Research on Hybrid Control Methods for Electromechanical Actuation Systems Under the Influence of Nonlinear Factors
Abstract
1. Introduction
- (1)
- Previous studies on EAS typically consider the control system and the mechanical transmission separately, focusing on one aspect at a time. In this work, we investigate the coupled interactions between drive control and mechanical nonlinearities. In addition, both friction and backlash are considered simultaneously, revealing their combined effect on system performance. This integrated approach provides a more comprehensive understanding of EAS dynamics and offers guidance for improving tracking accuracy under realistic mechanical conditions.
- (2)
- A hybrid control strategy is proposed to suppress the effects of nonlinear factors in electromechanical actuation systems. Hybrid control models are designed separately for the velocity loop and the position loop. In the velocity loop, a combination of super-twisting sliding mode control and a GPIO is employed to mitigate disturbances caused by nonlinearities while reducing the chattering inherent in sliding mode control. In the position loop, an RBF neural network is integrated with sliding mode control, where the RBF neural network approximates the nonlinear terms in the sliding mode controller, ensuring the stable operation of the electromechanical actuation system.
- (3)
- Considering that a single simulation platform cannot accurately replicate the actual operating conditions of EAS, this study employs a co-simulation platform combining SIMULINK and ADAMS 2019. This approach allows both kinematic analysis of the EAS and the design of nonlinear system controllers in MATLAB/SIMULINK 2021b. By building the control surface transmission system model in ADAMS and incorporating appropriate constraints and contact forces, the effects of backlash and friction on transmission accuracy can be effectively simulated. Meanwhile, the hybrid controller is implemented in SIMULINK to provide improved compensation for nonlinear factors in the EAS.
2. Materials and Methods
2.1. Mathematical Model of EAS
2.1.1. Mathematical Model of PMSM
- Stator voltage equation
- 2.
- Stator flux linkage equation
- 3.
- Electromagnetic torque equation
- 4.
- Mechanical motion equation
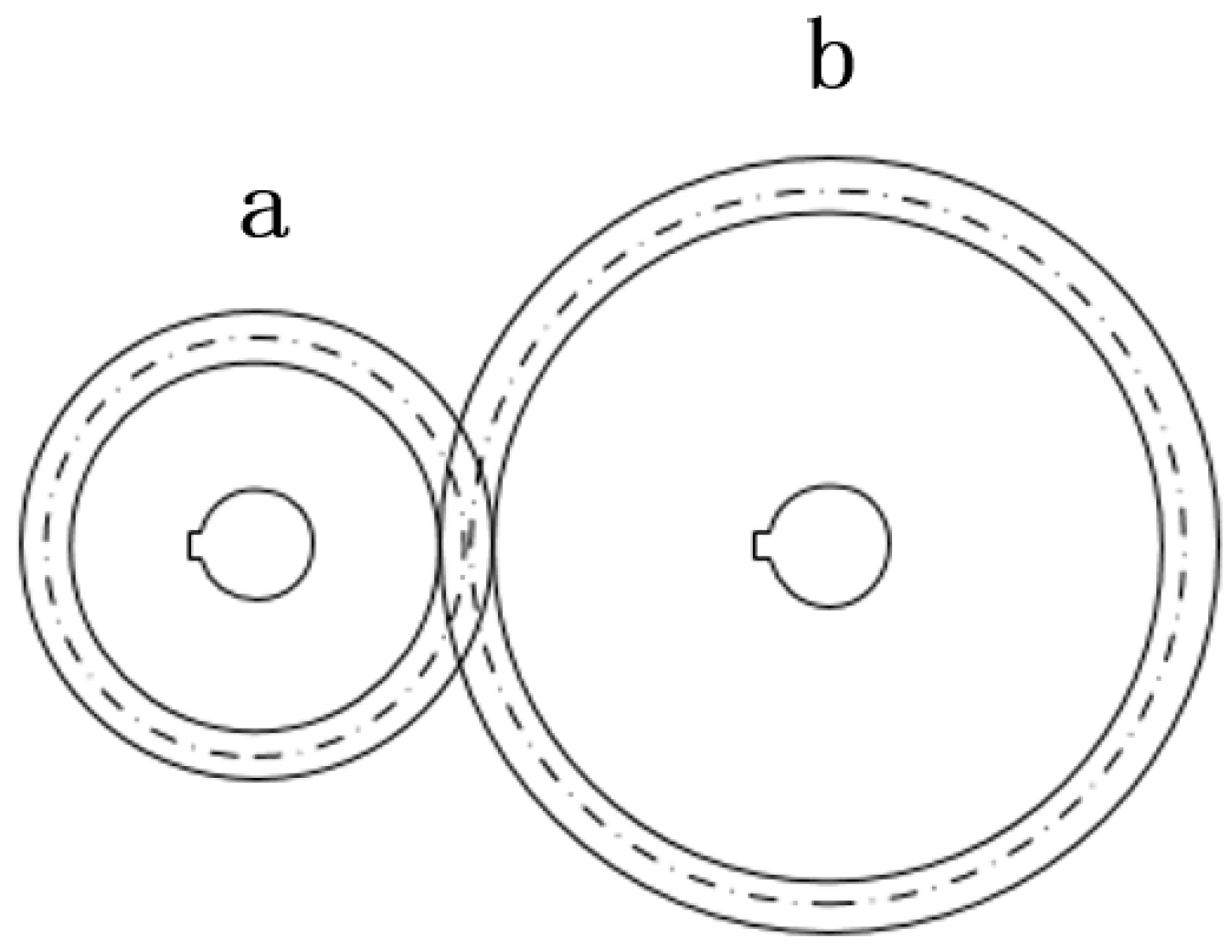
2.1.2. Mathematical Model of the Gearbox
2.1.3. Mathematical Model of the Planetary Roller Screw
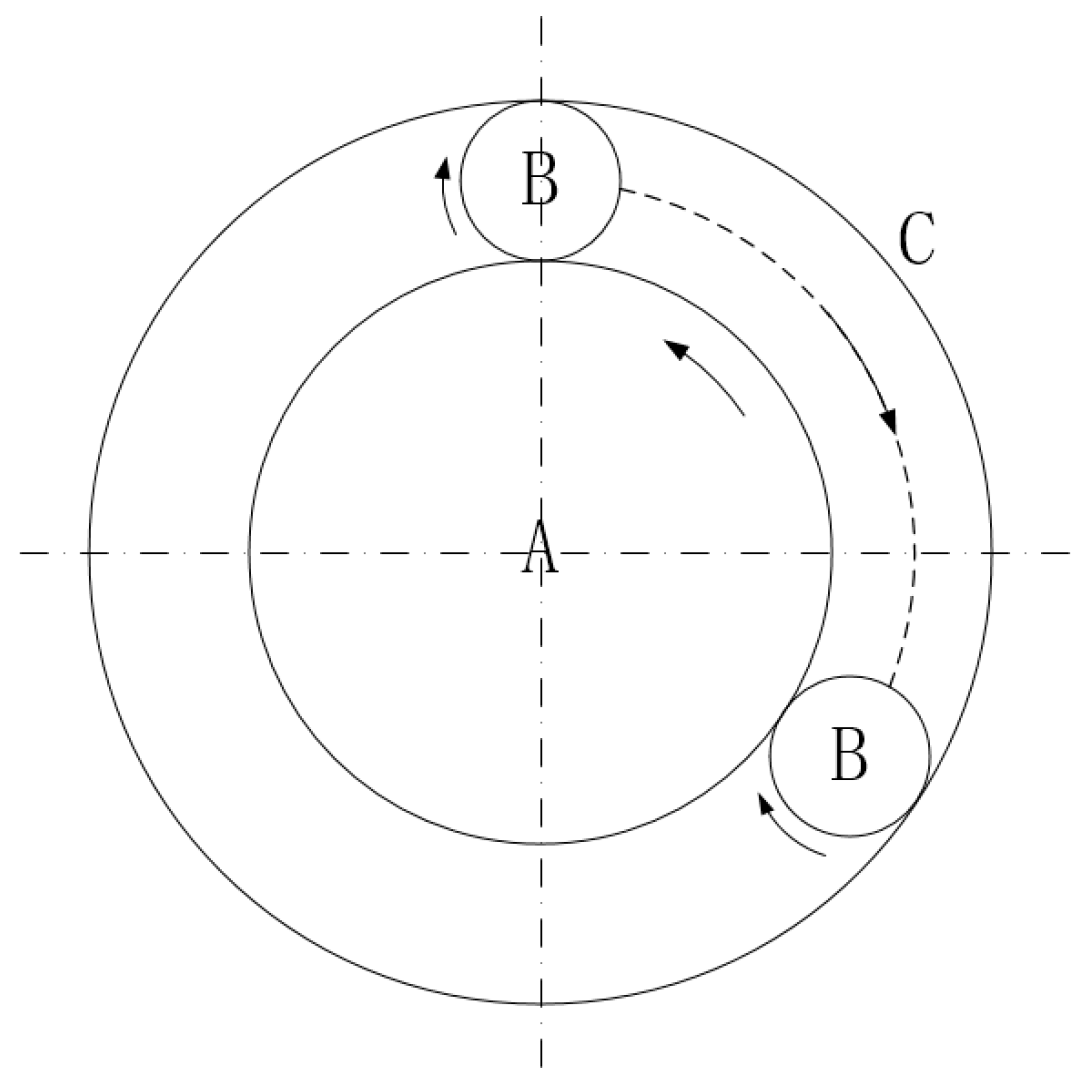
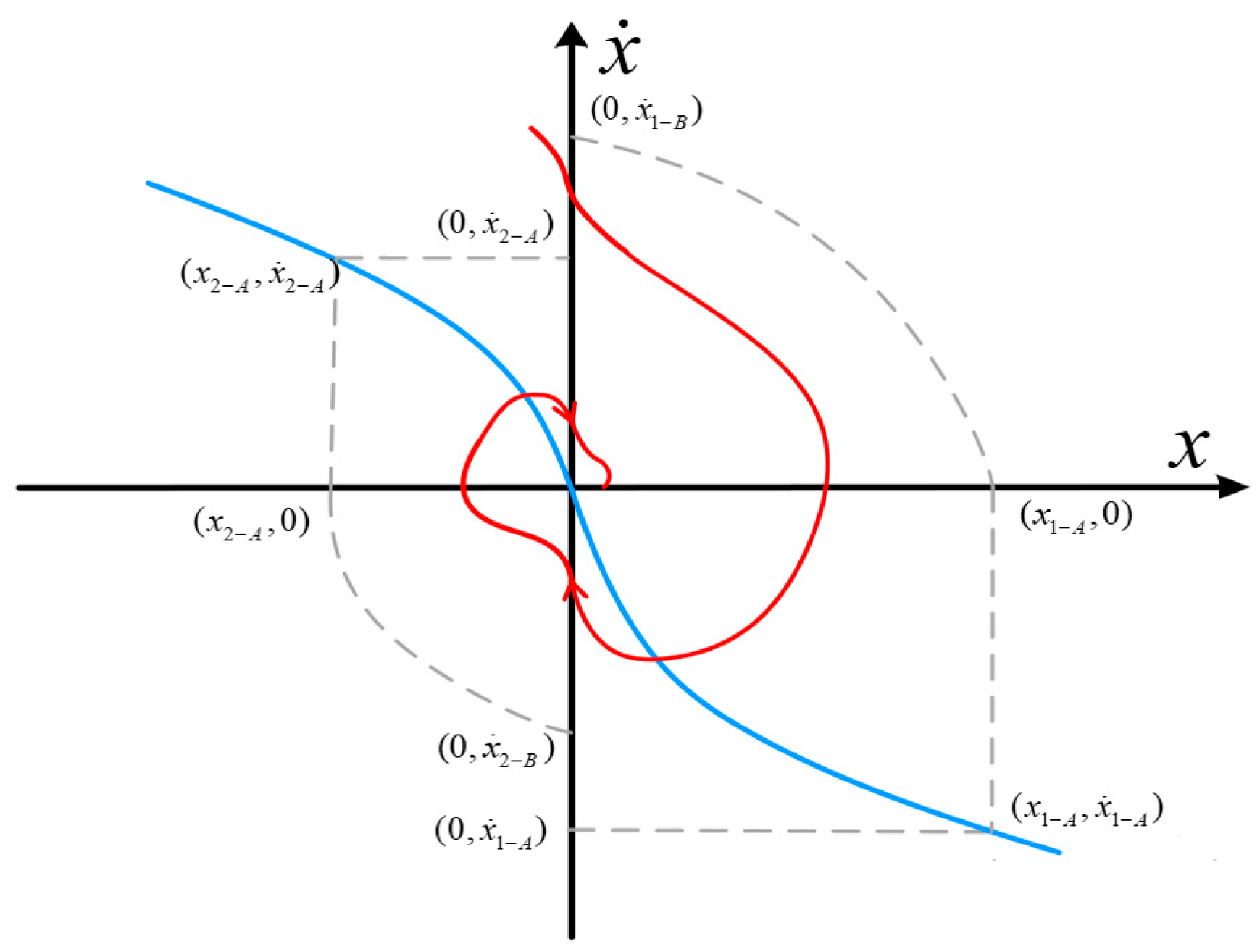
2.1.4. Mathematical Model of Nonlinear Factors
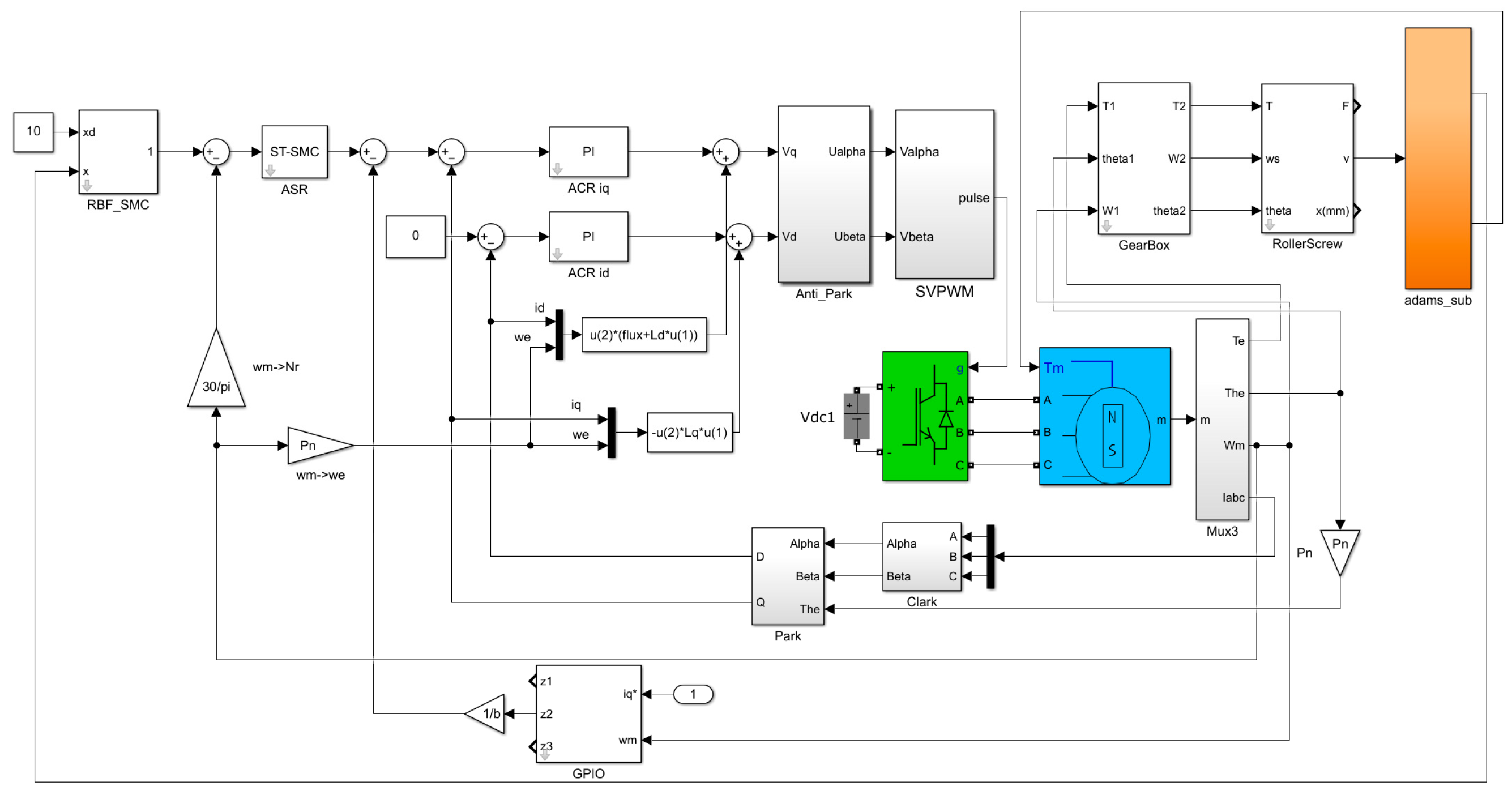
2.2. Hybrid Control Strategy Design for the EAS
2.2.1. Design of Super-Twisting Controller for the Speed Loop
2.2.2. Design of Generalized Proportional-Integral Observer for the Speed Loop
2.2.3. Design of Hybrid Controller for the Position Loop
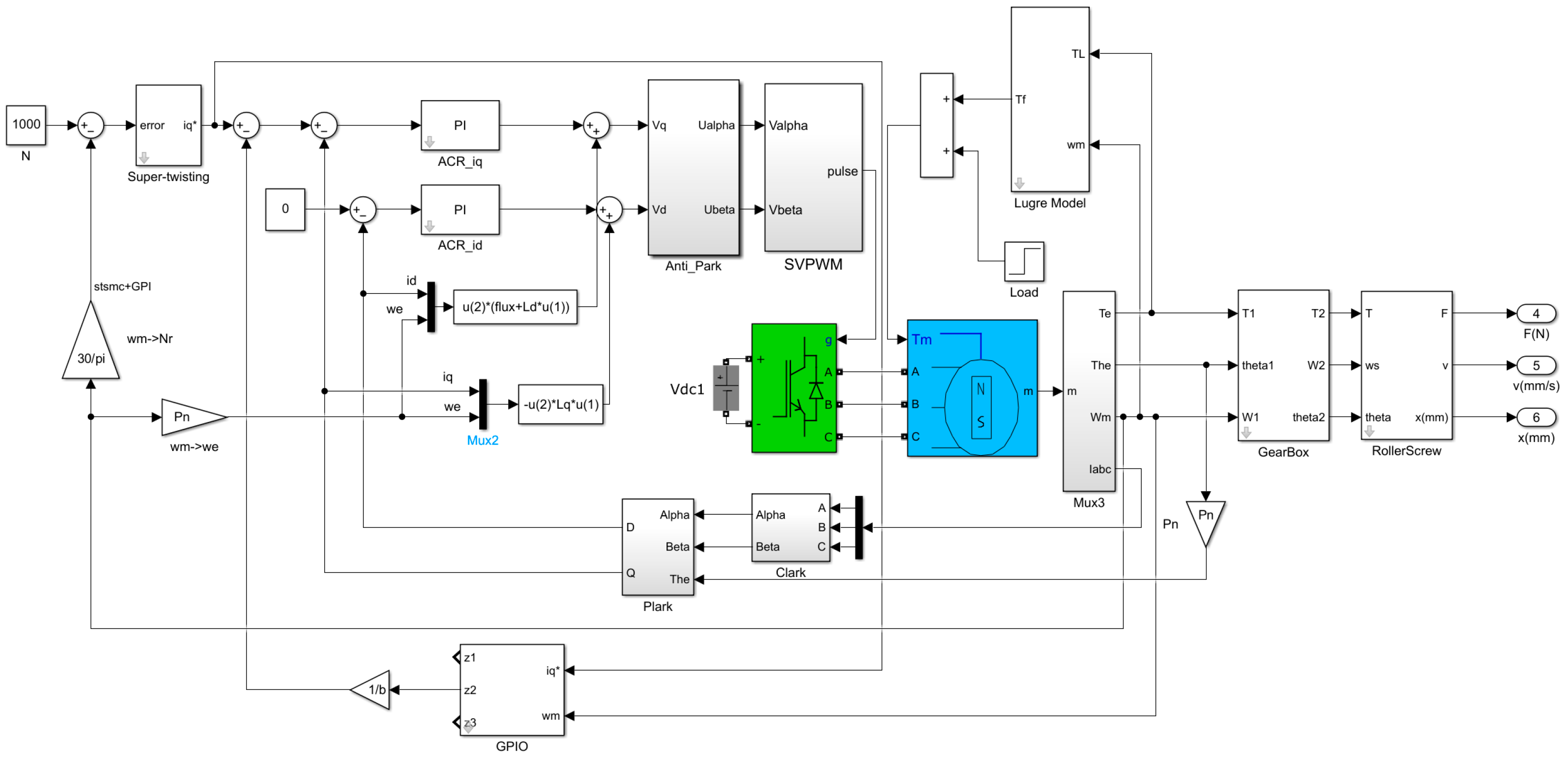
2.3. Co-Simulation Analysis of the Hybrid Control of the EAS
2.3.1. SIMULINK Simulation of the Speed Loop
2.3.2. SIMULINK Simulation of the Position Loop
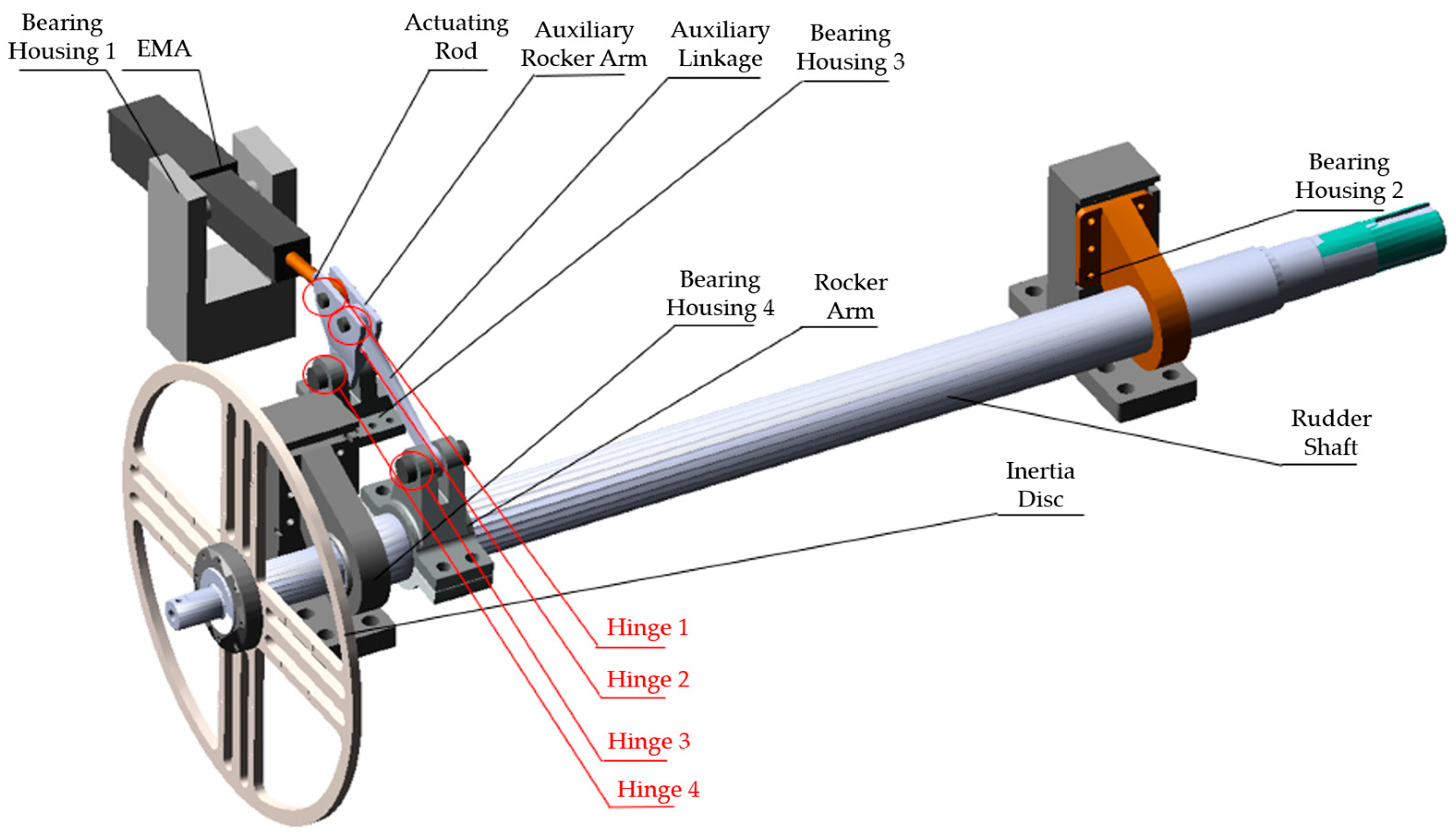
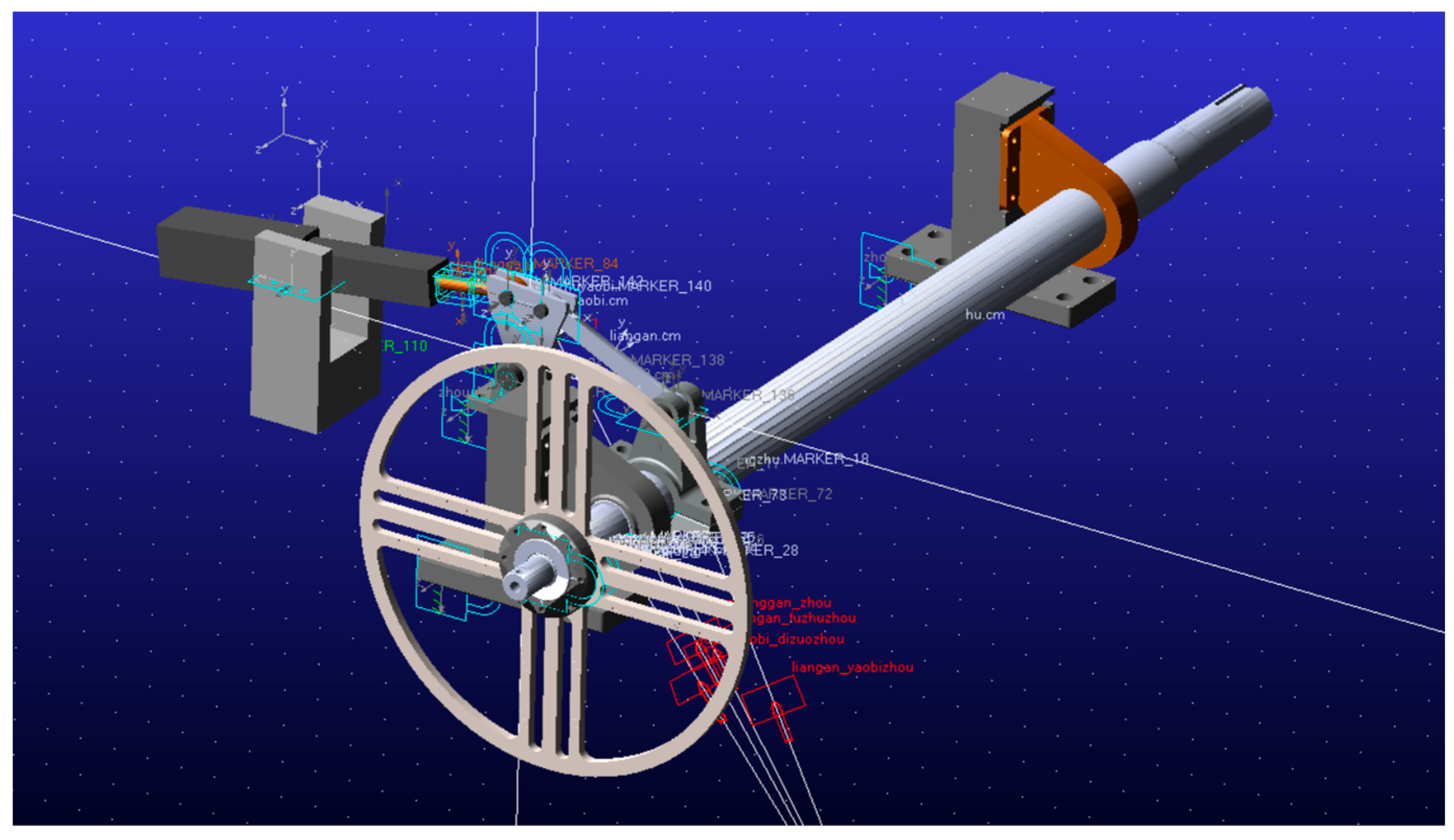
2.3.3. Construction of the ADAMS Dynamic Model
- Fixed joint
- 2.
- Revolute joint
- 3.
- Prismatic joint
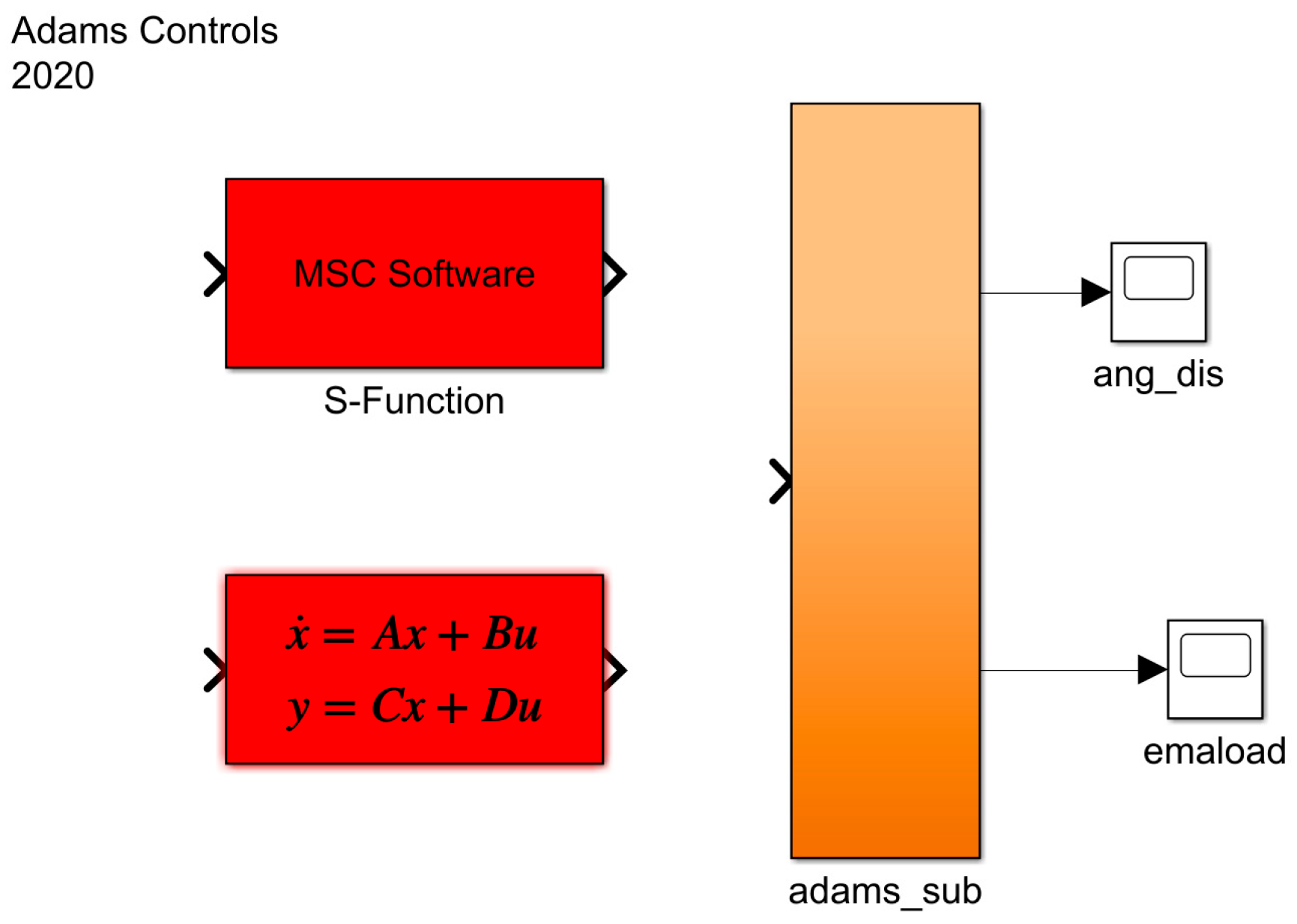
2.3.4. Co-Simulation Based on SIMULINK and ADAMS
3. Results
- Beijing AVIC torque sensor
- 2.
- Beijing AVIC tension–compression sensor
- 3.
- HEIDENHAIN incremental rotary encoder
- 4.
- FLTECH series magnetostrictive linear displacement sensor
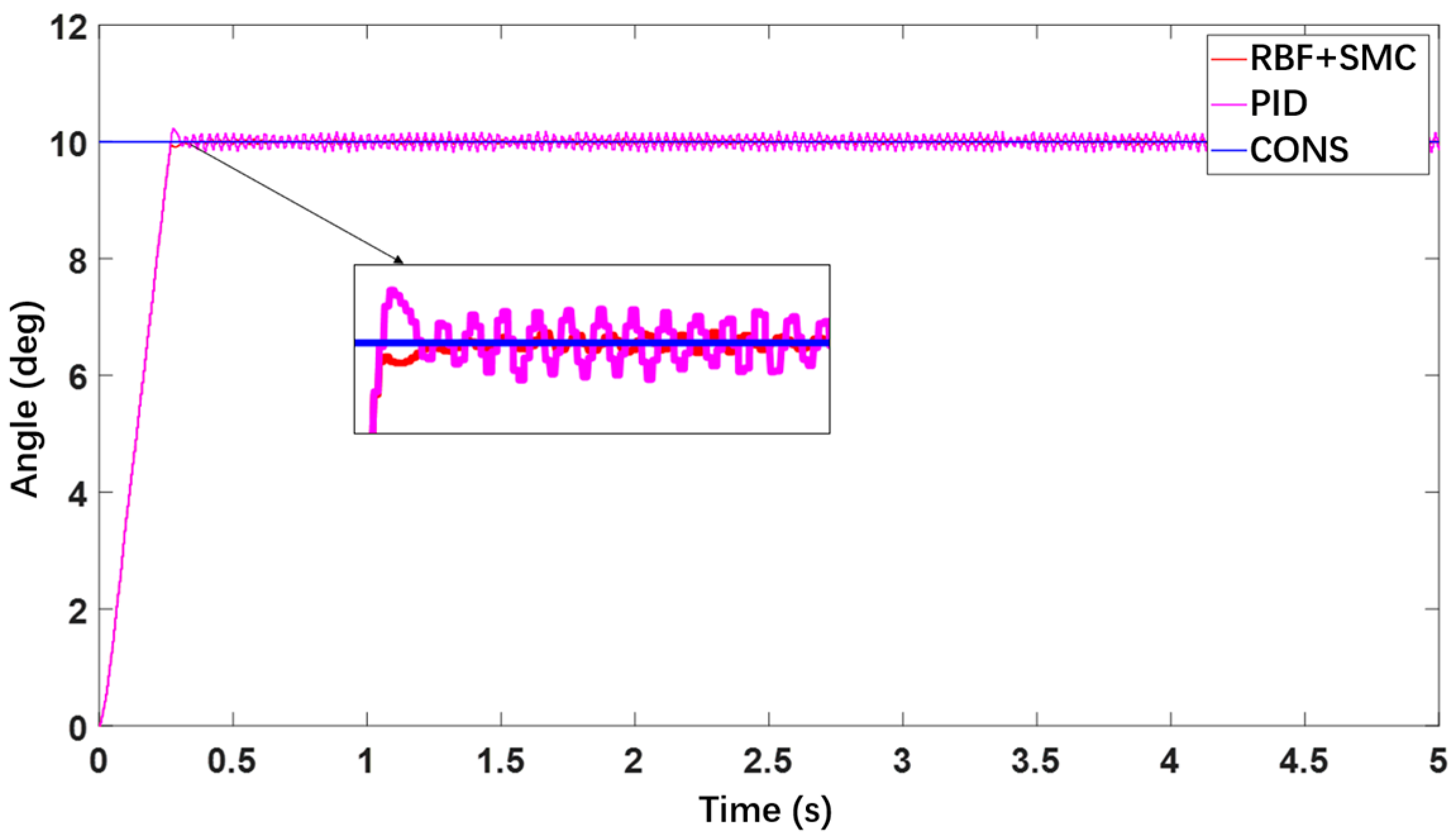
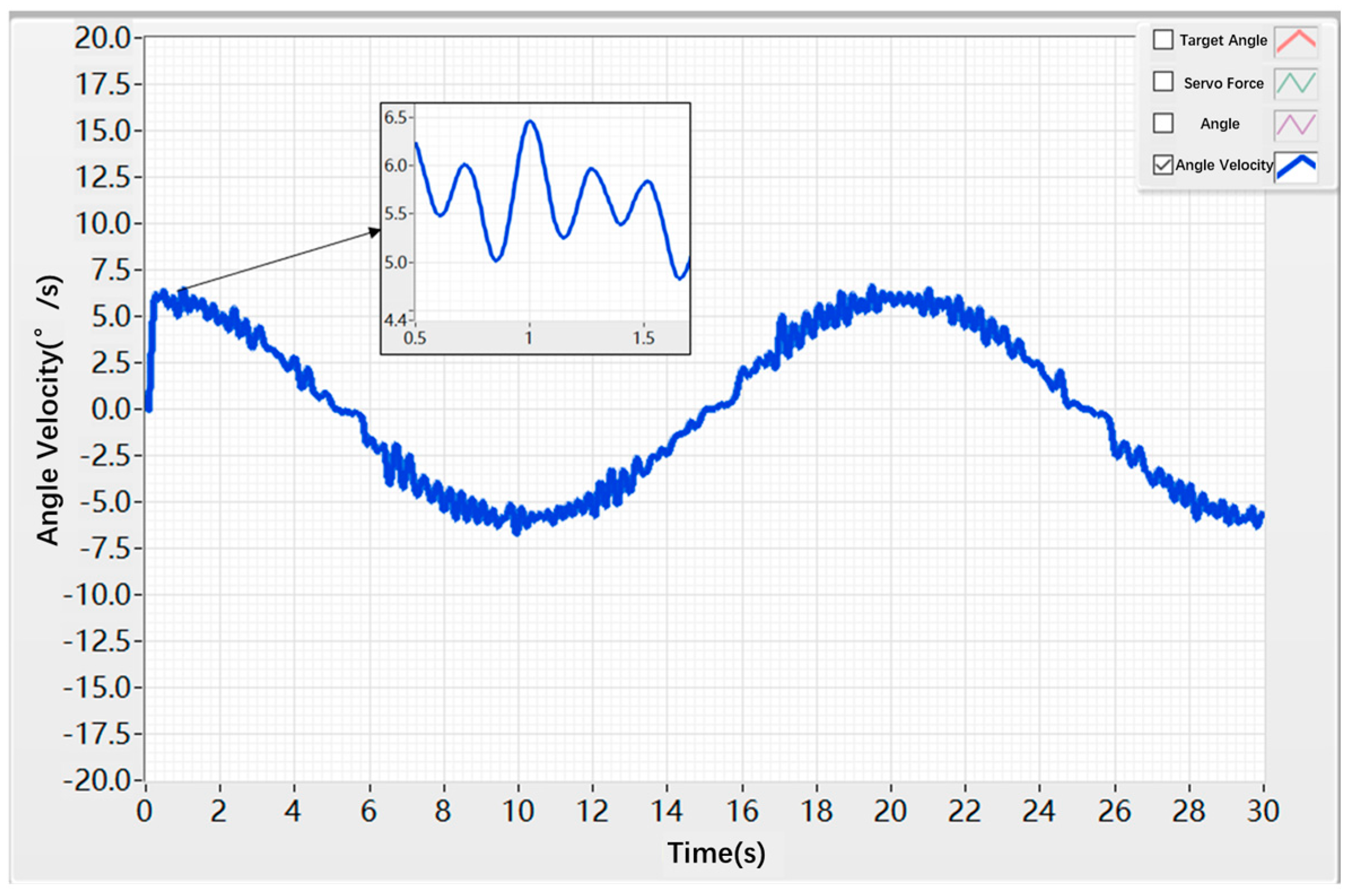
3.1. Step Response Test of the Hybrid Control Algorithm
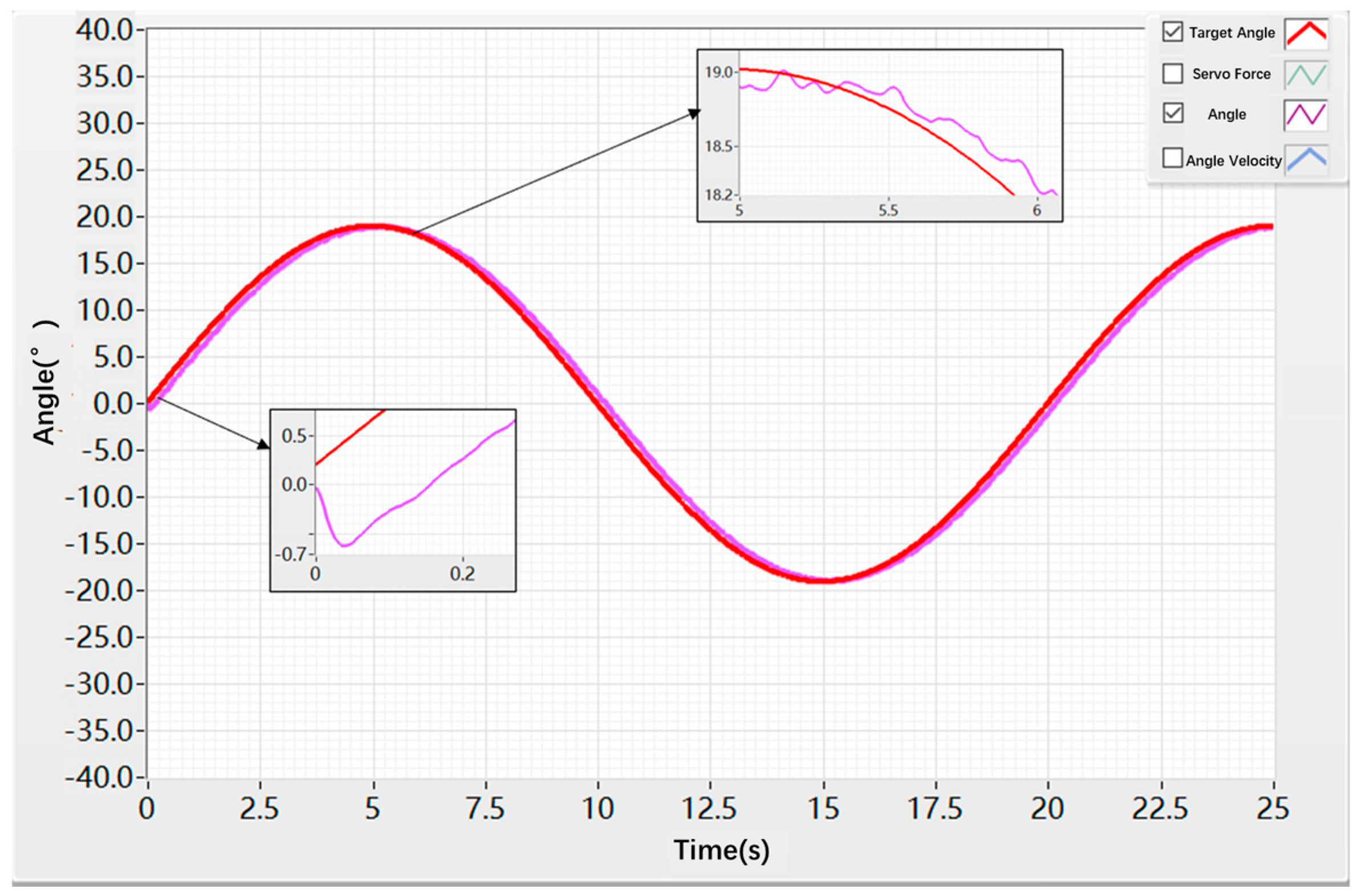
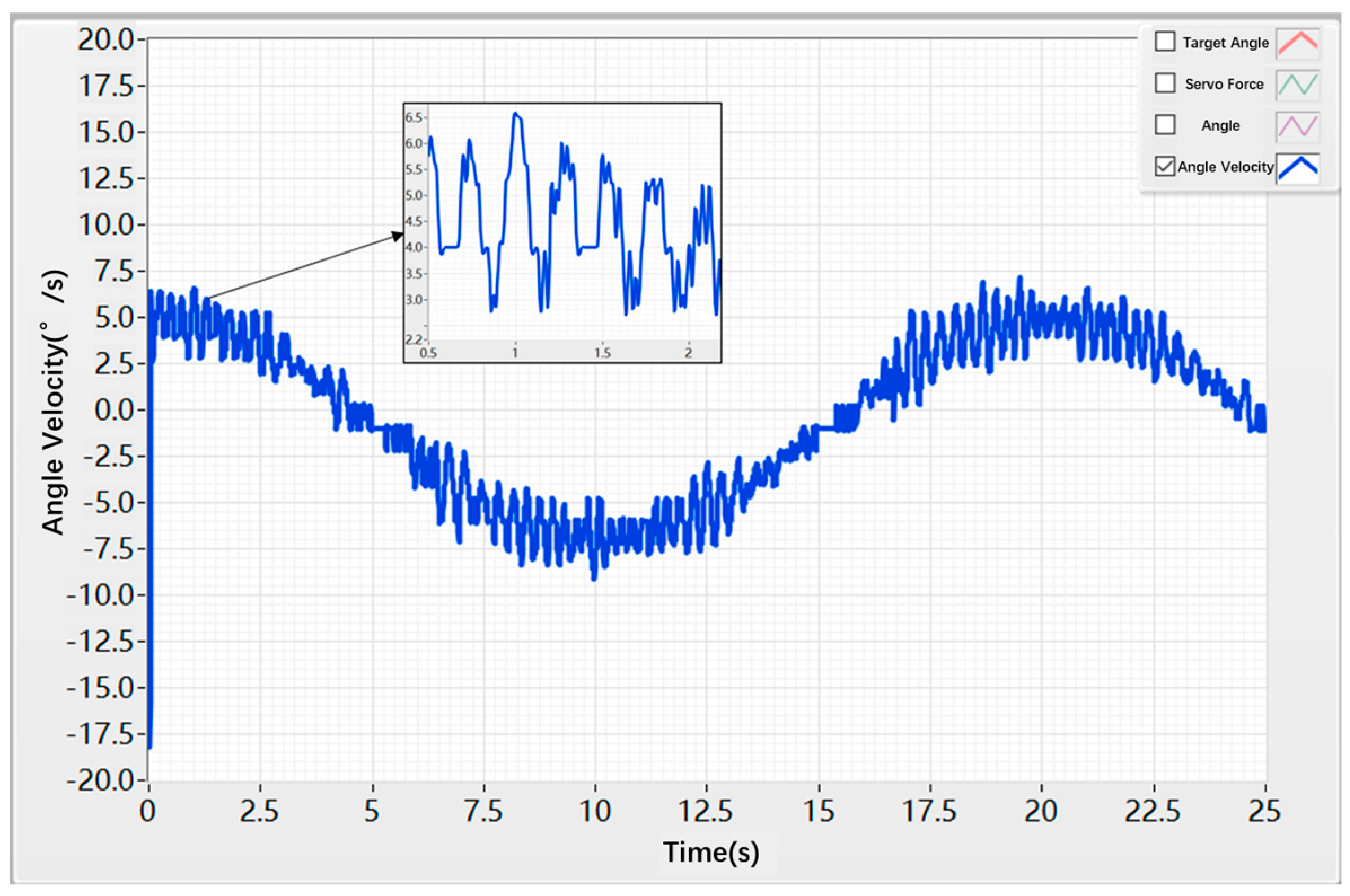
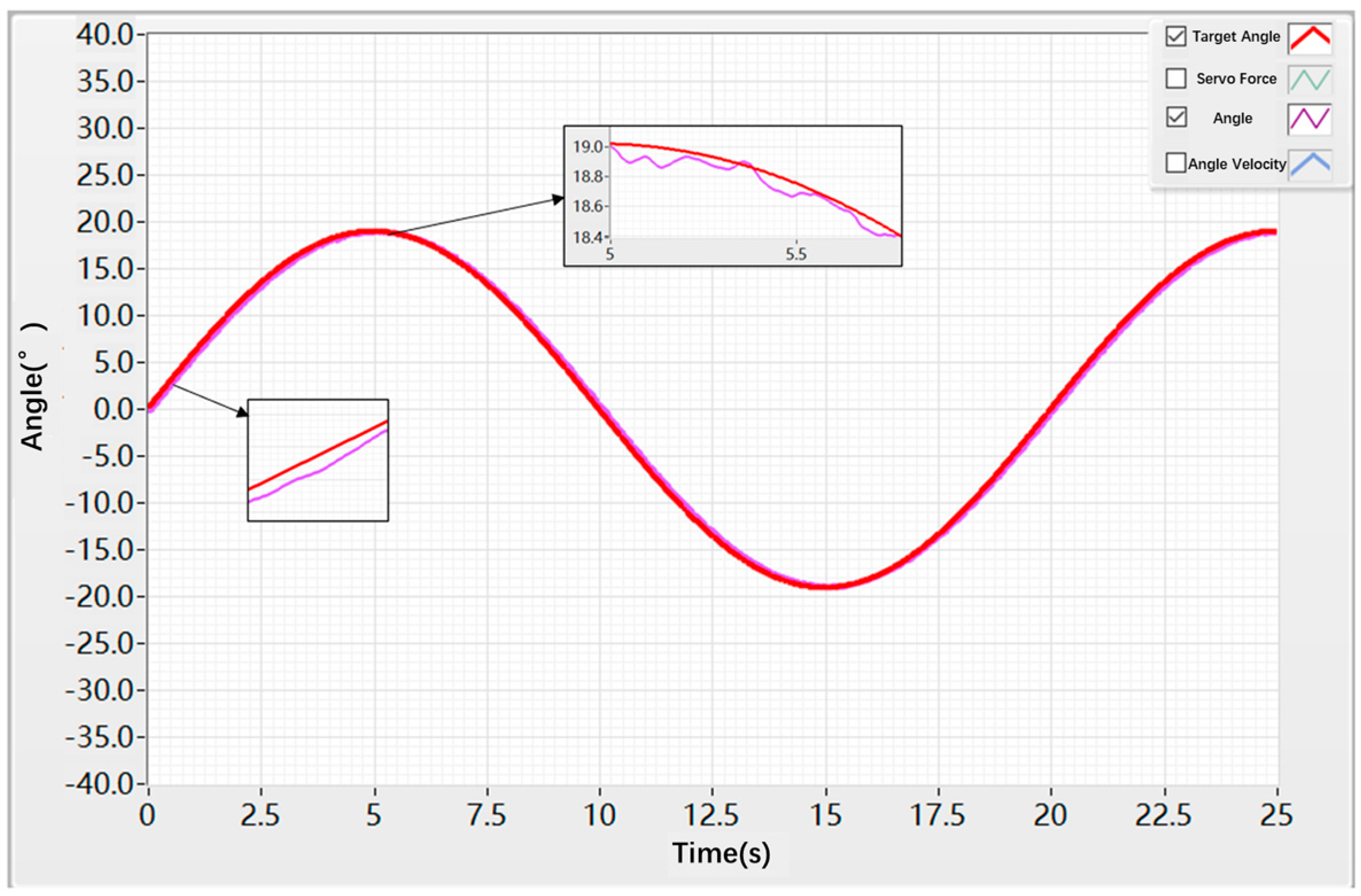
3.2. Sinusoidal Response Test of the Hybrid Control Algorithm
4. Discussion and Future Work
- In terms of mathematical modeling, the nonlinear factors of the mechanical system, such as backlash and friction, were simplified. As a result, the model lacks sufficient accuracy and requires further refinement.
- Regarding the hybrid control algorithm, the position loop employs an RBF neural network, which incurs a relatively high computational cost and thus requires further optimization.
- In the co-simulation, due to certain idealizations in the friction and backlash models, the nonlinear effects are smoothed. In contrast, in the actual control surface deflection experiments, the real system exhibits more pronounced friction, backlash, and mechanical flexibility effects, leading to discrepancies between the experimental and simulation peak speed results.
- Regarding system experiments, the nonlinear factors are primarily based on the intrinsic friction and backlash of the system, and the method of introducing these nonlinearities requires further refinement.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, W.; Yan, Y.; Qi, Y.; Huang, M.; Li, W. Recent development of aircraft electric propulsion system: A technical review. CES Trans. Electr. Mach. Syst. 2025, 9, 115–130. [Google Scholar] [CrossRef]
- Buticchi, G.; Wheeler, P.; Boroyevich, D. The more-electric aircraft and beyond. Proc. IEEE 2022, 111, 356–370. [Google Scholar] [CrossRef]
- Saha, A.; Ghassemi, M. A review of electrical insulation challenges for electrical powertrain components in the future more and all electric aircraft under low-pressure conditions. IEEE J. Emerg. Sel. Top. Power Electron. 2024, 13, 4521–4536. [Google Scholar] [CrossRef]
- Yuan, S.; Deng, W.; Yi, W.; Yao, J.; Yang, G.; Guan, J. Adaptive Robust Stable Tracking Control of Two-Axis Coupled Electromechanical Actuation System Based on Friction Compensation. Actuators 2025, 14, 396. [Google Scholar] [CrossRef]
- Qiao, G.; Zhang, X.; Liao, R.; Tang, S.; Ma, S. Fatigue analysis and lifespan prediction of the recirculating planetary roller screw mechanism. J. Mech. Sci. Technol. 2025, 39, 1951–1962. [Google Scholar] [CrossRef]
- Cao, J.; Li, Y.; Zhang, X.; Yang, J.; Fan, W. Torque-type backlash inverse control for an electromechanical actuator with active disturbance rejection. IEEE Access 2023, 11, 108688–108696. [Google Scholar] [CrossRef]
- Ruan, W.; Dong, Q.; Zhang, X.; Li, Z. Friction compensation control of electromechanical actuator based on neural network adaptive sliding mode. Sensors 2021, 21, 1508. [Google Scholar] [CrossRef] [PubMed]
- Quattrocchi, G.; Iacono, A.; Berri, P.C.; Vedova, M.D.L.D.; Maggiore, P. A new method for friction estimation in ema transmissions. Actuators 2021, 10, 194. [Google Scholar] [CrossRef]
- Fang, Q.; Zhou, Y.; Ma, S.; Zhang, C.; Wang, Y.; Huangfu, H. Electromechanical actuator servo control technology based on active disturbance rejection control. Electronics 2023, 12, 1934. [Google Scholar] [CrossRef]
- Khanh, N.D.; Kuznetsov, V.E.; Lukichev, A.N.; Chung, P.T. Adaptive control of electromechanical actuator taking into account nonlinear factors based on exo-model. In Proceedings of the 2022 Conference of Russian Young Researchers in Electrical and Electronic Engineering (ElConRus), Saint Petersburg, Russia, 25–28 January 2022. [Google Scholar]
- Gan, L.; Wang, L.; Huang, F. Adaptive backlash compensation for CNC machining applications. Machines 2023, 11, 193. [Google Scholar] [CrossRef]
- Xie, L.; Liu, L.; Zheng, X.; Wang, S. Sliding mode control of aircraft braking system based on LuGre model. J. Huazhong Univ. Sci. Technol. (Nat. Sci. Ed.) 2013, 41, 65–69. [Google Scholar]
- Zhang, K.; Shen, R.; Hu, Z.; Tang, J.; Sun, Z.; Ning, A.; Yang, S. Dynamic modeling and analysis considering friction-wear coupling of gear system. Int. J. Mech. Sci. 2024, 275, 109343. [Google Scholar] [CrossRef]
- Zhang, Q.; Yu, Z.; Liu, H.; Mo, J.; Xiang, Z.; Zhu, S.; Jin, W. Analysis of friction-induced vibration and wear characteristics during high-speed train friction braking process. Tribol. Int. 2024, 196, 109701. [Google Scholar] [CrossRef]
- Zhang, P.; Shi, Z.; Yu, B. Research on friction compensation method of electromechanical actuator based on improved active disturbance rejection control. Actuators 2023, 12, 445. [Google Scholar] [CrossRef]
- Maré, J.-C. Practical considerations in the modelling and simulation of electromechanical actuators. Actuators 2020, 9, 94. [Google Scholar] [CrossRef]
- Wan, Q.; Song, C.; Zhou, Y.; Tong, R.; Ma, S.; Liu, G. Modeling and analysis of the flap actuation system considering the nonlinear factors of EMA, joint clearance and flexibility. Aerospace 2024, 11, 440. [Google Scholar] [CrossRef]
- Fu, B.; Qi, H.; Xu, J.; Yang, Y. Composite sliding mode control of high precision electromechanical actuator considering friction nonlinearity. Actuators 2022, 11, 265. [Google Scholar] [CrossRef]
- Lee, H.-S.; Ko, Y.; Back, J.; Hong, K.-S.; Kim, C.-S. A double-loop robust position and speed control of an electromagnetic actuator against nonlinear model uncertainties. Control Eng. Pract. 2025, 160, 106318. [Google Scholar] [CrossRef]
- Scherer, S.P.; Speckmaier, M.; Gierszewski, D.; Steinert, A.; Holzapfel, F. Compensation of nonlinear transmission effects in electro-mechanical flight control systems. In Proceedings of the AIAA SciTech 2022 Forum, San Diego, CA, USA, 3–7 January 2022. [Google Scholar]
- Zuo, Q.; Wang, B.; Chen, J.; Dong, H. Model Predictive Control of Aero-Mechanical Actuators with Consideration of Gear Backlash and Friction Compensation. Electronics 2024, 13, 4021. [Google Scholar] [CrossRef]
- Maré, J.-C. Requirement-based system-level simulation of mechanical transmissions with special consideration of friction, backlash and preload. Simul. Model. Pract. Theory 2016, 63, 58–82. [Google Scholar] [CrossRef]
- Zhang, P.; Shi, Z.; Yu, B.; Qi, H. Research on the EMA Control Method Based on Transmission Error Compensation. Energies 2024, 17, 2528. [Google Scholar] [CrossRef]
- Hou, Q.; Ding, S. GPIO based super-twisting sliding mode control for PMSM. IEEE Trans. Circuits Syst. II Express Briefs 2020, 68, 747–751. [Google Scholar] [CrossRef]
- Xu, W.; Junejo, A.K.; Liu, Y.; Islam, R. Improved continuous fast terminal sliding mode control with extended state observer for speed regulation of PMSM drive system. IEEE Trans. Veh. Technol. 2019, 68, 10465–10476. [Google Scholar] [CrossRef]
- Yan, J.; Wang, H.; Huang, S.; Lan, Y. Disturbance Observer-Based Backstepping Control of PMSM for the Mine Traction Electric Locomotive. Math. Probl. Eng. 2018, 2018, 7253210. [Google Scholar] [CrossRef]
- Ding, S.; Park, J.H.; Chen, C.-C. Second-order sliding mode controller design with output constraint. Automatica 2020, 112, 108704. [Google Scholar] [CrossRef]
- Tian, M.; Wang, B.; Yu, Y.; Dong, Q.; Xu, D. Adaptive active disturbance rejection control for uncertain current ripples suppression of PMSM drives. IEEE Trans. Ind. Electron. 2023, 71, 2320–2331. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, X.; Wang, W.; Chen, K.; Cheung, N.C.; Pan, J. Enhanced sliding mode control for PMSM speed drive systems using a novel adaptive sliding mode reaching law based on exponential function. IEEE Trans. Ind. Electron. 2024, 71, 11978–11988. [Google Scholar] [CrossRef]
- Liu, X.; Deng, Y.; Liu, J.; Cao, H.; Xu, C.; Liu, Y. Fixed-time integral terminal sliding mode control with an adaptive RBF neural network for PMSM speed regulation. Control Eng. Pract. 2025, 156, 106236. [Google Scholar] [CrossRef]
- Guo, Z.; Li, J.; Yan, M.; Wang, G. Composite speed control based on an improved gain-adaptive super-twisting sliding mode observer for a permanent magnet synchronous motor. Control Eng. Pract. 2025, 157, 106241. [Google Scholar] [CrossRef]
- Ma, J.; Yao, Z.; Yao, J. Fixed-time sliding mode control of electro-hydrostatic actuators with adaptive neural network compensation. Control Eng. Pract. 2025, 165, 106616. [Google Scholar] [CrossRef]
- Zhao, K.; Jia, N.; She, J.; Dai, W.; Zhou, R.; Liu, W.; Li, X. Robust model-free super-twisting sliding-mode control method based on extended sliding-mode disturbance observer for PMSM drive system. Control Eng. Pract. 2023, 139, 105657. [Google Scholar] [CrossRef]
- Ghani, M.F.; Faudzi, A.A.M.; Ghazali, R.; Mohamaddan, S. Application of Fuzzy Logic Sliding Mode Control Approach with PID Structure for Electro-Hydraulic Actuator Tracking System. IEEE Access 2025, 13, 97818–97834. [Google Scholar] [CrossRef]
- Song, Z.; Zhou, W. PMSM disturbance resistant adaptive fast super-twisting algorithm speed control method. IEEE Access 2024, 12, 138155–138165. [Google Scholar] [CrossRef]
- Guan, M.; Qu, C.; Lv, J.; Yang, L.; Li, X. A novel RBF neural network–based sliding mode controller for a master–slave motor coordinated drive system. Int. J. Adv. Manuf. Technol. 2024, 133, 4907–4921. [Google Scholar] [CrossRef]
- Zhao, W.; Gu, L. RBF-Based Fractional-Order SMC Fault-Tolerant Controller for a Nonlinear Active Suspension. Machines 2024, 12, 270. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, Y. Adaptive RBF neural network based on sliding mode controller for active power filter. Int. J. Power Electron. 2020, 11, 460–481. [Google Scholar] [CrossRef]
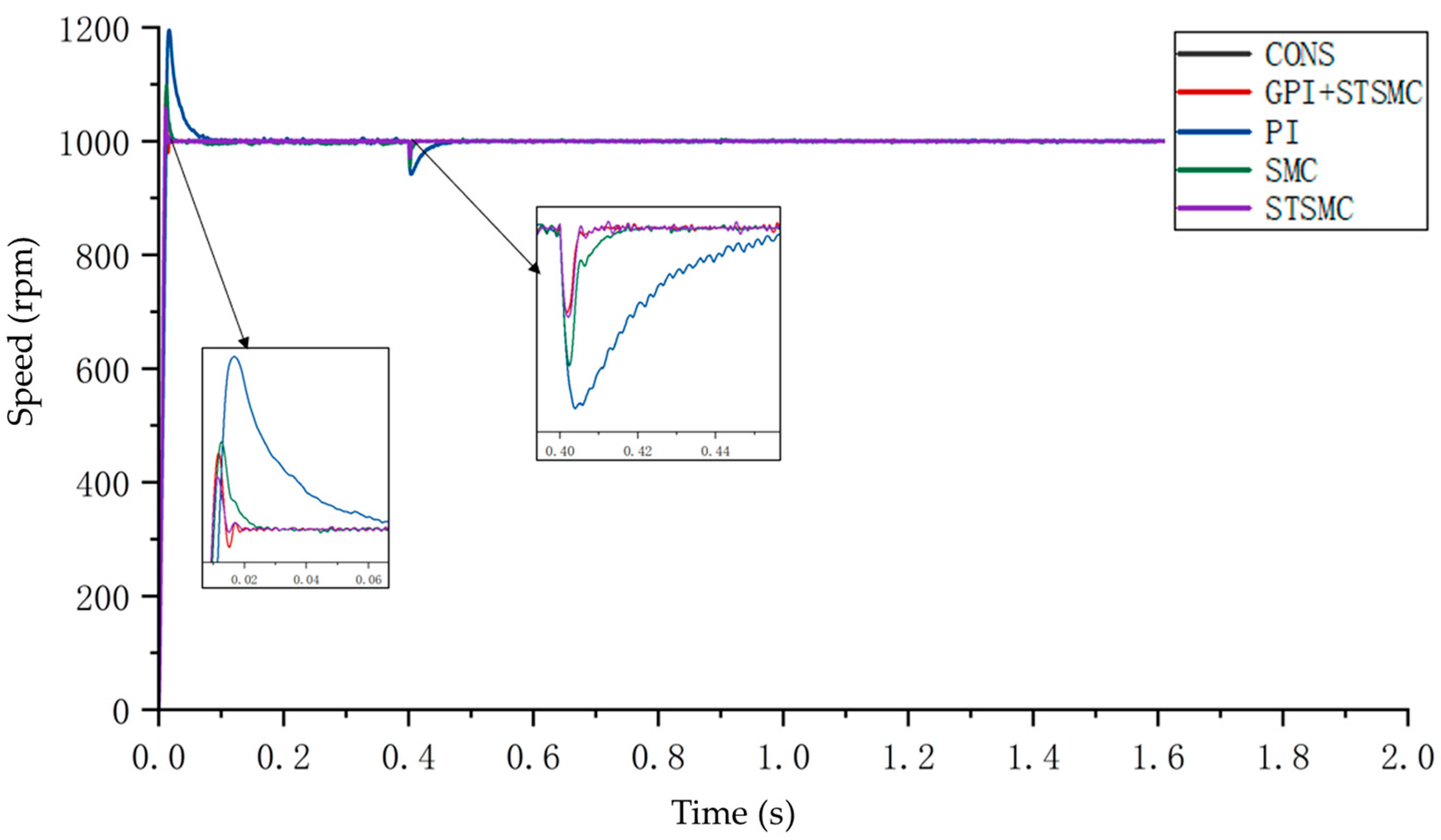
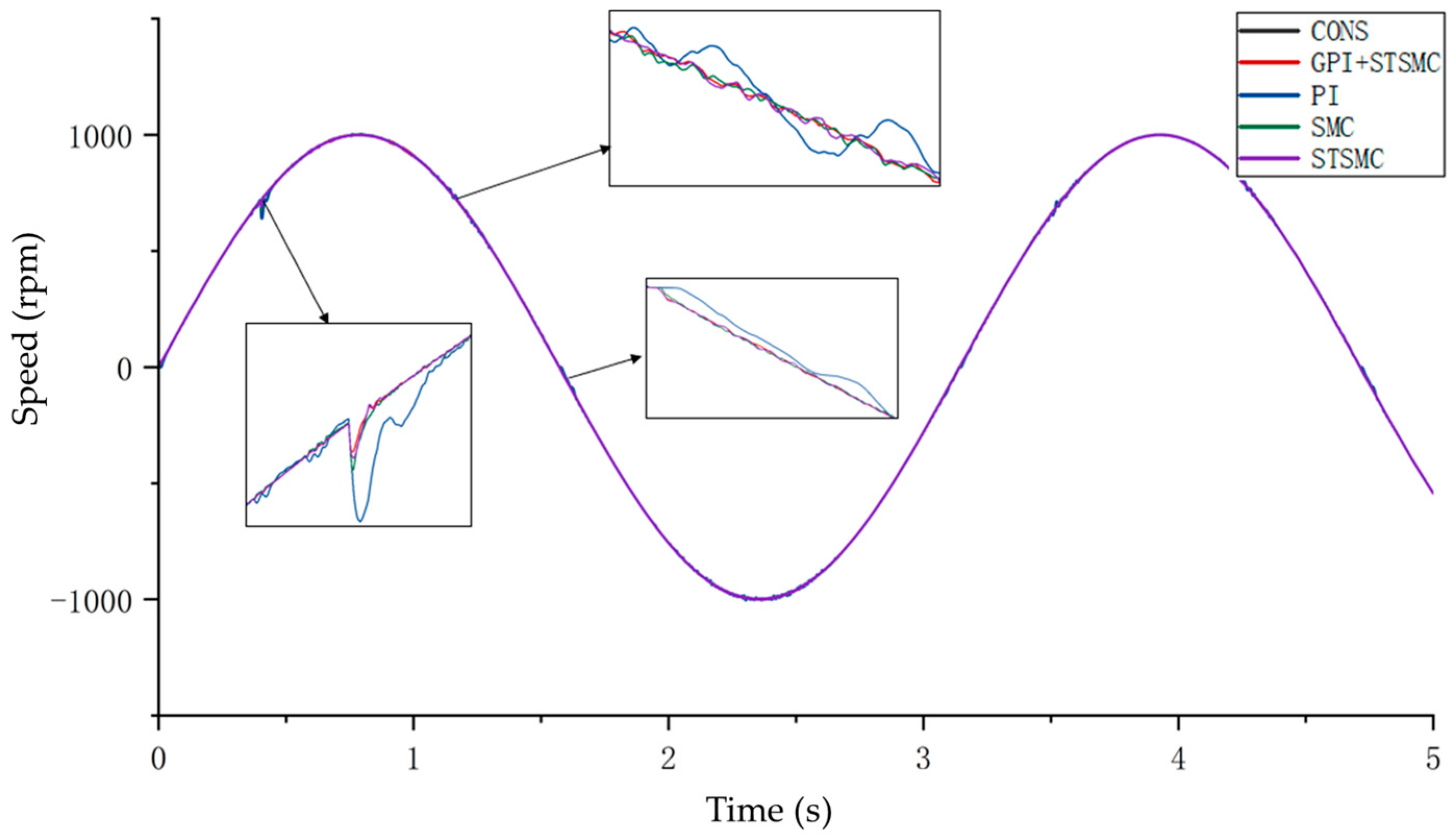

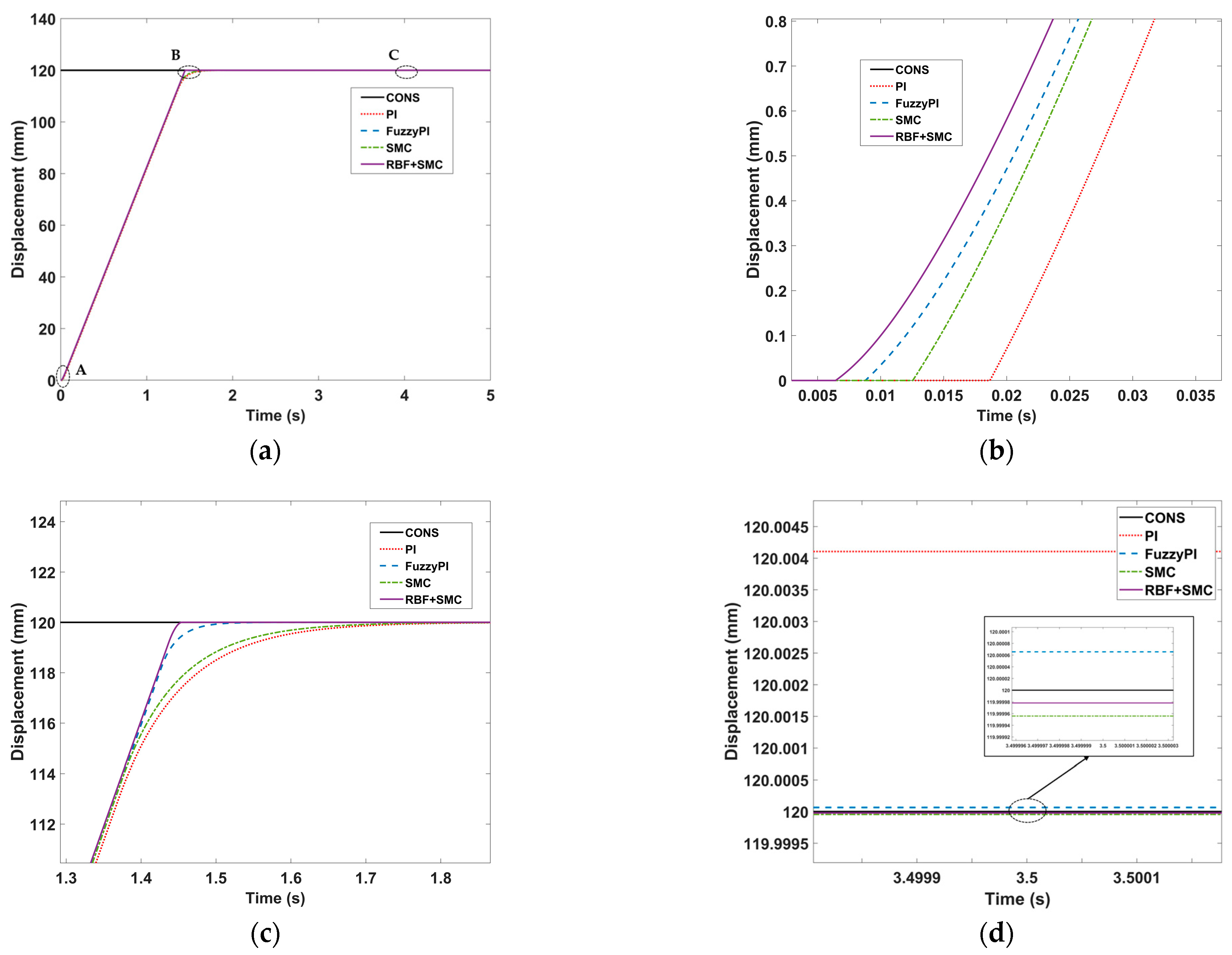


| Parameter | Value | Unit |
|---|---|---|
| K | 1 × 105 | N/mm |
| e | 2.2 | / |
| C | 10.0 | N·s/mm |
| δ | 0.1 | mm |
| μs | 0.3 | / |
| μd | 0.1 | / |
| Vs | 100.0 | mm/s |
| Vd | 1000.0 | mm/s |
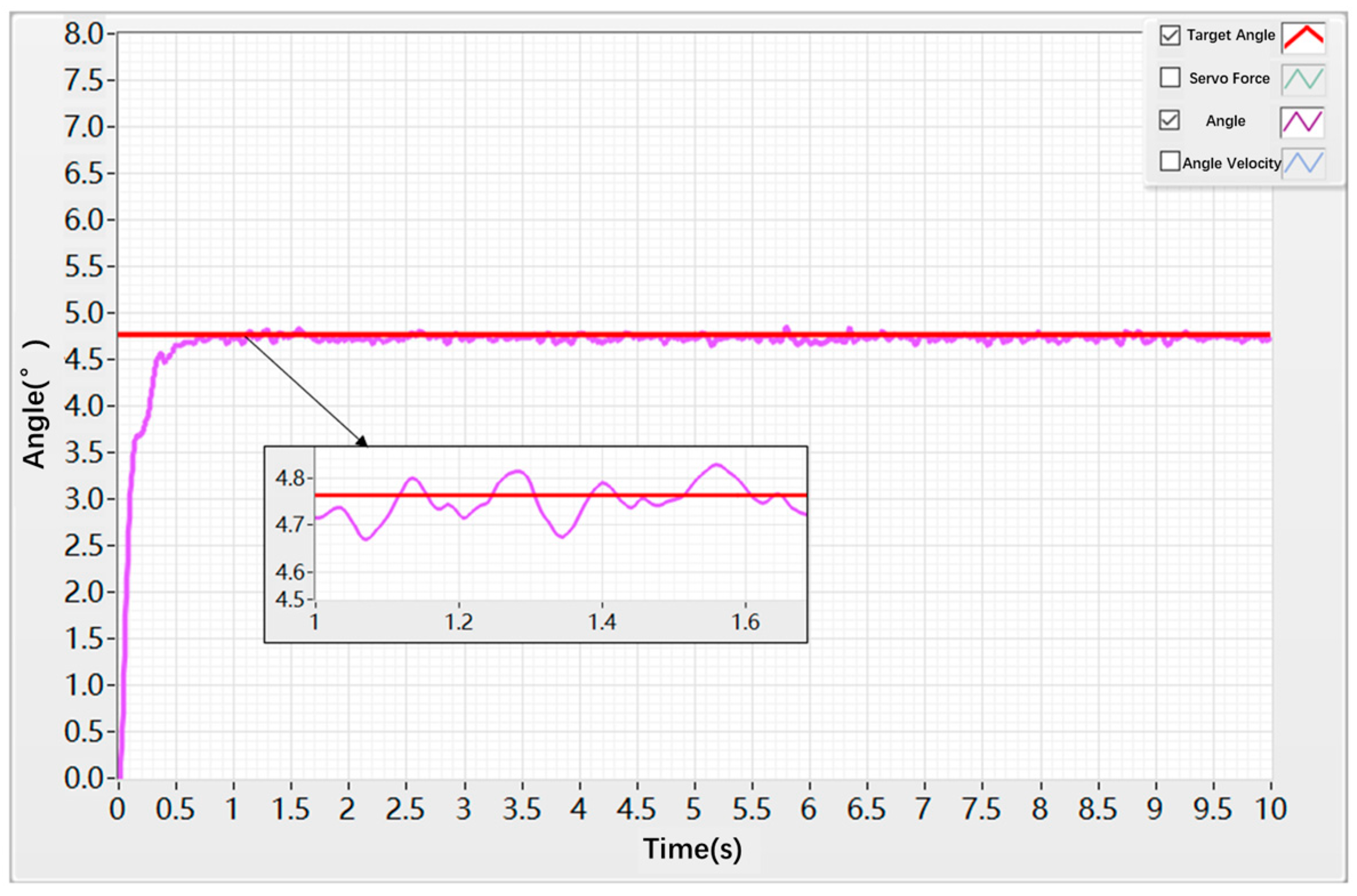
| Control Strategy | Step Command Amplitude (deg) | Settling Time (s) | Angle Chattering Amplitude (deg) | Angle Chattering Frequency |
|---|---|---|---|---|
| PID control | 4.72 | 0.9 | ±0.2 | High |
| Hybrid control | 4.72 | 0.5 | ±0.05 | Low |
| Control Strategy | Step Command Amplitude (deg) | Rise Time (s) | Mean Steady-State Error (deg) | Standard Deviations of Steady-State Error (deg) | RMS of Steady-State Error (deg) |
|---|---|---|---|---|---|
| PID control | 4.72 | 0.6 | 0.047 | 0.031 | 0.056 |
| Hybrid control | 4.72 | 0.3 | 0.023 | 0.022 | 0.032 |
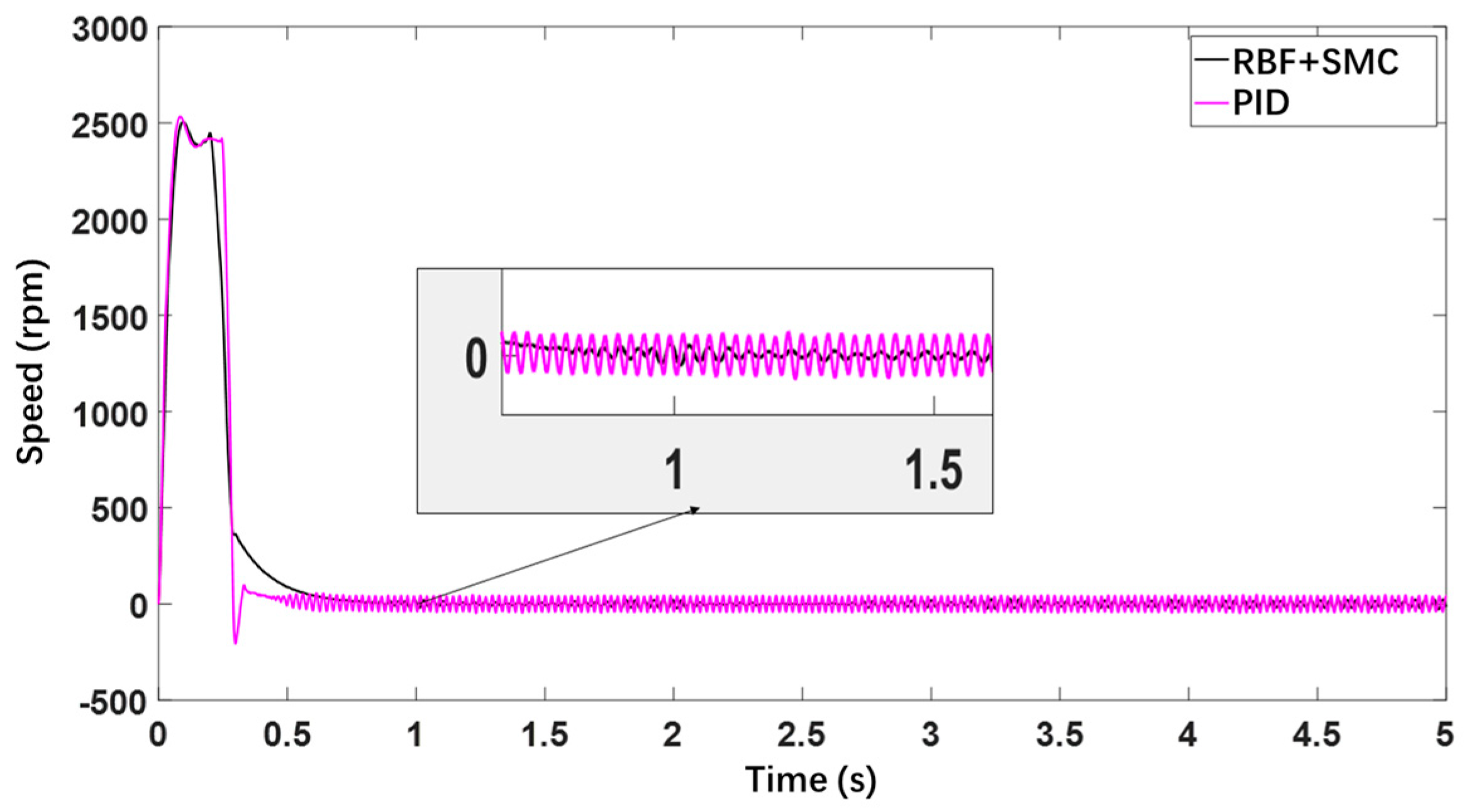
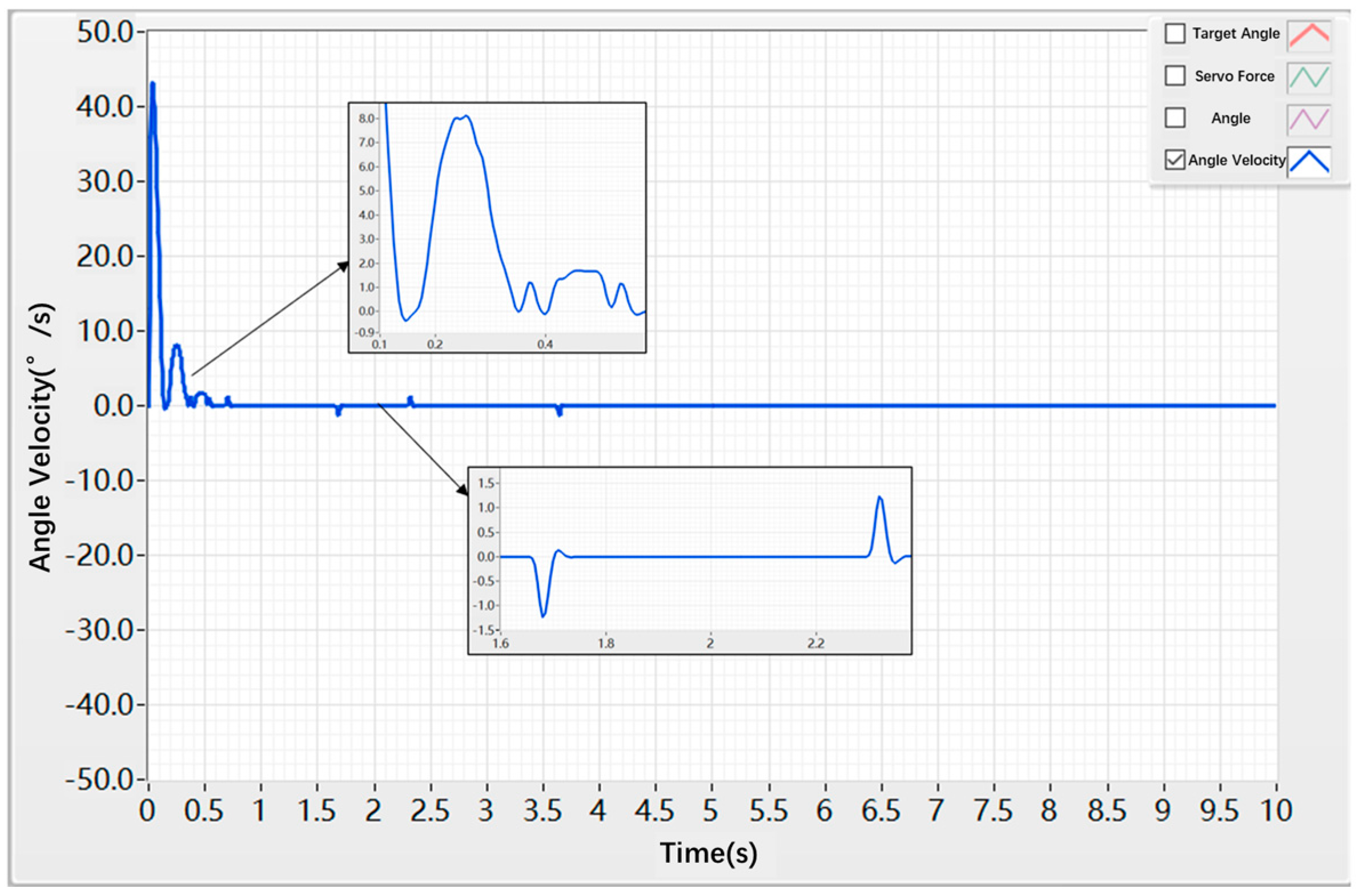
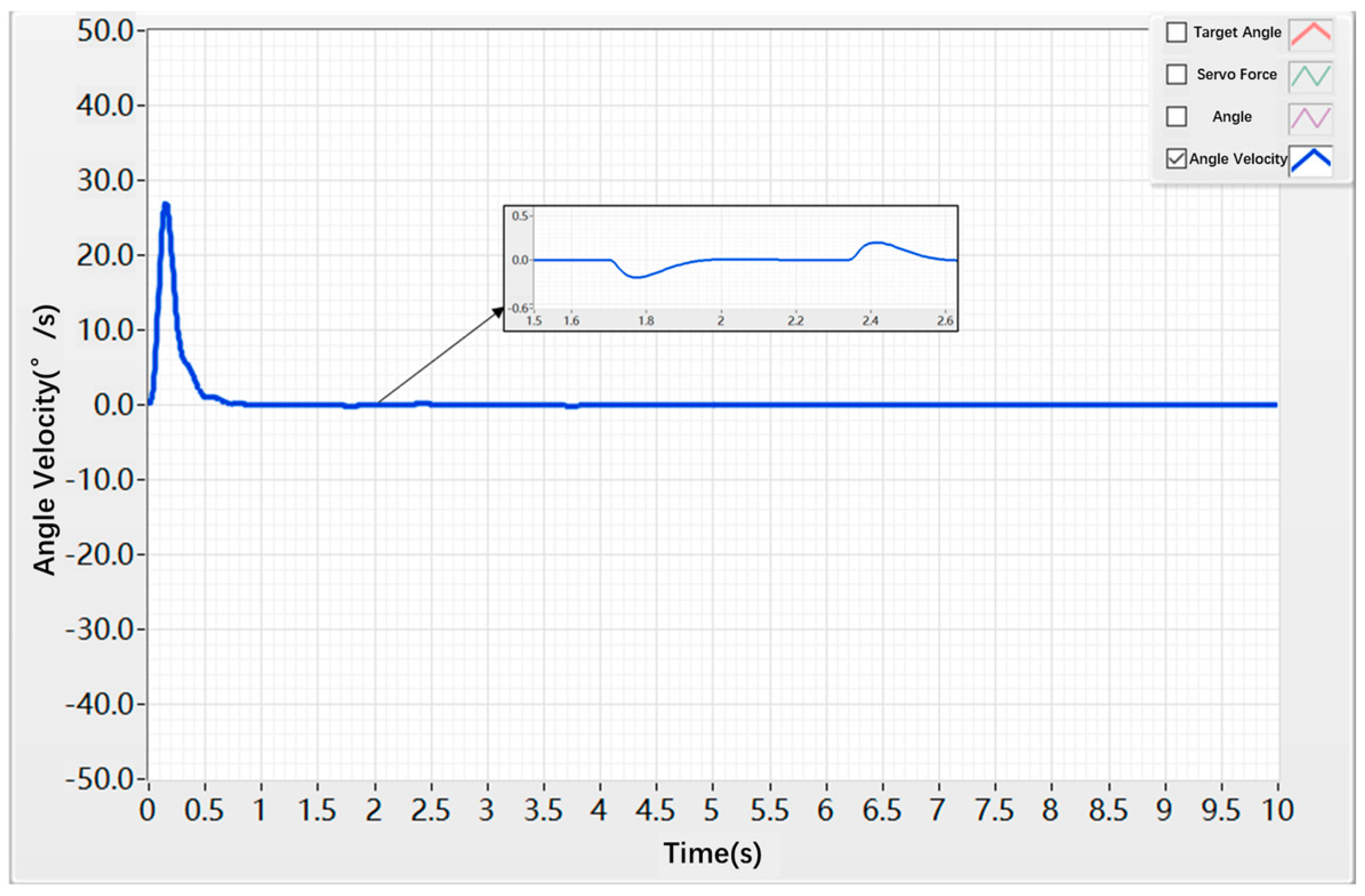
| Control Strategy | Peak Value (deg/s) | Vibration Behavior Between 0.3 s and 0.7 s | Amplitude of Fluctuation (deg/s) |
|---|---|---|---|
| PID control | 42 | Severe oscillation | ±1.3 |
| Hybrid control | 27 | No oscillation | ±0.2 |
| Control Strategy | Mean Steady-State Error (deg/s) | Standard Deviations of Steady-State Error (deg/s) | RMS of Steady-State Error (deg/s) |
|---|---|---|---|
| PID control | 1.412 | 0.135 | 1.418 |
| Hybrid control | 0.223 | 0.107 | 0.247 |
| Control Strategy | Sinusoidal Angle Amplitude (deg) | Sinusoidal Frequency (Hz) | Phase Lag Angle (deg) |
|---|---|---|---|
| PID control | 19 | 0.05 | ±1.3 |
| Hybrid control | 19 | 0.05 | ±0.3 |
| Control Strategy | Peak Value (deg/s) | Vibration Behavior | Amplitude of Fluctuation (deg/s) |
|---|---|---|---|
| PID control | −17.6 | Severe oscillation | ±2 |
| Hybrid control | 6 | Minor oscillation | ±1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, X.; Zhou, Y. Research on Hybrid Control Methods for Electromechanical Actuation Systems Under the Influence of Nonlinear Factors. Actuators 2025, 14, 526. https://doi.org/10.3390/act14110526
Ding X, Zhou Y. Research on Hybrid Control Methods for Electromechanical Actuation Systems Under the Influence of Nonlinear Factors. Actuators. 2025; 14(11):526. https://doi.org/10.3390/act14110526
Chicago/Turabian StyleDing, Xingye, and Yong Zhou. 2025. "Research on Hybrid Control Methods for Electromechanical Actuation Systems Under the Influence of Nonlinear Factors" Actuators 14, no. 11: 526. https://doi.org/10.3390/act14110526
APA StyleDing, X., & Zhou, Y. (2025). Research on Hybrid Control Methods for Electromechanical Actuation Systems Under the Influence of Nonlinear Factors. Actuators, 14(11), 526. https://doi.org/10.3390/act14110526






