Integral Reinforcement Learning-Based Stochastic Guaranteed Cost Control for Time-Varying Systems with Asymmetric Saturation Actuators

Abstract

This study explores a stochastic guarantee cost control (GCC) for time-varying systems with random parameters and asymmetric saturation actuators by employing the integral reinforcement learning (IRL) method in the dynamic event-triggered (DET) mode. Firstly, a modified Hamilton–Jacobi–Isaac (HJI) equation is formulated, and then the worst-case disturbance policy and the asymmetric saturation optimal control signal can be obtained. Secondly, the multivariate probabilistic collocation method (MPCM) is used to evaluate the value function at designated sampling points. The purpose of introducing the MPCM is to simplify the computational complexity of stochastic dynamic programming (SDP) methods. Furthermore, the DET mode is utilized to solve the SDP problem to reduce the computational burden on communication resources. Finally, the Lyapunov stability theorem is applied to analyze the stability of time-varying systems, and the simulation shows the feasibility of the designed method.

1. Introduction

Over the past few decades, stochastic control has been extensively studied across numerous practical domains, including robotic systems [1], microgrid setups [2], intelligent transportation networks [3], and other practical control fields. Compared with deterministic system control, stochastic system control has problems such as computational complexity and model mismatch, which makes its design challenging [4]. In [5], the stochastic control problem was studied in data-driven model predictive control by using neural networks (NNs) or establishing a stochastic sampling model. A stochastic control approach applicable to discrete-time nonlinear systems was put forward in [6]. The security issues of stochastic systems were also addressed in [7]. A novel stochastic control method was designed for a linear system with multiplicative noise and input constraints in [8]. Regarding stochastic discrete-time linear systems under bounded input constraints, a receding horizon control technique was formulated in [9]. However, none of the studies mentioned above considered optimal control under asymmetric saturation actuators (ASAs).

Actuator saturation is a common nonlinear problem that can affect system stability and performance and also pose significant challenges to controller design. In [10], a robust adaptive fuzzy fault-tolerant path planning control method was proposed to solve the actuator saturation problem. In [11], an adaptive compensation technique integrated into the backstepping framework was proposed for controlled systems with actuator saturation. In [12], an adaptive NN control method was proposed for systems with input saturation nonlinearities. These methods have symmetric saturation actuators, and in order to optimize control strategies, researchers have proposed ASA control strategies to ensure the safety and stability of the controlled system. In [13], a composite adaptive control method was proposed for tethered aircraft systems with ASAs. Ref. [14] proposed a sliding mode control method with ASAs for vehicle systems. In [15], an asymptotic stabilization method was proposed for unmanned surface vessels with actuator dead zones and bow constraints. However, the methods mentioned above do not consider the optimal performance of the controlled system. The adaptive dynamic programming (ADP) algorithm, which is a method that combines dynamic programming (DP) and integral reinforcement learning (RL) ideas, addresses the “curse of dimensionality” issue in conventional DP  [16,17,18,19]. For the Itô-type stochastic systems, the authors employed the ADP method to address the tracking control issue in [20]. In [21], a self-learning optimal operation control method based on a compensator and RL was proposed for input-constrained dual-time scale systems. A Q-learning-based fault-tolerant control method was designed without using the knowledge of system function in [22]. In [23], an RL-based optimal control (OC) method was devised for linear stochastic systems, with the least squares approach adopted to derive approximate optimal solutions. Further, an integral RL-based model-free tracking approach was developed for linear stochastic systems in [24]. In [25], an ADP-based GCC method was presented for nonlinear systems. By introducing the GCC approach, one can ensure that the control performance index is below a certain bound. The above methods may cause unnecessary waste of communication resources because these approaches are designed based on time-triggered control mechanisms.

Event-triggered control (ETC) is a non-periodic control strategy based on triggering conditions; the core idea of ETC is to determine when to update control signals or communicate through preset event-triggered conditions, rather than traditional periodic sampling or time triggering [26,27]. In [28], for Itô-type time-delayed stochastic systems subject to uncertainties, an OC strategy under the ETC mechanism was designed by using the ADP method and constructing an actor–critic architecture. Moreover, an optimal consensus control (OCC) strategy was proposed by using fuzzy technology for stochastic MASs with time delays in [29]. To further decrease control input update frequency and increase communication resource utilization, the dynamic event-triggered control (DETC) mechanism serves as an upgraded version of the conventional ETC approach. It is a dynamically adjustable mechanism that further optimizes resource usage, system performance, and adaptability [30]. In [31], under the DETC mechanism, the H2/H∞ problem was explored for partially unknown nonlinear stochastic systems by employing the ADP algorithm. In [32], focusing on uncertain microgrids, control inputs and external disturbances were treated as two participants in zero-sum differential game scenarios. Under the DETC mechanism, the authors put forward a frequency recovery control approach based on integral reinforcement learning (IRL). In [33], a dynamically adjustable triggering condition was designed based on the OC method for stochastic nonlinear systems by using backstepping technology and the RL algorithm in the DETC mode.

In addition, it is difficult to obtain accurate mathematical models for actual control systems, and estimating system dynamics through extended simulation experiments is a conventional method [34,35]. If random time-varying parameters exist in actual nonlinear controlled system dynamics, the expected control performance function is always estimated by using uncertainty evaluation methods [36], such as the Monte Carlo (MC) approach and its extensive version, which are implemented based on simulation experiments [37]. However, approximating the expected control performance index requires a large number of simulation experiments when using the MC method and its extensive version [38]. In [39], to simplify the computational complexity, the MPCM method, which is an effective technology for estimating uncertainties, was used to estimate the expected value of the cost function by taking values at certain specific sampling points. Stochastic GCC approaches have been put forward by using RL (or IRL) and MPCM methods in [36,40]. However, the issue of ASAs remains unaddressed. In our design, we put forward a GCC approach in DETC mode for stochastic systems subject to ASAs by employing the the MPCM integrated with IRL algorithms. The main contributions are as follows:

1.

This study develops an innovative DETC-based GCC approach for stochastic systems by using IRL algorithms with the MPCM. This approach can ensure that the system performance index is less than a certain upper bound.

2.

By solving an improved HJI equation by designing a modified long-term performance cost function, the control inputs under ASAs can be obtained via an actor–critic–disturbance NN structure.

3.

Through the introduction of dynamic parameters into triggering conditions in the DETC mechanism, the update rule for control inputs can be adjusted dynamically, which can reduce the computational complexity of sampling data.

This paper’s structure is arranged as follows. Section 2 presents the issue description. Section 3 develops stochastic systems’ optimal GCC design via a modified HJI equation. A stochastic GCC method is designed by using the MPCM and IRL in Section 4. Section 5 presents the event-triggered structure for optimal GCC. A simulation example is shown to verify the feasibility of the strategy in Section 6. The conclusion is shown in Section 7.

2. Problem Statement

Consider the following stochastic system [36,41]:

$$\begin{array}{c}\hfill \dot{\varsigma }=\chi \left(g\right)\varsigma +B\rho +Cd,\end{array}$$

(1)

where $\chi \left(g\right)\in R^{n\times n}$ represents a time-varying matrix related to the stochastic vector $g\left(t\right)$. Matrices $B\in R^{n\times q}$ and $C\in R^{n\times p}$ are the system functions. The disturbance policy, control input, and system state are $d\in R^p$, $\rho \in R^q$ and $\varsigma \left(t\right)\in R^n$, respectively. The control signal $\rho ={[{\rho }_1,{\rho }_2,\dots ,{\rho }_q]}^T$ satisfies ${\rho }_{min}\le {\rho }_i\le {\rho }_{max}$, $\left|{\rho }_{min}\right|\ne \left|{\rho }_{max}\right|$, for $i=1,2,\dots ,q$. ${\rho }_{min}$ and ${\rho }_{max}$ stand for the smallest and largest constraint limits of control inputs ${\rho }_i$. $g_p\left(t\right)$ is the sample function of the pth element in the random vector $g\left(t\right)$, and the dynamics of the sample system (1) are ordinary differential equations; $g_p\left(t\right)$ exhibits good behavior.

Assumption 1.

The system (1) satisfies Lipschitz continuity over the compact set ${\Omega }_{\varsigma }\subset R^n$ [36,42,43]. In addition, $\chi \left(g\right)\le b_a$, where $b_a$ is a positive constant.

Remark 1.

Unlike general stochastic models with drift and diffusion terms, Ref. [41] focused on zero-sum game studies of time-varying stochastic systems (1) with environment-influenced random variables. The system model (1) is applicable to practical scenarios. For example, aircraft systems have been modeled as $\dot{\varsigma }=-K\varsigma \left(t\right)+M_u\left(t\right)+M_d\left(t\right)$, where K is a weather-dependent random variable, $M_u\left(t\right)$ refers to regulated thrust, and $M_d\left(t\right)$ is the interference force. Other fields also explore such system dynamics [44].

Assumption 2.

Let ${\beta }_1$ denote a positive constant; the disturbance approach $d\left(\varsigma \right)$ is such that $d^T\left(\varsigma \right)d\left(\varsigma \right)\le {\beta }_1{\varsigma }^T\varsigma$, with $d\left(0\right)=0$.

The system (1) with nominal form becomes

$$\begin{array}{c}\hfill \dot{\varsigma }=\chi \left(g\right)\varsigma +B\rho .\end{array}$$

(2)

The positive definite matrix is represented as $Q\in R^{n\times n}$, and the long-term control performance function is

$$\begin{array}{c}\hfill \overline{\Theta }(\varsigma \left(0\right),\rho )=E\left[{\int }_0^{\infty }\left({\varsigma }^{T}Q\varsigma +\mathcal{W}\left(\rho \right)\right)dt\right].\end{array}$$

(3)

with

$$\begin{array}{c}\hfill \mathcal{W}\left(\rho \right)=2{\kappa }_2{\int }_{{\kappa }_1}^{\rho \left(\varsigma \right)}{\tilde{\rho }}_a^{-T}\left({\kappa }_2^{-1}(\vartheta -{\kappa }_1)\right)R\mathrm{d}\vartheta ,\\ \hfill {\kappa }_1={\displaystyle \frac{{\rho }_{max}+{\rho }_{min}}{2}},{\kappa }_2={\displaystyle \frac{{\rho }_{max}-{\rho }_{min}}{2}},\end{array}$$

where ${\tilde{\rho }}_a(·)=tanh(·)$. For ${\tilde{r}}_i>0,i=1,\dots ,q$, $R=diag\left({\tilde{r}}_1,{\tilde{r}}_2,\dots ,{\tilde{r}}_q\right)$.

By calculation, we have

$$\begin{array}{cc}\hfill \mathcal{W}\left(\rho \right)& =2{\kappa }_2{tanh}^{-T}\left({\displaystyle \frac{\rho \left(\varsigma \right)-{\kappa }_1}{{\kappa }_2}}\right)R(\rho \left(\varsigma \right)-{\kappa }_1)\hfill \\ \hfill & +{\kappa }_2^2{\overline{R}}^{T}ln\left(\overline{\mathbf{1}}-{\left({\displaystyle \frac{\rho \left(\varsigma \right)-{\kappa }_1}{{\kappa }_2}}\right)}^2\right),\hfill \end{array}$$

where $\overline{R}={\left[{\tilde{r}}_1,{\tilde{r}}_2,\dots ,{\tilde{r}}_q\right]}^T$ and $\overline{\mathbf{1}}=\underset{\underset{q}{︸}}{{[1,\dots ,1]}^{\top }}$.

Remark 2.

Ref. [36] studied the GCC problem of stochastic systems under an event-triggered mechanism. However, some practical systems face the nonlinear control problem of ASAs [13,14,15], which limits the application of the method in [36]. Therefore, this paper proposes a GCC strategy for stochastic systems under the ASA condition with $|{\rho }_{min}|\ne |{\rho }_{max}|$. By introducing a non-quadratic function $\mathcal{W}\left(\rho \right)$ related to the control input ρ to relax the asymmetric constraints and incorporating dynamic parameters into the triggering condition, the number of communications can be effectively reduced, and the utilization rate of communication resources can be further improved.

Within our design framework, the primary objective is to establish a GCC strategy for systems with ASAs by solving the HJI equation, which can ensure that the cost function is less than a certain upper bound and guarantee the stability and optimal control performance of stochastic systems under the DETC mechanism.

3. Stochastic Optimal GCC Design

In our design, an auxiliary policy is designed as ð, and the auxiliary system is established as

$$\begin{array}{c}\hfill \dot{\varsigma }=\chi \left(g\right)\varsigma +B\rho +Cð.\end{array}$$

(4)

Let $r(\varsigma ,\rho ,ð)={\varsigma }^{T}Q\varsigma +\mathcal{W}\left(\rho \right)-{\gamma }^2{ð}^Tð$, where $\gamma$ represents a pre-specified disturbance attenuation level.

The modified cost function is

$$\begin{array}{c}\hfill \Theta (\varsigma \left(0\right),\rho ,ð)=E\left[{\int }_0^{\infty }\left(r(\varsigma ,\rho ,ð)+{\gamma }^2{\beta }_1{\varsigma }^T\varsigma \right)dt\right].\end{array}$$

(5)

The value function is

$$\begin{array}{c}\hfill \mathsf{\Gamma }\left(\varsigma \left(t\right)\right)=E\left[{\int }_t^{\infty }\left(r(\varsigma ,\rho ,ð)+{\gamma }^2{\beta }_1{\varsigma }^T\varsigma \right)dt\right].\end{array}$$

(6)

The derivative value of $\mathsf{\Gamma }\left(\varsigma \right(t\left)\right)$ is

$$\begin{array}{c}\hfill E\left[\dot{\mathsf{\Gamma }}\left(\varsigma \left(t\right)\right)\right]=-{\gamma }^2{\beta }_1{\varsigma }^T\varsigma -r(\varsigma ,\rho ,ð).\end{array}$$

(7)

Let $\nabla \mathsf{\Gamma }\left(\varsigma \right)={\displaystyle \frac{\partial \mathsf{\Gamma }\left(\varsigma \right)}{\partial \varsigma }}$, inspired by [36,41], the Hamiltonian function is designed in the form of a mean, which is given by

$$\begin{array}{cc}\hfill \mathcal{H}(\varsigma ,\nabla \mathsf{\Gamma },\rho ,ð)=& E\left[{(\nabla \mathsf{\Gamma })}^T(\chi \left(g\right)\varsigma +B\rho +Cð)\right]\hfill \\ \hfill & +{\gamma }^2{\beta }_1{\varsigma }^T\varsigma +r(\varsigma ,\rho ,ð).\hfill \end{array}$$

(8)

Bellman’s equation refers to the principle of optimization in DP problems. In light of Bellman’s optimality principle, the following holds:

$$\begin{array}{c}\hfill \underset{\rho }{min}\underset{ð}{max}\mathcal{H}\left(\varsigma ,\nabla {\mathsf{\Gamma }}^{*},\rho ,ð\right)=0,\end{array}$$

(9)

with ${ð}^{*}$, ${\rho }^{*}$, and ${\mathsf{\Gamma }}^{*}\left(\varsigma \right)$ being the worst-case disturbance policy, optimal control signal, and optimal value function, respectively. By calculation, we have

$$\begin{array}{cc}\hfill {\rho }^{*}& =-{\kappa }_{2}tanh\left(N^{*}\right)+{\kappa }_1,\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill {ð}^{*}& ={\displaystyle \frac{1}{2{\gamma }^2}}{C}^T\nabla {\mathsf{\Gamma }}^{*}\left(\varsigma \right),\hfill \end{array}$$

(11)

where $N^{*}={\displaystyle \frac{1}{2{\kappa }_2}}{R}^{-1}{B}^T\nabla {\mathsf{\Gamma }}^{*}\left(\varsigma \right)$.

According to (10) and (11), we get

$$\begin{array}{cc}\hfill \mathcal{W}\left({\rho }^{*}\right)& =2{\kappa }_2{\int }_{{\kappa }_1}^{{\rho }^{*}\left(\varsigma \right)}{\tilde{\rho }}_a^{-T}\left({\kappa }_2^{-1}(\vartheta -{\kappa }_1)\right)R\mathrm{d}\vartheta \hfill \\ \hfill & =2{\kappa }_2{\int }_{{\kappa }_1}^{-{\kappa }_{2}tanh\left(N^{*}\right)+{\kappa }_1}{\tilde{\rho }}_a^{-T}\left({\kappa }_2^{-1}(\vartheta -{\kappa }_1)\right)R\mathrm{d}\vartheta \hfill \\ \hfill & =2{\kappa }_2^2{N}^{*T}Rtanh\left(N^{*}\right)+k_2^2{\overline{R}}^{T}ln\left(\overline{\mathbf{1}}-{tanh}^2\left(N^{*}\right)\right),\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill U_2^{*}& ={\gamma }^2{P}^{*T}{P}^{*},\hfill \end{array}$$

(13)

with $P^{*}={\displaystyle \frac{C^T\nabla {\mathsf{\Gamma }}^{*}}{2{\gamma }^2}}$ and $r(\varsigma ,{\rho }^{*},{ð}^{*})={\varsigma }^{T}Q\varsigma +\mathcal{W}\left({\rho }^{*}\right)-U_2^{*}$.

Based on (8), (12) and (13), the HJI equation is restructured as

$$\begin{array}{cc}\hfill & \mathcal{H}(\varsigma ,\nabla {\mathsf{\Gamma }}^{*},{\rho }^{*},{ð}^{*})\hfill \\ \hfill =& E\left[{(\nabla {\mathsf{\Gamma }}^{*})}^T(\chi \left(g\right)\varsigma +B{\rho }^{*}+C{ð}^{*})\right]+{\gamma }^2{\beta }_1{\varsigma }^T\varsigma +{\varsigma }^{T}Q\varsigma +\mathcal{W}\left({\rho }^{*}\right)-{\gamma }^2{ð}^{*T}{ð}^{*}\hfill \\ \hfill =& E\left[{\varsigma }^{T}Q\varsigma +\nabla {\mathsf{\Gamma }}^{*T}\chi \left(g\right)\varsigma +2{\kappa }_2^2{N}^{*T}Rtanh\left(N^{*}\right)+{\kappa }_2^2{\overline{R}}^{T}ln\left(\overline{\mathbf{1}}-{tanh}^2\left(N^{*}\right)\right)\right.\hfill \\ \hfill & \left.+{\gamma }^2{P}^{*T}{P}^{*}+{\gamma }^2{\beta }_1{\varsigma }^T\varsigma +2{\kappa }_2{N}^{*T}R\left(-{\kappa }_{2}tanh\left(N^{*}\right)+{\kappa }_1\right)\right]\hfill \\ \hfill =& E\left[{\varsigma }^T{Q}_1\varsigma +\nabla {\mathsf{\Gamma }}^{*T}\chi \left(g\right)\varsigma +{\gamma }^2{P}^{*T}{P}^{*}+{\kappa }_2^2{\overline{R}}^{T}ln\left(\overline{\mathbf{1}}-{tanh}^2\left(N^{*}\right)\right)+2{\kappa }_2{N}^{*T}R{\kappa }_1\right]=0\hfill \end{array}$$

(14)

where $I_{n\times n}$ is an $n\times n$ identity matrix, which satisfies $Q_1=Q+{\gamma }^2{\beta }_1{I}_{n\times n}$ and $\mathsf{\Gamma }\left(0\right)=0$.

Assumption 3.

${\lambda }_1$ and ${\lambda }_2$ are denoted as positive numbers. $\mathsf{\Gamma }\left(\varsigma \right)$ is continuously differentiable, which satisfies ${\lambda }_1{\parallel \varsigma \parallel }^2\le \mathsf{\Gamma }\left(\varsigma \right)\le {\lambda }_2{\parallel \varsigma \parallel }^2$.

Remark 3.

Due to the existence of uncertainty and random parameters, the OC problem of system (1) is difficult to solve. The GCC problem can obtain the upper bound of the cost function of system (1), which is the basic idea of the GCC problem. This article constructs an auxiliary system, and by solving the optimal value function of the auxiliary system, the guaranteed cost (GC) function of the original system (1) can be obtained; that is, the value function of the auxiliary system is the optimal GC function of the original system. A related theorem is given as follows.

Theorem 1.

Considering system (1), define the cost function of auxiliary system (4) as (5); the asymptotic stability characteristic in the mean of stochastic system (1) can be guaranteed if a differentiable value function ${\mathsf{\Gamma }}^{*}$ satisfies the HJI equation in (14) and the asymmetric cost control signal in (10) and the auxiliary policy in (11) are utilized.

Proof. 

Choose the candidate Lyapunov function as

$$\begin{array}{c}\hfill {\mathsf{\Gamma }}^{*}\left(\varsigma \left(t\right)\right)=E\left[{\int }_t^{\infty }\left({\varsigma }^T{Q}_1\varsigma +\mathcal{W}\left({\rho }^{*}\right)-{\gamma }^2{ð}^{*T}{ð}^{*}\right)d\varrho \right].\end{array}$$

When ${\rho }^{*}$ is substituted into (1), system (1) becomes

$$\begin{array}{c}\hfill \dot{\varsigma }=\chi \left(g\right)\varsigma +B{\rho }^{*}+Cd.\end{array}$$

(15)

Through the addition and substitution of $\nabla {\mathsf{\Gamma }}^{*T}\left(\varsigma \right)C{ð}^{*}$, we derive

$$\begin{array}{cc}\hfill E\left[{\dot{\mathsf{\Gamma }}}^{*}\left(\varsigma \right)\right]& =E\left[{\left(\nabla {\mathsf{\Gamma }}^{*}\left(\varsigma \right)\right)}^T\left(\chi \left(g\right)\varsigma +B{\rho }^{*}+Cd\right)\right]\hfill \\ \hfill & =E\left[{\left(\nabla {\mathsf{\Gamma }}^{*}\left(\varsigma \right)\right)}^T\left(\chi \left(g\right)\varsigma +B{\rho }^{*}+C{ð}^{*}\right)\right]\hfill \\ \hfill & +E\left[{\left(\nabla {\mathsf{\Gamma }}^{*}\left(\varsigma \right)\right)}^{T}C\left(d-{ð}^{*}\right)\right].\hfill \end{array}$$

(16)

Based on (8), (9) and (11), one gets

$$\begin{array}{cc}\hfill & E\left[{\left(\nabla {\mathsf{\Gamma }}^{*}\left(\varsigma \right)\right)}^T\left(\chi \left(g\right)\varsigma +B{\rho }^{*}+C{ð}^{*}\right)\right]+E\left[{\left(\nabla {\mathsf{\Gamma }}^{*}\left(\varsigma \right)\right)}^{T}C\left(d-{ð}^{*}\right)\right]\hfill \\ \hfill =& E\left[-{\gamma }^2{\beta }_1{\varsigma }^T\varsigma -{\varsigma }^{T}Q\varsigma -\mathcal{W}\left({\rho }^{*}\right)+{\gamma }^2{ð}^{*T}{ð}^{*}\right]\hfill \\ \hfill & +E\left[2{\gamma }^2{ð}^{*T}\left(d-{ð}^{*}\right)\right].\hfill \end{array}$$

(17)

Using Assumption 2 and the inequality $2{\gamma }^2{ð}^{*T}d\le {\gamma }^2{ð}^{*T}{ð}^{*}+{\gamma }^2{d}^{T}d$, one obtains

$$\begin{array}{c}\hfill E\left[{\dot{\mathsf{\Gamma }}}^{*}\left(\varsigma \right)\right]\le E\left[-{\varsigma }^{T}Q\varsigma -\mathcal{W}\left({\rho }^{*}\right)\right]\le 0.\end{array}$$

(18)

Integrating Equation (18) over the interval $[0,\infty )$, we have

$$\begin{array}{c}\hfill E\left[{\int }_0^{\infty }\left({\varsigma }^{T}Q\varsigma +\mathcal{W}({\rho }^{*}\right)d\varrho \right]\le {\mathsf{\Gamma }}^{*}\left(\varsigma \left(0\right)\right).\end{array}$$

(19)

From (18), [36] (Lemma 1) and Assumption 3, the asymptotic stability characteristic in the mean of stochastic system (1) can be guaranteed under the application of the control pairs $({\rho }^{*},{ð}^{*})$ given in (10) and (11). Additionally, based on (18), we have $\overline{\Theta }\left(\varsigma \left(0\right),{\rho }^{*}\right)\le {\mathsf{\Gamma }}^{*}\left(\varsigma \left(0\right)\right)$.    □

4. Stochastic GCC Method Design via MPCM and IRL Algorithm

In this section, a novel stochastic GCC method is proposed for the controlled system with asymmetric constrained inputs by using the MPCM and IRL algorithms.

Using (7), we derive the integral Bellman equation based on the optimality principle as ${\mathsf{\Gamma }}^{*}\left(\varsigma \left(t\right)\right)=E\left[{\int }_t^{t+T}({\gamma }^2{\beta }_1{\varsigma }^T\varsigma +r\left(\varsigma ,{\rho }^{*},{ð}^{*}\right))d\varrho +{\mathsf{\Gamma }}^{*}\left(\varsigma \left(t+T\right)\right)\right]$ with $T\in (0,t)$. For any admissible control policies $\left(\rho \right(\varsigma ),ð(\varsigma \left)\right)$, the value function satisfies the condition that

$$\begin{array}{cc}\hfill \mathsf{\Gamma }\left(\varsigma \right(t\left)\right)& =E\left[{\int }_t^{t+T}\left({\gamma }^2{\beta }_1{\varsigma }^T\varsigma +r(\varsigma ,\rho ,ð)\right)d\varrho +\mathsf{\Gamma }\left(\varsigma (t+T)\right)\right].\hfill \end{array}$$

(20)

Accordingly, one obtains

$$\begin{array}{cc}\hfill {\breve{e}}_B=& E[{\int }_t^{t+T}\left(r(\varsigma ,\rho ,ð)+{\gamma }^2{\beta }_1{\varsigma }^T\varsigma \right)d\varrho \hfill \\ \hfill & +\mathsf{\Gamma }\left(\varsigma \right(t+T\left)\right)]-\mathsf{\Gamma }(\varsigma \left(t\right))\hfill \end{array}$$

(21)

where ${\breve{e}}_B$ is the Bellman error.

Remark 4.

Equation (21) will be employed in the subsequent on-policy IRL design procedure. In our framework, the IRL algorithm serves to drive the Bellman error ${\breve{e}}_B$ in (21) toward zero.

As $t\to \infty$, $\left(\rho \left(\varsigma \right),d\left(\varsigma \right)\right)$ converges to $({\rho }^{*}\left(\varsigma \right),d^{*}\left(\varsigma \right))$ after several iterations in the learning process, and concurrently, $\mathsf{\Gamma }\left(\varsigma \right)$ approaches ${\mathsf{\Gamma }}^{*}\left(\varsigma \right)$.

4.1. On-Policy GCC Design

By designing an NN that includes the activation function, the expected weight vector and the approximation error are denoted as ${\phi }_c\left(\varsigma \right)$, ${\mathit{W}}_c$, and ${\epsilon }_c\left(\varsigma \right)$, respectively. We approximate the value function ${\mathsf{\Gamma }}^{*}\left(\varsigma \right)$ as

$$\begin{array}{c}\hfill {\mathsf{\Gamma }}^{*}\left(\varsigma \right)={\mathit{W}}_c^T{\phi }_c\left(\varsigma \right)+{\epsilon }_c\left(\varsigma \right).\end{array}$$

(22)

Let ${\widehat{\mathit{W}}}_c$ denote the estimated value for ${\mathit{W}}_c$. At time step $s+1$, the estimate value of $\mathsf{\Gamma }\left(\varsigma \right)$ is

$$\begin{array}{c}\hfill {\mathsf{\Gamma }}^{(s+1)}\left(\varsigma \right)={\widehat{\mathit{W}}}_c^{(s+1)T}{\phi }_c\left(\varsigma \right).\end{array}$$

(23)

Based on [40] (Th.2), we adopt the MPCM to reduce the number of simulations from $2^m{\prod }_{q=1}^m{N}_q$ to ${\prod }_{q=1}^m{N}_q$, which enables the prediction of the output mean of the system mapping $G\left({\eta }_1,{\eta }_2,\dots ,{\eta }_m\right)$. In this part, the GCC algorithm for random systems with stochastic uncertainty is presented in Algorithm 1.

The specific steps of Algorithm 1 include the following.

(1) Select a set of sampling points for the uncertain variable $g\left(t\right)$ based on the MPCM and calculate the cumulative cost function $G_{\mathsf{\Gamma }}$ for the future time period at each sampling point. This function is composed of the output estimate ${\widehat{\mathit{W}}}_c^T{\phi }_c$ of the next evaluation critic NN and the integral term containing control energy consumption and state cost in the current time period. (2) Calculate the mathematical expectation of the $G_{\mathsf{\Gamma }}$ function values at all sampling points to obtain the updated value function estimate for this iteration, denoted as ${\mathsf{\Gamma }}^{(s+1)}$. With this estimated value as the objective, update the weight vector ${\widehat{\mathit{W}}}_c$ of the evaluation NN by solving the HJI equation so that its output accurately matches the value function estimate. (3) Using the gradient information of the updated value function, design control strategy ${\rho }^{(s+1)}$ and disturbance strategy ${ð}^{(s+1)}$, respectively.

Algorithm 1 Model-based GCC algorithm for stochastic uncertain system (1).

Initialization Set initial admissible policies $\rho \left(0\right)$ and $ð\left(0\right)$. Step 1: A set of sampling points for the uncertain variable $g\left(t\right)$ is selected on the basis of the MPCM ([40], Section II). Compute the value of $G_{\mathsf{\Gamma }}$ at each sampling point: $$\begin{array}{cc}\hfill & G_{{\mathsf{\Gamma }}^{(s+1)}}\left(\varsigma ,{ð}^{\left(s\right)},{\rho }^{\left(s\right)},g\right)\hfill \\ \hfill =& {\widehat{\mathit{W}}}_c^{(s+1)T}{\phi }_c\left(\varsigma (t+T)\right)\hfill \\ \hfill & +{\int }_t^{t+T}(r(\varsigma \left(\varrho \right),{\rho }^{\left(s\right)}\left(\varrho \right),{ð}^{\left(s\right)}\left(\varrho \right))\hfill \\ \hfill & +{\gamma }^2{\beta }_1{\varsigma }^T\varsigma )d\varrho .\hfill \end{array}$$ (24) Step 2: Compute ${\mathsf{\Gamma }}^{(s+1)}\left(\varsigma \left(t\right)\right)$ by computing the mean value of $G_{{\mathsf{\Gamma }}^{(s+1)}}(·)$. $${\mathsf{\Gamma }}^{(s+1)}\left(\varsigma \left(t\right)\right)=E\left[G_{{\mathsf{\Gamma }}^{(s+1)}}\left(\varsigma ,{\rho }^{\left(s\right)},{ð}^{\left(s\right)},g\right)\right].$$ (25) Step 3: Update ${\mathit{W}}_c^{(s+1)}$ on the basis of solving the HJI equation: $${\widehat{\mathit{W}}}_c^{(s+1)T}{\phi }_c\left(\varsigma \left(t\right)\right)={\mathsf{\Gamma }}^{(s+1)}\left(\varsigma \left(t\right)\right).$$ (26) Step 4: Design the control pairs via $$\begin{array}{cc}\hfill {\rho }^{(s+1)}& =-{\kappa }_{2}tanh\left({\displaystyle \frac{1}{2{\kappa }_2}}{B}^T\nabla {\mathsf{\Gamma }}^{(s+1)}\left(\varsigma \right)\right)+{\kappa }_1,\hfill \end{array}$$ (27a) $$\begin{array}{cc}\hfill {ð}^{(s+1)}& ={\displaystyle \frac{1}{2{\gamma }^2}}{C}^T\nabla {\mathsf{\Gamma }}^{(s+1)}\left(\varsigma \right).\hfill \end{array}$$ (27b) Let s be updated as $s+1$. If $\parallel {\mathsf{\Gamma }}^{(s+1)}-{\mathsf{\Gamma }}^{\left(s\right)}\parallel \le \varsigma$ where $\varsigma$ is a small positive number and stops at step 4; Otherwise, please return to step 1.

Here, we define a new system function involving the uncertain parameter $g\left(t\right)$ as $G_{\mathsf{\Gamma }\left(t\right)}(\varsigma ,\rho ,ð,g)={\int }_t^{t+T}({\gamma }^2{\beta }_1{\varsigma }^T\varsigma +\gamma \left(\varsigma ,\rho ,ð\right))d\varrho +\mathsf{\Gamma }\left(\varsigma \left(t+T\right)\right)$. From (20), it follows that $\mathsf{\Gamma }\left(\varsigma \right)=E\left[G_{\mathsf{\Gamma }}(\varsigma ,\rho ,ð,g)\right]$. Specifically, select a set of samples according to the probability density functions (pdfs) $F_{{\chi }_q}\left(g_q\right)$ of the uncertain parameters $g\left(t\right)$, and then compute the value of $E\left[G_{\mathsf{\Gamma }\left(t\right)}(\varsigma ,\rho ,ð,g)\right]$ via simulating at these chosen samples. Suppose the degree of each uncertain variable $g_q$ is updated to $2N_q-1$; $G_{\mathsf{\Gamma }\left(t\right)}(\varsigma ,\rho ,ð,g)$ can be expressed as

$$\begin{array}{cc}\hfill & G_{\mathsf{\Gamma }\left(t\right)}(\varsigma ,\rho ,ð,g)\hfill \\ \hfill =& \sum _{p_1=0}^{2N_1-1}\sum _{p_2=0}^{2N_2-1}\dots \sum _{p_m=0}^{2N_m-1}{\mathsf{\Psi }}_{p_1,p_2,\dots ,p_m}(\varsigma ,\rho ,ð)\prod _{q=1}^m{g}_q^{p_q}.\hfill \end{array}$$

(28)

Using the MPCM, a low-order mapping is used to approximate $G_{\mathsf{\Gamma }\left(t\right)}(\varsigma ,\rho ,ð,g)$ as follows:

$$\begin{array}{cc}\hfill & G_{\mathsf{\Gamma }\left(t\right)}^{\prime }(\varsigma ,\rho ,ð,g)\hfill \\ \hfill =& \sum _{p_1=0}^{N_1-1}\sum _{p_2=0}^{N_2-1}\dots \sum _{p_m=0}^{N_m-1}{\Omega }_{p_1,p_2,\dots ,p_m}(\varsigma ,\rho ,ð)\prod _{q=1}^m{g}_q^{p_q}.\hfill \end{array}$$

(29)

On the basis of [40] (Th.2), one obtains $\mathsf{\Gamma }\left(\varsigma \left(t\right)\right)=E\left[G_{\mathsf{\Gamma }\left(t\right)}(\varsigma ,\rho ,ð,g)\right]=$$E\left[G_{\mathsf{\Gamma }\left(t\right)}^{\prime }(\varsigma ,\rho ,ð,g)\right]$.

Lemma 1.

The auxiliary system of controlled system (1) is given as (4), and the value function is obtained by (23). In each iteration, the MPCM is employed to sample the uncertainty space, and the policies ρ and ð obtained from Algorithm 1 remain optimal if Algorithm 1 converges.

Proof. 

Using [40] (Th.2) and the relation $\mathsf{\Gamma }\left(\varsigma \right)=E\left[G_{\mathsf{\Gamma }}(\varsigma ,\rho ,ð,g)\right]$, the control pairs $({\rho }^{*},{ð}^{*})$ can be derived from (10) and (11). To establish this theorem, we need to show that the optimal solution obtained by evaluating $G_{\mathsf{\Gamma }\left(t\right)}(\varsigma ,\rho ,ð,g)$ is identical to that derived from computing the reduced-order mapping $G_{\mathsf{\Gamma }\left(t\right)}^{\prime }(\varsigma ,\rho ,ð,g)$. The equivalence of these two optimal solutions are proven via a contradiction method, as detailed in [39] (Th.1).    □

4.2. IRL-Based GCC Design with Asymmetric Constrained Inputs

Unlike Algorithm 1, an IRL-based GCC method is developed for the system (1) without relying on the knowledge of function B and C. Based on [45], two exploration signals $e_1$ and $e_2$ are, respectively, added to the control policies ${\rho }^{\left(s\right)}$ and ${ð}^{\left(s\right)}$. Consequently, the system (4) becomes

$$\begin{array}{c}\hfill \dot{\varsigma }=\chi \left(g\right)\varsigma +B(\rho +e_1)+C(ð+e_2).\end{array}$$

(30)

The specific steps of Algorithm 2 include the following.

Algorithm 2 IRL-based GCC algorithm for system (1) with asymmetric constrained control.

Initialization Set the initial admissible policies $\rho \left(0\right)$ and $ð\left(0\right)$. Step 1: Choose a set of sampling points for the uncertain variable $g\left(t\right)$ based on MPCM ([40], Section II). For each sampling point, compute the value of $$\begin{array}{cc}\hfill & G_{{\mathsf{\Gamma }}^{(s+1)}}\left(\varsigma ,{\rho }^{\left(s\right)},d^{\left(s\right)},g\right)\hfill \\ \hfill =& {\int }_t^{t+T}({\gamma }^2{\beta }_1{\varsigma }^T\varsigma +r\left(\varsigma \left(\varrho \right),{\rho }^{\left(s\right)}\left(\varrho \right),{ð}^{\left(s\right)}\left(\varrho \right)\right)d\varrho \hfill \\ \hfill & +{\widehat{\mathit{W}}}_c^{(s+1)T}{\phi }_c\left(\varsigma (t+T)\right).\hfill \end{array}$$ (31) Step 2: Compute ${\mathsf{\Gamma }}^{(s+1)}\left(\varsigma \left(t\right)\right)$ by calculating the mean of $G_{{\mathsf{\Gamma }}^{(s+1)}}(·)$. $${\mathsf{\Gamma }}^{(s+1)}\left(\varsigma \left(t\right)\right)=E\left[G_{{\mathsf{\Gamma }}^{(s+1)}}\left(\varsigma ,{\rho }^{\left(s\right)},{ð}^{\left(s\right)},g\right)\right].$$ (32) Step 3: Update ${\mathsf{\Gamma }}^{(s+1)}$, ${\rho }^{(s+1)}$ and ${ð}^{(s+1)}$ through solving the HJI equation: $$\begin{array}{cc}\hfill & {\mathsf{\Gamma }}^{(s+1)}\left(\varsigma (t+T)\right)-{\mathsf{\Gamma }}^{(s+1)}\left(\varsigma \left(t\right)\right)\hfill \\ \hfill =& E\left[{\int }_t^{t+T}\left(-2{\kappa }_2{tanh}^{-T}\left({\kappa }_2^{-1}\left({\rho }^{(s+1)}-{\kappa }_1\right)\right)R{e}_1+2{\gamma }^2{ð}^{(s+1)T}{e}_2\right)d\varrho \right]\hfill \\ \hfill & +{\int }_t^{t+T}(-{\gamma }^2{\beta }_1{\varsigma }^T\varsigma -r^{\left(s\right)}(\varsigma ,\rho ,ð))d\varrho .\hfill \end{array}$$ (33) Set s to $s+1$. If $\parallel {\mathsf{\Gamma }}^{(s+1)}-{\mathsf{\Gamma }}^{\left(s\right)}\parallel \le \varsigma$, where $\varsigma$ is a chosen positive number, end at step 3; otherwise, return to step 1.

(1) Based on the MPCM, select a set of sampling points for the uncertain variable $g\left(t\right)$ and calculate the cumulative cost function $G_{\mathsf{\Gamma }}$ for the future time period at each sampling point. This function consists of the integral term containing the state penalty and control cost in the current time period, as well as the output estimate ${\widehat{\mathit{W}}}_c^{(s+1)T}{\phi }_c$ of the evaluation NN at the next time. (2) By calculating the mathematical expectation of the $G_{\mathsf{\Gamma }}$ function values at all sampling points, the updated value function estimate for this iteration, ${\mathsf{\Gamma }}^{(s+1)}$, is obtained. (3) Solve an HJI equation embedded with exploration signals $e_1$, $e_2$, while updating the value function ${\mathsf{\Gamma }}^{(s+1)}$, control strategy ${\rho }^{(s+1)}$, and disturbance strategy ${ð}^{(s+1)}$.

Taking (7) into account and utilizing (10) and (11), we have

$$\begin{array}{cc}\hfill & E\left[{\dot{\mathsf{\Gamma }}}^{(s+1)}\left(\varsigma \left(t\right)\right)\right]\hfill \\ \hfill =& E\left[\left(\nabla {\mathsf{\Gamma }}^{(s+1)\mathrm{T}}\left(\varsigma \right)\right)\left(\chi \left(g\right)\varsigma +B{\rho }^{\left(s\right)}+C{ð}^{\left(s\right)}\right)\right.\hfill \\ \hfill & \left.+\left(\nabla {\mathsf{\Gamma }}^{(s+1)\mathrm{T}}\left(\varsigma \right)\right)\left(B{e}_1+C{e}_2\right)\right]\hfill \\ \hfill =& E\left[-2{\kappa }_2{tanh}^{-T}\left({\kappa }_2^{-1}\left({\rho }^{(s+1)}-{\kappa }_1\right)\right)R{e}_1\right.\hfill \\ \hfill & \left.+2{\gamma }^2{ð}^{(s+1)\mathrm{T}}{e}_2\right]-{\gamma }^2{\beta }_1{\varsigma }^{\mathrm{T}}\varsigma -r^{\left(s\right)}(\varsigma ,\rho ,ð).\hfill \end{array}$$

(34)

Based on (34), one obtains

$$\begin{array}{cc}\hfill & E\left[{\mathsf{\Gamma }}^{(s+1)}\left(\varsigma (t+T)\right)\right]-{\mathsf{\Gamma }}^{(s+1)}\left(\varsigma \left(t\right)\right)\hfill \\ \hfill =& {\int }_t^{t+T}\left(-{\gamma }^2{\beta }_1{\varsigma }^T\varsigma -r^{\left(s\right)}(\varsigma ,\rho ,ð)\right)d\varrho \hfill \\ \hfill & +E\left[{\int }_t^{t+T}(-2{\kappa }_2{tanh}^{-T}\left({\kappa }_2^{-1}\left({\rho }^{(s+1)}-{\kappa }_1\right)\right)R{e}_1\right.\left.+2{\gamma }^2{d}^{(s+1)\mathrm{T}}{e}_2)d\varrho \right].\hfill \end{array}$$

(35)

Algorithm 2 presents the GCC approach via the MPCM and IRL algorithm, where the target control policies can be approximated through

$$\begin{array}{cc}\hfill {\rho }^{*}\left(\varsigma \right)& =-{\kappa }_{2}tanh\left({\mathit{W}}_{\rho }^T{\phi }_{\rho }\left(\varsigma \right)+{\epsilon }_{\rho }\left(\varsigma \right)\right)+{\kappa }_1,\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill {ð}^{*}\left(\varsigma \right)& ={\mathit{W}}_{ð}^T{\phi }_{ð}\left(\varsigma \right)+{\epsilon }_{ð}\left(\varsigma \right),\hfill \end{array}$$

(37)

where the activation functions are denoted as ${\phi }_{\rho }\left(\varsigma \right)$ and ${\phi }_{ð}\left(\varsigma \right)$, the expected weight vectors are denoted as ${\mathit{W}}_{\rho }$ and ${\mathit{W}}_{ð}$, and approximation errors are denoted as ${\epsilon }_{\rho }\left(\varsigma \right)$ and ${\epsilon }_{ð}\left(\varsigma \right)$. The subscripts $\rho$ and ð represent the actor NN and disturbance NN, respectively.

The control pairs in actual situations are

$$\begin{array}{cc}\hfill {\rho }^{(s+1)}\left(\varsigma \right)& =-{\kappa }_{2}tanh\left({\widehat{\mathit{W}}}_{\rho }^{(s+1)T}{\phi }_{\rho }\left(\varsigma \right)\right)+{\kappa }_1,\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill {ð}^{(s+1)}\left(\varsigma \right)& ={\widehat{\mathit{W}}}_{ð}^{(s+1)T}{\phi }_{ð}\left(\varsigma \right).\hfill \end{array}$$

(39)

Theorem 2.

The auxiliary system of controlled system (1) is given as (4). The value function and control pairs are approximated via (23), (38) and (39), respectively. Assume Algorithm 2 converges. At each iteration, the MPCM is used to sample from the uncertain parameters; ${\widehat{\mathsf{\Gamma }}}^{\left(s\right)}\left(\varsigma \right)$, ${\widehat{\rho }}^{\left(s\right)}\left(\varsigma \right)$ and ${\widehat{ð}}^{\left(s\right)}\left(\varsigma \right)$ given by (33) will ultimately converge to the optimal values ${\mathsf{\Gamma }}^{(*)}\left(\varsigma \right)$, ${\rho }^{(*)}\left(\varsigma \right)$, and ${ð}^{*}\left(\varsigma \right)$.

Proof. 

The solution obtained using the GCC algorithm based on IRL has been proven to be the same as the solution obtained using the GCC algorithm with asymmetric constraint control based on IRL in [46] (Th. 3). The prior conclusion derived via the MPCM for each sample point holds valid as well. Therefore, the two approaches achieve identical optimal value functions. □

5. Event-Triggered Construction of Optimal GCC

Time-triggered control strategies involve substantial data transmission, which causes computational overload. In contrast to time-triggered methods, this section presents a GCC approach in the DETC mode for the stochastic system (1) based on Theorems 1–2 and Lemma 1, aiming to decrease the unnecessary consumption of communication resources.

5.1. Event-Triggered GCC Design

The control pairs will update when the triggering condition is violated with the DETC strategy. At each triggering instant, $\varsigma \left(s_j\right)={\overline{\varsigma }}_j$, where $s_j$ stands for the j th sampling moment. The event-triggered error is

$$\begin{array}{c}\hfill e_j\left(t\right)=\varsigma \left(t\right)-{\overline{\varsigma }}_j,\forall t\in \left[s_j,s_{j+1}\right)\end{array}$$

(40)

For $j\in N$, $e_j\left(t\right)=0$ holds when $t=s_j$. Based on (40), at triggering instants, the ETC policies become

$$\begin{array}{cc}\hfill \rho \left({\overline{\varsigma }}_j\right)& =\rho \left(\varsigma \left(t\right)-e_j\right),\hfill \end{array}$$

(41)

$$\begin{array}{cc}\hfill ð\left({\overline{\varsigma }}_j\right)& =ð\left(\varsigma \left(t\right)-e_j\right).\hfill \end{array}$$

(42)

By applying (41) and (42), and considering system (4) for all $\forall t\in [s_j,s_j+1)$, the Hamiltonian function in (8) becomes

$$\begin{array}{cc}\hfill & \mathcal{H}\left(\varsigma ,\overline{\rho },\overline{ð},\nabla \mathsf{\Gamma }\left(\varsigma \right)\right)\hfill \\ \hfill & =E\left[{\left(\nabla \mathsf{\Gamma }\left(\varsigma \right)\right)}^T\left(\chi \left(g\right)\varsigma +B\overline{\rho }+C\overline{ð}\right)\right]\hfill \\ \hfill & +{\gamma }^2{\beta }_1{\varsigma }^T\varsigma +{\varsigma }^{T}Q\varsigma +\mathcal{W}\left(\overline{\rho }\right)-{\gamma }^2{\overline{ð}}^T\overline{ð}.\hfill \end{array}$$

(43)

where $\overline{\rho }=\rho \left({\overline{\varsigma }}_j\right)$ and $\overline{ð}=ð\left({\overline{\varsigma }}_j\right)$.

Using (10) and (11), the ETC policies can be constructed as

$$\begin{array}{cc}\hfill {\overline{\rho }}^{*}& =-{\kappa }_{2}tanh({\displaystyle \frac{1}{2{\kappa }_2}}{R}^{-1}{B}^T\nabla {\mathsf{\Gamma }}^{*}\left({\overline{\varsigma }}_j\right))+{\kappa }_1,\hfill \end{array}$$

(44)

$$\begin{array}{cc}\hfill {\overline{ð}}^{*}& ={\displaystyle \frac{1}{2{\gamma }^2}}{C}^T\nabla {\mathsf{\Gamma }}^{*}\left({\overline{\varsigma }}_j\right).\hfill \end{array}$$

(45)

with ${\overline{\rho }}^{*}={\rho }^{*}\left({\overline{\varsigma }}_j\right)$ and ${\overline{ð}}^{*}={ð}^{*}\left({\overline{\varsigma }}_j\right)$.

Substituting (44) and (45) into (43), the result is

$$\begin{array}{cc}\hfill & \mathcal{H}\left(\varsigma ,{\overline{\rho }}^{*},{\overline{ð}}^{*},\nabla {\mathsf{\Gamma }}^{*}\left(\varsigma \right)\right)\hfill \\ \hfill =& {\gamma }^2{\beta }_1{\varsigma }^T\varsigma +{\varsigma }^{T}Q\varsigma +\mathcal{W}\left({\overline{\rho }}^{*}\right)-{\gamma }^2{\overline{ð}}^{*T}{\overline{ð}}^{*}\hfill \\ \hfill & +E\left[{\left(\nabla {\mathsf{\Gamma }}^{*}\left(\varsigma \right)\right)}^T\left(\chi \left(g\right)\varsigma +B{\overline{\rho }}^{*}+C{\overline{ð}}^{*}\right)\right].\hfill \\ \hfill =& E[{\left(\nabla {\mathsf{\Gamma }}^{*}\left(\varsigma \right)\right)}^T\chi \left(g\right)\varsigma -{\kappa }_2{\left(\nabla {\mathsf{\Gamma }}^{*}\left(\varsigma \right)\right)}^{T}Btanh\left({\displaystyle \frac{1}{2{\kappa }_2}}{R}^{-1}{B}^T\nabla {\mathsf{\Gamma }}^{*}\left({\overline{\varsigma }}_j\right)\right)\hfill \\ \hfill & +{\left(\nabla {\mathsf{\Gamma }}^{*}\left(\varsigma \right)\right)}^{T}B{\kappa }_1+{\displaystyle \frac{1}{2{\gamma }^2}}{\left(\nabla {\mathsf{\Gamma }}^{*}\left(\varsigma \right)\right)}^{T}C{C}^T\nabla {\mathsf{\Gamma }}^{*}\left({\overline{\varsigma }}_j\right)\hfill \\ \hfill & -{\displaystyle \frac{1}{4{\gamma }^2}}{\left(\nabla {\mathsf{\Gamma }}^{*}\left({\overline{\varsigma }}_j\right)\right)}^{T}C{C}^T\nabla {\mathsf{\Gamma }}^{*}\left({\overline{\varsigma }}_j\right)]+{\gamma }^2{\beta }_1{\varsigma }^T\varsigma +{\varsigma }^{T}Q\varsigma +\mathcal{W}\left({\overline{\rho }}^{*}\right).\hfill \end{array}$$

(46)

Assumption 4.

The control pairs are Lipschitz-continuous, satisfying

$$\begin{array}{c}\hfill \parallel {\rho }^{*}-{\overline{\rho }}^{*}\parallel \le l_{\rho }\parallel E\left[e_j\left(t\right)\right]\parallel ,\end{array}$$

(47)

$$\begin{array}{c}\hfill \parallel {ð}^{*}-{\overline{ð}}^{*}\parallel \le l_{ð}\parallel E\left[e_j\left(t\right)\right]\parallel ,\end{array}$$

(48)

where $l_{\rho }$ and $l_{ð}$ are positive constants, ${\rho }^{*}={\rho }^{*}\left(\varsigma \right)$ and ${ð}^{*}={ð}^{*}\left(\varsigma \right)$.

Lemma 2.

Given that Assumption 4 is valid, the following inequality holds:

$$\begin{array}{cc}\hfill & ∥\mathcal{H}\left(\varsigma ,{\overline{\rho }}^{*},{\overline{ð}}^{*},\nabla {\mathsf{\Gamma }}^{*}\left(\varsigma \right)\right)-\mathcal{H}\left(\varsigma ,{\rho }^{*},{ð}^{*},\nabla {\mathsf{\Gamma }}^{*}\left(\varsigma \right)\right)∥\hfill \\ \hfill & \le m_1+(l_{\rho }^2+{\gamma }^2{l}_{ð}^2){∥\left[E\left(e_j\left(t\right)\right)\right]∥}^2,\hfill \end{array}$$

(49)

where $m_1$ is given in (52).

Proof. 

Subtracting (14) from (43), we have

$$\begin{array}{cc}\hfill & \mathcal{H}\left(\varsigma ,{\overline{\rho }}^{*},{\overline{ð}}^{*},\nabla {\mathsf{\Gamma }}^{*}\left(\varsigma \right)\right)-\mathcal{H}\left(\varsigma ,{\rho }^{*},{ð}^{*},\nabla {\mathsf{\Gamma }}^{*}\left(\varsigma \right)\right)\hfill \\ \hfill =& E\left[{\left(\nabla {\mathsf{\Gamma }}^{*}\left(\varsigma \right)\right)}^T\left(\chi \left(g\right)\varsigma +B{\overline{\rho }}^{*}+C{\overline{ð}}^{*}\right)\right]+{\gamma }^2{\beta }_1{\varsigma }^T\varsigma +r\left(\varsigma ,{\overline{\rho }}^{*},{\overline{ð}}^{*}\right)\hfill \\ \hfill & -E\left[{\left(\nabla {\mathsf{\Gamma }}^{*}\left(\varsigma \right)\right)}^T\left(\chi \left(g\right)\varsigma +B{\rho }^{*}+C{ð}^{*}\right)\right]-{\gamma }^2{\beta }_1{\varsigma }^T\varsigma -r\left(\varsigma ,{\rho }^{*},{ð}^{*}\right)\hfill \\ \hfill =& W\left({\overline{\rho }}^{*}\right)-W\left({\rho }^{*}\right)-{\gamma }^2{\overline{ð}}^{*T}{\overline{ð}}^{*}+{\gamma }^2{ð}^{*T}{ð}^{*}+2{\gamma }^2{ð}^{*T}{\overline{ð}}^{*}-2{\gamma }^2{ð}^{*T}{ð}^{*}\hfill \\ \hfill & +E\left[{\left(\nabla {\mathsf{\Gamma }}^{*}\left(\varsigma \right)\right)}^{T}B\left({\overline{\rho }}^{*}-{\rho }^{*}\right)\right]\hfill \\ \hfill =& W\left({\overline{\rho }}^{*}\right)-W\left({\rho }^{*}\right)-{\gamma }^2{\left({ð}^{*}-{\overline{ð}}^{*}\right)}^T\left({ð}^{*}-{\overline{ð}}^{*}\right)\hfill \\ \hfill & +E\left[{\left(\nabla {\mathsf{\Gamma }}^{*}\left(\varsigma \right)\right)}^{T}B\left({\overline{\rho }}^{*}-{\rho }^{*}\right)\right].\hfill \end{array}$$

(50)

Based on (47), we can get

$$\begin{array}{c}\hfill ∥\mathcal{W}\left({\overline{\rho }}^{*}\right)-\mathcal{W}\left({\rho }^{*}\right)∥=M_{\mathcal{W}}∥{\overline{\rho }}^{*}-{\rho }^{*}∥\le M_{\mathcal{W}}{l}_{\rho }\parallel E\left[e_j\left(t\right)\right]\parallel \end{array}$$

(51)

where $M_{\mathcal{W}}=\left|2{\kappa }_2{tanh}^{-T}\left({\displaystyle \frac{{\rho }_0-{\kappa }_1}{{\kappa }_2}}\right)R\right|$ with ${\rho }_0=\left|{\displaystyle \frac{{\overline{\rho }}^{*}+{\rho }^{*}}{2}}\right|$. Using Young’s inequality, we get $∥\mathcal{W}\left({\overline{\rho }}^{*}\right)-\mathcal{W}\left({\rho }^{*}\right)∥\le {\displaystyle \frac{M_{\mathcal{W}}^2}{2}}+{\displaystyle \frac{l_{\rho }^2{\parallel E\left[e_j\left(t\right)\right]\parallel }^2}{2}}$.

Based on (50), we have

$$\begin{array}{cc}\hfill & ∥\mathcal{H}\left(\varsigma ,{\overline{\rho }}^{*},{\overline{ð}}^{*},\nabla {\mathsf{\Gamma }}^{*}\left(\varsigma \right)\right)-\mathcal{H}(\varsigma ,{\rho }^{*},{ð}^{*},\nabla {\mathsf{\Gamma }}^{*}\left(\varsigma \right)∥\hfill \\ \hfill \le & {\displaystyle \frac{{∥E\left[\nabla {\mathsf{\Gamma }}^{*}\left(\varsigma \right)B\right]∥}^2+l_{\rho }^2{∥[E\left[e_j\left(t\right)\right]∥}^2}{2}}\hfill \\ \hfill & +{\displaystyle \frac{M_{\mathcal{W}}^2}{2}}+{\displaystyle \frac{l_{\rho }^2{\parallel E\left[e_j\left(t\right)\right]\parallel }^2}{2}}+{\gamma }^2{l}_{ð}^2{∥\left[E\left(e_j\left(t\right)\right)\right]∥}^2\hfill \\ \hfill =& m_1+(l_{\rho }^2+{\gamma }^2{l}_{ð}^2){∥\left[E\left(e_j\left(t\right)\right)\right]∥}^2.\hfill \end{array}$$

(52)

where $m_1={\displaystyle \frac{{∥E\left[\nabla {\mathsf{\Gamma }}^{*}\left(\varsigma \right)B\right]∥}^2}{2}}+{\displaystyle \frac{M_{\mathcal{W}}^2}{2}}$. □

Theorem 3.

Assuming that ${\mathsf{\Gamma }}^{*}\left(\varsigma \left(t\right)\right)>0$ is a continuous function satisfying the improved HJI Equation (14) and the OC pairs are given as (44) and (45), then system (1) is mean asymptotically stable if the following condition holds:

$$\begin{array}{c}\hfill \parallel E\left[e_j\left(t\right)\right]{\parallel }^2\le {\displaystyle \frac{\beta {\tilde{\sigma }}_a-{\alpha }^2{\lambda }_{min}\left(Q\right){\parallel \varsigma \parallel }^2-m_1}{l_{\rho }^2+2{\gamma }^2{l}_{ð}^2}}=e_T,\end{array}$$

(53)

where α is the designed parameter, $0<\alpha <1$, $\beta >0$, and $e_T$ is the trigger threshold. $m_1$ is given in (52). The internal dynamic signal is

$$\begin{array}{c}\hfill {\dot{\tilde{\sigma }}}_a=-\beta {\tilde{\sigma }}_a+{\lambda }_{min}\left(Q\right){\parallel \varsigma \parallel }^2.\end{array}$$

(54)

Proof. 

The Lyapunov function is $L=l_1+l_2=\mathsf{\Gamma }\left(\varsigma \right)+{\tilde{\sigma }}_a$, where $l_1=\mathsf{\Gamma }\left(\varsigma \right)$ and $l_2={\tilde{\sigma }}_a$.

In light of (43), the following holds:

$$\begin{array}{cc}\hfill & E\left[{\left(\nabla {\mathsf{\Gamma }}^{*}\left(\varsigma \right)\right)}^T\left(\chi \left(g\right)\varsigma +B{\overline{\rho }}^{*}+C{\overline{ð}}^{*}\right)\right]\hfill \\ \hfill =& -{\varsigma }^T{Q}_1\varsigma -\mathcal{W}\left({\overline{\rho }}^{*}\right)+{\gamma }^2{\overline{ð}}^{*T}{\overline{ð}}^{*}\hfill \\ \hfill & +\mathcal{H}\left(\varsigma ,{\overline{\rho }}^{*},{\overline{ð}}^{*},\nabla {\mathsf{\Gamma }}^{*}\left(\varsigma \right)\right).\hfill \end{array}$$

(55)

By substituting ${\overline{\rho }}^{*}$ from (44) and ${\overline{ð}}^{*}$ from (45) into (1), and relying on (55) and Lemma 2, one obtains

$$\begin{array}{cc}\hfill & E\left[{\dot{\mathsf{\Gamma }}}^{*}\left(\varsigma \left(t\right)\right)\right]\hfill \\ \hfill =& E\left[{\left(\nabla {\mathsf{\Gamma }}^{*}\left(\varsigma \right)\right)}^T\left(\chi \left(g\right)\varsigma +B{\overline{\rho }}^{*}+C{\overline{ð}}^{*}\right)+{\left(\nabla {\mathsf{\Gamma }}^{*}\left(\varsigma \right)\right)}^{T}C\left(d\left(\varsigma \right)-{\overline{ð}}^{*}\right)\right]\hfill \\ \hfill =& -{\varsigma }^T{Q}_1\varsigma -\mathcal{W}\left({\overline{\rho }}^{*}\right)+{\gamma }^2{\overline{ð}}^{*T}{\overline{ð}}^{*}+E\left[2{\gamma }^2{ð}^{*T}\left(d\left(\varsigma \right)-{\overline{ð}}^{*}\right)\right]\hfill \\ \hfill & +\mathcal{H}\left(\varsigma ,{\overline{\rho }}^{*},{\overline{ð}}^{*},\nabla {\mathsf{\Gamma }}^{*}\left(\varsigma \right)\right)\hfill \\ \hfill \le & E\left[{\gamma }^2{\left({ð}^{*}-{\overline{ð}}^{*}\right)}^T\left({ð}^{*}\left(\varsigma \right)-{\overline{ð}}^{*}\right)-{\varsigma }^{T}Q\varsigma +m_1+(l_{\rho }^2+{\gamma }^2{l}_{ð}^2){∥E\left[e_j\left(t\right)\right]∥}^2\right]\hfill \\ \hfill \le & E[-{\alpha }^2{\lambda }_{min}\left(Q\right){\parallel \varsigma \parallel }^2+{\gamma }^2{l}_{ð}^2{∥E\left[e_j\left(t\right)\right]∥}^2\hfill \\ \hfill & +m_1+(l_{\rho }^2+{\gamma }^2{l}_{ð}^2){∥E\left[e_j\left(t\right)\right]∥}^2-(1-{\alpha }^2){\lambda }_{min}\left(Q\right){\parallel \varsigma \parallel }^2],\hfill \end{array}$$

(56)

where ${\lambda }_{min}\left(Q\right)$ denotes the smallest eigenvalue of Q.

According to (54), we obtain

$$\begin{array}{c}\hfill {\dot{l}}_2=-\beta {\tilde{\sigma }}_a+{\lambda }_{min}\left(Q\right){\parallel \varsigma \parallel }^2,\end{array}$$

(57)

Taking (56) and (57) into account together, if the condition (53) holds, we derive $E\left[L\right]\le -{\alpha }^2{\lambda }_{min}\left(Q\right){\parallel \varsigma \parallel }^2<0$, for any $\varsigma =0$. According to [36] (Lemma 1) and Assumption 3, the system (1) achieves mean asymptotic stability. □

Theorem 4.

Consider system (2); when adopting the optimal ETC policy ${\rho }^{*}\left({\overline{\varsigma }}_j\right)$ from (44) and employing the OC signal ${\rho }^{*}={\overline{\rho }}^{*}$, the following result is obtained:

$$\begin{array}{c}\hfill \overline{\Theta }\left(\varsigma \left(0\right)\right),{\rho }^{*})\le {\Theta }^{*}\left(\varsigma \left(0\right),{\rho }^{*},{ð}^{*}\right).\end{array}$$

(58)

Proof. 

With respect to any admissible control function $\rho$, by referring to (4), (6), and (7) and calculating the system dynamics in (1), one obtains

$$\begin{array}{ccc}\hfill \overline{\Theta }(\varsigma \left(0\right),\rho )& =& E\left[{\int }_0^{\infty }\left({\varsigma }^{T}Q\varsigma +\mathcal{W}\left(\rho \right)+{\dot{\mathsf{\Gamma }}}^{*}\left(\varsigma \right)\right)d\varrho \right]+{\Theta }^{*}\left(\varsigma \left(0\right)\right)\hfill \\ \hfill & =& E[{\int }_0^{\infty }\left({\left(\nabla {\mathsf{\Gamma }}^{*}\left(\varsigma \right)\right)}^T\left(\chi \left(g\right)\varsigma +B\rho +Cd\right)+{\varsigma }^{T}Q\varsigma \right.\hfill \\ \hfill & & +\mathcal{W}\left(\rho \right)\left.\phantom{{\left(\nabla {\mathsf{\Gamma }}^{*}\left(\varsigma \right)\right)}^T}\right)d\varrho ]+{\Theta }^{*}\left(\varsigma \left(0\right)\right).\hfill \end{array}$$

(59)

On the basis of (8), one obtains

$$\begin{array}{cc}\hfill & E\left[{\left(\nabla {\mathsf{\Gamma }}^{*}\left(\varsigma \right)\right)}^T\left(\chi \left(g\right)\varsigma \right)\right]\hfill \\ \hfill =& E\left[-{\left(\nabla {\mathsf{\Gamma }}^{*}\left(\varsigma \right)\right)}^{T}B{\rho }^{*}\left(\varsigma \right)-{\gamma }^2{ð}^{*T}{ð}^{*}-{\gamma }^2{\beta }_1{\varsigma }^T\varsigma \right.\hfill \\ \hfill & \left.-{\varsigma }^{T}Q\varsigma -\mathcal{W}\left({\rho }^{*}\right)\right].\hfill \end{array}$$

(60)

Based on (60), we have

$$\begin{array}{cc}\hfill E& \left[{\int }_0^{\infty }\left({\left(\nabla {\mathsf{\Gamma }}^{*}\left(\varsigma \right)\right)}^T\left(\chi \left(g\right)\varsigma +B\rho +Cd\right)\right.\right.\hfill \\ \hfill & \left.\left.+{\varsigma }^{T}Q\varsigma +\mathcal{W}\left(\rho \right)\right)d\varrho \right]\hfill \\ \hfill =& E\left[{\left(\nabla {\mathsf{\Gamma }}^{*}\left(\varsigma \right)\right)}^{T}B\left(\rho -{\rho }^{*}\right)-{\gamma }^2{ð}^{*T}{ð}^{*}\right.\hfill \\ \hfill & \left.-{\gamma }^2{\beta }_1{\varsigma }^T\varsigma +\mathcal{W}\left(\rho \right)-\mathcal{W}\left({\rho }^{*}\right)+2{\gamma }^2{ð}^{*T}d\right].\hfill \end{array}$$

(61)

According to (61), Assumption 2, the Cauchy–Schwarz inequality, and $2{\gamma }^2{ð}^{*T}d\le {\gamma }^2{ð}^{*T}{ð}^{*}+{\gamma }^2{d}^{T}d$, we obtain

$$\begin{array}{cc}\hfill & E\left[{\int }_0^{\infty }\left(\nabla {\mathsf{\Gamma }}^{*T}\left(\varsigma \right)\left(\chi \left(g\right)\varsigma +B\rho +Cd\right)+{\varsigma }^{T}Q\varsigma +\mathcal{W}\left(\rho \right)\right)d\varrho \right]\hfill \\ \hfill \le & E\left[{\left(\nabla {\mathsf{\Gamma }}^{*}\left(\varsigma \right)\right)}^{T}B\left(\rho -{\rho }^{*}\right)+\mathcal{W}\left(\rho \right)-\mathcal{W}\left({\rho }^{*}\right)\right].\hfill \end{array}$$

(62)

Applying $\rho ={\overline{\rho }}^{*}$ to (62), one obtains the result (58). □

5.2. NN-Based Control Design

Based on Theorem 4, we have $\overline{\Theta }(\varsigma \left(0\right),{\rho }^{*})\le {\Theta }^{*}\left(\varsigma \left(0\right),{\rho }^{*}\left(\varsigma \right),{ð}^{*}\left(\varsigma \right)\right)$, and the GCC algorithm using IRL is used to achieve an approximation of ${\Theta }^{*}\left(\varsigma \left(0\right),{\rho }^{*}\left(\varsigma \right),{ð}^{*}\left(\varsigma \right)\right)$. In the proposed method, ${\mathsf{\Gamma }}^{*}\left(\varsigma \right)$ is approximated by (22). Based on the work in [47], the optimal GCC pairs are given as

$$\begin{array}{cc}\hfill {\rho }^{*}\left(\varsigma \right)& =-{\kappa }_{2}tanh\left({\mathit{W}}_{\rho }^T{\phi }_{\rho }\left({\overline{\varsigma }}_j\right)+{\epsilon }_{e,\rho }({\overline{\varsigma }}_j,e_j)\right)+{\kappa }_1\forall t\in [s_j,s_{j+1}),\hfill \end{array}$$

(63)

$$\begin{array}{cc}\hfill {ð}^{*}\left(\varsigma \right)& ={\mathit{W}}_{ð}^T{\phi }_{ð}\left({\overline{\varsigma }}_j\right)+{\epsilon }_{e,ð}({\overline{\varsigma }}_j,e_j)\forall t\in [s_j,s_{j+1}),\hfill \end{array}$$

(64)

where ${\epsilon }_{e,\rho }={\mathit{W}}_{\rho }^T\left[{\phi }_{\rho }({\overline{\varsigma }}_j+e_j)-{\phi }_{\rho }\left({\overline{\varsigma }}_j\right)\right]+{\epsilon }_{\rho }({\overline{\varsigma }}_j+e_j)$ and ${\epsilon }_{e,ð}={\mathit{W}}_{ð}^T[{\phi }_{ð}({\overline{\varsigma }}_j+e_j)-{\phi }_{ð}\left({\overline{\varsigma }}_j\right)]+{\epsilon }_{ð}({\overline{\varsigma }}_j+e_j)$ denote the event-sampled approximation errors.

Based on (14), (63) and (64), the HJI equation takes the form

$$\begin{array}{cc}\hfill & E\left[({\mathit{W}}_c^T\nabla {\phi }_c\left(\varsigma \right))\chi \left(g\right)\varsigma +{\mathit{W}}_c^T\nabla {\phi }_c\left(\varsigma \right)B{\rho }^{*}\right]+{\gamma }^2{\beta }_1{\varsigma }^T\varsigma \hfill \\ \hfill & +{\varsigma }^{T}Q\varsigma +\mathcal{W}\left({\rho }^{*}\right)+{\gamma }^2{\left({\mathit{W}}_{ð}^T{\phi }_{ð}\left({\overline{\varsigma }}_j\right)\right)}^T\left({\mathit{W}}_{ð}^T{\phi }_{ð}\left({\overline{\varsigma }}_j\right)\right)\hfill \\ \hfill & +{\epsilon }_{HJI}\hfill \\ \hfill =& {\varsigma }^T{Q}_1\varsigma +({\mathit{W}}_c^T\nabla {\phi }_c\left(\varsigma \right))\chi \left(g\right)\varsigma +{\kappa }_2^2{\overline{R}}^{T}ln\left(\overline{\mathbf{1}}-{tanh}^2\left(N_1\right)\right)\hfill \\ \hfill & +{\gamma }^2{P}_1^T{P}_1+2{\kappa }_2{N}_1^{T}R{\kappa }_1\hfill \\ \hfill & +{\epsilon }_{HJI1}\hfill \\ \hfill =& 0,\hfill \end{array}$$

(65)

where ${\epsilon }_{HJI}=\nabla {\epsilon }_c^T\chi \left(g\right)\varsigma +\nabla {\epsilon }_c^{T}B{\rho }^{*}+2{\gamma }^2{\mathit{W}}_{ð}^T{\phi }_{ð}\left({\overline{\varsigma }}_j\right){\epsilon }_{e,ð}+{\gamma }^2{\epsilon }_{e,ð}^T{\epsilon }_{e,ð}$. $P_1={\mathit{W}}_{ð}^T{\phi }_{ð}\left({\overline{\varsigma }}_j\right)$, ${\epsilon }_{HJI1}=\nabla {\epsilon }_c^T\chi \left(g\right)\varsigma +{\kappa }_2^2{\overline{R}}^{T}ln\left(\overline{\mathbf{1}}-{tanh}^2(N_1+{\epsilon }_{e,\rho })\right)-{\kappa }_2^2{\overline{R}}^{T}ln\left(\overline{\mathbf{1}}-{tanh}^2\left(N_1\right)\right)+{\gamma }^2{\epsilon }_{e,ð}^T{\epsilon }_{e,ð}+2{\gamma }^2{\mathit{W}}_{ð}^T{\phi }_{ð}{\epsilon }_{e,ð}+2{\kappa }_2{\epsilon }_{e,\rho }R{\kappa }_1$ and $N_1={\mathit{W}}_{\rho }^T{\phi }_{\rho }\left({\overline{\varsigma }}_j\right)$.

Assumption 5.

The actor, critic, and disturbance NNs, the NN weight vectors, activation function, reconstruction errors, and gradient of relevant parameters are bounded, which satisfy $\parallel {\mathit{W}}_c\parallel \le c_1,\parallel {\mathit{W}}_{\rho }\parallel \le c_2,\parallel {\mathit{W}}_{ð}\parallel \le c_3,\parallel {\mathit{W}}_a{\parallel }_F\le c_2^{\prime },{\parallel {\mathit{W}}_{ð}\parallel }_F\le c_3^{\prime }$; $∥{\phi }_{\rho }∥\le {\phi }_{\rho M}$, $\parallel {\phi }_{ð}\parallel \le {\phi }_{ðM}$, $\parallel \nabla {\phi }_c\parallel \le {\phi }_{cM}$, ${\epsilon }_c\left(\varsigma \right)\le {\epsilon }_{cM}$, ${\epsilon }_{\rho }\left(\varsigma \right)\le {\epsilon }_{\rho M}$, ${\epsilon }_{ð}\left(\varsigma \right)\le {\epsilon }_{ðM}$, $∥{\epsilon }_{ca}\left({\overline{\varsigma }}_j\right)∥\le b_{ca}$ and $\nabla {\epsilon }_c\le c_{\rho }$, respectively, where $c_1$, $c_2$, $c_3$, $c_2^{\prime }$, $c_3^{\prime }$, ${\phi }_{\rho M}$, ${\phi }_{ðM}$, ${\phi }_{cM}$, ${\epsilon }_{cM}$, ${\epsilon }_{\rho M}$, ${\epsilon }_{ðM}$, $b_{ca}$ and $c_{\rho }$ are positive constants.

The estimates for $\mathsf{\Gamma }$, $\rho$ and ð are expressed as

$$\begin{array}{cc}\hfill \widehat{\mathsf{\Gamma }}\left(\varsigma \right)& ={\widehat{\mathit{W}}}_c^T{\phi }_c\left(\varsigma \right),\hfill \end{array}$$

(66a)

$$\begin{array}{cc}\hfill \widehat{\rho }\left({\overline{\varsigma }}_j\right)& =-{\kappa }_{2}tanh\left({\widehat{\mathit{W}}}_{\rho }^T{\phi }_{\rho }\left({\overline{\varsigma }}_j\right)\right)+{\kappa }_1,\hfill \end{array}$$

(66b)

$$\begin{array}{cc}\hfill \widehat{ð}\left({\overline{\varsigma }}_j\right)& ={\widehat{\mathit{W}}}_{ð}^T{\phi }_{ð}\left({\overline{\varsigma }}_j\right),\hfill \end{array}$$

(66c)

where ${\widehat{\mathit{W}}}_c$, ${\widehat{\mathit{W}}}_{\rho }$ and ${\widehat{\mathit{W}}}_{ð}$ stand for the estimates of ${\mathit{W}}_c$, ${\mathit{W}}_{\rho }$ and ${\mathit{W}}_{ð}$, respectively.

Using (23) and (31)–(33), the residual error can be given as

$$\begin{array}{cc}\hfill {\breve{e}}_B& =E\left[{\overline{G}}_{{\mathsf{\Gamma }}^{(s+1)}}(\varsigma ,\widehat{\rho },\widehat{ð},g)\right]-{\widehat{\mathit{W}}}_c^T{\phi }_c\left(\varsigma \right)\hfill \\ \hfill & =E\left[{\int }_t^{t+T}\left({\varsigma }^T{Q}_1\varsigma +\mathcal{W}\left(\widehat{\rho }\right)-{\gamma }^2{\widehat{ð}}^T\widehat{ð}\right)d\varrho \right]\hfill \\ \hfill & -{\kappa }_2{\int }_t^{t+T}\left(\left(2e_1^{T}R\right)⨂{\phi }_{\rho }\left({\overline{\varsigma }}_j\right)\right)d\varrho ·\mathrm{vec}\left({\widehat{\mathit{W}}}_{\rho }\right)\hfill \\ \hfill & -{\int }_t^{t+T}\left(\left(2{\gamma }^2{e}_2^T\right)⨂{\phi }_{ð}\left({\overline{\varsigma }}_j\right)\right)d\varrho ·\mathrm{vec}\left({\widehat{\mathit{W}}}_{ð}\right)\hfill \\ \hfill & +E\left[{\widehat{\mathit{W}}}_c^T{\phi }_c\left(\varsigma (t+T)\right)\right]-{\widehat{\mathit{W}}}_c^T{\phi }_c\left(\varsigma \right).\hfill \end{array}$$

(67)

where $\widehat{\rho }=\widehat{\rho }\left({\overline{\varsigma }}_j\right)$ and $\widehat{ð}=\widehat{ð}\left({\overline{\varsigma }}_j\right)$. Design a new augmented weight vector as $\widehat{\mathit{W}}={\left[{\widehat{\mathit{W}}}_c,\mathrm{vec}\left({\widehat{\mathit{W}}}_{\rho }\right),\mathrm{vec}\left({\widehat{\mathit{W}}}_{ð}\right)\right]}^T$ and the target weight vector $\mathit{W}={\left[{\mathit{W}}_c,\mathrm{vec}\left({\mathit{W}}_{\rho }\right),\mathrm{vec}\left({\mathit{W}}_{ð}\right)\right]}^T$. Denote

$$\begin{array}{cc}\hfill S_1& =E\left[{\int }_t^{t+T}\left({\varsigma }^T{Q}_1\varsigma +\mathcal{W}\left(\widehat{\rho }\right)-{\gamma }^2{\widehat{ð}}^T\widehat{ð}\right)d\varrho \right],\hfill \\ \hfill S_2& =E\left[{\phi }_c\left(\varsigma (t+T)\right)-{\phi }_c\left(\varsigma \left(t\right)\right)\right],\hfill \\ \hfill S_3& =-{\kappa }_2{\int }_t^{t+T}\left(\left(2e_1^{T}R\right)⨂{\phi }_{\rho }\left({\overline{\varsigma }}_j\right)\right)d\varrho ,\hfill \\ \hfill S_4& =-{\int }_t^{t+T}\left(\left(2{\gamma }^2{e}_2^T\right)⨂{\phi }_{ð}\left({\overline{\varsigma }}_j\right)\right)d\varrho .\hfill \end{array}$$

(68)

Then, we have

$$\begin{array}{c}\hfill {\breve{e}}_B=E\left[\overline{S}\widehat{\mathit{W}}+S_1\right],\end{array}$$

(69)

with $\overline{S}=[S_2,S_3,S_4]$.

Let ${\xi }_1={\displaystyle \frac{1}{2}}{\breve{e}}_B^T{\breve{e}}_B$, ${\alpha }_1$ denote an adaptive gain parameter; the weight adjustment rule is developed as

$$\begin{array}{c}\hfill \dot{\widehat{\mathit{W}}}=-E\left[{\alpha }_1{\displaystyle \frac{{\overline{S}}^T}{{(\overline{S}{\overline{S}}^T+1)}^2}}{\breve{e}}_B\right],\end{array}$$

(70)

Assumption 6.

${\tilde{\eta }}_1$ is continuously excited within the interval of $\left[t,t+T\right]$, and one obtains

$$\begin{array}{c}\hfill {\gamma }_{1}I\le {\int }_t^{t+T}{\tilde{\eta }}_1{\tilde{\eta }}_1^{T}dt\le {\gamma }_{2}I,\end{array}$$

(71)

where ${\tilde{\eta }}_1=\left({\overline{S}}^T/\left(\overline{S}{\overline{S}}^T+1\right)\right)$, $T>0$, ${\gamma }_1\le {\gamma }_2$, and ${\gamma }_1$ and ${\gamma }_2$ are constants.

Considering $\dot{\varsigma }=\chi \left(g\right)\varsigma +B\widehat{\rho }+C\widehat{ð}$ and $\tilde{\mathit{W}}=\mathit{W}-\widehat{\mathit{W}}$, we define the augmented system state as $\mho ={\left[{\varsigma }^T,{\overline{\varsigma }}_j^T,{\tilde{\mathit{W}}}^T\right]}^T$, we have

$$\begin{array}{c}\hfill \dot{\mho }\left(t\right)=\left[\begin{array}{c}\chi \left(g\right)\varsigma +B\widehat{\rho }+C\widehat{ð}\\ 0\\ E\left[{\alpha }_1{\displaystyle \frac{{\overline{S}}^T}{{(\overline{S}{\overline{S}}^T+1)}^2}}{\breve{e}}_B\right]\end{array}\right],t\in [s_j,s_{j+1})\end{array}$$

(72)

Furthermore, one obtains

$$\begin{array}{c}\hfill \mho \left(t\right)=\mho \left(t^{-}\right)+\left[\begin{array}{c}0\\ \varsigma -{\overline{\varsigma }}_j\\ 0\end{array}\right],t=s_{j+1}\end{array}$$

(73)

Here, $\mho \left(t^{-}\right)={lim}_{\lambda \to 0}\mho (t-\lambda )$, where $\lambda \in (0,s_{j+1}-s_j)$.

Remark 5.

The residual error ${\breve{e}}_B$, which requires minimization in (67), is derived from the expectation of the function $E\left[{\overline{G}}_{{\mathsf{\Gamma }}^{(s+1)}}(\varsigma ,\widehat{\rho },\widehat{ð},g)\right]$. Detailed procedures for calculating this expectation are provided in [40].

5.3. Stability Analysis

Theorem 5.

The ETC policies are given as (66b) and (66c) for the dynamical system (4), and the weight adjustment law $\widehat{\mathit{W}}$ is designed as (70). The system states and NN weight estimation errors are uniformly bounded (UB) in the mean. The triggering condition is designed as

$$\begin{array}{c}\hfill \parallel E\left[e_j\left(t\right)\right]{\parallel }^2\le {\displaystyle \frac{\beta {\tilde{\sigma }}_b-{\varpi }^2{\lambda }_{min}\left(Q_1\right){\parallel \varsigma \parallel }^2-\mathsf{\Psi }\left({\overline{\varsigma }}_j\right)}{l_{\rho ð}}}-{\displaystyle \frac{C_0+{\gamma }^2{∥\widehat{ð}∥}^2}{l_{\rho ð}}}=e_T,\end{array}$$

(74)

where $C_0$ and $l_{\rho ð}$ are defined in (81), $\varpi \in (0,1)$. The internal dynamic signal is given by

$$\begin{array}{c}\hfill {\dot{\tilde{\sigma }}}_b=-\beta {\tilde{\sigma }}_b+{\lambda }_{min}\left(Q_1\right){\parallel \varsigma \parallel }^2.\end{array}$$

(75)

Proof. 

A Lyapunov function is chosen as

$$\begin{array}{c}\hfill {\Lambda }_{\mathsf{\Gamma }}\left(t\right)={\Lambda }_1\left(t\right)+{\Lambda }_2\left(t\right)+{\Lambda }_3\left(t\right)+{\Lambda }_4\left(t\right),\end{array}$$

(76)

with ${\Lambda }_1\left(t\right)=E\left[{\mathsf{\Gamma }}^{*}\left(\varsigma \right)\right]$, ${\Lambda }_2\left(t\right)=E\left[{\mathsf{\Gamma }}^{*}\left({\overline{\varsigma }}_j\right)\right]$, ${\Lambda }_3\left(t\right)=E\left[{\displaystyle \frac{1}{2{\alpha }_1}}{\tilde{\mathit{W}}}^T\tilde{\mathit{W}}\right]$ and ${\Lambda }_4\left(t\right)={\tilde{\sigma }}_b$.

Case 1: When $\forall t\in [s_j,s_{j+1})$,$j\in N$, based on (4), (66b) and (66c), one obtains

$$\begin{array}{ccc}\hfill {\dot{\Lambda }}_1\left(t\right)& =& E\left[{\left(\nabla {\mathsf{\Gamma }}^{*}\left(\varsigma \right)\right)}^T\left(\chi \left(g\right)\varsigma +B\widehat{\rho }+C\widehat{ð}\right)\right],\hfill \\ \hfill {\dot{\Lambda }}_2\left(t\right)& =& 0,\hfill \\ \hfill {\dot{\Lambda }}_3\left(t\right)& =& E\left[{\displaystyle \frac{1}{{\alpha }_1}}{\tilde{\mathit{W}}}^T\dot{\tilde{\mathit{W}}}\right],\hfill \\ \hfill {\dot{\Lambda }}_4\left(t\right)& =& {\dot{\tilde{\sigma }}}_b.\hfill \end{array}$$

Based on (22), we can obtain

$$\begin{array}{c}\hfill \nabla {\mathsf{\Gamma }}^{*}\left({\overline{\varsigma }}_j\right)={\left(\nabla {\phi }_c\left({\overline{\varsigma }}_j\right)\right)}^T{\mathit{W}}_c+\nabla {\epsilon }_c\left({\overline{\varsigma }}_j\right).\end{array}$$

(77)

According to $2a^{T}b\le {∥a∥}^2+{∥b∥}^2$ and Assumption 5, we get

$$\begin{array}{ccc}\hfill {\dot{\Lambda }}_1\left(t\right)& =& E\left[{\left(\nabla {\mathsf{\Gamma }}^{*}\left(\varsigma \right)\right)}^T\left(\chi \left(g\right)\varsigma +B{\rho }^{*}+C{ð}^{*}\right)\right]\hfill \\ \hfill & & +{\left(\nabla {\mathsf{\Gamma }}^{*}\left(\varsigma \right)\right)}^{T}B(\widehat{\rho }-{\rho }^{*})\hfill \\ \hfill & & +{\left(\nabla {\mathsf{\Gamma }}^{*}\left(\varsigma \right)\right)}^{T}C(\widehat{ð}-{ð}^{*})\hfill \\ \hfill & =& E\left[{\gamma }^2{ð}^{*T}{ð}^{*}-{\gamma }^2{\beta }_1{\varsigma }^T\varsigma \right.\hfill \\ \hfill & & -{\varsigma }^{T}Q\varsigma -\mathcal{W}\left({\rho }^{*}\right)+{\left(\nabla {\mathsf{\Gamma }}^{*}\left(\varsigma \right)\right)}^{T}B(\widehat{\rho }-{\rho }^{*})\hfill \\ \hfill & & \left.+2{\gamma }^2{ð}^{*T}(\widehat{ð}-{ð}^{*})\right]\hfill \\ \hfill & \le & E\left[{\gamma }^2{\widehat{ð}}^T\widehat{ð}-{\varsigma }^T{Q}_1\varsigma -\mathcal{W}\left({\rho }^{*}\right)\right.\hfill \\ \hfill & & \left.+{\displaystyle \frac{1}{2}}{∥B(\widehat{\rho }-{\rho }^{*})∥}^2-{\gamma }^2{∥{ð}^{*}-\widehat{ð}∥}^2+\left(c_{\rho }^2+{\phi }_{cM}^2{c}_1^2\right)\right]\hfill \\ \hfill & \le & E\left[{\gamma }^2{\widehat{ð}}^T\widehat{ð}-{\varsigma }^T{Q}_1\varsigma -\mathcal{W}\left({\rho }^{*}\right)\right.\hfill \\ \hfill & & \left.+{\displaystyle \frac{1}{2}}{∥B(\widehat{\rho }-{\rho }^{*})∥}^2+\left(c_{\rho }^2+{\phi }_{cM}^2{c}_1^2\right)\right]\hfill \end{array}$$

(78)

Substituting (77) into (10), one obtains

$$\begin{array}{cc}\hfill {\rho }^{*}\left({\overline{\varsigma }}_j\right)& =-{\kappa }_{2}tanh\left({\mathcal{N}}^{*}\right)+{\epsilon }_{ca}\left({\overline{\varsigma }}_j\right)+{\kappa }_1,t\in [s_l,s_{l+1}))\hfill \end{array}$$

(79a)

$$\begin{array}{cc}\hfill \widehat{\rho }\left({\overline{\varsigma }}_j\right)& =-{\kappa }_{2}tanh\left({\displaystyle \frac{1}{2{\kappa }_2}}{B}^T{\left(\nabla {\phi }_c\left({\overline{\varsigma }}_j\right)\right)}^T{\widehat{\mathit{W}}}_c\right)+{\kappa }_1,\hfill \end{array}$$

(79b)

where ${\mathcal{N}}^{*}=(1/\left(2{\kappa }_2\right))R^{-1}{B}^T{\left(\nabla {\phi }_c\left({\overline{\varsigma }}_j\right)\right)}^T{\mathit{W}}_c$ and ${\epsilon }_{ca}\left({\overline{\varsigma }}_j\right)=-(1/2)(I_q-\mathfrak{D}\left(ϵ\left({\overline{\varsigma }}_j\right)\right))R^{-1}{B}^T\left({\overline{\varsigma }}_j\right)\nabla {\epsilon }_c\left({\overline{\varsigma }}_j\right)$ with $\mathfrak{D}\left(ϵ\left({\overline{\varsigma }}_j\right)\right)=\mathrm{diag}\left\{{tanh}^2\left({ϵ}_i\left({\overline{\varsigma }}_j\right)\right)\right\}$, $i=1,2,\dots ,q$. $ϵ\left({\overline{\varsigma }}_j\right)=\left[{ϵ}_1\left({\overline{\varsigma }}_j\right),{ϵ}_2\left({\overline{\varsigma }}_j\right),\right.\dots ,{\left.{ϵ}_q\left({\overline{\varsigma }}_j\right)\right]}^T\in R^q$, $ϵ\left({\overline{\varsigma }}_j\right)$ is selected between ${\mathcal{N}}^{*}$ and $N^{*}$ and $\widehat{\rho }\left({\overline{\varsigma }}_j\right)$ is an approximate value of ${\rho }^{*}\left({\overline{\varsigma }}_j\right)$.

According to ${\parallel a+b\parallel }^2\le {2\parallel a\parallel }^2+2{\parallel b\parallel }^2$, (79a) and (79b), we get

$$\begin{array}{cc}\hfill & \parallel \widehat{\rho }-{\overline{\rho }}^{*}+{\overline{\rho }}^{*}-{\rho }^{*}{\parallel }^2\hfill \\ \hfill \le & 2\parallel \widehat{\rho }-{\overline{\rho }}^{*}{\parallel }^2+2{\parallel {\overline{\rho }}^{*}-{\rho }^{*}\parallel }^2\hfill \\ \hfill \le & 2\parallel {\kappa }_{2}tanh\left({\displaystyle \frac{1}{2{\kappa }_2}}{R}^{-1}{B}^T{\left(\nabla {\phi }_c\left({\overline{\varsigma }}_j\right)\right)}^T{\mathit{W}}_c\right)\hfill \\ \hfill & -{\kappa }_{2}tanh\left({\displaystyle \frac{1}{2{\kappa }_2}}{R}^{-1}{B}^T{\left(\nabla {\phi }_c\left({\overline{\varsigma }}_j\right)\right)}^T{\widehat{\mathit{W}}}_c\right)-{\epsilon }_{ca}\left({\overline{\varsigma }}_j\right){\parallel }^2+2{\parallel l_{\rho }E\left[e_j\left(t\right)\right]\parallel }^2\hfill \\ \hfill \le & 4\parallel {\kappa }_{2}tanh\left({\displaystyle \frac{1}{2{\kappa }_2}}{R}^{-1}{B}^T{\left({\phi }_c\left({\overline{\varsigma }}_j\right)\right)}^T{\mathit{W}}_c\right)\hfill \\ \hfill & -{\kappa }_{2}tanh\left({\displaystyle \frac{1}{2{\kappa }_2}}{R}^{-1}{B}^T{\left({\phi }_c\left({\overline{\varsigma }}_j\right)\right)}^T{\widehat{\mathit{W}}}_c\right){\parallel }^2+4{\parallel {\epsilon }_{ca}\left({\overline{\varsigma }}_j\right)\parallel }^2\hfill \\ \hfill & +2\parallel l_{\rho }E\left[e_j\left(t\right)\right]{\parallel }^2\hfill \\ \hfill \le & 8\parallel {\kappa }_{2}tanh\left({\displaystyle \frac{1}{2{\kappa }_2}}{R}^{-1}{B}^T{\left({\phi }_c\left({\overline{\varsigma }}_j\right)\right)}^T{\mathit{W}}_c\right){\parallel }^2\hfill \\ \hfill & +8\parallel {\kappa }_{2}tanh\left({\displaystyle \frac{1}{2{\kappa }_2}}{R}^{-1}{B}^T{\left({\phi }_c\left({\overline{\varsigma }}_j\right)\right)}^T{\widehat{\mathit{W}}}_c\right){\parallel }^2+4{\parallel {\epsilon }_{ca}\left({\overline{\varsigma }}_j\right)\parallel }^2\hfill \\ \hfill & +2\parallel l_{\rho }E\left[e_j\left(t\right)\right]{\parallel }^2\hfill \\ \hfill \le & 16{\kappa }_2^2+4b_{ca}^2+2l_{\rho }^2{∥E\left[e_j\left(t\right)\right]∥}^2.\hfill \end{array}$$

(80)

As proved in [48], $\mathcal{W}\left({\rho }^{*}\right)>0$, and one has

$$\begin{array}{cc}\hfill {\dot{\Lambda }}_1\left(t\right)& \le E\left[{\gamma }^2{\widehat{ð}}^T\widehat{ð}-{\varsigma }^T{Q}_1\varsigma +\left(c_{\rho }^2+{\phi }_{cM}^2{c}_1^2\right)\right.\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}{∥B∥}^2\left(16{\kappa }_2^2+4b_{ca}^2+2l_{\rho }^{2}E{\left[e_j\left(t\right)\right]}^2\right)]\hfill \\ \hfill & \le E\left[{\gamma }^2{\widehat{ð}}^T\widehat{ð}-{\varsigma }^T{Q}_1\varsigma +l_{\rho ð}{\parallel E\left[e_j\left(t\right)\right]\parallel }^2+C_0\right]\hfill \end{array}$$

(81)

where $C_0=\left(c_{\rho }^2+{\phi }_{cM}^2{c}_1^2\right)+{\displaystyle \frac{1}{2}}{∥B∥}^2\left(16{\kappa }_2^2+4b_{ca}^2\right)$ and $l_{\rho ð}={∥B∥}^2{l}_{\rho }^2$.

According to (12), we get

$$\begin{array}{ccc}\hfill \mathcal{W}\left(\widehat{\rho }\right)& =& 2{\kappa }_2{\int }_{{\kappa }_1}^{-{\kappa }_{2}tanh\left({\widehat{\mathit{W}}}_{\rho }^T{\phi }_{\rho }\left({\overline{\varsigma }}_j\right)\right)+{\kappa }_1}{\tilde{\rho }}_a^{-T}\left({\kappa }_2^{-1}(\vartheta -{\kappa }_1)\right)R\mathrm{d}\vartheta \hfill \\ \hfill & =& 2{\kappa }_2{\int }_{{\kappa }_1}^{-{\kappa }_{2}tanh\left({\widehat{\mathit{W}}}_{\rho }^T{\phi }_{\rho }\left({\overline{\varsigma }}_j\right)\right)+{\kappa }_1}{\tilde{\rho }}_a^{-T}\left({\kappa }_2^{-1}(\vartheta -{\kappa }_1)\right)R\mathrm{d}\vartheta \hfill \\ \hfill & =& 2{\kappa }_2^2{\int }_0^{-tanh\left({\widehat{\mathit{W}}}_{\rho }^T{\phi }_{\rho }\left({\overline{\varsigma }}_j\right)\right)}{\tilde{\rho }}_a^{-T}\left({\kappa }_2^{-1}(\vartheta -{\kappa }_1)\right)R\mathrm{d}\left({\kappa }_2^{-1}(\vartheta -{\kappa }_1)\right)\hfill \\ \hfill & =& 2{\kappa }_2^2{\phi }_{\rho }{\left({\overline{\varsigma }}_j\right)}^T{\widehat{\mathit{W}}}_{\rho }Rtanh\left({\widehat{\mathit{W}}}_{\rho }^T{\phi }_{\rho }\left({\overline{\varsigma }}_j\right)\right)+{\kappa }_2^2{\overline{R}}^{T}ln\left(\overline{\mathbf{1}}-{tanh}^2\left({\widehat{\mathit{W}}}_{\rho }^T{\phi }_{\rho }\left({\overline{\varsigma }}_j\right)\right)\right).\hfill \end{array}$$

(82)

By calculating Formula (69), the residual error ${\breve{e}}_B$ is re-expressed as follows:

$$\begin{array}{ccc}\hfill {\breve{e}}_B& =& E\left[\overline{S}(W-\tilde{W})+S_1\right]\hfill \\ \hfill & =& E\left[-\overline{S}\tilde{W}+\overline{S}W+{\int }_t^{t+T}\left({\varsigma }^T{Q}_1\varsigma +\mathcal{W}\left(\widehat{\rho }\right)-{\widehat{U}}_2\right)d\varrho \right],\hfill \end{array}$$

(83)

$$\begin{array}{cc}\hfill \mathcal{W}\left(\widehat{\rho }\right)& =2{\kappa }_2^2{\widehat{N}}^{T}Rtanh\left(\widehat{N}\right)+{\kappa }_2^2{\overline{R}}^{T}ln\left(\overline{\mathbf{1}}-{tanh}^2\left(\widehat{N}\right)\right),\hfill \end{array}$$

(84)

$$\begin{array}{cc}\hfill \widehat{N}& ={\widehat{\mathit{W}}}_{\rho }^T{\phi }_{\rho }\left({\overline{\varsigma }}_j\right),\hfill \end{array}$$

(85)

$$\begin{array}{cc}\hfill {\widehat{U}}_2& ={\gamma }^2{\widehat{P}}^T\widehat{P},\hfill \end{array}$$

(86)

$$\begin{array}{cc}\hfill \widehat{P}& ={\widehat{\mathit{W}}}_{ð}^T{\phi }_{ð}\left({\overline{\varsigma }}_j\right).\hfill \end{array}$$

(87)

Based on (65), one obtains

$$\begin{array}{c}\hfill {\breve{e}}_B=E\left[{\int }_t^{t+T}\left(-\mathcal{W}\left(\overline{\rho }\right)+\mathcal{W}\left(\widehat{\rho }\right)+{\overline{U}}_2-{\widehat{U}}_2-({\mathit{W}}_c^T\nabla {\phi }_c\left(\varsigma \right))\chi \left(g\right)\varsigma -{\epsilon }_{HJI1}+Z_0\right)d\varrho -\overline{S}\tilde{\mathit{W}}+\overline{S}\mathit{W}\right],\end{array}$$

(88)

where

$$\begin{array}{cc}\hfill Z_0& =-2{\kappa }_2{N}_1^{T}R{\kappa }_1-2{\gamma }^2{P}_1^T{P}_1+2{\kappa }_2^2{N}_1^{T}Rtanh\left(N_1\right),\hfill \\ \hfill \mathcal{W}\left(\overline{\rho }\right)& =2{\kappa }_2^2{N}_1^{T}Rtanh\left(N_1\right)+{\kappa }_2^2{\overline{R}}^{T}ln\left(\overline{\mathbf{1}}-{tanh}^2\left(N_1\right)\right),\hfill \\ \hfill {\overline{U}}_2& ={\gamma }^2{P}_1^T{P}_1.\hfill \end{array}$$

(89)

where ${\epsilon }_{HJI1}\le {\epsilon }_h$, with ${\epsilon }_h$ being a positive number.

Denote ${\overline{\mathcal{F}}}_1={\int }_t^{t+T}({\overline{U}}_2-\mathcal{W}\left(\overline{\rho }\right)-{\epsilon }_{HJI1}+Z_0)d\varrho$, ${\overline{\mathcal{F}}}_2={\int }_t^{t+T}(\mathcal{W}\left(\widehat{\rho }\right)-{\widehat{U}}_2)d\varrho$ and ${\overline{\mathcal{F}}}_3={\int }_t^{t+T}(-{\mathit{W}}_c^T\nabla {\phi }_c\left(\varsigma \right)\chi \left(g\right)\varsigma )d\varrho$, where T is a small positive number. Then, we have ${\overline{\mathcal{F}}}_1=T({\overline{U}}_2-\mathcal{W}\left(\overline{\rho }\right)-{\epsilon }_{HJI1}-Z_0)$, ${\overline{\mathcal{F}}}_2=T(\mathcal{W}\left(\widehat{\rho }\right)-{\widehat{U}}_2)$ and ${\overline{\mathcal{F}}}_3=T(-{\mathit{W}}_c^T\nabla {\phi }_c\chi \left(g\right)\varsigma )$. Based on Assumption 5, we have $∥{\overline{\mathcal{F}}}_1∥\le d_1$ with $d_1>0$.

Then, we have

$$\begin{array}{c}\hfill {\breve{e}}_B=E\left[\breve{\mathcal{F}}-\overline{S}\tilde{\mathit{W}}+\overline{S}\mathit{W}\right].\end{array}$$

(90)

where $\breve{\mathcal{F}}={\overline{\mathcal{F}}}_1+{\overline{\mathcal{F}}}_2+{\overline{\mathcal{F}}}_3$.

Based on (70) and (83), we have

$$\begin{array}{cc}\hfill E\left[{\displaystyle \frac{1}{{\alpha }_1}}{\tilde{W}}^T\dot{\tilde{W}}\right]& =E\left[{\displaystyle \frac{{\tilde{W}}^T{\overline{S}}^T}{{(\overline{S}{\overline{S}}^T+1)}^2}}\left(\breve{\mathcal{F}}-\overline{S}\tilde{W}+\overline{S}W\right)\right]\hfill \\ \hfill & \le E\left[-{\tilde{W}}^T{\tilde{\eta }}_1{\tilde{\eta }}_1^T\tilde{W}+{\tilde{W}}^T{\tilde{\eta }}_1{\tilde{\eta }}_1^{T}W+{\displaystyle \frac{1}{2}}{d}_1\parallel \tilde{W}\parallel +{\displaystyle \frac{1}{4}}{\parallel \tilde{W}\parallel }^2\right.\hfill \\ \hfill & \left.+\mathsf{\Psi }\left({\overline{\varsigma }}_j\right)+{\displaystyle \frac{1}{4}}\parallel \tilde{W}{\parallel }^2+{\displaystyle \frac{1}{4}}{\lambda }_m^2{\parallel \varsigma \parallel }^2\right]\hfill \\ \hfill & \le E\left[-\left({\displaystyle \frac{{\gamma }_1}{T}}-{\displaystyle \frac{1}{2}}\right)\parallel \tilde{W}{\parallel }^2+\mathsf{\Psi }\left({\overline{\varsigma }}_j\right)+{\displaystyle \frac{1}{4}}{\lambda }_m^2{\parallel \varsigma \parallel }^2\right.\hfill \\ \hfill & \left.+\left({\displaystyle \frac{{\gamma }_2}{T}}\sqrt{c_1^2+c_2^{\prime 2}+c_3^{\prime 2}}+{\displaystyle \frac{d_1}{2}}\right)\parallel \tilde{W}\parallel \right]\hfill \end{array}$$

(91)

where ${\tilde{\eta }}_1=\left({\overline{S}}^T/\left(\overline{S}{\overline{S}}^T+1\right)\right)$, $\mathsf{\Psi }\left({\overline{\varsigma }}_j\right)={\displaystyle \frac{T^2}{4}}{\left(\mathcal{W}\left(\widehat{\rho }\right)--{\gamma }^2{\widehat{ð}}^T\left({\overline{\varsigma }}_j\right)\widehat{ð}\left({\overline{\varsigma }}_j\right)\right)}^2$ and ${\lambda }_m=T{c}_1{\phi }_{cM}{b}_a$.

Using Equations (81) and (91), ${\dot{\Lambda }}_{\mathsf{\Gamma }}\left(t\right)$ becomes

$$\begin{array}{ccc}\hfill {\dot{\Lambda }}_{\mathsf{\Gamma }}\left(t\right)& \le & E\left[{\gamma }^2{\widehat{ð}}^T\widehat{ð}-{\varsigma }^T{Q}_1\varsigma +l_{\rho ð}{\parallel E\left[e_j\left(t\right)\right]\parallel }^2+C_0\right.\hfill \\ \hfill & & -\left({\displaystyle \frac{{\gamma }_1}{T}}-{\displaystyle \frac{1}{2}}\right)\parallel \tilde{W}{\parallel }^2+\mathsf{\Psi }\left({\overline{\varsigma }}_j\right)+{\displaystyle \frac{1}{4}}{\lambda }_m^2{\parallel \varsigma \parallel }^2\hfill \\ \hfill & & \left.+\left({\displaystyle \frac{{\gamma }_2}{T}}\sqrt{c_1^2+c_2^{\prime 2}+c_3^{\prime 2}}+{\displaystyle \frac{d_1}{2}}\right)\parallel \tilde{W}\parallel +{\dot{\tilde{\sigma }}}_b\right],\hfill \end{array}$$

(92)

If the triggering conditions (74) and (75) hold, one obtains

$$\begin{array}{ccc}\hfill {\dot{\Lambda }}_{\mathsf{\Gamma }}\left(t\right)& \le & E\left[{\gamma }^2{\widehat{ð}}^T\widehat{ð}-{\varsigma }^T{Q}_1\varsigma +l_{\rho ð}{\parallel E\left[e_j\left(t\right)\right]\parallel }^2+C_0\right.\hfill \\ \hfill & & -\left({\displaystyle \frac{{\gamma }_1}{T}}-{\displaystyle \frac{1}{2}}\right)\parallel \tilde{W}{\parallel }^2+\mathsf{\Psi }\left({\overline{\varsigma }}_j\right)+{\displaystyle \frac{1}{4}}{\lambda }_m^2{\parallel \varsigma \parallel }^2\hfill \\ \hfill & & \left.+\left({\displaystyle \frac{{\gamma }_2}{T}}\sqrt{c_1^2+c_2^{\prime 2}+c_3^{\prime 2}}+{\displaystyle \frac{d_1}{2}}\right)\parallel \tilde{W}\parallel +{\dot{\tilde{\sigma }}}_b\right]\hfill \\ \hfill & \le & E\left[-\left({\varpi }^2{\lambda }_{min}\left(Q_1\right)-{\displaystyle \frac{1}{4}}{\lambda }_m^2\right){\parallel \varsigma \parallel }^2-\left({\displaystyle \frac{{\gamma }_1}{T}}-{\displaystyle \frac{1}{2}}\right)\right.\hfill \\ \hfill & & \left.\times {\left(\parallel \tilde{W}\parallel -{\displaystyle \frac{2{\gamma }_2\sqrt{c_1^2+c_2^{\prime 2}+c_3^{\prime 2}}+T{d}_1}{2(2{\gamma }_1-T)}}\right)}^2+m\right],\hfill \end{array}$$

(93)

where $m={\displaystyle \frac{{\left(2{\gamma }_2\sqrt{c_1^2+c_2^{\prime 2}+c_3^{\prime 2}}+T{d}_1\right)}^2}{8T(2{\gamma }_1-T)}}$.

We select the interval T and the parameter ${\gamma }_1$, $\varpi$ under the condition that ${\varpi }^2{\lambda }_{min}\left(Q_1\right)-1/4{\lambda }_m^2>0$. Let parameter T be set such that ${\gamma }_1>T$; then ${\dot{\Lambda }}_{\mathsf{\Gamma }}\left(t\right)<0$ given that

$$\begin{array}{cc}\hfill \parallel \varsigma \parallel & >\sqrt{{\displaystyle \frac{m}{{\varpi }^2{\lambda }_{min}\left(Q_1\right)-\frac{1}{4}{\lambda }_m^2}}},\hfill \\ \hfill \parallel \tilde{\mathit{W}}\parallel & >\sqrt{{\displaystyle \frac{2Tm}{2{\gamma }_1-T}}}+{\displaystyle \frac{2{\gamma }_2\sqrt{c_1^2+c_2^{\prime 2}+c_3^{\prime 2}}+T{d}_1}{2(2{\gamma }_1-T)}}.\hfill \end{array}$$

Case 2: For any $\forall t=s_{j+1}$, the derivation of ${\Lambda }_{\mathsf{\Gamma }}\left(t\right)$ is given by

$$\begin{array}{ccc}\hfill & \Delta {\Lambda }_{\mathsf{\Gamma }}\left(t\right)\hfill & \\ \hfill =& E\left[{\displaystyle \frac{1}{2{\alpha }_1}}{\tilde{\mathit{W}}}^T\left(\overline{\varsigma }\left(s_j^{+}\right)\right)\tilde{\mathit{W}}\left(\overline{\varsigma }\left(s_j^{+}\right)\right)\right]-E\left[{\displaystyle \frac{1}{2{\alpha }_1}}{\tilde{\mathit{W}}}^T\left(\overline{\varsigma }\left(s_j\right)\right)\tilde{\mathit{W}}\left(\overline{\varsigma }\left(s_j\right)\right)\right]\hfill \\ \hfill & +{\mathsf{\Gamma }}^{*}\left({\overline{\varsigma }}_{j+1}\right)-{\mathsf{\Gamma }}^{*}\left({\overline{\varsigma }}_j\right)++{\tilde{\sigma }}_b\left(\overline{\varsigma }\left(s_j^{+}\right)\right)-{\tilde{\sigma }}_b\left(\overline{\varsigma }\left(s_j\right)\right)+{\mathsf{\Gamma }}^{*}\left(\overline{\varsigma }\left(s_j^{+}\right)\right)-{\mathsf{\Gamma }}^{*}\left(\overline{\varsigma }\left(s_j\right)\right).\hfill \end{array}$$

(94)

Considering Case 1, $\mathsf{\Gamma }\left(t\right)$ decreases strictly monotonically over the interval $[s_j,s_{j+1})$. This implies $\mathsf{\Gamma }(s_j+t_1)<\mathsf{\Gamma }\left(s_j\right)$ for all $\forall t_1\in (0,s_{j+1}-s_j)$. Then, we have $\Lambda \left(s_j^{+}\right)\le \Lambda \left(s_j\right)$ when calculating the limits on both sides of this inequality. Given this result, it follows that

$$\begin{array}{cc}\hfill & \sigma \left(\overline{\varsigma }\left(s_j^{+}\right)\right)+E\left[{\displaystyle \frac{1}{2{\alpha }_1}}{\tilde{\mathit{W}}}^T\left(\overline{\varsigma }\left(s_j^{+}\right)\right)\tilde{\mathit{W}}\left(\overline{\varsigma }\left(s_j^{+}\right)\right)\right]+{\mathsf{\Gamma }}^{*}\left(\overline{\varsigma }\left(s_j^{+}\right)\right)\hfill \\ \hfill \le & \sigma \left(\overline{\varsigma }\left(s_j\right)\right)+E\left[{\displaystyle \frac{1}{2{\alpha }_1}}{\tilde{\mathit{W}}}^T\left(\overline{\varsigma }\left(s_j\right)\right)\tilde{\mathit{W}}\left(\overline{\varsigma }\left(s_j\right)\right)\right]+{\mathsf{\Gamma }}^{*}\left(\overline{\varsigma }\left(s_j\right)\right).\hfill \end{array}$$

(95)

Furthermore, for $s_j$, $j\in N$, according to Case 1, ${\mathsf{\Gamma }}^{*}\left(\varsigma \right)$ constitutes a continuous difference function, so it follows that ${\mathsf{\Gamma }}^{*}\left({\overline{\varsigma }}_{j+1}\right)\le {\mathsf{\Gamma }}^{*}\left({\overline{\varsigma }}_j\right)$. Based on (94) and (95), we derive $\Delta {\Lambda }_{\mathsf{\Gamma }}\left(t\right)\le 0$.

Based on the above analysis, the proof is completed. □

6. Simulation

Consider the following stochastic system [36]:

$$\begin{array}{c}\hfill \dot{\varsigma }=\chi \left(g\right)\varsigma +B\rho +Cd,\end{array}$$

(96)

with the system states and control policy being denoted as $\varsigma ={[{\varsigma }_1,{\varsigma }_2]}^T\in R^2$ and $\rho \in R$, respectively. d is the disturbance policy. The control policy $\rho$ satisfies $-0.8\le \rho \le 1$. The uncertain term is $d\left(\varsigma \right)=0.5p_{1}sin\left(2p_2{\varsigma }_2\right)cos\left(p_3{\varsigma }_1\right)$ with $p_1\in (-1,1)$, $p_2\in (-0.5,0.5)$ and $p_3\in (0,0.5)$. ${\xi }_i\left(t\right),i=1,\dots ,4$, is a random variable that satisfies a uniform distribution, and its pdfs are the same as example 1 in the simulation in [36].

Through calculation, one obtains ${∥ð\left(\varsigma \right)∥}^2\le sin\left(0.5{\varsigma }_2^2\right)\le 0.5{∥\varsigma ∥}^2$. Set the following auxiliary system as

$$\begin{array}{c}\hfill \dot{\varsigma }=\chi \left(g\right)\varsigma +B\rho +Cð,\end{array}$$

(97)

where $ð\left(\varsigma \right)$ denotes the auxiliary disturbance policy. The original state is ${\varsigma }_0={[1,2]}^T$ and $Q=\mathrm{diag}\{1,1\}$. The activation function is defined as follows: ${\phi }_c={\left[{\varsigma }_1^2,{\varsigma }_1{\varsigma }_2,{\varsigma }_2^2\right]}^T$, ${\phi }_{\rho }={\phi }_{ð}={\left[{\varsigma }_1,{\varsigma }_2\right]}^T$; the weight vectors are ${\mathit{W}}_c={[{\mathit{W}}_{c1},{\mathit{W}}_{c2},{\mathit{W}}_{c3}]}^T$, ${\mathit{W}}_{\rho }={[{\mathit{W}}_{\rho 1},{\mathit{W}}_{\rho 2}]}^T$, and ${\mathit{W}}_{ð}={[{\mathit{W}}_{ð1},{\mathit{W}}_{ð2}]}^T$. The sample size used by the MPCM is 16. Table 1 shows the simulation parameters.

Table 1. Parameter settings.

Parameter	R	T	$\mathit{\gamma }$	$\mathit{\beta }$	${\mathit{\rho }}_{\mathbf{min}}$	${\mathit{\rho }}_{\mathbf{max}}$	$\mathit{\varpi }$	${\mathit{l}}_{\mathit{\rho }}$
value	1	0.005	5	0.5	−0.8	1	0.5	10

The weight curves of NNs are shown in Figure 1 and Figure 2. The weight updates of the critic, actor, and disturbance NNs gradually approach $[3.413,2.916,2.147]$, $[0.868,0.648]$, and $[0.576,0.208]$, respectively. Based on this weight convergence value of the critic NN, we can obtain that the GC of the original system is 17.86.

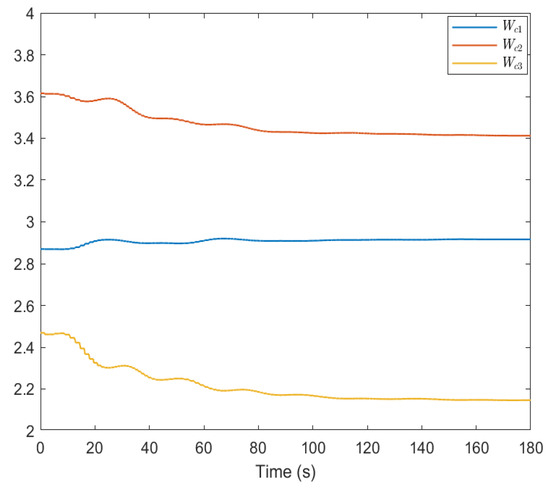
Figure 1. Weight trajectories of the critic NN in our design.

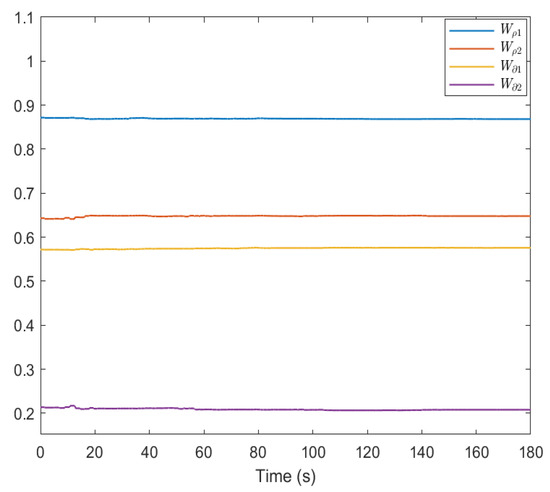
Figure 2. Weight curves of actor and disturbance NNs in our design.

Figure 3 shows the system state curves. Evidently, all state trajectories are capable of eventually converging to the equilibrium point.

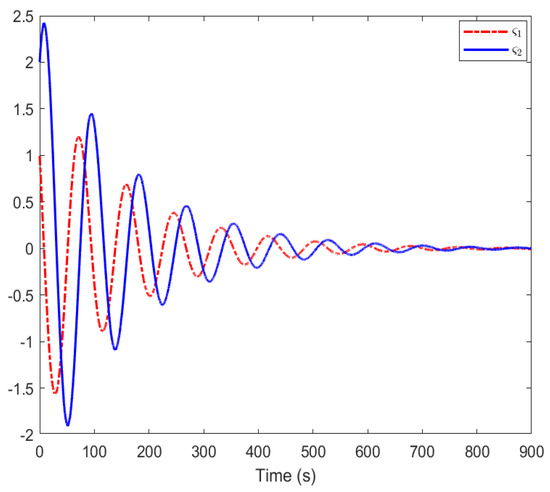
Figure 3. System state curves in our design.

Figure 4 gives the variation curves of control pairs according to the DETC mode. It is shown that, compared with the baseline, the curve of the control policy obtained by our designed method stays within the range of −0.8 to 1, which proves the effectiveness of the designed method with ASAs.

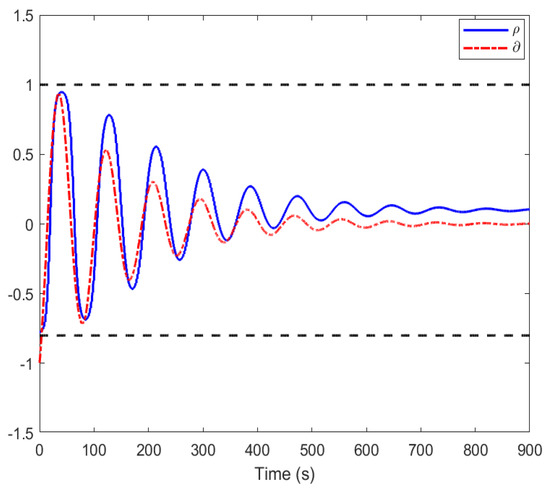
Figure 4. The change curves of the event-triggered optimization control strategy and worst-case disturbance strategy in our design.

Figure 5 shows the trajectories of $\left|\right|e_j{\left|\right|}^2$ and ${\overline{e}}_T$. By using the DETC method, the number of controller updates can be greatly reduced. The sampling period of ETC is given in Figure 6. It displays the time interval between the previous and the current triggering moment. The triggering frequency is dynamically adjusted according to the triggering condition.

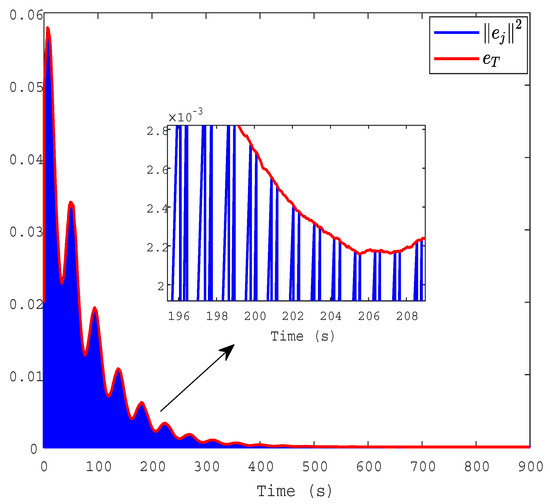
Figure 5. The triggering condition of $\left|\right|e_j{\left|\right|}^2$ and ${\overline{e}}_T$ in our design.

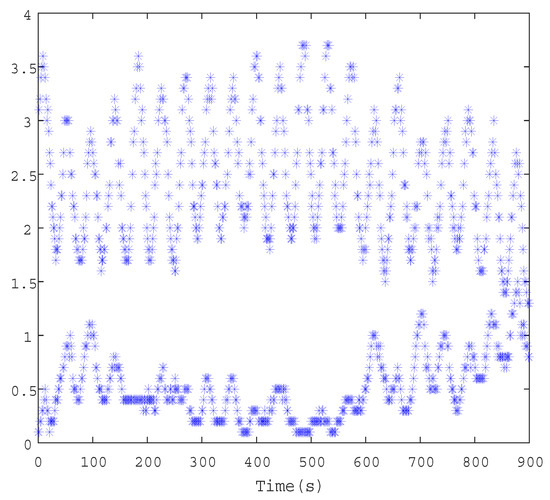
Figure 6. Sampling period of the learning stage in our design.

Figure 7 illustrates the dynamic evolution process of internal signals within the DETC framework. It is clear that the trajectory of internal parameter changes is always greater than 0 and decreasing.

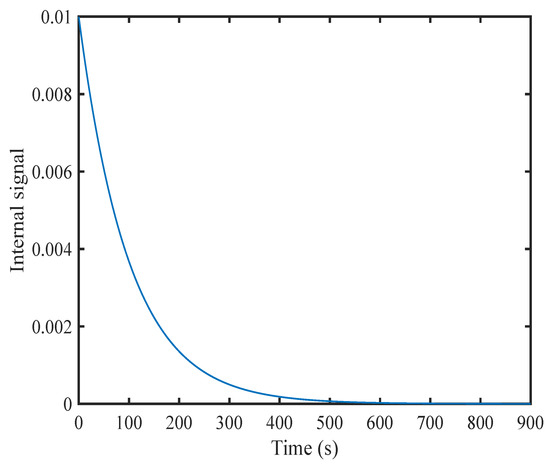
Figure 7. The change curve of the dynamic signal in the triggering condition in our design.

To demonstrate the control performance of the approach proposed in our design, a comparative simulation is given as follows by using the method proposed in [36].

Figure 8 and Figure 9 show the convergence of the NN weight vectors. The weight updates of the critic, actor and disturbance NNs gradually approach $[3.121,2.880,2.295]$, $[0.900,0.697]$ and $[0.599,0.301]$, respectively.

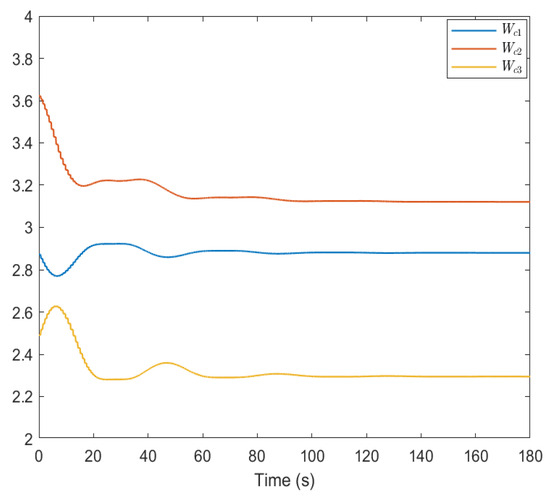
Figure 8. Weight trajectories of the critic NN by using the method in [36].

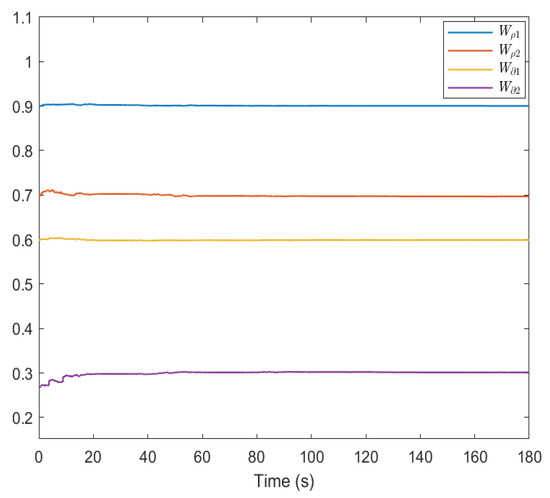
Figure 9. Weight curves of actor and disturbance NNs by using method in [36].

Figure 10 shows the system state curves obtained by using the method in [36].

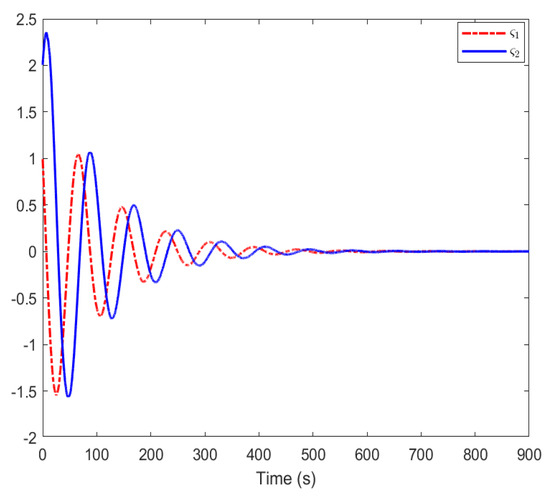
Figure 10. System state curves by using method in [36].

Figure 11 shows the variation curves of control pairs based on the ETC mode obtained by using the method in [36]. The blue line denotes the variation curve of the control input, indicating that it exceeds the range of −0.8 to 1. Figure 4 is within the range of −0.8 to 1. By comparing Figure 4 and Figure 11, it is clear that the control strategy in our design exhibits excellent performance.

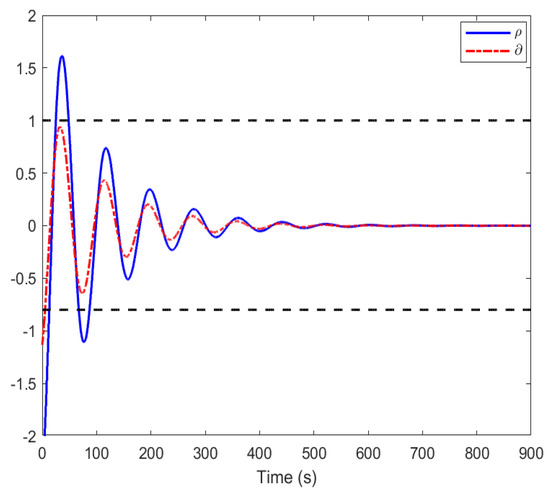
Figure 11. The change curves of the event-triggered optimization control signal and worst-case disturbance signal by using the method in [36].

Figure 12 shows the triggering conditions of $\left|\right|e_j{\left|\right|}^2$ and ${\overline{e}}_T$ under event-triggering mode. It is obvious that the ETC signal requires 2574 state samples, while the DETC strategy proposed in this paper only uses 2028 state samples. It is evident that the DETC proposed in this article can improve controller updates by up to 21.2%.

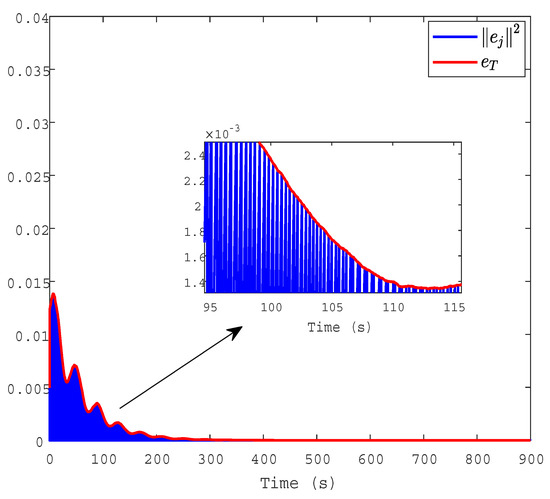
Figure 12. The triggering condition of $\left|\right|e_j{\left|\right|}^2$ and ${\overline{e}}_T$ by using the method in [36].

7. Conclusions

In our design, we have proposed dynamic event-triggered IRL-based control approach for a stochastic system with random parameters and ASAs. Firstly, a modified HJI equation has been formulated. Applying the actor–critic–disturbance NN architecture, both the OC signal under ASAs and the worst-case disturbance strategy have been derived by solving an improved HJI equation. Secondly, the MPCM has been employed to estimate the value function at specific sampling points. The utilization of the MPCM can reduce the computational complexity of sampling data in simulation experiments. Thirdly, through the introduction of dynamic parameters into the triggering conditions, the control input has been adjusted dynamically. Moreover, when the triggering condition is met, the weight values of NNs can be tuned in a synchronous manner, which has significantly enhanced the efficiency of communication resource usage. Furthermore, the Lyapunov stability theorem has been employed to analyze and verify the time-varying system’s stability. Finally, simulation results have confirmed the efficacy of the developed approach.