An Efficient Quadratic Programming Method for Kinematic Control of Redundant Manipulators under Joint Velocity Constraints
Abstract
1. Introduction
- -
- The proposal to integrate differential kinematics with the continuation method into a numerical iterative approach and to construct it as a constrained QP problem to ensure its practicality. Additionally, the design of the corresponding homotopy auxiliary functions enhances its convergence, thereby improving the computational efficiency and accelerating the computation speed to the level of unconstrained solutions.
- -
- Experimental validation on a variety of classical redundant robot kinematic chains. The proposed method has been tested and validated across various robotic kinematic chains, comparing it with classic IK methods. The experiments indicate that, compared to the classic unconstrained and constrained IK methods, the proposed method significantly optimizes several metrics, including the number of iterations, average computation time, accuracy, and precision.
2. Problem Statement
2.1. Unconstrained Jacobian-Based Inverse Kinematics
2.2. QP-Based Inverse Kinematics
3. Methodology
4. Results and Analysis
4.1. Benchmark Setup
4.2. Manipulator Models
4.3. Algorithms and Evaluations
| Algorithm 1: QP problem with continuation method | ||
| Input: Initial guess q, Target pd, Rd | ||
| Initialization: | ||
| Equation (1): pinit, Rinit = ForwardKinematics(q) | ||
| Equation (4): err = computeError(pd, Rd, pinit, Rinit) | ||
| Init parameters: t = 0, i = 0, dt, gt | ||
| Equation (17): Init G(q) | ||
| while not (stopping criterion = Equation (28)) do | ||
| s = tanh(t) | ||
| Equation (25): g0 = computeg0(G, s) | ||
| err = err + g0 | ||
| J = computeJacobian(q) | ||
| = ProxQP(J, err, q) | ||
| q = q + | ||
| pinit, Rinit = ForwardKinematics(q) | ||
| err = computeError(pd, Rd, pinit, Rinit) | ||
| t = t + dts | ||
| i = i + 1 | ||
| if i mod gt == 0 then | ||
| Init G(q) | ||
| end | ||
| end | ||
| Output: q | ||
4.4. Computation Range
4.5. Analysis of Iterations and Applications
4.6. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1

| Joint i | qi/rad | di/mm | ai/mm | αi/rad |
|---|---|---|---|---|
| 1 | q1 | −285.6 | 0 | π |
| 2 | q2 | 0 | 0 | π/2 |
| 3 | q3 | −458.6 | 0 | π/2 |
| 4 | q4 | 0 | 65 | π/2 |
| 5 | q5 | −455.4 | −52.8 | −π/2 |
| 6 | q6 + π | 0 | −12.2 | −π/2 |
| 7 | q7 | −116.9 | 87 | −π/2 |
Appendix A.2
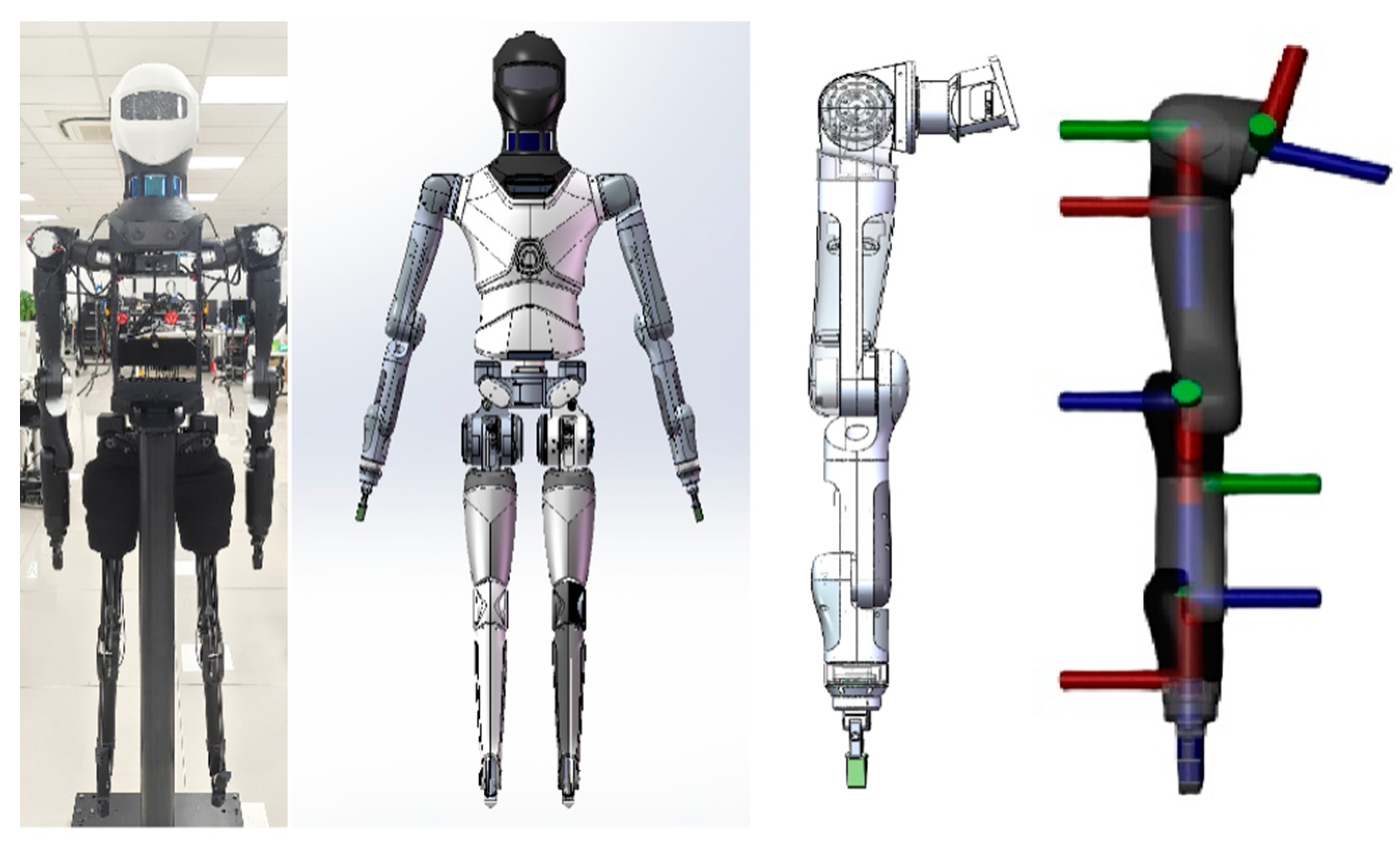
| Joint i | qi/rad | di/mm | ai/mm | αi/rad |
|---|---|---|---|---|
| 1 | 0 | 0 | ||
| 2 | 0 | 0 | ||
| 3 | −285 | 0 | ||
| 4 | 0 | 10 | ||
| 5 | −205 | −10 | ||
| 6 | 0 | 0 | ||
| 7 | 85.85 | 0 |
References
- Benati, M.; Morasso, P.; Tagliasco, V. The inverse kinematic problem for anthropomorphic manipulator arms. Trans. ASME J. Dyn. Syst. Meas. Control 1982, 104, 110–113. [Google Scholar] [CrossRef]
- Ortega, J.M.; Rheinboldt, W.C. Iterative Solution of Nonlinear Equations in Several Variables; SIAM: Philadelphia, PA, USA, 2000. [Google Scholar]
- Goldenberg, A.; Benhabib, B.; Fenton, R. A complete generalized solution to the inverse kinematics of robots. IEEE J. Robot. Autom. 1985, 1, 14–20. [Google Scholar] [CrossRef]
- Whitney, D.E. The Mathematics of Coordinated Control of Prosthetic Arms and Manipulators. J. Dyn. Syst. Meas. Control 1972, 94, 303–309. [Google Scholar] [CrossRef]
- Haviland, J.; Corke, P. Manipulator differential kinematics: Part I: Kinematics, velocity, and applications. IEEE Robot. Autom. Mag. 2023, 2–11. [Google Scholar] [CrossRef]
- Orin, D.E.; Schrader, W.W. Efficient computation of the Jacobian for robot manipulators. Int. J. Robot. Res. 1984, 3, 66–75. [Google Scholar] [CrossRef]
- Gonzalez-Palacios, M.A.; Angeles, J.; Ranjbaran, F. The kinematic synthesis of serial manipulators with a prescribed Jacobian. In Proceedings of the IEEE International Conference on Robotics and Automation, Atlanta, GA, USA, 2–6 May 1993; IEEE: New York, NY, USA, 1993; pp. 450–455. [Google Scholar]
- Gosselin, C.M.; Guillot, M. The synthesis of manipulators with prescribed workspace. J. Mech. Des. 1991, 113, 451–455. [Google Scholar] [CrossRef]
- Chiaverini, S.; Siciliano, B.; Egeland, O. Review of the damped least-squares inverse kinematics with experiments on an industrial robot manipulator. IEEE Trans. Control Syst. Technol. 1994, 2, 123–134. [Google Scholar] [CrossRef]
- Nakamura, Y.; Hanafusa, H. Inverse Kinematic Solutions With Singularity Robustness for Robot Manipulator Control. J. Dyn. Syst. Meas. Control 1986, 108, 163–171. [Google Scholar] [CrossRef]
- Zhao, J.; Xu, T.; Fang, Q.; Xie, Y.; Zhu, Y. A synthetic inverse kinematic algorithm for 7-DOF redundant manipulator. In Proceedings of the 2018 IEEE International Conference on Real-time Computing and Robotics (RCAR), Kandima, Maldives, 1–5 August 2018; IEEE: New York, NY, USA, 2018; pp. 112–117. [Google Scholar]
- Phuoc, L.M.; Martinet, P.; Lee, S.; Kim, H. Damped least square based genetic algorithm with Gaussian distribution of damping factor for singularity-robust inverse kinematics. J. Mech. Sci. Technol. 2008, 22, 1330–1338. [Google Scholar] [CrossRef]
- Moreno, L.A.O.; Ramírez, D.V.; Sánchez, M.P.; Rodríguez, L.R. Comparative Study of Iterative Methods for Inverse Kinematics of Redundant Serial Robots with Increasing Degrees of Freedom. In Proceedings of the 2023 IEEE International Autumn Meeting on Power, Electronics and Computing (ROPEC), Ixtapa, Mexico, 18–20 October 2023; IEEE: New York, NY, USA, 2023; Volume 7, pp. 1–6. [Google Scholar]
- Wang, L.-C.T.; Chen, C.-C. A combined optimization method for solving the inverse kinematics problems of mechanical manipulators. IEEE Trans. Robot. Autom. 1991, 7, 489–499. [Google Scholar] [CrossRef]
- Cheng, F.-T.; Chen, T.-H.; Sun, Y.-Y. Efficient algorithm for resolving manipulator redundancy—The compact QP method. In Proceedings of the 1992 IEEE International Conference on Robotics and Automation, Nice, France, 12–14 May 1992; IEEE Computer Society: Los Alamitos, CA, USA, 1992; pp. 508–509. [Google Scholar]
- Zhang, Z.; Zhang, Y. Variable joint-velocity limits of redundant robot manipulators handled by quadratic programming. IEEE/ASME Trans. Mechatron. 2012, 18, 674–686. [Google Scholar] [CrossRef]
- Kanoun, O.; Lamiraux, F.; Wieber, P.-B. Kinematic control of redundant manipulators: Generalizing the task-priority framework to inequality task. IEEE Trans. Robot. 2011, 27, 785–792. [Google Scholar] [CrossRef]
- Marić, F.; Giamou, M.; Khoubyarian, S.; Petrović, I.; Kelly, J. Inverse kinematics for serial kinematic chains via sum of squares optimization. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; IEEE: New York, NY, USA, 2020; pp. 7101–7107. [Google Scholar]
- Woliński, Ł.; Wojtyra, M. A novel QP-based kinematic redundancy resolution method with joint constraints satisfaction. IEEE Access 2022, 10, 41023–41037. [Google Scholar] [CrossRef]
- Khudher, D.; Powell, R. Quadratic programming for inverse kinematics control of a hexapod robot with inequality constraints. In Proceedings of the 2016 International Conference on Robotics: Current Trends and Future Challenges (RCTFC), Thanjavur, India, 19–20 December 2016; IEEE: New York, NY, USA, 2016; pp. 1–5. [Google Scholar]
- Bensadoun, R.; Gur, S.; Blau, N.; Wolf, L. Neural inverse kinematic. In Proceedings of the International Conference on Machine Learning (ICML), Baltimore, MD, USA, 17–23 July 2022; PMLR: New York, NY, USA, 2022; pp. 1787–1797. [Google Scholar]
- Aggogeri, F.; Pellegrini, N.; Taesi, C.; Tagliani, F.L. Inverse kinematic solver based on machine learning sequential procedure for robotic applications. J. Phys. Conf. Ser. 2022, 2234, 012007. [Google Scholar] [CrossRef]
- Malik, A.; Lischuk, Y.; Henderson, T.; Prazenica, R. A deep reinforcement-learning approach for inverse kinematics solution of a high degree of freedom robotic manipulator. Robotics 2022, 11, 44. [Google Scholar] [CrossRef]
- Guo, Z.; Huang, J.; Ren, W.; Wang, C. A reinforcement learning approach for inverse kinematics of arm robot. In Proceedings of the 2019 4th International Conference on Robotics, Control and Automation (ICRCA), Guangzhou, China, 26–28 July 2019; pp. 95–99. [Google Scholar]
- Ben-Israel, A. A Newton-Raphson method for the solution of systems of equations. J. Math. Anal. Appl. 1966, 15, 243–252. [Google Scholar] [CrossRef]
- Wu, T.-M. The inverse kinematics problem of spatial 4P3R robot manipulator by the Homotopy Continuation Method with an adjustable auxiliary Homotopy function. Nonlinear Anal. Theory Methods Appl. 2006, 64, 2373–2380. [Google Scholar] [CrossRef]
- Wu, T.-M. A study of convergence on the Newton-homotopy continuation method. Appl. Math. Comput. 2005, 168, 1169–1174. [Google Scholar] [CrossRef]
- Morgan, A.P. A method for computing all solutions to systems of polynomials equations. ACM Trans. Math. Softw. 1983, 9, 1–17. [Google Scholar] [CrossRef]
- Moe, S.; Antonelli, G.; Teel, A.R.; Pettersen, K.Y.; Schrimpf, J. Set-based tasks within the singularity-robust multiple task-priority inverse kinematics framework: General formulation, stability analysis, and experimental results. Front. Robot. AI 2016, 3, 16. [Google Scholar] [CrossRef]
- Lloyd, S.; Irani, R.A.; Ahmadi, M. Fast and robust inverse kinematics of serial robots using Halley’s method. IEEE Trans. Robot. 2022, 38, 2768–2780. [Google Scholar] [CrossRef]
- Wu, T.-M. Solving the nonlinear equations by the Newton-homotopy continuation method with adjustable auxiliary homotopy function. Appl. Math. Comput. 2006, 173, 383–388. [Google Scholar] [CrossRef]
- Egeland, O. Task-space tracking with redundant manipulators. IEEE J. Robot. Autom. 1987, 3, 471–475. [Google Scholar] [CrossRef]
- Chan, T.F.; Dubey, R.V. A weighted least-norm solution based scheme for avoiding joint limits for redundant joint manipulators. IEEE Trans. Robot. Autom. 1995, 11, 286–292. [Google Scholar] [CrossRef]
- Carpentier, J.; Saurel, G.; Buondonno, G.; Mirabel, J.; Lamiraux, F.; Stasse, O.; Mansard, N. The Pinocchio C++ library: A fast and flexible implementation of rigid body dynamics algorithms and their analytical derivatives. In Proceedings of the 2019 IEEE/SICE International Symposium on System Integration (SII), Paris, France, 14–16 January 2019; IEEE: New York, NY, USA, 2019; pp. 614–619. [Google Scholar]
- Bambade, A.; El-Kazdadi, S.; Taylor, A.; Carpentier, J. Prox-qp: Yet another quadratic programming solver for robotics and beyond. In Proceedings of the RSS 2022-Robotics: Science and Systems, New York, NY, USA, 27 June–1 July 2022. [Google Scholar]
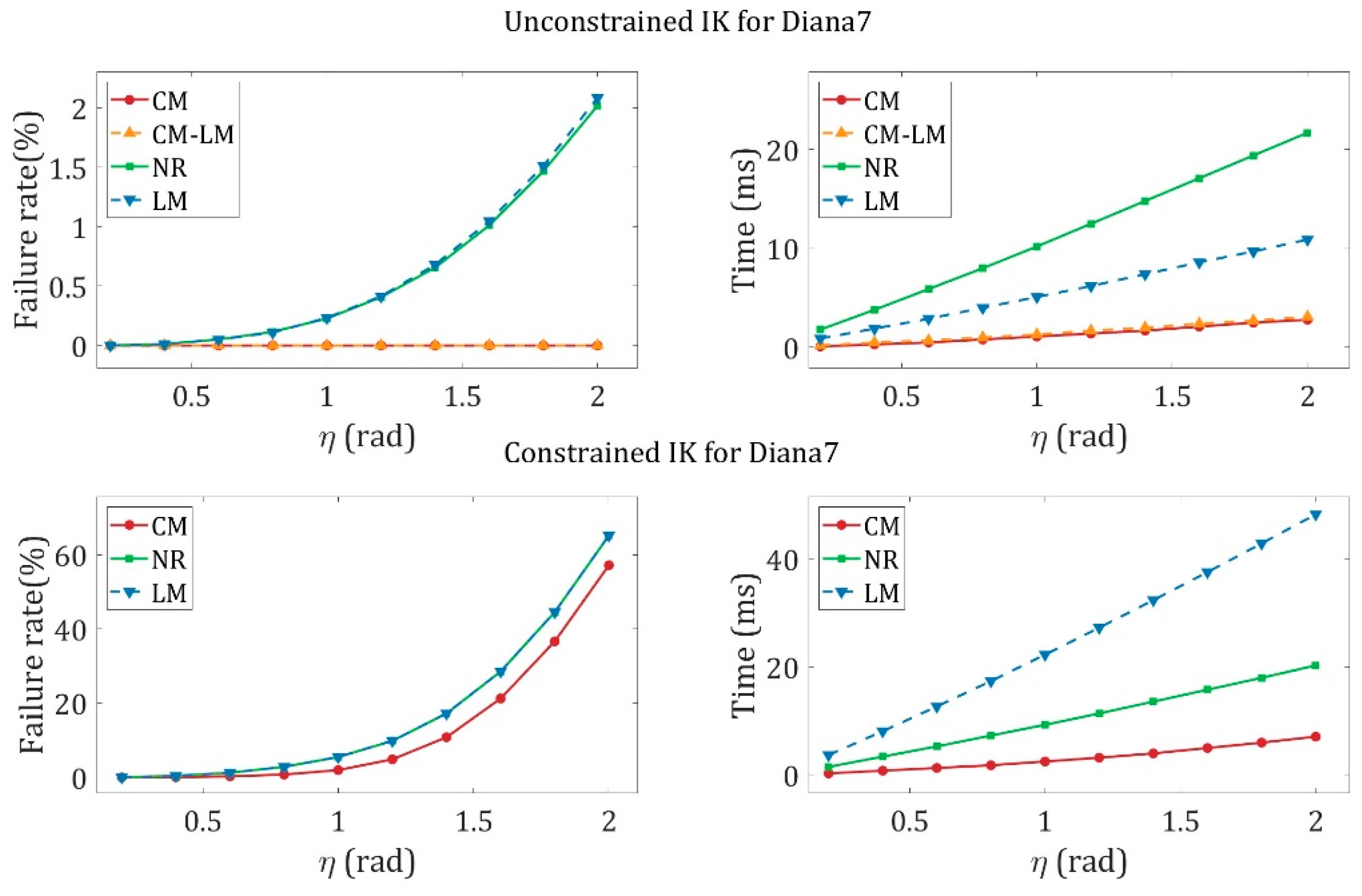
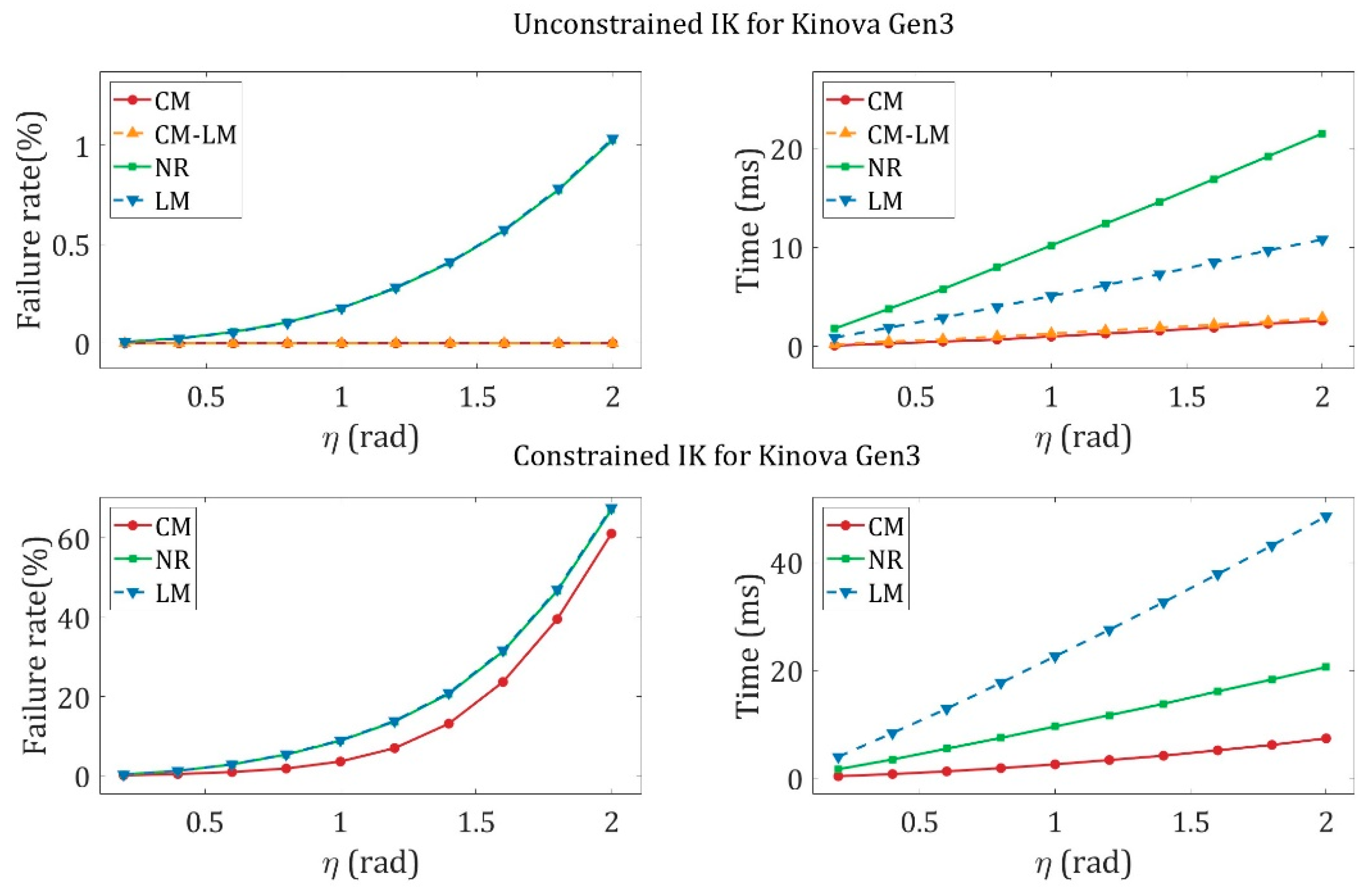

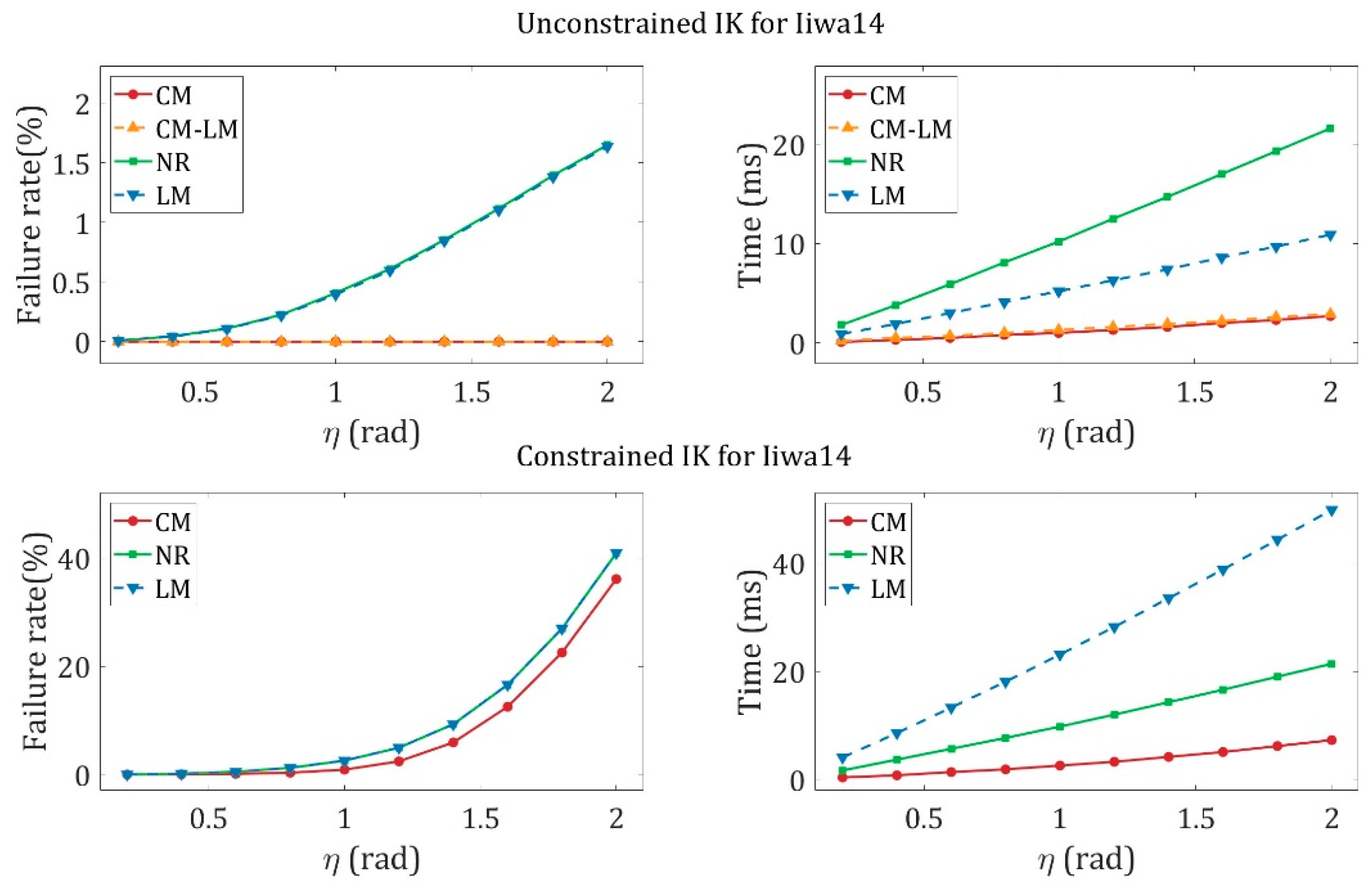
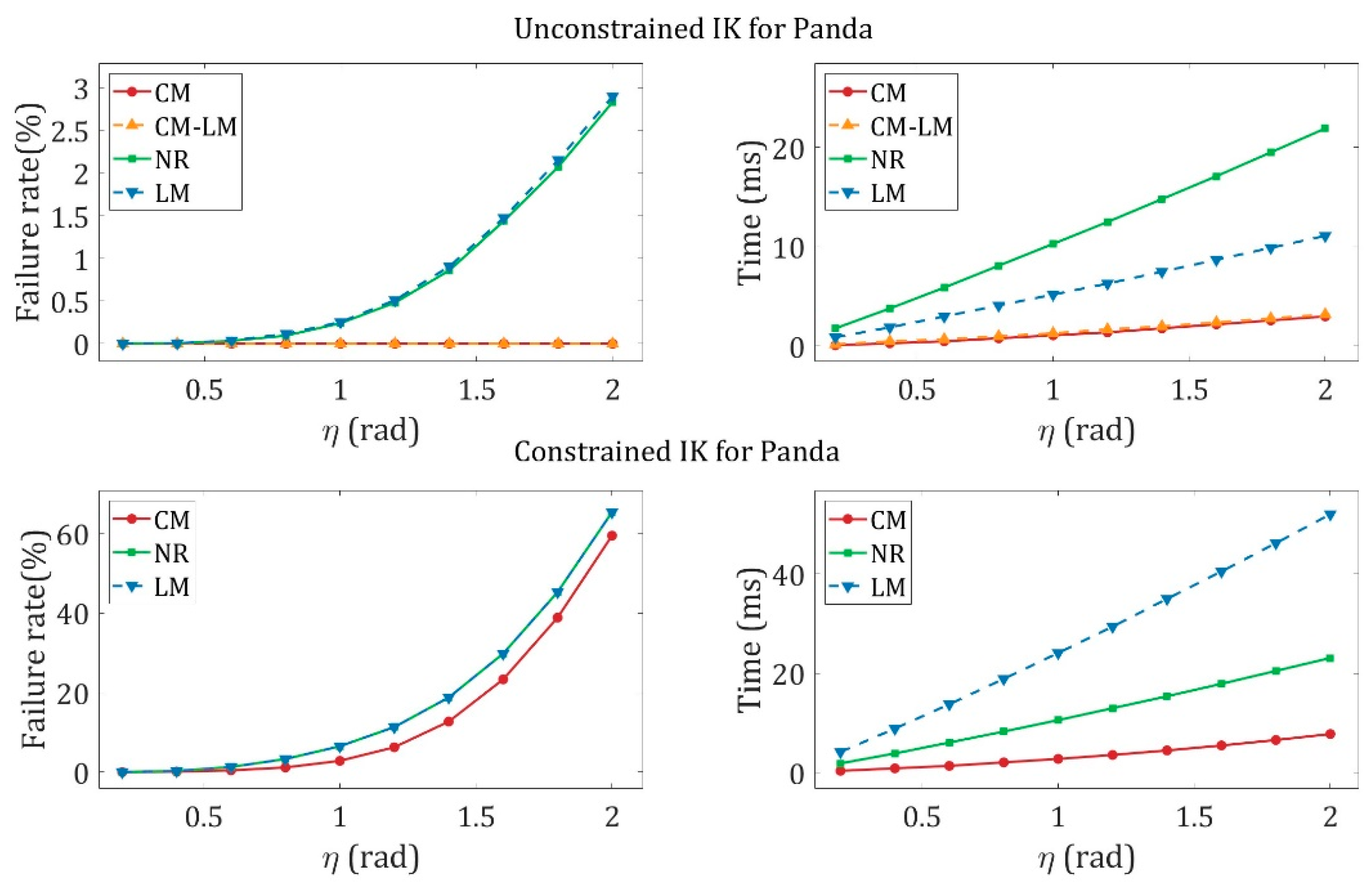
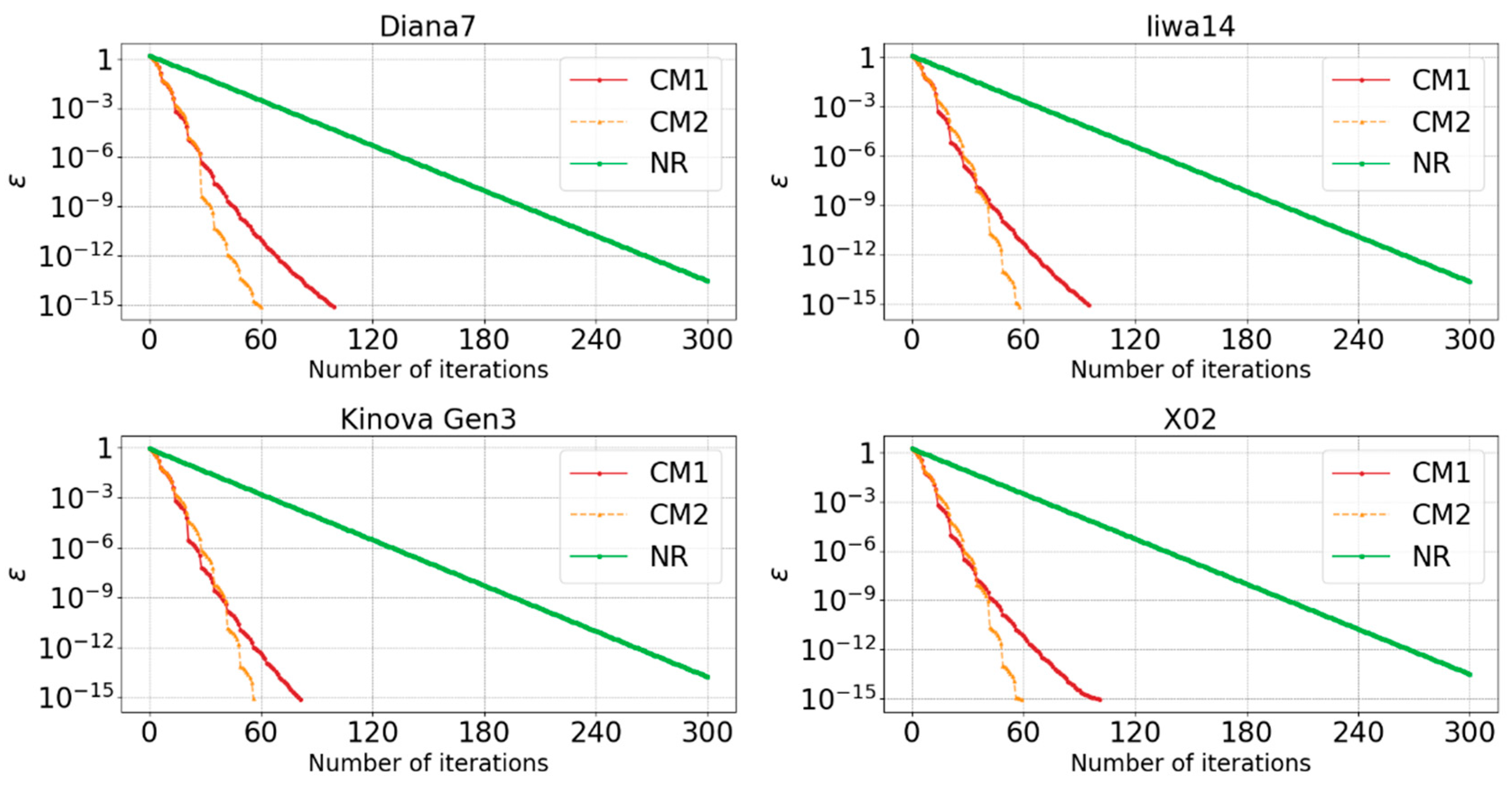
| Robot | Precision | Method | Accuracy | Times (ms) | Max Iterations | Max Iterations | Min Iterations |
|---|---|---|---|---|---|---|---|
| Diana7 | 1 × 10−4 | NR | 99.15% | 1.89 | 85.1 | 252 | 60 |
| LM | 99.15% | 4.53 | 85.1 | 252 | 60 | ||
| CM | 99.79% | 0.49 | 18.2 | 238 | 14 | ||
| 1 × 10−14 | NR | 19.82% | 6.39 | 297.6 | 300 | 277 | |
| LM | 19.82% | 15.71 | 297.6 | 300 | 277 | ||
| CM | 99.46% | 1.97 | 83.0 | 267 | 68 | ||
| Iiwa14 | 1 × 10−4 | NR | 99.64% | 1.74 | 85.1 | 174 | 64 |
| LM | 99.64% | 4.08 | 85.1 | 236 | 64 | ||
| CM | 99.92% | 0.44 | 18.0 | 248 | 14 | ||
| 1 × 10−14 | NR | 19.15% | 5.82 | 297.7 | 300 | 281 | |
| LM | 19.12% | 13.96 | 297.7 | 300 | 282 | ||
| CM | 97.86% | 1.77 | 82.8 | 264 | 70 | ||
| Kinova Gen3 | 1 × 10−4 | NR | 98.27% | 1.71 | 84.3 | 256 | 57 |
| LM | 98.27% | 4.25 | 84.3 | 290 | 57 | ||
| CM | 99.49% | 0.47 | 18.3 | 237 | 14 | ||
| 1 × 10−14 | NR | 23.32% | 5.72 | 297.4 | 300 | 281 | |
| LM | 23.31% | 13.76 | 297.4 | 300 | 281 | ||
| CM | 96.73% | 1.79 | 84.9 | 267 | 71 | ||
| Panda | 1 × 10−4 | NR | 99.06% | 1.87 | 84.9 | 270 | 57 |
| LM | 99.06% | 4.29 | 84.9 | 270 | 57 | ||
| CM | 99.71% | 0.48 | 18.1 | 188 | 14 | ||
| 1 × 10−14 | NR | 20.97% | 6.16 | 297.5 | 300 | 280 | |
| LM | 20.95% | 14.23 | 297.5 | 300 | 280 | ||
| CM | 99.49% | 1.88 | 82.9 | 266 | 70 | ||
| X02 | 1 × 10−4 | NR | 98.52% | 2.50 | 84.4 | 221 | 59 |
| LM | 98.52% | 5.10 | 84.4 | 223 | 59 | ||
| CM | 99.51% | 0.69 | 18.0 | 183 | 14 | ||
| 1 × 10−14 | NR | 24.66% | 8.83 | 297.2 | 300 | 275 | |
| LM | 24.65% | 17.63 | 297.2 | 300 | 275 | ||
| CM | 98.56% | 2.72 | 83.2 | 265 | 69 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Wang, P.; Zhao, W.; Wu, T.; Li, Q. An Efficient Quadratic Programming Method for Kinematic Control of Redundant Manipulators under Joint Velocity Constraints. Actuators 2024, 13, 273. https://doi.org/10.3390/act13070273
Li Z, Wang P, Zhao W, Wu T, Li Q. An Efficient Quadratic Programming Method for Kinematic Control of Redundant Manipulators under Joint Velocity Constraints. Actuators. 2024; 13(7):273. https://doi.org/10.3390/act13070273
Chicago/Turabian StyleLi, Zongdao, Pengfei Wang, Wenlong Zhao, Tao Wu, and Qingdu Li. 2024. "An Efficient Quadratic Programming Method for Kinematic Control of Redundant Manipulators under Joint Velocity Constraints" Actuators 13, no. 7: 273. https://doi.org/10.3390/act13070273
APA StyleLi, Z., Wang, P., Zhao, W., Wu, T., & Li, Q. (2024). An Efficient Quadratic Programming Method for Kinematic Control of Redundant Manipulators under Joint Velocity Constraints. Actuators, 13(7), 273. https://doi.org/10.3390/act13070273






