Structural Design and Control Performance Study of Flexible Finger Mechanisms for Robot End Effectors
Abstract
1. Introduction
2. Materials and Methods
2.1. Flexible Finger Structure Design
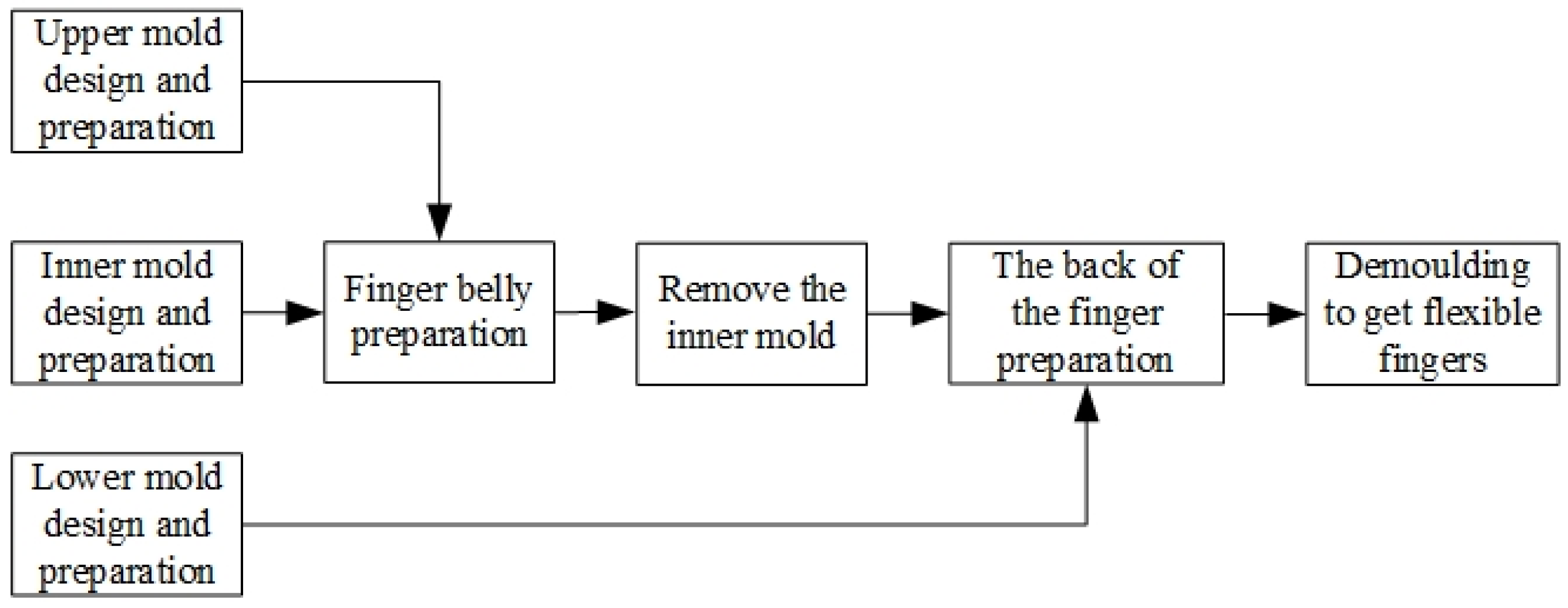
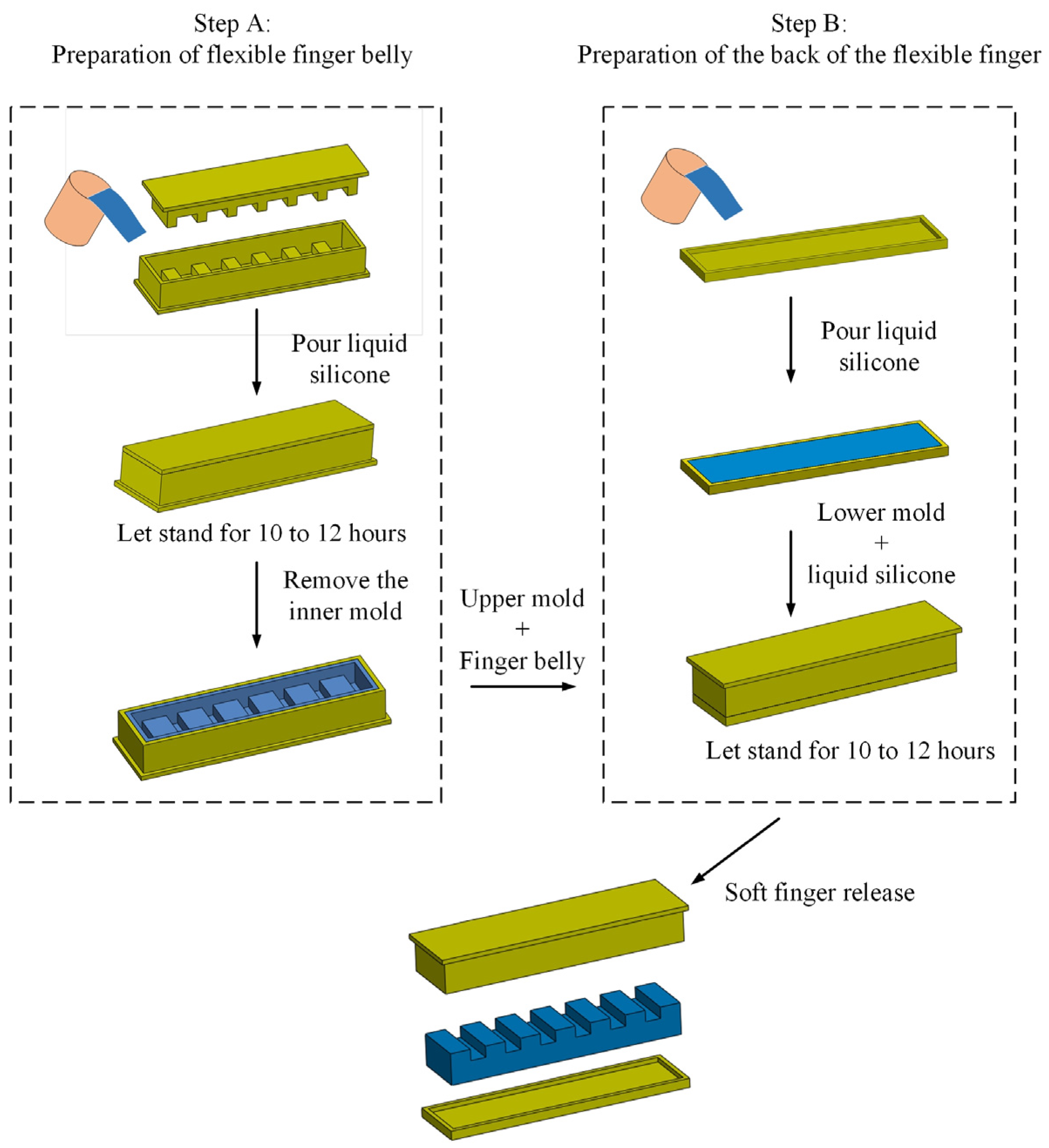
2.2. Design and Manufacture of Finger Molds and Flexible Fingers
3. Simulation and Experiment
3.1. Simulation Analysis of Flexible Finger
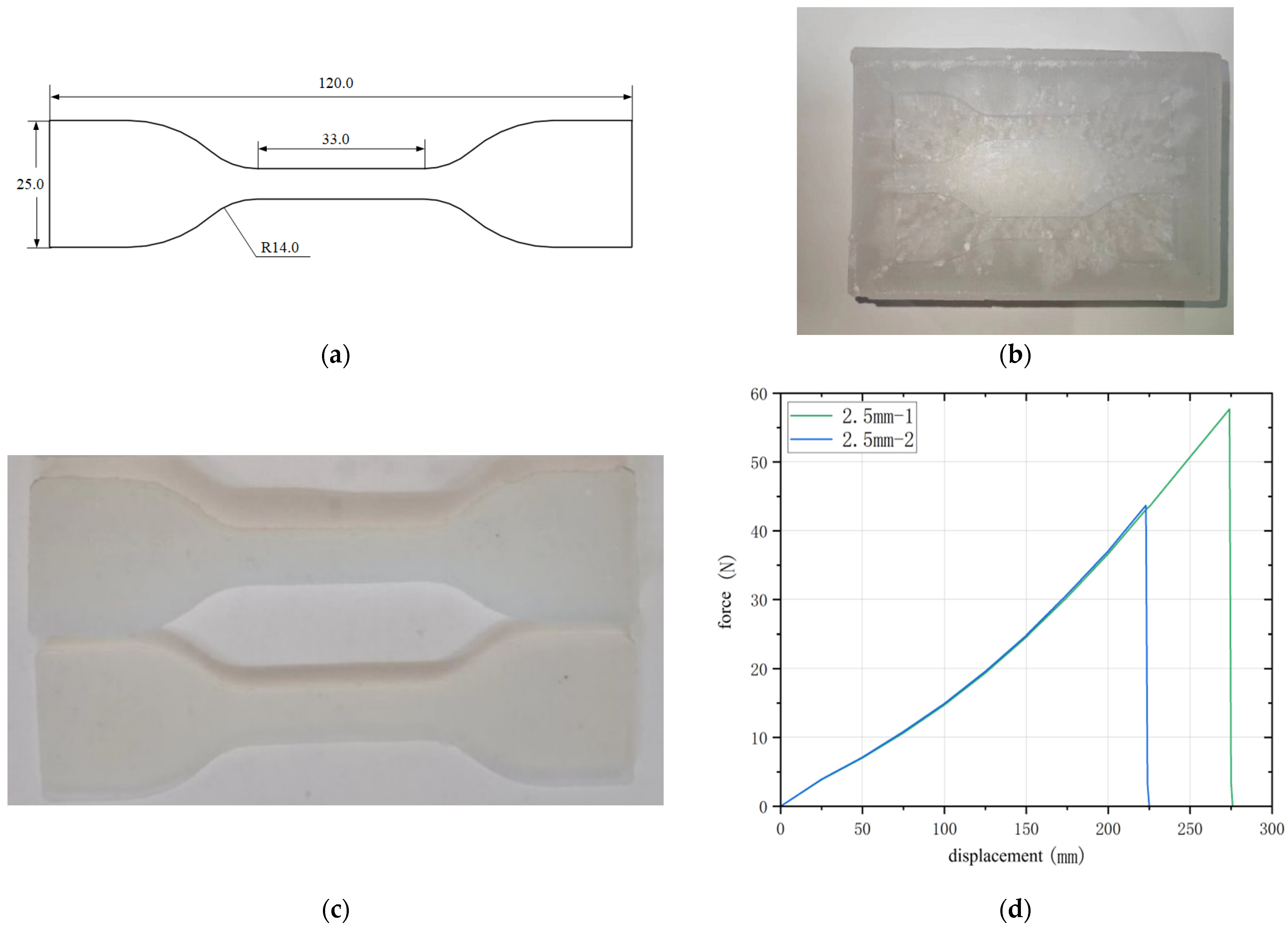
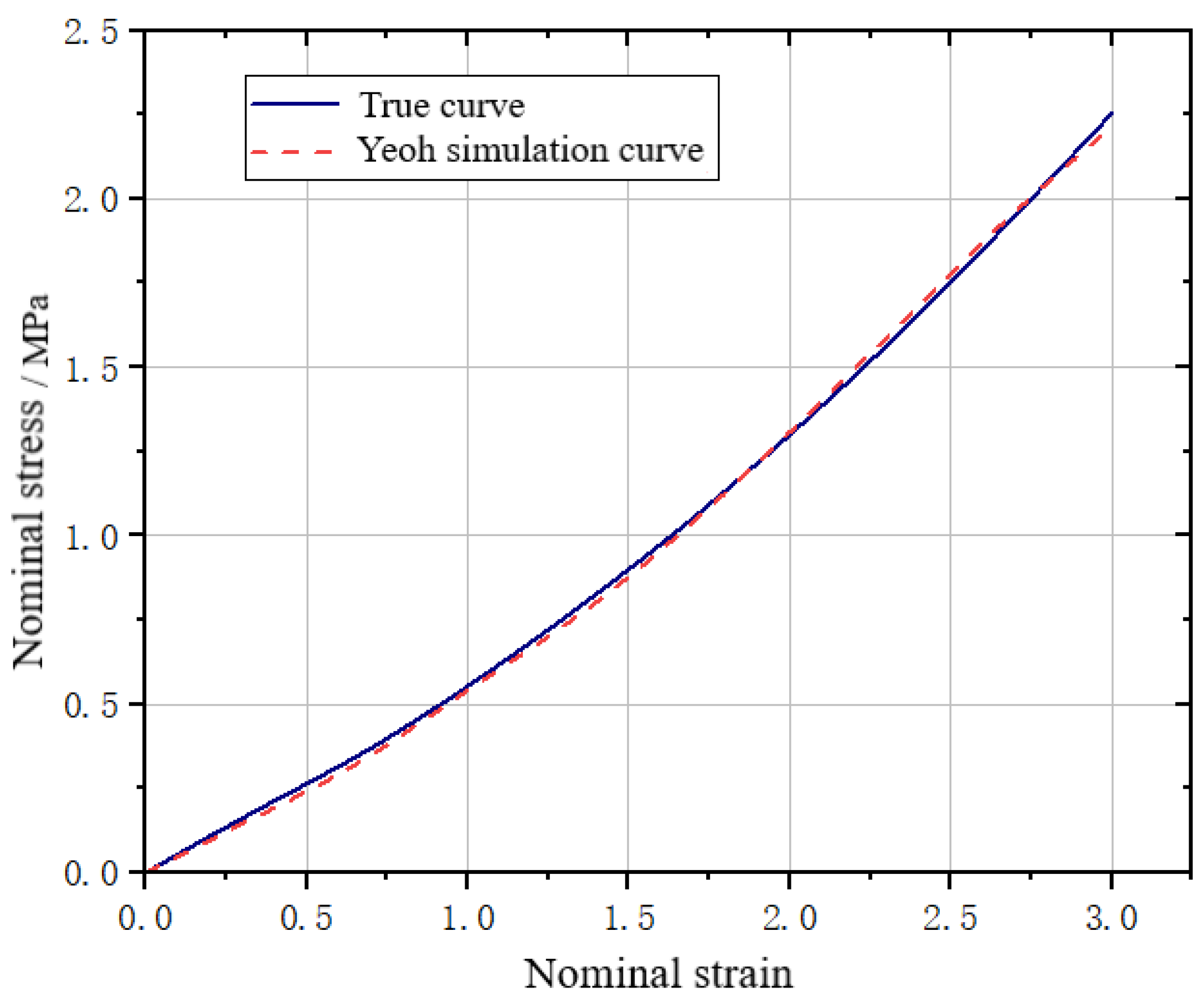
3.1.1. Experimental Testing of Material Parameters of Standard Samples
3.1.2. Simulation Analysis of Mechanical Parameters of Flexible Fingers
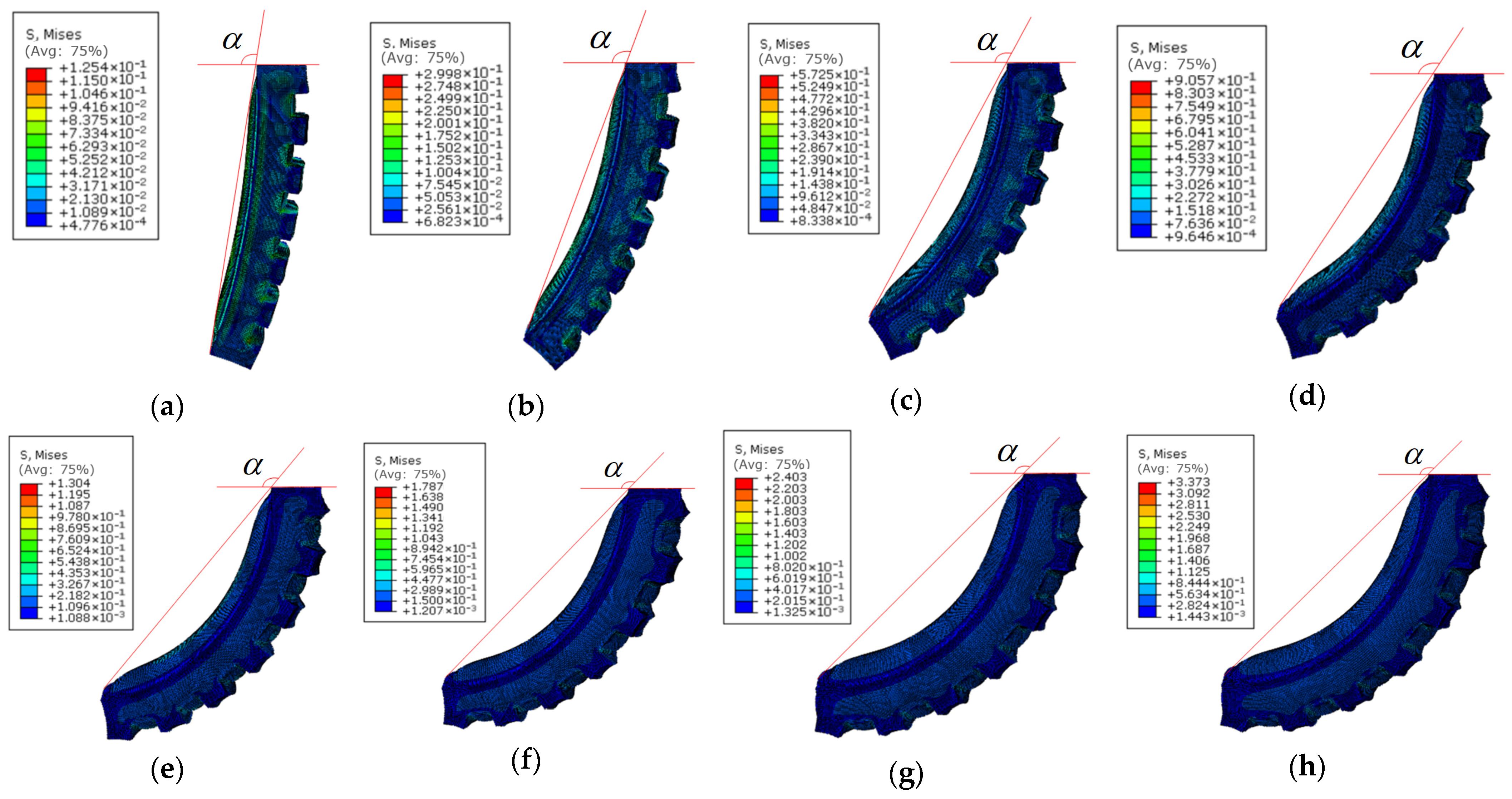
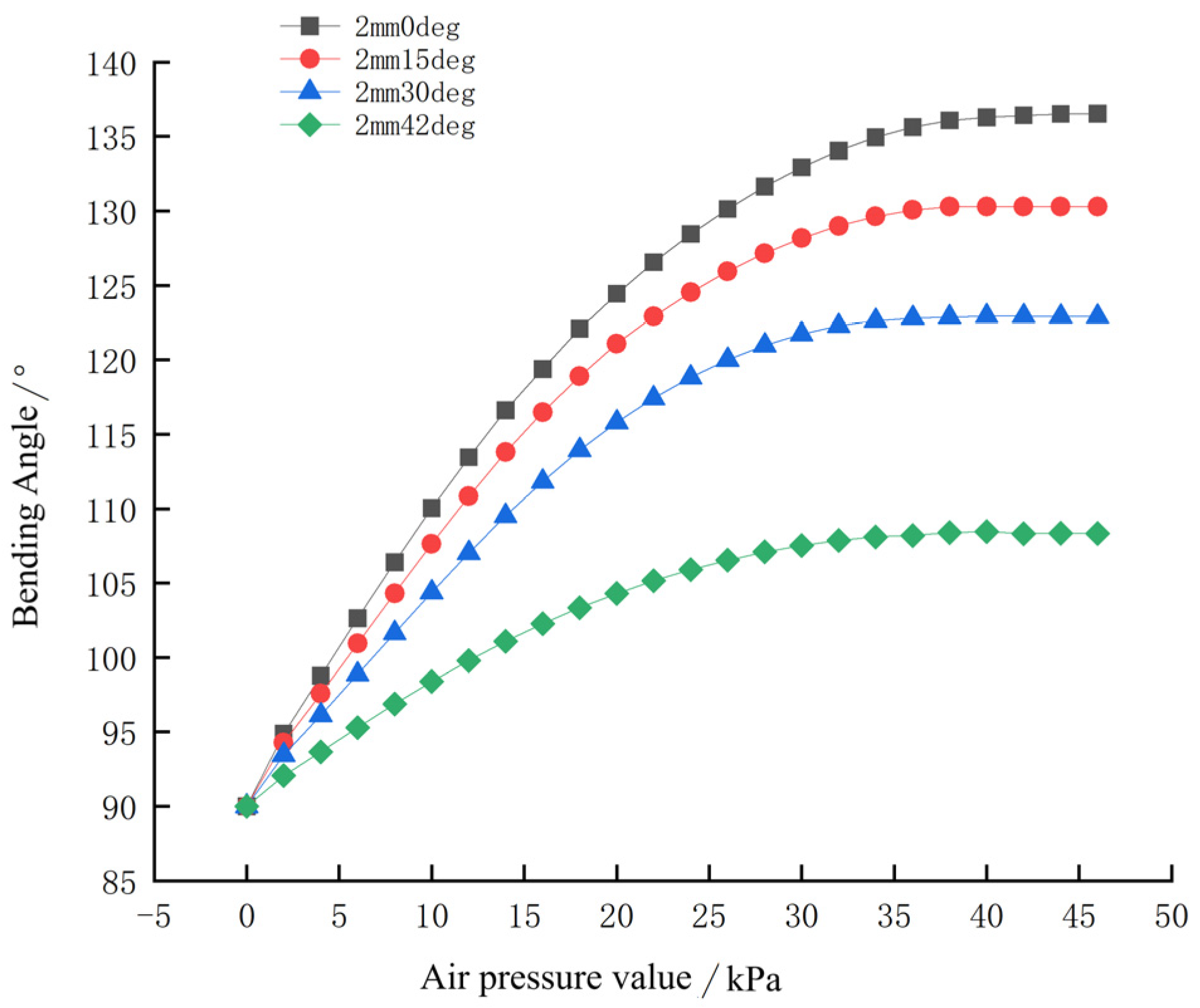
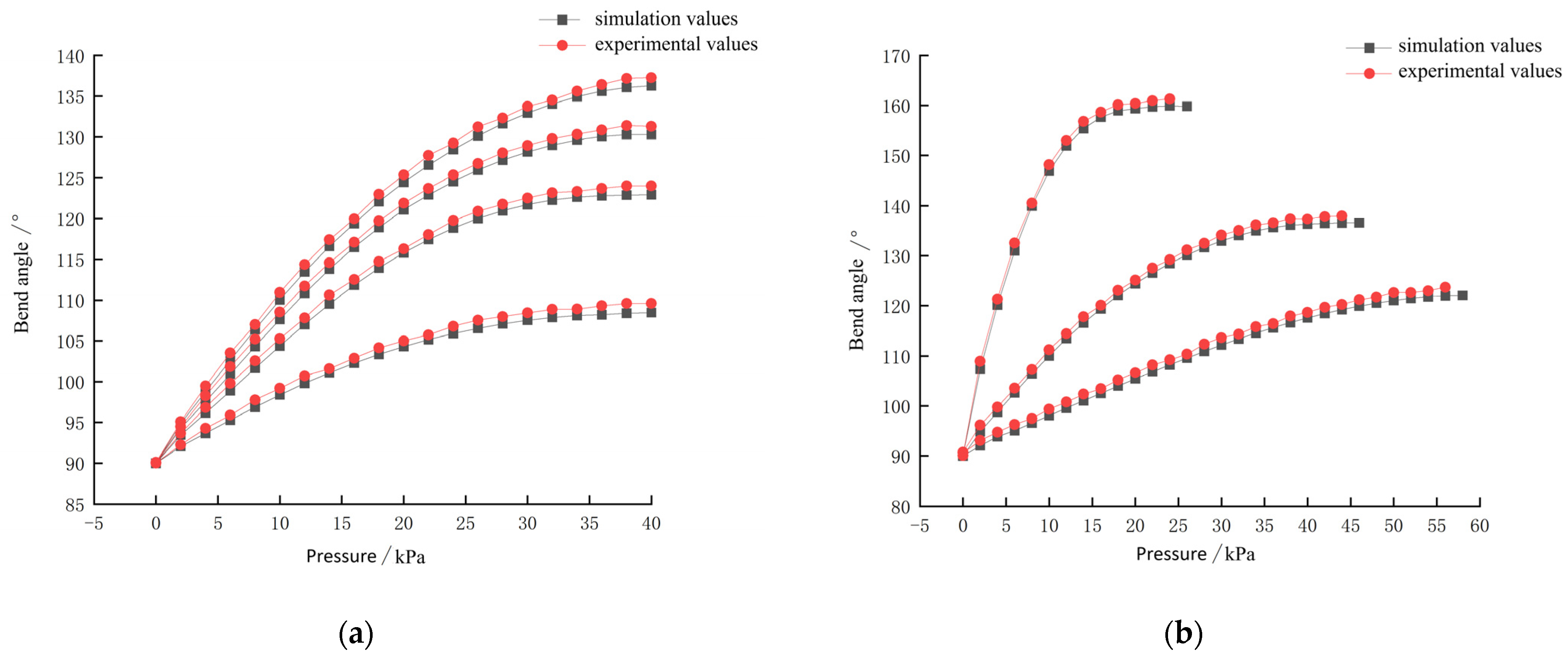
3.1.3. Influence of Finger Cavity Angle on Flexural Properties of Flexible Fingers
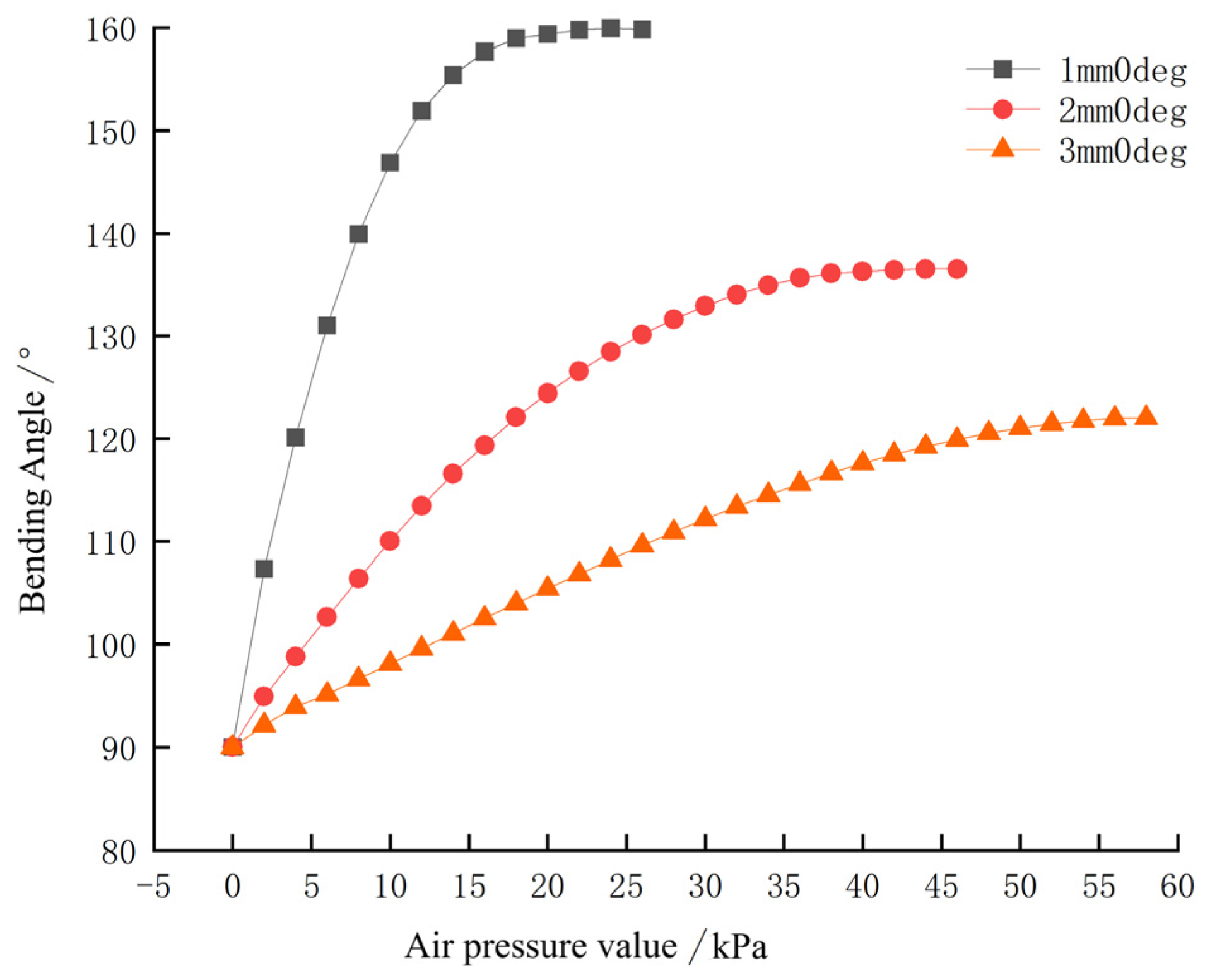
3.1.4. Influence of Finger Thickness on Flexural Properties of Flexible Fingers
3.2. Mechanical Properties of Flexible Fingers
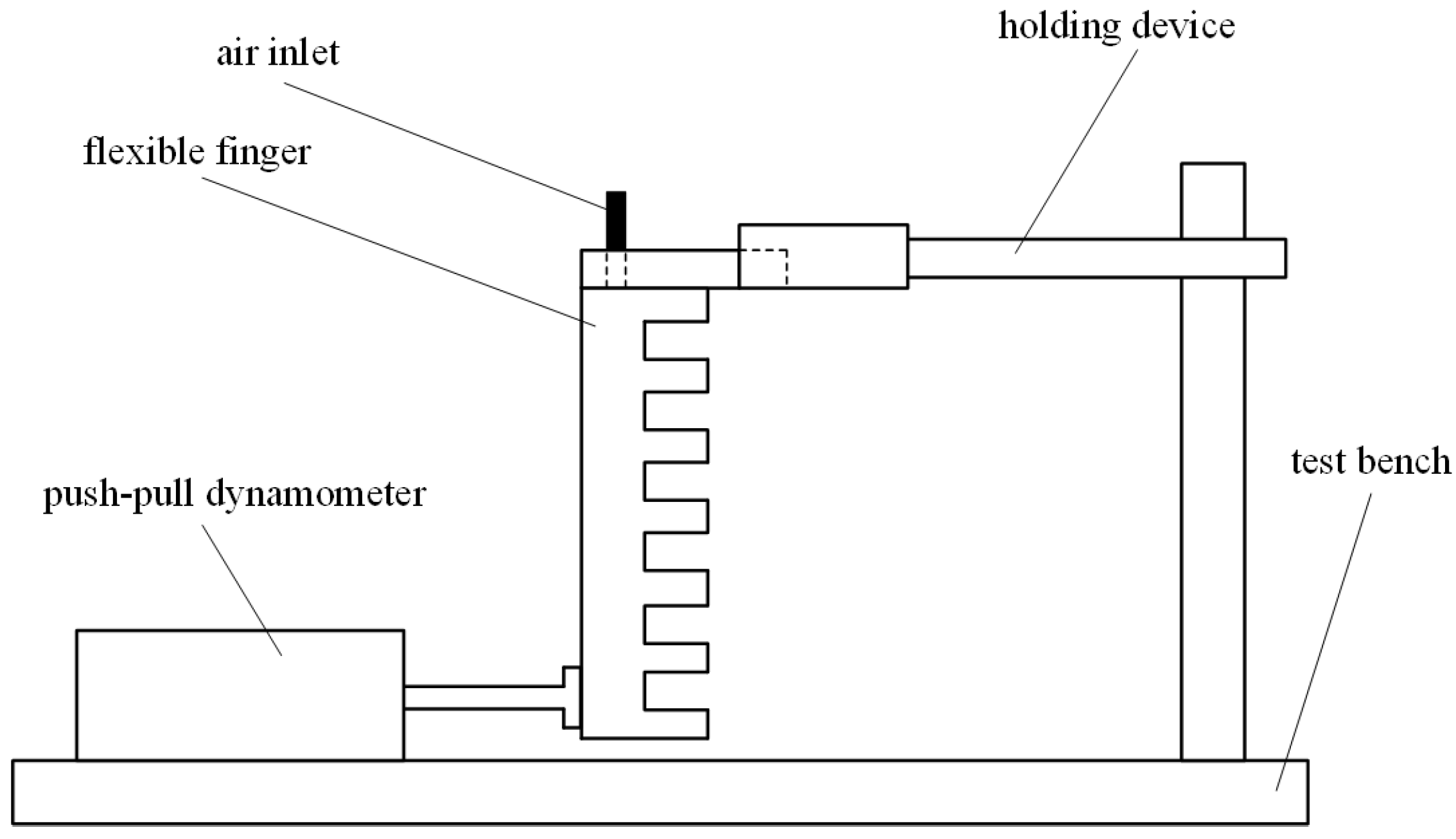
3.2.1. Experimental Platform Construction
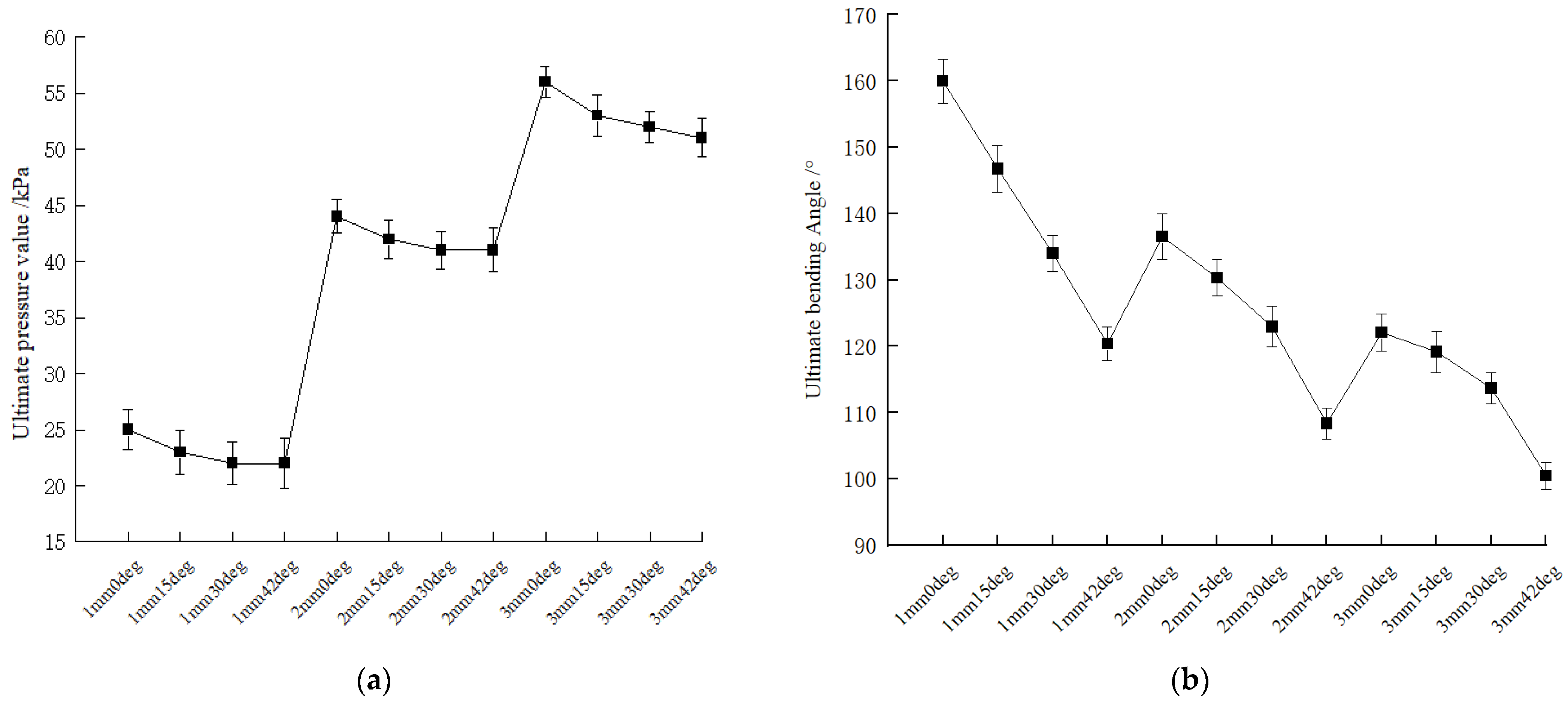
3.2.2. The Ultimate Pressure and Bending Angle of Fingers
3.2.3. Bending Angle Test Experiment
3.2.4. Contact Force Test
4. Control Algorithm Analysis
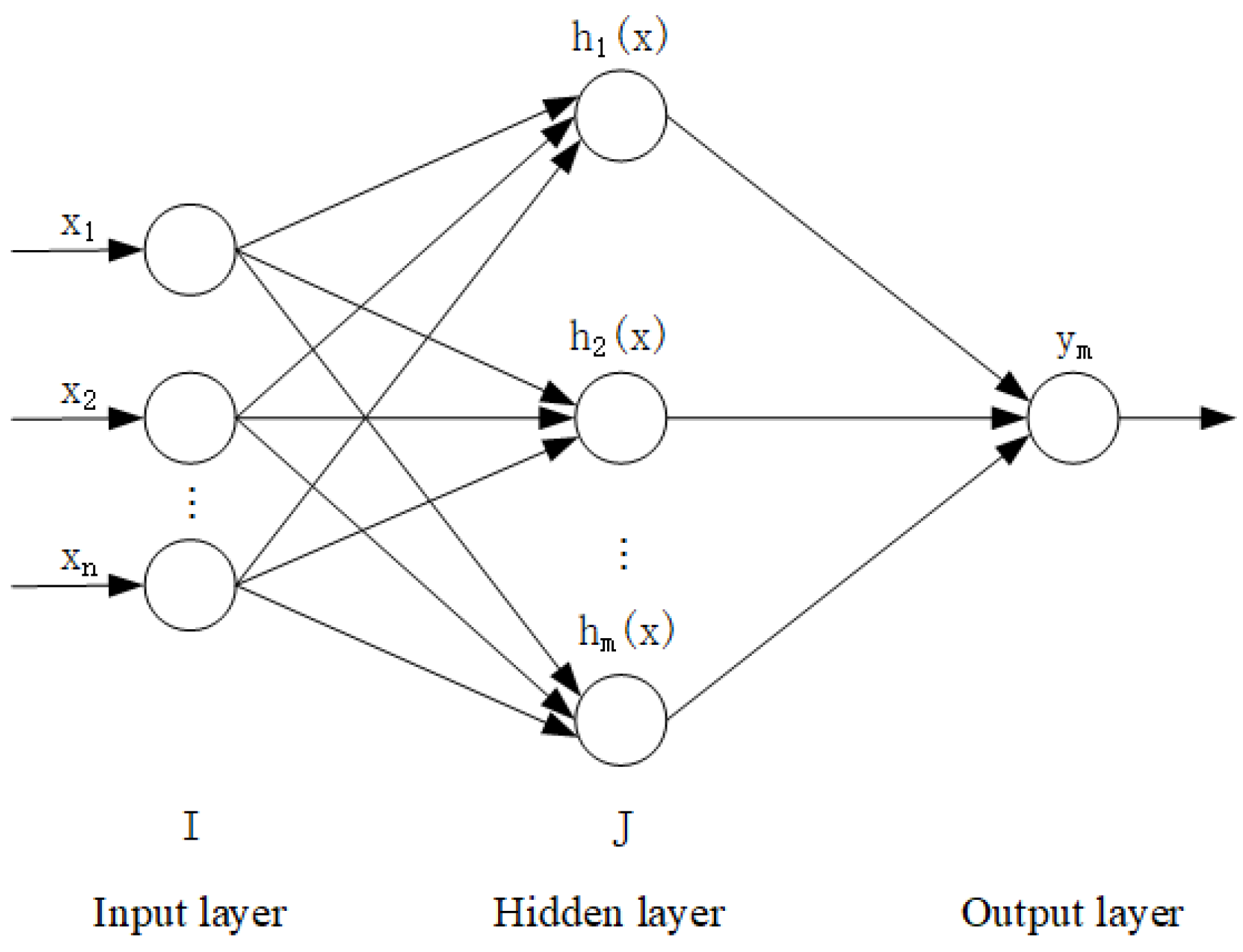
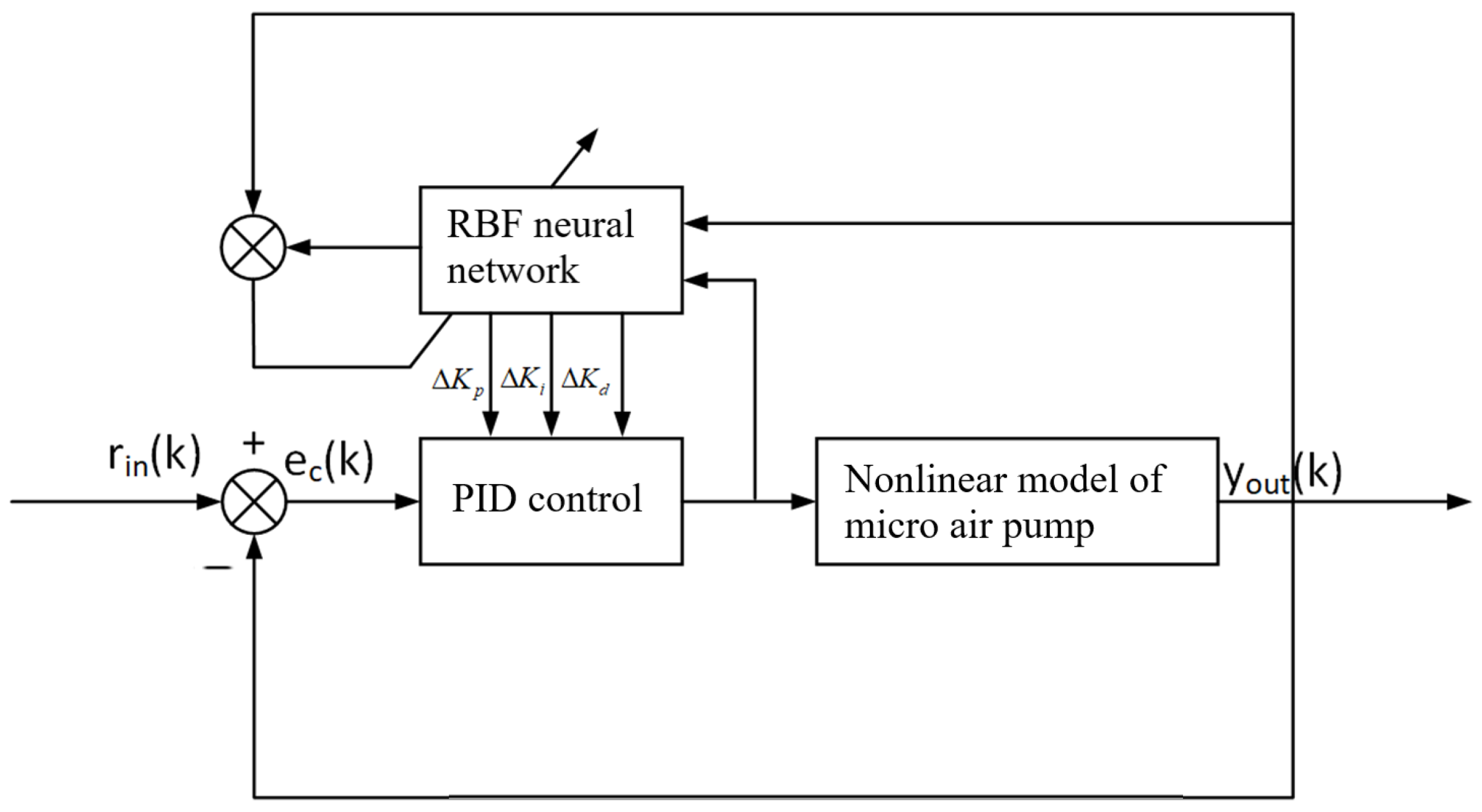
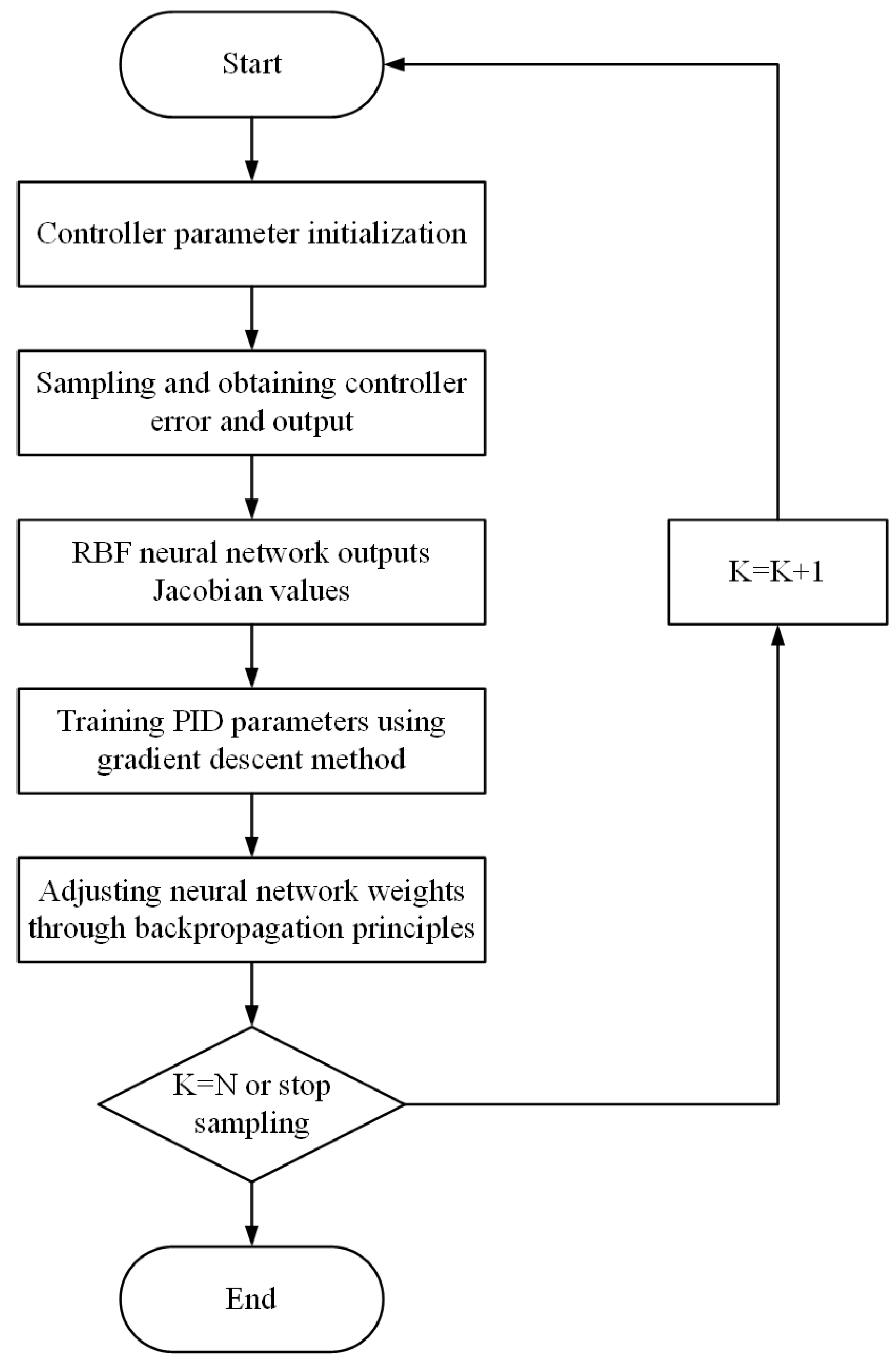
4.1. Flexible Finger Pressure Control Algorithm Based on RBF Neural Network Tuning PID Control
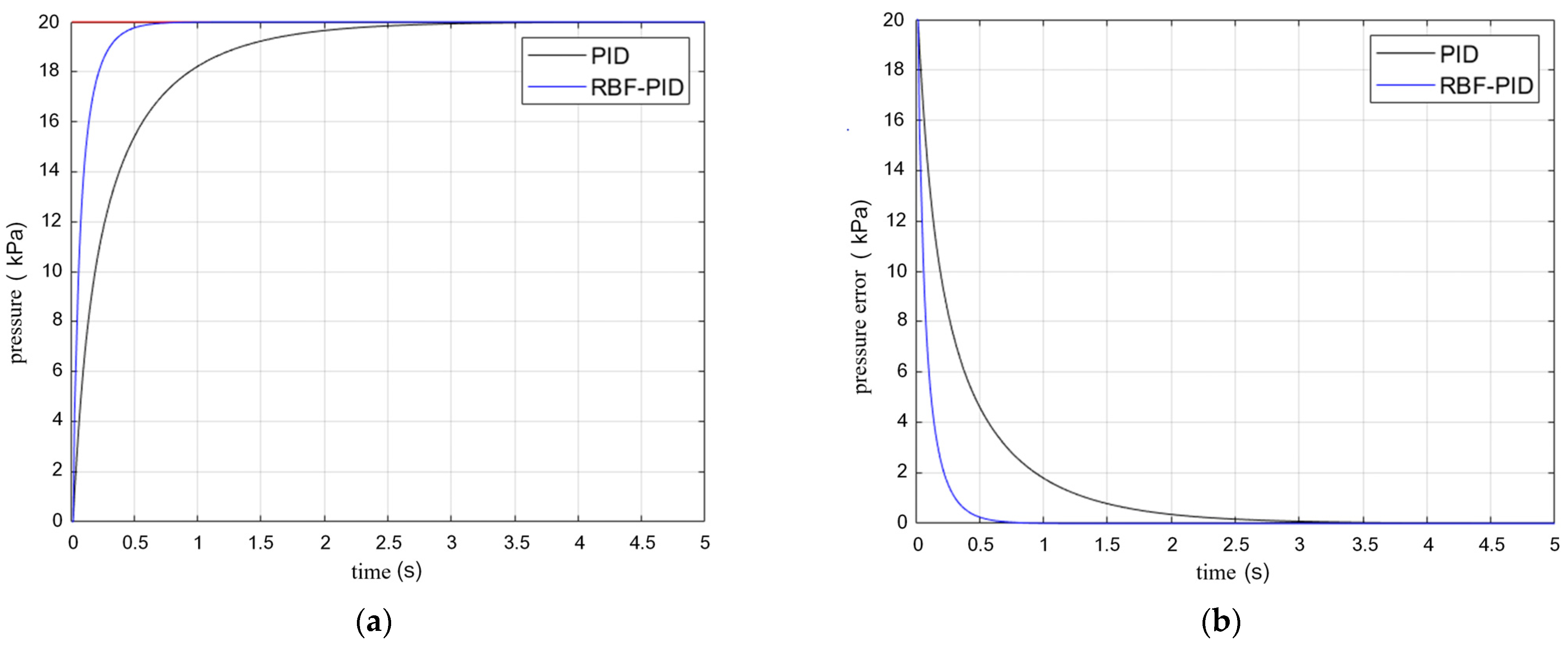
4.2. Flexible Finger Pressure Control Experiment Based on RBF Neural Network Tuning PID Control
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, B. Research on the Design of Manipulator Robot Claw. Mod. Ind. Econ. Inf. Technol. 2020, 10, 41–42. [Google Scholar]
- Tuleja, P.; Sidlovska, L. Unilateral gripping with active vacuum suction cup Calculation of gripping force and number of suction cups. Transf. Inovacii 2014, 29, 232–235. [Google Scholar]
- Shintake, J.; Cacucciolo, V.; Floreano, D.; Shea, H. Soft robotic grippers. Adv. Mater. 2018, 30, 1707035. [Google Scholar] [CrossRef] [PubMed]
- Rus, D.; Tolley, M.T. Design, fabrication and control of soft robots. Nature 2015, 521, 467–475. [Google Scholar] [CrossRef] [PubMed]
- Tramacere, F.; Beccai, L.; Mattioli, F.; Sinibaldi, E.; Mazzolai, B. Artificial Adhesion Mechanisms Inspired by Octopus Suckers. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; IEEE: Piscataway, NJ, USA, 2018; pp. 3846–3851. [Google Scholar]
- Zheng, Z.; Wang, K.; Wu, X.; Zhang, Q.; Li, K. Dynamic analysis of elastic projecting robot inspired by chameleon tongue. In Proceedings of the 2018 IEEE International Conference on Robotics and Biomimetics (ROBIO), Kuala Lumpur, Malaysia, 12–15 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 2088–2094. [Google Scholar]
- Zhang, Z.; Zhou, J.; Yi, B.; Wang, K. A flexible swallowing gripper for harvesting apples and its grasping force sensing model. Comput. Electron. Agric. 2023, 204, 107489. [Google Scholar] [CrossRef]
- Luo, Z.; Wang, S.; Cheng, G.; Yuan, N.; Ding, J. Design, manufacturing, and control of biomimetic hands based on elastic materials. J. Mech. Eng. 2019, 55, 11. [Google Scholar] [CrossRef]
- Barbieri, L.; Bruno, F.; Gallo, A.; Muzzupappa, M.; Russo, M.L. Design, Prototyping and Testing of a Modular Small-Sized Underwater Robotic Arm Controlled through a Master-Slave Approach. Ocean. Eng. 2018, 158, 253–262. [Google Scholar] [CrossRef]
- Hao, Y.; Gong, Z.; Xie, Z.; Guan, S.; Yang, X.; Ren, Z.; Wang, T.; Wen, L. Universal soft pneumatic robotic gripper with variable effective length. In Proceedings of the 2016 35th Chinese control conference (CCC), Chengdu, China, 27–29 July 2016; IEEE: Piscataway, NJ, USA, 2018; pp. 6109–6114. [Google Scholar]
- Sinatra, N.R.; Teeple, C.B.; Vogt, D.M.; Parker, K.K.; Gruber, D.F.; Wood, R.J. Ultragentle Manipulation of Delicate Structures Using a Soft Robotic Gripper. Sci. Robot 2019, 4, 5425. [Google Scholar] [CrossRef] [PubMed]
- Lau, G.K.; Heng, K.R.; Ahmed, A.S.; Shrestha, M. Dielectric elastomer fingers for versatile grasping and nimble pinching. Appl. Phys. Lett. 2017, 110, 18. [Google Scholar] [CrossRef]
- Li, L.; Fengming, X.; Tianhong, W.; Guopeng, W.; Yingzhong, T.; Tao, J.; Quan, Z. Stiffness-Tunable Soft Gripper with Soft-Rigid Hybrid Actuation for Versatile Manipulations. Soft Robot. 2022, 9, 1108–1119. [Google Scholar] [CrossRef]
- Homberg, B.S.; Katzschmann, R.K.; Dogar, M.R.; Rus, D. Haptic identification of objects using a modular soft robotic gripper. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1698–1705. [Google Scholar]
- Merces, L.; Ferro, L.M.M.; Thomas, A.; Karnaushenko, D.D.; Luo, Y.; Egunov, A.I.; Zhang, W.; Bandari, V.K.; Lee, Y.; McCaskill, J.S.; et al. Bio-Inspired Dynamically Morphing Microelectronics toward High-Density Energy Applications and Intelligent Biomedical Implants. Adv. Mater. 2024, 36, 2313327. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Birla, M.; Oldham, K.R.; Filipov, E.T. Elastically and Plastically Foldable Electrothermal Micro-Origami for Controllable and Rapid Shape Morphing. Adv. Funct. Mater. 2020, 30, 2003741. [Google Scholar] [CrossRef]
- Tawk, C.; Gillett, A.; in het Panhuis, M.; Spinks, G.M.; Alici, G. A 3D-Printed Omni-Purpose Soft Gripper. IEEE Trans. Robot. 2019, 35, 1268–1275. [Google Scholar] [CrossRef]
- Xavier, M.S.; Tawk, C.D.; Zolfagharian, A.; Pinskier, J.; Howard, D.; Young, T.; Jiewen, L.; Harrison, S.M.; Yong, Y.K.; Bodaghi, M.; et al. Soft pneumatic actuators: A review of design, fabrication, modeling, sensing, control and applications. IEEE Access 2022, 10, 59442–59485. [Google Scholar] [CrossRef]
- Pagoli, A.; Chapelle, F.; Corrales-Ramon, J.A.; Mezouar, Y.; Lapusta, Y. Review of soft fluidic actuators: Classification and materials modeling analysis. Smart Mater. Struct. 2021, 31, 013001. [Google Scholar] [CrossRef]
- Marchese, A.D.; Katzschmann, R.K.; Rus, D. A recipe for soft fluidic elastomer robots. Soft Robot. 2015, 1, 7–25. [Google Scholar] [CrossRef] [PubMed]
- Hu, W.; Mutlu, R.; Li, W.; Alici, G. A structural optimisation method for a soft pneumatic actuator. Robotics 2018, 7, 24. [Google Scholar] [CrossRef]
- Xavier, M.S.; Fleming, A.J.; Yong, Y.K. Design and control of pneumatic systems for soft robotics: A simulation approach. IEEE Robot. Autom. Lett. 2021, 6, 5800–5807. [Google Scholar] [CrossRef]
- Joshi, S.; Paik, J. Pneumatic supply system parameter optimization for soft actuators. Soft Robot. 2021, 8, 152–163. [Google Scholar] [CrossRef]
- Joshi, S.; Sonar, H.; Paik, J. Flow path optimization for soft pneumatic actuators: Towards optimal performance and portability. IEEE Robot. Autom. Lett. 2021, 6, 7949–7956. [Google Scholar] [CrossRef]
- Qian, P.; Luo, H.; Liu, L.; Lv, P.; Pu, C.; Meng, D.; Páez, L.M.R. A hybrid Gaussian mutation PSO with search space reduction and its application to intelligent selection of piston seal grooves for homemade pneumatic cylinders. Eng. Appl. Artif. Intell. 2023, 122, 106156. [Google Scholar] [CrossRef]
- Qian, P.; Liu, L.; Wu, J.; Pu, C.; Luo, H.; Fu, Y.; Zuo, Q. A novel double-acting, air-floating, frictionless pneumatic actuator. Sens. Actuators A Phys. 2023, 362, 114674. [Google Scholar] [CrossRef]
- Shi, Y.; Li, H.; Fu, X.; Luan, R.; Wang, Y.; Wang, N.; Wang, N.; Sun, Z.; Niu, Y.; Wang, C.; et al. Self-powered difunctional sensors based on sliding contact-electrification and tribovoltaic effects for pneumatic monitoring and controlling. Nano Energy 2023, 110, 108339. [Google Scholar] [CrossRef]
- Shi, Y.; Yang, Z.; Wang, Y.; Xu, S.; Sun, Z.; Wu, J.; Wang, C. Observer-Based Adaptive Finite-Time Contact Force Tracking Control for Pneumatic Polishing System. IEEE Sens. J. 2024, 24, 19801–19812. [Google Scholar] [CrossRef]
- Wang, C.; Shi, Y.; Wang, Y.; Xu, S.; Liang, M. Event-Triggered Adaptive Fuzzy Output Feedback Tracking Control for Pneumatic Servo System with Input Voltage Saturation and Position Constraint. IEEE Trans. Ind. Inform. 2024, 20, 4360–4369. [Google Scholar] [CrossRef]
- Wang, C.; Shi, Y.; Wang, Y.; Xu, S.; Sun, Z. Position Tracking Control for Pneumatic Servo System Subject to State Constraints and Voltage Saturation. IEEE/ASME Trans. Mechatron. 2023, 43, 1–11. [Google Scholar] [CrossRef]
- Wang, N.; Xu, L.; Xie, F.; Shi, Y.; Wang, Y. Research on the dynamic characteristics of pneumatic proportional regulator in pneumatic-loading system and design of fuzzy adaptive controller. Sci. China Technol. Sci. 2022, 65, 956–965. [Google Scholar] [CrossRef]
- Halladay, J.R.; Jaglowski, K.T. Sources of hysteresis in rubber compound. Rubber Plast. News 2017, 7, 13–17. [Google Scholar]
- McCulloch, A. Logival of the ideas imminent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Powell, M.J.; Radial, D. Basis Function for Multivariable Interpolation: A Review; Mason, J.C., Cox, M.G., Eds.; Algorithms for Approximation; Carendon Press: Oxford, UK, 1985; pp. 143–167. [Google Scholar]
- Broomhead, D.S.; Lowe, D. Multivariable functional interpolation and adaptive networks. Complex Syst. 1998, 2, 321–355. [Google Scholar]






| Device Name | Device Type | Input Voltage | Output Voltage | Input Air Pressure | Output Air Pressure |
|---|---|---|---|---|---|
| power supply A | D-30B | 100–240 V | 5–24 V | / | / |
| power supply B | S-35-12 | 115–230 V | 12 V | / | / |
| terminal board | CB-68LP | / | / | / | / |
| breadboard | ZY-60 | / | / | / | / |
| data acquisition card | PCI-E 6353 | −10–10 V | −10–10 V | / | / |
| driver module | L298N | 9–12 V | 0–12 V | / | / |
| air pressure sensor | XGZP6847A | / | 0.5–4.5 V | −100–700 kPa | / |
| micro-air pump | 370-B | 0–12 V | / | / | −60–160 kPa |
| two-way ball valve | VHK2-06F-06F | / | / | / | / |
| barometer | YN60 | / | / | 0–100 kPa | / |
| gas-stabilizing device | / | / | / | / | / |
| holding device | syj-02 | / | / | / | / |
| measuring paper | A4 | / | / | / | / |
| computer | / | / | / | / | / |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Wang, K.; Cai, M.; Shi, Y.; Gong, S.; Zhang, H.; Zhang, P. Structural Design and Control Performance Study of Flexible Finger Mechanisms for Robot End Effectors. Actuators 2024, 13, 271. https://doi.org/10.3390/act13070271
Zhang Y, Wang K, Cai M, Shi Y, Gong S, Zhang H, Zhang P. Structural Design and Control Performance Study of Flexible Finger Mechanisms for Robot End Effectors. Actuators. 2024; 13(7):271. https://doi.org/10.3390/act13070271
Chicago/Turabian StyleZhang, Yeming, Kai Wang, Maolin Cai, Yan Shi, Sanpeng Gong, Hui Zhang, and Pengyun Zhang. 2024. "Structural Design and Control Performance Study of Flexible Finger Mechanisms for Robot End Effectors" Actuators 13, no. 7: 271. https://doi.org/10.3390/act13070271
APA StyleZhang, Y., Wang, K., Cai, M., Shi, Y., Gong, S., Zhang, H., & Zhang, P. (2024). Structural Design and Control Performance Study of Flexible Finger Mechanisms for Robot End Effectors. Actuators, 13(7), 271. https://doi.org/10.3390/act13070271







