Disturbance Observer-Based Adaptive Fault Tolerant Control with Prescribed Performance of a Continuum Robot
Abstract
1. Introduction
- (1)
- Compared with the conventional prescribed performance results, in this paper, an asymmetric time-varying BLF is applied for uncertain continuum robot systems to avert the tracking error contravening the time-varying constraint, which has a faster convergence speed and higher tracking accuracy.
- (2)
- A function approximation technique (FAT) is introduced to effectively evaluate the lumped unknown term of the continuum robot. The proposed FAT has a good capability to approximate the discontinuous and continuous unknown functions, respectively. Furthermore, FAT has less computation, since there are fewer tuning parameters.
- (3)
- In contrast with the traditional DO-based AFTC methods, a nonlinear DO is operated to estimate the new compounded disturbance, which can erase the disturbance quickly and offer higher estimation accuracy. Furthermore, no matter when actuator faults occur, the proposed controller of the continuum robot can evaluate the uncertain disturbance in real time and has a good control performance.
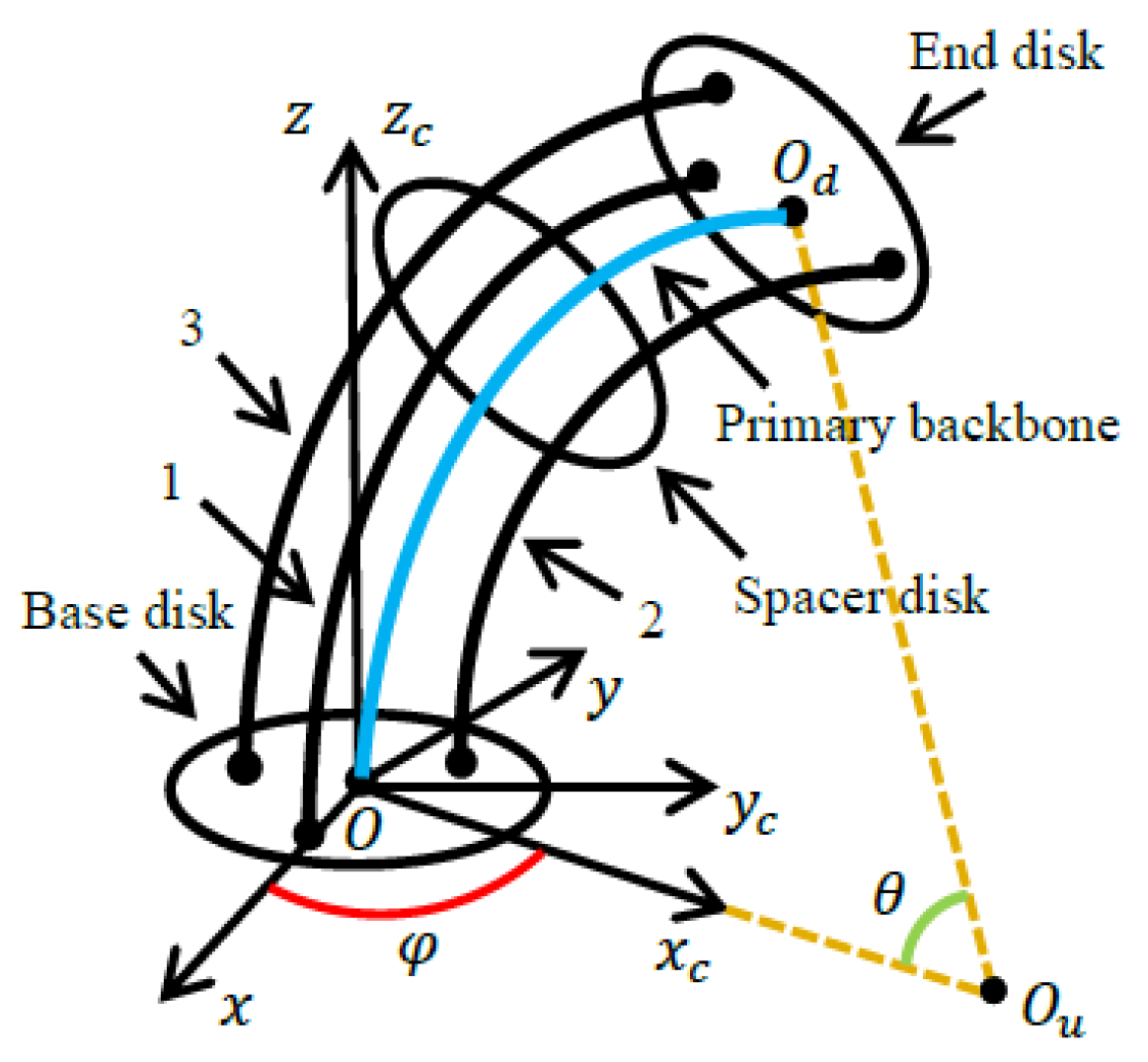
2. System Description and Problem Formulation
3. Design of AFTC
3.1. Controller Design
3.2. Stability Analysis
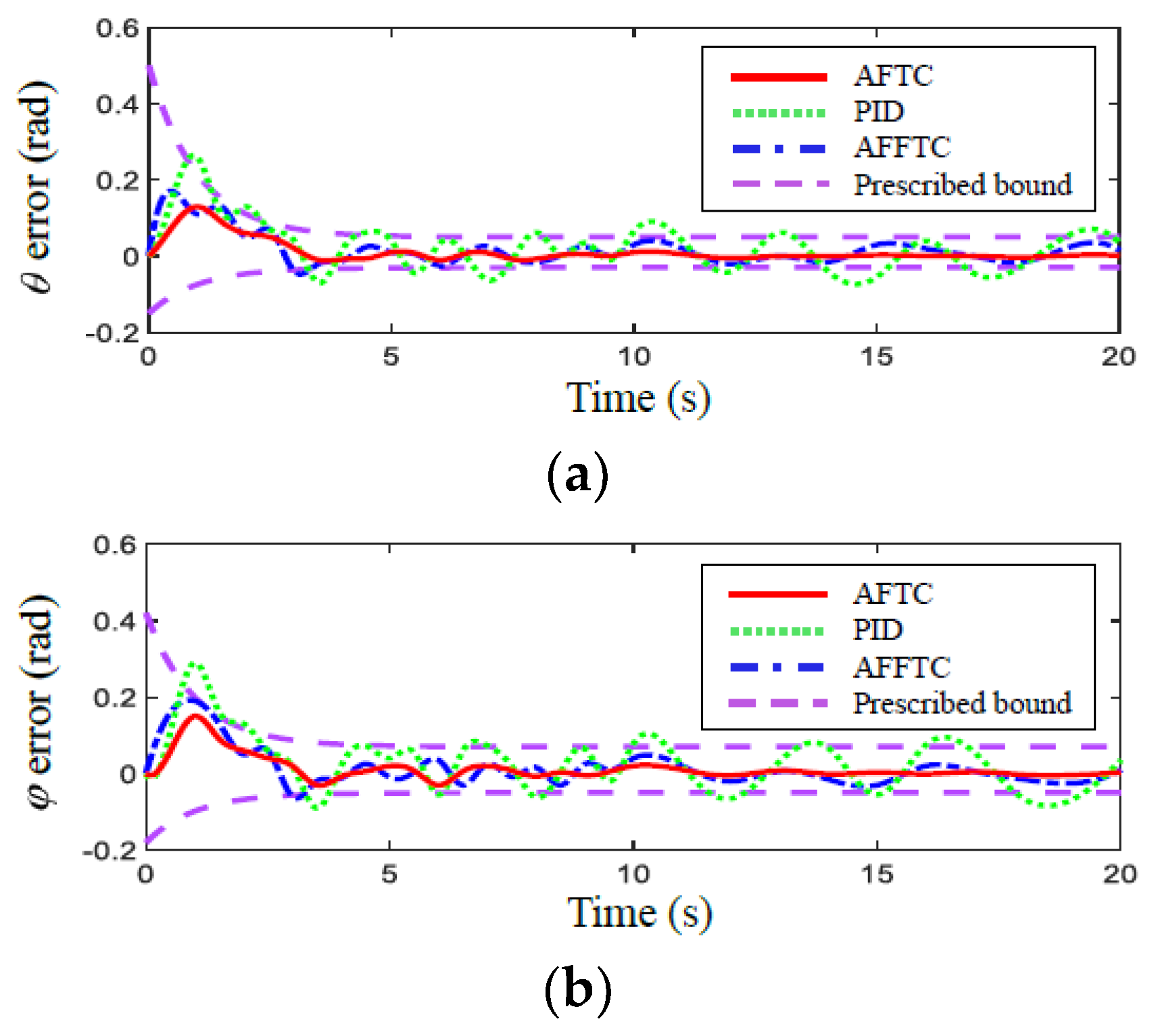
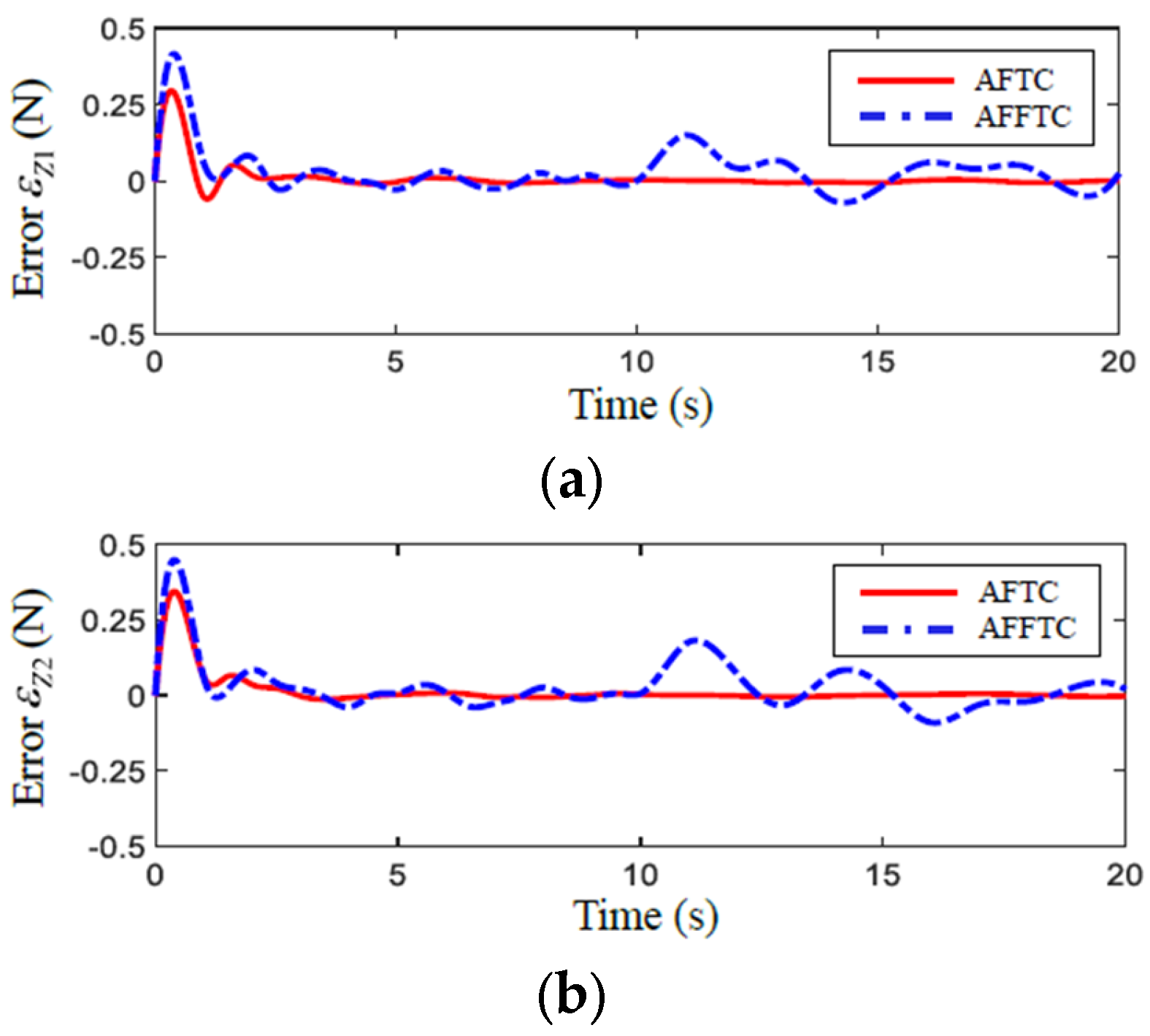
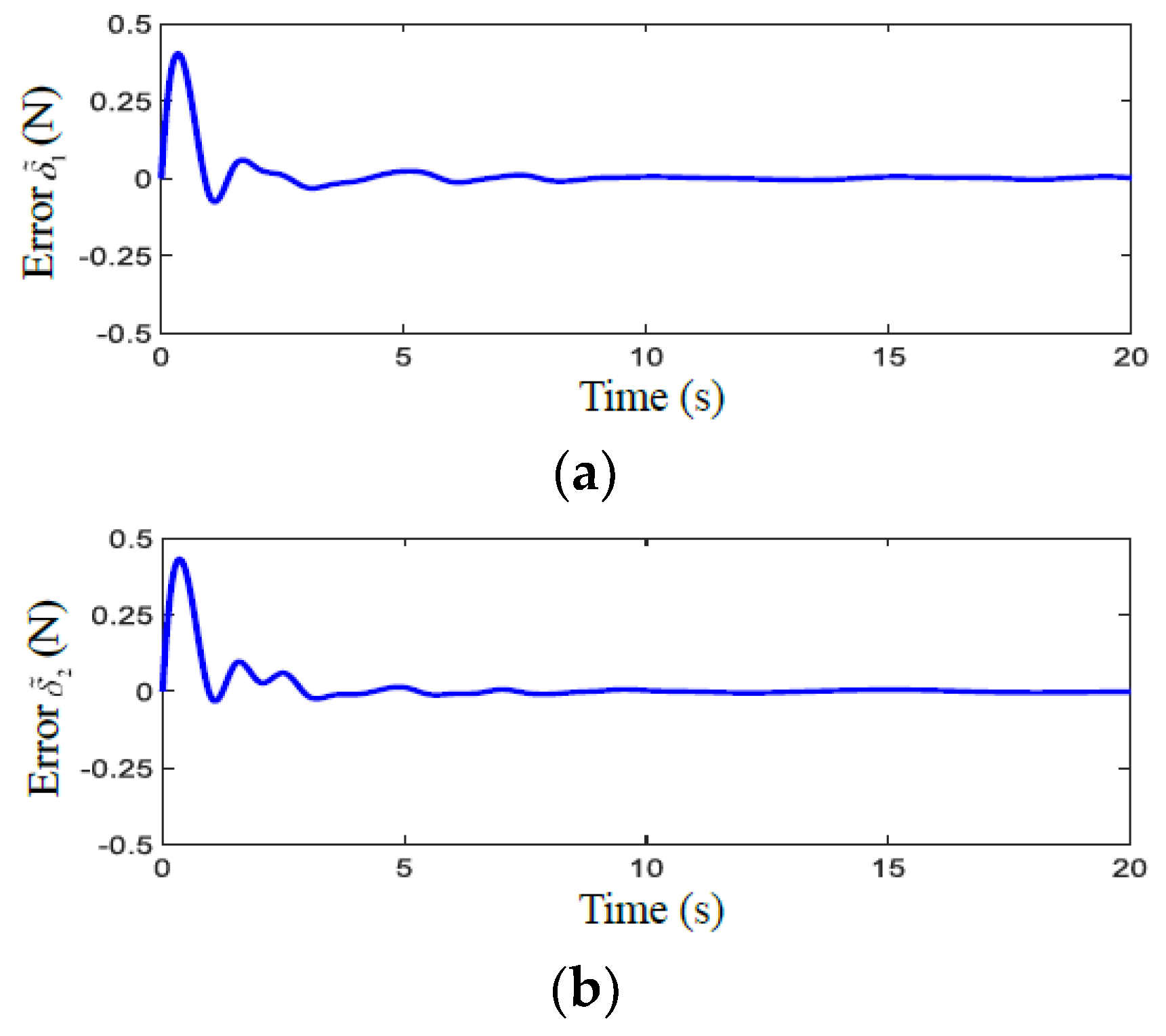
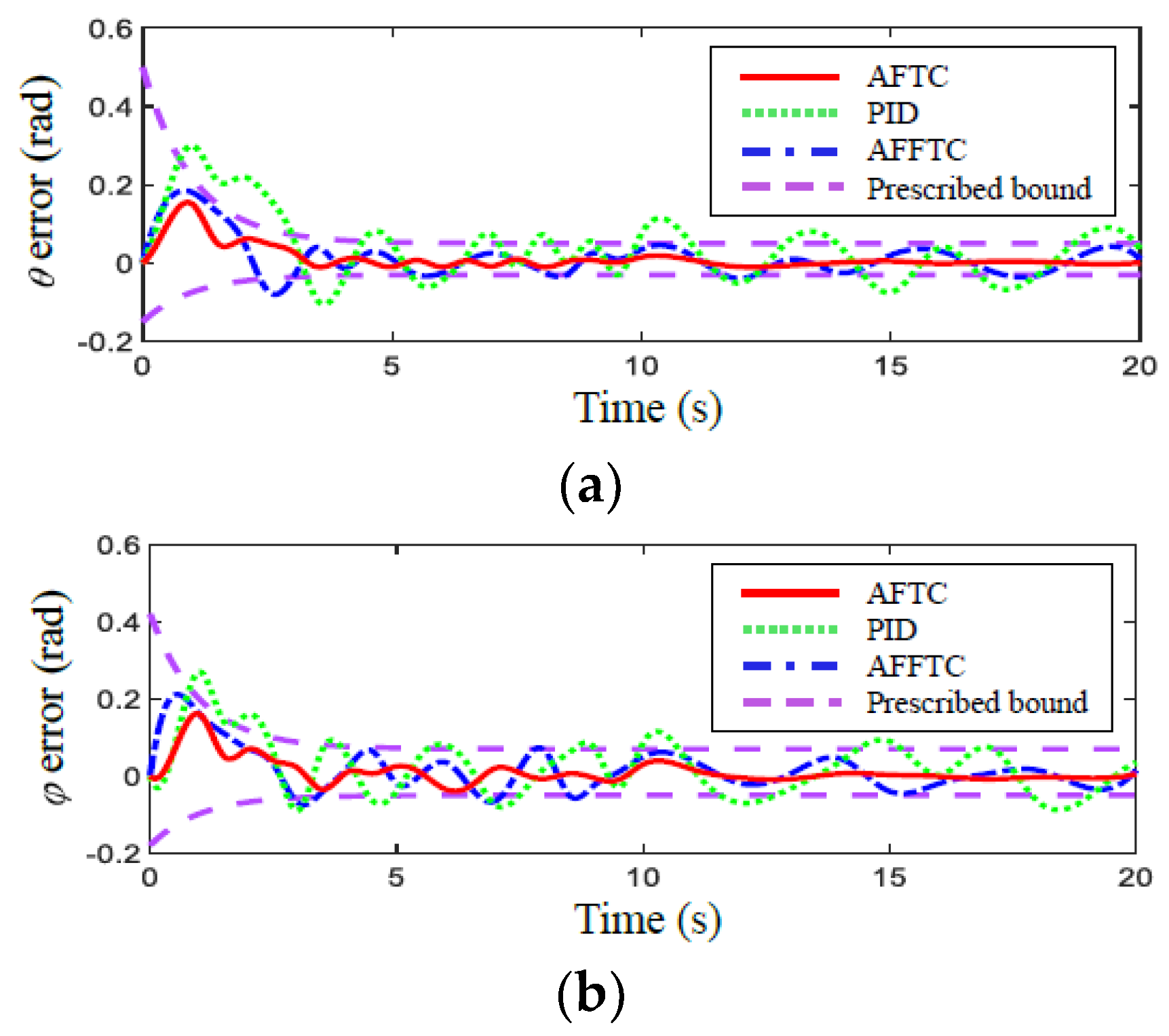
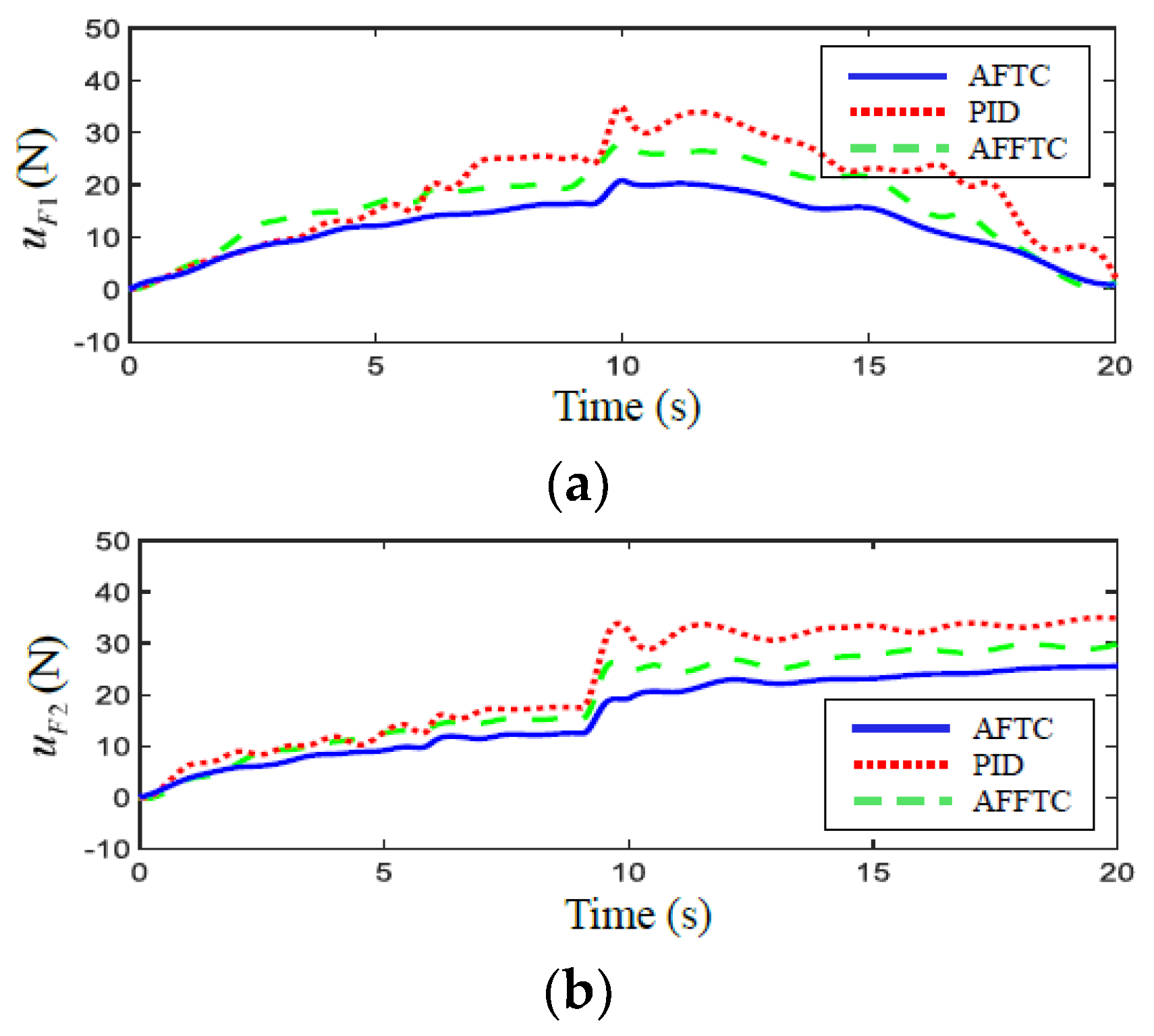
4. Simulation Results
5. Experiment Results
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Gao, Y.; Takagi, K.; Kato, T.; Shono, N.; Hata, N. Continuum robot with follow-the-leader motion for endoscopic third ventriculostomy and tumor biopsy. IEEE Trans. Biomed. Eng. 2020, 67, 379–390. [Google Scholar] [CrossRef] [PubMed]
- Xiao, B.; Cao, L.; Xu, S.; Liu, L. Robust tracking control of robot manipulators with actuator faults and joint velocity measurement uncertainty. IEEE/ASME Trans. Mechatron. 2020, 25, 1354–1365. [Google Scholar] [CrossRef]
- He, B.; Wang, Z.; Li, Q.; Xie, H.; Shen, R. An analytic method for the kinematics and dynamics of a multiple-backbone continuum robot. Int. J. Adv. Robot. Syst. 2013, 10, 84. [Google Scholar] [CrossRef]
- Jabari, M.; Zakeri, M.; Janabi-Sharifi, F.; Norouzi-Ghazbi, S. Inverse kinematics of concentric tube robots in the presence of environmental constraints. Appl. Bionics Biomech. 2021, 2021, 4107732. [Google Scholar] [CrossRef] [PubMed]
- Xu, S.; He, B. Adaptive approximation tracking control of a continuum robot with uncertainty disturbances. IEEE Trans. Cybern. 2024, 54, 230–240. [Google Scholar] [CrossRef] [PubMed]
- Lai, J.; Huang, K.; Lu, B.; Zhao, Q.; Chu, H. Verticalized-tip trajectory tracking of a 3D-printable soft continuum robot: Enabling surgical blood suction automation. IEEE/ASME Trans. Mechatron. 2022, 27, 1545–1556. [Google Scholar] [CrossRef]
- Xu, S. Adaptive approximation sliding-mode control of an uncertain continuum robot with input nonlinearities and disturbances. Appl. Bionics Biomech. 2024, 2024, 8533606. [Google Scholar] [CrossRef]
- Jin, X.; Che, W.; Wu, Z.; Wang, H. Analog control circuit designs for a class of continuous-time adaptive fault-tolerant control systems. IEEE Trans. Cybern. 2022, 52, 4209–4220. [Google Scholar] [CrossRef]
- Zhu, S.; Li, H.; Wang, G.; Kuang, C.; Chen, H.; Gao, J.; Xie, W. Research on fault-tolerant control of distributed-drive electric vehicles based on fuzzy fault diagnosis. Actuators 2023, 12, 246. [Google Scholar] [CrossRef]
- Chang, Y.; Wu, C.; Lin, H. Adaptive distributed fault-tolerant formation control for multi-robot systems under partial loss of actuator effectiveness. Int. J. Control Autom. Syst. 2018, 16, 2114–2124. [Google Scholar] [CrossRef]
- Lomakin, A.; Deutscher, J. Reliable algebraic fault detection and identification of robots. IEEE Trans. Autom. Sci. Eng. 2022, 19, 3821–3837. [Google Scholar] [CrossRef]
- Zhao, D.; Jiang, B.; Yang, H. Backstepping-based decentralized fault-tolerant control of hypersonic vehicles in PDE-ODE form. Int. J. Robust Nonlinear Control 2022, 67, 1210–1225. [Google Scholar] [CrossRef]
- Van, M.; Mavrovouniotis, M.; Ge, S.S. An adaptive backstepping nonsingular fast terminal sliding mode control for robust fault tolerant control of robot manipulators. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 1448–1458. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, G. Adaptive fuzzy fault-tolerant control of uncertain Euler-Lagrange systems with process faults. IEEE Trans. Fuzz. Syst. 2020, 28, 2619–2630. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, X.; Cheng, Y. Model free based finite time fault-tolerant control of robot manipulators subject to disturbances and input saturation. Int. J. Robust Nonlinear Control 2022, 32, 5281–5303. [Google Scholar] [CrossRef]
- Van, M.; Ge, S.S. Adaptive fuzzy integral sliding-mode control for robust fault-tolerant control of robot manipulators with disturbance observer. IEEE Trans. Fuzz. Syst. 2021, 29, 1284–1296. [Google Scholar] [CrossRef]
- He, W.; Huang, H.; Ge, S.S. Adaptive neural network control of a robotic manipulator with time-varying output constraints. IEEE Trans. Cybern. 2017, 47, 3136–3147. [Google Scholar] [CrossRef] [PubMed]
- Hu, B.; Guan, Z.; Lewis, F.; Chen, C.L.P. Adaptive tracking control of cooperative robot manipulators with markovian switched couplings. IEEE Trans. Ind. Electron. 2021, 68, 2427–2436. [Google Scholar] [CrossRef]
- Lin, C.; Sie, T. Design and experimental characterization of artificial neural network controller for a lower limb robotic exoskeleton. Actuators 2023, 12, 55. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, H.; Wang, Y.; Sun, S. Adaptive fuzzy control for nonstrict-feedback systems under asymmetric time-varying full state constraints without feasibility condition. IEEE Trans. Fuzz. Syst. 2021, 29, 976–985. [Google Scholar] [CrossRef]
- Lv, M.; Li, Y.; Pan, W.; Baldi, S. Finite-time fuzzy adaptive constrained tracking control for hypersonic flight vehicles with singularity-free switching. IEEE/ASME Trans. Mechatron. 2022, 27, 1594–1605. [Google Scholar] [CrossRef]
- Wang, S.; Yu, H.; Yu, J.; Na, J.; Ren, X. Neural-network-based adaptive funnel control for servo mechanisms with unknown dead-zone. IEEE Trans. Cybern. 2021, 50, 1383–1394. [Google Scholar] [CrossRef]
- Zhang, Y.; Niu, H.; Tao, J.; Li, X. Novel data and neural network-based nonlinear adaptive switching control method. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 789–797. [Google Scholar] [CrossRef]
- Huang, H.; Pan, H.; Cheng, Y. Tracking control for flexible joint robots based on adaptive fuzzy compensation with uncertain parameters. Int. J. Adapt. Control Signal Process. 2021, 35, 1633–1648. [Google Scholar] [CrossRef]
- Izadbakhsh, A. FAT-based robust adaptive control of electrically driven robots without velocity measurements. Nonlinear Dyn. 2017, 89, 289–304. [Google Scholar] [CrossRef]
- Wang, Y.; Bai, Y.; Svinin, M. Function approximation technique based adaptive control for chaos synchronization between different systems with unknown dynamics. Int. J. Control Autom. Syst. 2021, 19, 2611–2621. [Google Scholar] [CrossRef]
- Khodamipour, G.; Khorashadizadeh, S.; Farshad, M. Observer-based adaptive control of robot manipulators using reinforcement learning and the Fourier series expansion. Trans. Inst. Meas. Control 2021, 43, 2307–2320. [Google Scholar] [CrossRef]
- Bu, W.; Li, T.; Yang, J.; Yi, Y. Disturbance observer-based event-triggered tracking control of networked robot manipulator. Meas. Control 2020, 53, 892–898. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, W.; Shen, G.; Xia, Y. Disturbance observer-based adaptive finite-time attitude tracking control for rigid spacecraft. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 6606–6613. [Google Scholar] [CrossRef]
- Mao, Q.; Dou, L.; Yang, Z.; Tian, B.; Zong, Q. Fuzzy disturbance observer-based adaptive sliding mode control for reusable launch vehicles with aeroservoelastic characteristic. IEEE Trans. Ind. Inform. 2020, 16, 1214–1223. [Google Scholar] [CrossRef]
- Zhang, Q.; He, D. Disturbance-observer-based adaptive fuzzy control for strict-feedback switched nonlinear systems with input delay. IEEE Trans. Fuzz. Syst. 2021, 29, 1942–1952. [Google Scholar] [CrossRef]
- Li, Z.; Su, C.; Wang, L.; Chen, Z.; Chai, T. Nonlinear disturbance observer-based control design for a robotic exoskeleton incorporating fuzzy approximation. IEEE Trans. Ind. Electron. 2015, 62, 5763–5775. [Google Scholar] [CrossRef]
- Zhao, Z.; He, X.; Ahn, C. Boundary disturbance observer-based control of a vibrating single-link flexible manipulator. IEEE Trans. Syst. Man. Cybern. Syst. 2021, 51, 2382–2390. [Google Scholar] [CrossRef]
- Cui, G.; Yu, J.; Shi, P. Observer-based finite-time adaptive fuzzy control with prescribed performance for nonstrict-feedback nonlinear systems. IEEE Trans. Fuzz. Syst. 2022, 30, 767–778. [Google Scholar] [CrossRef]
- Zhou, Q.; Zhao, S.; Li, H.; Lu, R.; Wu, C. Adaptive neural network tracking control for robotic manipulators with dead zone. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 3611–3620. [Google Scholar] [CrossRef] [PubMed]
- Shao, X.; Hu, Q.; Shi, Y.; Jiang, B. Fault-tolerant prescribed performance attitude tracking control for spacecraft under input saturation. IEEE Trans. Control Syst. Technol. 2020, 28, 574–582. [Google Scholar] [CrossRef]
- Nai, Y.; Yang, Q.; Wu, Z. Prescribed performance adaptive neural compensation control for intermittent actuator faults by state and output feedback. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 4931–4945. [Google Scholar] [CrossRef]
- Shen, Z.; Wang, Q.; Dong, S.; Yu, H. Dynamic surface control for tracking of unmanned surface vessel with prescribed performance and asymmetric time-varying full state constraints. Ocean. Eng. 2022, 253, 111319. [Google Scholar] [CrossRef]
- Liu, Y.; Gong, M.; Liu, L.; Tong, S.; Chen, C.L.P. Fuzzy observer constraint based on adaptive control for uncertain nonlinear MIMO systems with time-varying state constraints. IEEE Trans. Cybern. 2021, 51, 1380–1389. [Google Scholar] [CrossRef]


| Controllers | Parameters |
|---|---|
| PID | , , |
| AFFTC | , , , , , , |
| AFTC | , , , ,, , , |
| Controllers | RMSE (rad) | RMSE (rad) |
|---|---|---|
| PID | 0.0216 | 0.0273 |
| AFFTC | 0.0183 | 0.0172 |
| AFTC | 0.0102 | 0.0118 |
| Controllers | RMSE (rad) | RMSE (rad) |
|---|---|---|
| PID | 0.0237 | 0.0295 |
| AFFTC | 0.0196 | 0.0183 |
| AFTC | 0.0112 | 0.0126 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, S. Disturbance Observer-Based Adaptive Fault Tolerant Control with Prescribed Performance of a Continuum Robot. Actuators 2024, 13, 267. https://doi.org/10.3390/act13070267
Xu S. Disturbance Observer-Based Adaptive Fault Tolerant Control with Prescribed Performance of a Continuum Robot. Actuators. 2024; 13(7):267. https://doi.org/10.3390/act13070267
Chicago/Turabian StyleXu, Shoulin. 2024. "Disturbance Observer-Based Adaptive Fault Tolerant Control with Prescribed Performance of a Continuum Robot" Actuators 13, no. 7: 267. https://doi.org/10.3390/act13070267
APA StyleXu, S. (2024). Disturbance Observer-Based Adaptive Fault Tolerant Control with Prescribed Performance of a Continuum Robot. Actuators, 13(7), 267. https://doi.org/10.3390/act13070267





