Fixed-Time Adaptive Neural Network-Based Trajectory Tracking Control for Workspace Manipulators

Abstract

This paper proposes a novel neural network-based control algorithm with fixed-time performance constraints for manipulator systems in workspaces. The algorithm efficiently controls the manipulator’s trajectory tracking by tuning a preset performance function, thereby optimizing both speed and accuracy within a fixed timeframe. Initially, a tangent-type error transformation, applied through homogeneous embryonic transformation, ensures rapid convergence of tracking errors to a specific region. Subsequently, integrating a predetermined control strategy into the fixed-time stability framework ensures the system’s state reaches a defined boundary within a finite period. Lastly, neural networks are employed to approximate dynamic parameters and adjust the controller, achieving optimal parameter approximation and significantly enhancing trajectory tracking robustness. Simulation analyses and comparisons confirm the controller’s effectiveness and superiority in enhancing both the transient and steady-state performance of the control system.

1. Introduction

As modern industry rapidly evolves, manipulators are increasingly utilized in industrial production. Owing to their high efficiency, flexibility, and precision, manipulators play a vital role in industrial production. However, the control of manipulators remains a challenging and keenly studied area due to their highly nonlinear, strongly coupled, and time-varying nature [1,2,3].

Addressing the manipulator’s trajectory tracking control, scholars globally have extensively researched and proposed methods including proportion integration differentiation (PID) control [4,5,6], inverse-step control [7,8], and sliding mode control [9,10]. Despite their simplicity and usability, these methods struggle to fulfill high accuracy and robustness requirements. To address these shortcomings, researchers have introduced additional methods like adaptive control [11,12,13,14], robust control [15,16,17,18], and fuzzy control [19,20,21,22]. While these methods improve control performance and handle system uncertainty, their slow convergence speed fails to meet rapid response requirements.

Recent years have seen the proposal of new control schemes to meet the growing demands for manipulator control accuracy in the industry. Within these control schemes, certain studies specifically address the manipulator system’s uncertainty. For instance, Ref. [23] describes combining adaptive backstepping control with fuzzy logic systems’ function approximation capabilities to create controllers for input-saturated manipulator systems. Moreover, Ref. [24] addresses how environmental or inherent conditions may limit a manipulator’s position and angular velocity, achieving indirect system state constraints through position error limitations using the obstacle Lyapunov function. Other studies have focused on addressing issues within traditional control schemes. The article [25] introduces an enhanced design method for a robust, optimal, flexible jointed manipulator interference observer, aiming to maximize interference suppression and ensure optimal trajectory tracking. While the paper primarily improves the steady-state accuracy of flexible jointed manipulator position tracking, it overlooks in-depth analysis of transient response and output constraints. Study [26] employs a nonlinear filter with a self-compensation feature to correct boundary layer errors and mitigate filter inaccuracies. While this scheme enhances control performance, the nonlinear filter significantly complicates the overall control system.

To further improve the control performance of manipulator systems, preset performance control [27,28,29] and fixed-time control [30,31] have received much attention. The fixed-time control ensures tracking error convergence to a steady state within a set period, yet it overlooks transient performance constraints. The preset performance control is able to satisfy both the transient and steady-state performance requirements of the manipulators, but it cannot explicitly provide the time at which the system enters the steady state. The control scheme proposed in study [32] ensures both transient and steady state performance of the system but does not allow the tracking error to converge within a predefined performance boundary in a predefined time. Study [33] merges finite time with predefined performance control, offering a trajectory tracking scheme. However, its convergence rate, tied to a fixed stopping time parameter, limits flexibility and transient performance enhancement.

Despite the extensive research, controller design frequently relies on fully available robot dynamics models, which are seldom accessible in real-world scenarios. Consequently, exploring advanced control strategies to address model uncertainties becomes critically important. Neural networks (NN) are renowned and utilized for their superior function approximation abilities, particularly in simplifying the modeling of nonlinear systems [34,35]. This implies new solution avenues for manipulator control issues, especially those lacking precise dynamic models, through the robust modeling and approximation prowess of neural networks. Employing neural networks comprehensively for control compensates for traditional model deficiencies, enhances system stability and accuracy, and facilitates the broader application and development of manipulator systems across various fields.

Building on the previous discussion, this study integrates a pre-programmed performance control strategy within a fixed-time stability framework and employs adaptive neural network control to devise a manipulator control strategy for superior performance under stringent constraints. Our study’s achievement of quicker response and heightened precision not only boosts the manipulators’ operational performance in intricate scenarios but also its adaptability and flexibility, all while maintaining constraint compliance and system safety, marking significant theoretical and practical advancements. Relative to existing methods, this paper’s primary contributions are as follows:

• The homogeneous embryo transformation enables tangent-type error transformation, ensuring tracking error convergence to a specific region and preventing “performance spikes” seen in traditional control methods;
• The integration of the preset performance control strategy into the fixed-time stability theoretical framework not only ensures that the state converges to a predetermined region within a predetermined time, but also further adjusts the convergence speed and accuracy to achieve better control performance;
• The use of neural networks to approximate the unknown dynamical parameters and compensate the prediction results to the controller improves the robustness and adaptive ability of the controller without the need of known uncertainty boundaries of the system.

This paper is structured as follows: Section 2 introduces the system model and performance function. Section 3 details the design of a neural network controller with fixed-time preset performance. Section 4 presents simulation validation to demonstrate the algorithm’s effectiveness. Section 5 concludes the paper and outlines future research directions.

2. System Modeling and Problem Formulation

2.1. Coordinate Transformation

To represent the model in the workspace, the manipulator joint coordinates $\left({\varphi }_1,{\varphi }_2\right)$ need to be transformed into the end-effector Cartesian coordinates $\left(x_1,x_2\right)$.

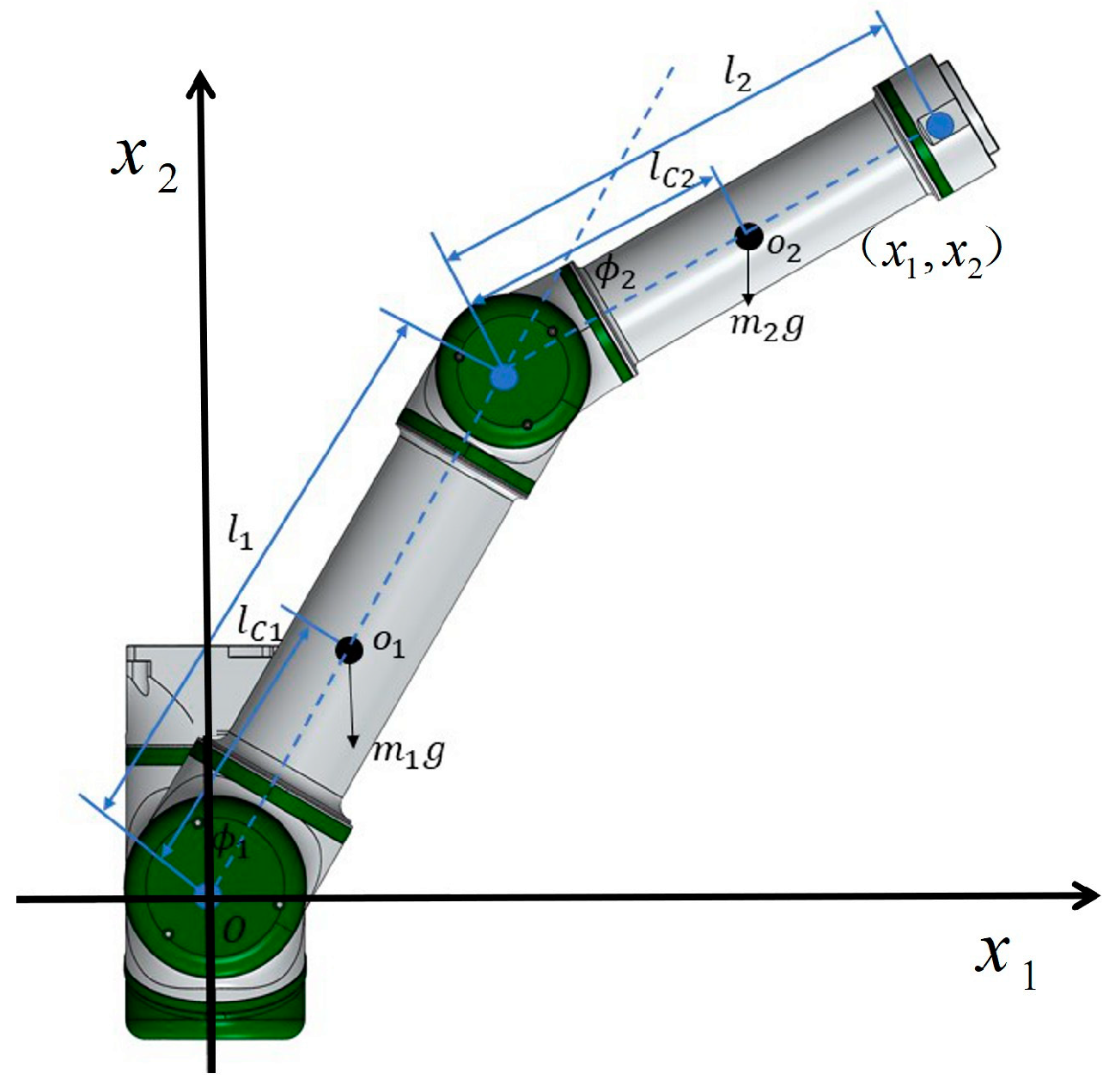
The schematic structure of the two-degree-of-freedom manipulator is shown in Figure 1, and modeling of the manipulator in Figure 1 yields

$$x_1=l_1\cos {\varphi }_1+l_2\cos ({\varphi }_1+{\varphi }_2)$$

(1)

$$x_2=l_1\sin {\varphi }_1+l_2\sin ({\varphi }_1+{\varphi }_2)$$

(2)

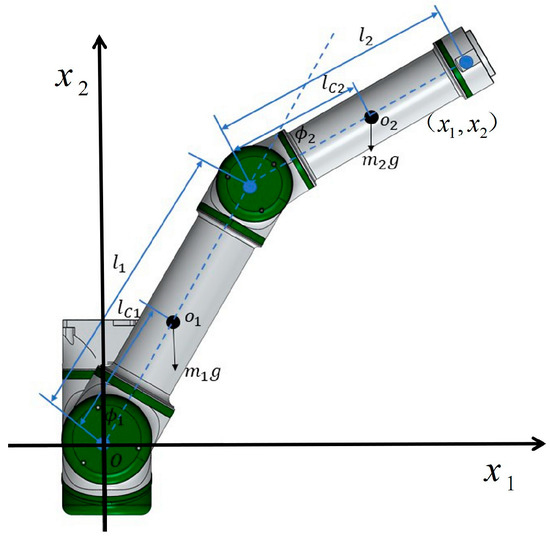
Figure 1. Schematic diagram of 2-DOF manipulator.

Combining Equations (1) and (2), we obtain

$$x_1^2+x_2^2=l_1^2+l_2^2+2l_1{l}_2\cos {\varphi }_2$$

(3)

Then

$${\varphi }_2=\arccos (\frac{x_1^2+x_2^2-l_1^2-l_2^2}{2l_1{l}_2})$$

(4)

Let $q_1=\arctan \frac{x_2}{x_1}$ and $q_2=\arccos \frac{x_1^2+x_2^2+l_1^2-l_2^2}{2l_1\sqrt{x_1^2+x_2^2}}$ and the following can be obtained:

$${\varphi }_1=\left\{\begin{array}{l}{q}_1-q_2,{\varphi }_2>0\\ q_1+q_2,{\varphi }_2⩽0\end{array}\right.$$

(5)

2.2. Neural Network Modeling of Manipulators

Consider a rigid 2-degree-of-freedom manipulator as the controlled object. The manipulator’s operation is assumed to be related to the end-effector’s spatial position. Let $x\in R^n$ represent the end-effector’s location and orientation within the workspace. The following is an expression of the manipulator’s dynamic properties in the workspace:

$$H_x(\varphi )\ddot{x}+C_x(\varphi ,\dot{\varphi })\dot{x}+g_x(\varphi )={\tau }_x$$

(6)

where $H_x\left(\varphi \right)$ is the $n\times n$ order rotational inertia matrix, $H_x\left(\varphi \right)=J^{-T}\left(\varphi \right)H\left(\varphi \right)J^{-1}\left(\varphi \right)$; $C_x\left(\varphi ,\dot{\varphi }\right)$ is the $n\times n$ order matrix of the Göttinger force and centrifugal force, $C_x\left(\varphi ,\dot{\varphi }\right)=J^{-T}\left(\varphi \right)\left(C\left(\varphi ,\dot{\varphi }\right)-H\left(\varphi \right)J^{-1}\left(\varphi \right)\dot{J}\left(\varphi \right)\right)J^{-1}\left(\varphi \right)$; $g_x\left(\varphi \right)$ is the $n\times 1$ order gravity vector, $g_x\left(\varphi \right)=J^{-T}\left(\varphi \right)g\left(\varphi \right)$; and ${\tau }_x\in R^n$ is the vector of joint torques exerted by the actuator. $J\left(\varphi \right)\in R^{n\times n}$ is the Jacobi matrix determined by the structure of the system, which is assumed to be non-singular in the bounded workspace.

The dynamic equations of the manipulator have the following properties:

Property 1.

The inertia matrix $H_x\left(\varphi \right)$ is symmetrically positive definite.

Property 2.

If $C_x\left(\varphi ,\dot{\varphi }\right)$ is defined via the Christoffel sign rule, the matrix ${\stackrel{.}{H}}_x\left(\varphi \right)-2C_x\left(\varphi ,\dot{\varphi }\right)$ is skew-symmetric.

The matrices $H_x$, $C_x$, and $g_x$ contain parametric uncertainties, which can negatively impact the control (6). Therefore, neural networks can be employed to handle these unknown dynamics.

Definition 1.

A class of Radial Basis Function Neural Networks (RBFNN) is commonly used to estimate unknown continuous functions as follows [36]:

$$f_i(\mathrm{\Xi })={{\widehat{W}}_i}^{*\mathrm{T}}{S}_i(\mathrm{\Xi })+{\overline{\epsilon }}_i(\mathrm{\Xi })\hspace{1em}i=1,2,\dots ,n$$

(7)

where ${{\widehat{W}}_i}^{\ast }\in R^{l\times n}$ is the ideal weight matrix, $S_i\left(\Xi \right)\in R^{l\times n}$ is the Gaussian radial basis function matrix, and ${\stackrel{-}{\epsilon }}_i(\Xi )=[{\stackrel{-}{\epsilon }}_1(\Xi ),\dots ,{\stackrel{-}{\epsilon }}_n(\Xi ){]}^T$ is the unknown estimated error column vector. The index i represents the i-th neuron in the RBFNN and ranges from 1 to n, where n is the total number of neurons. ${{\widehat{W}}_i}^{\ast }$ is unknown and its estimate ${\widehat{W}}_i$is used to design the controller and has ${\breve{W}}_i={\widehat{W}}_i-{W_i}^{\ast }$, denoting the error value of the weight matrix. ${\stackrel{-}{\epsilon }}_i\left(\Xi \right)$ satisfies ${\stackrel{-}{\epsilon }}_i\left(\Xi \right)\le \lambda <\infty$.

The radial basis element $s_j$ of $S_i\left(\Xi \right)$ is provided by the following equation:

$$s_j(\mathrm{\Xi })=\exp \left(\frac{-{(\mathrm{\Xi }-{\mu }_j)}^T(\mathrm{\Xi }-{\mu }_j)}{{\sigma }_j^2}\right)$$

(8)

where ${\mu }_j$ is the center of the receptive field, and ${\sigma }_j$ is the width of the Gaussian function.

Since $H_x\left(\varphi \right)$ and $g_x\left(\varphi \right)$ are functions of $\varphi$ only, they can be modeled using a static neural network.

$$H_{xkj}\left(\varphi \right)={\displaystyle \sum _l{\theta }_{kjl}}{\xi }_{kjl}\left(\varphi \right)+{\epsilon }_{hkj}\left(\varphi \right)={\theta }_{kj}^T{\xi }_{kj}\left(\varphi \right)+{\epsilon }_{hkj}\left(\varphi \right)$$

(9)

$$g_{xk}(\varphi )={\displaystyle \sum _l{m}_{kl}}{\zeta }_{kl}(\varphi )+{\epsilon }_{gk}(\varphi )=m_k^T{\zeta }_k(\varphi )+{\epsilon }_{gk}(\varphi )$$

(10)

where the weights of the neural network are represented by ${\theta }_{kjl},m_{kl}\in R$, the radial basis function with respect to the input vector ϕ is represented by ${\xi }_{kjl}\left(\varphi \right),{\zeta }_{kl}\left(\varphi \right)\in R$, and the modeling errors for $H_{xkj}\left(\varphi \right)$ and $g_{xk}\left(\varphi \right)$, respectively, are represented by ${\epsilon }_{mkj}\left(\varphi \right), {\epsilon }_{gk}\left(\varphi \right)\in R$, and they are presumptively limited.

The neural network model for $C_x\left(\varphi ,\dot{\varphi }\right)$ is based on a dynamic neural network with inputs $\varphi$ and $\dot{\varphi }$ for $C_{xkj}\left(\varphi ,\dot{\varphi }\right)$,

$$C_{xkj}\left(\varphi ,\dot{\varphi }\right)={\displaystyle \sum _l{n}_{kjl}}{\varsigma }_{kjl}\left(\mathrm{\Phi }\right)+{\epsilon }_{ckj}\left(\mathrm{\Phi }\right)=n_{kj}^T{\varsigma }_{kj}\left(\mathrm{\Phi }\right)+{\epsilon }_{ckj}\left(\mathrm{\Phi }\right)$$

(11)

where $\Phi =[{\varphi }^T{\dot{\varphi }}^T{]}^T\in R^{2n}$; $n_{kjl}\in R$ are the weights; ${\varsigma }_{kjl}\left(\Phi \right)\in R$ is the radial basis function whose inputs are the vectors $\Phi$; and ${\epsilon }_{ckj}\left(\Phi \right)$ is the modeling error of $C_{xkj}\left(\varphi ,\dot{\varphi }\right)$ and is assumed to be bounded as well.

2.3. Fixed-Time Preset Performance Function

This paper employs a performance-constrained control method that limits the tracking error within a preset range using an exponentially decaying performance function. However, the traditional exponential decay performance function only ensures convergence to the preset range in infinite time, but not within a specified time. To achieve better tracking performance within a specified time, a specified-time preconditioned performance function is introduced, defined as follows:

$${\beta }_i(t)=\left\{\begin{array}{cc}{\left(\frac{T_i-t}{T_i}\right)}^{\frac{{\rho }_i}{1-{\rho }_i}}\left({\beta }_i^0-{\beta }_i^{\infty }\right)+{\beta }_i^{\infty }& 0\le t\le T_i\\ {\beta }_i^{\infty }& t>T_i\end{array}\right.$$

(12)

where the performance function constants ${\beta }_i^0$ and ${\beta }_i^{\infty }$ have value domains of ${\beta }_i^0>{\beta }_i^{\infty }>0$ and ${\rho }_i=L_1-L_2\mathit{cos}(t\pi /T_i)$. $T_i$ are freely set time parameters. Here, $L_1$ represents the maximum value of the performance function, and $L_2$ represents the amplitude of the oscillation around the mean value defined by $L_1$.

Based on the proposed performance function, the boundary constraint of the position tracking error variable is as follows:

$$-{\underset{¯}{\eta }}_{\mathrm{i}}{\beta }_{\mathrm{i}}(\mathrm{t})<{\mathrm{e}}_{\mathrm{i}}<{\overline{\eta }}_{\mathrm{i}}{\beta }_{\mathrm{i}}(\mathrm{t})$$

(13)

where $-{\underset{¯}{\eta }}_{\mathrm{i}}$ and ${\stackrel{-}{\eta }}_i$ are constants. The initial value of Equation (13) is as follows:

$$-{\underset{¯}{\eta }}_{\mathrm{i}}{\beta }_{\mathrm{i}}(0)<{\mathrm{e}}_{\mathrm{i}}<{\overline{\eta }}_{\mathrm{i}}{\beta }_{\mathrm{i}}(0)$$

(14)

Since the performance function (12) cannot be used directly to design the controller, an error transformation function is needed to relate the tracking error to the specified time performance function, consider the error transformation function $\psi (·)$.

$$\psi \left({\epsilon }_i\right)=\frac{e_i\left(t\right)}{{\beta }_i\left(t\right)}=\frac{2{\eta }_{\mathrm{i}}}{\pi }\arctan \left({\epsilon }_i\right)$$

(15)

where ${\epsilon }_i$ is the transformed position tracking error, and function $\psi \left({\epsilon }_i\right)$ has the following properties:

(1)

The function $\psi \left({\epsilon }_i\right)$ is strictly growing and smooth;

(2)

$-{\underset{¯}{\eta }}_{\mathrm{i}}<\psi \left({\epsilon }_i\right)<{\stackrel{-}{\eta }}_i$;

(3)

$\underset{e_i\to -\infty }{lim}\psi \left({\epsilon }_i\right)=-{\eta }_i$, $\underset{e_i\to +\infty }{lim}\psi \left({\epsilon }_i\right)={\eta }_i$.

After the above transformation, the unconstrained tracking error $e_i$ is transformed into a constrained error variable ${\epsilon }_i$, which can reduce the difficulty of controller design.

3. Controller Design

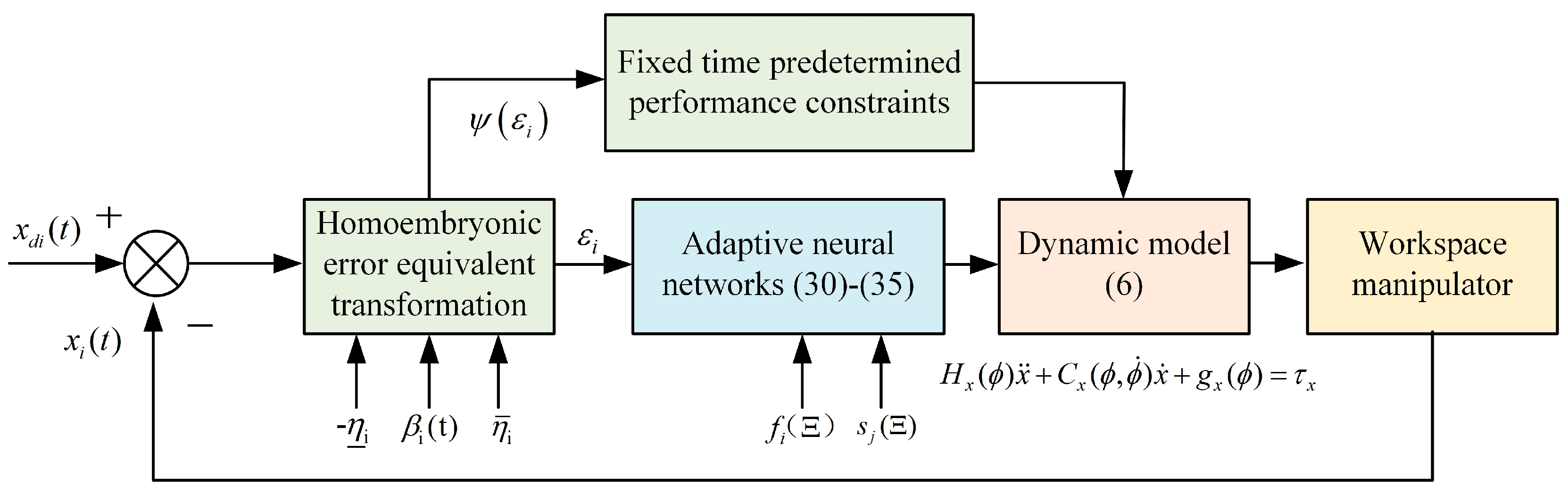
The control framework diagram for trajectory tracking control of a workspace manipulator based on a fixed-time adaptive neural network is illustrated in Figure 2. The control system begins with an error equivalent transformation using a homoembryonic approach, which ensures rapid convergence of tracking errors. This is followed by the application of fixed-time predetermined performance constraints. Adaptive neural networks are then employed to approximate dynamic parameters and adjust the controller. The dynamic model of the manipulator is controlled to achieve precise trajectory tracking within a fixed timeframe, optimizing both speed and accuracy. The workspace manipulator’s state is dynamically adjusted to meet the desired performance criteria.

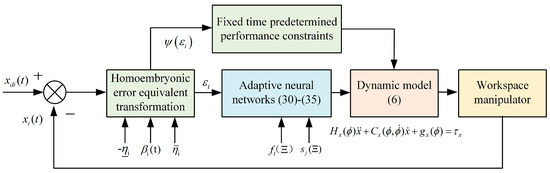
Figure 2. Control scheme block diagram.

3.1. Homoembryonic Error Equivalent Transformation

Let $x_d\left(t\right)$ be the ideal trajectory in the workspace, then ${\dot{x}}_d\left(t\right)$ and ${\ddot{x}}_d\left(t\right)$ are the ideal velocity and acceleration, respectively. Before controller design, the tracking error signal of the robot manipulator can be defined as follows:

$$e_i(t)=x_i(t)-x_{di}(t)$$

(16)

In order to make the actual trajectory $x\left(t\right)$ of the manipulator track the desired signal $x_d\left(t\right)$, and to make the system obtain better steady-state tracking performance, this paper is based on the theory of fixed-time stability, and, at the same time, combined with the predetermined performance control, the controller constraint strategy is designed to satisfy the following conditions:

(1)

The system’s adjustment time must be less than 1 s under any operating conditions and reference signal changes;

(2)

The steady state tracking error is less than 0.03;

(3)

The tracking error of the system is limited to the upper and lower bounds of the preset performance function.

To achieve the aforementioned control objectives, an error transformation is introduced. It converts the original nonlinear system with constrained tracking error behavior into an equivalent unconstrained system.

$${\epsilon }_i\left(t\right)={\psi }^{-1}\frac{e_i\left(t\right)}{{\beta }_i\left(t\right)}\triangleq \mathrm{{\rm Z}}\frac{e_i\left(t\right)}{{\beta }_i\left(t\right)}$$

(17)

where ${\epsilon }_i\left(t\right)\in R$ is the transformed error vector, $\psi \left({\epsilon }_i\right)=[\psi \left({\epsilon }_1\right),\dots ,\psi \left({\epsilon }_n\right){]}^T$.

$$\psi \left({\epsilon }_i\right)=\frac{2{\eta }_{\mathrm{i}}}{\pi }\arctan \left({\epsilon }_i\right)$$

(18)

$${\epsilon }_i\left(t\right)=\tan \frac{\pi \psi \left({\epsilon }_i\right)}{2{\eta }_i}$$

(19)

where ${\eta }_i$ is a design scalar constant which, together with ${\beta }_i$, imposes behavioral bounds on the system output tracking error, ${\beta }_i$, as shown in Equation (12). As can be seen, the transformation (17) is one-to-one, meaning that if the new error boundaries of ${\epsilon }_i\left(t\right)$ are fulfilled, a fixed-time prescribed performance control of the tracking error $e_i\left(t\right)$ may be obtained.

Additionally, the following equation provides the first- and second-order derivatives of $\psi \left({\epsilon }_i\right)$ for the controller design that comes next, derived from Equation (18):

$$\stackrel{.}{\dot{\psi }\left({\epsilon }_i\right)}=\frac{2{\dot{\eta }}_i}{\pi }\arctan ({\epsilon }_i)+\frac{2{\eta }_i}{\pi }\frac{{\dot{\epsilon }}_i}{1+{\epsilon }_i^2}$$

(20)

$$\stackrel{.}{\ddot{\psi }\left({\epsilon }_i\right)}=\frac{2{\ddot{\eta }}_i}{\pi }\arctan {\epsilon }_i+\frac{4{\dot{\eta }}_i}{\pi }\frac{{\dot{\epsilon }}_i}{1+{\epsilon }_i^2}+\frac{2{\eta }_i}{\pi }\frac{{\ddot{\epsilon }}_i(1+{\epsilon }_i^2)-2{\epsilon }_i{\dot{\epsilon }}_i^2}{{(1+{\epsilon }_i^2)}^2}$$

(21)

Remark 1.

The value of ${\epsilon }_i\left(t\right)$ will be big if $\psi \left({\epsilon }_i\right)$ deviates somewhat from the origin because the tan-type function (19) is sensitive to $\psi \left({\epsilon }_i\right)$. Our suggested controller, in conjunction with the tan-type error transformation function, guarantees that the error is kept within a certain, limited radius surrounding the origin.

In summary, our constraint control strategy is to make the tracking error converge to a predetermined region in a fixed time by means of the homogeneous embryo transformation, which facilitates the subsequent controller design and can be expressed as $\underset{t\to T_i}{lim}\left|e_i\left(t\right)\leftrightarrow {\epsilon }_i\left(t\right)\right|\le {\eta }_i$.

Definition 2.

Think about the system that follows [37],

$$\dot{x}(t)=f(x(t)),x(0)=0,f(0)=0$$

(22)

where $x\in R^n,f\left(\mathit{x}\right):U_0\to R^n$ is continuous in the open neighborhood of the origin. Assume that the system (22) has a unique solution in forward time for all initial conditions.

For any real numbers $\alpha ,\beta >0,\rho >1,0<q<1,$ there exists a positive definite Lyapunov function $V\left(x\right)=0\Rightarrow x=0$, and there is $V\left(x\right)\le -\alpha V^{\prime }\left(x\right)-\beta V^{\prime }\left(x\right)$. Then, the system (22) is globally fixed-time stable and the stability time function is bounded to be

$$T_i⩽T_{\max }=\frac{1}{\alpha (p-1)}+\frac{1}{\beta (q-1)}$$

(23)

Definition 3.

For any real number $x_i\left(i=\mathrm{1,2},\cdots ,n\right)$, there exist real numbers 0 < $q\le 1$, such that the following inequality is true [38]:

$${(\mid x_1\mid +\cdots +\mid x_n\mid )}^q\le \mid x_1{\mid }^q+\cdots +\mid x_n{\mid }^q$$

(24)

where $q=\frac{q_1}{q_2}$ and both $q_1$ and $q_2$ are positive odd numbers.

Definition 4.

For any real number $x_i\left(i=\mathrm{1,2},\cdots ,n\right)$, there exist real numbers $p>1$, such that the following inequality holds [39]:

$${\displaystyle \sum _{i=1}^n\mid }{x}_i{\mid }^p\le {\left({\displaystyle \sum _{i=1}^n\mid }{x}_i\mid \right)}^p\le n^{p-1}{\displaystyle \sum _{i=1}^n\mid }{x}_i{\mid }^p$$

(25)

3.2. Neural Network Controller Design

Let $x_d\left(t\right)$ be the ideal trajectory in the workspace, $x\left(t\right)$ be the actual trajectory, and $x_r\left(t\right)$ be the reference trajectory after transformation. The error vector $\epsilon \left(t\right)$ of the robot in the workspace is

$$\epsilon (t)=x(t)-x_d(t)$$

(26)

$${\dot{x}}_r(t)={\dot{x}}_d(t)+\Lambda \epsilon (t)$$

(27)

Define

$$r(t)={\dot{x}}_r(t)-\dot{x}(t)=\dot{\epsilon }(t)+\mathrm{\Lambda }\epsilon (t)$$

(28)

where the matrix Λ is positive definite.

From Section 2.2, the dynamic equation of the manipulator in the workspace after modeling with the neural network can be written as

$$H_x(\varphi )\ddot{x}+C_x(\varphi ,\dot{\varphi })\dot{x}+g_x(\varphi )={\tau }_x$$

(29)

where

$$H_{xkj}\left(\varphi \right)={\theta }_{kj}^T{\xi }_{kj}\left(\varphi \right)+{\epsilon }_{hkj}\left(\varphi \right)$$

(30)

$$C_{xkj}\left(\varphi ,\dot{\varphi }\right)=n_{kj}^T{\varsigma }_{kj}\left(\mathrm{\Phi }\right)+{\epsilon }_{ckj}\left(\mathrm{\Phi }\right)$$

(31)

$$g_{xk}(\varphi )=m_k^T{\zeta }_k(\varphi )+{\epsilon }_{gk}(\varphi )$$

(32)

Using GL matrices and their multiplication operations [36], $H_x\left(\varphi \right)$ can be written as

$$H_x\left(\varphi \right)=\left[{\left\{\mathrm{\Theta }\right\}}^T·\left\{\mathrm{\Xi }(\varphi )\right\}\right]+E_h(\varphi )$$

(33)

where $\left\{\Theta \right\}$ and $\Xi \left(\varphi \right)$ are GL matrices whose elements are ${\theta }_{kj}$ and ${\xi }_{kj}\left(\varphi \right)$, respectively, and $E_h\left(\varphi \right)\in R^{n\times n}$ is the matrix of the modeling error ${\epsilon }_{hkj}\left(\varphi \right)$.

Similarly, a GL matrix transformation of $C_x\left(\varphi ,\dot{\varphi }\right)$ and $g_{xk}\left(\varphi \right)$ has

$$C_x\left(\varphi ,\dot{\varphi }\right)=[{\left\{\mathrm{{\rm N}}\right\}}^T·\left\{\mathrm{\Gamma }\left(\mathrm{\Phi }\right)\right\}]+{\mathrm{{\rm E}}}_c\left(\mathrm{\Phi }\right)$$

(34)

$$g_x(\varphi )=[{\left\{\mathrm{{\rm M}}\right\}}^T·\left\{\mathrm{\Pi }(\varphi )\right\}]+{\mathrm{{\rm E}}}_g(\varphi )$$

(35)

where $\left\{{\rm N}\right\}, \Gamma \left(\Phi \right), \left\{{\rm M}\right\}$, and $\left\{\Pi \left(\varphi \right)\right\}$ are GL matrices whose elements are $n_{kj}$, ${\varsigma }_{kj}\left(\Phi \right)$, ${\beta }_k$, and ${\zeta }_k\left(\varphi \right)$ in Equations (31) and (32), and ${{\rm E}}_c\left(\Phi \right)\in R^{n\times n}$ and ${{\rm E}}_g\left(\varphi \right)\in R^{n\times n}$ are modeling error matrices.

Bringing Equations (33)–(35) into Equation (29), we obtain

$$\left[{\left\{\mathrm{\Theta }\right\}}^T·\left\{\mathrm{\Xi }\left(\varphi \right)\right\}+E_{\mathrm{h}}\left(\varphi \right)\right]\ddot{x}+\left[{\left\{\mathrm{{\rm N}}\right\}}^T·\left\{\mathrm{\Gamma }\left(\mathrm{\Phi }\right)\right\}+E_{\mathrm{c}}\left(\mathrm{\Phi }\right)\right]\dot{x}+\left[{\left\{M\right\}}^T·\left\{\mathrm{\Pi }\left(\mathrm{\varphi }\right)\right\}+E_{\mathrm{g}}\left(\varphi \right)\right]={\tau }_x$$

(36)

Selecting $\left(\widehat{·}\right)$ to stand in for the anticipated value of $(·)$, define $\left(\widetilde{·}\right)=(·)-\left(\widehat{·}\right)$. The design controller is

$${\tau }_x=\left[{\left\{\widehat{\mathrm{\Theta }}\right\}}^T·\left\{\mathrm{\Xi }\left(\varphi \right)\right\}\right]{\ddot{x}}_r+\left[{\left\{\widehat{\mathrm{{\rm N}}}\right\}}^T·\left\{\mathrm{\Gamma }\left(\mathrm{\Phi }\right)\right\}\right]{\dot{x}}_r+\left[{\left\{\widehat{M}\right\}}^T·\left\{\mathrm{\Pi }\left(\mathrm{\varphi }\right)\right\}\right]+K_r+E_s\mathrm{sgn}(r)$$

(37)

where $K_r\in R^{n\times n}>0$ and $E_s>‖E‖=E_h\left(\varphi \right){\ddot{x}}_r+E_c\left(\Phi \right){\dot{x}}_r+E_g\left(\varphi \right)$. Model-based control is represented by the first three terms of the controller, and proportional differential (PD) control is represented by the term $K_r$, and the robust term that suppresses the neural network’s modeling error is the last term of the control rule.

Combining Equations (36) and (37), it is obtained that

$$\begin{array}{r}\left[{\left\{\mathrm{\Theta }\right\}}^T·\left\{\mathrm{\Xi }\left(\varphi \right)\right\}+E_{\mathrm{h}}\left(\varphi \right)\right]\ddot{x}+\left[{\left\{\mathrm{{\rm N}}\right\}}^T·\left\{\mathrm{\Gamma }\left(\mathrm{\Phi }\right)\right\}+E_{\mathrm{c}}\left(\mathrm{\Phi }\right)\right]\dot{x}+\left[{\left\{M\right\}}^T·\left\{\mathrm{\Pi }\left(\varphi \right)\right\}+E_{\mathrm{g}}\left(\varphi \right)\right]\\ =\left[{\left\{\widehat{\mathrm{\Theta }}\right\}}^T·\left\{\mathrm{\Xi }\left(\varphi \right)\right\}\right]{\ddot{x}}_r+\left[{\left\{\widehat{\mathrm{{\rm N}}}\right\}}^T·\left\{\mathrm{\Gamma }\left(\mathrm{\Phi }\right)\right\}\right]{\dot{x}}_r+\left[{\left\{\widehat{M}\right\}}^T·\left\{\mathrm{\Pi }\left(\varphi \right)\right\}\right]+K_r+E_s\mathrm{sgn}(r)\end{array}$$

(38)

Bringing $\dot{x}={\dot{x}}_r-r$ and $\ddot{x}={\ddot{x}}_r-\dot{r}$ into the above equation yields

$$\begin{array}{c}\left[{\left\{\mathrm{\Theta }\right\}}^T·\left\{\mathrm{\Xi }\left(\varphi \right)\right\}+E_{\mathrm{h}}\left(\varphi \right)\right]({\ddot{x}}_r-\dot{r})+\left[{\left\{\mathrm{{\rm N}}\right\}}^T·\left\{\mathrm{\Gamma }\left(\mathrm{\Phi }\right)\right\}+E_{\mathrm{c}}\left(\mathrm{\Phi }\right)\right]({\dot{x}}_r-r)+\left[{\left\{M\right\}}^T·\left\{\mathrm{\Pi }\left(\varphi \right)\right\}+E_{\mathrm{g}}\left(\varphi \right)\right]\\ =\left[{\left\{\widehat{\mathrm{\Theta }}\right\}}^T·\left\{\mathrm{\Xi }\left(\varphi \right)\right\}\right]{\ddot{x}}_r+\left[{\left\{\widehat{\mathrm{{\rm N}}}\right\}}^T·\left\{\mathrm{\Gamma }\left(\mathrm{\Phi }\right)\right\}\right]{\dot{x}}_r+\left[{\left\{\widehat{M}\right\}}^T·\left\{\mathrm{\Pi }\left(\varphi \right)\right\}\right]+K_r+E_s\mathrm{sgn}(r)\end{array}$$

(39)

Simplification of the above equation yields

$$\begin{array}{r}\left[{\left\{\mathrm{\Theta }\right\}}^T·\left\{\mathrm{\Xi }\left(\varphi \right)\right\}+E_{\mathrm{h}}\left(\varphi \right)\right]\dot{r}+\left[{\left\{\mathrm{{\rm N}}\right\}}^T·\left\{\mathrm{\Gamma }\left(\mathrm{\Phi }\right)\right\}+E_{\mathrm{c}}\left(\mathrm{\Phi }\right)\right]r+K_r+E_s\mathrm{sgn}(r)\\ =\left[{\left\{\tilde{\mathrm{\Theta }}\right\}}^T·\left\{\mathrm{\Xi }\left(\varphi \right)\right\}\right]{\ddot{x}}_r+\left[{\left\{\widetilde{\mathrm{{\rm N}}}\right\}}^T·\left\{\mathrm{\Gamma }\left(\mathrm{\Phi }\right)\right\}\right]{\dot{x}}_r+\left[{\left\{\tilde{M}\right\}}^T·\left\{\mathrm{\Pi }\left(\varphi \right)\right\}\right]+E\end{array}$$

(40)

Substituting Equations (33) and (34), we obtain

$$\begin{array}{l}{H}_x\left(\varphi \right)\dot{r}+C_x\left(\varphi ,\dot{\varphi }\right)r+K_r+E_s\mathrm{sgn}(r)\\ =\left[{\left\{\tilde{\mathrm{\Theta }}\right\}}^T·\left\{\mathrm{\Xi }\left(\varphi \right)\right\}\right]{\ddot{x}}_r+\left[{\left\{\widetilde{\mathrm{{\rm N}}}\right\}}^T·\left\{\mathrm{\Gamma }\left(\mathrm{\Phi }\right)\right\}\right]{\dot{x}}_r+\left[{\left\{\tilde{M}\right\}}^T·\left\{\mathrm{\Pi }\left(\varphi \right)\right\}\right]+E\end{array}$$

(41)

The stability of the closed-loop system (41) is provided by the following theorem.

Theorem 1.

For a closed-loop system Equation (41) if $K_r>0,E_s>‖E‖$ and the adaptive law satisfies

$${\dot{\widehat{\theta }}}_k=A_k\cdot \{\left.{\xi }_k(\varphi )\right\}{\ddot{x}}_r{r}_k$$

(42)

$${\stackrel{.}{\widehat{n}}}_k=B_k\cdot \{\left.{\varsigma }_k(\mathrm{\Phi })\right\}{\dot{x}}_r{r}_k$$

(43)

$${\dot{\widehat{m}}}_k=C_k\cdot \{\left.{\zeta }_k(\varphi )\right\}{r}_k$$

(44)

where $A_k=A_k^T>0{;B}_k=B_k^T{;C}_k=C_k^T$, and ${\widehat{\theta }}_k$, ${\widehat{n}}_k$, ${\widehat{m}}_k$ are vectors of ${\widehat{\theta }}_{kj}$, ${\widehat{n}}_{kj}$, and ${\widehat{m}}_{kj}$, respectively, then ${\widehat{\theta }}_k, {\widehat{n}}_k,{\widehat{m}}_k\in L_{\infty }$, $\epsilon \in L_2^n\cap L_{\infty }^n$, and $\epsilon$is continuous, and $\epsilon ,\dot{\epsilon }\to 0$ when $t\to \infty$.

Proof of Theorem 1.

Consider the following Lyapunov function

$$V=\frac{1}{2}{r}^{\mathcal{T}}{H}_x(\varphi )r+\frac{1}{2}{\displaystyle \sum _{k=1}^n{\tilde{\theta }}_k^{\mathcal{T}}}{A}_k^{-1}{\tilde{\theta }}_k+\frac{1}{2}{\displaystyle \sum _{k=1}^n{\tilde{n}}_k^T{B}_k^{-1}{\tilde{n}}_k}+\frac{1}{2}{\displaystyle \sum _{k=1}^n{\tilde{m}}_k^T{C}_k^{-1}{\tilde{m}}_k}$$

(45)

where $A_k,B_k,C_k$ are positive definite matrices. Derivation of Equation (45) yields

$$\dot{V}=r^{\mathcal{T}}{H}_x(\varphi )\dot{r}+\frac{1}{2}{r}^{\mathcal{T}}{\dot{H}}_x(\varphi )r+{\displaystyle \sum _{k=1}^n{\tilde{\theta }}_k^{\mathcal{T}}}{A}_k^{-1}{\dot{\tilde{\theta }}}_k+{\displaystyle \sum _{k=1}^n{\tilde{n}}_k^T{B}_k^{-1}{\dot{\tilde{n}}}_k}+{\displaystyle \sum _{k=1}^n{\tilde{m}}_k^T{C}_k^{-1}{\dot{\tilde{m}}}_k}$$

(46)

Since the matrix ${\stackrel{.}{H}}_x\left(\varphi \right)-2C_x\left(\varphi ,\dot{\varphi }\right)$ is skew-symmetric, then $r^{\mathcal{T}}\left({\dot{H}}_x\right(\varphi )-2C_x\left.\left(\Phi \right)\right)r=0$. Using the fact that ${\dot{\tilde{\theta }}}_k=-{\dot{\widehat{\theta }}}_k,{\dot{\tilde{n}}}_k=-{\dot{\widehat{n}}}_k$ and ${\dot{\tilde{m}}}_k=-{\dot{\widehat{m}}}_k,$ substituting into the above equation

$$\dot{V}=r^{\mathcal{T}}\left(H_x(\varphi )\dot{r}+C_x\left(\mathrm{\Phi }\right)r\right)-{\displaystyle \sum _{k=1}^n{\tilde{\theta }}_k^{\mathcal{T}}}{A}_k^{-1}{\dot{\widehat{\theta }}}_k-{\displaystyle \sum _{k=1}^n{\tilde{n}}_k^T{B}_k^{-1}{\dot{\widehat{n}}}_k}-{\displaystyle \sum _{k=1}^n{\tilde{m}}_k^T{C}_k^{-1}{\dot{\widehat{m}}}_k}$$

(47)

Substituting (41) yields

$$\begin{array}{ll}\dot{V}=& -r^{\mathcal{T}}{K}_r-E_s{r}^{\mathcal{T}}\mathrm{sgn}(r)+{\displaystyle \sum _{k=1}^n\left\{{\tilde{\theta }}_k^{\mathcal{T}}\right\}}·\left\{{\xi }_k\left(\varphi \right)\right\}{\ddot{x}}_r{r}_k\\ & +{\displaystyle \sum _{k=1}^n\left\{{\tilde{n}}_k^{\mathcal{T}}\right\}}·\left\{{\varsigma }_k\left(\mathrm{\Phi }\right)\right\}{\dot{x}}_r{r}_k+{\displaystyle \sum _{k=1}^n\left\{{\tilde{m}}_k^{\mathcal{T}}\right\}}·\left\{{\zeta }_k\left(\varphi \right)\right\}{r}_k\\ & +r^{\mathcal{T}}E-{\displaystyle \sum _{k=1}^n{\tilde{\theta }}_k^{\mathcal{T}}}{A}_k^{-1}{\dot{\widehat{\theta }}}_k-{\displaystyle \sum _{k=1}^n{\tilde{n}}_k^T{B}_k^{-1}{\dot{\widehat{n}}}_k}-{\displaystyle \sum _{k=1}^n{\tilde{m}}_k^T{C}_k^{-1}{\dot{\widehat{m}}}_k}\end{array}$$

(48)

Substituting the adaptive laws (42), (43), and (44) into the above equation and combining them with $E_s>‖E‖$, we obtain

$$\dot{V}=-r^{\mathcal{T}}{K}_r-E_s{r}^{\mathcal{T}}\mathrm{sgn}(r)+r^{\mathcal{T}}E\le 0$$

(49)

Since $V\ge 0,\dot{V}\le 0$, hence, $r$, ${\tilde{\theta }}_k$, ${\tilde{n}}_k$, and ${\tilde{m}}_k$ are bounded. When $\dot{V}\equiv 0$ is satisfied $r=0$; the closed-loop system is asymptotically stable according to the LaSalle invariance principle. When $t\to \infty ,r\to 0$, there is $\epsilon ,\dot{\epsilon }\to 0$.□

4. Simulation Experiment Verification

To illustrate the effectiveness of the validation algorithm, a planar two-link manipulator, widely used in the literature, is considered in our simulation study. The kinetic equations of the manipulator are

$$H_x(\varphi )\ddot{x}+C_x(\varphi ,\dot{\varphi })\dot{x}+g_x(\varphi )={\tau }_x$$

(50)

where

$$H_x(\varphi )=J^{-T}(\varphi )H(\varphi )J^{-1}(\varphi )$$

(51)

$$g_x(\varphi )=J^{-T}(\varphi )g(\varphi )$$

(52)

$$C_x(\varphi ,\dot{\varphi })=J^{-T}(\varphi )(C(\varphi ,\dot{\varphi })-H(\varphi )J^{-1}(\varphi )\dot{J}(\varphi ))J^{-1}(\varphi )$$

(53)

$$H(\varphi )=\left[\begin{array}{cc}{p}_1+p_2+2p_3\cos {\varphi }_2& p_2+p_3\cos {\varphi }_2\\ p_2+p_3\cos {\varphi }_2& p_2\end{array}\right]$$

(54)

$$C(\varphi ,\dot{\varphi })=\left[\begin{array}{cc}-p_3{\dot{\varphi }}_2\sin {\varphi }_2& -p_3({\dot{\varphi }}_1+{\dot{\varphi }}_2)\sin {\varphi }_2\\ p_3{\dot{\varphi }}_1\sin {\varphi }_2 & 0\end{array}\right]$$

(55)

$$\mathrm{g}(\varphi )=\left[\begin{array}{c}{p}_{4}g\cos {\varphi }_1+p_{5}g\cos ({\varphi }_1+{\varphi }_2)\\ p_{5}g\cos ({\varphi }_1+{\varphi }_2)\end{array}\right]$$

(56)

$$J(\varphi )=\left[\begin{array}{cc}-l_1\sin ({\varphi }_1)-l_2\sin ({\varphi }_1+{\varphi }_2)& -l_2\sin ({\varphi }_1+{\varphi }_2)\\ l_1\cos ({\varphi }_1)+l_2\cos ({\varphi }_1+{\varphi }_2)& l_2\cos ({\varphi }_1+{\varphi }_2)\end{array}\right]$$

(57)

$$\begin{array}{c}\dot{J}(\varphi )=\left[\begin{array}{cc}-l_1\cos ({\varphi }_1)-l_2\cos ({\varphi }_1+{\varphi }_2)& -l_2\cos ({\varphi }_1+{\varphi }_2)\\ -l_1\sin ({\varphi }_1)-l_2\sin ({\varphi }_1+{\varphi }_2)& -l_2\sin ({\varphi }_1+{\varphi }_2)\end{array}\right]{\dot{\varphi }}_1\\ +\left[\begin{array}{cc}-l_2\cos ({\varphi }_1+{\varphi }_2)& -l_2\cos ({\varphi }_1+{\varphi }_2)\\ -l_2\sin ({\varphi }_1+{\varphi }_2)& -l_2\sin ({\varphi }_1+{\varphi }_2)\end{array}\right]{\dot{\varphi }}_2\end{array}$$

(58)

Take $P=\left[p_1 p_2{p}_3{p}_4{p}_5\right]={\left[2.90 0.76 0.87 3.04 0.87\right]}^T$. Since the tracking trajectory is a right-angle coordinate in the workspace, not an angular position in the joint space, the dijoint angular position should be converted to the joint end Cartesian coordinate in the workspace according to Equations (4) and (5). The Jacobian matrix $J\left(\varphi \right)$ is shown in Equations (57) and (58).

The ideal tracking trajectory in the workspace is taken as $x_{d1}\left(t\right)=0.5\cos \left(0.5\ast \pi t\right)+1.0, { x}_{d2}\left(t\right)=0.5\sin \left(0.5\ast \pi t\right)+1.0$, which is a circle with radius 0.5 m and a center at $\left(x_1,x_2\right)=\left(\mathrm{1.0,1.0}\right) \mathrm{m}$. For the initial condition, the end-effector of the manipulator is at the center of the circle, i.e., $x\left(0\right)=\left[1.0 1.0\right] \mathrm{m}$, $\dot{x}\left(0\right)=\left[0 0| \right]\mathrm{m}/\mathrm{s}$.

For the approximation of each element of $H_x\left(\varphi \right)$, $g_x\left(\varphi \right)$, and $C_x(\varphi ,\dot{\varphi })$, the RBF neural network accepts $\varphi$ and $\dot{ \varphi }$ as input, and its hidden layer has seven nodes by design.

All Gaussian functions’ parameters are assumed to be $b_i=10 \mathrm{a}\mathrm{n}\mathrm{d} c_i=\left[\begin{array}{ccccccc}-1.5& -1.0& -0.5& 0& 0.5& 1.0& 1.5\end{array}\right],$ putting the neural network’s starting value at 0. Equations (37) and (42)–(44) employ the adaptive law and the control law, respectively. The controller gains are chosen as $K=\left[\begin{array}{cc}30& 0\\ 0& 30\end{array}\right]$ and $E_s=0.5$. By Lemma 2, $\mathsf{\Lambda }=\left[\begin{array}{cc}15& 0\\ 0& 15\end{array}\right]$ is taken and the parameters of the adaptive law are taken as $A_k=\mathrm{diag}\left\{2.0\right\}$, ${{\rm B}}_k=\mathrm{diag}\left\{0.10\right\}$ and $C_k=\mathrm{diag}\left\{5.0\right\}$.

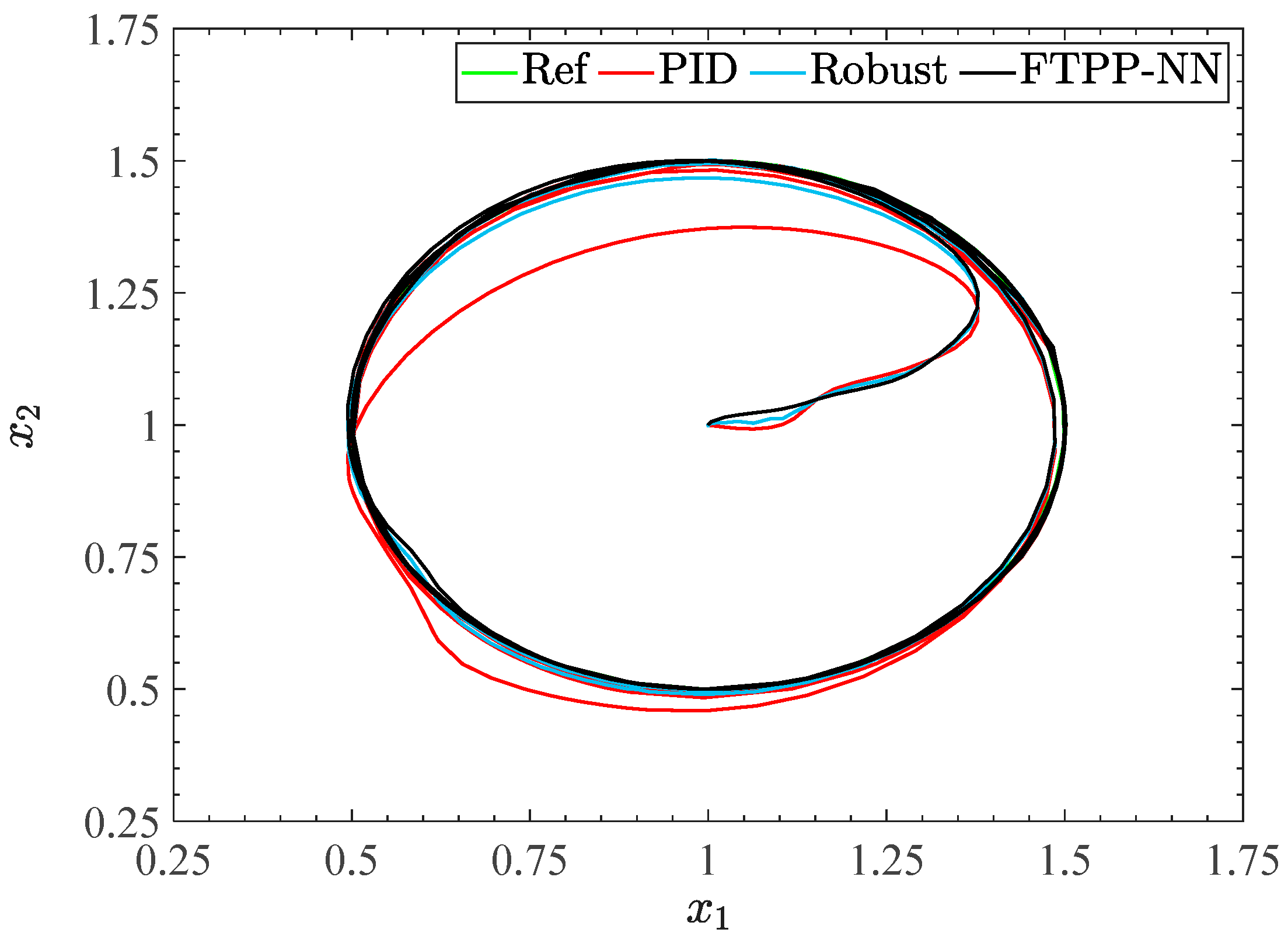
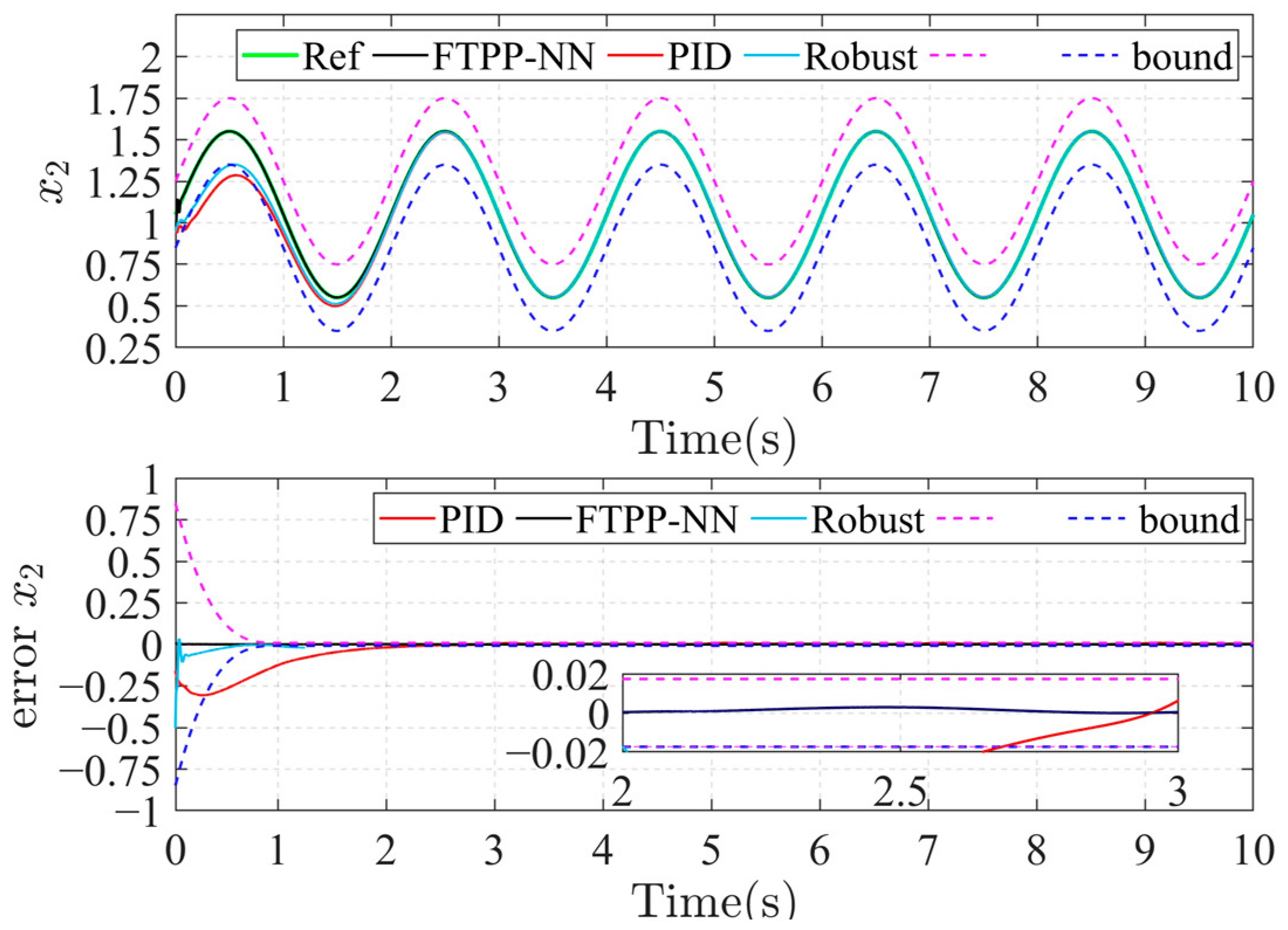
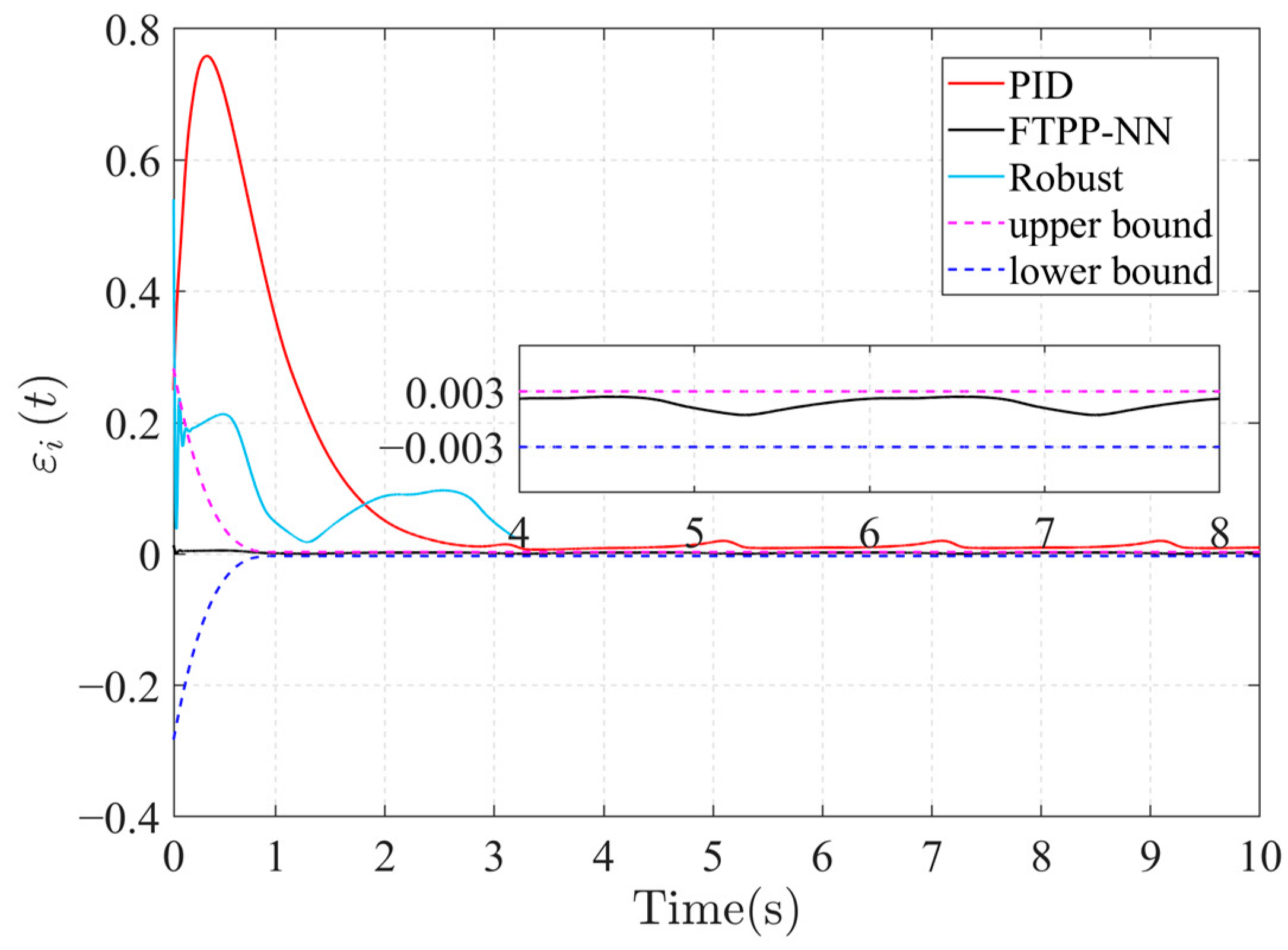
The simulation results are shown in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11. Figure 3 illustrates the trajectory tracking performance of the proposed algorithm applied to the manipulator and compares it with the PID and robust control algorithms under the same conditions. The results indicate that all three control methods can achieve the desired trajectory tracking. However, the proposed workspace manipulator adaptive neural network control method based on time preset performance (hereafter referred to as FTPP-NN) demonstrates faster tracking speed and higher accuracy, achieving precise tracking within the preset 1 s. Notably, the tracking errors of the PID and robust control methods exceed the boundaries during the initial phase, whereas the FTPP-NN method ensures that the tracking error remains constrained within the boundaries at all times, thereby improving both the transient and steady-state performance of the system.

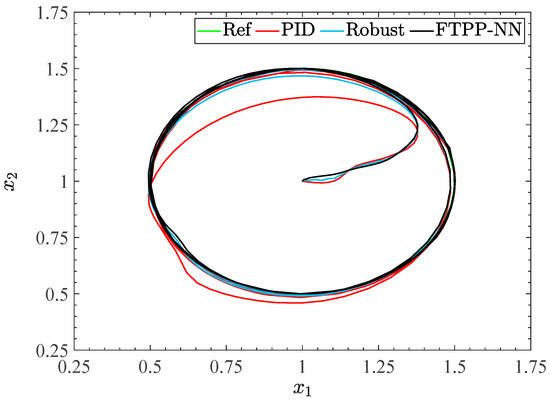
Figure 3. Tracking the trajectory of the end joint.

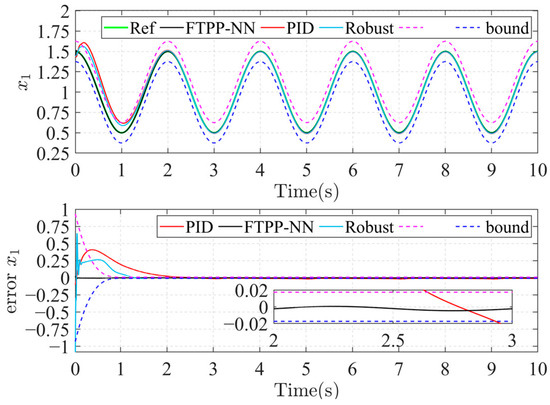
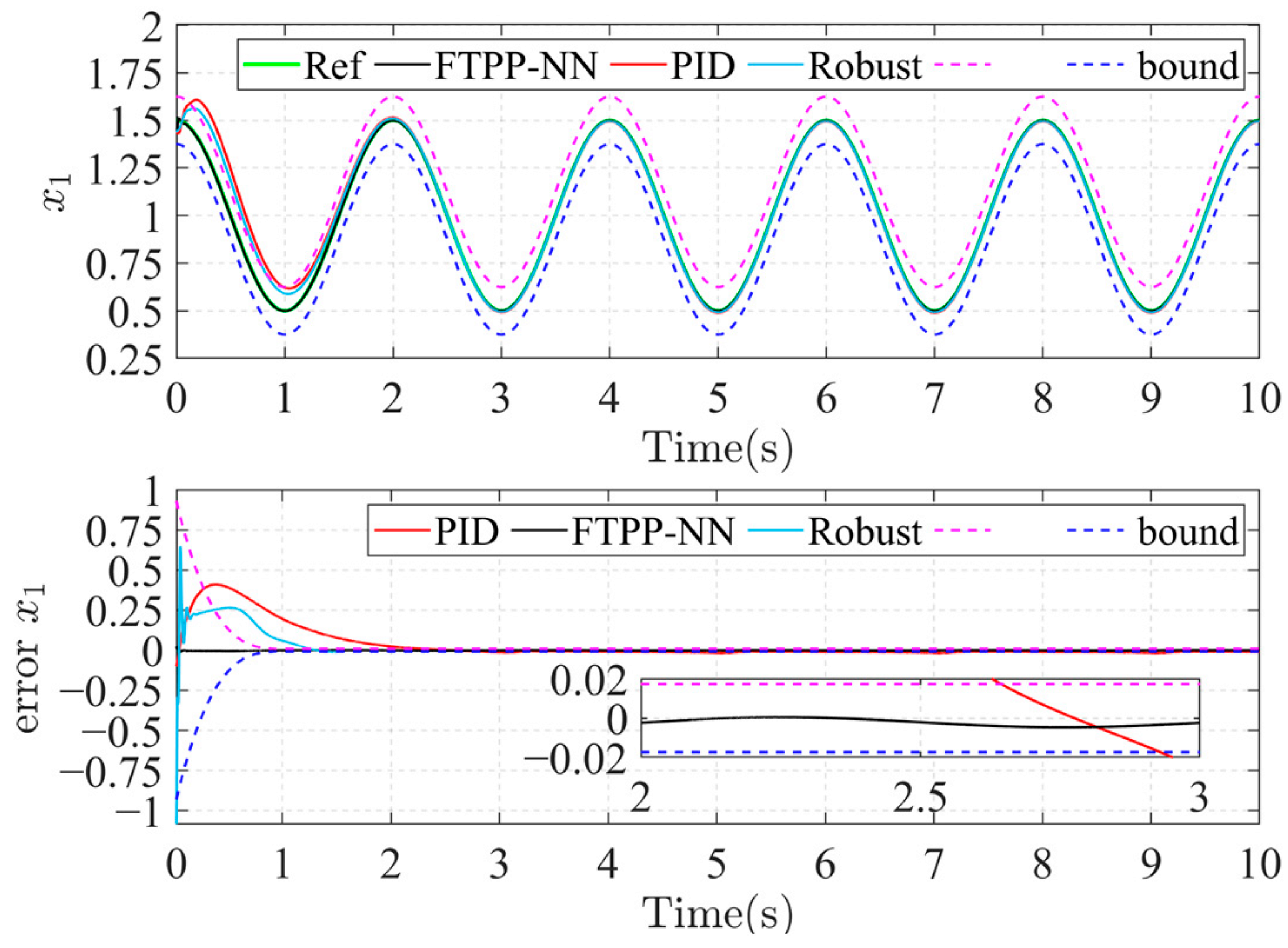
Figure 4. Trajectories and errors in the x₁ direction.

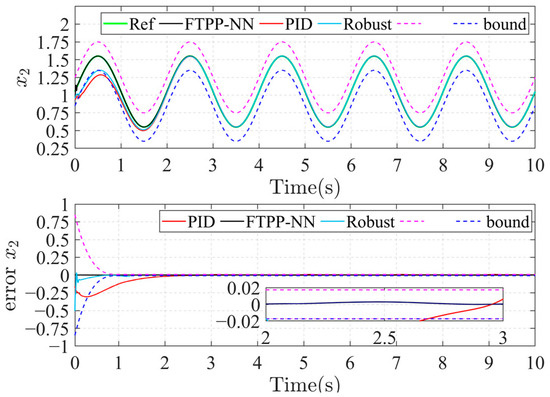
Figure 5. Trajectories and errors in the x₂ direction.

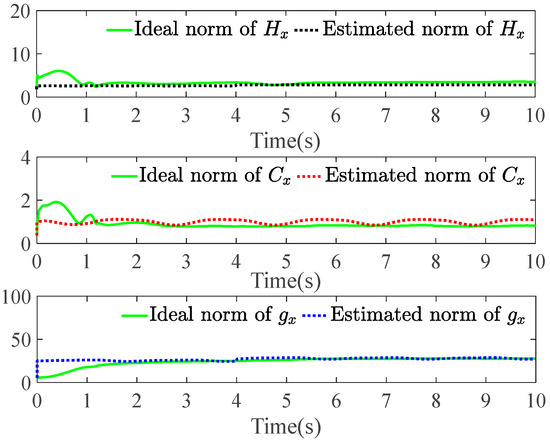
Figure 6. Approximation of kinetic parameters for $H_x$, $C_x$, and $g_x$.

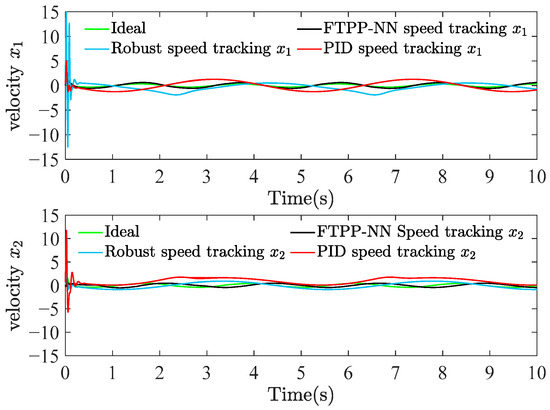
Figure 7. Angular velocity tracking of the end joints.

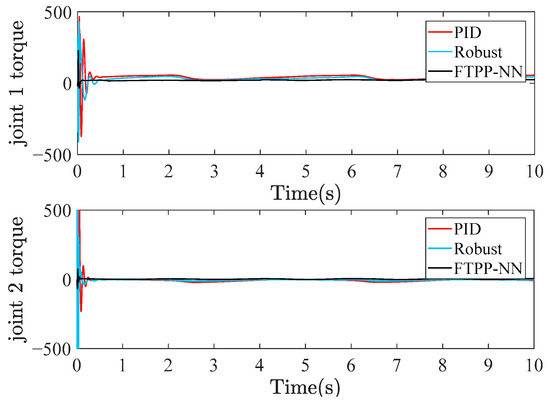
Figure 8. Control inputs for Joint 1 and Joint 2.

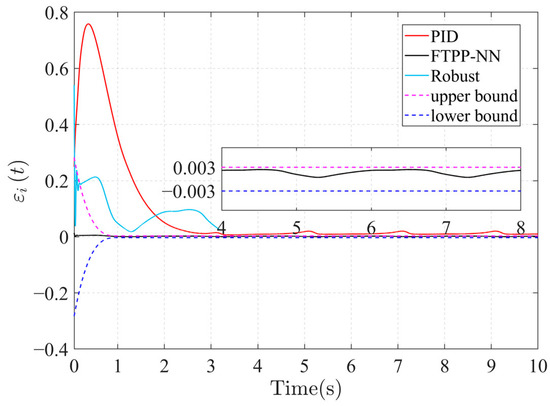
Figure 9. Trajectory tracking error for different control algorithms.

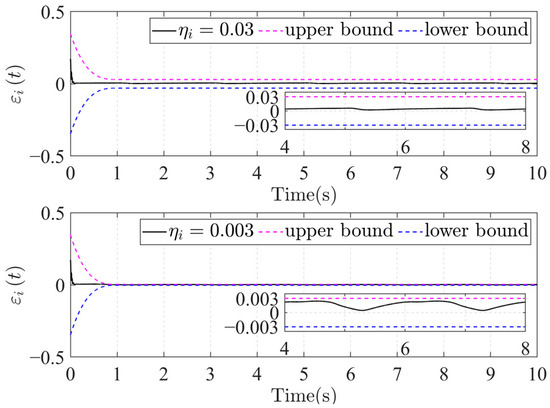
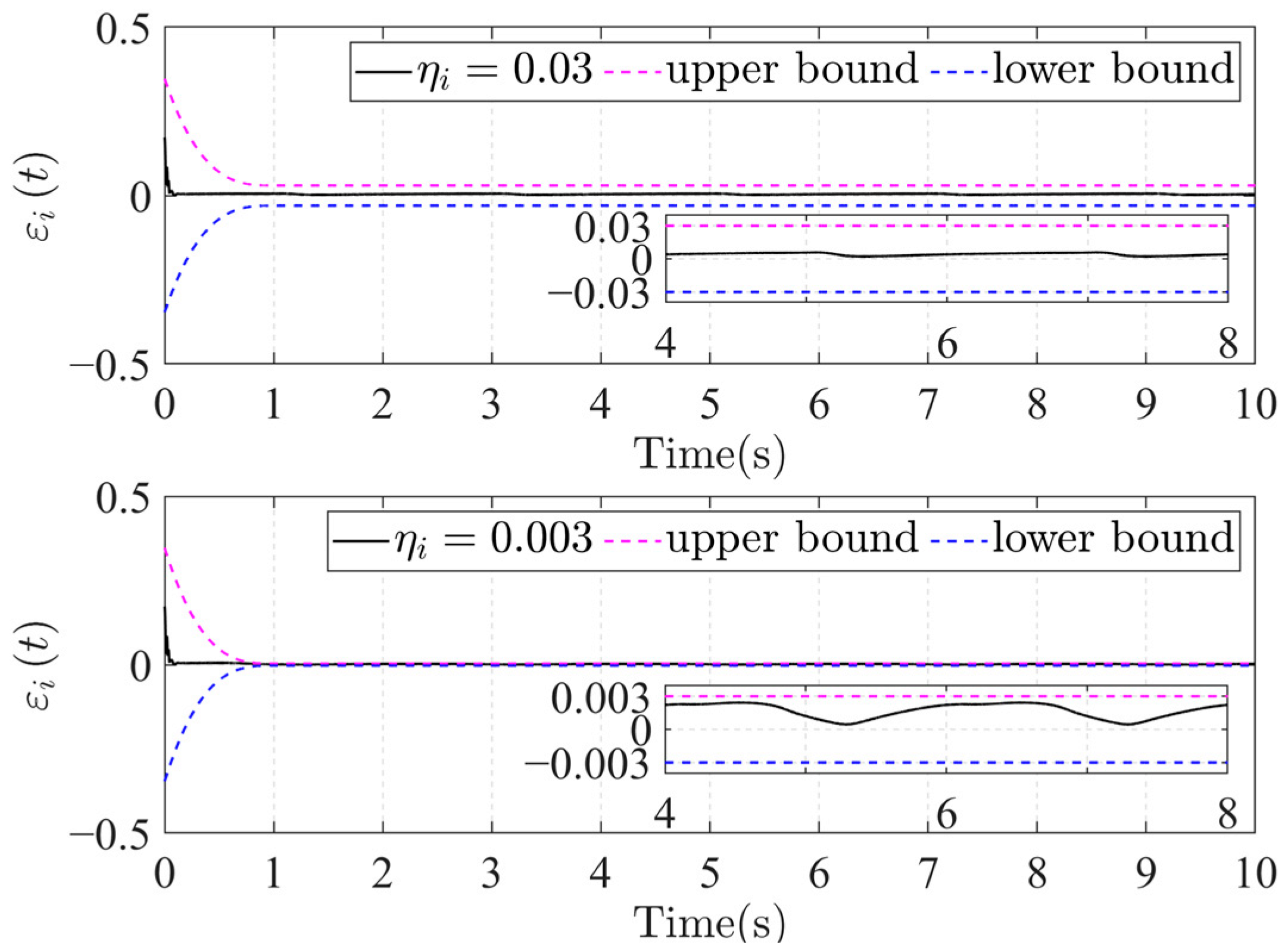
Figure 10. Trajectory tracking error for different preset boundaries.

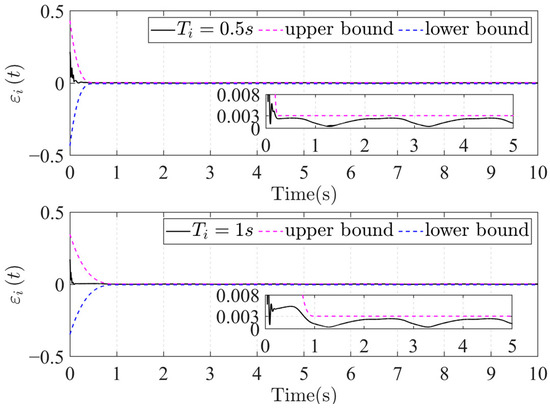
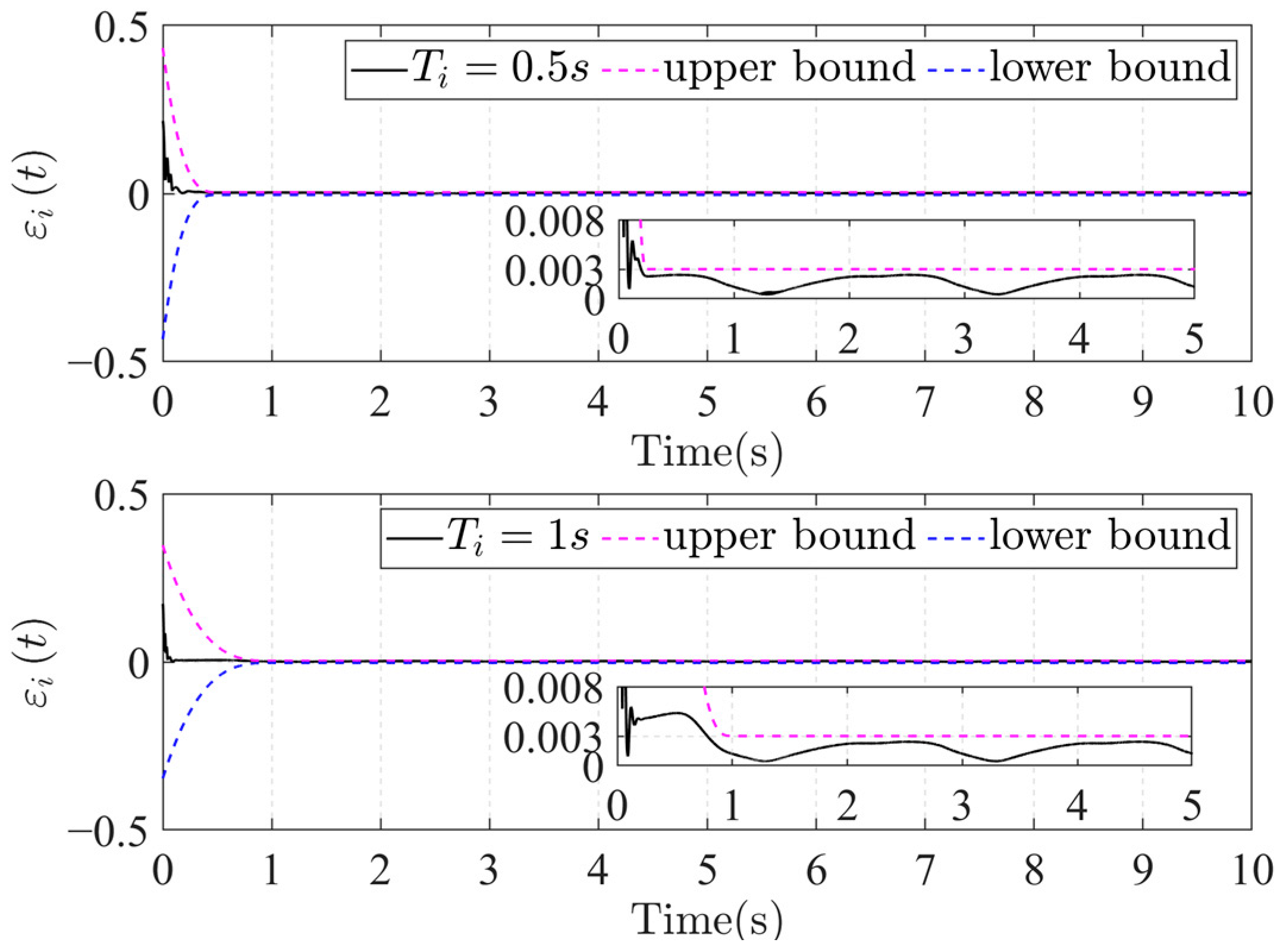
Figure 11. Trajectory tracking error for different preset times.

Figure 4 and Figure 5, respectively, show the errors in the x₁ and x₂ directions under the Cartesian coordinate system of the joint ends in the workspace. The FTPP-NN method demonstrates superior performance compared to both PID and robust control methods. The tracking errors in the x₁ and x₂ directions are significantly reduced, and the FTPP-NN method achieves stable and accurate tracking within the specified time frame.

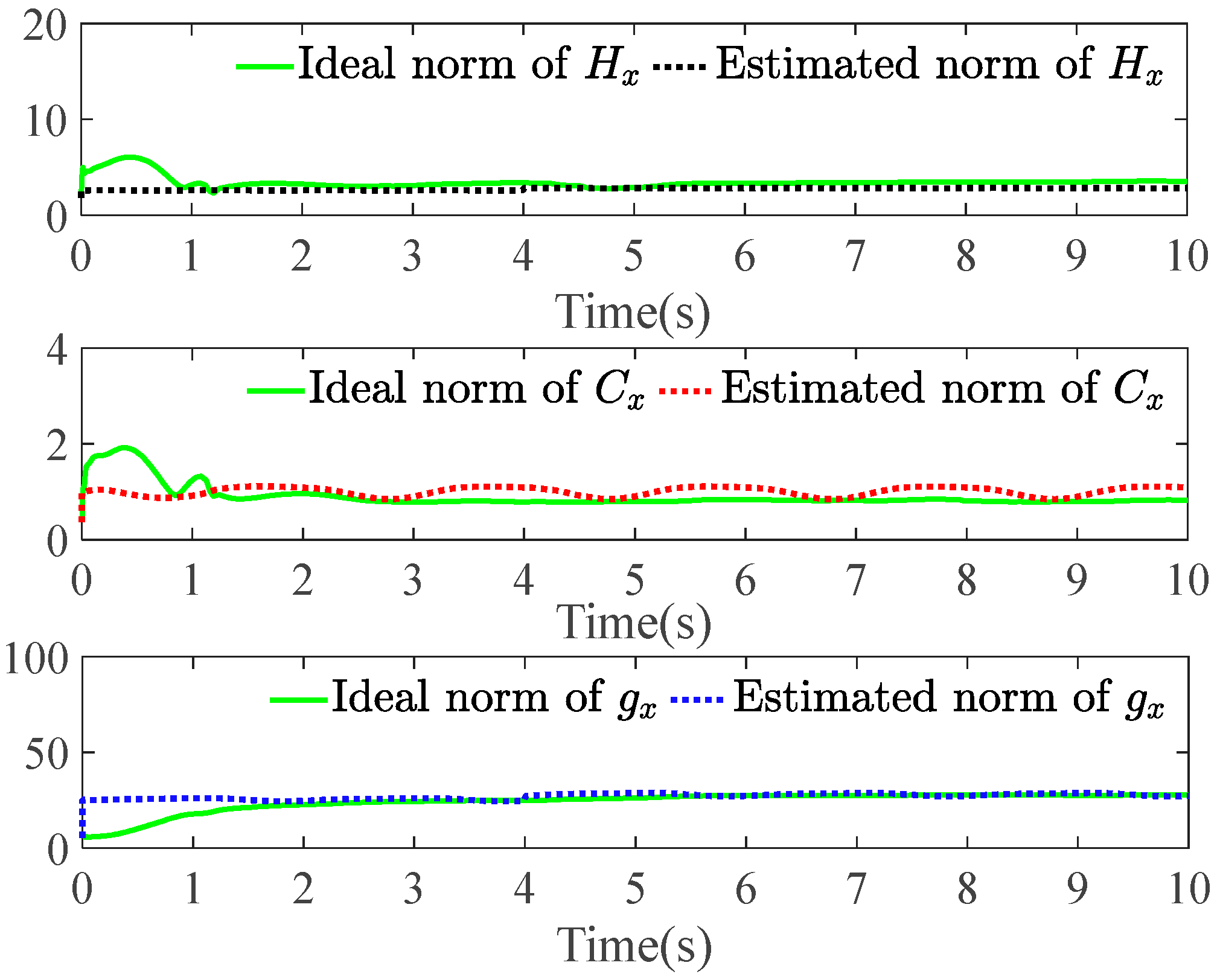
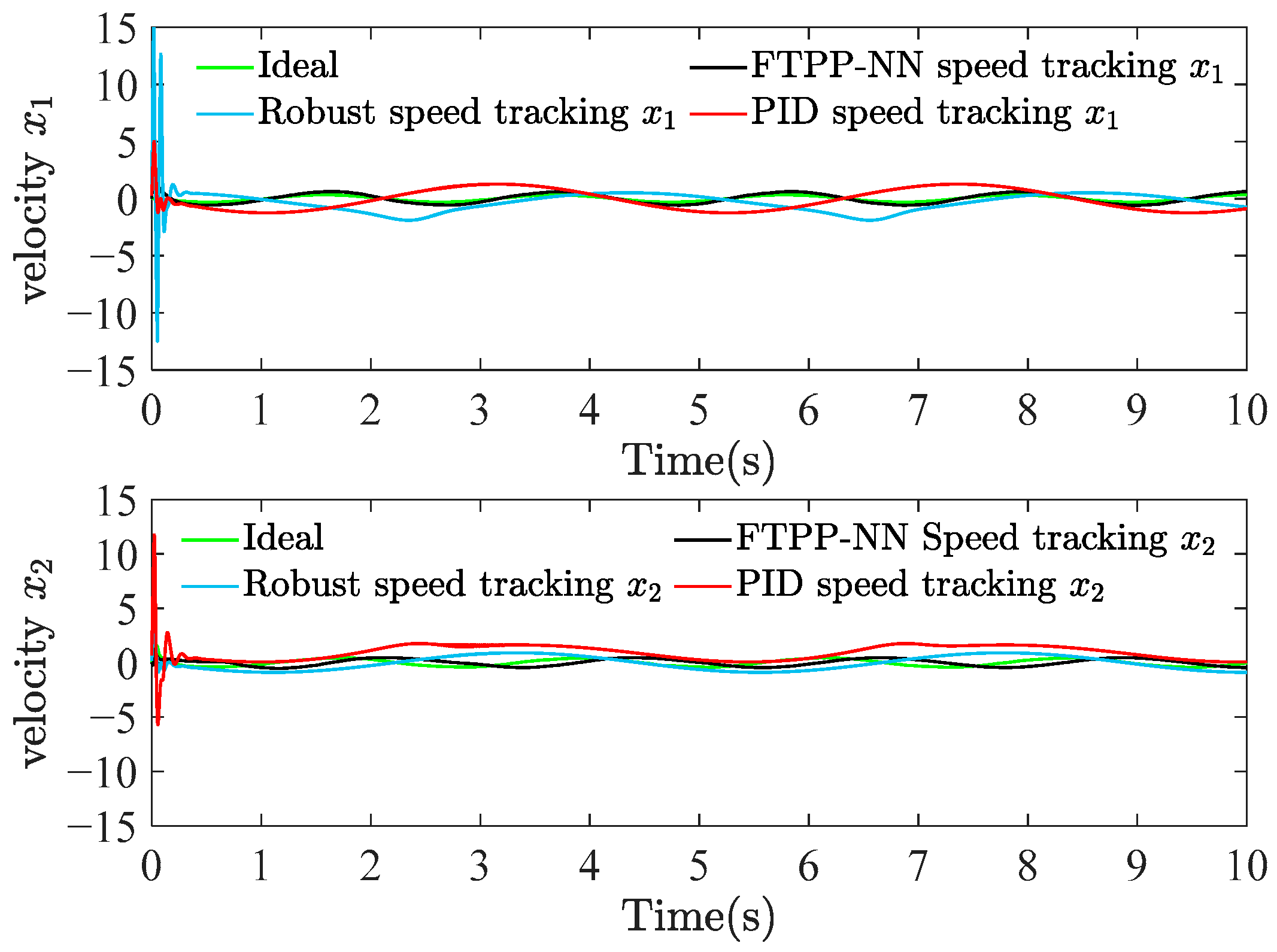
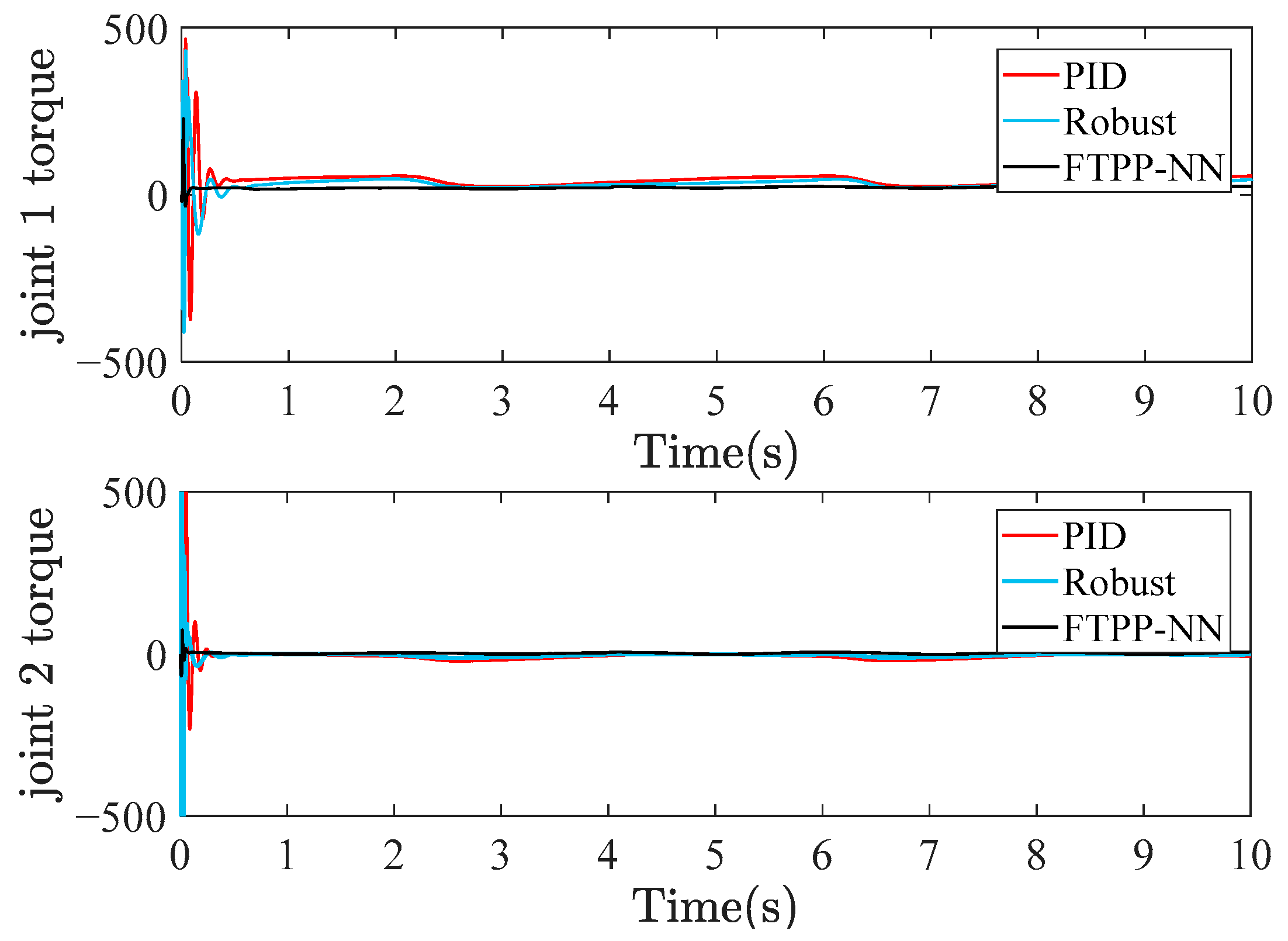
Figure 6 shows the ideal and estimated values of the kinetic parameters $H_x$, $C_x$, and $g_x$ over time. The estimation of the adaptive neural network for the kinetic parameters in the FTPP-NN algorithm maintains a high consistency with the ideal values, especially in the steady-state part of the system response. This demonstrates the robustness of the FTPP-NN method in accurately estimating and adapting to the system’s kinetic parameters. In terms of velocity tracking, Figure 7 demonstrates the velocity tracking capabilities of the three methods. When the system reaches a steady state, the velocity profiles show precise tracking of the desired velocity with minimal steady-state error. Compared to the PID and robust control algorithms, the FTPP-NN control strategy significantly reduces the steady-state error, demonstrating its superior performance in maintaining accurate velocity tracking. The joint torque analysis in Figure 8 shows that the FTPP-NN method can quickly reduce the high torque peaks caused by initial conditions and maintain a stable torque output thereafter.

The technique presented in this work may meet the criterion of trajectory tracking accuracy after homozygous error conversion, as shown in Figure 9. After appropriate transformation, the position tracking error ${\epsilon }_i$ is confined within the preset limits, offering explicit guidance for designing and tuning the control system. Error analysis in Figure 10 and Figure 11 shows that adjusting the convergence boundary ${\eta }_i$ and the time parameter $T_i$ enables the FTPP-NN method to maintain rapid and precise tracking control. The impact of various parameters on the dynamics of position tracking error is further elucidated, highlighting the FTPP-NN controller’s adaptability to diverse control tasks.

5. Conclusions

This paper introduces a fixed-time, performance-constrained control algorithm using an RBF neural network for workspace manipulators, aimed at enhancing the convergence speed and accuracy for trajectory tracking within defined time and steady-state limits. The controller design features a tangent-type error transformation through homogeneous embryonic transformation, directing the tracking error towards a specified region. Additionally, the control strategy is woven into a fixed-time stability framework, ensuring all system states are confined within a bounded region in a finite timeframe. Lastly, dynamic parameters estimated through a neural network are fed back to the controller for enhanced parameter optimization. The error from the fixed-time performance control strategy is integrated with neural network control in designing the controller, securing swift and precise manipulator trajectory tracking. Simulation results confirm the effectiveness and superior performance of the proposed controller. However, the current study does not include experimental validation, which is a limitation. In practice, akin to widely used multi-degree-of-freedom industrial manipulators, the next step involves extending this paper’s control method to such systems and conducting experimental studies to validate the simulation results. Additionally, we plan to explore time-specific performance-constrained trajectory tracking for a broader range of nonlinear mechanical systems.