Stable Rapid Sagittal Walking Control for Bipedal Robot Using Passive Tendon
Abstract
1. Introduction
2. Development of Bipedal Robot Using Passive Tendon
2.1. General Description of the Bipedal Robot Prototype
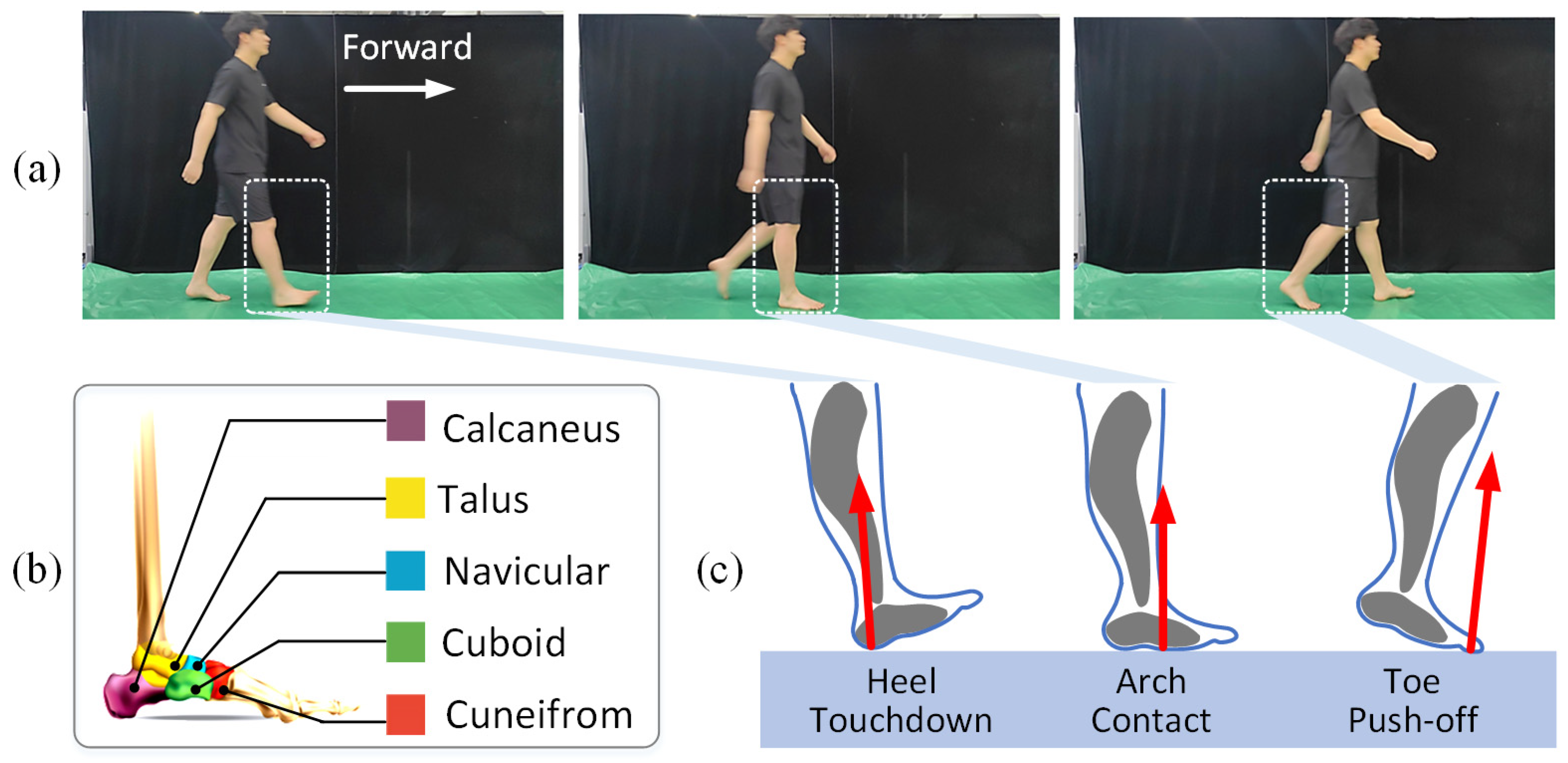
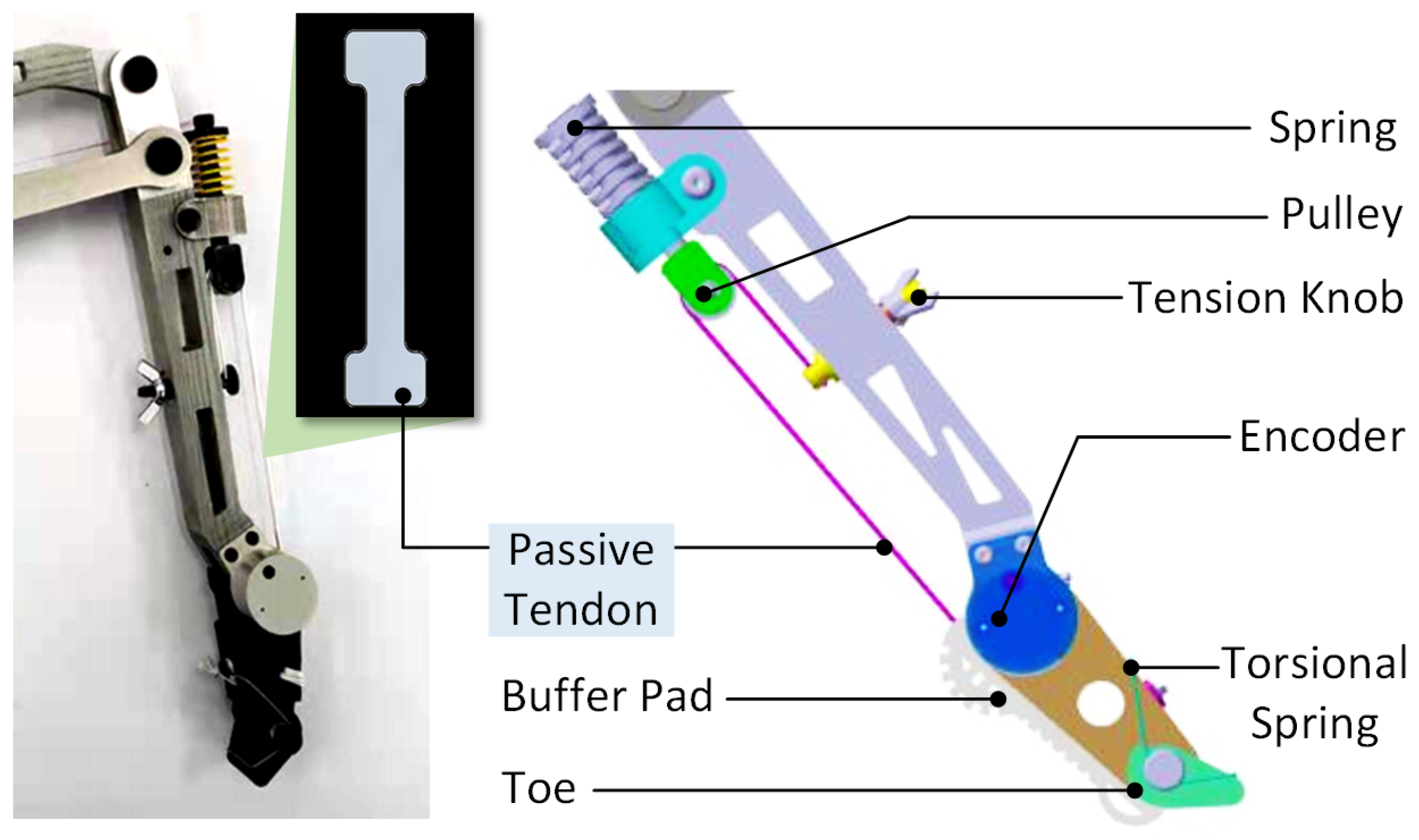
2.2. Inspiration and Design of Passive Tendon
2.3. Sensors and Electical Layout
3. Dynamic Modeling and Gait Synthesis of the Bipedal Robot
3.1. Kinematics of the Leg with Coaxial Actuations
3.2. Dynamic Model of the Bipedal Robot
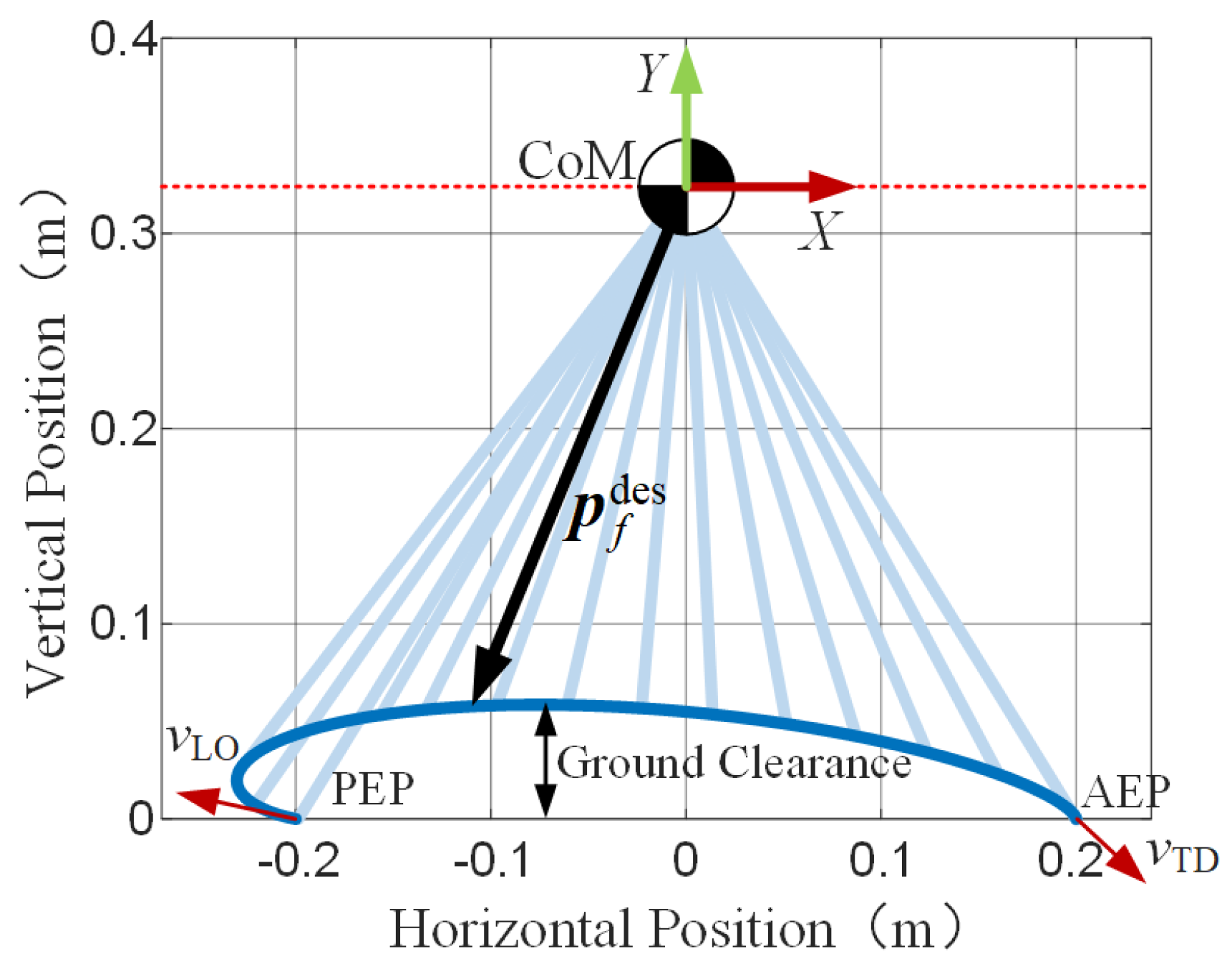
3.3. LIP Model-Based Walking Gait Synthesis
| Algorithm 1: Motion Planning of the LIP Model on the Sagittal Plane |
| Input: Desired CoM state at the ending of single support duration Sdes Desired walking speed at double support duration v0 Height of the CoM hCoM Position of the CoM Start time of the stance phase |
| Output: Trajectory of the CoM xCoM |
|
4. Control Framework of the Bipedal Robot
4.1. Swing Leg Control
4.2. Stance Leg Control
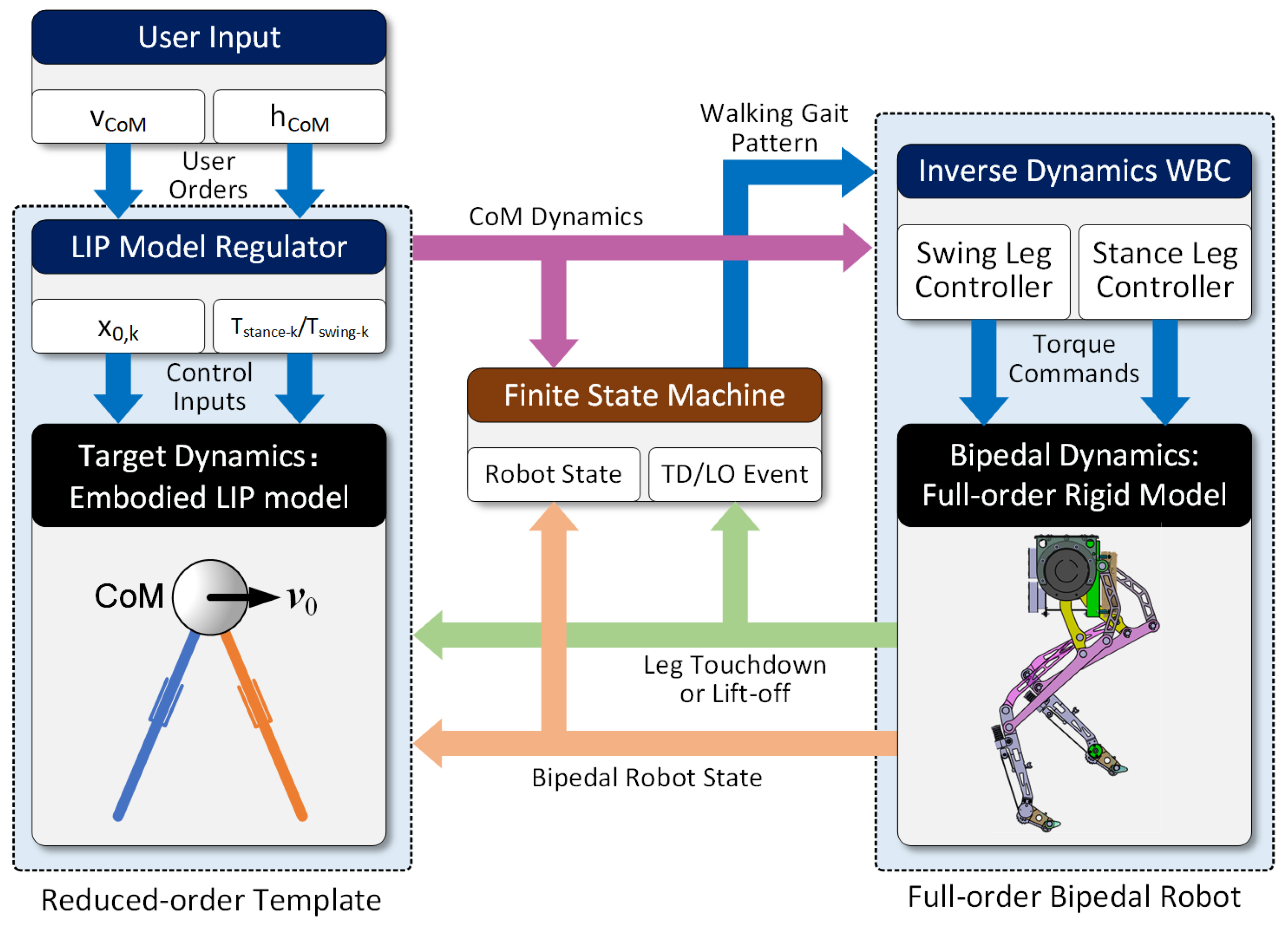
4.3. Whole-Body Control Framework of the Bipedal Robot
5. Experiments
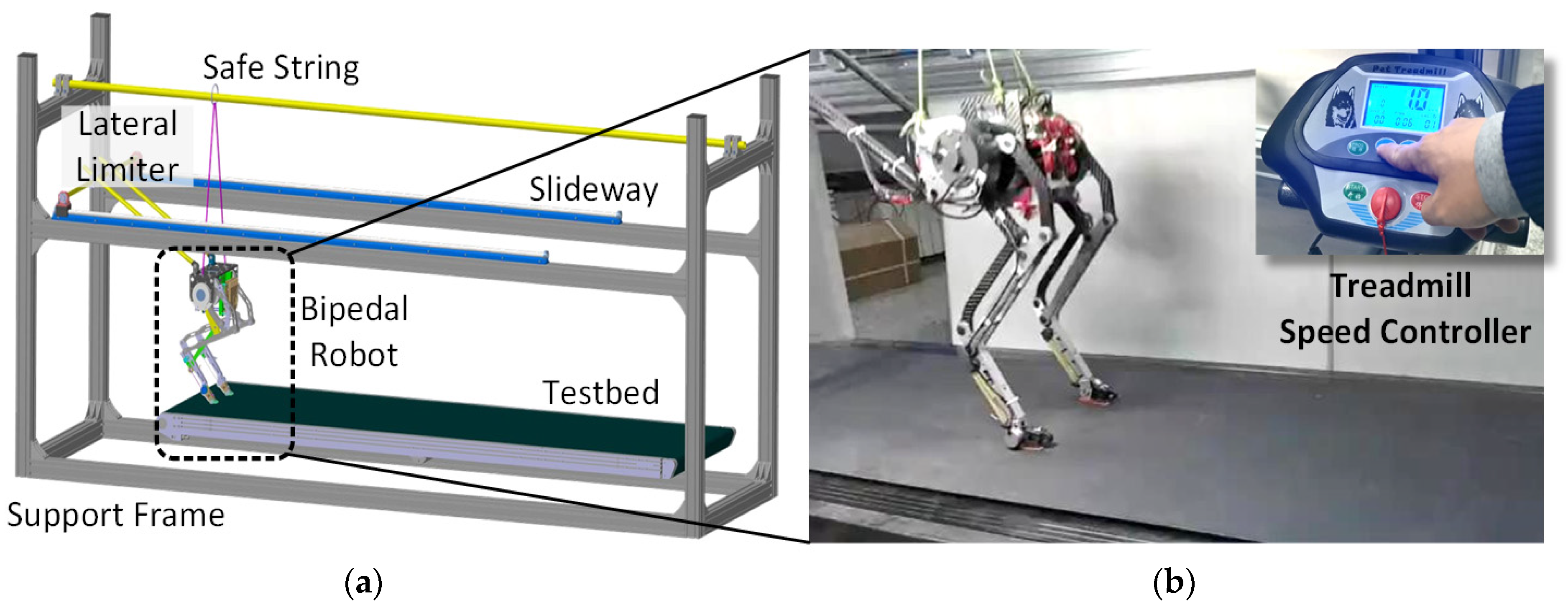
5.1. Experimental Setups
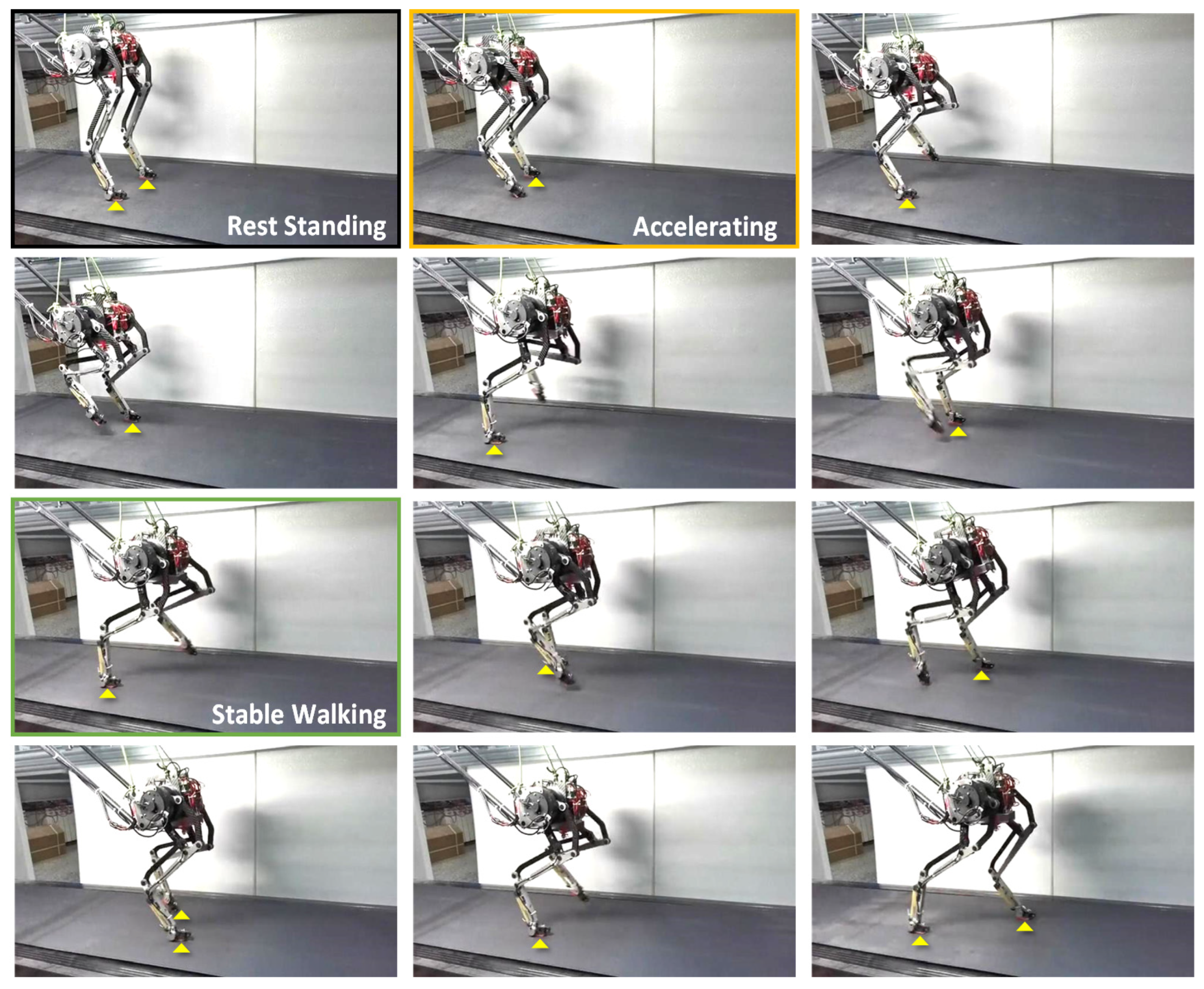
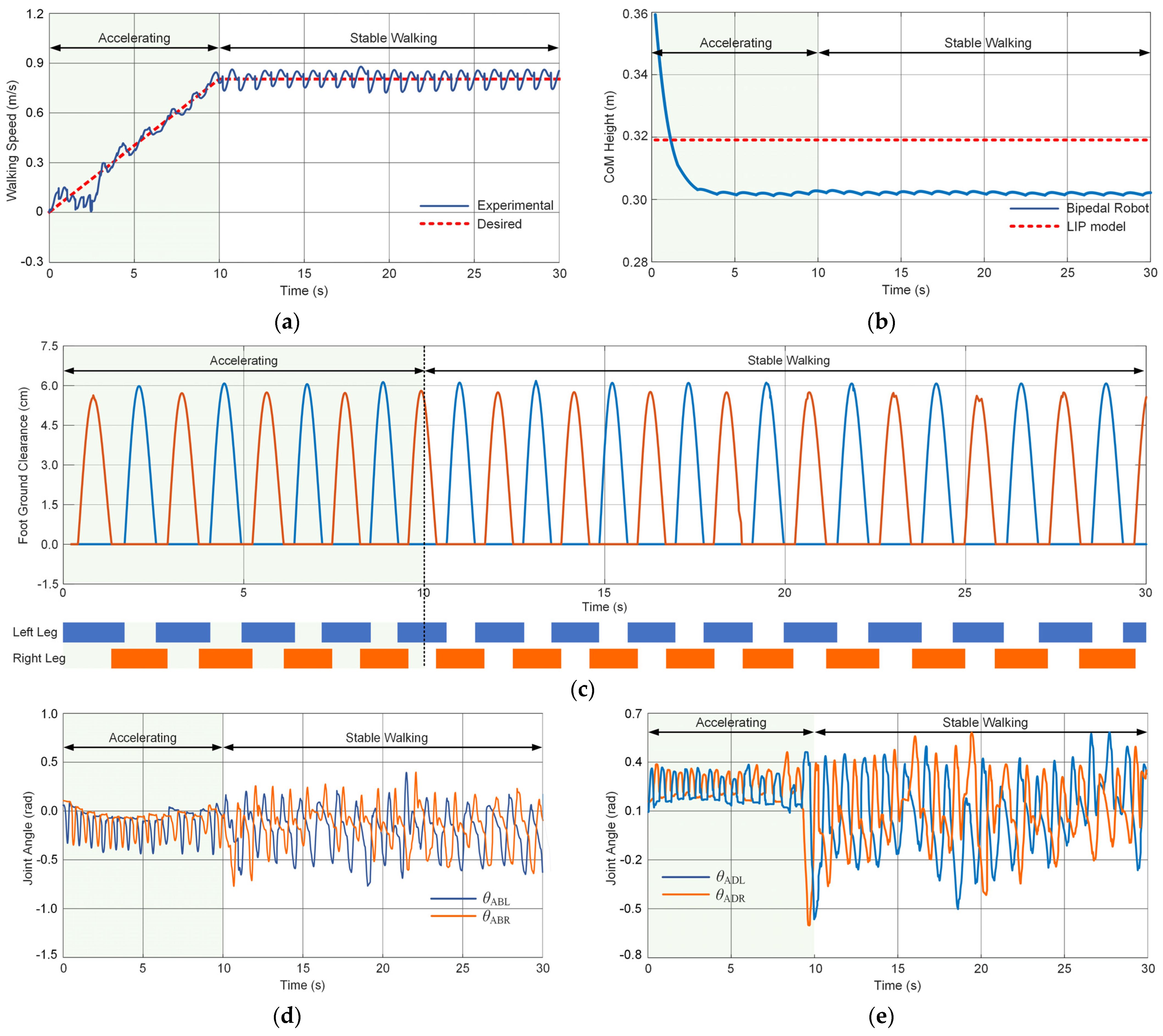
5.2. Stable Walking Test
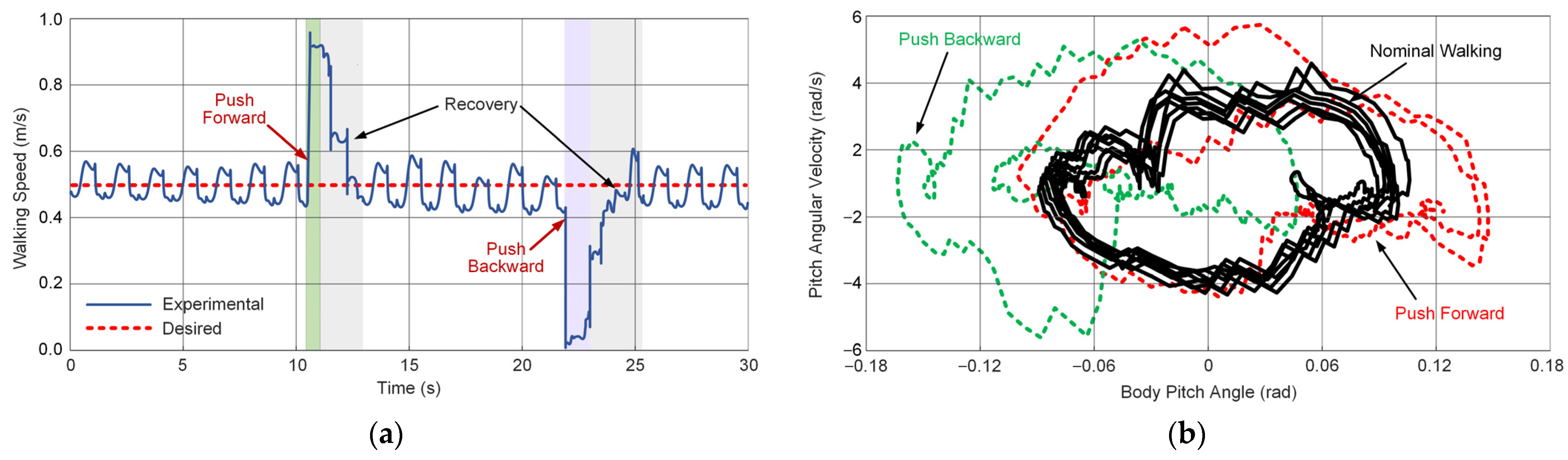
5.3. Push Recovery Test
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Raibert, M. Legged Robots That Balance, 1st ed.; The MIT Press: Cambridge, MA, USA, 1986; pp. 2–9. [Google Scholar]
- Yu, H.; Gao, H.; Ding, L.; Li, M.; Deng, Z.; Liu, G. Gait Generation with Smooth Transition Using CPG-Based Locomotion Control for Hexapod Walking Robot. IEEE Trans. Ind. Electron. 2016, 63, 5488–5500. [Google Scholar] [CrossRef]
- Hutter, M.; Gehring, C.; Höpflinger, M.; Blösch, M.; Siegwart, R. Toward Combining Speed, Efficiency, Versatility, and Robustness in an Autonomous Quadruped. IEEE Trans. Robot. 2014, 30, 1427–1440. [Google Scholar] [CrossRef]
- Yi, H.; Xu, Z.; Xin, X.; Zhou, L.; Luo, X. Bio-inspired Leg Design for a Heavy-Duty Hexapod Robot. J. Bionic. Eng. 2022, 19, 975–990. [Google Scholar] [CrossRef]
- Hurst, J.W.; Rizzi, A.A. Series Compliance for An Efficient Running Gait. IEEE Robot. Autom. Mag. 2008, 15, 42–51. [Google Scholar] [CrossRef]
- Park, H.W.; Ramezani, A.; Grizzle, J.W. A Finite-State Machine For Accommodating Unexpected Large Ground-Height Variations in Bipedal Robot Walking. IEEE Trans. Robot. 2013, 29, 331–345. [Google Scholar] [CrossRef]
- Liu, X.; Rossi, A.; Poulakakis, I. A Switchable Parallel Elastic Actuator and Its Application to Leg Design for Running Robots. IEEE/ASME Trans. Mech. 2018, 23, 2681–2692. [Google Scholar] [CrossRef]
- Yang, T.; Westervelt, E.R.; Schmiedeler, J.P.; Bockbrader, R.A. Design and Control of a Planar Bipedal Robot ERNIE with Parallel Knee Compliance. Auton. Robot. 2008, 25, 317–330. [Google Scholar] [CrossRef]
- Haeufle, D.F.B.; Taylor, M.D.; Schmitt, S.; Geyer, H. A Clutched Parallel Elastic Actuator Concept: Towards Energy Efficient Powered Legs in Prosthetics and Robotics. In Proceedings of the Fourth IEEE RAS/EMBS International Conference on Biomedical Robotics and Biomechatronics, Roma, Italy, 24–27 June 2012. [Google Scholar]
- Reher, J.; Ames, A.D. Dynamic Walking: Toward Agile and Efficient Bipedal Robots. Ann. Rev. Contr. Robot. 2021, 4, 535–572. [Google Scholar] [CrossRef]
- Sreenath, K.; Park, H.W.; Poulakakis, I.; Grizzle, J.W. Embedding Active Force Control within the Compliant Hybrid Zero Dynamics to Achieve Stable, Fast Running on MABEL. Int. J. Robot. Res. 2013, 32, 324–345. [Google Scholar] [CrossRef]
- Che, J.; Pan, Y.; Yan, W.; Yu, J. Leg Configuration Analysis and Prototype Design of Biped Robot Based on Spring Mass Model. Actuators 2022, 11, 75. [Google Scholar] [CrossRef]
- Yamamoto, K.; Kamioka, T.; Sugihara, T. Survey on Model-Based Biped Motion Control for Humanoid Robots. Adv. Robotics. 2020, 34, 1353–1369. [Google Scholar] [CrossRef]
- Yu, H.; Gao, H.; Deng, Z. Toward a Unified Approximate Analytical Representation For Spatially Running Spring-Loaded Inverted Pendulum. IEEE Trans. Robot. 2021, 37, 691–698. [Google Scholar] [CrossRef]
- Takenaka, T.; Matsumoto, T.; Yoshiike, T. Real Time Motion Generation and Control For Biped Robot-1st Report: Walking Gait Pattern Generation. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 10–15 October 2019. [Google Scholar]
- Geyer, H.; Seyfarth, A.; Blickhan, R. Compliant Leg Behavior Explains Basic Dynamics of Walking and Running. Proc. R. Soc. Lond. B. 2006, 273, 2861–2867. [Google Scholar]
- Ahmadi, M.; Buehler, M. Controlled Passive Dynamic Running Experiments with the ARL-Monopod II. IEEE Trans. Robot. 2006, 22, 974–986. [Google Scholar] [CrossRef]
- Hobbelen, D.G.E.; Wisse, M. Swing-Leg Retraction For Limit Cycle Walkers Improves Disturbance Rejection. IEEE Trans. Robot. 2008, 24, 377–389. [Google Scholar] [CrossRef]
- Posa, M.; Cantu, C.; Tedrake, R. A Direct Method For Trajectory Optimization of Rigid Bodies Through Contact. Int. J. Robot. Res. 2014, 33, 69–81. [Google Scholar] [CrossRef]
- Saab, L.; Ramos, O.E.; Keith, F.; Mansard, N.; Soueres, P.; Fourquet, J.Y. Dynamic Whole-Body Motion Generation Under Rigid Contacts and Other Unilateral Constraints. IEEE Trans. Robot. 2013, 29, 346–362. [Google Scholar] [CrossRef]
- Calanca, A.; Fiorini, P. Understanding Environment-Adaptive Force Control of Series Elastic Actuators. IEEE/ASME Trans. Mech. 2018, 23, 413–423. [Google Scholar] [CrossRef]
- Paine, N.; Oh, S.; Sentis, L. Design and Control Considerations for High-Performance Series Elastic Actuators. IEEE/ASME Trans. Mech. 2014, 19, 1080–1091. [Google Scholar] [CrossRef]
- Jafari, A.; Tsagarakis, N.; Caldwell, D. A Novel Intrinsically Energy Efficient Actuator with Adjustable stiffness (AwAS). IEEE/ASME Trans. Mech. 2013, 18, 355–365. [Google Scholar] [CrossRef]
- Mörl, F.; Siebert, T.; Häufle, D. Contraction Dynamics and Function of the Muscle-Tendon Complex Depend On the Muscle Fibre-Tendon Length Ratio: A Simulation Study. Biomech. Model Mechanobiol. 2016, 15, 245–258. [Google Scholar] [CrossRef] [PubMed]
- Sawicki, G.S.; Robertson, B.D.; Azizi, E.; Roberts, T.J. Timing matters: Tuning the Mechanics of a Muscle-Tendon Unit by Adjusting Stimulation Phase During Cyclic Contractions. J. Exp. Biol. 2015, 218, 3150–3159. [Google Scholar] [CrossRef] [PubMed]
- Lai, A.; Schache, A.G.; Lin, Y.; Pandy, M.G. Tendon Elastic Strain Energy in the Human Ankle Plantar-Flexors and Its Role with Increased Running Speed. J. Exp. Biol. 2014, 217, 3159–3168. [Google Scholar] [CrossRef] [PubMed]
- Jackson, R.W.; Dembia, C.L.; Delp, S.L.; Collins, S.H. Muscle-Tendon Mechanics Explain Unexpected Effects of Exoskeleton Assistance On Metabolic Rate During Walking. J. Exp. Biol. 2017, 220, 2082–2095. [Google Scholar] [CrossRef] [PubMed]
- Sovukluk, S.; Englsberger, J.; Ott, C. Highly Maneuverable Humanoid Running via 3D SLIP+Foot Dynamics. IEEE Robot. Autom. Let. 2024, 9, 1131–1138. [Google Scholar] [CrossRef]
- Xiong, X.; Ames, A. 3-D Underactuated Bipedal Walking via H-LIP Based Gait Synthesis and Stepping Stabilization. IEEE Trans. Robot. 2022, 38, 2405–2425. [Google Scholar] [CrossRef]
- Shamsha, A.; Gu, Z.; Warnke, J.; Zhao, Y.; Hutchinson, S. Integrated Task and Motion Planning For Safe Legged Navigation in Patially Observable Environments. IEEE Trans. Robot. 2023, 39, 4913–4934. [Google Scholar] [CrossRef]
- Kajita, S.; Kanehiro, F.; Kaneko, K.; Yokoi, K.; Hirukawa, H. The 3D linear Inverted Pendulum Model: A Simple Modeling For A Biped Walking Pattern Generation. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Maui, HI, USA, 29 October–3 November 2001. [Google Scholar]
- Ott, C.; Dietrich, A.; Schäffer, A.A. Prioritized multi-task compliance control of redundant manipulators. Automatica 2015, 53, 416–423. [Google Scholar] [CrossRef]






| Specifications | Value | Unit |
|---|---|---|
| Total mass | 4.08 | kg |
| Body mass | 3.36 | kg |
| Leg mass (single) | 0.34 | kg |
| Foot mass (single) | 0.04 | kg |
| Natural standing height | 0.45 | m |
| Body height | 0.25 | m |
| Body width | 0.38 | m |
| Foot pad length | 0.04 | m |
| Storage size (leg folded) | 0.35 × 0.27 × 0.19 | m3 |
| Foot Contact State | Left-Side χL | Right-Side χR | Gait Phase |
|---|---|---|---|
| Double support | 1 | 1 | Stance |
| Double take-off | 0 | 0 | Flight |
| Left-side leg in stance | 1 | 0 | Stance |
| Right-side leg in stance | 0 | 1 | Stance |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, H.; Wang, S.; Shan, K.; Mu, C.; Wang, X.; Su, B.; Yu, H. Stable Rapid Sagittal Walking Control for Bipedal Robot Using Passive Tendon. Actuators 2024, 13, 240. https://doi.org/10.3390/act13070240
Gao H, Wang S, Shan K, Mu C, Wang X, Su B, Yu H. Stable Rapid Sagittal Walking Control for Bipedal Robot Using Passive Tendon. Actuators. 2024; 13(7):240. https://doi.org/10.3390/act13070240
Chicago/Turabian StyleGao, Haibo, Shengjun Wang, Kaizheng Shan, Changxi Mu, Xin Wang, Bo Su, and Haitao Yu. 2024. "Stable Rapid Sagittal Walking Control for Bipedal Robot Using Passive Tendon" Actuators 13, no. 7: 240. https://doi.org/10.3390/act13070240
APA StyleGao, H., Wang, S., Shan, K., Mu, C., Wang, X., Su, B., & Yu, H. (2024). Stable Rapid Sagittal Walking Control for Bipedal Robot Using Passive Tendon. Actuators, 13(7), 240. https://doi.org/10.3390/act13070240






