Disturbance-Observer-Based Sliding-Mode Speed Control for Synchronous Reluctance Motor Drives via Generalized Super-Twisting Algorithm
Abstract
1. Introduction
2. Preliminaries
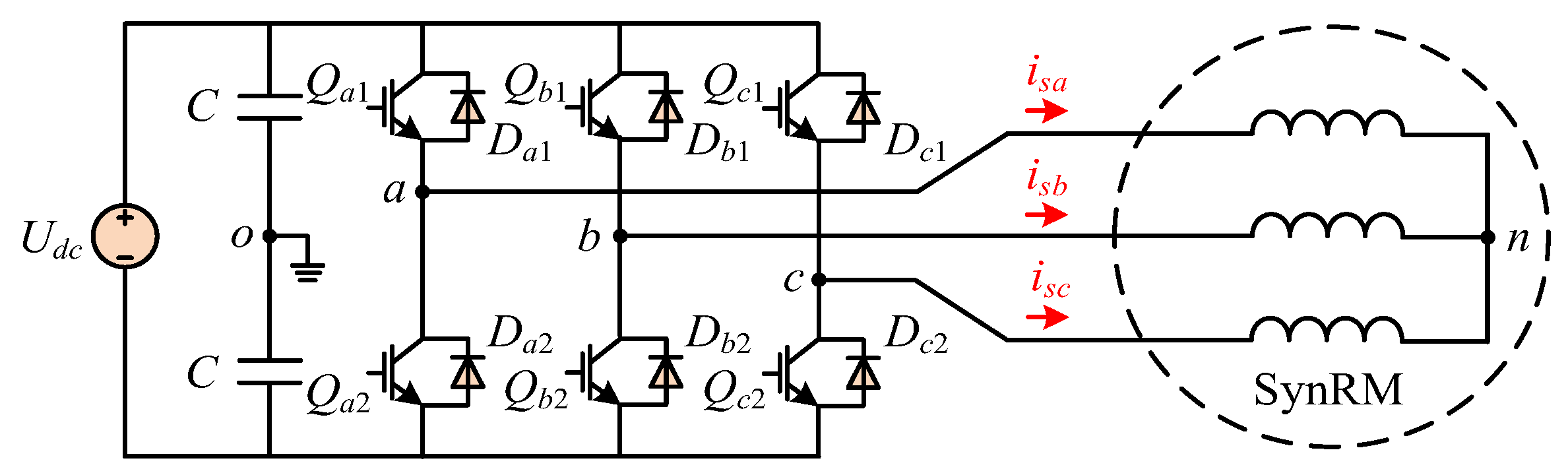
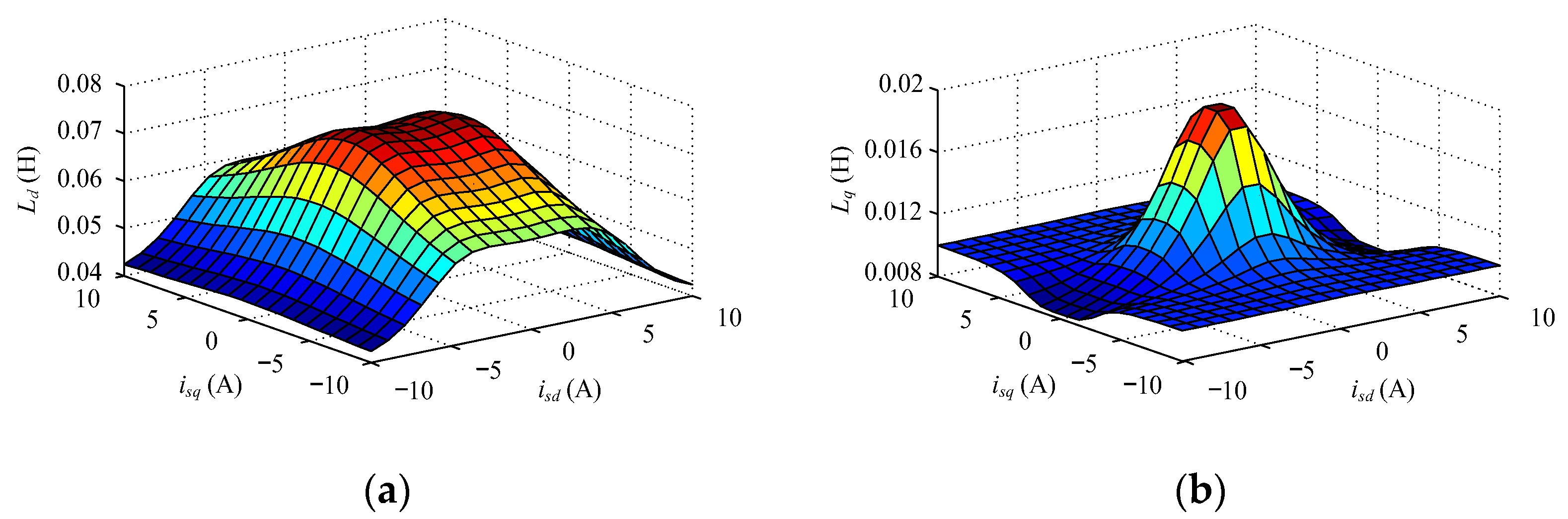
2.1. Dynamics of the SynRM Drive System
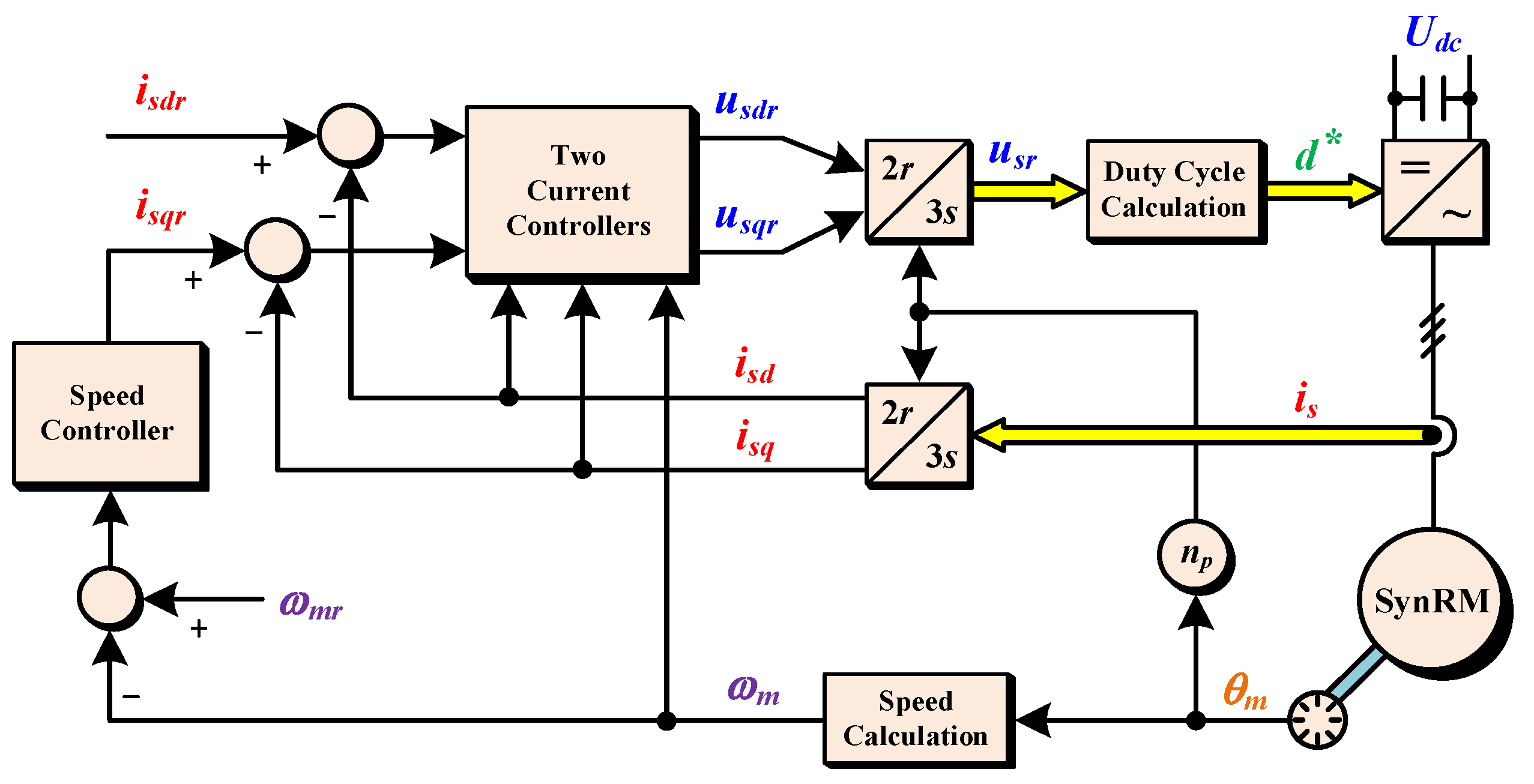
2.2. Adopted Vector Control Strategy
3. Controller Design
3.1. Speed Tracking Error Dynamics
3.2. GSTSM-DO Design
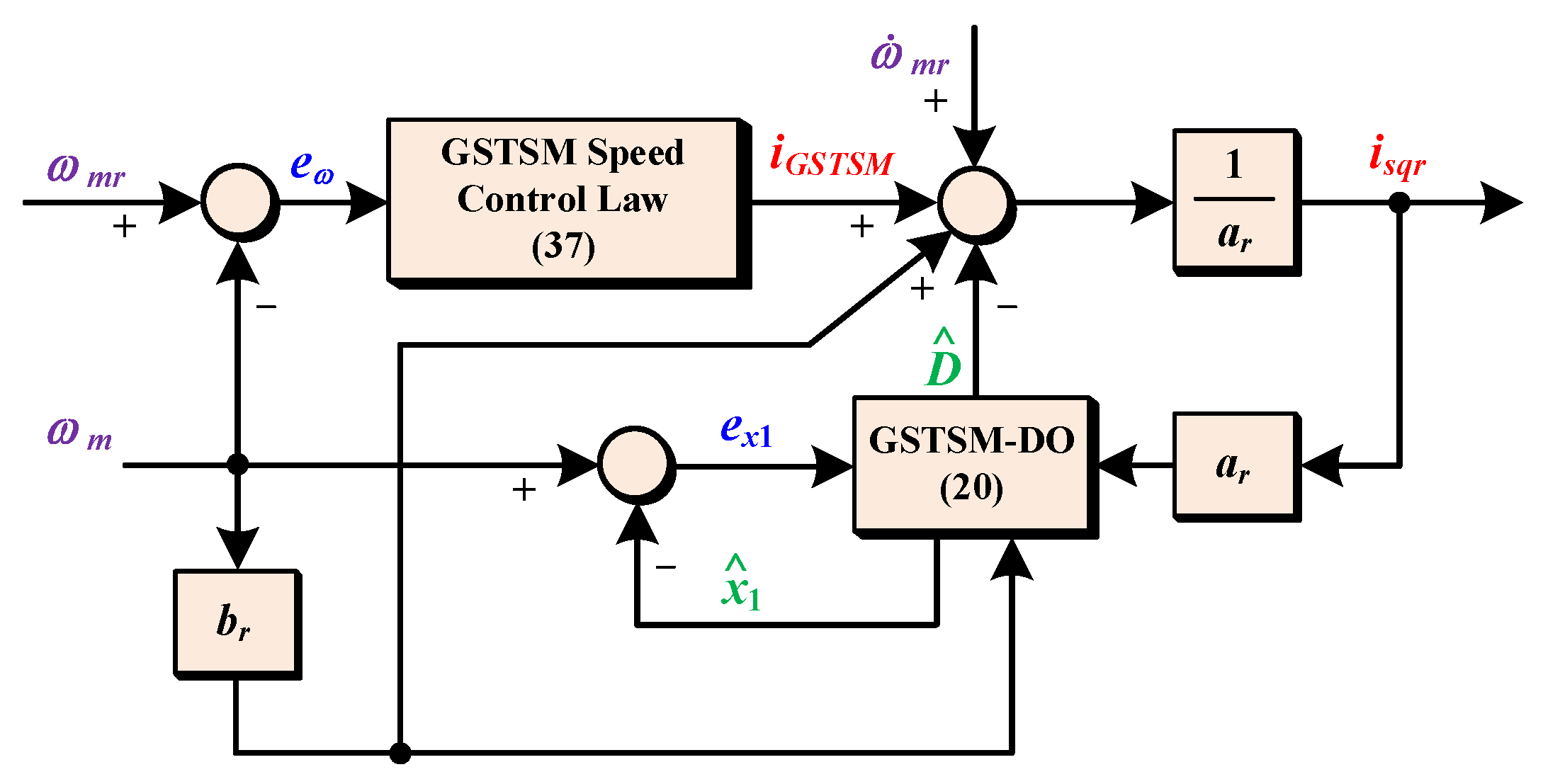
3.3. Proposed Composite Speed Controller Design
4. Simulation Results
5. Conclusions and Future Work
Funding
Data Availability Statement
Conflicts of Interest
References
- Pellegrino, G.; Jahns, T.M.; Bianchi, W.L.; Soong, W.L.; Cupertino, F. The Rediscovery of Synchronous Reluctance and Ferrite Permanent Magnet Motors; Springer: Basel, Switzerland, 2016. [Google Scholar]
- Moghaddam, R.R.; Magnussen, F.; Sadarangani, C. Theoretical and experimental reevaluation of synchronous reluctance machine. IEEE Trans. Ind. Electron. 2010, 57, 6–13. [Google Scholar] [CrossRef]
- Ozcelik, N.G.; Dogru, U.E.; Imeryuz, M.; Ergene, L.T. Synchronous reluctance motor vs. induction motor at low-power industrial applications: Design and comparison. Energies 2019, 12, 2190. [Google Scholar] [CrossRef]
- Heidari, H.; Rassõlkin, A.; Kallaste, A.; Vaimann, T.; Andriushchenko, E.; Belahcen, A.; Lukichev, D.V. A review of synchronous reluctance motor-drive advancements. Sustainability 2021, 13, 729. [Google Scholar] [CrossRef]
- Murataliyev, M.; Degano, M.; Di Nardo, M.; Bianchi, N.; Gerada, C. Synchronous reluctance machines: A comprehensive review and technology comparison. Proc. IEEE 2022, 110, 382–399. [Google Scholar] [CrossRef]
- Kostko, J.K. Polyphase reaction synchronous motors. J. Am. Inst. Elect. Eng. 1923, 42, 1162–1168. [Google Scholar] [CrossRef]
- Ferrari, M.; Bianchi, N.; Doria, A.; Fornasiero, E. Design of synchronous reluctance motor for hybrid electric vehicles. IEEE Trans. Ind. Appl. 2015, 51, 3030–3040. [Google Scholar] [CrossRef]
- Bianchi, N.; Bolognani, S.; Carraro, E.; Castiello, M.; Fornasiero, E. Electric vehicle traction based on synchronous reluctance motors. IEEE Trans. Ind. Appl. 2016, 52, 4762–4769. [Google Scholar] [CrossRef]
- Kumar, G.V.; Chuang, C.H.; Lu, M.Z.; Liaw, C.M. Development of an electric vehicle synchronous reluctance motor drive. IEEE Trans. Veh. Technol. 2020, 69, 5012–5024. [Google Scholar] [CrossRef]
- Boztas, G.; Aydogmus, O.; Caner, M.; Guldemir, H. Design, optimisation and implementation of low-voltage synchronous reluctance motor for solar-powered systems. IET Power Electron. 2019, 12, 1679–1685. [Google Scholar] [CrossRef]
- Ibrahim, M.N.; Rezk, H.; Al-Dhaifallah, M.; Sergeant, P. Solar array fed synchronous reluctance motor driven water pump: An improved performance under partial shading conditions. IEEE Access 2019, 7, 77100–77115. [Google Scholar] [CrossRef]
- Parveen, H.; Singh, B. PV Array fed synchronous reluctance motor driven water pumping system with grid integration and seamless operability. IEEE Trans. Ind. Appl. 2024, 60, 3724–3733. [Google Scholar] [CrossRef]
- Roshanfekr, P.; Lundmark, S.; Thiringer, T.; Alatalo, M. A synchronous reluctance generator for a wind application-compared with an interior mounted permanent magnet synchronous generator. In Proceedings of the 7th IET International Conference on Power Electronics, Machines and Drives, Manchester, UK, 8–10 April 2014. [Google Scholar]
- Moncada, R.H.; Young, H.A.; Pavez-Lazo, B.J.; Tapia, J.A. A commercial-off-the-shelf synchronous reluctance motor as a generator for wind power applications. In Proceedings of the 2015 IEEE International Electric Machines & Drives Conference, Coeur d’Alene, ID, USA, 10–13 May 2015. [Google Scholar]
- Singh, B.; Bhuvaneswari, G. Position sensor-less synchronous reluctance generator based grid-tied wind energy conversion system with adaptive observer control. IEEE Trans. Sustain. Energy 2019, 11, 693–702. [Google Scholar]
- Gorozhankin, A.N. The choice of the rotor geometry of synchronous reluctance machines for electric drives for cold-rolling tube mills. Russ. Electr. Eng. 2020, 91, 293–297. [Google Scholar] [CrossRef]
- Blagov, M.; Kushnarev, V.; Platonov, V. Application of a synchronous reluctance electric drive in a cold rolling mill. In Proceedings of the 2022 Conference of Russian Young Researchers in Electrical and Electronic Engineering, Saint Petersburg, Russia, 25–28 January 2022. [Google Scholar]
- Park, J.; Kalev, C.; Hofmann, H.F. Control of high-speed solid-rotor synchronous reluctance motor/generator for flywheel-based uninterruptible power supplies. IEEE Trans. Ind. Electron. 2008, 55, 3038–3046. [Google Scholar] [CrossRef]
- ABB. IE5 SynRM Motors Deliver Ultra-Premium Energy Efficiency. Available online: https://new.abb.com/news/detail/58874/abb-ie5-synrm-motors-deliver-ultra-premium-energy-efficiency (accessed on 15 June 2024).
- SIEMENS. Small Step, Big Impact: A New Dimension in Efficiency: The Innovative Synchronous-Reluctance Drive System with SIMOTICS Motors and SINAMICS Converters. Available online: https://cache.industry.siemens.com/dl/files/277/109757277/att_960984/v1/simotics-synchronous-reluctance-drive-system-en-2018.pdf (accessed on 15 June 2024).
- Pyrhönen, J.; Hrabovcová, V.; Semken, R.S. Electrical Machine Drives Control: An Introduction; Wiley: Chichester, UK, 2016. [Google Scholar]
- Yousefi-Talouki, A.; Pescetto, P.; Pellegrino, G.; Boldea, I. Combined active flux and high-frequency injection methods for sensorless direct-flux vector control of synchronous reluctance machines. IEEE Trans. Power Electron. 2018, 33, 2447–2457. [Google Scholar] [CrossRef]
- Liu, Y.-C.; Laghrouche, S.; N’Diaye, A.; Narayan, S.; Cirrincione, G.; Cirrincione, M. Sensorless control of synchronous reluctance motor drives based on the TLS EXIN neuron. In Proceedings of the 2019 IEEE International Electric Machines & Drives Conference, San Diego, CA, USA, 12–15 May 2019. [Google Scholar]
- Liu, Y.-C.; Laghrouche, S.; N’Diaye, A.; Cirrincione, M. Model predictive current and capacitor voltage control of post-fault three-level NPC inverter-fed synchronous reluctance motor drives. In Proceedings of the 2019 International Aegean Conference on Electrical Machines and Power Electronics & 2019 International Conference on Optimization of Electrical and Electronic Equipment, Istanbul, Turkey, 27–19 August 2019. [Google Scholar]
- Li, C.; Wang, G.; Zhang, G.; Zhao, N.; Xu, D. Adaptive pseudorandom high-frequency square-wave voltage injection based sensorless control for SynRM drives. IEEE Trans. Power Electron. 2020, 36, 3200–3210. [Google Scholar] [CrossRef]
- Heidari, H.; Rassõlkin, A.; Kallaste, A.; Vaimann, T.; Andriushchenko, E.; Belahcen, A. Design of a research laboratory drive system for a synchronous reluctance motor for vector control and performance analysis. Inventions 2021, 6, 64. [Google Scholar] [CrossRef]
- Hadla, H.; Santos, F. Performance comparison of field-oriented control, direct torque control, and model-predictive control for SynRMs. Chin. J. Electr. Eng. 2022, 8, 24–37. [Google Scholar] [CrossRef]
- Li, S.; Yang, J.; Chen, W.-H.; Chen, X. Disturbance Observer-Based Control Methods and Applications; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Farhan, A.; Abdelrahem, M.; Hackl, C.M.; Kennel, R.; Shaltout, A.; Saleh, A. Advanced strategy of speed predictive control for nonlinear synchronous reluctance motors. Machines 2020, 8, 44. [Google Scholar] [CrossRef]
- Mei, M.-Y.; Liu, T.-H. Design and implementation of an online tuning adaptive controller for synchronous reluctance motor drives. IEEE Trans. Ind. Electron. 2013, 60, 3644–3657. [Google Scholar]
- Pan, P.C.; Liu, T.H.; Madawala, U.K. Adaptive controller with an improved high-frequency injection technique for sensorless synchronous reluctance drive systems. IET Electr. Power Appl. 2016, 10, 240–250. [Google Scholar] [CrossRef]
- Daryabeigi, E.; Mirzaei, A.; Zarchi, H.A.; Vaez-Zadeh, S. Enhanced emotional and speed deviation control of synchronous reluctance motor drives. IEEE Trans. Energy Convers. 2019, 34, 604–612. [Google Scholar] [CrossRef]
- Cao, L.; Feng, D.; Diao, X.; Zhu, H. Decoupling control based on backstepping control for bearingless synchronous reluctance motor. In Proceedings of the 32nd Chinese Control Conference, Xi’an, China, 26–28 July 2013. [Google Scholar]
- Lin, F.-J.; Huang, M.-S.; Chen, S.-G.; Hsu, C.-W.; Liang, C.-H. Adaptive backstepping control for synchronous reluctance motor based on intelligent current angle control. IEEE Trans. Power Electron. 2020, 35, 7465–7479. [Google Scholar] [CrossRef]
- Liu, T.-H.; Ahmad, S.; Mubarok, M.S.; Chen, J.-Y. Simulation and implementation of predictive speed controller and position observer for sensorless synchronous reluctance motors. Energies 2020, 13, 2712. [Google Scholar] [CrossRef]
- Costin, M.; Lazar, C. Field-oriented predictive control structure for synchronous reluctance motors. Machines 2023, 11, 682. [Google Scholar] [CrossRef]
- Lin, C.-H. Comparative dynamic control for continuously variable transmission with nonlinear uncertainty using blend amend recurrent Gegenbauer-functional-expansions neural network. Nonlinear Dyn. 2017, 87, 1467–1493. [Google Scholar] [CrossRef]
- Lin, C.-H.; Chang, K.T. Admixed recurrent Gegenbauer polynomials neural network with mended particle swarm optimization control system for synchronous reluctance motor driving continuously variable transmission system. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2020, 234, 183–198. [Google Scholar] [CrossRef]
- Sharaf-Eldin, T.; Dunnigan, M.W.; Fletcher, J.E.; Williams, B.W. Nonlinear robust control of a vector-controlled synchronous reluctance machine. IEEE Trans. Power Electron. 1999, 14, 1111–1121. [Google Scholar] [CrossRef]
- Chiang, H.-K.; Tseng, C.-H. Design and implementation of a grey sliding mode controller for synchronous reluctance motor drive. Control Eng. Pract. 2004, 12, 155–163. [Google Scholar] [CrossRef]
- Chen, C.-A.; Chiang, H.-K.; Lin, B.-R. The novel adaptive sliding mode control for current sensorless synchronous reluctance motor speed drive. In Proceedings of the 2008 IEEE International Conference on Industrial Technology, Chengdu, China, 21–24 April 2008. [Google Scholar]
- Lin, F.-J.; Chen, S.-G.; Huang, M.-S.; Liang, C.-H.; Liao, C.-H. Adaptive complementary sliding mode control for synchronous reluctance motor with direct-axis current control. IEEE Trans. Ind. Electron. 2022, 69, 141–150. [Google Scholar] [CrossRef]
- Lin, W.B.; Chiang, H.K. Super-twisting algorithm second-order sliding mode control for a synchronous reluctance motor speed drive. Math. Probl. Eng. 2013, 2013, 632061. [Google Scholar] [CrossRef]
- Chiang, H.K.; Lin, W.B. Sub-optimal algorithm second-order sliding mode control for a synchronous reluctance motor speed drive. Trans. Can. Soc. Mech. Eng. 2016, 40, 897–908. [Google Scholar] [CrossRef]
- Ren, L.; Lin, G.; Zhao, Y.; Liao, Z.; Peng, F. Adaptive nonsingular finite-time terminal sliding mode control for synchronous reluctance motor. IEEE Access 2021, 9, 51283–51293. [Google Scholar] [CrossRef]
- Shtessel, Y.; Edwards, C.; Fridman, L.; Levant, A. Sliding Mode Control and Observation; Birkhäuser: New York, NY, USA, 2014. [Google Scholar]
- Utkin, V.I.; Guldner, J.; Shi, J.X. Sliding-Mode Control in Electro-Mechanical Systems, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Šabanovic, A. Variable structure systems with sliding modes in motion control-a survey. IEEE Trans. Ind. Inform. 2011, 7, 212–223. [Google Scholar] [CrossRef]
- Mohd Zaihidee, F.; Mekhilef, S.; Mubin, M. Robust speed control of PMSM using sliding mode control (SMC)-a review. Energies 2019, 12, 1669. [Google Scholar] [CrossRef]
- Derafa, L.; Benallegue, A.; Fridman, L. Super twisting control algorithm for the attitude tracking of a four rotors. J. Franklin Inst. 2012, 349, 685–699. [Google Scholar] [CrossRef]
- Vazquez, C.; Collado, J.; Fridman, L. Super twisting control of a parametrically excited overhead crane. J. Franklin Inst. 2014, 351, 2283–2298. [Google Scholar] [CrossRef]
- Liu, S.; Feng, Z.; Gu, Y.; Hai, K.L.; Wang, P. Second-order sliding-mode control of synchronous buck converter based on sub-optimal algorithm. In Proceedings of the 2017 Asian Conference on Energy, Power and Transportation Electrification, Singapore, 24–26 October 2017. [Google Scholar]
- Liu, Y.-C.; Laghrouche, S.; N’Diaye, A.; Cirrincione, M. Active-flux-based super-twisting sliding mode observer for sensorless vector control of synchronous reluctance motor drives. In Proceedings of the 2018 7th International Conference on Renewable Energy Research and Applications, Paris, France, 14–17 October 2018. [Google Scholar]
- Chen, J.; Shuai, Z.; Zhang, H.; Zhao, W. Path following control of autonomous four-wheel-independent-drive electric vehicles via second-order sliding mode and nonlinear disturbance observer techniques. IEEE Trans. Ind. Electron. 2021, 68, 2460–2469. [Google Scholar] [CrossRef]
- Basbas, H.; Liu, Y.-C.; Laghrouche, S.; Hilairet, M.; Plestan, F. Review on floating offshore wind turbine models for nonlinear control design. Energies 2022, 15, 5477. [Google Scholar] [CrossRef]
- Gutiérrez-Oribio, D.; Tzortzopoulos, G.; Stefanou, I.; Plestan, F. Earthquake control: An emerging application for robust control. theory and experimental tests. IEEE Trans. Control Syst. Technol. 2023, 31, 1747–1761. [Google Scholar] [CrossRef]
- Sadeghi, R.; Madani, S.M.; Ataei, M.; Kashkooli, M.A.; Ademi, S. Super-twisting sliding mode direct power control of a brushless doubly fed induction generator. IEEE Trans. Ind. Electron. 2018, 65, 9147–9156. [Google Scholar] [CrossRef]
- Wang, H.; Ge, X.; Liu, Y.-C. Second-order sliding-mode MRAS observer based sensorless vector control of linear induction motor drives for medium-low speed maglev applications. IEEE Trans. Ind. Electron. 2018, 65, 9938–9952. [Google Scholar] [CrossRef]
- Scalcon, F.P.; Fang, G.; Vieira, R.P.; Gründling, H.A.; Emadi, A. Discrete-time super-twisting sliding mode current controller with fixed switching frequency for switched reluctance motors. IEEE Trans. Power Electron. 2022, 37, 3321–3333. [Google Scholar] [CrossRef]
- Wang, H.; Yang, Y.; Ge, X.; Zuo, Y.; Feng, X.; Chen, D.; Liu, Y.-C. Speed-sensorless control of induction motor drives with a STA-FLL speed estimation scheme. IEEE Trans. Ind. Electron. 2023, 70, 12168–12180. [Google Scholar] [CrossRef]
- Moreno, J.; Osorio, M. A Lyapunov approach to second-order sliding mode controllers and observers. In Proceedings of the 47th IEEE conference on decision and control, Cancun, Mexico, 9–11 December 2008. [Google Scholar]
- Moreno, J.A. On strict Lyapunov functions for some non-homogeneous super-twisting algorithms. J. Franklin Inst. 2014, 351, 1902–1919. [Google Scholar] [CrossRef]
- Moreno, J.; Osorio, M. A linear framework for the robust stability analysis of a generalized super-twisting algorithm. In Proceedings of the 6th International Conference on Electrical Engineering, Computing Science and Automatic Control, Toluca, Mexico, 10–13 January 2009. [Google Scholar]
- Kali, Y.; Rodas, J.; Saad, M.; Gregor, R.; Benjielloun, K.; Doval-Gandoy, J.; Goodwin, G. Speed control of a five-phase induction motor drive using modified super-twisting algorithm. In Proceedings of the 2018 International Symposium on Power Electronics, Electrical Drives, Automation and Motion, Amalfi, Italy, 20–22 June 2018. [Google Scholar]
- Liu, Y.-C.; Laghrouche, S.; Depernet, D.; N’Diaye, A.; Djerdir, A.; Cirrincione, M. Disturbance-observer-based speed control for SPMSM drives using modified super-twisting algorithm and extended state observer. Asian J. Control 2023, 26, 1089–1102. [Google Scholar] [CrossRef]
- Shiralkar, A.; Kurode, S. Generalized super-twisting algorithm for control of electro-hydraulic servo system. IFAC-PapersOnLine 2016, 49, 742–747. [Google Scholar] [CrossRef]
- Zhao, L.; Zheng, C.; Wang, Y.; Liu, B. A finite-time control for a pneumatic cylinder servo system based on a super-twisting extended state observer. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 1164–1173. [Google Scholar] [CrossRef]
- Cao, Q.; Su, X. Generalized Super-Twisting Backstepping Sliding Mode Control for Electro-Hydraulic Servo Systems Considering the Coexistence of Matched and Mismatched Uncertainties. Appl. Sci. 2023, 13, 4931. [Google Scholar] [CrossRef]
- Sumantri, B.; Uchiyama, N.; Sano, S. Generalized super-twisting sliding mode control with a nonlinear sliding surface for robust and energy-efficient controller of a quad-rotor helicopter. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 231, 2042–2053. [Google Scholar] [CrossRef]
- Borlaug, I.L.G.; Pettersen, K.Y.; Gravdahl, J.T. Tracking control of an articulated intervention AUV in 6DOF using the generalized super-twisting algorithm. In Proceedings of the 2019 American Control Conference, Philadelphia, PA, USA, 10–12 July 2019. [Google Scholar]
- Kristiansen, B.A.; Grøtte, M.E.; Gravdahl, J.T. Quaternion-based generalized super-twisting algorithm for spacecraft attitude control. IFAC-PapersOnLine 2020, 53, 14811–14818. [Google Scholar] [CrossRef]
- Russo, A.; Canciello, G.; Cavallo, A. Generalized super-twisting control of a dual active bridge for more electric aircraft. In Proceedings of the 2021 European Control Conference, Delft, The Netherlands, 29 June–2 July 2021. [Google Scholar]
- Lee, J.; Deshpande, N.; Caldwell, D.G.; Mattos, L.S. Microscale precision control of a computer-assisted transoral laser microsurgery system. IEEE/ASME Trans. Mechatron. 2020, 25, 604–615. [Google Scholar] [CrossRef]
- Singh, P.; Agrawal, P.; Nandanwar, A.; Behera, L.; Verma, N.K.; Nahavandi, S.; Jamshidi, M. Multivariable event-triggered generalized super-twisting controller for safe navigation of nonholonomic mobile robot. IEEE Syst. J. 2021, 15, 454–465. [Google Scholar] [CrossRef]
- Chen, W.-H.; Yang, J.; Guo, L.; Li, S. Disturbance-observer-based control and related methods-an overview. IEEE Trans. Ind. Electron. 2016, 63, 1083–1095. [Google Scholar] [CrossRef]
- Wang, B.; Dong, Z.; Yu, Y.; Wang, G.; Xu, D. Static-errorless deadbeat predictive current control using second-order sliding-mode disturbance observer for induction machine drives. IEEE Trans. Power Electron. 2018, 33, 2395–2403. [Google Scholar] [CrossRef]
- Wu, S.; Zhang, J.; Chai, B. A robust backstepping sensorless control for interior permanent magnet synchronous motor using a super-twisting based torque observer. Asian J. Control 2019, 21, 172–183. [Google Scholar] [CrossRef]
- Liu, Y.-C.; Laghrouche, S.; Depernet, D.; N’Diaye, A.; Djerdir, A.; Cirrincione, M. Super-twisting sliding-mode observer-based model reference adaptive speed control for PMSM drives. J. Franklin Inst. 2023, 360, 985–1004. [Google Scholar] [CrossRef]
- Liu, Y.-C.; Laghrouche, S.; Depernet, D.; Djerdir, A.; Cirrincione, M. Disturbance-observer-based complementary sliding-mode speed control for PMSM drives: A super-twisting sliding-mode observer-based approach. IEEE J. Emerg. Sel. Topics Power Electron. 2021, 9, 5416–5428. [Google Scholar] [CrossRef]
- Nurettin, A.; İnanç, N. High-performance induction motor speed control using a robust hybrid controller with a supertwisting sliding mode load disturbance observer. IEEE Trans. Ind. Electron. 2023, 70, 7743–7752. [Google Scholar] [CrossRef]
- Choi, J.-W.; Sul, S.-K. Inverter output voltage synthesis using novel dead time compensation. IEEE Trans. Power Electron. 1996, 11, 221–227. [Google Scholar] [CrossRef]
- Liu, K.; Zhu, Z.Q. Online Estimation of the rotor flux linkage and voltage-source inverter nonlinearity in permanent magnet synchronous machine drives. IEEE Trans. Power Electron. 2014, 29, 418–427. [Google Scholar] [CrossRef]
- Qiu, T.; Wen, X.; Zhao, F. Adaptive-linear-neuron-based dead-time effects compensation scheme for PMSM drives. IEEE Trans. Power Electron. 2016, 31, 2530–2538. [Google Scholar] [CrossRef]
- Tang, Z.; Akin, B. A new LMS algorithm based dead-time compensation method for PMSM FOC drives. IEEE Trans. Ind. Appl. 2018, 54, 6472–6484. [Google Scholar] [CrossRef]
- Liu, Y.-C.; Laghrouche, S.; N’Diaye, A.; Cirrincione, M. Hermite neural network-based second-order sliding-mode control of synchronous reluctance motor drive systems. J. Franklin Inst. 2021, 358, 400–427. [Google Scholar] [CrossRef]
- Yamamoto, S.; Tomishige, K.; Ara, T. A method to calculate transient characteristics of synchronous reluctance motors considering iron loss and cross-magnetic saturation. IEEE Trans. Ind. Appl. 2007, 43, 47–56. [Google Scholar] [CrossRef]
- Gonzalez, T.; Moreno, J.A.; Fridman, L. Variable gain super-twisting sliding mode control. IEEE Trans. Autom. Control 2012, 57, 2100–2105. [Google Scholar] [CrossRef]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Prentice-Hall: Englewood Cliffs, NJ, USA, 2001. [Google Scholar]
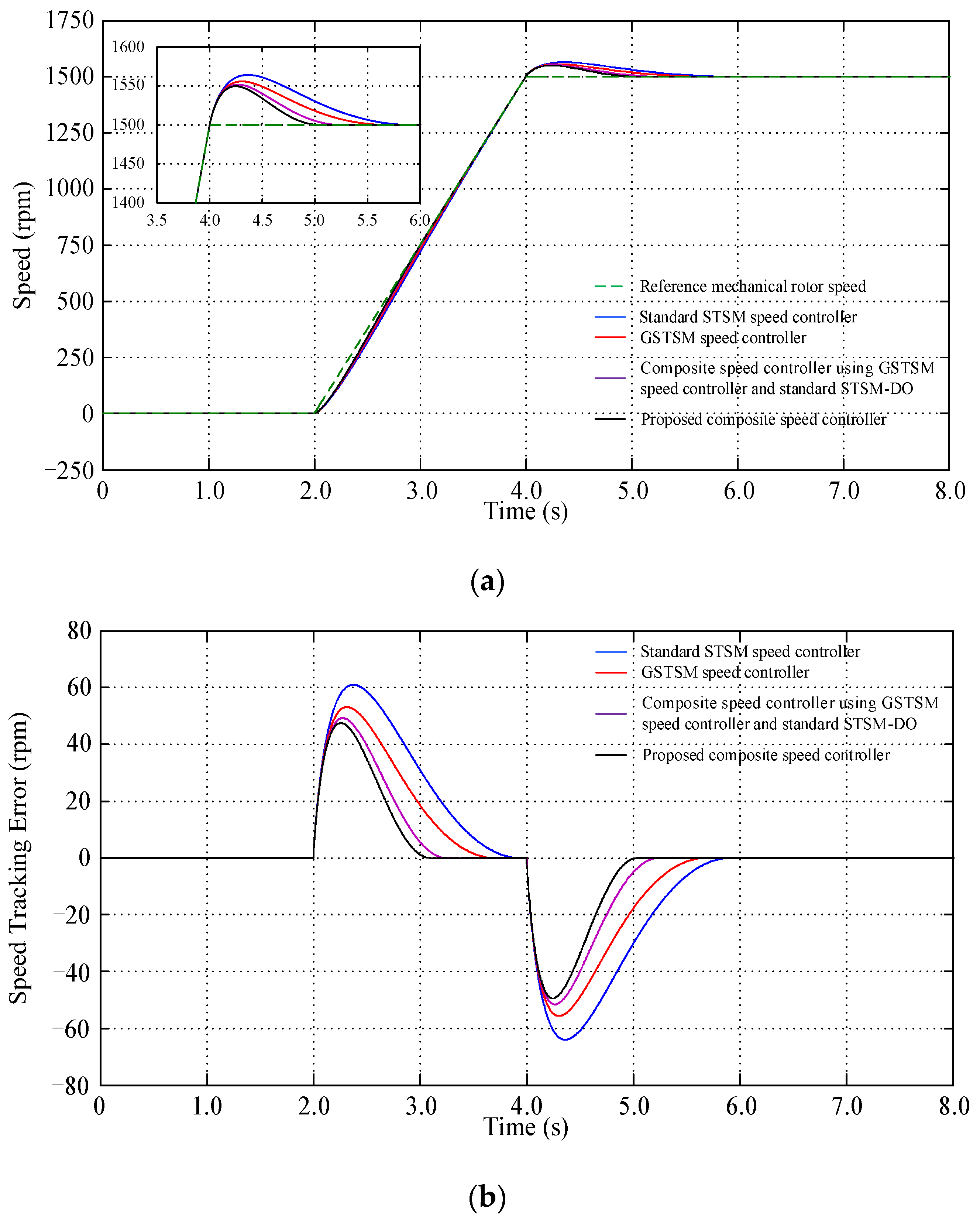
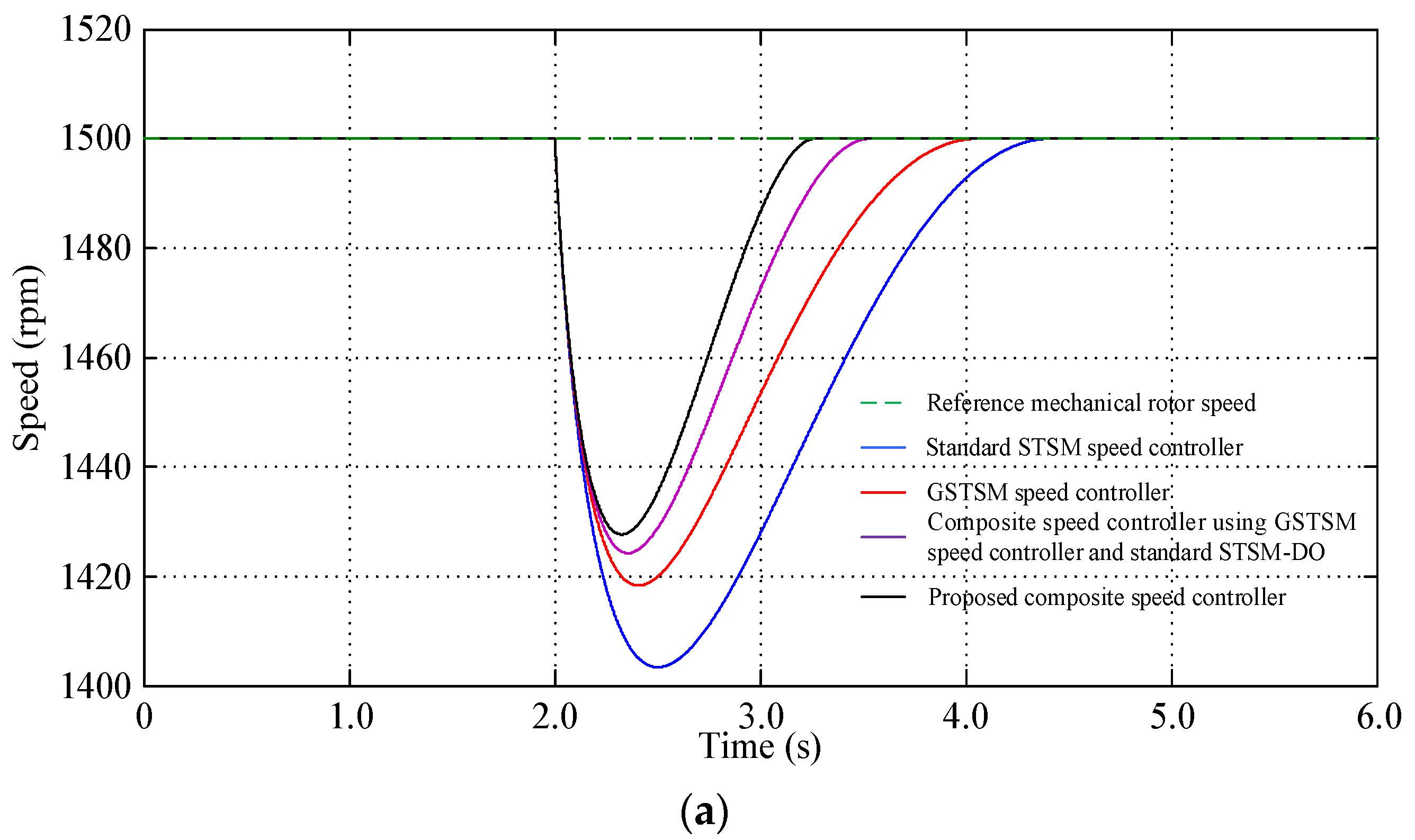
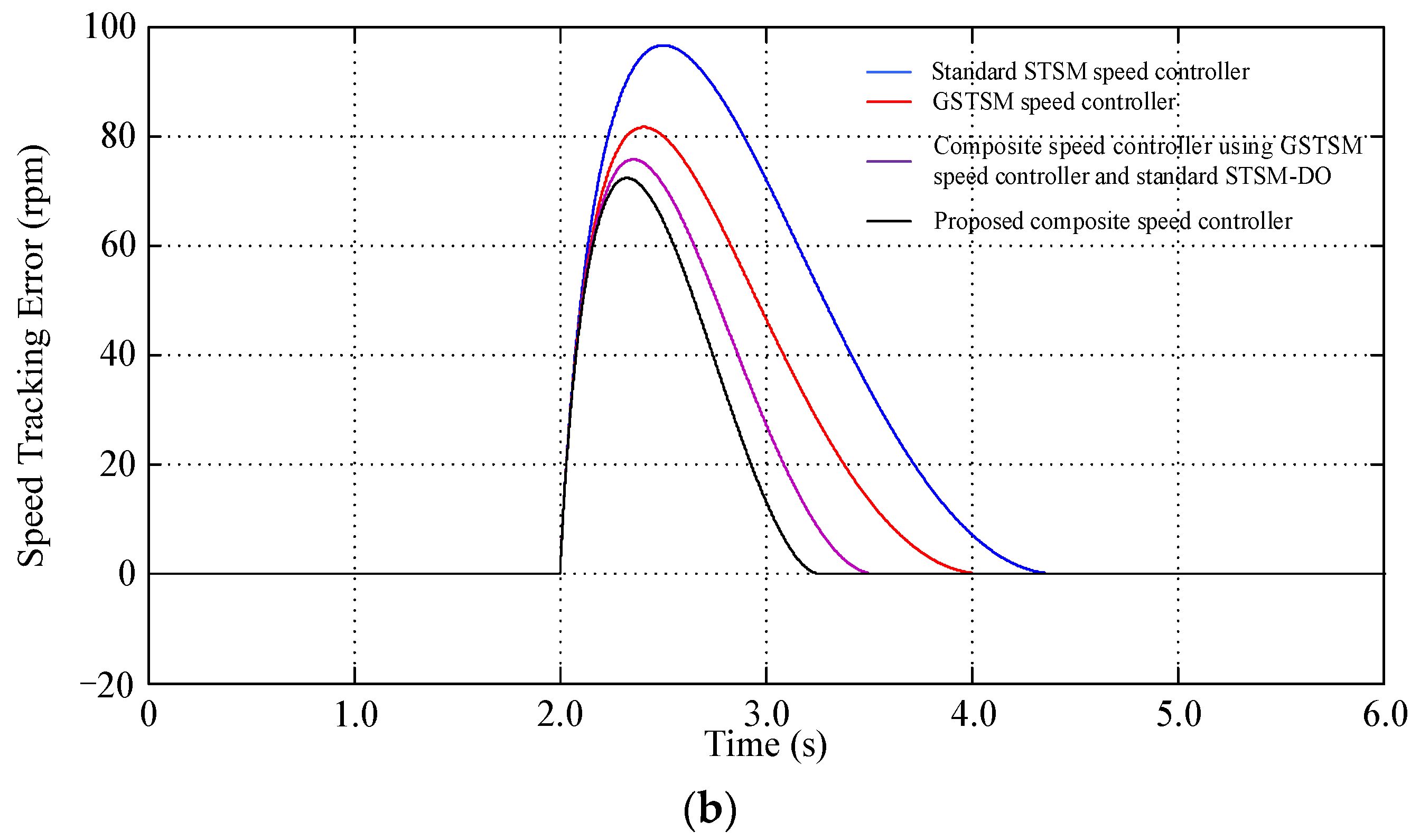
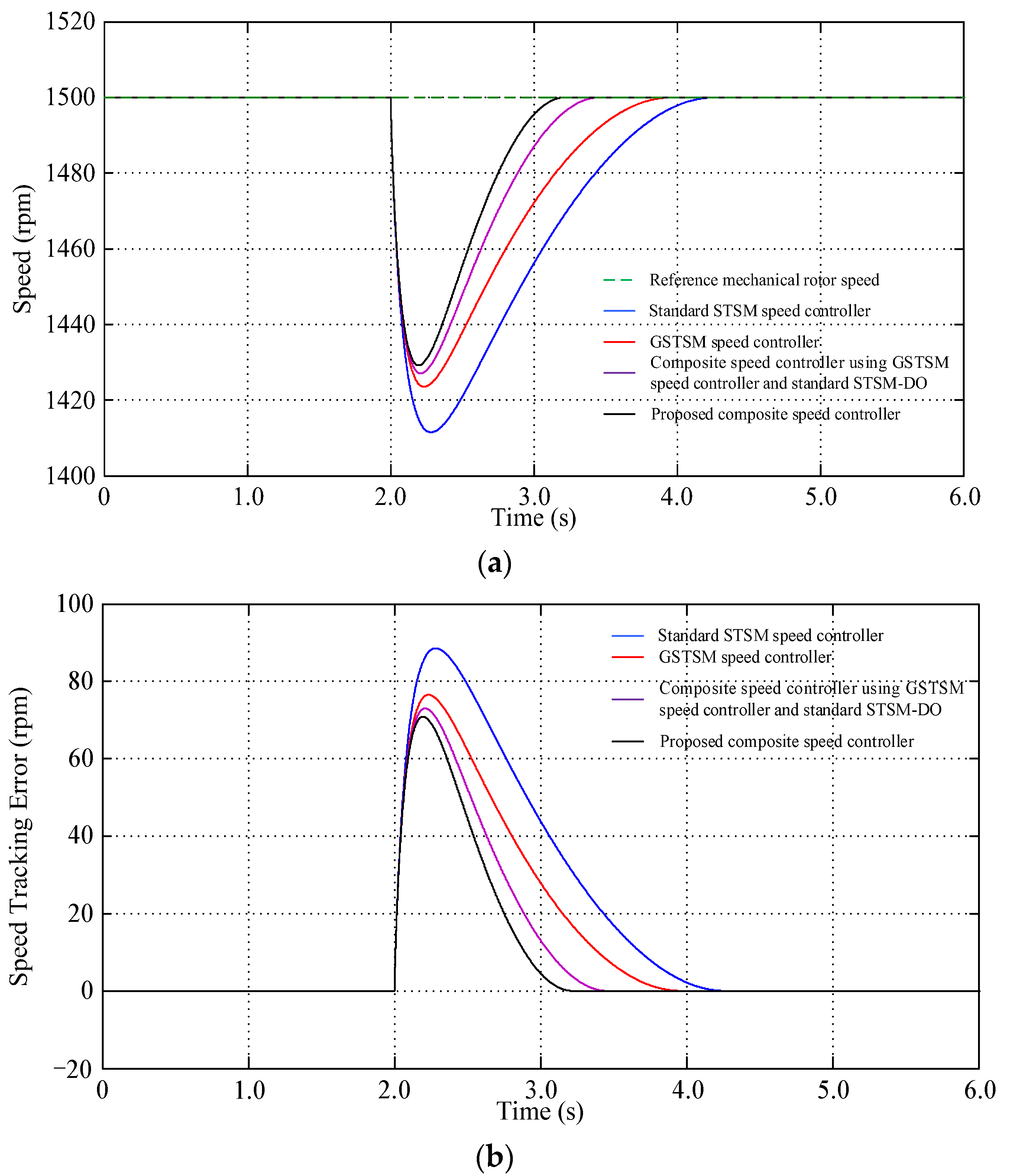
| Speed Controller | Controller Parameters | Observer Parameters |
|---|---|---|
| Standard STSM Speed Controller | , , | - |
| GSTSM Speed Controller | , , | - |
| Composite Speed Controller Using GSTSM Speed Controller and Standard STSM-DO | , , | , , |
| Proposed Composite Speed Controller | , , | , , |
| Speed Controller | Overshoot (rpm) | Settling Time (s) |
|---|---|---|
| Standard STSM Speed Controller | 63.98 | 3.74 |
| GSTSM Speed Controller | 55.69 | 3.52 |
| Composite Speed Controller Using GSTSM Speed Controller and Standard STSM-DO | 51.54 | 3.14 |
| Proposed Composite Speed Controller | 49.48 | 2.96 |
| Speed Controller | Maximum Tracking Error (rpm) | Settling Time (s) |
|---|---|---|
| Standard STSM Speed Controller | 96.59 | 2.27 |
| GSTSM Speed Controller | 81.65 | 1.91 |
| Composite Speed Controller Using GSTSM Speed Controller and Standard STSM-DO | 75.74 | 1.45 |
| Proposed Composite Speed Controller | 72.29 | 1.21 |
| Speed Controller | Maximum Tracking Error (rpm) | Settling Time (s) |
|---|---|---|
| Standard STSM Speed Controller | 88.53 | 2.09 |
| GSTSM Speed Controller | 76.49 | 1.79 |
| Composite Speed Controller Using GSTSM Speed Controller and Standard STSM-DO | 72.99 | 1.34 |
| Proposed Composite Speed Controller | 70.87 | 1.12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.-C. Disturbance-Observer-Based Sliding-Mode Speed Control for Synchronous Reluctance Motor Drives via Generalized Super-Twisting Algorithm. Actuators 2024, 13, 233. https://doi.org/10.3390/act13070233
Liu Y-C. Disturbance-Observer-Based Sliding-Mode Speed Control for Synchronous Reluctance Motor Drives via Generalized Super-Twisting Algorithm. Actuators. 2024; 13(7):233. https://doi.org/10.3390/act13070233
Chicago/Turabian StyleLiu, Yong-Chao. 2024. "Disturbance-Observer-Based Sliding-Mode Speed Control for Synchronous Reluctance Motor Drives via Generalized Super-Twisting Algorithm" Actuators 13, no. 7: 233. https://doi.org/10.3390/act13070233
APA StyleLiu, Y.-C. (2024). Disturbance-Observer-Based Sliding-Mode Speed Control for Synchronous Reluctance Motor Drives via Generalized Super-Twisting Algorithm. Actuators, 13(7), 233. https://doi.org/10.3390/act13070233






