Abstract
Automatic navigation based on dual-antenna real-time kinematic (RTK) positioning has been widely employed for unmanned agricultural machinery, whereas GNSS inevitably suffers from signal blocking and electromagnetic interference. In order to improve the reliability of an RTK-based navigation system in a GNSS-challenged environment, an integrated navigation system is preferred for autonomous navigation, which increases the complexity and cost of the navigation system. The information fusion of integrated navigation has been dominated by Kalman filter (KF) for several decades, but the KF cannot assimilate the known knowledge of the navigation context efficiently. In this paper, the geometric characteristics of the straight path and path-tracking error were employed to formulate the constraint measurement model, which suppresses the position error in the case of RTK-degraded scenarios. The pseudo-measurements were then imported into the KF framework, and the smoothed navigation state was generated as a byproduct, which improves the reliability of the RTK positioning without external sensors. The experiment result of the mobile vehicle automatic navigation indicates that the tracking error-constrained KF (EC-KF) outperforms the trajectory-constrained KF (TC-KF) and KF when the RTK system outputs a float or single-point position (SPP) solution. In the case where the duration of the SPP solution was 20 s, the positioning errors of the EC-KF and TC-KF were reduced by 38.50% and 24.04%, respectively, compared with those of the KF.
1. Introduction
With the flourishing of smart agriculture and unmanned farm-related applications, the automatic driving scenes in agricultural machinery have become increasingly diverse [1,2,3]. RTK-GNSS has been widely applied in precision agriculture in the past few decades, such as mapping the row crops and providing ground truth for vision-based navigation applications [4,5,6]. In the application of self-driving agricultural machinery, RTK-GNSS is often integrated with an attitude and heading reference system to correct the position drift resulting from vehicle attitude variation [7,8]. Recently, the dual-antenna RTK-GNSS navigation system has been applied alone for agricultural machinery automatic navigation working in large farmland [9]. However, the radiolocation-based navigation systems suffer from electromagnetic interference and disturbances from trees and high-voltage wires, inevitably leading to short-term RTK failure, which has a significant effect on the stability of unmanned agricultural machinery. In order to further enhance the reliability of agricultural machinery’s autonomous operations, improving the reliability of RTK-GNSS based on information fusion methods is of great significance [10,11,12].
The Kalman filter (KF) is derived under the criterion of the linear minimum mean square error (LMMSE), which achieves an optimal state estimation when given precise a priori knowledge on the state-space model (SSM) and noise properties [13]. In order to improve the position and heading accuracy of agricultural machinery, many KF-based integrated navigation systems have been developed [14,15,16]. Han et al. developed an integrated navigation system by fusing three single GPS receivers and an inertial measurement unit (IMU) based on the KF [17]. Li et al. proposed a fuzzy adaptive finite impulse response KF to fuse the position and attitude from the GNSS and IMU [18]. In order to handle the unknown a priori knowledge on an SSM or noise, Jing et al. developed an adaptive square root cubature KF (CKF) to improve the path-tracking accuracy of a land leveling system, where the process noise and measurement noise are estimated online by the Sage–Husa method [19]. Wang et al. further improved the robustness of the CKF by combining the maximum correntropy and resampling-free sigma-point update, which enhances the reliability of the GNSS/IMU under the GNSS-denied environment [20]. The above-mentioned methods try to improve GNSS reliability by focusing on either extra external sensors or an improved KF, which does not take the a priori knowledge of the navigation context into consideration.
The KF does not employ the a priori known state constraints on its recursive innovation assimilation, such as the physic constraint on the steering angle or trajectory shape of the autonomous vehicle. By projecting the solution of the KF into the constrained surface, the constrained KF achieves a more accurate result in case there is unmodeled uncertainty in the state estimation [21]. Liu et al. developed an adaptive KF by using road information to refine the state estimation of vehicle navigation, while neglecting that the road has a specific width [22]. Similarly, Zhou et al. constructed a pseudo-measurement based on the a priori known trajectory shape to develop a trajectory shape constraint KF, which improves the target tracking accuracy [23]. Li et al. employed the destination constraint and circular trajectory to improve the maneuvering target tracking, where the nonlinear pseudo-measurement was processed by an unscented Kalman filter [24]. Zhang et al. generalized the straight path and circular trajectory into the heading constraint state estimation, where the extended KF was employed to handle the nonlinearity in state-to-measurement [25]. Except for the trajectory shape, non-holonomic constraints have also been applied to reduce the drift of low-cost inertial sensors in the GNSS/IMU, which improves the positioning reliability of tractor navigation [26].
The above-mentioned state-constraint KFs have been verified by numerical simulation, and a few of them applied the state constraint for agricultural machinery navigation operations. Recently, Zhang et al. proposed a self-calibrating variable structure KF to bridge the BDS outages, which compensates for the drift of heading and biases of an IMU based on the assumption that the heading does not vary during straight path tracking [27]. Inspired by the work of Zhang et al., we take the operation context information of autonomous navigation vehicles as a priori knowledge in this paper. Not only does the navigation context include the predefined trajectory, but it also includes the path-tracking errors of the previous time instant. The automatic navigation mobile vehicle equipped with a dual-antenna RTK-GNSS was employed to verify the effectiveness of context-constrained KFs (CC-KFs), where different RTK short-term failures were stimulated to analyze the performance of the CC-KFs. The main contributions of this paper include the following: (1) the automatic navigation context of agricultural machinery was taken as the constraints to enhance the reliability of the RTK positioning; (2) both the equality and inequality constraints were imported into the dual-antenna RTK system; and (3) the CC-KFs were verified by an automatic navigation mobile vehicle with a dual-antenna RTK-GNSS, which improves the robustness of navigation without employing extra sensors.
The structure of this paper is as follows. Firstly, the principle of a state-constrained KF is presented in Section 2, and the operation context-constraint models are formulated, on whose basis the proposed CC-KFs are developed. In Section 3, the CC-KFs are verified by employing an automatic navigation mobile vehicle. Finally, Section 4 concludes this work.
2. Materials and Methods
The performance of the automatic navigation of agricultural machinery depends on the predefined field path and real-time position and heading output of the dual-antenna RTK. However, the dual-antenna RTK suffers from short-term signal degradation from time to time during the whole field navigation. Generally, the agricultural machinery works in a boustrophedon way, which consists of parallel straight lines and curves of fixed curvature, and most of the in-field working focuses on straight-line segments. Furthermore, the path-tracking errors of agricultural machinery have continuous change regularities, even if the vehicle suffers from soft soil surfaces or abrupt changes in position and heading. In order to improve the reliability of the positioning system, pseudo-measurements can be constructed based on the a priori information on the navigation operations of agricultural machinery.
2.1. Constrained Kalman Filter
Supposing the discrete linear model of the agricultural machinery navigation system can be written as
where is the state transition matrix from time k − 1 to time k; is the measurement matrix at time k; , are the system state vector and noise vector; and are the system measurement vector and noise vector; n and p are the state and measurement dimensions, respectively. The KF filtering includes time update and measurement update steps, which are formulated as
where (3) and (4) transform the posterior state at time k − 1 into the state a priori domain corresponding to time k, and then the observations’ innovation at time k is assimilated to approximate the posterior state by (6) and (7). Given the initial state values and , the system noise matrix and the measurement matrix R, the state estimate at time can be derived recursively after assimilating the measurement .
In practical engineering problems, the system designer sometimes has some a priori information about the parameters to be estimated or the saturation of the actuator inputs for the control system. However, the KF framework cannot fully utilize these a priori constraint relationships of the state quantities. By converting the a priori knowledge into constraint equations and importing them into the KF framework as pseudo-measurements, the estimation accuracy and robustness of the KF can be further improved under sensor malfunction or abnormal observation. The optimal solution of the equality-constrained KF can be expressed as
satisfying
where is a known constant matrix whose rank is less than n, is the number of linearly independent constraint equations, is an -dimensional constant vector, and is a symmetric positive definite weight matrix. Constructing a Lagrangian function to convert the conditional extreme value into the solution of the following function:
The optimal solution can then be found by solving
Then, we have
Usually, the symmetric positive definite weight matrix can be selected as the identity matrix I or .
2.2. Constraint Measurement Formulation
2.2.1. Trajectory-Constraint Equation
As shown in Figure 1, when the agricultural machinery travels along the predefined straight-line path at a constant speed v, its heading angle in the plane is . The actual tracking path is indicated by red dash line, and any three consecutive points are on the same straight line. Supposing the position of the agricultural machinery at time is (), and the positions at time and are (), (), respectively. Then, we have
Considering the consistency of the speed direction and heading during the straight-line following, the constraint relationship between the speed and position can be expressed as
where and are the velocity components at time , and and are the velocity components at time . According to Equations (15) and (16), the pseudo-measurement of the target state can be constructed as
where is the virtual measurement of the underlying position and velocity, and its mean and variance are both 0. Then, the augmented measurement equation can be defined as
Finally, the constraint equation of the straight path tracking of agricultural machinery can be constructed
where
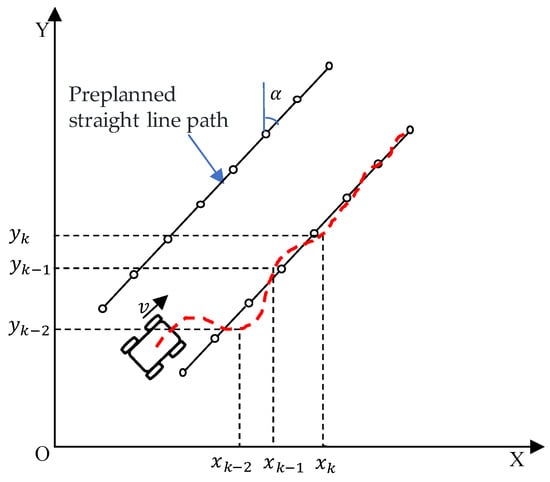
Figure 1.
Straight path constraint model.
2.2.2. Path-Tracking Error Constraint Equation
Unlike the predefined field working path, which is deterministic and static, the path-tracking errors of agricultural machinery are dynamic states that are generated by employing different path-tracking algorithms. The tracking errors for the automatic navigation of agricultural machinery mainly include the lateral error and heading error, where the former is defined as the distance from the current position to a selected path segment [28].
The path segment generation for U-turning involved in our experiment is presented, which makes it easier to follow the path-tracking error-derived pseudo-measurement. The predefined path of agricultural machinery is composed of parallel straight lines and curves of different curvatures, where the U-turning is a typical path for our whole field path planning. As shown in Figure 2, the U-turning path includes two straight lines and one turning curve with turning radius . The navigation computer generates the AB baseline after receiving two points A1 and B1 fixed by the dotting instrument, and the waypoints are then generated according to the given points interval value and calculated straight-line function. Similarly, the parallel straight line A2B2 can then be generated according to the implement width and turning form. As we can see from Figure 2, B1 is the ending point of line A1B1, and O is the center of the turning circle. Supposing N is the middle point of the turning curve, because the curvature of the turning path is constant, the position of the waypoint of the curve path can be decided by angle and the heading of line A1B1. Let the angular increment be , , and the length of line B1M be ; then, for an arbitrary point M, we have
If , then , and thus, for M, we define its position as , ; if , then , and the position of point M has , . A similar generation strategy can be applied for the straight lines of different heading values. Although the lateral tracking error may vary from several centimeters to several decimeters, it can also be applied for positioning reliability enhancement under a GNSS-challenged environment.
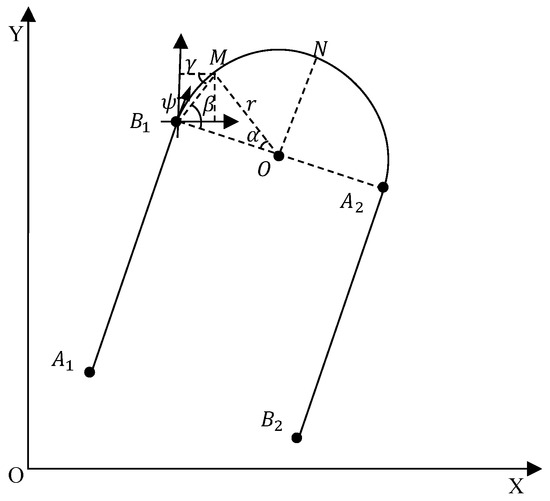
Figure 2.
Generation of U-turning path.
As is shown in Figure 3, suppose the lateral tracking error at time k is , which represents the distance of point from line segment . The equation of the line is Ax By C = 0, and according to the definition of the lateral tracking error, we have
After taking the square of both sides of Equation (23), we obtain
Solving the partial derivative of Equation (24), we obtain
And then a pseudo-measurement of the target state can be formulated as
where is the virtual measurement of the underlying position and velocity, and its mean and variance are both 0. Then, the augmented measurement equation can be written as
Finally, the constraint equation of the path-tracking error of the agricultural machinery can be constructed as
where
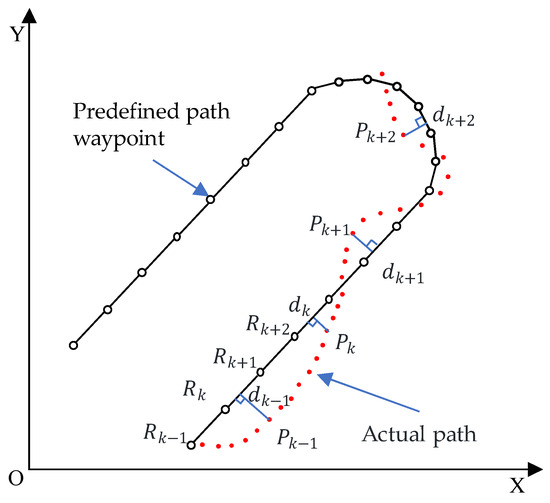
Figure 3.
Path-tracking error constraint model.
2.3. Operation Context Constrained KF
Suppose the navigation state of the agricultural machinery during the field operation can be written as , which represents the eastward and northward position and velocity of the agricultural machinery at time , and the eastward and northward position at time . The interval between and time is , and the system propagation matrix and measurement matrix can be formulated as
In case the straight path constraint model is employed, the augmented matrix can be written as
When the path-tracking error is taken as the pseudo-measurement, and the augmented matrix is
Based on the above derivation, the operation context-constrained KF for agricultural machinery navigation fusion can be summarized as Figure 4.
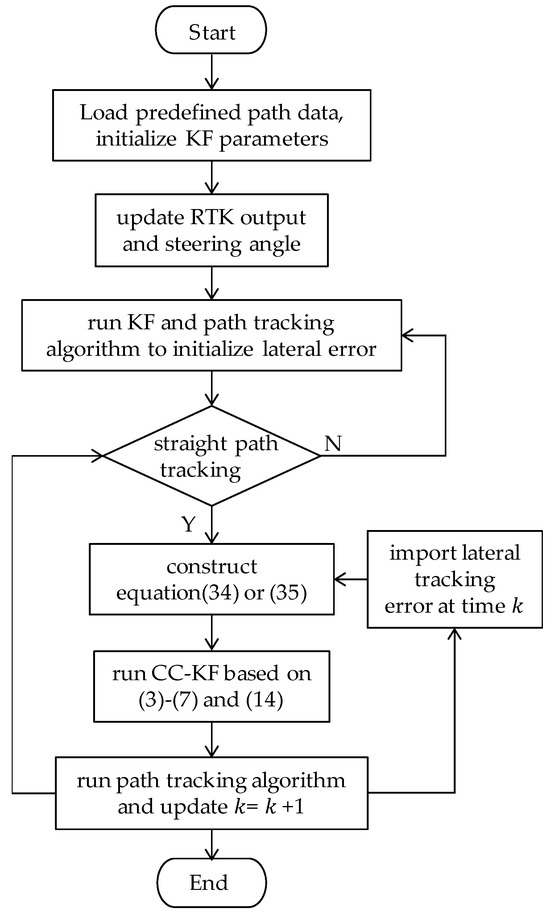
Figure 4.
Flowchart of context-constrained navigation fusion.
3. Results and Discussion
An autonomous vehicle was employed as an experimental platform to verify the effectiveness of CC-KFs, which consisted of a dual-antenna RTK and navigation controller. As shown in Figure 5, the OEM719 produced by NovAtel (Canada) was employed as the base station receiver, while the rover receiver was self-developed based on the UM482 chip module provided by Beijing Beidou Satellite Communication Group Co., Ltd. (Beijing, China). The positioning accuracy of the UM482 is 1cm+1ppm, and the antenna baseline for the dual-antenna mode is 0.785 m. In our test, the update frequency of the dual-antenna RTK is 5 Hz. The motor driver RMDS405 supports 30 A current, and the encoder is Omron E6B2, with a resolution of up to 3600 P/R. The host computer recorded the vehicle’s position and heading in real time and outputted the calculated navigation deviation based on predefined path data. The embedded controller calculated the desired steering angle after receiving the navigation deviation, and then sent the control information to the motor driver via the CAN bus at a frequency of 5 Hz. The motor driver converted the control information into voltage, and received encoder feedback in real time, forming a closed-loop steering control system to control the motor at a frequency of 100 Hz.
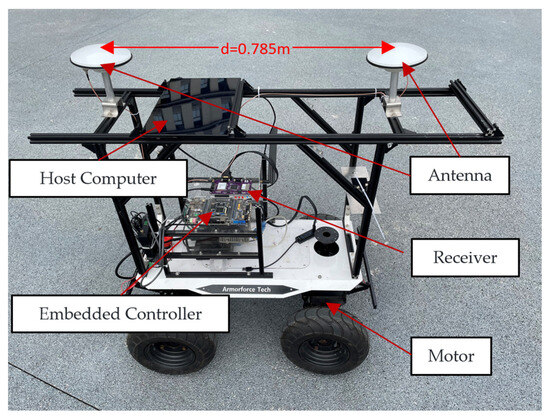
Figure 5.
Experimental verification platform.
The geometric-based path-tracking algorithm proposed in [29] was employed to control the vehicle to travel along the planned continuous U-shaped path. The average speed of the vehicle was about 1 m/s, and the tracking error, position, and heading results were collected and saved for analysis. As shown in Figure 6, the lateral tracking error settled at ±3 cm with a percentage of 86.30%, and the heading deviation settled at ±2° with a percentage of 90.61%, which indicates that the tracking error can be applied for navigation fusion assistance.
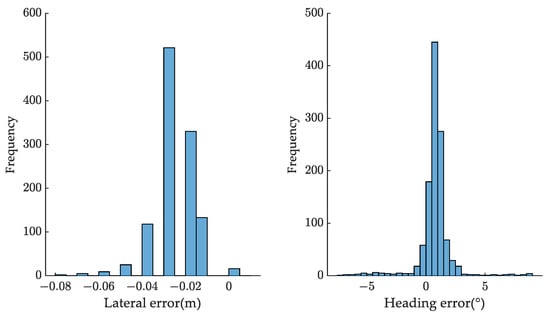
Figure 6.
Path-tracking errors distribution.
The dual-antenna RTK may suffer from disturbances and lead to four types of positioning results, which are integer ambiguity fixed, float solution (FS), single-point solution (SPP), and GNSS outage. The Gaussian noise with the variance of 0.3 m2 was used to stimulate the FS scenario, and the variance in the SPP solution was calculated by turning off the radio station and recording the position data for post-process analysis, and in our test, the variance corresponding to the SPP scenario was set as 3 m2. The duration ΔT for the FS and SPP were set as 5 s and 20 s, respectively. Accordingly, we randomly deleted RTK observations to stimulate the GNSS outage case, and the short-term GNSS outage duration ΔT was set to 5 s and 20 s. In the following discussion, the performance of the traditional KF, trajectory-constrained KF (TC-KF) [23], and lateral tracking error-constrained KF (EC-KF) are compared and discussed, and the parameter configuration of different filters, such as Q, R, and are fixed and set the same to make a fair comparison.
The trajectory tracking results are shown in Figure 7. It is noted that if the RTK outputs continuous and accurate position and heading data, the TC-KF and EC-KF achieve similar position results with the KF. A more specific result is shown in Figure 8 and Figure 9, where the position error is calculated with respect to the original RTK output without adding Gaussian noise. As we can see, under the FS, SPP, and GNSS outage scenario, all the algorithms show noticeable performance degradation compared with the first straight path tracking. However, the TC-KF and EC-KF outperform the KF under the GNSS-challenged environment, which demonstrates the effectiveness of the constraint model in mitigating the uncertainty of abnormal observation. Notice that, when the RTK works in the FS or SPP model, both constraint models enhance the positioning stability compared with the KF, which indicates the context model imports extra innovation into the calculation of the Kalman gain. With the increase in ΔT, the constraint model contains less useful information for the Kalman gain update, which makes the estimation error increase. The EC-KF shows a better performance than the TC-KF in the cases of the FS and SPP, which coincides with the fact that once there is an obvious lateral tracking error in the straight path tracking, Equation (17) is too strong for position estimation, and there should be significant uncertainty for this pseudo-measurement.
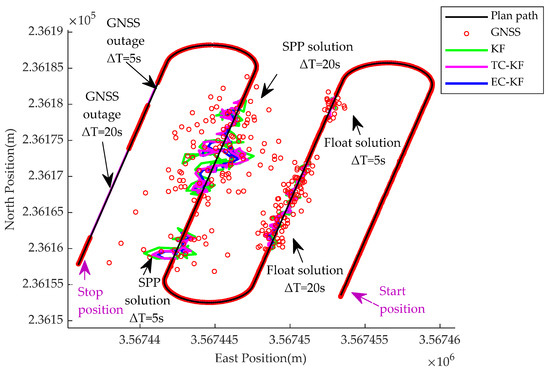
Figure 7.
Positioning result of continuous U-turning path tracking.
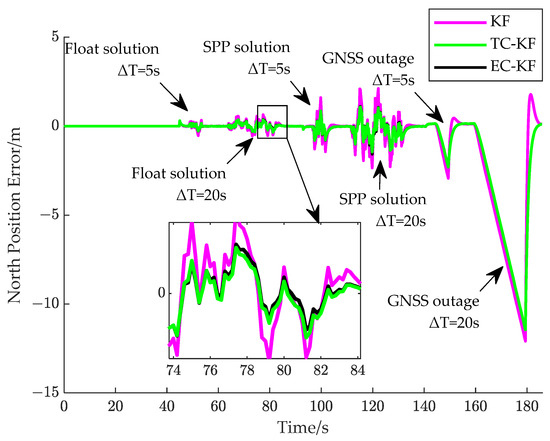
Figure 8.
North position error of continuous U-turning path tracking.
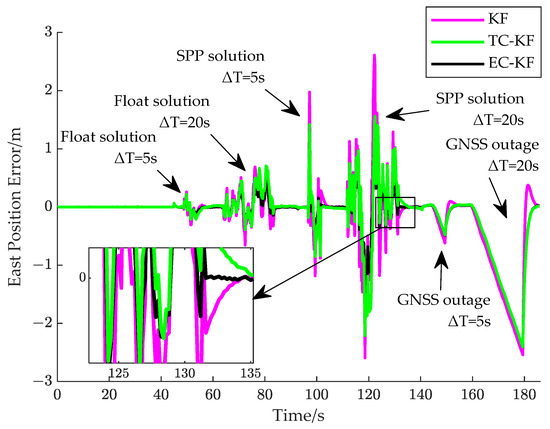
Figure 9.
East position error of continuous U-turning path tracking.
This conclusion is further confirmed by the result shown in the last straight path of Figure 7, where the TC-KF and EC-KF achieve the same result during the GNSS outage. In all the filters, the Kalman gain is calculated based on the last available RTK observation, and the measurement uncertainty is relatively larger compared with the extra information provided by Equations (17) and (27). However, as the TC-KF and EC-KF import more information than the KF when there is no new observation for the measurement update, they outperform the KF slightly during the GNSS outage. Once new observations are provided, the large uncertainty of the KF incurs a significant discrepancy between the state prediction distribution and likelihood function constructed from the RTK observation. Notice that, in Figure 8 and Figure 9, there is no obvious fluctuation for the TC-KF and EC-KF in case a new RTK position is provided, which may have two reasons. Firstly, the prediction uncertainty during the GNSS outage is mitigated to some extent by employing a pseudo-measurement. Secondly, the position noise of the RTK is very small, which makes the discrepancy between the prediction covariance and actual measurement noise significant, whereas the unignorable variance in the pseudo-measurement derived from the history states relieves this covariance inconsistency problem.
The cumulative distribution of the position error under different scenarios in terms of the root mean square error (RMSE) is shown in Figure 10, where the EC-KF outperforms the KF and TC-KF under the FS and SPP scenarios, whereas it shows a similar result with the TC-KF under the GNSS outage. The position error of the EC-KF under the FS scenario (with only the Float solution shown in Figure 7) is 0.2 m with a percentage of 80% and is 0.5 m with a percentage of 61% under the SPP scenario (with only the SPP solution shown in Figure 7). More detailed results are listed in Table 1. Under the FS scenario, in the case of ΔT = 5 s, the TC-KF and EC-KF reduce the position error by 33.20% and 42.58% compared to the KF, and in the case of ΔT = 20 s, these values become 17.51% and 38.32%. Under the SPP scenario, in the case of ΔT = 5 s, the TC-KF and EC-KF reduce the position error by 33.92% and 44.64% compared to the KF, and in the case of ΔT = 20 s, these values become 24.04% and 38.50%. As we can see, with the increase in the duration and level for RTK degradation, the EC-KF shows a much better robustness than the TC-KF. Both the TC-KF and EC-KF outperform the KF in the case of the GNSS outage, where the tracking error-constraint equation does not show a better result than the trajectory-constraint equation when no new observation is provided.
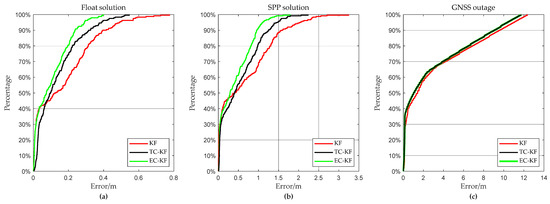
Figure 10.
Position error of different filters under RTK-degraded scenario. (a) Error distribution under FS; (b) error distribution under SPP; (c) error distribution under GNSS outage.

Table 1.
RMSE of position error under different scenarios.
4. Conclusions
This paper proposed an operation context-enhanced KF for agricultural machinery navigation based on a dual-antenna RTK. In order to improve the reliability of the RTK, the operation context of the unmanned agricultural machinery was augmented to the RTK measurement, which reduces the position error in case of RTK failure without employing additional sensors. The field test based on the autonomous vehicle indicates the EC-KF outperforms the TC-KF and KF obviously in the RTK-degraded environment, and the path-tracking error constraint shows more robustness than the trajectory constraint in handling different types of abnormal observation. Because the KF is the most popular information fusion method in navigation applications, and the agricultural machinery often works in a boustrophedon way, the context-constrained KFs can be easily implemented to enhance the stability of the RTK. As the tracking error-constraint model not only works for a straight path but also works for a curved path, the EC-KF can be applied for the whole field navigation of the agricultural machinery without switching the constraint model.
In this work, only the straight path and lateral tracking error were employed in deriving the context-constraint equations; in future work, more flexible data-driven models should be imported into the KF based on self-learning methods. Furthermore, because we focus on RTK-based automatic navigation in this paper, we only compared the EC-KF solution with the KF and TC-KF solutions, and a comparison with other integrated navigation solutions would demonstrate the superiority of context-constrained KFs more clearly. These context-constraint models were derived with the hypothesis that the pseudo-measurements are perfect measurements, i.e., without setting the measurement noise, which may not coincide with the practical application. In future work, assimilating the pseudo-measurement in a more efficient way is also under consideration.
Author Contributions
Conceptualization, B.C. and J.Z.; methodology, B.C. and Y.Z.; software, B.C. and J.Z.; validation, J.Z., X.C. and Z.S.; formal analysis, Z.S.; investigation, B.C.; resources, Y.L.; data curation, X.C.; writing—original draft preparation, J.Z. and B.C.; writing—review and editing, Y.Z. and X.W.; visualization, J.Z.; supervision, B.C.; project administration, X.W.; funding acquisition, B.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was jointly funded by the Natural Science Foundation of China, grant number 32271999, the Primary Research & Development Plan of Jiangsu Province, grant number BE2021313, the Jiangsu Province and Education Ministry Co-sponsored Synergistic Innovation Center of Modern Agricultural Equipment, grant number XTCX2009, the Primary Research & Development Plan of Danyang City (Modern Agricultural), grant number SNY202303, and Open Funding from the Key Laboratory of Modern Agricultural Equipment and Technology (Jiangsu University), Ministry of Education, grant number MAET202301. The APC was funded by MAET202301.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Xie, B.; Jin, Y.; Faheem, M.; Gao, W.; Liu, J.; Jiang, H.; Cai, L.; Li, Y. Research Progress of Autonomous Navigation Technology for Multi-Agricultural Scenes. Comput. Electron. Agric. 2023, 211, 107963. [Google Scholar] [CrossRef]
- Chen, T.T.; Xu, L.Z.; Ahn, H.S.; Lu, E.; Liu, Y.B.; Xu, R.B. Evaluation of headland turning types of adjacent parallel paths for combine harvesters. Biosyst. Eng. 2023, 233, 93–113. [Google Scholar] [CrossRef]
- Chen, J.; Song, J.; Guan, Z.H.; Lian, Y. Measurement of the distance from grain divider to harvesting boundary based on dynamic regions of interest. Int. J. Agric. Biol. Eng. 2021, 14, 226–232. [Google Scholar] [CrossRef]
- Garrido, M.S.; De Lacy, M.C.; Ramos, M.I.; Borque, M.J.; Susi, M. Assessing the accuracy of NRTK altimetric positioning for precision agriculture: Test results in an olive grove environment in Southeast Spain. Precision Agric. 2019, 20, 461–476. [Google Scholar] [CrossRef]
- Perez-Ruiz, M.; Slaughter, D.C.; Gliever, C.; Upadhyaya, S.K. Tractor-based Real-time Kinematic-Global Positioning System (RTK-GPS) guidance system for geospatial mapping of row crop transplant. Biosyst. Eng. 2012, 111, 64–71. [Google Scholar] [CrossRef]
- Ricardo, O.; Noboru, N. Simultaneous mapping and crop row detection by fusing data from wide angle and telephoto images. Comput. Electron. Agric. 2019, 162, 602–612. [Google Scholar] [CrossRef]
- Kanagasingham, S.; Ekpanyapong, M.; Chaihan, R. Integrating machine vision-based row guidance with GPS and compass-based routing to achieve autonomous navigation for a rice field weeding robot. Precis. Agric. 2020, 21, 831–855. [Google Scholar] [CrossRef]
- Han, X.Z.; Kim, H.J.; Kim, J.Y.; Yi, S.Y.; Moon, H.C.; Kim, J.H. Path-tracking simulation and field tests for an auto-guidance tillage tractor for a paddy field. Comput. Electron. Agric. 2015, 112, 161–171. [Google Scholar] [CrossRef]
- Yin, X.; An, J.; Wang, Y.; Wang, Y.; Jin, C. Development and experiments of the autonomous driving system for high-clearance spraying machines. Trans. CSAE 2021, 37, 22–30. [Google Scholar]
- Li, Y.; Jia, H.; Qi, J.; Sun, H.; Tian, X.; Liu, H.; Fan, X. An Acquisition Method of Agricultural Equipment Roll Angle Based on Multi-Source Information Fusion. Sensors 2020, 20, 2082. [Google Scholar] [CrossRef]
- Zhong, Y.; Xue, M.Q.; Yuan, H.L. Design of the GNSS/INS integrated navigation system for intelligent agricultural machinery. Trans. Chin. Soc. Agric. Eng. 2021, 37, 40–46. [Google Scholar] [CrossRef]
- Ma, Z.; Yin, C.; Du, X.; Zhao, L.; Li, L.; Zhang, G.; Wu, C. Rice row tracking control of crawler tractor based on the satellite and visual integrated navigation. Comput. Electron. Agric. 2022, 197, 106935. [Google Scholar] [CrossRef]
- Cui, B.; Wei, X.; Chen, X.; Li, J.; Li, L. On sigma-point update of cubature Kalman filter for GNSS/INS under GNSS-challenged environment. IEEE Trans. Veh. Technol. 2019, 68, 8671–8682. [Google Scholar] [CrossRef]
- Liu, J.; Liu, H.H.; Wang, J.J.; Gu, H.G. Coordinated Lateral Stability Control of Autonomous Vehicles Based on State Estimation and Path Tracking. Machines 2023, 11, 328. [Google Scholar] [CrossRef]
- Chen, T.; Chen, L.; Xu, X.; Cai, Y.F.; Jiang, H.B.; Sun, X.Q. Passive fault-tolerant path following control of autonomous distributed drive electric vehicle considering steering system fault. Mech. Syst. Signal Process. 2019, 123, 298–315. [Google Scholar] [CrossRef]
- Zhang, J.; Sun, T.R.; Liu, Z.L. Robust model predictive control for path-following of underactuated surface vessels with roll constraints. Ocean Eng. 2017, 143, 125–132. [Google Scholar] [CrossRef]
- Han, X.; Kim, H.-J.; Jeon, C.W.; Moon, H.C.; Kim, J.H. Development of a low-cost GPS/INS integrated system for tractor automatic navigation. Int. J. Agric. Biol. Eng. 2017, 10, 123–131. [Google Scholar] [CrossRef]
- Li, S.; Zhang, M.; Ji, Y.; Zhang, Z.; Cao, R.; Chen, B.; Li, H.; Yin, Y. Agricultural machinery GNSS/IMU-integrated navigation based on fuzzy adaptive finite impulse response Kalman filtering algorithm. Comput. Electron. Agric. 2021, 191, 106524. [Google Scholar] [CrossRef]
- Jing, Y.; Li, Q.; Ye, W.; Liu, G. Development of a GNSS/INS-based automatic navigation land levelling system. Comput. Electron. Agric. 2023, 213, 108187. [Google Scholar] [CrossRef]
- Wang, G.; Cui, B.; Tang, C. Robust cubature Kalman filter based on maximum correntropy and resampling-free sigma-point update framework. Dig. Signal Process. 2022, 126, 103495. [Google Scholar] [CrossRef]
- Simon, D. Kalman Filtering with State Constraints: A Survey of Linear and Nonlinear Algorithms. IET Control Theory Appl. 2010, 4, 1303–1318. [Google Scholar] [CrossRef]
- Liu, Y.W.; Liu, J.N.; Zhu, D.Y. Application of adaptive Kalman filter restricted by road information to vehicle-borne navigation. Geomat. Inf. Sci. Wuhan Univ. 2008, 33, 828–830. [Google Scholar]
- Zhou, G.; Li, K.; Kirubarajan, T.; Xu, L. State estimation with trajectory shape constraints using pseudo-measurements. IEEE Trans. Aerosp. Electron. Syst. 2018, 55, 2395–2407. [Google Scholar] [CrossRef]
- Li, K.Y.; Kirubarajan, T.; Zhou, G.J. State Estimation with Implicit Constraints of Circular Trajectory Using Pseudo-Measurements. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 4406–4425. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, K.; Zhou, G. State Estimation with Heading Constraints for on-Road Vehicle Tracking. IEEE Trans. Intell. Transp. Syst. 2022, 23, 13614–13635. [Google Scholar] [CrossRef]
- Zhang, Q.; Chen, Q.; Xu, Z.; Zhang, T.; Niu, X. Evaluating the Navigation Performance of Multi-information Integration Based on Low-end Inertial Sensors for Precision Agriculture. Precis. Agric. 2021, 22, 627–646. [Google Scholar] [CrossRef]
- Zhang, W.Y.; Wang, J.; Zhang, Z.G.; He, J.; Luo, X.W. Self-calibrating Variable Structure Kalman Filter for Tractor Navigation during BDS Outages. Trans. Chin. Soc. Agric. Mach. 2020, 51, 18–27. [Google Scholar]
- Zhang, Q.; Qiu, H. A dynamic path search algorithm for tractor automatic navigation. Trans. ASAE 2004, 47, 639–646. [Google Scholar] [CrossRef]
- Cui, X.; Cui, B.; Ma, Z. Integration of geometric-based path tracking controller and its application in agricultural machinery automatic navigation. J. Intell. Agric. Mech. 2023, 4, 24–31. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).