An Ice Protection System Based on Phased Piezoelectric Transducers
Abstract
1. Introduction
- The implementation of dedicated numerical tools for the accurate prediction of ice accretion mechanisms and the design of unconventional concepts;
2. Proposed Ice Protection System Layout and Working Principle
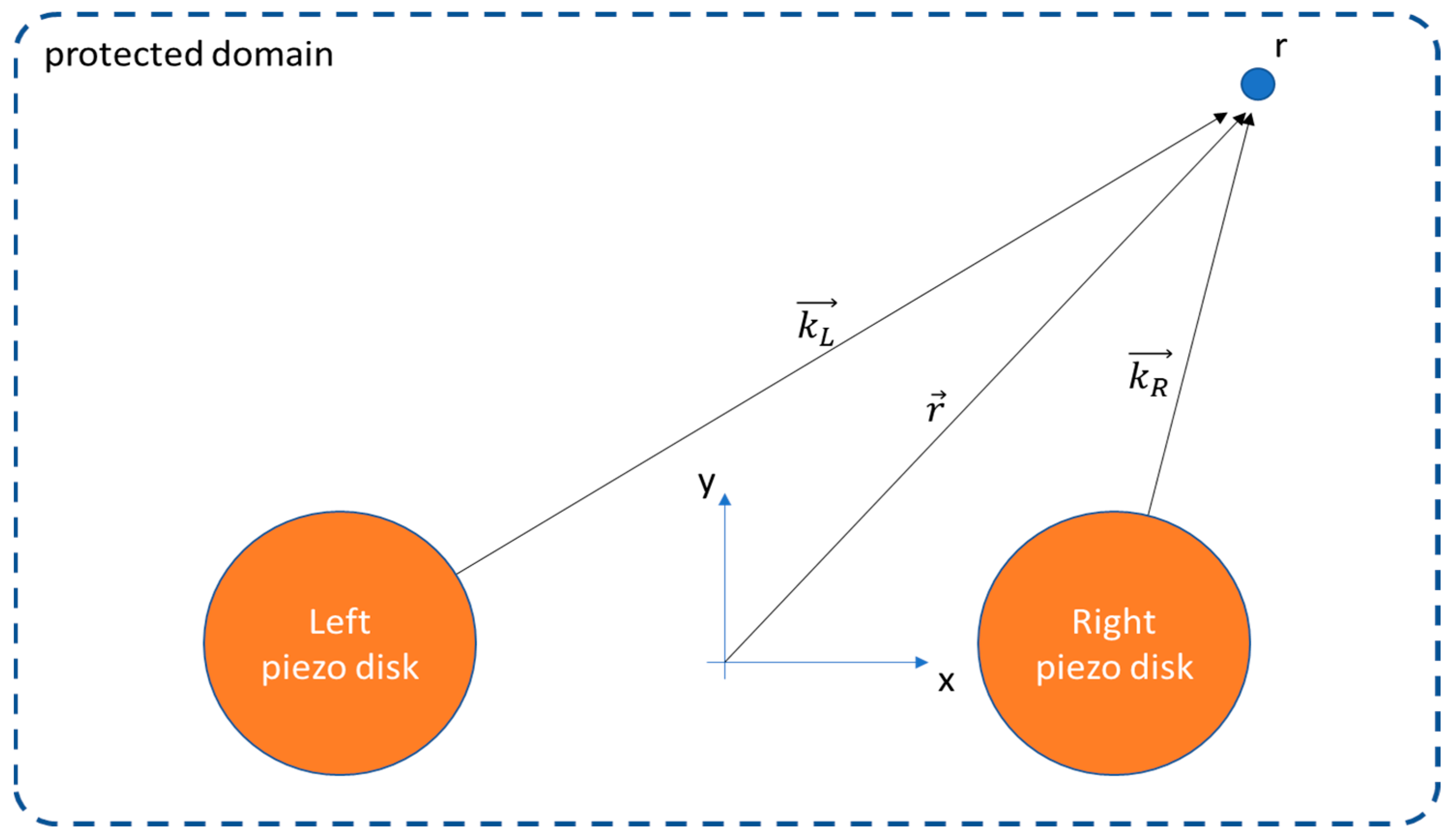
- The distance of the sources from the point: this parameter causes both a phase shift and an attenuation of the signals;
- The geometry of the protected component: thickness or curvature variations, local discontinuities, junctions, or constraints may generate wave reflections, worsening system effectiveness;
- The distribution of the ice: ice accretions behave as lumped masses that modify the dynamic response and also result in the reflection of waves;
- The temperature: the distribution of temperature may vary, for instance, along the chord, as shown in [53]; this parameter may produce thermal distortions within the different materials of the system; moreover, it may alter the mechanical properties of the ice;
- The transmission of shear: this aspect is crucial for its impact on the magnitude of the transmitted actions. It is influenced by different parameters; the theoretical model built by Crawley and de Luis [56] highlights the effect of some parameters, corresponding to the quality of the bonding layer and, thus, the effectiveness of the transmission. In particular, the non-dimensional parameter Γ was identified for a 1D PZT patch of extension L:
3. Operational Range
- The applications can be categorized into two primary families based on the frequency of excitation: low bandwidth, arriving at a few kHz, and high bandwidth, over 20 kHz. In the first band, the typical modal shapes of plate elements are excited, while in the higher band, thickness resonances are exploited. It is noteworthy that applications operating at low frequencies typically employ a greater number of piezoelectric patches with an overall capacitance compliant with the frequency limitations of the amplifier;
- Another classification, even if not so sharp, can be performed on the basis of the voltage of excitation; two parameters seem to be related to it: the stiffness of the structure (in turn determined by material and geometry) and the frequency itself: generally stiffer structures and lower frequencies are accompanied by higher voltages; it is also worth noting that higher frequencies require amplification systems with an adequately high cut-off band, compatible with the capacitances of bulky piezoelectrics;
- Protected part: flat (rectangular or circular, free or constrained) and curved plates representative of wing leading edges; with specific reference to this last typology and in particular to the work [60]; it is worth noting the implementation of an opposite phase delay to better harmonize the waves produced by different piezoelectrics acting on a complex structure;
- The ice distribution: the applications are characterized by ice accretions with different thicknesses, up to 12 mm, with an average of 4 mm.
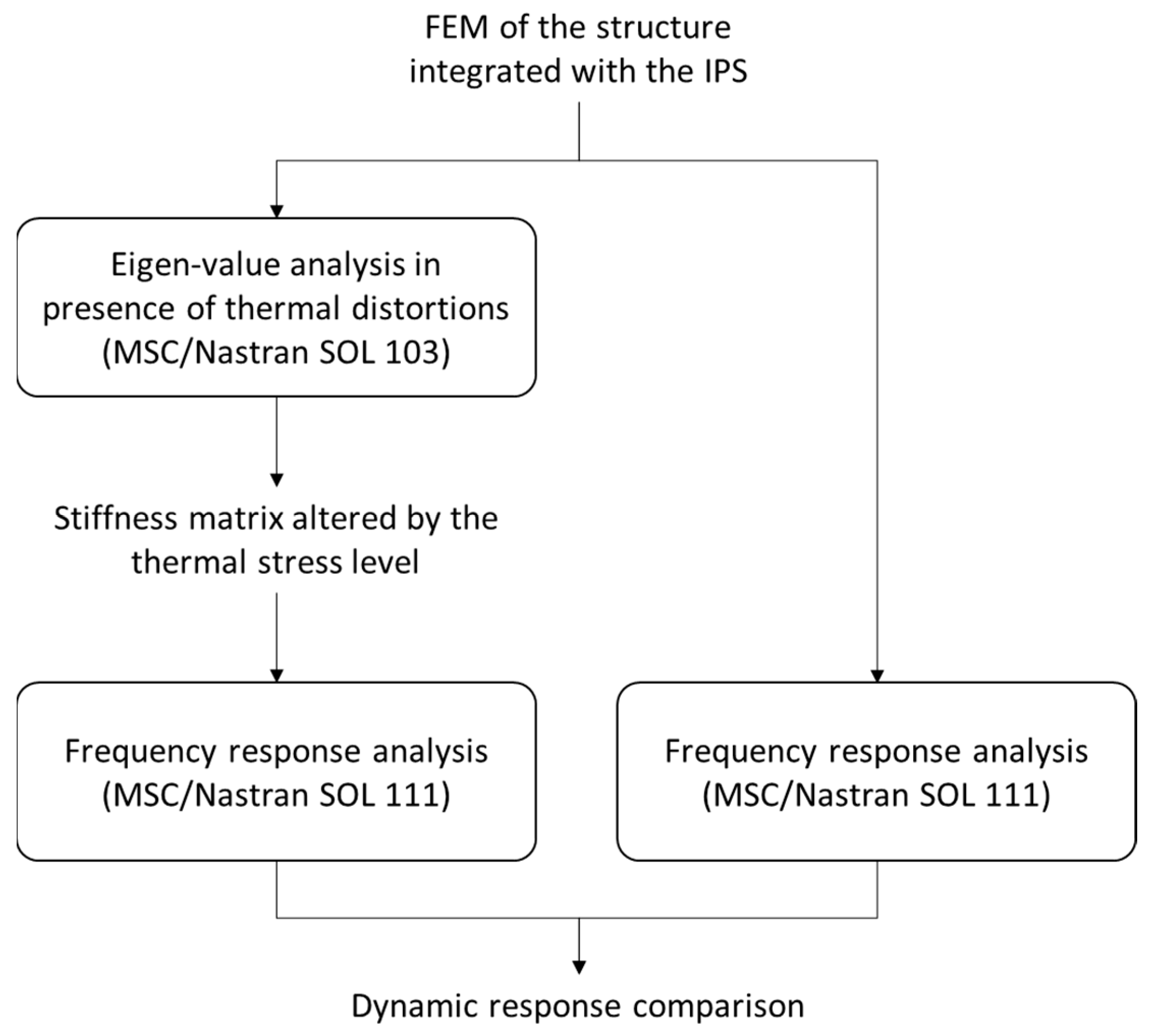
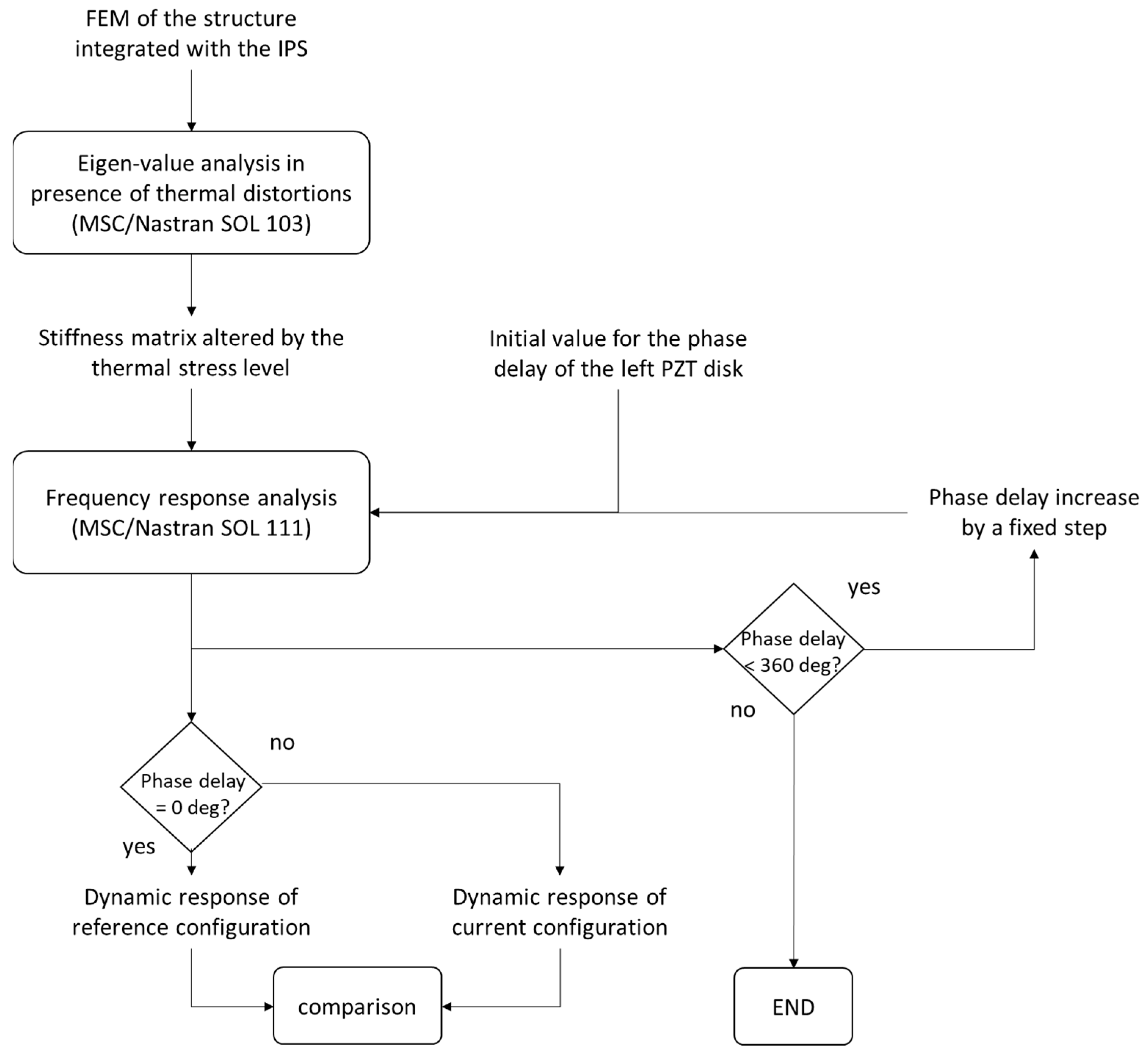
4. Modeling and Parameter Sensitivity
5. Optimal Delay Effects
6. Ice Protection Effectiveness
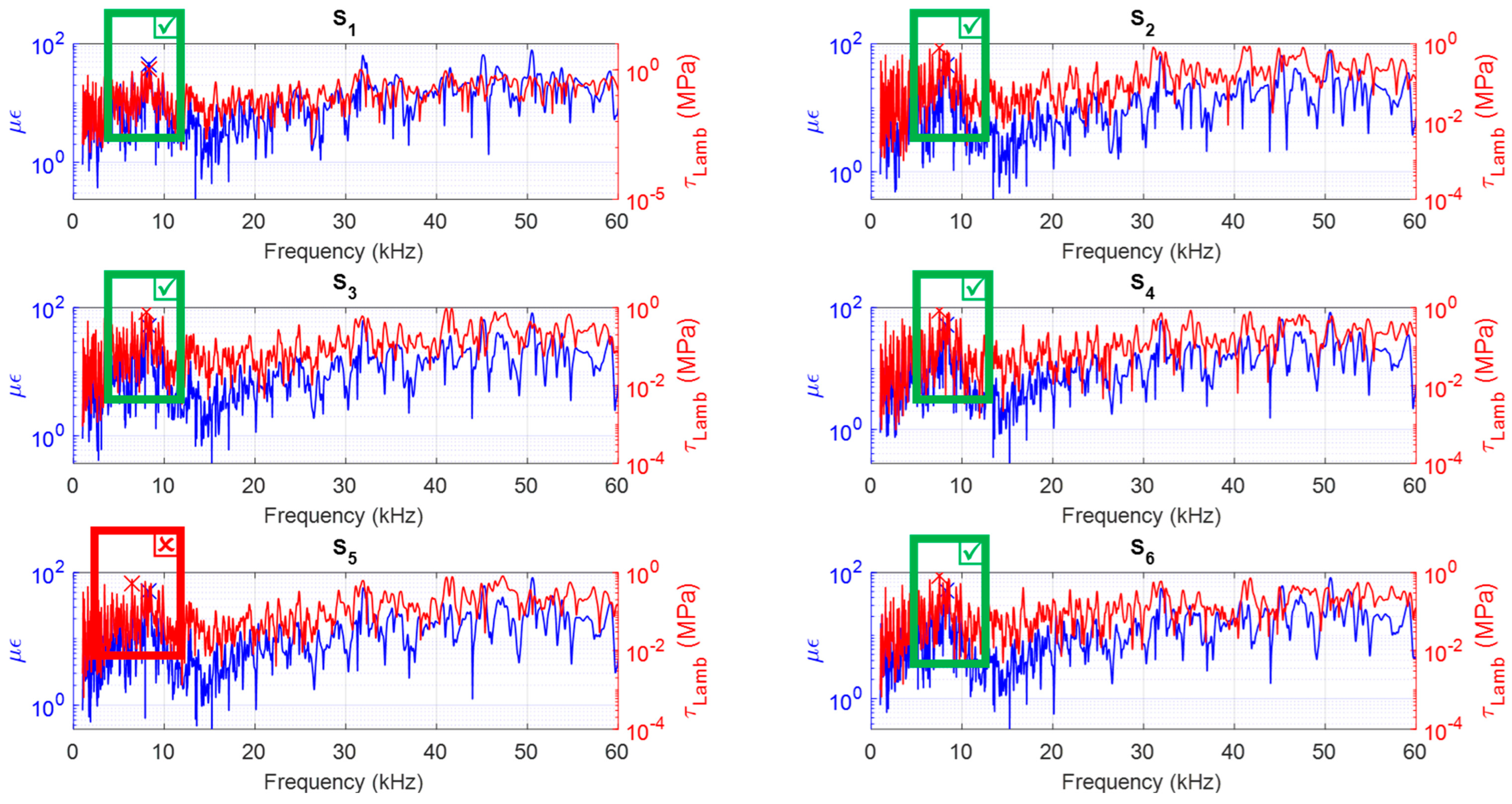
7. Preliminary Experimental Validation
- The experimental data without optimal phase delay, averaged over all the sensors and over the entire thickness and temperatures ranges, lead to an average transmitted strain of 5 µε.
- The same average, for the optimal phase delay, gives an increase of about 0.6 µε; that is to say, an intensification of the transmitted action of about 12%.
8. Conclusions and Further Steps
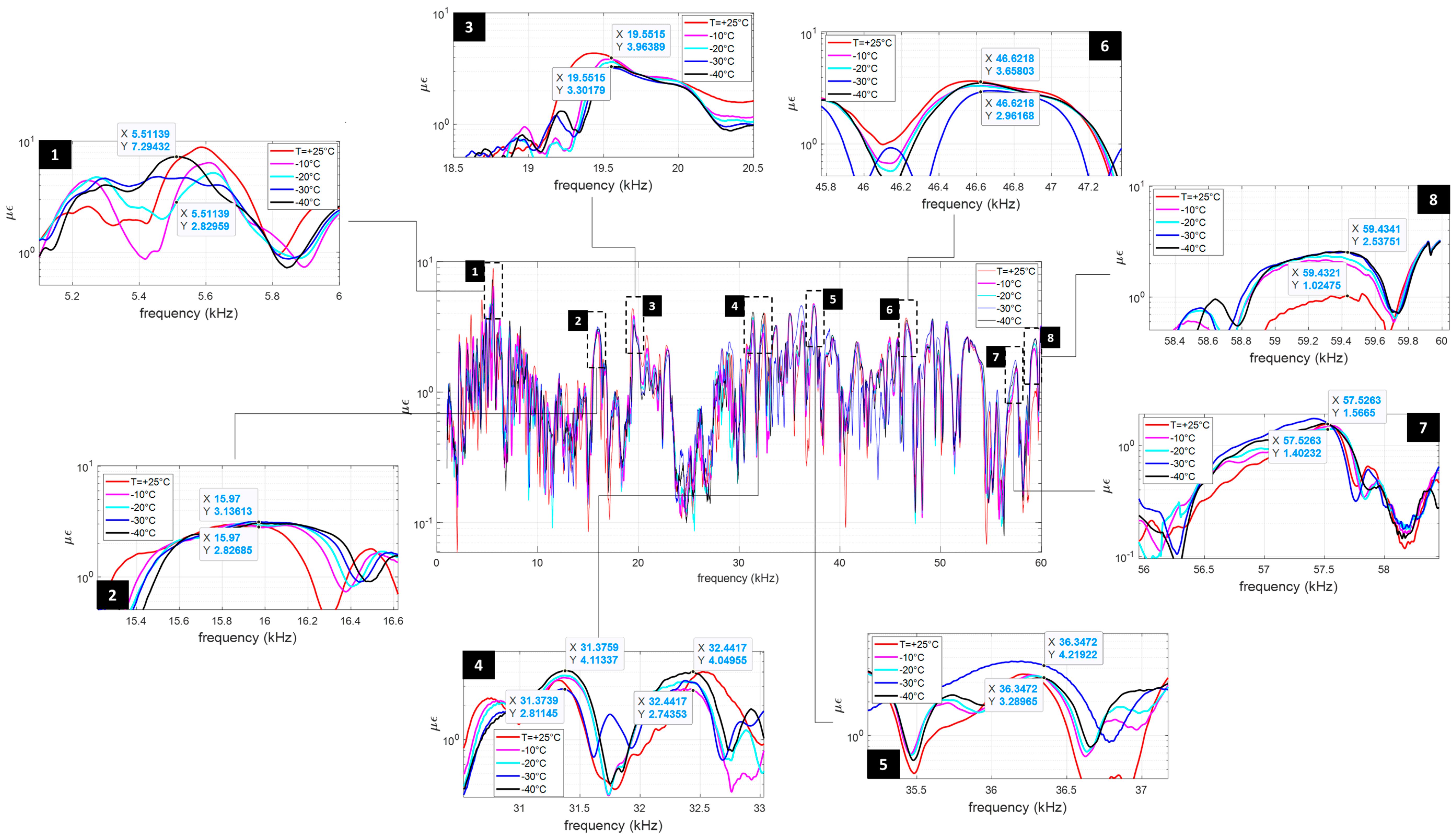
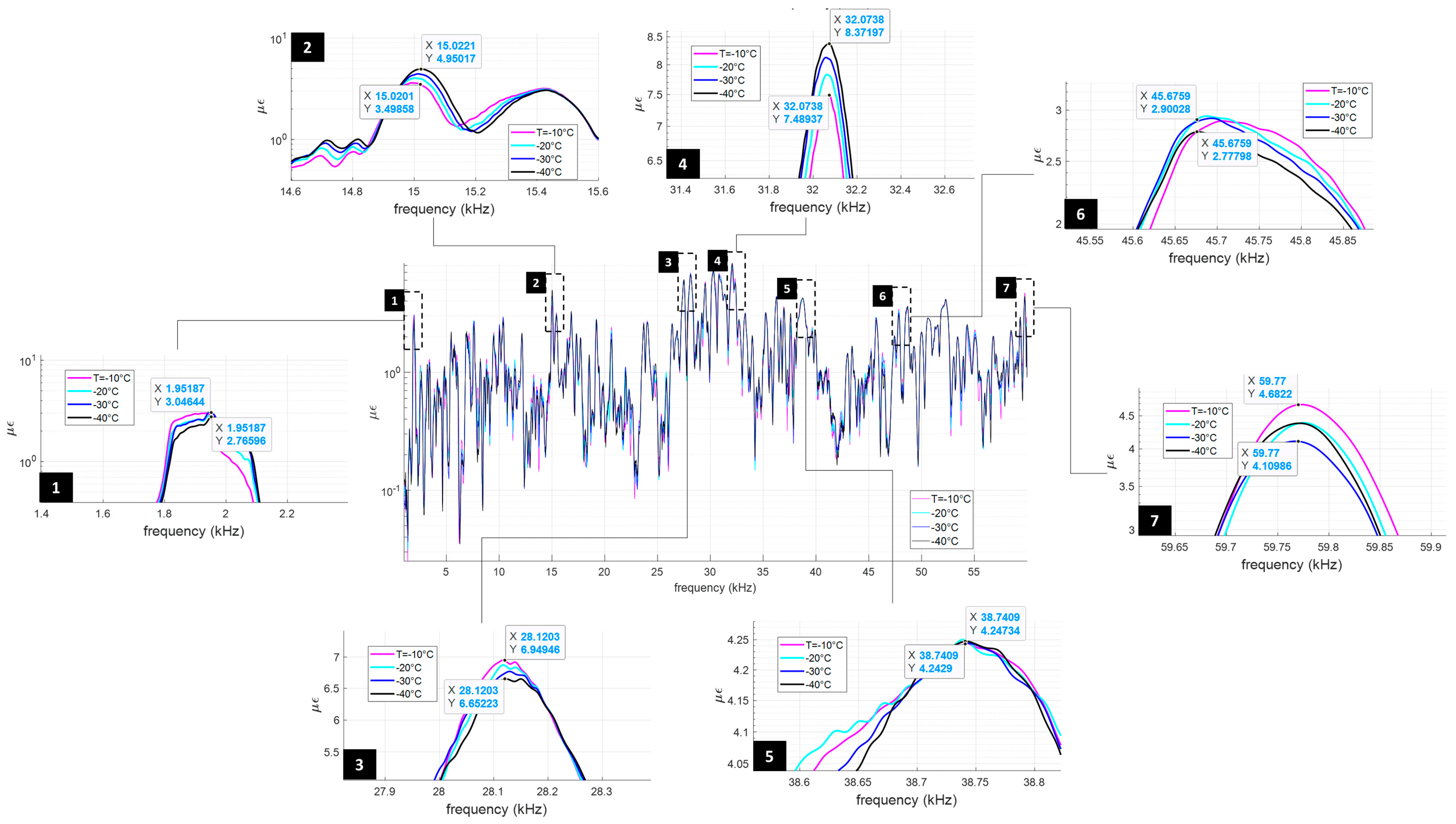
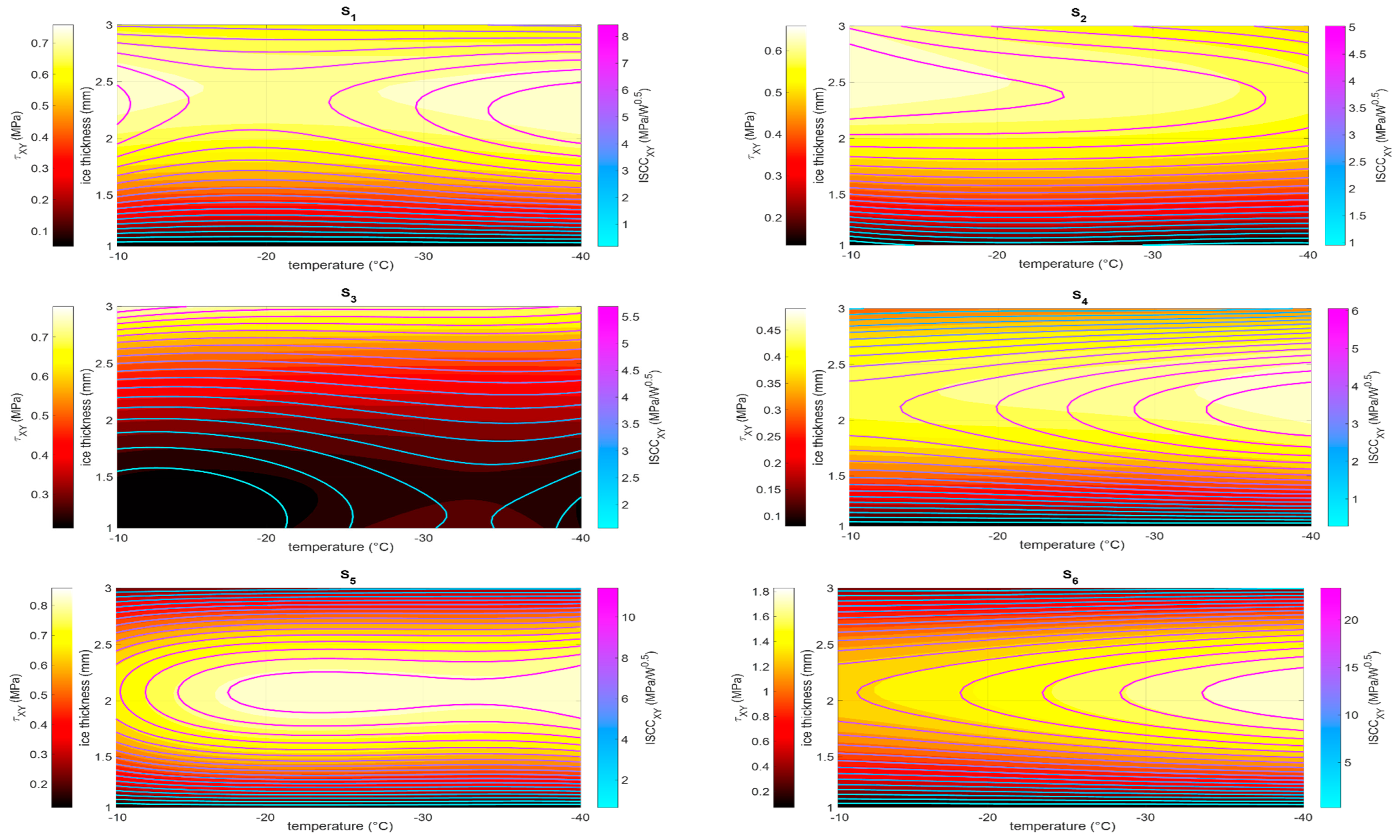
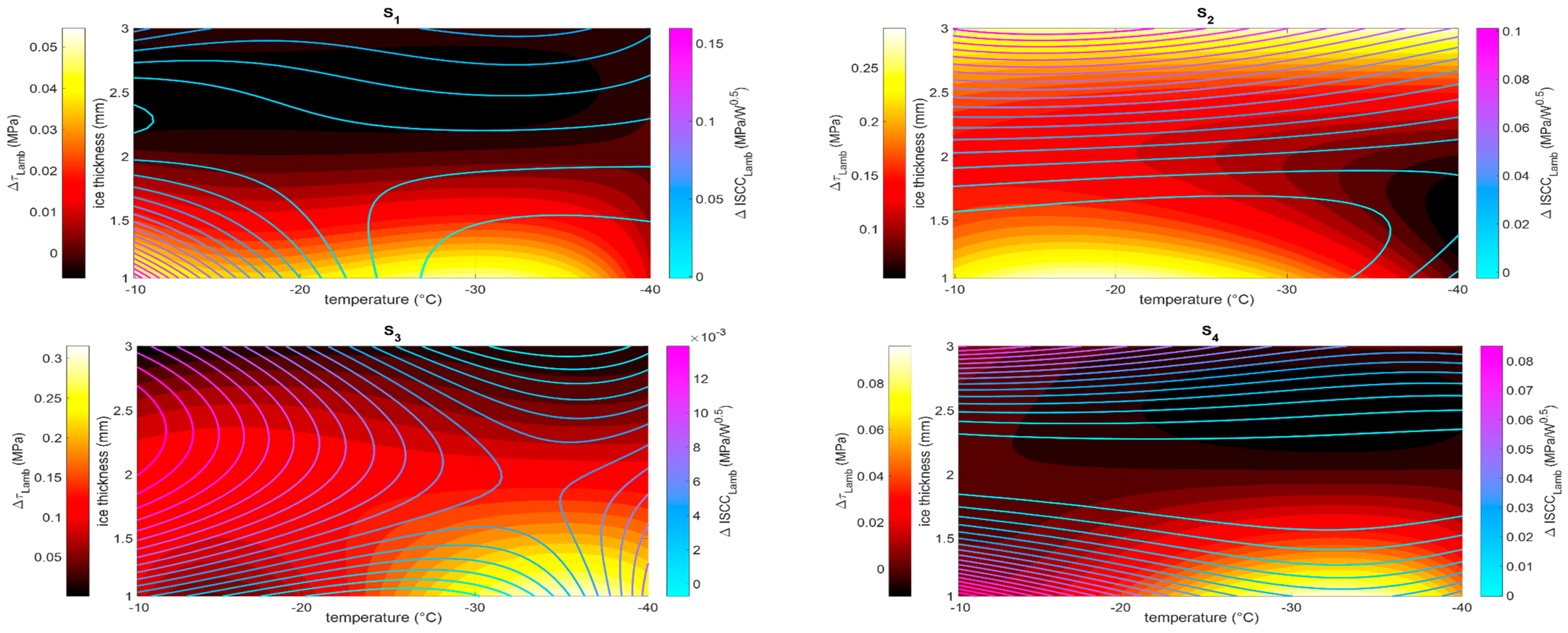
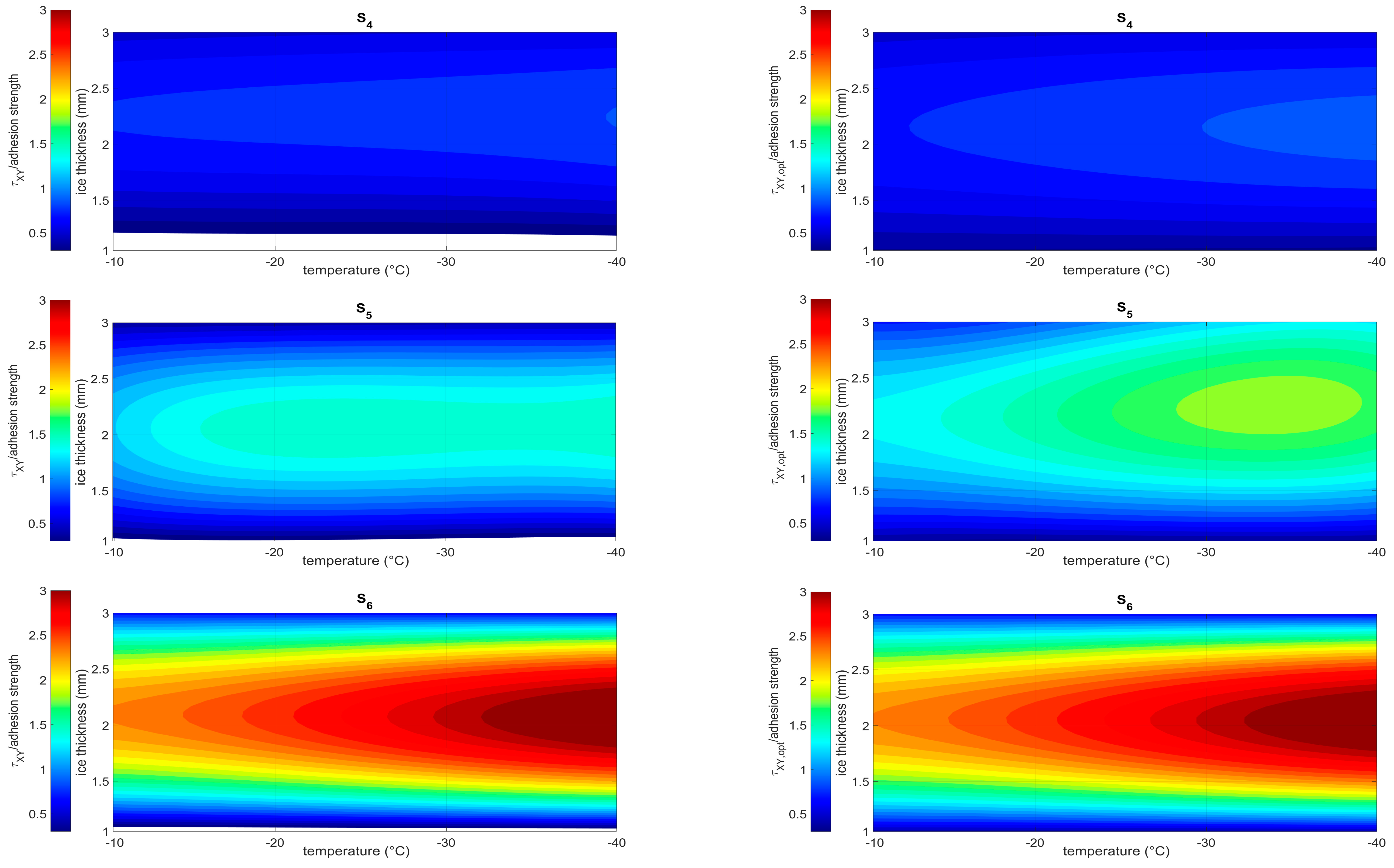
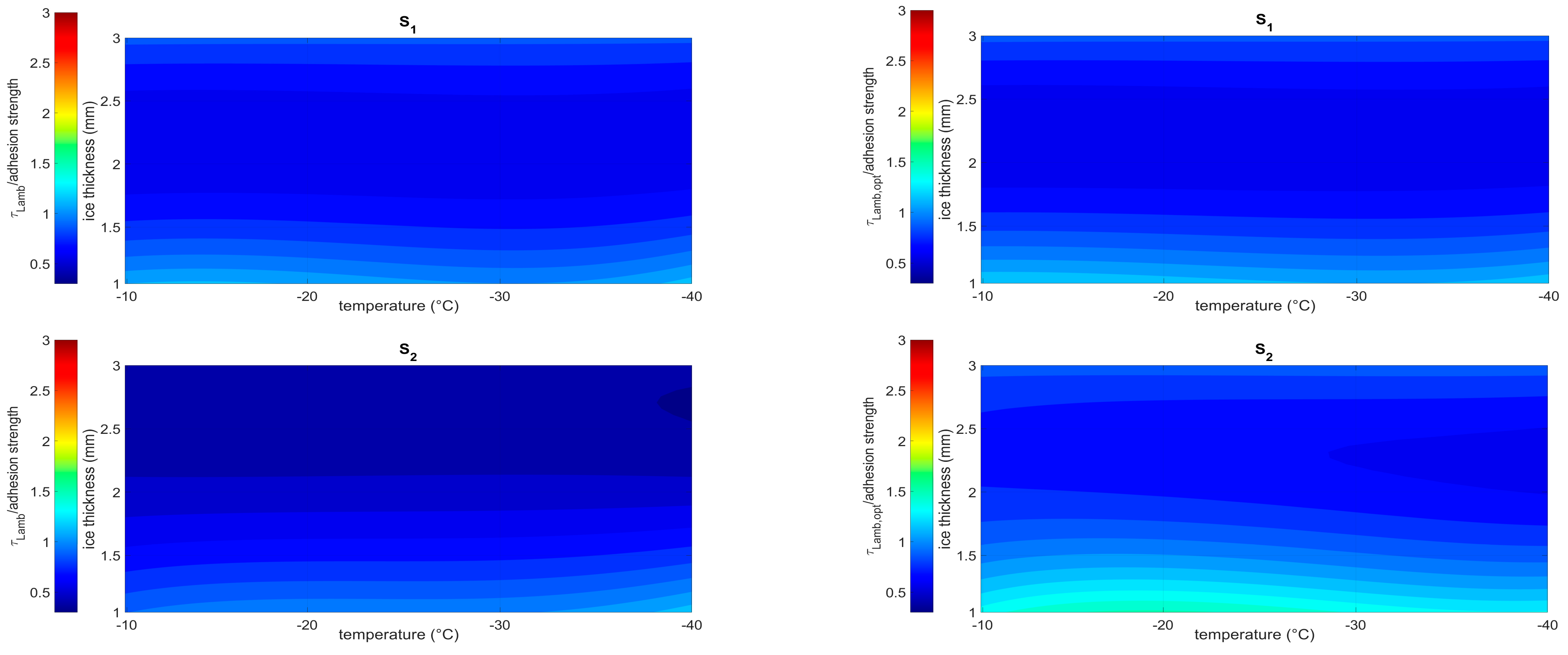
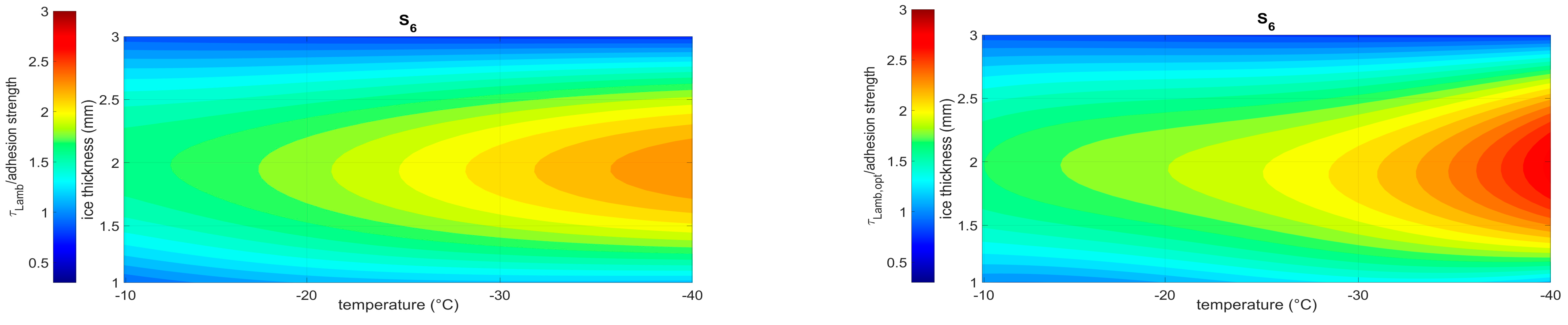
- The temperature of the structure dramatically alters not only the ice features but also the dynamic of the structure itself. In particular, the stress level due to the thermal distortions determines the shift of the frequency peaks that are potentially exploitable for exciting shear waves. Thus, the ice protection system may not work in nominal conditions, with a consequent a loss of effectiveness. Within the operational range [−40 °C, −10 °C] a reduction of up to 62% of the magnitude of shear was estimated at the interface with the ice.
- The ice thickness may alter the dynamic behavior of the system even more significantly, both in terms of amplitude and the position of the peaks. A reduction of up to 95% of the shear amplitude was estimated within the ice thickness range of 1–3 mm. Even higher variations seem plausible in the case of non-uniform ice accretions.
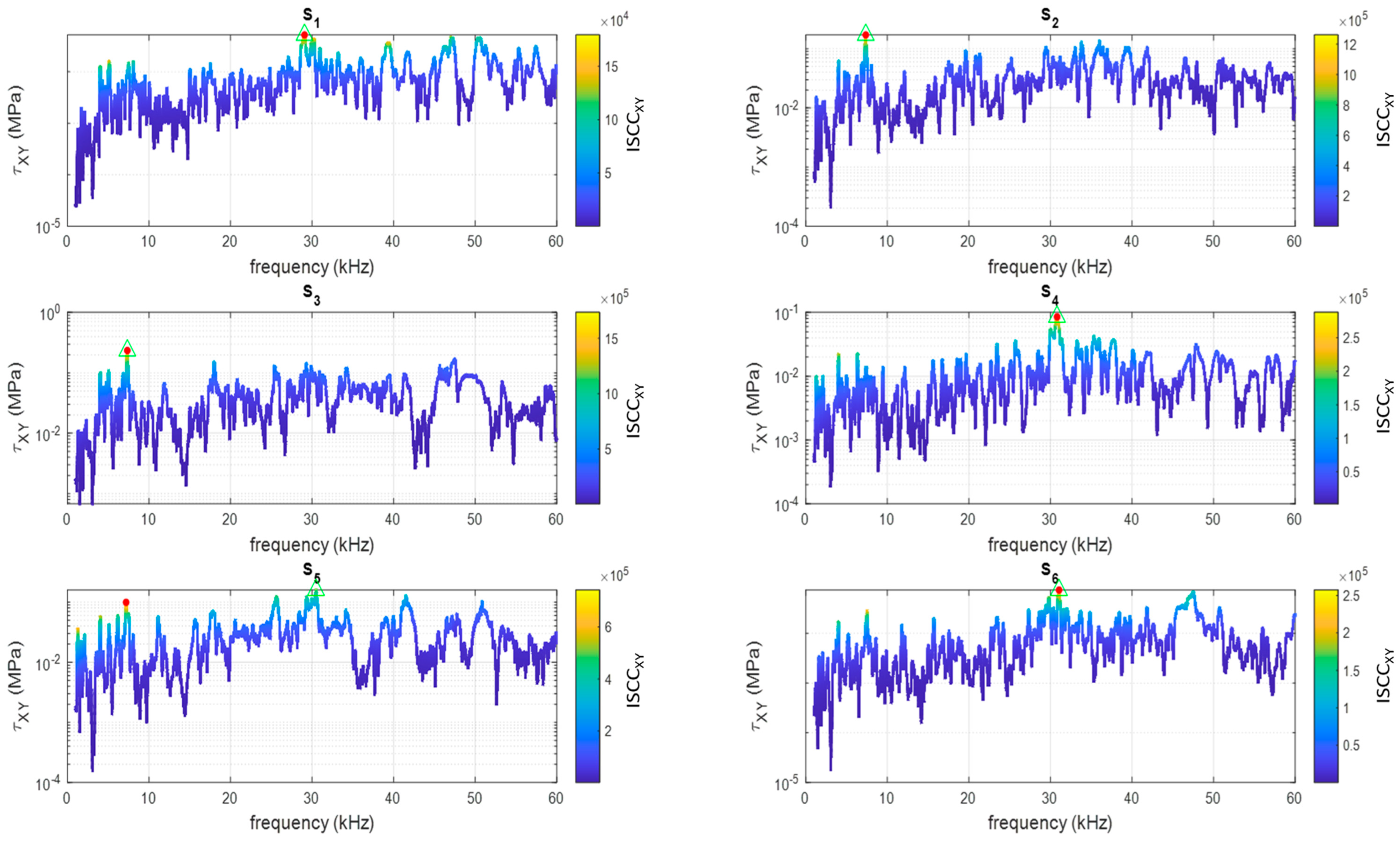
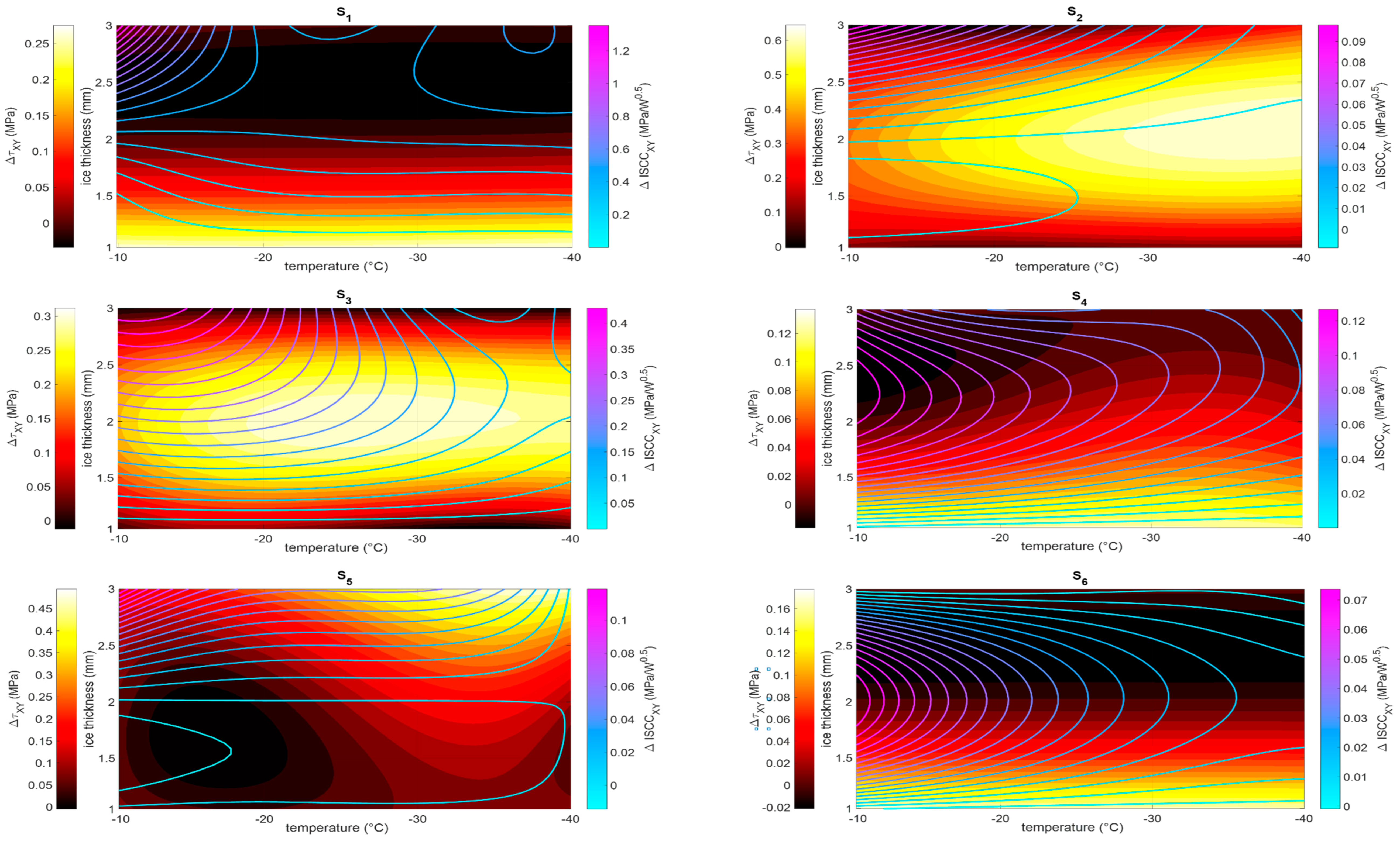
- The maximum shear magnitude and the ISCC in the case of 0-phase delay (reference) generally coincide. On the contrary, different trends were observed within the temperature–ice thickness domain when the logic of the optimal phase is implemented. This highlights the importance of a strategy of selection between one target, the magnitude of the shear, and the best compromise between this and needed power, that is to say, the ISCC.
- An increase of the shear magnitude up to 0.6 and 0.3 MPa for the in-plane and out-of-plane actions, respectively, was estimated. These figures indicate that an increase of one order blow the reference configuration (0-phase delay) can be obtained to the optimal phase delay strategy.
- The ISCC was most benefited by the strategy. Here, the best increase of ISCC was estimated at 1.2 MPa/√W for the in-plane actions, over a reference value of 8 MPa/√W, that is to say, 15%. The ISCC for the in-plane actions was enhanced but in a much modest way, with a net increase of 0.16 MPa/√W over a basic value of 16 MPa/√W, practically 1%.
- The thickness of the ice generally has a more severe impact on the effectiveness of the system than the temperature. Moreover, depending on the location of the sensor, the values of the thickness for which the best performance is achieved changes. This suggests the influence of the modal shapes on the local deformation field.
- A global enhancement of the power of the ice protection system was also observed through a preliminary experimental campaign; a rough maximum value of 12% of improvement of the power within the operational range was estimated, even in a direct comparison in terms of shear since the transducers were suited for linear and not angular strain.
- Readiness of the technology: this aspect is achieved through redundant architectures that rely on the synergistic use of multiple network elements, ensuring an acceptable level of performance even in the event of temporary faults in some transducers.
- Integration and impact on the other on-board systems: the phase delay approach contributes to enhanced performance and, in turn, to a reduction of the power consumption of the system; this, in some way, simplifies necessary upgrade operations, mitigating the upheaval of the pre-existing on-board equipment.
- Compliance with new configurations: the technology herein investigated seems particularly prone to new configurations, such as full electric or hybrid aircraft; the main reason is the type of energy, electrical energy, that the technology uses and handles, requiring limited operations of conversion before reaching the end user.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Marongiu, C.; Vitagliano, P.L.; Zanazzi, G.; Narducci, R. Aerodynamic Analysis of an Iced Airfoil at Medium/High Reynolds Number. AIAA J. 2008, 46, 2469–2478. [Google Scholar] [CrossRef]
- Federal Aviation Administration (FAA). Aircraft Icing. Available online: https://www.faa.gov/documentlibrary/media/advisory_circular/ac%2000-6a%20chap%2010-12.pdf (accessed on 7 March 2024).
- Parent, O.; Ilinca, A. Anti-icing and de-icing techniques for wind turbines: Critical review. Cold Reg. Sci. Technol. 2011, 65, 88–96. [Google Scholar] [CrossRef]
- Li, S.; Paoli, R. Modeling of Ice Accretion over Aircraft Wings Using a Compressible OpenFOAM Solver. Intl. Jnl. Aerospace Eng. 2019, 4864927. [Google Scholar] [CrossRef]
- Potapczuk, M.G. Aircraft Icing Research at NASA Glenn Research Center. J. Aerosp. Eng. 2013, 26. [Google Scholar] [CrossRef]
- Veldhuis, S.; Dam, C.J.; Hoeijmakers, H.W.M. Aircraft icing: A review of the fundamental mechanisms. Appl. Therm. Eng. 2003, 23, 2245–2266. [Google Scholar] [CrossRef]
- Thomas, S.K.; Cassoni, R.P.; MacArthur, C.D. Aircraft Anti-Icing and De-Icing Techniques and Modeling. J. Aircr. 1996, 33, 841–854. [Google Scholar] [CrossRef]
- Venna, S.; Lin, Y.-J.; Botura, G. Piezoelectric Transducer Actuated Leading Edge De-Icing with Simultaneous Shear and Impulse Forces. J. Aircr. 2007, 44, J052113. [Google Scholar] [CrossRef]
- Palacios, J.L. Design, Fabrication, and Testing of an Ultrasonic De-Icing System for Helicopter Rotor Blades. Ph.D. Thesis, The Pennsylvania State University, University Park, PA, USA, 2008. Available online: https://catalog.libraries.psu.edu/catalog/4753586 (accessed on 7 March 2024).
- Palacios, J.; Smith, E.; Rose, J.; Royer, R. Instantaneous De-Icing of Freezer Ice via Ultrasonic Actuation. AIAA J. 2011, 49, 1158–1167. [Google Scholar] [CrossRef]
- Zhang, Z.; Hu, H.; Bai, X.; Hu, H. An Experimental Study on the Detrimental Effects of Deicing Fluids on the Performance of Icephobic Coatings for Aircraft Icing Mitigation. Aerosp. Sci. Technol. 2021, 119, 107090. [Google Scholar] [CrossRef]
- Yakovlieva, A.; Boichenko, S.; Shkilniuk, I.; Bakhtyn, A.; Kale, U.; Nagy, A. Assessment of Influence of Anti-Icing Fluids Based on Ethylene and Propylene Glycol on Environment and Airport Infrastructure. Int. J. Sustain. Aviat. 2022, 8, 54–74. [Google Scholar] [CrossRef]
- Yamazaki, M.; Jemcov, A.; Sakaue, H. A Review on the Current Status of Icing Physics and Mitigation in Aviation. Aerospace 2021, 8, 188. [Google Scholar] [CrossRef]
- SKYbrary Aviation Safety. Chapter 15: Ice and Rain Protection. Available online: https://skybrary.aero (accessed on 13 March 2024).
- Abdelghany, E.S.; Sarhan, H.H.; El Saleh, A.; Farghaly, M.B. High Bypass Turbofan Engine and Anti-Icing System Performance: Mass Flow Rate of Anti-Icing Bleed Air System Effect. Case Studies in Thermal Engineering. 2023. Available online: https://researchgate.net (accessed on 13 March 2024).
- Wong, S.-H.; Papadakis, M.; Zamora, A. Computational Investigation of a Bleed Air Ice Protection System. In Proceedings of the Fluid Dynamics and Co-Located Conferences, Chicago, IL, USA, 28 June–1 July 2010. AIAA 2009-3966. [Google Scholar] [CrossRef]
- Papadakis, M.; Wong, S.-H.; Yeong, H.-W.; Wong, S.-C. Experimental Investigation of a Bleed Air Ice Protection System; SAE Technical Paper 2007-01-3313; SAE: Warrendale, PA, USA, 2007. [Google Scholar] [CrossRef]
- Papadakis, M.; Zamora Rodriguez, A.; Domingos, R. Experimental and Computer Model Results for a Bleed Air Ice Protection System; SAE Technical Paper 2011-38-0034; SAE: Warrendale, PA, USA, 2011. [Google Scholar] [CrossRef]
- Zanon, A.; De Gennaro, M. Design of the Thermoelectric Ice Protection System for a Tiltrotor Application. AIAA J. 2023, 59, 1337–1350. [Google Scholar] [CrossRef]
- Morita, K.; Kimura, S.; Sakaue, H. Hybrid System Combining Ice-Phobic Coating and Electrothermal Heating for Wing Ice Protection. Aerospace 2020, 7, 102. [Google Scholar] [CrossRef]
- Yu, L.; Wu, Y.; Zhao, H.; Zhu, D. A Study on the Sensitivities of an Ice Protection System Combining Thermoelectric and Superhydrophobic Coating to Icing Environment Parameters. Appl. Sci. 2023, 13, 6607. [Google Scholar] [CrossRef]
- Yang, S.; Yi, X.; Guo, Q.; Xiao, C.; Luo, Z.; Zhou, Y. Novel Hybrid Ice Protection System Combining Thermoelectric System and Synthetic Jet Actuator. AIAA J. 2021, 59, 4. [Google Scholar] [CrossRef]
- Bendarkar, M.V.; Chakraborty, I.; Garcia, E.; Mavris, D.N. Rapid Assessment of Power Requirements and Optimization of Thermal Ice Protection Systems. AIAA J. 2018, 59, 4136. [Google Scholar]
- Ingram, R.B.; Codner, G.W.; Gerardi, J.J. Electro-Magnetic Expulsion De-Icing System. WO Patent 1996037406A1, 28 November 1996. [Google Scholar]
- Petrenko, V.F. System and Method for Icemaker and Aircraft Wing with Combined Electromechanical and Electrothermal Pulse Deicing. U.S. Patent 20100206990A1, 19 August 2010. [Google Scholar]
- Lei, T.; Min, Z.; Gao, Q.; Song, L.; Zhang, X.; Zhang, X. The Architecture Optimization and Energy Management Technology of Aircraft Power Systems: A Review and Future Trends. Energies 2022, 15, 4109. [Google Scholar] [CrossRef]
- Righi, F.; Sullivan, D.B.; Hartl, D.J.; Rogers, J. Shape Memory Alloy Rotor Blade Deicing. In Proceedings of the 54th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Boston, MA, USA, 8–11 April 2013. [Google Scholar] [CrossRef]
- Tamer, O.; Kyriazis, A.; Sinapius, M. Parameter Study and Experimental Analysis of a Thermo-Mechanical De-Icing Concept. Smart Mater. Struct. 2020, 29, 045021. [Google Scholar] [CrossRef]
- Villeneuve, E.; Ghinet, S.; Volat, C. Experimental Study of a Piezoelectric De-Icing System Implemented to Rotorcraft Blades. Appl. Sci. 2021, 11, 9869. [Google Scholar] [CrossRef]
- Jomaa, M.; Vasic, D.; Costa, F.; Lévy, P.-E.; Ali, M. Driving Power Supply for an Avionic Piezoelectric Deicing System. In Proceedings of the SPIE 12483, Active and Passive Smart Structures and Integrated Systems XVII, 124831N, Long Beach, CA, USA, 28 April 2023. [Google Scholar] [CrossRef]
- Song, N.; Benmeddour, A. Erosion Resistant Hydrophobic Coatings for Passive Ice Protection of Aircraft. Appl. Sci. 2022, 12, 9589. [Google Scholar] [CrossRef]
- Piscitelli, F.; Palazzo, S.; De Nicola, F. Icing Wind Tunnel Test Campaign on a Nacelle Lip-Skin to Assess the Effect of a Superhydrophobic Coating on Ice Accretion. Appl. Sci. 2023, 13, 5183. [Google Scholar] [CrossRef]
- Ingram, R.B.; Gerardi, J.J. Shape Memory Alloy De-Icing Technology. U.S. Patent US5686003A, 11 November 1997. [Google Scholar]
- Liu, X.; Xing, Y.; Zhao, L. Study of Shape Memory Alloy De-icing Device for Nonrotating Components of Aircrafts. Proc. IOP Conf. Ser. Mater. Sci. Eng. 2018, 394, 032106. [Google Scholar] [CrossRef]
- Tamer, O.; Walter, F.; Sinapius, M.; Böl, M. A Computational Geometric Parameter Optimization of the Thermomechanical Deicing Concept. Actuators 2022, 11, 223. [Google Scholar] [CrossRef]
- Bhakta, B. Novel Ice Protection System Suitable for Unmanned Aerial Vehicle Wing. Ph.D. Thesis, Cranfield University, Cranfield, UK, 1 February 2005. [Google Scholar]
- Muhammed, M.; Virk, M.S. Ice Accretion on Fixed-Wing Unmanned Aerial Vehicle—A Review Study. Drones 2022, 6, 863. [Google Scholar] [CrossRef]
- European Commission. JEDI ACE—Japanese-European De-Icing Aircraft Collaborative Exploration. Available online: https://cordis.europa.eu/project/id/314335 (accessed on 7 March 2024).
- European Commission. SENS4ICE—SENSors and Certifiable Hybrid Architectures FOR Safer Aviation in ICing Environment [Internet]. Available online: https://www.sens4ice-project.eu/ (accessed on 7 March 2024).
- European Commission. ICE GENESIS Environment. Available online: https://www.ice-genesis.eu/page/bm/ldo-101.php (accessed on 7 March 2024).
- Jiang, X.; Wang, Y. Studies on the Electro-Impulse De-Icing System of Aircraft. Aerospace 2019, 6, 67. [Google Scholar] [CrossRef]
- Airport Cooperative Research Program. Available online: https://www.skybrary.aero/sites/default/files/bookshelf/4867.pdf (accessed on 7 March 2024).
- Meggitt PLC. GAINS—Green Airframe Icing Novel Systems. Available online: https://www.meggitt.com/insights/new-tunes-to-break-the-ice/ (accessed on 7 March 2024).
- Liu, J.; Janjua, Z.A.; Roe, M.; Xu, F.; Turnbull, B.; Choi, K.S.; Hou, X. Super-Hydrophobic/Icephobic Coatings Based on Silica Nanoparticles Modified by Self-Assembled Monolayers. Nanomaterials 2016, 6, 232. [Google Scholar] [CrossRef]
- Liu, J.; Wang, J.; Memon, H.; Fu, Y.; Barman, T.; Choi, K.S.; Hou, X. Hydrophobic/Icephobic Coatings Based on Thermal Sprayed Metallic Layers with Subsequent Surface Functionalization. Surf. Coat. Technol. 2019, 357, 267–272. [Google Scholar] [CrossRef]
- Dassault Group. Falcon 7X—The Benchmark for the 21st Century Business Jet. Available online: https://www.dassaultfalcon.com/en/Aircraft/Models/7X/Pages/overview.aspx (accessed on 7 March 2024).
- Yeoh, S.S.; Rashed, M.; Sanders, M.; Bozhko, S. Variable-Voltage Bus Concept for Aircraft Electrical Power System. IEEE Trans. Ind. Electron. 2019, 66, 5634–5643. [Google Scholar] [CrossRef]
- Memon, H.; Liu, J.; De Focatiis, D.S.A.; Choi, K.; Hou, X. Intrinsic Dependence of Ice Adhesion Strength on Surface Roughness. Surf. Coat. Technol. 2020, 385, 125352. [Google Scholar] [CrossRef]
- Memon, H.; Liu, J.; Weston, N.; Wang, J.; De Focatiis, D.S.A.; Choi, K.; Hou, X. In-Situ Icing and Water Condensation Study on Different Topographical Surfaces. Cold Reg. Sci. Technol. 2019, 165, 102778. [Google Scholar] [CrossRef]
- Tenebre, P.; Six, M.-F. Anti-Icing/De-Icing System and Method and Aircraft Structure Incorporating This System. U.S. Patent 8,146,866, 3 April 2012. [Google Scholar]
- Endres, M.; Sommerwerk, H.; Mendig, C.; Sinapius, M.; Horst, P. Experimental Study of Two Electro-Mechanical De-Icing Systems Applied on a Wing Section Tested in an Icing Wind Tunnel. CEAS Aeronaut. J. 2017, 8, 429–439. [Google Scholar] [CrossRef]
- Budinger, M.; Pommier-Budinger, V.; Bennani, L.; Rouset, P.; Bonaccurso, E.; Dezitter, F. Electromechanical Resonant Ice Protection Systems: Analysis of Fracture Propagation Mechanisms. AIAA J. 2018, 56, 4412–4422. [Google Scholar] [CrossRef]
- Chang, S.; Tang, H.; Wu, H.; Su, X.; Lewis, A.; Ji, C. Three-Dimensional Modelling and Simulation of the Ice Accretion Process on Aircraft Wings. Int. J. Astronaut. Aeronaut. Eng. 2018, 3, 1–25. [Google Scholar]
- Royer, R.L., Jr.; Rose, J.L.; Smith, E.C.; Palacios, J.L. Ultrasonic Vibration System and Method for Removing/Avoiding Unwanted Build-Up on Structures. U.S. Patent 20100031972A1, 11 February 2010. [Google Scholar]
- Lamb, H. On Waves in an Elastic Plate. Proc. R. Soc. A 1917, 93, 114–128. [Google Scholar]
- Crawley, E.F.; Luis, J.D. Use of Piezoelectric Actuators as Elements of Intelligent Structures. AIAA J. 1987, 25, 1373–1385. [Google Scholar] [CrossRef]
- Henkel. Brochure: Structural Adhesive Solutions for Composite Repair. Henkel Corporation. Available online: https://dm.henkel-dam.com/is/content/henkel/brochure-structural-adhesive-solutions-composite-repair-loctite (accessed on 1 April 2024).
- Lu, Z.; Brennan, M.; Ding, H.; Chen, L. High-Static-Low-Dynamic-Stiffness Vibration Isolation Enhanced by Damping Nonlinearity. Sci. China Technol. Sci. 2019, 62, 1103–1110. [Google Scholar] [CrossRef]
- Kovacic, I.; Brennan, M.; Waters, T. A Study of a Non-Linear Vibration Isolator with Quasi-Zero Stiffness Characteristic. J. Sound Vib. 2008, 315, 700–711. [Google Scholar] [CrossRef]
- Bai, T.; Zhu, C.; Miao, B.; Li, K.; Zhu, C. Vibration De-Icing Method with Piezoelectric Actuators. J. Vibroeng. 2015, 17, 61–73. [Google Scholar]
- Di Placido, N.; Soltis, J.; Palacios, J. Enhancement of Ultrasonic De-Icing via Tone Burst Excitation. J. Aircr. 2016, 53, 1821–1829. [Google Scholar] [CrossRef]
- Budinger, M.; Pommier-Budinger, V.; Reysset, A.; Palanque, V. Electromechanical Resonant Ice Protection Systems: Energetic and Power Considerations. AIAA J. 2021, 59, 2590–2602. [Google Scholar] [CrossRef]
- Budinger, M.; Pommier-Budinger, V.; Napias, G.; Costa da Silva, A. Ultrasonic Ice Protection Systems: Analytical and Numerical Models for Architecture Tradeoff. J. Aircr. 2016, 53, 680–690. [Google Scholar] [CrossRef]
- Memmolo, V.; Moll, J. Investigation on Guided Waves Propagation Across Ice Layers. In Proceedings of the SPIE Health Monitoring of Structural and Biological Systems XIV Conference, Online, 11 May 2020; Volume 11381. [Google Scholar]
- Pierrick, R.; Pommier-Budinger, V.; Budinger, M. Electromechanical Resonant Ice Protection Systems: How to Favour Fractures Propagation. In Proceedings of the International Conference on Icing of Aircraft, Engines, and Structures, Minneapolis, MN, USA, 17–21 June 2019. [Google Scholar]
- Shi, Y.; Yu, J. Multimodal Shear Wave Deicing Using Fibre Piezoelectric Actuator on Composite for Aircraft Wings. IEEE/ASME Trans. Mechatron. 2018, 23, 2090–2098. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, Q. Numerical Simulation and Experiment of the Piezoelectric De-Icing System. In Proceedings of the 3rd International Conference on Machinery, Materials and Information Technology Applications, Qingdao, China; 2015. [Google Scholar]
- MSC Nastran. Quick Reference Guide; MSC Software Corporation: Newport Beach, CA, USA, 2015; pp. 3442–3443. [Google Scholar]
- Xue, X.; Qiang, G.; Feng, Y.; Luo, T. Experimental Study on the Adhesion Strength of the Frozen Ice for Aircraft Moving Parts. Aerospace 2022, 9, 589. [Google Scholar] [CrossRef]
- Farahani, E.; Liberati, A.C.; Mahdavi, A.; Stoyanov, P.; Moreau, C.; Dolatabadi, A. Ice Adhesion Evaluation of PTFE Solid Lubricant Film Applied on TiO2 Coatings. Coatings 2023, 13, 1049. [Google Scholar] [CrossRef]
- Bleszynski, M.; Clark, E. Current Ice Adhesion Testing Methods and the Need for a Standard: A Concise Review. Standards 2021, 1, 117–133. [Google Scholar] [CrossRef]
- Work, A.; Lian, Y. A Critical Review of the Measurement of Ice Adhesion to Solid Substrates. Prog. Aerosp. Sci. 2018, 98, 1–26. [Google Scholar] [CrossRef]
- National Instruments. PXIe-5423 Specifications. Available online: https://www.ni.com/docs/en-US/bundle/pxie-5423-specs/page/specs.htmlt (accessed on 11 April 2024).
- National Instruments. PXIe 5105 Specifications. Available online: https://www.ni.com/docs/en-US/bundle/pxie-5105-specs/page/specs.html (accessed on 11 April 2024).












| Ice Prevention/ Removal System | Advantages | Disadvantages | Power Consumption (kW/m2) | Weight (kg/m2) | References |
|---|---|---|---|---|---|
| Fluid | Effective for both preventing and removing ice. Applicable to any surface. It can be cooled and used with various energy sources. | It can freeze or contaminate. It can affect surface aerodynamics. | 0.5–2 | 0.5–2 | [11,12,13] |
| Hot Air | Reliable for continuous ice protection. | It can cause thermal and fatigue on the surface. It can increase fuel consumption and emissions. It takes longer to remove ice. | 10–20 | 13 | [14,15,16,17,18] |
| Thermoelectrical | Versatile and manageable, it can utilize electricity from a multitude of sources. Prone to use various configurations of heating elements. | It requires high electrical power and insulation. It can cause arcing and sparks and affect the structural integrity of composite materials. | 5–15 | 0.5–1.5 | [19,20,21,22,23] |
| Electromagnetic Actuator | It can prevent and remove ice. It is capable of utilizing electrical power at various frequencies. | It can cause electromagnetic interference. It can affect the durability of the embedded metallic mesh in the material. | 10–30 | 0.1–0.5 | [24,25] |
| Electrohydraulic Actuator | Efficient and cost-effective; it can mechanically remove ice. It has the capability to harness hydraulic power from the engine or alternative sources. | It requires periodic activation and maintenance. It can cause noise and vibrations and affect the quality of the components. | 1–5 | 1–4 | [26] |
| Shape Memory Alloy Actuator | It can mechanically remove ice through shape alteration or torsional motion. It is capable of functioning with direct thermal input or through the Joule effect. | It requires accurate design and calibration. It can cause fatigue issues. It can affect the aerodynamic performance of the surface. | 0.5–2 | 0.5–2 | [27,28] |
| Piezoelectric Actuator | It can mechanically remove ice by generating vibrations or shear waves. It is capable of operating with low electrical power consumption. Prone to use various configurations of vibrating elements. Particularly compliant to full electric aircraft or hybrid aircraft configurations | It can require complex control and actuation systems. It can cause structural damage or cracks. | 1.1–1 | 0.05–0.5 | [29,30] |
| Hydrophobic Coatings | It can prevent ice formation and/or facilitate detachment under aerodynamic loads or in synergy with active systems | It can lose effectiveness over time, due to weathering or other factors | Depends on the composition: from 0.010 to 0.200 kg/m2 | Depends on the type and thickness of the coating: from 0.05 to 0.5 kg/m2 | [31,32] |
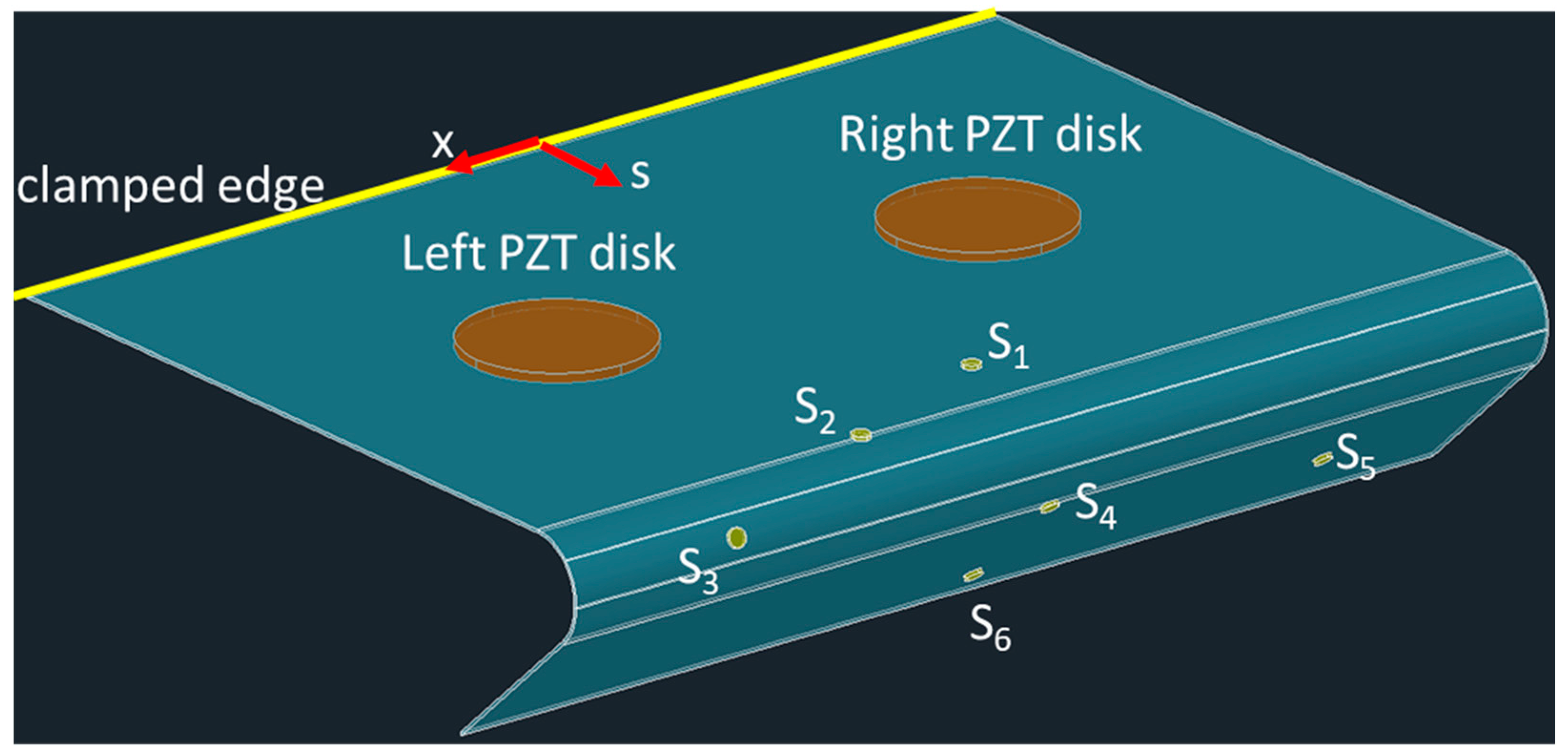
| Item | Curvilinear Abscissa, s (m) | Span Wise Coordinate, x (m) |
|---|---|---|
| Left actuator disk | 0.080 | 0.065 |
| Right actuator disk | 0.080 | −0.065 |
| Sensor S1 | 0.149 | 0 |
| Sensor S2 | 0.161 | 0.065 |
| Sensor S3 | 0.173 | 0.105 |
| Sensor S4 | 0.221 | 0 |
| Sensor S5 | 0.241 | −0.122 |
| Sensor S6 | 0.262 | 0 |
| Main Features of the Protected Element | Environment | De-Icing System | Actuator | Excitation Frequency | Voltage | Phase | Ice | Reference |
|---|---|---|---|---|---|---|---|---|
|
|
| 10 PZTs inner side leading edge placed next to spar and next to the tip | 1 kHz | −250–750 V | The actuators next to the tip are in opposite phase to the ones next to the spar |
| [51] |
| Freezer at temperatures in the range −20 °C, −15 °C | 6 PZTs, 20 × 20 × 1 mm | Sweep (100, 6000) Hz | 200 Vpp | Purified water poured in patches 20 × 20 mm and 2 or 6 mm thick | [60] | ||
| PZT 3.81 cm | Burst 67.5 kHz with 0.55 kHz variation | 24 patches of freezer ice | [61] | ||||
| Plate 154 × 52 × 1.5 mm | Freezer | Analytical and numerical model of fracture propagation | 1 PZT, 50 × 25 × 0.5 mm | 10, 15, and 26 kHz | 2/4 mm glaze ice | [62] | ||
| Clamped Plate 290 × 200 × 1.5 mm | Freezer | Compare different architectures | Langevin PZT |
| 150–180 | 2 mm glaze ice | [63] | |
| Fiberglass plate | Climate chamber | Guided waves for ice detection | 1 PZT | [64] | ||||
|
|
|
|
| Glaze ice | [65] | ||
| Prepreg Plate 175 × 45 × 2 mm | Freezer | PZT | 990 Hz | 10 Vpp | 1.5 mL frozen water | [66] | ||
| Freezer | 650 V | [67] |
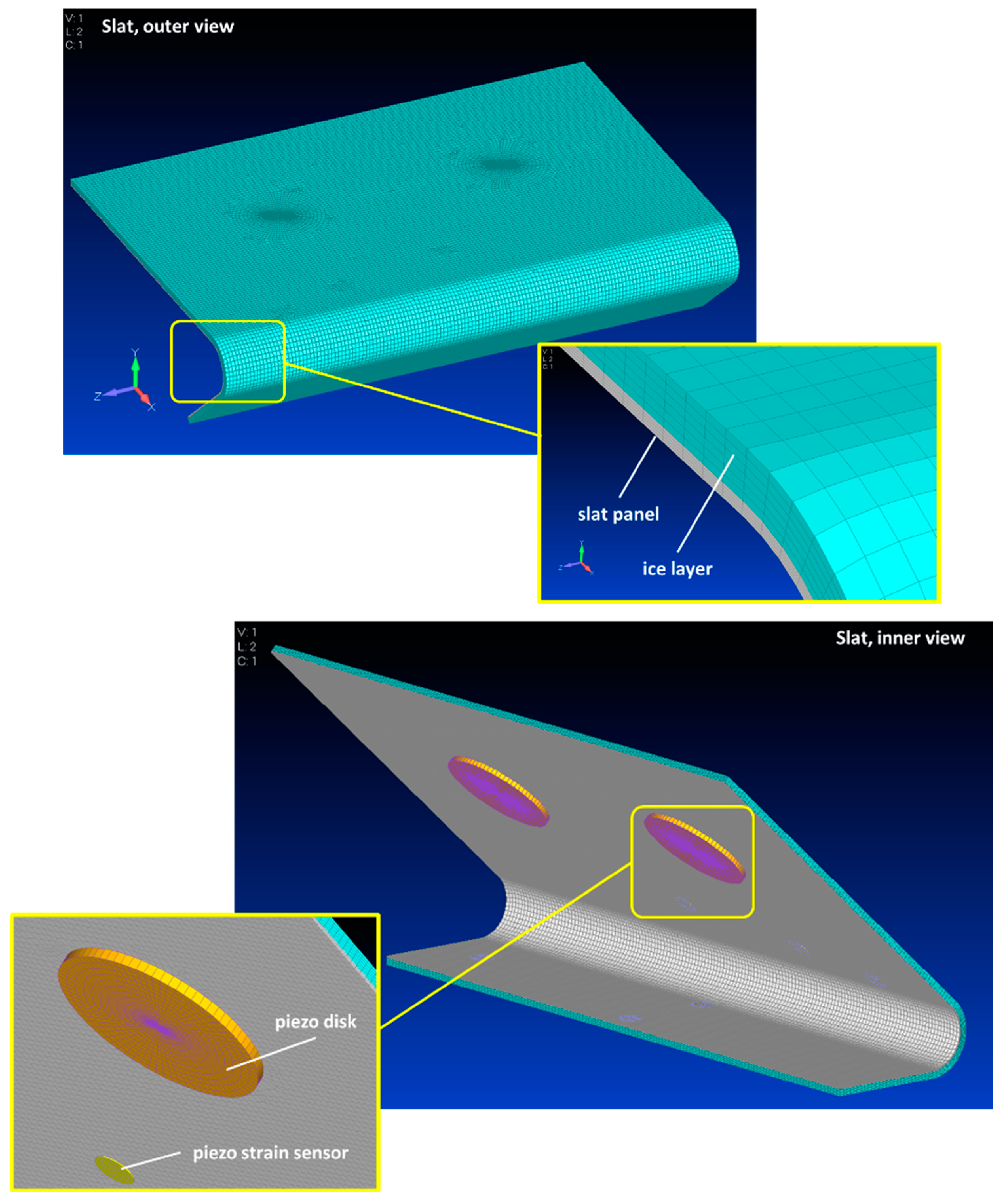
| FE Features | Slat Material | Piezo Actuators | Piezo Sensors |
|---|---|---|---|
| 255,112 solid elements; 624,311 3-dof nodes | Type: 7075 T6 Aluminum alloy; Young’s modulus: 70 GPa; Poisson ratio: 0.32; Density: 2750 kg/m3; | Number: 2 disks | Number: 6 disks |
| Thickness: 0.8 mm | Thickness: 2.5 mm | Thickness: 0.3 mm | |
| Diameter: 50 mm | Diameter: 10 mm | ||
| Piezoelectric characteristics: Table 5 | |||
| Transducer | Type of Material | Young’s Modulus, Poisson Ratio | Density | Piezoelectric Charge Constants | Piezoelectric Voltage Constants |
|---|---|---|---|---|---|
| Actuator disks | Pz26 | YE, 77.0 GPa ν, 0.334 | ρ, 7700 kg/m3 | −1.28 × 10−10 C/N 3.28 × 10−10 C/N | −10.9 × 10−3 Vm/N 28.0 × 10−3 Vm/N |
| Sensor disks | PIC155 | YE, 56.6 GPa ν, 0.334 | ρ, 7800 kg/m3 | −1.65 × 10−10 C/N 3.60 × 10−10 C/N | −12.9 × 10−3 Vm/N 27.0 × 10−3 Vm/N |
| Sensor | Ratio for In-Plane Shear | Ratio for Out-of-Plane Shear |
|---|---|---|
| S1 | 12.77% | 52.01% |
| S2 | 100.62% | 316.89% |
| S3 | 260.01% | 62.32% |
| S4 | - | 8.80% |
| S5 | 31.48% | 13.85% |
| S6 | 3.08% | 0.01% |
| Equipment | Number of Channels | Maximum Output Overload | Max Sample Frequency |
|---|---|---|---|
| PXIe 5423 generator | 2 | 12.0 Vpp | 40.0 MHz |
| PXIe 5105 oscilloscope | 8 | 6.0 V | 60.0 MHz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ameduri, S.; Concilio, A.; Brindisi, A.; Galasso, B. An Ice Protection System Based on Phased Piezoelectric Transducers. Actuators 2024, 13, 158. https://doi.org/10.3390/act13050158
Ameduri S, Concilio A, Brindisi A, Galasso B. An Ice Protection System Based on Phased Piezoelectric Transducers. Actuators. 2024; 13(5):158. https://doi.org/10.3390/act13050158
Chicago/Turabian StyleAmeduri, Salvatore, Antonio Concilio, Angela Brindisi, and Bernardino Galasso. 2024. "An Ice Protection System Based on Phased Piezoelectric Transducers" Actuators 13, no. 5: 158. https://doi.org/10.3390/act13050158
APA StyleAmeduri, S., Concilio, A., Brindisi, A., & Galasso, B. (2024). An Ice Protection System Based on Phased Piezoelectric Transducers. Actuators, 13(5), 158. https://doi.org/10.3390/act13050158








