Dielectric Elastomer-Based Actuators: A Modeling and Control Review for Non-Experts
Abstract
1. Introduction
2. Applications/Configurations of DEAs
2.1. General Application Domains and Functionalities
2.1.1. Application Domains
- DEAs
- DESs
- DEGs
2.1.2. Basic Functionalities
- Movement
- Vibration Suppression
- Transformation (Structure/Property Changes)
- Wave Manipulation
2.1.3. Feedback
2.2. Configurations
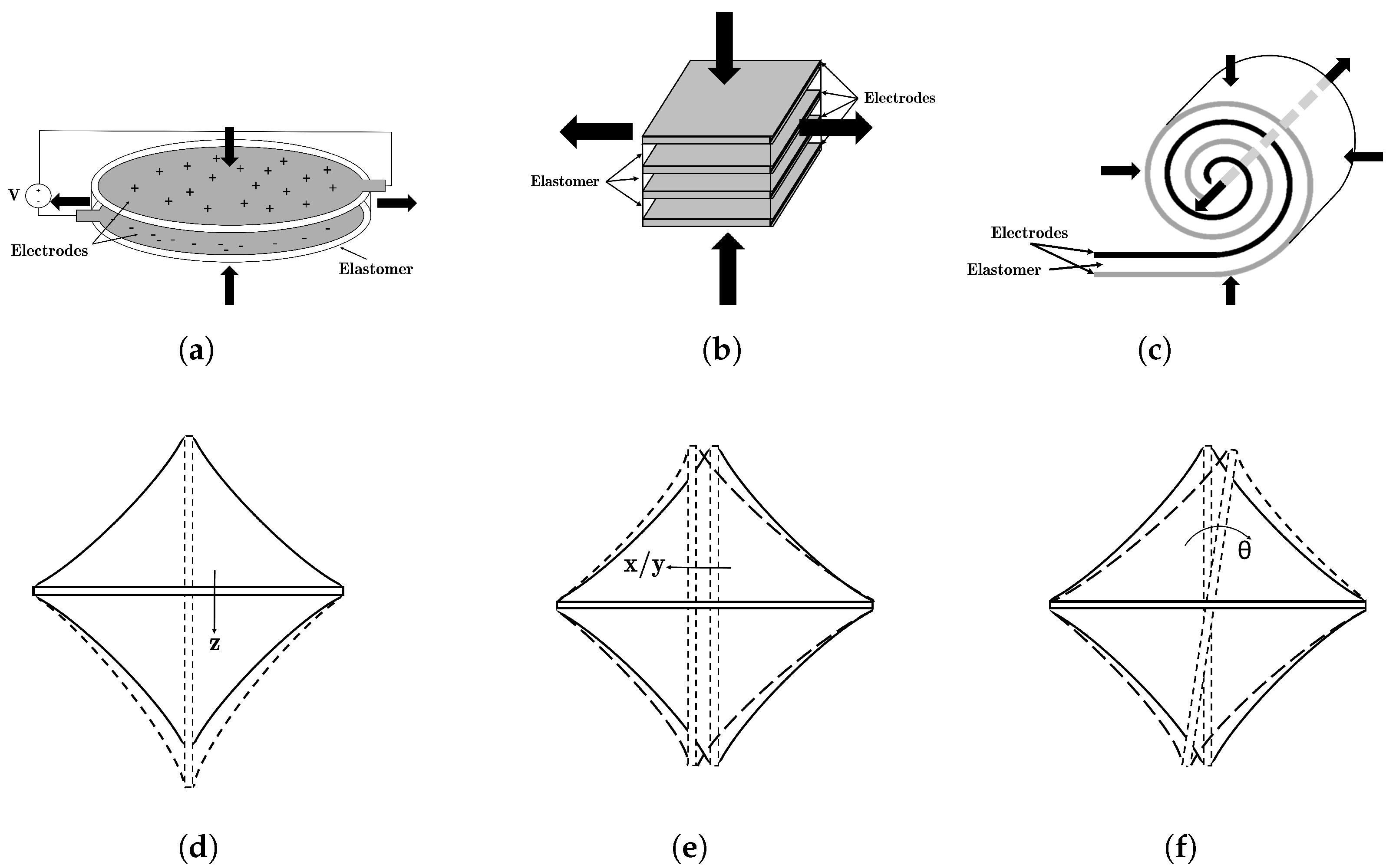
2.2.1. Planar Actuators
2.2.2. Conical Actuators
2.2.3. Complex Structures
2.3. Design Optimization Techniques
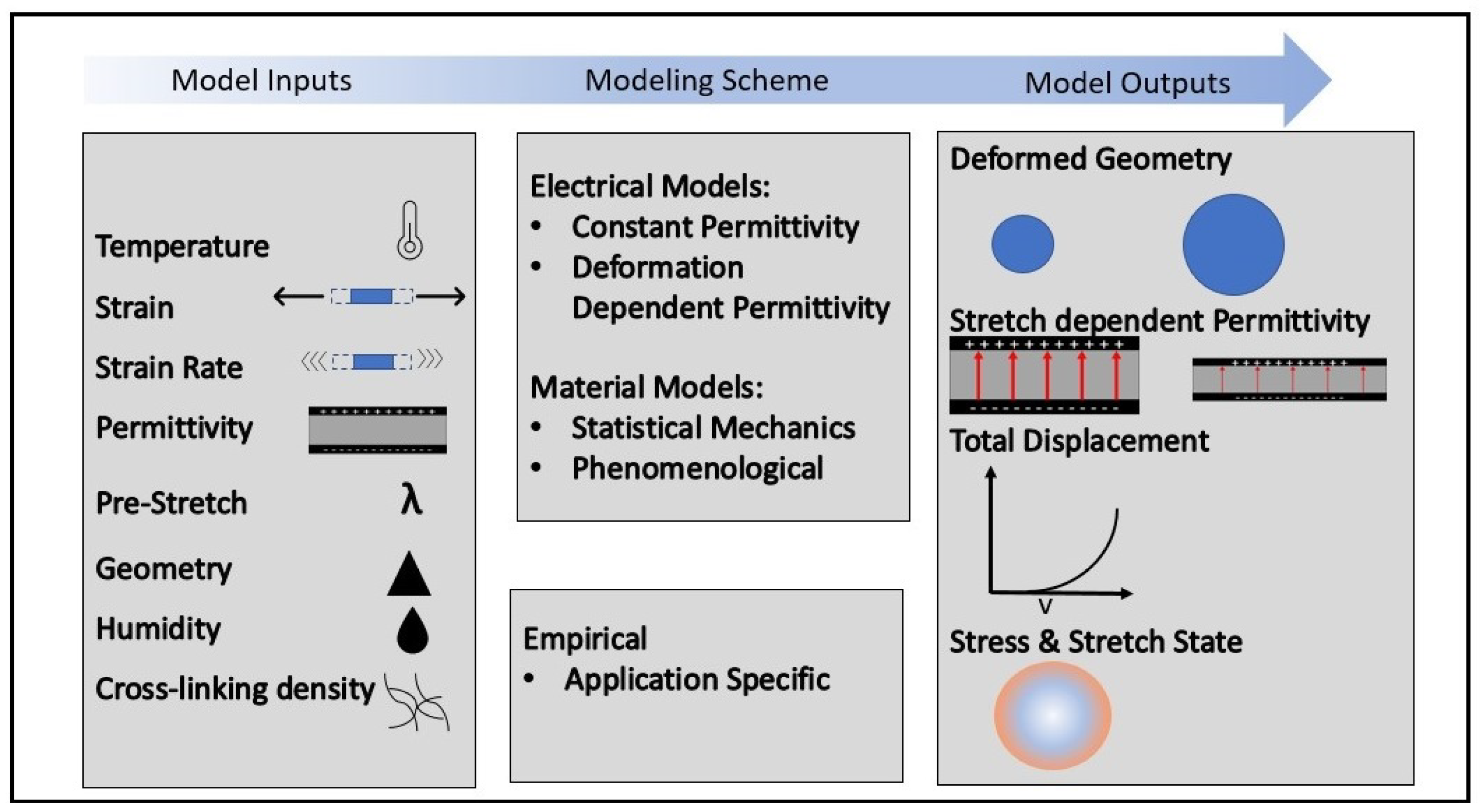
3. Material Models
3.1. Hyperelasticity
- Mooney–Rivlin [119]where denotes material constants found from best-fitting stress–strain data.
- Neo–Hookean [122]where is the small strain shear modulus.
- Ogden [121]where and are material constants determined from best-fitting stress–strain data.
- Gent [13]where represents the limiting stretch in the material.
- Yeoh [120]where are material constants determined by best-fitting stress–strain data.
- Arruda–Boyce [113]where N is the number of unit chains, is the Boltzmann constant, is the absolute temperature, is the inverse Langevin function of , where is the unit chain length, l is the chain length, n is the chain density, and is the limiting stretch of the chain.
- General Constitutive Model [115]where is the initial network modulus and is the entanglement modulus.
- Edwards–Vilgis [114]where , . represents the number of cross-links per volume. represents the number of sliplinks per volume. Finally, and represent the measurement of chain extensibility and average slip displacement, respectively.
- Nonaffine Network [116]where is the maximum stretch of the affine vector.
3.2. Deformation-Dependent Permittivity
3.3. Other Considerations for Material Modeling Include the Effect of Hysteresis
4. Material Limitations and Challenges
4.1. Electro-Mechanical Instabilities
4.2. Wrinkling
4.3. Electrical Breakdown
4.4. Pre-Stretch
4.5. Other Limitations
5. Treatments of Dielectric Elastomers
5.1. Interpenetration
5.2. Treatments to Achieve Self-Healing
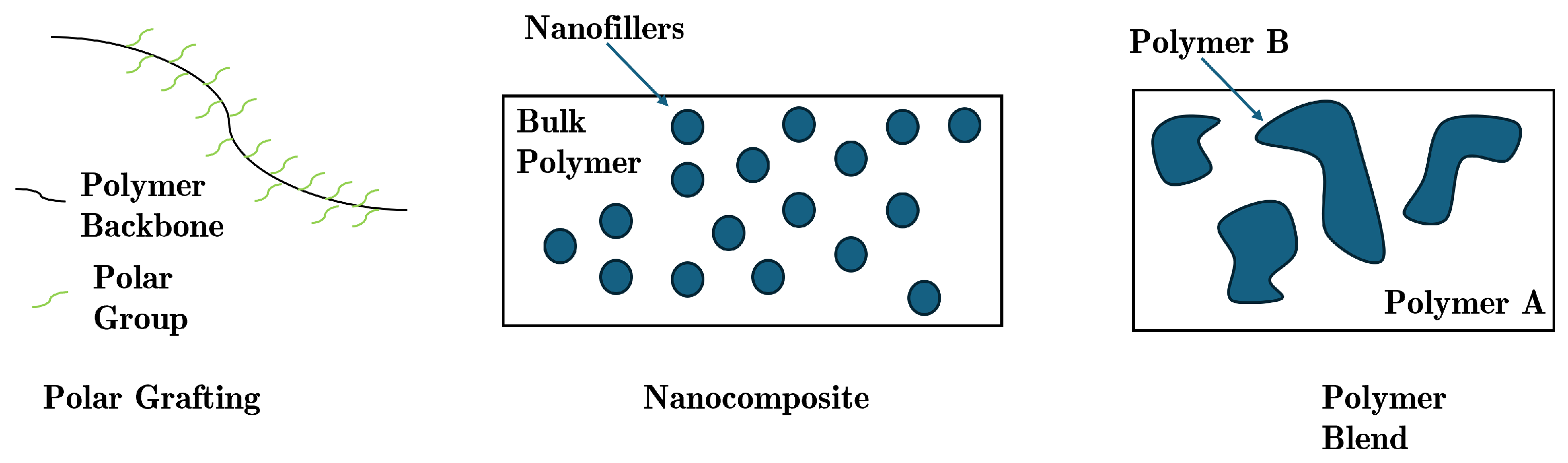
5.3. Addition of Fillers
5.4. Blending with Another Polymer
5.5. Polar Grafting
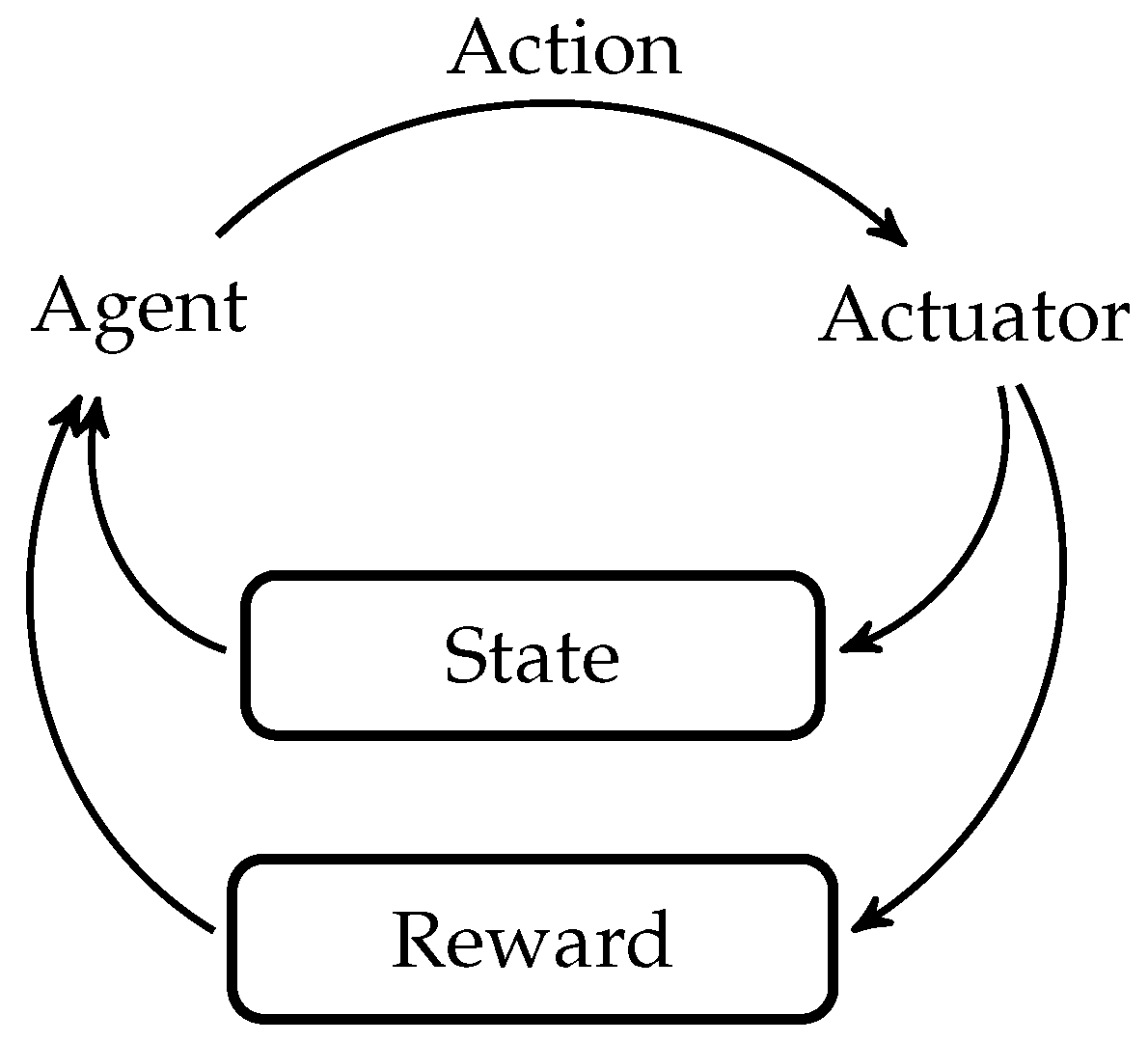
6. Controls
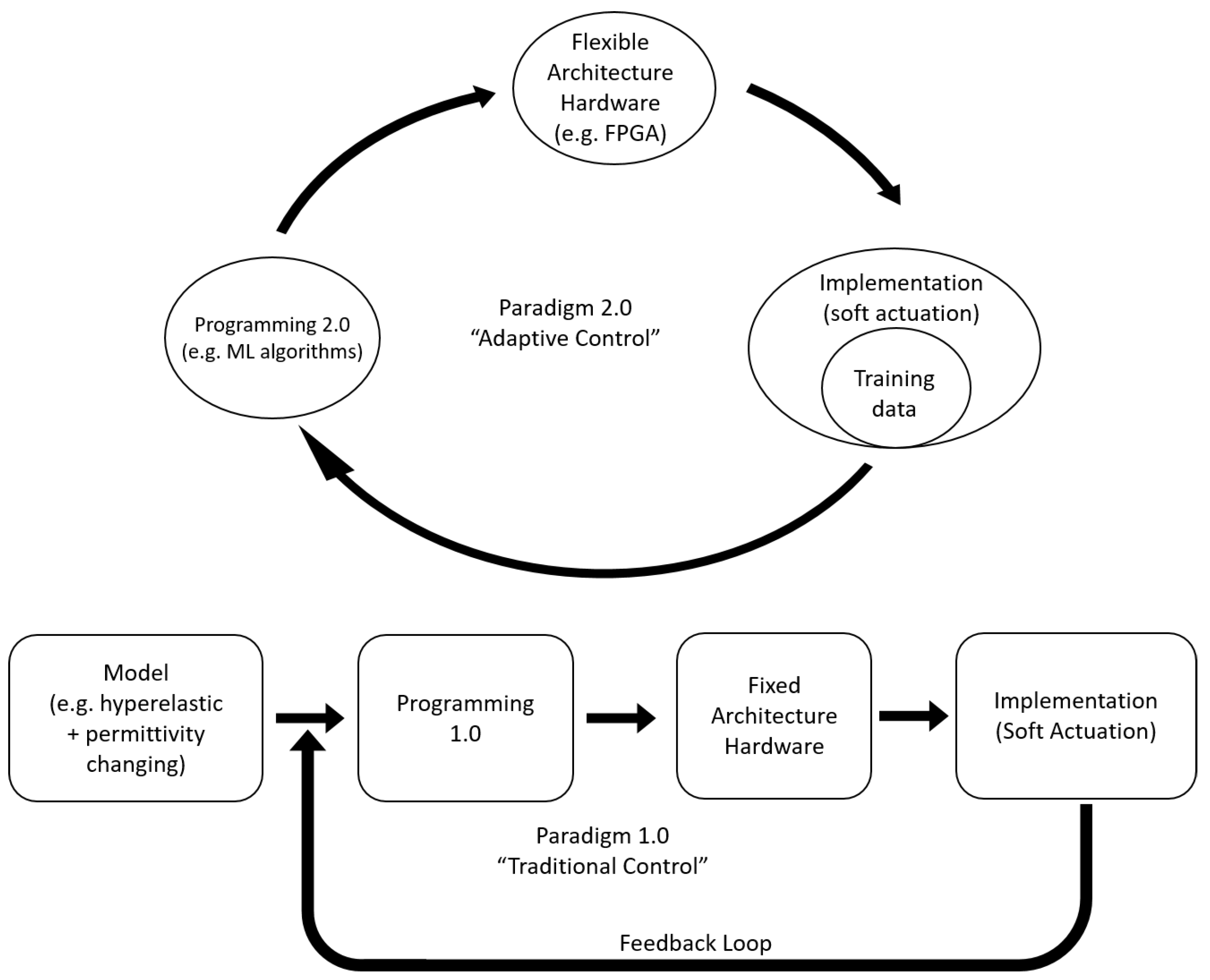
6.1. Traditional Control Techniques
6.2. Modern Control Techniques
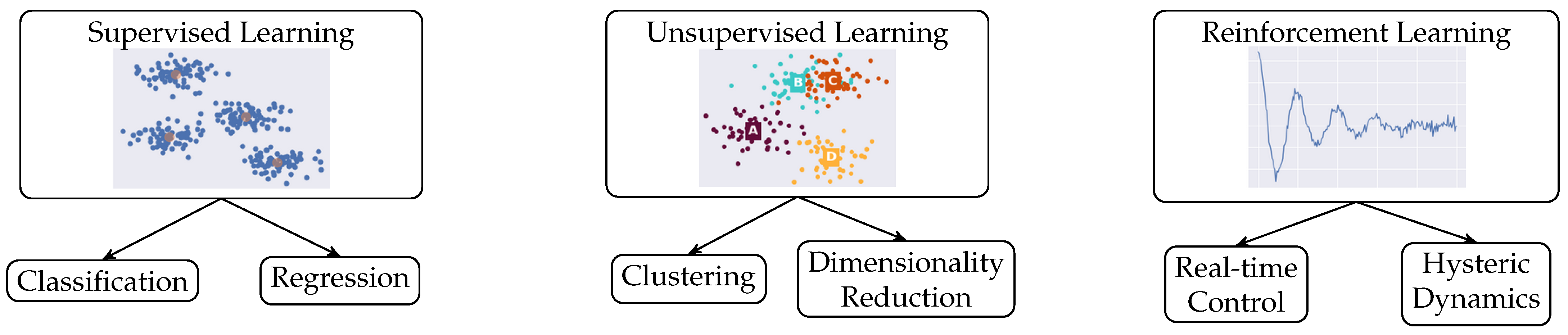
6.2.1. Introduction to Machine Learning
6.2.2. Established Machine Learning for DEA Control
6.2.3. Further Investigations into Machine Learning
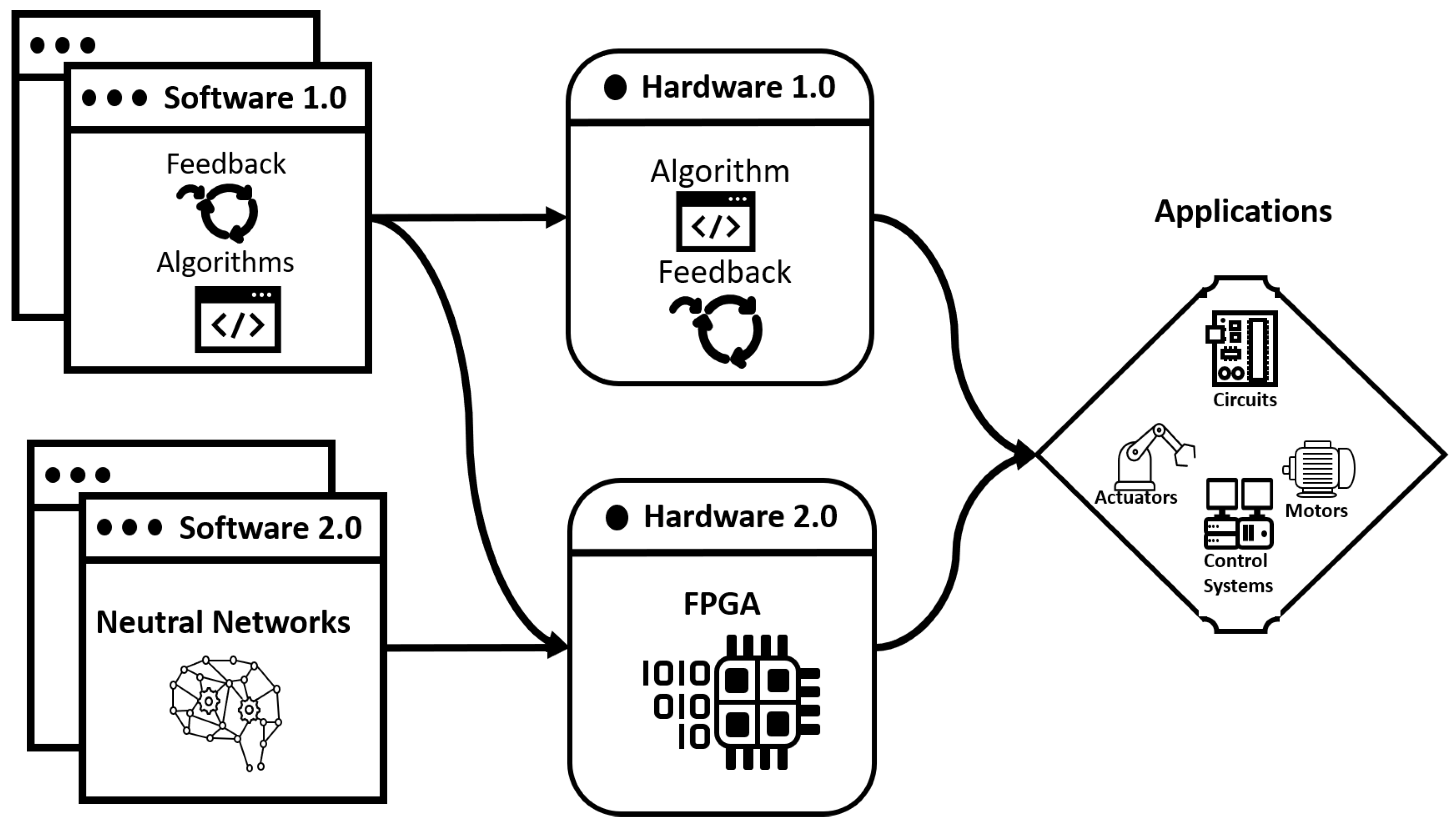
7. Field-Programmable Gate Arrays for Control Applications
7.1. Introduction to FPGAs
7.2. Control Applications with FPGAs
7.3. Implementation
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pfeil, S.; Henke, M.; Katzer, K.; Zimmermann, M.; Gerlach, G. A Worm-Like Biomimetic Crawling Robot Based on Cylindrical Dielectric Elastomer Actuators. Front. Robot. AI 2020, 7, 9. [Google Scholar] [CrossRef] [PubMed]
- Minaminosono, A.; Shigemune, H.; Okuno, Y.; Katsumata, T.; Hosoya, N.; Maeda, S. A deformable motor driven by dielectric elastomer actuators and flexible mechanisms. Front. Robot. AI 2019, 6, 1. [Google Scholar] [CrossRef] [PubMed]
- Christianson, C.; Goldberg, N.N.; Deheyn, D.D.; Cai, S.; Tolley, M.T. Translucent soft robots driven by frameless fluid electrode dielectric elastomer actuators. Sci. Robot. 2018, 3, eaat1893. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, C.T.; Phung, H.; Nguyen, T.D.; Jung, H.; Choi, H.R. Multiple-degrees-of-freedom dielectric elastomer actuators for soft printable hexapod robot. Sens. Actuators A Phys. 2017, 267, 505–516. [Google Scholar] [CrossRef]
- Duduta, M.; Clarke, D.R.; Wood, R.J. A high speed soft robot based on dielectric elastomer actuators. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 4346–4351. [Google Scholar]
- Wang, N.; Guo, H.; Chen, B.; Cui, C.; Zhang, X. Design of dielectric elastomer actuator using topology optimization method based on genetic algorithm. Smart Mater. Struct. 2019, 28, 065013. [Google Scholar] [CrossRef]
- Park, B.J.; Park, S.; Choi, M.; Park, S.K.; Yun, S.; Shin, E.; Yoon, J.W. Monolithic focus-tunable lens technology enabled by disk-type dielectric-elastomer actuators. Sci. Rep. 2020, 10, 16937. [Google Scholar] [CrossRef] [PubMed]
- Hajiesmaili, E.; Clarke, D.R. Reconfigurable shape-morphing dielectric elastomers using spatially varying electric fields. Nat. Commun. 2019, 10, 183. [Google Scholar] [CrossRef]
- Shian, S.; Diebold, R.M.; Clarke, D.R. Tunable lenses using transparent dielectric elastomer actuators. Opt. Express 2013, 21, 8669–8676. [Google Scholar] [CrossRef] [PubMed]
- Nam, S.; Yun, S.; Yoon, J.W.; Park, S.; Park, S.K.; Mun, S.; Park, B.; Kyung, K.U. A robust soft lens for tunable camera application using dielectric elastomer actuators. Soft Robot. 2018, 5, 777–782. [Google Scholar] [CrossRef]
- Daheshpour, K.; Mazlouman, S.J.; Mahanfar, A.; Yun, J.X.; Han, X.; Menon, C.; Carpi, F.; Vaughan, R.G. Pattern reconfigurable antenna based on moving V-shaped parasitic elements actuated by dielectric elastomer. Electron. Lett. 2010, 46, 886–888. [Google Scholar] [CrossRef]
- Mazlouman, S.J.; Soleimani, M.; Mahanfar, A.; Menon, C.; Vaughan, R.G. Pattern reconfigurable square ring patch antenna actuated by hemispherical dielectric elastomer. Electron. Lett. 2011, 47, 164–165. [Google Scholar] [CrossRef]
- Gent, A.N. A new constitutive relation for rubber. Rubber Chem. Technol. 1996, 69, 59–61. [Google Scholar] [CrossRef]
- Treloar, L. The elasticity of a network of long-chain molecules. I. Trans. Faraday Soc. 1943, 39, 36–41. [Google Scholar] [CrossRef]
- Zhao, X.; Koh, S.J.A.; Suo, Z. Nonequilibrium thermodynamics of dielectric elastomers. Int. J. Appl. Mech. 2011, 3, 203–217. [Google Scholar] [CrossRef]
- Xiang, Y.; Zhong, D.; Wang, P.; Yin, T.; Zhou, H.; Yu, H.; Baliga, C.; Qu, S.; Yang, W. A physically based visco-hyperelastic constitutive model for soft materials. J. Mech. Phys. Solids 2019, 128, 208–218. [Google Scholar] [CrossRef]
- Zhang, J.; Ru, J.; Chen, H.; Li, D.; Lu, J. Viscoelastic creep and relaxation of dielectric elastomers characterized by a Kelvin-Voigt-Maxwell model. Appl. Phys. Lett. 2017, 110, 044104. [Google Scholar] [CrossRef]
- Jiménez, S.M.; McMeeking, R.M. Deformation dependent dielectric permittivity and its effect on actuator performance and stability. Int. J. Non-Linear Mech. 2013, 57, 183–191. [Google Scholar] [CrossRef]
- Jiménez, S.M.; McMeeking, R.M. A constitutive law for dielectric elastomers subject to high levels of stretch during combined electrostatic and mechanical loading: Elastomer stiffening and deformation dependent dielectric permittivity. Int. J. Non-Linear Mech. 2016, 87, 125–136. [Google Scholar] [CrossRef]
- Farmer, C.; Medina, H. Effects of electrostriction on the bifurcated electro-mechanical performance of conical dielectric elastomer actuators and sensors. Robotica 2023, 41, 215–235. [Google Scholar] [CrossRef]
- Pu, J.; Meng, Y.; Xie, Z.; Peng, Z.; Wu, J.; Shi, Y.; Plamthottam, R.; Yang, W.; Pei, Q. A unimorph nanocomposite dielectric elastomer for large out-of-plane actuation. Sci. Adv. 2022, 8, eabm6200. [Google Scholar] [CrossRef]
- Wang, Y.; Kim, S.; Li, G.; Sun, L. Filler orientation effect on relative permittivity of dielectric elastomer nanocomposites filled with carbon nanotubes. Comput. Mater. Sci. 2015, 104, 69–75. [Google Scholar] [CrossRef]
- Gu, G.Y.; Gupta, U.; Zhu, J.; Zhu, L.M.; Zhu, X.Y. Feedforward deformation control of a dielectric elastomer actuator based on a nonlinear dynamic model. Appl. Phys. Lett. 2015, 107, 042907. [Google Scholar] [CrossRef]
- Kelley, C.R.; Kauffman, J.L. Tremor suppression controller for dielectric elastomer orthosis. In Proceedings of the Electroactive Polymer Actuators and Devices (EAPAD) XX, Denver, CO, USA, 5–8 March 2018; International Society for Optics and Photonics: Bellingham, WA, USA, 2018; Volume 10594, p. 105940U. [Google Scholar]
- Rizzello, G.; Naso, D.; York, A.; Seelecke, S. Closed loop control of dielectric elastomer actuators based on self-sensing displacement feedback. Smart Mater. Struct. 2016, 25, 035034. [Google Scholar] [CrossRef]
- Jones, R.W.; Sarban, R. Inverse grey-box model-based control of a dielectric elastomer actuator. Smart Mater. Struct. 2012, 21, 075019. [Google Scholar] [CrossRef]
- Hoffstadt, T.; Maas, J. Model-based self-sensing algorithm for dielectric elastomer transducers based on an extended Kalman filter. Mechatronics 2018, 50, 248–258. [Google Scholar] [CrossRef]
- Gu, G.Y.; Zhu, J.; Zhu, L.M.; Zhu, X. A survey on dielectric elastomer actuators for soft robots. Bioinspiration Biomim. 2017, 12, 011003. [Google Scholar] [CrossRef]
- Gupta, U.; Qin, L.; Wang, Y.; Godaba, H.; Zhu, J. Soft robots based on dielectric elastomer actuators: A review. Smart Mater. Struct. 2019, 28, 103002. [Google Scholar] [CrossRef]
- Youn, J.H.; Jeong, S.M.; Hwang, G.; Kim, H.; Hyeon, K.; Park, J.; Kyung, K.U. Dielectric elastomer actuator for soft robotics applications and challenges. Appl. Sci. 2020, 10, 640. [Google Scholar] [CrossRef]
- Wang, J.; Li, S.; Gao, D.; Xiong, J.; Lee, P.S. Reconfigurable and programmable origami dielectric elastomer actuators with 3D shape morphing and emissive architectures. NPG Asia Mater. 2019, 11, 71. [Google Scholar] [CrossRef]
- Ashby, J.; Rosset, S.; Henke, E.F.M.; Anderson, I. Inflatable dielectric elastomer robots for space. In Proceedings of the Electroactive Polymer Actuators and Devices (EAPAD) XXI, Denver, CO, USA, 4–7 March 2019; International Society for Optics and Photonics: Bellingham, WA, USA, 2019; Volume 10966, p. 109661L. [Google Scholar]
- Rossiter, J.; Conn, A.; Cerruto, A.; Winters, A.; Roke, C. Colour gamuts in polychromatic dielectric elastomer artificial chromatophores. In Proceedings of the Electroactive Polymer Actuators and Devices (EAPAD), San Diego, CA, USA, 10–13 March 2014; International Society for Optics and Photonics: Bellingham, WA, USA, 2014; Volume 9056, p. 905620. [Google Scholar]
- Zhao, Y.; Guo, Q.; Wu, S.; Meng, G.; Zhang, W. Design and experimental validation of an annular dielectric elastomer actuator for active vibration isolation. Mech. Syst. Signal Process. 2019, 134, 106367. [Google Scholar] [CrossRef]
- Kornbluh, R.D.; Pelrine, R.; Pei, Q.; Heydt, R.; Stanford, S.; Oh, S.; Eckerle, J. Electroelastomers: Applications of dielectric elastomer transducers for actuation, generation, and smart structures. In Proceedings of the Smart Structures and Materials 2002: Industrial and Commercial Applications of Smart Structures Technologies, San Diego, CA, USA, 18–21 March 2002; International Society for Optics and Photonics: Bellingham, WA, USA, 2002; Volume 4698, pp. 254–270. [Google Scholar]
- Waché, R.; McCarthy, D.N.; Risse, S.; Kofod, G. Rotary motion achieved by new torsional dielectric elastomer actuators design. IEEE/ASME Trans. Mechatron. 2014, 20, 975–977. [Google Scholar] [CrossRef]
- Cao, C.; Burgess, S.; Conn, A.T. Toward a dielectric elastomer resonator driven flapping wing micro air vehicle. Front. Robot. AI 2019, 5, 137. [Google Scholar] [CrossRef] [PubMed]
- Shintake, J.; Cacucciolo, V.; Shea, H.; Floreano, D. Soft biomimetic fish robot made of dielectric elastomer actuators. Soft Robot. 2018, 5, 466–474. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Z.; Shuai, C.; Gao, Y.; Rustighi, E.; An, Y. An application review of dielectric electroactive polymer actuators in acoustics and vibration control. In Proceedings of the Journal of Physics: Conference Series, Indore, India, 13–14 February 2016; Volume 744, p. 012162. [Google Scholar]
- Lin, P.W.; Liu, C.H. Bio-inspired soft proboscis actuator driven by dielectric elastomer fluid transducers. Polymers 2019, 11, 142. [Google Scholar] [CrossRef] [PubMed]
- Christianson, C.; Goldberg, N.N.; Tolley, M.T. Elastomeric diaphragm pump driven by fluid electrode dielectric elastomer actuators (FEDEAs). In Proceedings of the Electroactive Polymer Actuators and Devices (EAPAD) XX, Denver, CO, USA, 5–8 March 2018; International Society for Optics and Photonics: Bellingham, WA, USA, 2018; Volume 10594, p. 105940O. [Google Scholar]
- Cho, K.H.; Kim, Y.; Yang, S.Y.; Kim, K.; Park, J.H.; Rodrigue, H.; Moon, H.; Koo, J.C.; Choi, H.R. Artificial musculoskeletal actuation module driven by twisted and coiled soft actuators. Smart Mater. Struct. 2019, 28, 125010. [Google Scholar] [CrossRef]
- Choi, J.H.; Ahn, J.; Kim, J.B.; Kim, Y.C.; Lee, J.Y.; Oh, I.K. An electroactive, tunable, and frequency selective surface utilizing highly stretchable dielectric elastomer actuators based on functionally antagonistic aperture control. Small 2016, 12, 1840–1846. [Google Scholar] [CrossRef] [PubMed]
- Kubo, M.; Li, X.; Kim, C.; Hashimoto, M.; Wiley, B.J.; Ham, D.; Whitesides, G.M. Stretchable microfluidic radiofrequency antennas. Adv. Mater. 2010, 22, 2749–2752. [Google Scholar] [CrossRef] [PubMed]
- She, A.; Zhang, S.; Shian, S.; Clarke, D.R.; Capasso, F. Large Area Electrically Tunable Lenses Based on Metasurfaces and Dielectric Elastomer Actuators. arXiv 2017, arXiv:1708.01972. [Google Scholar] [CrossRef]
- Aschwanden, M.; Beck, M.; Stemmer, A. Diffractive transmission grating tuned by dielectric elastomer actuator. IEEE Photonics Technol. Lett. 2007, 19, 1090–1092. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, Z.Y.; Zhang, D.W.; Huang, Y.S.; Ni, Z.J.; Zhuang, S.L. Tunable guided-mode resonance filter based on dielectric elastomer actuators. Optik 2014, 125, 1990–1992. [Google Scholar] [CrossRef]
- Lu, Z.; Godaba, H.; Cui, Y.; Foo, C.C.; Debiasi, M.; Zhu, J. An electronically tunable duct silencer using dielectric elastomer actuators. J. Acoust. Soc. Am. 2015, 138, EL236–EL241. [Google Scholar] [CrossRef] [PubMed]
- Jia, K.; Wang, M.; Lu, T.; Zhang, J.; Wang, T. Band-gap tunable dielectric elastomer filter for low frequency noise. Smart Mater. Struct. 2016, 25, 055047. [Google Scholar] [CrossRef]
- Zhang, R.; Lochmatter, P.; Kunz, A.; Kovacs, G.M. Spring roll dielectric elastomer actuators for a portable force feedback glove. In Proceedings of the Smart Structures and Materials 2006: Electroactive Polymer Actuators and Devices (EAPAD), San Diego, CA, USA, 26 February–2 March 2006; International Society for Optics and Photonics: Bellingham, WA, USA, 2006; Volume 6168, p. 61681T. [Google Scholar]
- Opris, D.M.; Molberg, M.; Walder, C.; Ko, Y.S.; Fischer, B.; Nueesch, F.A. New silicone composites for dielectric elastomer actuator applications in competition with acrylic foil. Adv. Funct. Mater. 2011, 21, 3531–3539. [Google Scholar] [CrossRef]
- Kanno, R.; Watanabe, S.; Shimizu, K.; Shintake, J. Self-sensing McKibben artificial muscles embedded with dielectric elastomer sensor. IEEE Robot. Autom. Lett. 2021, 6, 6274–6280. [Google Scholar] [CrossRef]
- Zhu, Y.; Giffney, T.; Aw, K. A dielectric elastomer-based multimodal capacitive sensor. Sensors 2022, 22, 622. [Google Scholar] [CrossRef] [PubMed]
- Nie, B.; Geng, J.; Yao, T.; Miao, Y.; Zhang, Y.; Chen, X.; Liu, J. Sensing arbitrary contact forces with a flexible porous dielectric elastomer. Mater. Horiz. 2021, 8, 962–971. [Google Scholar] [CrossRef]
- Gratz-Kelly, S.; Krüger, T.; Rizzello, G.; Seelecke, S.; Moretti, G. An audio-tactile interface based on dielectric elastomer actuators. Smart Mater. Struct. 2023, 32, 034005. [Google Scholar] [CrossRef]
- Ciarella, L.; Richter, A.; Henke, E.F.M. Integrated logic for dielectric elastomers: Replicating the reflex of the venus flytrap. Adv. Mater. Technol. 2023, 8, 2202000. [Google Scholar] [CrossRef]
- Antillon, D.W.O.; Walker, C.; Rosset, S.; Anderson, I.A. The challenges of hand gesture recognition using dielectric elastomer sensors. In Proceedings of the Electroactive Polymer Actuators and Devices (EAPAD) XXII, Online, 27 April–8 May 2020; SPIE: Bellingham, WA, USA, 2020; Volume 11375, pp. 231–241. [Google Scholar]
- Shrestha, M.; Lu, Z.; Lau, G.K. High humidity sensing by ‘hygromorphic’dielectric elastomer actuator. Sens. Actuators B Chem. 2021, 329, 129268. [Google Scholar] [CrossRef]
- Kornbluh, R.D.; Pelrine, R.; Prahlad, H.; Wong-Foy, A.; McCoy, B.; Kim, S.; Eckerle, J.; Low, T. Dielectric elastomers: Stretching the capabilities of energy harvesting. MRS Bull. 2012, 37, 246. [Google Scholar] [CrossRef]
- Du, X.; Du, L.; Cai, X.; Hao, Z.; Xie, X.; Wu, F. Dielectric elastomer wave energy harvester with self-bias voltage of an ancillary wind generator to power for intelligent buoys. Energy Convers. Manag. 2022, 253, 115178. [Google Scholar] [CrossRef]
- Zhang, C.; Lai, Z.; Zhang, G.; Yurchenko, D. Energy harvesting from a dynamic vibro-impact dielectric elastomer generator subjected to rotational excitations. Nonlinear Dyn. 2020, 102, 1271–1284. [Google Scholar] [CrossRef]
- Zhang, C.; Lai, Z.; Li, M.; Yurchenko, D. Wind energy harvesting from a conventional turbine structure with an embedded vibro-impact dielectric elastomer generator. J. Sound Vib. 2020, 487, 115616. [Google Scholar] [CrossRef]
- Vertechy, R.; Papini Rosati, G.P.; Fontana, M. Reduced model and application of inflating circular diaphragm dielectric elastomer generators for wave energy harvesting. J. Vib. Acoust. 2015, 137, 011004. [Google Scholar] [CrossRef]
- Zhang, J.; Lai, Z.; Rao, X.; Zhang, C. Harvest rotational energy from a novel dielectric elastomer generator with crank-connecting rod mechanisms. Smart Mater. Struct. 2020, 29, 065005. [Google Scholar] [CrossRef]
- Vertechy, R.; Fontana, M.; Papini, G.R.; Bergamasco, M. Oscillating-water-column wave-energy-converter based on dielectric elastomer generator. In Proceedings of the Electroactive Polymer Actuators and Devices (EAPAD), San Diego, CA, USA, 10–14 March 2013; International Society for Optics and Photonics: Bellingham, WA, USA, 2013; Volume 8687, p. 86870I. [Google Scholar]
- Lai, H.; Reid, K. Investigation of dielectric elastomer human energy harvesting to reduce knee joint torque deviation due to bracing. J. Rehabil. Assist. Technol. Eng. 2019, 6, 1–9. [Google Scholar] [CrossRef]
- Moretti, G.; Rosset, S.; Vertechy, R.; Anderson, I.; Fontana, M. A review of dielectric elastomer generator systems. Adv. Intell. Syst. 2020, 2, 2000125. [Google Scholar] [CrossRef]
- Brochu, P.; Pei, Q. Dielectric elastomers for actuators and artificial muscles. In Electroactivity in Polymeric Materials; Rasmussen, L., Ed.; Springer: Boston, MA, USA, 2012; pp. 1–56. [Google Scholar] [CrossRef]
- Jiaxin, Z.; Weiping, Z.; Chenyang, W.; Yang, Z.; Jiahao, W. Current status of insect-inspired flapping wing micro air vehicles. In Proceedings of the 2019 IEEE International Conference on Unmanned Systems (ICUS), Beijing, China, 17–19 October 2019; pp. 894–898. [Google Scholar]
- Pelrine, R.; Kornbluh, R.D.; Pei, Q.; Stanford, S.; Oh, S.; Eckerle, J.; Full, R.J.; Rosenthal, M.A.; Meijer, K. Dielectric elastomer artificial muscle actuators: Toward biomimetic motion. In Proceedings of the Smart Structures and Materials 2002: Electroactive Polymer Actuators and Devices (EAPAD), San Diego, CA, USA, 17–21 March 2002; International Society for Optics and Photonics: Bellingham, WA, USA, 2002; Volume 4695, pp. 126–137. [Google Scholar]
- Anderson, I.A.; Calius, E.P.; Gisby, T.; Hale, T.; McKay, T.; O’Brien, B.; Walbran, S. A dielectric elastomer actuator thin membrane rotary motor. In Proceedings of the Electroactive Polymer Actuators and Devices (EAPAD), San Diego, CA, USA, 8–12 March 2009; International Society for Optics and Photonics: Bellingham, WA, USA, 2009; Volume 7287, pp. 470–479. [Google Scholar] [CrossRef]
- Sarban, R.; Jones, R.; Mace, B.; Rustighi, E. A tubular dielectric elastomer actuator: Fabrication, characterization and active vibration isolation. Mech. Syst. Signal Process. 2011, 25, 2879–2891. [Google Scholar] [CrossRef]
- Kajiwara, I.; Kitabatake, S.; Hosoya, N.; Maeda, S. Design of dielectric elastomer actuators for vibration control at high frequencies. Int. J. Mech. Sci. 2019, 157, 849–857. [Google Scholar] [CrossRef]
- Sarban, R.; Jones, R.W. Physical model-based active vibration control using a dielectric elastomer actuator. J. Intell. Mater. Syst. Struct. 2012, 23, 473–483. [Google Scholar] [CrossRef]
- Sarban, R.; Jones, R.W. Electromechanical model-based vibration isolation using a dielectric elastomer actuator. In Proceedings of the 2011 IEEE International Conference on Mechatronics, Istanbul, Turkey, 13–15 April 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 603–608. [Google Scholar]
- Kelley, C.R.; Kauffman, J.L. Tremor-active controller for dielectric elastomer-based pathological tremor suppression. IEEE/ASME Trans. Mechatron. 2020, 25, 1143–1148. [Google Scholar] [CrossRef]
- Kelley, C.R.; Kauffman, J.L. Necessary dielectric elastomer parameters for wearable tremor suppression. In Proceedings of the Electroactive Polymer Actuators and Devices (EAPAD) XXI, Denver, CO, USA, 4–7 March 2019; SPIE: Bellingham, WA, USA, 2019; Volume 10966, pp. 250–260. [Google Scholar]
- Aksoy, B.; Shea, H. Reconfigurable and latchable shape-morphing dielectric elastomers based on local stiffness modulation. Adv. Funct. Mater. 2020, 30, 2001597. [Google Scholar] [CrossRef]
- Li, Y.; Gong, Z.; Zhang, T. Design Method of Minimum Energy Structural Dielectric Elastomer Actuators for Origami Robots. In Proceedings of the 2022 IEEE International Conference on Mechatronics and Automation (ICMA), Guilin, China, 7–10 August 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 675–679. [Google Scholar]
- Yin, X.; Zhou, P.; Wen, S.; Zhang, J. Origami Improved Dielectric Elastomer Actuation for Tunable Lens. IEEE Trans. Instrum. Meas. 2022, 71, 1–9. [Google Scholar] [CrossRef]
- Zhao, P.; Cai, Y.; Liu, C.; Ge, D.; Li, B.; Chen, H. Study on the bio-inspired electrochromic device enabled via dielectric elastomer actuator. Opt. Mater. 2021, 111, 110569. [Google Scholar] [CrossRef]
- Xiao, M.; Mao, J.; Kollosche, M.; Hwang, V.; Clarke, D.R.; Manoharan, V.N. Voltage-tunable elastomer composites that use shape instabilities for rapid structural color changes. Mater. Horiz. 2022, 9, 1954–1961. [Google Scholar] [CrossRef] [PubMed]
- Bauer, S.; Bauer-Gogonea, S.; Graz, I.; Kaltenbrunner, M.; Keplinger, C.; Schwödiauer, R. 25th anniversary article: A soft future: From robots and sensor skin to energy harvesters. Adv. Mater. 2014, 26, 149–162. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Wang, Y.; Gupta, U.; Liu, J.; Zhang, L.; Du, D.; Foo, C.C.; Ouyang, J.; Zhu, J. Transparent soft robots for effective camouflage. Adv. Funct. Mater. 2019, 29, 1901908. [Google Scholar] [CrossRef]
- Christodoulou, C.G.; Tawk, Y.; Lane, S.A.; Erwin, S.R. Reconfigurable antennas for wireless and space applications. Proc. IEEE 2012, 100, 2250–2261. [Google Scholar] [CrossRef]
- Jiang, X.J.; Mazlouman, S.J.; Mahanfar, A.; Vaughan, R.G.; Menon, C. DEA deformed stretchable patch antenna. Smart Mater. Struct. 2012, 21, 055020. [Google Scholar] [CrossRef]
- Saghlatoon, H.; Honari, M.M.; Mirzavand, R.; Mousavi, P.; Kumar, A.; La, T.G.; Chung, H.J. A novel investigation on printed stretchable WLAN antennas. In Proceedings of the 2017 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, San Diego, CA, USA, 9–14 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 2537–2538. [Google Scholar]
- Pang, W.; Cheng, X.; Zhao, H.; Guo, X.; Ji, Z.; Li, G.; Liang, Y.; Xue, Z.; Song, H.; Zhang, F.; et al. Electro-mechanically controlled assembly of reconfigurable 3D mesostructures and electronic devices based on dielectric elastomer platforms. Natl. Sci. Rev. 2020, 7, 342–354. [Google Scholar] [CrossRef]
- Yu, N.; Genevet, P.; Kats, M.A.; Aieta, F.; Tetienne, J.P.; Capasso, F.; Gaburro, Z. Light propagation with phase discontinuities: Generalized laws of reflection and refraction. Science 2011, 334, 333–337. [Google Scholar] [CrossRef] [PubMed]
- Landgraf, M.; Zorell, U.; Wetzel, T.; Reitelshofer, S.; Yoo, I.S.; Franke, J. Dielectric elastomer actuators as self-sensing devices: A new method of superimposing actuating and sensing signals. In Proceedings of the Electroactive Polymer Actuators and Devices (EAPAD), San Diego, CA, USA, 1 April 2015; Bar-Cohen, Y., Ed.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2015; Volume 9430, pp. 272–280. [Google Scholar] [CrossRef]
- Huang, P.; Wu, J.; Meng, Q.; Wang, Y.; Su, C.Y. Self-Sensing Motion Control of Dielectric Elastomer Actuator Based on NARX Neural Network and Iterative Learning Control Architecture. In IEEE/ASME Transactions on Mechatronics; IEEE: Piscataway, NJ, USA, 2023; pp. 1–11. [Google Scholar] [CrossRef]
- Chortos, A.; Hajiesmaili, E.; Morales, J.; Clarke, D.R.; Lewis, J.A. 3D Printing of Interdigitated Dielectric Elastomer Actuators. Adv. Funct. Mater. 2020, 30, 1907375. [Google Scholar] [CrossRef]
- Zou, J.; Gu, G. Dynamic modeling of dielectric elastomer actuators with a minimum energy structure. Smart Mater. Struct. 2019, 28, 085039. [Google Scholar] [CrossRef]
- Li, W.B.; Zhang, W.M.; Gao, Q.H.; Guo, Q.W.; Wu, S.; Zou, H.X.; Yan, H.; Peng, Z.K.; Meng, G. Electrostatic field induced coupling actuation mechanism for dielectric elastomer actuators. Extrem. Mech. Lett. 2020, 35, 100638. [Google Scholar] [CrossRef]
- Jia, K.; Lu, T.; Wang, T. Deformation study of an in-plane oscillating dielectric elastomer actuator having complex modes. J. Sound Vib. 2019, 463, 114940. [Google Scholar] [CrossRef]
- Medina, H.; Farmer, C.W. Improved Model for Conical Dielectric Elastomer Actuators with Fewer Electrical Connections. J. Mech. Robot. 2020, 12, 031016. [Google Scholar] [CrossRef]
- Farmer, C.; Medina, H. Dimensionless parameter-based numerical model for double conical dielectric elastomer actuators. Eng. Res. Express 2020, 2, 035020. [Google Scholar] [CrossRef]
- He, T.; Zhao, X.; Suo, Z. Dielectric elastomer membranes undergoing inhomogeneous deformation. J. Appl. Phys. 2009, 106, 083522. [Google Scholar] [CrossRef]
- Cao, C.; Gao, X.; Burgess, S.; Conn, A.T. Power optimization of a conical dielectric elastomer actuator for resonant robotic systems. Extrem. Mech. Lett. 2020, 35, 100619. [Google Scholar] [CrossRef]
- Xue, J.; Du, Y.; Zhao, W.; Gao, X. A Modular Crawling Robot Driven by A Single-layer Conical Dielectric Elastomer. In Proceedings of the 2022 IEEE International Conference on Robotics and Biomimetics (ROBIO), Jinghong, China, 5–9 December 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 783–788. [Google Scholar]
- Cao, C.; Hill, T.L.; Li, B.; Wang, L.; Gao, X. Nonlinear dynamics of a conical dielectric elastomer oscillator with switchable mono to bi-stability. Int. J. Solids Struct. 2021, 221, 18–30. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, J.; Huang, P.; Su, C.Y.; Wang, Y. Inverse dynamics modelling and tracking control of conical dielectric elastomer actuator based on GRU neural network. Eng. Appl. Artif. Intell. 2023, 118, 105668. [Google Scholar] [CrossRef]
- Mulembo, T.; Njeri, W.; Nagai, G.; Tamagawa, H.; Naito, K.; Nitta, T.; Sasaki, M. Linear-Quadratic Regulator for Control of Multi-Wall Carbon Nanotube/Polydimethylsiloxane Based Conical Dielectric Elastomer Actuators. Actuators 2020, 9, 18. [Google Scholar] [CrossRef]
- Zou, J.; Gu, G. Feedforward control of the rate-dependent viscoelastic hysteresis nonlinearity in dielectric elastomer actuators. IEEE Robot. Autom. Lett. 2019, 4, 2340–2347. [Google Scholar] [CrossRef]
- Sun, W.; Liu, F.; Ma, Z.; Li, C.; Zhou, J. Soft mobile robots driven by foldable dielectric elastomer actuators. J. Appl. Phys. 2016, 120, 084901. [Google Scholar] [CrossRef]
- Timmer, J.; Häußler, S.; Lauk, M.; Lücking, C.H. Pathological tremors: Deterministic chaos or nonlinear stochastic oscillators? Chaos Interdiscip. J. Nonlinear Sci. 2000, 10, 278–288. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Yan, Z.; Luo, K.; Tian, Q. Optimal design of electrode topology of dielectric elastomer actuators based on the parameterized level set method. Soft Robot. 2023, 10, 106–118. [Google Scholar] [CrossRef] [PubMed]
- Chen, F.; Liu, K.; Wang, Y.; Zou, J.; Gu, G.; Zhu, X. Automatic design of soft dielectric elastomer actuators with optimal spatial electric fields. IEEE Trans. Robot. 2019, 35, 1150–1165. [Google Scholar] [CrossRef]
- Wang, N.; Guo, H.; Chen, B.; Cui, C.; Zhang, X. Integrated design of actuation and mechanism of dielectric elastomers using topology optimization based on fat Bezier curves. Soft Robot. 2019, 6, 644–656. [Google Scholar] [CrossRef]
- Zhao, X.; Suo, Z. Method to analyze programmable deformation of dielectric elastomer layers. Appl. Phys. Lett. 2008, 93, 251902. [Google Scholar] [CrossRef]
- Garnell, E.; Aksoy, B.; Rouby, C.; Shea, H.; Doaré, O. Geometric optimization of dielectric elastomer electrodes for dynamic applications. Appl. Acoust. 2021, 181, 108120. [Google Scholar] [CrossRef]
- Nalbach, S.; Banda, R.M.; Croce, S.; Rizzello, G.; Naso, D.; Seelecke, S. Modeling and design optimization of a rotational soft robotic system driven by double cone dielectric elastomer actuators. Front. Robot. AI 2020, 6, 150. [Google Scholar] [CrossRef]
- Arruda, E.M.; Boyce, M.C. A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials. J. Mech. Phys. Solids 1993, 41, 389–412. [Google Scholar] [CrossRef]
- Edwards, S.; Vilgis, T. The effect of entanglements in rubber elasticity. Polymer 1986, 27, 483–492. [Google Scholar] [CrossRef]
- Xiang, Y.; Zhong, D.; Wang, P.; Mao, G.; Yu, H.; Qu, S. A general constitutive model of soft elastomers. J. Mech. Phys. Solids 2018, 117, 110–122. [Google Scholar] [CrossRef]
- Davidson, J.D.; Goulbourne, N.C. A nonaffine network model for elastomers undergoing finite deformations. J. Mech. Phys. Solids 2013, 61, 1784–1797. [Google Scholar] [CrossRef]
- Rivlin, R. Large elastic deformations of isotropic materials. I. Fundamental concepts. Philos. Trans. R. Soc. Lond. Ser. A 1948, 240, 459–490. [Google Scholar]
- Rivlin, R. Large elastic deformations of isotropic materials IV. Further developments of the general theory. Philos. Trans. R. Soc. Lond. Ser. A 1948, 241, 379–397. [Google Scholar]
- Mooney, M. A theory of large elastic deformation. J. Appl. Phys. 1940, 11, 582–592. [Google Scholar] [CrossRef]
- Yeoh, O.H. Some forms of the strain energy function for rubber. Rubber Chem. Technol. 1993, 66, 754–771. [Google Scholar] [CrossRef]
- Ogden, R.W. Large deformation isotropic elasticity–on the correlation of theory and experiment for incompressible rubberlike solids. Proc. R. Soc. Lond. A 1972, 326, 565–584. [Google Scholar] [CrossRef]
- Treloar, L. Stress-strain data for vulcanized rubber under various types of deformation. Rubber Chem. Technol. 1944, 17, 813–825. [Google Scholar] [CrossRef]
- Farmer, C.; Medina, H. Hyperelastics.jl: A Julia package for hyperelastic material modelling with a large collection of models. J. Open Source Softw. 2024, 9, 6314. [Google Scholar] [CrossRef]
- Suo, Z. Theory of dielectric elastomers. Acta Mech. Solida Sin. 2010, 23, 549–578. [Google Scholar] [CrossRef]
- Di Lillo, L.; Schmidt, A.; Carnelli, D.A.; Ermanni, P.; Kovacs, G.; Mazza, E.; Bergamini, A. Measurement of insulating and dielectric properties of acrylic elastomer membranes at high electric fields. J. Appl. Phys. 2012, 111, 024904. [Google Scholar] [CrossRef]
- Wissler, M.; Mazza, E. Electromechanical coupling in dielectric elastomer actuators. Sens. Actuators A Phys. 2007, 138, 384–393. [Google Scholar] [CrossRef]
- Jean-Mistral, C.; Sylvestre, A.; Basrour, S.; Chaillout, J. Dielectric properties of polyacrylate thick films used in sensors and actuators. Smart Mater. Struct. 2010, 19, 075019. [Google Scholar] [CrossRef]
- Tröls, A.; Kogler, A.; Baumgartner, R.; Kaltseis, R.; Keplinger, C.; Schwödiauer, R.; Graz, I.; Bauer, S. Stretch dependence of the electrical breakdown strength and dielectric constant of dielectric elastomers. Smart Mater. Struct. 2013, 22, 104012. [Google Scholar] [CrossRef]
- Kuhn, W.; Grün, F. Beziehungen zwischen elastischen Konstanten und Dehnungsdoppelbrechung hochelastischer Stoffe. Kolloid Z. 1942, 101, 248–271. [Google Scholar] [CrossRef]
- Sheng, J.; Chen, H.; Li, B.; Wang, Y. Influence of the temperature and deformation-dependent dielectric constant on the stability of dielectric elastomers. J. Appl. Polym. Sci. 2013, 128, 2402–2407. [Google Scholar] [CrossRef]
- Brokate, M.; Sprekels, J. Hysteresis and Phase Transitions; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 121. [Google Scholar]
- Khurana, A.; Kumar, A.; Raut, S.K.; Sharma, A.K.; Joglekar, M.M. Effect of viscoelasticity on the nonlinear dynamic behavior of dielectric elastomer minimum energy structures. Int. J. Solids Struct. 2021, 208, 141–153. [Google Scholar] [CrossRef]
- Alibakhshi, A.; Heidari, H. Nonlinear dynamics of dielectric elastomer balloons based on the Gent-Gent hyperelastic model. Eur. J. Mech. -A/Solids 2020, 82, 103986. [Google Scholar] [CrossRef]
- Chen, Y.; Kang, G.; Yuan, J.; Hu, Y.; Li, T.; Qu, S. An electro-mechanically coupled visco-hyperelastic-plastic constitutive model for cyclic deformation of dielectric elastomers. Mech. Mater. 2020, 150, 103575. [Google Scholar] [CrossRef]
- Alibakhshi, A.; Chen, W.; Destrade, M. Nonlinear vibration and stability of a dielectric elastomer balloon based on a strain-stiffening model. J. Elast. 2023, 153, 533–548. [Google Scholar] [CrossRef]
- Chiang Foo, C.; Cai, S.; Jin Adrian Koh, S.; Bauer, S.; Suo, Z. Model of dissipative dielectric elastomers. J. Appl. Phys. 2012, 111, 034102. [Google Scholar] [CrossRef]
- Zhao, X.; Hong, W.; Suo, Z. Electromechanical hysteresis and coexistent states in dielectric elastomers. Phys. Rev. B 2007, 76, 134113. [Google Scholar] [CrossRef]
- Amin, A.; Lion, A.; Sekita, S.; Okui, Y. Nonlinear dependence of viscosity in modeling the rate-dependent response of natural and high damping rubbers in compression and shear: Experimental identification and numerical verification. Int. J. Plast. 2006, 22, 1610–1657. [Google Scholar] [CrossRef]
- Rey, T.; Chagnon, G.; Le Cam, J.B.; Favier, D. Influence of the temperature on the mechanical behaviour of filled and unfilled silicone rubbers. Polym. Test. 2013, 32, 492–501. [Google Scholar] [CrossRef]
- Bergström, J.S.; Boyce, M.C. Constitutive modeling of the large strain time-dependent behavior of elastomers. J. Mech. Phys. Solids 1998, 46, 931–954. [Google Scholar] [CrossRef]
- Lion, A. On the large deformation behaviour of reinforced rubber at different temperatures. J. Mech. Phys. Solids 1997, 45, 1805–1834. [Google Scholar] [CrossRef]
- Lion, A. Constitutive modelling in finite thermoviscoplasticity: A physical approach based on nonlinear rheological models. Int. J. Plast. 2000, 16, 469–494. [Google Scholar] [CrossRef]
- Lion, A. Thixotropic behaviour of rubber under dynamic loading histories: Experiments and theory. J. Mech. Phys. Solids 1998, 46, 895–930. [Google Scholar] [CrossRef]
- Miehe, C.; Keck, J. Superimposed finite elastic–viscoelastic–plastoelastic stress response with damage in filled rubbery polymers. Experiments, modelling and algorithmic implementation. J. Mech. Phys. Solids 2000, 48, 323–365. [Google Scholar] [CrossRef]
- Guélin, P. Remarques sur L’hysteresis Mecanique. Les Bases d’un Schema Thermomecanique a Structure Hereditaire. J. Mec. 1980, 19, 217–247. [Google Scholar]
- Krempl, E.; Khan, F. Rate (time)-dependent deformation behavior: An overview of some properties of metals and solid polymers. Int. J. Plast. 2003, 19, 1069–1095. [Google Scholar] [CrossRef]
- Laiarinandrasana, L.; Piques, R.; Robisson, A. Visco-hyperelastic model with internal state variable coupled with discontinuous damage concept under total Lagrangian formulation. Int. J. Plast. 2003, 19, 977–1000. [Google Scholar] [CrossRef]
- Haupt, P.; Sedlan, K. Viscoplasticity of elastomeric materials: Experimental facts and constitutive modelling. Arch. Appl. Mech. 2001, 71, 89–109. [Google Scholar] [CrossRef]
- Hasanpour, K.; Ziaei-Rad, S.; Mahzoon, M. A large deformation framework for compressible viscoelastic materials: Constitutive equations and finite element implementation. Int. J. Plast. 2009, 25, 1154–1176. [Google Scholar] [CrossRef]
- Kilian, H.; Strauss, M.; Hamm, W. Universal properties in filler-loaded rubbers. Rubber Chem. Technol. 1994, 67, 1–16. [Google Scholar] [CrossRef]
- Mathew, A.T.; Vo, T.V.K.; Koh, S.J.A. A molecular perspective to analytical modeling that reveals new instabilities in dielectric elastomer transducers. J. Mech. Phys. Solids 2019, 132, 103703. [Google Scholar] [CrossRef]
- Li, B.; Chen, H.; Qiang, J.; Hu, S.; Zhu, Z.; Wang, Y. Effect of mechanical pre-stretch on the stabilization of dielectric elastomer actuation. J. Phys. D Appl. Phys. 2011, 44, 155301. [Google Scholar] [CrossRef]
- Plante, J.S.; Dubowsky, S. Large-scale failure modes of dielectric elastomer actuators. Int. J. Solids Struct. 2006, 43, 7727–7751. [Google Scholar] [CrossRef]
- Godaba, H.; Zhang, Z.Q.; Gupta, U.; Foo, C.C.; Zhu, J. Instabilities in dielectric elastomers: Buckling, wrinkling, and crumpling. Soft Matter 2019, 15, 7137–7144. [Google Scholar] [CrossRef]
- Zhu, J.; Kollosche, M.; Lu, T.; Kofod, G.; Suo, Z. Two types of transitions to wrinkles in dielectric elastomers. Soft Matter 2012, 8, 8840–8846. [Google Scholar] [CrossRef]
- Mao, G.; Wu, L.; Liang, X.; Qu, S. Morphology of voltage-triggered ordered wrinkles of a dielectric elastomer sheet. J. Appl. Mech. 2017, 84, 111005. [Google Scholar] [CrossRef]
- Zurlo, G.; Destrade, M.; DeTommasi, D.; Puglisi, G. Catastrophic thinning of dielectric elastomers. Phys. Rev. Lett. 2017, 118, 078001. [Google Scholar] [CrossRef]
- Sheima, Y.; Caspari, P.; Opris, D.M. Artificial muscles: Dielectric elastomers responsive to low voltages. Macromol. Rapid Commun. 2019, 40, 1900205. [Google Scholar] [CrossRef]
- Kumar, D.; Sarangi, S. Pre-stretch and frequency variation effect on the dielectric permittivity of a dielectric elastomer: An amended permittivity model. Sādhanā 2019, 44, 173. [Google Scholar] [CrossRef]
- Pelrine, R.; Kornbluh, R.; Pei, Q.; Joseph, J. High-speed electrically actuated elastomers with strain greater than 100%. Science 2000, 287, 836–839. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Suo, Z. Theory of dielectric elastomers capable of giant deformation of actuation. Phys. Rev. Lett. 2010, 104, 178302. [Google Scholar] [CrossRef]
- Liu, L.; Liu, Y.; Li, B.; Yang, K.; Li, T.; Leng, J. Thermo-electro-mechanical instability of dielectric elastomers. Smart Mater. Struct. 2011, 20, 075004. [Google Scholar] [CrossRef]
- Huang, J.; Shian, S.; Diebold, R.M.; Suo, Z.; Clarke, D.R. The thickness and stretch dependence of the electrical breakdown strength of an acrylic dielectric elastomer. Appl. Phys. Lett. 2012, 101, 122905. [Google Scholar] [CrossRef]
- Kofod, G.; Sommer-Larsen, P.; Kornbluh, R.; Pelrine, R. Actuation response of polyacrylate dielectric elastomers. J. Intell. Mater. Syst. Struct. 2003, 14, 787–793. [Google Scholar] [CrossRef]
- Zhao, Y.; Zha, J.W.; Yin, L.J.; Gao, Z.S.; Wen, Y.Q.; Dang, Z.M. Remarkable electrically actuation performance in advanced acrylic-based dielectric elastomers without pre-strain at very low driving electric field. Polymer 2018, 137, 269–275. [Google Scholar] [CrossRef]
- Kofod, G. The static actuation of dielectric elastomer actuators: How does pre-stretch improve actuation? J. Phys. D Appl. Phys. 2008, 41, 215405. [Google Scholar] [CrossRef]
- Khanh, V.T.V.; Mathew, A.T.; Short, J.S.; Quek, Z.F.; Ang, M.H.; Koh, S.J.A. Displacement improvement from variable pre-stretch diaphragm type Dielectric Elastomer Actuator. In Proceedings of the 2018 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Auckland, New Zealand, 9–12 July 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 545–550. [Google Scholar]
- Pelrine, R.; Sommer-Larsen, P.; Kornbluh, R.D.; Heydt, R.; Kofod, G.; Pei, Q.; Gravesen, P. Applications of dielectric elastomer actuators. In Proceedings of the Smart Structures and Materials 2001: Electroactive Polymer Actuators and Devices, San Diego, CA, USA, 17–21 March 2001; International Society for Optics and Photonics: Bellingham, WA, USA, 2001; Volume 4329, pp. 335–349. [Google Scholar]
- Dughaish, Z.H. Dielectric properties of (BaTiO3)(1-x) (SnO2)x ceramics. J. Nat. Sci. Math. 2013, 6, 107–121. [Google Scholar] [CrossRef]
- Zou, J.; Gu, G.Y.; Zhu, L.M. Open-loop control of creep and vibration in dielectric elastomer actuators with phenomenological models. IEEE/ASME Trans. Mechatron. 2016, 22, 51–58. [Google Scholar] [CrossRef]
- McKay, T.; O’Brien, B.; Calius, E.; Anderson, I. An integrated, self-priming dielectric elastomer generator. Appl. Phys. Lett. 2010, 97, 062911. [Google Scholar] [CrossRef]
- Zhang, J.; Tang, L.; Liu, L.; Zhao, J.; Yang, Z.; Li, P. Modeling of humidity effect on electromechanical properties of viscoelastic dielectric elastomer. Int. J. Mech. Sci. 2021, 193, 106177. [Google Scholar] [CrossRef]
- Zuo, Y.; Ding, Y.; Zhang, J.; Zhu, M.; Liu, L.; Zhao, J. Humidity effect on dynamic electromechanical properties of polyacrylic dielectric elastomer: An experimental study. Polymers 2021, 13, 784. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, J.; Chen, H. Ambient humidity altering electromechanical actuation of dielectric elastomers. Appl. Phys. Lett. 2019, 115, 184101. [Google Scholar] [CrossRef]
- Albuquerque, F.B.; Shea, H. Influence of humidity, temperature and prestretch on the dielectric breakdown strength of silicone elastomer membranes for DEAs. Smart Mater. Struct. 2020, 29, 105024. [Google Scholar] [CrossRef]
- Plante, J.S.; Dubowsky, S. On the properties of dielectric elastomer actuators and their design implications. Smart Mater. Struct. 2007, 16, S227. [Google Scholar] [CrossRef]
- Mathew, A.T.; Koh, S.J.A. Operational limits of a non-homogeneous dielectric elastomer transducer. Int. J. Smart Nano Mater. 2017, 8, 214–231. [Google Scholar] [CrossRef]
- Seifi, S.; Park, H.S. Electro-elastocapillary Rayleigh–plateau instability in dielectric elastomer films. Soft Matter 2017, 13, 4305–4310. [Google Scholar] [CrossRef]
- Romasanta, L.J.; Lopez-Manchado, M.Á.; Verdejo, R. Increasing the performance of dielectric elastomer actuators: A review from the materials perspective. Prog. Polym. Sci. 2015, 51, 188–211. [Google Scholar] [CrossRef]
- Ha, S.M.; Yuan, W.; Pei, Q.; Pelrine, R.; Stanford, S. Interpenetrating polymer networks for high-performance electroelastomer artificial muscles. Adv. Mater. 2006, 18, 887–891. [Google Scholar] [CrossRef]
- Ha, S.M.; Yuan, W.; Pei, Q.; Pelrine, R.; Stanford, S. Interpenetrating networks of elastomers exhibiting 300% electrically-induced area strain. Smart Mater. Struct. 2007, 16, S280. [Google Scholar] [CrossRef]
- Sahu, D.; Sahu, R.K.; Patra, K. Effects of crosslink density on the behavior of VHB 4910 dielectric elastomer. J. Macromol. Sci. Part A 2019, 56, 821–829. [Google Scholar] [CrossRef]
- Tugui, C.; Bele, A.; Tiron, V.; Hamciuc, E.; Varganici, C.D.; Cazacu, M. Dielectric elastomers with dual piezo-electrostatic response optimized through chemical design for electromechanical transducers. J. Mater. Chem. C 2017, 5, 824–834. [Google Scholar] [CrossRef]
- Xu, J.; Dong, Y.; Jiang, Z.; Tang, L.; Chen, X.; Yao, Z.; Cao, K. Self-healing high-performance dielectric elastomer actuator with novel liquid-solid interpenetrating structure. Compos. Part A Appl. Sci. Manuf. 2021, 149, 106519. [Google Scholar] [CrossRef]
- Utrera-Barrios, S.; Verdejo, R.; López-Manchado, M.A.; Santana, M.H. Evolution of self-healing elastomers, from extrinsic to combined intrinsic mechanisms: A review. Mater. Horiz. 2020, 7, 2882–2902. [Google Scholar] [CrossRef]
- Bilodeau, R.A.; Kramer, R.K. Self-healing and damage resilience for soft robotics: A review. Front. Robot. AI 2017, 4, 48. [Google Scholar] [CrossRef]
- Bortot, E.; Springhetti, R.; Gei, M. Enhanced soft dielectric composite generators: The role of ceramic fillers. J. Eur. Ceram. Soc. 2014, 34, 2623–2632. [Google Scholar] [CrossRef]
- Gallone, G.; Galantini, F.; Carpi, F. Perspectives for new dielectric elastomers with improved electromechanical actuation performance: Composites versus blends. Polym. Int. 2010, 59, 400–406. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, L.; Fan, J.; Yu, K.; Liu, Y.; Shi, L.; Leng, J. New silicone dielectric elastomers with a high dielectric constant. In Proceedings of the Modeling, Signal Processing, and Control for Smart Structures, San Diego, CA, USA, 9–13 March 2008; International Society for Optics and Photonics: Bellingham, WA, USA, 2008; Volume 6926, p. 692610. [Google Scholar]
- Gallone, G.; Carpi, F.; De Rossi, D.; Levita, G.; Marchetti, A. Dielectric constant enhancement in a silicone elastomer filled with lead magnesium niobate–lead titanate. Mater. Sci. Eng. C 2007, 27, 110–116. [Google Scholar] [CrossRef]
- Carpi, F.; Rossi, D.D. Improvement of electromechanical actuating performances of a silicone dielectric elastomer by dispersion of titanium dioxide powder. IEEE Trans. Dielectr. Electr. Insul. 2005, 12, 835–843. [Google Scholar] [CrossRef]
- Ruan, M.; Yang, D.; Guo, W.; Zhang, L.; Wu, Y.; Li, S. Mussel-inspired synthesis of barium titanate@ poly (dopamine)@ graphene oxide multilayer core-shell hybrids for high-performance dielectric elastomer actuator. Mater. Lett. 2018, 219, 109–113. [Google Scholar] [CrossRef]
- Ning, N.; Ma, Q.; Liu, S.; Tian, M.; Zhang, L.; Nishi, T. Tailoring dielectric and actuated properties of elastomer composites by bioinspired poly (dopamine) encapsulated graphene oxide. ACS Appl. Mater. Interfaces 2015, 7, 10755–10762. [Google Scholar] [CrossRef]
- Banet, P.; Zeggai, N.; Chavanne, J.; Nguyen, G.T.; Chikh, L.; Plesse, C.; Almanza, M.; Martinez, T.; Civet, Y.; Perriard, Y.; et al. Evaluation of dielectric elastomers to develop materials suitable for actuation. Soft Matter 2021, 17, 10786–10805. [Google Scholar] [CrossRef]
- Skov, A.L.; Yu, L. Optimization Techniques for Improving the Performance of Silicone-Based Dielectric Elastomers. Adv. Eng. Mater. 2018, 20, 1700762. [Google Scholar] [CrossRef]
- Tan, M.W.M.; Thangavel, G.; Lee, P.S. Enhancing dynamic actuation performance of dielectric elastomer actuators by tuning viscoelastic effects with polar crosslinking. NPG Asia Mater. 2019, 11, 62. [Google Scholar] [CrossRef]
- Yu, L.; Madsen, F.B.; Hvilsted, S.; Skov, A.L. High energy density interpenetrating networks from ionic networks and silicone. In Proceedings of the Electroactive Polymer Actuators and Devices (EAPAD), San Diego, CA, USA, 8–12 March 2015; SPIE: Bellingham, WA, USA, 2015; Volume 9430, pp. 196–206. [Google Scholar]
- Zhang, Y.; Ellingford, C.; Zhang, R.; Roscow, J.; Hopkins, M.; Keogh, P.; McNally, T.; Bowen, C.; Wan, C. Electrical and mechanical self-healing in high-performance dielectric elastomer actuator materials. Adv. Funct. Mater. 2019, 29, 1808431. [Google Scholar] [CrossRef]
- Fan, F.; Szpunar, J. Characterization of viscoelasticity and self-healing ability of VHB 4910. Macromol. Mater. Eng. 2015, 300, 99–106. [Google Scholar] [CrossRef]
- Chen, Y.; Agostini, L.; Moretti, G.; Fontana, M.; Vertechy, R. Dielectric elastomer materials for large-strain actuation and energy harvesting: A comparison between styrenic rubber, natural rubber and acrylic elastomer. Smart Mater. Struct. 2019, 28, 114001. [Google Scholar] [CrossRef]
- Madsen, F.B.; Daugaard, A.E.; Hvilsted, S.; Skov, A.L. The current state of silicone-based dielectric elastomer transducers. Macromol. Rapid Commun. 2016, 37, 378–413. [Google Scholar] [CrossRef]
- Cameron, C.G.; Underhill, R.S.; Rawji, M.; Szabo, J.P. Conductive filler: Elastomer composites for Maxwell stress actuator applications. In Proceedings of the Smart Structures and Materials 2004: Electroactive Polymer Actuators and Devices (EAPAD), San Diego, CA, USA, 14–18 March 2004; International Society for Optics and Photonics: Bellingham, WA, USA, 2004; Volume 5385, pp. 51–59. [Google Scholar]
- Zhang, Q.P.; Liu, J.H.; Liu, H.D.; Jia, F.; Zhou, Y.L.; Zheng, J. Tailoring chain length and cross-link density in dielectric elastomer toward enhanced actuation strain. Appl. Phys. Lett. 2017, 111, 152901. [Google Scholar] [CrossRef]
- Yang, D.; Tian, M.; Kang, H.; Dong, Y.; Liu, H.; Yu, Y.; Zhang, L. New polyester dielectric elastomer with large actuated strain at low electric field. Mater. Lett. 2012, 76, 229–232. [Google Scholar] [CrossRef]
- Sun, H.; Liu, X.; Yan, H.; Feng, Z.; Yu, B.; Ning, N.; Tian, M.; Zhang, L. The role of dipole structure and their interaction on the electromechanical and actuation performance of homogeneous silicone dielectric elastomers. Polymer 2019, 165, 1–10. [Google Scholar] [CrossRef]
- Su, Y.; Sui, G.; Lan, J.; Yang, X. A highly stretchable dielectric elastomer based on core–shell structured soft polymer-coated liquid-metal nanofillers. Chem. Commun. 2020, 56, 11625–11628. [Google Scholar] [CrossRef]
- Ziegmann, A.; Schubert, D.W. Influence of the particle size and the filling degree of barium titanate filled silicone elastomers used as potential dielectric elastomers on the mechanical properties and the crosslinking density. Mater. Today Commun. 2018, 14, 90–98. [Google Scholar] [CrossRef]
- Chen, T.; Lin, M.; Zhao, Y.; Pan, L.; Tang, Q. Electromechanical response of polyol-polyurethane blends as dielectric elastomer flexible mirco-actuator material. J. Mater. Sci. Mater. Electron. 2017, 28, 3560–3570. [Google Scholar] [CrossRef]
- Ning, N.; Qin, H.; Wang, M.; Sun, H.; Tian, M.; Zhang, L. Improved dielectric and actuated performance of thermoplastic polyurethane by blending with XNBR as macromolecular dielectrics. Polymer 2019, 179, 121646. [Google Scholar] [CrossRef]
- Ye, Z.; Chen, Z.; Asmatulu, R.; Chan, H. Robust control of dielectric elastomer diaphragm actuator for human pulse signal tracking. Smart Mater. Struct. 2017, 26, 085043. [Google Scholar] [CrossRef]
- Massenio, P.R.; Rizzello, G.; Comitangelo, G.; Naso, D.; Seelecke, S. Reinforcement Learning-Based Minimum Energy Position Control of Dielectric Elastomer Actuators. IEEE Trans. Control Syst. Technol. 2020, 29, 1674–1688. [Google Scholar] [CrossRef]
- Li, L.; Li, J.; Qin, L.; Cao, J.; Kankanhalli, M.S.; Zhu, J. Deep Reinforcement Learning in Soft Viscoelastic Actuator of Dielectric Elastomer. IEEE Robot. Autom. Lett. 2019, 4, 2094–2100. [Google Scholar] [CrossRef]
- Huang, P.; Wu, J.; Zhang, P.; Wang, Y.; Su, C.Y. Dynamic modeling and tracking control for dielectric elastomer actuator with a model predictive controller. IEEE Trans. Ind. Electron. 2021, 69, 1819–1828. [Google Scholar] [CrossRef]
- Tao, B.; Luo, K.; Tian, Q.; Hu, H. Inverse dynamic design for motion control of soft machines driven by dielectric elastomer actuators. Int. J. Mech. Sci. 2024, 273, 109213. [Google Scholar] [CrossRef]
- Branz, F.; Francesconi, A. Modelling and control of double-cone dielectric elastomer actuator. Smart Mater. Struct. 2016, 25, 095040. [Google Scholar] [CrossRef]
- Braganza, D.; Dawson, D.M.; Walker, I.D.; Nath, N. A Neural Network Controller for Continuum Robots. IEEE Trans. Robot. 2007, 23, 1270–1277. [Google Scholar] [CrossRef]
- Xian, B.; Dawson, D.; de Queiroz, M.; Chen, J. A Continuous Asymptotic Tracking Control Strategy for Uncertain Nonlinear Systems. IEEE Trans. Autom. Control 2004, 49, 1206–1211. [Google Scholar] [CrossRef]
- Chin, K.; Hellebrekers, T.; Majidi, C. Machine Learning for Soft Robotic Sensing and Control. Adv. Intell. Syst. 2020, 2, 1900171. [Google Scholar] [CrossRef]
- Abbeel, P.; Quigley, M.; Ng, A.Y. Using Inaccurate Models in Reinforcement Learning. In Proceedings of the 23rd International Conference on Machine Learning—ICML ’06, Pittsburgh, PA, USA, 25–29 June 2006; ACM Press: Pittsburgh, PA, USA, 2006; pp. 1–8. [Google Scholar] [CrossRef]
- Medina, H.; Gentry, N.; Farmer, C. Remote Laboratory for Machine Learning Training of a Soft Actuator’s Control: A Case Study. In Proceedings of the 2021 ASEE Southeastern Section Conference, Virtual, 7–10 March 2021. [Google Scholar]
- Francois-Lavet, V.; Henderson, P.; Islam, R.; Bellemare, M.G.; Pineau, J. An Introduction to Deep Reinforcement Learning. Found. Trends Mach. Learn. 2018, 11, 219–354. [Google Scholar] [CrossRef]
- Kirkpatrick, K.; Valasek, J.; Haag, C. Characterization and Control of Hysteretic Dynamics Using Online Reinforcement Learning. J. Aerosp. Inf. Syst. 2013, 10, 297–305. [Google Scholar] [CrossRef][Green Version]
- Osman, H.E. On Reinforcement Memory for Non-Markovian Control. In Research and Development in Intelligent Systems XXVII; Bramer, M., Petridis, M., Hopgood, A., Eds.; Springer: London, UK, 2011; pp. 179–192. [Google Scholar] [CrossRef]
- Hausknecht, M.; Stone, P. Deep recurrent q-learning for partially observable mdps. In Proceedings of the 2015 AAAI Fall Symposium Series, Arlington, Virginia, 12–14 November 2015. [Google Scholar]
- Liu, V.; Adeniji, A.; Lee, N.; Zhao, J.; Srouji, M. Recurrent Control Nets for Deep Reinforcement Learning. arXiv 2019, arXiv:1901.01994. [Google Scholar] [CrossRef]
- Chen, C.; Ying, V.; Laird, D. Deep Q-Learning with Recurrent Neural Networks. Stanf. Cs229 Course Rep. 2016, 4, 6. [Google Scholar]
- Kalashnikov, D.; Irpan, A.; Pastor, P.; Ibarz, J.; Herzog, A.; Jang, E.; Quillen, D.; Holly, E.; Kalakrishnan, M.; Vanhoucke, V.; et al. Scalable Deep Reinforcement Learning for Vision-Based Robotic Manipulation. In Proceedings of the 2nd Conference on Robot Learning, Zurich, Switzerland, 29–31 October 2018; Billard, A., Dragan, A., Peters, J., Morimoto, J., Eds.; Proceedings of Machine Learning Research; PMLR. 2018; Volume 87, pp. 651–673. [Google Scholar]
- Rueckert, E.; Nakatenus, M.; Tosatto, S.; Peters, J. Learning Inverse Dynamics Models in O(n) Time with LSTM Networks. In Proceedings of the 2017 IEEE-RAS 17th International Conference on Humanoid Robotics (Humanoids), Birmingham, UK, 15–17 November 2017; IEEE: Birmingham, UK, 2017; pp. 811–816. [Google Scholar] [CrossRef]
- Thuruthel, T.G.; Shih, B.; Laschi, C.; Tolley, M.T. Soft Robot Perception Using Embedded Soft Sensors and Recurrent Neural Networks. Sci. Robot. 2019, 4, eaav1488. [Google Scholar] [CrossRef]
- Veeramani, A.S.; Crews, J.H.; Buckner, G.D. Hysteretic Recurrent Neural Networks: A Tool for Modeling Hysteretic Materials and Systems. Smart Mater. Struct. 2009, 18, 075004. [Google Scholar] [CrossRef]
- Gonzalez, J.; Yu, W. Non-Linear System Modeling Using LSTM Neural Networks. IFAC-Pap. 2018, 51, 485–489. [Google Scholar] [CrossRef]
- Omidshafiei, S.; Pazis, J.; Amato, C.; How, J.P.; Vian, J. Deep Decentralized Multi-task Multi-Agent Reinforcement Learning under Partial Observability. In Proceedings of the 34th International Conference on Machine Learning; Sydney, NSW, Australia, 6–11 August 2017, Precup, D., Teh, Y.W., Eds.; Proceedings of Machine Learning Research; PMLR; 2017; Volume 70, pp. 2681–2690. [Google Scholar]
- Yang, T.; Xiao, Y.; Zhang, Z.; Liang, Y.; Li, G.; Zhang, M.; Li, S.; Wong, T.W.; Wang, Y.; Li, T.; et al. A Soft Artificial Muscle Driven Robot With Reinforcement Learning. Sci. Rep. 2018, 8, 14518. [Google Scholar] [CrossRef]
- Larson, C.; Spjut, J.; Knepper, R.; Shepherd, R. A Deformable Interface for Human Touch Recognition Using Stretchable Carbon Nanotube Dielectric Elastomer Sensors and Deep Neural Networks. Soft Robot. 2019, 6, 611–620. [Google Scholar] [CrossRef] [PubMed]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-Informed Neural Networks: A Deep Learning Framework for Solving Forward and Inverse Problems Involving Nonlinear Partial Differential Equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Gaskett, C.; Wettergreen, D.; Zelinsky, A. Q-learning in continuous state and action spaces. In Proceedings of the Australasian Joint Conference on Artificial Intelligence, Sydney, Australia, 6–10 December 1999; Springer: Berlin/Heidelberg, Germany, 1999; pp. 417–428. [Google Scholar]
- Baydere, B.A.; Talas, S.K.; Samur, E. A novel highly-extensible 2-DOF pneumatic actuator for soft robotic applications. Sens. Actuators A Phys. 2018, 281, 84–94. [Google Scholar] [CrossRef]
- Rizzello, G.; Naso, D.; York, A.; Seelecke, S. A self-sensing approach for dielectric elastomer actuators based on online estimation algorithms. IEEE/ASME Trans. Mechatron. 2016, 22, 728–738. [Google Scholar] [CrossRef]
- Sánchez-Solano, S.; Cabrera, A.J.; Baturone, I.; Moreno-Velo, F.J.; Brox, M. FPGA implementation of embedded fuzzy controllers for robotic applications. IEEE Trans. Ind. Electron. 2007, 54, 1937–1945. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, J.; Han, Y.; Li, H.; Li, X. DeepBurning: Automatic generation of FPGA-based learning accelerators for the neural network family. In Proceedings of the 2016 53nd ACM/EDAC/IEEE Design Automation Conference (DAC), Austin, TX, USA, 5–9 June 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–6. [Google Scholar]
- Su, J.; Liu, J.; Thomas, D.B.; Cheung, P.Y. Neural network based reinforcement learning acceleration on FPGA platforms. ACM SIGARCH Comput. Archit. News 2017, 44, 68–73. [Google Scholar] [CrossRef]
- Zhang, C.; Li, P.; Sun, G.; Guan, Y.; Xiao, B.; Cong, J. Optimizing fpga-based accelerator design for deep convolutional neural networks. In Proceedings of the 2015 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Monterey, CA, USA, 22–24 February 2015; pp. 161–170. [Google Scholar]
- Da Silva, L.M.; Torquato, M.F.; Fernandes, M.A. Parallel implementation of reinforcement learning q-learning technique for fpga. IEEE Access 2018, 7, 2782–2798. [Google Scholar] [CrossRef]
- Leong, P.H.W.; Tsoi, K.H. Field Programmable Gate Array technology for robotics applications. In Proceedings of the 2005 IEEE International Conference on Robotics and Biomimetics-ROBIO, Shatin, China, 5–9 July 2005; IEEE: Piscataway, NJ, USA, 2005; pp. 295–298. [Google Scholar]
- Arish, S.; Sharma, R. Run-Time-Reconfigurable Multi-Precision Floating-Point Matrix Multiplier Intellectual Property Core on FPGA. Circuits Syst. Signal Process. 2017, 36, 998–1026. [Google Scholar] [CrossRef][Green Version]
- Wei, H.; Li, C.; Chen, D.; Wang, J.; Wang, T. Research on reconfigurable robot controller based on ARM and FPGA. In Proceedings of the 2008 6th IEEE International Conference on Industrial Informatics, Daejeon, Republic of Korea, 13–16 July 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 123–128. [Google Scholar]
- Astarloa, A.; Lázaro, J.; Bidarte, U.; Jiménez, J.; Zuloaga, A. FPGA technology for multi-axis control systems. Mechatronics 2009, 19, 258–268. [Google Scholar] [CrossRef]
- Upegui, A.; Moeckel, R.; Dittrich, E.; Ijspeert, A.; Sanchez, E. An FPGA dynamically reconfigurable framework for modular robotics. In Proceedings of the Workshop Procedings of the 18th International Conference on Architecture of Computing Systems 2005 (ARCS’05), Innsbruck, Austria, 14–17 March 2005; VDE Verlag: Berlin, Germany, 2005. number CONF. [Google Scholar]
- Hill, M.; Rizzello, G.; Seelecke, S. Development of a fatigue testing setup for dielectric elastomer membrane actuators. In Proceedings of the Electroactive Polymer Actuators and Devices (EAPAD), Portland, OR, USA, 26–29 March 2017; International Society for Optics and Photonics: Bellingham, WA, USA, 2017; Volume 10163, p. 101630X. [Google Scholar]
- Atalik, T.; Deniz, M.; Koc, E.; Gercek, C.O.; Gultekin, B.; Ermis, M.; Cadirci, I. Multi-DSP and -FPGA-Based Fully Digital Control System for Cascaded Multilevel Converters Used in FACTS Applications. IEEE Trans. Ind. Inform. 2012, 8, 511–527. [Google Scholar] [CrossRef]
- Bonato, V.; Peron, R.; Wolf, D.F.; de Holanda, J.A.; Marques, E.; Cardoso, J.M. An FPGA implementation for a Kalman filter with application to mobile robotics. In Proceedings of the 2007 International Symposium on Industrial Embedded Systems, Lisbon, Portugal, 4–6 July 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 148–155. [Google Scholar]
- Van Duong, L.; Asahina, R.; Wang, J. Development of a vision-based soft tactile muscularis. In Proceedings of the 2019 2nd IEEE International Conference on Soft Robotics (RoboSoft), Seoul, Republic of Korea, 14–18 April 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 343–348. [Google Scholar]
- Gankidi, P.R. Fpga Accelerator Architecture for Q-Learning and Its Applications in Space Exploration Rovers. Ph.D. Thesis, Arizona State University, Tempe, AZ, USA, 2016. [Google Scholar]
- Deiss, S.R.; Douglas, R.J.; Whatley, A.M.; Maass, W. A pulse-coded communications infrastructure for neuromorphic systems. Pulsed Neural Netw. 1999, 157–178. [Google Scholar] [CrossRef]
- Upegui, A.; Pena-Reyes, C.A.; Sanchez, E. An FPGA platform for on-line topology exploration of spiking neural networks. Microprocess. Microsyst. 2005, 29, 211–223. [Google Scholar] [CrossRef]
| Category | Classification | Application | Sources |
|---|---|---|---|
| Actuators | Shape-Changing | Origami Structures | [31] |
| Inflatable Structures | [32] | ||
| Camouflage | [33] | ||
| Object Control | Vibration Compensation | [34] | |
| Involuntary Tremor | [24] | ||
| Movement | Valve | [35] | |
| Deformable Motors | [2] | ||
| Rotary Motors | [36] | ||
| Hexapod-like movement | [4] | ||
| Insect-like movement | [37] | ||
| Fish-like movement | [38] | ||
| Loudspeaker | [39] | ||
| Spiral Proboscis Pump Actuator | [40] | ||
| Elastomeric Pump | [41] | ||
| Muscle-Inspired | [42] | ||
| Electromagnetic Wave Manipulation | Frequency Selective Surfaces | [43] | |
| Stretchable Microfluid Channels | [44] | ||
| Parasitic Elements | [11] | ||
| Hemispherical Ring Patch Antenna | [12] | ||
| Optical Manipulation | Expansion-type Tunable Lenses | [10] | |
| Liquid Lenses | [9] | ||
| Metasurface Lenses | [45] | ||
| Tunable Diffraction Transmission Grating | [46] | ||
| Tunable Resonance Filter | [47] | ||
| Sound Isolation | Duct Silencer | [48] | |
| Band gap Low Frequency Noise Filter | [49] | ||
| Sensing | Feedback | Deformation Sensing | [50] |
| Tactile Display | [51] | ||
| Combined | McKibben Muscle Sensors | [52] | |
| Pressure Sensing | Multi-modal pressure-displacement sensor | [53] | |
| Pressure Sensing | [54] | ||
| Audio-tactile interface | [55] | ||
| Venus Fly-trap mimicry | [56] | ||
| Gesture Recognition | Hand Gesture Detection | [57] | |
| Humidity Detection | Hygromorphic DEA | [58] | |
| Energy Generation | Environmental | Tidal Wave Generation | [59,60] |
| Wind Energy Generation | [61,62] | ||
| Human | Heel Strike Generator | [63] | |
| Mechanical | Crankshaft Generator | [64] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Medina, H.; Farmer, C.; Liu, I. Dielectric Elastomer-Based Actuators: A Modeling and Control Review for Non-Experts. Actuators 2024, 13, 151. https://doi.org/10.3390/act13040151
Medina H, Farmer C, Liu I. Dielectric Elastomer-Based Actuators: A Modeling and Control Review for Non-Experts. Actuators. 2024; 13(4):151. https://doi.org/10.3390/act13040151
Chicago/Turabian StyleMedina, Hector, Carson Farmer, and Isaac Liu. 2024. "Dielectric Elastomer-Based Actuators: A Modeling and Control Review for Non-Experts" Actuators 13, no. 4: 151. https://doi.org/10.3390/act13040151
APA StyleMedina, H., Farmer, C., & Liu, I. (2024). Dielectric Elastomer-Based Actuators: A Modeling and Control Review for Non-Experts. Actuators, 13(4), 151. https://doi.org/10.3390/act13040151





