Wind Turbine Bearing Failure Diagnosis Using Multi-Scale Feature Extraction and Residual Neural Networks with Block Attention
Abstract
1. Introduction
- A reconstruction method is proposed to convert one-dimensional vibration signals into two-dimensional images.
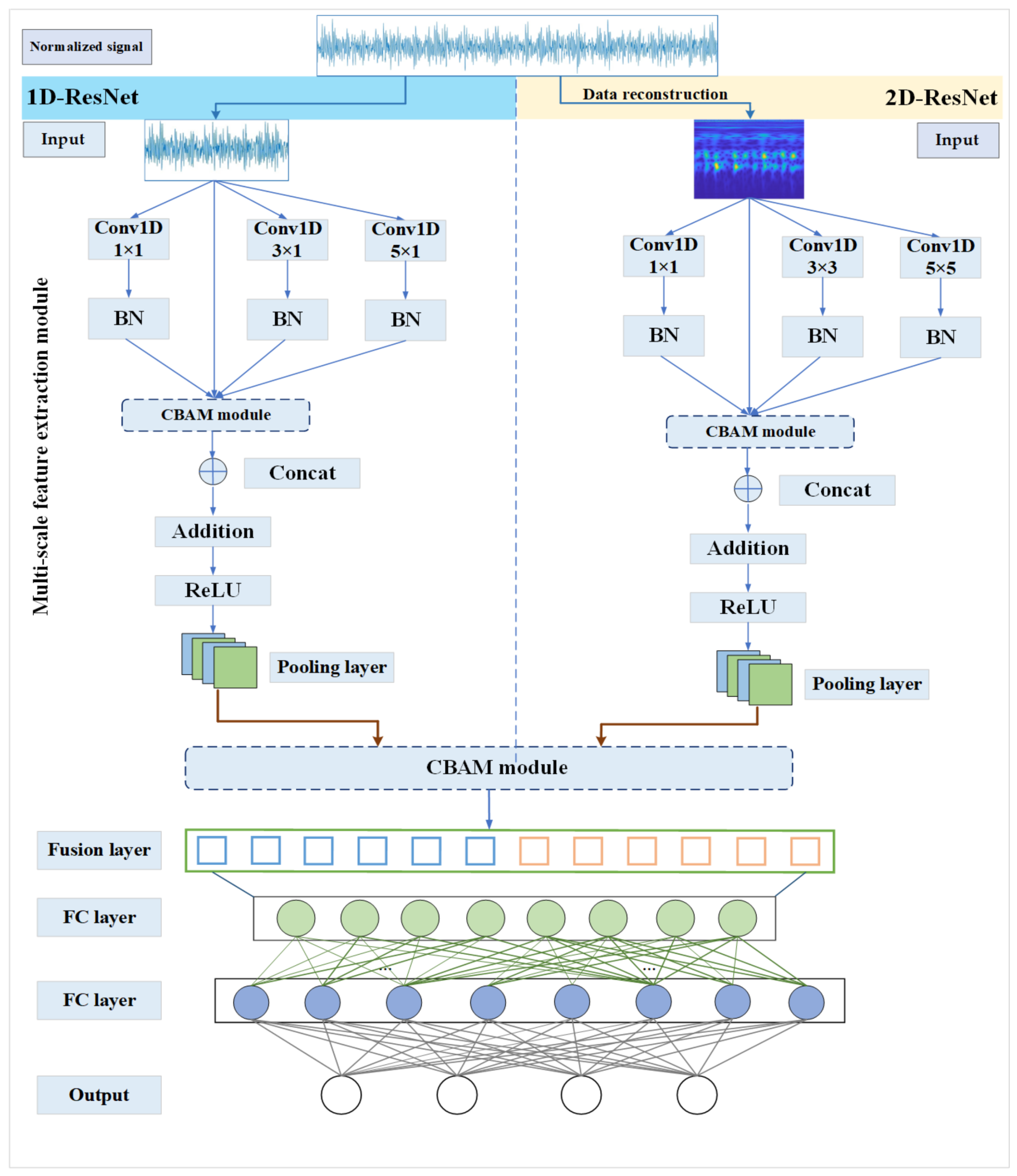
- A multi-scale feature extraction module combining 1D-ResNet and 2D-ResNet was designed and implemented, using parallel convolutional kernels to extract features.
- After feature extraction, a CBAM module is added before fusion to enhance the network’s ability to capture key features by focusing on important features in specific channels or spatial areas. After feature fusion, CBAM is introduced again to further enhance the effect of feature fusion, ensuring that the features extracted by different network branches can be effectively integrated, ultimately providing more accurate input features for the classification task of the fully connected layer.
2. Materials and Methods
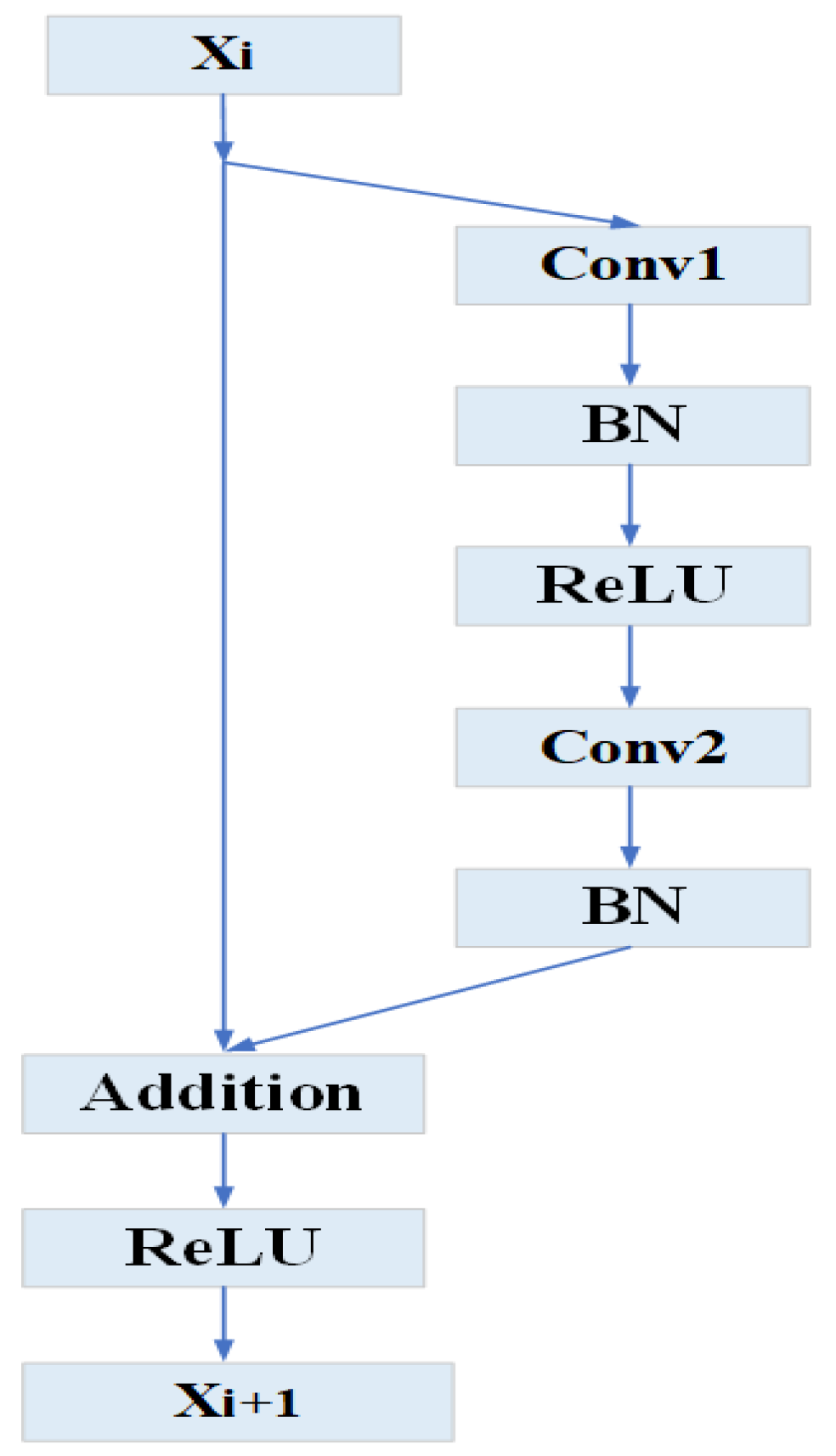
2.1. Residual Network
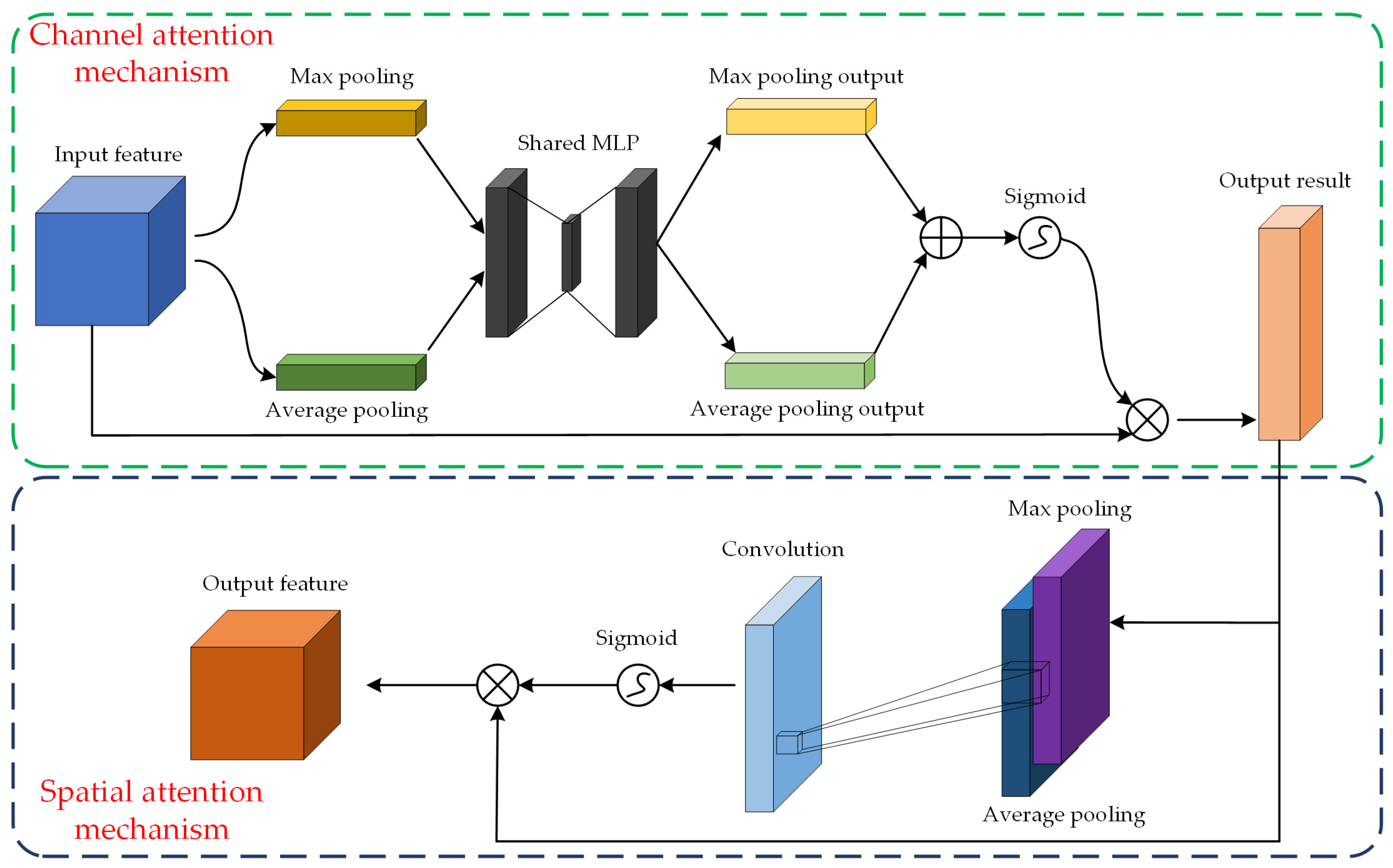
2.2. CBAM Module
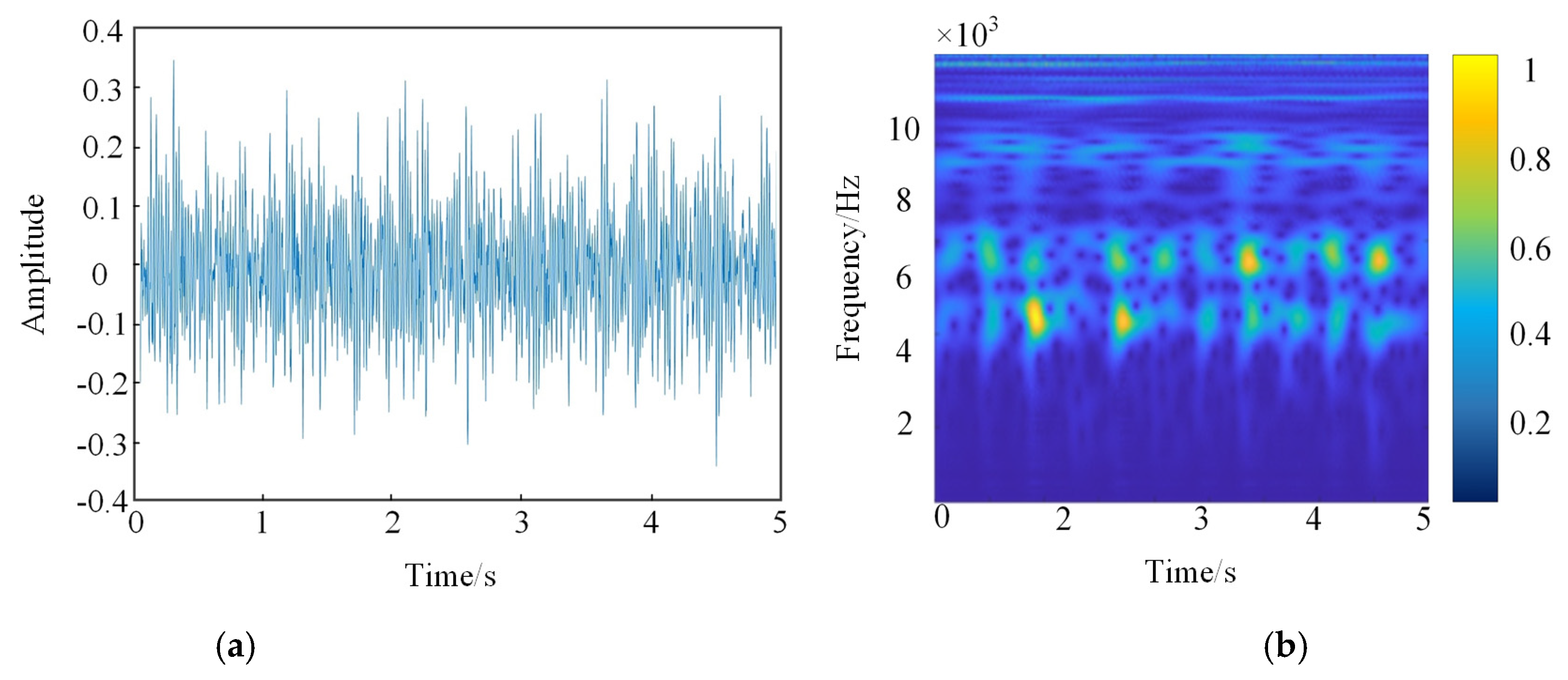
2.3. Continuous Wavelet Transform
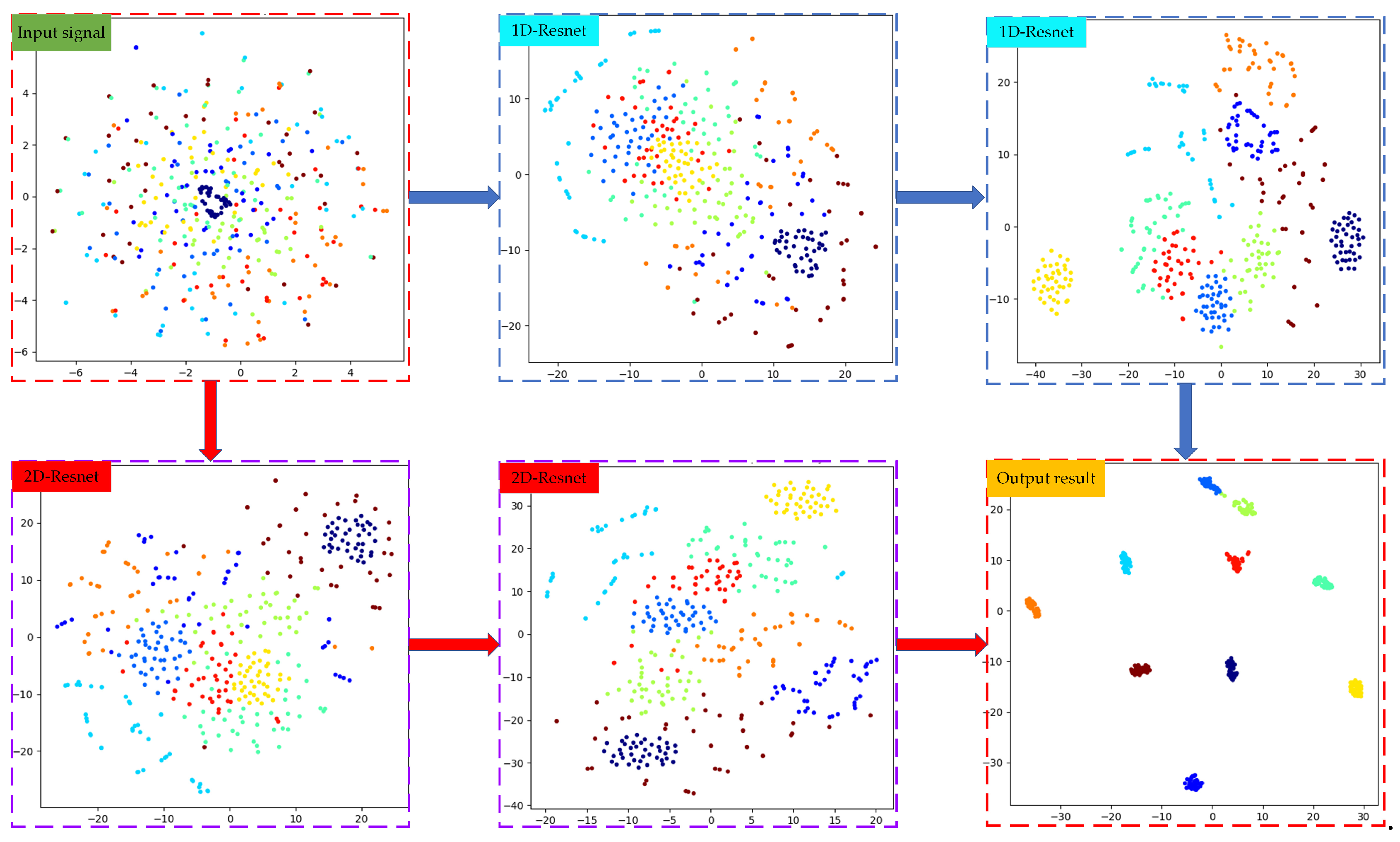
2.4. Multi-Scale Feature Extraction Module
2.5. TSFFResNet-Net
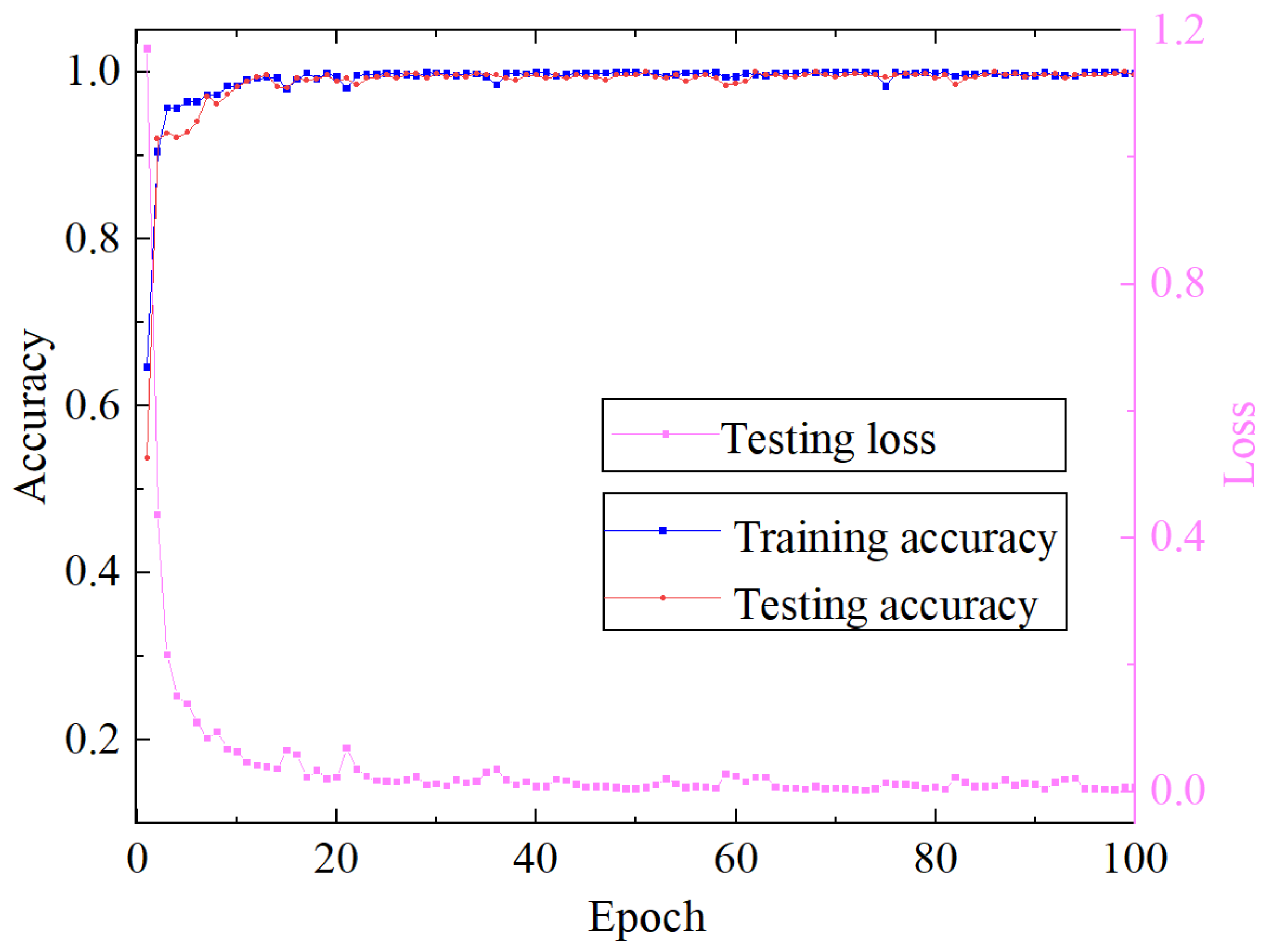
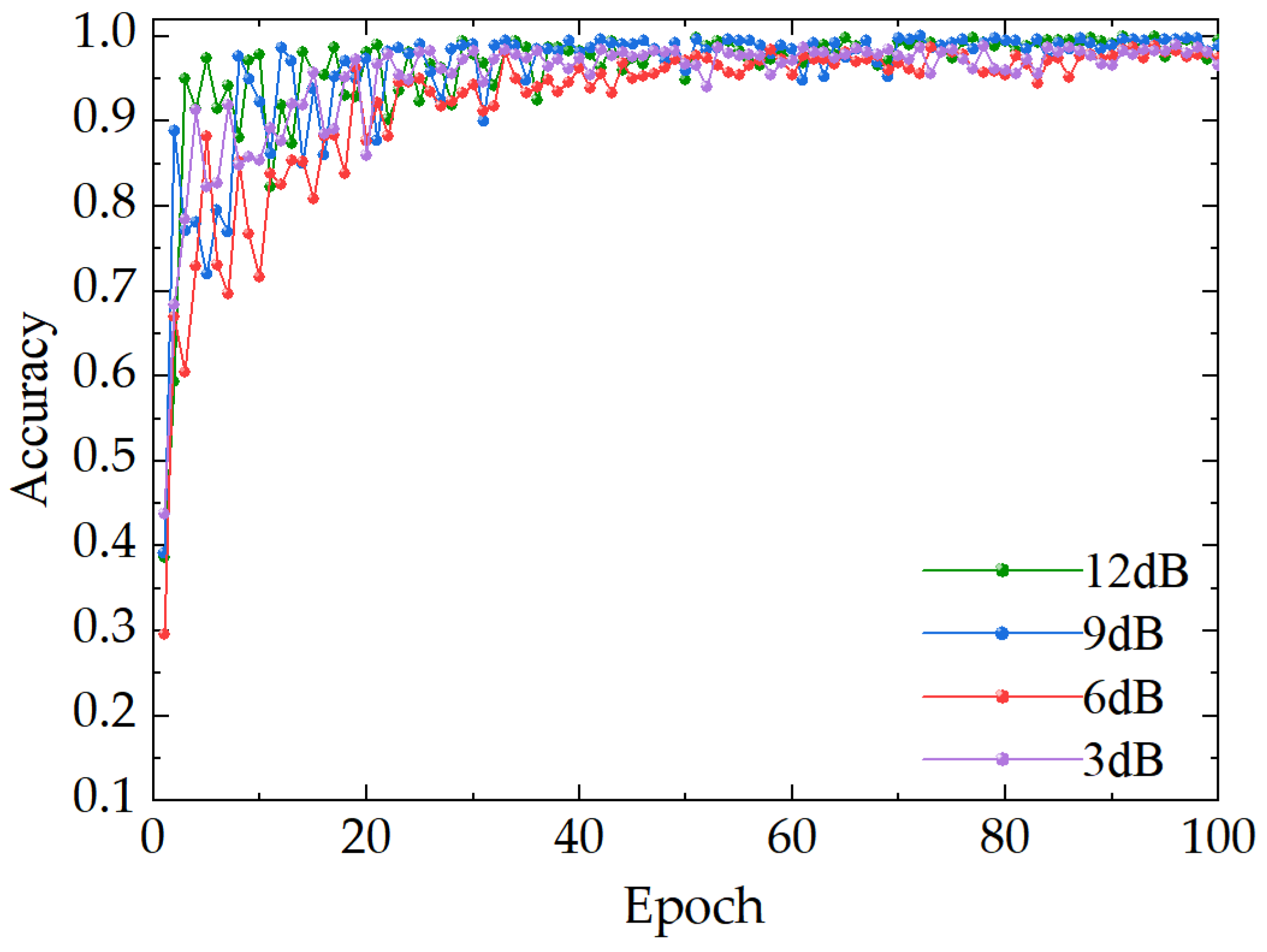
3. Results
3.1. Case 1
3.2. Case 2
4. Discussion and Conclusions
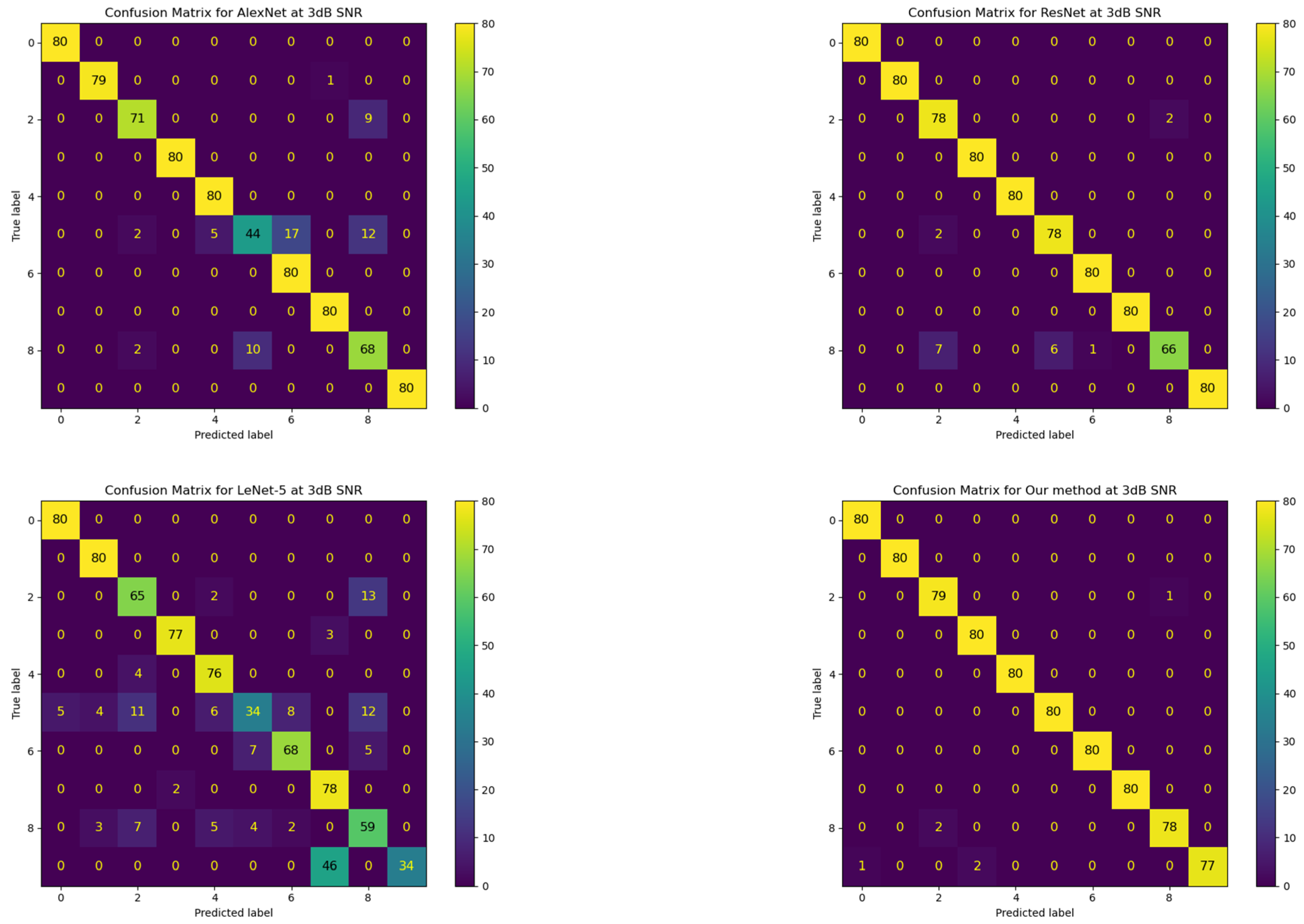
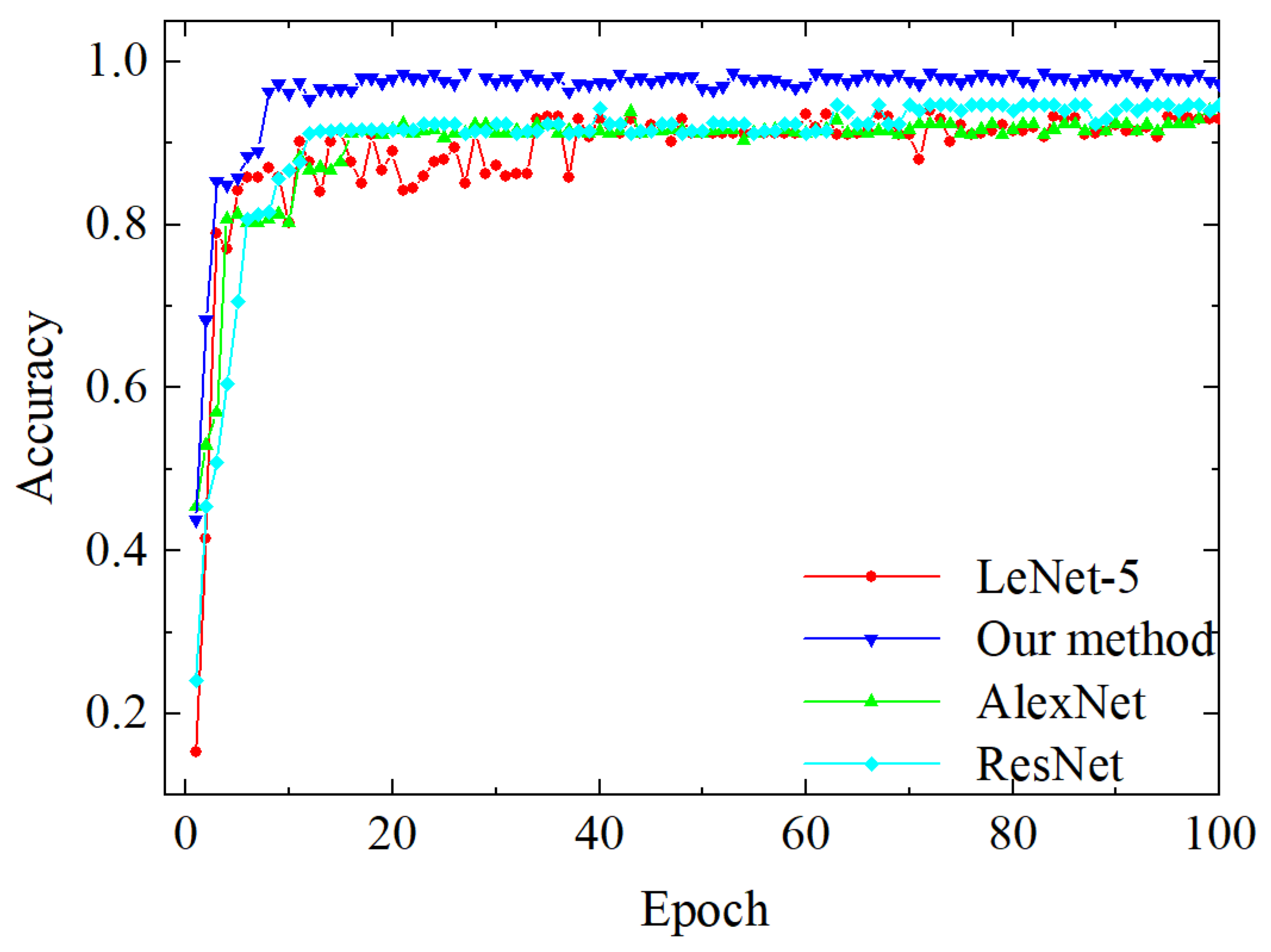
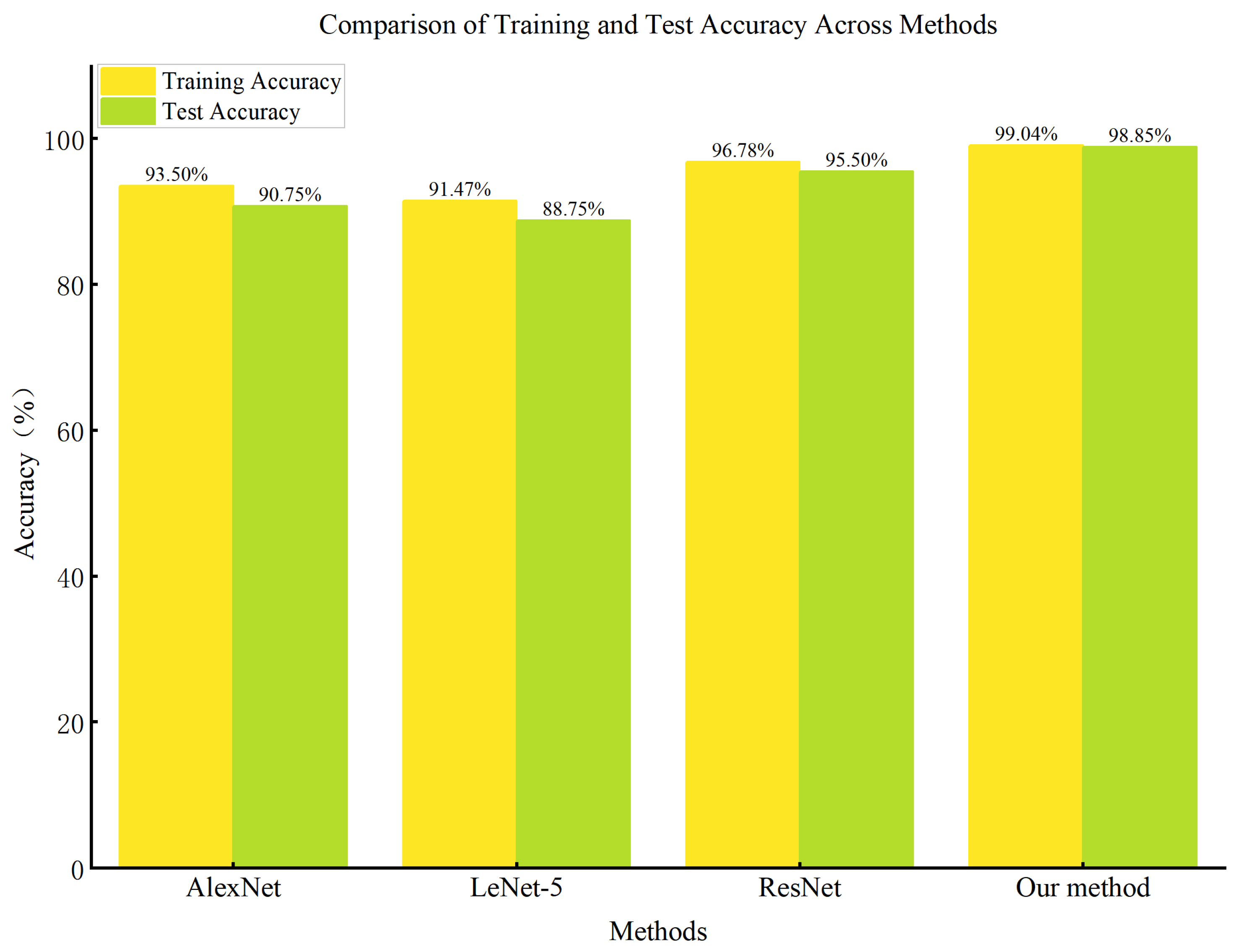
- The proposed wind turbine rolling bearing fault diagnosis method, based on one-dimensional and two-dimensional convolutional neural networks combined with the empirical wavelet transform method, demonstrated excellent performance in various signal-to-noise ratios and different datasets, showing higher diagnostic accuracy and better robustness. Compared to other classic convolutional neural network methods (such as LeNet-5, AlexNet, and ResNet), this method achieved significantly higher diagnostic accuracy under various signal-to-noise ratio conditions, especially in low signal-to-noise ratio situations, highlighting its superiority in handling noise and complex working conditions.
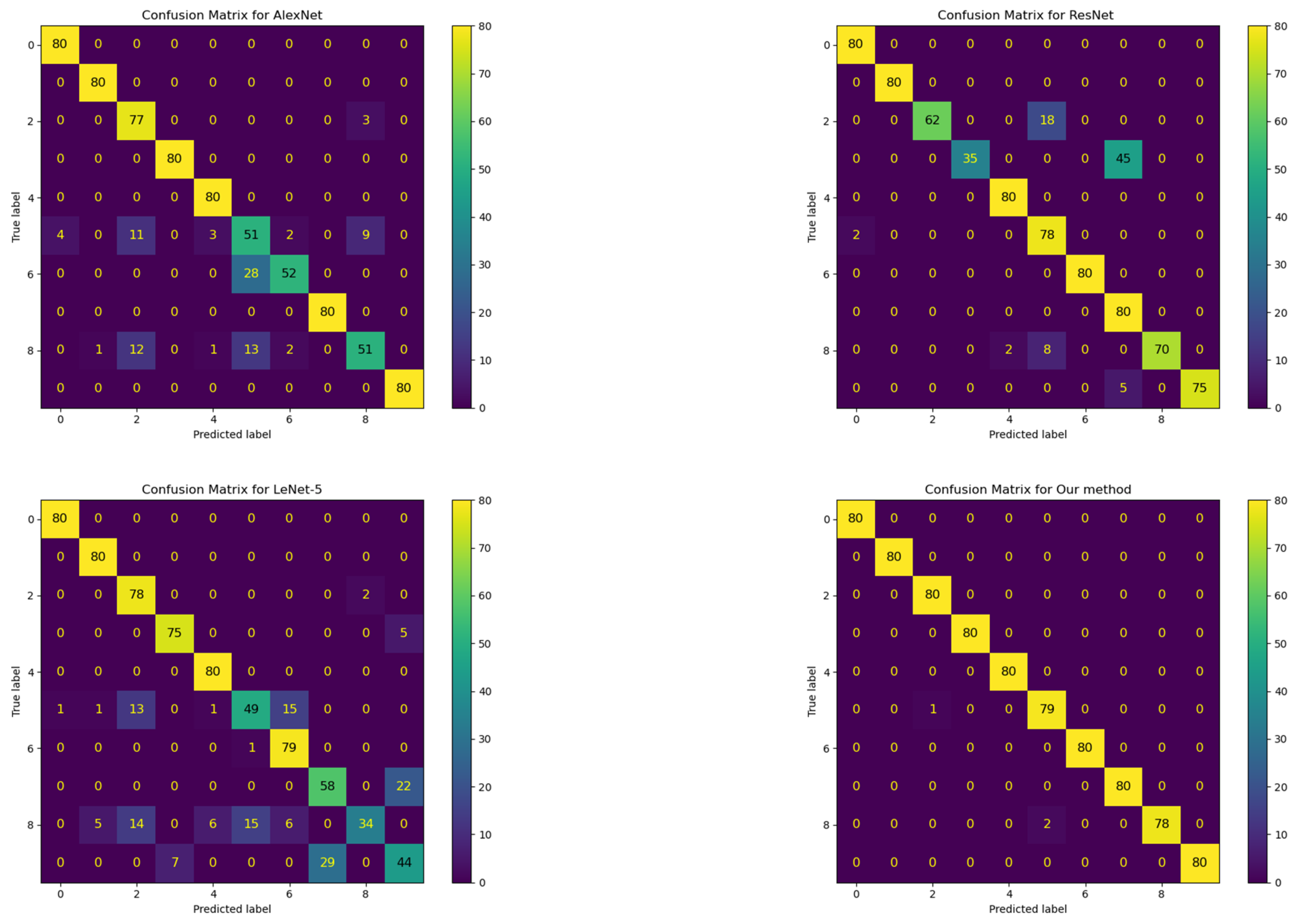
- Through comprehensive comparison with different methods, the proposed method achieved an accuracy of over 99% on the test set, significantly outperforming other comparison methods. Additionally, in the confusion matrix analysis, it showed high recognition rates for various fault modes, further demonstrating its outstanding performance in multi-class fault diagnosis tasks.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Niu, G.X.; Liu, E.H.; Wang, X.; Zhang, B. A Hybrid Bearing Prognostic Method with Fault Diagnosis and Model Fusion. IEEE Trans. Ind. Inform. 2024, 20, 864–872. [Google Scholar] [CrossRef]
- Ma, Z.P.; Zhao, M.; Dai, X.B.; Bi, H.N. Compound fault diagnosis of wind turbine bearing under ultra-low speed operations using generalized sparse spectral coherence. Mech. Syst. Signal Process. 2024, 208, 111027. [Google Scholar] [CrossRef]
- Damou, A.; Ratni, A.; Benazzouz, D. Intelligent multi-fault identification and classification of defective bearings in gearbox. Adv. Mech. Eng. 2024, 16, 1–6. [Google Scholar] [CrossRef]
- Li, X.M.; Wang, Y.X.; Yao, J.C.; Li, M.; Gao, Z.K. Multi-sensor fusion fault diagnosis method of wind turbine bearing based on viewable neural networks. Reliab. Eng. Syst. Saf. 2024, 245, 109980. [Google Scholar] [CrossRef]
- Hu, B.Q.; Liu, J.; Xu, Y.; Huo, T.L. An Integrated Bearing Fault Diagnosis Method Based on Multibranch SKNet and Enhanced Inception-ResNet-v2. Shock. Vib. 2024, 2024, 9071328. [Google Scholar] [CrossRef]
- Liang, P.F.; Tian, J.Y.; Wang, S.Y.; Yuan, X.M. Multi-source information joint transfer diagnosis for rolling bearing with unknown faults via wavelet transform and an improved domain adaptation network. Reliab. Eng. Syst. Saf. 2024, 242, 109788. [Google Scholar] [CrossRef]
- Ding, Y.F.; Jia, M.P.; Zhuang, J.C.; Cao, Y.D.; Zhao, X.L.; Lee, C.G. Deep imbalanced domain adaptation for transfer learning fault diagnosis of bearings under multiple working conditions. Reliab. Eng. Syst. Saf. 2023, 230, 108890. [Google Scholar] [CrossRef]
- Tan, H.C.; Xie, S.C.; Liu, R.D.; Cheng, J.Q.; Jing, K.K. Fatigue condition diagnosis of rolling bearing based on normalized balanced multiscale sample entropy. Int. J. Fatigue 2023, 172, 107642. [Google Scholar] [CrossRef]
- Xu, F.; Fang, Y.J.; Wang, D.; Liang, J.Q.; Tsui, K.L. Combining DBN and FCM for Fault Diagnosis of Roller Element Bearings without Using Data Labels. Shock. Vib. 2018, 2018, 3059230. [Google Scholar] [CrossRef]
- Wang, C.Y.; Zhu, G.Y.; Liu, T.Y.; Xie, Y.H.; Zhang, D. A Sub-Domain Adaptive Transfer Learning Base on Residual Network for Bearing Fault Diagnosis. JVC/J. Vib. Control. 2023, 29, 105–117. [Google Scholar] [CrossRef]
- Liu, C.Y.; Ban, Y.X.; Li, H.Y.; Guo, N.; Ma, X.Q.; Yang, F.; Sui, X.; Huang, Y. Accurate Recognition Method for Rolling Bearing Failure of Mine Hoist in Strong Noise Environment. Machines 2023, 11, 632. [Google Scholar] [CrossRef]
- Zhou, F.N.; Yang, S.; Fujita, H.; Chen, D.M.; Wen, C.L. Deep learning fault diagnosis method based on global optimization GAN for unbalanced data. Knowl.-Based Syst. 2020, 187, 104837. [Google Scholar] [CrossRef]
- Liu, Y.; Xiang, H.; Jiang, Z.S.; Xiang, J.W. Second-order transient-extracting S transform for fault feature extraction in rolling bearings. Reliab. Eng. Syst. Saf. 2023, 230, 108955. [Google Scholar] [CrossRef]
- Liu, X.Y.; Chen, G.; Wei, X.K.; Liu, Y.B.; Wang, H. A rolling bearing fault evolution state indicator based on deep learning and its application. J. Mech. Sci. Technol. 2023, 37, 2755–2769. [Google Scholar] [CrossRef]
- Han, Y.F.; Li, B.Z.; Huang, Y.K.; Li, L.; Yan, K. Imbalanced fault classification of rolling bearing based on an improved oversampling method. J. Braz. Soc. Mech. Sci. Eng. 2023, 45, 223. [Google Scholar] [CrossRef]
- Deng, J.; Liu, H.; Fang, H.R.; Shao, S.Y.; Wang, D.; Hou, Y.M.; Chen, D.S.; Tang, M.C. MgNet: A fault diagnosis approach for multi-bearing system based on auxiliary bearing and multi-granularity information fusion. Mech. Syst. Signal Process. 2023, 193, 110253. [Google Scholar] [CrossRef]
- Wang, Q.H.; Yang, C.G.; Wan, H.Q.; Deng, D.H.; Nandi, A.K. Bearing fault diagnosis based on optimized variational mode decomposition and 1D convolutional neural networks. Meas. Sci. Technol. 2022, 32, 104007. [Google Scholar] [CrossRef]
- Niu, G.X.; Liu, E.H.; Wang, X.; Ziehl, P.; Zhang, B. Enhanced Discriminate Feature Learning Deep Residual CNN for Multitask Bearing Fault Diagnosis with Information Fusion. IEEE Trans. Ind. Inform. 2023, 19, 762–770. [Google Scholar] [CrossRef]
- Bai, R.X.; Meng, Z.; Xu, Q.S.; Fan, F.J. Fractional Fourier and time domain recurrence plot fusion combining convolutional neural network for bearing fault diagnosis under variable working conditions. Reliab. Eng. Syst. Saf. 2023, 232, 109076. [Google Scholar] [CrossRef]
- Han, C.K.; Lu, W.; Wang, H.Q.; Song, L.Y.; Cui, L.L. Multistate fault diagnosis strategy for bearings based on an improved convolutional sparse coding with priori periodic filter group. Mech. Syst. Signal Process. 2023, 188, 109995. [Google Scholar] [CrossRef]
- Dubey, R.; Sharma, R.R.; Upadhyay, A.; Pachori, R.B. Automated Variational Nonlinear Chirp Mode Decomposition for Bearing Fault Diagnosis. IEEE Trans. Ind. Inform. 2023, 19, 10873–10882. [Google Scholar] [CrossRef]
- Zhang, Y.C.; Ji, J.C.; Ren, Z.H.; Ni, Q.; Gu, F.S.; Feng, K.; Yu, K.; Ge, J.; Lei, Z.H.; Liu, Z. Digital twin-driven partial domain adaptation network for intelligent fault diagnosis of rolling bearing. Reliab. Eng. Syst. Saf. 2023, 234, 109186. [Google Scholar] [CrossRef]
- Chen, J.Y.; Lin, C.Y.; Yao, B.Q.; Yang, L.C.; Ge, H.J. Intelligent fault diagnosis of rolling bearings with low-quality data: A feature significance and diversity learning method. Reliab. Eng. Syst. Saf. 2023, 237, 109343. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, C.H.; Jiang, X.X. Imbalanced fault diagnosis of rolling bearing using improved MsR-GAN and feature enhancement-driven CapsNet. Mech. Syst. Signal Process. 2022, 168, 108664. [Google Scholar] [CrossRef]
- Xu, M.; Shi, Y.M.; Deng, M.Q.; Liu, Y.; Ding, X.; Deng, A.D. An improved multi-scale branching convolutional neural network for rolling bearing fault diagnosis. PLoS ONE 2023, 18, e0291353. [Google Scholar] [CrossRef]
- Cheng, Z.W.; Li, X.J.; Guo, P.; Deng, Y.; Xie, Z.H.; Lian, L. Transfer Deep Learning Network for Rolling Bearing Fault Diagnosis of Wind Turbines. J. Phys. Conf. Ser. 2023, 2503, 012095. [Google Scholar] [CrossRef]
- Chen, X.H.; Lou, W.; Zhao, W.H.; Yang, G.X.; Ding, K.; Zhang, J.W. A Rolling Bearing Fault Diagnosis Method Via 2D Feature Map of CSCoh after Denoising and MSCNN under Different Conditions. J. Vib. Control. 2023, 30, 1241–1253. [Google Scholar] [CrossRef]
- Fu, H.Y.; Yu, D.; Zhan, C.S.; Zhu, X.Z.; Xie, Z.J. Unsupervised Rolling Bearing Fault Diagnosis Method across Working Conditions Based on Multiscale Convolutional Neural Network. Meas. Sci. Technol. 2024, 35, 035018. [Google Scholar] [CrossRef]
- Yin, P.Z.; Nie, J.; Liang, X.Y.; Yu, S.S.; Wang, C.L.; Nie, W.Z.; Ding, X.Q. A Multiscale Graph Convolutional Neural Network Framework for Fault Diagnosis of Rolling Bearing. IEEE Trans. Instrum. Meas. 2023, 72, 2520713. [Google Scholar] [CrossRef]
- Hou, X.L.; Guo, W.C.; Ren, S.J.; Li, Y.; Si, Y.; Su, L.Z. Bolt-Loosening Detection Using 1D and 2D Input Data Based on Two-Stream Convolutional Neural Networks. Materials 2022, 15, 6757. [Google Scholar] [CrossRef]
- Xue, F.; Zhang, W.M.; Xue, F.; Li, D.D.; Xie, S.L.; Fleischer, J. A novel intelligent fault diagnosis method of rolling bearing based on two-stream feature fusion convolutional neural network. Measurement 2021, 176, 109226. [Google Scholar] [CrossRef]
- Li, B.; Lima, D. Facial Expression Recognition via ResNet-50. Int. J. Cogn. Comput. Eng. 2021, 2, 57–64. [Google Scholar] [CrossRef]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. CBAM: Convolutional Block Attention Module. In Proceedings of the Computer Vision—ECCV 2018, Munich, Germany, 8–14 September 2018; Volume 11211, pp. 3–19. [Google Scholar]
- Chen, Y.T.; Zhang, X.Z.; Chen, W.N.; Li, Y.Y.; Wang, J.S. Research on Recognition of Fly Species Based on Improved RetinaNet and CBAM. IEEE Access 2020, 8, 102907–102919. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Lu, Y.; Zhu, W.Q.; Wei, X.; Wei, Z. Traffic Sign Detection Based on Multi-Scale Feature Extraction and Cascade Feature Fusion. J. Supercomput. 2023, 79, 2137–2152. [Google Scholar] [CrossRef]




| Category | Bearing Condition | Fault Diameter/mm | Length | Sample Size | Rotation/(r·min−1) |
|---|---|---|---|---|---|
| 1 | Normal | 0 | 1024 | 400 | 1730~1797 |
| 2 | Inner ring fault 1 | 0.1778 | 1024 | 400 | 1730~1797 |
| 3 | Inner ring fault 2 | 0.3556 | 1024 | 400 | 1730~1797 |
| 4 | Inner ring fault 3 | 0.5334 | 1024 | 400 | 1730~1797 |
| 5 | Rolling element fault 1 | 0.1778 | 1024 | 400 | 1730~1797 |
| 6 | Rolling element fault 2 | 0.3556 | 1024 | 400 | 1730~1797 |
| 7 | Rolling element fault 3 | 0.5334 | 1024 | 400 | 1730~1797 |
| 8 | Outer ring fault 1 | 0.1778 | 1024 | 400 | 1730~1797 |
| 9 | Outer ring fault 2 | 0.3556 | 1024 | 400 | 1730~1797 |
| 10 | Outer ring fault 3 | 0.5334 | 1024 | 400 | 1730~1797 |
| Layer | Name | Kernel Parameter |
|---|---|---|
| Input | 1024 × 1 | |
| 1-1 | Convolution layer | 24 & 1 × 1 |
| Convolution layer | 24 & 3 × 1 | |
| Convolution layer | 24 & 5 × 1 | |
| 1-2 | CBAM module | - |
| 1-3 | Pooling layer | 1 × 64 |
| 1-4 | CBAM module | - |
| 1-5 | Fully connected layer 1 | 256 × 64 |
| 1-6 | Fully connected layer 2 | 64 × 10 |
| Layer | Name | Kernel Parameter |
|---|---|---|
| Input | 64 × 64 | |
| 2-1 | Convolution layer | 24 & 1 × 1 |
| Convolution layer | 24 & 3 × 3 | |
| Convolution layer | 24 & 5 × 5 | |
| 2-2 | CBAM module | - |
| 2-3 | Pooling layer | 64 × 64 |
| 2-4 | CBAM module | - |
| 2-5 | Fully connected layer 1 | 256 × 64 |
| 2-6 | Fully connected layer 2 | 64 × 10 |
| Method | Diagnostic Accuray | |||
|---|---|---|---|---|
| 3 dB | 6 dB | 9 dB | 12 dB | |
| Alexnet | 83.04 | 85.86 | 88.50 | 90.50 |
| ResNet | 90.59 | 91.38 | 94.80 | 95.25 |
| LetNet-5 | 85.81 | 86.35 | 88.00 | 89.25 |
| Our method | 96.55 | 97.50 | 98.85 | 99.62 |
| Category | Bearing Condition | Training Set Size | Test Set Size |
|---|---|---|---|
| 0 | Normal | 320 | 80 |
| 1 | Inner ring fault 1 | 320 | 80 |
| 2 | Inner ring fault 2 | 320 | 80 |
| 3 | Inner ring fault 3 | 320 | 80 |
| 4 | Rolling element fault 1 | 320 | 80 |
| 5 | Rolling element fault 2 | 320 | 80 |
| 6 | Rolling element fault 3 | 320 | 80 |
| 7 | Outer ring fault 1 | 320 | 80 |
| 8 | Outer ring fault 2 | 320 | 80 |
| 9 | Outer ring fault 3 | 320 | 80 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Y.; Yang, Y.; Kang, S.; Tian, X.; Liu, S.; Sun, F. Wind Turbine Bearing Failure Diagnosis Using Multi-Scale Feature Extraction and Residual Neural Networks with Block Attention. Actuators 2024, 13, 401. https://doi.org/10.3390/act13100401
Luo Y, Yang Y, Kang S, Tian X, Liu S, Sun F. Wind Turbine Bearing Failure Diagnosis Using Multi-Scale Feature Extraction and Residual Neural Networks with Block Attention. Actuators. 2024; 13(10):401. https://doi.org/10.3390/act13100401
Chicago/Turabian StyleLuo, Yuanqing, Yuhang Yang, Shuang Kang, Xueyong Tian, Shiyue Liu, and Feng Sun. 2024. "Wind Turbine Bearing Failure Diagnosis Using Multi-Scale Feature Extraction and Residual Neural Networks with Block Attention" Actuators 13, no. 10: 401. https://doi.org/10.3390/act13100401
APA StyleLuo, Y., Yang, Y., Kang, S., Tian, X., Liu, S., & Sun, F. (2024). Wind Turbine Bearing Failure Diagnosis Using Multi-Scale Feature Extraction and Residual Neural Networks with Block Attention. Actuators, 13(10), 401. https://doi.org/10.3390/act13100401







