Flow Separation Control of Nacelle Inlets in Crosswinds by Dielectric Barrier Discharge Plasma Actuation
Abstract
1. Introduction
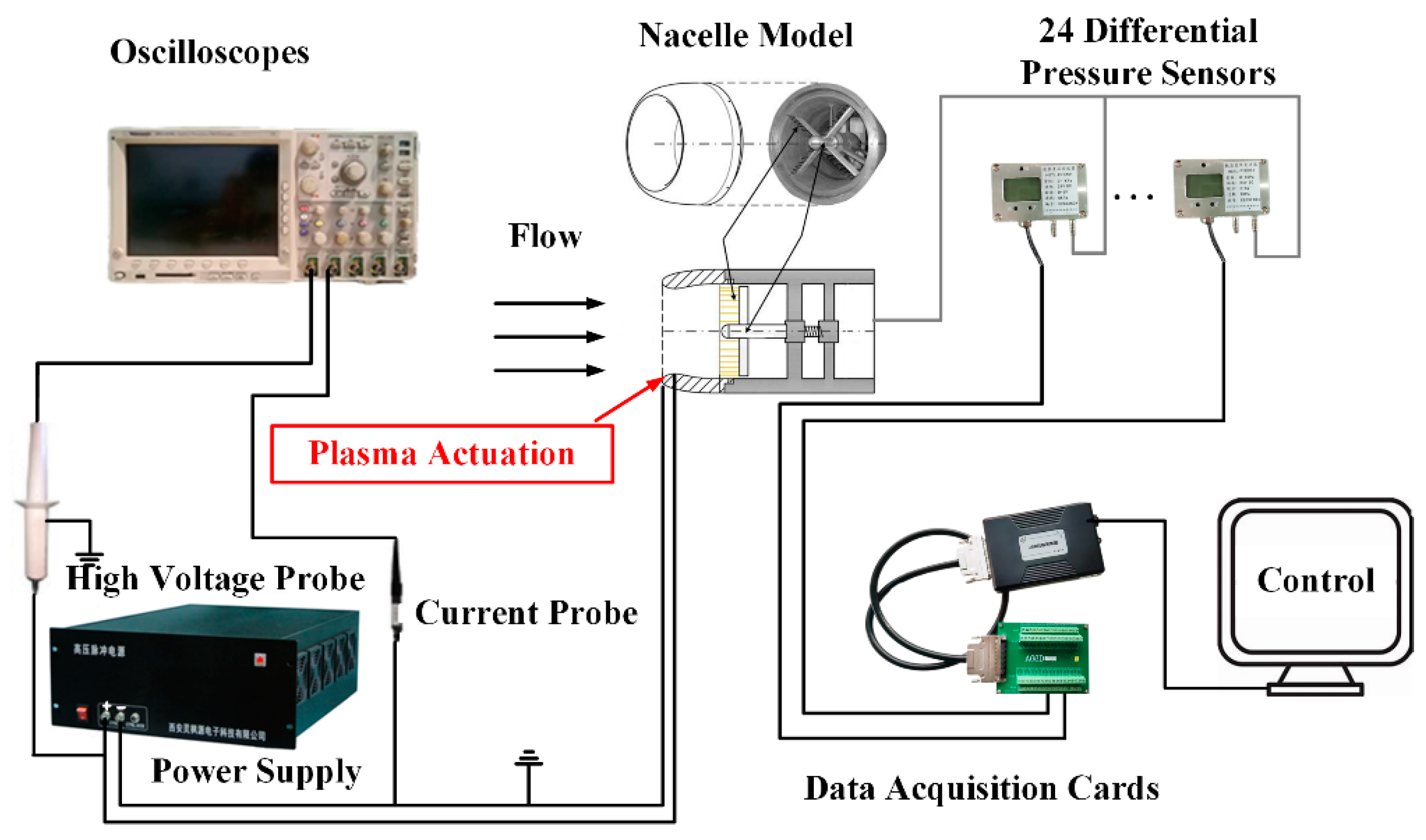
2. Experimental Systems
2.1. Experimental Systems for Nacelles
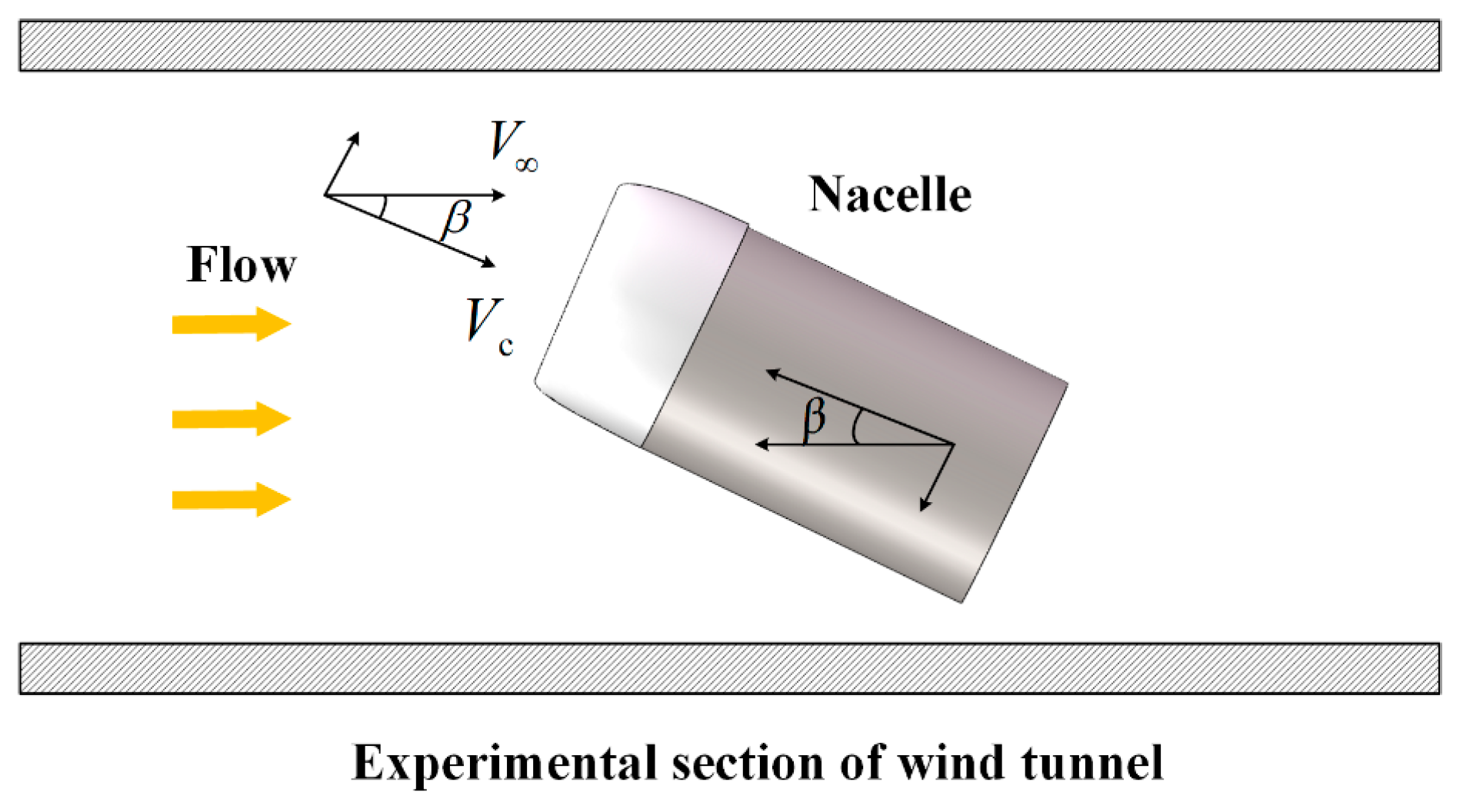
2.2. Wind Tunnel Systems
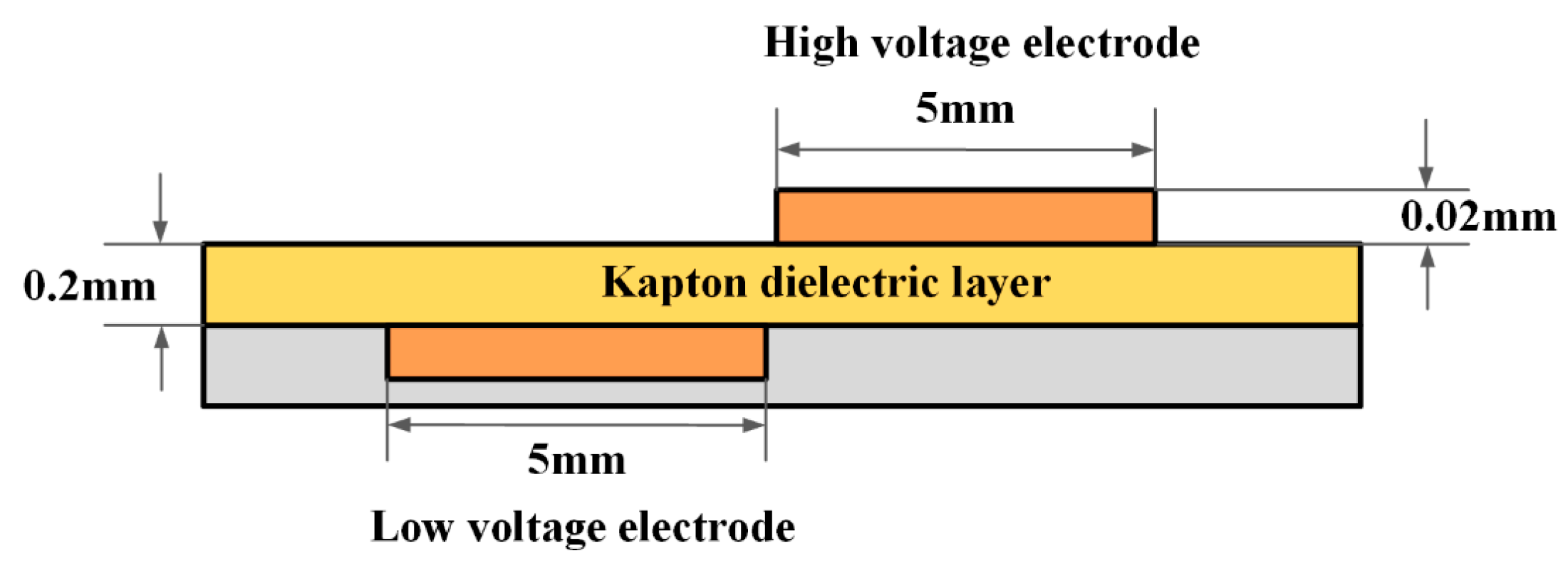
2.3. Plasma Actuation Systems
2.4. Electrical Parameter Measurement System
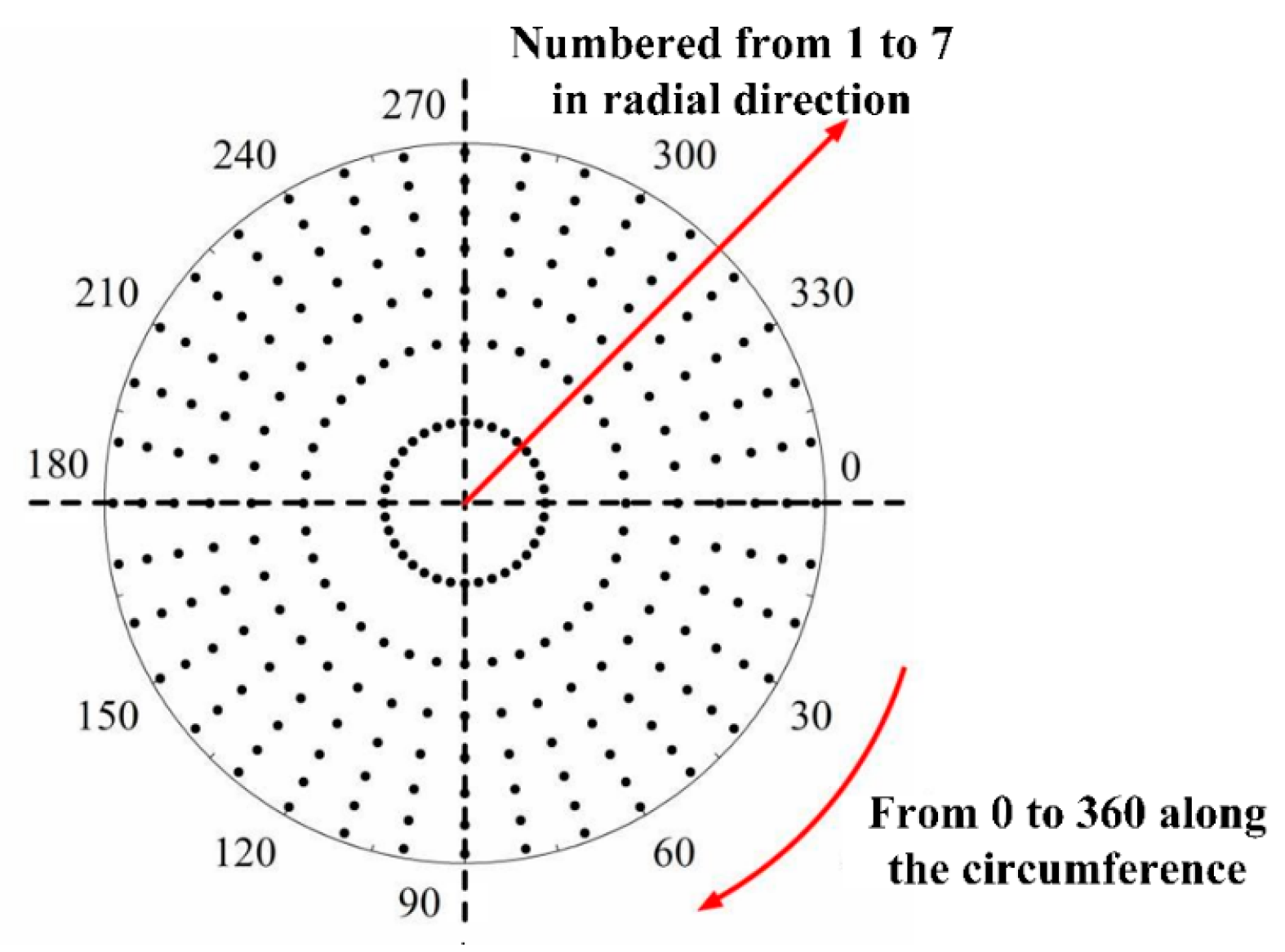
2.5. Flow Field Evaluation Index
3. Results and Discussion
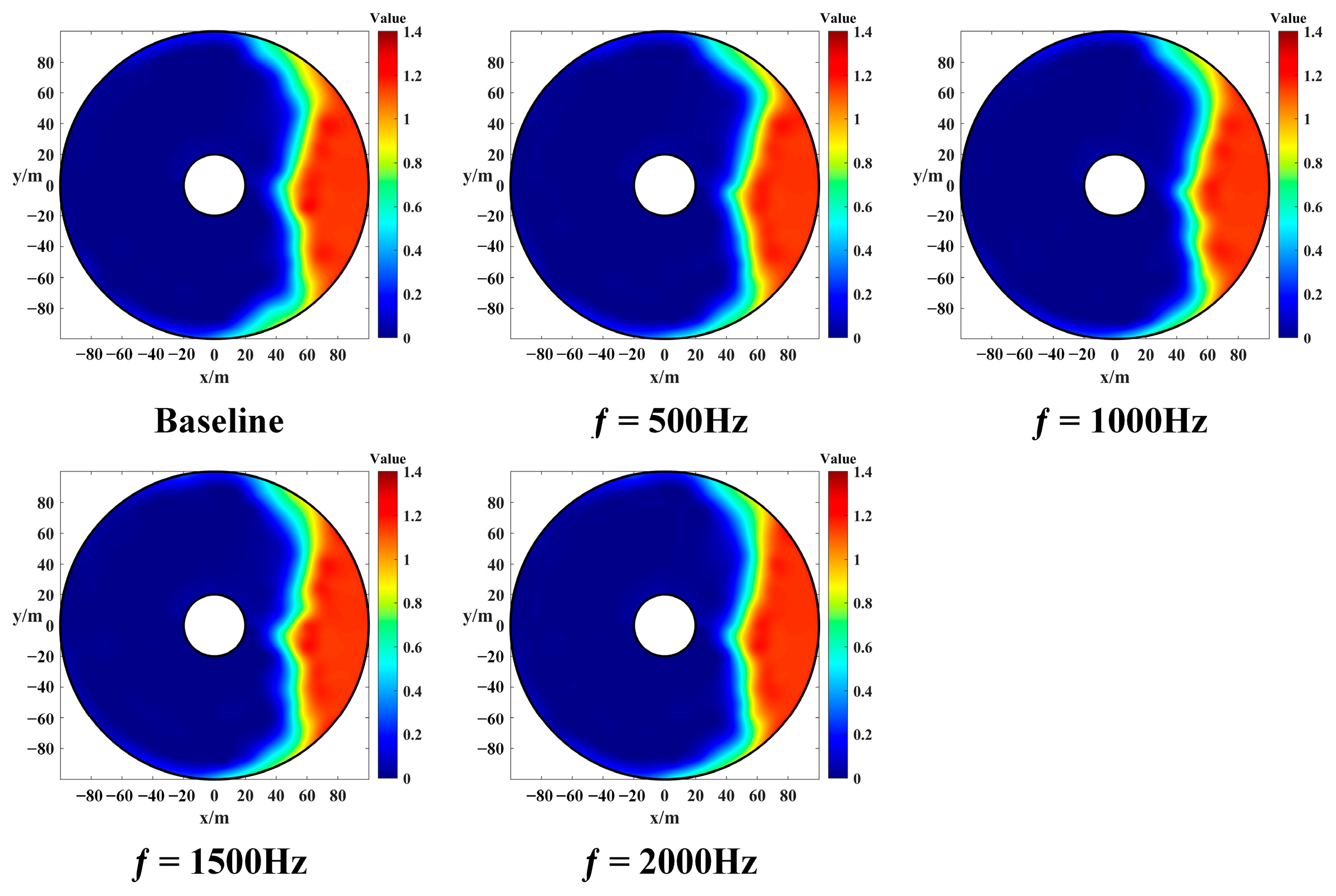
3.1. Experiment on Nacelle Inlet under Crosswind Conditions
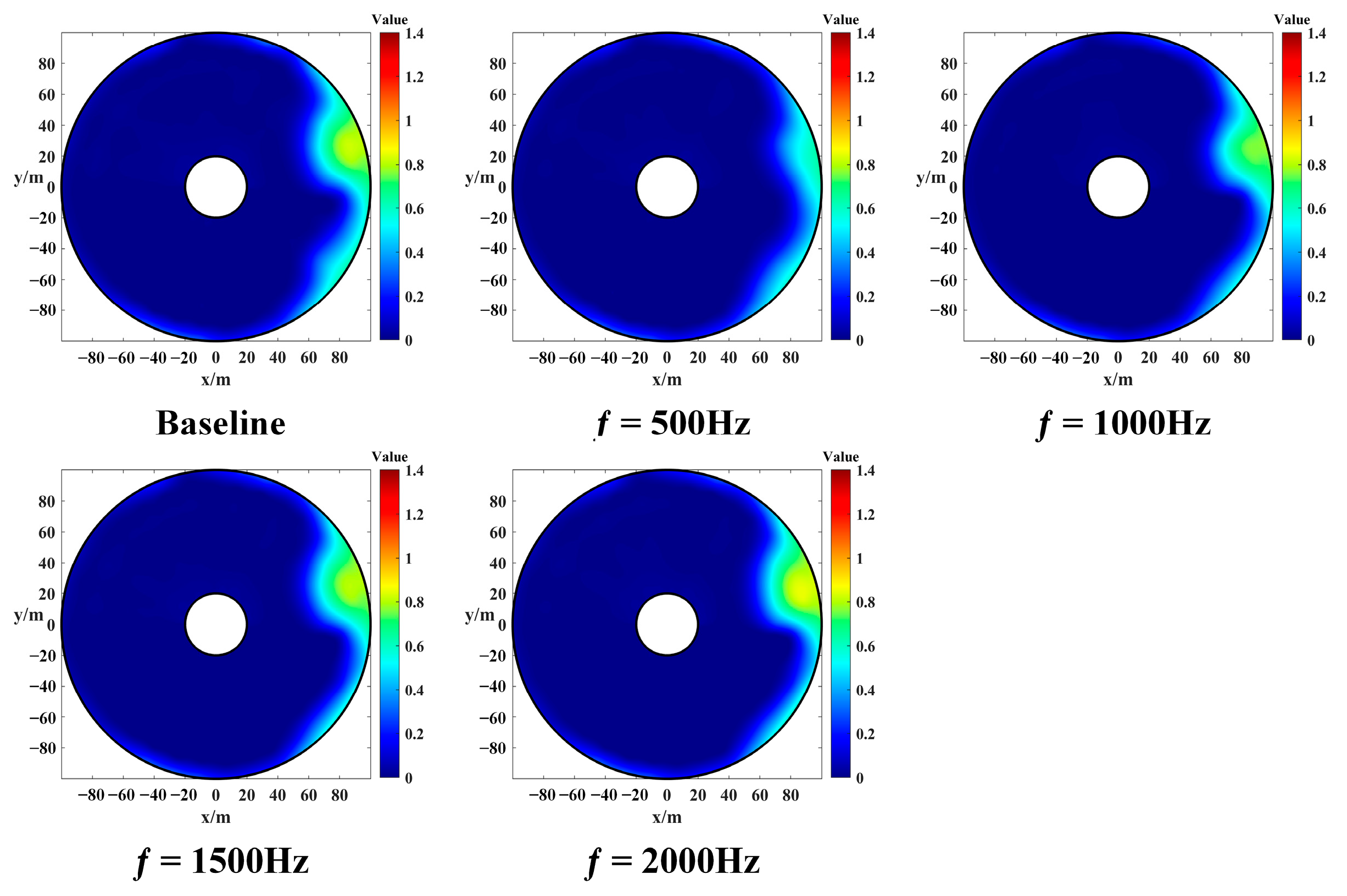
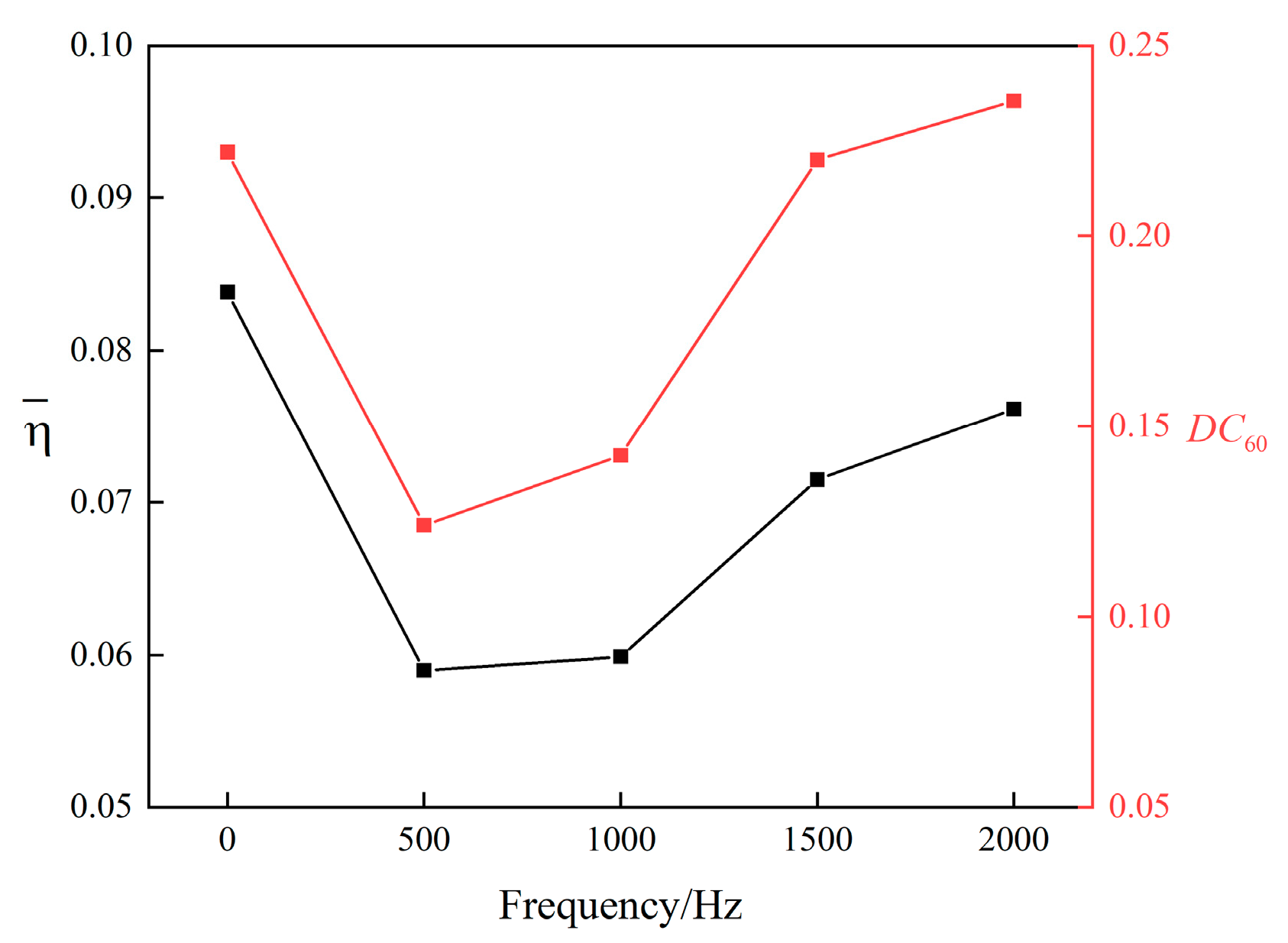
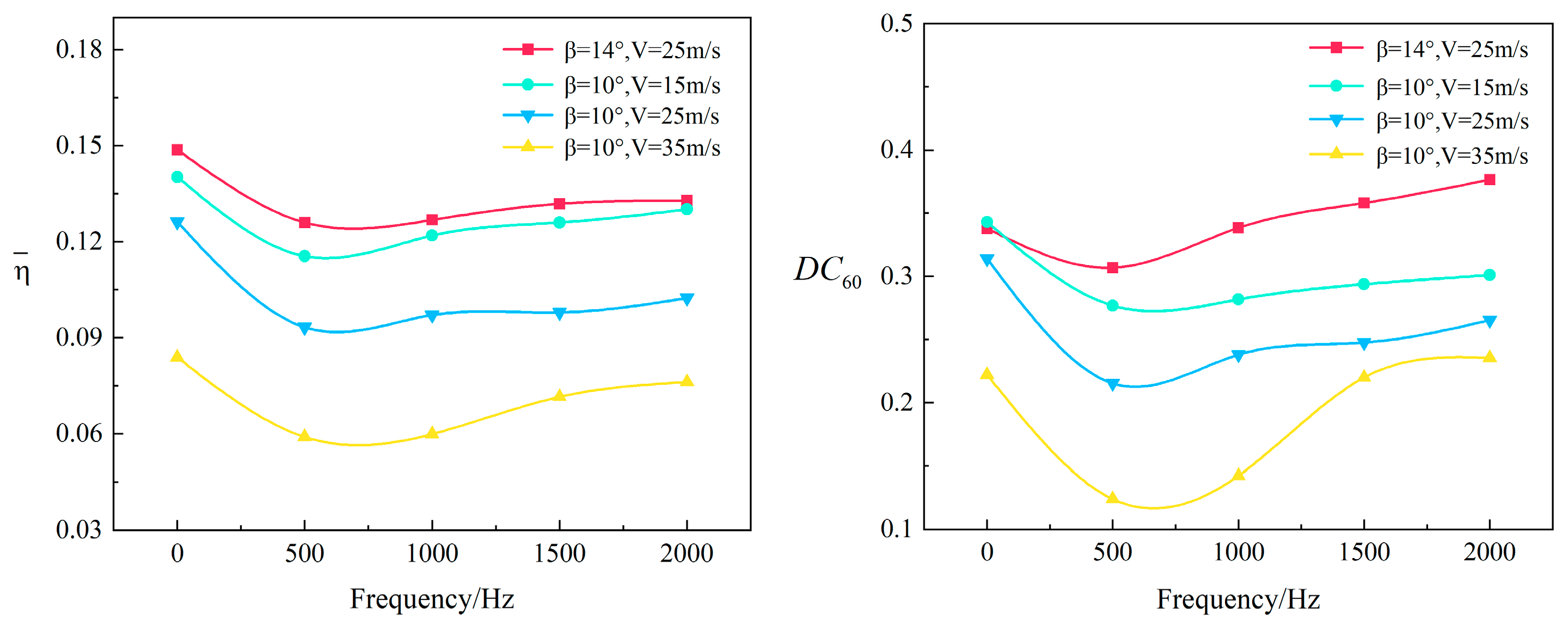
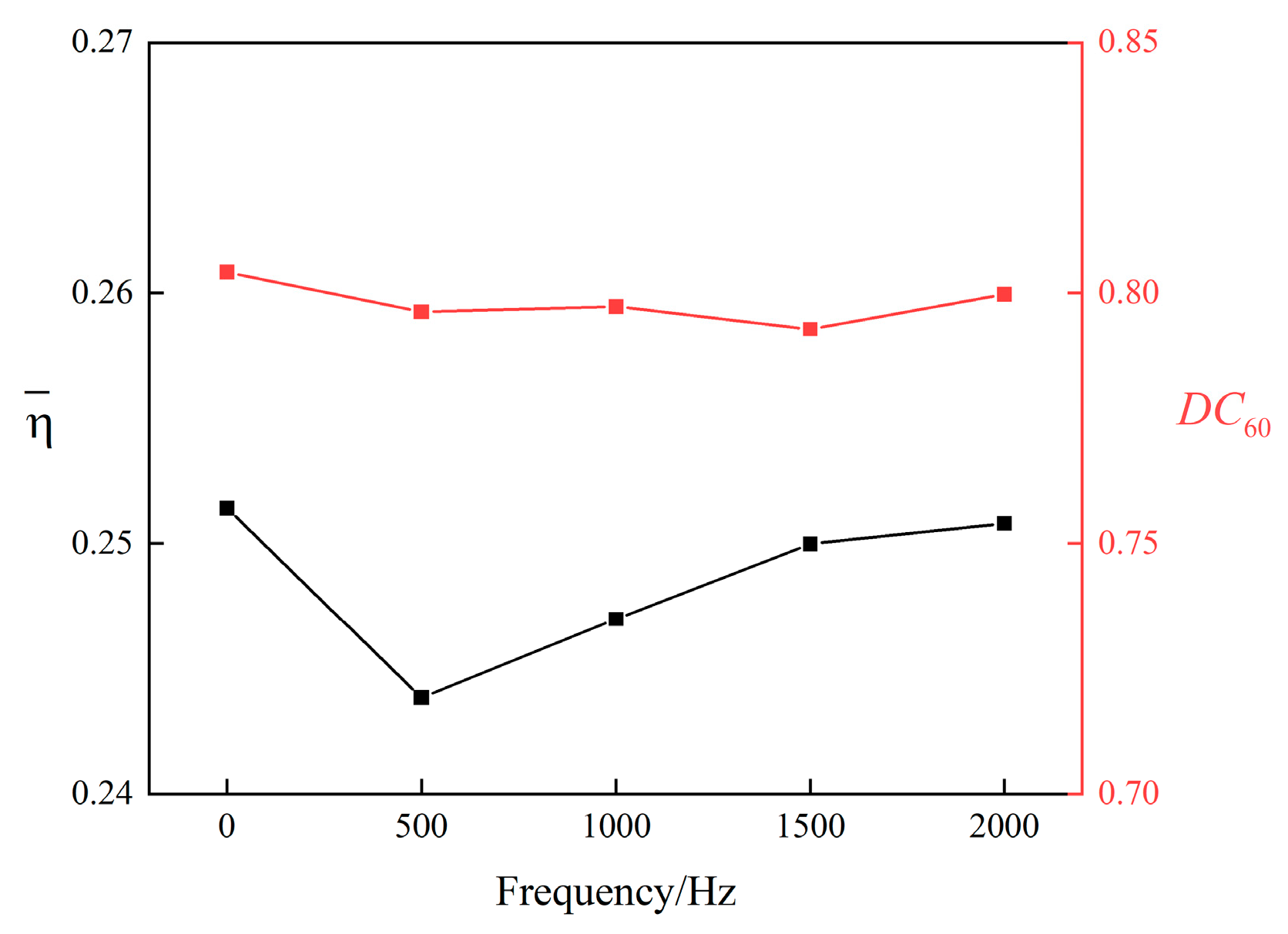
3.2. Flow Separation Control of Nacelle Inlets in Crosswinds by NS-DBD
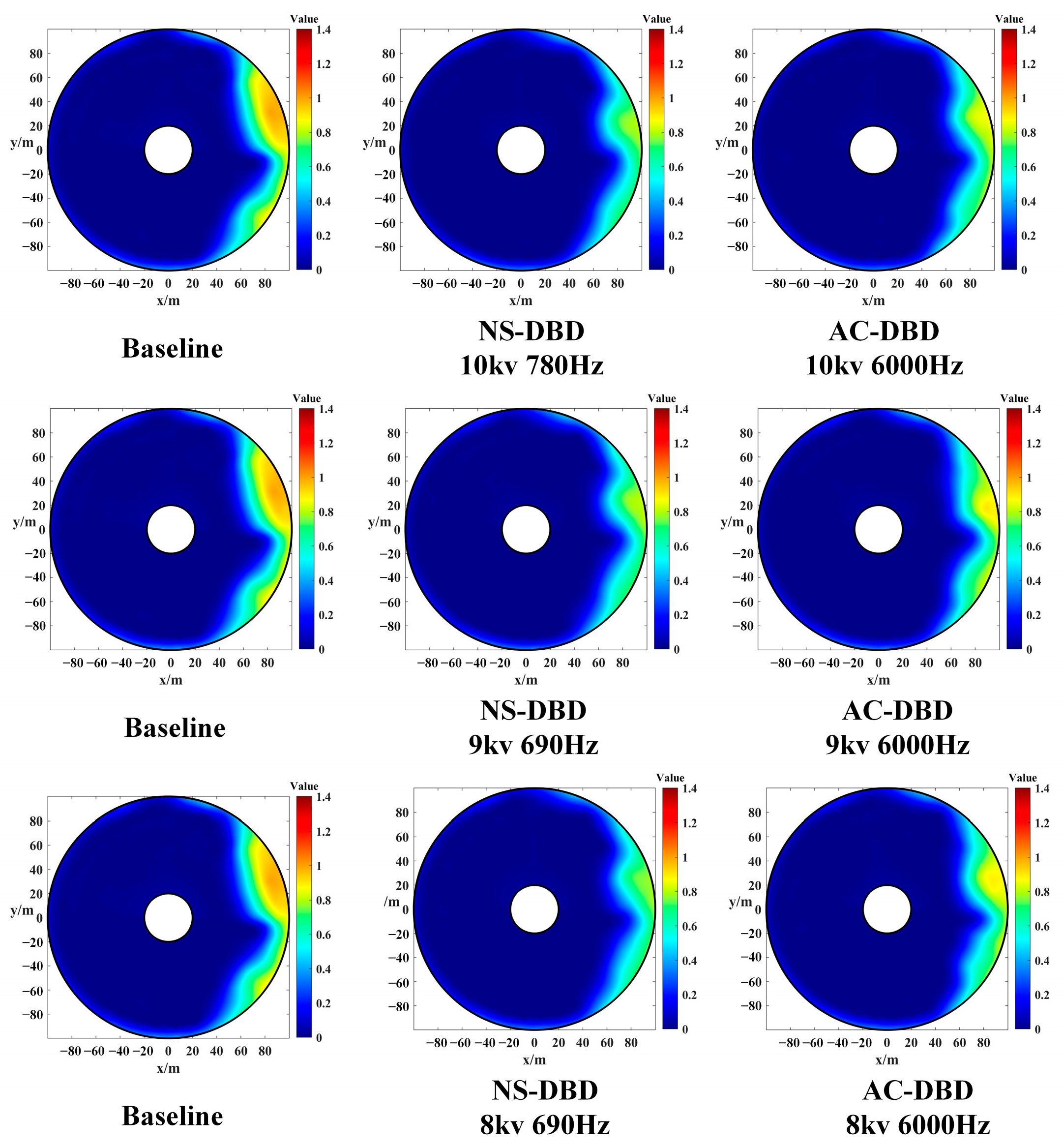
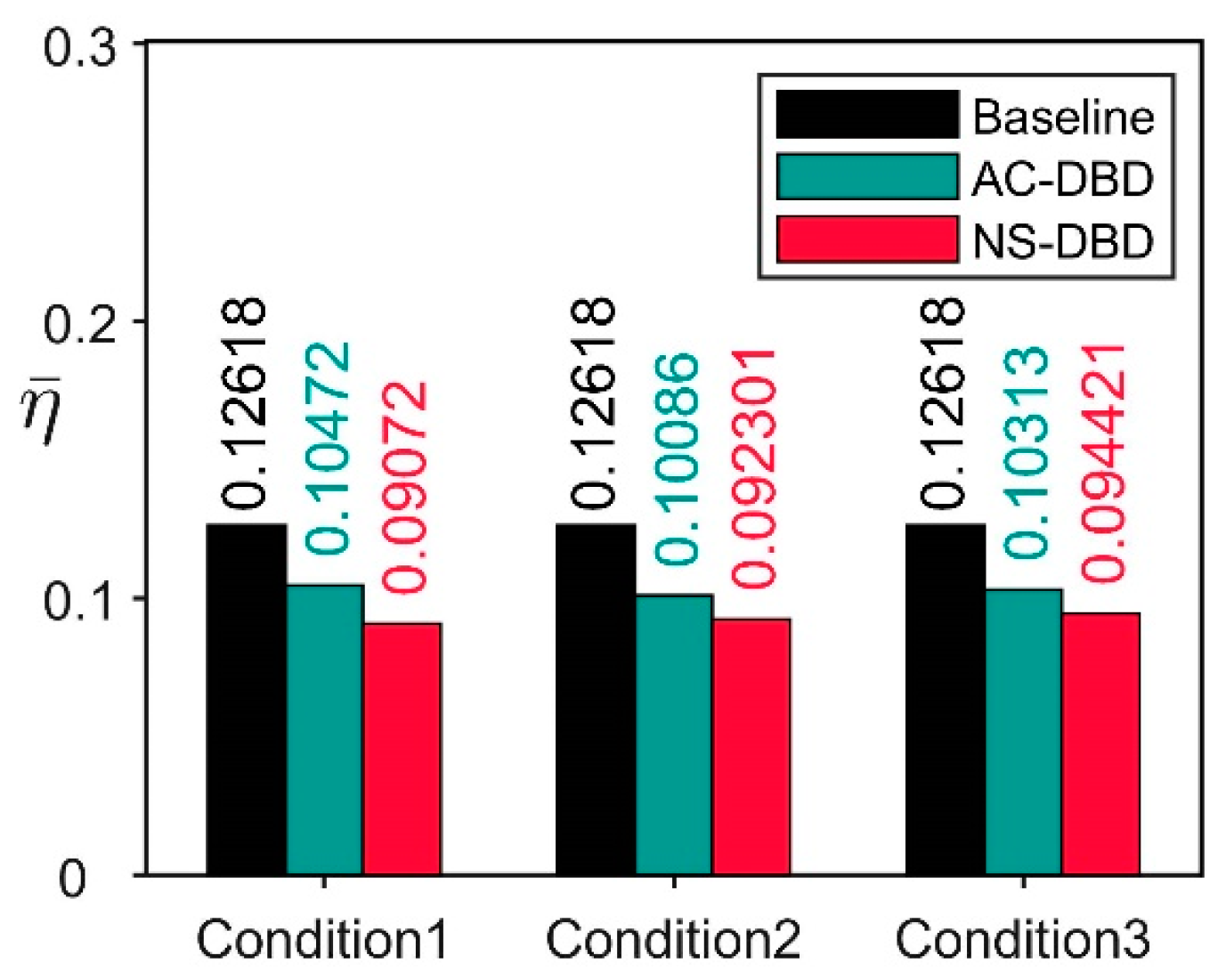
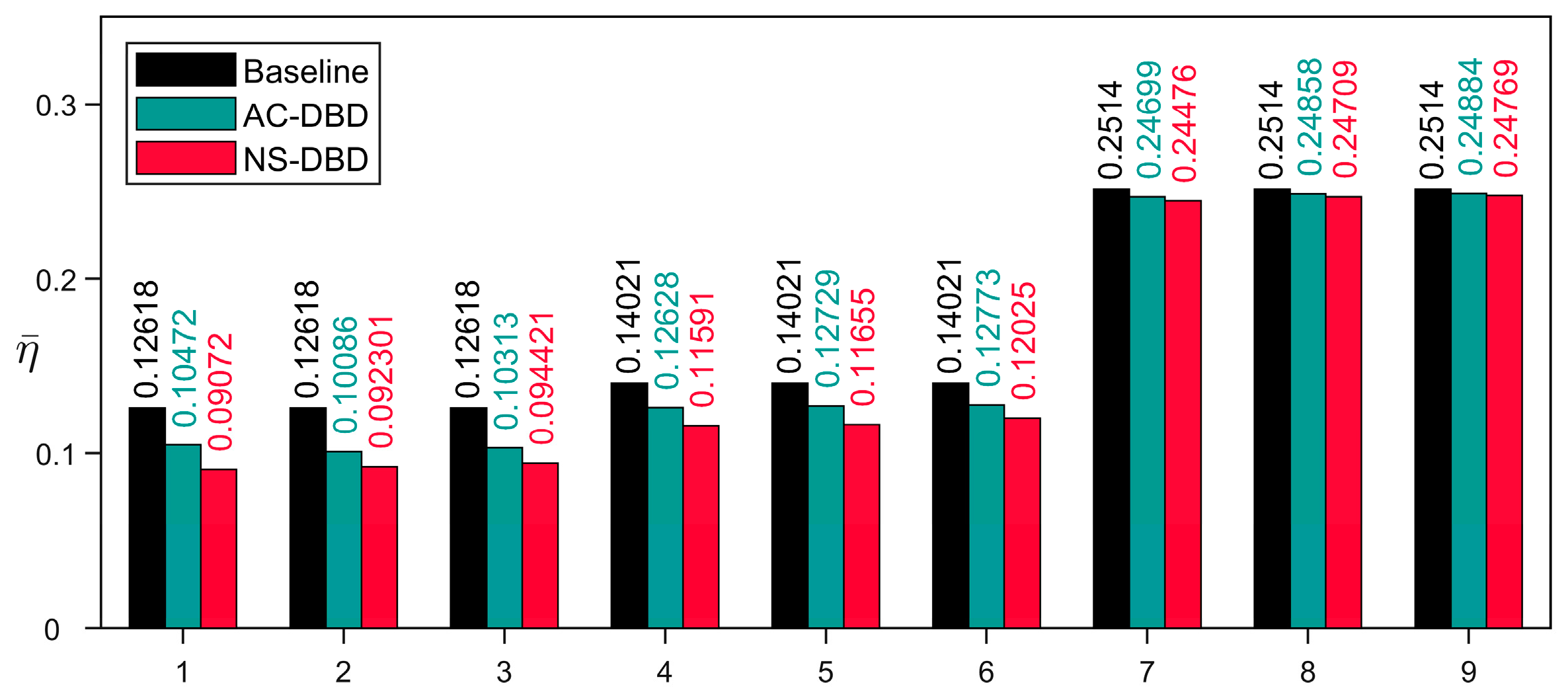
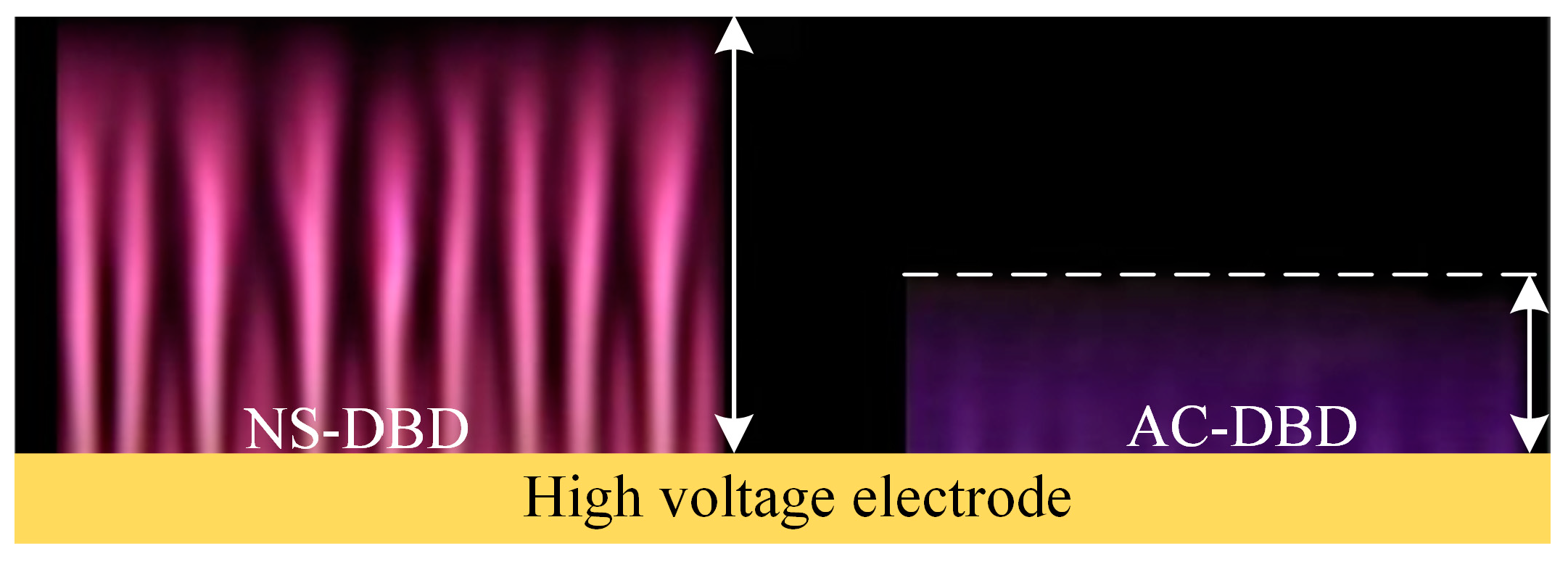
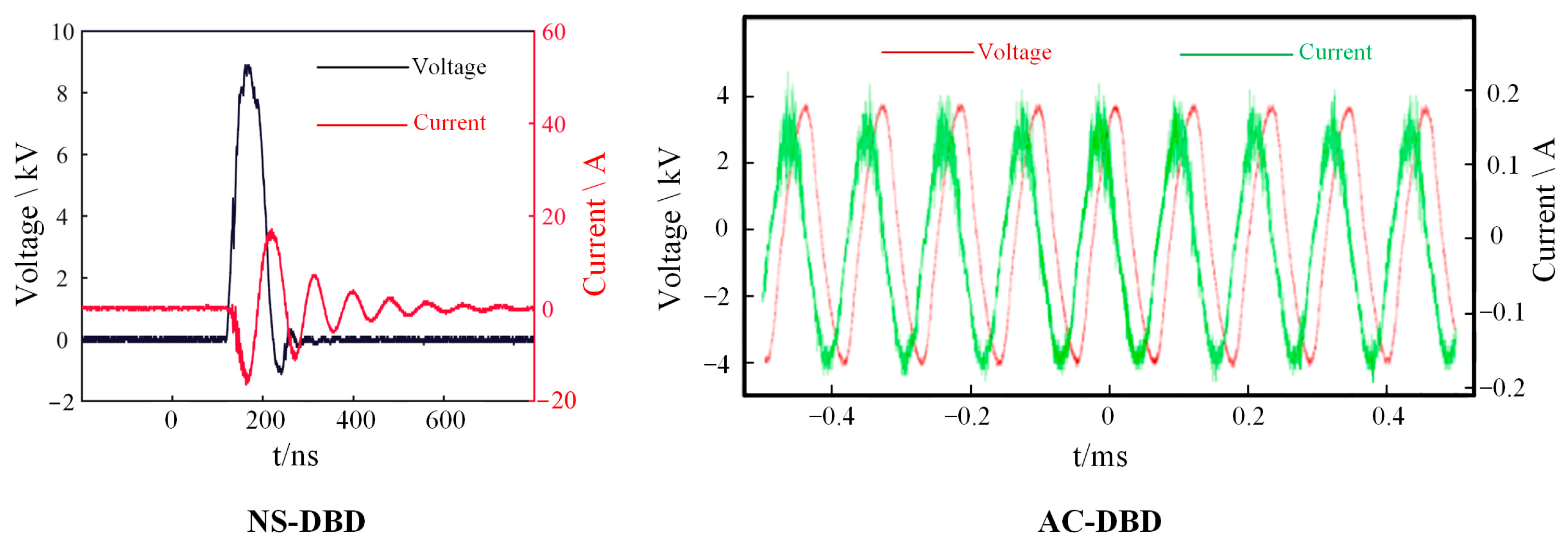
3.3. Comparative Experiment of Flow Control between NS-DBD and AC-DBD
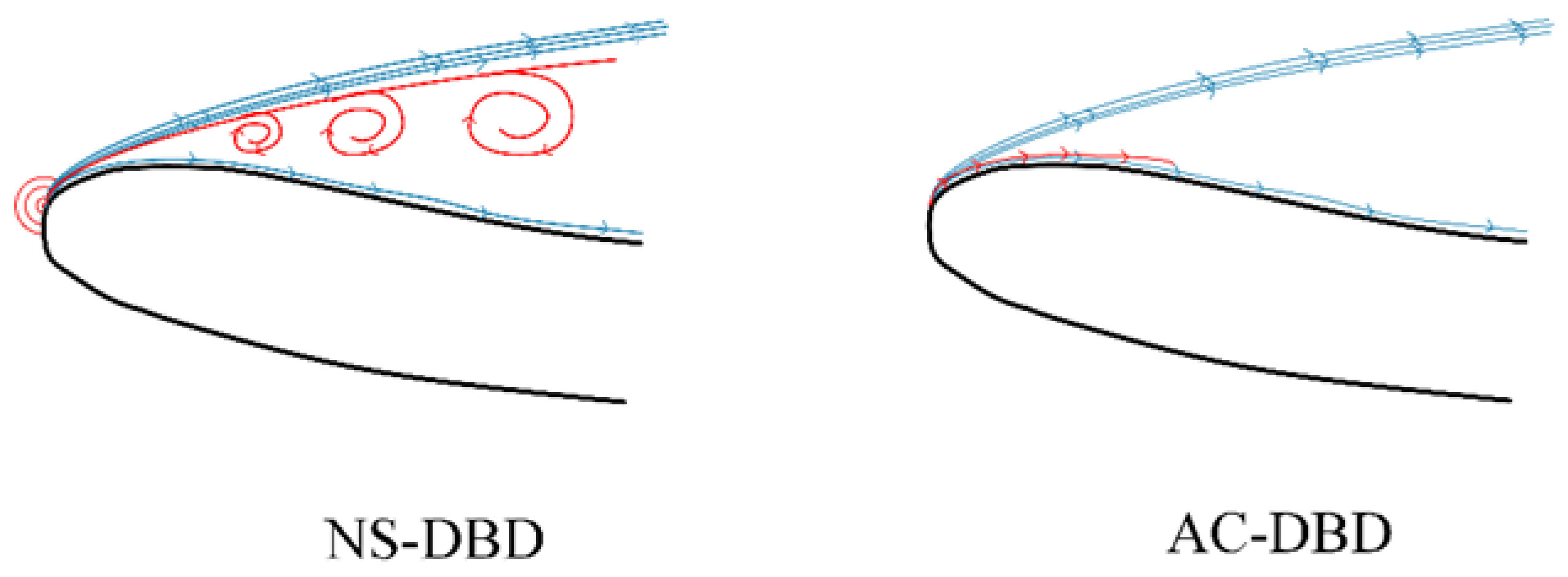
3.4. Mechanism of Dielectric Barrier Discharge Flow Control in Crosswinds
4. Conclusions
- (1)
- NS-DBD can reduce the total pressure loss coefficient and flow separation range. Under the condition that = 10° and = 35 m/s, the total pressure distortion basically disappears;
- (2)
- There is an inherent optimal coupling frequency of NS-DBD, under which the total pressure distortion of the crosswind separation flow field is minimal;
- (3)
- NS-DB has an obvious flow control effect, mainly in the case of small separation distortion. However, the control effect on the separation field is limited when the separation distortion is large;
- (4)
- AC-DBD can also improve total pressure distortion, but under the same actuation power, the control effect of NS-DBD is better than AC-DBD;
- (5)
- Compared with AC-DBD, the “impact mechanism” and the attached vortex structure of NS-DBD are more conducive to promoting the mixing momentum exchange of the boundary layer between the mainstream zone and the separation zone, and the flow control effect is better. Therefore, NS-DBD should be preferred in the problem of flow separation of nacelles under crosswind conditions.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vunnam, K.; Hoover, R. Modeling of Inlet Distortion using a Combined Turbofan and Nacelle Inlet Model during Crosswind and Low Speed Forward Operation. In Proceedings of the ASME 2011 Turbo Expo: Turbine Technical Conference and Exposition, Vancouver, BC, Canada, 6–10 June 2011. [Google Scholar]
- Motycka, D.L. Reynolds number and fan/inlet coupling effects on subsonic transport inlet distortion. J. Propuls. Power 1985, 1, 229–234. [Google Scholar] [CrossRef]
- Murphy, J.P.; MacManus, D.G. Ground vortex aerodynamics under crosswind conditions. Exp. Fluids 2011, 50, 109–124. [Google Scholar] [CrossRef]
- Brix, S.; Neuwerth, G.; Jacob, D. The inlet-vortex system of jet engines operating near the ground. In Proceedings of the 18th Applied Aerodynamics Conference, Denver, CO, USA, 14–17 August 2000. [Google Scholar]
- Zantopp, S.; MacManus, D.; Murphy, J. Computational and experimental study of intake ground vortices. Aeronaut. J. 2010, 114, 769–784. [Google Scholar] [CrossRef]
- Hall, C.A.; Hynes, T.P. Measurements of intake separation hysteresis in a model fan and nacelle rig. J. Propuls. Power 2006, 22, 872–879. [Google Scholar] [CrossRef]
- Majić, F.; Efraimsson, G.; O’Reilly, C.J. Potential improvement of aerodynamic performance by morphing the nacelle inlet. Aerosp. Sci. Technol. 2016, 54, 122–131. [Google Scholar] [CrossRef]
- Yeung, A.; Vadlamani, N.R.; Hynes, T.; Sarvankar, S. Quasi 3D nacelle design to simulate crosswind flows: Merits and challenges. Int. J. Turbomach. Propuls. Power 2019, 4, 25. [Google Scholar] [CrossRef]
- Minaker, Q.J.; Defoe, J.J. Prediction of crosswind separation velocity for fan and nacelle systems using body force models: Part 1: Fan body force model generation without detailed stage geometry. Int. J. Turbomach. Propuls. Power 2019, 4, 43. [Google Scholar] [CrossRef]
- Minaker, Q.J.; Defoe, J.J. Prediction of crosswind separation velocity for fan and nacelle systems using body force models: Part 2: Comparison of crosswind separation velocity with and without detailed fan stage geometry. Int. J. Turbomach. Propuls. Power 2019, 4, 41. [Google Scholar] [CrossRef]
- Harjes, L.; Bode, C.; Grubert, J.; Frantzheld, P.; Koch, P.; Friedrichs, J. Investigation of jet engine intake distortions caused by crosswind conditions. J. Glob. Power Propuls. Soc. 2020, 4, 48–62. [Google Scholar] [CrossRef]
- Laroussi, M.; Lu, X.; Keidar, M. Perspective: The physics, diagnostics, and applications of atmospheric pressure low temperature plasma sources used in plasma medicine. J. Appl. Phys. 2017, 122, 020901. [Google Scholar] [CrossRef]
- Laroussi, M.; Tendero, C.; Lu, X. Inactivation of bacteria by the plasma pencil. Plasma Process. Polym. 2006, 3, 470–473. [Google Scholar] [CrossRef]
- Woedtke, T.V.; Reuter, S.; Masur, K. Plasmas for medicine. Phys. Rep. 2013, 530, 291–320. [Google Scholar] [CrossRef]
- Hoffmann, C.; Berganza, C.; Zhang, J. Cold Atmospheric Plasma: Methods of production and application in dentistry and oncology. Med. Gas Res. 2013, 3, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Xie, J.; Chen, Q.; Suresh, P. based plasma sanitizers. Proc. Natl. Acad. Sci. USA 2017, 114, 5119–5124. [Google Scholar] [CrossRef]
- Choudhury, B.; Revazishvili, T.; Lozada, M. Distributed compact plasma reactor decontamination for planetary protection in space missions. Sci. Rep. 2023, 13, 1928. [Google Scholar] [CrossRef] [PubMed]
- Penetrante, B.M.; Hsiao, M.C.; Bardsley, J.N. Electron beam and pulsed corona processing of volatile organic compounds in gas streams. Pure Appl. Chem. 1996, 68, 1083–1087. [Google Scholar] [CrossRef]
- Kim, H.H. Nonthermal plasma processing for air-pollution control: A historical review, current issues, and future prospects. Plasma Process. Polym. 2004, 1, 91–110. [Google Scholar] [CrossRef]
- Oda, T.; Takahashi, T.; Nakano, H. Decomposition of fluorocarbon gaseous contaminants by surface discharge-induced plasma chemical processing. IEEE Trans. Ind. Appl. 1993, 29, 787–792. [Google Scholar] [CrossRef]
- Jiang, Z.; Fang, D.; Liang, Y. Catalytic degradation of benzene over non-thermal plasma coupled Co-Ni binary metal oxide nanosheet catalysts. J. Environ. Sci. (China) 2023, 132, 1–11. [Google Scholar] [CrossRef]
- Toko, S.; Hasegawa, T.; Okumura, T. Optical emission spectroscopy study in CO2 methanation with plasma. Jpn J. Appl. Phys. 2023, 62, SI1008. [Google Scholar] [CrossRef]
- Wallis, A.E.; Whitehead, J.C.; Zhang, K. Plasma-assisted catalysis for the destruction of CFC-12 in atmospheric pressure gas streams using TiO2. Catal. Lett. 2007, 113, 29–33. [Google Scholar] [CrossRef]
- Guo, Y.F.; Ye, D.Q.; Chen, K.F. Toluene decomposition using a wire-plate dielectric barrier discharge reactor with manganese oxide catalyst in situ. J. Mol. Catal. A Chem. 2006, 245, 93–100. [Google Scholar] [CrossRef]
- Morozumi, J.; Goya, T.; Kuyama, T. In-situ electrical monitoring of SiO2/Si structures in low-temperature plasma using impedance spectroscopy. Jpn J. Appl. Phys. 2023, 62, SI1010. [Google Scholar] [CrossRef]
- Morshed, M.M.; Alam, M.M.; Daniels, S.M. Plasma treatment of natural jute fibre by RIE 80 plus plasma tool. Plasma Sci. Technol. 2010, 12, 325. [Google Scholar] [CrossRef]
- Vanneste, J.; Ennaert, T.; Vanhulsel, A. Unconventional pretreatment of lignocellulose with low-temperature plasma. ChemSusChem 2017, 10, 14–31. [Google Scholar] [CrossRef]
- Corke, T.C.; Post, M.L.; Orlov, D.M. Single-dielectric barrier discharge plasma enhanced aerodynamics: Concepts, optimization, and applications. J. Propuls. Power 2008, 24, 935–945. [Google Scholar] [CrossRef]
- Yang, H.; Liang, H.; Zhao, G.; Wang, B.; Zhang, S.; Kong, W. Experimental study on dynamic stall control based on AC-DBD actuation. Plasma Sci. Technol. 2021, 23, 115502. [Google Scholar] [CrossRef]
- Yang, H.; Zhao, G.; Liang, H.; Wei, B. Dynamic stall control over an airfoil by NS-DBD actuation. Chinese Phys. B 2020, 29, 105203. [Google Scholar] [CrossRef]
- Veerakumar, R.; Raul, V.; Liu, Y.; Wang, X.; Leifsson, L.; Hu, H. Metamodeling-based parametric optimization of DBD plasma actuation to suppress flow separation over a wind turbine airfoil model. Acta Mech. Sin. 2020, 36, 260–274. [Google Scholar] [CrossRef]
- Little, J.; Singh, A.; Ashcraft, T.; Durasiewicz, C. Post-stall flow control using nanosecond pulse driven dielectric barrier discharge plasma actuators. Plasma Sources Sci. Technol. 2019, 28, 014002. [Google Scholar] [CrossRef]
- Sekimoto, S.; Fujii, K.; Anyoji, M.; Miyakawa, Y.; Ito, S.; Shimomura, S.; Nishida, H.; Nonomura, T.; Matsuno, T. Flow Control around NACA0015 Airfoil Using a Dielectric Barrier Discharge Plasma Actuator over a Wide Range of the Reynolds Number. Actuators 2023, 12, 43. [Google Scholar] [CrossRef]
- Matsunuma, T. Effects of the Installation Location of a Dielectric Barrier Discharge Plasma Actuator on the Active Passage Vortex Control of a Turbine Cascade at Low Reynolds Numbers. Actuators 2022, 11, 129. [Google Scholar] [CrossRef]
- Geng, X.; Shi, Z.; Cheng, K.; Dong, H.; Zhao, Q.; Chen, S. Experimental investigations on characteristics of boundary layer and control of transition on an airfoil by AC-DBD. Mod. Phys. Lett. B. 2018, 32, 1850108. [Google Scholar] [CrossRef]
- Kriegseis, J.; Simon, B.; Grundmann, S. Towards in-flight applications? A review on dielectric barrier discharge-based boundary-layer control. Appl. Mech. Rev. 2016, 68, 020802. [Google Scholar] [CrossRef]
- Im, S.; Do, H.; Cappelli, M.A. Dielectric barrier discharge control of a turbulent boundary layer in a supersonic flow. Appl. Phys. Lett. 2010, 97, 041503. [Google Scholar] [CrossRef]
- Schatzman, D.M.; Thomas, F.O. Turbulent boundary-layer separation control with single dielectric barrier discharge plasma actuators. AIAA J. 2010, 48, 1620–1634. [Google Scholar] [CrossRef]
- Grundmann, S.; Tropea, C. Active cancellation of artificially introduced Tollmien–Schlichting waves using plasma actuators. Exp. Fluids 2008, 44, 795–806. [Google Scholar] [CrossRef]
- Arnob, D.G.; Subrata, R. Modification of energetic modes for transitional flow control. AIP Adv. 2022, 12, 035149. [Google Scholar]
- Yao, J.; Zhou, D.; He, H.; He, C.; Shi, Z.; Du, H. Experimental investigation of lift enhancement for flying wing aircraft using nanosecond DBD plasma actuators. Plasma Sci. Technol. 2017, 19, 044002. [Google Scholar] [CrossRef]
- Iranshahi, K.; Mani, M. Dielectric barrier discharge actuators employed as alternative to conventional high-lift devices. J. Aircr. 2018, 55, 2104–2113. [Google Scholar] [CrossRef]
- Xu, Z.; Wu, B.; Gao, C.; Wang, N. Numerical simulation of dynamic stall flow control using a multi-dielectric barrier discharge plasma actuation strategy. Phys. Plasmas 2022, 29, 103503. [Google Scholar] [CrossRef]
- Xie, L.; Liang, H.; Zong, H.; Liu, X.; Li, Y. Multipurpose distributed dielectric-barrier-discharge plasma actuation: Icing sensing, anti-icing, and flow control in one. Phys. Fluids 2022, 34, 071701. [Google Scholar] [CrossRef]
- Jia, Y.; Liang, H.; Zong, H.; Wei, B.; Xie, L.; Hua, W.; Li, Z. Ice shape modulation with nanosecond pulsed surface dielectric barrier discharge plasma actuator towards flight safety. Aerosp. Sci. Technol. 2022, 120, 631–651. [Google Scholar] [CrossRef]
- Rodrigues, F.; Abdollahzadehsangroudi, M.; Nunes-Pereira, J.; Páscoa, J. Recent Developments on Dielectric Barrier Discharge (DBD) Plasma Actuators for Icing Mitigation. Actuators 2023, 12, 5. [Google Scholar] [CrossRef]
- Moreira, M.; Rodrigues, F.; Cândido, S.; Santos, G.; Páscoa, J. Development of a Background-Oriented Schlieren (BOS) System for Thermal Characterization of Flow Induced by Plasma Actuators. Energies 2023, 16, 540. [Google Scholar] [CrossRef]
- Lilley, A.J.; Roy, S.; Michels, L. Performance recovery of plasma actuators in wet conditions. J. Phys. D 2022, 55, 155201. [Google Scholar] [CrossRef]
- Vassberg, J.; Tinoco, E.; Mani, M. Summary of the third AIAA CFD drag prediction workshop, 45th AIAA aerospace sciences meeting and exhibit. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2007. [Google Scholar]
- Trapp, L.G.; Girardi, R. Evaluation of nacelle drag using Computational Fluid Dynamics. J. Aerosp. Technol. Manag. 2010, 2, 145–153. [Google Scholar] [CrossRef]
- Trapp, L.G.; Girardi, R.M. Characteristics of Inlet Trailing Vortex. J. Aircr. 2020, 57, 305–316. [Google Scholar] [CrossRef]
- Trapp, L.G. Crosswind effects on engline inlets: The inlet vortex. J. Aircr. 2010, 47, 577–590. [Google Scholar] [CrossRef]
- Jia, Y.; Liang, H.; He, Q.; Su, Z.; Song, G. Flow separation control of nacelle in crosswind by microsecond pulsed surface dielectric barrier discharge plasma actuator. Flow Turbul. Combust. 2021, 107, 631–651. [Google Scholar] [CrossRef]
- Zheng, H.; Liang, H.; Jie, C.; Zong, H.; Xiang, M.; Xie, L.; Li, Y. Experimental study on plasma actuation characteristics of nanosecond pulsed dielectric barrier discharge. Plasma Sci. Technol. 2021, 24, 015505. [Google Scholar] [CrossRef]
- Yang, Z.; Song, H.; Wang, H.; Guo, S.; Jia, M.; Wang, K. Aerodynamic actuation characteristics of radio-frequency discharge plasma and control of supersonic flow. Chin. Phys. B 2019, 28, 024701. [Google Scholar] [CrossRef]
- Li, Y.; Wu, Y.; Liang, H. Principle of plasma impingement flow control for improving the ability of in hibiting flow separation. Chin. Sci. Bull. 2010, 55, 3060–3068. [Google Scholar]
- Chen, J.; Liang, H.; Wei, B. Discharge Characteristics of Surface Dielectric Barrier Discharge Driven by Parameterized Nanosecond Pulsed Power Supply. High Volt. Eng. 2019, 45, 3365–3374. [Google Scholar]
- Correale, G.; Michelis, T.; Ragni, D. Nanosecond-pulsed plasma actuation in quiescent air and laminar boundary layer. J. Phys. D Appl. Phys. 2014, 47, 105201. [Google Scholar] [CrossRef]
- Li, Y.; Wu, Y.; Liang, H. The mechanism of plasma shock flow control for enhancing flow separation control capability. Chin. Sci. Bull. 2010, 55, 3060. [Google Scholar]

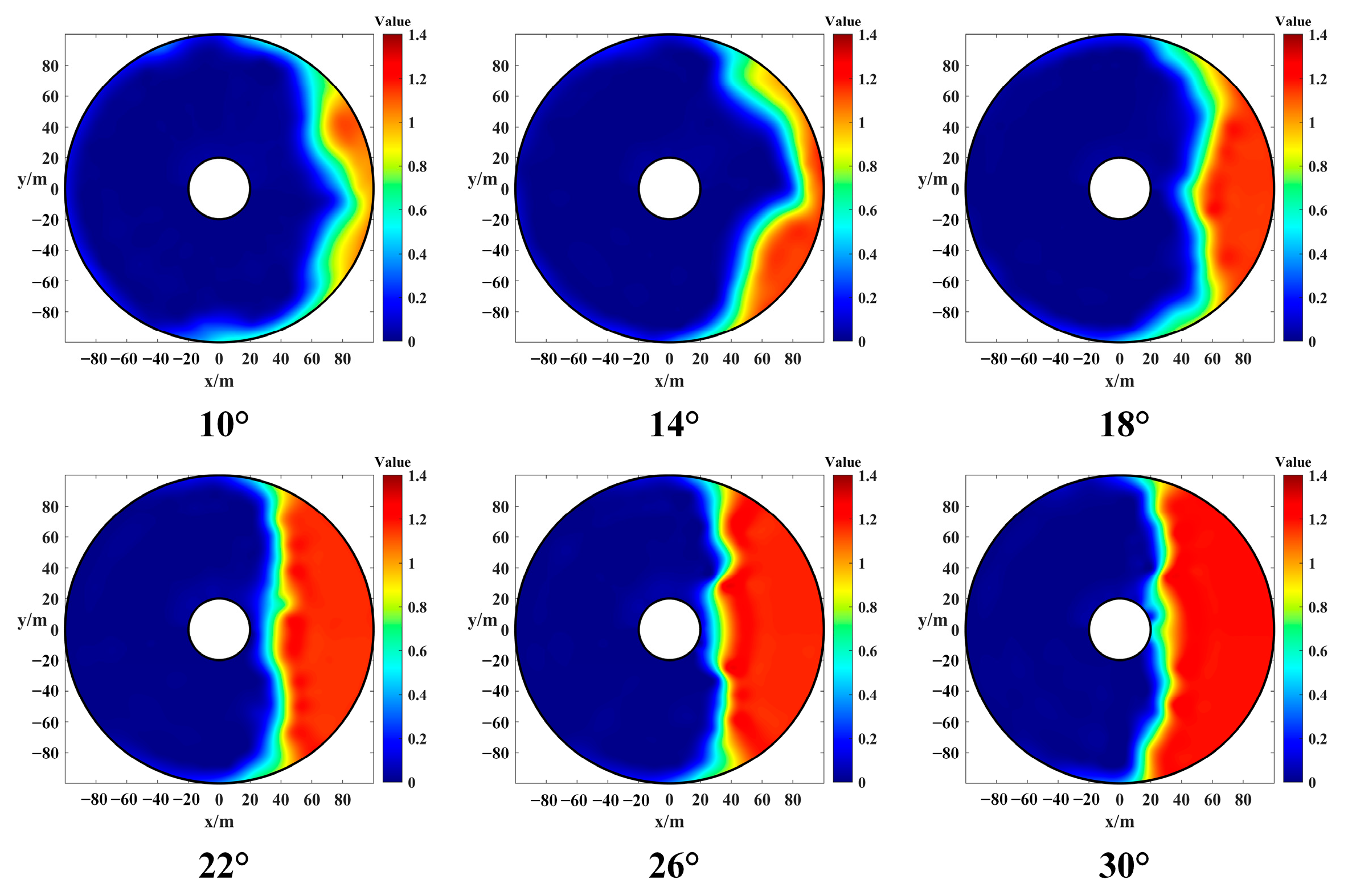
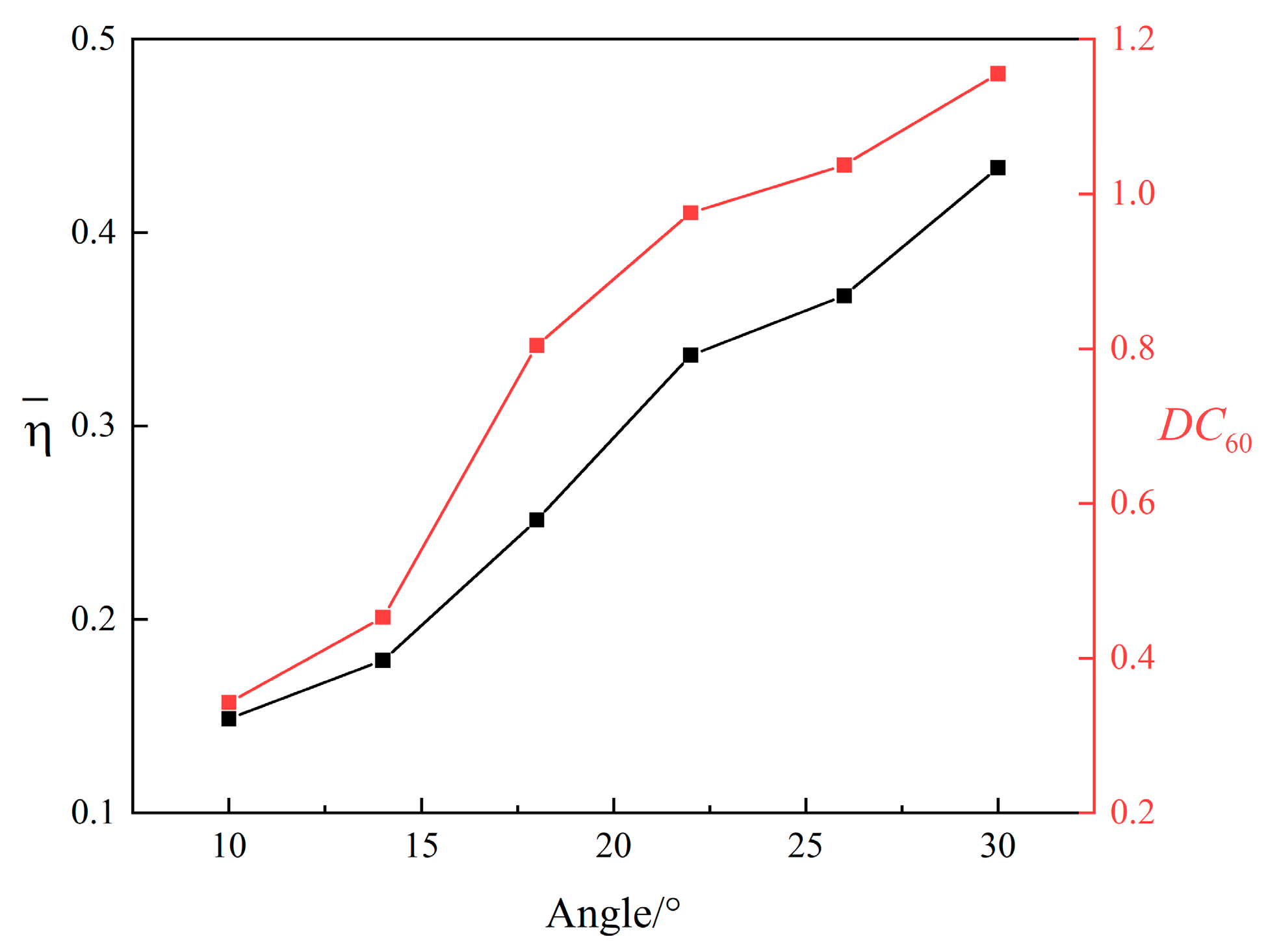
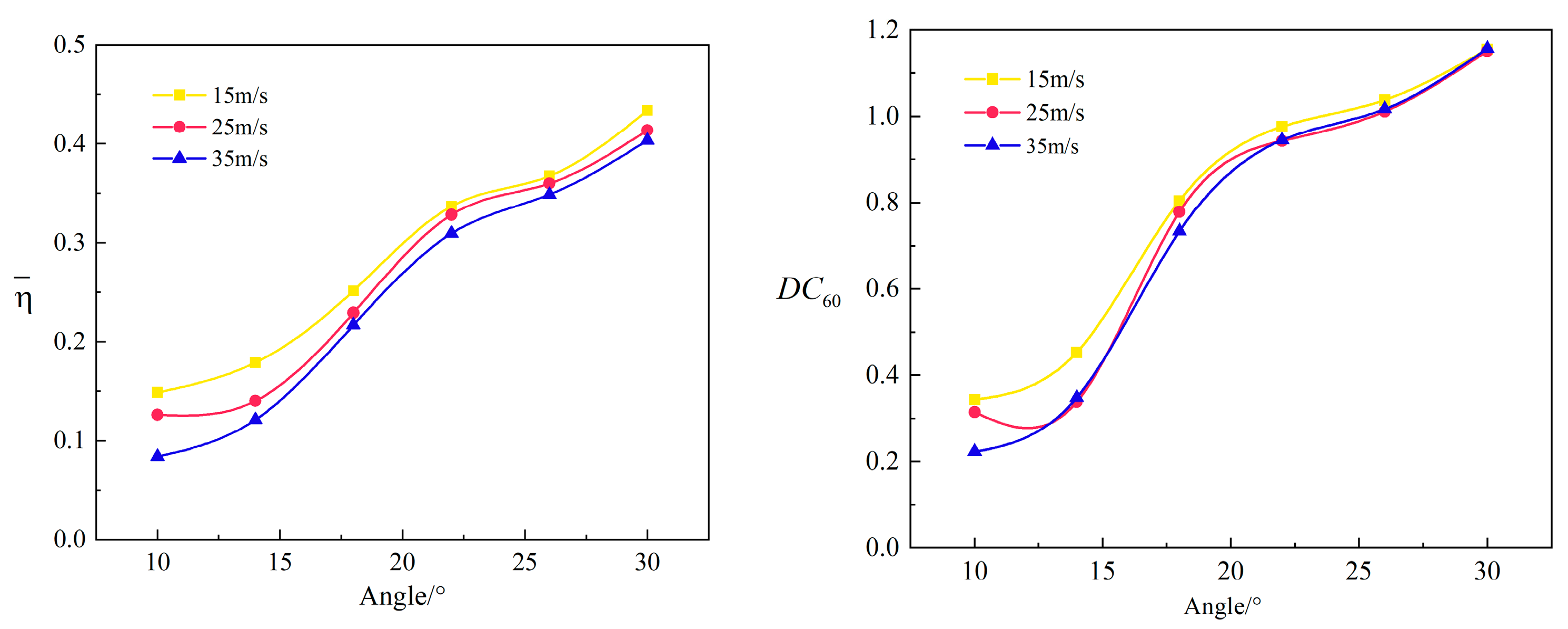
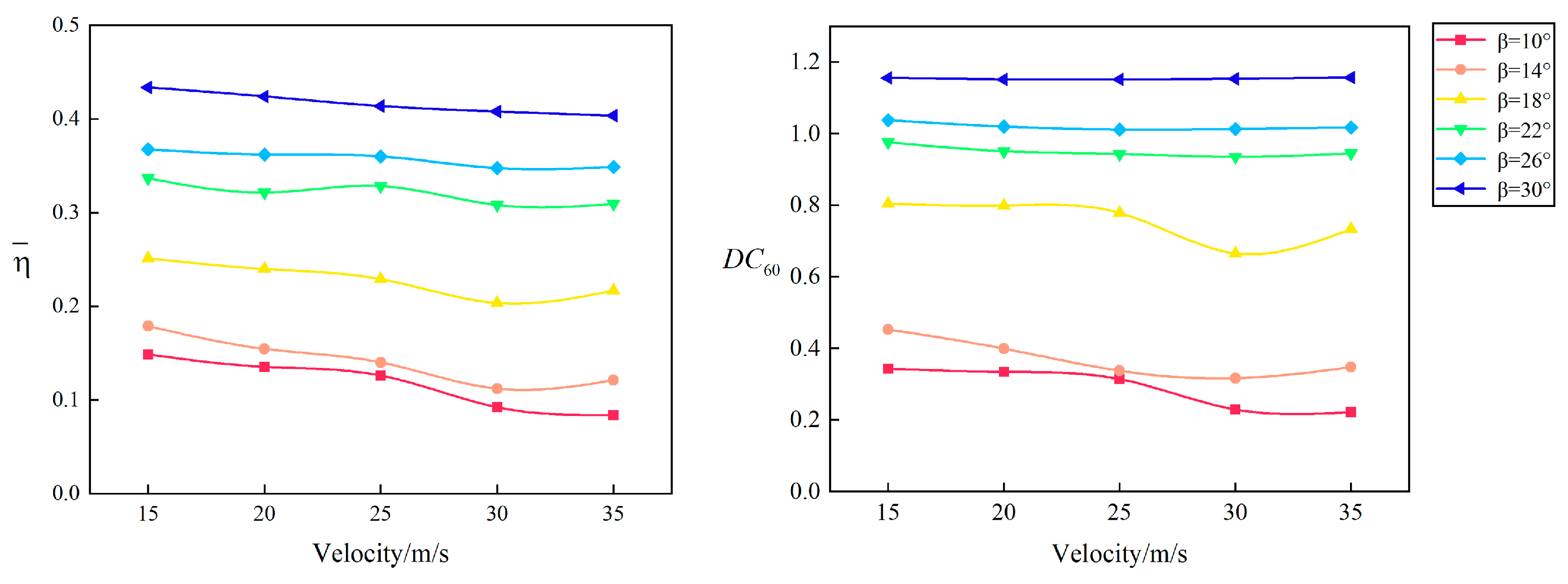


| Condition Number | ||
|---|---|---|
| 1 | 10° | 15 m/s |
| 2 | 10° | 35 m/s |
| 3 | 10° | 25 m/s |
| 4 | 14° | 25 m/s |
| 5 | 18° | 15 m/s |
| Number | Actuation Mode | Power | ||
|---|---|---|---|---|
| 1 | AC-DBD | 10 kV | 6000 Hz | 29.9704 |
| NS-DBD | 10 kV | 780 Hz | 29.8803 | |
| 2 | AC-DBD | 9 kV | 6000 Hz | 19.9858 |
| NS-DBD | 9 kV | 690 Hz | 20.1304 | |
| 3 | AC-DBD | 8 kV | 6000 Hz | 14.1942 |
| NS-DBD | 8 kV | 690 Hz | 14.2513 |
| Number | |||
|---|---|---|---|
| 1 | 10° | 25 m/s | 10 kV |
| 2 | 9 kV | ||
| 3 | 8 kV | ||
| 4 | 14° | 25 m/s | 10 kV |
| 5 | 9 kV | ||
| 6 | 8 kV | ||
| 7 | 18° | 25 m/s | 10 kV |
| 8 | 9 kV | ||
| 9 | 8 kV |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, D.; Liang, H.; Yang, H.; Su, Z.; Zhang, C.; Liu, S. Flow Separation Control of Nacelle Inlets in Crosswinds by Dielectric Barrier Discharge Plasma Actuation. Actuators 2023, 12, 229. https://doi.org/10.3390/act12060229
Zhang D, Liang H, Yang H, Su Z, Zhang C, Liu S. Flow Separation Control of Nacelle Inlets in Crosswinds by Dielectric Barrier Discharge Plasma Actuation. Actuators. 2023; 12(6):229. https://doi.org/10.3390/act12060229
Chicago/Turabian StyleZhang, Dongsheng, Hua Liang, Hesen Yang, Zhi Su, Chuanbiao Zhang, and Shimin Liu. 2023. "Flow Separation Control of Nacelle Inlets in Crosswinds by Dielectric Barrier Discharge Plasma Actuation" Actuators 12, no. 6: 229. https://doi.org/10.3390/act12060229
APA StyleZhang, D., Liang, H., Yang, H., Su, Z., Zhang, C., & Liu, S. (2023). Flow Separation Control of Nacelle Inlets in Crosswinds by Dielectric Barrier Discharge Plasma Actuation. Actuators, 12(6), 229. https://doi.org/10.3390/act12060229






