Implementation of a Cascade Fault Tolerant Control and Fault Diagnosis Design for a Modular Power Supply
Abstract
1. Introduction
2. Problem Formulation and Contribution of the Paper
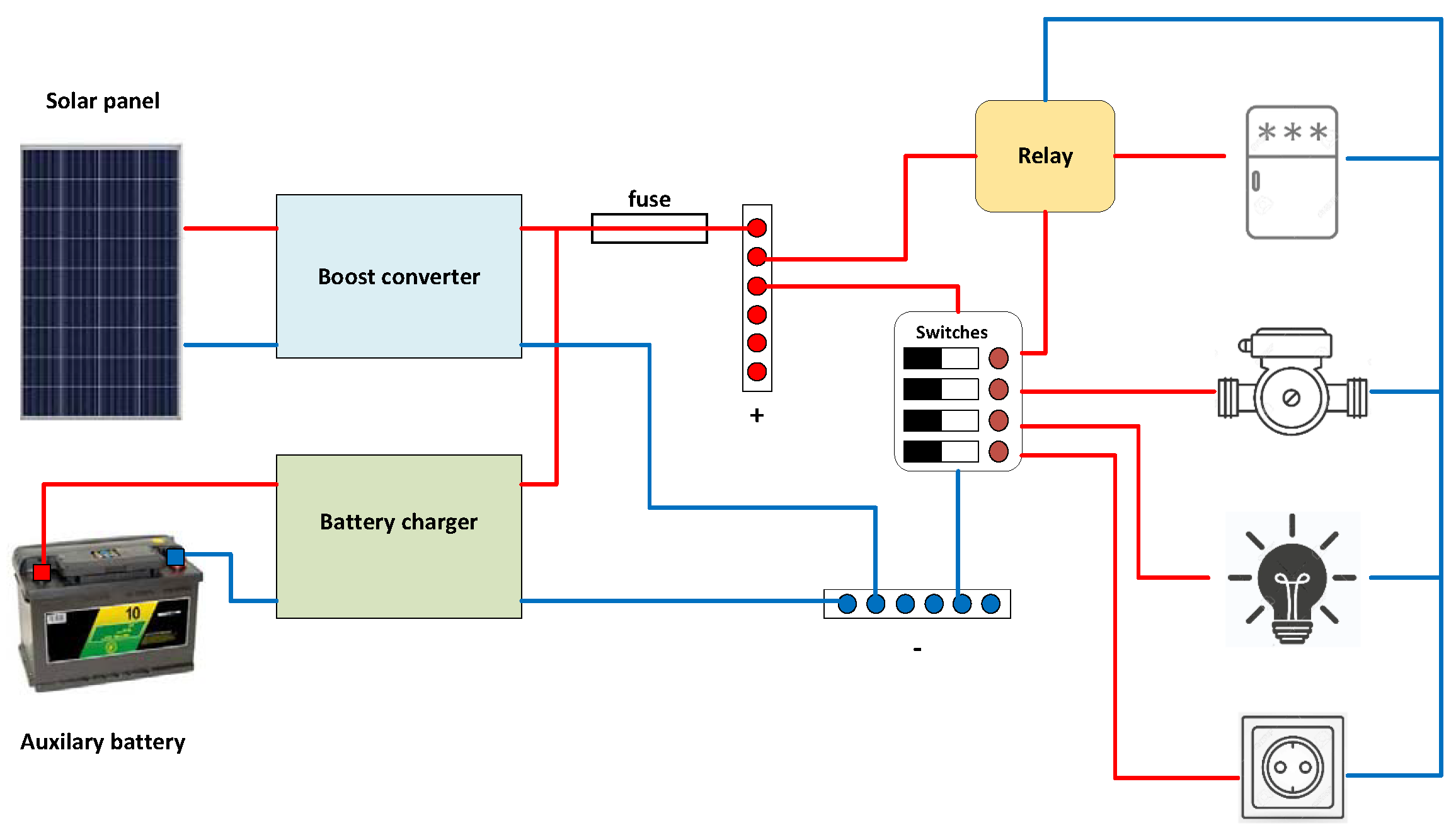
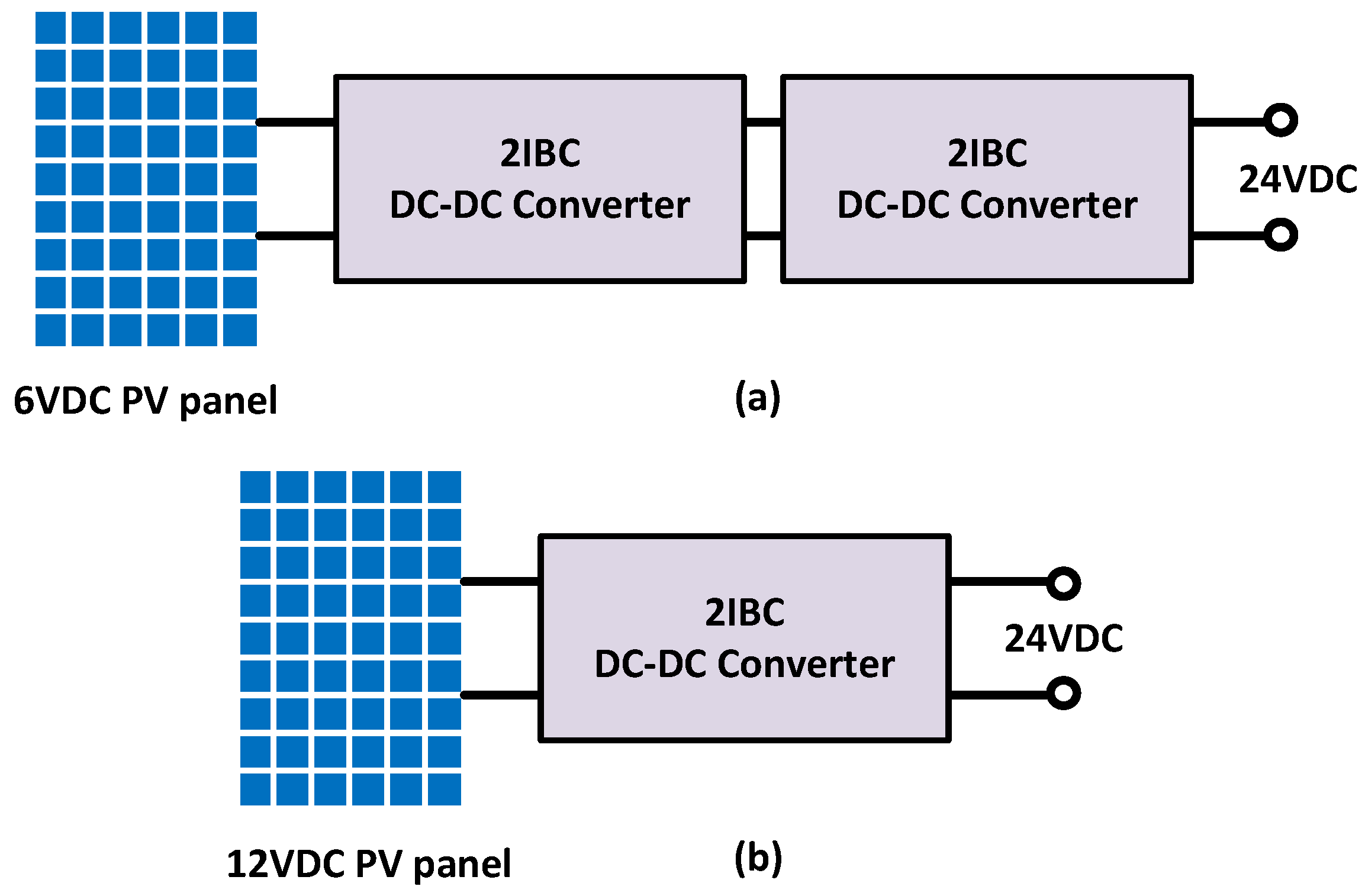
2.1. Case of Using the Modular Power Supply
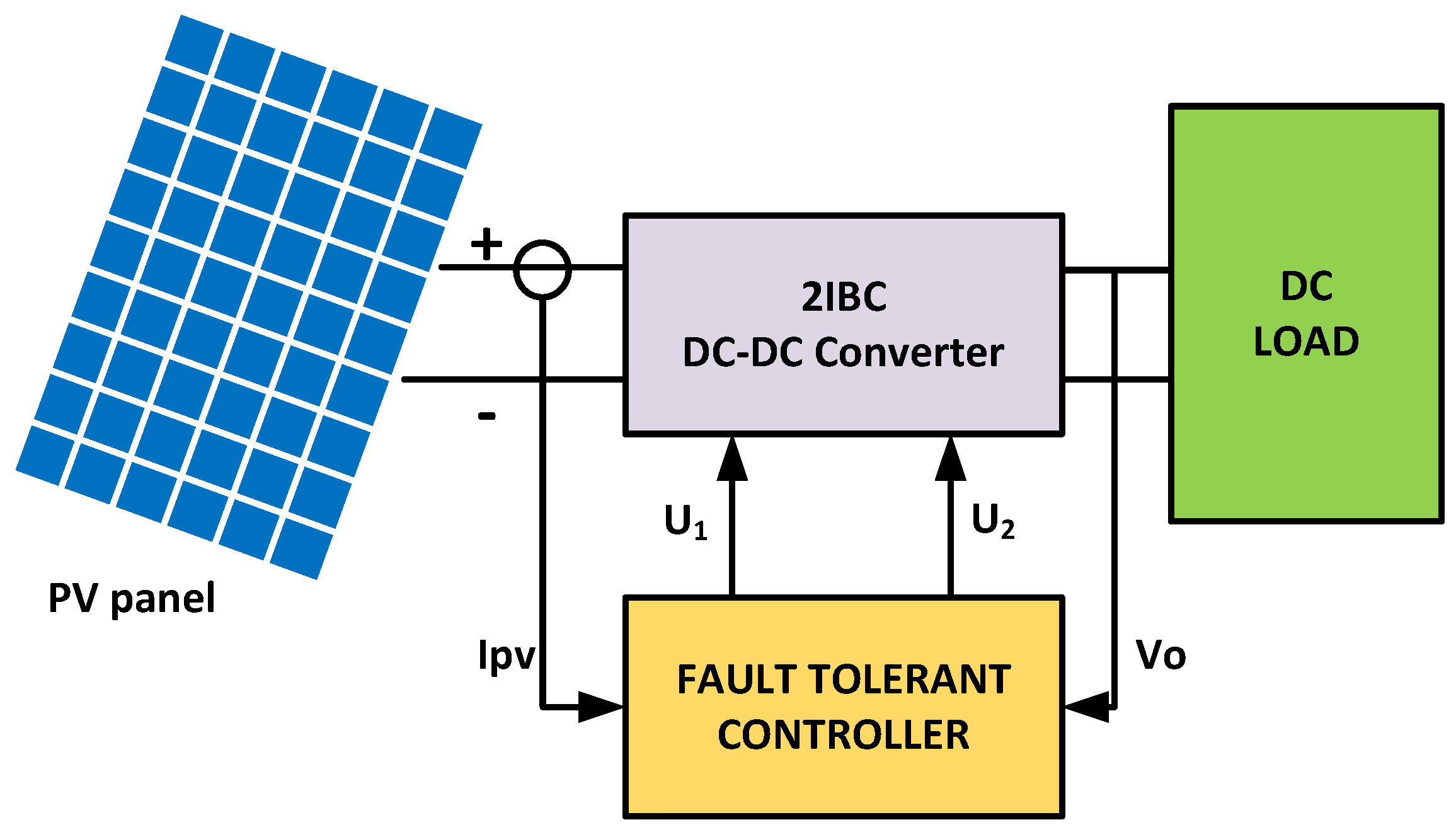
2.2. The Proposed Supervision Scheme and the Fault Tolerance of the Controller
3. The Cascade PI-Sliding Mode Control Applied to the Photovoltaic Power Supply
3.1. The Renewable Energy Power Supply
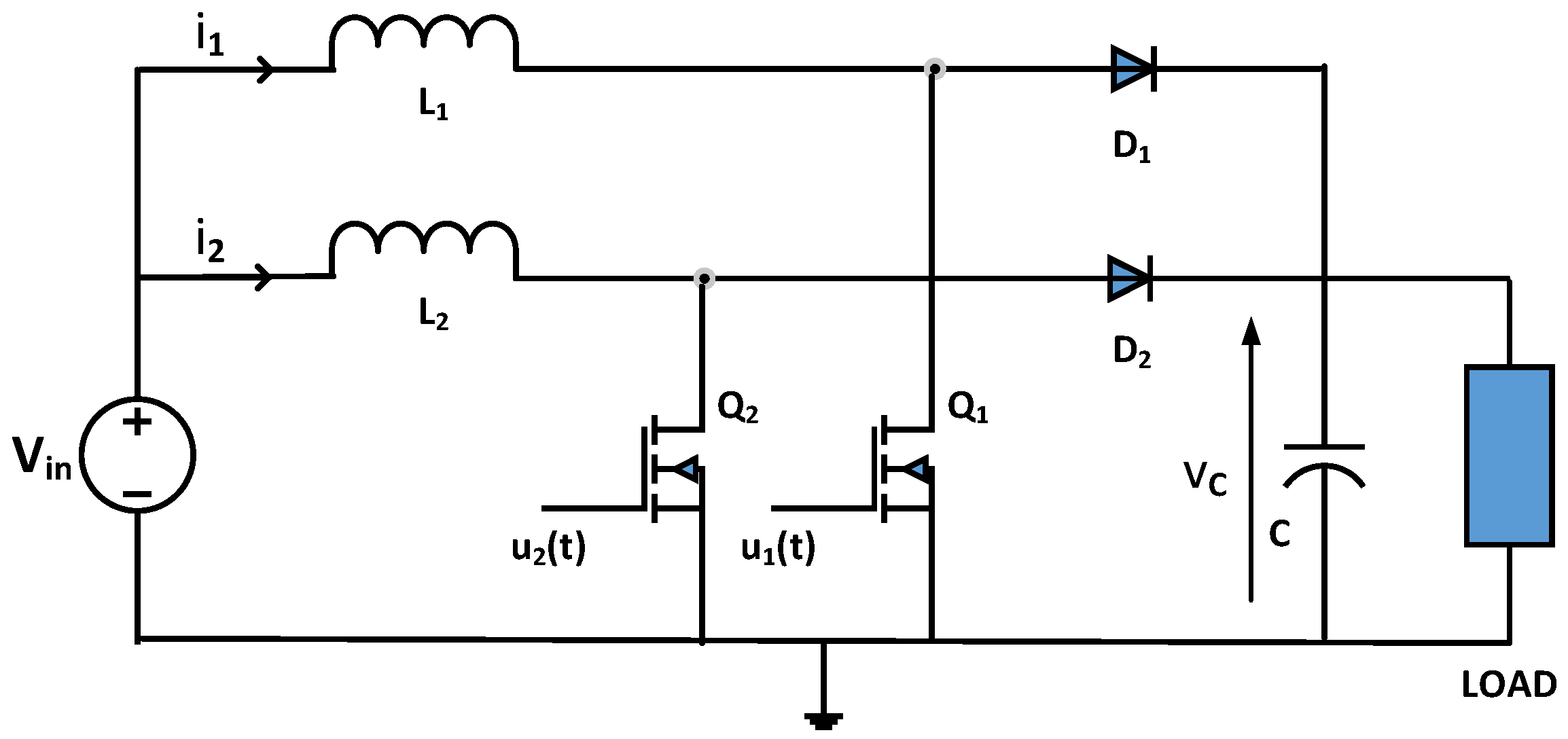
3.2. The Two-Stage Boost Converter Model
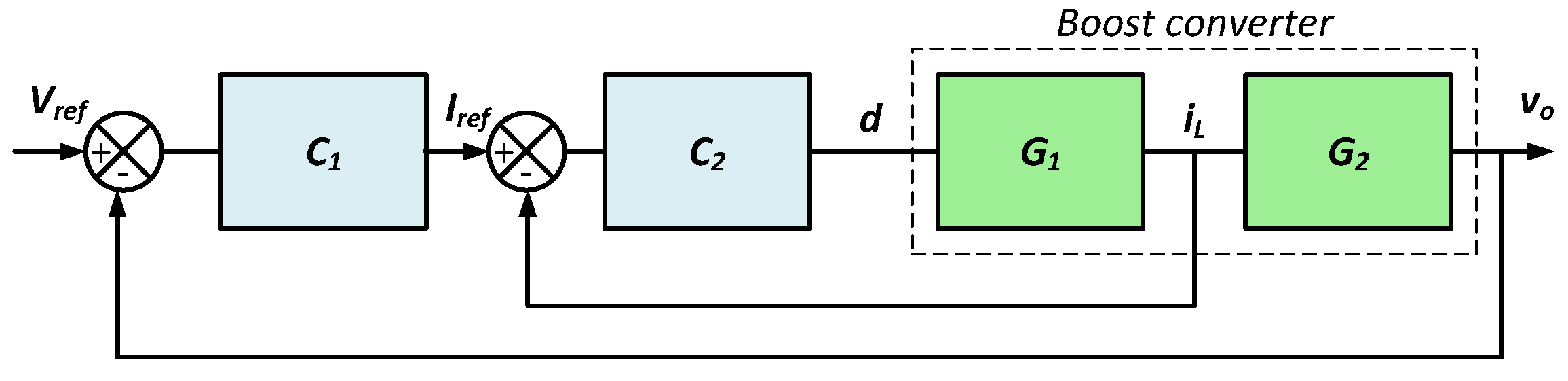
3.3. The Application of the PI-SMC Control Approach
4. Fault Diagnosis Using Analytic Redundancy Relations
4.1. Illustrative Example
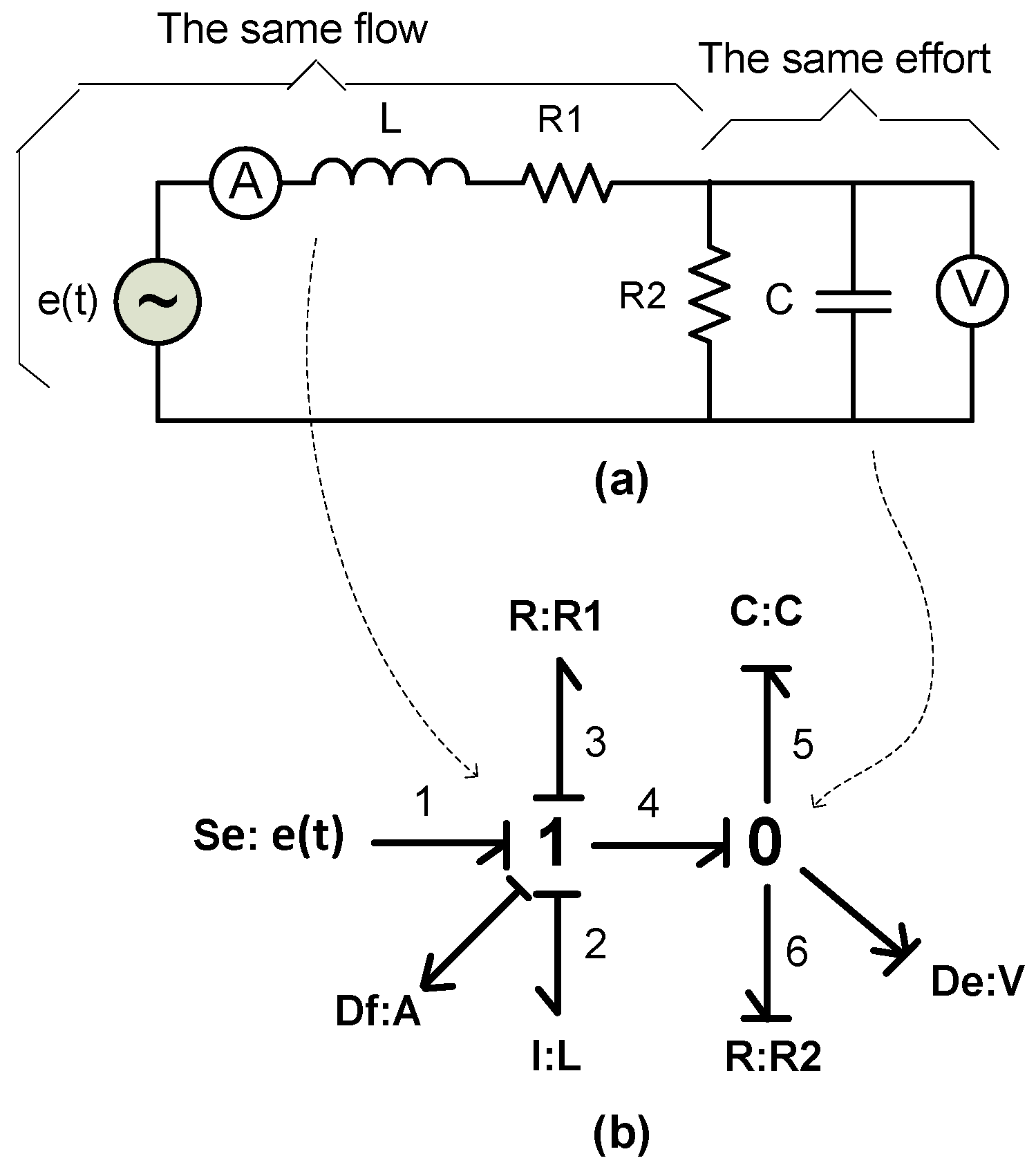
4.2. The Bond Graph Model of the Interleaved Power Converter
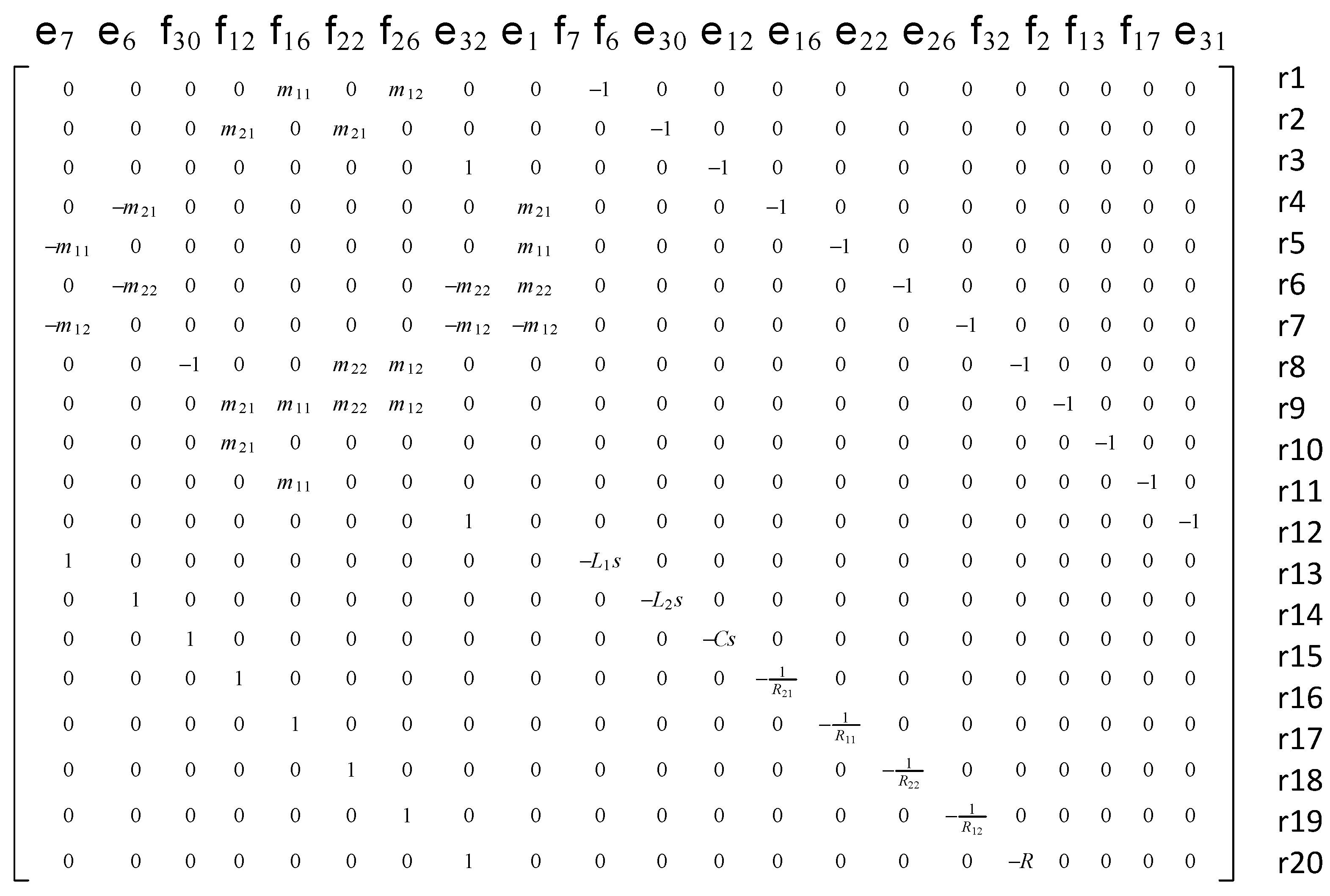
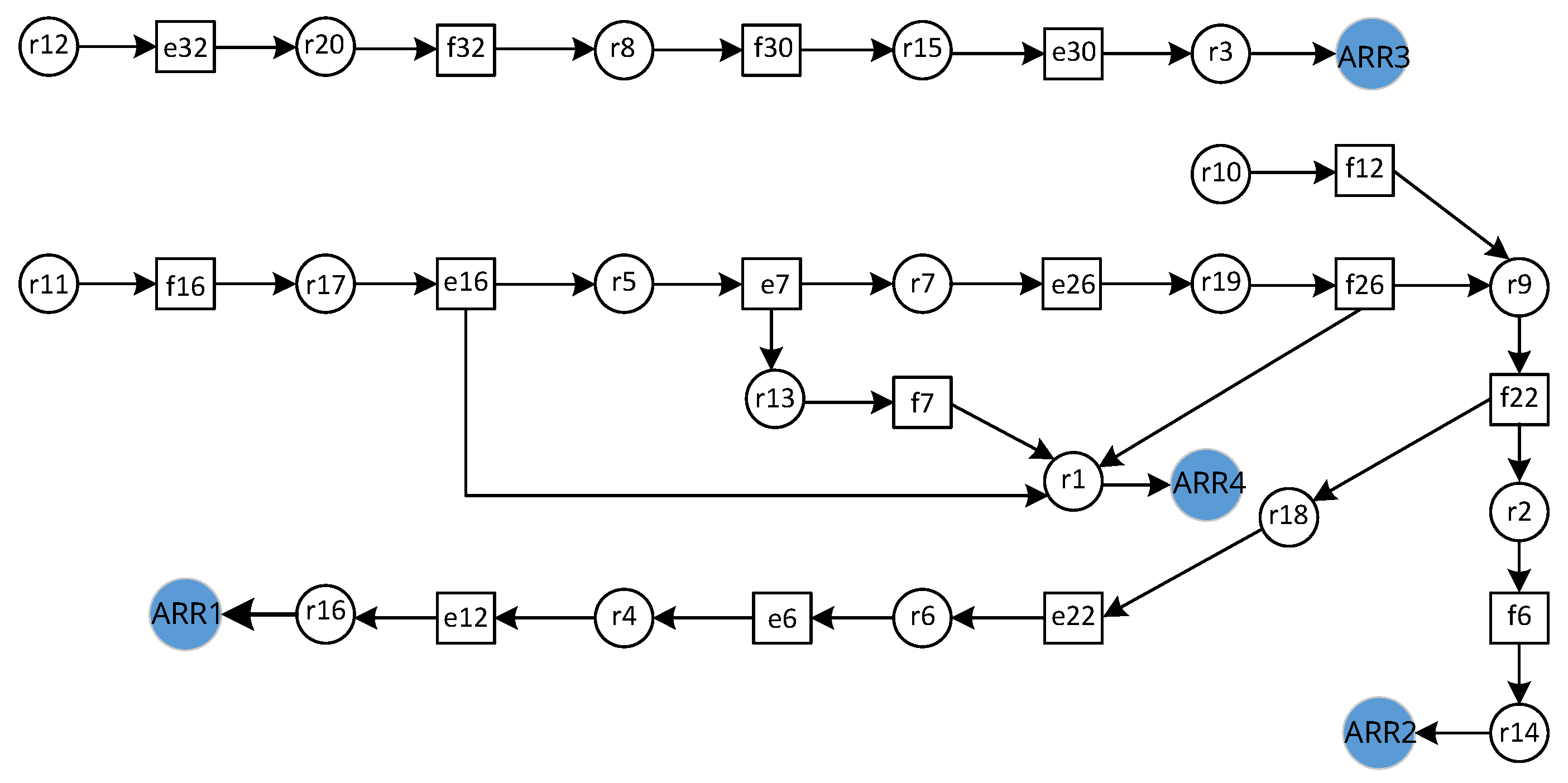
4.3. Analytic Redundancy Relations Based Diagnosis
- -
- Discretization with an appropriate frequency;
- -
- Digital filtering to reduce false alarms;
- -
- Numerical limitation to reduce the amplitude of non-desired harmonics. The limit should be higher than the threshold value;
- -
- The decision must be averaged to an appropriate number of sampling periods to escape the fugitive faults.
5. Simulation and Experimental Results
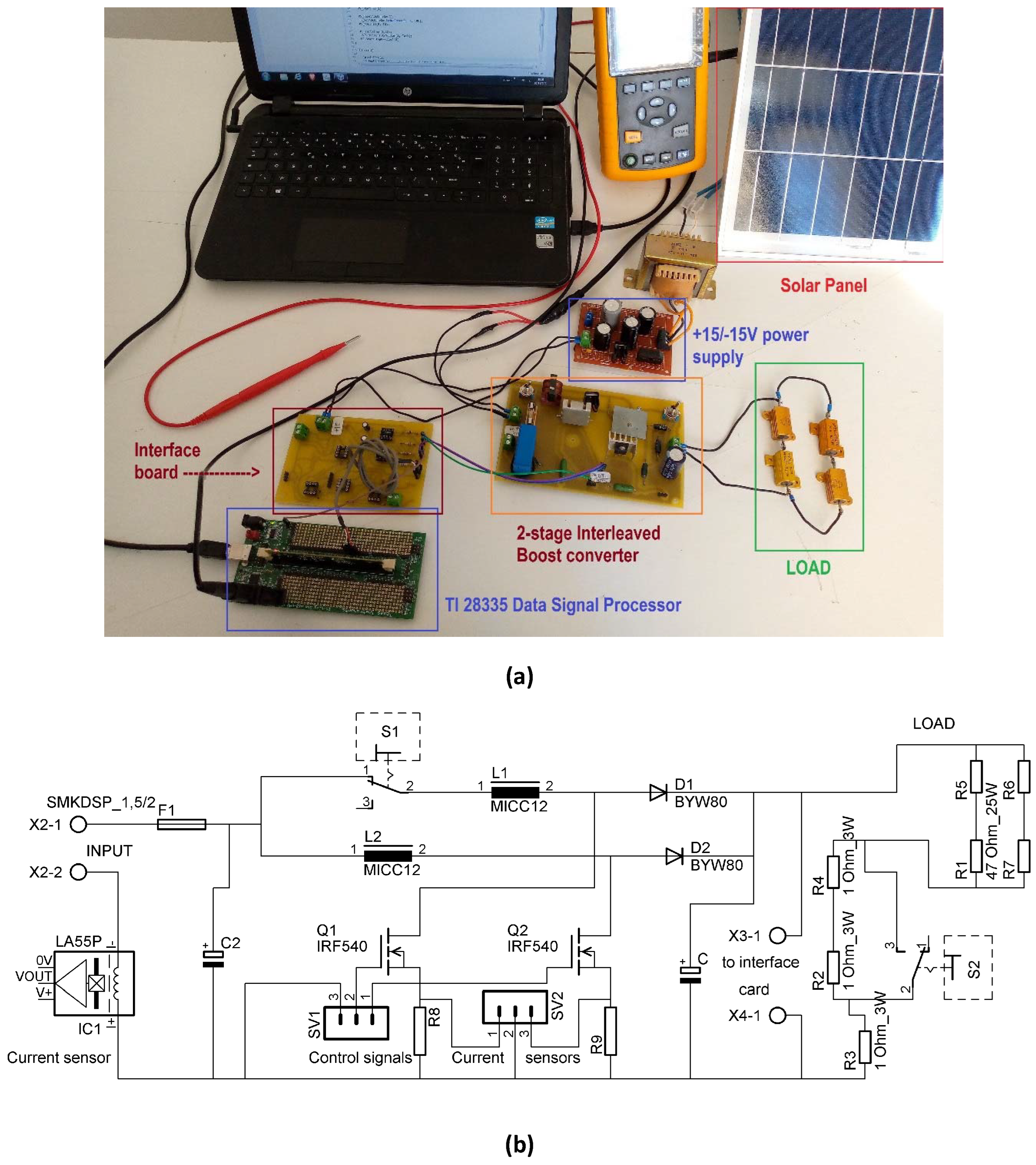
5.1. The Experimental Prototype
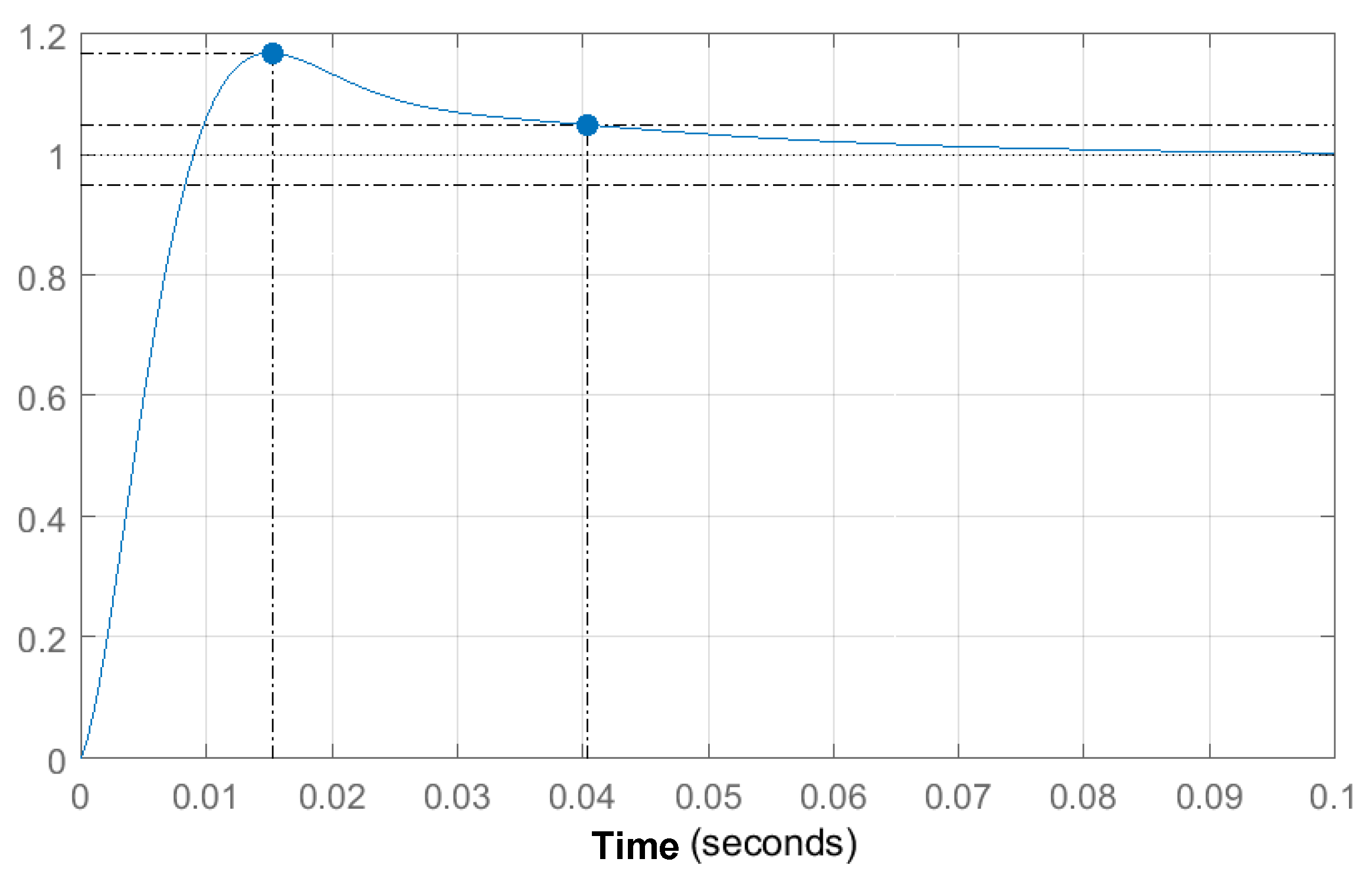
5.2. Implementation of the Control Algorithm
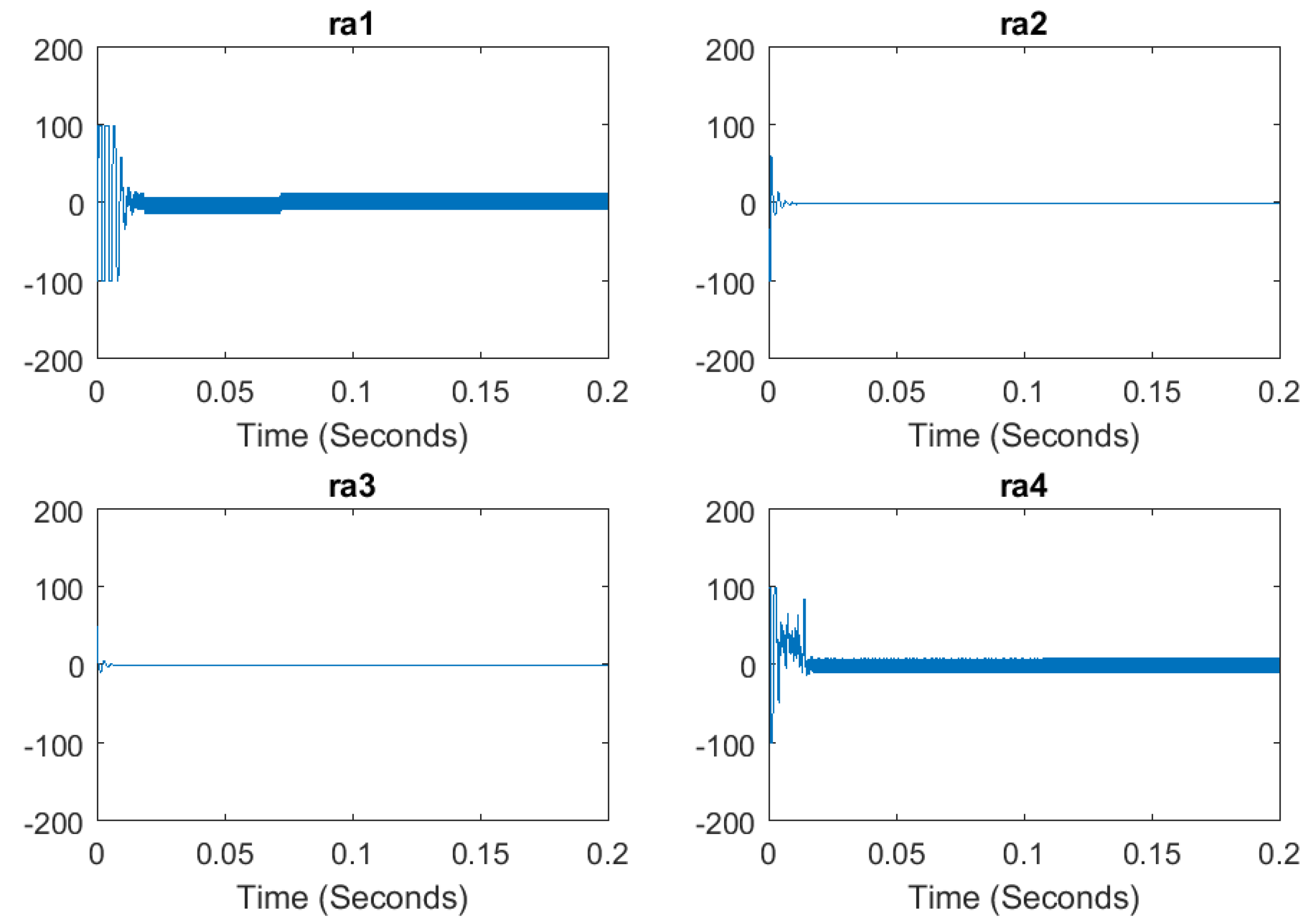
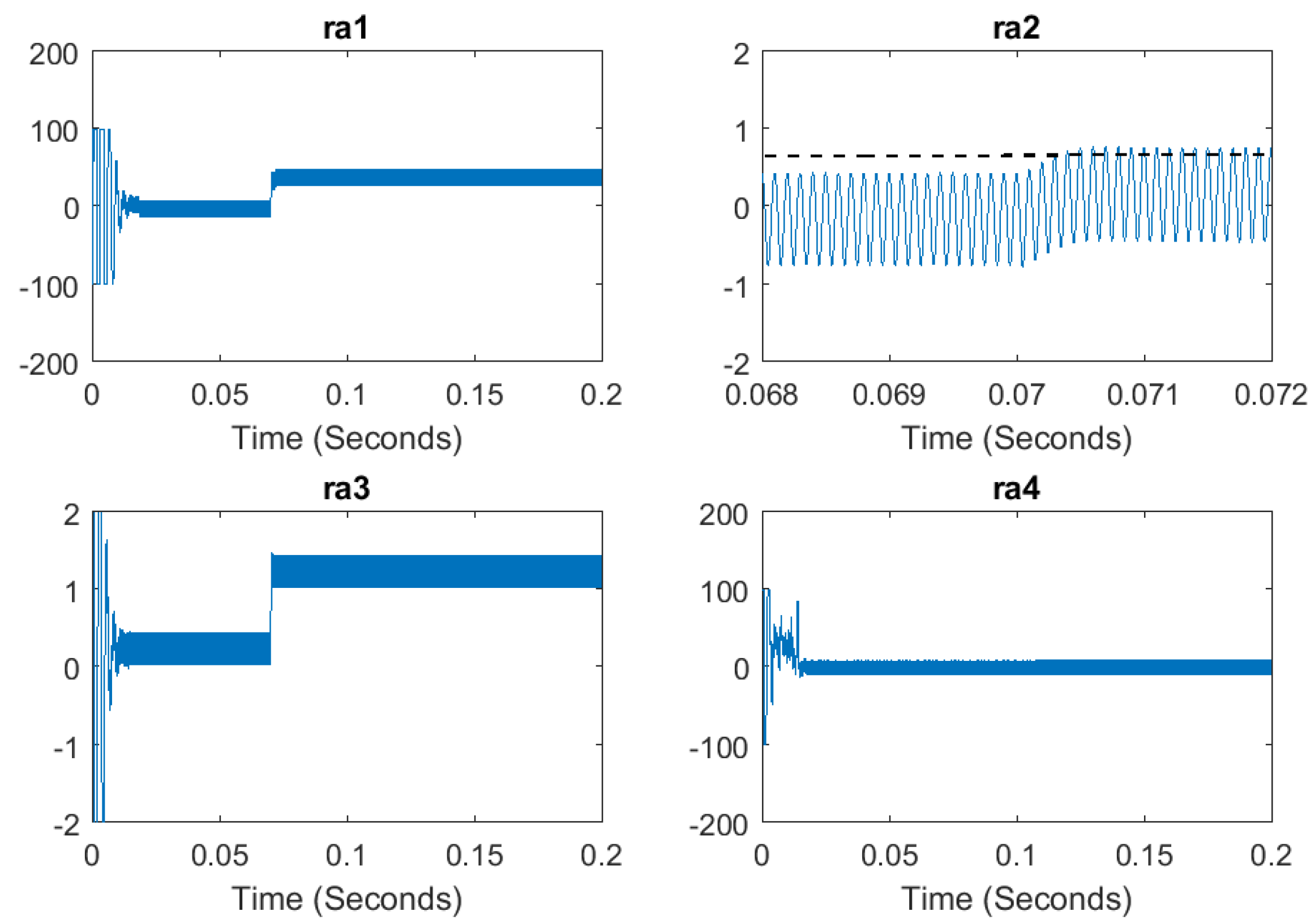
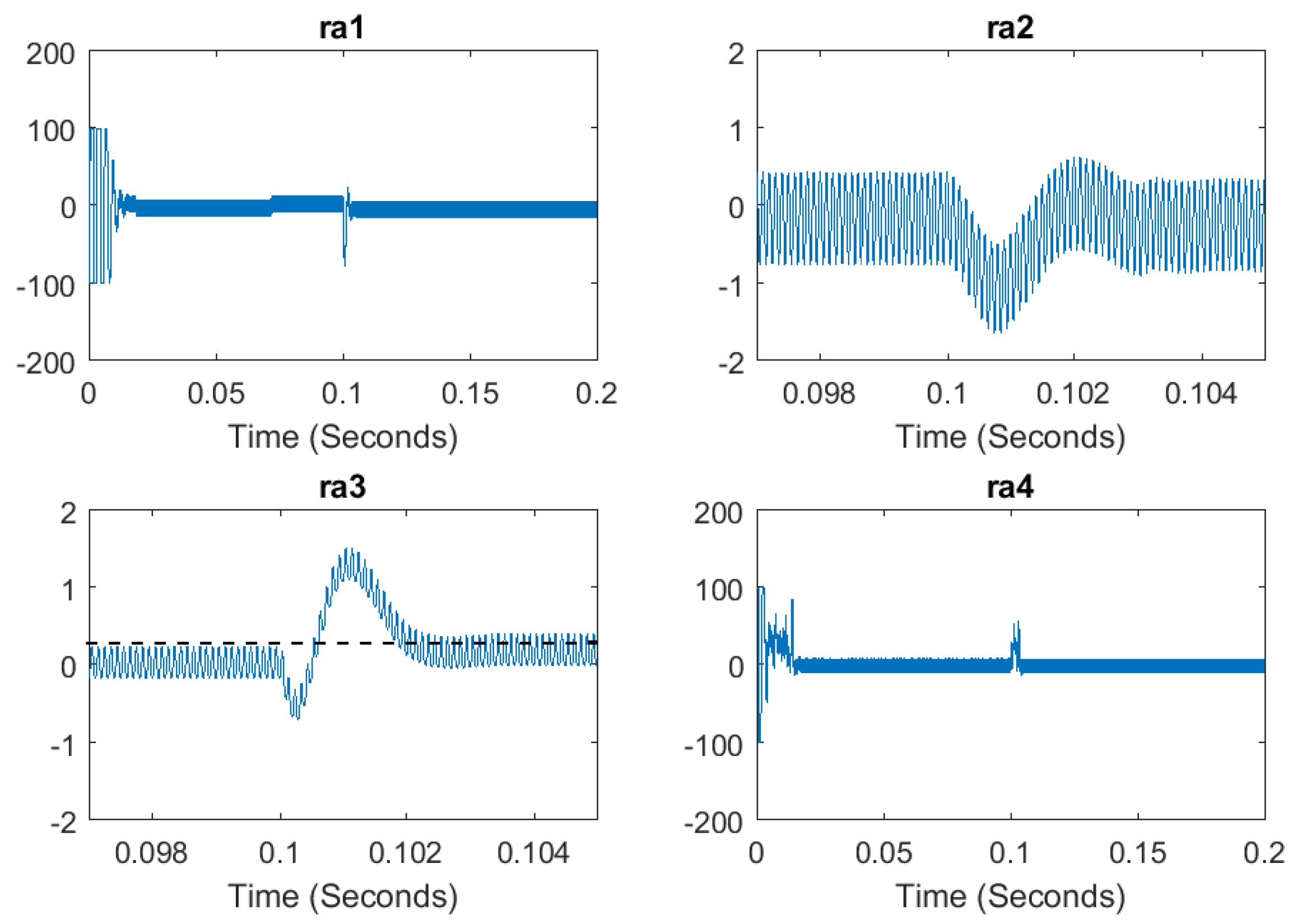
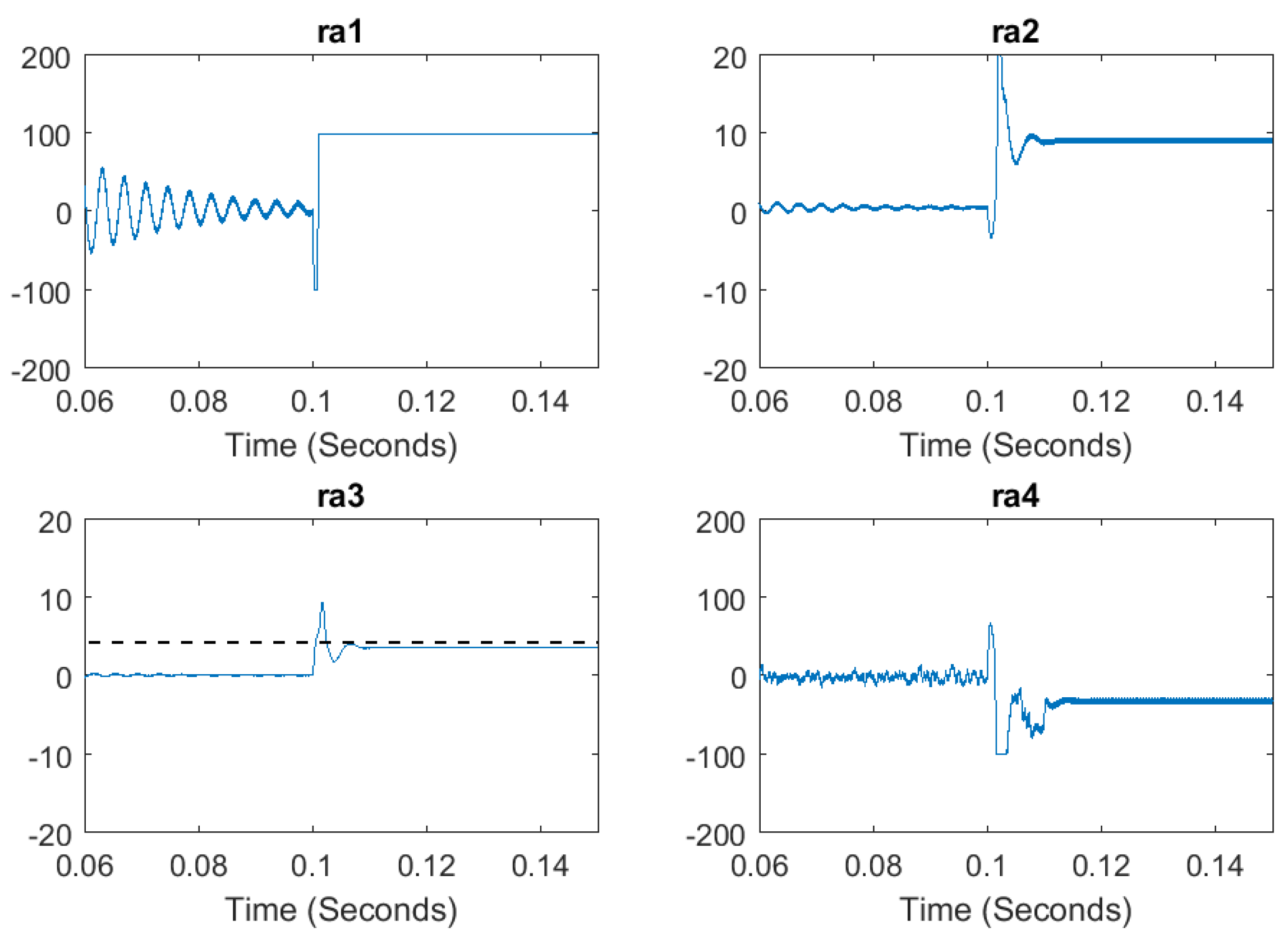
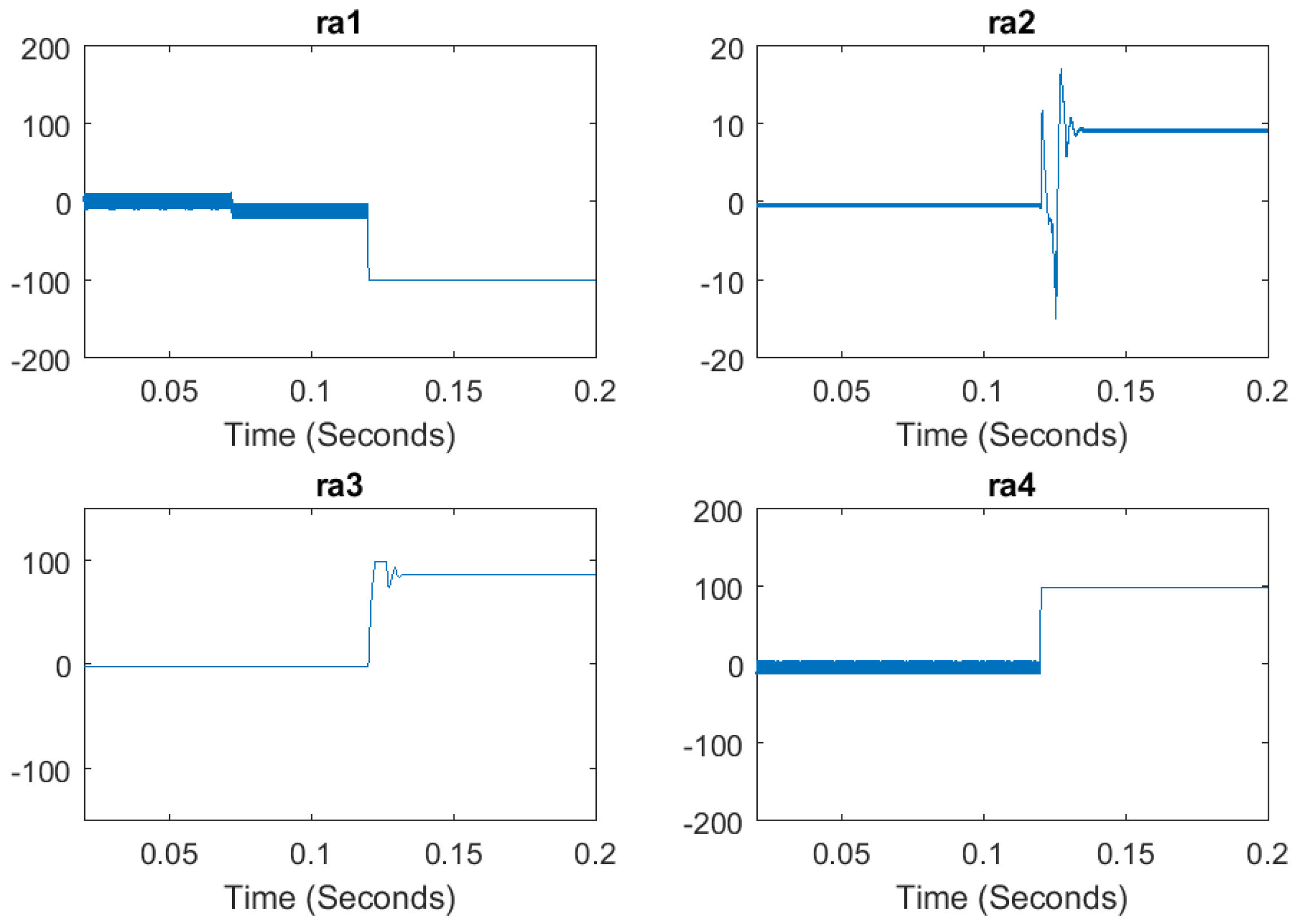
5.3. Simulation of the Diagnosis Approach
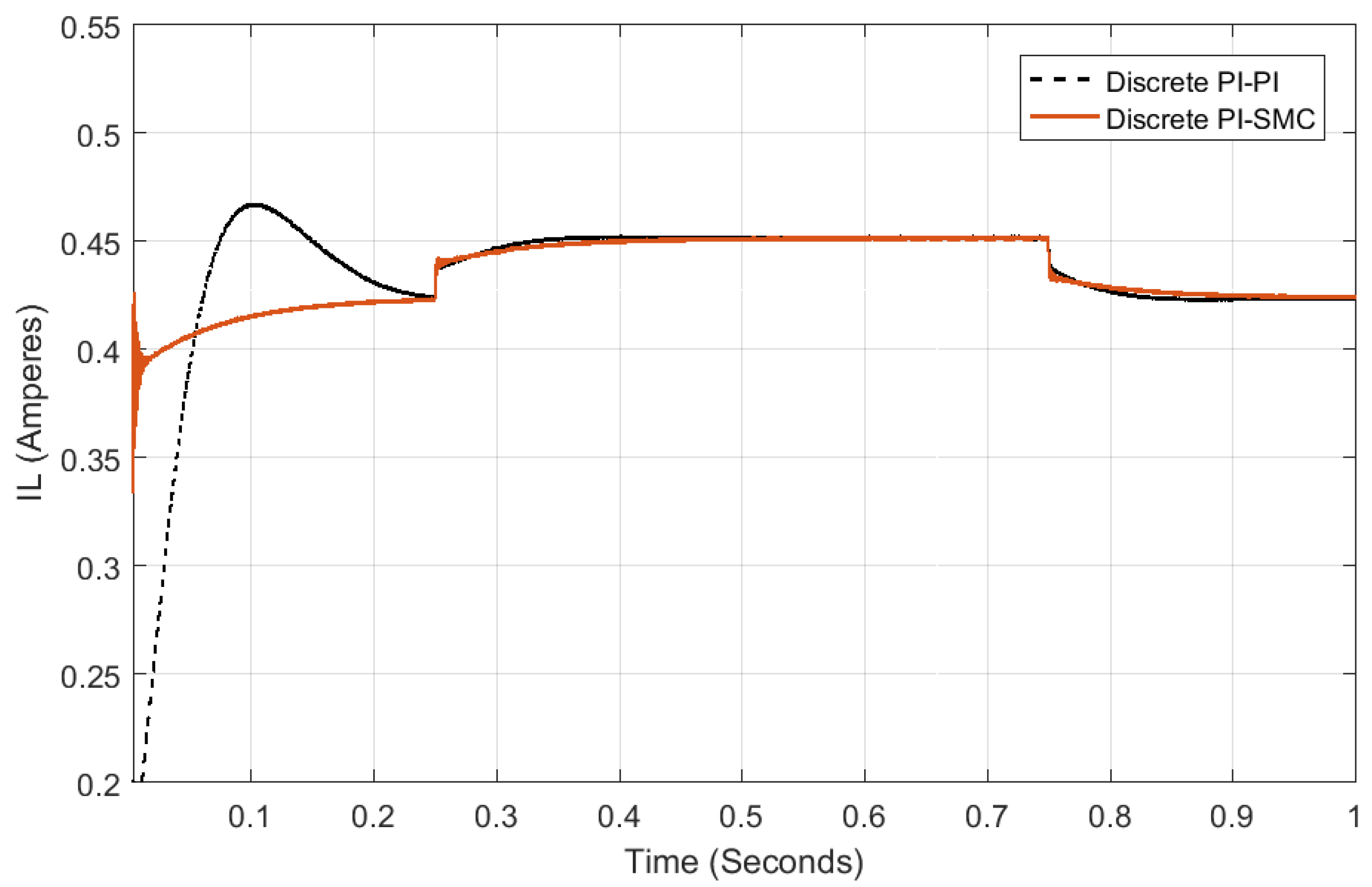
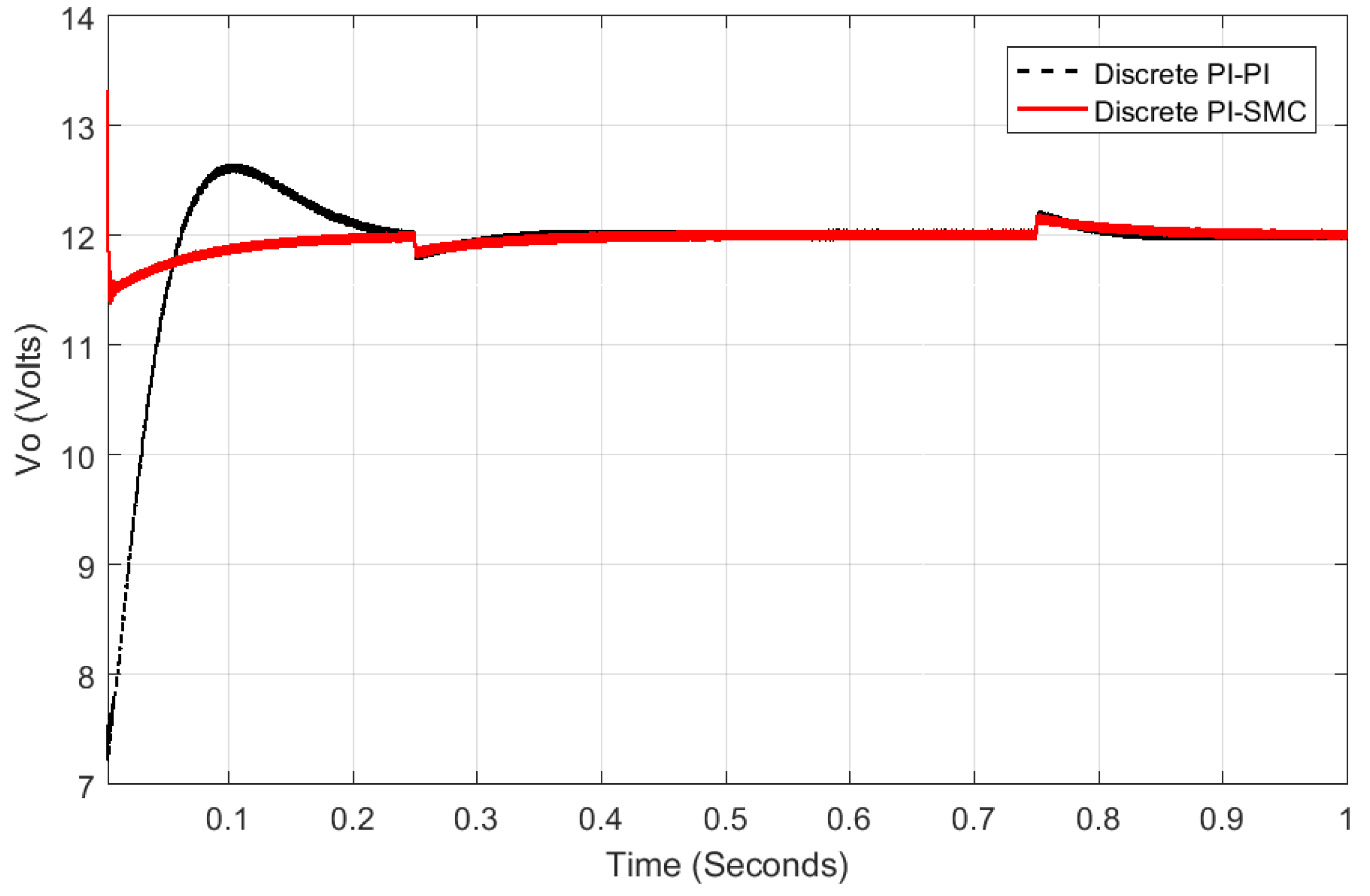
5.4. Experimental Results and Discussion
6. Conclusions and Perspective Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SMC | Sliding Mode Control |
| PI | Proportional–Integral |
| PV | Photovoltaic |
| RE | Renewable Energy |
| AI | Artificial Intelligence |
| FD | Fault Diagnostic |
| FDI | Fault Detection and Identification |
| NIBC | N-stage Interleaved Boost Converter |
| 2IBC | 2-stage Interleaved Boost converter |
| BC | Boost Converter |
| MPPT | Maximum Power Point Tracking |
| CCM | Continuous Conduction Mode |
| BG | Bond Graph |
| ARR | Analytic Redundancy Relation |
| PWM | Pulse-Width Modulation |
| DSP | Digital Signal Processor |
| ADC | Analog-to-Digital Converter |
Appendix A

- -
- X: the state vector (composed of the variables generalized momentum p on elements I and generalized displacement q on elements C) split into the and vectors associated with the causal components in integral and derivative causalities.
- -
- : the derivative with respect to the time of the state vector (variables e on the I and f on the C).
- -
- Z: the complement of X (variables f on the I and e on the C) split into and
- -
- U: input vector (sources).
- -
- Y: output vector (sensors).
- -
- : input of the dissipative module R.
- -
- : output of the dissipative module R.
References
- Zaidi, A.; Barambones, O.; Charaabi, A.; Zanzouri, N. Fault Tolerant Robust Passivity-Based Control Design for a Proton Exchange Membrane Fuel Cell Power Supply. J. Energy Resour. Technol. 2022, 144, 101304. [Google Scholar] [CrossRef]
- Reshma Gopi, R.; Sreejith, S. Converter topologies in photovoltaic applications: A review. Renew. Sustain. Energy Rev. 2018, 94, 1–14. [Google Scholar] [CrossRef]
- Sheik Mohammed, S.; Devaraj, D. Simulation of incremental conductance MPPT based two phase interleaved boost converter using MATLAB/simulink. In Proceedings of the IEEE International Conference on Electrical, Computer and Communication Technologies (ICECCT), Coimbatore, India, 5–7 March 2015. [Google Scholar] [CrossRef]
- Thounthong, P.; Mungporn, P.; Guilbert, D.; Takorabet, N.; Pierfederici, S.; Nahid-Mobarakeh, B.; Hu, Y.; Bizon, N.; Huangfu, Y.; Kumam, P. Design and control of multiphase interleaved boost converters-based on differential flatness theory for PEM fuel cell multi-stack applications. Int. J. Electr. Power Energy Syst. 2021, 124, 106346. [Google Scholar] [CrossRef]
- Olmos-Lopez, A.; Guerrero, G.; Arau, J.; Aguilar, C.; Yris, J.C. Passivity-based control for current sharing in PFC interleaved boost converters. In Proceedings of the Twenty-Sixth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Fort Worth, TX, USA, 6–11 March 2011; pp. 475–480. [Google Scholar] [CrossRef]
- Charaabi, A.; Barambones, O.; Zaidi, A.; Zanzouri, N. A Novel Two Stage Controller for a DC-DC Boost Converter to Harvest Maximum Energy from the PV Power Generation. Actuators 2020, 9, 29. [Google Scholar] [CrossRef]
- Arnaoutakis, G.E.; Kocher-Oberlehner, G.; Katsaprakakis, D.A. Criteria-Based Model of Hybrid Photovoltaic–Wind Energy System with Micro-Compressed Air Energy Storage. Mathematics 2023, 11, 391. [Google Scholar] [CrossRef]
- Ragusa, M.A.; Tachikawa, A. On some regularity results of minimizers of energy functionals. Aip Conf. Proc. 2014, 1637, 854–863. [Google Scholar]
- Ramos-Paja, C.A.; Montoya, O.D.; Grisales-Noreña, L.F. Adaptive Sliding-Mode Controller for Flyback-Based PV Systems Featuring Constant Switching Frequency. Mathematics 2022, 10, 1255. [Google Scholar] [CrossRef]
- Al-Wesabi, I.; Fang, Z.; Wei, Z.; Dong, H. Direct Sliding Mode Control for Dynamic Instabilities in DC-Link Voltage of Standalone Photovoltaic Systems with a Small Capacitor. Electronics 2022, 11, 133. [Google Scholar] [CrossRef]
- Charaabi, A.; Zaidi, A.; Zanzouri, N. Dual loop control of DC-DC boost converter based cascade sliding mode control. In Proceedings of the International Conference on Green Energy Conversion Systems (GECS), Hammamet, Tunisia, 23–25 March 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Frivaldsky, M.; Morgos, J.; Hanko, B.; Prazenica, M. The Study of the Operational Characteristic of Interleaved Boost Converter with Modified Coupled Inductor. Electronics 2019, 8, 1049. [Google Scholar] [CrossRef]
- Zenteno-Torres, J.; Cieslak, J.; Dávila, J.; Henry, D. Sliding Mode Control with Application to Fault-Tolerant Control: Assessment and Open Problems. Automation 2021, 2, 1–30. [Google Scholar] [CrossRef]
- Liu, Z.; Xu, Z.; Zhang, X. A Novel Real-Time Fast Fault-Tolerance Diagnosis and Fault Adjustment Strategy for m-Phase Interleaved Boost Converter. IEEE Access 2021, 9, 11776–11786. [Google Scholar] [CrossRef]
- Abouobaida, H.; Abouelmahjoub, Y.; Marques Cardoso, A.J.; Chikhy, H.; Beid, S.E. Open-Circuit Fault Diagnosis and Fault-Tolerent Control Strategies for Interleaved Boost Converter. In Proceedings of the 2020 IEEE 2nd International Conference on Electronics, Control, Optimization and Computer Science (ICECOCS), Kenitra, Morocco, 2–3 December 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Ahmad, M.W.; Gorla, N.B.Y.; Malik, H.; Panda, S.K. A Fault Diagnosis and Postfault Reconfiguration Scheme for Interleaved Boost Converter in PV-Based System. IEEE Trans. Power Electron. 2021, 36, 3769–3780. [Google Scholar] [CrossRef]
- Xu, L.; Ma, R.; Zhuo, S.; Xie, R.; Wang, X.; Huangfu, Y. Observer Based Switch Open-Circuit Diagnosis for Interleaved Boost Converter. In Proceedings of the IECON 2020: The 46th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 18–21 October 2020; pp. 5012–5017. [Google Scholar] [CrossRef]
- Salman, M.; Dardouri, M.; El Khil, S.K.; Boccaletti, C. Open Switch Fault Diagnosis and Current Sensor Fault Tolerant Control of a DC-DC Interleaved Boost Converter using Generalized Proportional Integral Observer. In Proceedings of the 2021 IEEE 13th International Symposium on Diagnostics for Electrical Machines, Power Electronics and Drives (SDEMPED), Dallas, TX, USA, 22–25 August 2021; pp. 247–253. [Google Scholar] [CrossRef]
- Xu, L.; Ma, R.; Zhuo, S.; Xie, R.; Wang, X.; Huangfu, Y. Open-Circuit Switch Fault Diagnosis and Fault- Tolerant Control for Output-Series Interleaved Boost DC–DC Converter. IEEE Trans. Transp. Electrif. 2021, 7, 2054–2066. [Google Scholar] [CrossRef]
- He, W.; Shang, Y. Finite-Time Parameter Observer-Based Sliding Mode Control for a DC/DC Boost Converter with Constant Power Loads. Electronics 2022, 11, 819. [Google Scholar] [CrossRef]
- Pazouki, E.; De Abreu-Garcia, J.A.; Sozer, Y. Fault tolerant control method for interleaved DC-DC converters under open and short circuit switch faults. In Proceedings of the 2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1–5 October 2017; pp. 1137–1142. [Google Scholar] [CrossRef]
- Guilbert, D.; N’Diaye, A.; Gaillard, A.; Djerdir, A. Fuel Cell Systems Reliability and Availability Enhancement by Developing a Fast and Efficient Power Switch Open-Circuit Fault Detection Algorithm in Interleaved DC/DC Boost Converter Topologies. Int. J. Hydrogen Energy 2016, 41, 15505–15517. [Google Scholar] [CrossRef]
- Dieste-Velasco, M.I. Application of a Pattern-Recognition Neural Network for Detecting Analog Electronic Circuit Faults. Mathematics 2021, 9, 3247. [Google Scholar] [CrossRef]
- Yang, N.-C.; Ismail, H. Voting-Based Ensemble Learning Algorithm for Fault Detection in Photovoltaic Systems under Different Weather Conditions. Mathematics 2022, 10, 285. [Google Scholar] [CrossRef]
- Jamshidpour, E.; Poure, P.; Saadate, S. Common Switch Fault Diagnosis for Two-Stage DC-DC Converters Used in Energy Harvesting Applications. Electronics 2019, 8, 293. [Google Scholar] [CrossRef]
- Kumar, G.K.; Elangovan, D. Review on fault-diagnosis and fault-tolerance for DC–DC converters. IET Power Electron. 2020, 13, 1–13. [Google Scholar] [CrossRef]
- Sladic, S.; De Santis, M.; Zivic, E.; Giemacki, W. Paradigm Changes in Power Electronics Caused by Emerging Materials. In Proceedings of the International Congress on Advanced Materials Sciences and Engineering (AMSE), Opatija, Croatia, 22–24 July 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, X.; Ren, P. Fault Diagnosis and Identification of Power Capacitor Based on Edge Cloud Computing and Deep Learning. Math. Probl. Eng. 2020, 2020, 3120805. [Google Scholar] [CrossRef]
- Lu, S.-D.; Sian, H.-W.; Wang, M.-H.; Kuo, C.-C. Fault diagnosis of power capacitors using a convolutional neural network combined with the chaotic synchronisation method and the empirical mode decomposition method. IET Sci. Meas. Technol. 2021, 15, 551–561. [Google Scholar] [CrossRef]
- Chaouch, H.; Charfeddine, S.; Ben Aoun, S.; Jerbi, H.; Leiva, V. Multiscale Monitoring Using Machine Learning Methods: New Methodology and an Industrial Application to a Photovoltaic System. Mathematics 2022, 10, 890. [Google Scholar] [CrossRef]
- Edstrom, K.; Strömberg, J.E.; Söderman, U.; Top, J. Modelling and simulation of a switched power converter. Simul. Ser. 1997, 29, 195–200. [Google Scholar]
- Tagina, M.; Cassar, J.P.; Dauphin-Tanguy, G.; Staroswiecki, M. Bond Graph Models for Direct Generation of Formal Fault Detection Systems. Int. J. Syst. Anal. Model. Simul. (SAMS) 1996, 23, 1–17. [Google Scholar]
- Zaidi, A.; Tagina, M.; Ould Bouamama, B. Improvement of Bond Graph Model Based Diagnosis with Bayesian Networks Approach. Int. J. Simul. Syst. Sci. Technol. 2020, 12, 5. [Google Scholar] [CrossRef]
- Ould Bouamama, B.; Medjaher, K.; Samantaray, A.K.; Staroswiecki, M. Supervision of an industrial steam generator. Part I: Bond graph modelling. Control. Eng. Pract. 2006, 14, 71–83. [Google Scholar] [CrossRef]
- Bouamama, B.O.; Samantaray, A.K.; Medjaher, K.; Staroswiecki, M.; Dauphin-Tanguy, G. Model builder using functional and bond graph tools for FDI design. Control. Eng. Pract. 2005, 13, 875–891. [Google Scholar] [CrossRef]
- Yu, M.; Lu, H.; Wang, H.; Xiao, C.; Lan, D. Compound Fault Diagnosis and Sequential Prognosis for Electric Scooter with Uncertainties. Actuators 2020, 9, 128. [Google Scholar] [CrossRef]
- Yu, M.; Xiao, C.; Wang, H.; Jiang, W.; Zhu, R. Adaptive Cuckoo Search-Extreme Learning Machine Based Prognosis for Electric Scooter System under Intermittent Fault. Actuators 2021, 10, 283. [Google Scholar] [CrossRef]
- Jantharamin, N.; Zhang, L. Analysis of multiphase interleaved converter by using state-space averaging technique. In Proceedings of the 2009 6th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology, Chonburi, Thailand, 6–9 May 2009; pp. 288–291. [Google Scholar] [CrossRef]
- Chen, Z.; Gao, W.; Hu, J.; Ye, X. Closed-Loop Analysis and Cascade Control of a Nonminimum Phase Boost Converter. IEEE Trans. Power Electron. 2011, 26, 1237–1252. [Google Scholar] [CrossRef]
- Slotine, J.-J.E. Sliding controller design for non-linear systems. Int. J. Control 1948, 40, 421–434. [Google Scholar] [CrossRef]
- Paynter, H. Analysis and Design of Engineering Systems; MIT Press: Cambridge, MA, USA, 1961. [Google Scholar]
- Soderman, U.; Top, J.; Stromberg, J.E. The Conceptual Side of Mode Switching. In Proceedings of the IEEE Systems Man and Cybernetics Conference—SMC, Le Touquet, France, 17–20 October 1993; pp. 245–250. [Google Scholar]
- Mosterman, P.J. Implicit Modeling and Simulation of Discontinuities in Physical System Models. In Proceedings of the 4th International Conference on Automation of Mixed Processes: Hybrid Dynamic Systems, Dortmund, Germany, 18–19 September 2000; pp. 35–40. [Google Scholar]
- Back, A.; Guckenheimer, J.; Myers, M. A Dynamical Simulation Facility for Hybrid Systems; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1993; Volume 736, pp. 255–267. [Google Scholar]
- Borutzky, W. Bond graph modelling and simulation of fault scenarios in switched power electronic systems. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2012, 226, 1381–1393. [Google Scholar] [CrossRef]
- Tagina, M. Application de la Modélisation Bond Graph à la Surveillance des Systèmes Complexes. Ph.D. Thesis, Université de Lille, Lille, France, 1995. [Google Scholar]
- Borutzky, W. Fault indicators and unique mode-dependent state equations from a fixed-causality diagnostic bond graph of linear models with ideal switches. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2018, 232, 695–708. [Google Scholar] [CrossRef]
- Zaidi, A. Integration of Bayesian Networks and Bond Graphs for Supervision of Dynamic Systems. Ph.D. Thesis, Université de Lille, Lille, France, 2012. [Google Scholar]


| L | C | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 0 | 1 | 1 | |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | |
| D | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| I | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| C | R | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | |
| 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | |
| 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | |
| D | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| I | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| Parameter | Value |
|---|---|
| Input voltage | 6 V |
| Output voltage | 12 V |
| Inductance | 300 mH |
| Output capacitor C | 47 F |
| Input capacitor | 1000 F |
| Static duty cycle D | 0.5 |
| Load resistor R | 50 |
| Transistor parasitic resistor | 0.16 |
| Inductance parasitic resistor | 1.1 |
| Output capacitor parasitic resistor | 2.1 |
| Switching frequency | 10 KHz |
| Maximum power | 30 W |
| Maximum power voltage | 6 V |
| Maximum power current | 5 A |
| Open-circuit voltage | 7.2 V |
| Short-circuit current | 6 A |
| Size | 350 × 530 × 17 mm |
| Case Test | Load (%) | (V) | (V) | Error (%) |
|---|---|---|---|---|
| Open-loop 2IBC | 100 | 6.89 | 14.54 | 21.16 |
| Closed-loop 2IBC | 100 | 6.51 | 12.03 | 0.25 |
| Closed-loop 2IBC | 104 | 5.92 | 12.03 | 0.25 |
| Closed-loop BC | 100 | 6.36 | 11.94 | 0.5 |
| Closed-loop BC | 104 | 6.32 | 11.94 | 0.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaidi, A.; Barambones, O.; Zanzouri, N. Implementation of a Cascade Fault Tolerant Control and Fault Diagnosis Design for a Modular Power Supply. Actuators 2023, 12, 135. https://doi.org/10.3390/act12030135
Zaidi A, Barambones O, Zanzouri N. Implementation of a Cascade Fault Tolerant Control and Fault Diagnosis Design for a Modular Power Supply. Actuators. 2023; 12(3):135. https://doi.org/10.3390/act12030135
Chicago/Turabian StyleZaidi, Abdelaziz, Oscar Barambones, and Nadia Zanzouri. 2023. "Implementation of a Cascade Fault Tolerant Control and Fault Diagnosis Design for a Modular Power Supply" Actuators 12, no. 3: 135. https://doi.org/10.3390/act12030135
APA StyleZaidi, A., Barambones, O., & Zanzouri, N. (2023). Implementation of a Cascade Fault Tolerant Control and Fault Diagnosis Design for a Modular Power Supply. Actuators, 12(3), 135. https://doi.org/10.3390/act12030135







