Optimization of the Storage Spaces and the Storing Route of the Pharmaceutical Logistics Robot
Abstract
1. Introduction
2. Storage Unit Structure
2.1. Description of the Storage
- (1)
- The drug storage and distribution system is a rectangular frame structure, as shown in Figure 3. The drug storage and distribution system is composed of six storage units, each of which is composed of multi-layer drug storage tanks, and each of which is composed of multiple storage locations;
- (2)
- The length of each tank is the same, but the width and height are different. The storage height of the same layer is the same. After the equipment runs, each storage location can only store a certain drug;
- (3)
- Set the drug storage and distribution system to be composed of M drug storage tanks. Since the width of drugs that can be stored in each unit is limited when setting, the storage unit needs to be optimized first;
- (4)
- Set the drug r to be stored for the first time, the drug width is lr, where the inventory of the drug storage tank is s = 0, and the length of the drug storage tank is L, and then, the number of replenishment required for the drug storage tank is ;
- (5)
- For the storage of a certain drug, the number of storage units allocated is N. Since the length of storage units is the same, the number of this drug stored in each unit is the same;
- (6)
- It is set that there are n rows of m layers in the reservoir rectangle, and the reservoirs in row j of layer i are recorded as (i, j), where i = 1, 2, …, m; j = 1, 2, …, n;
- (7)
- Each chemical storage tank has a unique number, among which, the storage location number in column j of layer i is , and the chemical storage tank code is arranged from small to large. If a chemical storage tank has been allocated, the corresponding mark is 1, otherwise it is idle, and the mark is 0.
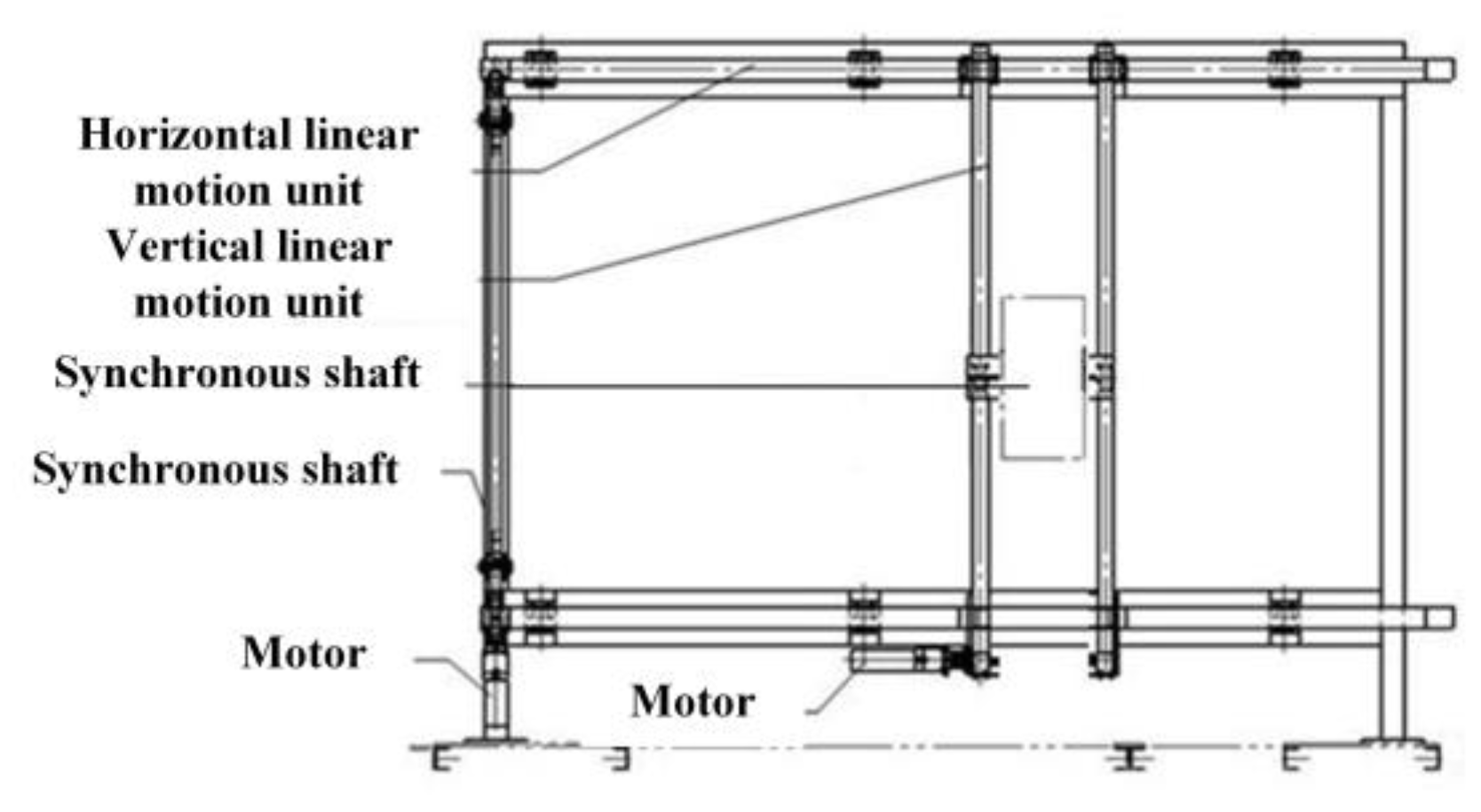
2.2. Description of the Sorting Mechanical Configuration and Sorting Process
3. Optimization of Sorting Route
3.1. Amount of Storing with a Kind Drug
3.2. Design of the Ant Colony Algorithm
3.3. The Process of the Algorithm
| Algorithm 1. (improved ant colony algorithm sequence (iacs) |
| Initialize α, β, τ0, ρ, Q, n, Nc_max, Sx, Sy, Vx, Vy, ax, ay While( nc <= Nc_max) Initalize refilling time Tk, tabUk, and allowedk For (k=1; k< m; k++) While ( allowedk != null) Build tabUk by applying n-1 times the following step tabUk = tabUk + (i, j) and allowedk = allowedk - (i, j) Choose the next node j probability, calculate Pijk according to the Formula (11): Calculate the optimal tour Lk of ant k End while For every edge (i, j) Update the pheromone according to the Formulas (9) and (12): by applying the rule: where is the same as Equation (15): End for End for Update the historical optimal storing path where is updated as Equation (13) For every edge (i, j) do τij = (nc+1)=τij (nc) End For End while |
4. Experiments and Analysis
4.1. Test Samples
4.2. Results and Analysis of Test Samples
- (1)
- In the first test sample, compare the recovery paths between the three models. They were completely different from other models. The recovery path includes all recovery paths in the storage process of a drug. The recovery path lengths of rs, acs, and iacs were 14.8050, 11.3332, and 12.1811, respectively. Based on this, we can see that the recovery path of acs was the shortest. Compared with rs, the best recovery path rate of acs and iacs was more than 23.45% and 17.72%, respectively. It can be seen that the optimized rate between the acs and the iacs based on the rs was more than 5.37%. Moreover, restoring time of the acs and the iacs were the difference. Both of them required shorter time than the rs on restoring route. The optimized rate of restoring time of both the acs and the iacs were shorter than 15.08% and 18.67% when compared with that of the rs. It can be seen that the acs can search shorter sorting routes than the rs and the iacs. In terms of storing time, the iacs was better than the rs and the acs. Accordingly, the objective function of the iacs was to achieve the shortest sorting time, and the objective function of the acs was to search the shortest storing route.
- (2)
- In the second test sample, comparing restoring paths among the three models, the rs were different from the acs and the iacs. Only one storing route was same as the acs and the iacs in four storing paths. Because it included two picking points which only has kind of storing route. it could not be optimized. The lengths of storing route of the rs, the acs, and the iacs were 11.1096, 9.0186, and 9.6906, respectively. Therefore, the acs is the best storing model to search the shortest storing route. The results showed that when the storage path of rs was properly arranged, the storage path of iacs was longer than that of rs. However, this rarely happens. However, iacs was better than rs and ac in terms of storage time. Compared with rs and acs, the optimal storage time of iacs was 16.35% and 3.27% shorter, respectively. It can be seen that iacs was the best storage model for searching storage paths and needed the shortest time.
- (3)
- In Table 6, as the number of pickings increased, the optimized rate on the storing route value and storing time also increased. The iacs was obviously shorter than the acs on storing time.
- (1)
- In Table 7, comparing with the operation time or storing route time of the first test sample, the iacs was better than the rs and the acs. The optimized rate of operation time was more than 4.61% when comparing the iacs with the rs. Additionally, the optimized rate of operation time was more than 18.67% when comparing the iacs with the rs. The reason for this is that the storage time included in the operation time was not optimized. Optimization of the acs and the iacs were negative to the storing route. It can be seen that the iacs was better than the acs. The reason for this is that acceleration and deceleration of motor were set as “S” curve in actual operation and were set as oblique straight line in the simulation. The storing route of the iacs was longer than the acs’s in the first test sample. However, the iacs required less time to operate through this storing path than the acs. Additionally, the time used in operation, which was spent on storing path, was less than that used in the simulation when the storing path was short.
- (2)
- In Table 7, comparing with the operation time and storing route time of the second test sample, the iacs was also better than the rs and the acs. The optimized rate of operation time was more than 4.77% when comparing the iacs with the rs. The optimized rate of operation time was more than 16.35% when comparing the iacs with the rs. It can be seen that the optimized effect was similar to the first test sample. The optimization of the iacs was better than the acs. Compared with the rs, optimized rate of operation storing time with the iacs and the acs were both reducing instead. The reason for this is that with the increase in selection, more rs storage time was required, which was set as the denominator and had a greater impact.
- (3)
- In conclusion, the iacs was better than the rs on storing time. As picking increased, the iacs was obviously better than the acs. Based on the storing time of the rs, compared with the acs, the optimized rate of storing time with the iacs was more than 0.35%, even up to 1.57%.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tan, L.; Chen, W.; He, B.; Zhu, J.; Cen, X.; Feng, H. A survey of prescription errors in paediatric outpatients in multi-primary care settings: The implementation of an electronic pre-prescription system. Front. Pediatr. 2022, 10. [Google Scholar] [CrossRef] [PubMed]
- Anjalee, J.A.L.; Rutter, V.; Samaranayake, N.R. Application of failure mode and effects analysis (FMEA) to improve medication safety in the dispensing process—A study at a teaching hospital, Sri Lanka. BMC Public Health 2021, 21, 1430. [Google Scholar] [CrossRef]
- Nermeen, A.; Safa, A.; Sayed, S.; Mojeba, H. Studying the medication prescribing errors in the egyptian community pharmacies. Asian J. Pharm. 2018, 12, 25–30. [Google Scholar]
- Hesse, M.; Thylstrup, B.; Seid, A.K.; Tjagvad, C.; Clausen, T. A retrospective cohort study of medication dispensing at pharmacies: Administration matters! Drug Alcohol Depend. 2021, 225, 108792. [Google Scholar] [CrossRef] [PubMed]
- Jacobson, M.G.; Chang, T.Y.; Earle, C.C.; Newhouse, J.P. Physician agency and patient survival. J. Econ. Behav. Organ. 2017, 134, 27–47. [Google Scholar] [CrossRef]
- Chen, F.Y. Current situation and new progress of automated pharmacy. Mingyi Dr. 2020, 4, 277. [Google Scholar]
- Cai, Y.X.; Zhang, M.L. Study on dispensing optimization of integrated traditional Chinese medicine dispensing system. Light Ind. Mach. 2019, 37, 80–88. [Google Scholar]
- Jin, H.; Yun, C.; Wang, W.; Li, D.J. Application and research of the Clip Type Manipulator. In Mechanisms and Machine Science; Springer: Cham, Switzerland, 2016; pp. 841–851. [Google Scholar] [CrossRef]
- Lin, Y.; Cai, Z.; Huang, M.; Gao, X.; Yu, G. Evaluation of development status and application effect of outpatient pharmacy automatic dispensing system in mainland China. Chin. J. Mod. Appl. Pharm. 2020, 37, 1131–1138. [Google Scholar]
- Ozden, S.G.; Smith, A.E.; Gue, K.R. A computational software system to design order picking warehouses. Comput. Oper. Res. 2021, 132, 105311. [Google Scholar] [CrossRef]
- Mulac, A.; Mathiesen, L.; Taxis, K.; Granås, A.G. Barcode medication administration technology use in hospital practice: A mixed-methods observational study of policy deviations. BMJ Qual. Saf. 2021, 30, 1021–1030. [Google Scholar] [CrossRef]
- Jin, H.; He, Q.; He, M.; Lu, S.; Hu, F.; Hao, D. Optimization for medical logistics robot based on model of traveling salesman problems and vehicle routing problems. Int. J. Adv. Robot. Syst. 2021, 18, 17298814211022539. [Google Scholar] [CrossRef]
- Sng, Y.L.; Ong, C.K.; Lai, Y.F. Approaches to outpatient pharmacy automation: A systematic review. Eur. J. Hosp. Pharm. 2019, 26, 157–162. [Google Scholar] [CrossRef]
- Ahtiainen, H.K.; Kallio, M.M.; Airaksinen, M.; Holmström, A.R. Safety, time and cost evaluation of automated and semi-aut-omated drug distribution systems in hospitals:a systematic review. Eur. J. Hosp. Pharm. 2020, 27, 253–262. [Google Scholar] [CrossRef] [PubMed]
- Zhu, S.; Wang, H.; Zhang, X.; He, X.; Tan, Z. A decision model on human-robot collaborative routing for automatic logis-tics. Adv. Eng. Inform. 2022, 53, 101681. [Google Scholar] [CrossRef]
- Keung, K.; Lee, C.; Ji, P. Industrial internet of things-driven storage location assignment and order picking in a resource synchronization and sharing-based robotic mobile fulfillment system. Adv. Eng. Inform. 2022, 52, 101540. [Google Scholar] [CrossRef]
- Boysen, N.; de Koster, R.; Füßler, D. The forgotten sons: Warehousing systems for brick-and-mortar retail chains. Eur. J. Oper. Res. 2020, 288, 361–381. [Google Scholar] [CrossRef]
- Jin, H.; Yun, C.; Gao, X. Application and research of the refilling process with Clip Type Manipulator. In Proceedings of the 2015 IEEE International Conference on Robotics and Biomimetics (ROBIO), Zhuhai, China, 6–9 December 2015; pp. 775–780. [Google Scholar] [CrossRef]
- Jin, H.; He, Q.; He, M.; Hu, F.; Lu, S. New method of path optimization for medical logistics robots. J. Robot. Mechatronics 2021, 33, 944–954. [Google Scholar] [CrossRef]
- Yang, D.; Wu, Y.; Ma, W. Optimization of storage location assignment in automated warehouse. Microprocess. Microsyst. 2020, 80, 103356. [Google Scholar] [CrossRef]
- Wu, L.; Huang, X.; Cui, J.; Liu, C.; Xiao, W. Modified adaptive ant colony optimization algorithm and its application for solving path planning of mobile robot. Expert Syst. Appl. 2023, 215, 1–22. [Google Scholar] [CrossRef]
- Li, S.; Zhang, M.; Wang, N.; Cao, R.; Zhang, Z.; Ji, Y.; Li, H.; Wang, H. Intelligent scheduling method for multi-machine cooperative operation based on NSGA-III and improved ant colony algorithm. Comput. Electron. Agric. 2023, 204, 107532. [Google Scholar] [CrossRef]
- Shi, E.; Lou, L.; Warburton, L.; Rubinsky, B. 3D Printing in Combined Cartesian and Curvilinear Coordinates. J. Med. Devices 2022, 16, 044502. [Google Scholar] [CrossRef]
- Lanza, G.; Passacantando, M.; Scutellà, M.G. Assigning and sequencing storage locations under a two level storage policy: Optimization model and matheuristic approaches. Omega 2021, 108, 102565. [Google Scholar] [CrossRef]
- Xu, X.; Ren, C. A novel storage location assignment in multi-pickers picker-to-parts systems integrating scattered storage, demand correlation, and routing adjustment. Comput. Ind. Eng. 2022, 172, 1–15. [Google Scholar] [CrossRef]
- Ma, Z.; Wu, G.; Ji, B.; Wang, L.; Luo, Q.; Chen, X. A novel scattered storage policy considering commodity classification and correlation in robotic mobile fulfillment systems. IEEE Trans. Autom. Sci. Eng. 2022, 1–14. [Google Scholar] [CrossRef]
- Zuñiga, J.B.; Martínez, J.A.S.; Fierro, T.E.S.; Saucedo, J.A.M. Optimization of the storage location assignment and the picker-routing problem by using mathematical programming. Appl. Sci. 2020, 10, 534. [Google Scholar] [CrossRef]
- Lu, F.; Feng, W.; Gao, M.; Bi, H.; Wang, S. The fourth-party logistics routing problem using ant colony system-improved grey wolf optimization. J. Adv. Transp. 2020, 2020, 8831746. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, Z.; Luan, S.; Li, X.; Sun, Y. Opposition-Based Ant Colony Optimization Algorithm for the Traveling Salesman Problem. Mathematics 2020, 8, 1650. [Google Scholar] [CrossRef]
- Jin, H.; Wang, W.; Cai, M.; Wang, G.; Yun, C. Ant colony optimization model with characterization-based speed and multi driver for the refilling system in hospital. Adv. Mech. Eng. 2017, 9, 1687814017713700. [Google Scholar] [CrossRef]


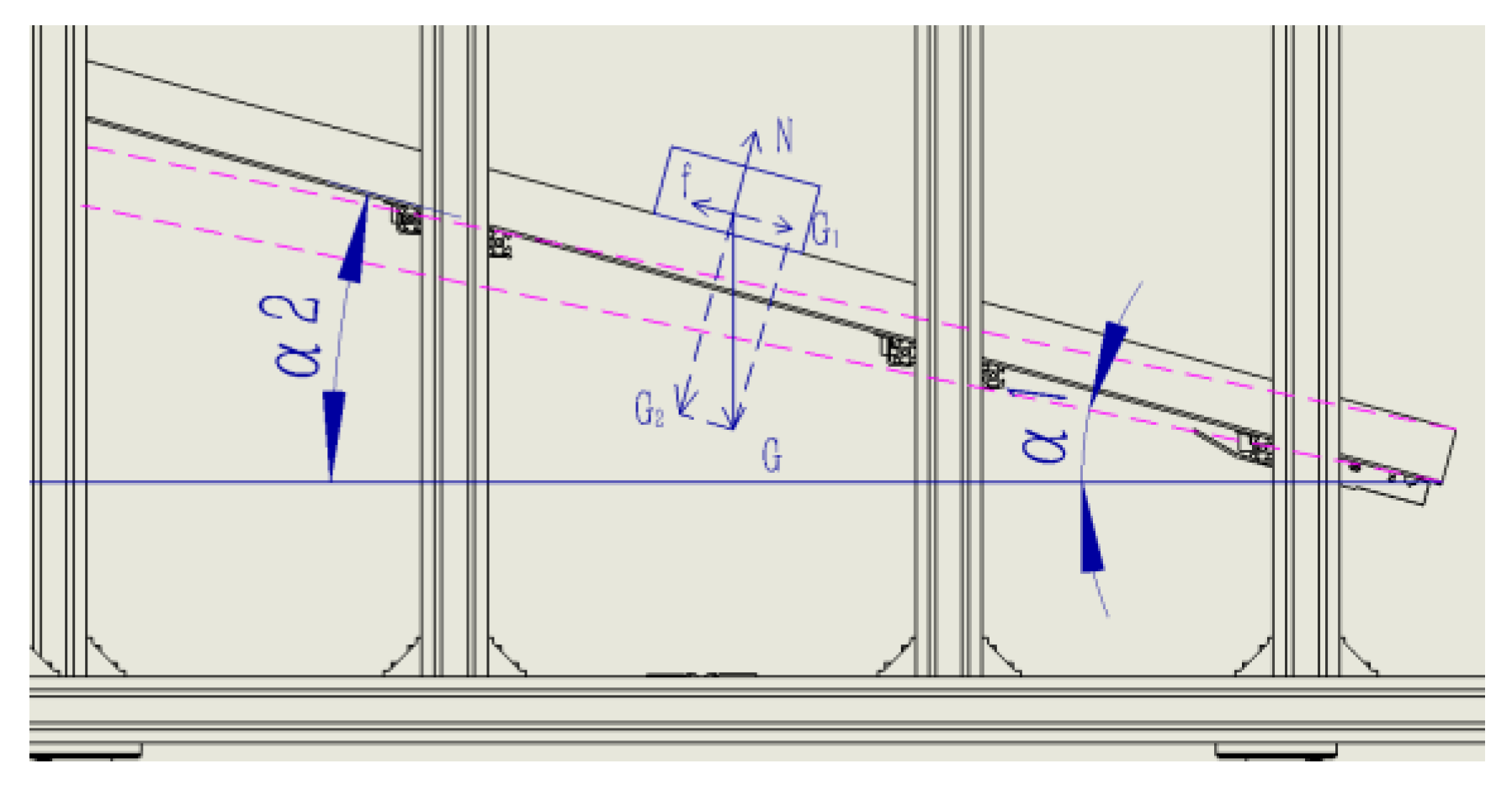
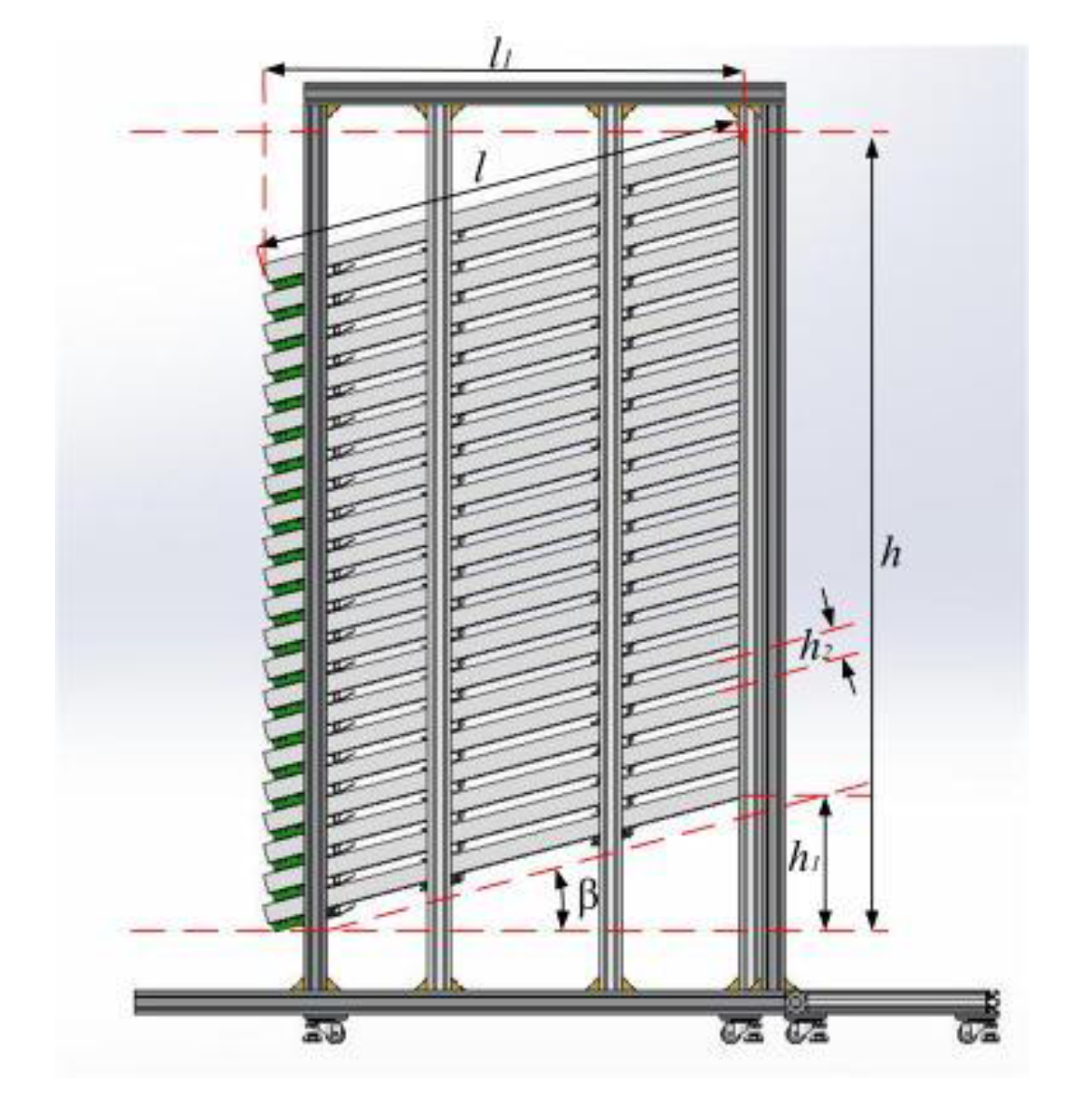



| β | h1 (m) | h2 (m) | m |
|---|---|---|---|
| 18° | 0.4095 | 1.640 | 20 |
| 20° | 0.4586 | 1.591 | 19 |
| 21.8° | 0.5040 | 1.546 | 18 |
| Number of Remaining Medicine Boxes in the Medicine Storage Tank | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|
| Single Box Dispensing Time | 0.311 | 0.328 | 0.335 | 0.334 | 0.369 | 0.392 | 0.468 |
| Kit Size (mm) | Delivery Time (s) | No Drug Delivery |
|---|---|---|
| 167 × 67 × 17 | 0.655 | Two boxes and above |
| 130 × 95 × 12 | 0.362 | nothing |
| 98 × 47 × 12 | 0.377 | One box |
| Number | Medicine Name | Pharmaceutical Manufacturers | H (mm) | Max |
|---|---|---|---|---|
| 1 | Ritodrine Hydrochloride Tablets | Biotech, Ltd. TAIWAN | 10.85 | 30 |
| 2 | Polyferose Capsules | Qingdao Guofeng Pharmaceutical Co., Ltd. | 15.90 | 20 |
| Number | Picking | 101 | 103 | 109 | 202 | 208 | 211 | 212 | 303 | 305 | 307 |
| 1 | ORT SPP | 11 6 | 5 3 | 19 4 | 17 5 | 6 7 | 3 5 | 18 2 | 10 7 | 14 7 | 20 10 |
| Picking | 408 | 409 | 502 | 507 | 512 | 601 | 608 | 707 | 709 | 711 | |
| ORT SPP | 16 4 | 15 6 | 8 3 | 4 8 | 12 4 | 7 4 | 13 5 | 2 8 | 9 7 | 1 3 | |
| Number | Picking | 103 | 104 | 107 | 201 | 207 | 202 | 210 | 302 | 305 | 301 |
| 2 | ORT SPP | 19 5 | 1 4 | 4 2 | 16 6 | 20 5 | 14 1 | 3 2 | 8 1 | 2 4 | 13 6 |
| Picking | 409 | 403 | 404 | 509 | 108 | 602 | 606 | 611 | 706 | 707 | |
| ORT SPP | 10 4 | 7 3 | 12 1 | 18 10 | 17 3 | 6 3 | 11 2 | 15 2 | 5 1 | 9 3 |
| Number | Storing Model | Route | Storing Route Value (m) | Route Rate | Storing Time (s) | Time Rate |
|---|---|---|---|---|---|---|
| a1-1 b1-1 c1-1 | rs acs iacs | 0-103-507-211-707-711-0 0-103-211-711-707-507-0 0-103-507-707-211-711-0 | 3.7261 3.0827 3.5261 | 0 17.26% 5.37% | 11.3895 10.3353 10.1490 | 0 9.26% 10.89% |
| a1-2 b1-2 c1-2 | rs acs iacs | 0-208-601-502-709-303-0 0-303-208-709-502-601-0 0-208-709-601-502-303-0 | 7.3718 6.0045 6.4561 | 0 18.55% 12.42% | 22.8189 19.7200 19.2517 | 0 13.58% 15.63% |
| a1-3 b1-3 c1-3 | rs acs iacs | 0-512-608-305-409-101-0 0-305-409-512-608-101-0 0-512-409-608-305-101-0 | 10.9175 8.7301 9.3088 | 0 20.03% 14.74% | 33.9041 29.6905 28.3970 | 0 12.43% 16.24% |
| a1-4 b1-4 c1-4 | rs acs iacs | 0-408-202-212-109-307-0 0-109-212-408-307-202-0 0-212-109-307-408-202-0 | 14.8050 11.3332 12.1811 | 0 23.45% 17.72% | 45.9859 39.0516 37.3981 | 0 15.08% 18.67% |
| a2-1 b2-1 c2-1 | rs acs iacs | 0-104-305-210-107-706-602-403-302-0 0-104-305-107-210-706-602-403-302-0 0-302-104-305-107-210-706-403-602-0 | 3.2082 3.0132 3.3867 | 0 6.08% -5.56% | 12.0624 11.1822 10.8914 | 0 7.30% 9.71% |
| a2-2 b2-2 c2-2 | rs acs iacs | 0-611-202-301-404-707-409-606-0 0-202-309-611-707-606-404-301-0 0-611-409-707-606-404-202-301-0 | 7.8976 5.7759 6.4479 | 0 26.87% 18.36% | 25.3772 20.9768 19.7844 | 0 17.34% 22.04% |
| a2-3 b2-3 c2-3 | rs acs iacs | 0-108-509-207-0 0-108-207-509-0 0-108-207-509-0 | 10.2047 8.1137 8.7857 | 0 20.49% 13.91% | 32.5624 27.8004 26.6080 | 0 14.62% 18.29% |
| a2-4 b2-4 c2-4 | rs acs iacs | 0-103-204-0 0-103-204-0 0-103-204-0 | 11.1096 9.0186 9.6906 | 0 18.82% 12.77% | 36.4167 31.6547 30.4623 | 0 13.08% 16.35% |
| Number | Storing Model | Operation Time (s) | Storing Route Time (s) | Operation Rate | Storing Rate |
|---|---|---|---|---|---|
| a1-1 b1-1 c1-1 | rs acs iacs | 46.490 45.435 45.249 | 11.390 10.335 10.149 | 0 2.32% 2.67% | 0 9.26% 10.89% |
| a1-2 b1-2 c1-2 | rs acs iacs | 94.319 91.220 90.752 | 22.819 19.720 19.252 | 0 3.29% 3.78% | 0 13.58% 15.63% |
| a1-3 b1-3 c1-3 | rs acs iacs | 141.804 137.591 136.297 | 33.904 29.691 28.397 | 0 2.97% 3.88% | 0 12.43% 16.24% |
| a1-4 b1-4 c1-4 | rs acs iacs | 186.386 179.452 177.798 | 45.986 39.052 37.398 | 0 3.72% 4.61% | 0 15.08% 18.67% |
| a2-1 b2-1 c2-1 | rs acs iacs | 38.062 37.182 36.891 | 12.062 11.182 10.891 | 0 2.31% 3.08% | 0 7.30% 9.71% |
| a2-2 b2-2 c2-2 | rs acs iacs | 76.077 71.677 70.484 | 25.377 20.977 19.784 | 0 5.78% 7.35% | 0 17.34% 22.04% |
| a2-3 b2-3 c2-3 | rs acs iacs | 107.962 103.200 102.008 | 32.562 27.800 26.608 | 0 4.41% 5.51% | 0 14.62% 18.29% |
| a2-4 b2-4 c2-4 | rs acs iacs | 124.817 120.055 118.862 | 36.417 31.655 30.462 | 0 3.82% 4.77% | 0 13.08% 16.35% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Lu, S.; Luo, M.; Dong, B. Optimization of the Storage Spaces and the Storing Route of the Pharmaceutical Logistics Robot. Actuators 2023, 12, 133. https://doi.org/10.3390/act12030133
Zhang L, Lu S, Luo M, Dong B. Optimization of the Storage Spaces and the Storing Route of the Pharmaceutical Logistics Robot. Actuators. 2023; 12(3):133. https://doi.org/10.3390/act12030133
Chicago/Turabian StyleZhang, Ling, Shiqing Lu, Mulin Luo, and Bin Dong. 2023. "Optimization of the Storage Spaces and the Storing Route of the Pharmaceutical Logistics Robot" Actuators 12, no. 3: 133. https://doi.org/10.3390/act12030133
APA StyleZhang, L., Lu, S., Luo, M., & Dong, B. (2023). Optimization of the Storage Spaces and the Storing Route of the Pharmaceutical Logistics Robot. Actuators, 12(3), 133. https://doi.org/10.3390/act12030133





