Abstract
It has been nearly 60 years since the introduction of the Gough–Stewart manipulator (GSM). With the advantages of superior load capacity and high precision, the GSM still plays an important role in many fields. However, the GSM has limitations such as a small workspace and complex singularities. To overcome these problems, a novel kinematically redundant parallel robot is designed with three redundant actuators added on the basis of the GSM. First, the structure of the proposed robot is introduced, and the kinematics of the proposed robot is established. Second, the workspaces of the proposed robot are analyzed, and the results show that the position workspace volume and the maximum torsion and orientation angles of the proposed robot can be improved effectively. Third, the singularities of the proposed robot and the GSM are compared based on the Jacobian matrices. Finally, the multi-parameter, multi-objective optimization is used to optimize the geometric parameters of the proposed robot, and an experimental prototype of the proposed robot is designed based on the optimization results.
1. Introduction
Parallel robots have become a research hotspot in the past two decades due to their advantages of high stiffness, high load-to-weight ratio, fast speed, compact structure, and small motion inertia [1]. Benefiting from these advantages, parallel robots can be used in a variety of applications, including satellite antennas, telescope positioning systems, medical robots, high-speed picking and placing, etc. [2,3,4]. However, the parallel robots have problems such as limited workspace and complex singularities, which may limit the potential use of parallel robots. Many scholars have conducted deeper research on these problems of parallel robots.
Workspace is an important performance index for parallel robots. Constrained by the closed-loop multi-legs of the parallel robot, the workspace of the parallel robot is relatively small compared with that of the series robot. Therefore, the workspace has become the focus of research in parallel robots. Gosselin proposed an algorithm for calculating the position workspace of a 6-DOF parallel mechanism, and the volume of the workspace can be evaluated [5]. Kim et al. obtained the dexterous workspace of a 6-DOF parallel platform by using geometric methods and compared the results with the position workspace calculated by Gosselin [6]. Merlet proposed an algorithm to compute the 6D workspace; this algorithm can verify whether a given 6D space is an effective workspace [7]. Pernkopf et al. made a complete analysis of the reachable workspace of the spatial Gough–Stewart platform with a planar base; further, they derived the method of calculating the size of a minimal building enclosing all motion instances of the manipulator [8]. In addition to the position workspace, the orientation workspace is also the focus of research. Bonev et al. studied an orientation workspace algorithm for a 6-DOF parallel manipulator that can represent all reachable orientations when a point on the moving platform is fixed [9]. Jiang et al. studied the maximum singularity-free orientation workspace of the Gough–Stewart platform [10]. Yan et al. compared the workspace and dexterity of two over-constrained parallel manipulators [11]. Li et al. modified the existing 3-CRU mechanism and obtained its reachable workspace by using forward kinematics [12].
Singularity is another important performance index for the parallel robots. Several DOFs may be lost or gained when the parallel robot is in its singularity configuration, resulting in the robot not operating properly. Therefore, it is necessary to study the singularity of parallel robots. Gosselin et al. presented an analysis of direct kinematic singularity and inverse kinematic singularity, and explained the physical significance of these singularities [13]. Zlatanov et al. defined constrained singularities in constrained parallel mechanisms and studied the causes and effects of these singularities [14]. St-Onge et al. studied the singular trajectories of the Gough–Stewart platform, and expressed these singular trajectories in image form [15]. Conconi et al. presented an assessment of singularities of general parallel kinematic chains and proposed a comprehensive taxonomy [16]. Sarigul et al. analyzed the singularity by constructing a specific Gough–Stewart platform, and the influence of geometric parameters on singularity was studied [17].
To solve the problem of small workspace and complex singularity of the parallel robot, many scholars have adopted the approach of introducing redundancy. Saglia et al. presented a redundant actuated parallel mechanism by adding a central strut to the 3UPS mechanism and analyzed the advantages of eliminating singularities and improving dexterity by introducing redundancy [18]. Wang et al. designed a redundant actuated ankle rehabilitation robot and compared redundant robots with non-redundant robots using singularity, dexterity, and stiffness as performance indices. The conclusions showed that redundant robots have better performance [19]. Gosselin et al. developed a 9-DOF redundant parallel mechanism based on the Gough–Stewart platform, which improved the torsion angle of the mechanism [20]. Wen et al. designed a backdrivable kinematic redundancy mechanism that has a very large position and orientation workspace, and can avoid type II singularities [21]. Yan et al. proposed a 5-DOF redundant actuated mechanism with a large tilt angle, which can be used for five-face machining [22]. The above studies proved that the introduction of redundancy has a very large effect on improving the workspace of parallel robots and avoiding singularity.
The GSM was proposed in 1965 [23] and is still applied in many fields, such as surgical robots. Raabe et al. designed a fracture reduction surgery robot based on the GSM [24]. Li et al. designed a robot based on the GSM for diaphyseal fracture reduction [25]. This paper tries to design a new redundant parallel robot to solve the problems of small workspace and complex singularities of the GSM, making the parallel robot available for practical applications such as medical surgery as early as possible. The rest of this paper is organized as follows. In Section 2, the structure of the robot is described and the kinematics of the robot is derived. In Section 3, the algorithm for calculating the workspace of the redundant parallel robot is proposed. In Section 4, the singularity of the redundant parallel robot is analyzed by using the homogeneous dimensional Jacobian matrix. In Section 5, the multi-objective optimization method is used to optimize the size of the proposed robot. In Section 6, the full paper is concluded.
2. Structure and Kinematics
For the GSM, Ma et al. defined the neutral poses in the literature [26]—that is, the orientation of the moving platform is zero, and the center position of moving platform is , where denotes the pose height variable. Neutral poses can obtain the minimum condition number; then, the robot can be kept as far away from the singularity as possible. However, the moving platform cannot be in neutral poses in most operating situations. When the moving platform is not parallel to the base, to make the mechanism move as close to neutral poses as possible, redundancy is introduced in this paper to reduce the angle between the moving platform and the plane where the bottom of the legs are located.
In this section, a new kinematically redundant parallel robot is introduced, which is based on the GSM. The new robot has six legs and three linear actuators on the base. Each leg is a prismatic actuator, and the three linear actuators are mounted on the base at a tilt angle . The three linear actuators located on the base are introduced as redundant actuators, which include active sliders and linear rails. The new kinematically redundant parallel robot is called redundant parallel robot with inclined rail (RPRI) in this paper. In the case that the three redundant actuators are locked, the RPRI becomes a non-redundant GSM. When the tilt angle of the moving platform is not equal to 0, through the motion of the redundant actuators, the plane formed by the bottom of the six lateral actuators can be as parallel as possible to the moving platform; then, the moving platform is closer to the neutral poses. The 3D model and structural sketch are shown in Figure 1a and Figure 1b, respectively.

Figure 1.
Redundant parallel robot with inclined rail. (a) 3D model. (b) Diagram of PRMIR.
To analyze the RPRI, the moving platform frame and base frame are established, as shown in Figure 2a,b. The origin of the base frame is located at the common intersection of the projection of the three linear rails on the base, and a diagram of the base is shown in Figure 2b. The x-axis is co-linear with the projection of a linear rail, and the z-axis is perpendicular to the base. The angle between the projection of the three linear rails is 2/3. The origin of the moving platform frame is located at its center. The -axis is perpendicular to line and passes through the midpoint of the line, and the -axis is perpendicular to the moving platform.
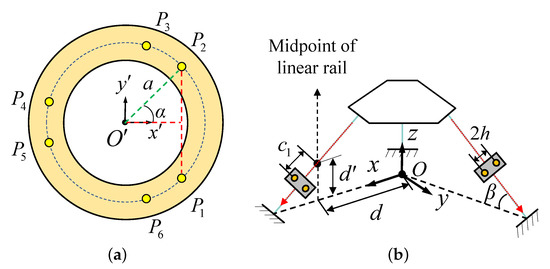
Figure 2.
(a) Diagram of moving platform. (b) Diagram of base.
To obtain the kinematic inverse solution of the moving platform, the fixed X–Y–Z Euler angles are used to represent the orientation of the moving platform relative to the base frame. The transformation matrix from the base frame to the moving platform frame can be obtained by referring to the literature [27].
The position vector of in the base frame can be represented by
where represents the position vector of in the base frame. represents the position vector of in the moving platform frame with . We can obtain
where . a denotes the radius of the circle in which is located, and represents half of the angle between and , and , and and , as illustrated in Figure 2a.
Since two adjacent on the moving platform are distributed as an array of , we have , , and . Similarly, we can obtain the position vector of
where d represents the distance between the projection of the midpoint of the linear rail on the x-axis and the point O. represents the distance value from the base slider to the midpoint of the k-th linear rail with . The direction that the base slider moves down the linear rail is regarded as the positive direction, as shown by the red arrows in Figure 2b. When the base slider passes the midpoint of the linear rail and moves down, is a positive value; otherwise, it is a negative value. h represents half the distance between the bottoms of two adjacent legs. represents the distance between the midpoint of the linear rail and its projection. The relationship between k and i is that when or 2, ; when or 4, ; and when or 6, .
Then, the length of each legchain can be expressed as
By the time derivative of Equation (1), the velocity vector of can be obtained as
where is the skew-symmetric matrix of , and . represents the angular velocity of the moving platform with respect to the base frame, and . The derivative of Equation (3) can be written as
where .
The point on the moving platform can also be expressed as
where denotes the unit vector corresponding to the leg of the RPRI.
The derivative of Equation (8) can be written as
where denotes the angular velocity of the leg. According to the literature [27], it can be obtained that
Let the velocity of the moving platform be , and define the length of the legs as with and ; then, Equation (10) can be rewritten as
where and are
where
It can be seen that the matrix is dimensionally inhomogeneous; so, this matrix is physically meaningless. To overcome this problem, the characteristic length link is used to homogenize the matrix [26]. In this paper, is chosen as the characteristic length link [27]. The dimensional homogeneous matrix can be obtained by dividing the fourth, fifth, and sixth columns of the by C.
3. Workspace Analysis
Workspace is an important performance index for parallel robots. Compared with the series robots, parallel robots have a smaller workspace. In this section, the redundancy is introduced to increase the workspace of parallel robots, and the effect of introducing redundancy is evaluated by comparing with the non-redundant GSM. To reduce the influence of other factors, the same moving platform, linear rail, and leg are used for the two manipulators. In fact, when the sliders of the redundant actuator of the RPRI are locked in the same horizontal plane, the proposed robot can be regarded as a non-redundant GSM. In this paper, the RPRI that the slider of the redundant actuators are locked to at the midpoint of each linear rail was regarded as the comparison GSM. The geometric parameters of the RPRI are listed in Table 1, where the values of and are chosen with reference to existing linear actuator commodities. The selection and principle for d and h is to avoid interference between the actuators. Parameters a and are chosen to avoid oversizing the moving platform.

Table 1.
Geometric parameters.
3.1. Position Workspace
Gosselin defined the position workspace of the parallel platform [5]. In this paper, the position discrete calculation algorithm is proposed to calculate the position workspace of the RPRI. is chosen as the maneuver point. The RPRI’s position workspace is made up of the position set of , and the position of can be obtained by solving its inverse kinematics. Different from the unique solution of non-redundant robots’ inverse kinematics, infinite sets of solutions can be derived for the inverse kinematics of redundant parallel robots. In this paper, the positions of three sliders are traversed to obtain a practicable solution for each leg.
The designed calculation framework for solving the RPRI’s position workspace is given by Figure 3. When calculating the workspace, the range of possible movements of point are estimated and a cuboid based on the estimates is set up. The cuboid is discretized into many points and the points are then traversed. The maximum and minimum values of the cuboid along the x-direction are defined as and . The y- and z-directions have similar definitions. To initialize and , set and . Leg length, interference between legs, and singular positions will affect the workspace of the proposed robot. The constraints condition in Figure 3 are listed below:
- Constraint of leg lengthThe obtained by Equation (5) is required to satisfy the following condition:
- The interference between each legWhen calculating the workspace, legs should avoid interference with each other. According to the literature [28], the constraint condition of interference between legs can be expressed aswhere D is the minimum distance between the central axis of the two arbitrary legs and is the diameter of the legs.
- Singular positionsWhen the robot reaches its singular configuration, the condition number of Jacobian matrix tends to infinity. However, the robot’s motion performance has deteriorated when it is close to the singular configuration. According to the literature [19], the judging condition of a singularity point is selected as for the convenience of calculation when calculating the workspace. The definition of is given in Equation (17). If , in this paper, we deem that the point is a singular position and it will be removed from the position workspace; otherwise, it is not a singular position. The position workspace of the RPRI is shown in Figure 4.

Figure 3.
The calculation framework for solving the position workspace of RPRI.
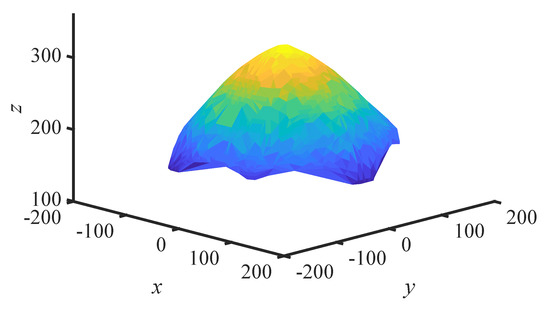
Figure 4.
Position workspace of the RPRI.
3.2. Orientation Workspace
The orientation workspace represents all possible orientations of the moving platform when the position of is fixed. According to the literature [29], the cylindrical coordinate system is utilized to represent the orientation workspace in this paper, where represents the direction of tilt of the moving platform, r represents the tilt angle , and z represents the torsion angle of the moving platform. Similar to Figure 3, the orientation workspace is calculated using the orientation discrete calculation algorithm. The orientation workspace of the RPRI is shown in Figure 5.

Figure 5.
Orientation workspace of the RPRI.
3.3. Comparison with the GSM
The non-redundant GSM adopts the same algorithm as the RPRI to calculate the position and orientation workspace, and the results are shown in Figure 6.

Figure 6.
(a) Position workspace of GSM. (b) Orientation workspace of GSM.
The results of workspace analysis for the non-redundant GSM and the RPRI are shown in Table 2, where “Volume” represents the volume enclosed by the outermost boundary of the position workspace. It can be seen from Table 2 that compared with the non-redundant robots, the RPRI has larger position workspace volume, tilt angle, and torsion angle. These results prove that the workspace of the parallel robot can be increased by introducing redundancy.

Table 2.
Workspace analysis results.
4. Singularity Analysis
When the robot runs in the singular configuration, it will be uncontrolled; so, the robot should avoid working in singular configurations. However, when the robot works in the vicinity of the singular configuration, its performance already begins to deteriorate sharply. In this paper, the condition number is chosen as a criterion to evaluate the singularity performance of the RPRI and GSM.
The singular value of the Jacobian matrix can be expressed as
where is the eigenvalue of . Then, the condition number of can be calculated as
where . The smaller the condition number, the better the singularity performance of the robot. When the condition number goes to infinity, the robot will be in singular configuration.
To clearly show the condition number distribution of the RPRI and GSM, their orientations of the moving platform are kept constant to move in a horizontal plane. Then, are calculated in different positions. The condition number of the GSM is calculated for comparison. For simplicity, let denote the centre point of the position workspace, and , where . When , it represents the RPRI; when , it represents the GSM. and represent the minimum and maximum z-values of all points in the position workspace, separately. The condition number distributions of the RPRI and the GSM in different configurations are given in Figure 7, Figure 8 and Figure 9.
It can be seen from Figure 7, Figure 8 and Figure 9 that the condition numbers of the Jacobian matrix of the RPRI are all smaller than those of the GSM. It indicates that the proposed robot has a better ability to avoid singularity after the introduction of redundancy. Moreover, we drew the projection outline of the condition number distributions on the plane in Figure 7, Figure 8 and Figure 9. It can be seen that the contours of the GSM are all inside the RPRI, which proves that the workspace of the robot increases after the introduction of redundancy.
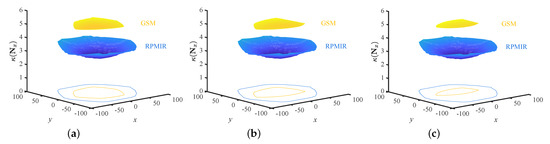
Figure 7.
The condition number distributions of the RPRI and the GSM with under different orientations. (a) Torsion and tilt angles . (b) Torsion and tilt angles . (c) Torsion and tilt angles .
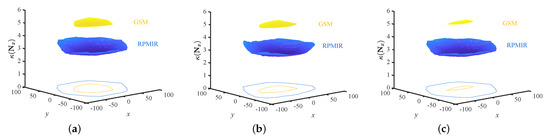
Figure 8.
The condition number distributions of the RPRI and the GSM with under different orientations. (a) Torsion and tilt angles . (b) Torsion and tilt angles . (c) Torsion and tilt angles .

Figure 9.
The condition number distributions of the RPRI and the GSM with under different orientations. (a) Torsion and tilt angles . (b) Torsion and tilt angles . (c) Torsion and tilt angles .
5. Optimization and Application
The RPRI is designed by introducing redundancy into the GSM. The parameters of the robot need to be optimized for the best performance after introducing redundancy. For the RPRI, d and in Equation (3) are chosen as the optimization variables. Since the genetic algorithm is able to easily obtain the global optimal solutions [30], the multi-parameter, multi-objective genetic algorithm is used to optimize the geometric parameters of the RPRI in this paper.
It is hoped that the RPRI has a large workspace while each point inside its workspace is far away from the singularities. The global condition index (GCI) is defined to measure the robot’s ability to avoid singularity as follows:
where W represents the set of points in the position workspace. Then, the multi-parameter, multi-objective optimization problem can be expressed as
where is the objective function, , V denotes the position workspace volume, , and . The range of the variables is shown in Table 3.

Table 3.
Range of the optimized variables.
For the parallel robots, the projection of the bottom of the leg onto the base is generally outside the projection of the moving platform onto the base. To ensure this geometric constraint condition, is defined as follows:
The options of the genetic algorithm are set as follows: PopulationSize = 30, InitialPopulation = , Generations = 50, ParetoFraction = 0.35. The results obtained by the multi-objective genetic algorithm are called the Pareto front solutions. In this paper, the Pareto front solutions for problem (19) are shown in Table 4 and the variables corresponding to each set of Pareto front solutions are shown in Table 5.

Table 4.
Optimized V and GCI of the RPRI.

Table 5.
Optimized parameters.
In the multi-objective optimization problems, it may not be able to find a unique optimal solution. For different application scenarios, we need to choose the most appropriate solution from the set of Pareto front solutions. The comprehensive performance index (CPI) is constructed to choose the compromised data. CPI can be expressed as
where and denote the weight coefficients, and . In subsequent studies, we hope that the RPRI will be used in fracture reduction surgery. According to the literature [31], the surgical robot usually needs a large workspace; so, here, we make . In this case, the CPIs of the 11-th data are the largest; then, the 11-th data are chosen as the machining parameters for the experimental prototype. Based on the parameters in Table 1 and Table 5, an experimental prototype of the RPRI is manufactured, as shown in Figure 10.

Figure 10.
Prototype of the RPRI.
6. Conclusions
In this paper, a novel kinematically redundant parallel robot called RPRI was designed, based on the GSM. The performance of the RPRI was analyzed and compared with the GSM.
- (1)
- The kinematic analysis of the RPRI was presented, and the position and orientation workspaces of the RPRI were calculated. The position and orientation workspaces of the GSM were calculated and compared with the RPRI. The comparison showed that after the introduction of redundancy, the volume of the position workspace increased by 362%, the maximum torsion angle increased by 77%, and the maximum tilt angle increased by 63%.
- (2)
- The dimensionally homogeneous Jacobian matrices were constructed to compare the singularities of the RPRI and the GSM. The condition number distributions of the RPRI and the GSM in different configurations are illustrated to show that RPRI has greater performance in avoiding singularity than the GSM.
- (3)
- The multi-parameter, multi-objective genetic algorithm was used to optimize the geometric parameters of the RPRI. On the basis of the optimized results, the experimental prototype of the RPRI was built with the target of fracture reduction surgery.
There are still several issues that remain to be solved in this study, which are the subjects of future work. One vital issue is that the workspace of the proposed robot needs to be validated by experiment. In addition, the optimal singularity-free trajectories need to be planned based on the RPRI’s ability to avoid singularities.
Author Contributions
Conceptualization, G.L. and X.Z.; methodology, X.L.; data curation, formal analysis, and simulation, X.Z and T.S.; supervision, G.H. and W.C.; investigation, X.Z. and W.C.; writing—original draft preparation, X.Z.; writing—review and editing, X.L. and G.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Beijing Natural Science Foundation (Project Nos. L202020 and L222053), the National Natural Science Foundation of China (Project Nos. 62103412, 62003005, U22A2056, and 62103007), the R&D Program of Beijing Municipal Education Commission (Project Nos. KM202110009009 and KM202210009010), the Natural Science Foundation of Beijing (Project Nos. 4204097 and L222058), the Yuyou Talent Support Project of North China University of Technology, and the Fundamental Research Funds for Beijing Municipal Universities.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, J.; Liu, X.; Wu, C. Optimal design of a new spatial 3-DOF parallel robot with respect to a frame-free index. Sci. China Ser. E-Technol. Sci. 2009, 52, 986–999. [Google Scholar] [CrossRef]
- Furqan, M.; Suhaib, M.; Ahmad, N. Studies on Stewart platform manipulator: A review. J. Mech. Sci. Technol. 2017, 31, 4459–4470. [Google Scholar] [CrossRef]
- Yang, J.; Sun, T.; Cheng, L.; Hou, Z. Spatial repetitive impedance learning control for robot-assisted rehabilitation. IEEE/ASME Trans. Mechatron 2022, 1–11. [Google Scholar] [CrossRef]
- Lu, S.; Ding, B.; Li, Y. Minimum-jerk trajectory planning pertaining to a translational 3-degree-of-freedom parallel manipulator through piecewise quintic polynomials interpolation. Adv. Mech. Eng. 2020, 12, 1–18. [Google Scholar] [CrossRef]
- Gosselin, C. Determination of the workspace of 6-DOF parallel manipulators. J. Mech. Des. 1990, 112, 331–336. [Google Scholar] [CrossRef]
- Kim, D.; Chung, W.; Youm, Y. Geometrical approach for the workspace of 6-DOF parallel manipulators. In Proceedings of the International Conference on Robotics and Automation, Albuquerque, NM, USA, 20–25 April 1997; Volume 4, pp. 2986–2991. [Google Scholar] [CrossRef]
- Merlet, J.P. Determination of 6D workspaces of Gough-Type parallel manipulator and comparison between different geometries. Int. J. Robot. Res. 1999, 18, 902–916. [Google Scholar] [CrossRef]
- Pernkopf, F.; Husty, M.L. Workspace analysis of Stewart-Gough-Type parallel manipulators. Proc. Inst. Mech. Eng. C Mech. Eng. Sci. 2006, 220, 1019–1032. [Google Scholar] [CrossRef]
- Bonev, I.A.; Ryu, J. A new approach to orientation workspace analysis of 6-DOF parallel manipulators. Mech. Mach. Theory 2001, 36, 15–28. [Google Scholar] [CrossRef]
- Jiang, Q.; Gosselin, C.M. Determination of the maximal singularity-free orientation workspace for the Gough–Stewart platform. Mech. Mach. Theory 2009, 44, 1281–1293. [Google Scholar] [CrossRef]
- Yan, Q.; Li, B.; Li, Y.; Zhao, X. Kinematics comparative study of two overconstrained parallel manipulators. Math. Probl. Eng. 2016, 2016, 5091405. [Google Scholar] [CrossRef]
- Li, B.; Li, Y.M.; Zhao, X.H.; Ge, W.M. Kinematic analysis of a novel 3-CRU translational parallel mechanism. Mech. Sci. 2015, 6, 57–64. [Google Scholar] [CrossRef]
- Gosselin, C.; Angeles, J. Singularity analysis of closed-loop kinematic chains. IEEE Trans. Robot. Autom. 1990, 6, 281–290. [Google Scholar] [CrossRef]
- Zlatanov, D.; Bonev, I.; Gosselin, C. Constraint singularities of parallel mechanisms. In Proceedings of the 2002 IEEE International Conference on Robotics and Automation (Cat. No.02CH37292), Washington, DC, USA, 11–15 May 2002; Volume 1, pp. 496–502. [Google Scholar] [CrossRef]
- St-Onge, B.M.; Gosselin, C.M. Singularity analysis and representation of the general Gough-Stewart platform. Int. J. Robot. Res. 2000, 19, 271–288. [Google Scholar] [CrossRef]
- Conconi, M.; Carricato, M. A new assessment of singularities of parallel kinematic chains. IEEE Tran. Robot. 2009, 25, 757–770. [Google Scholar] [CrossRef]
- Sarigul, A.S.; Guneri, B. Some geometric, kinematic, and dynamic considerations on Stewart-Gough platforms with singularity analysis. Robotica 2014, 32, 953–966. [Google Scholar] [CrossRef]
- Saglia, J.A.; Dai, J.S.; Caldwell, D.G. Geometry and kinematic analysis of a redundantly actuated parallel mechanism that eliminates singularities and improves dexterity. J. Mech. Des. 2008, 130. [Google Scholar] [CrossRef]
- Wang, C.; Fang, Y.; Guo, S.; Chen, Y. Design and kinematical performance analysis of a 3-RUS/RRR redundantly actuated parallel mechanism for ankle rehabilitation. J. Mech. Robot. 2013, 5, 041003. [Google Scholar] [CrossRef]
- Gosselin, C.; Schreiber, L.T. Kinematically redundant spatial parallel mechanisms for singularity avoidance and large orientational workspace. IEEE Trans. Robot. 2016, 32, 286–300. [Google Scholar] [CrossRef]
- Wen, K.; Nguyen, T.S.; Harton, D.; Laliberté, T.; Gosselin, C. A backdrivable kinematically redundant (6+3)-degree-of-freedom hybrid parallel robot for intuitive sensorless physical human–robot interaction. IEEE Trans. Robot. 2021, 37, 1222–1238. [Google Scholar] [CrossRef]
- Yan, P.; Huang, H.; Li, B.; Zhou, D. A 5-DOF redundantly actuated parallel mechanism for large tilting five-face machining. Mech. Mach. Theory 2022, 172, 104785. [Google Scholar] [CrossRef]
- Stewart, D. A platform with six degrees of freedom. Proc. Inst. Mech. Eng. 1965, 180, 371–386. [Google Scholar] [CrossRef]
- Raabe, D.; Dogramadzi, S.; Atkins, R. Semi-automatic percutaneous reduction of intra-articular joint fractures - An initial analysis. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, St Paul, MN, USA, 14–18 May 2012; pp. 2679–2684. [Google Scholar] [CrossRef]
- Li, C.; Wang, T.; Hu, L.; Tang, P.; Wang, L.; Zhang, L.; Guo, N.; Tan, Y. A novel master–slave teleoperation robot system for diaphyseal fracture reduction: A preliminary study. Comput. Assist. Surg. 2016, 21, 162–167. [Google Scholar] [CrossRef]
- Ma, O.; Angeles, J. Optimum architecture design of platform manipulators. In Proceedings of the Fifth International Conference on Advanced Robotics ’Robots in Unstructured Environments, Pisa, Italy, 19–22 June 1991; Volume 2, pp. 1130–1135. [Google Scholar] [CrossRef]
- Bahman, N.; Farid, M.; Mahzoon, M. Redundancy resolution and control of a novel spatial parallel mechanism with kinematic redundancy. Mech. Mach. Theory 2019, 133, 112–126. [Google Scholar] [CrossRef]
- Dong, K.; Li, D.; Xue, X.; Xu, C.; Wang, H.; Gao, X. Workspace and accuracy analysis on a novel 6-UCU bone-attached parallel manipulator. Chin. J. Mech. Eng. 2022, 35, 35. [Google Scholar] [CrossRef]
- Bonev, I.; Zlatanov, D.; Gosselin, C.M. Advantages of the modified Euler angles in the design and control of PKMs. In Proceedings of the 2002 Parallel Kinematic Machines International Conference, Chemnitz, Germany, 23–25 April 2002; pp. 171–188. [Google Scholar]
- Du, J.; Huang, Z.; Yang, R. Optimization of the motion control mechanism of the hatch door of airliner. Struct. Multidiscip. Optim. 2015, 51, 1173–1186. [Google Scholar] [CrossRef]
- Essomba, T.; Nguyen Phu, S. Kinematic analysis and design of a six-degrees of freedom 3-RRPS mechanism for bone reduction surgery. J. Med. Devices 2020, 15, 011101. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).