Abstract
This paper presents a method on how to compute the position of a robotic arm in the 2D and 3D spaces. This method is slightly different from the well-known methods, such as forward or inverse kinematics. The method presented in this paper is an optical method, which uses two video cameras in stereo vision configuration to locate and compute the next move of a robotic arm in space. The method recognizes the coordinates of the markers placed at the joints of the robotic arm using the two video cameras. The coordinate points of these markers are connected with straight lines. Around certain points, circles are drawn. From the tangent to the circles, a non-Cartesian (orthogonal) coordinate system is drawn, which is enough to compute the target position of the robotic arm. All of these drawings are overlaid on the live video feed. This paper also presents another method for calculating the stereo distance using the triangulation method. An alternative method is also presented when a non-Cartesian (orthogonal) 3D coordinate system is created, which is used to compute the target position of the robotic arm in the 3D space. Because the system is in a loop, it can make micro-adjustments of the robotic arm, in order to be exactly in the desired position. In this way, there is no need to make calibrations for the robotic arm. In an industrial system, there is no need to stop the production line, which can be a really big cost saver.
1. Introduction
The idea of controlling a robotic arm has always been of great interest for mankind because it is the only way to produce many products for today’s users with high demand [1]. Consumerism made today’s world really hard to survive in without machines or robots. In a traditional robotic system, robots are controlled with forward or inverse kinematics, but in this paper we try to present an alternative method, maybe a complementary method, which can help to control a robotic arm optically using video cameras [2] in stereo vision configuration. Video cameras can be used to auto-calibrate a robotic arm that can shift from its movement path, due to repeated movement operations [3].
In a traditional robotic system with forward or inverse kinematics, the robot needs maintenance and calibration. If the robotic arm shifts, it will offset its predefined movement path [4].
A robotic arm control method will be presented, which will be controlled using information received from video cameras mounted on the side of the room [5]. With strong image processing techniques, the robotic arm can be controlled quite precisely.
There are also deep learning and reinforcement learning methods to control the manipulator for dexterous operation, which can achieve good results [6,7,8,9,10]. The method presented in this article can be comparable to these methods [11,12,13,14,15,16,17,18,19,20], when we refer to precision, but with the advantage that there is no need for the calibration process, so no time is lost like with other methods.
The robotic arm’s position computing method is implemented in a real robotic arm control system.
Table 1 shows a comparison between the system presented in this manuscript and other robotic arm control systems using video cameras, made by other researchers and presented in specialized journals. The method presented was currently implemented to control only three joints of the robotic arm.

Table 1.
Comparison between the presented method and other similar methods.
It can be seen that the parameters of the proposed approach are comparable to the implementations in the specialized journals. The method presented in this paper can be extended to several joints. The presented algorithm controls three joints: left-right base rotation ( axis), forward-backward shoulder movement ( axis) and up-down elbow movement ( axis). To scale up the system to robotic arms with more than three DoF, up-down wrist movement can be added, for example, or rotation of certain joints. All of this can be achieved by the usage of extra algorithms, such as the forward or inverse kinematics. The proposed algorithm is not made to work alone, but alongside other known algorithms, thus it can also control robotic arms with seven joints, which are used in the aerospace industry.
Park et al. [24] can control a robotic arm with seven joints, in the simulation program and another robotic arm with four joints, in the real experiment using classical Jacobian matrix methods, but uses calibration and adjustments with a system of lasers mounted on the end effector. The experiment also uses the help of a video camera, which tracks the two laser points projected on a wall. The video camera was used because the classical Jacobian matrix system has some shortcomings. For example, sometimes the position computed by the algorithm is not correct, and there are some positions in the space where the robotic arm cannot reach [24]. In this way, a video camera system was used to solve this problem. The approach is a bit unusual, as the camera is behind the robotic arm and follows the laser point projected onto a wall from the end effector, thus not viewing the robotic arm itself or the object being manipulated.
It can be seen that, in the article presented by Park et al. [24], there are at least 25 calibration steps, which are not present in the method disclosed in this paper because the calibration is performed in real time during execution. In the method presented in this paper, only two calibration parameters are needed, which can be measured in the beginning and will not change over time. The rest of the calibration is conducted automatically in real-time during execution. In other words, in the worst case, the position is recalculated and the robotic arm is moved more precisely to the target position. In an unfavorable case, the robotic arm on the first attempt will not get very close to the target position and will have tolerances on the order of millimeters. At this moment, the video cameras will sense this and will give a command to recalculate the position. From this moment on, the target position of the robotic arm will be recalculated from the new position, from this smaller distance, and in this way the error will be corrected. From the tests, it has been seen that the position is recalculated a maximum of three times, but in most cases, the robotic arm manages to reach exactly the target position on the first try.
In the article written by Seelinger et al. [21], an interesting and rather rare approach can be seen, as three video cameras are used, which can control a robotic arm with six joints. One camera is placed in front and two on the side of the robotic arm. The approach is quite interesting because, in the article, only the movements of the robotic arm are tracked, but they are not actually controlled by the cameras. The control is carried out by forward or inverse kinematics, so it is completed by classical methods.
Behera et al. [23] presented an approach similar to that disclosed in this paper. Two video cameras are used and a robotic arm with three joints is controlled. In this approach, classical methods such as forward or inverse kinematics are also used, but cameras are also partially used to control the robotic arm. In the paper [23], one camera is placed on the back and the other camera is placed on one side of the robotic arm.
A stereo camera system is not created because the cameras are not on the same side, but still the control is made using another algorithm, which complements the classical methods such as the forward or inverse kinematics. The algorithm in this approach is not used on its own either, but it is a complex method, which controls the robotic arm using video cameras, and also incorporates classical methods too.
In the article written by Kelly et al. [22], a slightly different approach is observed, since only one camera is used, which is mounted on the end effector of the robotic arm. The robotic arm has only two joints. It can be said that two cameras are too much for this movement because, with two joints, the robotic arm can only move in one plane, and, in this way, one camera is enough for computing this movement. This approach is quite different from the one presented in this paper, as the camera views the manipulated object and not the robotic arm itself. The approach, however, has advantages because it deals with the dynamics of the robotic arm, which were not taken into account in this paper. Until now, the dynamics have not affected the system because the system moved relatively light objects from one position to another [25]. In the case where the movement velocity does not matter too much, there are no problems [26]. For moving large objects at high speed, handling the dynamics of a robotic arm is of great interest [27].
The goal of this work is to create a novel computational method for determining the position of a robotic arm in space [28]. The idea was to create an alternative, or at least a complementary method to the classic forward or inverse kinematics. This can be achieved by creating an optical method in which the position of a robotic arm can be computed using video cameras [29]. To recognize a robotic arm in space, markers are placed on each joint of the robotic arm. The coordinates of these markers are connected with straight lines. Circles around certain points are also drawn. From the tangent to the circles, a non-Cartesian (orthogonal) coordinate system is drawn, which is good enough to compute the target position of the robotic arm [30]. All of these drawings are overlaid on the live video feed. The coordinates of the markers placed on the joints of the robotic arm are the initial information from which the movement angles of each motor can be computed to know how much each motor from the joints of the robotic arm has to rotate in order to move the robotic arm in the desired position [31]. The coordinates of the markers placed on the joints of the robotic arm are read using two video cameras. In a standard forward or inverse kinematics computed robotic arm system, the robotic arm can shift or offset after repeated movements [32]. For this, a re-calibration is needed to place the robotic arm on track in the desired movement path [33]. When this happens, the production line must be stopped, which can cause great financial losses for an industrial system and can increase manufacturing costs [34]. An optical method can be an advantage because there is no need to perform periodic calibrations of a robotic arm [35]. This can be a really big cost saver [36]. The optical method can make repeated micro-adjustments to reach the target position of the robotic arm because the system is in a loop [37].
2. Problem Solving
2.1. Presenting the Proposed Algorithm
In this section, the proposed method is presented, which can compute the target position of the robotic arm in the 3D space. This proposed approach is based on the combination of two algorithms. The first algorithm is the joint detection method in the 2D space (axes and ), using image processing techniques. The second algorithm is the stereo distance calculation algorithm, which computes distances in the third dimension (axis ), using two video cameras in stereo mode.
The algorithm used involves the usage of some guide lines and circles overlaid on the image captured in real-time by the video cameras. These video cameras provide the initial information (the coordinates of the joints) to calculate distances.
In Figure 1, it can be seen how the guide lines and circles will be drawn on the live video stream with the robotic arm. Here, a 3D model of the Lynxmotion AL5X robotic arm is shown with the guide lines and circles drawn for the position calculation. The 3D model was used only to show the basic idea of the algorithm. Other alternative methods will be shown on a real robotic arm.
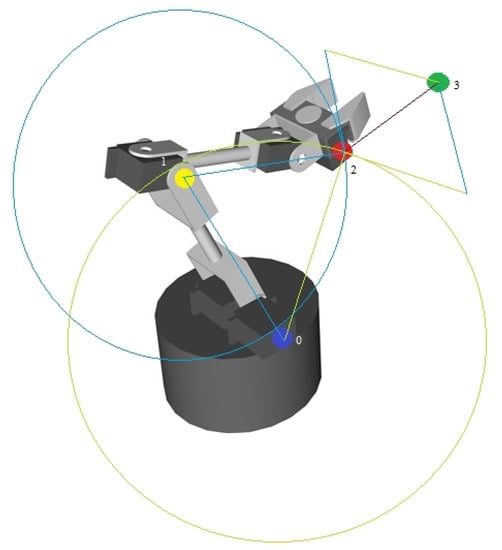
Figure 1.
Auxiliary drawings on the 3D model of the robotic arm.
In Figure 2, the drawings overlaid on the live video stream can be seen.
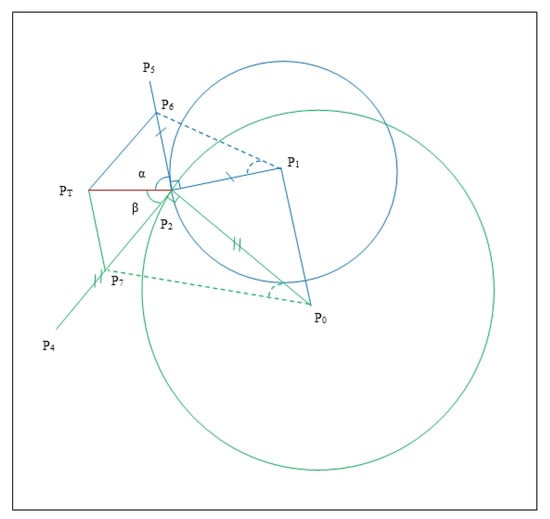
Figure 2.
Guide lines and circles for calculating distances in the 2D space overlaid on the live video stream.
The point refers to the blue bottle cap placed on the base of the robotic arm, the point refers to the yellow bottle cap placed on the elbow of the robotic arm, and the point refers to the red bottle cap placed on the end effector of the robotic arm. The point is the target point, the point at which the end effector must reach, and is marked with the green bottle cap.
Points , and with are connected with blue lines, the point is connected with the point using a green line, in this way obtaining the skeleton of the robotic arm. The blue lines are overlaid directly on the robotic arm because they connect the joints of the robotic arm (these lines have a fixed length), and the green line shows the “opening distance” of the robotic arm, or the distance between the bottom and the end joints (this line is variable in length). Finally, the point is connected with the point using a red line (this line is also variable in length, depending on the position where the target point is placed).
A blue circle is drawn around the point , and a green circle is drawn around the point . The blue circle has a fixed radius and a variable origin, and the green circle has a fixed origin and a variable radius. After this step, the tangents are drawn to the blue and green circles. The simplest method is to calculate the orthogonal vector for the blue segment and the orthogonal vector for the green segment by drawing perpendicular segments of equal lengths to the radius of the circles. The green segment is equal and perpendicular to the green segment , and the blue segment is equal and perpendicular to the blue segment .
This way, a coordinate system was obtained, which is not a Cartesian (orthogonal) coordinate system, but it can be used for the intended purpose to compute the robotic arm’s position in space. The points of interest are and , which need to be determined.
A parallel line to the green line can be drawn; this line also passes through the point , which will certainly intersect the blue line. In addition, the points and are on this line. The intersection is made through the point . A parallel line can be drawn, with the blue line; also, the points and are on this line; this parallel line also passes through the point , which will surely intersect the green line; also, the points and are on this line. The intersection is made through the point . Thus, the parallelogram is obtained. This parallelogram is actually the coordinate system from which useful information can be obtained; the useful information is the length of the segments and . In addition, the length of the segments and is known (the position of the points , , and is known, and the coordinates of these points were obtained with the help of a single camera). The coordinates of the target point and the intersection points and are also known.
The length of the segments and is also known, which are the lengths of the legs of the green right triangle, for which the motion angle of the base motor of the robotic arm using trigonometric functions must be computed by computing the angle arctangent. The system could compute singularities at specific positions. The robotic arm is mechanically made in such a way that it does not move when a singularity point is computed. If the system computes a singularity point, the robotic arm would move as close to the target position by repeating the position computation algorithm again. The system is made to move in a loop.
Knowing the length of the segments and (the lengths of the legs of the blue right triangle) for which the angle of motion of the robotic arm elbow motor needs to be computed.
This drawing refreshes on the robotic arm’s live video stream dynamically every time the robotic arm changes its position. The dimensions differ, but the symmetry is the same; the sides of the parallelogram will always be parallel to each other. Certain segments of the final overlaid image are hidden for readability (e.g., segments , , , ).
Angles must be converted into robotic values, and these values can be decoded by the robotic arm microcontroller; in other words, these values are “understood” by the robotic arm. These robotic values are actually pulse widths in microseconds () which are used to control each motor from the joints of the robotic arm, and the “robotic values” are the positions of each servo motor of the robotic arm.
The three-dimensional extension of the present 2D algorithm is performed using a secondary video camera used to calculate distances on the axis.
In the following, the formulas for generating the overlaid drawings applied in the real-time video stream are presented [38].
The values of the robot commands have been determined. These were obtained by converting the “” (pulse widths) for the servomotors as shown in Equation (1):
The “” (pulse widths) are between 500 and 2500, and the maximum angle of movement of a servomotor is , so the relationship between the angles and “” (pulse widths) is presented in Equation (2):
As seen in (2), the “” were rounded to integer values because the microcontroller, which controls the servomotors from the robotic arm’s joints, can accept only integer values. We can accept (2); then, the error of our rounding will be a movement of a joint with , which is not a big error, but even in this situation, this error will be also corrected by the micro adjustments made by the robotic arm controlled by the two video cameras used in the stereo vision configuration.
The difference between the vectors was calculated as shown in Equation (3):
The length of the Euclidean norm vector is computed as shown in Equation (4):
The orthogonal vector was calculated as shown in Equation (5):
Combining Equation (3) with Equation (5), we obtain the coordinates of the points and as shown in Equation (6) and in Equation (7).
The parallelogram was calculated as follows:
The line passing through the point for the end effector of the robotic arm is expressed by Equation (9):
Or:
Using Equation (10) twice for x and twice for y, for both slopes ( and ), Equations (11)–(14) were obtained:
Finally, the coordinates of the point were obtained as presented in Equation (16):
Performing the same calculations for , the coordinates for the point were obtained with Equations (17) and (18):
Next, how to calculate the distance using the stereo cameras is described.
In Figure 3, the right triangle has one leg that represents the object “”, and the other leg represents the distance between the cameras, or, in the terms used in this paper, represents “”.
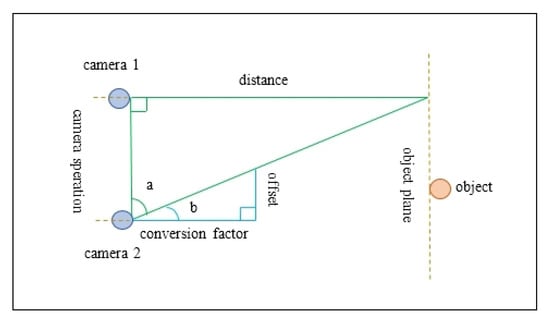
Figure 3.
Stereo distance calculation.
In the smaller (calibration) right triangle, one leg is the difference between the two images, and the other leg is the conversion factor, which is a calibration parameter. The system thus provides a self-calibration function, as the conversion factor is recalculated each time the distance is computed; this event occurs each time the robot changes direction [39]. The only pre-calibration, which the system needs, is the distance between the cameras (“”) and knowledge the initial distance from the cameras to the robotic arm (“”). This can be measured in advance. In industrial systems and in our system, too, the robotic arm is fixed to the ground [40,41,42] with screws, so these distances will not change. The offset can be computed by reading the coordinates, with the video cameras, of a certain marker placed at a specific joint of the robotic arm. In our case, the marker number 2, is placed at the end effector joint of the robotic arm.
Two distances were calculated, one to the blue dot, which represents the base of the robot, and the other to the green dot, which represents the target point, where the end effector must reach [38]. These two distances are subtracted from each other. This difference represents the leg of the right triangle, and the other leg is the green segment , as shown in Figure 2.
Using the following formulas, the measured distance values can be transformed from the real-world coordinates to the pixel coordinates to synchronize them with the values obtained from Figure 2. With trigonometric functions, the value of the angle of movement of the robotic arm will be calculated on the axis and after that this value will be converted into a command “understood” by the robot. The image in Figure 2 is doubled for redundancy and is also used to obtain the distance parameters measured using stereo cameras [38]. In Figure 2, the distances for the and axes are determined, and, in Figure 3, the distances for the axis are determined. The position of the robotic arm in the 3D space is obtained by combining the two algorithms [38], the first algorithm presented in Figure 2 is doubled for redundancy, using the two cameras, and the other algorithm is presented in Figure 3, which also uses the parameters obtained with the algorithm shown in Figure 2.
In the following, the formulas for calculating the stereo distance will be presented according to Figure 3.
The tangent of the angles and was calculated as shown in Equation (19):
The offset was calculated as the difference between the initial points of the left and right images, acquired by the two cameras, as shown in Equation (20):
The conversion factor results are shown in Equation (21):
The offset was calculated relative to the point as shown below in Equation (22):
The final distance was calculated as seen in Equation (23):
The angle in degrees will be obtained as shown in Equation (24):
The values for the final “robotic commands” were calculated as presented in Equation (25):
The real-world coordinates were converted into pixels as follows. The computer display used is a display, and the resolution for the captured image has 320 × 240 pixels [43] as shown in Equation (26):
The pixel density was obtained from Equation (26). From Equation (27), the data for the image size were obtained for a specific computer display size, which in the case of the experiment was 21.05 PPI [43]. This value was taken from the PPI table [43], where initially the height and width of a computer display needed to be measured and, after being computed, the area in square inches. For each computer display area, in square inches, there is a correspondence in PPI, which is a constant, which we can use to convert real-world values into pixels:
The screen resolution needed to be introduced because the robotic arm’s position detection in the 2D space (for axes and ) makes distance calculations on the computer screen at pixel level. For the third dimension (for the axis), the stereo distance measurement makes calculations in the real world, which needs to be converted to pixels, to be combined with the robotic arm position detection in the 2D space, which uses pixel level calculations. To convert real-world coordinates to pixels, as presented, the screen size and resolution is a factor, which needs to be taken into account (some screens have more, others have less pixels).
The method to compute the distance in the 3D space is made using a combined algorithm. The movement in 2D (on the and axes) is computed with Equations (3)–(18) and, for the movement in the third dimension (for the axis), the stereo distance calculation is used, which is calculated with Equations (19)–(23). There are two images for redundancy, so for the and axis in the 2D space, the calculations are made twice, using Equations (3)–(18). The second camera is actually needed for the distance measurement for the axis, for the stereo distance calculation.
As geometric conclusions, it can be said that the position of the robotic arm in space cannot be computed with only forward and inverse kinematics or coordinate system transformations, but also with another type of parallelogram-shaped coordinate system, which is not a Cartesian (orthogonal) coordinate system, but it is good enough to compute the position of the robotic arm in space.
In Figure 4, the graphical representation of the steps on how to control a robotic arm using the proposed method is presented. Also, a pseudocode with the implementation is shown in Appendix A.

Figure 4.
Graphical representation of the steps on how to control a robotic arm using the proposed method.
2.2. Method Evaluation with Six-Sigma Tools
Six-Sigma (6) is a set of tools and methods to improve the process. These tools try to improve the quality of manufacturing by removing defective products. This can be carried out using statistical or empirical quality management methods with the goal of increasing customer satisfaction. The term Six Sigma comes from statistics, indicating the percentage of products without defects, or how many standard deviations of a Gaussian distribution correspond to the number of products without defect. These tools can be successfully used for any measurement system, in our case the distance measurement system. If our distance measurement system passes the Six-Sigma tests, it means that we have a robust system that can be easily used in the industry and also in other fields.
In Table 2, the method is tested by taking measurements at different distances. The system was tested by comparing the computed distance measurement method to a laser distance measurement tool. In total, 30 measurements for the distances from 100 mm to 3000 mm, with an increment of 100 mm.

Table 2.
Distance measurement using video cameras at different distances in [mm] with a highlight on the measurement delta (error) in [mm] and the relative error.
The measuring error for the and axes was not computed because the computations are at the pixel level. Everything being computed in the 2D space is computed on the computer screen, and this error could not be relevant for a motor movement. This is considered to be much under 1 of the motor movement. For the axis, the measurement error was computed, due to the fact that depth movement is measured using two video cameras. The measuring error for the axis is presented in the table. Here, the actual measured distance with a laser measurement tool and the distance computed by the presented algorithm using video cameras can be seen. The delta (error) was also computed, which is the difference between the value measured by the presented algorithm using video cameras and the real distance measured by the laser measurement tool.
In Equation (29), the relative error is presented, and this is also presented in Table 2:
where is the relative error, is the real distance measured with the laser distance measurement tool, and is the distance calculated with the algorithm. In Equation (30), the tracking error is presented:
where is the tracking error, is the real distance measured with the laser distance measurement tool, is the distance calculated with the algorithm, and N is the number of measurements made. As can be seen, the tracking error is just below 3.5 mm at distances between 100 and 3000 mm, which is quite acceptable, due to the fact that the system can make corrections using the optical self-calibration because the system is in a loop.
Figure 5 shows the normal probability plot, with a 95% confidence interval, of the delta (error), which is the difference between the real value and the measured value. The mean of the delta (error) is −0.7667 mm, which is acceptable. The standard deviation is 3.38 mm. This could cause the robotic arm to oscillate, but with the auto-calibration method, the system being in a loop, the robotic arm can easily get in the desired target position, by the repeated use of the presented algorithm. The authors made video recordings to demonstrate that the robotic arm can reach the desired position. The (Anderson–Darling) value is 0.643, and the p-value is 0.084, which is greater than = 0.05, so we fail to reject the null hypothesis and the delta (error) is not statistically significant because it has too few values. However, even in this situation, the values are very close to the real distance.
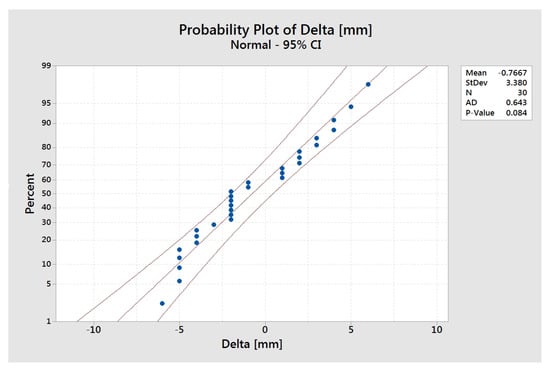
Figure 5.
Normal probability plot for the error (delta).
In Figure 6, a capability analysis of the 30 distance measurements is presented. The charts (individual value and moving range) are in limits. The histogram has a Gaussian trend, but for a histogram, 30 values are not enough. It is also observed in the histogram that there are no measured values where the delta (error) is 0. This means that there is no measurement without error, but this is not a big issue because these errors are very low. In the normal probability plot, the (Anderson–Darling) value is 0.643, and the p-value is 0.084. Thus, it is greater than = 0.05, so we fail to reject the null hypothesis, and it can be said that the delta (error) is not statistically significant because we do not have enough values. However, in this situation, the values are also very close to the real distance. The most important part is the values in the conclusions, where the standard deviation is 2.965 mm within the subgroup and 3.38 mm in the overall measurements. The value is 1.38, which is more than 4, which is a very good result for a real system. The is 1.46, is 1.28, and is 1.21. All the values are very close to 4, which is a very good result for a real system. The (the error per one million measurements) is 20.21 within the subgroup and 171.11 in overall the measurements. This value is also a very good result.
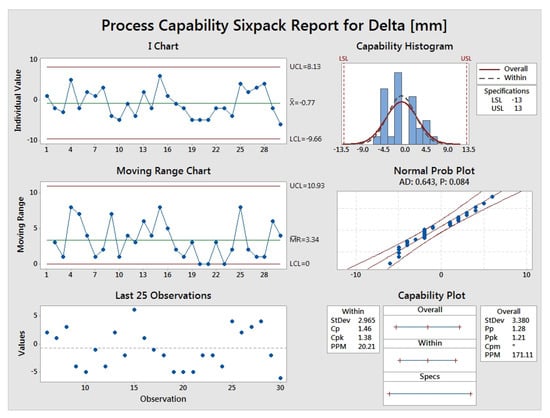
Figure 6.
Capability analysis for the actual distance and distance computed by the method using video cameras.
Only a distance measurement with a laser distance measuring tool was performed, and this was considered standard for distance measurement. Therefore, only a comparison to this value was performed, a validation of the distance measurement with video cameras, using the Six Sigma (6) tools. A comparison to a calibrated device (the laser distance measuring tool) was made, and this can be considered as the calibration error.
3. Results
3.1. Calibrations
All of the methods presented in this paper needed some initial calibrations or some calibrations before running the experiment. Using a video controlled system in a loop, which can make micro-adjustments during execution, can be of great benefit in multiple ways. The presented system has the ability to re-calibrate itself during execution by recomputing the target distance in a loop as the end effector of the robotic arm gets closer to the target object. The advantage of this can be time saving and also cost saving, due to the fact that there is no need to pre-calibrate or re-calibrate the system after the robotic arm shifts from its movement path during repeated movement operations.
3.2. Experimental Results
Figure 7 shows the block diagram for the experiment of the detection of robotic arms in space. On the hardware side, there are two web cameras connected to the USB port, and the robotic arm is connected to the RS-232 port [38] of the PC. In the software part, histogram equalization is carried out to unify the image. Then, an HSV (hue, saturation, value) filter was used, the contours of the colored dots were detected (using edge detection), and finally the centers of the circles were computed, which were drawn around the colored dots detected. The colored dots are actually the markers placed at the joints of the robotic arm. The markers are made by using colored bottle caps. Mathematical calculations are made again, and circles and lines are drawn on the image to guide the calculations [38]. The colored dots detected are connected with lines and the circles are drawn around the detected colored dots. The center of the circles around the detected colored dots helps to connect the colored dots through their center. After mathematical calculations, the movement distance of each motor is converted into “robotic commands” (SCPI commands) and then sent to the robot using the RS-232 Linux driver.
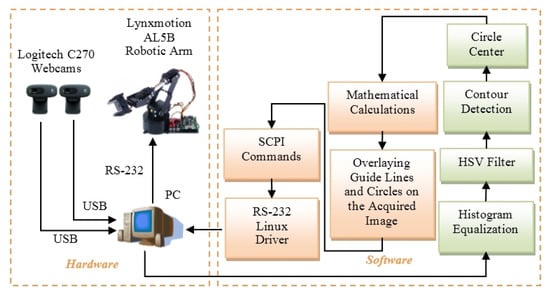
Figure 7.
Block diagram for the robotic arm controlling experiment in the 3D space made in Linux implemented in C language and OpenCV.
Figure 8 shows the block diagram for the Lynxmotion AL5B robotic arm control experiment with the ZedBoard and web cameras on the USB interface. The experiment is very similar to the one in Figure 7; the only difference is that the system is embedded because, instead of a PC, a development board [44] is used. The ZedBoard contains a Zynq-7000 SoC, which has an ARM Cortex-A9 dual-core microprocessor clocked between 866 and 1000 MHz, more than the microprocessor on the Zybo board, which has an ARM Cortex-A9 dual-core microprocessor clocked at 650 MHz. The Zynq-7000 SoC has an Artix-7 FPGA on both the ZedBoard and the Zybo boards. An Ubuntu Linux operating system was installed on the ZedBoard system. Then, the OpenCV library was installed and finally everything was coded in the C programming language [44]. The ZedBoard has some differences from the Zybo board. The ZedBoard has a USB port with a microUSB connector, and the Zybo board has a USB port with a USB type A (standard) connector. To connect a keyboard or mouse to the USB port on the ZedBoard, a male microUSB to a female USB A adapter cable is also needed. On the Zybo board, the UART serial interface and the programming interface are on the same interface, and a single microUSB connector is used. On the ZedBoard, there are separate connectors for these two interfaces. The ZedBoard has a more complex audio module than the Zybo board because the Zybo board has only three analog audio ports: line-in, microphone, and headphone. In addition to these analog audio ports, the ZedBoard has one more analog audio port: line-out. The audio system is not used in this experiment, but it is a plus that the ZedBoard has a more complex analog sound circuit. A big difference between two boards is that the video output is set in the Ubuntu Linux operating system to the ZedBoard on the VGA port and on the Zybo board to the HDMI port. The use of the VGA port can be quite noticeable in image quality since the microprocessor has not integrated a separate graphic processor. The system has not implemented a GPU, so when the analog VGA port is used, the pixels can be much more pronounced compared to the digital HDMI port. Even if there is no GPU on these systems, the marker detection method works smoothly.
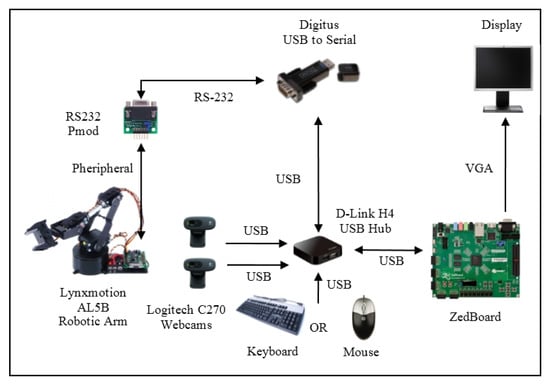
Figure 8.
Block diagram of the Lynxmotion AL5B robotic arm control experiment using the ZedBoard FPGA board.
In Figure 9, the stereo image with the auxiliary drawings applied directly to the live video feed can be seen. With their help, the amount of movement for each motor can be calculated, so that the robotic arm can reach the target position. In other words, the end effector, marked with the red bottle cap, reaches close to the green bottle cap. This first approach uses a combined algorithm using the distance calculation algorithm in the 2D space of the robotic arm and the stereo distance calculation algorithm. The distance calculation algorithm in the 2D space calculates the distance for movement in the coordinate system. The movement around point 0 (the base joint marked with the blue bottle cap) is the movement on the axis. The movement around point 1 (the elbow joint marked with the yellow bottle cap) is the movement on the axis. For the axis, two images are used (from the two cameras) and the depth distance is calculated using the stereo distance calculation algorithm. Positions are identified in the 3D space using image processing methods (color recognition (histogram equalization, HSV filter, contour detection, circle center detection) for different colored bottle caps placed on the joints of the robotic arm).

Figure 9.
The image of the guide lines and circles drawn for computing the position of the robotic arm in the 3D space using two combined algorithms: distance calculation in the 2D space and stereo distance calculation.
The noise problem of the proposed computer vision techniques would not be a problem. Actually, the system is made for robotic arms, which in the industry are screwed to the ground, so they are not moving from their position, and they are in an environment with good light because in a factory the lighting is usually good. Low light conditions can make noise in a live video feed, but this is not the case in our experiment. In addition to this, several image processing techniques such as histogram equalization or HSV filtering are used (for color recognition, to recognize the colored bottle caps placed on the joints of the robotic arm), which can correct an image with noise.
3.3. Discussion
The advantages of the presented method are that there is no need to calibrate or re-calibrate a robotic arm because the calibration is carried out during execution, with the help of the video cameras because the system is in a loop. Another advantage is that the system can be combined with other known methods, such as forward or inverse kinematics. The system can be implemented on any actual robotic arm, with current technology, due to the fact that video cameras nowadays are very popular and easy to find.
The disadvantages of the system can be that it is made up of two combined algorithms and sometimes it can be hard to implement a combined algorithm in a system.
4. Conclusions
The robotic arm position computation algorithm, using video cameras in the 3D space, was presented. The algorithm was validated using Six-Sigma (6) tools. The method of computation was implemented in software and tested on a real robotic arm.
The method and basic idea of the algorithms used were presented. Similar studies from the specialized literature were compared with the original model and the differences and advantages of the presented method were highlighted.
The formulas used in the robotic arm control programs were presented.
Several algorithms for computing distances were presented in the 2D and 3D spaces.
Since the mass of the robots used in the experimental part is not significant and the payload is reduced, an aspect corroborated by the servomotor control, the dynamics problems, was not taken into account, considering the optical self-calibration to be sufficient.
Further enhancements can be achieved by implementing the method on other platforms, such as FPGA boards with the Zynq-7000 SoC, like the Zybo. The system can also be implemented on a Raspberry Pi. The method can be ported to other programming languages, such as Python or Java, with the actual system being implemented in the C programming language. The best enhancement could be porting the system to another robot, such as the SCORBOT-ER III robotic arm.
Author Contributions
Conceptualization, R.S. and R.-S.R.; methodology, R.S. and R.-S.R.; software, R.S.; validation, R.S.; formal analysis, R.S. and R.-S.R.; investigation, R.S. and R.-S.R.; resources, R.S.; data curation, R.S.; writing—original draft preparation, R.S.; writing—review and editing, R.S.; visualization, R.S.; supervision, R.S.; project administration, R.S.; funding acquisition, R.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Academy of Romanian Scientists, Splaiul Independentei 54, 050044 Bucharest, Romania. This research was also funded by Politehnica University Timisoara and the Applied Electronics Department.
Data Availability Statement
All the images are available on request from the corresponding author.
Acknowledgments
The authors would like to thank the Academy of Romanian Scientists, Splaiul Independentei 54, 050044 Bucharest, Romania for the given support. The authors would also like to thank Politehnica University Timisoara and the Applied Electronics Department for the given support.
Conflicts of Interest
The authors declare no conflict of interest.
Notations
The following symbols and abbreviations are used in this manuscript:
| 2D | 2 Dimensions |
| 3D | 3 Dimensions |
| DoF | Degrees of Freedom |
| difference between robotic values (pulse widths) of the motors of the robotic arm | |
| difference between vectors | |
| vectors | |
| length of the Euclidean norm vector | |
| orthogonal vectors | |
| slopes of the two tangents to the circles | |
| right and left points of the offset | |
| pi = 3.14 | |
| inch | |
| Pixels Per Inch | |
| right, left | |
| coordinates | |
| d | distance |
| f | focal distance |
| angle | |
| coordinates in space | |
| vectors of the coordinates in space | |
| unit vectors | |
| vectors | |
| scalars | |
| vectors | |
| USB | Universal Serial Bus |
| RS-232 | Recommended Standard 232 (serial communication) |
| PC | Personal Computer |
| HSV | Hue, Saturation, Value |
| SCPI | Standard Commands for Programmable Instruments |
| ARM | Advanced RISC (Reduced Instruction Set Computer) Machine |
| SoC | System-on-a-Chip |
| FPGA | Field Programmable Gate Array |
| OpenCV | Open Computer Vision |
| UART | Universal Asynchronous Receiver-Transmitter (serial communication) |
| VGA | Video Graphics Array |
| HDMI | High-Definition Multimedia Interface |
| GPU | Graphics Processing Unit |
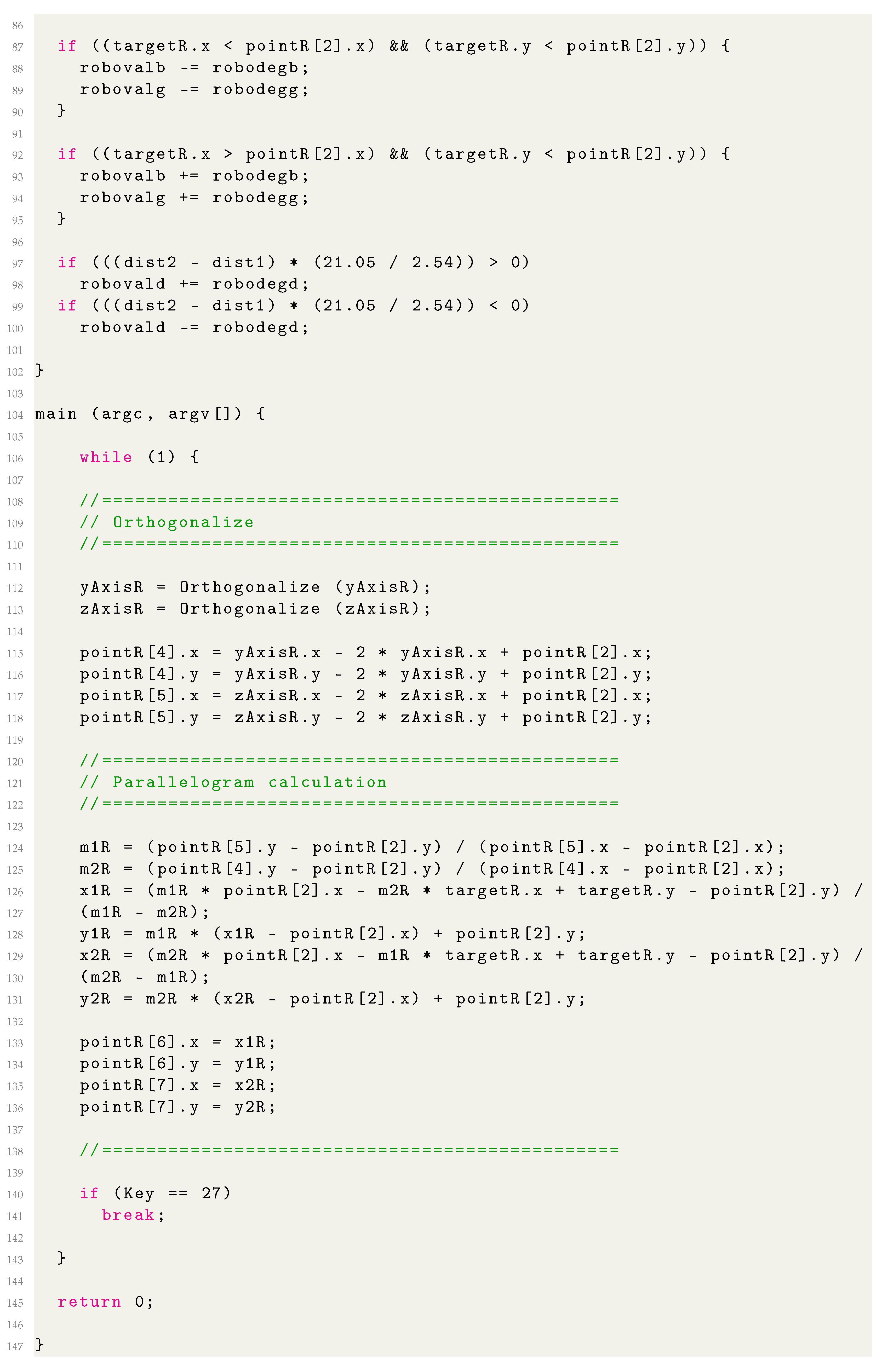
Appendix A
A pseudo code containing the computation method of the guidelines for calculating distances in the 3D space is listed below.

References
- Lippiello, V.; Ruggiero, F.; Siciliano, B.; Villani, L. Visual Grasp Planning for Unknown Objects Using a Multifingered Robotic Hand. IEEE/ASME Trans. Mechatron. 2013, 18, 1050–1059. [Google Scholar] [CrossRef]
- Kazemi, M.; Gupta, K.K.; Mehrandezh, M. Randomized Kinodynamic Planning for Robust Visual Servoing. IEEE Trans. Robot. 2013, 29, 1197–1211. [Google Scholar] [CrossRef]
- Fomena, R.T.; Tahri, O.; Chaumette, F. Distance-Based and Orientation-Based Visual Servoing from Three Points. IEEE Trans. Robot. 2011, 27, 256–267. [Google Scholar] [CrossRef]
- Heuring, J.J.; Murray, D.W. Modeling and copying human head movements. IEEE Trans. Robot. Autom. 1999, 15, 1095–1108. [Google Scholar] [CrossRef]
- Chaumette, F.; Hutchinson, S. Visual servo control. II. Advanced approaches [Tutorial]. IEEE Robot. Autom. Mag. 2007, 14, 109–118. [Google Scholar] [CrossRef]
- Naceri, A.; Schumacher, T.; Li, Q.; Calinon, S.; Ritter, H. Learning Optimal Impedance Control during Complex 3D Arm Movements. IEEE Robot. Autom. Lett. 2021, 6, 1248–1255. [Google Scholar] [CrossRef]
- Li, S.; Zhang, Y.; Jin, L. Kinematic Control of Redundant Manipulators Using Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 2243–2254. [Google Scholar] [CrossRef]
- Jiang, Y.; Wang, Y.; Miao, Z.; Na, J.; Zhao, Z.; Yang, C. Composite-Learning-Based Adaptive Neural Control for Dual-Arm Robots With Relative Motion. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 1010–1021. [Google Scholar] [CrossRef]
- Vazquez, L.A.; Jurado, F.; Castaneda, C.E.; Santibanez, V. Real-Time Decentralized Neural Control via Backstepping for a Robotic Arm Powered by Industrial Servomotors. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 419–426. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, C.; Zhang, Y.; Chen, C.L.P. Adaptive Neural Control for Dual-Arm Coordination of Humanoid Robot With Unknown Nonlinearities in Output Mechanism. IEEE Trans. Cybern. 2015, 45, 507–518. [Google Scholar]
- Cheng, B.; Wu, W.; Tao, D.; Mei, S.; Mao, T.; Cheng, J. Random Cropping Ensemble Neural Network for Image Classification in a Robotic Arm Grasping System. IEEE Trans. Instrum. Meas. 2020, 69, 6795–6806. [Google Scholar] [CrossRef]
- Freire, E.O.; Rossomando, F.G.; Soria, C.M. Self-tuning of a Neuro-Adaptive PID Controller for a SCARA Robot Based on Neural Network. IEEE Lat. Am. Trans. 2018, 16, 1364–1374. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, S.; Li, S.; Zhang, Z. Adaptive Projection Neural Network for Kinematic Control of Redundant Manipulators with Unknown Physical Parameters. IEEE Trans. Ind. Electron. 2018, 65, 4909–4920. [Google Scholar] [CrossRef]
- Hu, Z.; Han, T.; Sun, P.; Pan, J.; Manocha, D. 3D Deformable Object Manipulation Using Deep Neural Networks. IEEE Robot. Autom. Lett. 2019, 4, 4255–4261. [Google Scholar] [CrossRef]
- Huang, X.; Wu, W.; Qiao, H.; Ji, Y. 3D Brain-Inspired Motion Learning in Recurrent Neural Network with Emotion Modulation. IEEE Trans. Cogn. Dev. Syst. 2018, 10, 1153–1164. [Google Scholar] [CrossRef]
- Yang, Y.; Ni, Z.; Gao, M.; Zhang, J.; Tao, D. Collaborative Pushing and Grasping of Tightly Stacked Objects via Deep Reinforcement Learning. IEEE/CAA J. Autom. Sin. 2022, 9, 135–145. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, K.; Lin, J.; Louie, W.-Y.G.; Huang, H. Sim2real Learning of Obstacle Avoidance for Robotic Manipulators in Uncertain Environments. IEEE Robot. Autom. Lett. 2022, 7, 65–72. [Google Scholar] [CrossRef]
- Hsieh, Y.-Z.; Lin, S.-S. Robotic Arm Assistance System Based on Simple Stereo Matching and Q-Learning Optimization. IEEE Sens. J. 2020, 20, 10945–10954. [Google Scholar] [CrossRef]
- James, S.; Davison, A.J. Q-Attention: Enabling Efficient Learning for Vision-Based Robotic Manipulation. IEEE Robot. Autom. Lett. 2022, 7, 1612–1619. [Google Scholar] [CrossRef]
- Yang, D.; Liu, H.A. EMG-Based Deep Learning Approach for Multi-DOF Wrist Movement Decoding. IEEE Trans. Ind. Electron. 2022, 69, 7099–7108. [Google Scholar] [CrossRef]
- Seelinger, M.; Gonzalez-Galvan, E.; Robinson, M.; Skaar, S. Towards a robotic plasma spraying operation using vision. IEEE Robot. Autom. Mag. 1998, 5, 33–38. [Google Scholar] [CrossRef]
- Kelly, R.; Carelli, R.; Nasisi, O.; Kuchen, B.; Reyes, F. Stable visual servoing of camera-in-hand robotic systems. IEEE/ASME Trans. Mechatron. 2000, 5, 39–48. [Google Scholar] [CrossRef]
- Behera, L.; Kirubanandan, N. A hybrid neural control scheme for visual-motor coordination. IEEE Control Syst. 1999, 19, 34–41. [Google Scholar]
- Park, I.-W.; Lee, B.-J.; Cho, S.-H.; Hong, Y.-D.; Kim, J.-H. Laser-Based Kinematic Calibration of Robot Manipulator Using Differential Kinematics. IEEE/ASME Trans. Mechatron. 2012, 17, 1059–1067. [Google Scholar] [CrossRef]
- Li, Z.; Li, S.; Luo, X. Using Quadratic Interpolated Beetle Antennae Search to Enhance Robot Arm Calibration Accuracy. IEEE Robot. Autom. Lett. 2022, 7, 107202–107213. [Google Scholar] [CrossRef]
- Tan, N.; Yu, P.; Zhong, Z.; Ni, F. A New Noise-Tolerant Dual-Neural-Network Scheme for Robust Kinematic Control of Robotic Arms with Unknown Models. IEEE/CAA J. Autom. Sin. 2022, 9, 1778–1791. [Google Scholar] [CrossRef]
- Costanzo, M.; De Maria, G.; Natale, C. Tactile Feedback Enabling In-Hand Pivoting and Internal Force Control for Dual-Arm Cooperative Object Carrying. IEEE Robot. Autom. Lett. 2022, 7, 11466–11473. [Google Scholar] [CrossRef]
- AlBeladi, A.; Ripperger, E.; Hutchinson, S.; Krishnan, G. Hybrid Eye-in-Hand/Eye-to-Hand Image Based Visual Servoing for Soft Continuum Arms. IEEE Robot. Autom. Lett. 2022, 7, 11298–11305. [Google Scholar] [CrossRef]
- Ruan, Q.; Yang, F.; Yue, H.; Li, Q.; Xu, J.; Liu, R. An Accurate Position Acquisition Method of a Hyper-Redundant Arm with Load. IEEE Sens. J. 2022, 22, 8986–8995. [Google Scholar] [CrossRef]
- Rakshit, A.; Konar, A.; Nagar, A.K. A hybrid brain-computer interface for closed-loop position control of a robot arm. IEEE/CAA J. Autom. Sin. 2020, 7, 1344–1360. [Google Scholar] [CrossRef]
- Li, F.; Jiang, Y.; Li, T. A Laser-Guided Solution to Manipulate Mobile Robot Arm Terminals within a Large Workspace. IEEE/ASME Trans. Mechatron. 2021, 26, 2676–2687. [Google Scholar] [CrossRef]
- Tang, Z.; Wang, P.; Xin, W.; Laschi, C. Learning-Based Approach for a Soft Assistive Robotic Arm to Achieve Simultaneous Position and Force Control. IEEE Robot. Autom. Lett. 2022, 7, 8315–8322. [Google Scholar] [CrossRef]
- Min, J.-K.; Kim, D.-W.; Song, J.-B. A Wall-Mounted Robot Arm Equipped with a 4-DOF Yaw-Pitch-Yaw-Pitch Counterbalance Mechanism. IEEE Robot. Autom. Lett. 2020, 5, 3768–3774. [Google Scholar] [CrossRef]
- Lu, W.; Tang, B.; Wu, Y.; Lu, K.; Wang, D.; Wang, X. A New Position Detection and Status Monitoring System for Joint of SCARA. IEEE/ASME Trans. Mechatron. 2021, 26, 1613–1623. [Google Scholar] [CrossRef]
- Khaled, T.A.; Akhrif, O.; Bonev, I.A. Dynamic Path Correction of an Industrial Robot Using a Distance Sensor and an ADRC Controller. IEEE/ASME Trans. Mechatron. 2021, 26, 1646–1656. [Google Scholar] [CrossRef]
- Kamtikar, S.; Marri, S.; Walt, B.; Uppalapati, N.K.; Krishnan, G.; Chowdhary, G. Visual Servoing for Pose Control of Soft Continuum Arm in a Structured Environment. IEEE Robot. Autom. Lett. 2022, 7, 5504–5511. [Google Scholar] [CrossRef]
- Liu, X.; Madhusudanan, H.; Chen, W.; Li, D.; Ge, J.; Ru, C.; Sun, Y. Fast Eye-in-Hand 3D Scanner-Robot Calibration for Low Stitching Errors. IEEE Trans. Ind. Electron. 2021, 68, 8422–8432. [Google Scholar] [CrossRef]
- Szabo, R.; Gontean, A. Controlling a Robotic Arm in the 3D Space with Stereo Vision. In Proceedings of the 21st Telecommunications Forum (TELFOR), Belgrade, Serbia, 26 November 2013; pp. 916–919. [Google Scholar]
- Santoni, F.; De Angelis, A.; Skog, I.; Moschitta, A.; Carbone, P. Calibration and Characterization of a Magnetic Positioning System Using a Robotic Arm. IEEE Trans. Instrum. Meas. 2019, 68, 1494–1502. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, W.; Cai, Y.; Li, J.; Zeng, Y.; Chen, L.; Yuan, F.; Ji, Z.; Wang, Y.; Wyrwa, J. A Novel Single-Arm Stapling Robot for Oral and Maxillofacial Surgery—Design and Verification. IEEE Robot. Autom. Lett. 2022, 7, 1348–1355. [Google Scholar] [CrossRef]
- Ozguner, O.; Shkurti, T.; Huang, S.; Hao, R.; Jackson, R.C.; Newman, W.S.; Cavusoglu, M. Cenk Camera-Robot Calibration for the Da Vinci Robotic Surgery System. IEEE Trans. Autom. Sci. Eng. 2020, 17, 2154–2161. [Google Scholar] [CrossRef]
- Pan, Y.; Wang, H.; Li, X.; Yu, H. Adaptive Command-Filtered Backstepping Control of Robot Arms with Compliant Actuators. IEEE Trans. Control Syst. Technol. 2018, 26, 1149–1156. [Google Scholar] [CrossRef]
- PPI Computation. Available online: https://www.sven.de/dpi (accessed on 15 September 2022).
- Szabo, R.; Gontean, A. Lynxmotion AL5 Type Robotic Arm Control with Color Detection on FPGA Running Linux OS. In Proceedings of the 24th Telecommunications Forum (TELFOR), Belgrade, Serbia, 22–23 November 2016; pp. 818–821. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).