1. Introduction
Due to current advanced hardware and software technologies, data acquisition, storage, computing, and communication allow for the processing of increased amounts of data online. In this way, a new method referred to as data-driven control (DDC) has been developed, by which the controllers are directly designed using input–output data collected from the control system without process modeling. Through the development of information technology, the industrial processes have become more complex, making their modeling difficult. An alternative to the model-based control method is DDC, which has rapidly developed in recent decades. Overviews on the model-based control and data-driven control techniques are presented in [
1,
2], while the DDC theory is covered in books such as [
3,
4,
5]. At the same time, the data-driven tuning techniques were developed to optimize the controller parameters, distinguishing two classes based on the controller structure. The first class is intended for controllers with a fixed structure. Among these, the iterative feedback tuning (IFT) algorithm [
6] iteratively optimizes the controller parameters by estimating the gradient of a cost function in relation to the input and output signals; the virtual reference feedback tuning (VRFT) method [
7] is a direct data-driven method to optimize the controller parameters, which does not require iterations. The second class includes tuning methods that do not require knowledge of the regulator structure, such as iterative learning control [
8] or model-free adaptive control [
4].
One DDC method is the model-free control (MFC) algorithm, which was developed by Fliess and Join [
9] and has been successfully applied in many fields. It is based on the use of the ultralocal model, which is valid for a short time interval and is on the embedded of a PID controller in the control law, which is called an intelligent PID (iPID). The tuning parameters of the iPID controller are the usual tuning gains of the PID controller, to which the non-physical constant parameter α from the ultralocal model is added. Considering the ultralocal model and closing the tuning loop with the iPID controller, a description of the control system is obtained through a linear differential equation of the control error, which only depends on the tuning gains of the PID, if a good estimate of the term including the unknown parts of the ultralocal model is available [
8]. Hence, the conclusion from [
8] is made, where tuning the iPID controller is easy to perform by enforcing the condition that the differential equation must have stable roots, thus canceling the steady-state error. Furthermore, in accordance with a condition from [
9,
10], the user will choose the parameter α. Although it seems easy to tune an iPID controller, the use of only the linear differential equation does not directly lead to achieving the tuning gains.
For tuning the iPID controllers, several methods have been reported in the literature. Starting from the tuning proposed in [
8] based on the cancellation of the control error in the steady-state, in [
11,
12], domains were determined in the tuning gains space, for which the stability of the roots of the error differential equation is ensured, thus obtaining a zero steady-state error. The VRFT one-shot data-driven tuning algorithm can be used to tune the iPID controllers. Thus, in [
13], the method is shown regarding how the VRFT algorithm can be used to tune the iP, iPI, and iPID model-free controllers, where the three tuned controllers are validated on modular servo system laboratory equipment. Another hybrid method is generated by mixing the model-free control with the sliding mode control (SMC) [
14], resulting in a simple design method that ensures the stability of the tracking error dynamics specific to MFC. If the MFC in [
14] is of the iPI type, the method in [
15] presents the MFC-SMC with an iPD controller intended for the attitude and position control of a quadrotor.
The design methods above lead to the acquisition of the tuning gains of the iPID controllers without the possibility of finding a suitable value for
, which remains a constant design parameter to be chosen by the user according to [
9,
10]. However, other methods have been proposed to determine the parameter, such as in [
16], where
is found using an algorithm based on the ultralocal model. Another approach considers
as a time-varying parameter for which the values are instantly estimated [
17,
18].
The data-driven IFT method for tuning controllers with a fixed structure is a gradient descent-based iterative algorithm presented in [
6], are both theoretical aspects and applications regarding the tuning of controllers for mechanical and chemical systems. The tuning objective is to obtain the step response of the closed-loop system with a minimal settling time and small overshoot. The advantages of applying the IFT method for tuning PID controllers in relation to the classic methods are presented in [
19]. To ensure the con-vergence for the initial parameters of the controller, [
20] presents a solution based on a domain of attraction (DoA) approach. With respect to the regulatory control system, several solutions have proposed the use of the IFT algorithm. By using a special experiment, the authors of [
21] describe the gradient estimate method based on a spectral analysis; in [
22], the authors suggest the correlation-based IFT algorithm to reduce the influence of noise from the collected data. Solutions that do not require a special experiment to estimate the gradient related to the feedforward controller have also been proposed, such as those presented in [
23,
24]. A constrained IFT method was introduced in [
25] for the robust cascade path-tracking control of a networked robot. For a model-free adaptive iterative learning controller, the IFT algorithm was used in [
26] for controller parameters tuning. A first attempt of using the IFT algorithm for tuning a model-free iP controller intended for the speed control of an engine was presented in [
27].
This paper proposes a new method for tuning the model-free iPID controllers based on the IFT data-driven algorithm. Being a data-driven approach, a process model is not required to tune the controller parameters; it only requires the sets of input–output data collected from the control system. Because the IFT algorithm is a method for tuning the parameters of a controller with a fixed structure, this study first determined a structure for the iPID controller using the connections between the iPID and PID discrete-time controllers. Only the first and second order derivatives related to the ultralocal model, which is the basis of the model-free control concept, were considered. Using the derivative approximation method based on the backward difference, the fixed structures of the iPID controllers were obtained, which were described by discrete transfer functions that were parameterized with a parameter vector. Based on these discrete transfer functions, behaviors that assimilated to those of conventional PID controllers were found, which allowed for the selection of intelligent controllers with behaviors like the PID ones and the removal of those with unusual behaviors in the control engineering process. Knowing the fixed structures of the iPID controllers, the IFT data-driven algorithm was applied, and the optimal tuning parameters of the controllers were obtained. The proposed tuning method based on IFT data-driven algorithms has the advantage of generating iPID tuning parameters related to the PID control law, but also the parameter , which was usually chosen by the user. The new iPID controller tuning method based on the IFT algorithm is illustrated by real-time experiments that are aimed to validate the tuned controllers. The experiments were conducted with Quanser AERO 2 laboratory equipment in the one degree of freedom (1-DOF) configuration, with two DC motors for driving the propellers, for which the pitch angle was controlled.
This laboratory equipment, due to offering a wide range of system structures obtained through half-quad (pitch-locked, yaw-free), 1-DOF (yaw-locked, pitch-free), or 2-DOF con-figurations [
28], was often used for testing and validating new control methods. For all configurations, the control with PID regulators is presented in [
28]. New control algorithms for the 2-DOF configuration can also be found in the literature, such as adaptive neural control [
29], approximation-based quantized state feedback tracking [
30], observer-based sliding mode control [
31], fuzzy neural networks [
32], or adaptive attitude control with input and output quantization [
33].
This paper proposes the following new contributions with respect to the state-of-the-art:
- (i)
A new method of tuning model-free iPID controllers based on the IFT algorithm;
- (ii)
The calculation of both the tuning gains of the iPID controller and the parameter ;
- (iii)
The determination of a fixed structure for iPID controllers based on the connections between the iPID and PID discrete-time controllers to make it possible to apply the IFT tuning algorithm;
- (iv)
An analysis of the connections between the iPID and PID controllers; model-free control laws that correspond to some variants of the classical PID were determined, and those which are uncommon in the control engineering process were eliminated;
- (v)
The tuning of the iPID controllers using the IFT algorithm was tested and validated experimentally on Quanser AERO 2 laboratory equipment.
The paper is organized as follows.
Section 2 discusses the connections between the iPID and PID controllers, and based on them, the fixed structure of the iPID controller is presented.
Section 3 first briefly introduces the IFT approach and then describes how to tune the iPID controller using the IFT algorithm. The experimental validation of the tuned iPID controllers is shown in
Section 4, and
Section 5 concludes the paper.
2. iPID Fixed Structure Based on Connections between the iPID and PID Discrete-Time Controllers
The IFT technique is a model-free technique used to iteratively optimize the parameters of a fixed-order controller using data coming from the closed-loop system operation. Applying the IFT technique for tuning an iPID controller first requires the determination of a fixed structure for this type of controller, which is parametrized by a vector . For this reason, the discrete form of the iPID controllers has been related to the classical PID, which has a fixed structure.
The MFC method is designed around the concept of the ultralocal model [
9], which is obtained from signals of the system and is available for a very short time frame. The equation that describes the ultralocal model, with notations from the operational calculus, is:
where
is the output signal of the system,
is the control signal,
is a parameter chosen by the practitioner, and
is a function which contains all of the unmodelled components of the ultralocal model. The derivative order
of
is usually chosen as 1 or 2 [
9]. The control law iPID is defined as:
where
is the reference signal,
is the control error, and
,
, and
are the tuning gains of a classical PID controller.
The discrete-time ultralocal model is obtained using the backward difference approximation, as suggested in [
34], by replacing
with
, where
is the sampling period, resulting in:
Using Equation (3), the estimation of the unmodelled components of the ultralocal model is defined as:
In the following, the estimation error between the actual and its estimation is considered negligible.
Applying the backward difference approximation to Equation (2) and using the estimation from Equation (4), the discrete-time iPID control law is obtained:
From Equation (5), the discrete-time classical PID control law is easily deduced:
Next, the connections between the discrete-time iPID and PID controllers will be investigated, considering the two recommended values for the derivative order .
First, for
, from Equation (5) after a simple calculation, the following form of the iPID
1 regulator results:
which highlights a classical PI-I
2 type controller. The subscript of iPID
1 indicates the derivative order
.
Using Equation (7), the following equations are obtained for the intelligent controllers iP
1, iPI
1, and iPD
1, by setting the appropriate tuning parameters. Thus, for
, the iP
1 control law is found:
which corresponds to a classical PI controller. If only
, the result is the iPI
1 control law:
which has the form of a PI-I
2 controller, as in the case of the iPID
1 controller, but with different tuning parameters. Setting
, the iPD
1 control law is obtained:
which is a classical PI controller, as in the case of the iP
1 controller, but with different tuning parameters. When analyzing the comparisons between the iPID
1 and classical PID controllers for
, it is discovered that the intelligent controllers behave like PI or PI-I
2. For the iP
1 and iPD
1 controllers that behave like PI, by applying the Z transform to Equations (8) and (10), the discrete transfer function results:
whose tuning parameters grouped in the vector
are determined according to the type of the intelligent controller, as follows:
Applying the Z transform to Equations (7) and (9), the discrete transfer function of the iPI
1 and iPID
1 controllers that behave like PI-I
2 is obtained:
with the following tuning parameters grouped in the vector
:
In conclusion, for , the intelligent controllers iP1 and iPD1 behave as a PI controller, having a fixed structure given by the discrete transfer function from Equation (11), parametrized by a vector ; the intelligent controllers iPI1 and iPID1 behave like a PI-I2 controller with a fixed-order structure, given by the discrete transfer function from the Equation (14), parametrized by a vector .
For
, using Equation (5), the iPID
2 control law is obtained:
which highlights a classical PID-I
2 controller. The subscript of iPID
2 indicates the derivative order
.
Similar to the case of
, by setting the tuning parameters in Equation (17), the control laws iP
2, iPI
2, and iPD
2 for
are obtained. Therefore, for
, the iP
2 control law is achieved:
with a classical ID controller behavior, which is uncommon in the control engineering. Considering only
, the control law iPI
2 is obtained:
which is equivalent to a classical ID-I
2 controller, also unused in the control engineering. Setting
, the iPD
2 control law results in:
having a classical PID behavior.
Considering only the iPD
2 and iPID
2 controllers and applying the Z transform to Equations (17) and (20), which are related to the two controllers, the iPD
2 discrete transfer function is obtained:
and, respectively, for iPID
2:
The parameter vectors for the two controllers and the expressions of the tuning parameters are:
Analyzing for the case of in the comparisons between the iPID2 and the classic PID controllers, it turned out that the iP2 and iPI2 controllers behave similarly to equivalent classical controllers, which is unusual in the control engineering. The iPD2 and iPID2 controllers, PID and PID-I2 type behaviors, and fixed structures expressed by the transfer functions from Equations (21) and (22) were found, which were parameterized by the vectors given by Equations (23) and (24).
The connections analyzed between the iPID and PID showed that both for and for , the intelligent controllers have either an integrator or an integrator supplemented by a double integrator. It also resulted that a derivative behavior of the iPID controllers was only obtained for .
The parameters vector will be determined using the model-free IFT approach. Because the tuning parameters , , , and are obtained based on the vector, only the iP1 and iPI1 controllers were chosen for ; this is because from Equations (12) and (15), unique solutions for the tuning gains and are obtained. At the same time, for the case of , the neglected controllers iPD1 and iPID1 have the same type of behavior as the iP1 and iPI1 controllers; however, from Equations (13) and (16), unique solutions for the tuning parameters and are not obtained.
In the following, we will consider for the controllers iP1 and iPI1, having the fixed structure described by the transfer functions and , given by Equations (11) and (14); we will also consider for the controllers iPD2 and iPID2 with the fixed structure described by the transfer functions and , provided by Equations (21) and (22).
4. Case Studies—Real-Time Control of Pitch Angle for Aero 2 Laboratory Equipment
To test and validate the iPID controllers tuning using the IFT algorithm, we considered a real-time application for controlling the pitch angle for the dual-motor aerospace system Aero 2, provided by Quanser. The system has two rotors that can be used for various aerospace applications, with the possibility to control the pitch and yaw angles as suggested in [
28,
29,
30,
31,
32,
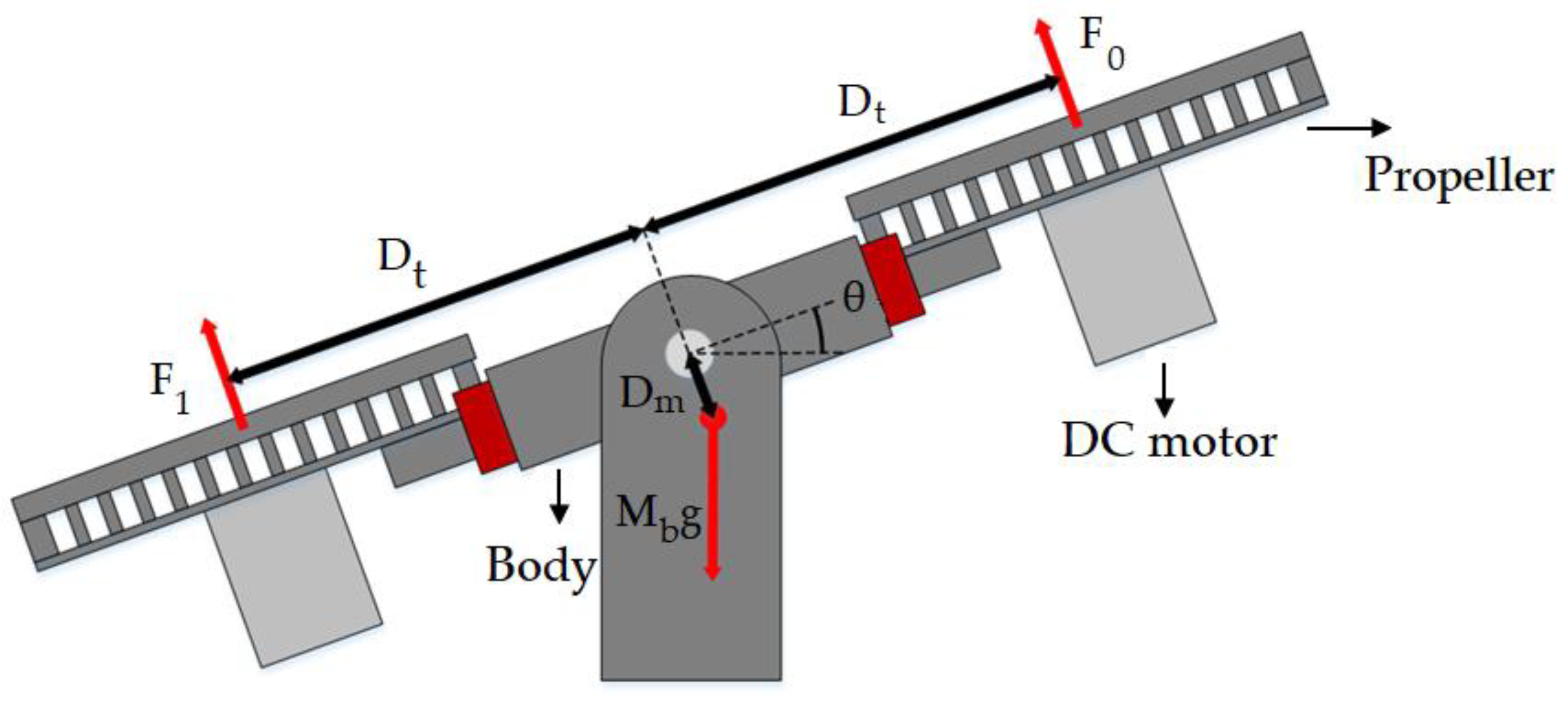
33]. To control the pitch angle, the 1-DOF configuration was chosen for the Aero 2 platform, which locks the yaw and has the pitch as free. This configuration, represented in
Figure 1, was used for real-time experiments, having both propellers horizontal and ensuring a variation of the pitch angle of 90° degrees, 45° degrees for each side.
Single-ended optical shaft encoders were used to measure the pitch of the Aero body and the angular speed of the DC motors [
28]. The pitch encoder is 2880 counts per revolution in quadrature mode, and the angular speed encoder is a counter that returns the number of the encoder counts every second.
The scheme of the 1-DOF Aero 2 plant for the pitch angle control is shown in
Figure 2, where
is the aero body mass,
is the thrust displacement,
is the center of mass displacement, and
is the pitch angle to the equilibrium position;
and
are the thrust forces generated by propellers that are driven by two DC motors, and
g is the gravitational acceleration. To introduce nonlinearities, an asymmetry was created by using a single propeller operating in both positive and negative thrust and by shifting the center of mass towards thruster 1.
Each propeller was driven by a DC motor, its supply voltage being considered the input variable, and the output variable is the pitch angle . The plant model was obtained based on the DC motor and propeller models.
The DC motor dynamics are described by [
28]:
where
is the motor current,
and
are the resistance and inductances of the rotor,
is the back electromotive force (emf),
is the rotor inertia,
is the motor angular speed,
is the motor torque,
is the drag torque and
and
are the motor back EMF and torque constant. Neglecting the rotor inductance, an assumption valid for low-power motors, the following model of the DC motor results from Equation (44):
The dynamic behavior of the propeller system can be modeled by taking into account [
28] and [
29,
31]:
where
is the moment of inertia related to the pitch motion,
is the viscous damping coefficient,
is the stiffness,
is the force thrust gain relative to the rotor speed,
is the distance from the pivot point to the center of the rotor, and
is the torque acting on the pitch axis, created by the thrust force
.
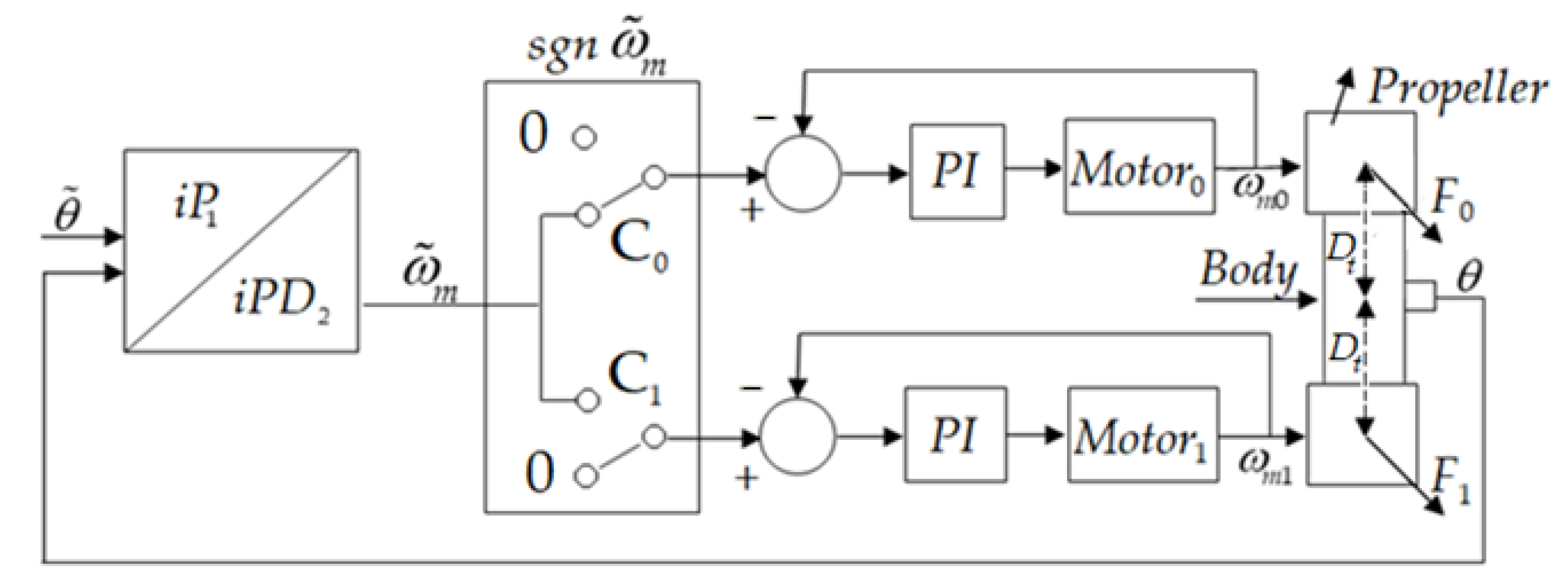
Considering the models of the two components of the plant, a cascade control structure was chosen, with a faster inner loop for controlling the motor angular speed
and an outer loop for controlling the pitch angle
. In this way, the disturbance introduced by the drag torque
will be rejected. The cascade control structure is a special one, whose scheme is represented in
Figure 3.
The
and
switches, which depend on the sign of the angular velocity reference
, have been introduced to activate a single motor. Thus, for
, the related internal propeller loop that generates the thrust force
will come into operation, and for
, it will be the propeller that generates the thrust force
. The presence of the two switches, through which a single inner loop is activated depending on the sign of
, introduces a nonlinearity in the control system. Another nonlinearity from Equation (46) is created by the asymmetric placement of the center of gravity, as seen in
Figure 2.
For each inner loop, a PI controller described by [
28]:
was designed, starting from the simplified model (45) of the DC motor and considering the overshoot
and peak time
as desired performances, as in [
28]. Applying the Laplace transform to the DC motor model (45), a first-order transfer function is obtained with gain
and time constant
. Using the plant transfer function, in [
28], the following tuning parameters of the PI controller were obtained based on a pole placement method:
where the damping ratio
and natural frequency
are calculated based on the desired performances. Employing the DC motor parameters and the desired performances from [
28], the following tuning parameters of the inner loop PI controller were obtained:
.
For the outer loop, two model-free controllers were tested to validate the proposed design method based on the data-driven IFT algorithm. The first one tested was an iP
1 controller with a PI-type behavior, as shown in
Section 2, which ensures a zero steady-state error; the second one was an iPD
2 with a PID-type behavior, for which the influence of the derivative component was analyzed. The structures of the two model-free controllers are depicted in
Figure 4.
In the model-free controller structure, the Discrete Derivative block DD computes the discrete-time derivative using the backward difference approximation; the block implements the discrete transfer function of the P or PD controller, resulting in the iP1 or iPD2 controllers. The sample time for both controllers was considered due to the small value of the time constants of the inner loop.
The outer loop plant is formed by the closed-loop transfer function of the inner loop, to which the propeller model from Equation (46) is added. Although the closed-loop model of the inner loop is known by designing with the pole placement method, the propeller model is considered as totally unknown. The design of the model-free controller was conducted only based on the data collected from the control system without using any outer loop plant model.
The Aero 2 system from Quanser was connected with a PC, where the control scheme from
Figure 2 was implemented using MATLAB/Simulink 2021b software tools.
For tuning the two model-free controllers, the IFT algorithm from
Section 3 was used, which is based on two closed-loop experiments and the collection of input and output data related to the real-time experiments. The proposed aero pitch controller tuning methodology is the following:
In the first step of the IFT algorithm, the tuning parameters of the two controllers that lead to a stable response must be found. These parameters were determined as in [
11] and [
12] based on the characteristic polynomial of the error, for which it was required that the roots be stable, thus cancelling the error in the steady-state. For iP
1, it follows from [
11] that the roots of the characteristic polynomial of the error are stable if
. Applying the Jury test, the domain in the plane of gains parameters, where the roots of the characteristic polynomial are stable, was obtained in [
12] for the iPD
2 controller, defined by:
For the two model-free controllers, the initial tuning parameters were chosen using values from the stability domains of the roots. With the tuning parameters thus determined, an experiment is carried out, and if undesirable performances are obtained, proceed to Step 2 of the IFT algorithm.
- 2.
At each iteration , two experiments of length are performed:
- (a)
The reference is applied to the pitch control system, and the input/output signals are collected ;
- (b)
The reference is applied to the control system, and the input/output signals are collected .
- 3.
Based on the data collected in the special experiment (b), the estimates of the gradients for and and the estimates of the gradient of the cost function and for the matrix , described by (37), are computed.
- 4.
Using the estimates from Step 3, the new vector of parameters
is calculated; based on the vector, the tuning parameters are determined using
Table 1.
- 5.
With the tuning parameters determined in Step 4, the performances of the pitch control system are tested in a real-time experiment.
- 6.
If the performances obtained with the tuning parameters from Step 5 are not satisfactory, restart the tuning procedure by repeating Step 2–5 until the desired performances are reached.
The penalty factor
from Equation (26) and the step size
from Equation (29) were determined through a trial-and-error procedure, while the matrix
was considered the identity matrix
, one of possibilities mentioned by [
6] and [
36]. To test the performances of the control system for each iteration
of the tuning procedure, the ITAE (integral time-weighted absolute error) criterion defined by:
was used, where
is the discrete-time expressed in seconds. This criterion is helpful because the objective is to have a smooth response without oscillations around the reference value.
4.1. Control of Pitch Angle with iP1 Controller
Based on the stability condition of the roots of the characteristic polynomial, the iP
1-0 controller with the tuning parameters from
Table 2 were chosen for the initial step. Using step size
, penalty factor
, and matrix
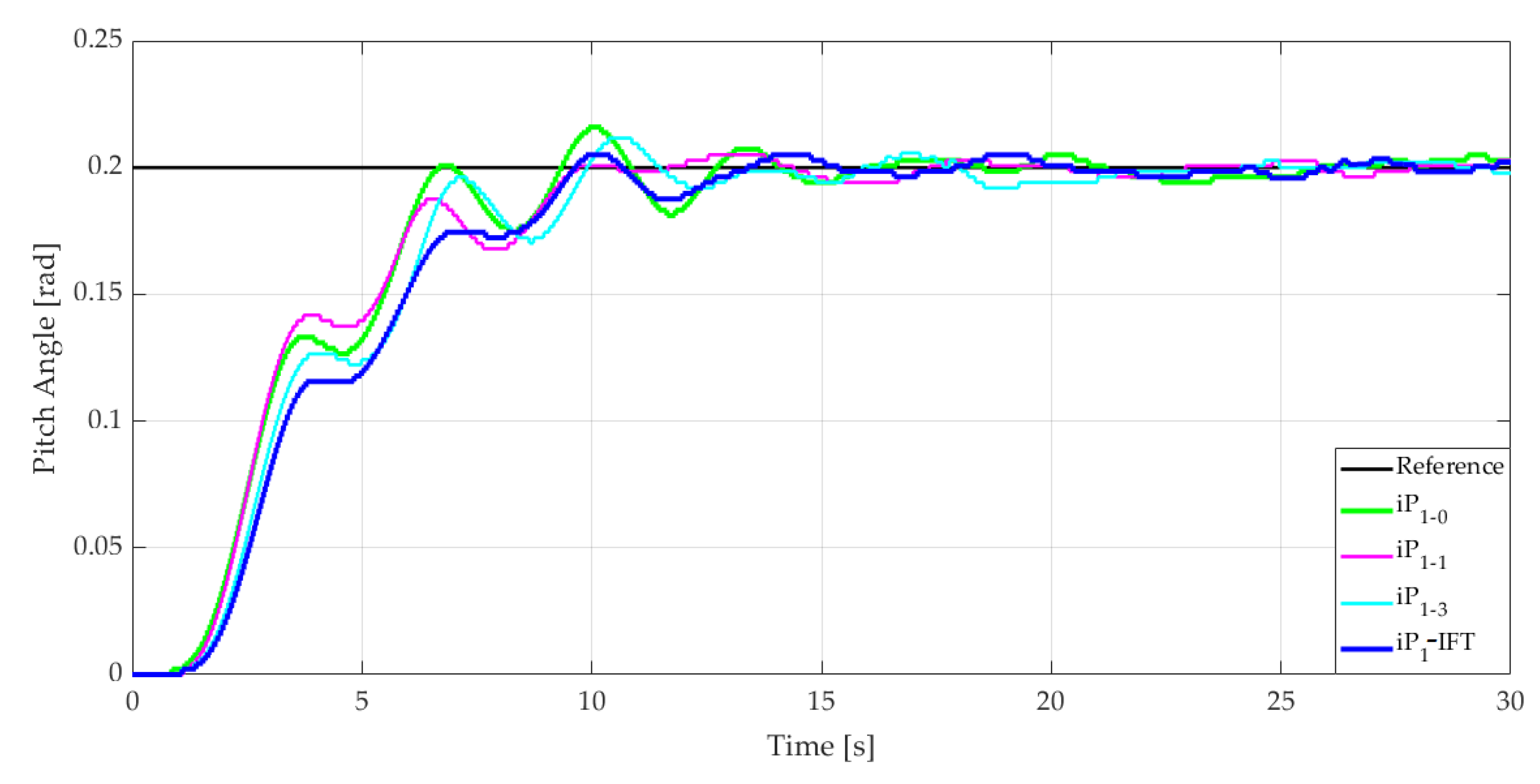
, four iterations of the IFT algorithm have been created, resulting in the controllers iP
1-1,2,3 and finally the fourth controller, iP
1-IFT. The stopping point was determined based on the optimum performance criterion defined by Equation (50). The responses of the iP
1 controllers are shown in
Figure 4, where the unsatisfactory performances of the iP
1-0 controller are visible. The IFT tuning procedure was applied in order to improve the performances. The initial response of the control system and other several intermediate responses results obtained with the iP
1-1,3 and iP
1-IFT controllers during the tuning procedure are shown in
Figure 5.
In
Figure 5, the system responses obtained with the iP
1 controllers are represented by considering the tuning parameters found using the tuning methodology. The optimal values have been obtained in the fourth step. The responses from the figure show that during the application of the IFT algorithm, the oscillations of the output signal become more damped and thus, the settling time decreases.
The parameters
and the values of the tuning parameters of the iP
1 controllers, which were determined with the relationships from
Table 1, are presented in
Table 2 together with the values of the ITAE criteria for each iteration.
In
Table 2, the values of the ITAE criterion decrease with the increase in the number of iterations, indicating the performances improvement.
The iP
1-0 and iP
1-IFT controllers are used in a comparative experiment, which in-volves modifications of the reference signal, with different steps, in both directions of the pitch axis. The result of the comparison is depicted in
Figure 6, from which the good behavior of the iP
1-IFT controller in relation to iP
1-0 is shown.
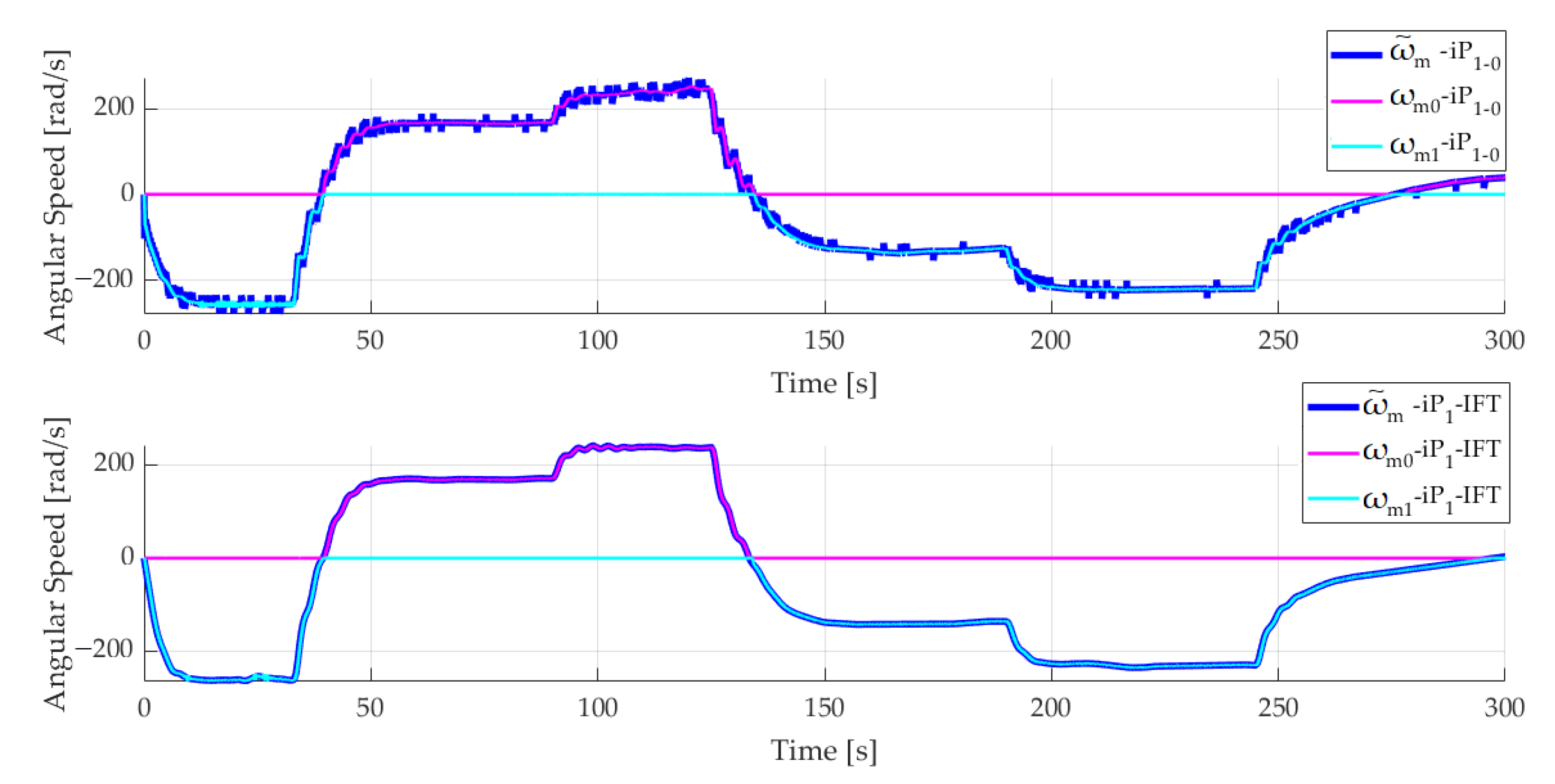
The control signals for the iP
1-
0 and iP
1-IFT controllers during the comparison experiments are presented in
Figure 7. Therein represented are the reference angular speed of the motors
and, at the same time, the responses of the two inner loops generated by the
C0 and
C1 switches from
Figure 3, depending on
. When
, the reference generated by the iP
1 controller of the outer loop will be applied through
C0 to the inner loop related to the motor
0, and the inner loop of the motor
1 will have the reference equal to zero through switch
C1. For
, the switches change their position and thus, the inner loop related to the motor
1 will receive the reference; for motor
0, the reference will be zero. The operation of the switches according to
introduces a nonlinearity in the plant model related to the outer loop.
From
Figure 7, an oscillating operation is observed for the DC motors, which actuate the propellers for the iP
1-0 controller, which can cause the wear of the Aero 2 system. These oscillations disappear in the case of the iP
1-IFT controller.
4.2. Control of Pitch Angle with the iPD2 Controller
As shown in the conclusions from
Section 2, the iPD
2 controller will introduce a derivative component that accelerates the control loop and leads to a faster response of the system, but at the same time amplifying the high-frequency signals. A similar procedure with the iP
1 case presented in
Section 4.1 was created, starting with a stable response of the system with an iPD
2-0 controller that was now determined based on the Jury test. For the iPD
2 controller, five iterations of the IFT algorithm have been achieved with step size
, penalty factor
, and matrix
. The responses obtained during the tuning phase with the initial controller iPD
2-0, with some intermediate controllers iPD
2-2,3 and the final controller iPD
2-IFT, are presented in
Figure 8.
The system controlled with iPD
2-0 shows oscillations with high amplitude, which are reduced after five iterations of the IFT algorithm. This gives the system a high range, where it can reach the reference for the pitch angle. The iPD
2-5 from the final iteration, noted as iPD
2-IFT, was chosen due to the obtained performances, which have been evaluated according to the ITAE criterion from Equation (50). The damping of the oscillations during the tuning phase leads to the decrease in the settling time, which becomes smaller than the one obtained with the iP
1-IFT controller in
Figure 5 due to the derivative component. In
Table 3, the parameters
and the values of the tuning parameters of the iPD
2 controllers are summarized together with the ITAE criteria values. As
Table 3 shows, the values of the ITAE criterion are decreasing from the initial response iPD
2-0 to the fifth iteration of the IFT algorithm due to the improvement of the performances.
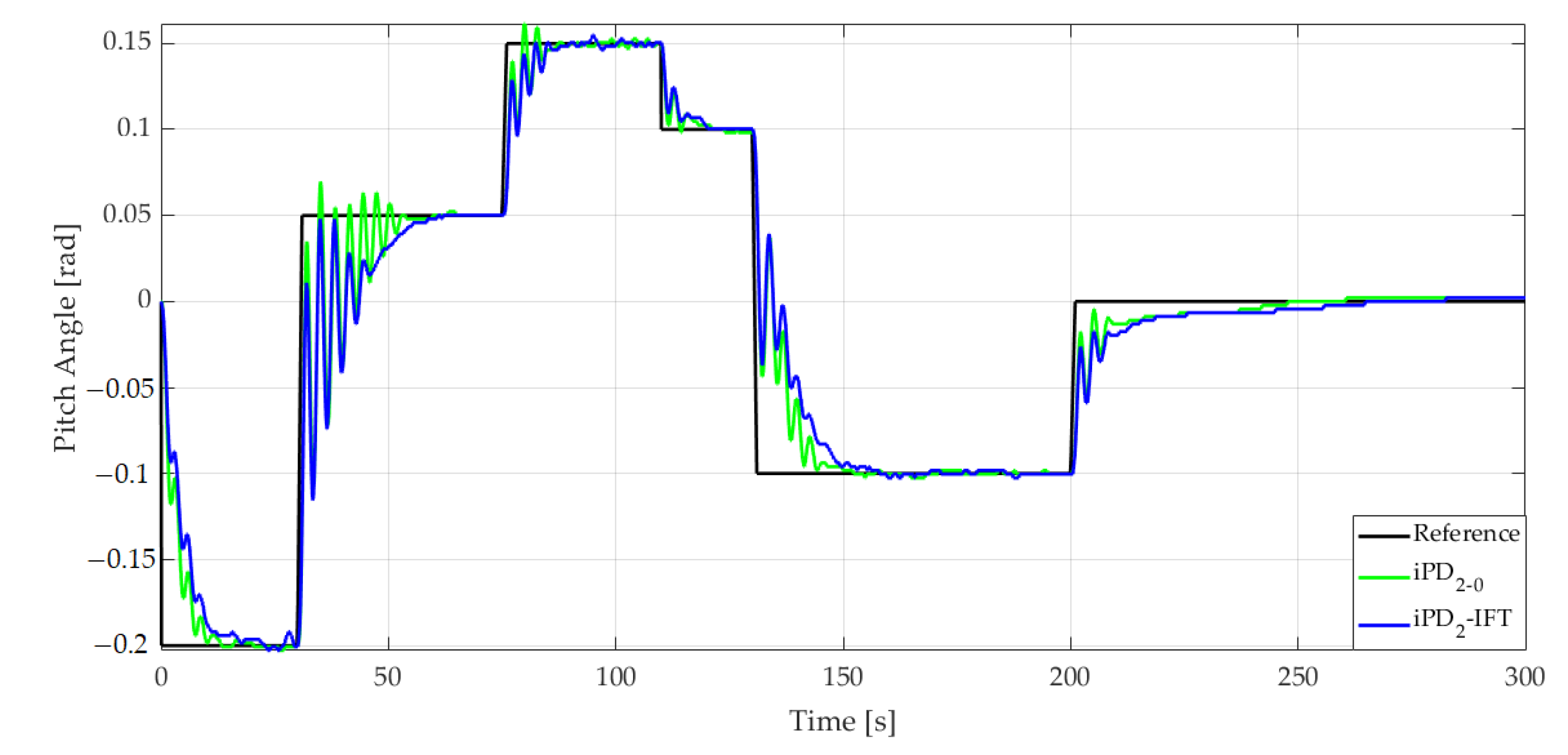
To analyze the behavior of the tuned controllers, a comparison between the initial iPD
2-0 and the final version of iPD
2-IFT for the step variations of the reference signal is made, and the results are presented in
Figure 9.
The figure reveals a similar behavior with the previous one presented in
Figure 8 for the tuning phase, with the iPD
2-0 controller having larger oscillations than the iPD
2-IFT when the reference is modified. This aspect is important with respect to achieving a high interval of movement on
the pitch axis. The initial set of parameters is limited to variations of angle under 0.25 radians (around 15°) because the oscillations introduced make the system unstable. Considering this limitation, a different reference for the pitch angle is used compared with the iP
1 one depicted in
Figure 6. The control signals for the iPD
2 controllers are shown in
Figure 10 with the reference control signal
and controlled signals
,
.
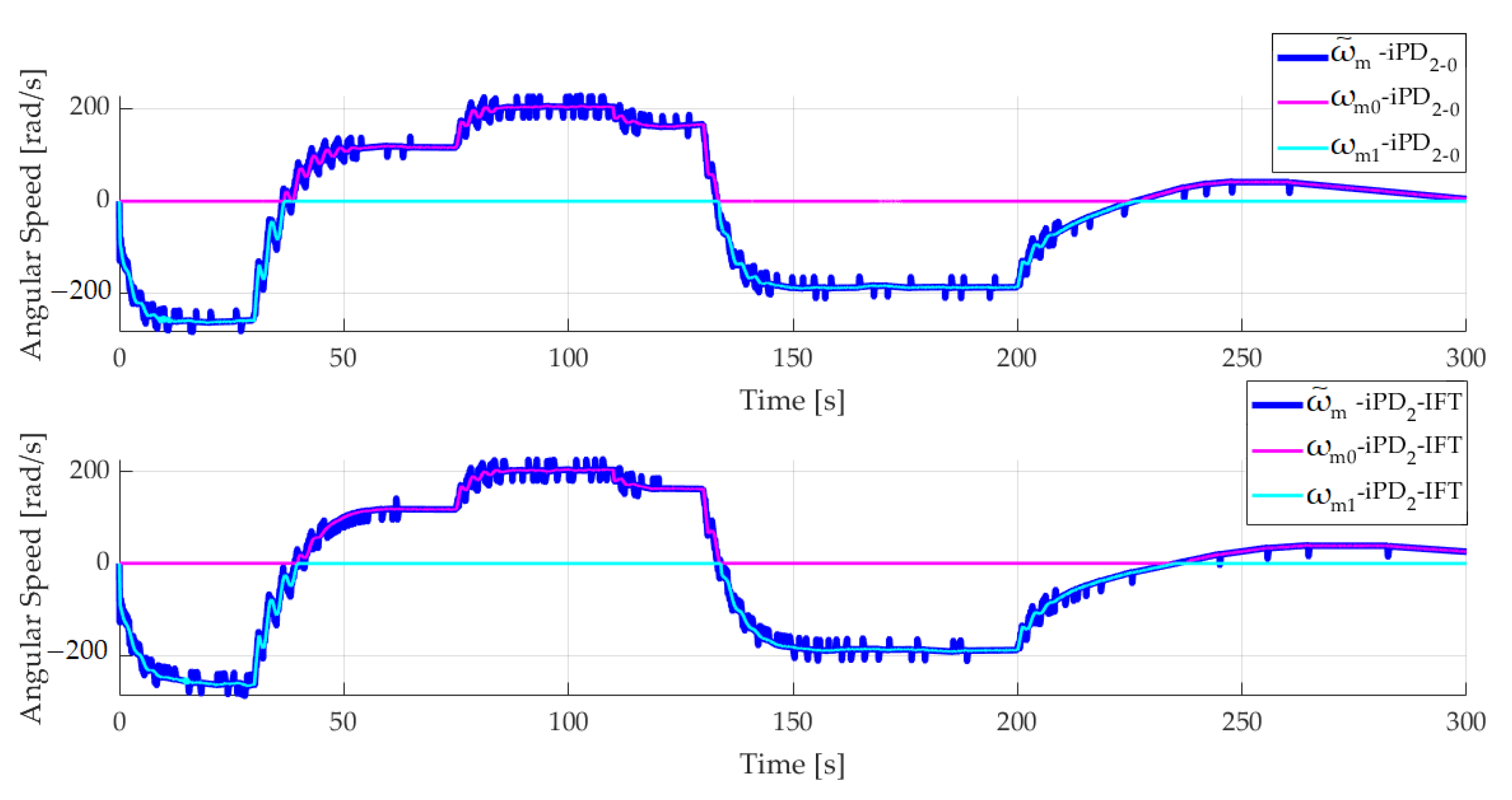
The reference angular speed of the motors
for the experiment presented in
Figure 9 can take positive or negative values, as
Figure 10 reveals. Taking into account the sign of
, the
C0 and
C1 switches from
Figure 3 make it possible to use motor
0 for the positive values and motor
1 for the negative values of the reference angular speed signal.
4.3. Control of Pitch Angle with iP1-IFT and iPD2-IFT Controllers
The controllers tuned with the IFT algorithm that were presented in
Section 4.1 and
Section 4.2 are used for a performance comparison with the step variations of the reference signal. The reference profile from
Figure 6 used for the iP
1 comparison was considered for the experiments against the iPD
2-IFT controller. Moreover, it is necessary to analyze which type of MFC controller can offer better results for the pitch angle control of an Aero System. The results are depicted in
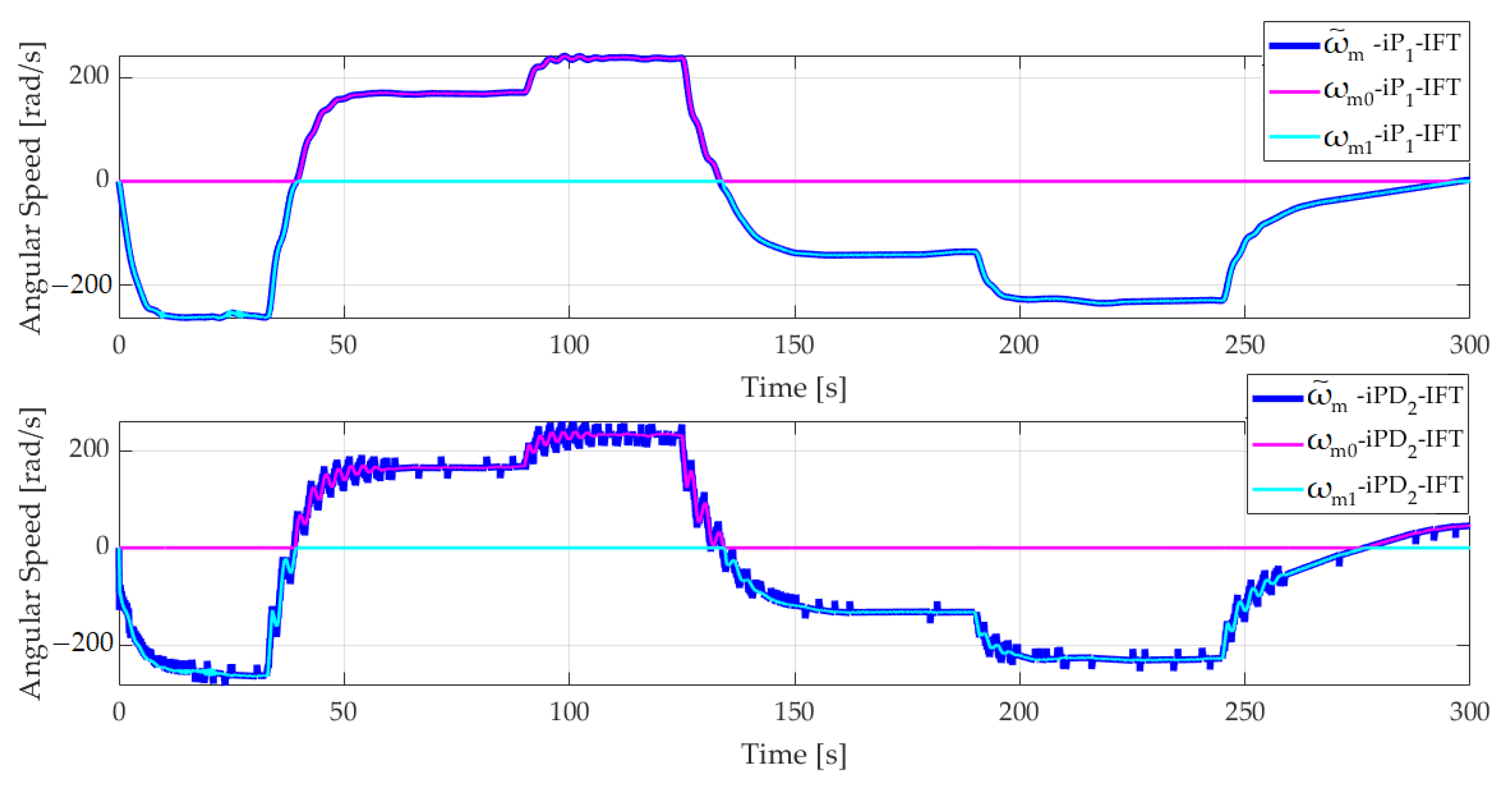
Figure 11.
The comparison reveals a response with larger oscillations for iPD
2-IFT in relation to iP
1-IFT to the step variations of the reference signal. However, due to the derivative component, iPD
2-IFT will generate a shorter settling time. The control signals obtained from the comparative experiment are depicted in
Figure 12 together with the angular speeds of the two DC motors.
The control signal of the iP1-IFT controller is smooth compared with that of the iPD2-IFT controller, which exhibits oscillations due to the amplification of the high-frequency signals from the control system by the derivative component. These oscillations propagate at the output of the inner loops and finally at the output of the control system, determining less satisfactory performances of the control system with iPD2-IFT compared with those obtained using iP1-IFT.
5. Conclusions
In this paper, a new method for tuning model-free iPID controllers based on the IFT data-driven algorithm is described. Considering that the IFT algorithm can only be used for the tuning controllers with a fixed structure, such a structure was first determined for the iPID controllers. Thus, starting from the connections between the iPID and PID discrete-time controllers, a fixed structure of the iPID controller was obtained, described by an equivalent transfer function that were parametrized with the parameters vector. Moreover, analyzing the behaviors of the iPID controllers in relation to the PID control laws, two intelligent controllers were established for and , respectively, with the others being eliminated because they had unusual behaviors in the control engineering. The IFT algorithm could be applied by having the iPID controllers with a fixed structure, whose transfer functions were used to estimate the gradients of the input/output variables. At the same time, based on two experiments in the closed loop, the input and output signals were collected, which together with the above derivative estimates allowed for the estimation of the gradients of the cost function and the matrix used to update the direction. Finally, the parameters grouped in vector of the fixed structure of the controller were determined; based on these parameters, the tuning gains and parameter were found. The methodology for tuning the iPID controllers based on the IFT algorithm was tested and experimentally validated using a real-time application for controlling the pitch angle of the dual-motor Aero 2 aerospace system, which was provided by Quanser.
The main advantages of the proposed tuning method based on the IFT algorithm consist of the following: the determination of both the gain parameters related to the PID algorithm and the α parameter; the IFT tuning of the iPID parameters does not require knowledge of the plant model; and the gradients of the quadratic control criterion can be easily estimated based on the data collected after the two experiments. Among the disadvantages, it is mentioned that the selection of the starting values of the iPID tuning parameters must be conducted in such a way so as to obtain a stable response and the two experiments must be performed to determine the tuning parameters at each step. The initial choice of tuning parameters, along with finding the related values of the step size and the penalty factor of the control effort through a trial-and-error procedure, are the main design challenges.
For future research, some techniques will be considered for tuning the parameters related to the step size and penalty factor of the control effort as well as the extending of the proposed method to multivariable systems.