Modeling and Fault Simulation of a New Double-Redundancy Electro-Hydraulic Servo Valve Based on AMESim
Abstract
:1. Introduction
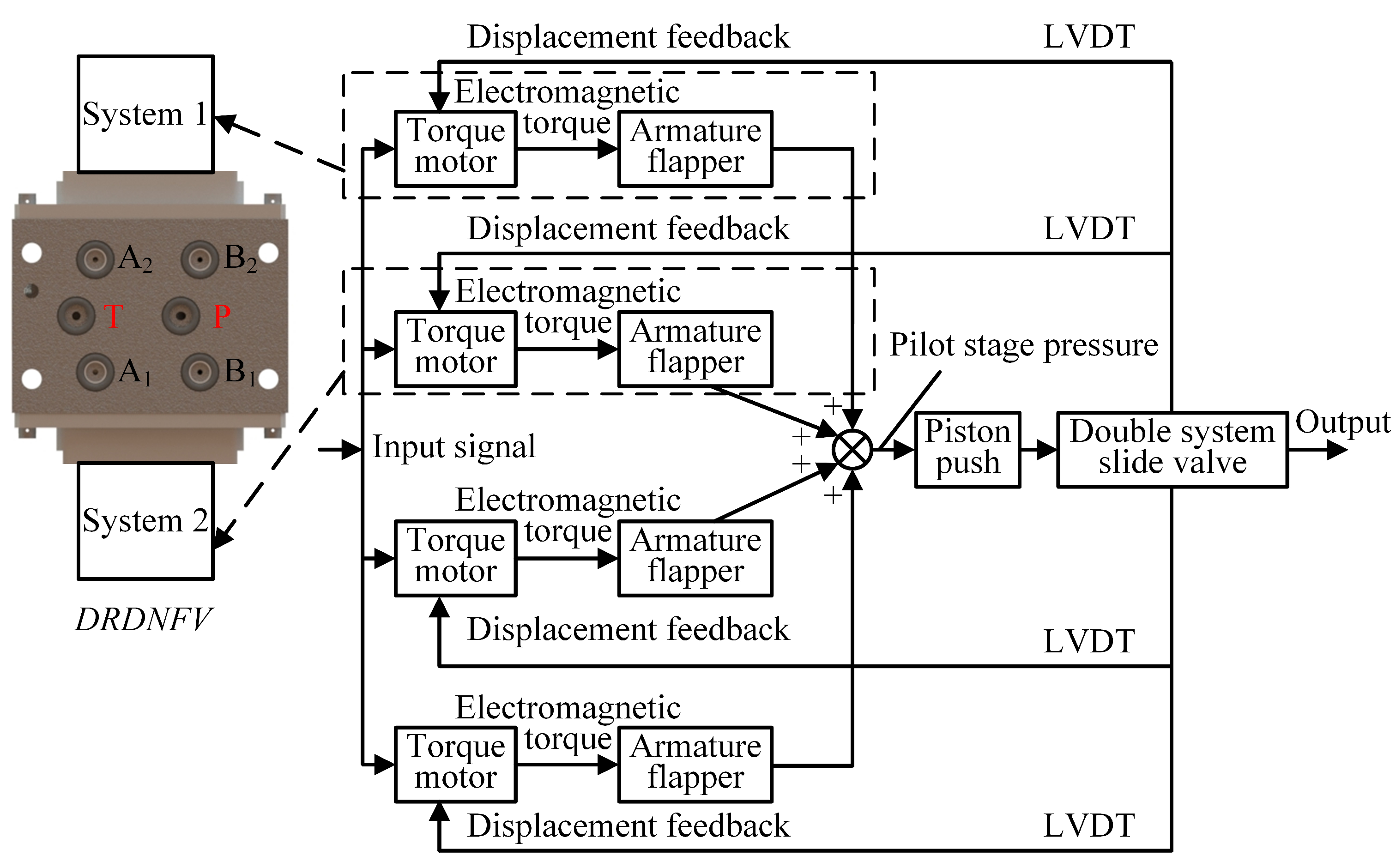
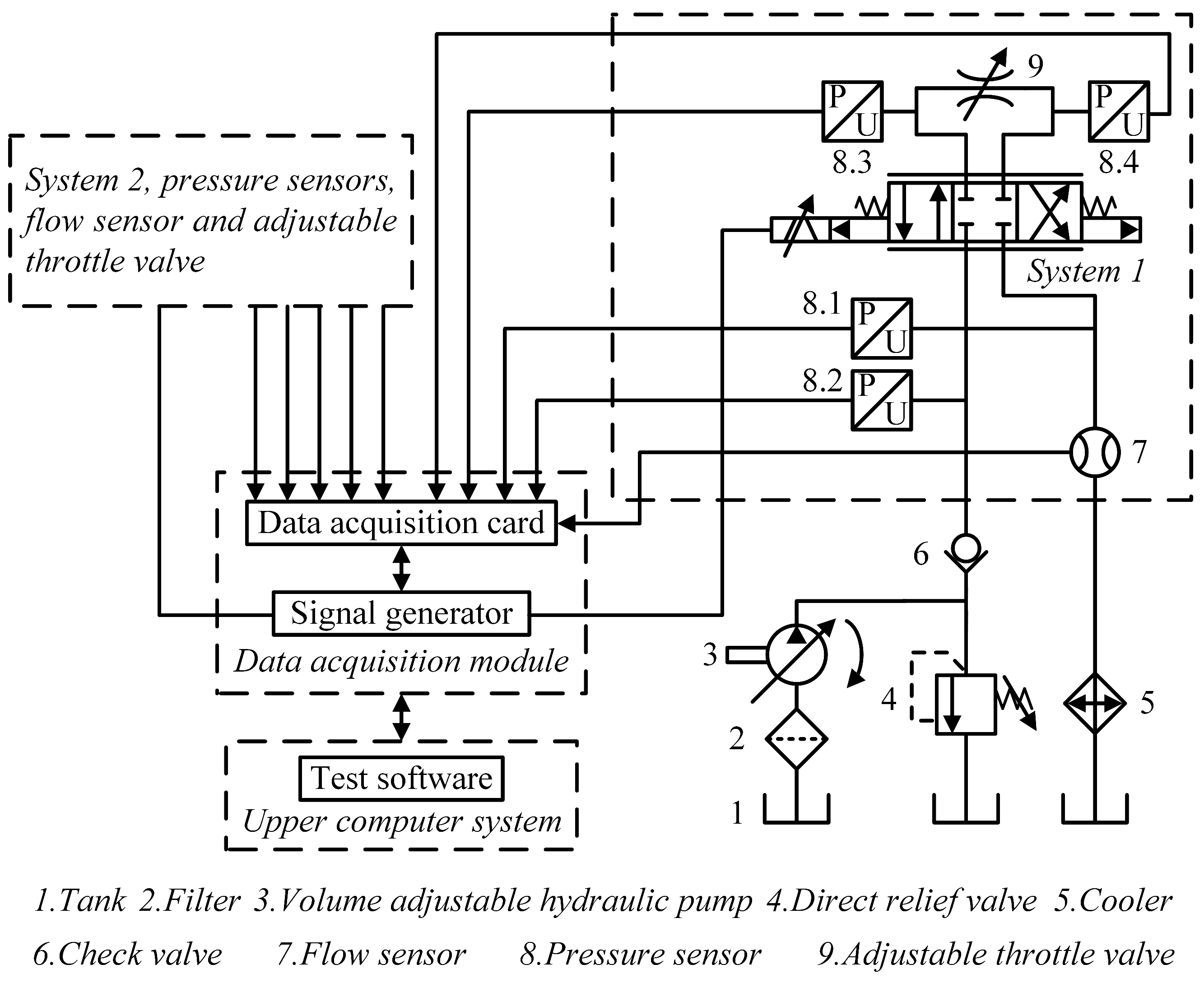
2. Working Principles
3. DREHSV Modeling
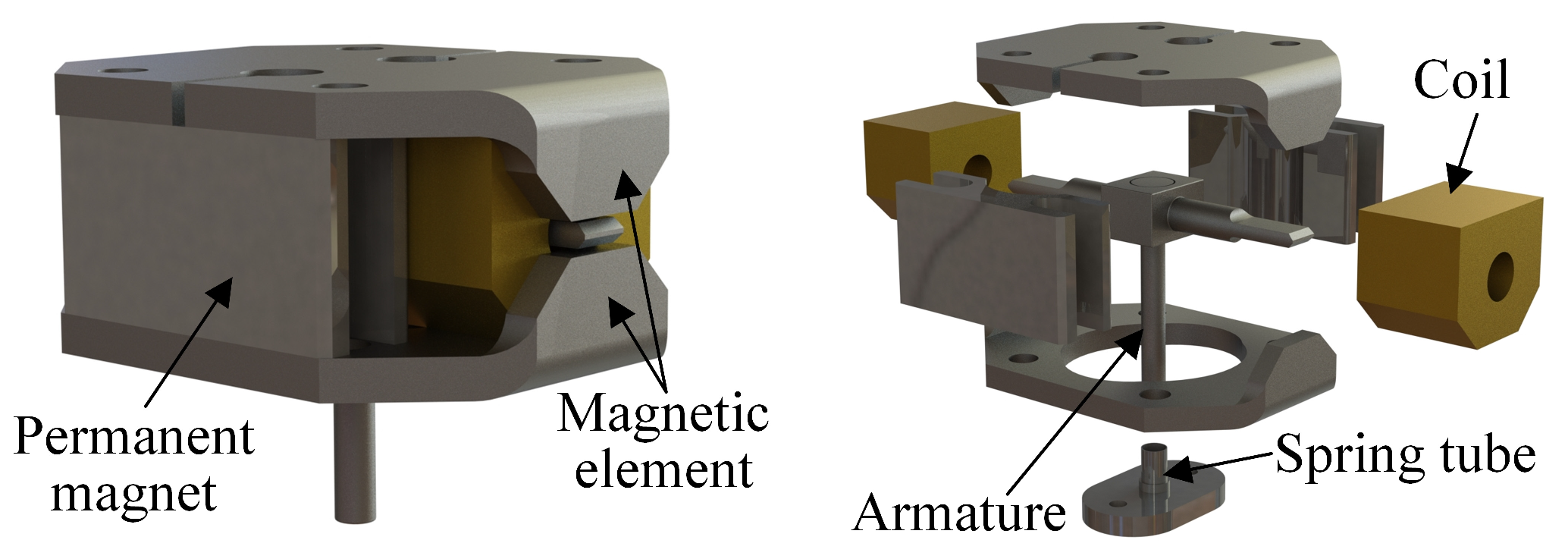
3.1. Torque Motor Modeling
3.2. Armature Assembly Modeling
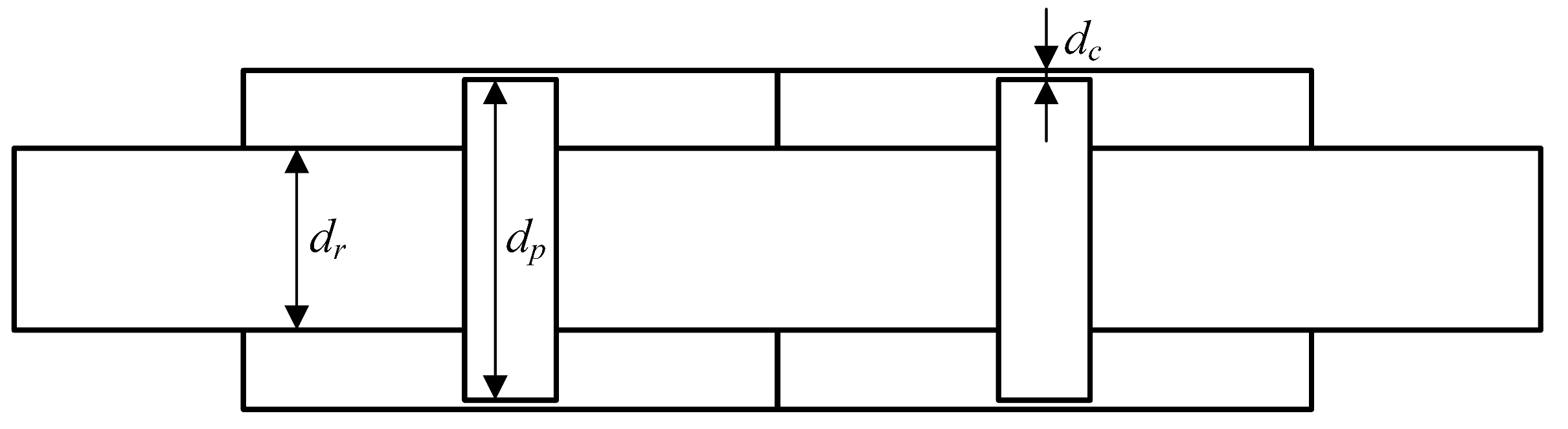
3.3. Double-System Slide Valve Modeling
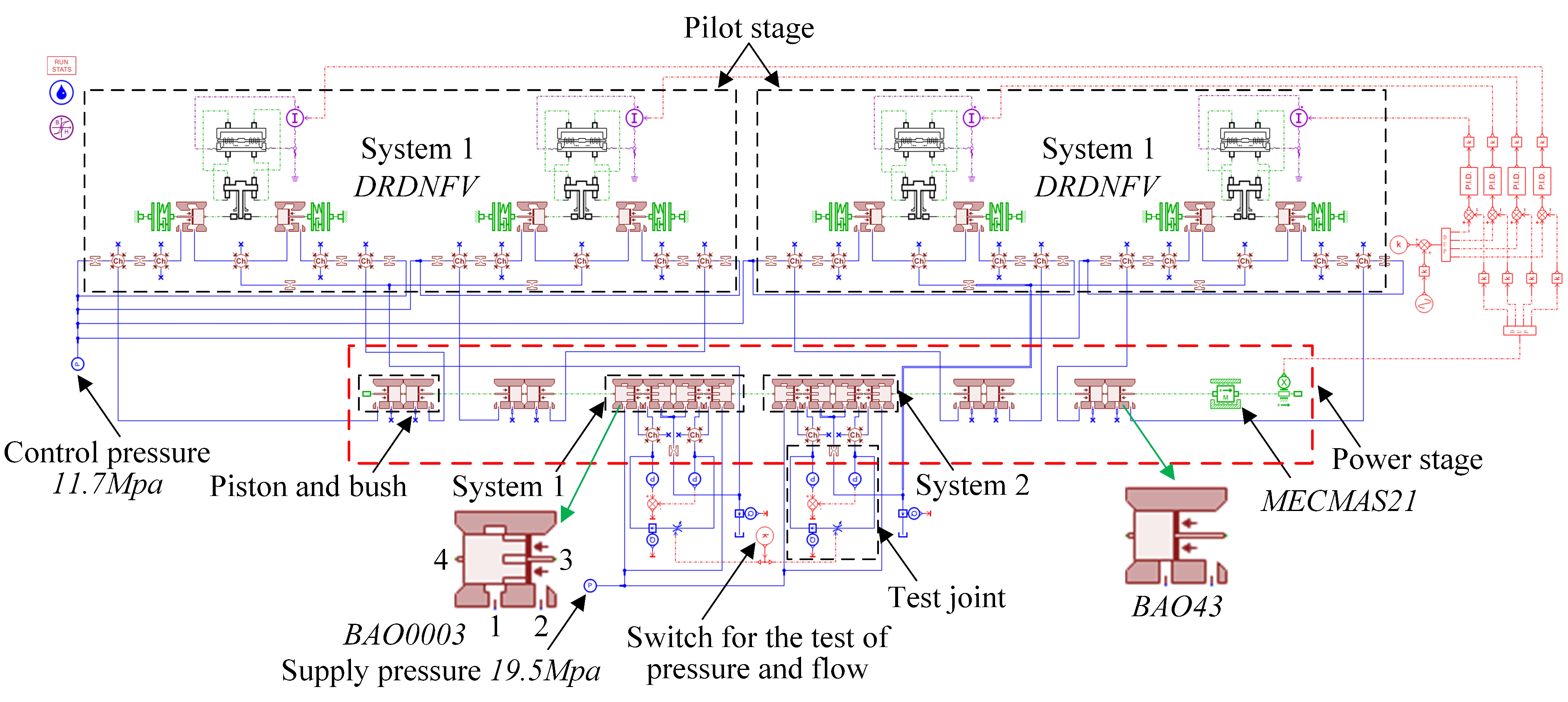
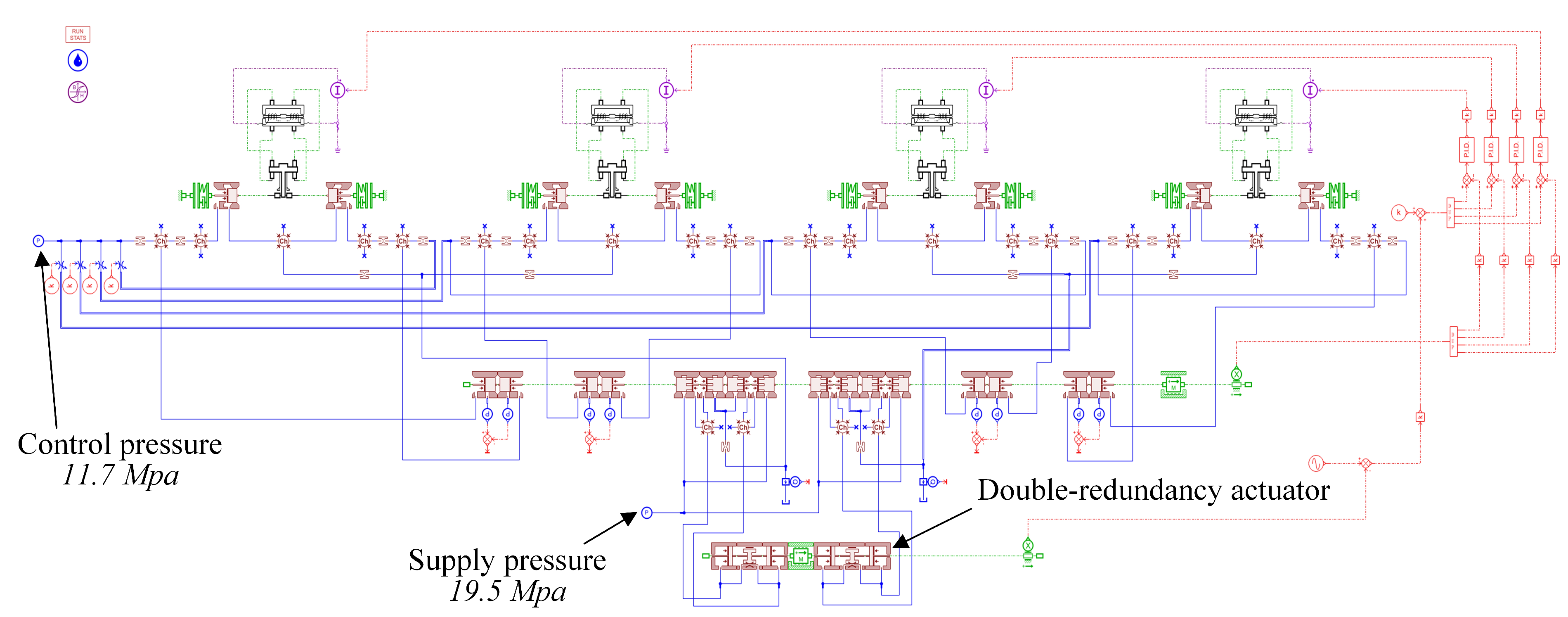
3.4. AMESim Overall Simulation Model
4. Simulation and Fault Research
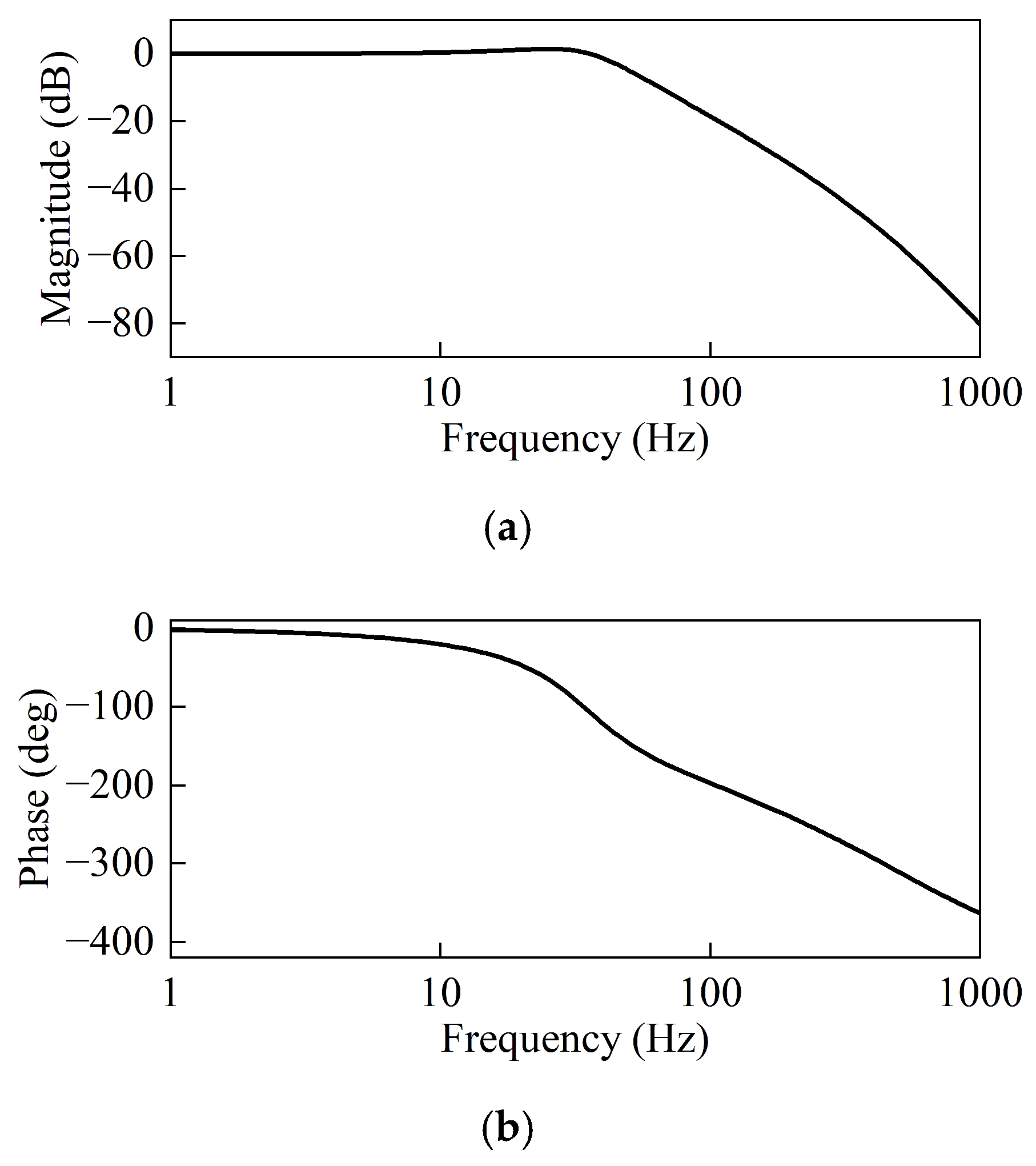
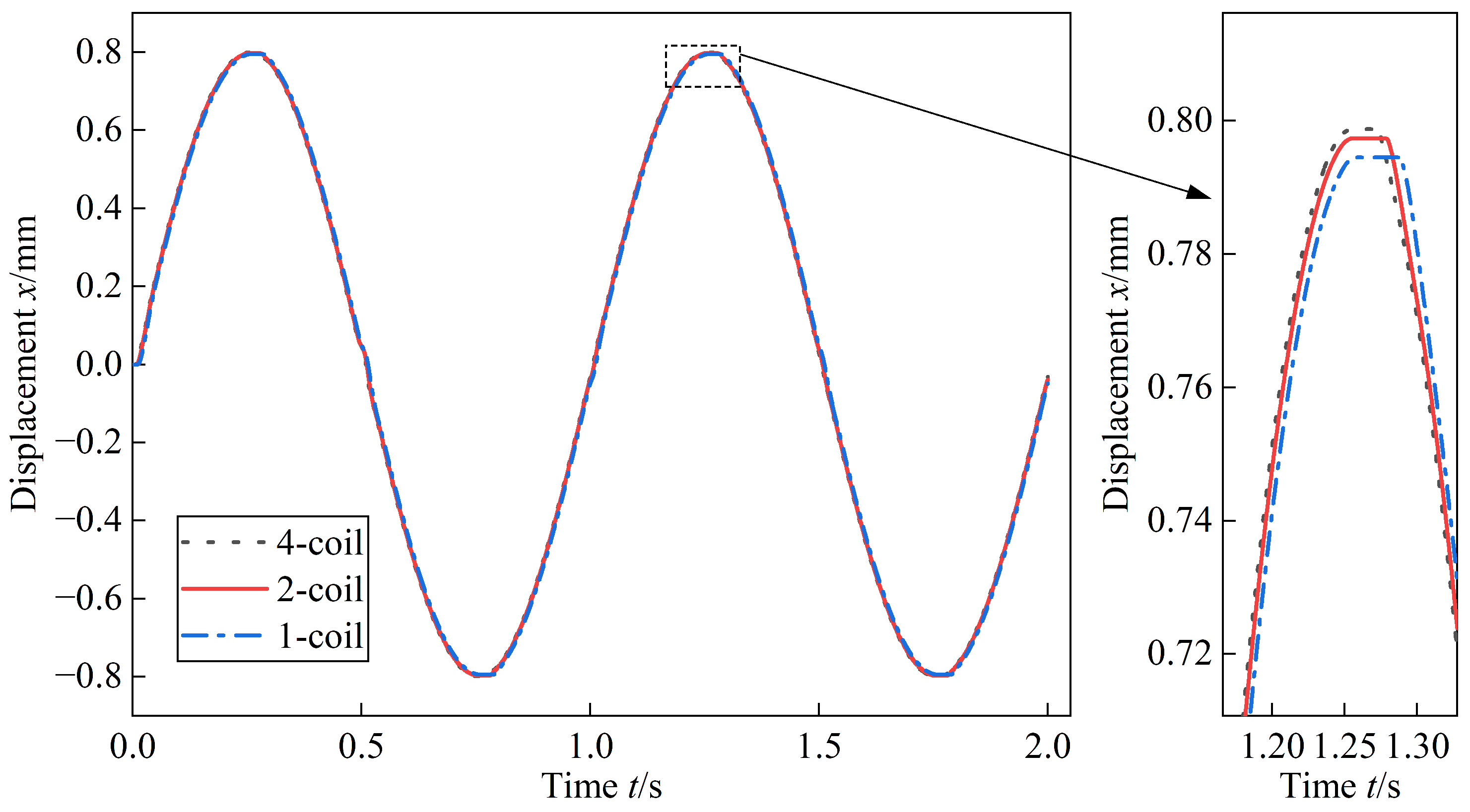
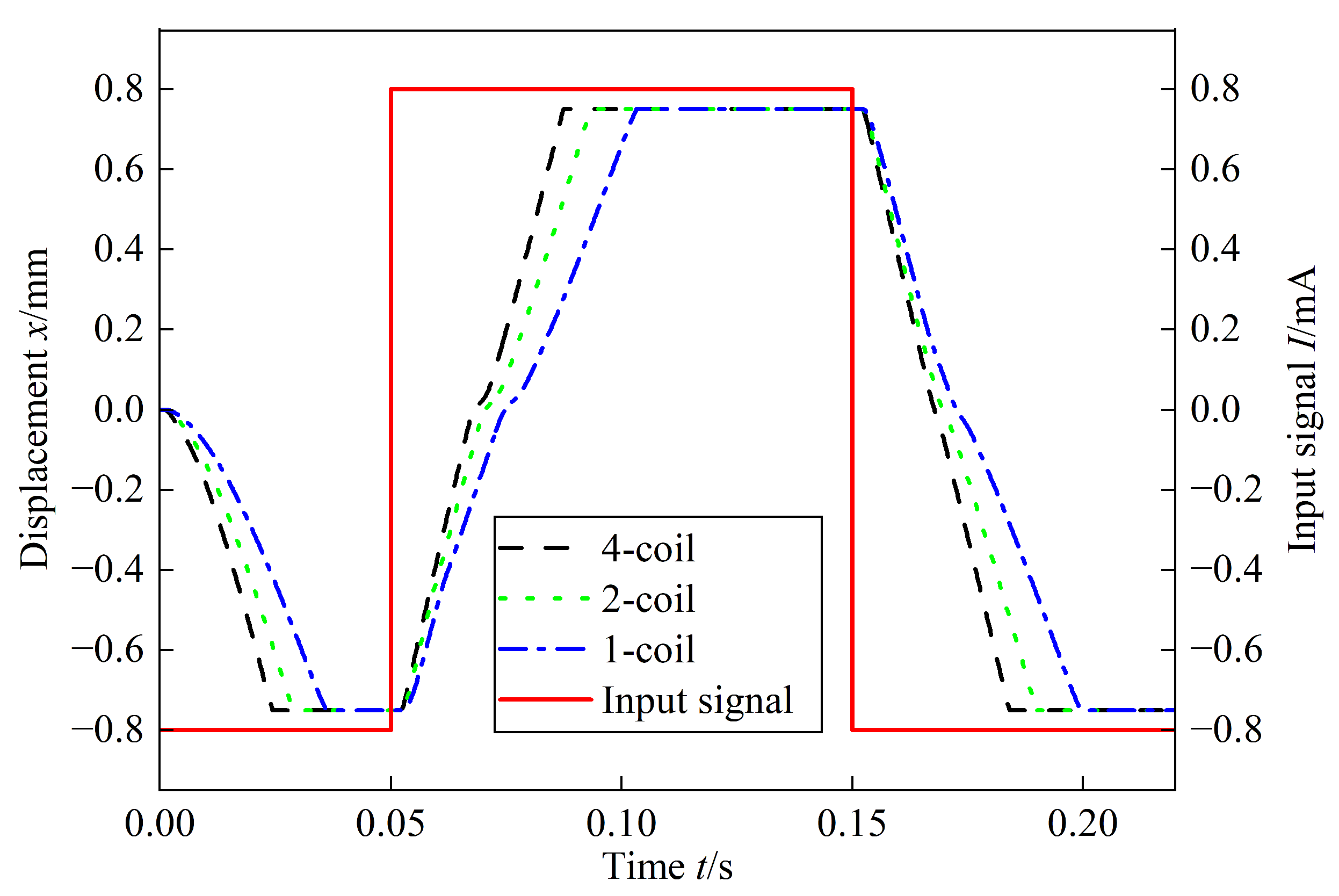
4.1. DREHSV Normal Mode
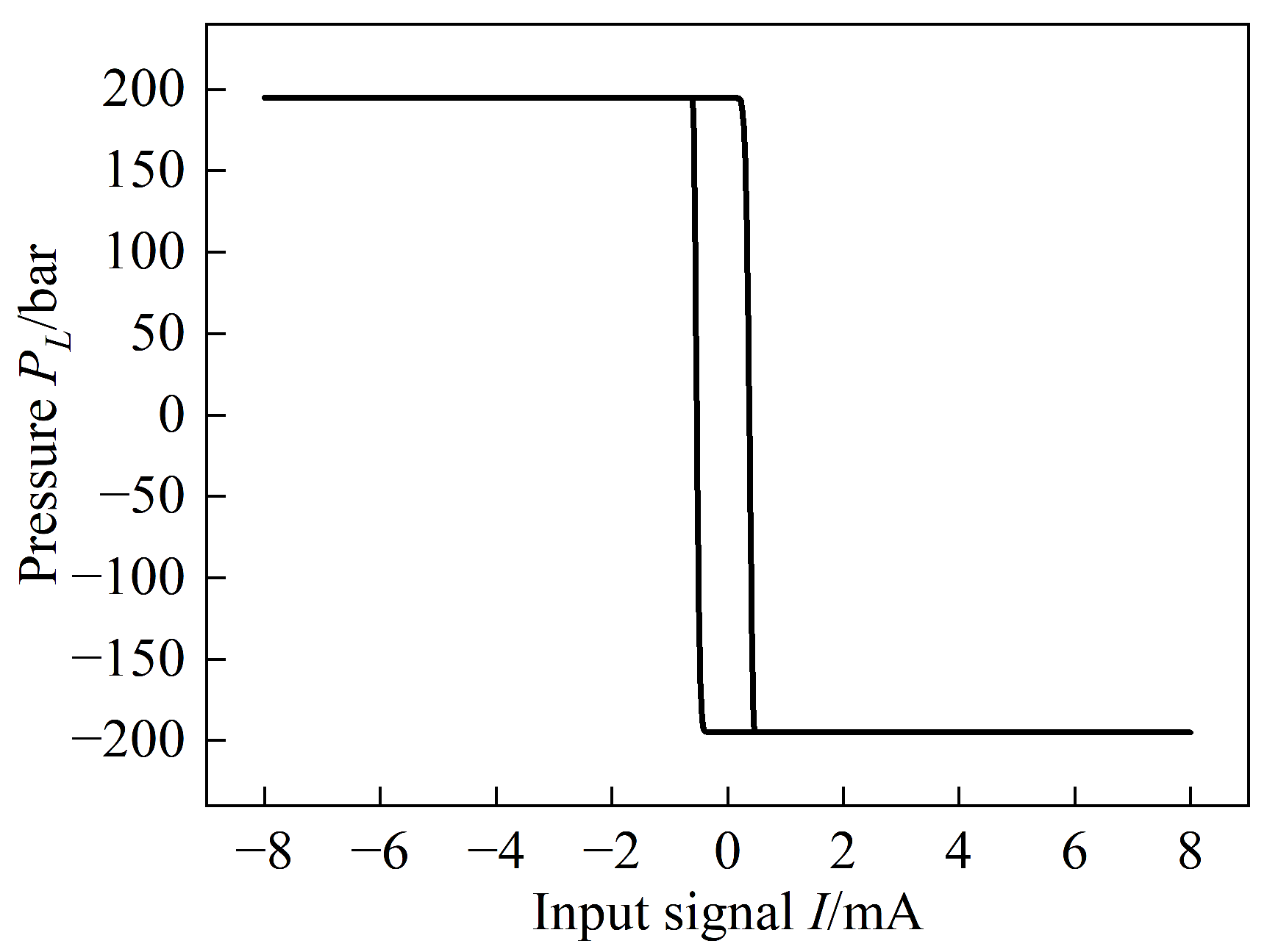

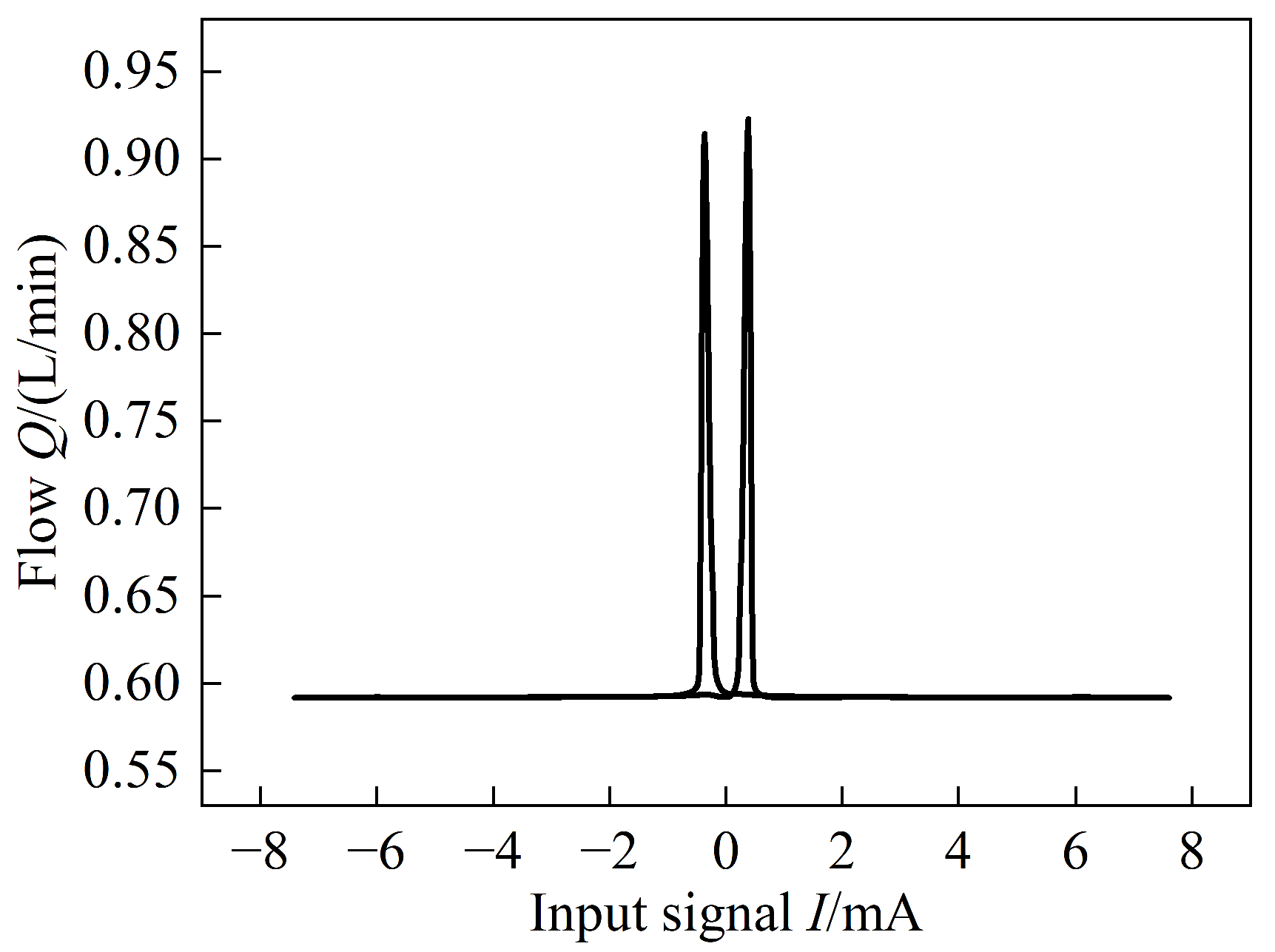
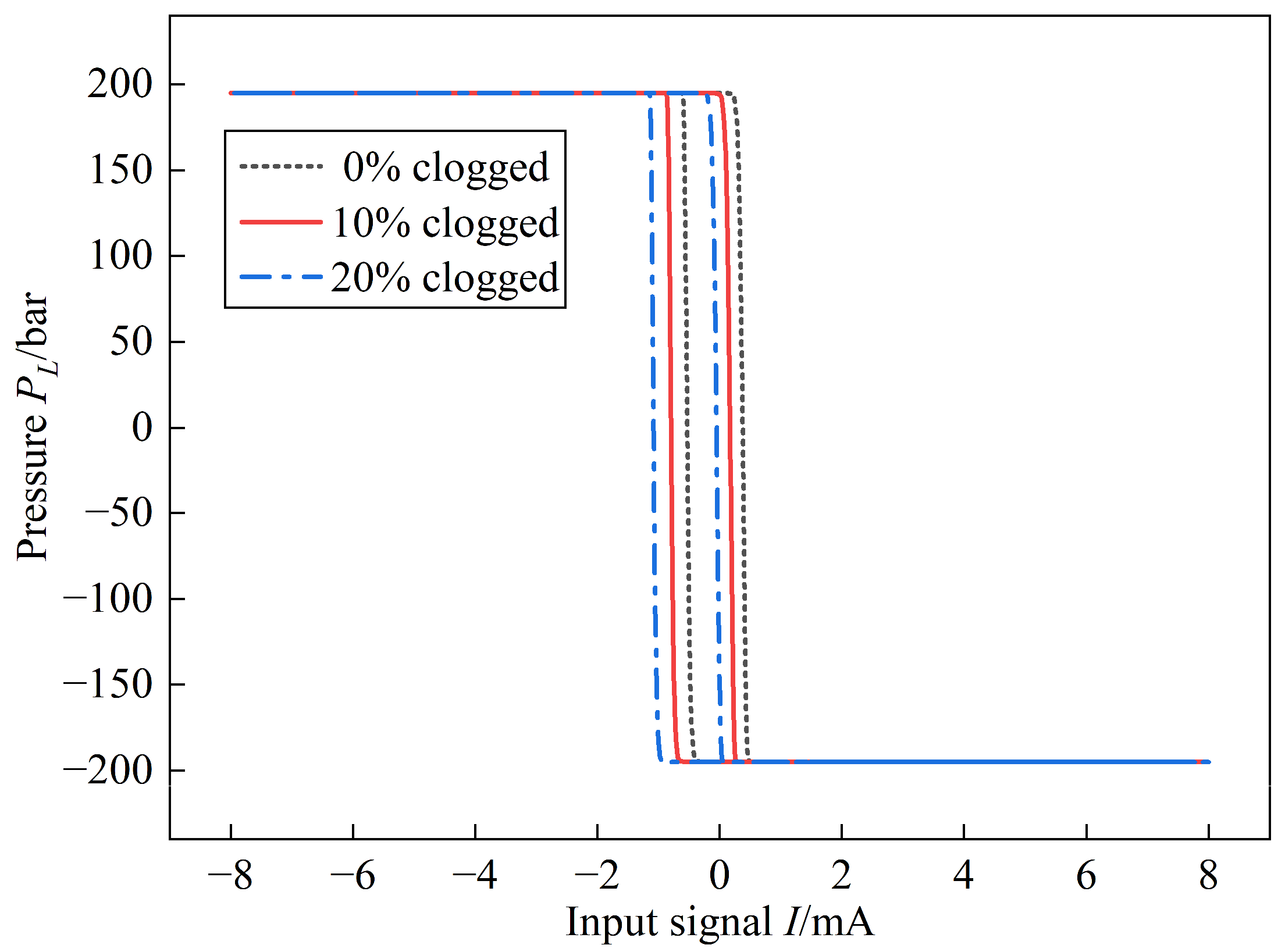
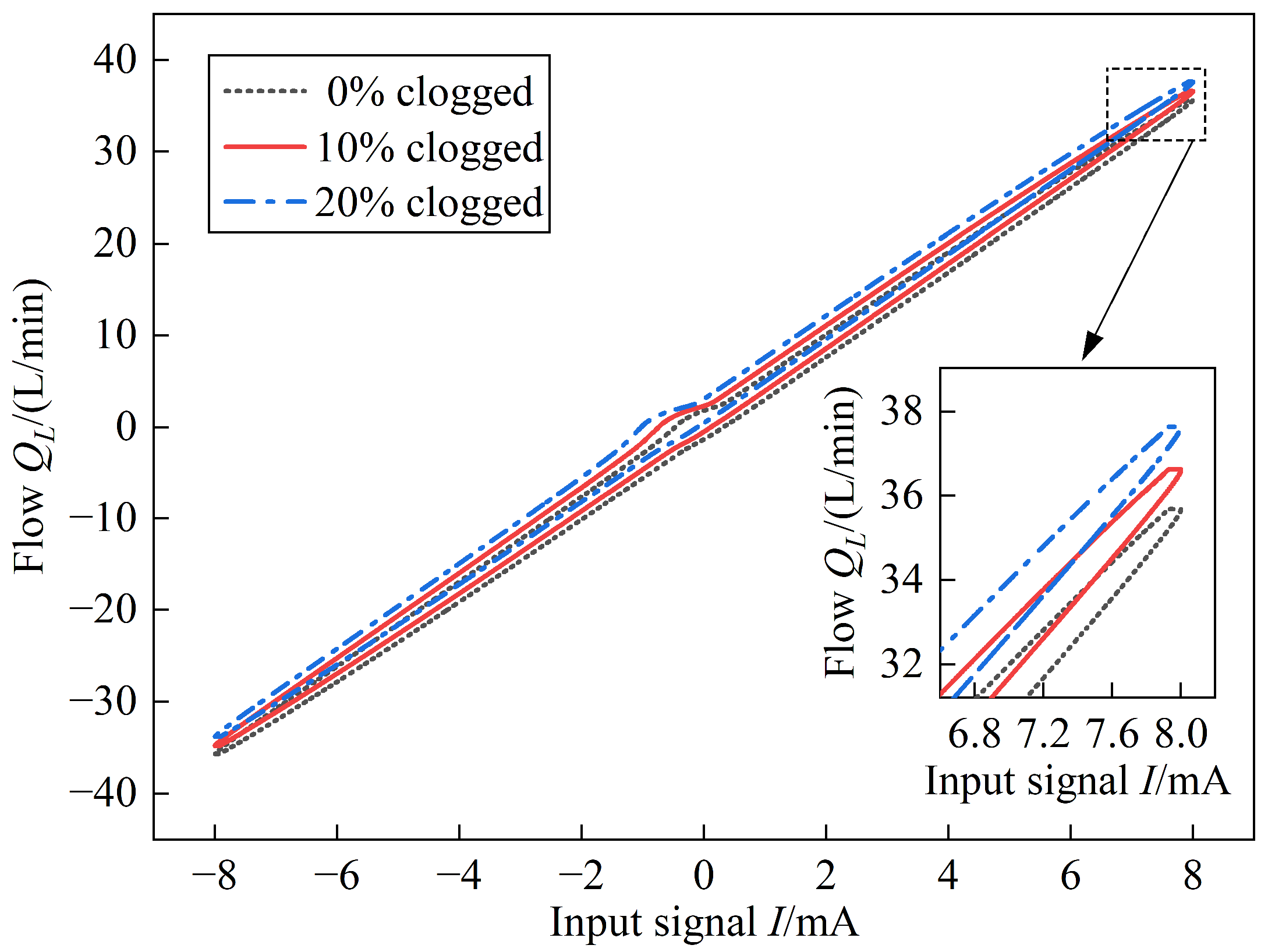
4.2. Pilot Stage Nozzle Clogged
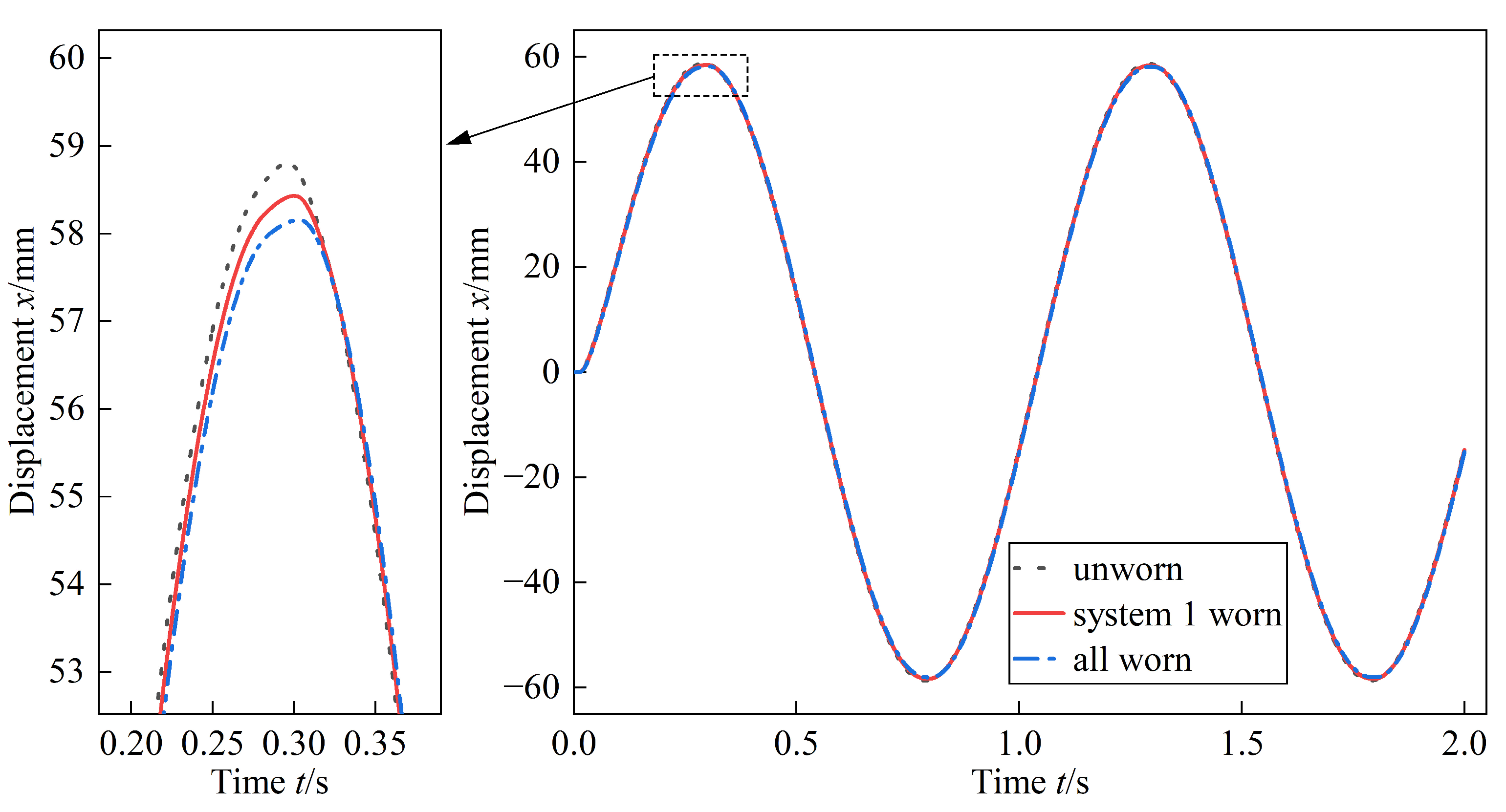
4.3. Power Stage Spool Worn
4.4. Redundant Design Advantage
5. Experiment
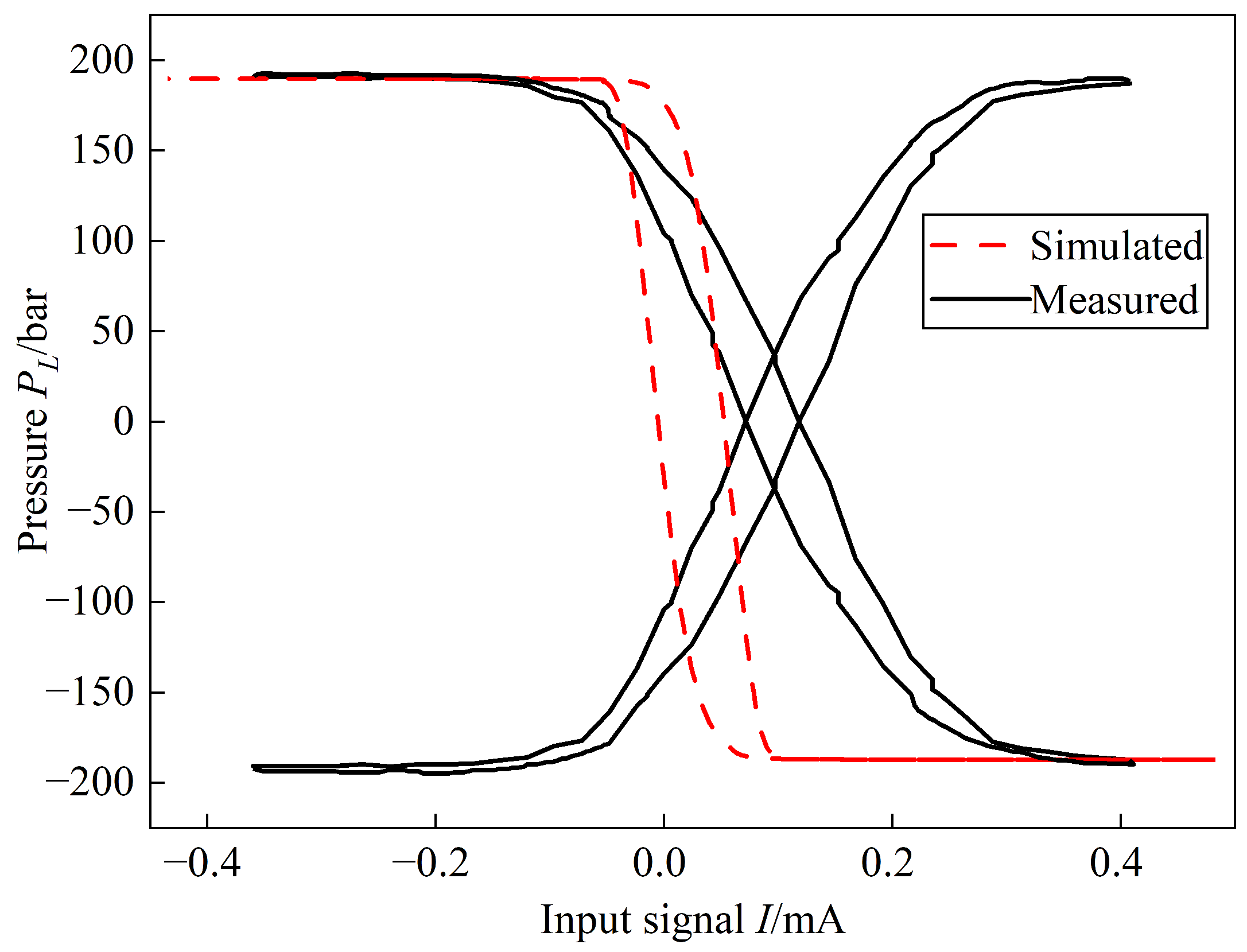
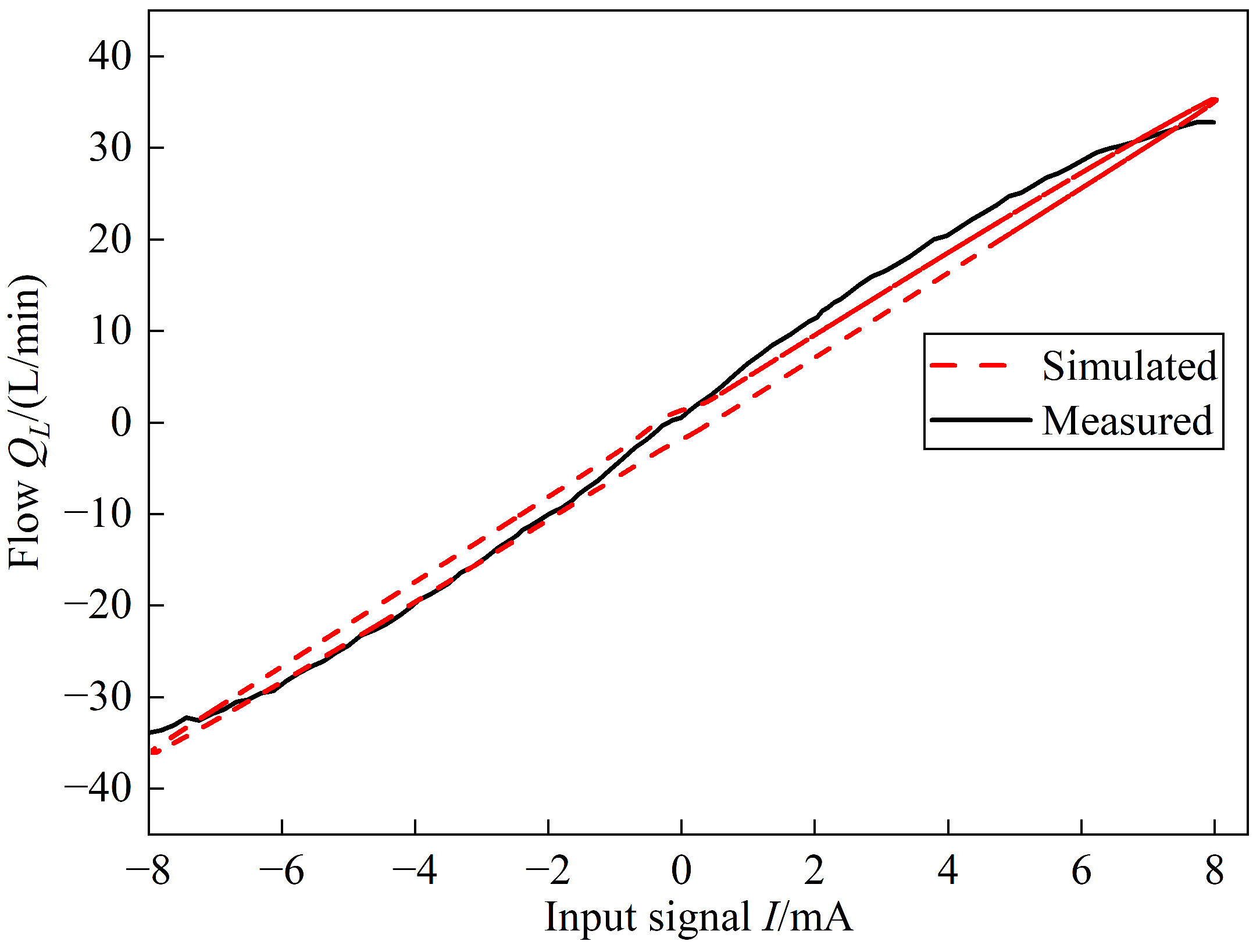
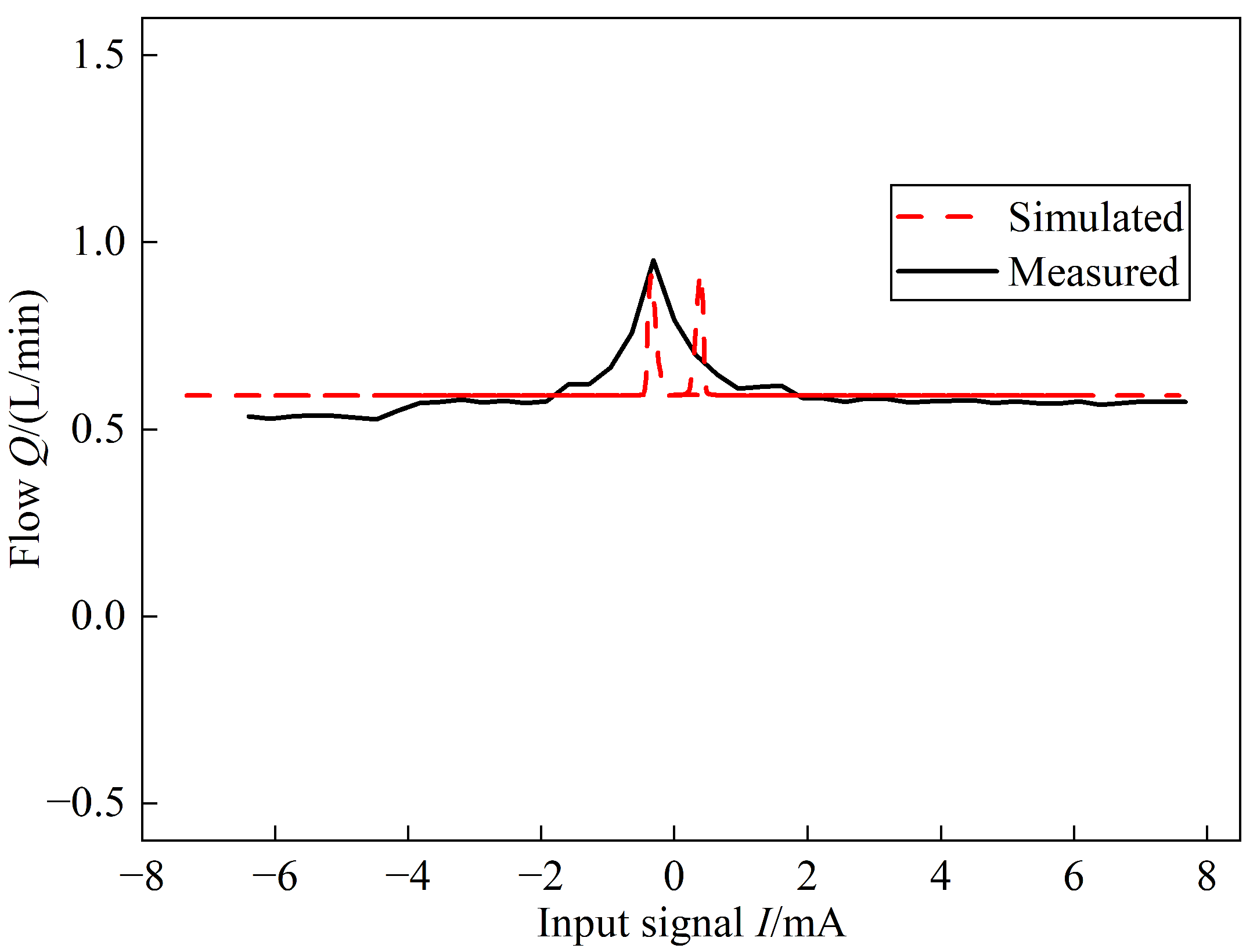
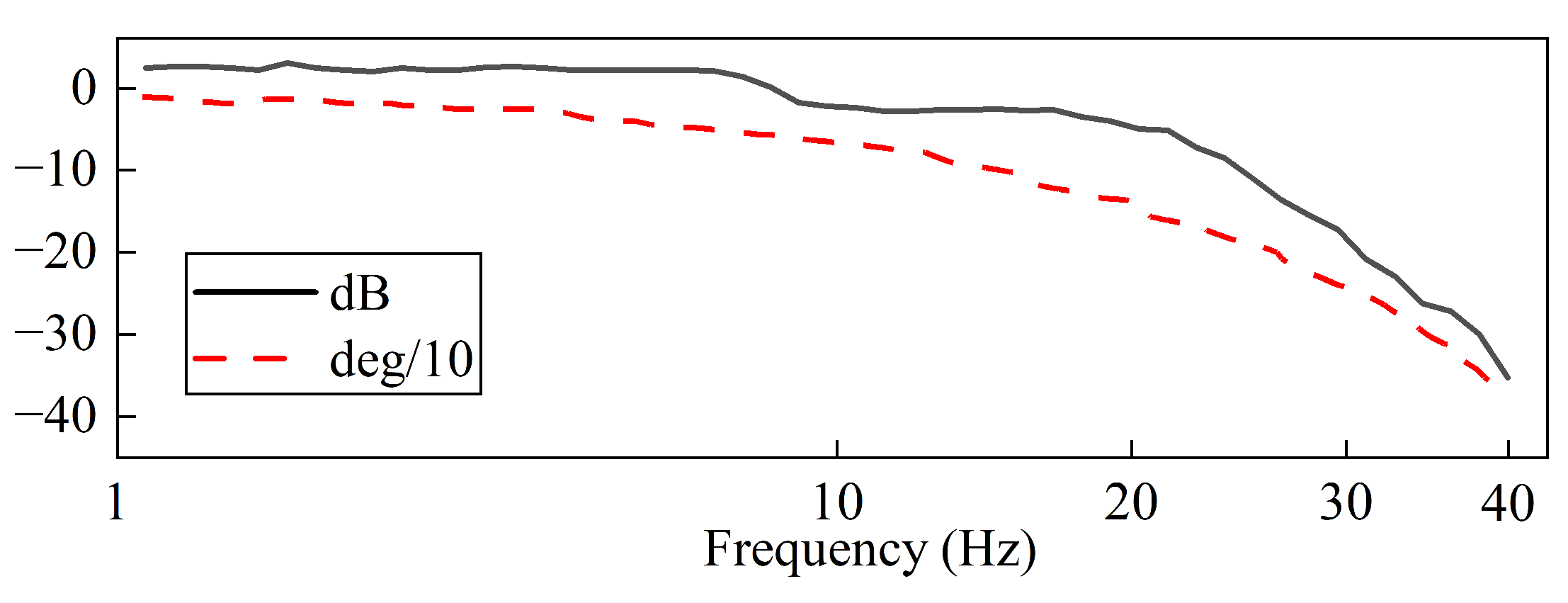
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fang, Q.; Huang, Z. Developing process, research actuality and trend of electrohydraulic servo valve. Mach. Tool Hydraul. 2007, 35, 162–165. [Google Scholar]
- Ye, H.; Zeng, G.S. Structure design and reliability analysis of the triplex redundance digital servo control system. J. Solid Rocket. Technol. 2002, 25, 69–72. [Google Scholar]
- Anderson, R.T.; Li, P.Y. Mathematical modeling of a two spools flow control servovalve using a pressure control pilot. J. Dyn. Syst. Meas. Control. 2002, 124, 420–427. [Google Scholar] [CrossRef]
- Chen, Z.G.; Ding, F.; Cai, Y.H. Research on characteristics of single-stage twin flapper-nozzle electrohydraulic servo valve. Mach. Tool Hydraul. 2007, 35, 114–116, 135. [Google Scholar]
- Mu, D.J.; Li, C.C.; Yan, H.; Sun, M. Nonlinear simulation and linearization of twin flapper-nozzle servo valve. J. Mech. Eng. 2012, 48, 193–198. [Google Scholar] [CrossRef]
- Wang, D.W. Flow Field Characteristics Research and Malfunction Simulation Analyses on the Three-Stage Servo Valve. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2013. [Google Scholar]
- Liu, C.H. Study on Modeling and Simulation of Two-Stage Nozzle-Flapper Servo Valve with Force Feedback. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2013. [Google Scholar]
- Wang, X.Q.; Wang, W.F. Modeling and simulation of armature assembly of double-stage double-nozzle-flapper electro-hydraulic servo valve. Mach. Tool Hydraul. 2014, 42, 161–165, 199. [Google Scholar]
- Gordic, D.; Babic, M.; Jovicic, N. Modelling of spool position feedback servo valves. Int. J. Fluid Power 2014, 5, 37–50. [Google Scholar] [CrossRef]
- Gordic, D.; Babic, M.; Milovanovic, D.M. Effects of the variation of torque motor parameters on servo valve performance. Stroj. Vestn. J. Mech. Eng. 2008, 54, 866–873. [Google Scholar]
- Li, L.F.; Yu, M.H.; Ma, C.F.; Guo, X.; Dong, M. Simulation and fault research for two stage double nozzle flapper electro-hydraulic servo valve based on AMESim. Mach. Tool Hydraul. 2017, 45, 177–180. [Google Scholar]
- Li, Y.S. Physical model of two-stage nozzle-flapper electrohydraulic servo-valve with force feedback. Chin. Hydraul. Pneum. 2021, 45, 69–73. [Google Scholar]
- Shi, S.M. The Fault Diagnosis of the Electro-Hydraulic Servo Valve Based on Neural Network. Ph.D. Thesis, Yanshan University, Qinhuangdao, China, 2022. [Google Scholar]
- Yan, H.; Yao, L.; Qiu, L.; Yan, H. Modelling and fault tolerance analysis of triplex redundancy servo valve. Int. J. Model. Identif. Control 2019, 31, 27–38. [Google Scholar] [CrossRef]
- Chen, K.Q.; Zhao, S.J.; Liu, H.X. The study on the high power redundant electro-hydraulic actuator for launch vehicles. Missiles Space Veh. 2020, 6, 79–84+122. [Google Scholar]
- Han, T.Y.; Im, D.S.; Hahn, B. Force-fighting phenomena and disturbance rejection in aircraft dual-redundant electro-mechanical actuation systems. Actuators 2023, 12, 310–328. [Google Scholar] [CrossRef]
- Yan, P.Y. Design of Industrial Two-Dimensional (2D) Servo Valve and Its Double Redundant Controller. Ph.D. Thesis, Zhejiang University of Technology, Hangzhou, China, 2020. [Google Scholar]
- Qin, J.Y.; Li, C.C.; Yan, H. Effect of temperature on torque motor air gap reluctance and permanent magnet polarization magnetomotive force. Mach. Tool Hydraul. 2017, 45, 105–109. [Google Scholar]
- Yin, Y.B.; Guo, W.K.; Li, R.H. Magnetic circuit modeling and characteristic analysis of torque motor considering magnetic leakage. J. Harbin Eng. Univ. 2020, 41, 1840–1846. [Google Scholar]
- Huang, C.C.; Yan, C.K.; Zhang, J.N.; Xu, D.F.; Jin, Z. Analysis of influencing factors of servo torque motor output torque. Chin. Hydraul. Pneum. 2021, 45, 65–70. [Google Scholar]
- Kang, J.; Yuan, Z.H.; Sadip, M.T. Numerical simulation and experimental research on flow force and pressure stability in a nozzle-flapper Servo Valve. Processes 2020, 8, 1404. [Google Scholar] [CrossRef]
- Lu, J.T.; Xie, H.B.; Chen, Y.M.; Yang, H. Flow-reduced double valve actuation for improving the dynamic performance of electro-hydraulic servo drive. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2023, 237, 294–305. [Google Scholar] [CrossRef]
- Wu, W.; Wei, C.H.; Zhou, J.J.; Hu, J.; Yuan, S. Numerical and experimental nonlinear dynamics of a proportional pressure-regulating valve. Nonlinear Dyn. 2021, 103, 1415–1425. [Google Scholar] [CrossRef]
- Aung, N.Z.; Li, S. A numerical study of cavitation phenomenon in a flapper-nozzle pilot stage of an electrohydraulic servo-valve with an innovative flapper shape. Energy Convers. Manag. 2014, 77, 31–39. [Google Scholar] [CrossRef]
- Wu, D.F.; Wang, X.; Ma, Y.X.; Wang, J.; Tang, M.; Liu, Y. Research on the dynamic characteristics of water hydraulic servo valves considering the influence of steady flow force. Flow Meas. Instrum. 2021, 80, 101966. [Google Scholar] [CrossRef]
- Huang, Z.P.; Yu, B.; Wang, Y.H.; Zhang, Q.W.; Xie, Y.; Xie, Z.J.; Kong, X.D. Structural analysis and improvement design of brake pressure valve feedback stage in multivalve parallel brake system. Shock. Vib. 2021, 2021, 4551799. [Google Scholar] [CrossRef]
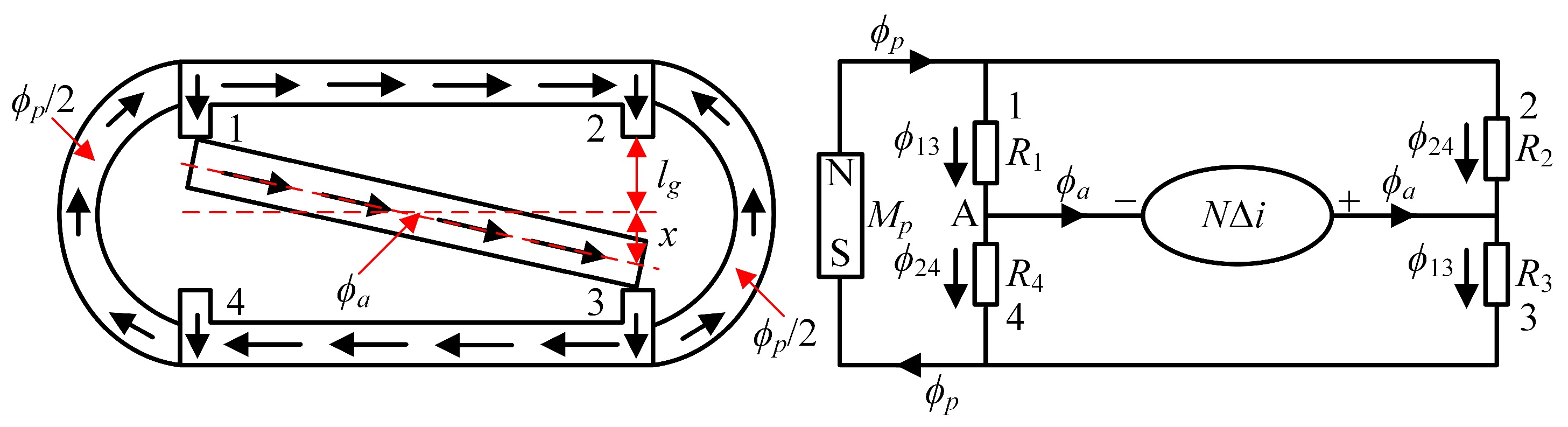
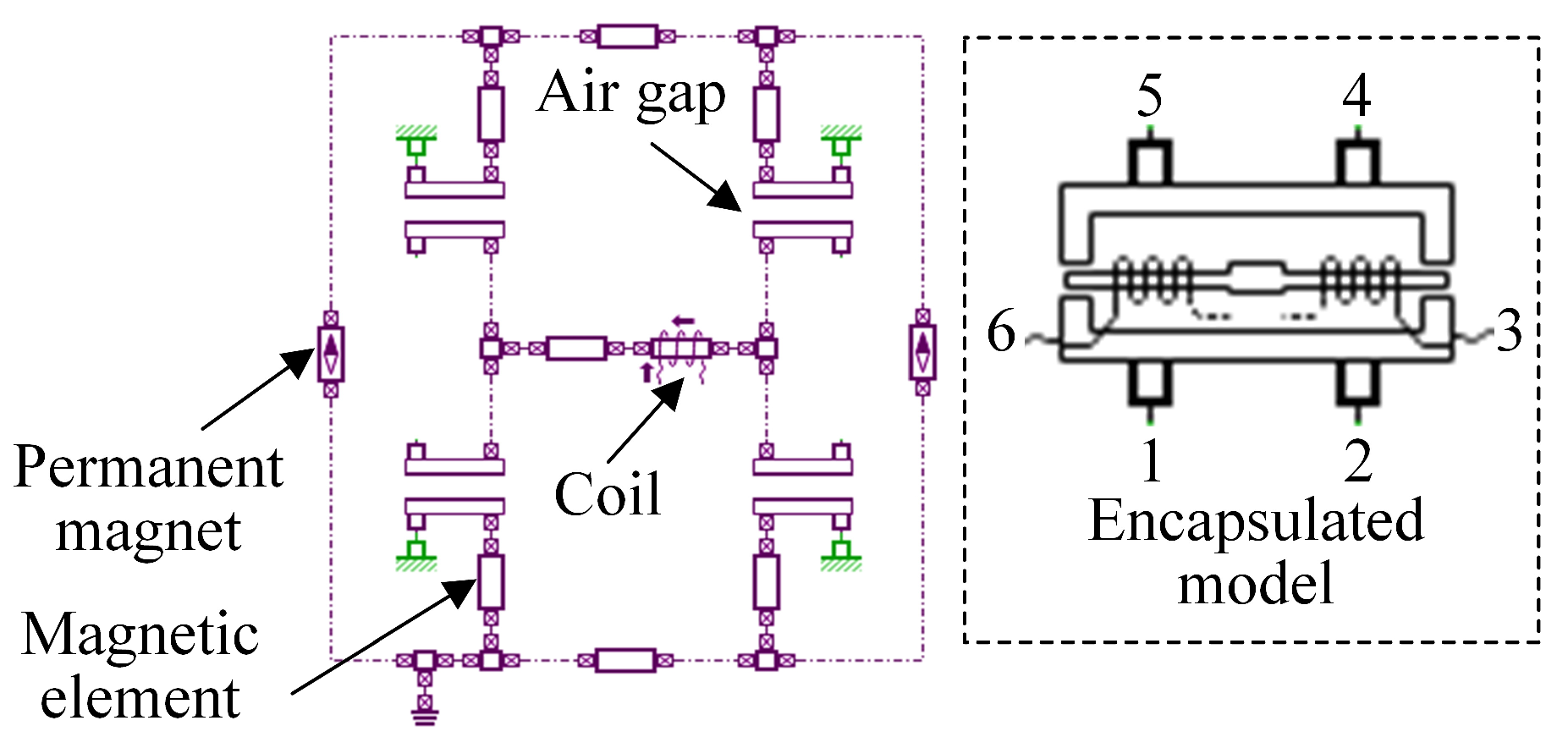
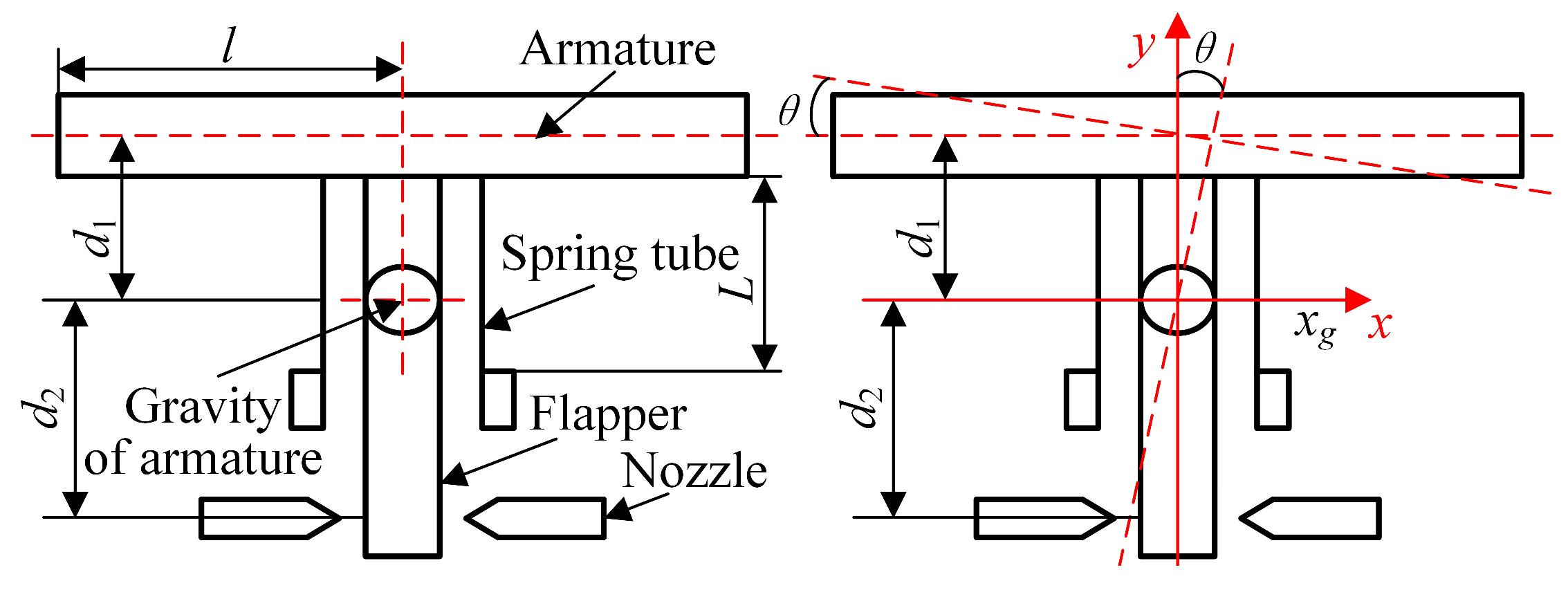
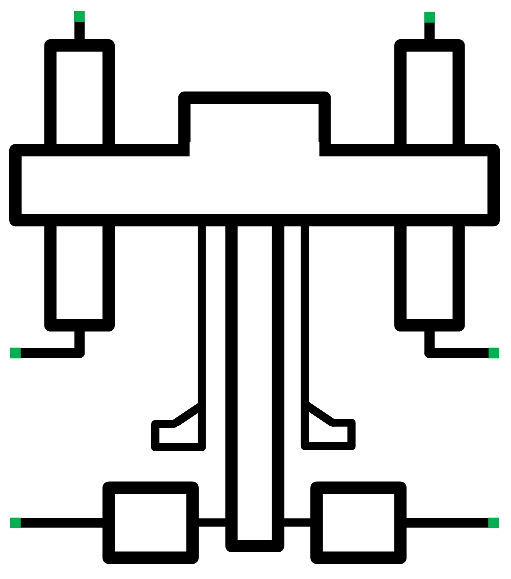

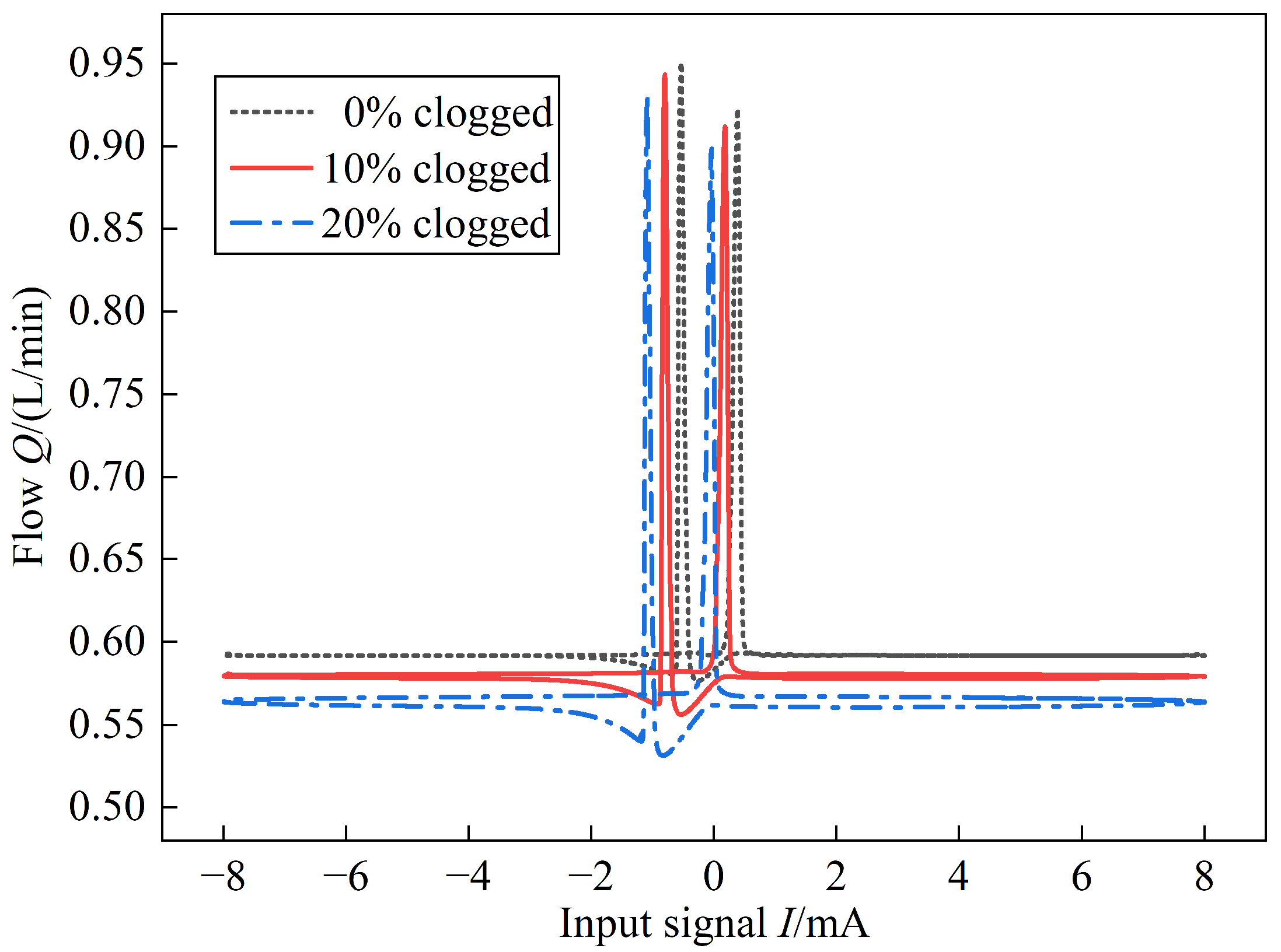

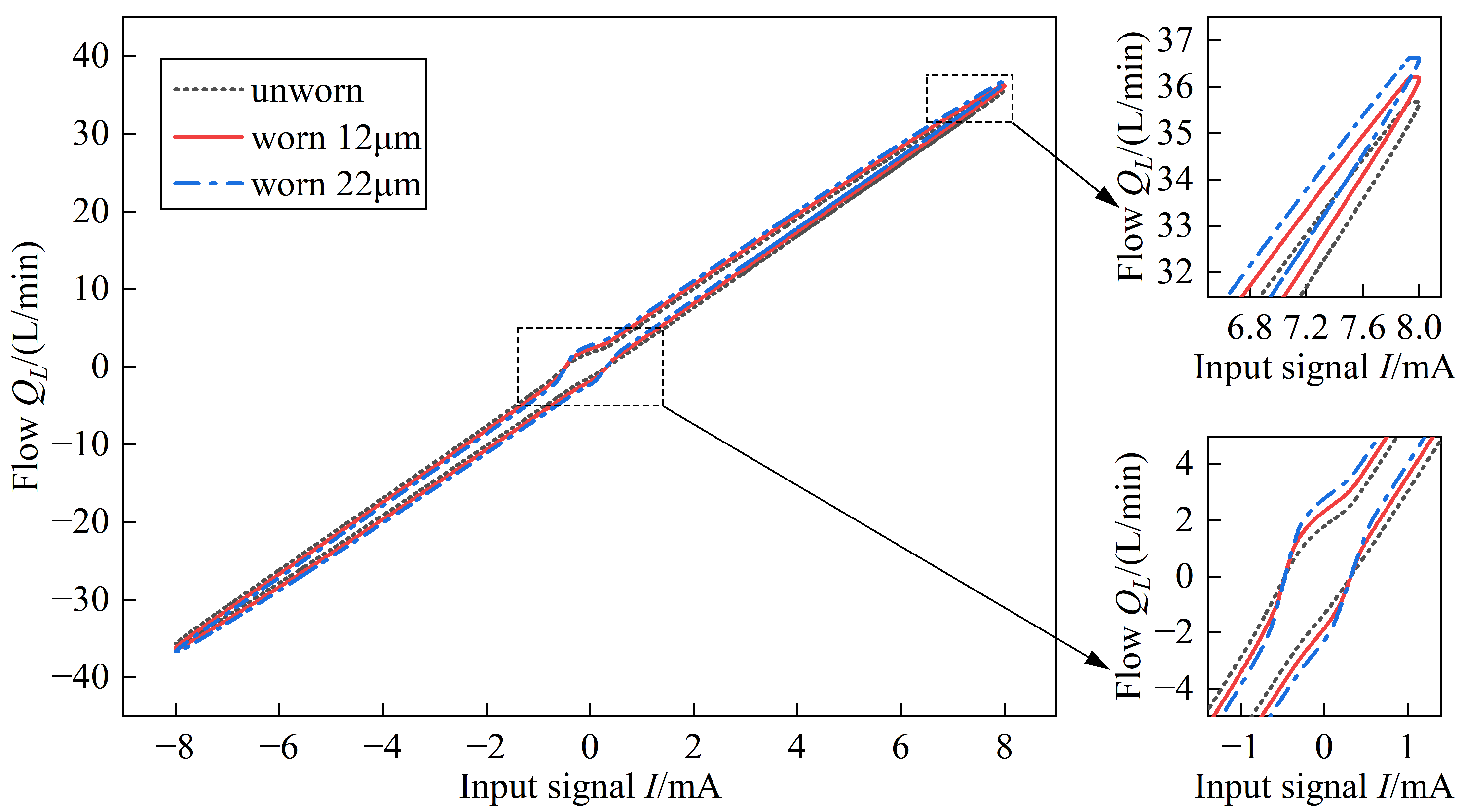
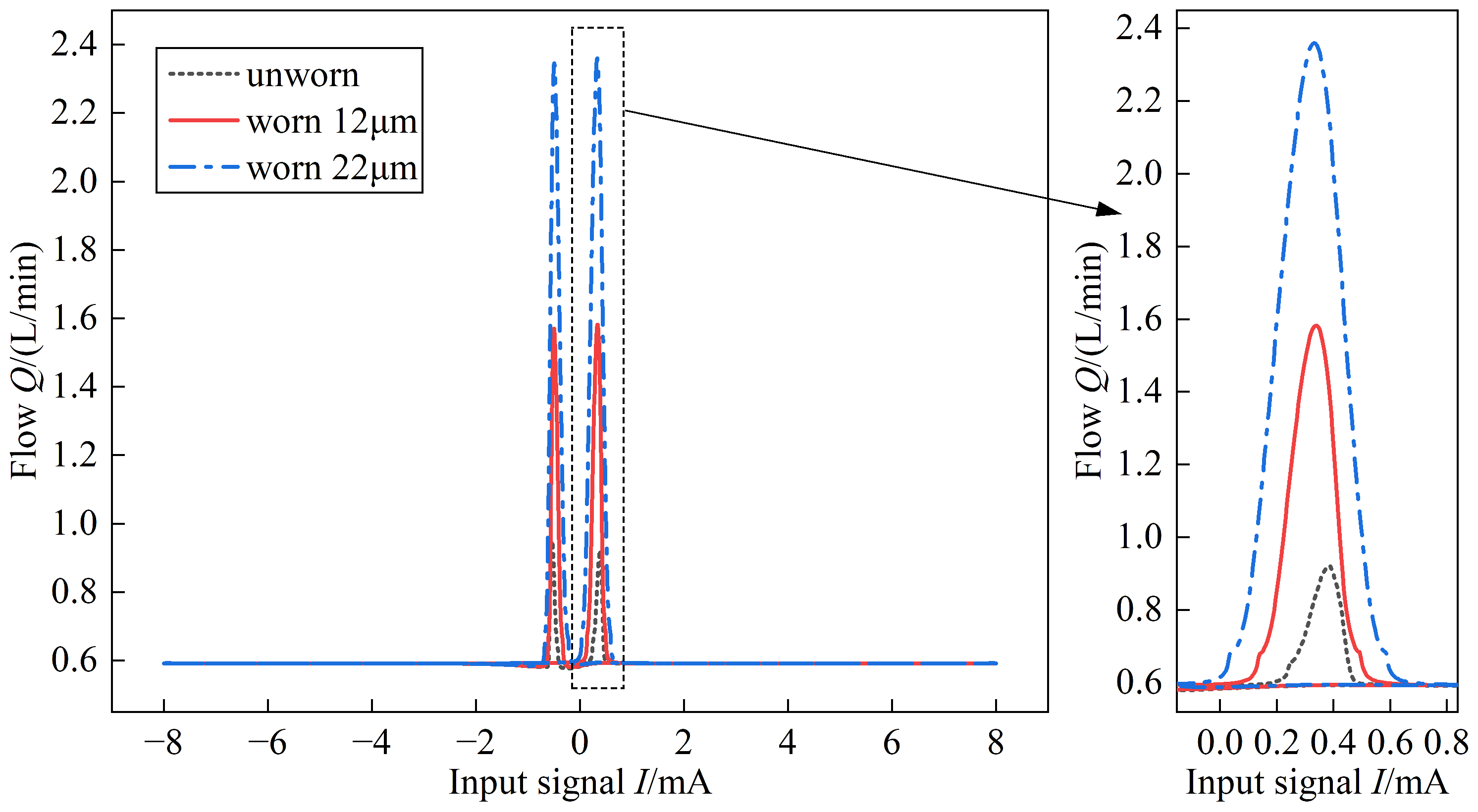
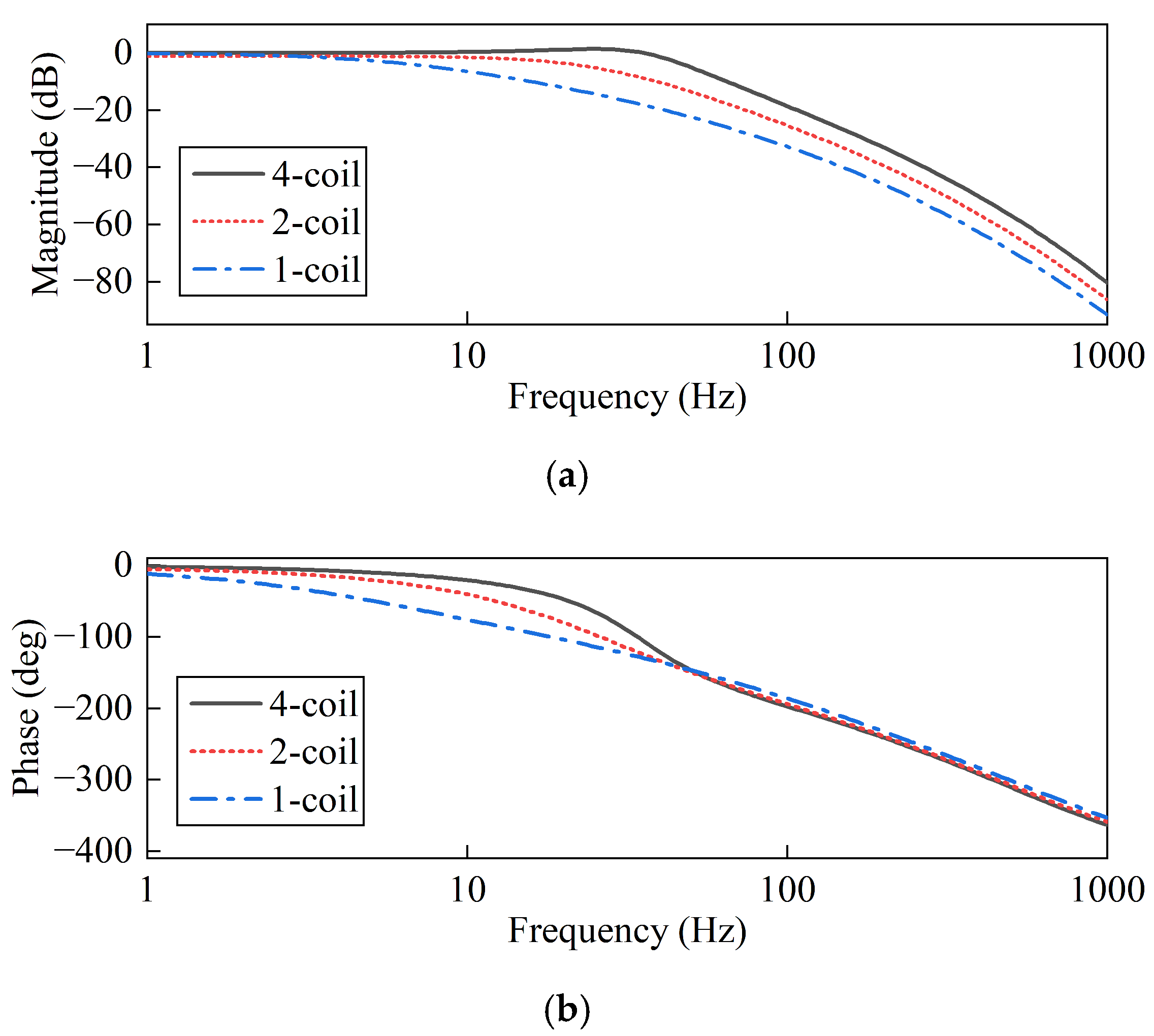

| Component | Parameter | Value |
|---|---|---|
| Air gap | Initial air gap (lg) | 0.3 mm |
| Pole area (Ag) | 15 mm2 | |
| Permanent magnet | Length of the element (lp) | 28 mm |
| Effective area of the element (Ap) | 65 mm2 | |
| Remanent induction (Bri) | 0.3 T | |
| Minimum coercive field (Hmc) | −20,000 A/m | |
| Minimum induction (Bmi) | 0.16 T | |
| Coil | Number of turns (N) | 4200 tr |
| Internal resistor | 400 Ohm |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| m | 0.0048 kg | d1 | 2.8 mm |
| J | 5.3 × 10−7 kg·m2 | d2 | 12.8 mm |
| L | 4.5 mm | br | 0.001 Nm/(rad/s) |
| E | 1.2 × 106 bar | bt | 100 N/(m/s) |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Spool diameter | 14.18 mm | Critical flow number | 100 |
| Rod diameter | 11.3 mm | Underlap corresponding to zero displacement | 0.008 mm |
| Width of a slot | 1.95 mm | Rounded corner radius | 0.007 mm |
| Depth of a slot | 0.87 mm | Clearance on diameter | 0.006 mm |
| Number of Coils | Amplitude | Phase |
|---|---|---|
| 4 | 39.835 Hz | 31.386 Hz |
| 2 | 17.983 Hz | 22.931 Hz |
| 1 | 5.497 Hz | 14.871 Hz |
| Number of Coils | Maximum Displacement | Required Time |
|---|---|---|
| 4 | 0.798 mm | 0.271 s |
| 2 | 0.797 mm | 0.278 s |
| 1 | 0.794 mm | 0.286 s |
| Different Wear Parts | Maximum Displacement | Time |
|---|---|---|
| Unworn | 58.807 mm | 0.296 s |
| System 1 worn | 58.431 mm | 0.300 s |
| All worn | 58.156 mm | 0.303 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, Q.; Wang, W.; Zhai, Y.; Sun, Y.; Zhang, W. Modeling and Fault Simulation of a New Double-Redundancy Electro-Hydraulic Servo Valve Based on AMESim. Actuators 2023, 12, 417. https://doi.org/10.3390/act12110417
Liang Q, Wang W, Zhai Y, Sun Y, Zhang W. Modeling and Fault Simulation of a New Double-Redundancy Electro-Hydraulic Servo Valve Based on AMESim. Actuators. 2023; 12(11):417. https://doi.org/10.3390/act12110417
Chicago/Turabian StyleLiang, Qiuhui, Wentao Wang, Yifei Zhai, Yanan Sun, and Wei Zhang. 2023. "Modeling and Fault Simulation of a New Double-Redundancy Electro-Hydraulic Servo Valve Based on AMESim" Actuators 12, no. 11: 417. https://doi.org/10.3390/act12110417
APA StyleLiang, Q., Wang, W., Zhai, Y., Sun, Y., & Zhang, W. (2023). Modeling and Fault Simulation of a New Double-Redundancy Electro-Hydraulic Servo Valve Based on AMESim. Actuators, 12(11), 417. https://doi.org/10.3390/act12110417






