Performance Analysis of Magnetorheological Damper with Folded Resistance Gaps and Bending Magnetic Circuit
Abstract
:1. Introduction
2. Design of the Proposed MR Damper
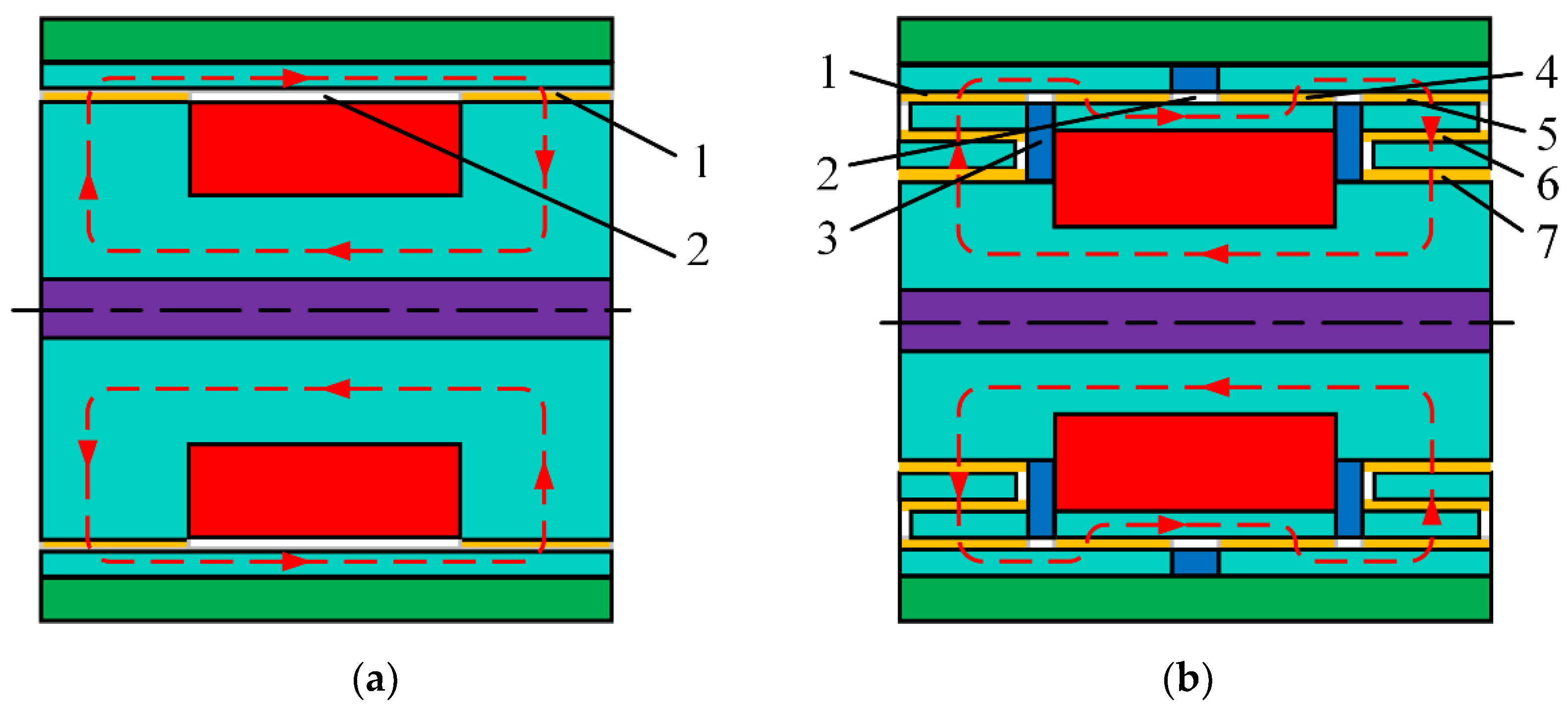
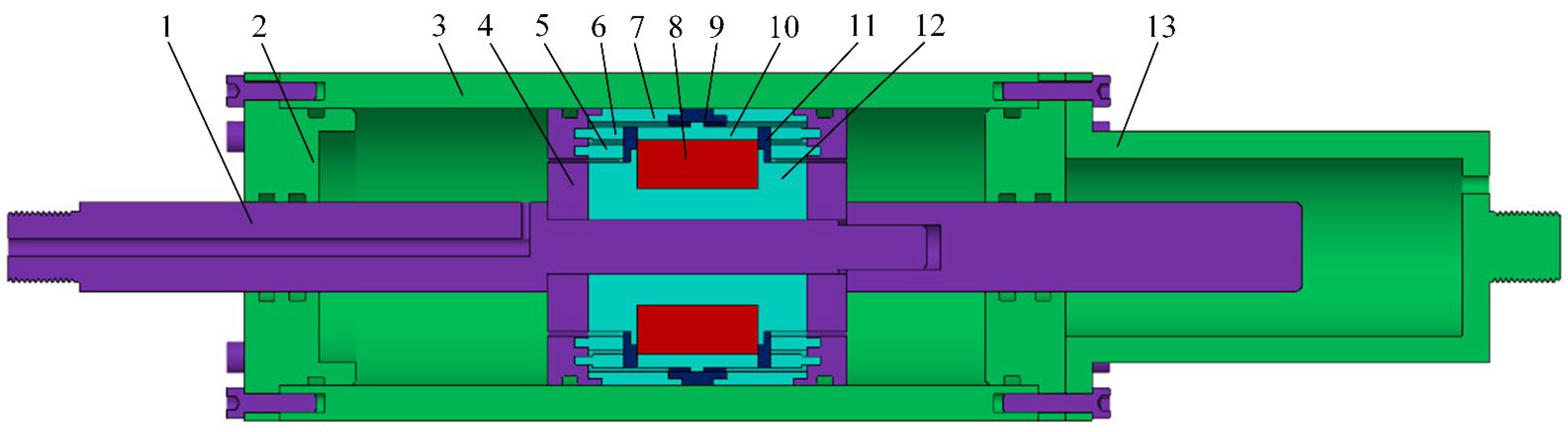
2.1. Structural Principle and Design
2.2. Magnetic Circuit of the Developed MR Damper
2.3. Design of Main Structural Dimensions
3. Mathematic Modeling of the Proposed MR Damper
4. Modeling and Simulation Analysis
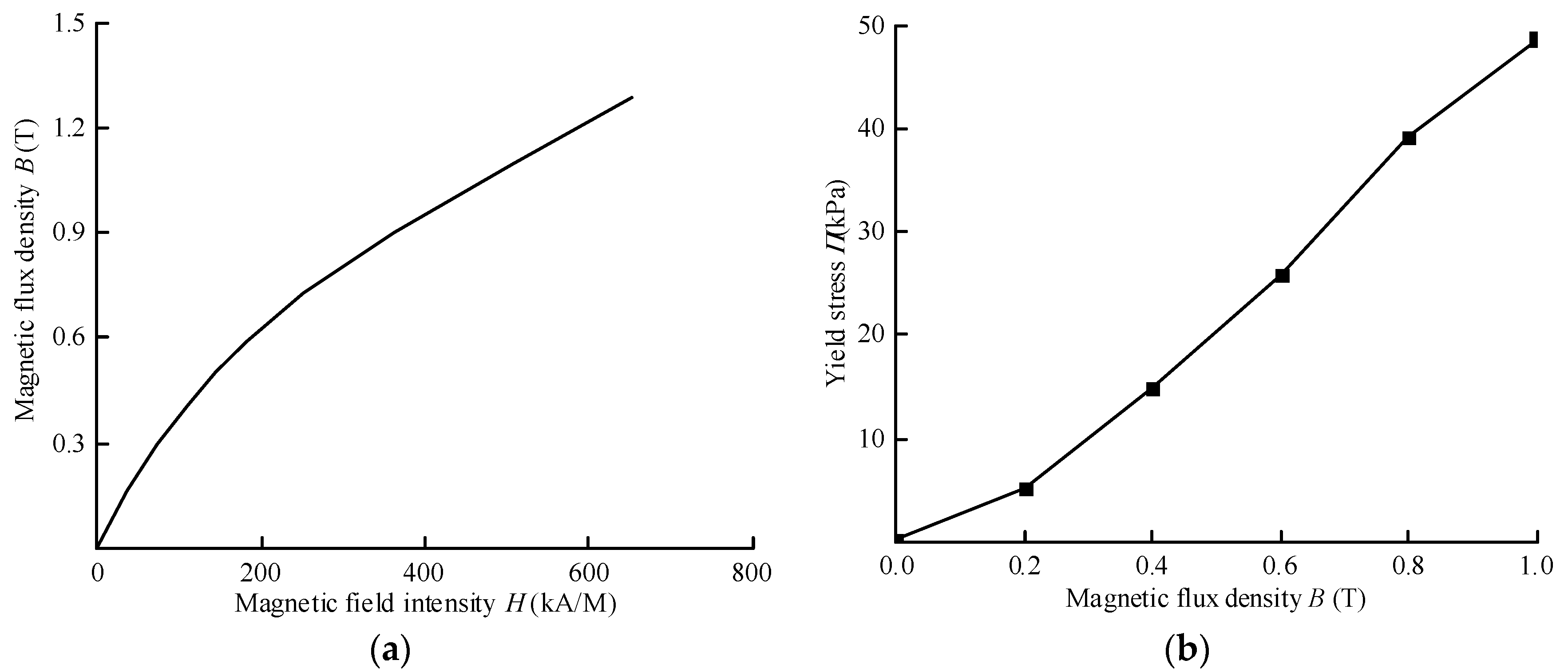
4.1. Properties of the MR Fluid
4.2. Finite Element Analysis
5. Experimental Analysis and Discussions
5.1. Prototype and Test System Setup
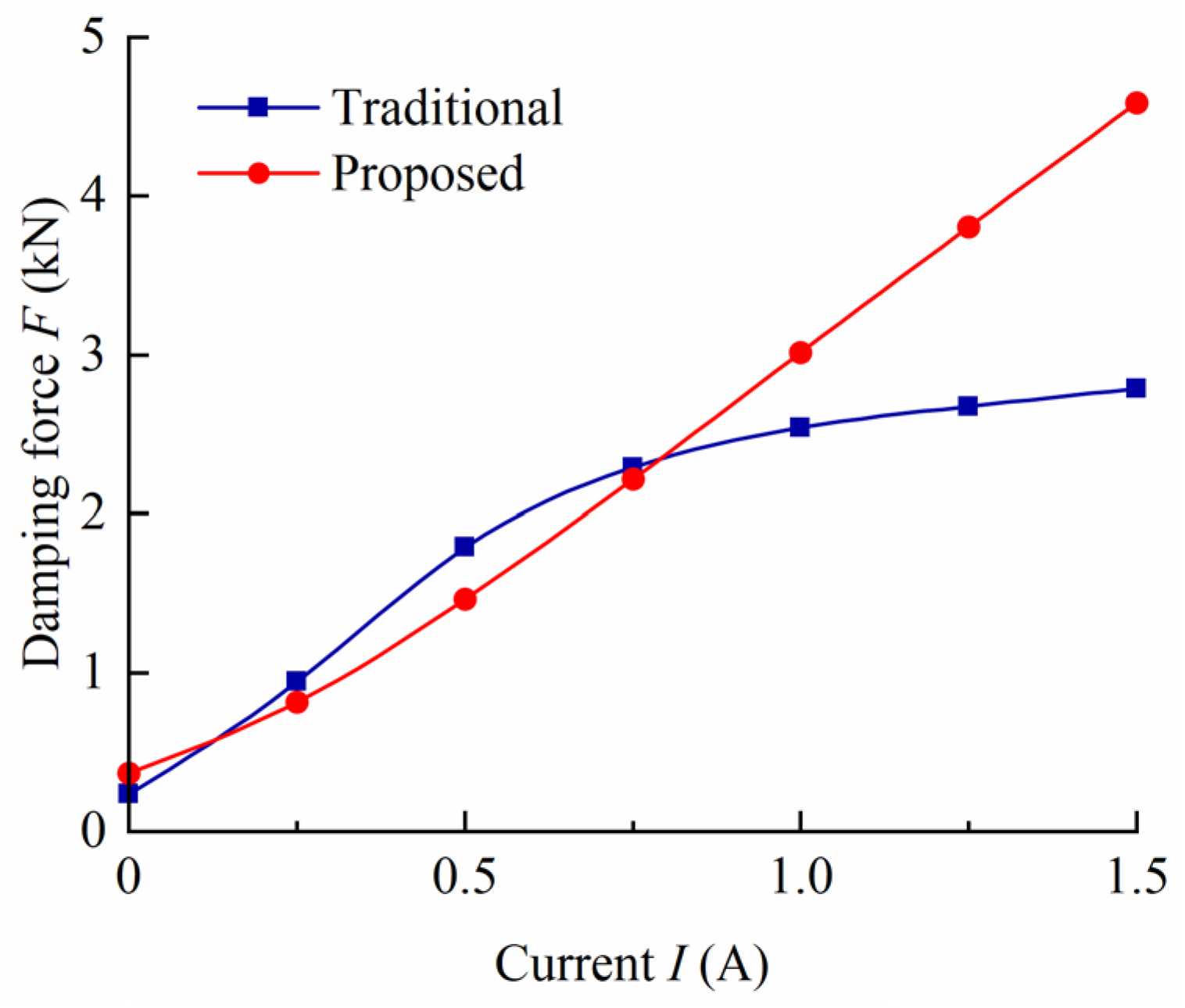
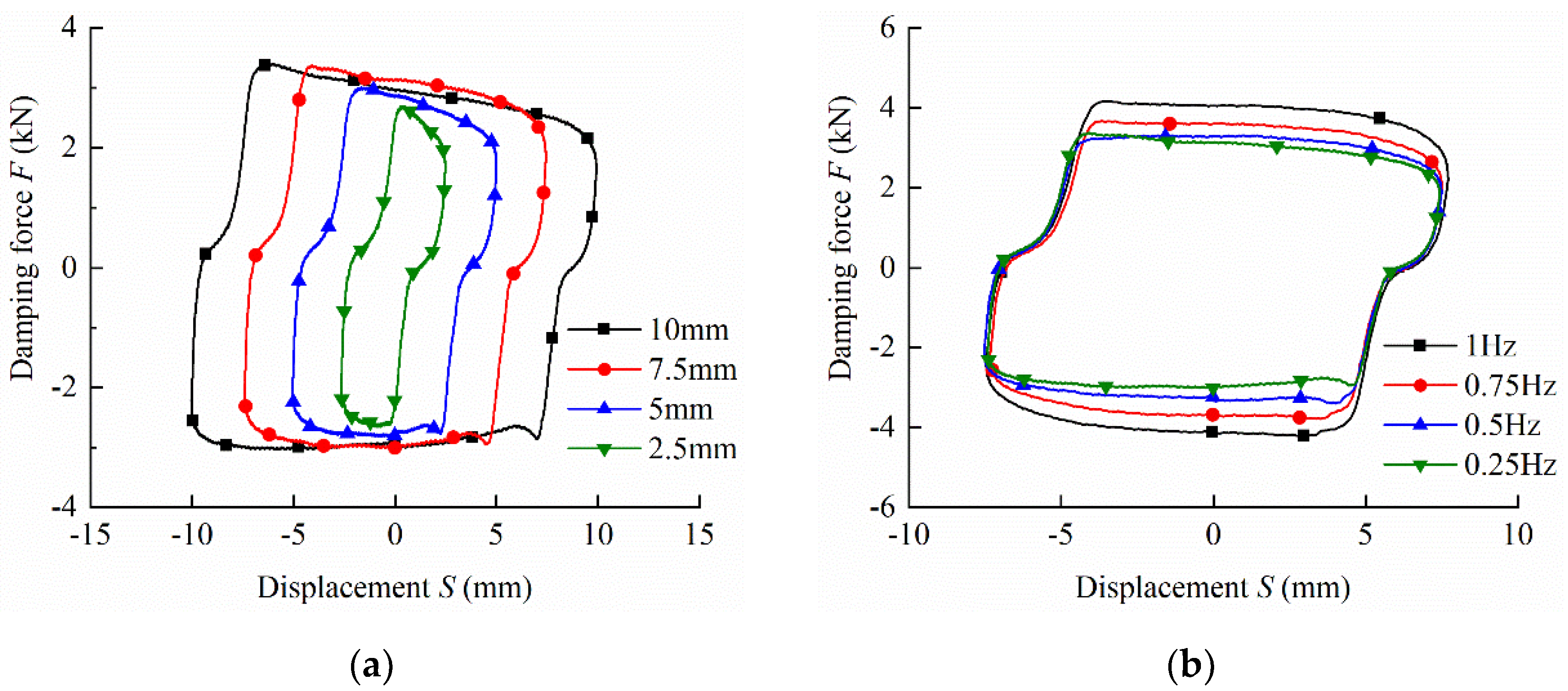
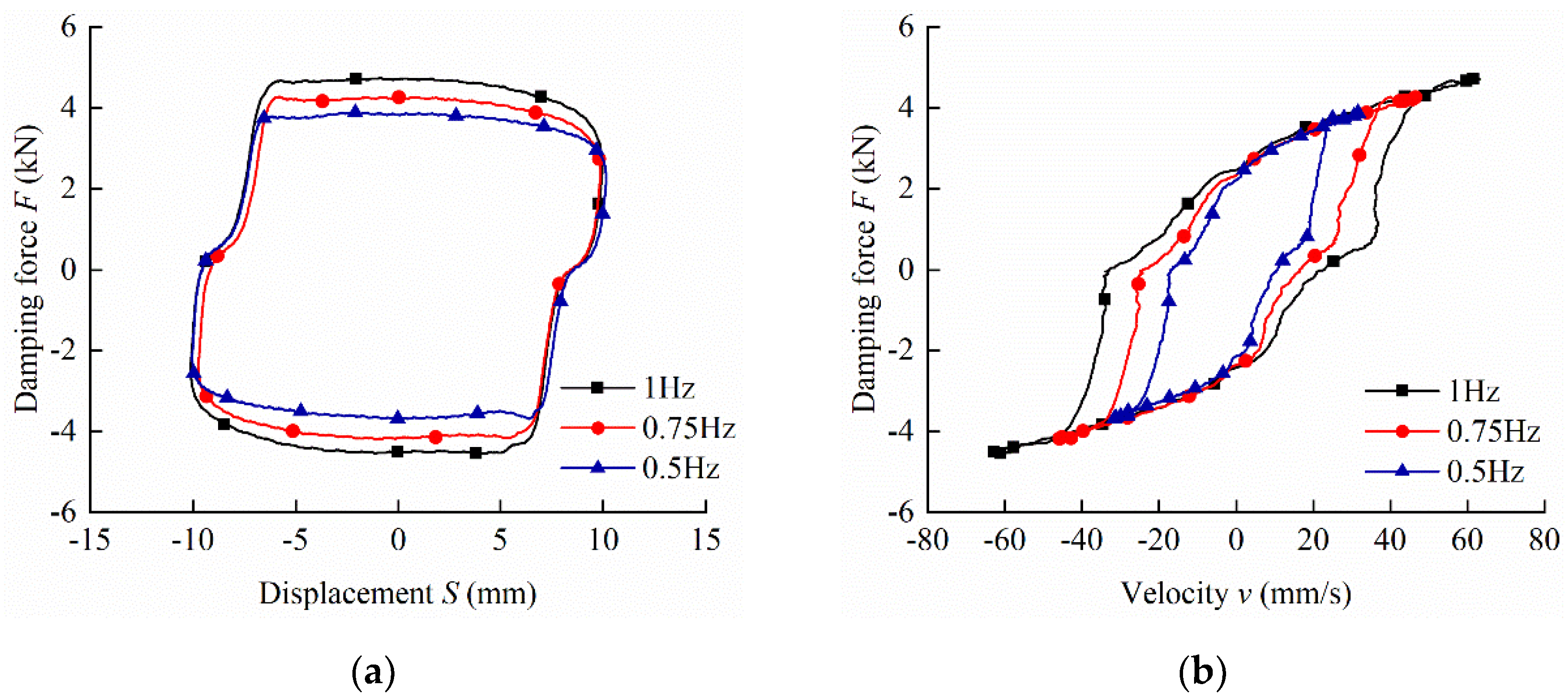
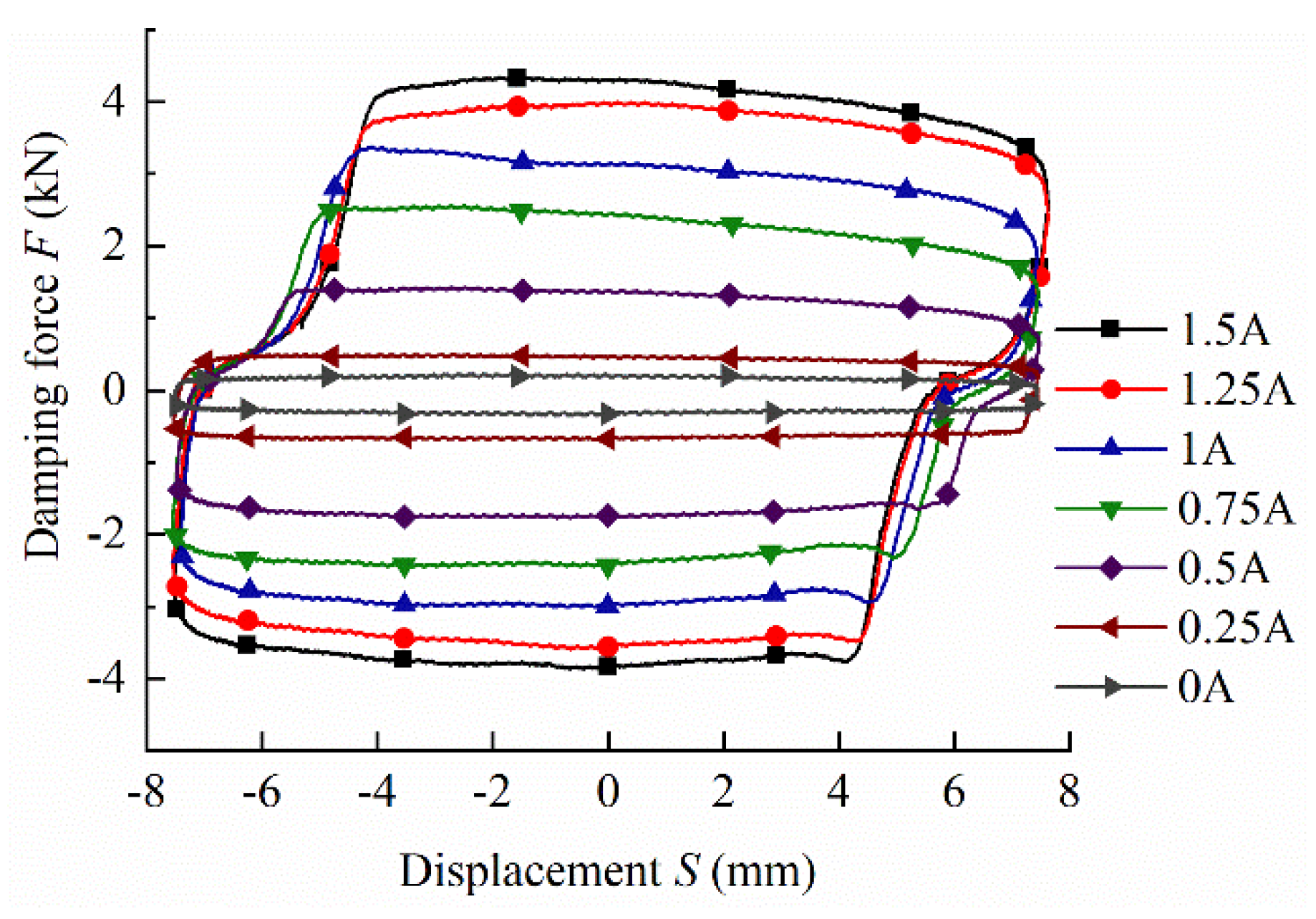
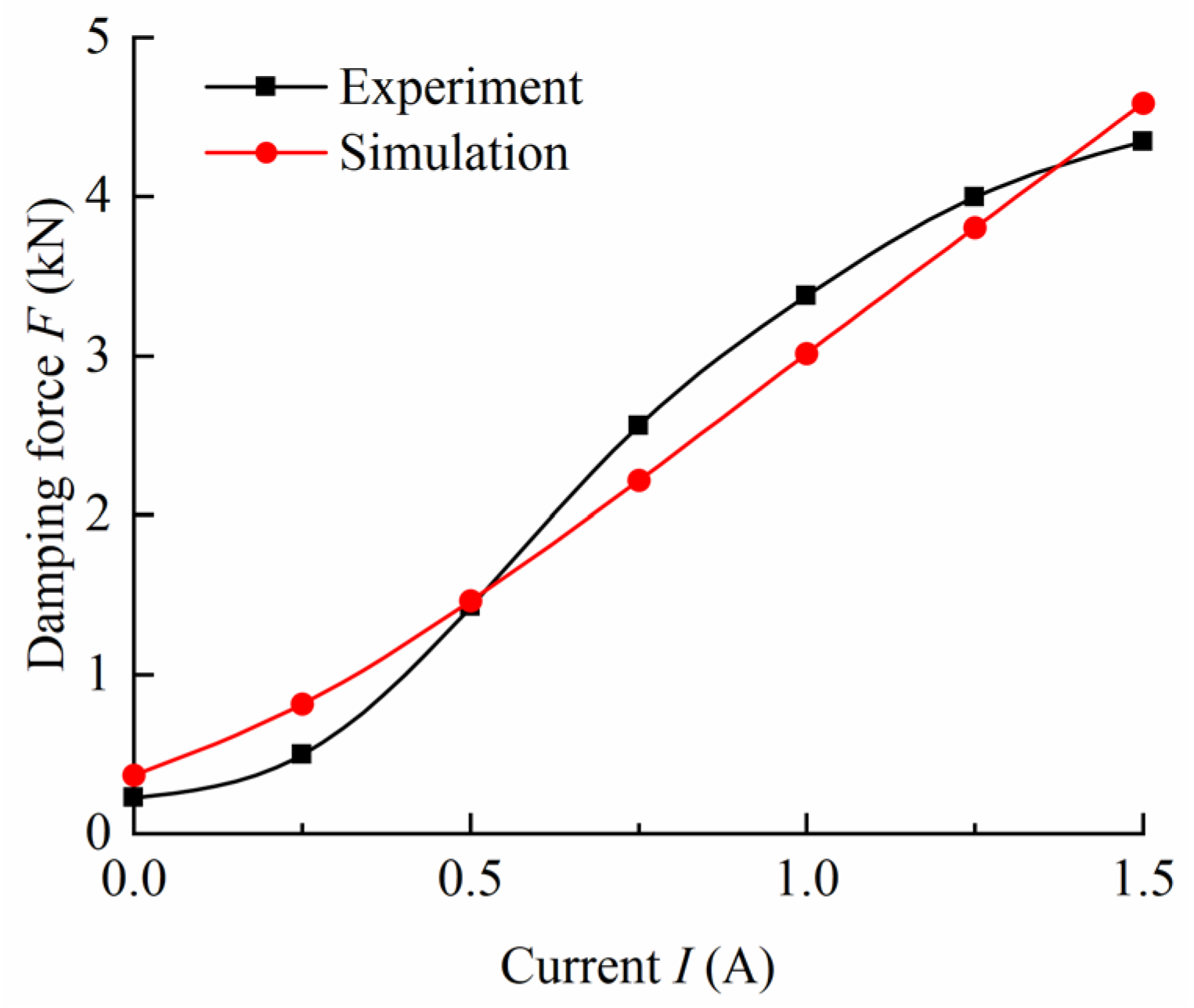
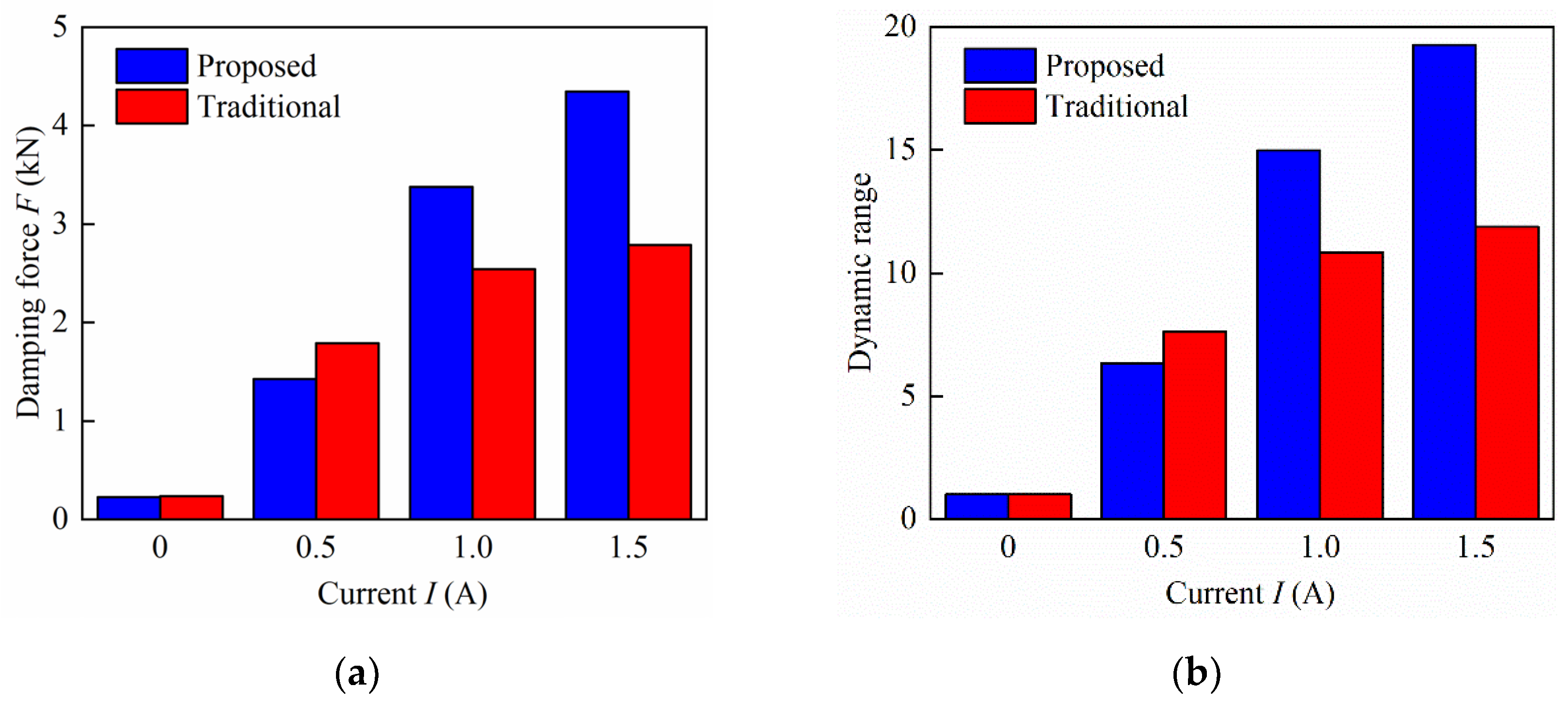
5.2. Damping Performance Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Deng, Z.X.; Wei, X.X.; Li, X.Q.; Zhao, S.E.; Zhu, S.K. Design and multi-objective optimization of magnetorheological damper considering vehicle riding comfort and operation stability. J. Intell. Mater. Syst. Struct. 2021, 10, 1215–1228. [Google Scholar] [CrossRef]
- Yang, J.; Ning, D.; Sun, S.S.; Zheng, J.; Lu, H.; Nakano, M.; Zhang, S.; Du, H.; Li, W.H. A semi-active suspension using a magnetorheological damper with nonlinear negative-stiffness component. Mech. Syst. Signal Process. 2021, 147, 107071. [Google Scholar] [CrossRef]
- Tang, X.; Du, H.P.; Sun, S.S.; Ning, D.H.; Xing, Z.W.; Li, W.H. Takagi-sugeno fuzzy control for semi-active vehicle suspension with a magnetorheological damper and experimental validation. IEEE Asme Trans. Mechatron. 2017, 22, 291–300. [Google Scholar] [CrossRef]
- Hu, G.L.; Wu, L.F.; Deng, Y.J.; Yu, L.F.; Luo, B. Damping performance analysis of magnetorheological damper based on multiphysics coupling. Actuators 2021, 10, 176. [Google Scholar] [CrossRef]
- Xu, Z.D.; Xu, Y.W.; Wang, C.; Zhao, Y.L.; Ji, B.H.; Du, Y.L. Force tracking model and experimental verification on a novel magnetorheological damper with combined compensator for stay cables of bridge. Structures 2021, 32, 1971–1985. [Google Scholar] [CrossRef]
- He, M.; Zheng, Z.P.; He, B.; Zhu, H. Optimising intelligent control of a highway bridge with magnetorheological dampers. Proc. Inst. Civ. Eng. Struct. Build. 2020, 173, 210–216. [Google Scholar] [CrossRef]
- Bhaiya, V.; Bharti, S.D.; Shrimali, M.K.; Datta, T.K. Hybrid seismic control of buildings using tuned mass and magnetorheological dampers. Proc. Inst. Civ. Eng. Struct. Build. 2020, 173, 471–487. [Google Scholar] [CrossRef]
- Luong, Q.V.; Jang, D.S.; Hwang, J.H. Semi-active control for a helicopter with multiple landing gears equipped with magnetorheological dampers. Appl. Sci. Basel 2021, 11, 3667. [Google Scholar] [CrossRef]
- Wang, C.; Nie, H.; Chen, J.B.; Lee, H.P. The design and dynamic analysis of a lunar lander with semi-active control. Acta Astronaut. 2019, 157, 145–156. [Google Scholar] [CrossRef]
- Wang, C.; Chen, J.B.; Li, X.L.; Chen, H.; Nie, H.; Lin, F. Design, dynamic analysis, and experiments of mrf dampers for lunar landers. Adv. Space Res. 2021, 68, 3012–3025. [Google Scholar] [CrossRef]
- Huber, M.; Eschbach, M.; Kazerounian, K.; Ilies, H. Functional evaluation of a personalized orthosis for knee osteoarthritis: A motion capture analysis. J. Med. Devices Trans. Asme 2021, 15, 041003. [Google Scholar] [CrossRef]
- Zuo, Q.; Zhao, J.P.; Mei, X.; Yi, F.; Hu, G.L. Design and trajectory tracking control of a magnetorheological prosthetic knee joint. Appl. Sci. Basel 2021, 11, 8305. [Google Scholar] [CrossRef]
- Lv, H.Z.; Sun, Q.; Zhang, W.J. A comparative study of four parametric hysteresis models for magnetorheological dampers. Actuators 2021, 10, 257. [Google Scholar] [CrossRef]
- Rossi, A.; Orsini, F.; Scorza, A.; Botta, F.; Belfiore, N.P.; Sciuto, S.A. A review on parametric dynamic models of magnetorheological dampers and their characterization methods. Actuators 2018, 7, 16. [Google Scholar] [CrossRef] [Green Version]
- Zhu, X.C.; Jing, X.J.; Cheng, L. Magnetorheological fluid dampers: A review on structure design and analysis. J. Intell. Mater. Syst. Struct. 2012, 23, 839–873. [Google Scholar] [CrossRef]
- Hu, G.L.; Zhang, J.W.; Zhong, F.; Yu, L.F. Performance evaluation of an improved radial magnetorheological valve and its application in the valve controlled cylinder system. Smart Mater. Struct. 2019, 28, 047003. [Google Scholar] [CrossRef]
- Ioan, B. Damper with magnetorheological suspension. J. Magn. Magn. Mater. 2002, 241, 196–200. [Google Scholar]
- Ioan, B. Magnetorheological suspension electromagnetic brake. J. Magn. Magn. Mater. 2004, 270, 321–326. [Google Scholar]
- Bai, X.X.; Hu, W.; Wereley, N.M. Magnetorheological damper utilizing an inner bypass for ground vehicle suspensions. IEEE Trans. Magn. 2013, 49, 3422–3425. [Google Scholar] [CrossRef]
- Hu, G.L.; Liu, F.S.; Xie, Z.; Xu, M. Design, analysis, and experimental evaluation of a double coil magnetorheological fluid damper. Shock. Vib. 2016, 2016, 4184726. [Google Scholar] [CrossRef]
- Aydar, G.; Wang, X.; Gordaninejad, F. A novel two-way-controllable magneto-rheological fluid damper. Smart Mater. Struct. 2010, 19, 065024. [Google Scholar]
- Cheng, M.; Chen, Z.B.; Xing, J.W. Design, analysis, and experimental evaluation of a magnetorheological damper with meandering magnetic circuit. IEEE Trans. Magn. 2018, 54, 1–10. [Google Scholar] [CrossRef]
- Idris, M.H.; Imaduddin, F.; Ubaidillah, U.; Mazlan, S.A.; Choi, S.B. A concentric design of a bypass magnetorheological fluid damper with a serpentine flux valve. Actuators 2020, 9, 16. [Google Scholar] [CrossRef] [Green Version]
- Yazid, I.I.M.; Mazlan, S.A.; Kikuchi, T.; Zamzuri, H.; Imaduddin, F. Design of magnetorheological damper with a combination of shear and squeeze modes. Mater. Des. (1980–2015) 2014, 54, 87–95. [Google Scholar] [CrossRef]
- Mughni, M.J.; Zeinali, M.; Mazlan, S.A.; Zamzuri, H.; Abdul Rahman, M.A. Experiments and modeling of a new magnetorheological cell under combination of flow and shear-flow modes. J. Non-Newton. Fluid Mech. 2015, 215, 70–79. [Google Scholar] [CrossRef]
- Ruan, X.; Xuan, S.; Zhao, J.; Bian, H.; Gong, X. Mechanical performance of a novel magnetorheological fluid damper based on squeeze-valve bi-mode of mrf. Smart Mater. Struct. 2020, 29, 055018. [Google Scholar] [CrossRef]
- Zhu, S.; Tang, L.; Liu, J.; Tang, X.; Liu, X. A novel design of magnetorheological damper with annular radial channel. Shock. Vib. 2016, 2016, 8086504. [Google Scholar] [CrossRef] [Green Version]
- Liao, C.R.; Zhao, D.X.; Xie, L.; Liu, Q. A design methodology for a magnetorheological fluid damper based on a multi-stage radial flow mode. Smart Mater. Struct. 2012, 21, 085005. [Google Scholar]
- Bai, X.X.; Wang, D.H.; Fu, H. Principle, modeling, and testing of an annular-radial-duct magnetorheological damper. Sens. Actuators A Phys. 2013, 201, 302–309. [Google Scholar] [CrossRef]
- Wang, M.; Chen, Z.; Wereley, N.M. Magnetorheological damper design to improve vibration mitigation under a volume constraint. Smart Mater. Struct. 2019, 28, 114003. [Google Scholar] [CrossRef]
- Mao, M.; Hu, W.; Choi, Y.T.; Wereley, N.M. A magnetorheological damper with bifold valves for shock and vibration mitigation. J. Intell. Mater. Syst. Struct. 2016, 18, 1227–1232. [Google Scholar] [CrossRef]
- Kim, K.; Chen, Z.; Yu, D.; Rim, C. Design and experiments of a novel magneto-rheological damper featuring bifold flow mode. Smart Mater. Struct. 2016, 25, 075004. [Google Scholar] [CrossRef]
- Hu, G.L.; Qi, H.N.; Chen, M.; Yu, L.F.; Li, G.; Zheng, H. Optimal design of magnetorheological damper with multiple axial fluid flow channels using bp neural network and particle swarm optimization methodologies. Int. J. Appl. Electromagn. Mech. 2021, 67, 339–360. [Google Scholar] [CrossRef]
- Hu, G.; Liu, H.; Duan, J.; Yu, L. Damping performance analysis of magnetorheological damper with serial-type flow channels. Adv. Mech. Eng. 2019, 11, 1687814018816842. [Google Scholar] [CrossRef] [Green Version]
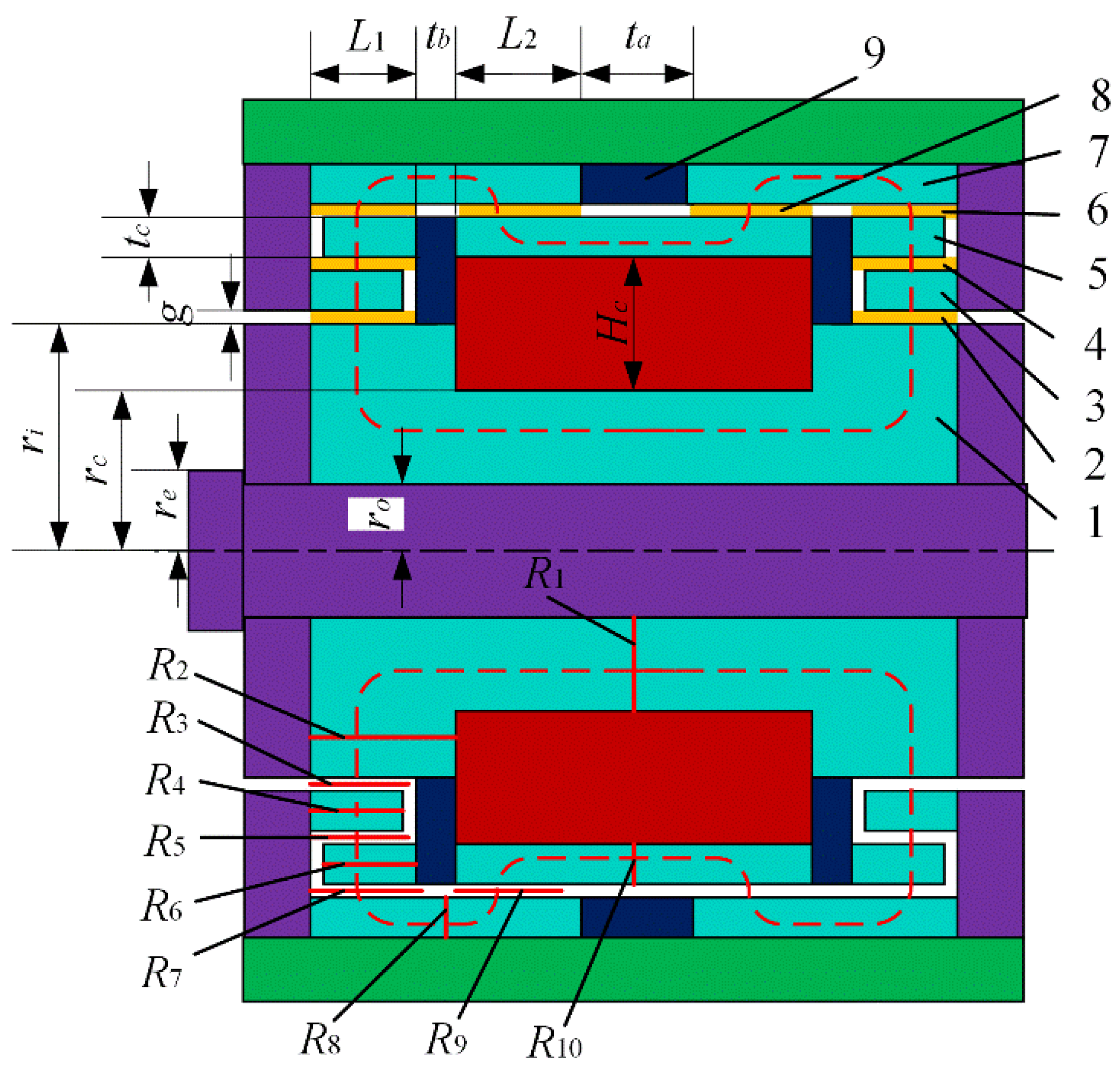
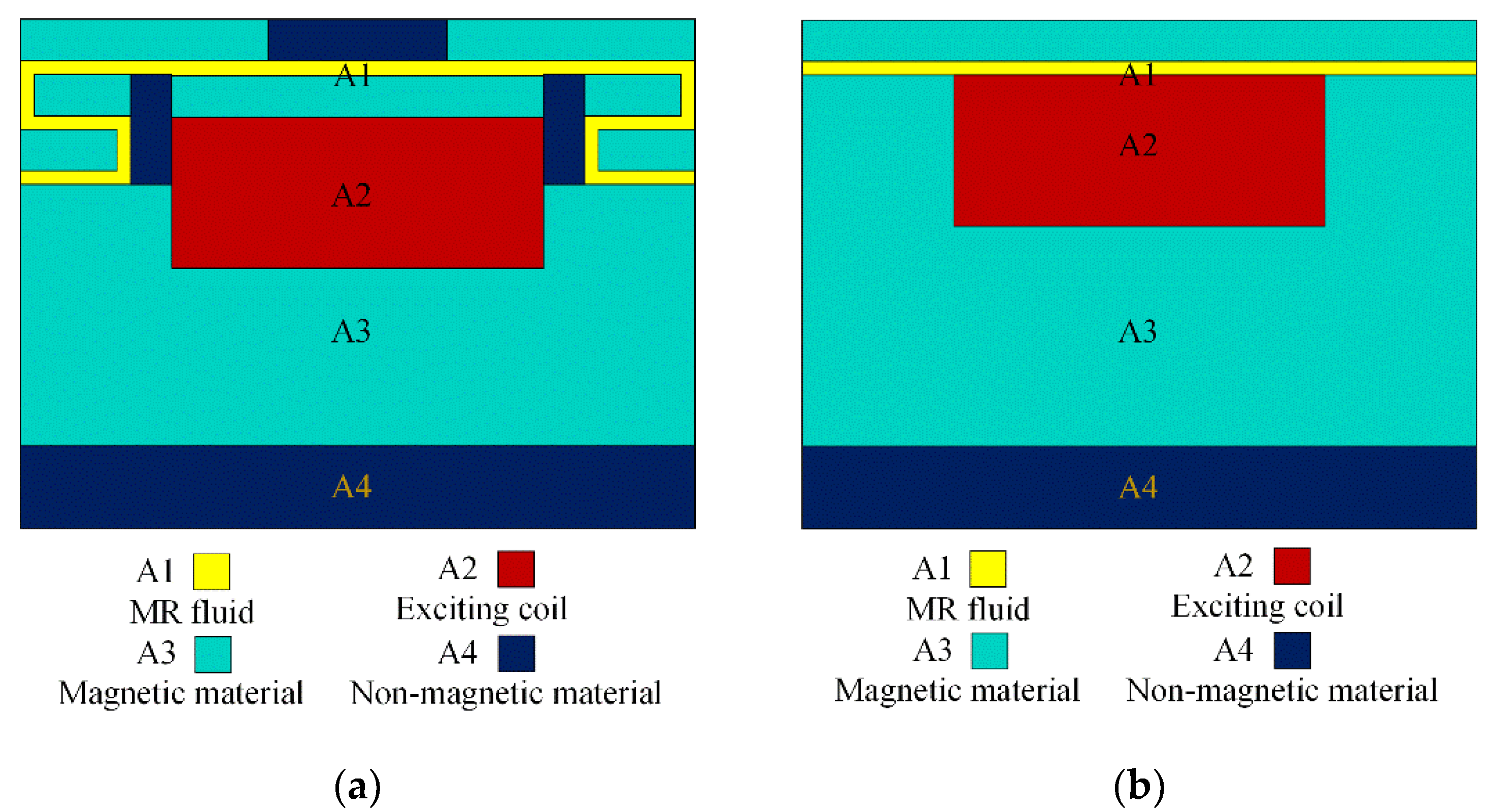
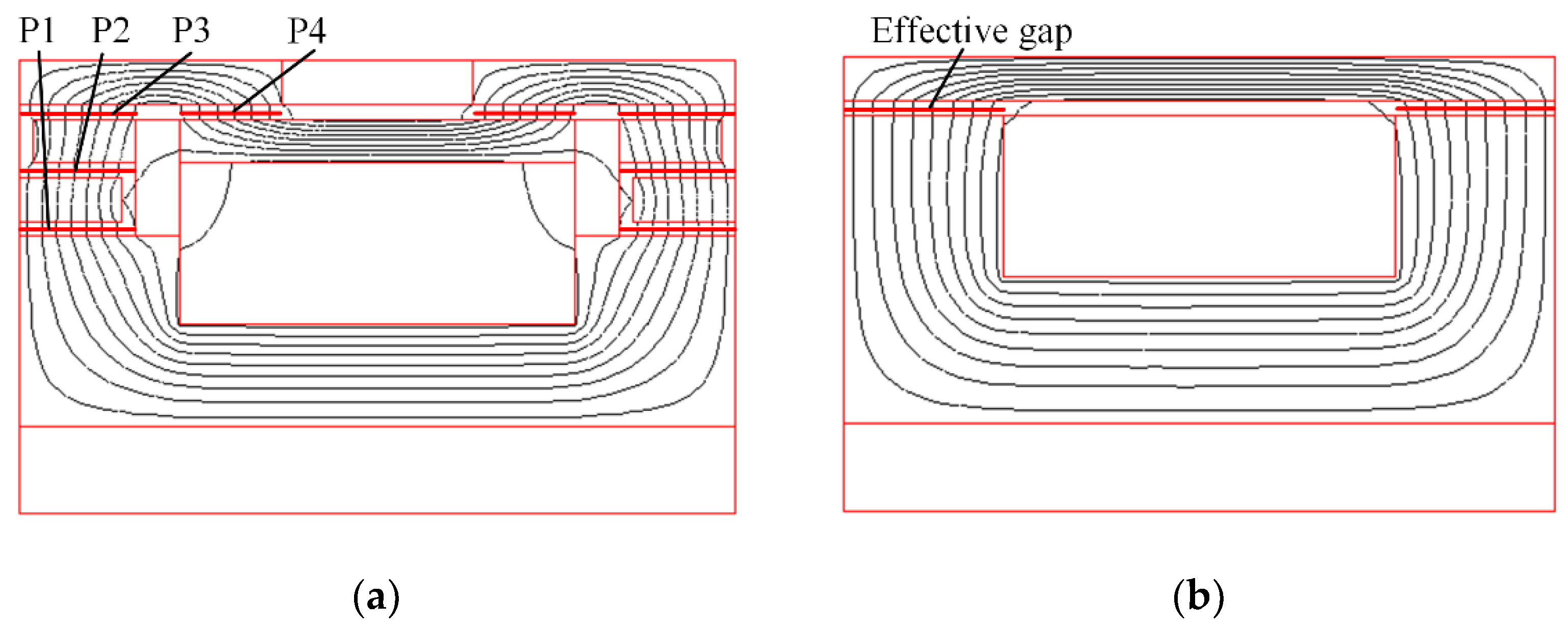
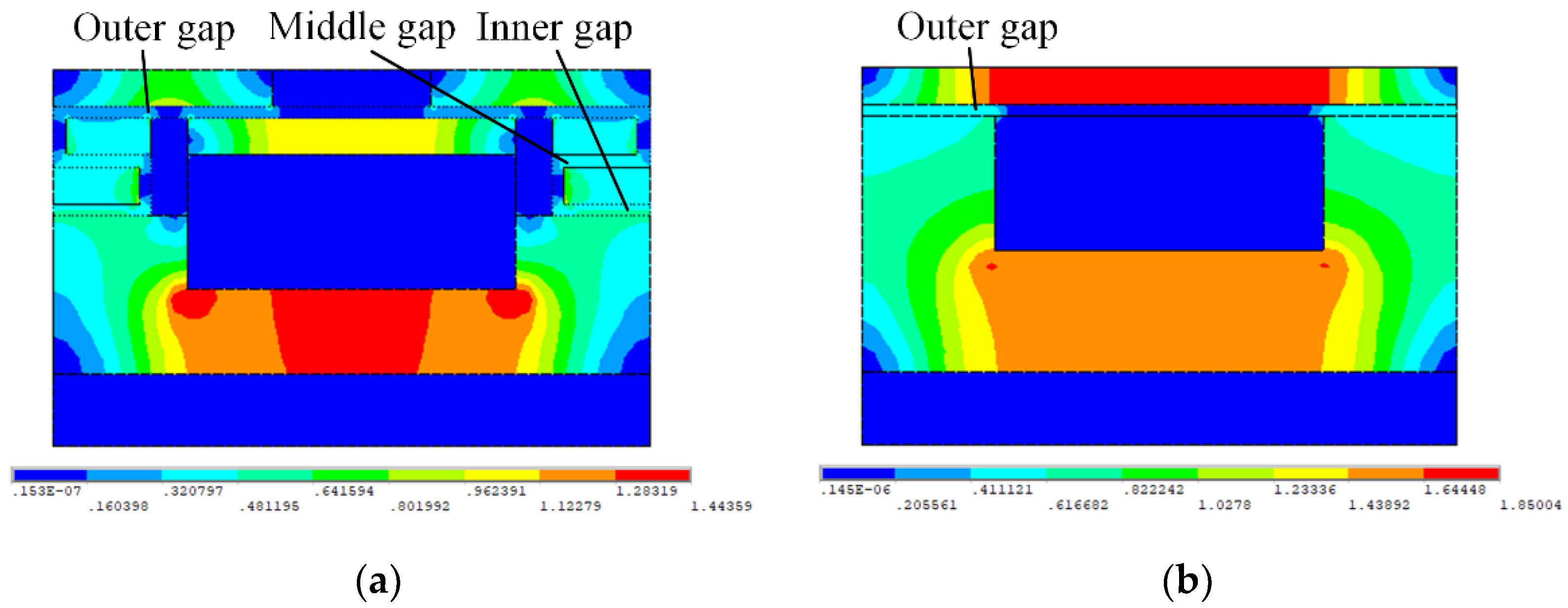
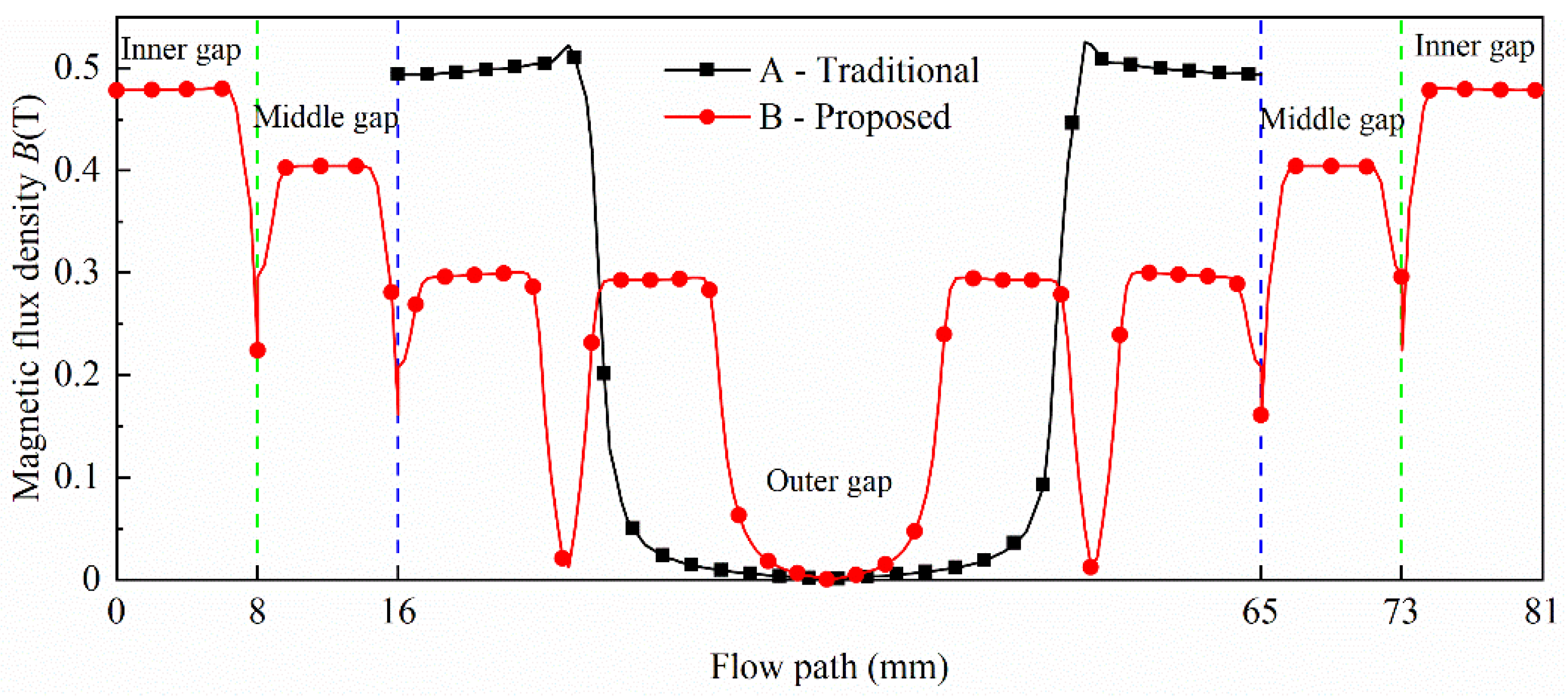
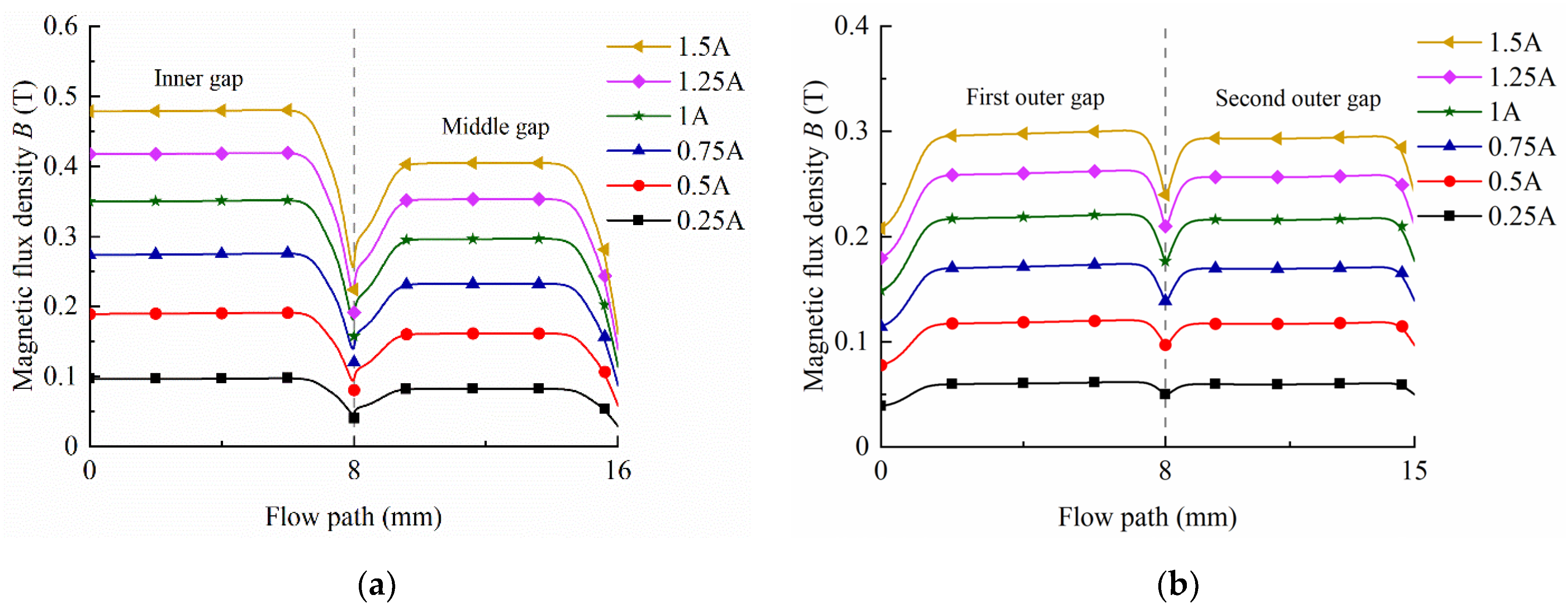
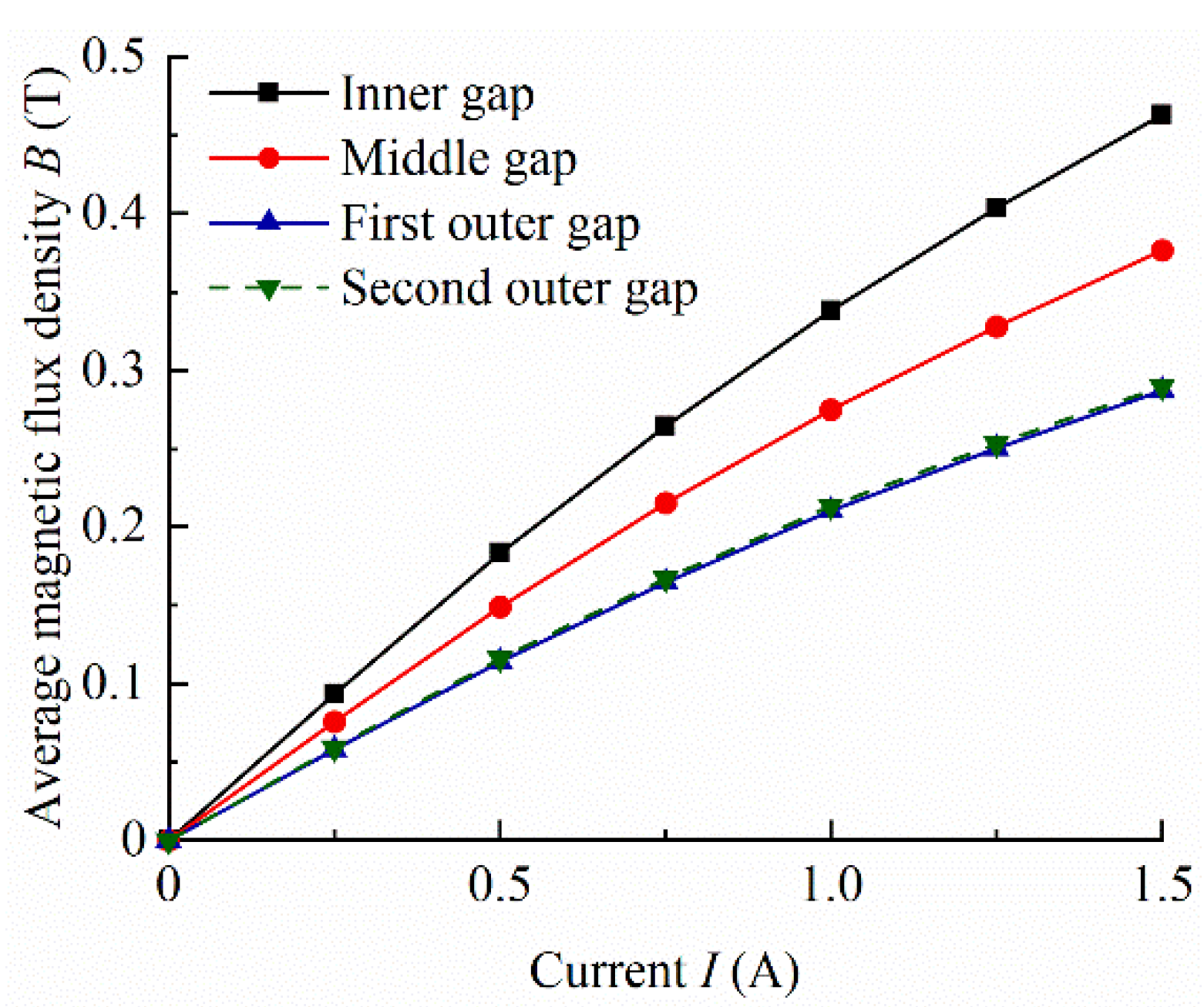


| Parameter | Value (mm) | Parameter | Value (mm) |
|---|---|---|---|
| Inside radius of piston rod (ro) | 7 | Length of first outer gap (L1) | 8 |
| External radius of core (rc) | 13 | Length of second outer gap (L2) | 7 |
| Radius of piston (rp) | 31 | Length of non-magnetic ring (ta) | 13 |
| Radius of inner gap (ri) | 19 | Thickness of non-magnetic disk (tb) | 3 |
| External radius of piston rod (rd) | 10 | Thickness of sleeve (tc) | 3 |
| Thickness of gap (g) | 1 | Height of exciting coil (Hc) | 11 |
| MR Damper | Radius of Piston (mm) | Maximum Positive Damping Force (N) | Damping Force Per Unit Volume (kN/m3) | Dynamic Range |
|---|---|---|---|---|
| Traditional MR damper | 31 | 2789 | 2.4 × 104 | 11.8 |
| MR damper in Reference [32] | 35.7 | 5486 | 2.92 × 104 | 7 |
| Proposed MR damper | 31 | 4346 | 2.93 × 104 | 19.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Xu, Y.; Zhou, F.; Hu, G.; Yu, L. Performance Analysis of Magnetorheological Damper with Folded Resistance Gaps and Bending Magnetic Circuit. Actuators 2022, 11, 165. https://doi.org/10.3390/act11060165
Liu L, Xu Y, Zhou F, Hu G, Yu L. Performance Analysis of Magnetorheological Damper with Folded Resistance Gaps and Bending Magnetic Circuit. Actuators. 2022; 11(6):165. https://doi.org/10.3390/act11060165
Chicago/Turabian StyleLiu, Leping, Yinan Xu, Feng Zhou, Guoliang Hu, and Lifan Yu. 2022. "Performance Analysis of Magnetorheological Damper with Folded Resistance Gaps and Bending Magnetic Circuit" Actuators 11, no. 6: 165. https://doi.org/10.3390/act11060165
APA StyleLiu, L., Xu, Y., Zhou, F., Hu, G., & Yu, L. (2022). Performance Analysis of Magnetorheological Damper with Folded Resistance Gaps and Bending Magnetic Circuit. Actuators, 11(6), 165. https://doi.org/10.3390/act11060165






