Control-Force Spectrum Considering Both Natural Period and Damping Ratio for Active Base-Isolated Building
Abstract
1. Introduction
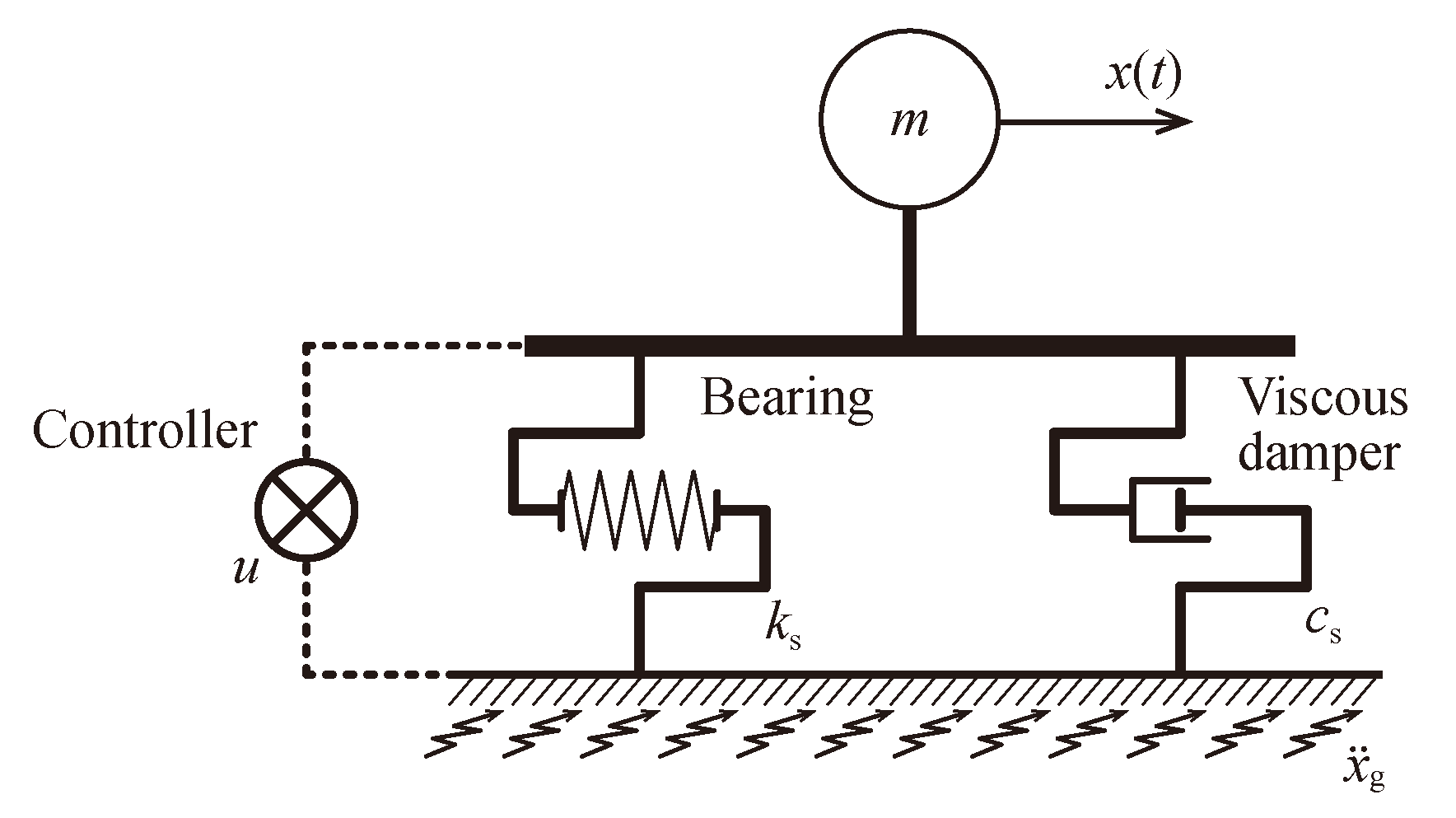
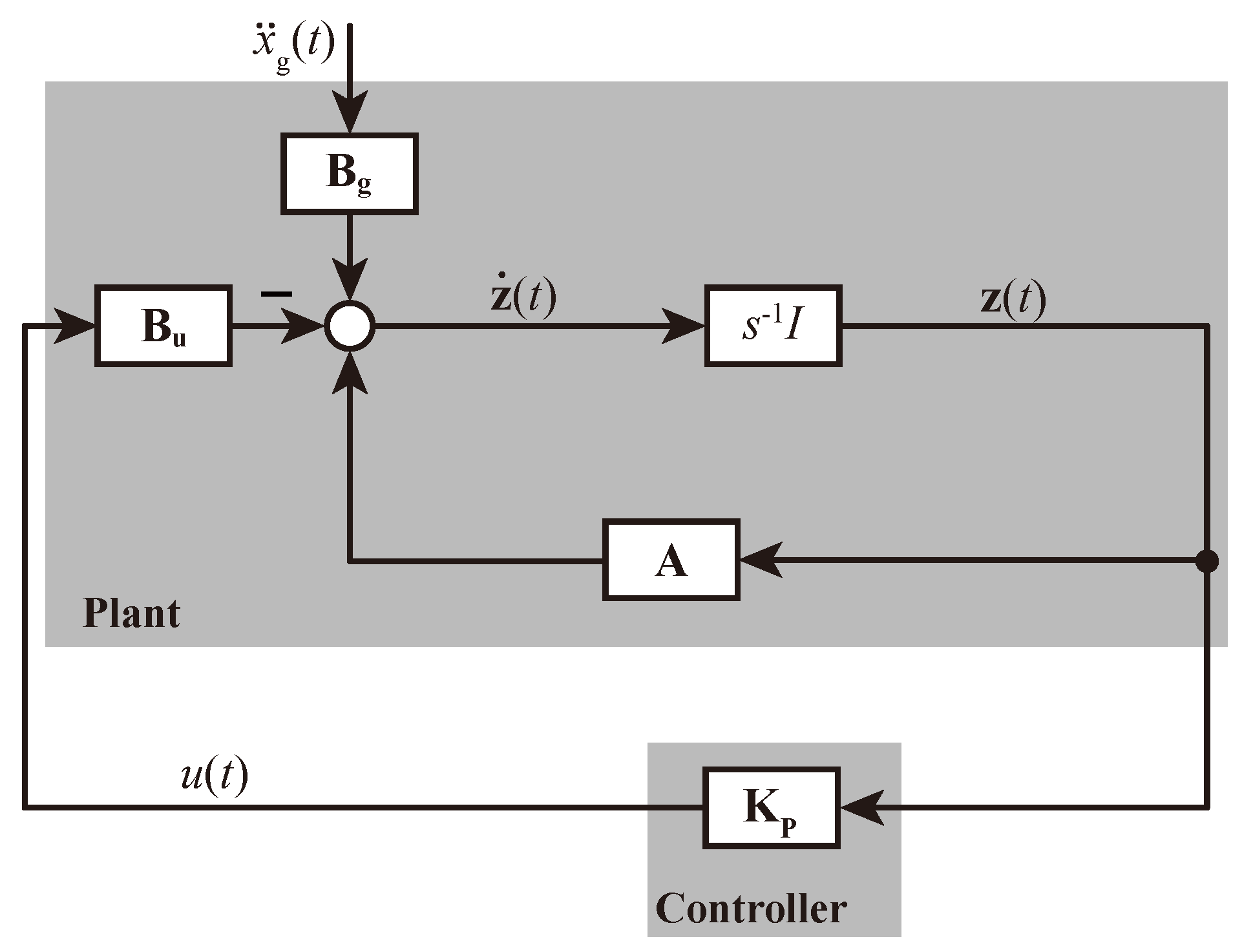
2. Mathematic Model
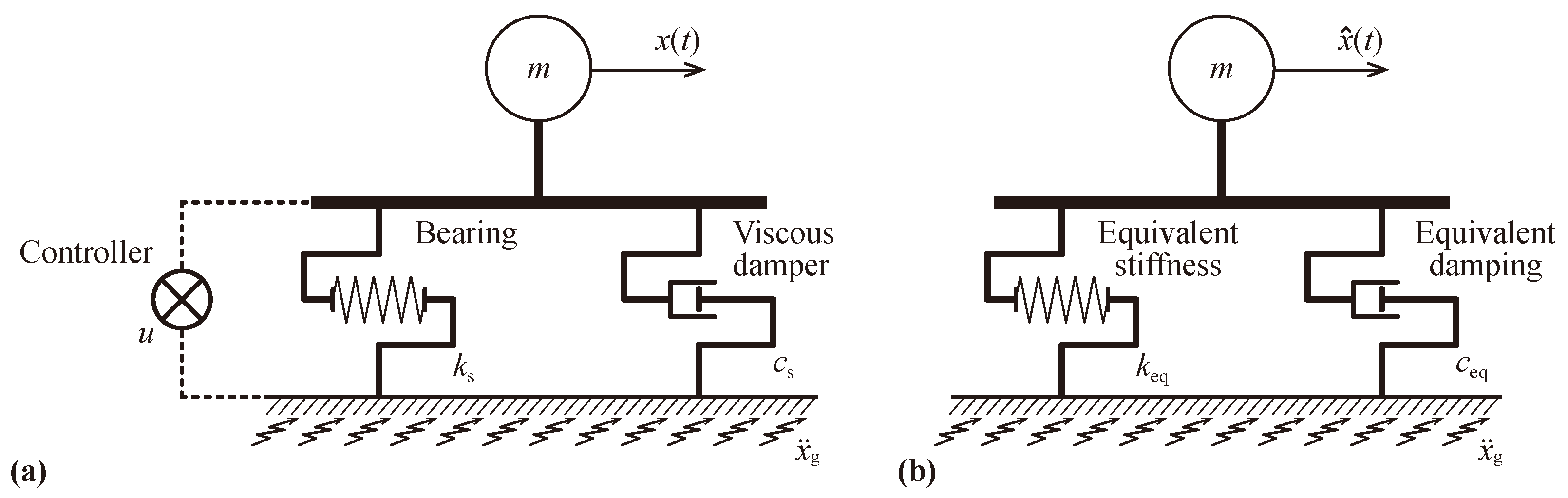
3. Equivalent Model
4. Control-Force Spectrum
4.1. Derivation of the Control-Force Spectrum
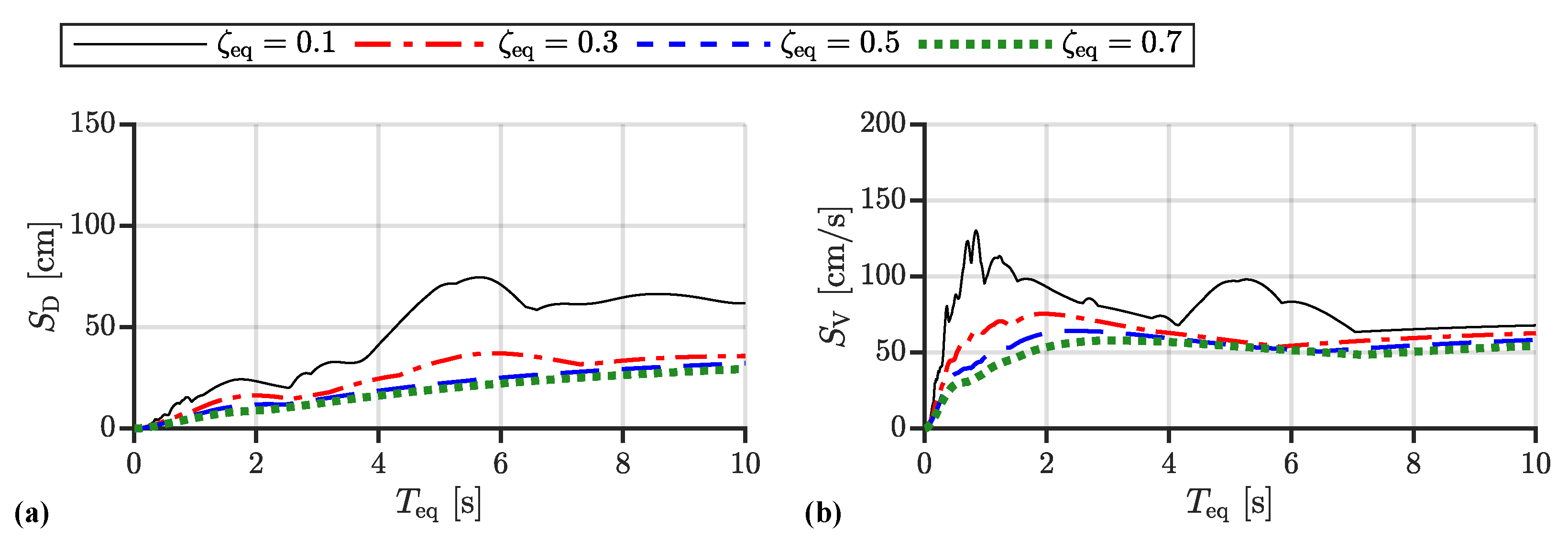
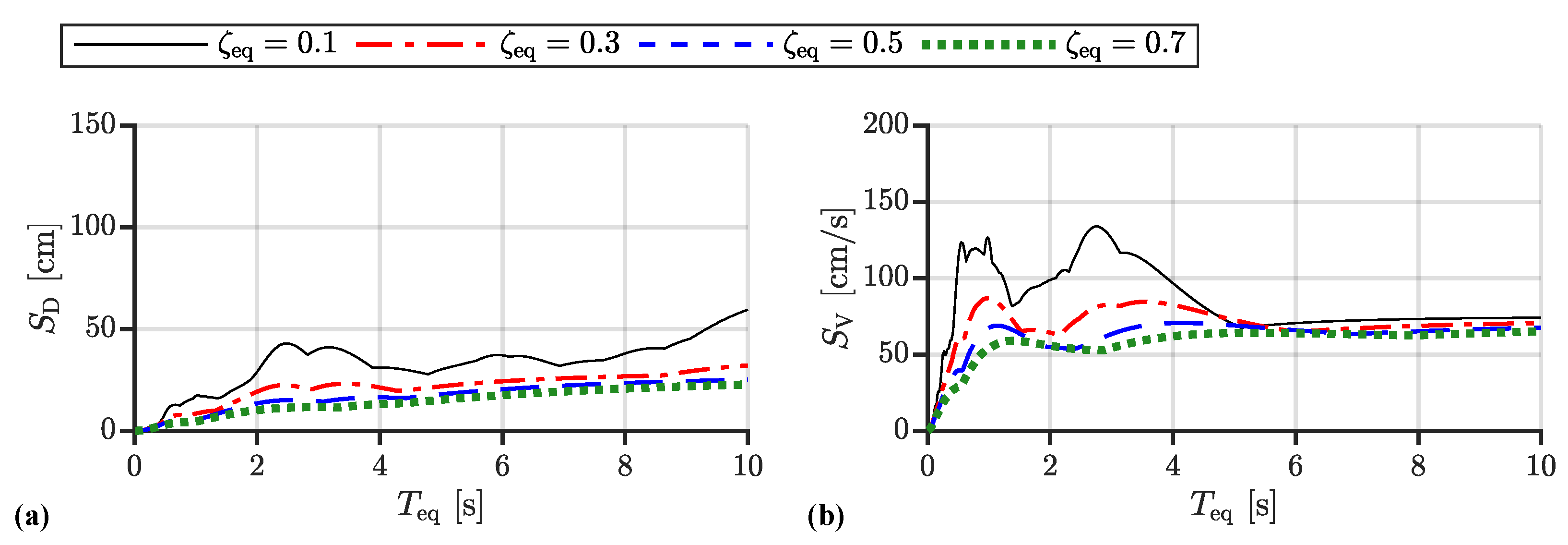
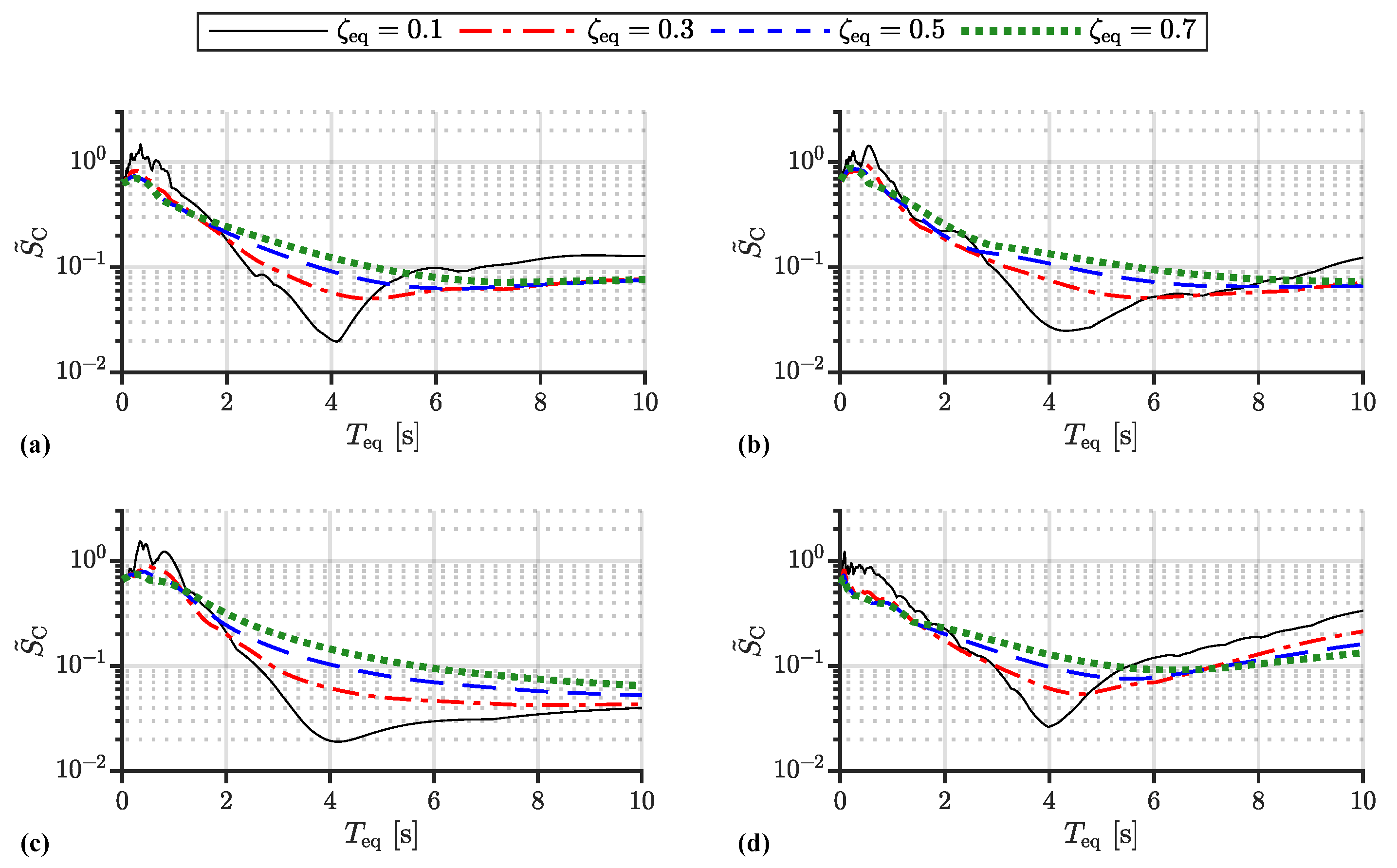
4.2. Numerical Example
- 1.
- The maximum control force decreases as the equivalent damping, , ratio increases if .
- 2.
- The maximum control force increases as the equivalent damping ratio, , increases if .
- 3.
- The maximum control force increases as the equivalent natural period, , increases if only for the case of Code Hachinohe.
5. Design Method
5.1. Design Algorithm
- Step 1.
- Specifies the design conditions:design earthquake wave,mass of the structure (m),restrictions of the maximum responses (displacement, , velocity, , and absolute acceleration, ),restrictions of natural period and damping ratio of structure ( and ), and restriction of shear-force coefficient of control force ().
- Step 2.
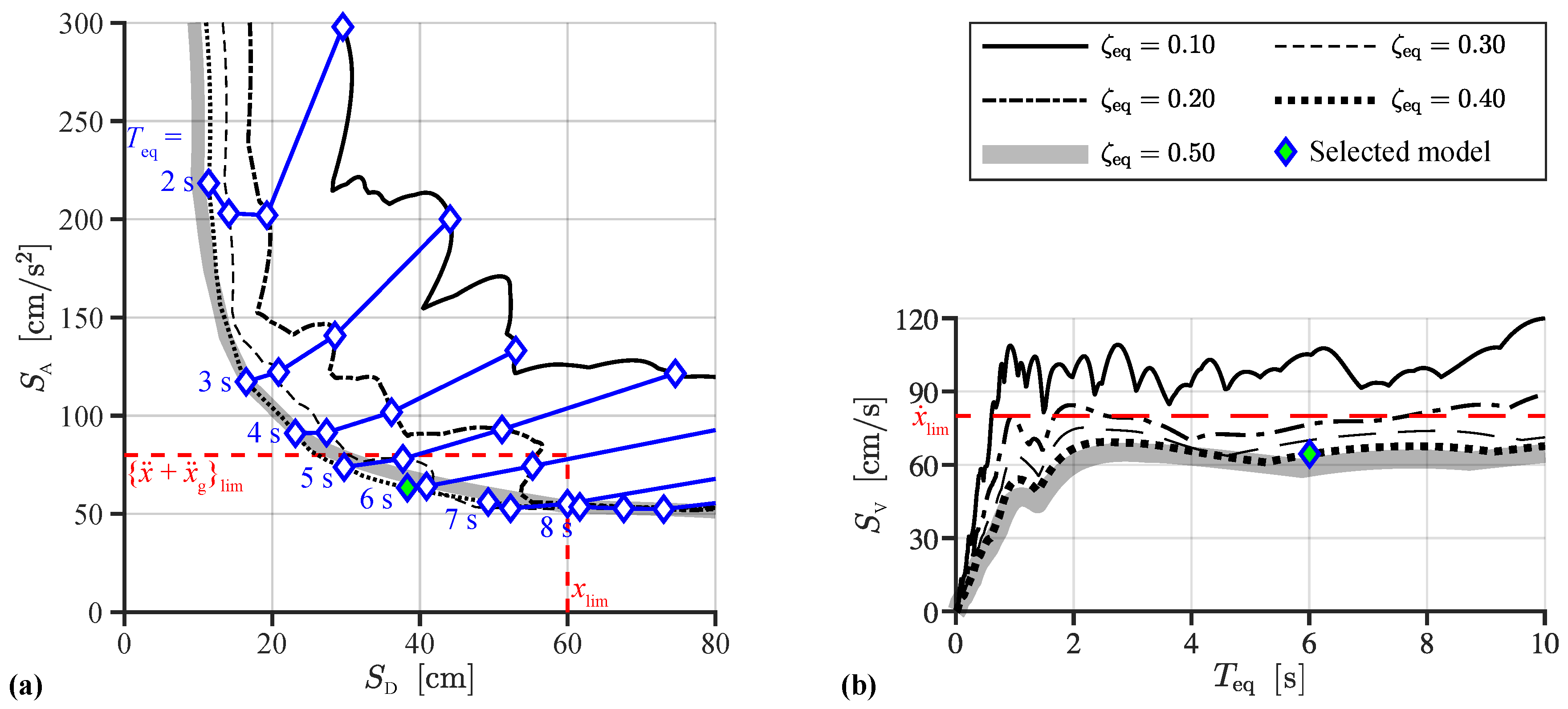
- Uses the response spectra of the design earthquake wave to select the target equivalent model (equivalent natural period, , and equivalent damping ratio, ) that satisfies the limitations on the maximum responses set at Step 1.
- Step 3.
- Uses the control force prediction spectrum to estimate the maximum control force of the equivalent model selected at Step 2. If all design limitations (, , and ) are satisfied, specifies appropriate values for and , then go to the next step. If not, go back to Step 2 and select another equivalent model.
- Step 4.
- Calculate the stiffness and damping coefficient by the following steps:
- Calculate the target equivalent stiffness and target equivalent damping coefficient ( and ) by substituting and , which were selected at Step 2, into (11).
- Calculate the stiffness and damping coefficient of the structure ( and ) by substituting and , which were selected at Step 3, into (10).
- Step 5.
- Calculate the feedback gain, , by substituting , , , and , which were obtained at Step 4, into (10).
5.2. Design Example
- Step 1.
- Design earthquake wave:Code Hachinohe wave (Figure 7).Mass of the structure:kg.Restrictions of the maximum response:,, and.Restrictions of natural period and damping ratio of structure:and.Restriction of shear-force coefficient of control force:.
- Step 2.
- Figure 9 shows the response spectra of the Code Hachinohe wave. Note that the blue plots in Figure 9a show the maximum responses of models with a specified equivalent natural period and equivalent damping ratio, and the plots with the same equivalent natural period are connected by the blue lines. From Figure 9, it can be seen that increasing the damping ratio over 40% cannot achieve a higher performance; thus, we do not consider the cases with a damping ratio large than 40%. We select the following equivalent model:andwhich satisfies the restrictions on the maximum responses set at Step 1.
- Step 3.
- Step 4.
- Substituting the target equivalent natural period, , and target equivalent damping ratio, into (11), the value of the target equivalent stiffness and target equivalent damping coefficient is obtained:N/m and Ns/m;.substituting the natural period of the structure, , and damping ratio of the structure, into (3), the value of the stiffness of the structure and damping coefficient of the structure is obtained:N/m and Ns/m.
- Step 5.
- Substituting the target equivalent stiffness, , stiffness of the structure, , target equivalent damping coefficient, , and damping coefficient of the structure, , into (10), the feedback gain is obtained: .

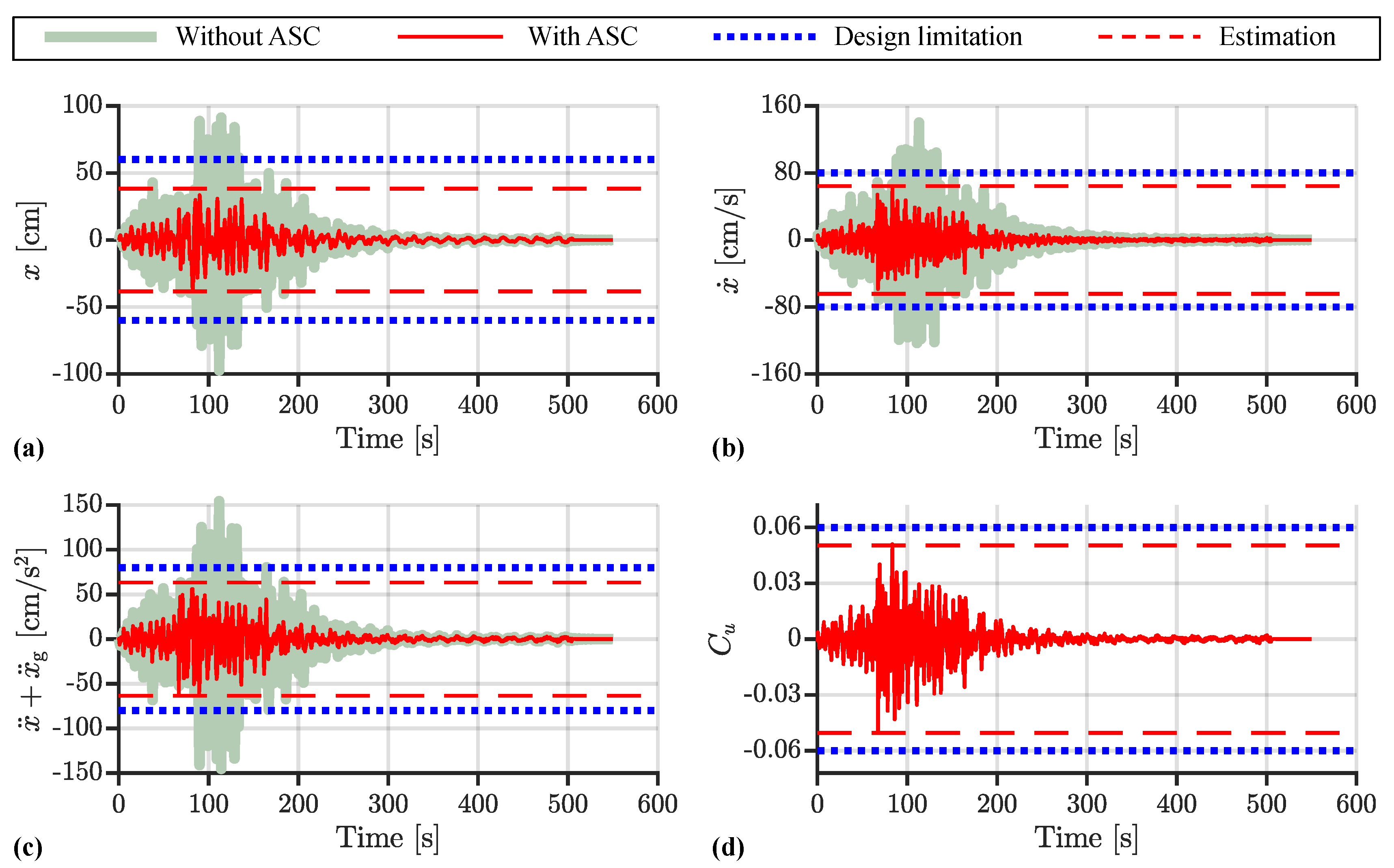
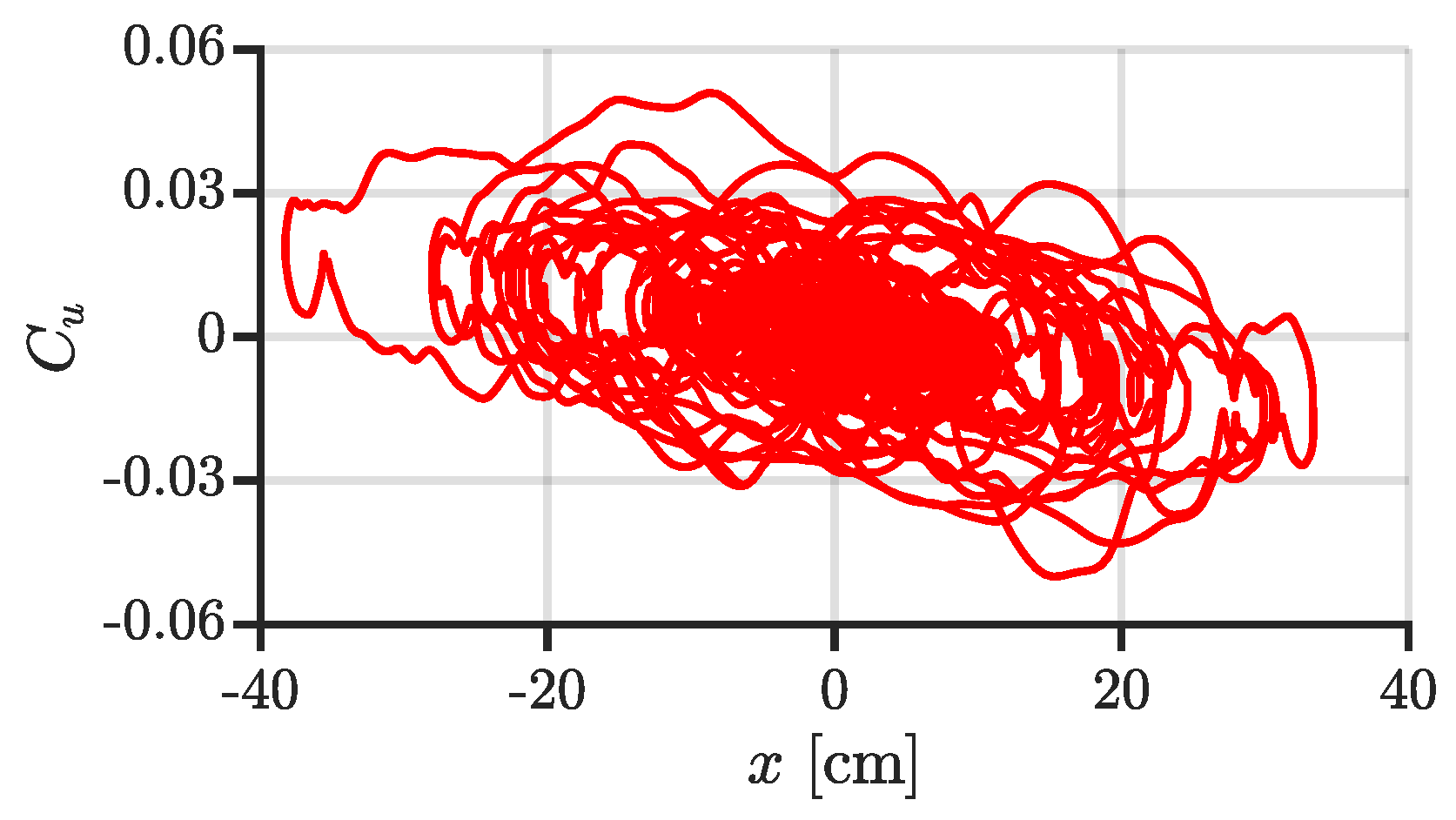
- The responses of the control system are suppressed by ASC.
- The limitations on the maximum responses and maximum control force are met.
- The estimated maximum responses and maximum control force match simulation results.
- The controller provides additional negative stiffness and positive damping to the system.
6. Conclusions
- (1)
- If , there are no estimation errors for all cases. The reason for this is that the control force only contains the velocity component when .
- (2)
- Since the phase difference usually occurs between the displacement and velocity, the estimation error may occur if .
- (3)
- The maximum control force decreases as the equivalent damping ratio increases in the resonance range.
- (4)
- The maximum shear-force coefficient of control force increases as the equivalent damping ratio, , increases if .
- (5)
- The responses of the design example are suppressed by ASC.
- (6)
- The controller of the design example provides additional negative stiffness and positive damping.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Accuracy Verification of the Control-Force Spectrum
| No. | Name | Recording Station | Year-M. | PGA [cm/s2] | PGV [cm/s] | ||
|---|---|---|---|---|---|---|---|
| comp. 1 | comp. 2 | comp. 1 | comp. 2 | ||||
| 1 | Northridge | Beverly Hills—Mulhol | 1994-6.7 | 407.00 | 506.00 | 58.89 | 62.57 |
| 2 | Northridge | Canyon Country—WLC | 1994-6.7 | 344.00 | 472.00 | 22.00 | 44.86 |
| 3 | Duzce | Bolu | 1999-7.1 | 713.00 | 806.00 | 56.43 | 62.03 |
| 4 | Hector Mine | Hector | 1999-7.1 | 260.00 | 330.00 | 28.52 | 41.67 |
| 5 | Imperial Valley | Delta | 1979-6.5 | 233.00 | 344.00 | 25.93 | 32.93 |
| 6 | Imperial Valley | El Centro Array #11 | 1979-6.5 | 357.00 | 372.00 | 34.41 | 42.09 |
| 7 | Kobe | Nishi—Akashi | 1995-6.9 | 499.00 | 493.00 | 37.24 | 36.54 |
| 8 | Kobe | Shin—Osaka | 1995-6.9 | 238.00 | 208.00 | 37.77 | 27.85 |
| 9 | Kocaeli | Duzce | 1999-7.5 | 306.00 | 351.00 | 58.80 | 46.33 |
| 10 | Kocaeli | Arcelik | 1999-7.5 | 214.00 | 147.00 | 17.67 | 39.53 |
| 11 | Landers | Yermo Fire Station | 1992-7.3 | 240.00 | 148.00 | 51.27 | 29.72 |
| 12 | Landers | Coolwater | 1992-7.3 | 278.32 | 408.66 | 275.47 | 433.74 |
| 13 | Loma Prieta | Capitola | 1989-6.9 | 518.00 | 434.00 | 34.94 | 29.16 |
| 14 | Loma Prieta | Gilroy Array #3 | 1989-6.9 | 544.00 | 360.00 | 35.66 | 44.61 |
| 15 | Manjil | Abbar | 1990-7.4 | 504.70 | 487.06 | 42.41 | 50.69 |
| 16 | Superstition Hills | El Centro Imp. Co. | 1987-6.5 | 351.00 | 253.00 | 46.30 | 40.82 |
| 17 | Superstition Hills | Poe Road (temp) | 1987-6.5 | 437.00 | 294.00 | 35.65 | 32.74 |
| 18 | Cape Mendocino | Rio Dell Overpass | 1992-7.0 | 378.00 | 538.00 | 43.72 | 41.81 |
| 19 | Chi-Chi | CHY101 | 1999-7.6 | 346.00 | 431.00 | 70.52 | 114.93 |
| 20 | Chi-Chi | TCU045 | 1999-7.6 | 487.06 | 348.88 | 12.67 | 20.54 |
| 21 | San Fernando | LA—Hollywood Stor | 1971-6.6 | 206.00 | 171.00 | 18.81 | 14.81 |
| 22 | Friuli | Tolmezzo | 1976-6.5 | 344.00 | 309.00 | 22.00 | 30.75 |
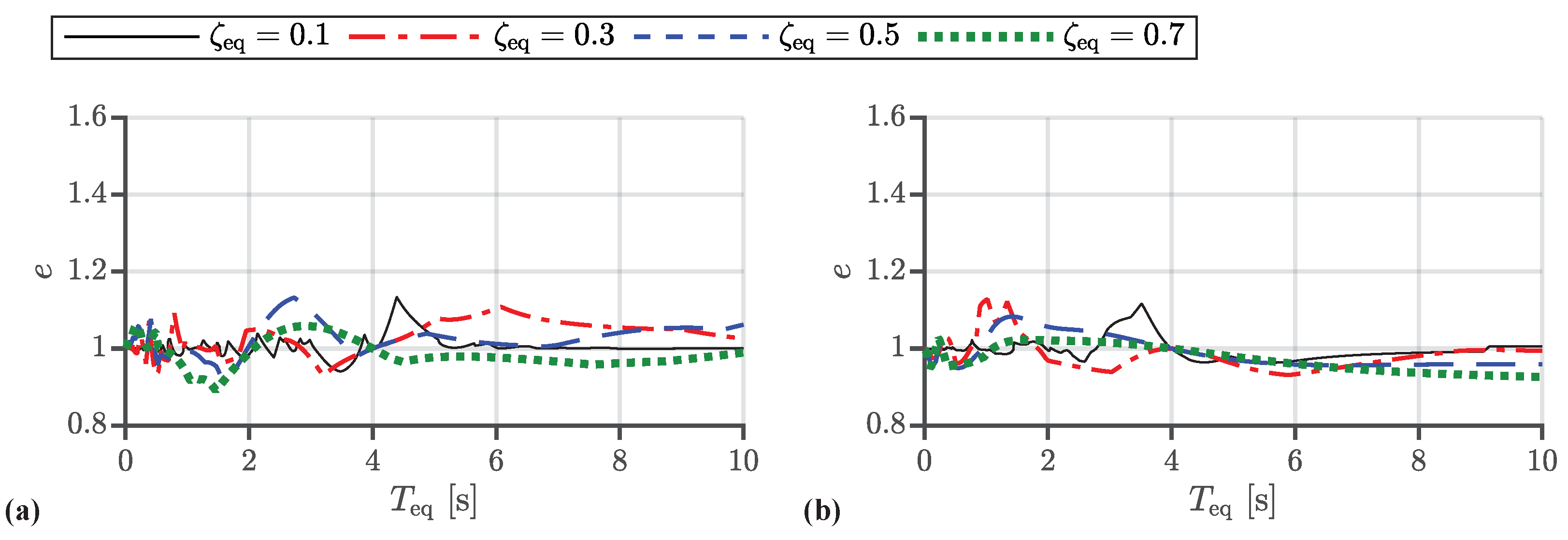
- (1)
- The estimation error of the ABS method is obviously larger than that of the SRSS method.
- (2)
- The estimation error of the ABS method is always larger than 0.
- (3)
- The estimation error of the SRSS method is less than 20% for the two selected cases.
- (4)
- (1)
- The mean value and standard derivation of the maximum estimation errors of the SRSS method are larger than that of the ABS method.
- (2)
- The estimation errors of the SRSS method are less than 20% for most cases.
- (1)
- Both the mean value of the estimation error and the standard derivation of the estimation error of the SRSS method are obviously less than that of the ABS method.
- (2)
- The mean values of the standard derivation of the estimation error of the SRSS method for each case are less than 8%.

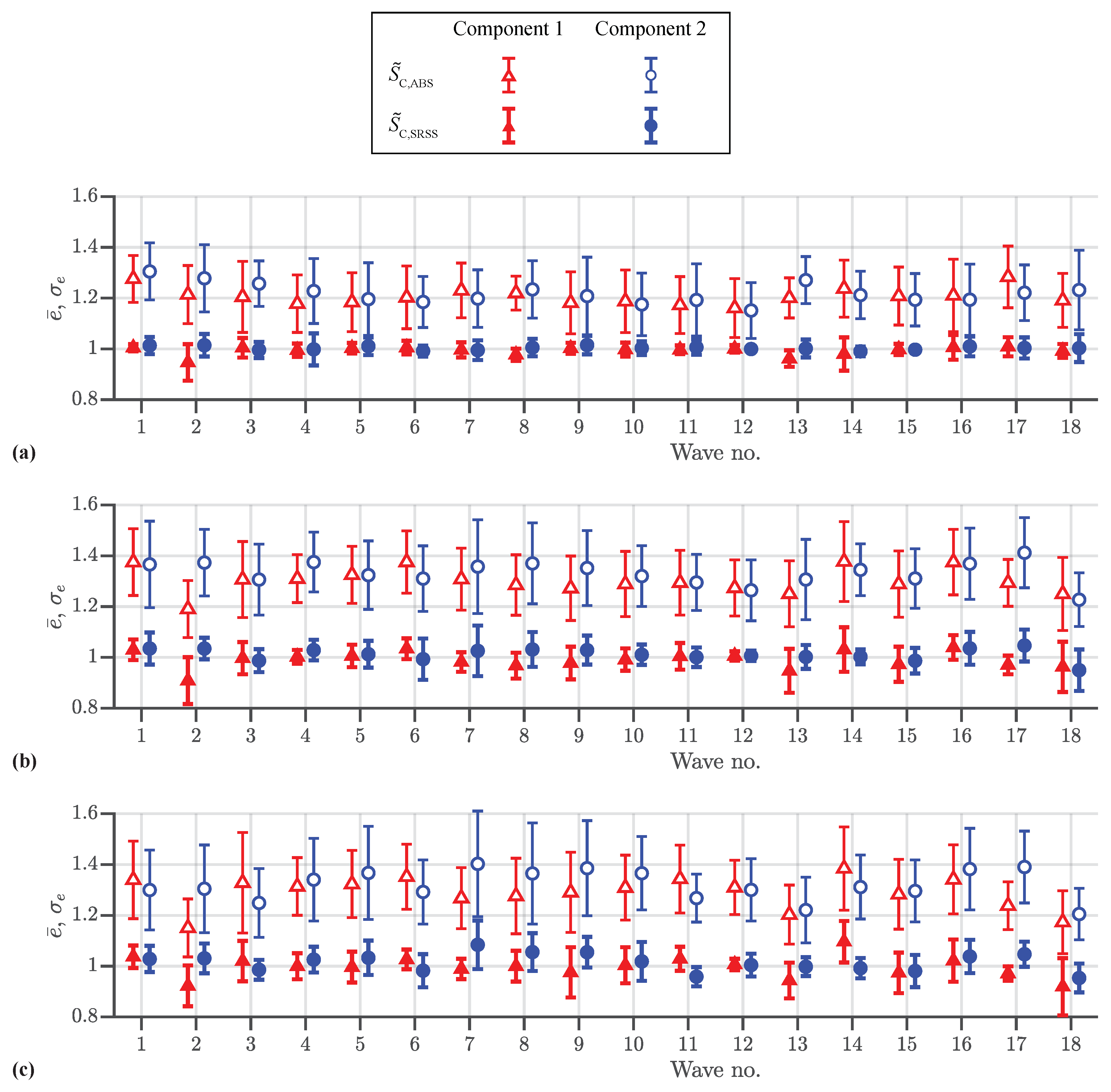
| ABS Method | SRSS Method | |||||
|---|---|---|---|---|---|---|
| 2 s | 0.01 | 0.10 | 10.79% | 11.92% | −0.04% | 2.26% |
| 0.30 | 21.21% | 14.00% | −0.26% | 4.46% | ||
| 0.50 | 25.93% | 14.22% | −0.30% | 6.04% | ||
| 0.70 | 27.74% | 14.26% | −0.64% | 6.86% | ||
| 0.05 | 0.10 | 7.98% | 10.17% | −0.04% | 1.69% | |
| 0.30 | 17.36% | 15.31% | −0.09% | 4.07% | ||
| 0.50 | 23.30% | 14.59% | −0.23% | 5.46% | ||
| 0.70 | 26.16% | 14.31% | −0.52% | 6.51% | ||
| 4 s | 0.01 | 0.10 | 21.47% | 12.46% | −0.27% | 4.16% |
| 0.30 | 31.56% | 14.05% | 0.04% | 6.82% | ||
| 0.50 | 30.23% | 15.89% | 0.49% | 7.88% | ||
| 0.70 | 26.06% | 15.33% | 0.23% | 7.45% | ||
| 0.05 | 0.10 | 14.52% | 13.42% | −0.10% | 3.10% | |
| 0.30 | 30.31% | 13.81% | −0.07% | 6.35% | ||
| 0.50 | 30.72% | 15.73% | 0.55% | 7.76% | ||
| 0.70 | 26.86% | 15.45% | 0.30% | 7.52% | ||
| 6 s | 0.01 | 0.10 | 27.40% | 12.53% | −0.32% | 5.60% |
| 0.30 | 29.21% | 15.03% | −0.26% | 7.30% | ||
| 0.50 | 23.45% | 15.54% | −0.28% | 6.70% | ||
| 0.70 | 19.23% | 14.82% | 0.16% | 6.25% | ||
| 0.05 | 0.10 | 22.58% | 12.32% | −0.23% | 4.22% | |
| 0.30 | 30.29% | 14.83% | −0.22% | 7.38% | ||
| 0.50 | 24.32% | 15.58% | −0.27% | 6.85% | ||
| 0.70 | 19.79% | 14.88% | 0.15% | 6.37% | ||
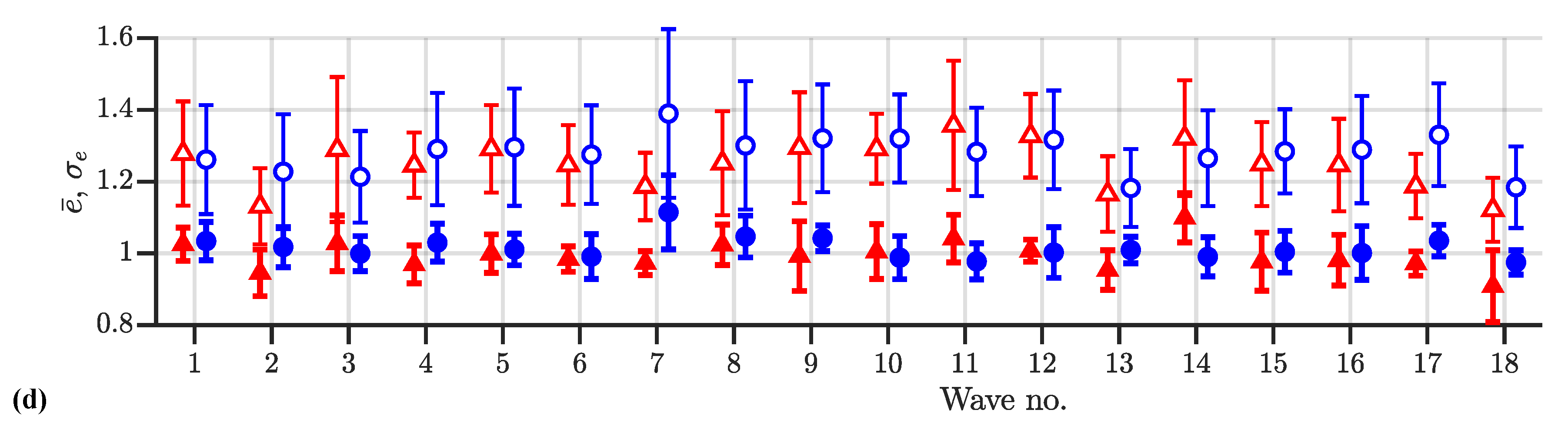
Appendix B. Analysis of Numerical Examples of Control-Force Spectrum
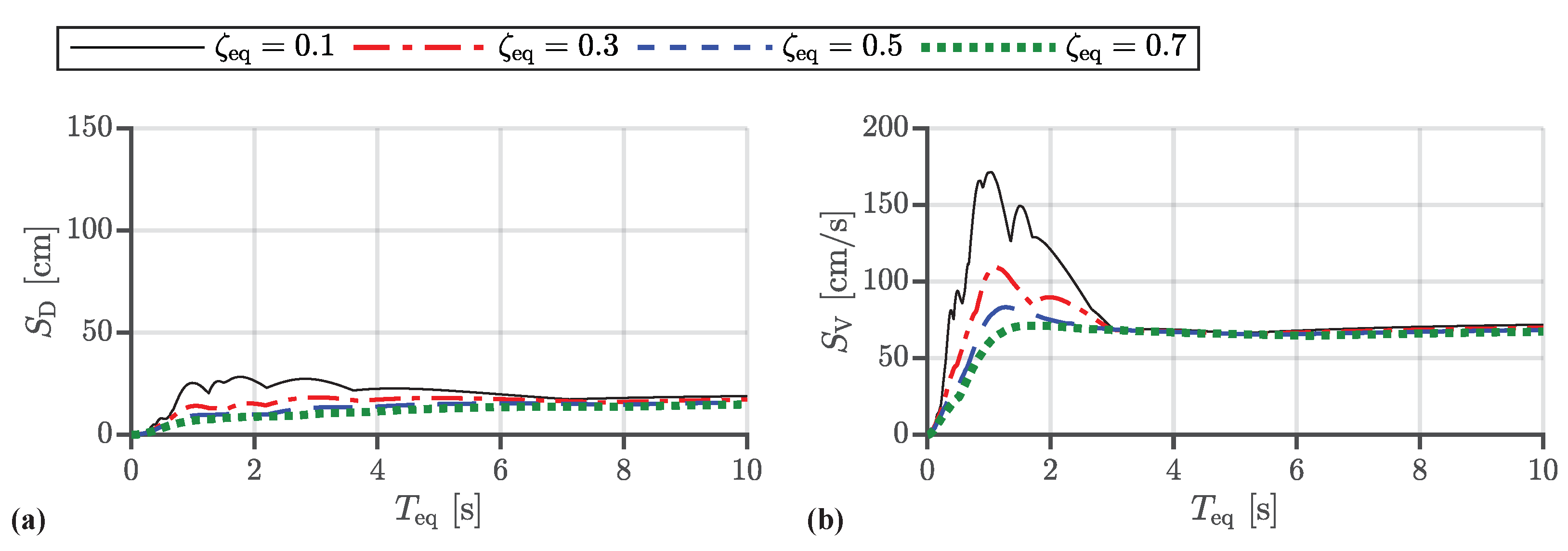

References
- Sheikh, H.; Van Engelen, N.C.; Ruparathna, R. A review of base isolation systems with adaptive characteristics. Structures 2022, 38, 1542–1555. [Google Scholar] [CrossRef]
- Beirami Shahabi, A.; Zamani Ahari, G.; Barghian, M. Base Isolation Systems—A State of the Art Review According to Their Mechanism. J. Rehabil. Civ. Eng. 2020, 8, 37–61. [Google Scholar] [CrossRef]
- Yutaka, N.; Keiichi, O. Review on seismic isolation and response control methods of buildings in Japan. Geoenviron. Disasters 2019, 6, 7. [Google Scholar] [CrossRef]
- Mazza, F. Base-isolation of a hospital pavilion against in-plane-out-of-plane seismic collapse of masonry infills. Eng. Struct. 2021, 228, 111504. [Google Scholar] [CrossRef]
- Warn, G.P.; Ryan, K.L. A Review of Seismic Isolation for Buildings: Historical Development and Research Needs. Buildings 2012, 2, 300. [Google Scholar] [CrossRef]
- Architectural Institute of Japan. Design Recommendations for Seismically Isolated Buildings; Architectural Institute of Japan: Tokyo, Japan, 2016. [Google Scholar]
- Kelly, J.M. The role of damping in seismic isolation. Earthq. Eng. Struct. Dyn. 1999, 28, 3–20. [Google Scholar] [CrossRef]
- Ibrahim, R. Recent advances in nonlinear passive vibration isolators. J. Sound Vib. 2008, 314, 371–452. [Google Scholar] [CrossRef]
- Zhao, Y.; Cui, J.; Zhao, J.; Bian, X.; Zou, L. Improving Low Frequency Isolation Performance of Optical Platforms Using Electromagnetic Active-Negative-Stiffness Method. Appl. Sci. 2020, 10, 7342. [Google Scholar] [CrossRef]
- Septimiu, L.; Chira, F.; Roşca, V.O. Passive, Active and Semi-Active Control Systems in Civil Engineering. Constr. Arhit. 2005, 3, 23–32. [Google Scholar]
- Fisco, N.; Adeli, H. Smart structures: Part I—Active and semi-active control. Sci. Iran. 2011, 18, 275–284. [Google Scholar] [CrossRef]
- Nagarajaiah, S.; Sahasrabudhe, S. Seismic response control of smart sliding isolated buildings using variable stiffness systems: An experimental and numerical study. Earthq. Eng. Struct. Dyn. 2006, 35, 177–197. [Google Scholar] [CrossRef]
- Kataria, N.P.; Jangid, R. Seismic protection of the horizontally curved bridge with semi-active variable stiffness damper and isolation system. Adv. Struct. Eng. 2016, 19, 1103–1117. [Google Scholar] [CrossRef]
- Chen, Y.; Sato, D.; Miyamoto, K.; She, J. Estimating the maximum response and maximum control force for high-rise base-isolated buildings with active structural control in along-wind direction. Eng. Struct. 2020, 216, 110712. [Google Scholar] [CrossRef]
- Miyamoto, K.; She, J.; Sato, D.; Yasuo, N. Automatic determination of LQR weighting matrices for active structural control. Eng. Struct. 2018, 174, 308–321. [Google Scholar] [CrossRef]
- Shivashankar, P.; Gopalakrishnan, S. Review on the use of piezoelectric materials for active vibration, noise, and flow control. Smart Mater. Struct. 2020, 29, 053001. [Google Scholar] [CrossRef]
- Horiguchi, C.; Kohiyama, M. Simultaneous optimization of structural and control systems of a SDOF buildings with a linear quadratic regulator controller aiming at performance-based design. J. Struct. Constr. Eng. 2012, 77, 715–722. (In Japanese) [Google Scholar] [CrossRef][Green Version]
- Kohiyama, M. Prediction of maximum control force of PD-controlled system under stationary white noise. In Proceedings of the 11th International Conference on Structural Safety and Reliability, New York, NY, USA, 16–20 June 2013; pp. 3871–3878. [Google Scholar] [CrossRef]
- Sato, D.; Chen, Y.; Miyamoto, K.; She, J. A spectrum for estimating the maximum control force for passive-base-isolated buildings with LQR control. Eng. Struct. 2019, 199, 109600. [Google Scholar] [CrossRef]
- Architectural Institute of Japan. AIJ Recommendations for Loads on Buildings; Architectural Institute of Japan: Tokyo, Japan, 2015. [Google Scholar]
- Federal Emergency Management Agency. Quantification of Building Seismic Performance Factors-FEMA P695; Federal Emergency Management Agency: Washington, DC, USA, 2009.
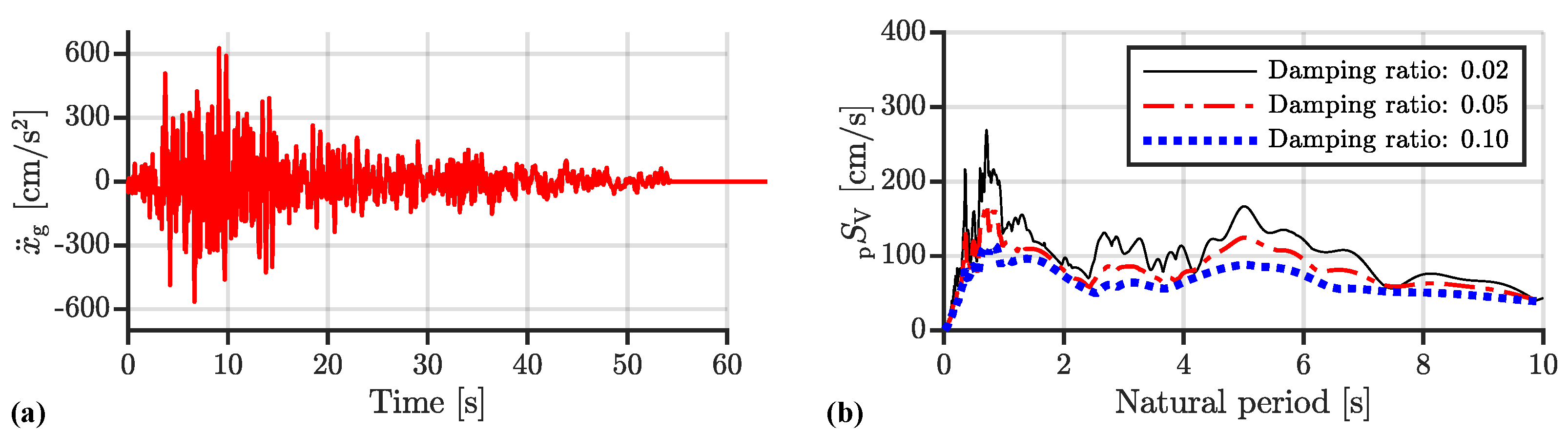

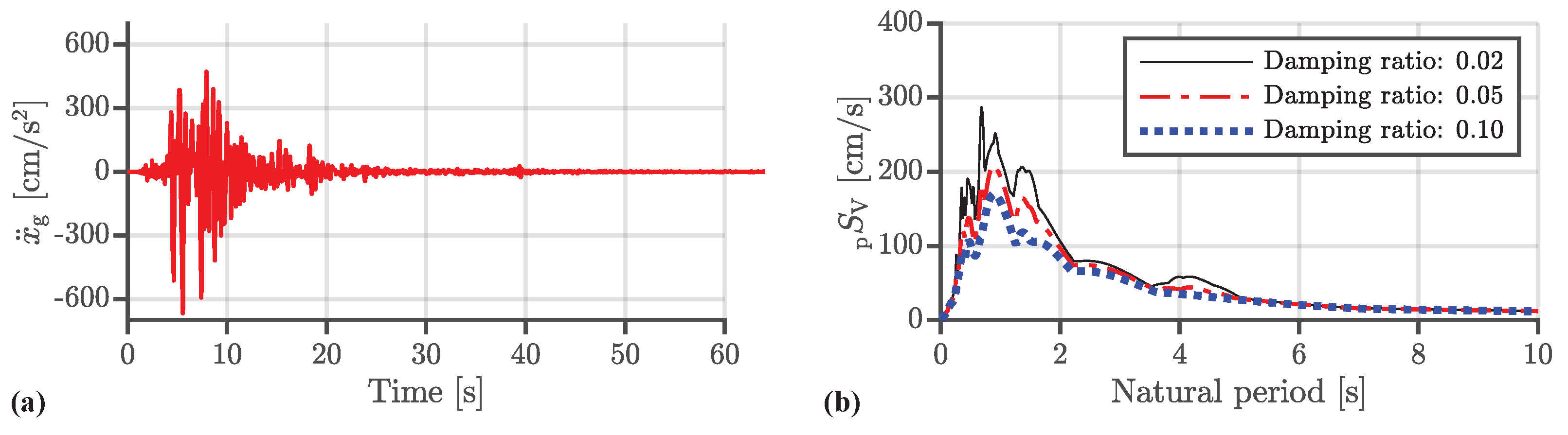
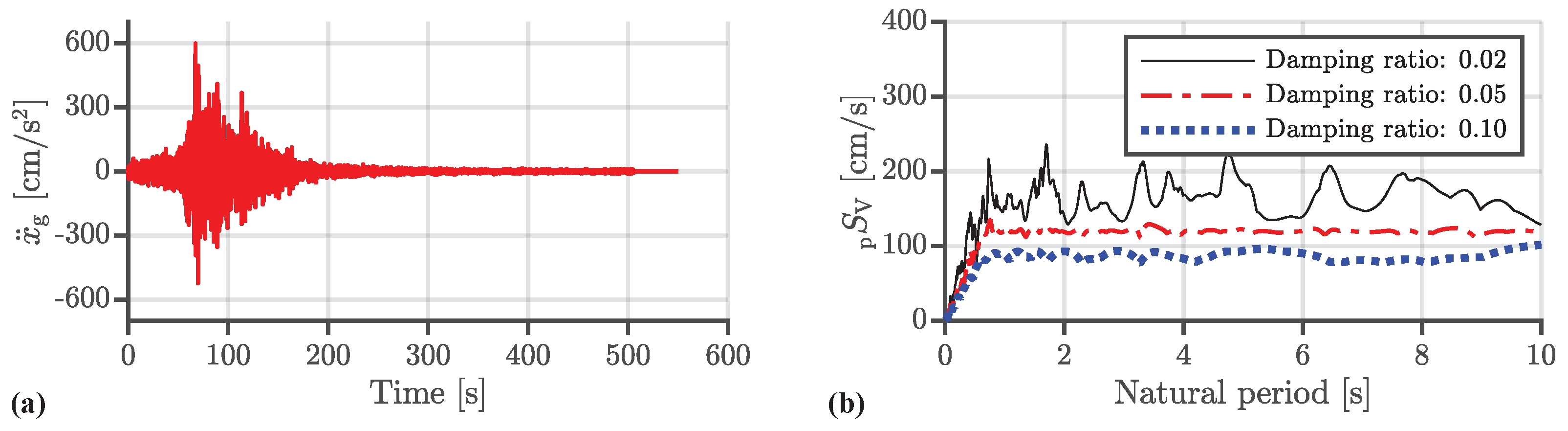
| Earthquake Wave | PGA [cm/s2] | PGV [cm/s] |
|---|---|---|
| Taft NS | 626.6 | 75.0 |
| El Centro 1940 NS | 748.5 | 75.0 |
| JMA Kobe NS | 667.2 | 75.0 |
| Code Hachinohe | 599.1 | 65.6 |
| Parameter | Symbol | Value |
|---|---|---|
| mass | m | 1.00 kg |
| stiffness | 2.46 N/m | |
| damping coefficient | 0.03 Ns/m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Sato, D.; Miyamoto, K.; She, J. Control-Force Spectrum Considering Both Natural Period and Damping Ratio for Active Base-Isolated Building. Actuators 2022, 11, 156. https://doi.org/10.3390/act11060156
Chen Y, Sato D, Miyamoto K, She J. Control-Force Spectrum Considering Both Natural Period and Damping Ratio for Active Base-Isolated Building. Actuators. 2022; 11(6):156. https://doi.org/10.3390/act11060156
Chicago/Turabian StyleChen, Yinli, Daiki Sato, Kou Miyamoto, and Jinhua She. 2022. "Control-Force Spectrum Considering Both Natural Period and Damping Ratio for Active Base-Isolated Building" Actuators 11, no. 6: 156. https://doi.org/10.3390/act11060156
APA StyleChen, Y., Sato, D., Miyamoto, K., & She, J. (2022). Control-Force Spectrum Considering Both Natural Period and Damping Ratio for Active Base-Isolated Building. Actuators, 11(6), 156. https://doi.org/10.3390/act11060156







