Abstract
This article proposes an analytical methodology for the optimal design of a magnetorheological (MR) valve constrained in a specific volume. The analytical optimization method is to identify geometric dimensions of the MR valve, and to determine whether the performance of the valve has undergone major improvement. Initially, an enhanced radial MR valve structure with effective annular and radial composite flow paths was designed. After describing the schematic configuration and operating principle of the proposed MR valve, a mathematical model of the pressure drop was derived on the basis of the Bingham model of a MR fluid. Sequentially, the multi-objective optimization problem had been formulated for the constructed approximate model exploiting the NSGA-II algorithm to find the global optimum geometrical dimensions of the enhanced radial MR valve. Meanwhile, influences of the geometrical design variables of the MR valve were analytically investigated by mapping finite element analysis numerical responses with response surface techniques. Lastly, the experimental test rig was setup to explore the pressure drop and dynamic response time of the initial and optimal MR valve, as well as the dynamic performance of the enhanced radial MR valve controlled cylinder system under different excitation conditions. The experimental results revealed that under the applied current of 1.6 A, the pressure drop and power consumption of the optimal MR valve improved significantly with values of 4.46 MPa and 16.84 W, respectively, when compared to 4.03 MPa and 27.65 W of their respective initial values. Additionally, the average response time efficiency improved by 14.29%, with its optimal value being 81 ms and initial value as 94.5 ms. Moreover, the damping force of the optimal MR valve-controlled cylinder system was 4.34 kN, which was 12.44% larger than the initial one of 3.86 kN at the applied current of 1.6 A.
1. Introduction
With years of development and exploration, some new types of intelligent materials, such as magnetorheological (MR) fluids [1] and MR elastomers [2], have gradually attracted the attention of researchers. MR fluid is a kind of functional fluid with variable yield stress whose rheological properties can be dramatically and reversibly varied by the application of an external magnetic field in milliseconds [3,4]. It is mainly a stable colloidal suspension composed of magnetically conductive base fluid, tiny solid iron particles and additives. Plus, MR fluids have a widespread foothold in various engineering applications due to their inherent features, such as quick response, low energy requirement, and excellent controllability, mostly in various MR intelligent devices [5,6,7,8], transportation vehicles [9,10], building suspensions [11], and biomedical applications [12,13,14].
The controllability of MR device is provided by regulating magnetic flux density across a damping gap through which the MR fluid flows. Therefore, in order to maximize the effective damping gap within a limited volume, a variety of MR valve structures have been developed successively. Aydar et al. [15] presented an MR valve based on the combined excitation of a coil and a permanent magnet. The electromagnetic field and the static magnetic field in the MR valve could be superimposed on each other by adjusting the excitation current, thereby controlling the effective magnetic flux intensity of the damping gap. Sahin et al. [16] proposed an MR valve with the disc damping gap. The MR fluid in the valve could flow between the two discs, and its flow direction was perpendicular to the magnetic flux lines in the damping gap. The experimental results show that the pressure drop and response time characteristics of the disc MR valve were better than those of the circular MR valve. Hu et al. [17,18] investigated a compact annular-radial-orifice flow MR valve, which had a high magnetic field utilization rate and a sufficiently large pressure differential. In addition, the application range of the MR valve could also be effectively expanded by changing the thickness of the radial damping gap. Imaduddin et al. [19,20] introduced a curved flow channel method to increase the effective working gap of the developed MR valve. The experimental results show that the maximum pressure drop of the MR valve could reach more than 2.5 MPa at the outer diameter of 50 mm. Bai et al. [21] studied an MR energy absorber with double concentric annular valve, which had the characteristics of high dynamic range and fail-safe damping force. Meanwhile, the double concentric annular valve was designed to reduce the reference damping force while maintaining an appropriate dynamic range to improve shock and vibration. Yang et al. [22] developed an annular multi-channel MR valve, which realized the effect of annular multi-channel multiplexing by adding a magnetic isolation ring to the winding groove, so that the magnetic flux line vertically passed through the annular channel. Hu et al. [23] designed a multi-stage radial MR valve in which the magnetic flux lines of the four radial damping gaps were substantially perpendicular to the fluid flow direction. Thus, the valve structure could not only make full use of the high magnetic flux density, but also enlarge the effective area. To sum up, although the flow path in MR valve can be effectively lengthened by implementing various structural optimization designs, these optimized valve structures are more complex, which will make their key performance indicators worse.
Recently, the geometric optimization design of MR device plays a crucial role in evaluating its dynamic performance, such as the pressure drop and the power consumption. Nguyen et al. [24,25] had performed optimization problem for MR valves of different configurations by considering the control energy and response time constant as its objective functions. In addition, the optimization procedure utilizing a golden-section algorithm and a local quadratic fitting technology was constructed via a finite element method. Keshav et al. [26] pointed out a methodology that combines the results of the finite element model built in the ANSYS software with the neural network technology to construct a neural network model for magnetic flux density prediction. Shamieh et al. [27] optimized the geometry of the MR brake by utilizing a combination of genetic algorithm and sequential quadratic programming algorithm. Plus, the objective of the work was to maximize dynamic range and minimize response time, and the initial and optimal MR brake were also experimentally tested on a quarter vehicle seat suspension test rig. Naserimojarad et al. [28] reported an analytical optimization design method for an MR damper based on applied mathematical analysis and finite element analysis, thus ensuring that the final solution of the cost equation was a global extremum.
Compared with the traditional hydraulic control valve, the MR valve designed based on MR mechanism has noteworthy dominances, which provides a new thought for the development of hydraulic technology. Salloom et al. [29] combined four identical MR valves into a three-position four-way proportional directional valve, which could control the speed and precise position of the hydraulic actuator by adjusting the fluid flow. Paweł et al. [30] introduced a rotary vibration damper with an MR valve that confines the MR valve with an annular fluid gap in a cylindrical hole. Henceforth, its dynamic performance was experimentally studied. Kubik et al. [31] displayed an MR valve with a short response time, the magnetic circuit of which was composed of ferrite materials to reduce the influence of eddy currents. Additionally, the proposed MR valve was coupled in the damper as the kernel element, which, in turn, constitutes a semi-active control vibration isolation test bench. Yoo et al. [32] surveyed an MR valve structure for pump-driven hydraulic actuators in a Wheatstone bridge hydraulic power circuit. Thereafter, the feasibility of the proposed MR valve to replace the traditional mechanical servo valve was verified based on the experimental performance data of the MR valve.
Consequently, this work emphasizes a design optimization methodology to optimally design the enhanced radial MR valve structure with effective annular and radial composite flow paths. The optimization methodology combines the finite element model implemented in COMSOL software with the orthogonal experimental analysis and response surface techniques to build an approximate model with the best fitting accuracy for identified design variables. Meanwhile, the NSGA-II algorithm is adopted to find the optimal geometry of the MR valve, so as to realize maximize the overall performance under a given constrained volume. Furthermore, the pressure drop performance and dynamic response time of the initial and optimal MR valve are evaluated on the dynamic performance test rig. The proposed MR valve is employed as the control unit of the valve-controlled cylinder system, and its dynamic performance is also experimentally studied.
2. Design and Development of an Enhanced Radial MR Valve
2.1. Principle and Structure Analysis
Figure 1 represents the schematic configuration of the enhanced radial MR valve. Its components mainly composed of the end cover, positioning plate, magnetic ring, nonmagnetic ring, excitation coil, damping disk, and nonmagnetic disk. Among them, the valve spool can be configured to pass through the left and right damping disks and nonmagnetic disk arranged sequentially. Two radial flow paths are then formed between the two positioning plates and the valve spool through the convex platform positioning. Likewise, an annular flow path is also formed between the outer circumference of the valve spool and the inner circumference of the magnetic ring. In addition, the central through hole is machined on the positioning plate to form two central pipe flow paths. In working condition, the MR fluid can flow in from the left end cover, and then flow through the left centric pipe, the left radial damping gap, the annular damping gap, the right radial damping gap, and the right centric pipe. At last, the MR fluid flows out from the right end cover.
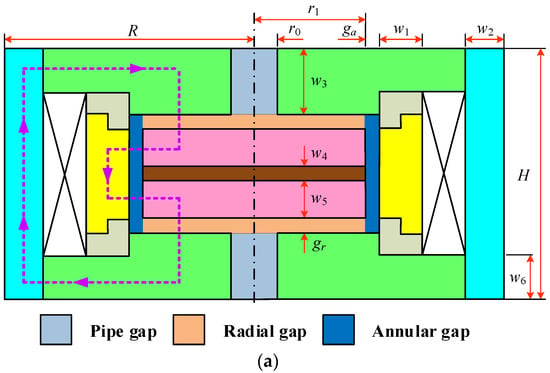
Figure 1.
Schematic configuration of the enhanced radial MR valve: (a) Schematic diagram, (b) 3D diagram. 1. End cover, 2. Nonmagnetic ring, 3. Damping disk, 4. Excitation coil, 5. Valve body, 6. Nonmagnetic disk, 7. Magnetic ring, 8. Positioning plate.
The structure of the proposed MR valve is configuration featured with nonmagnetic components arranged in an orderly manner, which can maximize the utilization of magnetic field within a limited volume. When the excitation coil of the valve is energized, the magnetic field is imposed perpendicularly to the MR fluid while passing through the radial damping gap and the annular damping gap in sequence, thus causing a field-dependent resistance on the flow. After that, the space of the damping channel of the MR valve can be fully exploited, which can effectively increase the pressure drop of the MR valve. Simultaneously, with the increment of applied current, the viscosity and shear yield stress of the MR fluid in the damping channel will also have a conspicuous variation. As a result, it is possible to control the pressure drop generated by the MR valve with modulating the current applied to the exciting coil. Table 1 lists the dimensional parameter values of the initial enhanced radial MR valve.

Table 1.
Primary structural dimension of the initial MR valve.
2.2. Mathematical Model of MR Valve
Performance indicators of the valve are assessed based on the quasi-static model of MR valves, where the equations are also derived based on the assumption that the MR fluid exhibits Bingham plastic behavior. By employing the viscoplastic Bingham model, the shear stress τ of the MR fluid can be expressed as
where τy represents the magnetic yield stress, is the shear strain rate of the MR fluid, B is the magnetic flux density of the applied magnetic field, η is the dynamic viscosity of the zero magnetic field with a value of 0.8 Pa·s. It is noted that the fluid viscosity after yielding is assumed to be a constant in the Bingham model. In this article, the MRF-J25T MR fluid prepared by Chongqing Materials Research Institute was used for simulation experiments. The least square method is employed to fit the τy based on each magnetic flux density, and the relationship between the yield stress τy and the magnetic flux density B is obtained as follows:
Figure 1 displays the five fluid flow zones divided by the proposed MR valve, which are divided into three different types of fluid flow channels. More specifically, the pressure drop at the circular pipe flow paths can be approximately calculated by
where q is the system flow rate, its value is 4 L/min, w3 is the thickness of the positioning plate, r0 is the radius of the center orifice.
The pressure drop at the radial disk flow paths can be written as
where r1 is radius of the damping disk, ga is the annular damping gap, gr is the radial damping gap, τy1 is the shear yield stress generated by the magnetic field at the radial disk flow path, c is the correction coefficient, and the value range is 2~3.
The pressure drop at the axial annular flow path is deduced by
where w4 is the thickness of the nonmagnetic disk, w5 is the thickness of the damping disk, τy2 is the shear yield stress generated by the magnetic field at the axial annular flow path.
The total pressure drop Δp can be mathematically determined using the following equation
The power consumption of the MR valve mainly comes from the thermal power consumption when the coil is energized, and its equation can be described as
where I is the excitation current, Aw is the cross-sectional area of the coil wire, ρ represents the resistivity of the wire, and L is the total length of the wire.
3. Flow Field Simulation of the Enhanced Radial MR Valve
To ascertain the variations in the rheological properties of MR fluids, it is essential to comprehend the dynamic flow field characteristics generated in the effective shear region of the MR valve. According to the structural dimensions in Table 1, the 2D axisymmetric model shown in Figure 2 was established in COMSOL software.
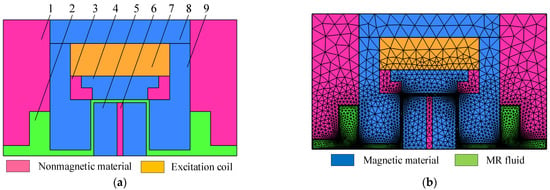
Figure 2.
A 2D finite element model of the MR valve: (a) entity model, (b) meshed model. 1. End cover, 2. MR fluid, 3. Nonmagnetic ring, 4. Magnetic ring, 5. Damping disk, 6. Nonmagnetic disk, 7. Excitation coil, 8. Valve body, 9. Positioning plate.
Figure 2a depicts the entity model, which can be divided into four segments according to the material properties defined in each region. Among which: the nonmagnetic disk, nonmagnetic ring, and end cover are made of stainless-steel material with better magnetic isolation performance; the valve body, magnetic ring, positioning plate and damping disk are made of No.10 steel material with excellent magnetic conductivity; the MRF-J25T type MR fluid is selected as the working fluid; the excitation coil is made of enameled copper wire evenly wound. Thereafter, the finite element model is constructed after meshing, which is illustrated in Figure 2b. The simulated solid model uses a triangular mesh for intelligent division, and the division of distinctive colors represents the material with different properties.
Figure 3a,b displays the velocity streamlines and the pressure variation in the MR valve when the applied current is 1 A, respectively. Observing Figure 3a, the streamlines in the damping channel of the MR valve are dense and straight, indicating that the flow velocity inside the channel is large and relatively stable. On the contrary, the streamline trajectories at both ends of the damping channel are complex and turbulent, indicating that the flow field at the entrance and exit of the channel varies dramatically. In Figure 3b, the internal pressure of the damping channel of the MR valve gradually decreases along the flow direction, and the pressure changes continuously without transient saltation.
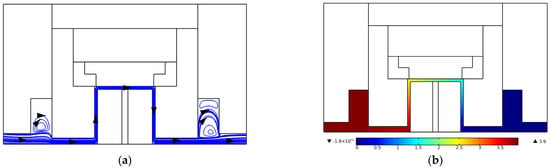
Figure 3.
Internal flow field distribution of the MR valve: (a) velocity streamlines, (b) pressure.
As can be seen from Figure 4a, when different current amplitudes are applied to the excitation coil, the pressure variation trend in the flow channel of the MR valve is completely consistent, and the pressure falling gradient in the radial flow path is greater than that in the annular flow path. It is also noticeable from Figure 4b that the pressure drop of the proposed MR valve increases rapidly with the augment in the currents before the current of 1.4 A. With the further increase in the current, the magnetic flux density in the working gap increased slowly and the growth rate of pressure drop gradually slowed down. Especially, the pressure drop of the initial MR valve can reach 4.4 MPa at the applied current of 1.6 A.
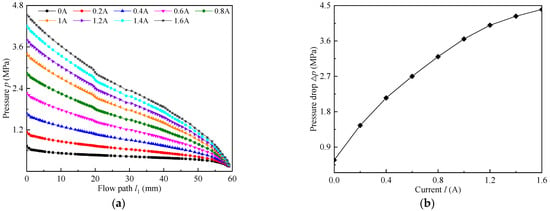
Figure 4.
Pressure distribution in the damping channel under different currents: (a) pressure varies with flow path, (b) pressure drop varies with current.
Figure 5 portrays the power consumption of the initial MR valve at different pressure drops. It can be distinctly found that the power consumption significantly rises with the increment of pressure drop. This is because, as the current increases, the internal magnetic field of the MR valve will gradually reach the magnetic saturation state, and the pressure drop will also tend to the maximum value, resulting in a substantial improve in the power consumption of the MR valve. Normally, the power consumption of the initial MR valve can reach 27.1 W at the applied current of 1.6 A.
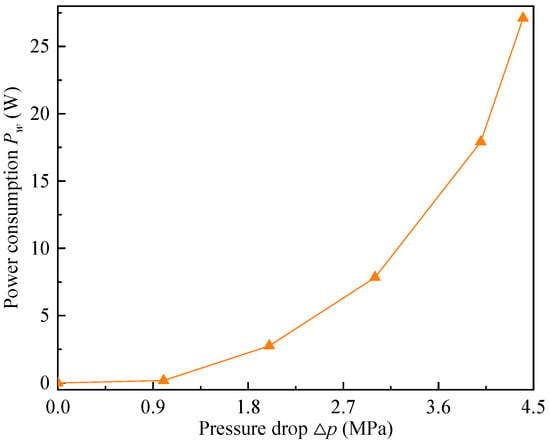
Figure 5.
Power consumption of MR valve under different pressure drops.
4. Multi-Objective Optimization Design of the Enhanced Radial MR Valve
Based on the Design-Expert platform, the multi-objective optimization design of the MR valve was carried out by coupling the DOE orthogonal experiment analysis and the approximate model. The optimization process was demonstrated in Figure 6. Firstly, the finite element analysis had been sequentially executed on the training data of different level combinations of each optimization variable obtained from the orthogonal experimental analysis to calculate the pressure drop and power consumption of the proposed MR valve. Then, the response surface technology was subsequently employed to fit the second-order approximate model of each target response. In the meantime, the analysis of variance was utilized for estimating the interaction between the design variables and to verify the desirable variables which were having a significant influence on the response. Finally, the geometric optimization problem had been formulated for the approximate model exploiting the NSGA-II algorithm to find the Pareto optimal solution. As an aside, the optimum geometrical dimensions were selected from the solution set according to the actual situation.
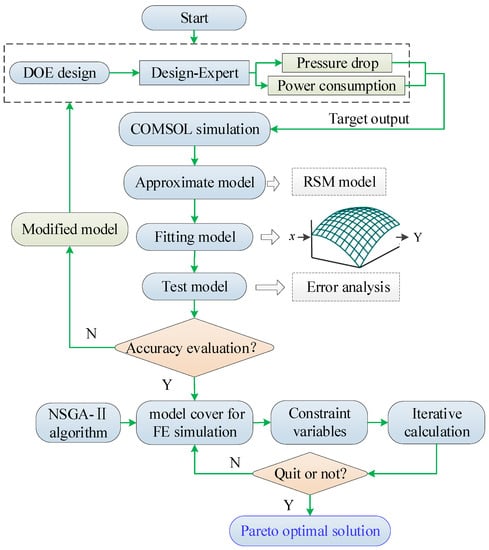
Figure 6.
Multi-objective optimization design process.
4.1. Orthogonal Experimental Analysis
In order to ensure that the proposed MR valve can enhance its dynamic performance as much as possible under the condition of constrained volume, take the radial damping gap gr, the thickness of the damping disk w5, the annular damping gap ga, and the radius of the damping disk r1 are utilized as design variables. The detailed of sampling range of each design variable is tabulated in Table 2.

Table 2.
Sampling range of each design variable.
Some design variable parameters of the initial and optimal MR valve will be adjusted, which will lead to a greater variation in the magnetic circuit reluctance and the cross-sectional area of winding groove. Accordingly, this optimization design takes the pressure drop generated by the initial MR valve as a reference at a current of 1.6 A, and takes the power consumption by the optimal MR valve as the target when the same pressure drop as before optimization is generated. Importantly, considering the accuracy and design efficiency of the approximate model, the pressure drop Δp and power consumption Pw at a current of 1.6 A are taken as the target response, and 29 simulation experiments have to be performed based on the orthogonal experimental analysis.
The results of the main effects analysis of the design matrix generated by 29 sampling times are exhibited in Figure 7. The greater the slope of the main effects diagram, the greater the influence of the design variables on the target response. According to Figure 7a, except that the thickness of the damping disk w5 has an approximately linear effect on the pressure drop, the other design variables have nonlinear effects on the pressure drop, among which the radial damping gap gr has the greatest effect on the pressure drop. It can be observed from Figure 7b that each design variable has an approximate linear impact on the power consumption, in which the radius of the damping disk r1 has the greatest impact on the power consumption, and the two damping gaps have little impact on the power consumption.
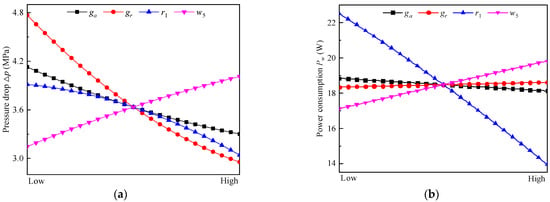
Figure 7.
Main effect diagram: (a) design variables on Δp, (b) design variables on Pw.
4.2. Construction of Approximate Model
The relationship between the design variables of the approximate model and the target response can be written as
where y(x) is the actual value of simulation, is the predicted value obtained in the approximate model, ε is the error between the simulated value and the predicted value.
The typically used quantities to judge the ability of the approximate models are the root mean square error (RMSE) and the multiple determination coefficients R2 which identifies the variation within the target response. Specifically, the RMSE is a quantity employed to reflect how close the predicted results to the actual response. Likewise, the determination coefficient R2 values are varied between 0 and 1, where values close to 1 manifest that the approximate model has high fitting accuracy to explain the response in the design space. The corresponding equation is defined as
where yi is the actual response value of the samples of part i, is the predicted value of part i of samples in the response surface model (RSM), is the average value of the actual response for the samples of part i.
Taking the matrix generated by the simulation model sampling 29 times as the original data, and the RSM is exploited to approximate fit the pressure drop Δp and power consumption Pw. The fitting indicators under the RSM are presented in Table 3.

Table 3.
Fitting indicator of response surface model.
As shown in Table 3, the values of RSME and R2 of the second-order response surface of pressure drop Δp are 1.4% and 99.5%, respectively. In addition, the values of RSME and R2 of the second-order response surface of power consumption Pw are 2% and 99.99%, respectively. The results exhibit that the constructed approximate model has a small fitting error and a high fitting accuracy, which is very close to the actual response of the finite element simulation, and can be subsequently optimized with the fitted approximation model.
In order to comprehend the fitting effect of the constructed approximate model more explicitly, the predicted values of the approximate model are compared with the simulated values of the finite element model, which are portrayed in Figure 8. It is noted that the predicted values of the pressure drop Δp and power consumption Pw can well approximate the simulated values, which demonstrates that the approximate model built by the RSM can accurately reflect the actual simulation in the whole range of design variables.
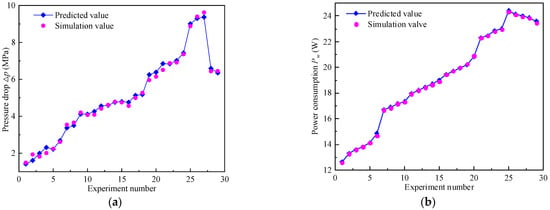
Figure 8.
Comparison between predicted value and simulation value: (a) pressure drop Δp, (b) power consumption Pw.
To examine whether the data points come from a normally distributed population, a normality examine is performed. Figure 9 reveals the standard residuals plotted against the percentage probability distributions of the pressure drop Δp and power consumption Pw. It can be clearly observed that the residuals data points closely follow the reference normal distribution line, which confirms that the analysis data from the population of normal distribution.
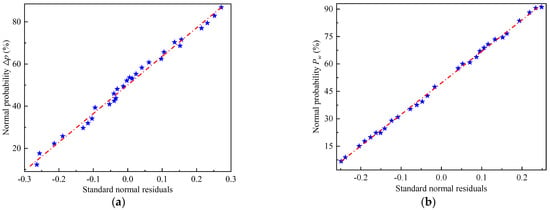
Figure 9.
Normal plot of residuals: (a) pressure drop Δp, (b) power consumption Pw.
Figure 10 depicts the fitting surface of the model when the annular damping gap and the thickness of the damping disk remain unchanged. It can be directly observed that the pressure drop Δp and power consumption Pw reduce with increment of the radius of the damping disk. Nevertheless, the Δp increases with the decrease in the radial damping gap, and the radial damping gap has little influence on the Pw. As an aside, Figure 11 reveals the fitting surface of the model when keeping the radial damping gap and the annular damping gap unchanged.
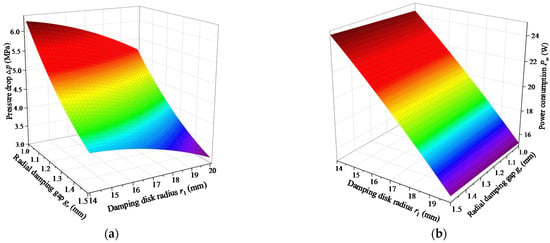
Figure 10.
Fitting surface of model for ga = 1.25 mm, w5 = 7.5 mm: (a) pressure drop Δp, (b) power consumption Pw.
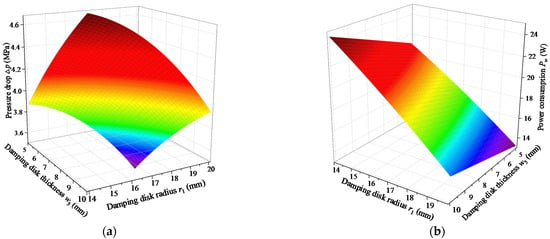
Figure 11.
Fitting surface of model for ga = 1.25 mm, gr = 1.25 mm: (a) pressure drop Δp, (b) power consumption Pw.
4.3. Multi-Objective Optimization Formulation
Some predefined constraints, such as length and radius of the valve, should be incorporated into the optimization process to guarantee the worst-case performance in practical applications. Hence, the geometry of the MR valve is constrained within a reasonable range, which is as follows
According to the upper and lower limits of each design variable, the performance indicators of the MR valve are transformed into a multi-objective optimization problem. The design space for the optimal solution is given by
On the other hand, an m file containing the approximate model of pressure drop Δp and power consumption Pw is established in Matlab software, and the m file is solved by multi-objective optimization utilizing the NSGA-II algorithm. In the optimization, the objective is to maximize pressure drop and minimize power consumption. Moreover, the population size was set as 100, the maximum evolution algebra was set as 200, and the crossover rate, crossover distribution index and mutation distribution index were set as 0.9, 10, and 20, respectively. At last, 700 Pareto optimal solutions can be obtained by running the solution, and the distribution of the Pareto fronts is displayed in Figure 12.
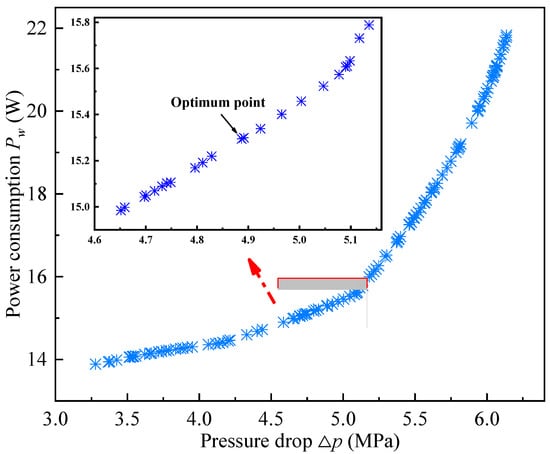
Figure 12.
Optimal Pareto front.
From Figure 12, it is worth mentioning that increasing the output pressure drop of the MR valve and reducing the power consumption are contradictory under certain conditions, that is, the realization of one optimization goal is at the expense of the loss of another optimization goal. Considering that the application of the MR valve is a small and medium hydraulic system, the optimum point in the plot is selected as the optimization result. Table 4 summarizes the initial and optimal values of each design variable and each performance indicator at the applied current of 1.6 A. It can also be realized that general improvement in the performance of the MR valve with the optimal indicators has been achieved compared with those in the initial indicators.

Table 4.
Optimization results.
4.4. Analysis of Optimization Results
Figure 13 implies the comparison curves of pressure drop and power consumption for the initial and optimal MR valve. It is found that the pressure drop and power consumption of the optimal MR valve at each current are greater than those initial, and the differentials between them linearly enhanced with the increment of current. Meanwhile, at an applied current of 1.6 A, the performance indicators, such as the pressure drop and power consumption, increased significantly with the optimal values of 4.84 MPa and 15.26 W separately, when compared to 4.4 MPa and 27.1 W of their respective initial values. In consequence, the simulation optimization results indicate that the performance indicators of the optimal MR valve have a substantial improvement, which preliminarily verifies the effectiveness of the optimization design in this study.
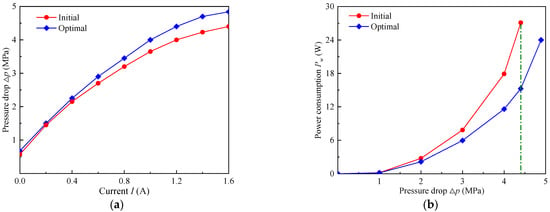
Figure 13.
Comparison of the initial and optimal performance indicators: (a) pressure drop Δp, (b) power consumption Pw.
5. Performance Analysis of the Enhanced Radial MR Valve
5.1. Prototype and Experimental Test Rig Setup
According to the structural parameters of the initial and optimal MR valve in Table 1 and Table 4, the prototype of the enhanced radial MR valve as shown in Figure 14 was manufactured, and the performance test rig was also built up that was shown schematically in Figure 15. The motor drives the gear pump to work, which could deliver the MR fluid to the MR valve. The pressure sensor (a) and (b) were adopted to measure the inlet and outlet pressure of the MR valve, respectively. The relief valve (A) acts as a safety valve to protect the hydraulic system, and the relief valve (B) acts as a back pressure valve to stabilize the outlet pressure, while providing the load cases for the test system. The DC power supply could provide power to the exciting coil of the MR valve. The data acquisition device was adopted to control the current of the MR valve and collect the pressure data of the system. After connecting the experimental equipment, the pressure drop under different currents could be easily collected through the control rocker on the data acquisition device.

Figure 14.
Prototype of the initial and optimal MR valve: (a) valve parts, (b) valve assembly. 1. Left end cover, 2. Valve body, 3. Left positioning plate, 4. Magnetic ring, 5. Right end cover, 6. Damping disk, 7. Nonmagnetic disk, 8. Right positioning plate, 9. Nonmagnetic ring.

Figure 15.
Experimental test rig of the enhanced radial MR valve: (a) performance test system, (b) data acquisition device. 1. Motor, 2. MR fluid tank, 3. Relief valve (A), 4. Gear pump, 5. Pressure sensor (a), 6. Relief valve (B), 7. Pressure sensor (b), 8. MR valve, 9. DC power supply, 10. Data acquisition device.
5.2. Experimental Analysis of Pressure Drop Performance
Figure 16 portrays the variation curve of the pressure of the optimal MR valve with current under load case 0. It is obvious that as the applied current enhances, the inlet pressure and pressure drop are growing in the same upward trend, while the outlet pressure remains basically unchanged. The maximum pressure drop of the proposed MR valve can reach about 4.46 MPa at the current of 1.6 A.
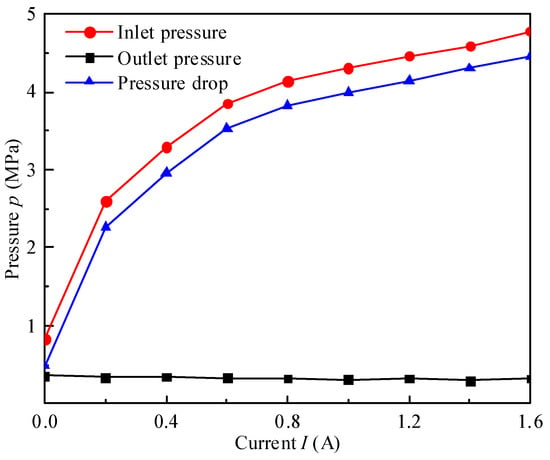
Figure 16.
Pressure change of the optimal MR valve under different currents.
Figure 17 shows the variation of pressure drop of the optimal MR valve with load cases and flow rates. It was observed that the viscosity pressure drop of the optimal MR valve rises with the increment of the load under different load cases. The total pressure drop of the optimal MR valve is not affected by load changes based on different currents. In addition, the pressure drop when the flow rate is 10 L/min is larger than that of 4 L/min under each current, and the difference between the two pressure drops is quite small. Among them, the pressure drop deviation at 4 L/min and 10 L/min varies from 0.05 MPa at 0.8 A current to 0.04 MPa at 1.6 A current, respectively.
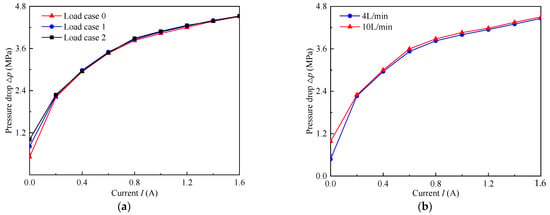
Figure 17.
Pressure drop change of the optimal MR valve under different excitations: (a) load cases, (b) flow rates.
The experimental pressure drops were compared for 0.4 A to 1.6 A current in steps of 0.4 A, and the results are presented in Figure 18. It can be clearly noted that the pressure drop of the initial and optimal MR valve has exactly alike variation tendency with the excitation current, and the optimal pressure drop is greater than that of the initial. As observed, based on load case 0 and a flow rate of 4 L/min, the pressure drop of the initial MR valve gradually enhanced from 2.65 MPa at 0.4 A current to 4.03 MPa at 1.6 A current, and simultaneously the pressure drop of the optimal MR valve also went up gradually in a nonlinear fashion from 2.96 MPa at 0.4 A current to 4.46 MPa at 1.6 A current. In other words, the increment amplitude in the pressure drop of the optimal MR valve is 11.7% at 0.4 A current and 10.67% at 1.6 A current, respectively, compared with the initial MR valve.
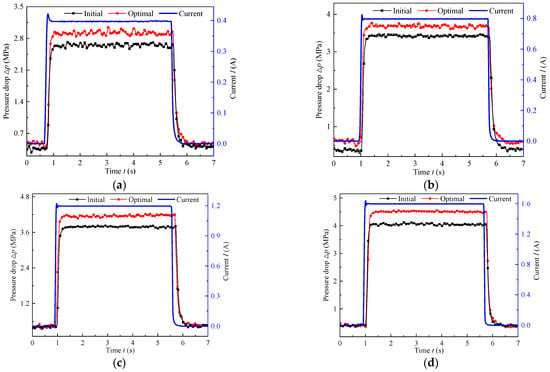
Figure 18.
Pressure drop change of the initial and optimal MR valve under different currents: (a) 0.4 A, (b) 0.8 A, (c) 1.2 A, (d) 1.6 A.
5.3. Experimental Analysis of Dynamic Response Time
In order to investigate the dynamic response time of the enhanced radial MR valve, a square wave control signal was activated under a steady flow. Additionally, the data acquisition device could periodically collect the pressure drop and response time data of the initial and optimal MR valve, and the dynamic response time of the MR valve needs to consider the current step response time generated before the pressure drop response time, which was since the current and pressure drop were part of the same test system. In this article, the rising response time was defined as the time required for a system property to rise from its initial state to 95% of its maximum value. Conversely, the falling response time was defined as the time required for a system property to fall from its initial maximum state to 5% of its maximum value, which was displayed in Figure 19.
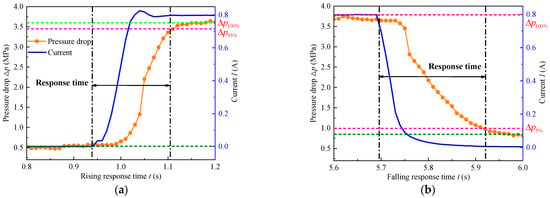
Figure 19.
Definition of dynamic response time: (a) rising response time, (b) falling response time.
The rising and falling response time of the MR valve varies with the applied current under load case 0 and a flow rate of 4 L/min, as shown in Figure 20 and Table 5. It is noteworthy to mention that the dynamic response time of the MR valve with hybrid flow geometry gradually decreases with the increment of the applied current. The average response times of the initial MR valve under the four current amplitudes are 170.5 ms, 133.5 ms, 106.5 ms and 94.5 ms, respectively, while the average response times of the optimal MR valve are 181 ms, 130.5 ms, 91 ms, 94.5 ms and 81 ms, respectively. More specifically, under the applied current of 1.6 A, the rising response time efficiency improved by 12.64%, having its optimal value as 76 ms and initial value as 87 ms. Likewise, it is found that there is a 15.69% increase in falling response time, with 86 ms as its optimal value compared to 102 ms as initial value.
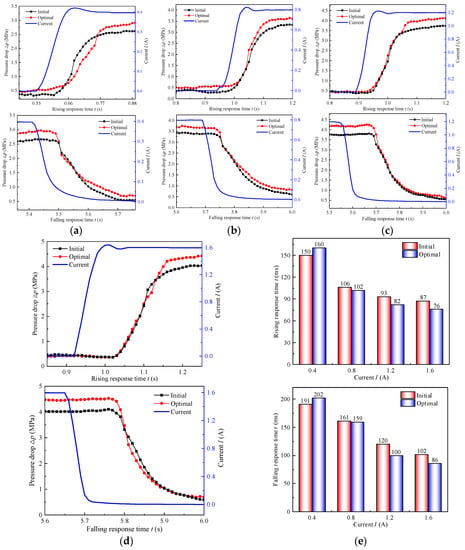
Figure 20.
Dynamic response times in rise and fall phases of the initial and optimal MR valve: (a) 0.4 A, (b) 0.8 A, (c) 1.2 A, (d) 1.6 A, (e) response time.

Table 5.
Response characteristic of the proposed MR valve.
In summary, the MR valve in hybrid flow geometry has a very slow falling response time compared to the rising response time. This is attributed to that the attenuation of induced electromotive force (EMF) in the excitation coil will grow in the current and pressure drop falling time. In addition, its induced EMF will also cause surge current, which will do some harm to the circuit. In order to reduce the harm caused by the induced EMF, a freewheeling diode can be connected in parallel at both ends of the MR valve coil.
Figure 21a plots the experimental results that the pressure drop of the optimal MR valve under each current is decidedly larger than that before optimization, and the gap between them increases with the augment of current. When the applied current is 1.6 A, the pressure drop of the optimal MR valve is 4.46 MPa which is 10.67% more than that of the initial MR valve with a pressure drop of 4.03 MPa. Similarly, Figure 21b represents the power consumption of the initial and optimal MR valve increases exponentially with the lift of pressure drop. Under the applied current of 1.6 A, the optimal MR valve has power consumption of 16.84 W, which is 39.1% greater than that of the initial MR valve with a power consumption of 27.65 W. It can be concluded that the performance indicators of the optimal MR valve have arresting betterment when compared with the initial MR valve, which further verifies the effectiveness of the optimized design in this study.
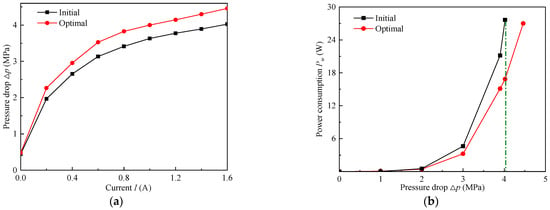
Figure 21.
Comparison of the initial and optimal performance indicators: (a) pressure drop Δp, (b) power consumption Pw.
6. Performance Analysis of the Enhanced Radial MR Valve Controlled Cylinder System
6.1. Test System of the Proposed MR Valve Controlled Cylinder System
Figure 22 displays the prototype of the enhanced radial MR valve-controlled cylinder system, and a schematic of the experimental test rig was exhibited in Figure 23. In this test rig, the lower end of the hydraulic cylinder was fixed on the fixture of the damper test system, and the upper end was connected with the power rod and the sensor. The DC power supply was exploited to provide current for the proposed MR valve, the damper test system was adopted to provide different excitations for the hydraulic cylinder, and the data of the damping force and displacement could be transmitted to the computer through the sensor.

Figure 22.
Prototype of the proposed MR valve-controlled cylinder system: 1. Enhanced radial MR valve, 2. Hydraulic pipe, 3. Double rod hydraulic cylinder.

Figure 23.
Experimental test rig of the proposed MR valve-controlled cylinder system: 1. Damper test system, 2. MR valve-controlled cylinder system, 3. DC power supply, 4. Electro-hydraulic servo controller, 5. Computer.
6.2. Dynamic Performance of the Initial and Optimal MR Valve Controlled Cylinder System
Figure 24 shows the measured damping force versus the displacement of the initial and optimal MR valve controlled hydraulic cylinder system at a frequency of 0.25 Hz and an amplitude of 7.5 mm. It can be distinctly noticed that the output damping force of the initial and optimal MR valve-controlled cylinder system stringent enhance with the increment of the excitation current. The main reason is that the increment of the excitation current will lead to the increase in the field-dependent pressure drop in the valve, which will enhance the damping force in the valve-controlled cylinder system. Additionally, the curve presented in Figure 24 has some distortion and missing in the upper left and lower right parts, which is mainly due to the fact that a certain volume of air is mixed into the MR fluid during fluid filling, resulting in a small empty stroke of the valve-controlled cylinder system due to the failure to timely compensate for the missing fluid in the chamber during the up and down stretching process. When the excitation current is 0.8 A, the maximum damping force of the initial and optimal MR valve-controlled cylinder system are 3.18 kN and 3.55 kN, the maximum deviation of calculation results for the initial and optimal output damping force is 11.62%.
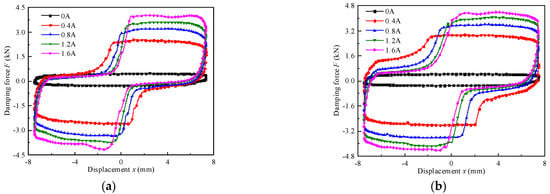
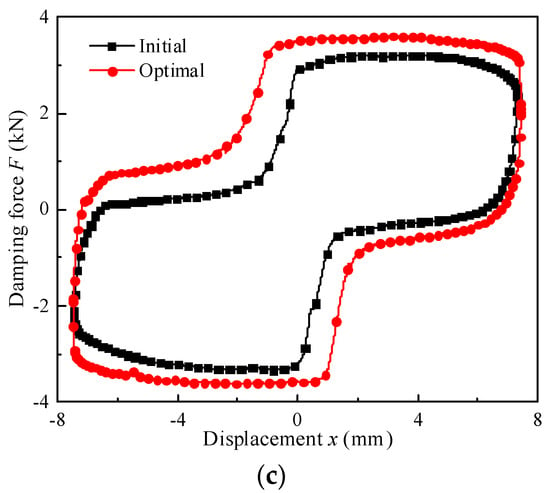
Figure 24.
Damping force versus displacement at constant frequency and amplitude: (a) initial, (b) optimal, (c) comparison of the initial and optimal damping force.
Figure 25 illustrates the variation of the damping force and the displacement for the proposed MR valve-controlled cylinder system with variable amplitudes at a current of 0.8 A and a frequency of 0.25 Hz. It is obvious that as the amplitude changes, the damping force is slightly influenced under the same current and frequency, which implies that the damping force of the MR valve-controlled cylinder system is not critically dependent on the amplitude. At the amplitude of 10 mm, the maximum damping force of the MR valve-controlled cylinder system for the optimal is 3.75 kN which is larger than that of the initial which has a value of 3.11 kN. Among them, the damping force increases with the increase in amplitude, which is mainly due to the increase in the fluid flow rate in the valve-controlled cylinder system, which increases the pressure drop at both ends of the MR valve, thereby increasing the output damping force.
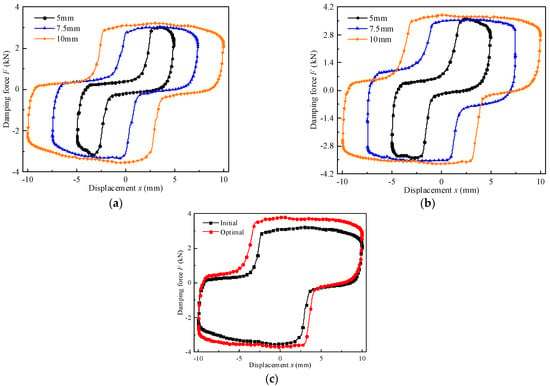
Figure 25.
Damping force versus displacement at constant current and frequency: (a) initial, (b) optimal, (c) comparison of the initial and optimal damping force.
Figure 26 displays the force-displacement performance of the proposed MR valve-controlled cylinder system. The control frequency varies from 0.25 Hz to 0.75 Hz, the test machine is set at sinusoidal loading with an amplitude of 7.5 mm and a current of 0.8 A. It is also apparent that the damping force of the valve-controlled cylinder system rises sequentially with the augment of the control frequency. In addition, when the control frequency is fixed at 0.5 Hz, there is 26.4% promote in the damping forces of the MR valve-controlled cylinder system with 3.83 kN as its optimal value compared to 3.03 kN as initial values.
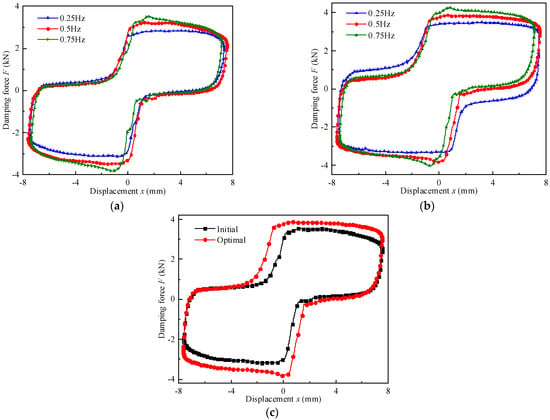
Figure 26.
Damping force versus displacement at constant amplitude and current: (a) initial, (b) optimal, (c) comparison of the initial and optimal damping force.
The dynamic performance of the initial and optimal MR valve-controlled cylinder system with variable currents is compared, as depicted in Figure 27. It can be seen that the damping force and dynamic range of the optimal MR valve-controlled cylinder system at each current are larger than those initial, and the disparity between them enlarges with the increment of the excitation current. When the applied current is 1.6 A, the measured damping force of the optimal MR valve-controlled cylinder system is 4.34 kN, which is 12.44% higher than the initial one of 3.86 kN. Analogously, the dynamic range of the optimal MR valve-controlled cylinder system is 10.14, which is 1.4% higher than the initial one of 10. Therefore, the experimental results demonstrate that the dynamic performance of the optimal MR valve-controlled cylinder system has prominent improvement from that of the initial one.
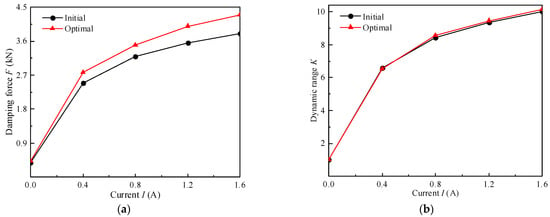
Figure 27.
Dynamic performance of the initial and optimal MR valve-control cylinder system at variable currents: (a) damping force, (b) dynamic range.
7. Conclusions
An enhanced radial MR valve with nonmagnetic disk in the intermediate of the valve spool was developed to improve the magnetic field characteristics in the design of the MR valve structure. A mathematical model of the viscosity and field-dependent pressure drop of each flow path was derived to investigate the relationship between the internal flow field and various structural parameters of the MR valve.
An analytical method for the optimal design of the enhanced radial MR valve was systematically developed, which could provide an optimization for some internal geometrical parameters of the MR valve in view of volume limitation using a multi-objective design space with predefined constraints. In particular, the orthogonal experimental analysis was employed to find the optimal location of the variables in the defined design domain. The finite element analysis had then been executed on the points identified by orthogonal experimental analysis to evaluate the pressure drop and power consumption of the proposed MR valve. As an aside, the response surface technology was subsequently employed to fit the approximate model of the pressure drop and power consumption. Lastly, the NSGA-II algorithm was adopted as an optimization tool to accurately obtain the Pareto optimal solution of the MR valve. The simulation results demonstrate that the performance indicators of the optimal MR valve had been greatly improved.
A test system was setup to investigate the pressure drop and dynamic response time of the enhanced radial MR valve. When the current was 1.6 A, the pressure drop of the optimal MR valve increased by 10.67%, and the power saving rate increased by 39.1% compared with the initial MR valve. Meanwhile, under the applied current of 1.6 A, the rising response time efficiency improved by 12.64%, having its optimal value as 76 ms and initial value as 87 ms. Likewise, it was found that there was 15.69% increase in falling response time with 86 ms as its optimal value compared to 102 ms as initial value. Furthermore, the dynamic performance of the enhanced radial MR valve control cylinder system was also validated by a series of dynamic tests at different currents, amplitudes, and frequencies. When the applied current was 1.6 A, the damping force and dynamic range of the proposed MR valve-controlled cylinder system increment from 3.86 kN and 10 of initial design to 4.34 kN and 10.14 of optimal design, respectively. Hence, it could be concluded that pressure drop and dynamic performance of the optimal MR valve had advantages over the initial one with the same structure dimension.
Author Contributions
J.R. conducted theoretical analysis and set up the experimental test rig; F.Z. conducted experimental research and wrote the first draft; N.W. carried out the simulation and optimal design; and G.H. developed the enhanced radial MR valve and revised the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research was financially supported by the National Natural Science Foundation of China (No. 52165004), Key Project of Natural Science Foundation of Jiangxi Province of China (No. 20212ACB204002), and the Special Foundation for Postgraduate Innovation in Jiangxi Province of China (No. YC2021-S460).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Elsaady, W.; Oyadiji, S.O.; Nasser, A. A review on multi-physics numerical modelling in different applications of magnetorheological fluids. J. Intell. Mater. Syst. Struct. 2020, 31, 1855–1897. [Google Scholar] [CrossRef]
- Bose, H.; Rabindranath, R.; Ehrlich, J. Soft magnetorheological elastomers as new actuators for valves. J. Intell. Mater. Syst. Struct. 2012, 23, 989–994. [Google Scholar] [CrossRef]
- Arief, I.; Mukhopadhyay, P.K. Magnetorheology in CoNi nanoplatelet-based MRFs: Effect of platelet orientation and oscillatory shear. J. Magn. Magn. Mater. 2019, 479, 326–331. [Google Scholar] [CrossRef]
- Arief, I.; Mukhopadhyay, P.K. Two-step yielding in novel CoNi nanoplatelet-based magnetic fluids under oscillatory rheology. Mater. Lett. 2016, 167, 192–196. [Google Scholar] [CrossRef]
- Hu, G.L.; Long, M.; Yu, L.F.; Li, W.H. Design and performance evaluation of a novel magnetorheological valve with a tunable resistance gap. Smart Mater. Struct. 2014, 23, 127001. [Google Scholar] [CrossRef]
- Hu, G.L.; Zhang, J.W.; Zhong, F.; Yu, L.F. Performance evaluation of an improved radial magnetorheological valve and its application in the valve controlled cylinder system. Smart Mater. Struct. 2019, 28, 47003. [Google Scholar] [CrossRef]
- Bai, X.X.; Cai, F.; Chen, P. Resistor-capacitor (RC) operator-based hysteresis model for magnetorheological (MR) dampers. Mech. Syst. Signal Process. 2019, 117, 157–169. [Google Scholar] [CrossRef]
- Hu, G.L.; Yi, F.; Tong, W.; Yu, L.F. Development and evaluation of a MR damper with enhanced effective gap lengths. IEEE Access 2020, 8, 156347–156361. [Google Scholar] [CrossRef]
- Jamadar, M.-E.-H.; Desai, R.M.; Saini, R.S.T.; Kumar, H.; Joladarashi, S. Dynamic analysis of a quarter car model with semi-active seat suspension using a novel model for magneto-rheological (MR) damper. J. Vib. Eng. Technol. 2021, 9, 161–176. [Google Scholar] [CrossRef]
- Sun, S.S.; Ning, D.H.; Yang, J. Development of an MR seat suspension with self-powered generation capability. Smart Mater. Struct. 2017, 26, 085025. [Google Scholar] [CrossRef]
- Yu, Y.; Royel, S.; Li, Y.; Li, J.; Yousefi, A.M.; Gu, X.; Li, S.; Li, H. Dynamic modelling and control of shear-mode rotational MR damper for mitigating hazard vibration of building structures. Smart Mater. Struct. 2020, 29, 114006. [Google Scholar] [CrossRef]
- Andrade, R.M.; Filho, A.B.; Vimieiro, C.B.S.; Pinotti, M. Optimal design and torque control of an active magnetorheological prosthetic knee. Smart Mater. Struct. 2018, 27, 168–176. [Google Scholar] [CrossRef]
- Gao, F.; Liu, Y.; Liao, W. Optimal design of a magnetorheological damper used in smart prosthetic knees. Smart Mater. Struct. 2017, 26, 035034. [Google Scholar] [CrossRef]
- Fu, Q.; Wang, D.H.; Xu, L.; Yuan, G. A magnetorheological damper-based prosthetic knee and sliding mode tracking control method for an MRPK-based lower limb prosthesis. Smart Mater. Struct. 2017, 26, 045030. [Google Scholar] [CrossRef]
- Aydar, G.; Wang, X.J.; Gordaninejad, F. A novel two-way-controllable magneto-rheological fluid damper. Smart Mater. Struct. 2010, 19, 065024. [Google Scholar] [CrossRef]
- Sahin, H.; Gordaninejad, F.; Wang, X.; Liu, Y. Response time of magnetorheological fluids and magnetorheological valves under various flow conditions. J. Intell. Mater. Syst. Struct. 2012, 23, 949–957. [Google Scholar] [CrossRef]
- Hu, G.L.; Liao, M.K.; Li, W.H. Analysis of a compact annular-radial-orifice flow magnetorheological valve and evaluation of its performance. J. Intell. Mater. Syst. Struct. 2017, 28, 1322–1333. [Google Scholar] [CrossRef] [Green Version]
- Hu, G.L.; Zhou, F.; Liao, M.K.; Yu, L.F. Dynamic performance analysis of a compact annular-radial-orifice flow magnetorheological valve and its application in the valve controlled cylinder system. Actuators 2021, 10, 104. [Google Scholar] [CrossRef]
- Imaduddin, F.; Mazlan, S.A.; Zamzuri, H.; Yazid, I.I.M. Design and performance analysis of a compact magnetorheological valve with multiple annular and radial gaps. J. Intell. Mater. Syst. Struct. 2015, 26, 1038–1049. [Google Scholar] [CrossRef]
- Idris, M.H.; Imaduddin, F.; Mazlan, S.A.; Choi, S.B. A concentric design of a bypass magnetorheological fluid damper with a serpentine flux valve. Actuators 2020, 9, 16. [Google Scholar] [CrossRef] [Green Version]
- Bai, X.X.; Wereley, N.M.; Choi, Y.T. Magnetorheological energy absorber with dual concentric annular valves. J. Intell. Mater. Syst. Struct. 2016, 27, 944–958. [Google Scholar] [CrossRef]
- Yang, X.L.; Chen, Y.J.; Liu, Y.T.; Zhang, R.B. Modeling and experiments of an annular multi-channel magnetorheological valve. Actuators 2022, 11, 19. [Google Scholar] [CrossRef]
- Hu, G.L.; Zhong, F.; Zhang, H.Y.; Ding, R.Q. Structure optimization and performance analysis of a multiple radial magnetorheological valve. J. Beijing Inst. Technol. 2017, 26, 458–467. [Google Scholar]
- Nguyen, Q.H.; Choi, S.B.; Lee, Y.S. An analytical method for optimal design of MR valve structures. Smart Mater. Struct. 2009, 18, 095032. [Google Scholar] [CrossRef]
- Nguyen, Q.H.; Choi, S.B. Selection of magnetorheological brake types via optimal design considering maximum torque and constrained volume. Smart Mater. Struct. 2012, 21, 015012. [Google Scholar] [CrossRef]
- Keshav, M.; Chandramohan, S. Geometric optimization of magnetorheological valve using feedforward neural networks for distribution of magnetic flux density inside the valve. Smart Mater. Struct. 2019, 28, 105018. [Google Scholar] [CrossRef]
- Shamieh, H.; Sedaghati, R. Multi-objective design optimization and control of magnetorheological fluid brakes for automotive applications. Smart Mater. Struct. 2017, 26, 125012. [Google Scholar] [CrossRef]
- Naserimojarad, M.M.; Moallem, M.; Arzanpour, S. A comprehensive approach for optimal design of magnetorheological dampers. J. Intell. Mater. Syst. Struct. 2018, 29, 3648–3655. [Google Scholar] [CrossRef]
- Salloom, M.; Samad, Z. Magnetorheological directional control valve. Int. J. Adv. Manuf. Technol. 2012, 58, 279–292. [Google Scholar] [CrossRef]
- Paweł, M.; Sławomir, K.; Arkadiusz, M. Rotary shock-absorber with magnetorheological valves. Adv. Mater. Res. 2013, 628, 505–511. [Google Scholar]
- Kubík, M.; Macháček, O.; Strecker, Z.; Roupec, J.; Mazůrek, I. Design and testing of magnetorheological valve with fast force response time and great dynamic force range. Smart Mater. Struct. 2017, 26, 047002. [Google Scholar] [CrossRef]
- Yoo, J.H.; John, S.; Chaudhuri, A. A magnetorheological actuation system: Test and model. Smart Mater. Struct. 2008, 17, 025023. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).