Abstract
For an electro-hydrostatic actuator (EHA), the position, speed, and current cascade three-loop control architecture are dominant in existing active disturbance rejection control (ADRC). However, this architecture suffers from many problems, such as severe noise sensitivity of the extended state observer (ESO), excessive complexity of control structure, and too many tuned parameters, which makes the controller not easy to implement in practice. Aiming at the above drawbacks, a novel cascade double-loop ADRC strategy that is automatic current-constrained is proposed, which makes the whole ADRC architecture simplified to the position and the integrated speed–current double-loop architecture. Firstly, for the position control loop, the singular perturbation theory is used to reasonably reduce the order of the model for the position subsystem of EHA. A reduced order ADRC controller (ROADRC) is synthesized, which not only effectively reduces the noise sensitivity of ESO, but also circumvents use of the actuation acceleration information in the controller design process. Secondly, the integrated speed–current ADRC controller is designed by taking the speed and current subsystems of EHA into synthesis, which avoids the problem of excessive current loop bandwidth in conventional three-loop control architecture, and the number of tuned parameters is significantly reduced. Additionally, an uncomplicated and effective automatic current-constrained ADRC controller (CACADRC) is designed to solve the problem in the integrated speed–current ADRC that the current cannot be automatically constrained. Finally, by comparing the three-loop PI controller with the traditional three-loop ADRC, a detailed simulation analysis is carried out to verify the effectiveness and merits of the proposed controller. The simulation results show that the proposed controller not only inherits the advantages of high precision and strong disturbance rejection performance of the conventional ADRC, but can also efficiently decrease the noise sensitivity of ESO and effectively achieve the current-constrained control.
1. Introduction
Electro-hydrostatic actuator (EHA) is a typical self-contained pump-controlled servo system, which has the preponderances of high integration, sizeable power-to-weight ratio, high reliability, high efficiency, and convenient installation and maintenance. It has been popular in many fields, such as main flight rudder control systems of more-electric aircraft, robots, vehicle active suspension devices, and injection molding machines [1,2,3,4,5,6,7]. However, EHA is a high-order complex nonlinear system with strong coupling to mechanical, electrical, and hydraulic. Moreover, there are a lot of parameter uncertainties and external disturbances in the system, which will degenerate the control performance of EHA. Therefore, a control strategy with high dynamic performance and strong robustness is urgently needed.
Currently, many advanced control methods have been extensively studied to improve the control performance of EHA. In [8], an adaptive backstepping control method was put forward, which combines a special adaptive law with an improved backstepping algorithm to handle all uncertainties and nonlinearities in the EHA system. In [9], an asymptotically stable controller was presented based on a two-degree-of-freedom (2DOF) disturbance observer to compensate for the adverse effects of friction and internal leakage. A new adaptive damping variable sliding mode controller for EHA was developed to improve position step performance [10]. In [11], a composite adaptive control method based on a robust integral of the sign of error (RISE) was proposed, in which the parameter adaptive law was utilized to deal with unknown parameters, and RISE was adopted to repress the effects of the lumped disturbance on the system. To improve the position tracking performance of a novel EHA with a constant-torque variant-displacement pump, an adaptive control method combining backstepping and nonlinear projection was proposed in [12].
Recently, active disturbance rejection control (ADRC) has attracted more attention thanks to its strong robustness to uncertainties in the system [13,14]. ADRC is a 2DOF control method that does not completely lean upon the system model, which regards all kinds of uncertainties (parameter uncertainty, structural uncertainty, and external disturbance) in the system as a total disturbance, and the unique extended state observer (ESO) was utilized to real-time observe and compensate the total disturbance. At present, ADRC has been widely studied and applied in many fields, such as motor control, valve-controlled electro-hydraulic servo system, aircraft control, and robot control [15,16,17,18,19,20,21]. However, there is still very little ADRC research literature on EHA. A position and pressure cascade double-loop ADRC control architecture for single-rod EHA was proposed in [22], whereas this controller requires the pressure information of the hydraulic cylinder, and the dynamics of the motor’s speed and current were neglected. The position, speed, and current cascade three-loop ADRC control structure were employed in [23]. Unfortunately, this method needs acceleration information in the design process of ADRC, which will lead to the oscillation of the control signal and even the system’s instability due to the severe noise amplification effect of the acceleration signal. In [24], the position, pressure, speed, and current cascade four-loop control architecture was proposed, and ADRC was adopted for each control loop to improve the disturbance rejection ability, whereas this method requires the pressure information of the hydraulic cylinder two chambers and too many parameters need to be tuned. In addition, speed and current double-loop control architecture were adopted in [23,24]. Due to the excessive requirement on the bandwidth of the current loop, which results in employing power electronic devices with high operation frequency, then the hardware cost of the controller and the power consumption of power electronics were both increased.
For EHA, the existing ADRC control architecture often adopts the position, speed, and current cascaded three-loop ADRC control architecture, but this ADRC control architecture has the following defects: (1) the order of position loop ESO is 4 order, so ESO is very sensitive to noise, which makes it difficult for ESO to accurately estimate the disturbance; (2) in the design process of position loop ADRC, the acceleration information is required, and the acceleration information has an amplification effect on noise, which leads to control output oscillation and even system instability; (3) the speed and current are controlled by a cascaded double loop. As the current loop is the inner loop, the control bandwidth of the current loop required by the current loop is larger than that of the speed loop, which results in a larger switching frequency of the power electronic devices; (4) the position, speed, and current cascaded three-loop ADRC control structure is more complicated, and so many parameters need to be tuned, so it is not conducive to practical application in engineering. To solve these problems, this paper proposes a novel cascade double-loop ADRC method composed of the position loop and integrated speed–current loop based on singular perturbation theory. The main outstanding works of this paper are summarized as follows:
- 1.
- A novel cascade double-loop ADRC control architecture, including a reduced order position control loop and an integrated speed–current control loop, is presented, which has a simpler structure and fewer tuning parameters compared with the existing architecture.
- 2.
- For the position control loop, a reduced-order ADRC controller (ROADRC) is synthesized based on singular perturbation theory. ROADRC does not need the acceleration information. Moreover, the noise sensitivity of ESO is significantly weakened. Hence, the control output signal of ROADRC is smoother, and the practical application difficulty of ROADRC is easier.
- 3.
- An effectively integrated speed–current ADRC with automatic current-constrained (CACADRC) is designed based on the barrier function. CACADRC not only solves the problem of excessive bandwidth of the current loop but also effectively solves the problem that the current cannot be constrained automatically after the integrated design. Furthermore, the detailed stability proof of CACADRC is given according to the Lyapunov theory.
2. System Description
2.1. Basic Principle
The basic schematic diagram of EHA is illustrated in Figure 1. It is primarily composed of a permanent magnet synchronous motor (PMSM), reversible plunger pump, check valves, relief valves, accumulator, mode switching valve, cylinder, sensors and drive controller, etc. Among them, the current sensor, resolver, and displacement sensor are responsible for measuring the current, speed of PMSM, and displacement of the piston rod, respectively. According to the desired position signal, the drive controller executes the corresponding control algorithm to generate the drive control signal to control the speed and direction of PMSM, and then control the output flow and pressure of the reversible piston pump to make the piston of the hydraulic cylinder perform telescopic movement, and finally realizes the control of the position, speed, and direction of the load. The accumulator fills the system with oil through check valve 1 or 2 to prevent the system from damaging the hydraulic components due to the “cavitation” phenomenon caused by the low oil pressure, and relief valve 1 or 2 is used to prevent the excessive high oil pressure of the system for safety.
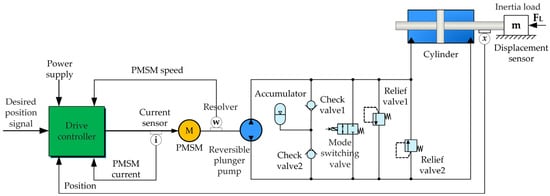
Figure 1.
Schematic diagram of EHA.
2.2. Mathematical Modelling
2.2.1. Equations for Voltage and Motion of PMSM
Assuming the PMSM’s rotor is surface-mounted, then the voltage equations of the q-axis and d-axis in the q, d rotor reference frame are mathematically depicted as:
where uq and ud are q, d axis voltage components; Rh is the stator resistance; iq and id are q, d axial current components; Lq and Ld are the equivalent inductance of q, d axis; ωm is the mechanical angular speed of PMSM; p is the number of pole pairs; and ψf is the flux linkage of the rotor permanent magnet.
The motion equation of the PMSM can be given by:
where Jp is the rotor inertia of PMSM; Bp is the viscous friction coefficient of the reversible plunger pump; Dp is the displacement of the reversible plunger pump; and pa and pb are the oil outlet and inlet pressures of the pump, respectively.
2.2.2. Flow Equation of Reversible Plunger Pump
Regarding the reversible plunger pump, the flow equation can be described as follows:
where Qa and Qb are the oil outlet and inlet flow of the pump, respectively; Qip, Qopa, and Qopb are the internal and external leakage flow of the pump, respectively; βe is the effective oil bulk modulus; and Va and Vb are respectively the volumes of oil outlet chamber and oil return chamber of the pump.
2.2.3. Flow Equation of Hydraulic Cylinder
Ignoring the external leakage flow of the hydraulic cylinder, the flow equation in two chambers of the hydraulic cylinder can be written as:
where Q1 and Q2 are, respectively, the inflow and outflow flow of the two chambers of the hydraulic cylinder; A is the effective working area of the hydraulic cylinder piston; x is the displacement of the piston rod of the hydraulic cylinder; p1 and p2 are respectively the pressure of the two chambers of the hydraulic cylinder; Qic is the internal leakage flow in the hydraulic cylinder; and V10 and V20 are the volumes of the closed chamber on both sides of the hydraulic cylinder, respectively.
2.2.4. Motion Equation of the Hydraulic Cylinder
The balance equation that denotes the connection between the load and the output force of the hydraulic cylinder can obtain the following:
where mt is the total mass of the piston, piston rod, and load; Bt is the total viscous friction coefficient of the hydraulic cylinder and the load; and FL is the external load force applied to the piston rod.
2.2.5. Equation of Pressure Dynamics
According to the flow continuity characteristics, the flow equation can be written as follows:
where Qc1, Qc2, Qr1, and Qr2 are the flow through the check valve and the relief valve, respectively.
Assuming that the pressure loss from the pump to the hydraulic cylinder line is zero because the flow channel in the valve block is very short, then pa = p1, pb = p2. In addition, Va = V10 + Ax, Vb = V20−Ax, considering Equations (3), (4), and (6), we can obtain the following:
where Qv1 = −Qc1 + Qr1; Qv2 = −Qc2 + Qr2.
Assuming that the piston is in the middle position of the hydraulic cylinder at the initial stage, namely V10 ≈ V20 = V0, and considering that the hydraulic cylinder is symmetric, it is approximately . Equation (7) is taken into consideration to obtain:
where pL = p1−p2 is the load pressure; Ct is the total leakage coefficient of the pump and the hydraulic cylinder; and Qun = −(Qopa−Qopb)/2 + (Qv1 + Qv2)/2.
Defining state variables as X = (x1, x2, x3, x4, x5, x6)T= (x, , pL, ωm, iq, id)T, the state equation of EHA can be depicted as follows:
where dLm = −FL; dLp = −DppL.
With ud, uq as the direct control quantity, EHA is a 5-order, 2-input single-output system. For the purpose of simplifying the controller design process, the whole system is divided into three subsystems; namely, the position subsystem composed of state variables x, , pL, the speed subsystem composed of state variable ωm, and the current subsystem composed of state variables id, iq.
2.3. Reduced Order Model of EHA Based on Singular Perturbation Theory
Because the design order of position loop ESO in the conventional three-loop ADRC architecture of EHA is 4 order and the acceleration information in the controller has an amplification effect on noise, ESO is very sensitive to noise. Therefore, if the position loop ESO can be reduced-order processed, the practicability of the position loop ADRC controller will be significantly increased. Based on the above idea, the singular perturbation theory is utilized to reduce the order of the position subsystem. First, the position subsystem is written into the singular perturbation form, and then the order of the position subsystem model is reduced [25].
It is noted that the effective oil bulk modulus βe is a numerically sizeable physical quantity in Equation (8); usually, its value is (7~15) × 108 Pa, so ɛs = βe−1V0 is chosen as the singular perturbation parameter. Defining the state variables Xs= (x, )T and Zs = pL, Equations (5) and (8) can be written in the singularly perturbed standard form:
Let ɛs = 0, the following formula of Equation (10) can degenerate into an algebraic equation:
The quasi-steady state quantity of pL can be obtained as follows:
Define yτ = pL − , then:
Set ɛs = 0, τs = t/ɛs, then Equation (13) can be converted into the new timescale τs framework, then the boundary layer model equation can obtain the following:
It is clear that the boundary layer model is asymptotically stable concerning the equilibrium point yτ = 0. According to Tikhonov theorem, it can be known that:
, when satisfies , we have for , and we have for .
The quasi-steady state quantity is substituted into the upper formula of Equation (10), and the reduced order model can be obtained as follows:
Define the state variables X = (x1, x2)T = (x,)T, then Equation (15) can be written as the following state space form:
where gx0 is the nominal value of gx = ADp/(mtCt); dx = Δgxωm−[A2(mtCt)−1 + mt−1Bt]‧ + A(mtCt)−1Qun−mt−1FL; and Δgx is the perturbation value of parameter gx.
3. Design of Novel ADRC for EHA
If the two-position two-way mode switching valve in Figure 1 is closed, then the system is in position control mode. The EHA control architecture diagram of the proposed method is shown in Figure 2.
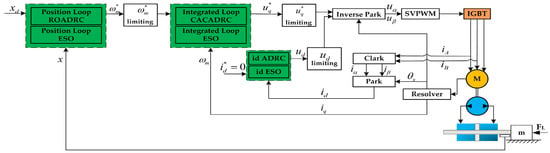
Figure 2.
The control architecture diagram of the EHA.
While the two-position two-way mode switching valve is switched on, the system is in speed control mode. The position loop in Figure 2 is removed to obtain the EHA control architecture diagram of the CACADRC.
3.1. ROADRC Design
By designing ESO to accurately estimate dx, converting it into a corresponding control quantity to cancel the disturbance, and then considering it as a nominal model without any disturbance to design the controller, the difficulty of controller design will be significantly reduced.
Assuming that ωmc represents the disturbance compensation control quantity and ωm0 represents the nominal control quantity, then the output of the ROADRC controller is ωm* = ωm0 + ωmc.
In the following, ESO is designed to estimate dx, and the total disturbance dx is expanded into an additional state denoted by x3, and its derivative satisfies this condition: = hx. Then, the ESO can be constructed as:
where lx1, lx2 and lx3 > 0 are satisfying the Hurwitz condition, and , and are the estimated values of x1, x2, and x3, respectively.
Then, ωm* can be designed as:
where xd is the position reference, and kx1 and kx2 are the control parameters of ROADRC.
It can be seen from Equation (17) that three parameters lx1 ~ lx3 need to be tuned, and the characteristic equation s3 + lx1s2 + lx2s + lx3 of ESO can be integrated into the mode of multiple poles, namely (s + ωox)3. In this way, lx1 ~ lx3 is only related to the ESO bandwidth ωox, so ESO only needs to set one parameter ωox. Then, lx1 ~ lx3 can be easily calculated as [26]:
Similarly, the control system is of order 2, and the characteristic equation s2 + kx2s + kx1 is integrated into the mode of multiple poles, namely (s + ωcx)2. ωcx is the control bandwidth, so one only needs to adjust the ωcx parameter. In this case, kx1 ~ kx2 can be easily calculated as:
3.2. CACADRC Design
In conventional three-loop control architecture, the bandwidth of the current loop is usually required to be larger than that of the speed loop, so it requires a higher operating frequency of power electronic devices, which leads to the increase in the hardware cost of the controller and the power consumption of power electronics. Moreover, this architecture needs to set more parameters. To deal with these problems, the speed loop, and current loop can be regarded as a whole to design the controller.
Rewrite motor motion Equation (2) as follows:
where aω = −Jp−1Bpωm−Jp−1DpPL.
By taking the derivative of both sides of Equation (21) and considering Equation (1), it can be obtained:
where gωq0 is the nominal value of gωq = 3/2∙pψfJp−1Lq−1; dωq = Δgωquq + gω[−Lq−1Rhiq−Lq−1pωm(Ldid + ψf)] , and Δgωq is the perturbation value of parameter gωq.
Defining the state variables ωm = (ωm1, ωm2)T = (ωm, )T and rewriting Equation (22) as the following state space form:
Assuming that uqc represents the disturbance compensation control quantity and uq0 represents the nominal control quantity, the output of the integrated speed–current control is uqi* = uq0 + uqc.
In the following, ESO is designed to estimate dωq, and the total disturbance dωq is expanded into a state, namely ωm3 = dωq, denoted as = hωq, ESO needs to be designed as order 3, and the ESO is constructed as:
where lωq1, lωq2, and lωq3 > 0 are satisfying Hurwitz condition, and , and are the estimated values of ωm1, ωm2, and ωm3, respectively.
Defining the speed tracking error is as eωq1 = ωmd −, eωq2=− , then uqi* is designed as:
where ωmd is the speed reference, and kωq1 and kωq2 are the control parameters of the integrated speed–current loop controller.
However, it should be noted that after the integration of ωm and iq is processed, iq is in an uncontrollable state, which means the amplitude of iq cannot be limited as the traditional ADRC architecture; namely, iq may be larger than iqmax. To deal with this problem, a CACADRC controller that can automatically constrain iq is developed here. Therefore, Equation (25) is amended as follows:
where is the barrier function; l is the current penalty coefficient; and iqmax is the limiting value of iq.
Remark 1:

The differential term eωq2 of speed tracking error eωq1 characterizes the damping or angular acceleration of the system to some extent. The larger the damping is, the slower the tracking speed of the rotating speed is, but the more stable the tracking transient is. As can be seen fromFigure 3, when iq approaches iqmax, the nonlinear current penalty term increases, the damping of the system increases, and the angular acceleration decreases. It is noted that the angular acceleration is proportional to the current, so iq decreases. As iq moves away from iqmax, the nonlinear current penalty term decreases, the damping of the system decreases, the angular acceleration increases, and iq begins to increase again. Finally, iq fluctuates around iqmax.

Figure 3.
Automatic current-constrained mechanism of barrier function fbr.
The ESO bandwidth of CACADRC is represented by ωoωq. At the same time, since the ESO of CACADRC is also of order 3, similar to the ESO’s parameter tuning process of the position loop, lωq1 ~ lωq3 can be easily calculated as:
The control system is of order 2, and the control bandwidth of CACADRC is ωcωq. In this case, it is easy to calculate kωq1 ~ kωq2 as:
4. Stability Proof of the System
4.1. Stability Proof of ROADRC
4.1.1. Proof of Convergence of ESO
Considering Equation (17), then the characteristic polynomial of ROADRC’s ESO is denoted by:
where ωox > 0, according to the binomial theorem:
Let ei = xi−,i = 1, 2, 3, subtract Equation (17) from Equation (16), and we have:
Substituting Equation (30) into Equation (31), we can obtain:
Make ɛi = ei/ωoxi−1, i = 1, 2, 3, then:
Writing the above equation in matrix form:
where .
Since A satisfies Hurwitz’s condition, there exists a positive definite matrix P, such that ATP + PA = −I. Defining the Lyapunov function V(ɛ) = ɛTPɛ, and taking the derivative about time:
If hx is bounded, i.e., |hx| < M, when , is always satisfied, then will converge to the range , so is bounded. Considering ɛi = ei/ωoxi−1, i = 1, 2, 3, and inequality (35), we can obtain the following:
Thus, is bounded. In particular, when hx = 0, e is asymptotically stable, namely .
4.1.2. Stability Proof of Controller
Substituting Equation (18) into Equation (16), we can obtain:
Rearranging Equation (37), we have:
Writing the above equation in matrix form:
where , , , .
Since kx1 and kx2 satisfy Hurwitz’s condition, there exists a positive definite matrix Px, such that . Defining the Lyapunov function , taking the derivative of V about time:
where λmax (Px) is the largest eigenvalue of Px.
When , is always satisfied, then must converge to the range , i.e., is bounded. Especially when the ESO estimation error is , , then .
4.2. Stability Proof of CACADRC
4.2.1. Proof of Convergence of ESO
The proof process of ESO convergence is similar to that of position loop ESO.
4.2.2. Stability Proof of Controller
Combined with Equations (23) and (26), the closed-loop system can be given as:
Therefore, the control system can be written as follows:
Theorem 1.
If the initial value iq(0) ϵ (-iqmax, iqmax), (ewq1, ewq2) asymptotically converges to a bounded closed set, where βkωq is indicated below. In the meantime, iq(t) ϵ (-iqmax, iqmax) always hold.
Proof:
The Lyapunov function is defined as:
According to the system (42), to find the differentiation of V(eωq):
If the controller parameters kωq1 > 1 and , then:
where βkωq = min {kωq1−1, kωq1 + 2kωq2−2 + 2l/tan−1(iqmax2−iq2)} is a positive number.
At the moment, according to Lyapunov’s theorem, (ewq1, ewq2) asymptotically converges ΩE.
Next, according to Equation (42):
F(eωq1,eωq2) is a continuous function when (−iqmax, iqmax). If iq approaches ±iqmax, . There is a constant , such that there must be when , which means always hold. Thus, the inequality (45) is always true for any time.
Especially when = 0, the closed loop system (41) is asymptotically stable at the equilibrium point. Meanwhile, iq(t) ϵ (−iqmax, iqmax) always hold. □
5. Simulation Results
For the purpose of verifying the control performance and the effectiveness of the proposed method, a detailed simulation analysis was conducted by comparing it with different methods, which was performed by using MATLAB/Simulink. For the convenience of analysis, these methods are abbreviated as follows:
- 2PI: the conventional PI controller is employed in the speed and current double-loop.
- 2ADRC: the conventional ADRC is employed in the speed and current double-loop.
- 3PI: the conventional PI controller is employed in the position, speed, and current three-loop.
- 3ADRC: the conventional ADRC is employed in the position, speed, and current three-loop.
- 3ADRC1: the position loop ADRC of 3ADRC.
- Proposed method: ROADRC is employed in the position loop, and CACADRC is adopted for the integrated speed–current loop.
The EHA system parameters are detailed in Table 1 below.

Table 1.
The EHA system parameters.
5.1. Performance Simulation Analysis of CACADRC
In this simulation study, the speed tracking performance, disturbance rejection performance, and automatic current-constraint effectiveness of CACADRC are demonstrated. The current constraint is 16A, and the speed reference ωmd is 500 rad/s.
The simulation is divided into two cases. The first case is used to illustrate the current limiting effect of the current penalty coefficient l and provide guidance for choosing l. The second case is used to compare the tracking performance and disturbance rejection performance of 2PI, 2ADRC, and CACADRC.
CACADRC parameters:
ωcωq = 85 rad/s, ωoωq = 5ωcωq; the control bandwidth of the current loop in d-axis is ωcd = 1257 rad/s; and the ESO bandwidth is ωod = 10ωcd.
Case 1: Figure 4a–c shows ωm, iq and uq response curves under the action of different current penalty coefficients l, respectively. It can be seen that iq is constrained within the amplitude limit of 16A when l = 0.1kωq2, kωq2, and 2kωq2, which means that the CACADRC can effectively realize automatic current-constraint control, and by adjusting the current penalty coefficient l in the barrier function, the current limiting intensity can be effectively adjusted. When l increases, the current iq will decrease, resulting in a decrease in the response speed of ωm. It should be noted that if the value of l is too large, the transient performance of the system will suffer a certain loss. On the contrary, if the value of l is too small, the current iq will exceed the amplitude limit, which makes the circuit safety threatened. Therefore, a compromise should be considered in practical applications.
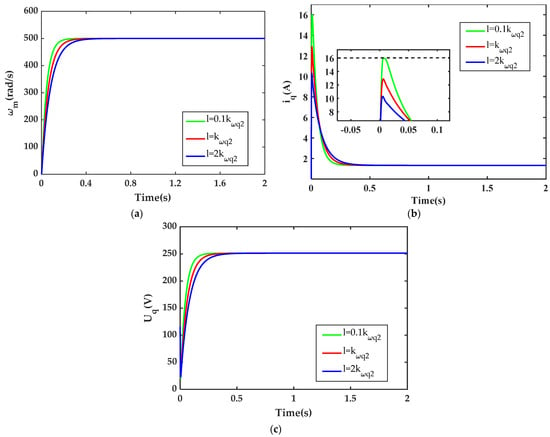
Figure 4.
Performance comparisons under CACADRC with different current penalty coefficients l. (a) Speed response curves; (b) q-axis current response curves; and (c) q-axis voltage response curves.
Figure 5a–c, respectively, shows ωm, iq and uq response curves. To quantitatively analyze the performance of the different methods, the performance evaluation indices are employed, which are listed in Table 2, including overshoot (OS), settling time (ST), peak current (PC), speed drop (SD), recovery time (RT) and the number of parameters (PN).
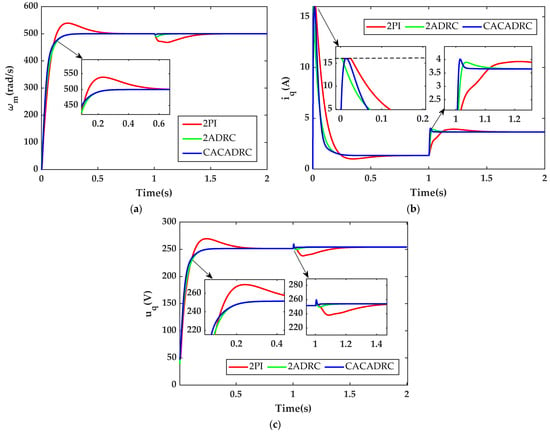
Figure 5.
Speed step response comparison curves with ωmd = 500 rad/s. (a) Speed response curves; (b) q-axis current response curves; and (c) q-axis voltage response curves.

Table 2.
Performance evaluation indices.
2PI parameters:
Speed loop: KPω = 0.05, KIω = 0.3; q-axis current loop: KPq = 2.2, KIq = 564.8; d-axis current loop: KPd = 20, KId = 2011.
2ADRC parameters:
The control bandwidth of the speed loop is ωcω = 21.4 rad/s, and the ESO bandwidth is ωoω = 10ωcω; the control bandwidth of the current loop in the d-axis, q-axis is ωcd = 1257 rad/s, ωcq = 1257 rad/s, respectively; and the ESO bandwidth is ωod = ωcd, ωoq = ωcq, respectively.
CACADRC parameters:
Take l = 0.01 kωq2, ωcωq = 72 rad/s, ωoωq = 10 ωcωq; ωcd = 1257 rad/s, ωod = 10 ωcd.
Case 2: In the startup phase, it is observed in Figure 5a and Table 2 that, when compared with 2PI and 2ADRC, both CACADRC and 2ADRC can realize tracking without overshoot, while 2PI has a large overshoot. CACADRC and 2ADRC have the similar OS and ST, i.e., comparable tracking performance, which indicates that CACADRC does not need an excessive inner loop control bandwidth and requires fewer tuning parameters to have a similar dynamic performance as 2ADRC. In addition, in accordance with the requirement of iq < 16A, it can be seen from Figure 5b and Table 2 that the iq of 2PI, 2ADRC, and CACADRC are all kept within the current restricted range. The reason is that 2PI and 2ADRC constrain the current by limiting the control output iq*, while CACADRC constrains the current by adding the barrier function to the controller, which has the same current limiting effect as well as 2ADRC and 2PI.
An external load of 2000 N‧m is suddenly applied at t = 1s. It can be seen from Figure 5a and Table 2 that CACADRC has a slightly better disturbance rejection ability than 2ADRC. While the 2PI has a larger SD and longer RT, that is, the disturbance rejection ability is poor. The reason is, on the one hand, the PI controller does not explicitly consider the speed regulation performance and disturbance rejection performance, it is to choose appropriate parameters to meet these performances in a compromise, while ADRC is a 2DOF controller, which can separately consider the speed regulation performance and disturbance rejection performance. On the other hand, the disturbance rejection effect of the PI controller is mainly realized by the integration effect, and the integration has a cumulative effect, so the disturbance compensation will inevitably be delayed. Although the delay effect can be alleviated by increasing the integral gain of the controller, a large integral gain will lead to a larger overshoot of the step response when there is no external load.
5.2. Performance Simulation Analysis of ROADRC
In this simulation study, the position tracking performance, disturbance rejection performance, and ESO noise reduction effect of ROADRC are demonstrated.
The simulation is divided into two cases. The first case is the position tracking performance, disturbance rejection performance, and sensitivity to noise of 3PI, 3ADRC, and the proposed method when the position reference is a step signal. The second case is the position tracking performance, disturbance rejection performance, and sensitivity to noise of 3PI, 3ADRC, and the proposed method when the position reference is a time-varying signal.
3PI parameters:
Position loop: KPx = 12661.58, KIx = 48091.89. KPω = 0.05, KIω = 0.3; KPq = 2.2, KIq = 564.8; KPd = 20, KId = 2011.
3ADRC parameters:
The control bandwidth of 3ADRC1 is ωcx = 94 rad/s, and the ESO bandwidth is ωox = 10 ωcx. ωcω = 628 rad/s, ωoω = 5 ωcω; ωcd = 1257 rad/s, ωcq = 1257 rad/s; ωod = ωcd, ωoq = ωcq.
The proposed method parameters:
Take l = 19 kωq2, ωcx = 94 rad/s, ωox = 10 ωcx; ωcωq = 628 rad/s, ωoωq = 5 ωcωq; ωcd = 1257 rad/s, ωod = ωcd.
Case 1: The position reference xd is 0.1m, and a uniformly distributed noise signal with an amplitude of 1 × 10−5 is added to the position signal x. The comparison curves of position step performance are shown in Figure 6. As shown in Figure 6a, it is seen that although 3PI has the fastest response speed, it produces a 10% overshoot, while the proposed method and 3ADRC achieve almost the same tracking performance without overshoot.
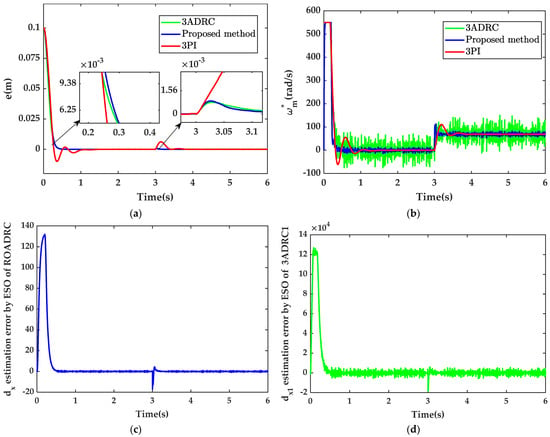
Figure 6.
Position step response comparison curves with xd = 0.1m. (a) Comparison curves of position tracking errors of 3ADRC, the proposed method and 3PI; (b) control output ωm* response curves; (c) disturbance estimation error by ESO of ROADRC; and (d) disturbance estimation error by ESO of 3ADRC1.
The external load force of 1000 N is suddenly applied at t = 3 s. It can be seen from Figure 6a that the 3PI produces a position error of about 0.0062 m, and the position recovery time is about 0.84 s. Although 3PI can recover to its original position eventually, the recovery time is very long, while 3ADRC produces a position error of about 0.0012 m with a position recovery time of about 0.35 s, and the proposed method produces a position error of about 0.001 m with a position recovery time of about 0.35 s. It can be seen that the proposed method and 3ADRC have similar disturbance rejection capabilities, because both of them estimate and compensate for the disturbance in real-time through ESO, while the disturbance rejection ability of 3PI is significantly worse than that of 3ADRC and the proposed method because PI controller is used to suppress the disturbance through integration.
Moreover, it can be calculated:
The disturbance quantity dx of ROADRC:
The disturbance quantity dx1 of 3ADRC1:
Figure 6c,d shows that the ESO to disturbance estimation curve of ROADRC is smoother than that of 3ADRC1 because the ESO order of ROADRC is lower than that of 3ADRC1, in other words, the disturbance estimation of ROADRC is more accurate than that of 3ADRC1.
In addition, it can be seen from Figure 6b that the control output ωm* of 3ADRC1 is more seriously polluted by noise than that of ROADRC. The reason is the ESO order of 3ADRC1 is one order higher than that of ROADRC, so it is sensitive to noise, and the 3ADRC1 introduces the actuation acceleration information, which has an amplification effect on noise. However, the control output curve ωm* of the position loop PI is the smoothest, because only the proportional term of the position loop PI introduces noise, and the integral term can suppress the noise to a certain extent.
Case 2: The position reference xd is 0.001 sin (4πt) m, and a uniformly distributed noise signal with an amplitude of 1 × 10−5 is added to the position signal x. In order to verify the influence of interference force and parameter mutation on system performance, it is assumed that external load FL = 500 sin (2πt) N is applied at t = 0 s, while total mass of the piston, piston rod and load mt and total leakage coefficient of the pump and the hydraulic cylinder Ct become twice the original value, respectively.
The comparison curves of position tracking performance are manifested in Figure 7. It can be seen from Figure 7a that 3PI has the largest tracking error, and the tracking error of ROADRC is slightly smaller than that of 3ADRC, which indicates that the disturbance rejection ability of the proposed method is slightly better than that of 3ADRC and significantly better than that of 3PI. As can be seen from Figure 7c,d, the disturbance estimation error curve of ROADRC’s ESO is smoother than that of 3ADRC1, since the ESO order of ROADRC is lower than that of 3ADRC1. In addition, it can be indicated from Figure 7b that the control output ωm* of 3ADRC1 is more seriously polluted by noise than that of ROADRC.
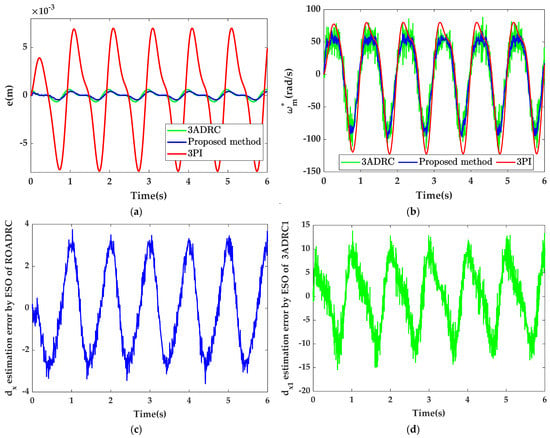
Figure 7.
Position time-varying signal response comparison curves under complex disturbance when xd = 0.001 sin (4πt) m. (a) Comparison curves of position tracking errors of 3ADRC, the proposed method and 3PI; (b) control output ωm* response curves; (c) disturbance estimation error by ESO of ROADRC; and (d) disturbance estimation error by ESO of 3ADRC1.
6. Conclusions
In this paper, a novel cascade double-loop ADRC control architecture, including the reduced order position control loop and an integrated speed–current control loop, was proposed to improve the control performance of EHA. By comparing with traditional three-loop PI controller and traditional three-loop ADRC, the following conclusions can be given:
- The barrier function introduced in CACADRC can effectively achieve automatic current-constraint control, and by adjusting the current penalty coefficient l in the barrier function, the current limiting intensity can be effectively adjusted. Compared with 2PI and 2ADRC, both CACADRC and 2ADRC can realize tracking without overshoot, while 2PI has a large overshoot. In terms of anti-disturbance ability, CACADRC and 2ADRC have a more excellent anti-disturbance performance than 2PI, and CACADRC has a slightly better anti-disturbance ability than 2ADRC.
- When the position reference is a step signal, both the proposed method and 3ADRC can achieve tracking without overshoot, while 3PI has a large overshoot. Moreover, the disturbance rejection performance of the proposed method is similar to that of 3ADRC and superior to that of 3PI when subjected to step disturbance. In addition, when the position reference is a sinusoidal time-varying signal, the disturbance rejection ability of the proposed method is slightly better than that of 3ADRC and significantly better than that of 3PI.
- Due to the reduced order processing of the position subsystem, the order of the ESO of ROADRC is lower than that of the ESO of 3ADRC1, and the noise sensitivity is effectively weakened, which makes the disturbance estimation of the ROADRC’s ESO smoother than that of 3ADRC1. Moreover, in the process of ROADRC design, the use of acceleration information is avoided, so the control output signal ωm* of ROADRC is smoother than that of 3ADRC1.
- The proposed novel cascaded double-loop ADRC control architecture is simpler than the traditional cascaded three-loop ADRC control architecture and requires fewer parameters to be tuned, which is more conducive to the application in practical engineering.
Author Contributions
Conceptualization, R.Y., Y.M. and L.Z.; methodology, R.Y. and Y.M.; software, R.Y. and Y.M.; validation, R.Y., Y.M. and L.Z.; formal analysis, Y.M., L.Z. and H.H.; investigation, J.Z.; resources, H.H.; data curation, L.Z. and H.H.; writing—original draft preparation, R.Y. and Y.M.; writing—review and editing, R.Y., Y.M., J.Z. and L.Z.; visualization, R.Y., L.Z. and J.Z.; supervision, J.Z., L.Z. and H.H.; project administration, J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (grant number: 51565030) and the Science and Technology Program of Gansu Province (grant number: 20JR10RA175).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Not applicable.
Acknowledgments
The authors acknowledge the English review process conducted by MDPI services.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Symbol | Comment |
| EHA | electro-hydrostatic actuator |
| ADRC | active disturbance rejection control |
| ESO | extended state observer |
| ROADRC | reduced-order ADRC controller |
| CACADRC | automatic current-constrained ADRC controller |
| PI | proportional integral controller |
| 2DOF | two-degree-of-freedom |
| RISE | the robust integral of the sign of error |
| PMSM | permanent magnet synchronous motor |
| uq, ud | q,d axis voltage components |
| Rh | stator resistance |
| ig, id | q,d axial current components |
| Lq, Ld | the equivalent inductance of q, d axis |
| ωm | the mechanical angular speed of PMSM |
| p | the number of pole pairs |
| ψf | flux linkage of the rotor permanent magnet |
| Jp | rotor inertia |
| Bp | the coefficient of viscous friction of the reversible plunger pump |
| Dp | displacement of the reversible plunger pump |
| pa, pb | oil outlet and inlet pressures of the pump |
| Qa, Qb | oil outlet and inlet flow of the pump |
| Qip, Qopa, Qopb | internal and external leakage flow of the pump |
| βe | effective oil bulk modulus |
| Va, Vb | volumes of the oil outlet chamber and oil return chamber of the pump |
| Q1, Q2 | inflow and outflow flow of the two chambers of the hydraulic cylinder |
| A | the effective working area of the hydraulic cylinder piston |
| x | displacement of the piston rod of the hydraulic cylinder |
| p1, p2 | the pressure of the two chambers of the hydraulic cylinder |
| Qic | internal leakage flow in the hydraulic cylinder |
| V10, V20 | volumes of the closed chamber on both sides of the hydraulic cylinder |
| mt | the total mass of the piston, piston rod, and load |
| Bt | the total viscous friction coefficient of the hydraulic cylinder and the load |
| FL | the external load force applied to the piston rod |
| Qc1, Qc2 | flow through the check valve |
| Qr1, Qr2 | flow through the relief valve |
| pL | load pressure |
| Ct | total leakage coefficient of the pump and the hydraulic cylinder |
| quasi-steady state quantity | |
| ωmc | disturbance compensation control quantity of ROADRC |
| ωm0 | nominal control quantity of ROADRC |
| ωm* | control output of ROADRC |
| lx1, lx2, lx3 | ESO gains of ROADRC |
| Xd | position reference |
| kx1, kx2 | control parameters of ROADRC |
| ωox | ESO bandwidth of the position loop |
| ωcx | control bandwidth of the position loop |
| uqc | disturbance compensation control quantity of the integrated speed–current control |
| uq0 | nominal control quantity of the integrated speed–current control |
| uqi* | the output of the integrated speed–current control |
| lωq1, lωq2, lωq3 | ESO gains of the integrated speed–current control |
| ωmd | speed reference |
| kωq1, kωq2 | control parameters of the integrated speed–current controller |
| uq* | control output of CACADRC |
| fbr | barrier function |
| l | current penalty coefficient |
| iqmax | limiting value of iq |
| ωoωq | ESO bandwidth of CACADRC |
| ωcωq | control bandwidth of CACADRC |
| 2PI | the conventional PI controller is employed in the speed and current double-loop |
| 2ADRC | the conventional ADRC is employed in the speed and current double-loop |
| 3PI | the conventional PI controller is employed in the position, speed, and current three-loop |
| 3ADRC | the conventional ADRC is employed in the position, speed, and current three-loop |
| 3ADRC1 | the position loop ADRC of 3ADRC |
| Proposed method | ROADRC is employed in the position loop, and CACADRC is adopted for the integrated speed–current loop |
| ωcd | control bandwidth of the current loop in the d-axis |
| ωod | ESO bandwidth of the current loop in the d-axis |
| D | piston diameter of the hydraulic cylinder |
| d | piston rod diameter of hydraulic cylinder |
| L | piston stroke |
| V | the total volume of the hydraulic cylinder |
| V0 | the initial one-sided volume of the hydraulic cylinder |
| uN | PMSM-rated voltage |
| IN | PMSM-rated current |
| TN | PMSM-rated torque |
| ωmN | PMSM-rated rotating speed |
| OS | overshoot |
| ST | settling time |
| PC | peak current |
| SD | speed drop |
| RT | recovery time |
| PN | number of parameters |
| KPω, KIω | proportion and integral gains of speed loop of 2PI |
| KPq, KIq | proportion and integral gains of the q-axis current loop of 2PI |
| KPd, KId | proportion and integral gains of the d-axis current loop |
| ωcω | control bandwidth of the speed loop of 2ADRC |
| ωoω | ESO bandwidth of the speed loop of 2ADRC |
| ωcq | control bandwidth of the current loop in the q-axis of 2ADRC |
| ωoq | ESO bandwidth of the current loop in the q-axis of 2ADRC |
| KPx, KIx | proportion and integral gains of the position loop of 3PI |
| ωcx | control bandwidth of the position loop |
| ωox | ESO bandwidth of the position loop |
| dx | disturbance quantity of ROADRC |
| dx1 | disturbance quantity of 3ADRC1 |
References
- Fu, Y.L.; Han, X.; Yang, R.R.; Qi, H.T.; Fu, J. Review on Design Method of Electro-hydrostatic Actuator. J. Beijing Univ. Aeronaut. Astronaut. 2017, 43, 1939–1952. (In Chinese) [Google Scholar] [CrossRef]
- Mare, J.C.; Fu, J. Review on Signal-by-Wire and Power-by-Wire Actuation for More Electric Aircraft. Chin. J. Aeronaut. 2017, 30, 857–870. [Google Scholar] [CrossRef]
- Alle, N.; Hiremath, S.S.; Makaram, S.; Subramaniam, K.; Talukdar, A. Review on Electro-hydrostatic Actuator for Flight Control. Int. J. Fluid Power 2016, 17, 125–145. [Google Scholar] [CrossRef]
- Ko, T.; Murotani, K.; Yamamoto, K.; Nakamura, Y. Whole-Body Compliant Motion by Sensor Integration of an EHA-Driven Humanoid Hydra. Int. J. Hum. Robot. 2021, 18, 2150002. [Google Scholar] [CrossRef]
- Kou, F.R. The Control Study of Vehicle Active Suspension with Electro-hydrostatic Actuator. Appl. Mech. Mater. 2011, 97–98, 716–720. [Google Scholar] [CrossRef]
- Sun, W.C.; Gao, H.J.; Yao, B. Adaptive Robust Vibration Control of Full-Car Active Suspensions with Electro-hydraulic Actuators. IEEE Trans. Control Syst. Technol. 2013, 21, 2417–2422. [Google Scholar] [CrossRef]
- Chiang, M.H.; Chen, C.C.; Kuo, C.F.J. The High Response and High Efficiency Velocity Control of a Hydraulic Injection Molding Machine Using a Variable Rotational Speed Electro-hydraulic Pump-Controlled System. Int. J. Adv. Manuf. Technol. 2009, 43, 841–851. [Google Scholar] [CrossRef]
- Ahn, K.K.; Nam, D.N.C.; Jin, M. Adaptive Backstepping Control of an Electro-hydraulic Actuator. IEEE/ASME Trans. Mechatron. 2013, 19, 987–995. [Google Scholar] [CrossRef]
- Lee, W.; Kim, M.J.; Chung, W.K. Asymptotically Stable Disturbance Observer-Based Compliance Control of Electro-hydrostatic Actuators. IEEE/ASME Trans. Mechatron. 2019, 25, 195–206. [Google Scholar] [CrossRef]
- Li, L.J.; Wang, M.K.; Yang, R.R.; Fu, Y.L.; Zhu, D.M. Adaptive Damping Variable Sliding Mode Control for an Electro-hydrostatic Actuator. Actuators 2021, 10, 83. [Google Scholar] [CrossRef]
- Ge, Y.W.; Yang, X.W.; Deng, W.X.; Yao, J.Y. Rise-Based Composite Adaptive Control of Electro-hydrostatic Actuator with Asymptotic Stability. Machines 2021, 9, 181. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, M.K.; Fu, J.; Fu, Y.L. Adaptive Control of an Aerospace Electro-hydrostatic Actuator with a Constant-Torque Variable-Displacement Pump. J. Aerosp. Eng. 2022, 35, 04022028. [Google Scholar] [CrossRef]
- Han, J.Q. From PID to Active Disturbance Rejection Control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Gao, Z.Q.; Huang, Y.; Han, J.Q. An Alternative Paradigm for Control System Design. In Proceedings of the 40th IEEE Conference on Decision and Control, Orlando, FL, USA, 4–7 December 2001; pp. 4578–4585. [Google Scholar] [CrossRef]
- Wang, Y.C.; Fang, S.H.; and Hu, J.X. Active Disturbance Rejection Control based on Deep Reinforcement Learning of PMSM for More Electric Aircraft. IEEE Trans. Power Electron. 2023, 38, 406–416. [Google Scholar] [CrossRef]
- Zhu, L.H.; Zhang, G.Q.; Jing, R.Z.; Bi, G.D. Nonlinear Active Disturbance Rejection Control Strategy for Permanent Magnet Synchronous Motor Drives. IEEE Trans. Energy Convers. 2022, 37, 2119–2129. [Google Scholar] [CrossRef]
- Xu, Z.B.; Deng, W.X.; Shen, H.; Yao, J.Y. Extended-State-Observer-Based Adaptive Prescribed Performance Control for Hydraulic Systems with Full-State Constraints. IEEE/ASME Trans. Mechatron. 2022, 1–11. [Google Scholar] [CrossRef]
- Liu, C.; Yue, X.K.; Zhang, J.Q.; Shi, K.K. Active Disturbance Rejection Control for Delayed Electromagnetic Docking of Spacecraft in Elliptical Orbits. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 2257–2268. [Google Scholar] [CrossRef]
- Xu, L.X.; Ma, H.J.; Guo, D.; Xie, A.H.; Song, D.L. Backstepping Sliding-Mode and Cascade Active Disturbance Rejection Control for a Quadrotor UAV. IEEE/ASME Trans. Mechatron. 2020, 25, 2743–2753. [Google Scholar] [CrossRef]
- Lara-Ortiz, V.; Guarneros, A.; Llorente-Vidrio, D.; Cruz-Ortiz, D.; Salgado, I.; Chairez, I. Active Disturbance Rejection Controller for a Flexible Walking Bioinspired Inchworm Mobile Robot Actuated with Shape Memory Alloy Devices. IEEE Trans. Control Syst. Technol. 2022, 30, 1790–1797. [Google Scholar] [CrossRef]
- Blas, L.A.; Dávila, J.; Salazar, S.; Bonilla, M. Robust Trajectory Tracking for an Uncertain UAV Based on Active Disturbance Rejection. IEEE Control Syst. Lett. 2022, 6, 1466–1471. [Google Scholar] [CrossRef]
- Han, X.X.; Chen, Z.X.; Feng, Y.B.; Xie, J.; Wei, X.L.; Wei, L.J. Cascade Active Disturbance Rejection Control of Single-Rod Electro-hydrostatic Actuator. Asian J. Control 2022, 1–17. [Google Scholar] [CrossRef]
- Yang, R.R. Research on Control Strategy for Electro-Hydrostatic Actuation System Based on a Novel Integrated Electro-hydraulic Pump. Ph.D. Thesis, Beijing University of Aeronautics and Astronautics, Beijing, China, 2019; pp. 76–77. (In Chinese). [Google Scholar]
- Wang, M.K.; Wang, Y.; Fu, Y.L.; Yang, R.R.; Zhao, J.A.; Fu, J. Experimental Investigation of an Electro-hydrostatic Actuator based on the Novel Active Compensation Method. IEEE Access 2020, 8, 170635–170649. [Google Scholar] [CrossRef]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Pearson Education: Hoboken, NJ, USA, 2002; pp. 423–430. [Google Scholar]
- Gao, Z.Q. Scaling and Bandwidth-Parameterization based Controller Tuning. In Proceedings of the American Control Conference, Denver, CO, USA, 4–6 June 2003; pp. 4989–4996. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).