Performance Assessment of a Low-Cost Miniature Electrohydrostatic Actuator
Abstract
:1. Introduction
2. Materials and Methods
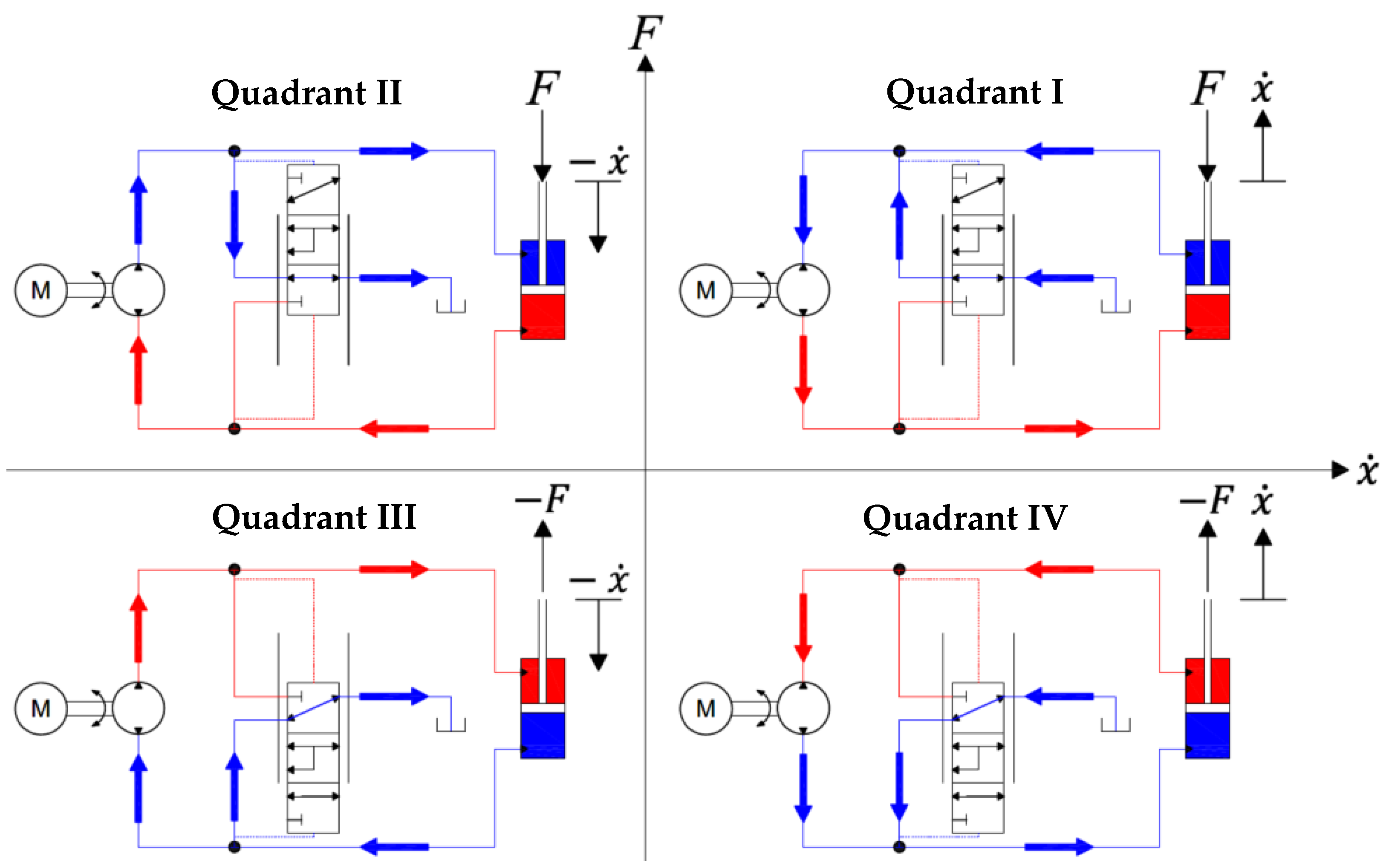
2.1. Testing Methodology
- characterizing the performance of the pump and motor combination
- identifying the EHA speed and force limits
- measuring the hydraulic efficiency of the EHA system excluding the pump
- measuring the step response of the EHA system, and
- assessing the thermal limits of the EHA system.
2.1.1. Pump Characterization Methods
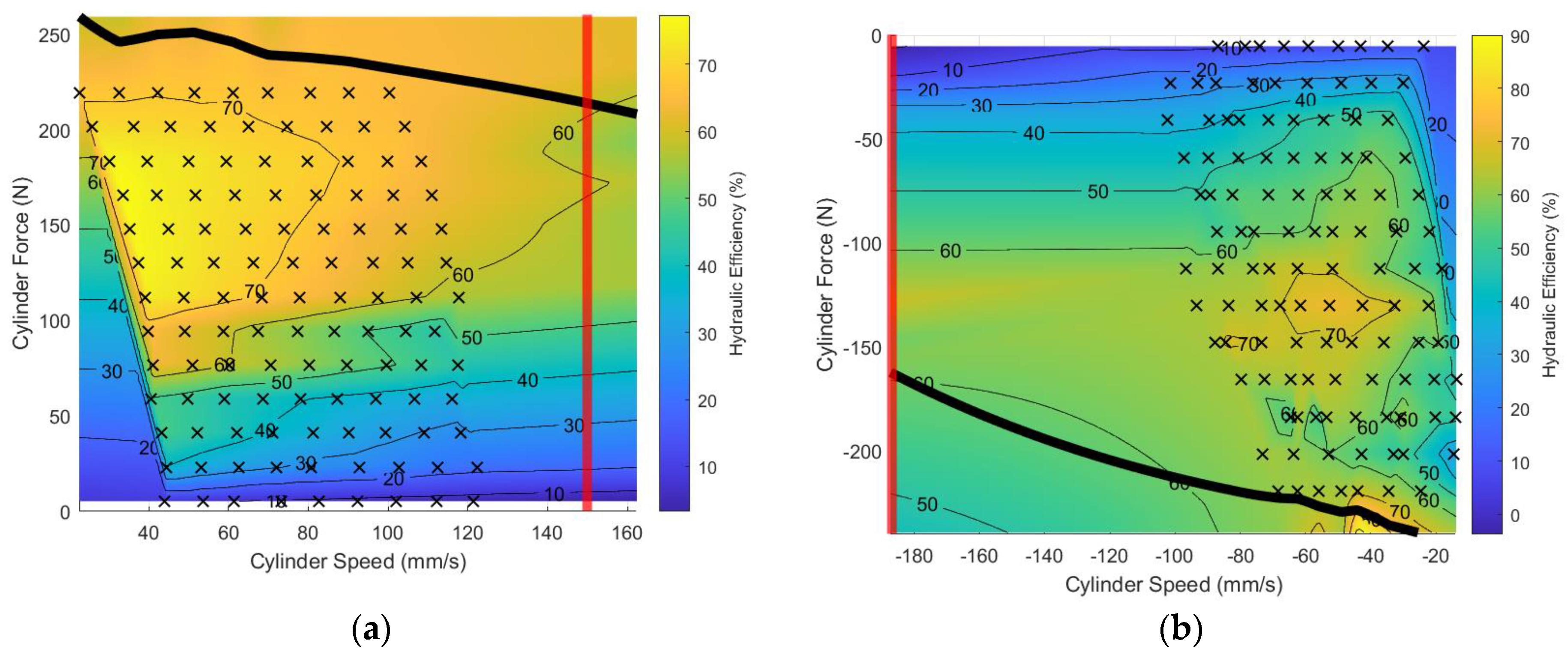
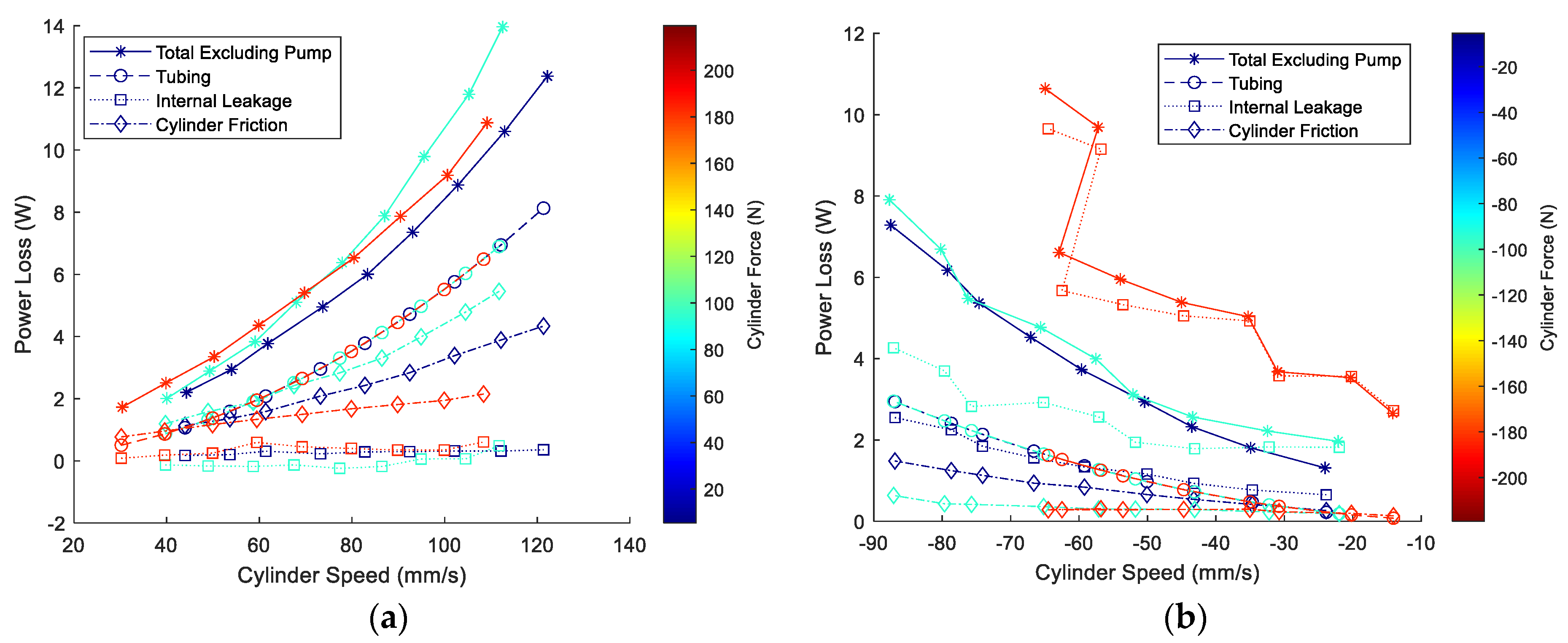
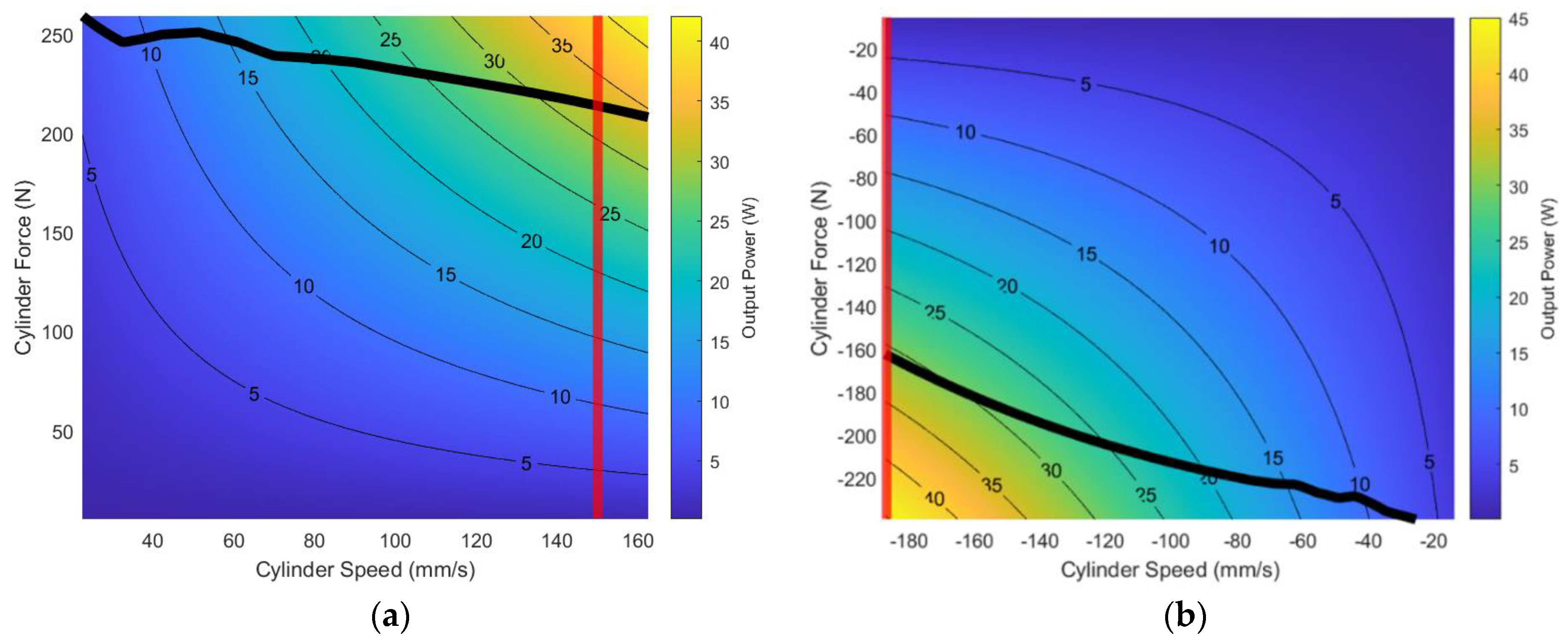
2.1.2. Steady State EHA System Performance Methods
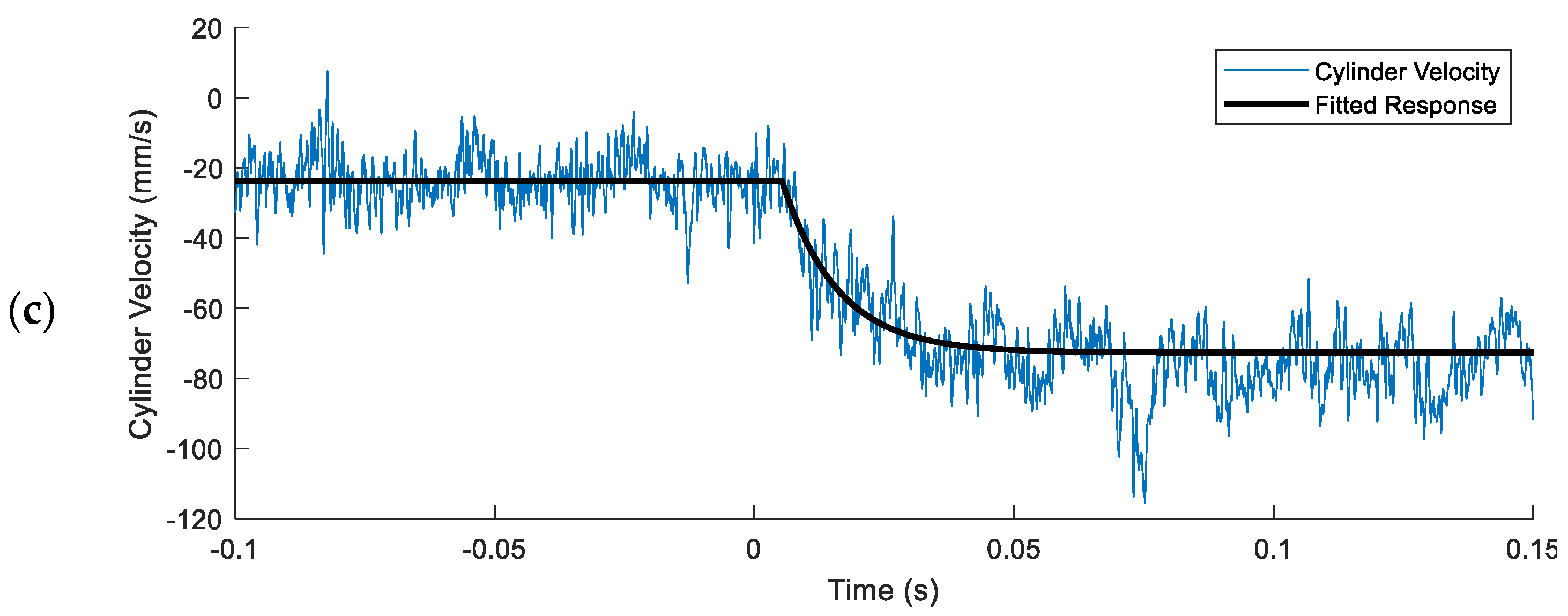
2.1.3. Dynamic Step Response Methods
2.1.4. Thermal Performance Methods
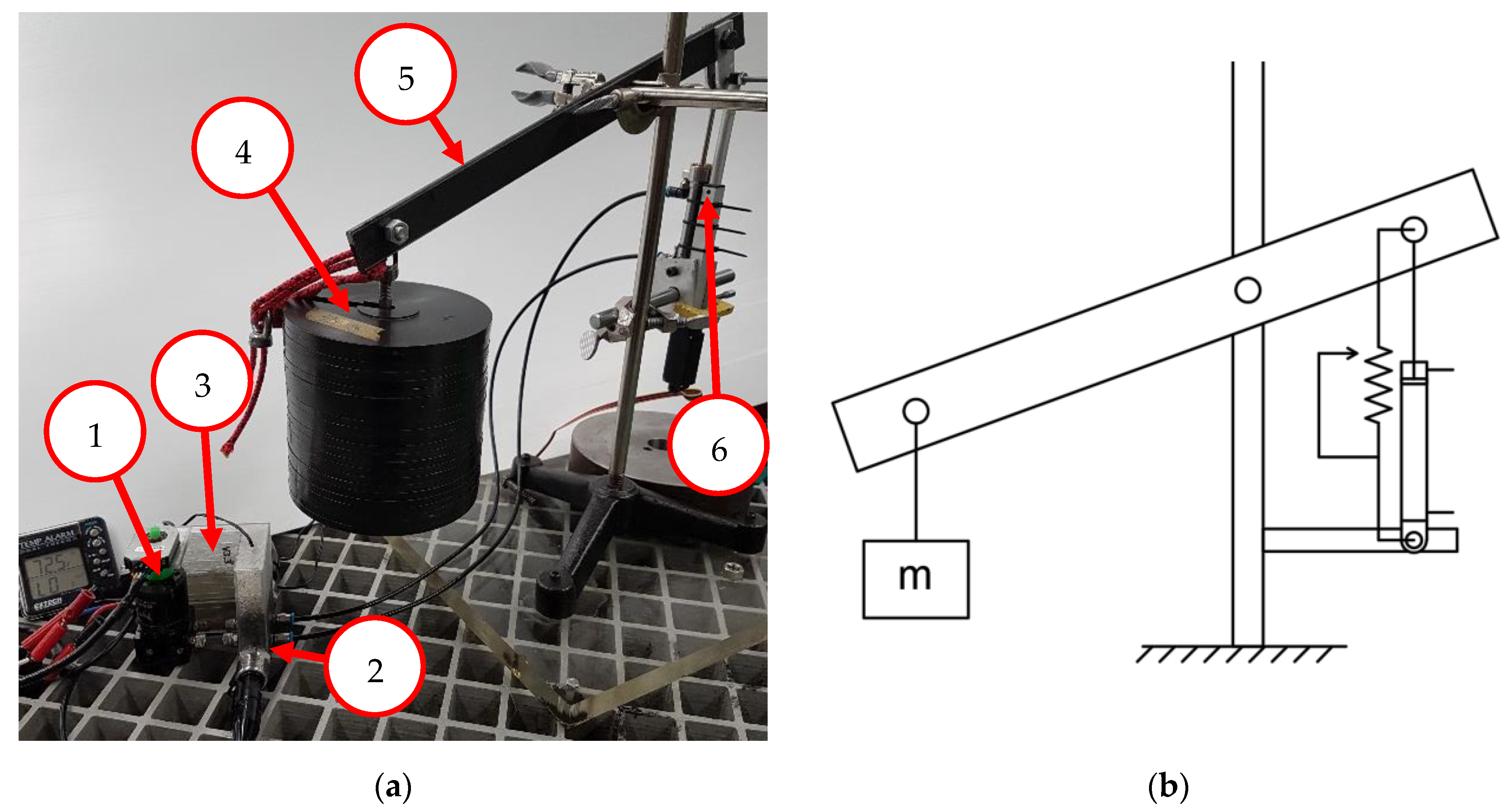
2.2. Apparatus and Instrumentation
3. Results and Discussion
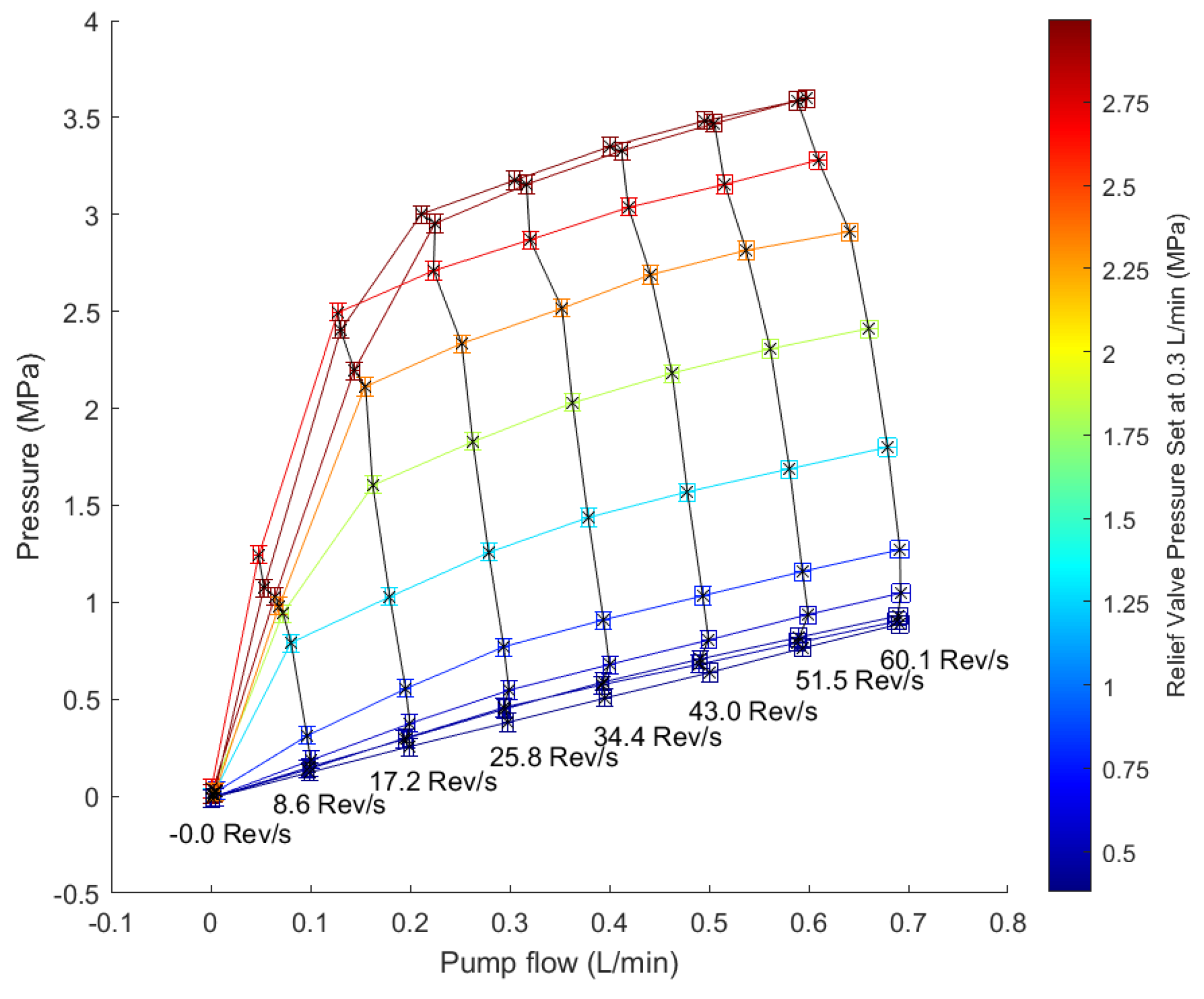
3.1. Pump Characterization Results
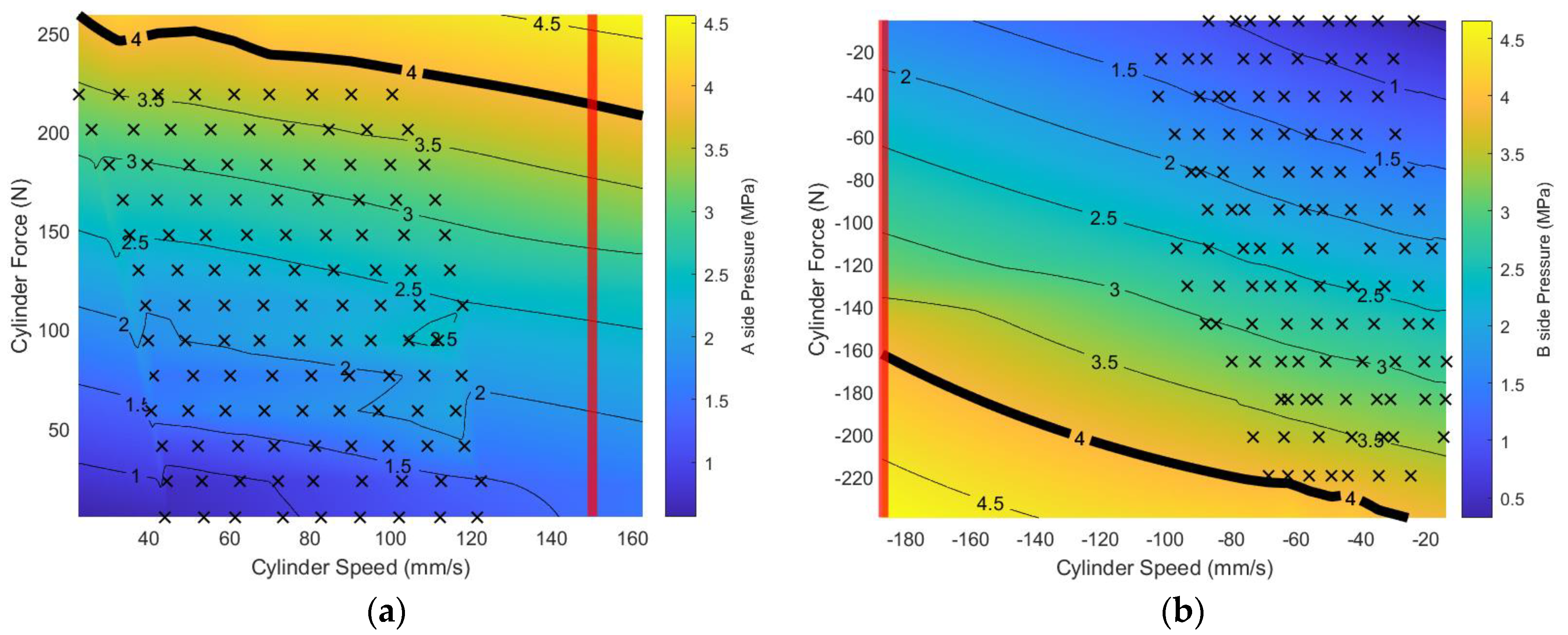
3.2. Steady State System Performance Results
3.3. Dynamic Step Response Results
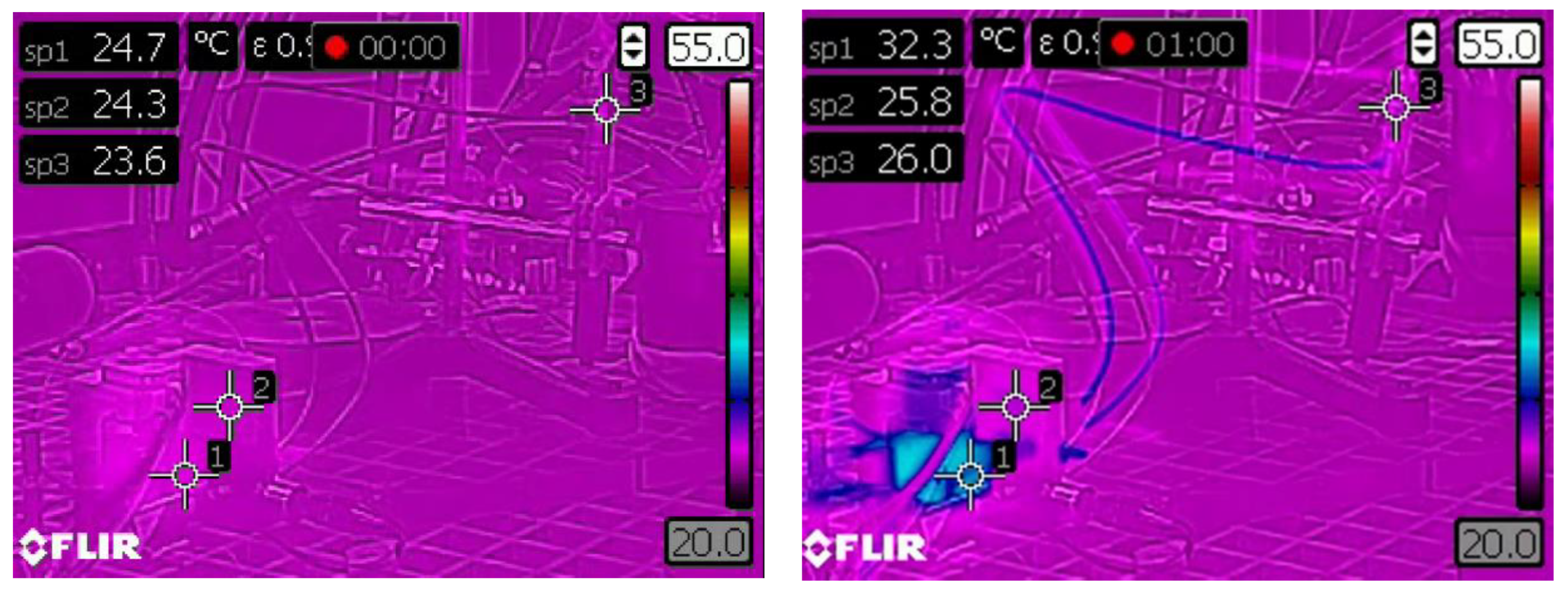
3.4. Thermal Performance Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Ketelsen, S.; Padovani, D.; Andersen, T.O.; Ebbesen, M.K.; Schmidt, L. Classification and Review of Pump-Controlled Differential Cylinder Drives. Energies 2019, 12, 1293. [Google Scholar] [CrossRef] [Green Version]
- Alle, N.; Hiremath, S.S.; Makaram, S.; Subramaniam, K.; Talukdar, A. Review on Electro Hydrostatic Actuator for Flight Control. Int. J. Fluid Power 2016, 17, 125–145. [Google Scholar] [CrossRef]
- Van den Bossche, D. The A380 flight control electrohydrostatic actuators, achievements and lessons learnt. In Proceedings of the ICAS 25TH International Congress of the Aeronautical Sciences, Hamburg, Germany, 3 September 2006. [Google Scholar]
- Xia, J.; Durfee, W.K. Analysis of Small-Scale Hydraulic Actuation Systems. J. Mech. Des. 2013, 135, 091001. [Google Scholar] [CrossRef] [Green Version]
- Houle, K.L. A Power Transmission Design for an Untethered Hydraulic Ankle Orthosis. Master’s Thesis, University of Minnesota, Minnesota, MN, USA, 2012. [Google Scholar]
- Neubauer, B.C. Principles of Small-Scale Hydraulic Systems for Human Assistive Machines. Ph.D. Thesis, University of Minnesota, Minnesota, MN, USA, 2017. [Google Scholar]
- Wiens, T.; Deibert, B. A Low-Cost Miniature Electrohydrostatic Actuator System. Actuators 2020, 9, 130. [Google Scholar] [CrossRef]
- Hagen, D.; Pawlus, W.; Ebbesen, M.K.; Andersen, T.O. Feasibility Study of Electromechanical Cylinder Drivetrain for Offshore Mechatronic Systems. Model. Identif. Control. A Nor. Res. Bull. 2017, 38, 59–77. [Google Scholar] [CrossRef] [Green Version]
- Ristic, M.; Whaler, M. Electrification of hydraulics opens new ways for intelligent energy-optimized systems. In Proceedings of the 11th International Fluid Power Conference, Aachen, Germany, 19 March 2018. [Google Scholar]
- Wiens, T.; Deibert, B. A Low-cost miniature electrohydrostatic actuator. In Proceedings of the 1st International Electronic Conference on Actuator Technology: Materials, Devices and Applications MDPI, Online, 20 November 2020. [Google Scholar]
- Deibert, B.; Scott, S.; Dolovich, A.; Wiens, T. The use of additive manufactured plastic in small-scale poppet valves and pressure vessels (Accepted). In Proceedings of the BATH/ASME 2022 Symposium on Fluid Power and Motion Control, American Society of Mechanical Engineers, Bath, UK, 14–16 September 2020. [Google Scholar]
- Parker Hannifin Corp. Parker Legris Technical Tubing & Hose. 2014. Available online: https://www.farnell.com/datasheets/1905436.pdf (accessed on 25 July 2022).
- AliExpress Brushless Hydraulic Lift Oil Pump for 1/14 Tamiya RC Truck Trailer Tipper Scania Actros Volvo MAN LESU JDM Excavator DIY Parts|Parts & Accessories|. Available online: //www.aliexpress.com/item/1005003462607936.html?src=ibdm_d03p0558e02r02&sk=&aff_platform=&aff_trace_key=&af=&cv=&cn=&dp= (accessed on 25 May 2022).
- ODrive. Available online: https://odriverobotics.com (accessed on 3 February 2022).
- Parker Hannifin Corp. Fixed Displacement Gear Pumps D/H/HD Series. 2002. Available online: https://www.parker.com/Literature/Pump%20&%20Motor%20Division/Catalogs/PDFs/DHHD_0910.pdf (accessed on 5 October 2022).
- Parker Hannifin Corp. Gear Pumps/Motors Series PGP/PGM. 2017. Available online: https://www.parker.com/literature/PMDE/Catalogs/Gear_Units/PGP_PGM/HY30-3300-UK.pdf (accessed on 4 October 2022).
- Duplomatic MS S.p.A GP External Gear Pumps Series 20. 2020. Available online: https://duplomaticmotionsolutions.com/docs/2020/11100-ed_4d72e112c3.pdf (accessed on 4 October 2022).
- Bucher Hydraulics S.p.A Gear Pumps AP100. 2015. Available online: https://www.bucherhydraulics.com/datacat/files/Katalog/Pumpen/Aussenzahnradpumpen/Aussenzahnradpumpen%20AP100/AP100_200-P-991218-en.pdf (accessed on 5 October 2022).
- Ketelsen, S.; Michel, S.; Andersen, T.O.; Ebbesen, M.K.; Weber, J.; Schmidt, L. Thermo-Hydraulic Modelling and Experimental Validation of an Electro-Hydraulic Compact Drive. Energies 2021, 14, 2375. [Google Scholar] [CrossRef]
- Technical Data Sheet Prusament PETG by Prusa Polymers. Available online: https://prusament.com/media/2020/01/PETG_TechSheet_ENG.pdf (accessed on 1 March 2022).








| Parameter | Fitted Value |
|---|---|
| [RPM/V] | 1108 (1088–1128) |
| [-] | 0.98 (0.94–1.03) |
| [Pa∙s] | 885 (678–1093) |
| [Nm] | 1.91 × 10−3 (0.66 × 10−3–3.2 × 10−3) |
| [m3/rev] | 2.02 × 10−7 (2.01 × 10−7–2.04 × 10−7) |
| [1/(Pa∙s)] | 2.65 × 10−6 (2.49 × 10−6–2.80 × 10−6) |
| Fitted Time Constant τvel (ms) | ||
|---|---|---|
| Load Mass (kg) | Average | Standard Deviation |
| 0 | 3.89 | 1.72 |
| 4.8 | 7.65 | 1.34 |
| 9.4 | 12.5 | 1.01 |
| Cylinder Load, F (N) | Heat Generated, Q (W) | (s) | Steady Temperature, T∞ (°C) |
|---|---|---|---|
| 50 | 8.6 | 242 | 36.3 |
| 94 | 13.8 | 246 | 43.6 |
| 139 | 20.4 | 440 | 67.1 |
| 184 | 26.4 | 459 | 84.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deibert, B.; Wiens, T. Performance Assessment of a Low-Cost Miniature Electrohydrostatic Actuator. Actuators 2022, 11, 334. https://doi.org/10.3390/act11110334
Deibert B, Wiens T. Performance Assessment of a Low-Cost Miniature Electrohydrostatic Actuator. Actuators. 2022; 11(11):334. https://doi.org/10.3390/act11110334
Chicago/Turabian StyleDeibert, Brendan, and Travis Wiens. 2022. "Performance Assessment of a Low-Cost Miniature Electrohydrostatic Actuator" Actuators 11, no. 11: 334. https://doi.org/10.3390/act11110334





