A Pneumatic Control Method for Commercial Vehicle Electronic Brake System Based on EPV Module
Abstract
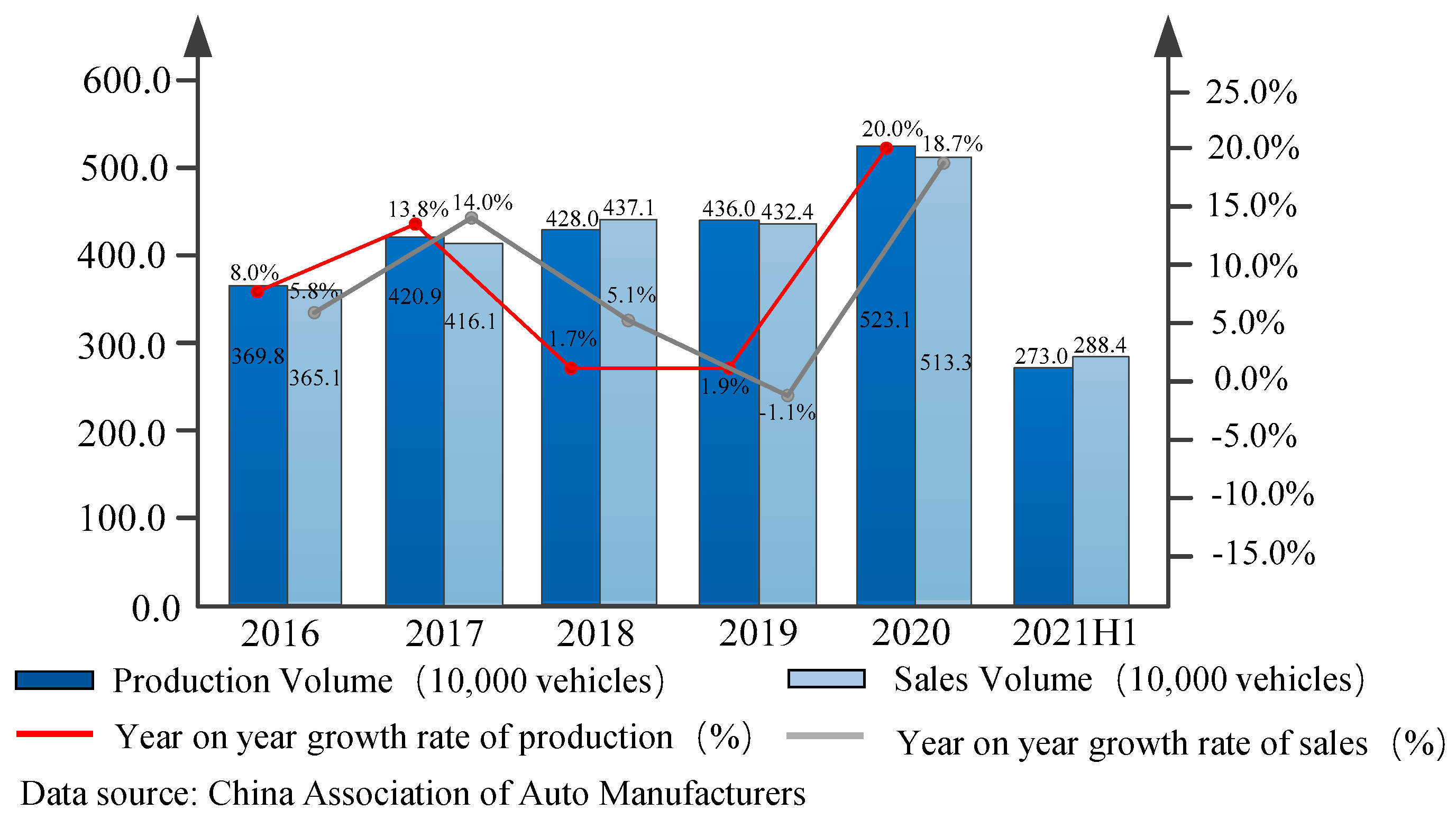
:1. Introduction
- (1)
- A novel EBS system based on the EPV module is designed by integrating various pneumatic valves, which improves the structure layout of the system and optimizes the precision of pressure regulation.
- (2)
- A novel SPWM air pressure control method is proposed to achieve different pressure-increasing and decompressing speeds by controlling the duration of the pressure-increasing and decompressing states of the valve in one cycle.
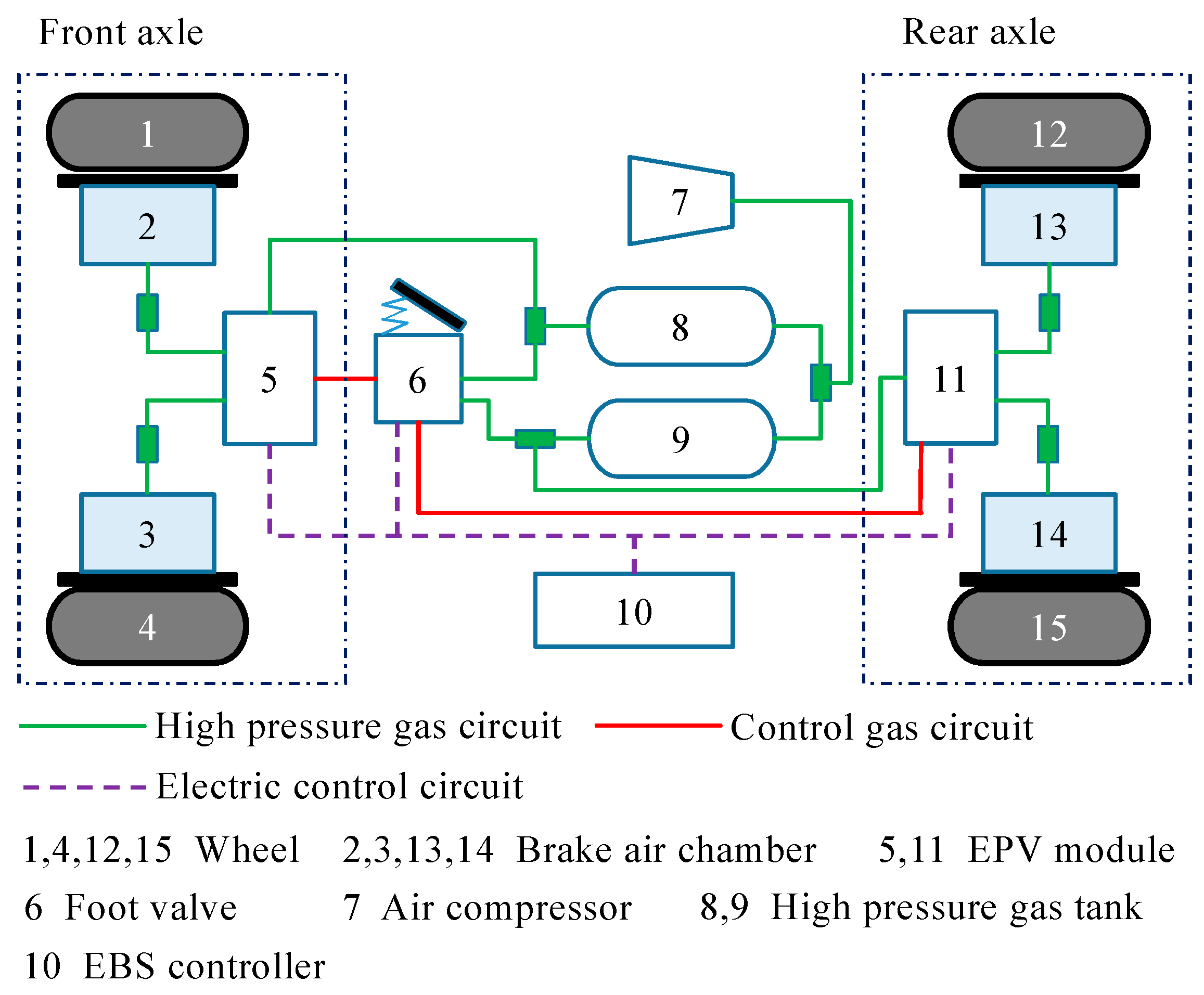
2. Structure Design of Commercial Vehicle EBS Based on the EPV Module
3. Dynamic Model of the EPV Module
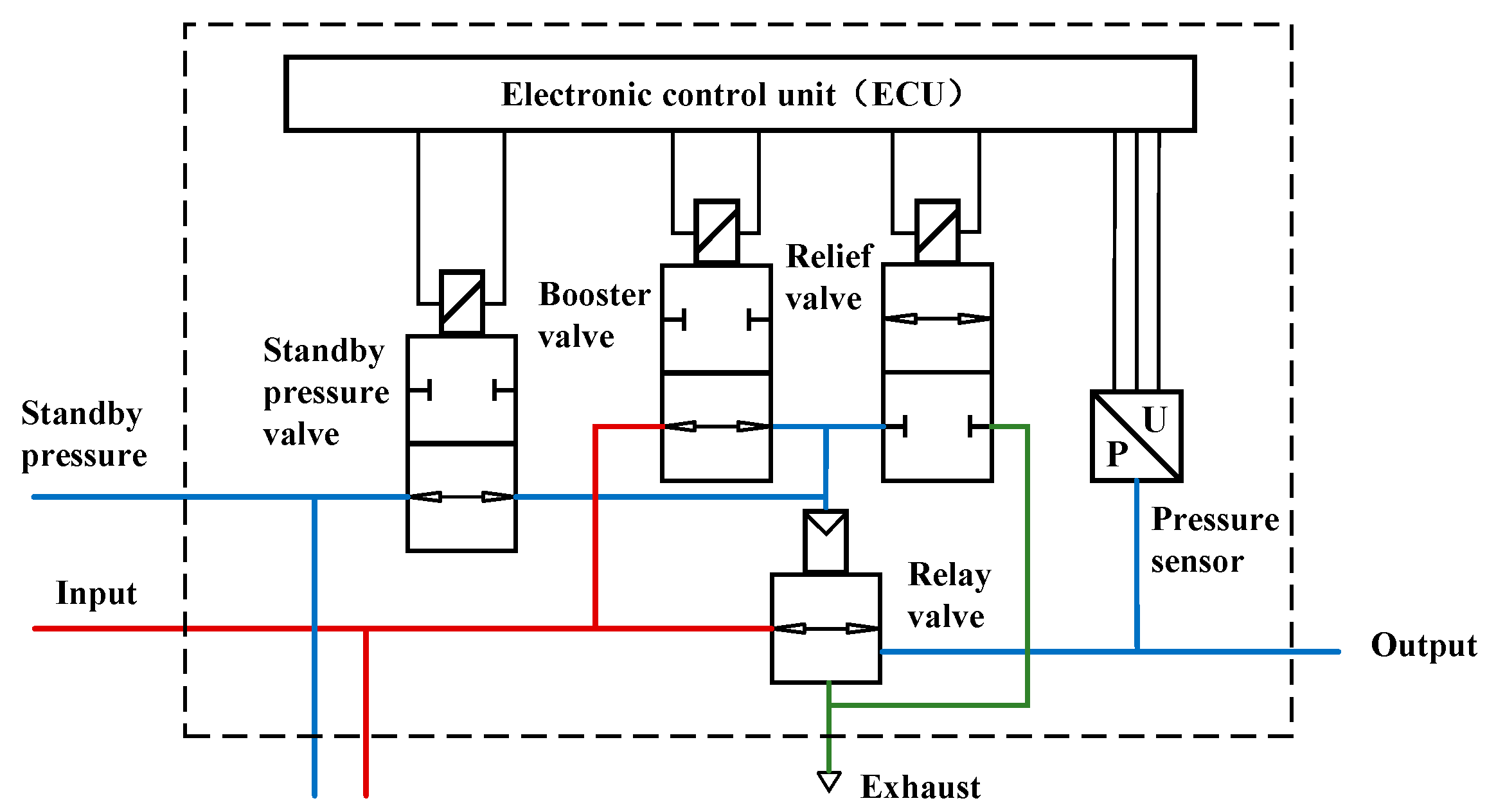
3.1. Characteristics Analysis of the EPV Module
3.2. Dynamics Model of the EPV Module
4. Design of Commercial Vehicle EBS Bottom Controller Based on EPV
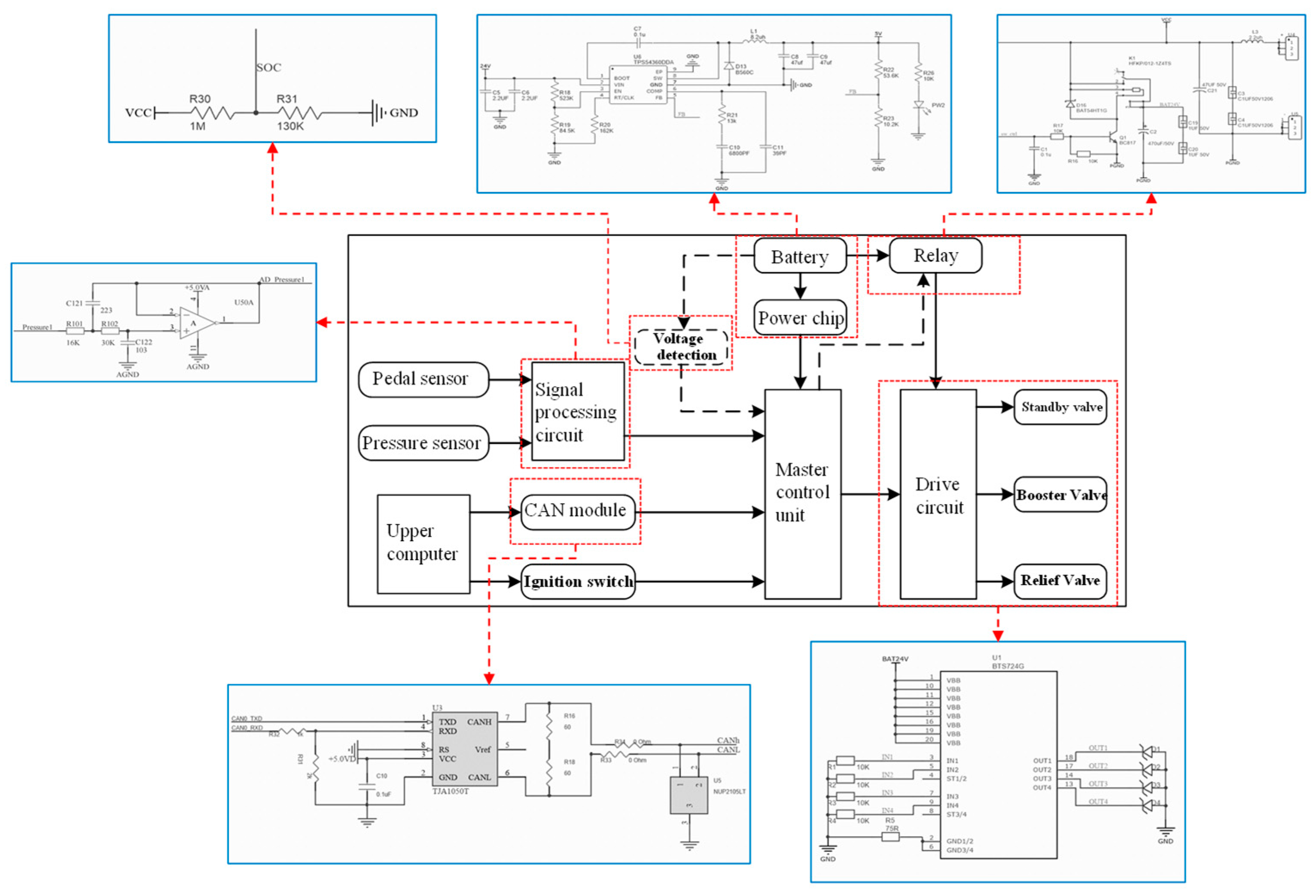
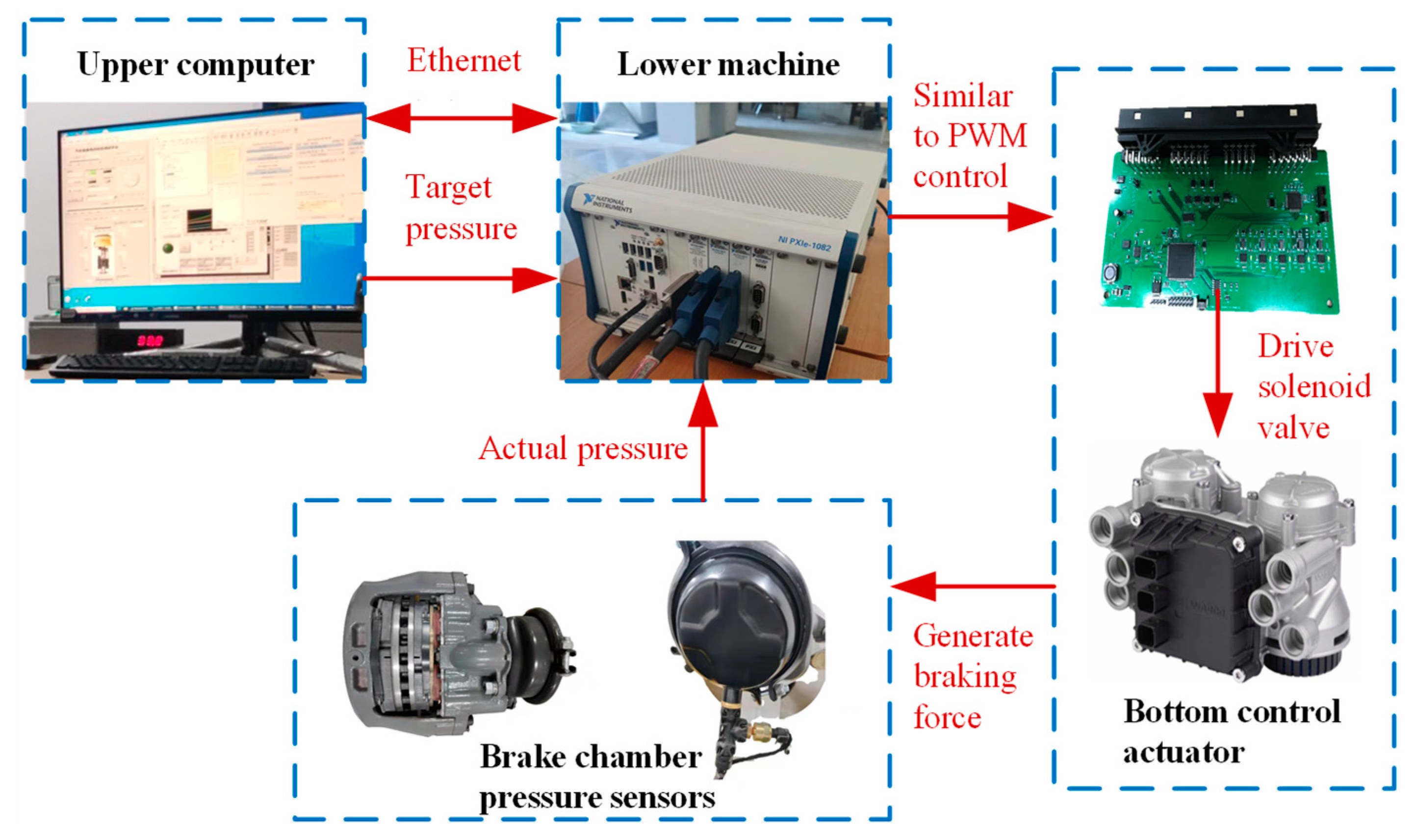
4.1. Hardware Architecture of Commercial Vehicle EBS Bottom Controller Based on EPV
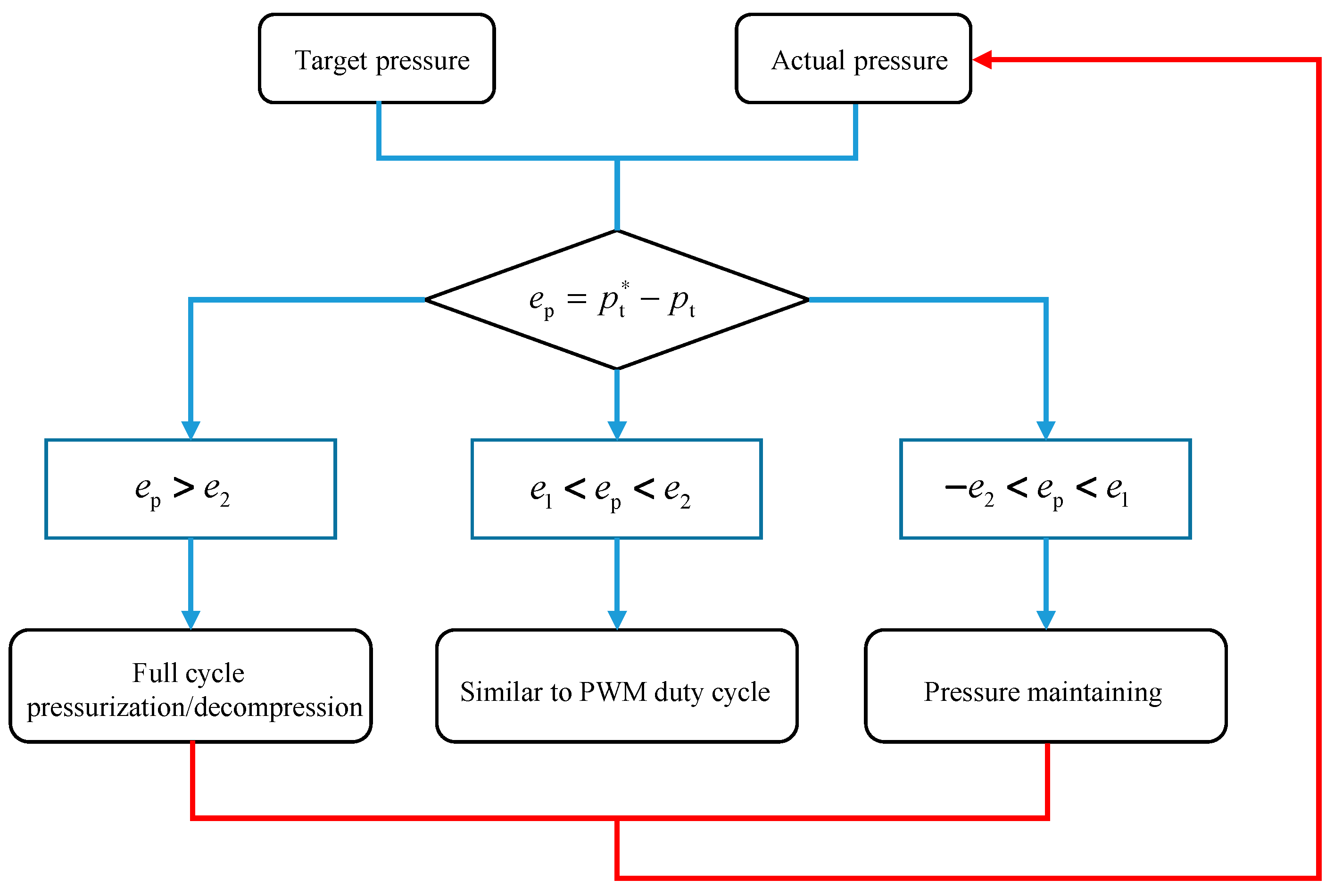
4.2. Air Pressure Close-Loop Control Logic of EBS Controller Based on EPV Module
4.3. Air Pressure Control Method of the EPV Module Based on SPWM
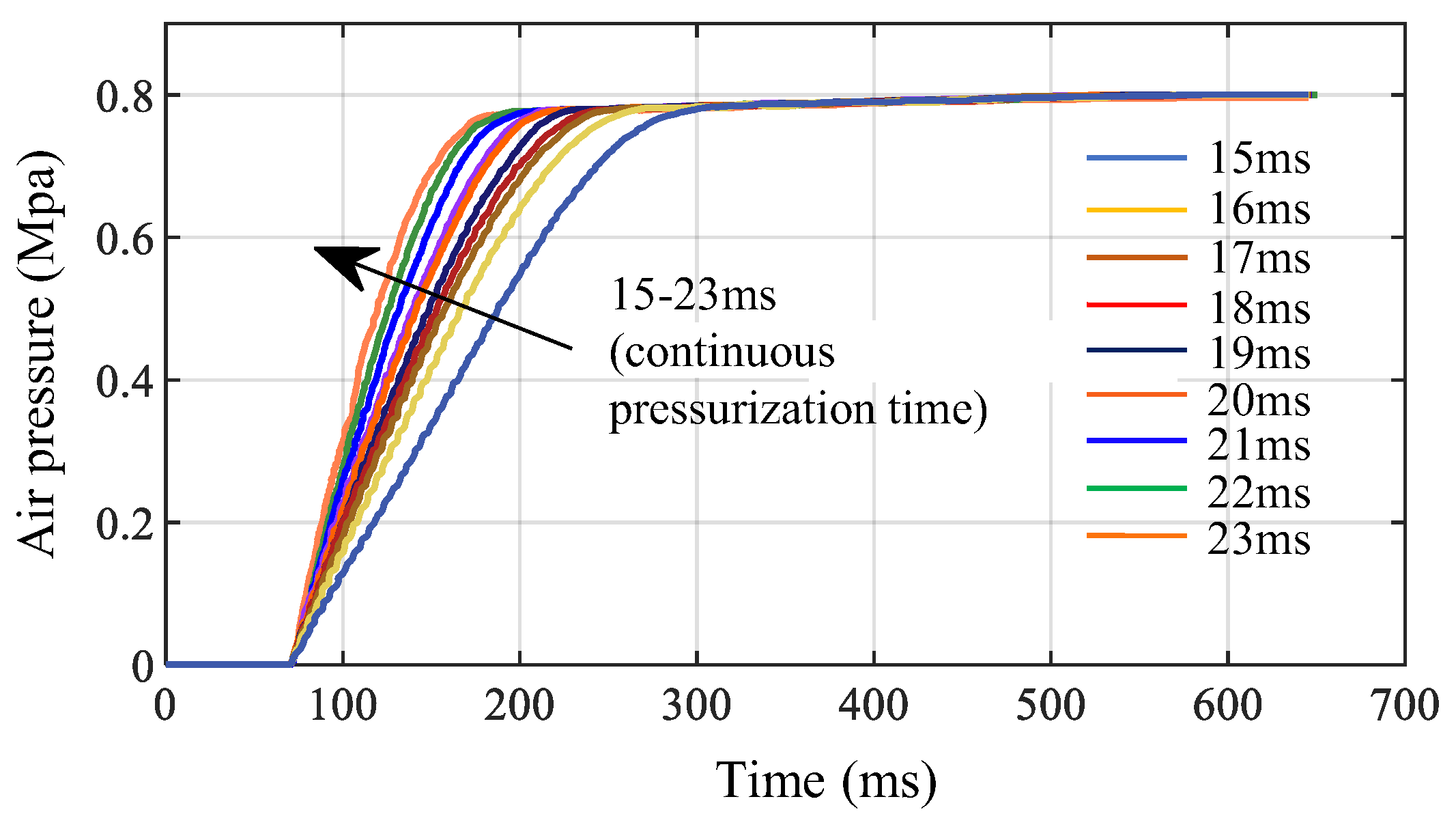
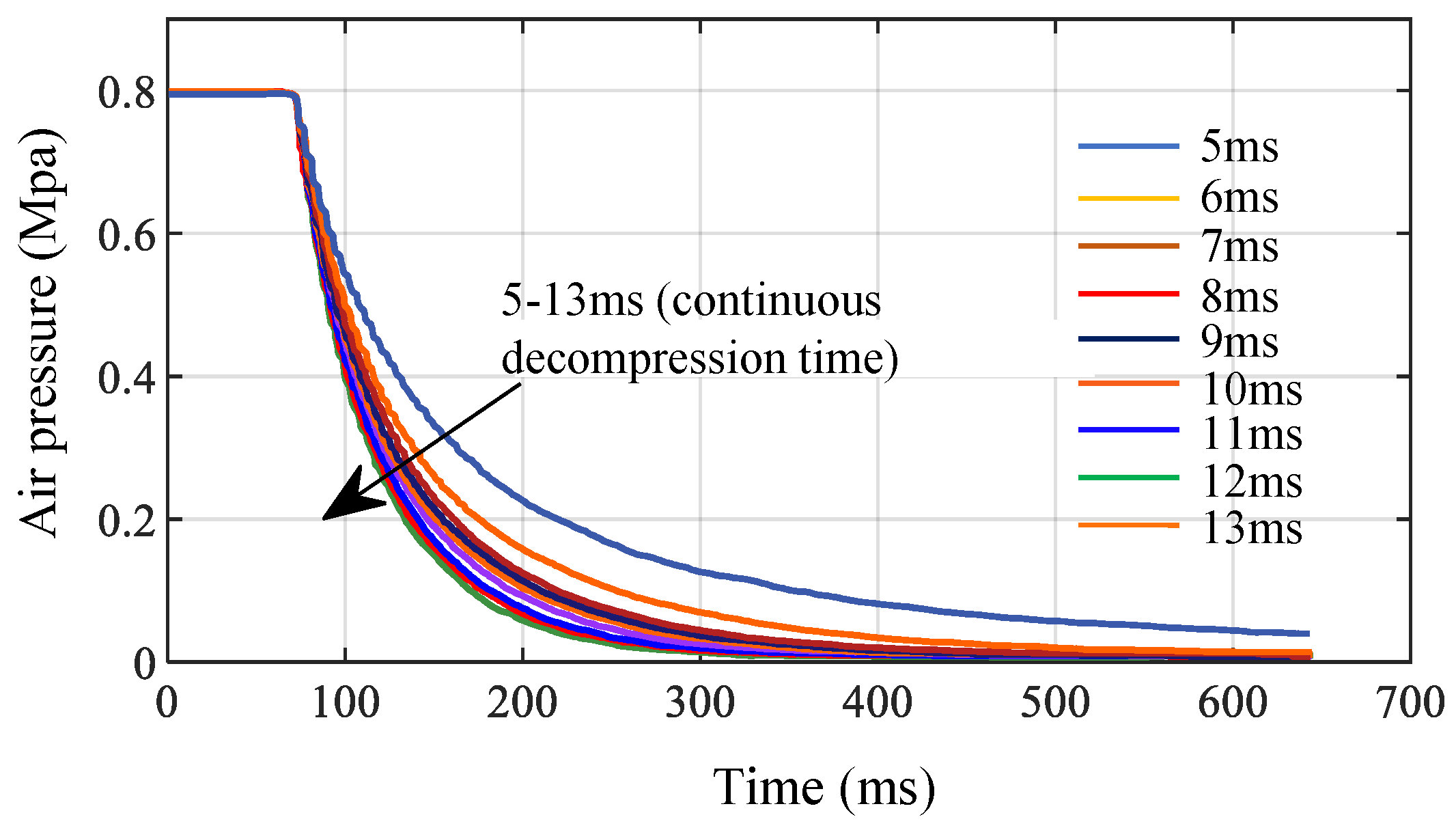
4.4. Determination of Air Pressure Control Parameters Based on SPWM
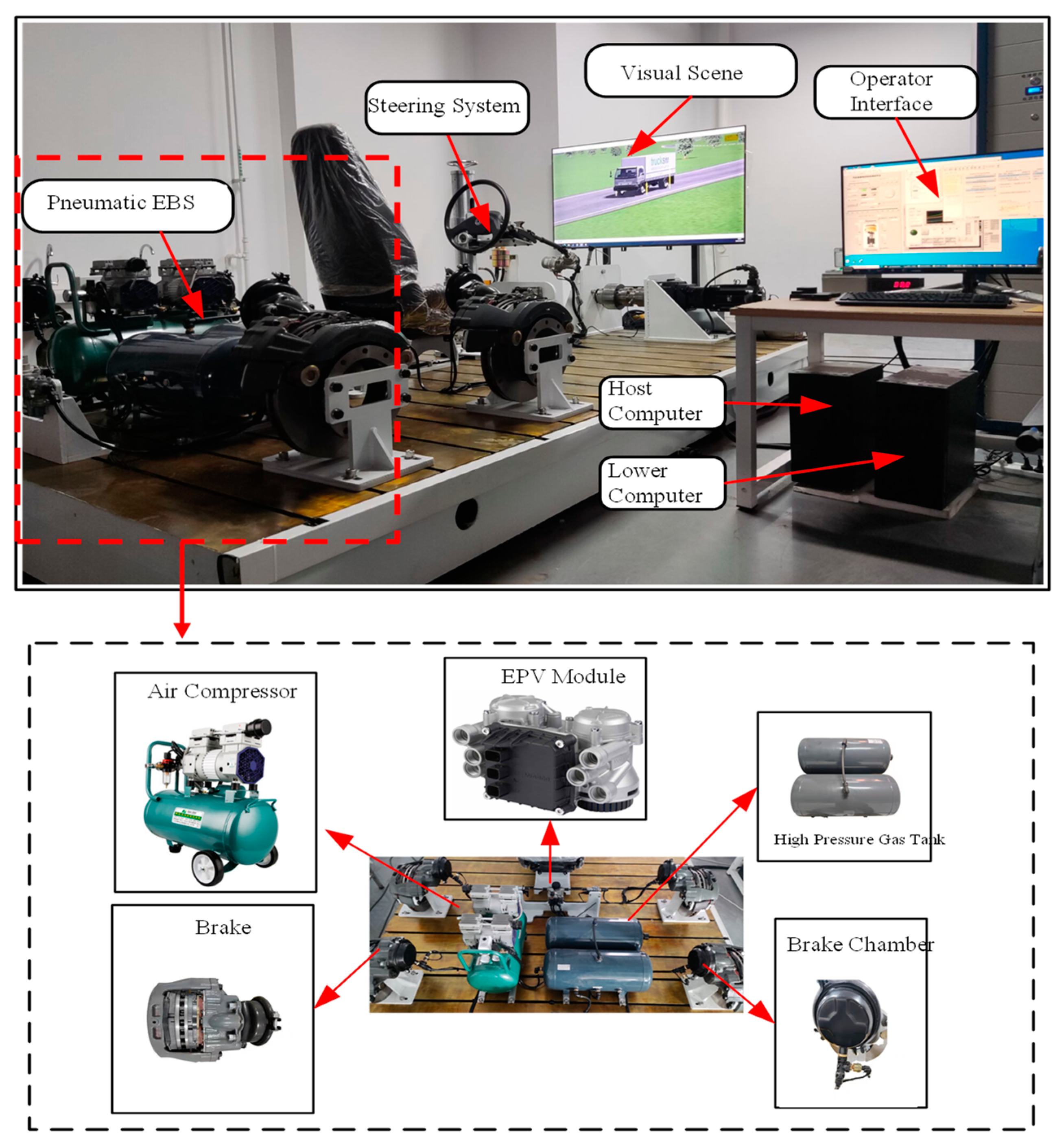
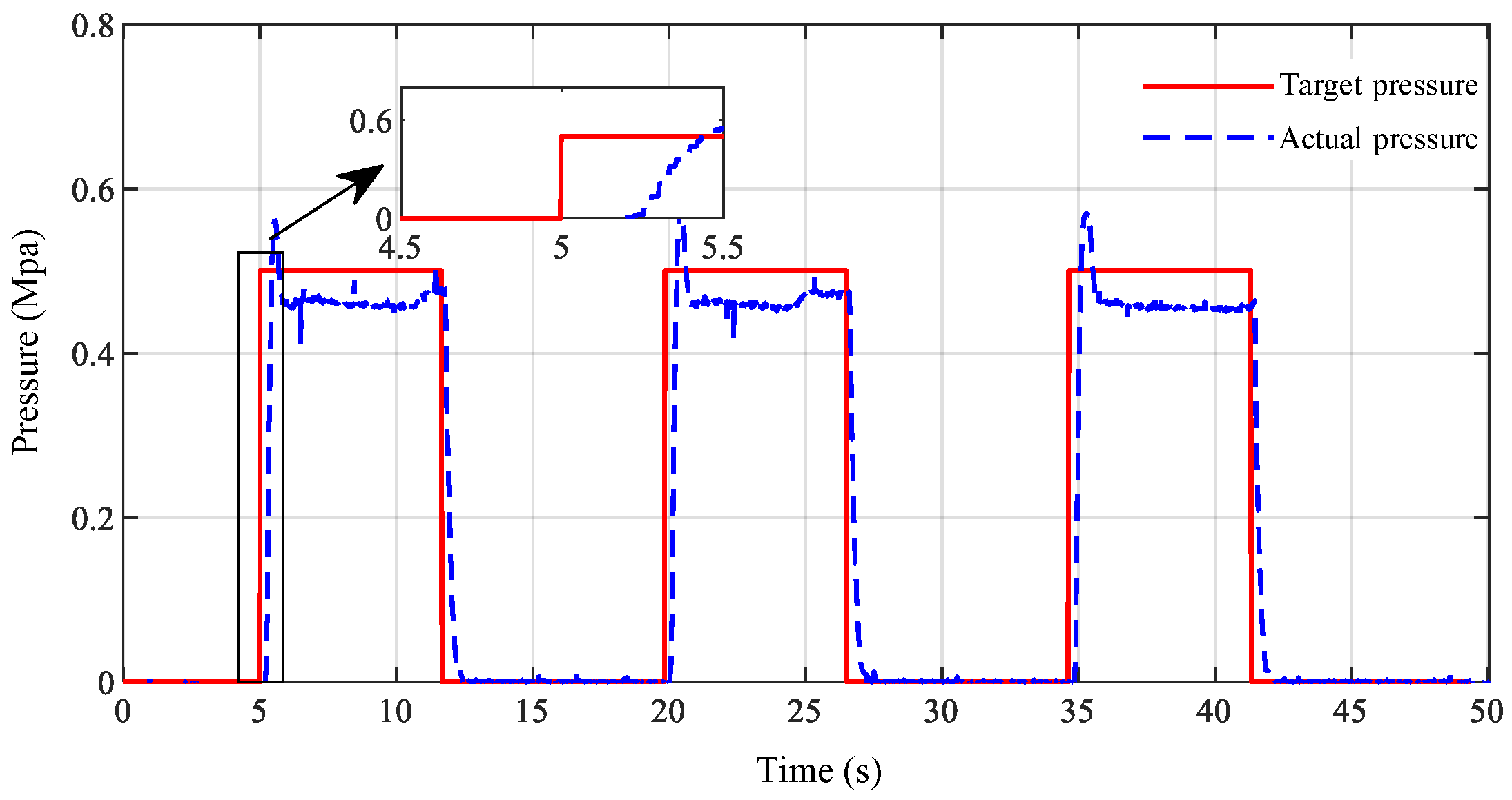
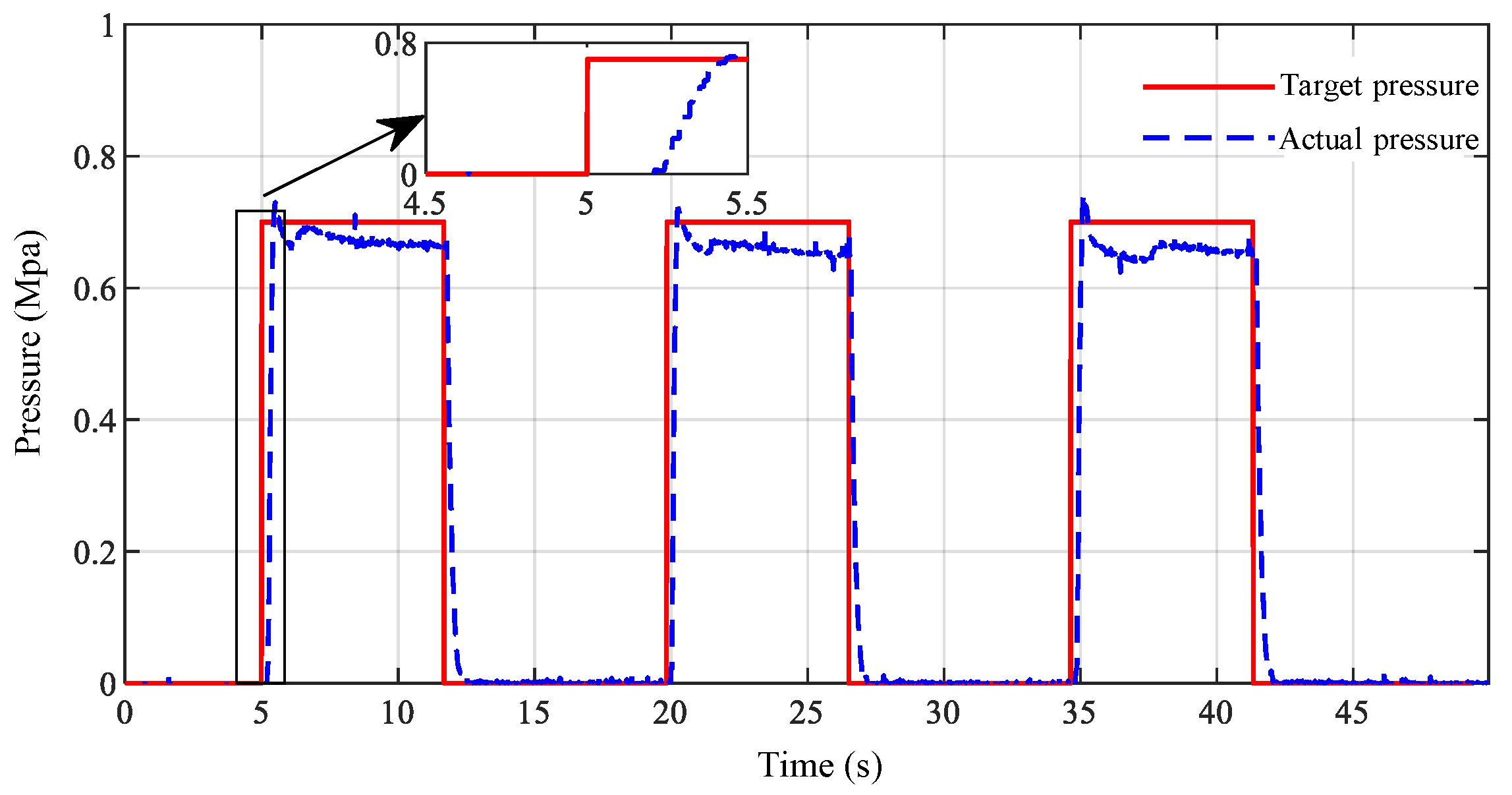
5. Dynamic Response Verification of Air Pressure Closed-Loop Control of EBS Bottom Controller Based on EPV Module
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Miller, J.I. Advanced Braking Systems for Heavy Vehicles. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 2010. [Google Scholar]
- Liu, Q.; Dong, Y.; Zhao, L.; Ma, C. Modeling, Control and Test of a Novel Electronic Pneumatic Brake System. IOP Conf. Ser. Mater. Sci. Eng. 2019, 631, 042030. [Google Scholar] [CrossRef]
- Zhang, D.; Zong, C.; Yang, S.; Zhao, W. Development and Verification of Electronic Braking System ECU Software for Commercial Vehicle; SAE Technical Paper 2013-01-2736; Society of Automotive Engineers (SAE): Warrendale, PA, USA, 2013. [Google Scholar] [CrossRef]
- Bao, H.; Wang, Z.; Liu, Z.; Li, G. Study on Pressure Change Rate of the Automatic Pressure Regulating Valve in the Electronic-Controlled Pneumatic Braking System of Commercial Vehicle. Processes 2021, 9, 938. [Google Scholar] [CrossRef]
- Zhang, D.; Zong, C.; Wan, Y.; Zheng, H.; Zhao, W.Q. Development and Research on Control Strategy of Advanced Electronic Braking Systems for Commercial Vehicle; SAE Technical Paper 2014-01-2285; Society of Automotive Engineers (SAE): Warrendale, PA, USA, 2014. [Google Scholar] [CrossRef]
- Miller, J.I.; Henderson, L.M.; Cebon, D. Designing and Testing an Advanced Pneumatic Braking System for Heavy Vehicles. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2013, 227, 1715–1729. [Google Scholar] [CrossRef]
- Bao, H.; Wang, Z.; Wei, X.; Li, G. Study on the Structural Configurations and Pressure Regulation Characteristics of the Automatic Pressure Regulating Valve in the Electronically Controlled Pneumatic Brake System of Commercial Vehicles. Appl. Sci. 2021, 11, 10603. [Google Scholar] [CrossRef]
- Leontiev, D.; Klimenko, V.; Mykhalevych, M.; Don, Y.; Frolov, A. Simulation of Working Process of the Electronic Brake System of the Heavy Vehicle. In Mathematical Modeling and Simulation of Systems (MODS): Advances in Intelligent Systems and Computing; Springer: Cham, Switzerland, 2019; Volume 1019. [Google Scholar] [CrossRef]
- Day, A.J.; Ho, H.P.; Hussain, K.; Johnstone, A. Brake System Simulation to Predict Brake Pedal Feel in a Passenger Car; SAE Technical Papers 2014, Report No. 09BC-0077; SAE International: Warrendale, PA, USA, 2009. [Google Scholar]
- Ma, T.; Qian, C. The Modeling and Simulation of Pneumatic ABS Pressure Regulator Based on AMESim. Adv. Mater. Res. 2014, 971–973, 811–815. [Google Scholar] [CrossRef]
- David, R.; Neumann, R.; Murrenhoff, H. Simplified Fluid Transmission Line Model for Pneumatic Control Applications. In Proceedings of the 14th Scandinavian International Conference on Fluid Power (SICFP15), Tampere, Finland, 20–22 May 2015; Volume 6. [Google Scholar]
- Chen, L.; Wang, H.; Cao, D. High-precision Hydraulic Pressure Control Based on Linear Pressure-Drop Modulation in Valve Critical Equilibrium State. IEEE Trans. Ind. Electron. 2017, 64, 7984–7993. [Google Scholar]
- Farid, B.; Helmus, T.; Lumkes, J. The Impact of Peak-and-Hold and Reverse Current Solenoid Driving Strategies on the Dynamic Performance of Commercial Cartridge Valves in a Digital Pump/Motor. Int. J. Fluid Power 2016, 17, 37–47. [Google Scholar]
- Edmond, R.; Hurmuzlu, Y. A high performance pneumatic force actuator system: Part I—Nonlinear mathematical model. ASME J. Dyn. Syst. Meas. Control 2000, 122, 416–425. [Google Scholar]
- Chol, H.J.; Zhao, W.Q.; Zong, C.F.; Zheng, H.Y. Simulation and HIL Test for Proportional Relay Valve of Commercial Vehicle Pneumatic EBS. Appl. Mech. Mater. 2013, 437, 418–422. [Google Scholar] [CrossRef]
- Seung, C.J.; Kim, J.; Jeon, J. New brake by wire concept with mechanical backup. SAE Int. J. Passeng. Cars-Mech. Syst. 2012, 5, 1194–1198. [Google Scholar]
- Barlsen, H.; Stender, A.; Tha, I.; Witte, N.; Wolf, M. Electronic Braking System and Method for Drawbar Trailers. U.S. Patent 8,267,485, 18 September 2012. [Google Scholar]
- Lei, M. Simulation Research and Detection System Development of ABS Relay Valve. Master’s Thesis, China Institute of Metrology, Hangzhou, China, 2012. [Google Scholar]
- Li, Y. Hardware in the Loop Simulation of Pneumatic ABS for Commercial Vehicles. Master’s Thesis, Yanshan University, Qinhuangdao, China, 2018. [Google Scholar]
- Shi, Y.; Lu, Y.; Wang, X.; Luo, Z. Analysis of the brake Valve Dynamic Characteristics Based on AMEsim. Instrum. Tech. Sens. 2014, 23–26. [Google Scholar] [CrossRef]
- An, Z. Design of Relay Valve Detection System. Master’s Thesis, China Institute of Metrology, Hangzhou, China, 2013. [Google Scholar]
- Wan, Y.; Zhang, D.; Weiqiang, Z.; Zong, C.; Han, J. Development of Simulation Platform and Compensation Control Strategy for Pneumatic Electric Control Braking System. J. Jilin Univ. Eng. Ed. 2016, 46, 711–717. [Google Scholar]
- Wang, S.; Zhang, B.; Zhong, Q.; Yang, H. Study on Control Performance of Pilot High-Speed Switching Valve. Adv. Mech. Eng. 2017, 9, 1687814017708908. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Chen, H.; Yuan, J. Research on Control Method of Proportional Relay Valve for EBS of Commercial Vehicle. In Proceedings of the Annual Meeting of China Society of Automotive Engineering, Changchun, China, 15–18 July 2010. [Google Scholar]
- You, M.; Zhang, J.; Sun, D.; Gou, J. Characteristics Analysis and Control Study of a Pneumatic Proportional Valve. In Proceedings of the 2015 IEEE Advanced Information Technology, Electronic and Automation Control Conference (IAEAC 2015), Chongqing, China, 19–20 December 2015; pp. 242–247. [Google Scholar] [CrossRef]
- Zheng, H.; Ma, S.; Liu, Y. Vehicle Braking Force Distribution with Electronic Pneumatic Braking and Hierarchical Structure for Commercial Vehicle. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2018, 232, 481–493. [Google Scholar] [CrossRef]
- Wan, Y.; Zhang, D.; Weiqiang, Z.; Zong, C.; Han, J. Development of Simulation Platform and Control Strategy of Electronic Braking System for Commercial Vehicles; SAE Technical Paper, 2014-01-2286; Society of Automotive Engineers (SAE): Warrendale, PA, USA, 2014. [Google Scholar] [CrossRef]
- Kong, X.; Zhang, J.; Li, T.; Chang, L. Research on Liner Pressure Control of Force Control System of High-speed Switch Solenoid Valve. J. Mech. Eng. 2014, 50, 192–199. [Google Scholar] [CrossRef]
- Bali, E.; Erzan Topcu, E. Design of On-Off Type Solenoid Valve for Electro-Pneumatic Brake Systems and Investigation of Its Static Characteristics. Int. J. Adv. Automot. Technol. 2018, 2, 175–184. [Google Scholar]
- Wu, J.; Zhang, J.; Nie, B.; Liu, Y.; He, X. Adaptive Control of PMSM Servo System for Steering-by-Wire System with Disturbances Observation. IEEE Trans. Transp. Electrif. 2021, 8, 2015–2028. [Google Scholar] [CrossRef]
- Wu, J.; Kong, Q.; Yang, K.; Liu, Y.; Cao, D.; Li, Z. Research on the Steering Torque Control for Intelligent Vehicles Co-Driving With the Penalty Factor of Human-Machine Intervention. IEEE Trans. Syst. Man Cybern. Syst. 2022, 1–12. [Google Scholar] [CrossRef]
- Yan, Y.; Wu, J.; Liu, X.; Zhao, Y.; Wang, S. A lateral trajectory tracking control method for intelligent commercial vehicles considering active anti-roll decision based on Stackelberg equilibrium. IET Intell. Transp. Syst. 2022, 16, 1193–1208. [Google Scholar] [CrossRef]
- Wu, J.; Tian, Y.; Walker, P.; Li, Y. Attenuation reference model based adaptive speed control tactic for automatic steering system. Mech. Syst. Signal Process. 2021, 156, 107631. [Google Scholar] [CrossRef]

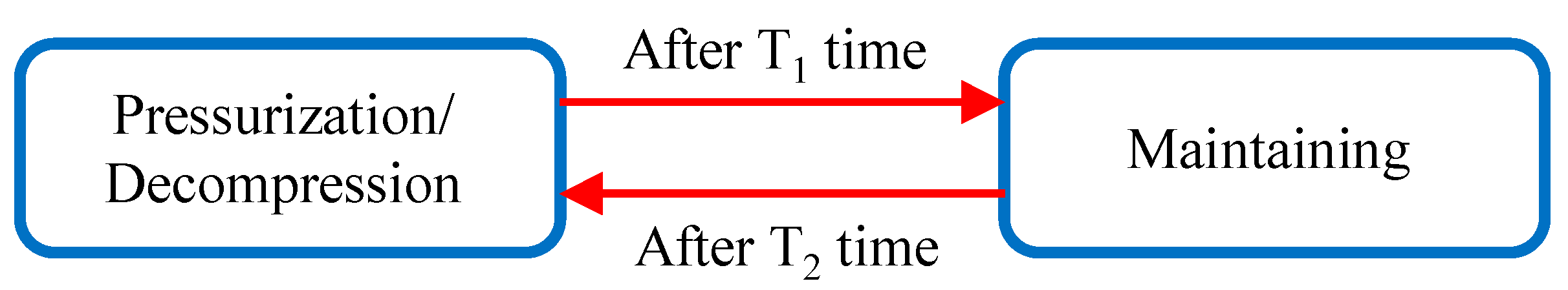
| Signal Names | Parameters | Numbers |
|---|---|---|
| Displacement sensor of the brake pedal | voltage nominal value: 24 V current top limit: 1 A | 1 channel |
| Ignition switch | voltage nominal value: 24 V current top limit: 1 A | 1 channel |
| Booster/Relief valve | voltage nominal value: 24 V current top limit: 2 A | 4 channels |
| Standby pressure valve | voltage nominal value: 24 V current top limit: 2 A | 2 channels |
| 24 V Power supply | Rated output voltage: 24 V capacity:105 Ah | 1 channel |
| CAN signals | Baud rate: 250 K | 2 channels |
| Pressure sensor of the brake air chamber | Output voltage: 0.5–4.5 V | 4 channels |
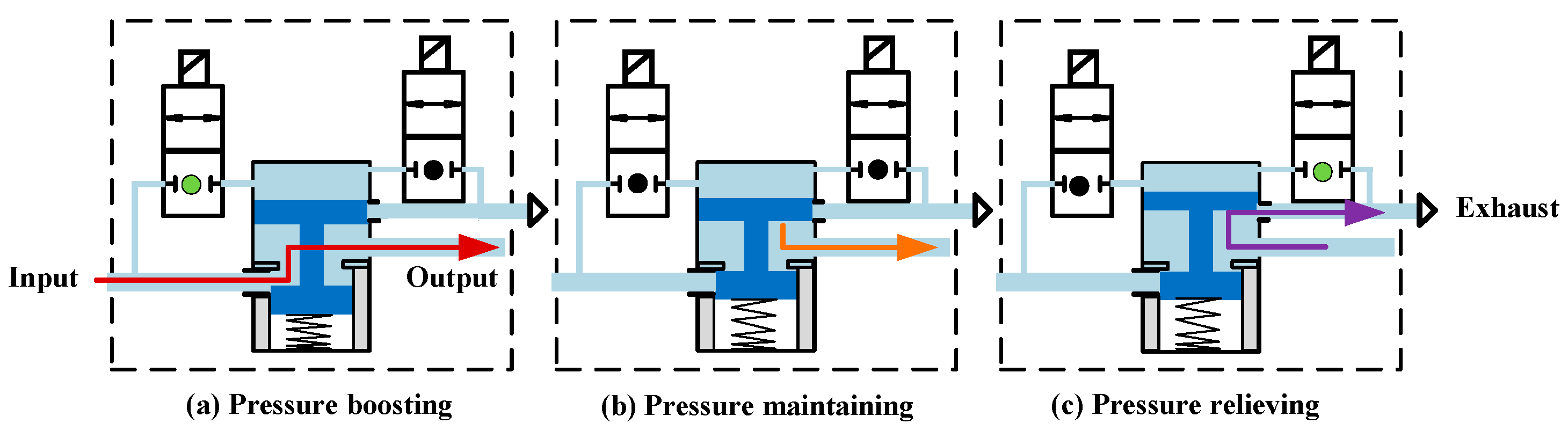
| Process | Booster Valve State | Relief Valve State | ||
|---|---|---|---|---|
| Pressure boosting | Power off | Open | Power off | Close |
| Pressure maintaining | Power on | Close | Power off | Close |
| Pressure relieving | Power on | Close | Power on | Open |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Yan, Y.; Zhu, Q.; Zhao, G.; Feng, D.; Wu, J. A Pneumatic Control Method for Commercial Vehicle Electronic Brake System Based on EPV Module. Actuators 2022, 11, 316. https://doi.org/10.3390/act11110316
Zhang L, Yan Y, Zhu Q, Zhao G, Feng D, Wu J. A Pneumatic Control Method for Commercial Vehicle Electronic Brake System Based on EPV Module. Actuators. 2022; 11(11):316. https://doi.org/10.3390/act11110316
Chicago/Turabian StyleZhang, Lanjiang, Yang Yan, Qingwei Zhu, Gang Zhao, Deying Feng, and Jian Wu. 2022. "A Pneumatic Control Method for Commercial Vehicle Electronic Brake System Based on EPV Module" Actuators 11, no. 11: 316. https://doi.org/10.3390/act11110316
APA StyleZhang, L., Yan, Y., Zhu, Q., Zhao, G., Feng, D., & Wu, J. (2022). A Pneumatic Control Method for Commercial Vehicle Electronic Brake System Based on EPV Module. Actuators, 11(11), 316. https://doi.org/10.3390/act11110316






