Design of an Acoustic Synthetic Jet Actuator for Flow Control
Abstract
1. Introduction
2. Acoustic Synthetic Jet Actuator
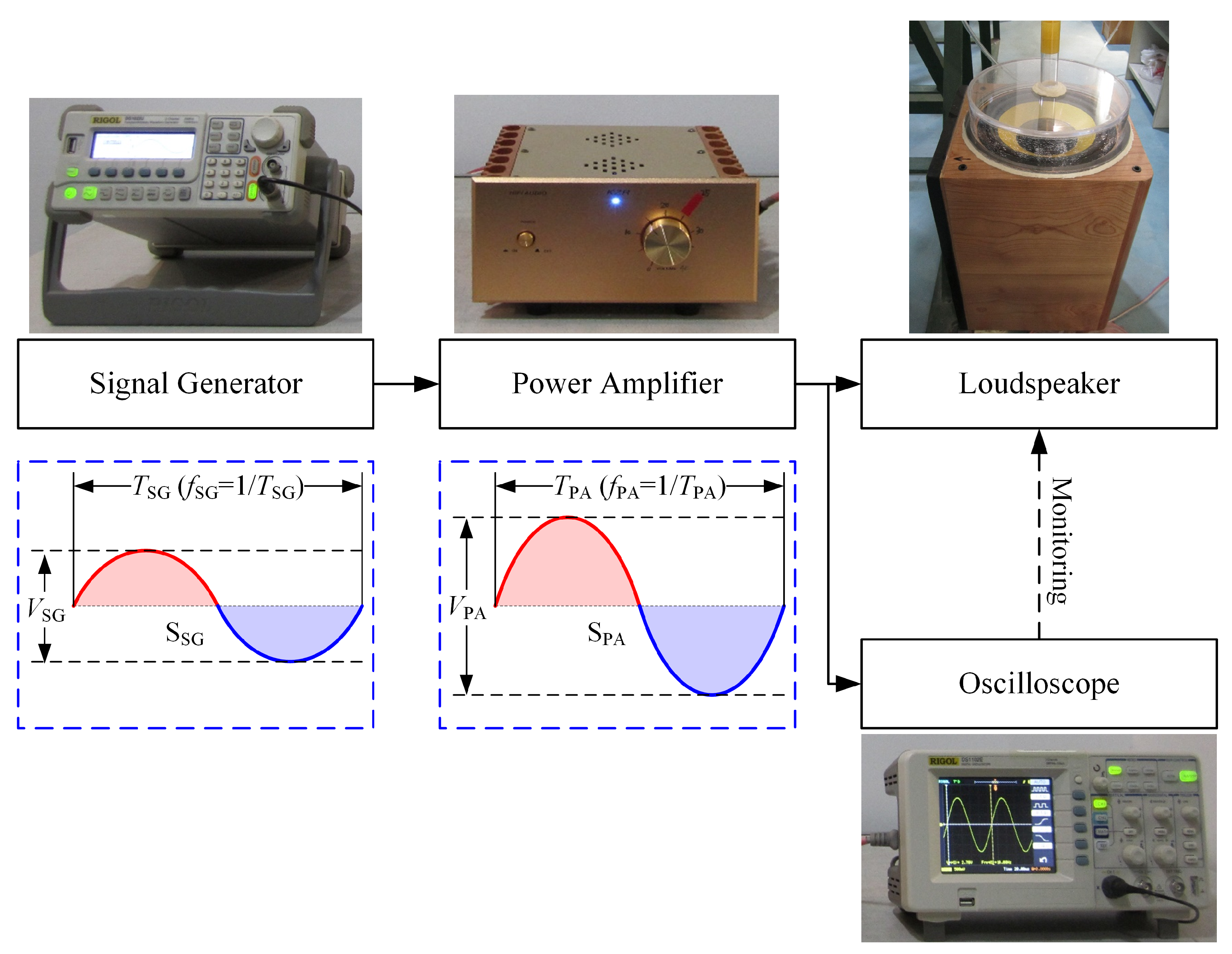
2.1. Actuation System
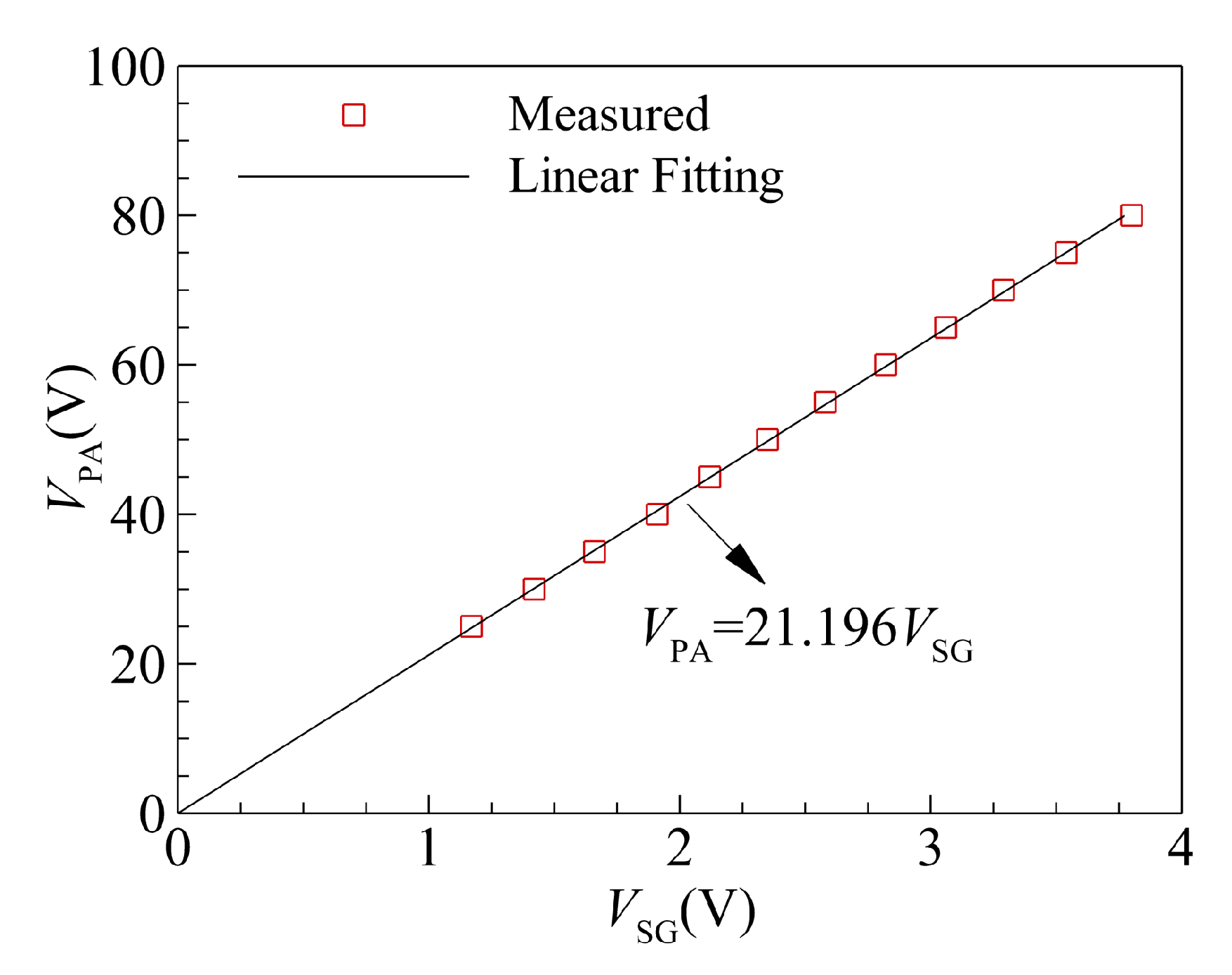
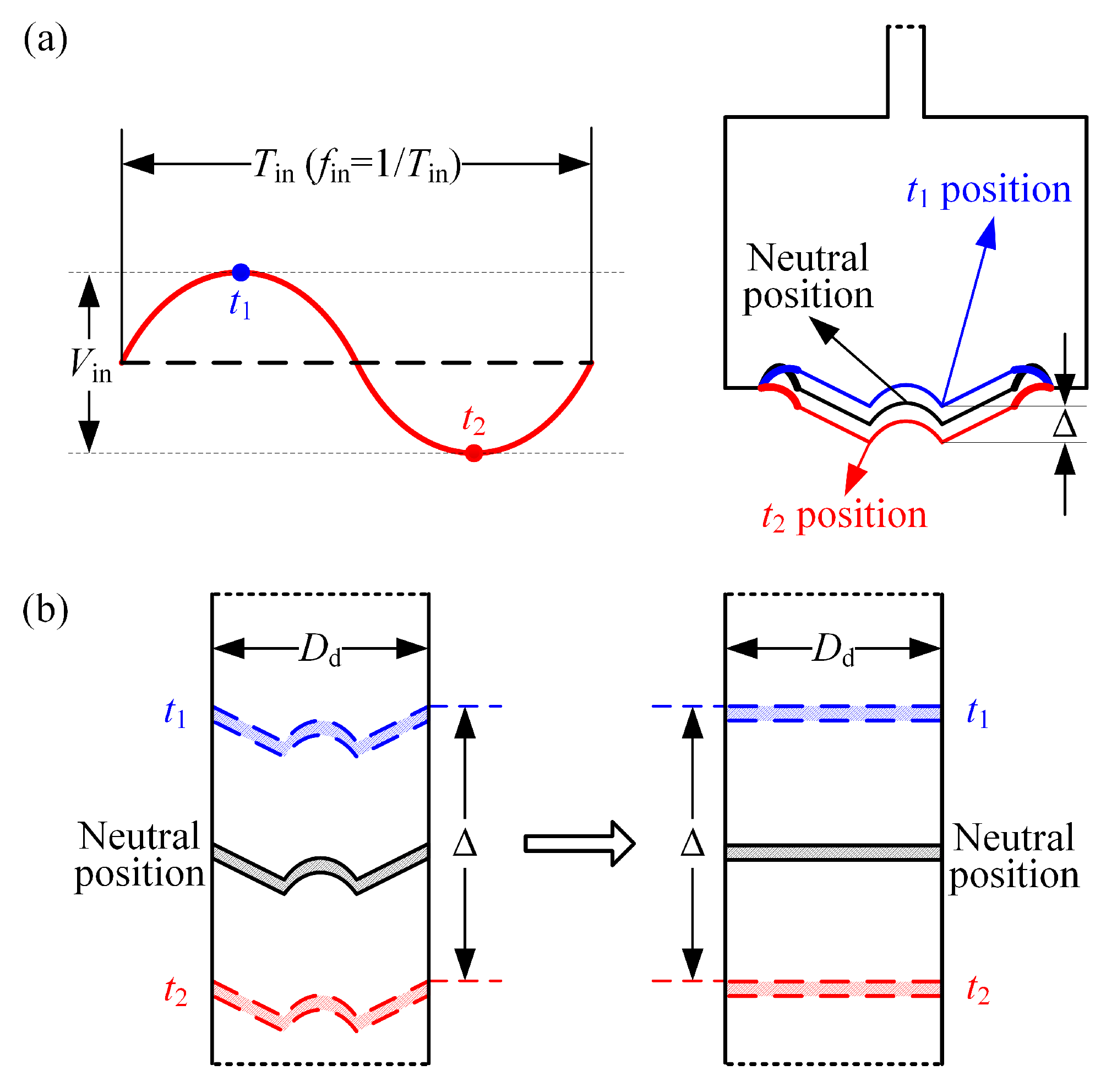
2.2. Input Signal Modulation
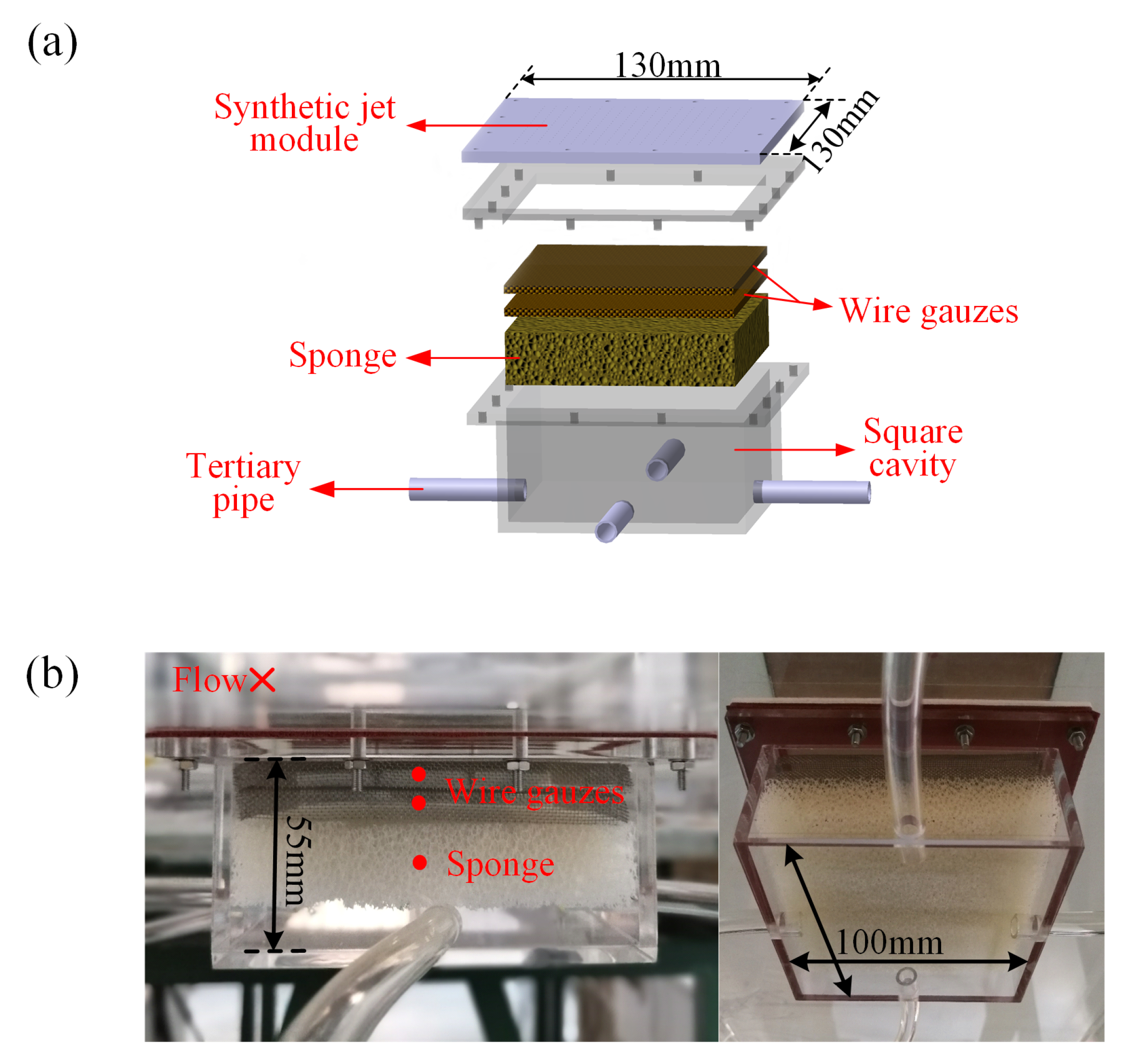
2.3. Implementation of Multiple Orifices Corresponding to One Diaphragm
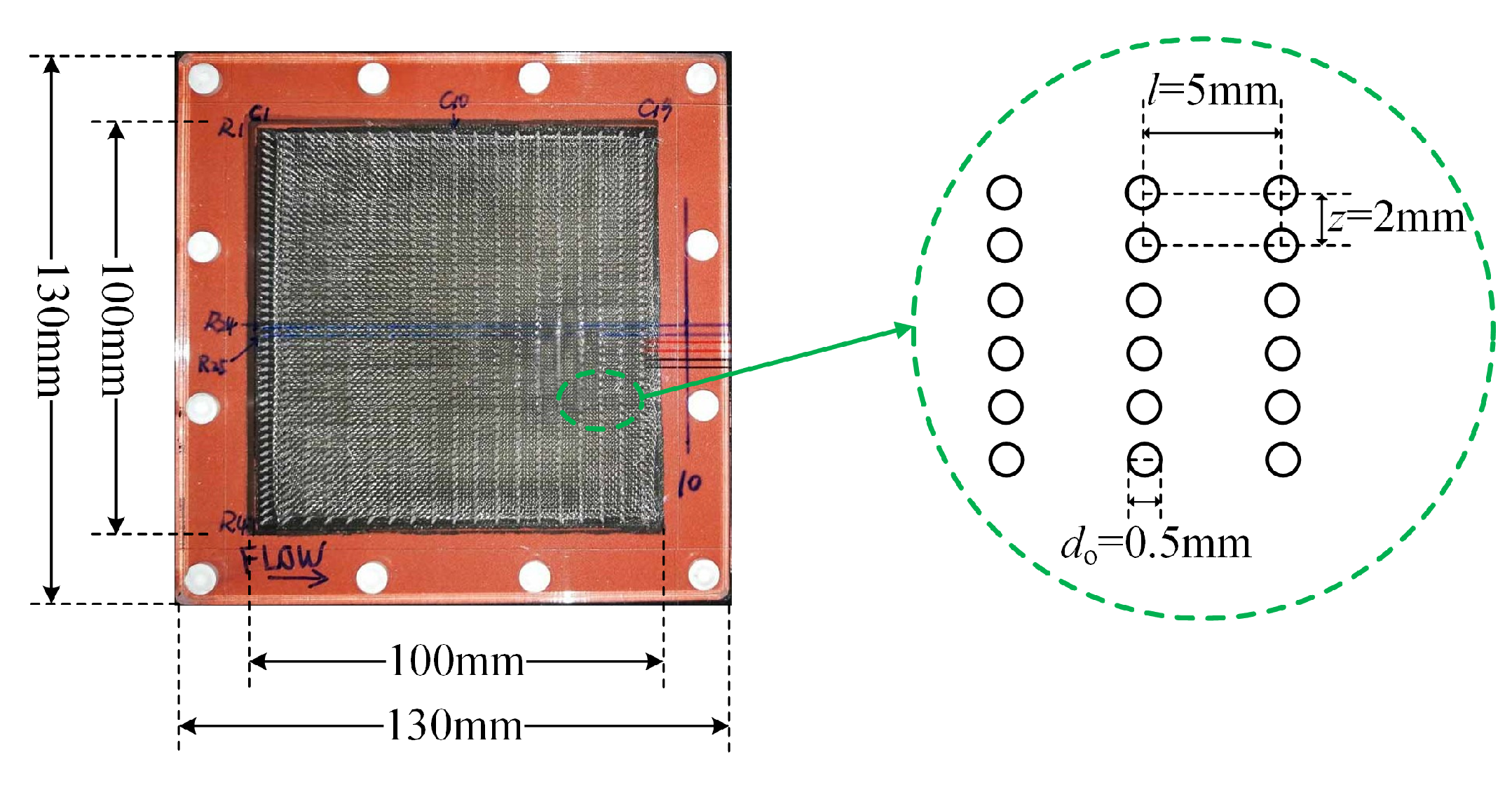
2.4. Orifice Array
2.5. Parameters Determining the Performance of Distributed Synthetic Jets
3. Characteristics of Distributed Synthetic Jets
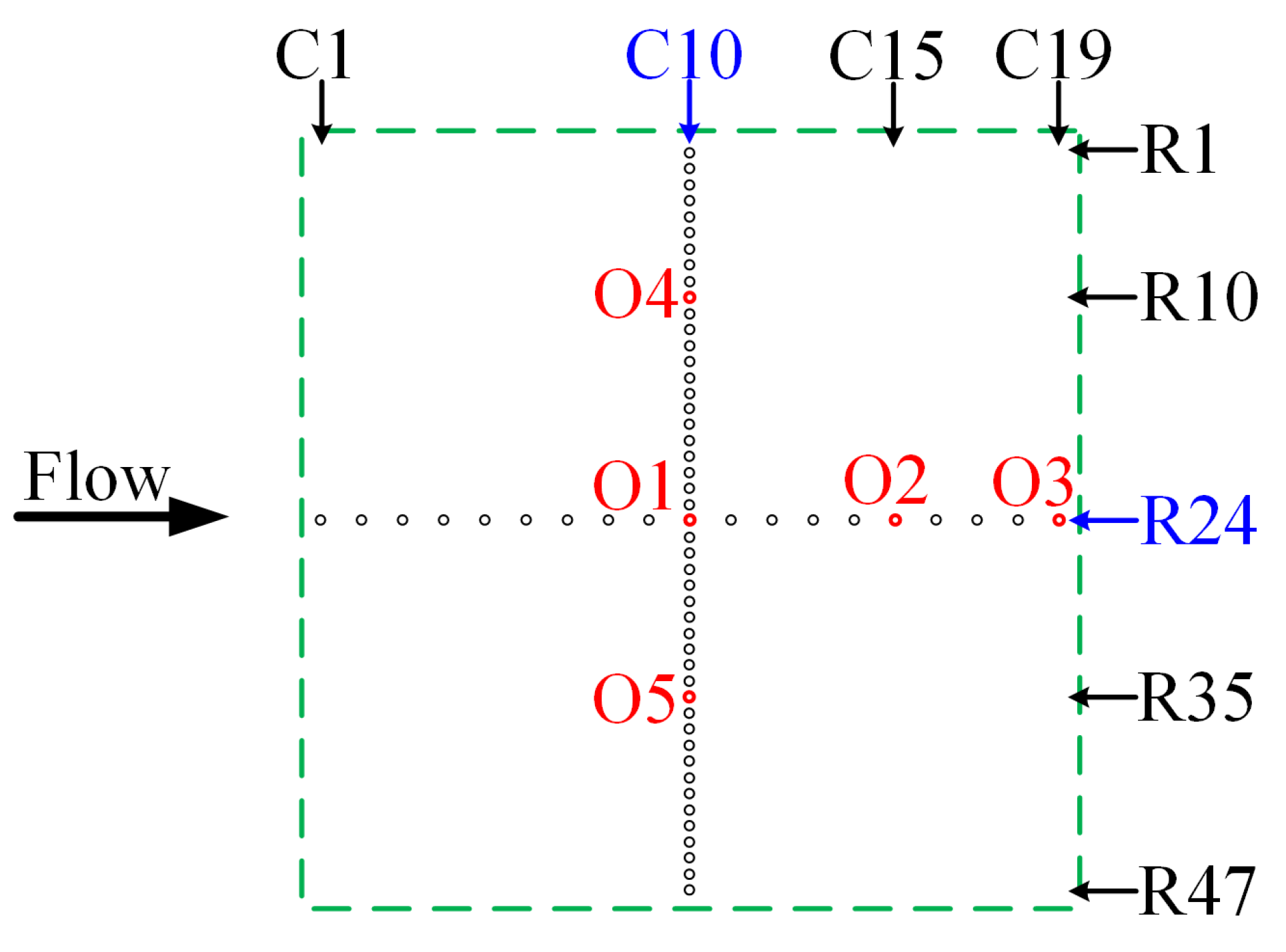
3.1. Measurement Method
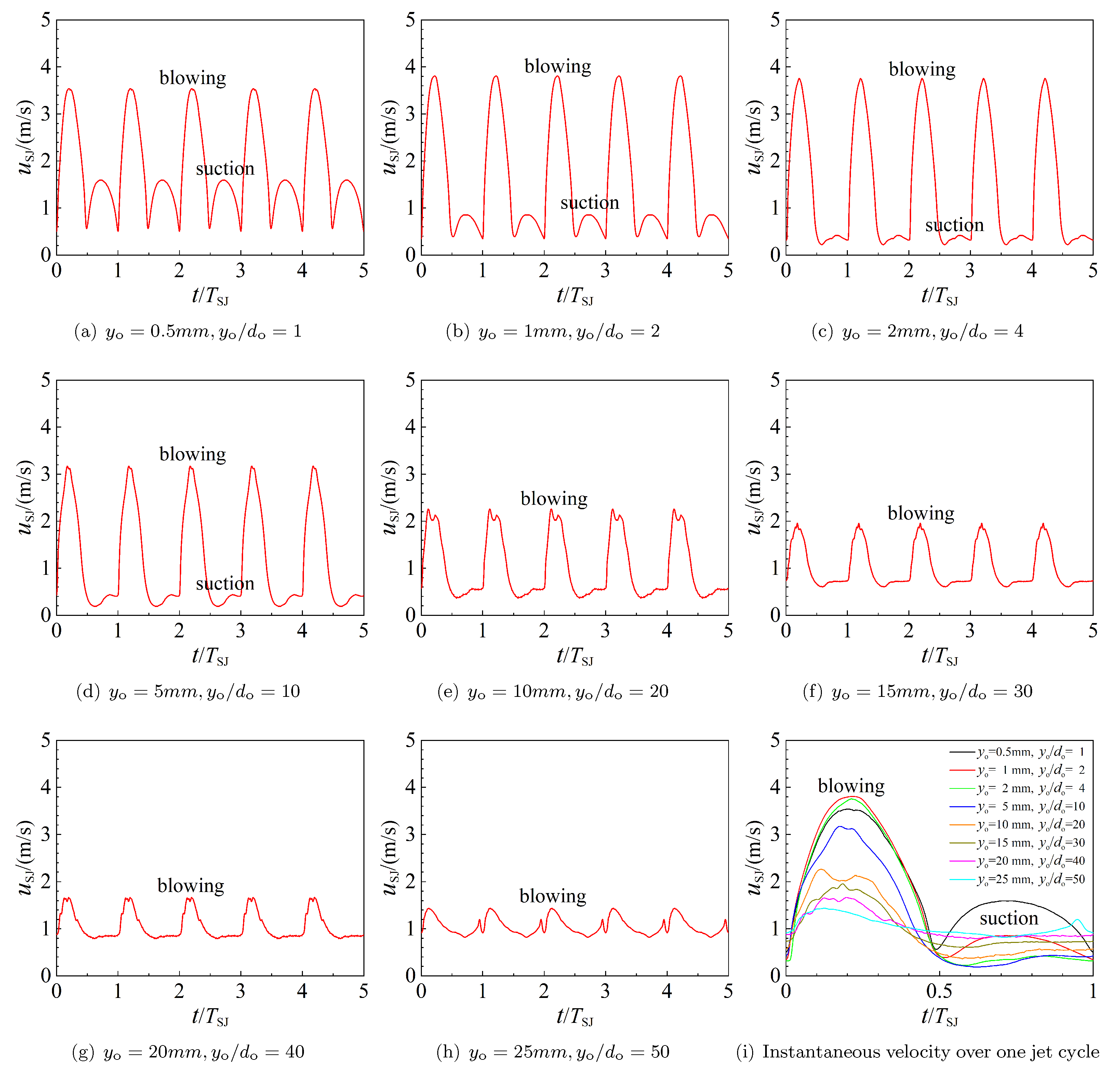
3.2. Instantaneous Velocity
3.3. Centerline Velocity
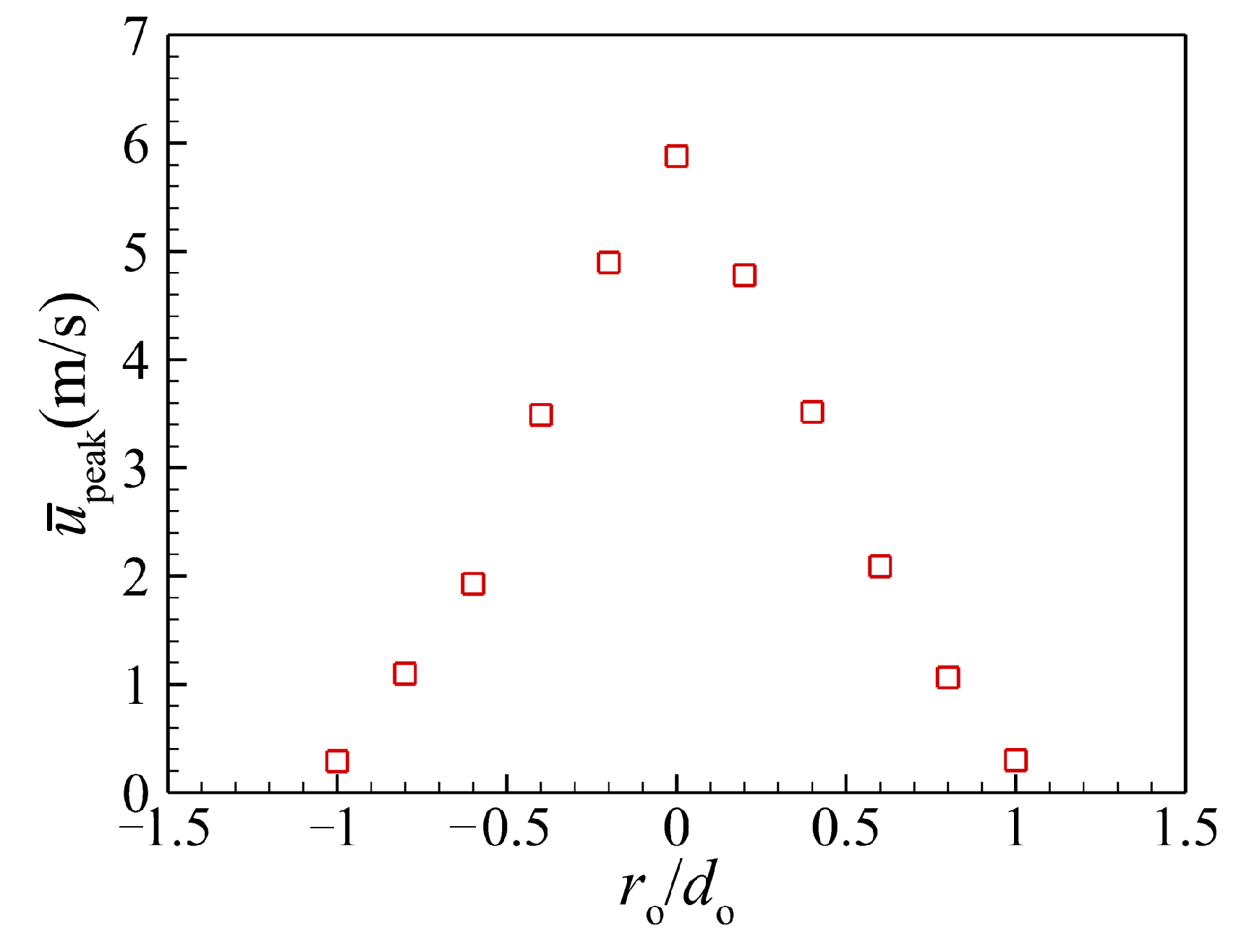
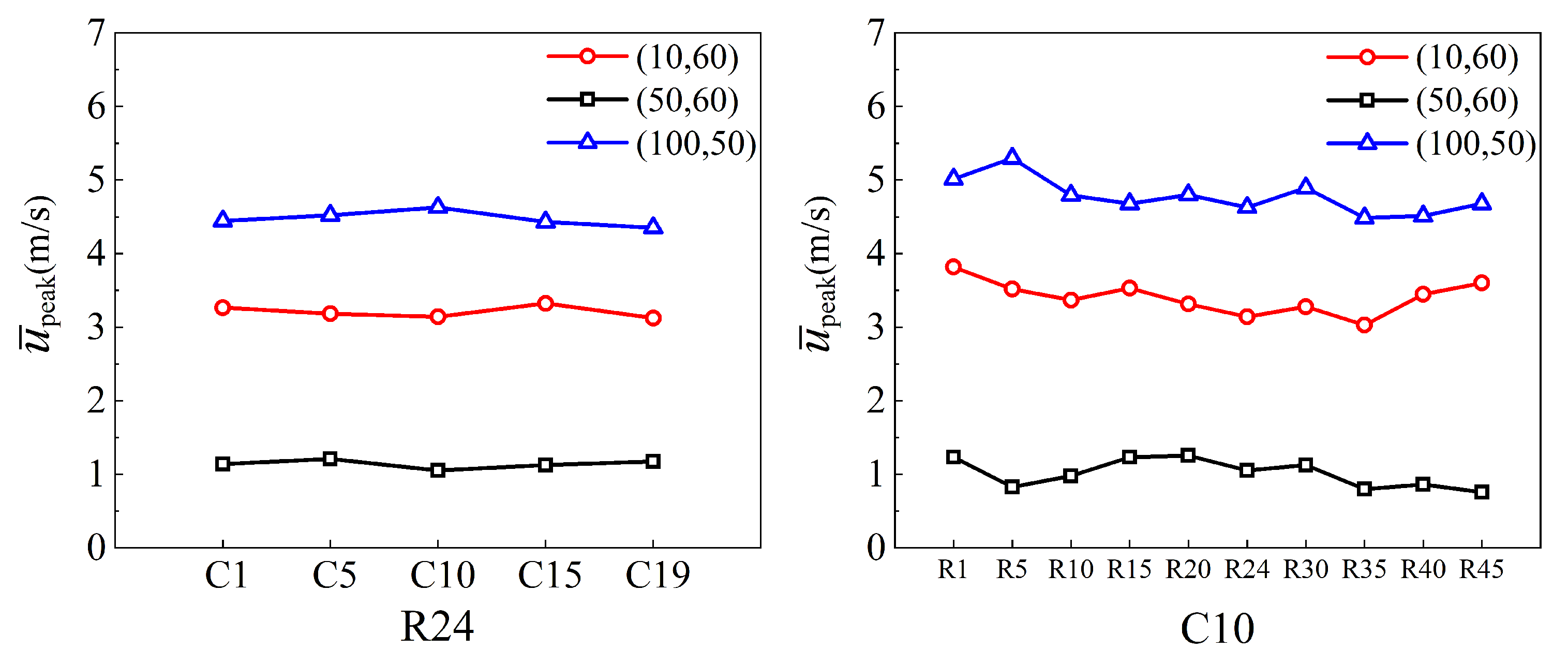
3.4. Synthetic Jet Uniformity
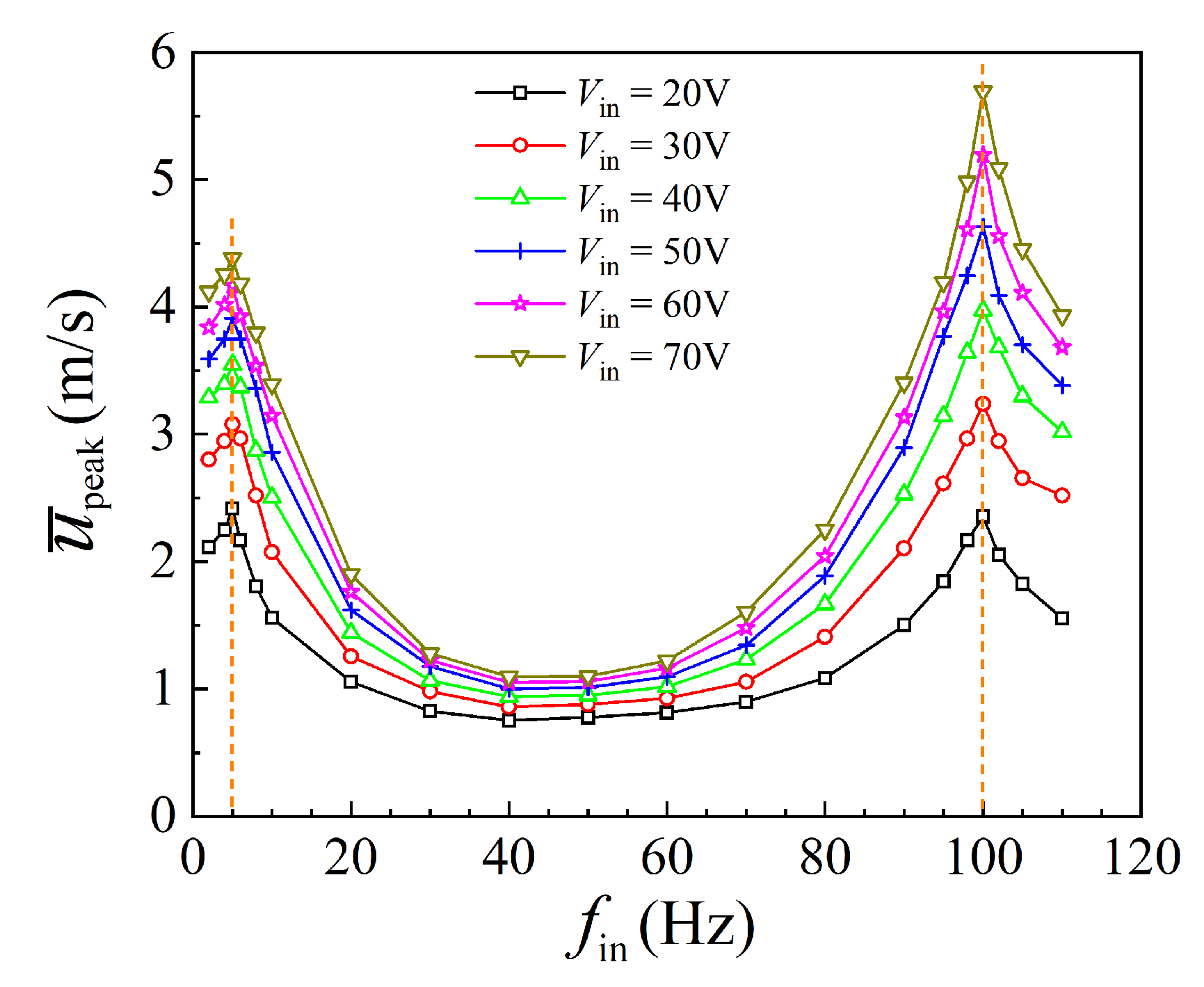
3.5. Parameter Space
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Glezer, A.; Amitay, M. Synthetic Jets. Annu. Rev. Fluid Mech. 2002, 34, 503–529. [Google Scholar] [CrossRef]
- Murugan, T.; Deyashi, M.; Dey, S.; Rana, S.C.; Chatterjee, P.K. Recent developments on synthetic jets. Def. Sci. J. 2016, 66, 489–498. [Google Scholar] [CrossRef]
- Smith, B.L.; Glezer, A. The formation and evolution of synthetic jets. Phys. Fluids 1998, 10, 2281–2297. [Google Scholar] [CrossRef]
- Holman, R.; Utturkar, Y.; Mittal, R.; Smith, B.L.; Cattafesta, L. Formation criterion for synthetic jets. AIAA J. 2005, 43, 2110–2116. [Google Scholar] [CrossRef]
- Garcillan, L.; Zhong, S.; Pokusevski, Z.; Wood, N. A PIV study of synthetic jets with different orifice shape and orientation. In Proceedings of the 2nd AIAA Flow Control Conference, Portland, OR, USA, 28 June–1 July 2004. AIAA 2004-2213. [Google Scholar]
- Crook, A.; Wood, N.J. Measurements and visualizations of synthetic jets. In Proceedings of the 39th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2001. AIAA 2001-0145. [Google Scholar]
- Tang, H.; Salunkhe, P.; Zheng, Y.; Du, J.; Wu, Y. On the use of synthetic jet actuator arrays for active flow separation control. Exp. Therm. Fluid Sci. 2014, 57, 1–10. [Google Scholar] [CrossRef]
- Chatlynne, E.; Rumigny, N.; Amitay, M.; Glezer, A. Virtual aero-shaping of a Clark-Y airfoil using synthetic jet actuators. In Proceedings of the 39th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2001. AIAA 2001-0732. [Google Scholar]
- Cheng, X.; Ma, C.; Liu, H.; Yang, C. Influence of synthetic jet on aerodynamic characteristics of blunt trailing edge wind turbine airfoil. J. Mech. Eng. 2016, 52, 148–156. [Google Scholar] [CrossRef]
- Wu, C.; Ahmed, N. Vectoring of a wall bounded planar jet using synthetic jet actuator. In Proceedings of the 31st AIAA Applied Aerodynamics Conference, San Diego, CA, USA, 24–27 June 2013. AIAA 2013-2515. [Google Scholar]
- Xia, Q.; Zhong, S. Liquids mixing enhanced by multiple synthetic jet pairs at low Reynolds numbers. Chem. Eng. Sci. 2013, 102, 10–23. [Google Scholar] [CrossRef]
- Zhang, J.; Gao, S.; Tan, X. Convective heat transfer on a flat plate subjected to normally synthetic jet and horizontally forced flow. Int. J. Heat Mass Transf. 2013, 57, 321–330. [Google Scholar] [CrossRef]
- Hafsteinsson, H.; Eriksson, L.E.; Cuppoletti, D.; Gutmark, E.; Prisell, E. Active suppression of supersonic jet noise using pulsating micro-jets. In Proceedings of the 50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Nashville, TN, USA, 9–12 January 2012. AIAA 2012-0246. [Google Scholar]
- Gilarranz, J.L.; Traub, L.W.; Rediniotis, O.K. A new class of synthetic jet actuators-part I: Design, fabrication and bench top characterization. J. Fluids Eng. 2005, 127, 367–376. [Google Scholar] [CrossRef]
- Chaudhari, M.; Verma, G.; Puranik, B.; Agrawal, A. Frequency response of a synthetic jet cavity. Exp. Therm. Fluid Sci. 2009, 33, 439–448. [Google Scholar] [CrossRef]
- Smyk, E.; Gil, P.; Gałek, R.; Przeszłowski, Ł. Acoustic and flow aspects of novel synthetic jet actuator. Actuators 2020, 9, 100. [Google Scholar] [CrossRef]
- Gil, P.; Wilk, J. Experimental investigations of different loudspeakers applied as synthetic jet actuators. Actuators 2021, 10, 224. [Google Scholar] [CrossRef]
- Bailo, K.C.; Brei, D.E.; Calkins, F.T. Investigation of PVdF active diaphragms for synthetic jets. In Proceedings of the SPIE’s 7th Annual International Symposium on Smart Structures and Materials, Newport Beach, CA, USA, 6 March 2000. [Google Scholar]
- Liang, Y.; Kuga, Y.; Taya, M. Design of membrane actuator based on ferromagnetic shape memory alloy composite for synthetic jet applications. Sens. Actuat. A-Phys. 2006, 125, 512–518. [Google Scholar] [CrossRef]
- Grossman, K.R.; Cybyk, B.Z.; Rigling, M.C.; VanWie, D.M. Characterization of sparkjet actuators for flow control. In Proceedings of the 42nd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 5–8 January 2004. AIAA 2004-89. [Google Scholar]
- Caruana, D.; Barricau, P.; Hardy, P.; Cambronne, J.P.; Belinger, A. The “plasma synthetic jet” actuator. Aero-thermodynamic characterization and first flow control applications. In Proceedings of the 47th AIAA Aerospace Sciences Meeting Including The New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 5–8 January 2009. AIAA 2009-1307. [Google Scholar]
- Zhang, Z.; Li, D. Characteristics of a synthetic jet actuator and its application on control of flow over a backward facing step. J. Mech. Eng. 2018, 54, 224–232. [Google Scholar] [CrossRef]
- Zhong, S.; Jabbal, M.; Tang, H.; Garcillan, L.; Guo, F.; Wood, N.; Warsop, C. Towards the design of synthetic-jet actuators for full-scale flight conditions—Part 1: The fluid mechanics of synthetic-jet actuators. Flow Turbul. Combust. 2007, 78, 283–307. [Google Scholar] [CrossRef]
- Tang, H.; Zhong, S.; Jabbal, M.; Garcillan, L.; Guo, F.; Wood, N.; Warsop, C. Towards the design of synthetic-jet actuators for full-scale flight conditions—Part 2: Low-dimensional performance prediction models and actuator design method. Flow Turbul. Combust. 2007, 78, 309–329. [Google Scholar] [CrossRef]
- Tang, H.; Zhong, S. Incombressible Flow Model of Synthetic Jet Actuators. AIAA J. 2006, 44, 908–912. [Google Scholar] [CrossRef]
- Gil, P.; Strzelczyk, P. Performance and efficiency of loudspeaker driven synthetic jet actuator. Exp. Therm. Fluid Sci. 2016, 76, 163–174. [Google Scholar] [CrossRef]
- Shuster, J.M.; Smith, D.R. A study of the formation and scaling of a synthetic jet. In Proceedings of the 42nd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 5–8 January 2004. AIAA 2004-90. [Google Scholar]
- Luca, L.; Girfoglio, M.; Coppola, G. Modeling and experimental validation of the frequency response of synthetic jet actuators. AIAA J. 2014, 52, 1733–1748. [Google Scholar] [CrossRef]
- Mark, A.F.; Philippe, L.; Pierre, E.S. Influence of cavity shape on synthetic jet performance. Sens. Actuat. A-Phys. 2015, 223, 1–10. [Google Scholar]
- Zhao, Z.; Ding, J.; Shi, S.; Kaufmann, R.; Ganapathisubramani, B. Volumetric flow characterisation of a rectangular orifice impinging synthetic jet with single-camera light-field PIV. Exp. Therm. Fluid Sci. 2021, 123, 110327. [Google Scholar] [CrossRef]
- Palumbo, A.; Luca, L. Experimental and CFD characterization of a double-orifice synthetic jet actuator for flow control. Actuators 2021, 10, 326. [Google Scholar] [CrossRef]
- Chaudhari, M.; Puranik, B.; Agrawal, A. Multiple orifice synthetic jet for improvement in impingement heat transfer. Int. J. Heat Mass Transf. 2011, 54, 2056–2065. [Google Scholar] [CrossRef]
- Mangate, L.; Yadav, H.; Agrawal, A.; Chaudhari, M. Experimental investigation on thermal and flow characteristics of synthetic jet with multiple-orifice of different shapes. Int. J. Therm. Sci. 2019, 140, 344–357. [Google Scholar] [CrossRef]
- Gil, P. Experimental investigation on heat transfer enhancement of air-cooled heat sink using multiple synthetic jets. Int. J. Therm. Sci. 2021, 166, 106949. [Google Scholar] [CrossRef]
- Gil, P.; Smyk, E.; Gałek, R.; Przeszłowski, Ł. Thermal, flow and acoustic characteristics of the heat sink integrated inside the synthetic jet actuator cavity. Int. J. Therm. Sci. 2021, 170, 107171. [Google Scholar] [CrossRef]
- Kline, S.J.; Reynolds, W.C.; Schraub, F.A.; Runstadler, P.W. The structure of turbulent boundary layers. J. Fluid Mech. 1967, 30, 741–773. [Google Scholar] [CrossRef]
- Kim, H.T.; Kline, S.J.; Reynolds, W.C. The production of turbulence near a smooth wall in a turbulent boundary layer. J. Fluid Mech. 1971, 50, 133–160. [Google Scholar] [CrossRef]
- Smith, C.R.; Metzler, S.P. The characteristics of low-speed streaks in the near-wall region of a turbulent boundary layer. J. Fluid Mech. 1983, 129, 27–54. [Google Scholar] [CrossRef]
- Chiatto, M.; Palumbo, A.; Luca, L. Design approach to predict synthetic jet formation and resonance amplifications. Exp. Therm. Fluid Sci. 2019, 107, 79–87. [Google Scholar] [CrossRef]
- Zong, H.; Chiatto, M.; Kotsonis, M.; Luca, L. Plasma synthetic jet actuators for active flow control. Actuators 2018, 7, 77. [Google Scholar] [CrossRef]






| z | l | ||
|---|---|---|---|
| mm | mm | mm | mm |
| - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, L.; Li, D.; Zhang, Z.; Yang, Y.; Liu, D.; Tao, Y.; Lu, B. Design of an Acoustic Synthetic Jet Actuator for Flow Control. Actuators 2022, 11, 300. https://doi.org/10.3390/act11100300
Lu L, Li D, Zhang Z, Yang Y, Liu D, Tao Y, Lu B. Design of an Acoustic Synthetic Jet Actuator for Flow Control. Actuators. 2022; 11(10):300. https://doi.org/10.3390/act11100300
Chicago/Turabian StyleLu, Lianshan, Dong Li, Zhenhui Zhang, Yin Yang, Dawei Liu, Yang Tao, and Bo Lu. 2022. "Design of an Acoustic Synthetic Jet Actuator for Flow Control" Actuators 11, no. 10: 300. https://doi.org/10.3390/act11100300
APA StyleLu, L., Li, D., Zhang, Z., Yang, Y., Liu, D., Tao, Y., & Lu, B. (2022). Design of an Acoustic Synthetic Jet Actuator for Flow Control. Actuators, 11(10), 300. https://doi.org/10.3390/act11100300






