Fixed Points on Active and Passive Dynamics of Active Hydraulic Mounts with Oscillating Coil Actuator
Abstract
:1. Introduction
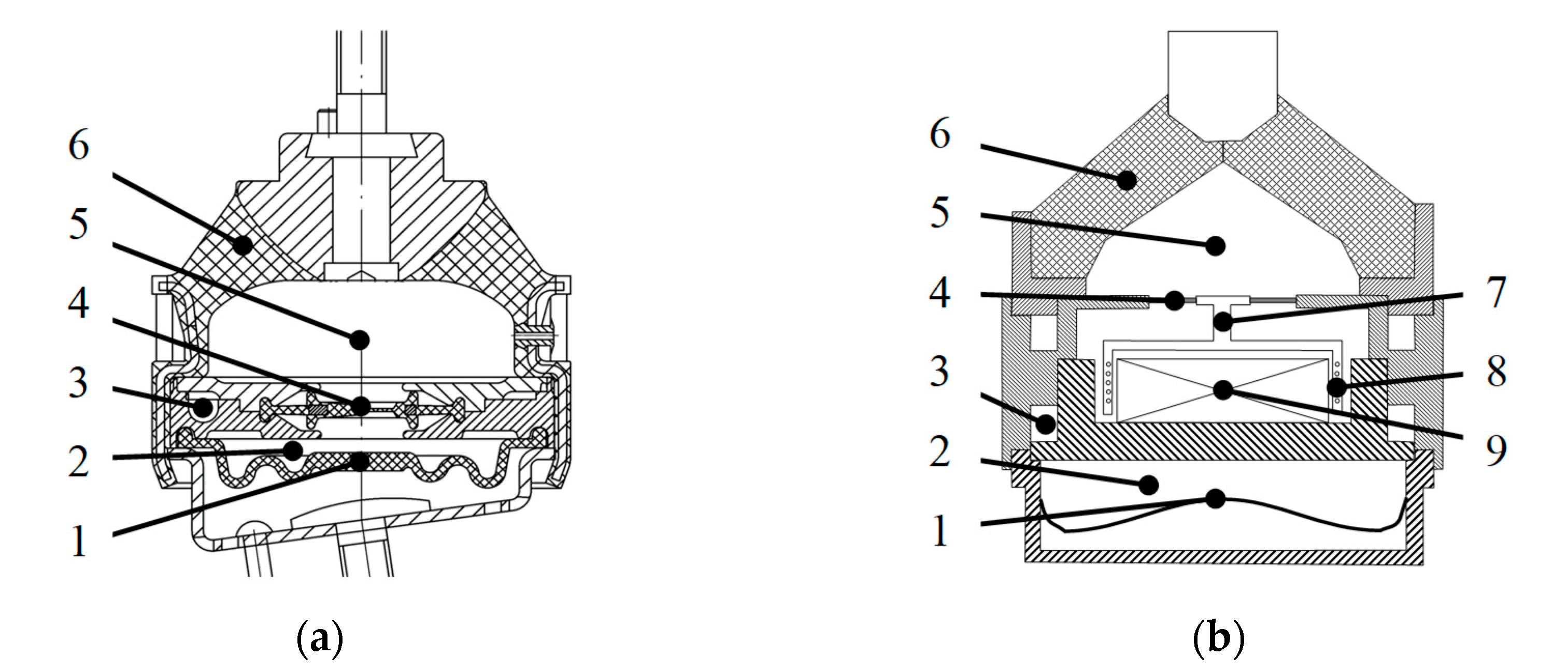
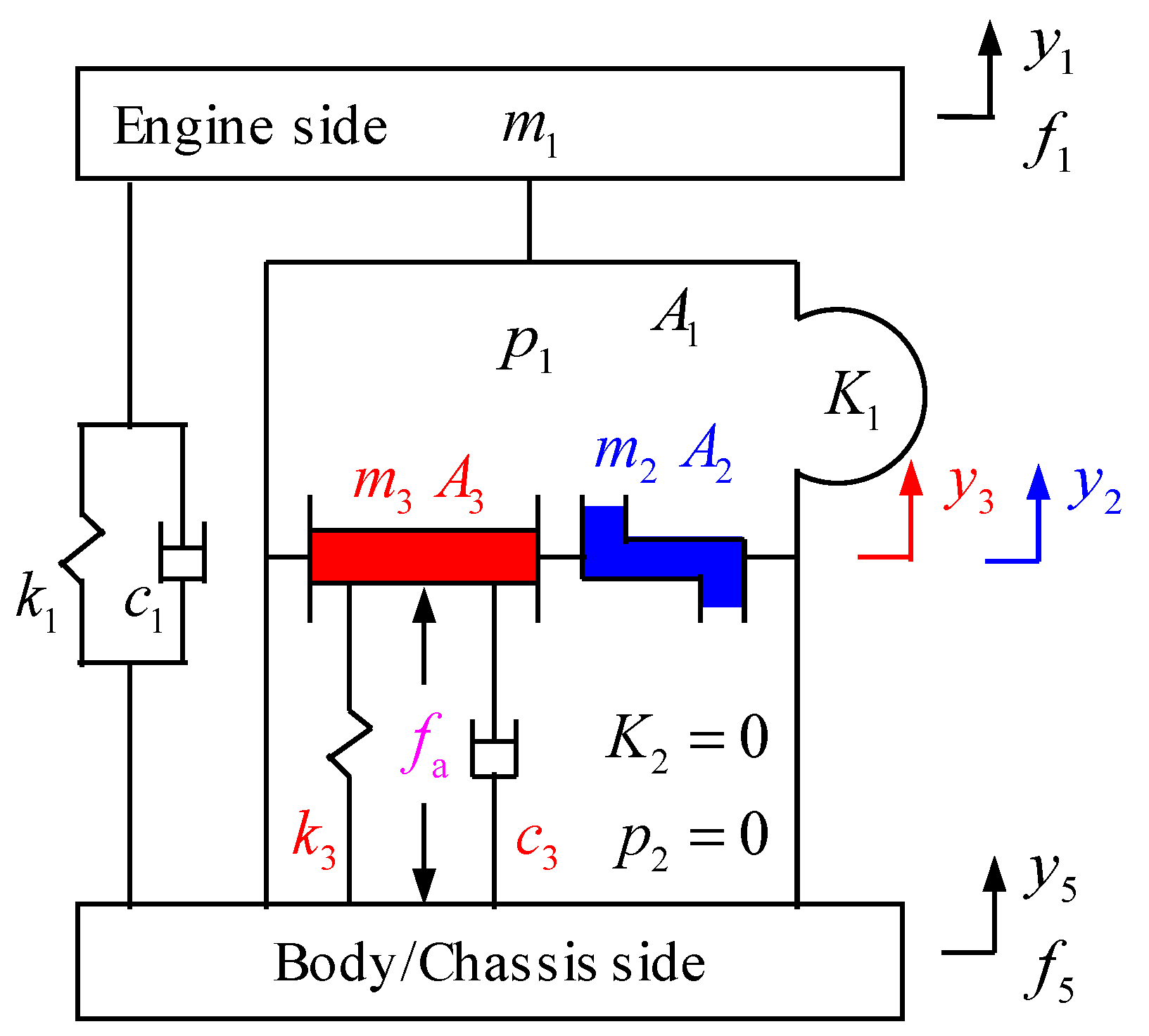
2. Mechanical Model of Active Hydraulic Mount (AHM)
3. Analysis and Experimental Validation of Passive Dynamics
3.1. Nonlinear Lumped Parameter Mathematical Model for Passive Dynamics
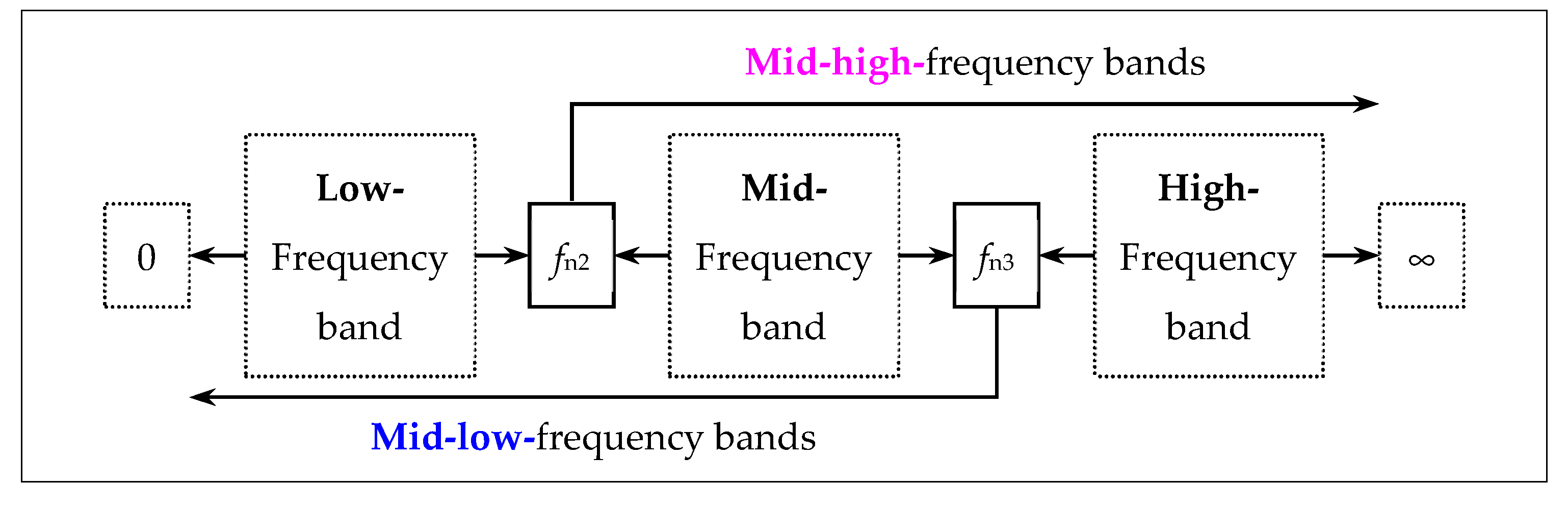
3.2. Analysis of Mid-Low-Frequency Passive Dynamics and the Amplitude Dependence and Fixed Points (f << fn3)
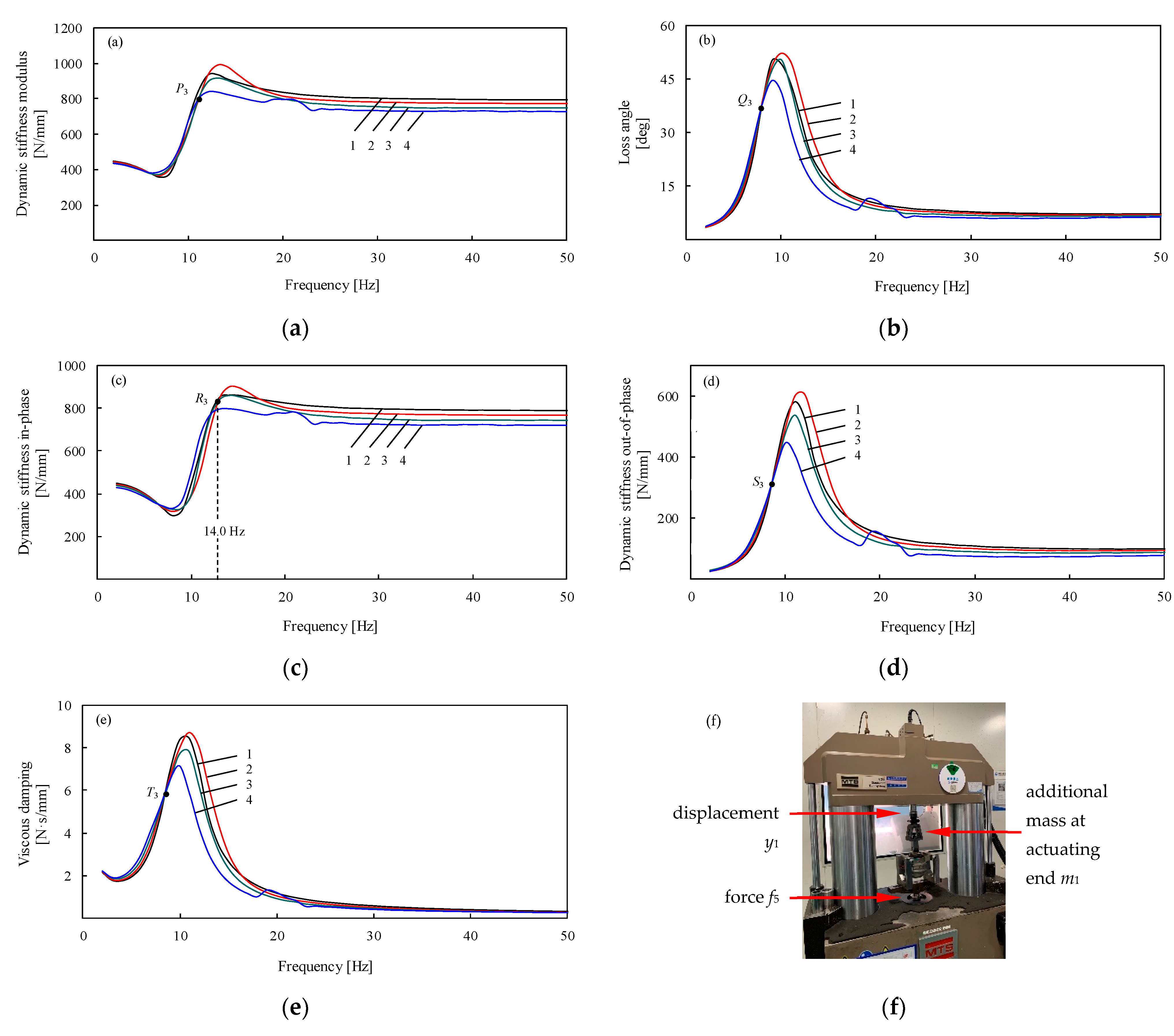
3.3. Experimental Validation of Amplitude Dependence and Fixed Point for Mid-Low-Frequency Passive Dynamics
4. Analysis and Experimental Validation of Active Dynamics
4.1. Nonlinear Lumped Parameter Zodel for Active Dynamics
4.2. Analysis of Mid-Low-Frequency Active Dynamics and the Amplitude Dependence and Fixed Points (f << fn3)
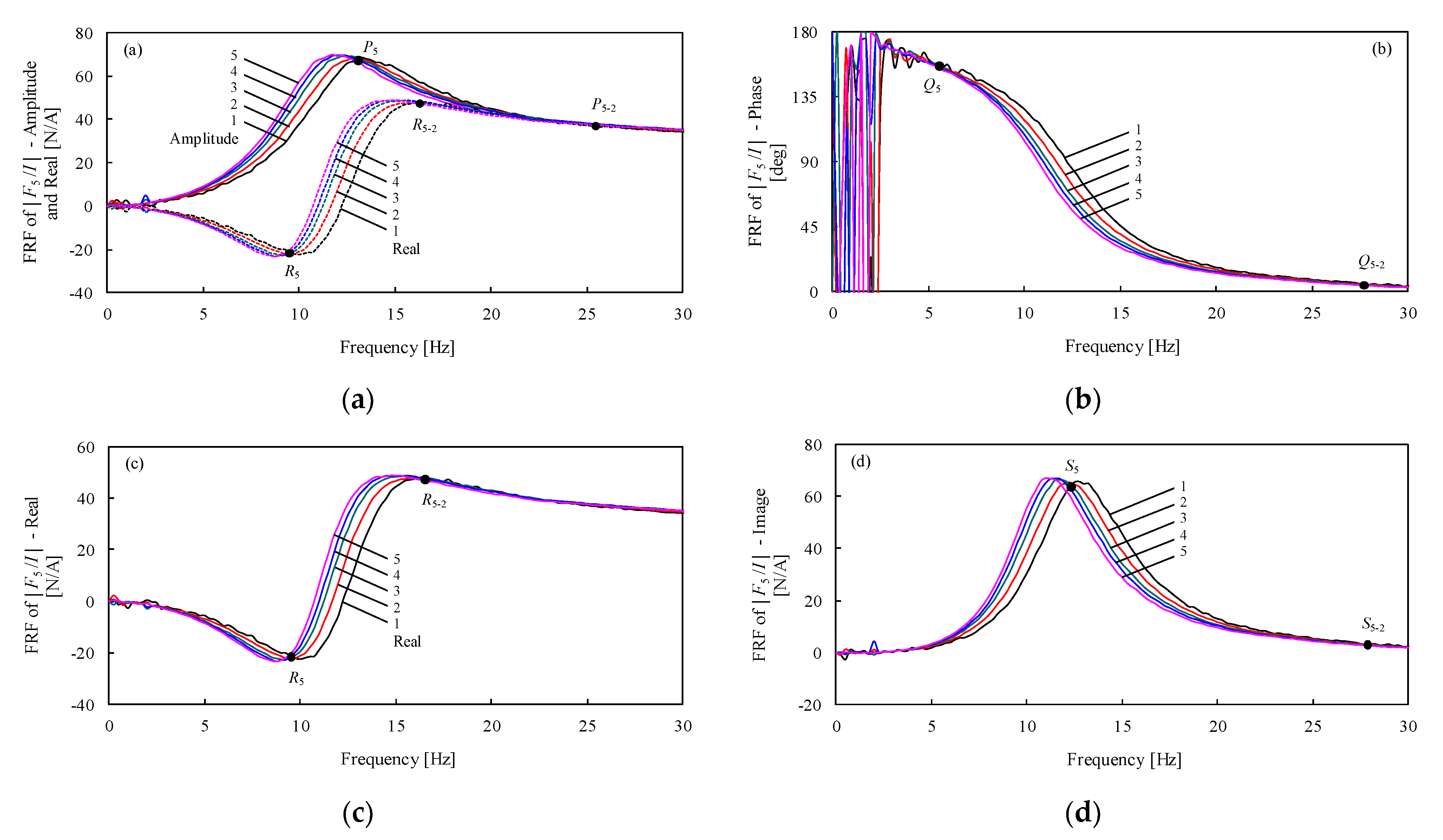
4.3. Experimental Validation of Amplitude Dependence and Fixed Point for Mid-Low-Frequency Active Dynamics
5. Conclusions
- A unified lumped parameter mechanical model with two DOFs is established for PHM-IT-DMs and AHM-IT-DMs. Considering that the fluid channel resonance frequency is far less than the resonance frequency of the decoupler/mover, the active and passive dynamics may be divided into mid-low-frequency dynamics and mid-high-frequency dynamics. In mid-low-frequency bands, the inertia and damping forces of decoupler/mover may be neglected, and a 1-DOF nonlinear lumped parameter mathematical model can be obtained.
- The 1-DOF nonlinear lumped parameter mathematical model for mid-low-frequency bands exhibits several distinct features in active and passive dynamics, such as amplitude dependence, fixed point, resonance peak, and horizontal segment.
- The fundamental reason for amplitude-dependent dynamics is the amplitude dependence of local loss at the entrance and outlet. Amplitude-dependent dynamics represent a precondition for the existence of a fixed point.
- Since the inertia of the decoupler/mover may be neglected in mid-low-frequency bands, the drive point and cross point dynamics are identical.
- A single fixed point in passive dynamics for an AHM-IT-DM-OCA is revealed in the analysis and experiment. In the meantime, a pair of fixed points in active dynamics is newly revealed in the experiment. This paired appearance of fixed points is a new issue, and its mechanism should be investigated considering the dynamic characteristics of electromagnetic induction.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Ormondroyd, J.; Den Hartog, J.P. The theory of the dynamic vibration absorber. ASME J. Appl. Mech 1928, 50, 9–22. [Google Scholar]
- Hahnkamm, E. The damping of the foundation vibrations at varying excitation frequency. Master Arch. 1932, 4, 192–201. [Google Scholar]
- Brock, J.E. A note on the damped vibration absorber. Trans. Am. Soc. Mech. Eng. 1946, 68, 284. [Google Scholar]
- Den Hartog, J.P. Mechanical Vibrations, 4th ed.; McGraw-Hill: New York, NY, USA, 1956. [Google Scholar]
- Fan, R.-L.; Lu, Z.-H. Fixed points on the nonlinear dynamic properties of hydraulic engine mounts and parameter identification method: Experiment and theory. J. Sound Vib. 2007, 305, 703–727. [Google Scholar] [CrossRef]
- He, S.; Singh, R. Estimation of amplitude and frequency dependent parameters of hydraulic engine mount given limited dynamic stiffness measurements. Noise Control Eng. J. 2005, 53, 271–285. [Google Scholar] [CrossRef] [Green Version]
- Hausberg, F.; Christian, S.; Peter, P.; Manfred, P.; Simon, H.; Markus, R. Experimental and analytical study of secondary path variations in active engine mounts. J. Sound Vib. 2015, 340, 22–38. [Google Scholar] [CrossRef]
- Fan, R.-L.; Dou, Y.-F.; Yao, F.-H.; Qi, S.-Q.; Han, C. Experimental and analytical study of secondary path transfer function in active hydraulic mount with solenoid actuator. Actuators 2021, 10, 150. [Google Scholar] [CrossRef]
- Fan, R.-L.; Wang, P.; Han, C.; Wei, L.-J.; Liu, Z.-J.; Yuan, P.-J. Summarisation, simulation and comparison of nine control algorithms for an active control mount with an oscillating coil actuator. Algorithms 2021, 14, 256. [Google Scholar] [CrossRef]
- Gao, Z.-Q.; Wang, B.-R. Fluid Mechanics; Science Press: Beijing, China, 2017. [Google Scholar]
- Zhang, Y.-M. Mechanical Vibrations; Tsinghua University Press: Beijing, China, 2019. [Google Scholar]
- Fan, R.-L.; Fei, Z.-N.; Zhou, B.-Y.; Gong, H.-B.; Song, P.-J. Two-step dynamics of a semiactive hydraulic engine mount with four-chamber and three-fluid-channel. J. Sound Vib. 2020, 480, 115403. [Google Scholar] [CrossRef]
- Wen, B.-C. Engineering Nonlinear Vibrations; Science Press: Beijing, China, 2007. [Google Scholar]
- Khovanskii, A. Topological Galois Theory. Solvability and Unsolvability of Equations in Finite Terms; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Esterov, A. Galois theory for general systems of polynomial equations. Compos. Math. 2019, 155, 229–245. [Google Scholar] [CrossRef] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, R.-L.; Dou, Y.-F.; Ma, F.-L. Fixed Points on Active and Passive Dynamics of Active Hydraulic Mounts with Oscillating Coil Actuator. Actuators 2021, 10, 225. https://doi.org/10.3390/act10090225
Fan R-L, Dou Y-F, Ma F-L. Fixed Points on Active and Passive Dynamics of Active Hydraulic Mounts with Oscillating Coil Actuator. Actuators. 2021; 10(9):225. https://doi.org/10.3390/act10090225
Chicago/Turabian StyleFan, Rang-Lin, Yu-Fei Dou, and Fu-Liang Ma. 2021. "Fixed Points on Active and Passive Dynamics of Active Hydraulic Mounts with Oscillating Coil Actuator" Actuators 10, no. 9: 225. https://doi.org/10.3390/act10090225
APA StyleFan, R.-L., Dou, Y.-F., & Ma, F.-L. (2021). Fixed Points on Active and Passive Dynamics of Active Hydraulic Mounts with Oscillating Coil Actuator. Actuators, 10(9), 225. https://doi.org/10.3390/act10090225





