Modeling and Analysis in Trajectory Tracking Control for Wheeled Mobile Robots with Wheel Skidding and Slipping: Disturbance Rejection Perspective
Abstract
:1. Introduction
2. Methods
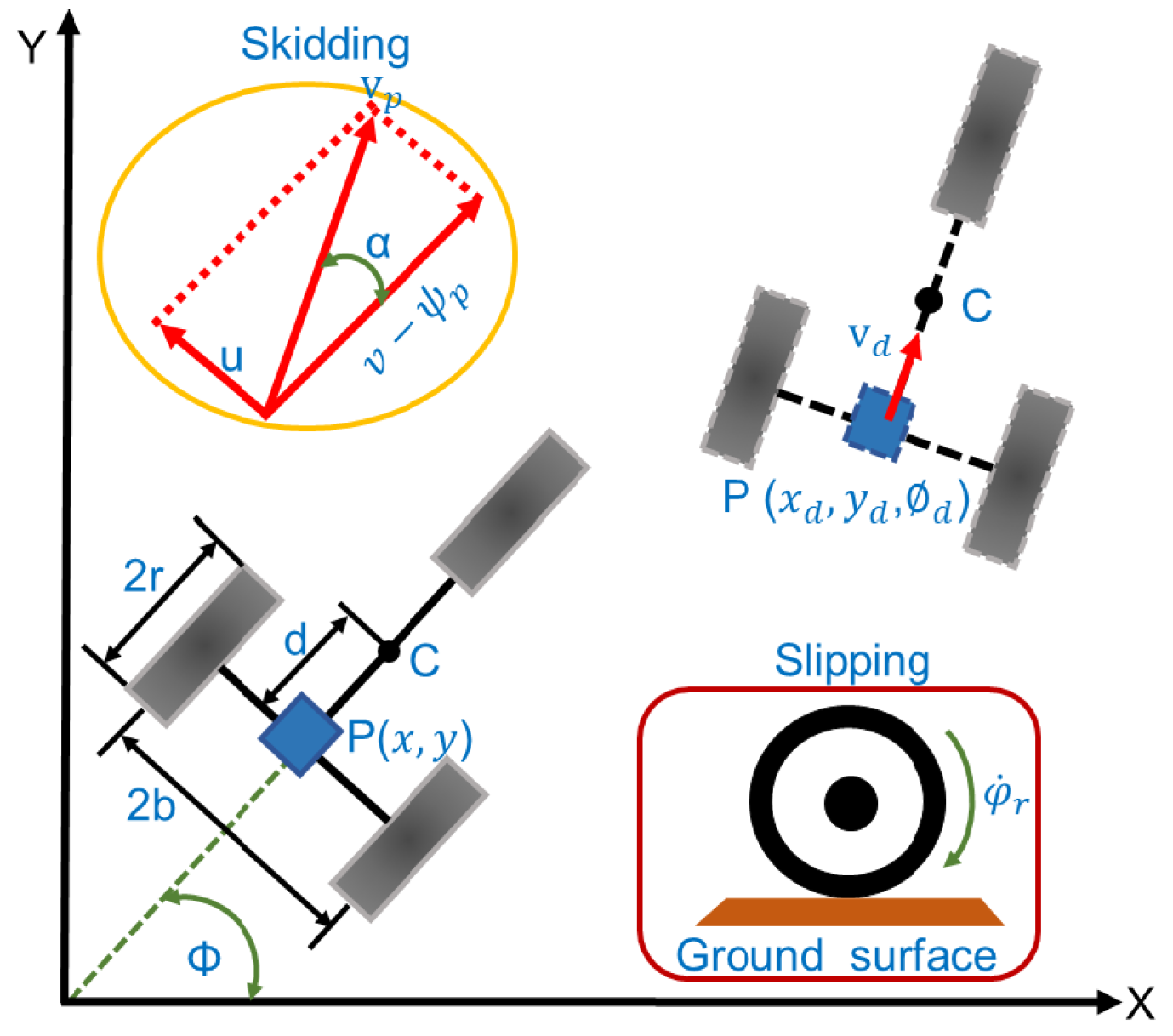
2.1. System Modeling
2.2. Tracking Problem for Nonholonomic WMR
2.3. Control Design and Stability Analysis
3. Results
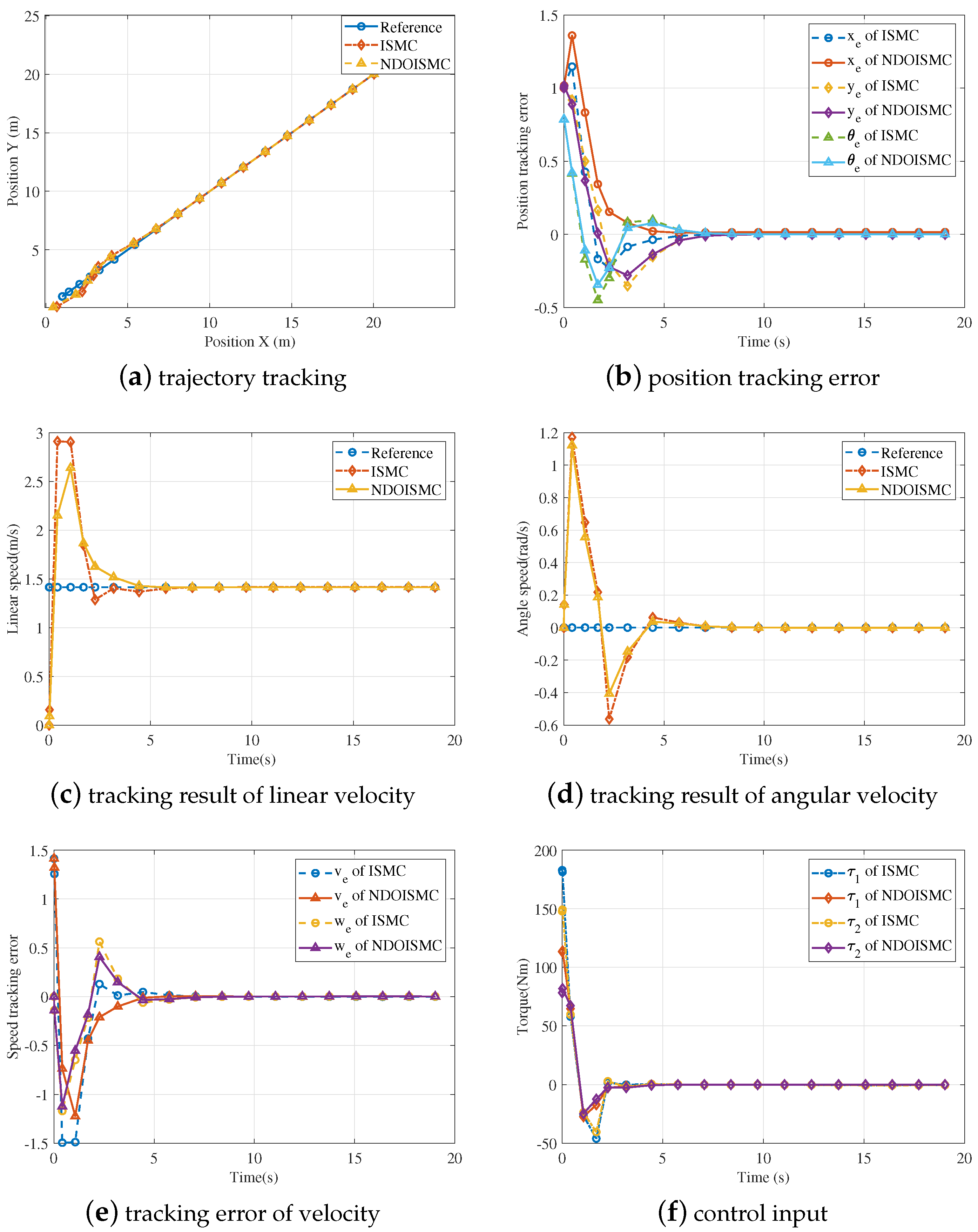
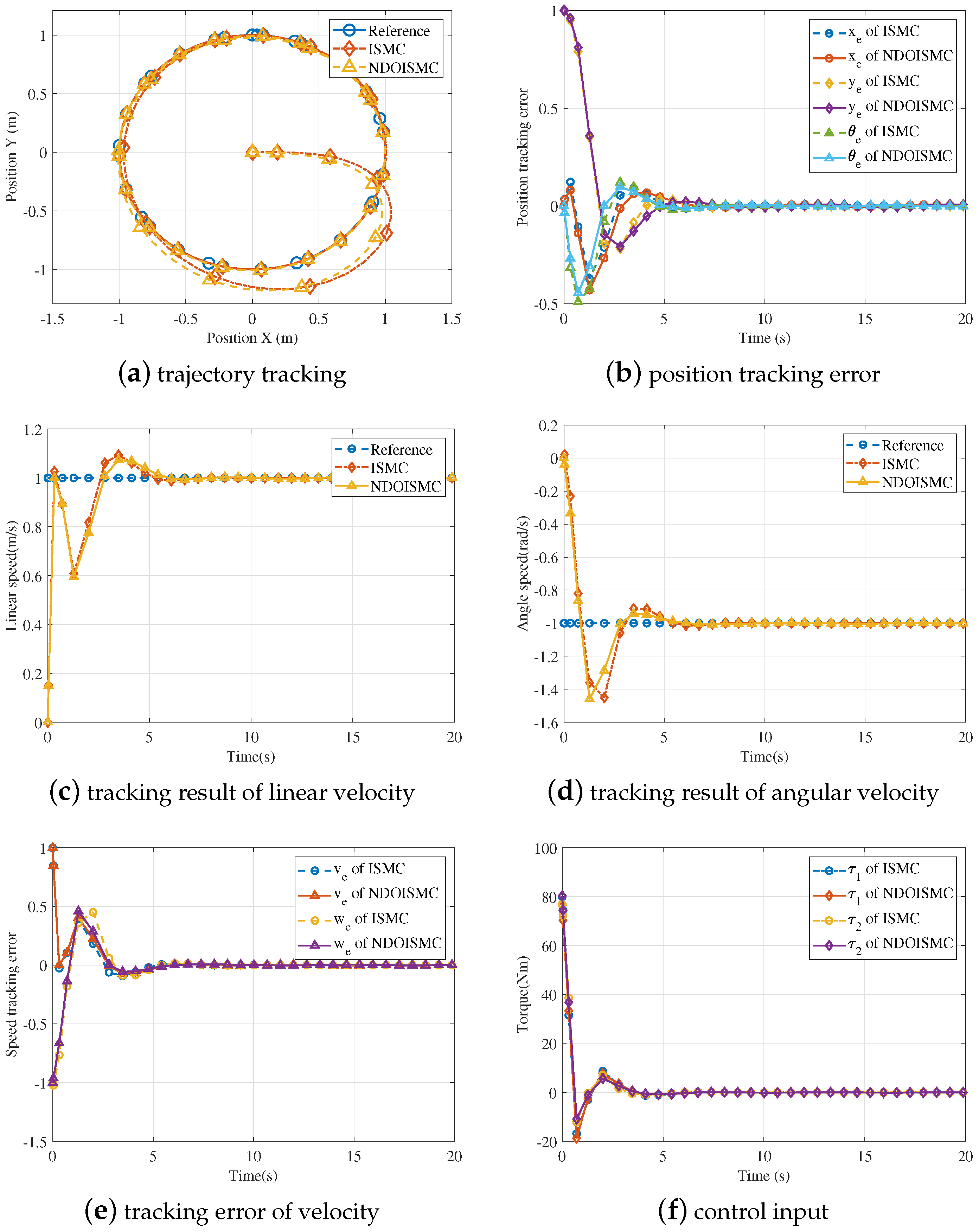
3.1. Simulation Works
3.2. Experiment Works
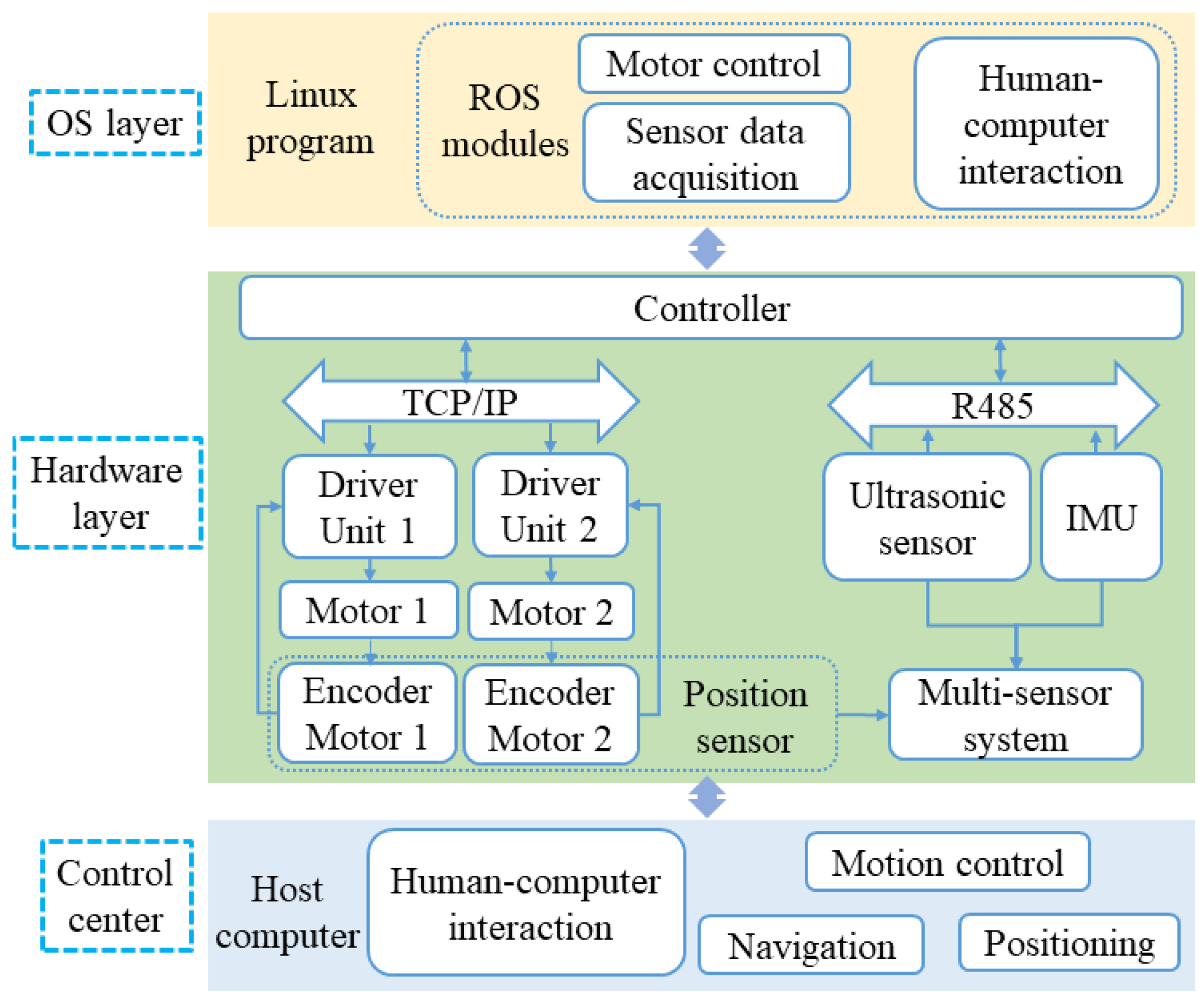
3.2.1. Experimental Setup
3.2.2. Experimental Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| WMR | Wheeled mobile robot |
| NDO | Nonlinear disturbance observer |
| ISMC | Integral sliding mode controller |
References
- Filipescu, A.; Minca, E.; Filipescu, A.; Coanda, H.G. Manufacturing technology on a mechatronics line assisted by autonomous robotic systems, robotic manipulators and visual servoing systems. Actuators 2020, 9, 127. [Google Scholar] [CrossRef]
- Ding, L.; Li, S.; Liu, Y.J.; Gao, H.; Chen, C.; Deng, Z. Adaptive neural network-based tracking control for full-state constrained wheeled mobile robotic system. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 2410–2419. [Google Scholar] [CrossRef]
- Noh, M.; Kwon, E.; Park, S.H.; Park, Y.-W. Modeling of attractive force by magnetic wheel used for mobile robot. Actuators 2020, 9, 67. [Google Scholar] [CrossRef]
- Tzafestas, S.G. Mobile robot control and navigation: A global overview. J. Intell. Robot. Syst. 2018, 91, 35–58. [Google Scholar] [CrossRef]
- Fierro, R.; Lewis, F.L. Control of a nonholomic mobile robot: Backstepping kinematics into dynamics. J. Robot Syst. 1997, 14, 149–163. [Google Scholar] [CrossRef]
- Binh, N.T.; Tung, N.A.; Nam, D.P.; Quang, N.H. An adaptive backstepping trajectory tracking control of a tractor trailer wheeled mobile robot. Int. J. Control Autom. Syst. 2019, 17, 465–473. [Google Scholar] [CrossRef]
- Yang, J.M.; Kim, J.H. Sliding mode control for trajectory tracking of nonholonomic wheeled mobile robots. IEEE Trans. Robot. Autom. 1999, 15, 578–587. [Google Scholar] [CrossRef] [Green Version]
- Liu, K.; Gao, H.; Ji, H.; Hao, Z. Adaptive sliding mode based disturbance attenuation tracking control for wheeled mobile robots. Int. J. Control Autom. Syst. 2020, 18, 1288–1298. [Google Scholar] [CrossRef]
- Zhai, J.Y.; Song, Z.B. Adaptive sliding mode trajectory tracking control for wheeled mobile robots. J. Control 2019, 92, 2255–2262. [Google Scholar] [CrossRef]
- Ding, L.; Li, S.; Gao, H.; Chen, C.; Deng, Z. Adaptive partial reinforcement learning neural network-based tracking control for wheeled mobile robotic systems. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 2512–2523. [Google Scholar] [CrossRef]
- Fierro, R.; Lewis, F.L. Control of a nonholonomic mobile robot using neural networks. IEEE Trans. Neural Netw. 1998, 9, 589–600. [Google Scholar] [CrossRef] [Green Version]
- Jhang, J.Y.; Lin, C.J.; Lin, C.T.; Young, K.Y. Navigation control of mobile robots using an interval type-2 fuzzy controller based on dynamic-group particle swarm optimization. Int. J. Control Autom. Syst. 2018, 16, 2446–2457. [Google Scholar] [CrossRef]
- Guo, Y.; Yu, L.; Xu, J. Robust finite-time trajectory tracking control of wheeled mobile robots with parametric uncertainties and disturbances. Int. J. Syst. Sci. 2019, 32, 1358–1374. [Google Scholar] [CrossRef]
- Khalaji, A.K.; Jalalnezhad, M. Robust forward\backward control of wheeled mobile robots. ISA Trans. 2021, 115, 32–45. [Google Scholar] [CrossRef]
- Wang, D.W.; Low, C.B. Modeling and analysis of skidding and slipping in wheeled mobile robots: Control design perspective. IEEE Trans. Robot. 2008, 24, 676–687. [Google Scholar] [CrossRef]
- Low, C.B.; Wang, D.W. Maneuverability and path following control of wheeled mobile robot in the presence of wheel skidding and slipping. J. Field Robot. 2010, 27, 127–144. [Google Scholar] [CrossRef]
- Dixon, W.E.; Dawson, D.M.; Zergeroglu, E. Robust control of a mobile robot system with kinematic disturbances. In Proceedings of the IEEE International Conference on Control Applications. Conference Proceedings (Cat. No.00CH37162), Anchorage, AK, USA, 27 September 2000; pp. 437–442. [Google Scholar]
- Dixon, W.E.; Dawson, D.M.; Zergeroglu, E.; Behal, A. Nonlinear control of wheeled mobile robot. In Lecture Notes in Control and Information Sciences; Springer: New York, NY, USA, 2000. [Google Scholar]
- Gonzalez, R.; Fiacchini, M.; Alamo, T.; LuisGuzman, J.; Rodriguez, F. Adaptive control for a mobile robot under slip conditions using an LMI-Based approach. Eur. J. Control 2010, 16, 144–155. [Google Scholar] [CrossRef]
- Cui, M.; Sun, D.; Liu, W.; Zhao, M.; Liao, X. Adaptive tracking and obstacle avoidance control for mobile robots with unknown sliding. Int. J. Adv. Robot. Syst. 2012, 9, 1–14. [Google Scholar] [CrossRef]
- Gao, H.; Song, X.; Ding, L.; Xia, K.; Li, N.; Deng, Z. Adaptive motion control of wheeled mobile robot with unknown slippage. Int. J. Control 2014, 87, 1513–1522. [Google Scholar] [CrossRef]
- Li, S.; Ding, L.; Gao, H.; Chen, C.; Liu, Z.; Deng, Z. Adaptive neural network tracking control-based reinforcement learning for wheeled mobile robots with skidding and slipping. Neurocomput 2018, 283, 20–30. [Google Scholar] [CrossRef]
- Fernández, C.P.; Cerqueira, J.J.F.; Lima, A.M.N. Nonlinear trajectory tracking controller for wheeled mobile robots by using a flexible auxiliary law based on slipping and skidding variations. Rob. Auton. Syst. 2019, 118, 231–250. [Google Scholar] [CrossRef]
- Wang, S.; Zhai, J. A Trajectory Tracking Method for Wheeled Mobile Robots Based on Disturbance Observer. Int. J. Control Autom. Syst. 2020, 18, 2165–2169. [Google Scholar] [CrossRef]
- Cui, M. Observer-Based Adaptive Tracking Control of Wheeled Mobile Robots With Unknown Slipping Parameters. IEEE Access 2019, 7, 169646–169655. [Google Scholar] [CrossRef]
- Chen, C.; Gao, H.; Ding, L.; Li, W.; Yu, H.; Deng, Z. Trajectory tracking control of WMRs with lateral and longitudinal slippage based on active disturbance rejection control. Rob. Auton. Syst. 2018, 107, 236–245. [Google Scholar] [CrossRef]
- Chen, M. Disturbance attenuation tracking control for wheeled mobile robots with skidding and slipping. IEEE Trans. Industr. Inform. 2017, 64, 3359–3368. [Google Scholar] [CrossRef]
- Kang, H.S.; Kim, Y.T.; Hyun, C.H.; Park, M. Generalized extended state observer approach to robust tracking control for wheeled mobile robot with skidding and slipping. Int. J. Adv. Robot. Syst. 2013, 10, 1–10. [Google Scholar] [CrossRef]
- Kang, H.S.; Hyun, C.H.; Kim, S. Robust tracking control using fuzzy disturbance observer for wheeled mobile robots with skidding and slipping. Int. J. Adv. Robot. Syst. 2014, 11, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Kanayama, Y.; Kimura, Y.; Miyazaki, F.; Noguchi, T. A stable tracking control method for an autonomous mobile robot. In Proceedings of the IEEE International Conference on Robotics and Automation, Cincinnati, OH, USA, 13–18 May 1990; pp. 384–389. [Google Scholar]


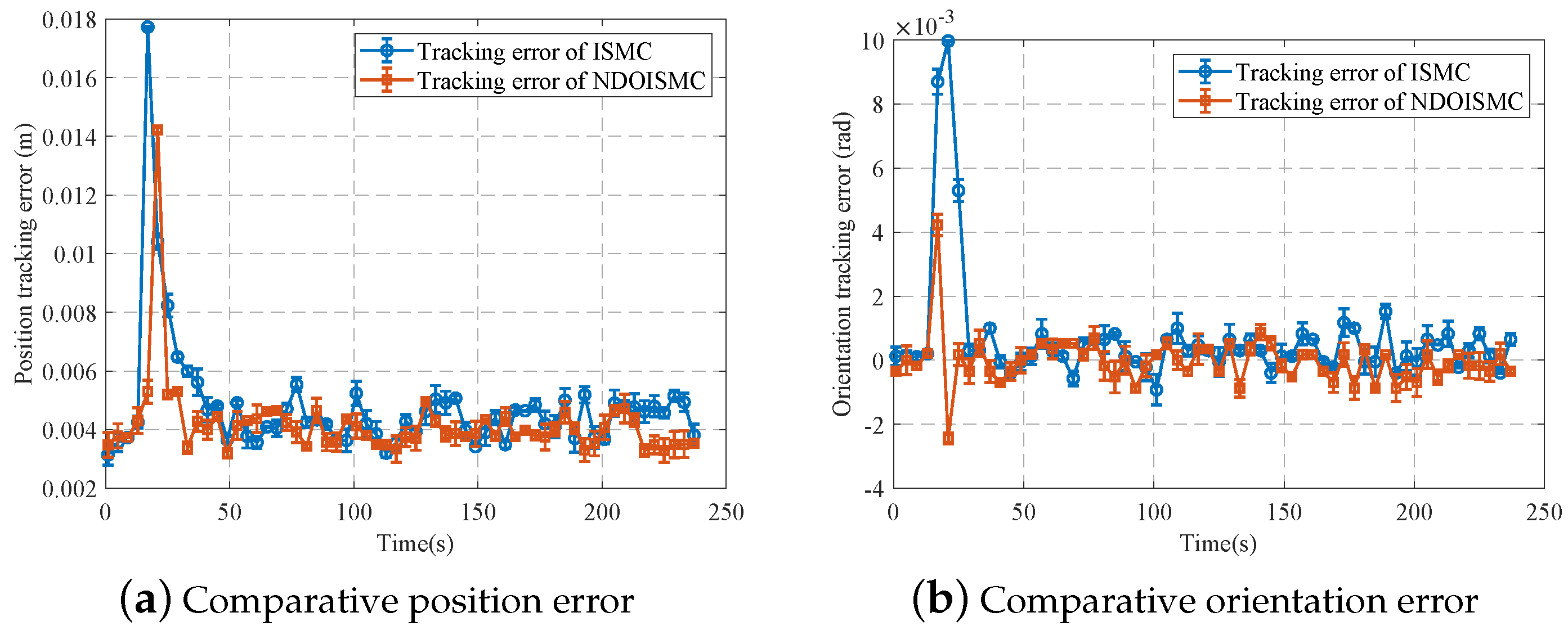
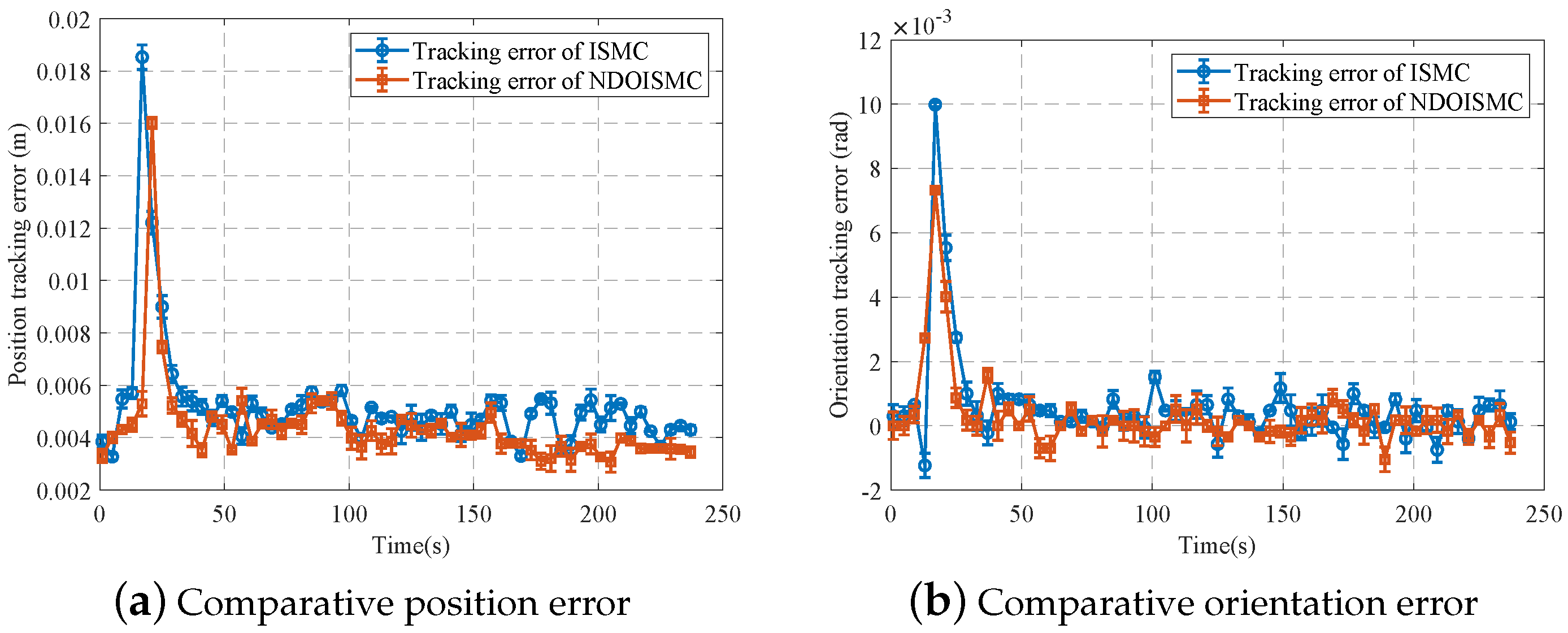
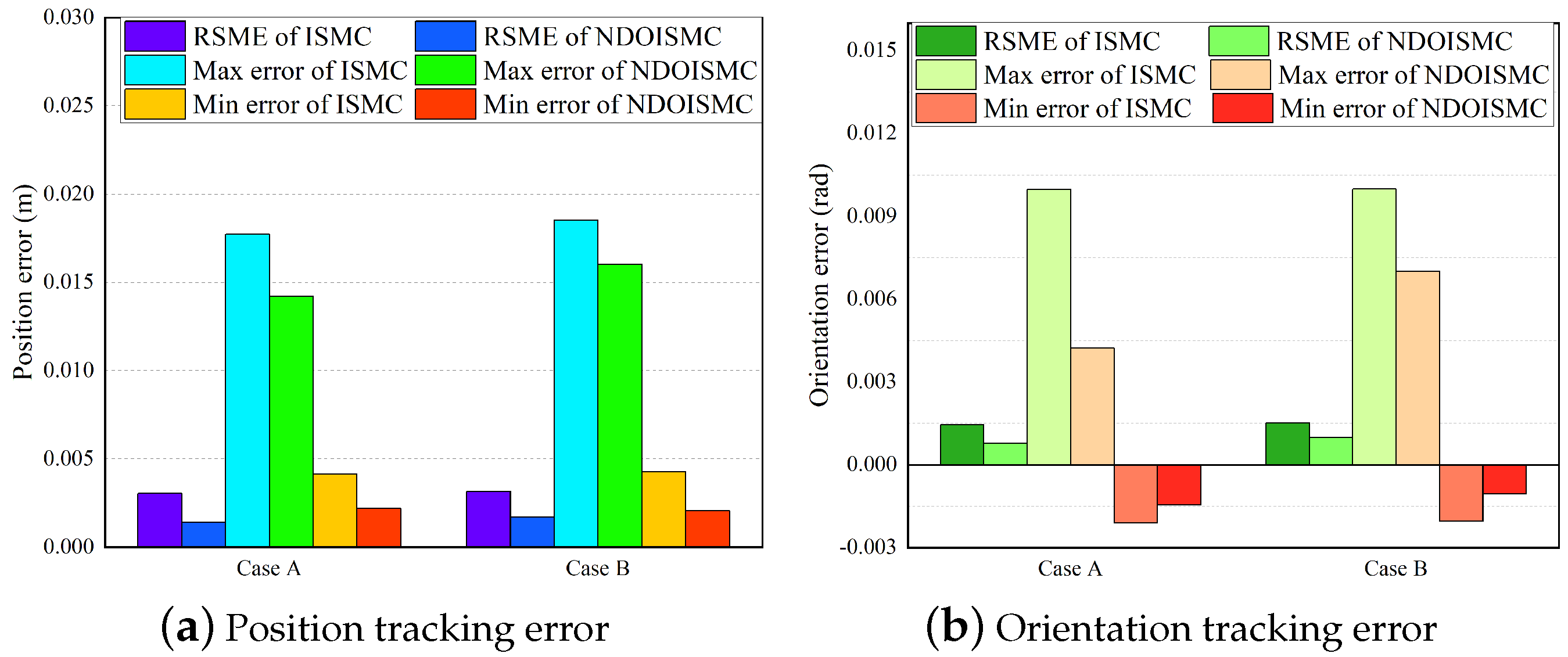
| Physical Meaning | Symbolic Notation | Value |
|---|---|---|
| Mass of WMR | m | 69.263 |
| Moment of inertia of WMR | I | 4.729 |
| Moment of inertia of each wheel | Ic | 0.000718 |
| Wheels radius | r | 0.0625 m |
| Half distance between left and right wheels | b | 0.206 m |
| Distance between C and P | d | 0.183 m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, X.; Yan, L.; Gerada, C. Modeling and Analysis in Trajectory Tracking Control for Wheeled Mobile Robots with Wheel Skidding and Slipping: Disturbance Rejection Perspective. Actuators 2021, 10, 222. https://doi.org/10.3390/act10090222
Gao X, Yan L, Gerada C. Modeling and Analysis in Trajectory Tracking Control for Wheeled Mobile Robots with Wheel Skidding and Slipping: Disturbance Rejection Perspective. Actuators. 2021; 10(9):222. https://doi.org/10.3390/act10090222
Chicago/Turabian StyleGao, Xiaoshan, Liang Yan, and Chris Gerada. 2021. "Modeling and Analysis in Trajectory Tracking Control for Wheeled Mobile Robots with Wheel Skidding and Slipping: Disturbance Rejection Perspective" Actuators 10, no. 9: 222. https://doi.org/10.3390/act10090222
APA StyleGao, X., Yan, L., & Gerada, C. (2021). Modeling and Analysis in Trajectory Tracking Control for Wheeled Mobile Robots with Wheel Skidding and Slipping: Disturbance Rejection Perspective. Actuators, 10(9), 222. https://doi.org/10.3390/act10090222





