Abstract
In the context of automated driving, Electric Power Steering (EPS) systems represent an enabling technology. They introduce the ergonomic function of reducing the physical effort required by the driver during the steering maneuver. Furthermore, EPS gives the possibility of high precision control of the steering system, thus paving the way to autonomous driving capability. In this context, the present work presents a performance assessment of an EPS system designed for a full-electric all-wheel-drive electric prototype racing in Formula Student Driverless (FSD) competitions. Specifically, the system is based on the linear actuation of the steering rack by using a ball screw. The screw nut is rotated through a belt transmission driven by a brushless DC motor. Modeling and motion control techniques for this system are presented. Moreover, the numerical model is tuned through a grey-box identification approach. Finally, the performance of the proposed EPS system is tested experimentally on the vehicle through both sine-sweep profiles and co-simulated driverless sessions. The system performance is assessed in terms of reference tracking capability, thus showing favorable results for the proposed actuation solution.
1. Introduction
The automotive industry is currently facing a substantial shift towards new mobility trends: electrification, spreading of car sharing services and autonomous driving [1]. Features like autonomous emergency braking and lane keeping assistance are referred to as Advanced Driver Assistance Systems (ADAS). These features expand from premium to mass-offering markets and represent a key-point in the progressive transition towards autonomous driving. In this context, Waymo-Google launched a self-driving car project in 2009. Later, Tesla Motor Company rolled out autopilot software on their Model S in October 2015. Ongoing efforts by most carmakers like Volvo head towards the design of autonomous vehicles [2]. A disruptive SAE Level 4 autonomy is expected to be available between 2020 and 2022 [3], while full autonomy with Level 5 technology is supposed to arrive by 2030 [2].
In this challenging scenario, Electric Power Steering (EPS) is a key technology for highly automated driving. Currently, such systems are employed to help the driver in the steering maneuvers by reducing the physical effort required, especially at low speed. Furthermore, EPS systems are used to provide the forces acting on the steering wheel as feedback to the user to preserve the driving sensation. In fact, EPS systems act on the rack-pinion steering box through an electric motor that provides the required torque to the steering column or directly to the rack. Another steering assistance technology is represented by hydraulic power systems. They exploit the pressure generated through a motor- or engine-driven pump to assist the turning of the steering wheel. Nevertheless, such technology is less efficient than the electric one, as witnessed in [4,5]. Therefore, EPS is regarded as a key technology for implementing autonomous driving features in the context of assisted and efficient mobility [6].
Intense research efforts have been dedicated to the control of EPS systems in the last decades. Research works presented by Mehrabi et al. in 2011 [4], Liao & Du [7] in 2003, Frankem & Müller in 2014 [8] and Chen & Chen in 2006 [9] focus on the control of such systems for ADAS applications. Specifically, torque control is addressed with the goal of comfort and safety optimization, as well as disturbance rejection. As stated by Groll et al. in 2006 [10], the most relevant frequencies of the driver input are below 4 Hz. Therefore, the control system must operate to reject the disturbances efficiently to avoid high-frequency oscillatory behavior [11]. For industrial applications, the tendency is to adopt PID control as a cost-effective and easy-to-tune solution. However, this control scheme may present important drawbacks when dealing with the multi-order nature of the steering system. Therein, induced resonant behavior can affect the stability or tracking performance of an EPS angle control, as demonstrated in [12]. The work presented by Govender et al. [11] with a PID for front steering angle control gives an insight into the above-mentioned robustness drawbacks. It suggests the adoption of filters, anti-windup and non-zero structures enhance the stability of the control system. Liao & Du [13] proposed a solution for the modeling and co-simulation of the EPS system and vehicle dynamics. Other efforts deal with active front steering control for automated driving applications through model predictive control (MPC) [14]. Further works enhance the MPC solution with path tracking and trajectory planning methods [15]. In [16], Daimler AG presents an EPS model and the design of a controller to ensure accurate, robust and smooth tracking of the desired trajectories of the front steering angle. The developed steering model shows significant nonlinear behavior due to the elastic elements, friction and gear ratios. Thereby, different control techniques are proposed and compared in [16,17].
Despite these comprehensive efforts, minor attention has been paid to the performance assessment of EPS systems applied to a driverless application from an actuation standpoint. The design and control target for such applications pose important challenges. During manual driving, the driver can constantly adjust the steering wheel input to compensate for disturbances from the road. Conversely, the EPS in autonomous vehicles is no longer used as an amplifier for the driver’s torque since it must actuate the entire steering system [11]. Therefore, the extension of EPS systems to driverless applications is not straightforward and has not been addressed properly by the available literature.
In this context, the main contributions provided by the present work are: (i) the performance assessment of the proposed EPS actuator through a dedicated on-vehicle experimental campaign aimed at identifying the dynamic capabilities of the system for a driverless application; (ii) the validation of the discussed actuator in a driverless maneuver generated by the complete vehicle MPC controller.
The integration of the steering control system in the complete autonomous vehicle model needs the characterization of the actuator to define its dynamic behavior and the system capability for the specific automated driving scenario. Furthermore, a precise mathematical model of the controlled plant is essential to properly design a control strategy of the complete vehicle. In the case of MPC, the compensator is aimed at minimizing the vehicle lateral deviation and relative yaw angle with respect to the reference trajectory, as described in [18]. For this purpose, correct system identification of the controlled plant is fundamental. The work presented in [19] addresses the estimation of the parameters of an EPS by using different algorithms to improve the robustness of the designed controller. Nevertheless, the estimation was performed in a test bench scenario thus implying model mismatch when the system is mounted on a vehicle.
The performance assessment of an EPS system for the autonomous driving application, through in-vehicle experimental tests, is discussed in [20]. However, this paper focuses only on the tracking performance of the proposed controller, without identifying and discussing the dynamic capabilities of the actuator for the considered application.
In this perspective, this paper presents a custom EPS system for a driverless racing vehicle participating at Formula Student Driverless (FSD) events. In detail, the presented work is focused on the implementation and performance assessment of the actuator and system identification using a grey-box model. The work addresses the dynamic performance of the steering actuator integrated with the complete driverless vehicle. To this end, an in-vehicle experimental campaign is carried out to validate the identified model that will be integrated with the MPC controller of the complete driverless vehicle.
The proposed actuator layout consists of a ball screw assembly acting in parallel to the steering rack. The screw nut is actuated by using a toothed belt transmission driven by a brushless DC electric motor. Hence, the screw translates thus actuating the steering rack. This work examines the characteristics of the chosen layout and deals with its integration in the reference racing vehicle. Specifically, the system has been optimized for the integration with the considered vehicle to be compliant with the guidelines of FSD competitions [21], while also accomplishing the autonomous driving function. Electric motor, mechanical system and vehicle dynamic models have been developed and implemented in a MATLAB/Simulink environment, by using a linear grey-box model for the estimation of the unknown parameters. The EPS system is controlled through a PID with a feedforward position control loop, whereas a classic PI is used for the electric motor current control. A pole placement technique is used for the controller tuning. To validate the system and assess performance, in-vehicle experimental tests were conducted. Then, the validity of the proposed layout is demonstrated by testing the racing vehicle equipped with the developed EPS system in a driverless scenario. In particular, the steering profile computed by a vehicle dynamics MPC controller is used as a realistic reference for this verification [18].
This paper is organized as follows. Section 2 describes the considered system layout along with the selected design choices. Section 3 illustrates the system modeling and the implemented control techniques. Finally, Section 4 focuses on the system identification and on the discussion of the experimental results obtained during different maneuvers.
2. System Layout
The EPS layout for the FSD application is chosen and designed to be compliant with the regulations and guidelines provided by Formula SAE [21] and to fit into the already existing reference vehicle. The driverless class was introduced in FSD competitions in 2018. It consists of static and dynamic events aimed at evaluating the autonomous vehicle’s ability to adapt to the tested driving scenario. The academic activities for developing a driverless single-seated race car provide a platform to develop and validate new technologies under challenging conditions. Self-driving racecars represent a unique opportunity to design and test software required in autonomous transport, such as redundant perception, failure detection and control in challenging conditions [22].
The steering system of the reference vehicle is a mechanical rack and pinion with a herringbone-like gear profile. The steering rack is a custom solution starting from the zRack provided by Zedaro. It presents a rack length of 264 mm to fit the limited available space in the front cross-sectional area of the monocoque, as shown in Figure 1. The C-Factor and the steering ratio are 85.5 mm and 4.3:1, respectively, with a steering wheel working angle ranging from −90 to +90 degrees. The steering column is equipped with a rotary encoder, which provides the feedback signal for the autonomous steering system control loop.
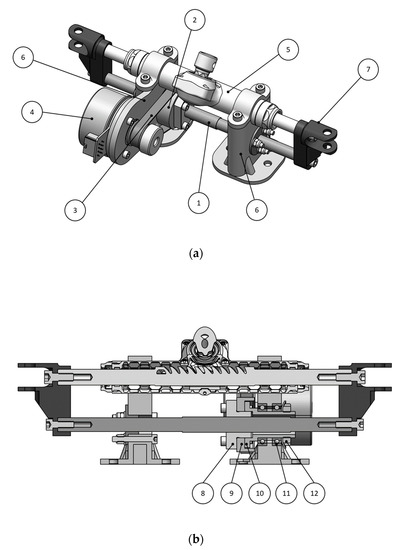
Figure 1.
(a) Autonomous Steering System actuator view: 1—Ball screw; 2—Ball screw nut and bearing assembly; 3—HTD belt; 4—BLDC motor; 5—Steering rack; 6—Support structure; 7—Clevises. (b) Autonomous Steering System cross-section to highlight the ball screw nut and bearing assembly: 8—Ball screw nut; 9—HTD pulley; 10—Nut bearing support; 11—Ball bearings; 12—Lock nut washer.
The proposed solution design is subject to specific constraints, which can be summarized as follows:
- Small rack assembly with a rack length equal to 264 mm.
- Required total rack travel equal to 45 mm, by considering a steering wheel working angle from −90 to +90 degrees.
- Required actuation speed , by taking as target the capability of the driver to actuate the steering wheel from full left to full right in 1 s.
- Reversibility between driverless and with-driver modes must be guaranteed without mechanically dismounting any physical part, according to the competition rules [21].
Specifically, the reversibility constraint implies an integration of the EPS solution with the existing steering rack, thus reducing the available space inside the cockpit.
In this scenario, the chosen solution (Figure 1) consists of a rack that is linearly actuated by using a ball screw (1). The power unit is a brushless DC (BLDC) motor provided by Maxon Motor AGTM (Sachseln, Switzerland) (4). The nut (8) is rotated through a belt-drive transmission (3), while its translation is constrained. By converse, the screw is free to translate, thus providing a linear actuation of the rack (5).
The required rack force for the considered application is . It is due to the required torque needed to move the steering rack at standstill, as a worst-case scenario [22]. Then, the required ball screw torque and the motor speed and power are computed. A Bosch Rexroth ball screw with a diameter of 12 mm and a lead of 2 mm is chosen for the present application. It features an efficiency .
According to the calculated power request and due to the constraints on the available space, the MaxonTM EC 60 Flat 150 W motor is selected for its compact size. It offers a nominal speed and torque of 3480 rpm and 0.401 Nm, respectively. The ball screw is parallel to the vehicle steering rack, as shown in Figure 1. The rack supports have been modified to mount the motor and accommodate the ball screw within a single assembly. The screw and the rack ends are rigidly connected by means of two clevises. The latter are coupled with the steering tie rods.
The ball screw drive is a reversible mechanism that allows the vehicle to be driven in both driverless and with-driver modes, without mechanically disconnecting the autonomous actuator. The selected belt and pulley system have a standard HTD profile with a pitch of 3 mm and a width of 9 mm. The belt drive system was sized to comply with the power transmission for this application. The bearing assembly uses two SKF four-point contact ball bearings in the “O” arrangement (11).
The BLDC motor is controlled and driven by a MaxonTM EPOS 4 electronic control unit that communicates via CAN with a dSPACETM (Paterborn, Germany) MicroAutoBox. The latter is the onboard CPU of the vehicle. The reference steering angle for the control loop is computed by the trajectory planning and control algorithm implemented on the dSPACETM unit, as described in [18,23]. The algorithm receives the signals from the stereo camera, LiDAR and inertial measurement unit (IMU) sensors. The control also provides the steering command to follow the desired path. Then, the reference steering angle is compared with the feedback provided by the steering encoder. The EPOS ECU closes the position feedback loop and provides the voltage command to the electric motor to drive the autonomous steering actuator, as subsequently discussed in Section 3.3.
Figure 2a shows the positioning of the steering actuator assembly in the vehicle CAD model. In Figure 2b, we show the installation of the real prototype, together with its components.
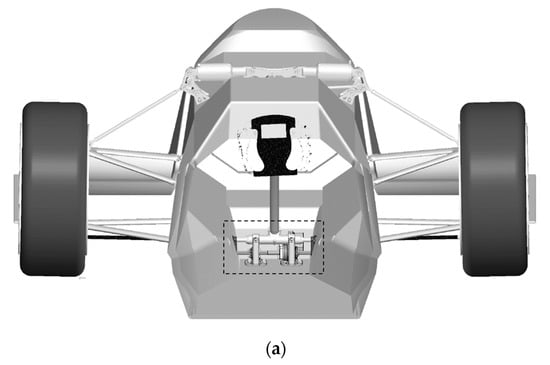
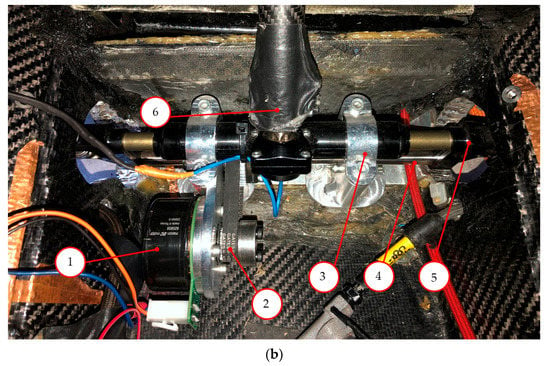
Figure 2.
(a) Autonomous EPS system positioning in the vehicle CAD model. (b) EPS positioning in the actual vehicle: 1—BLDC motor; 2—HTD belt; 3—Support structure; 4—Ball screw; 5—Clevises; 6—Steering column.
3. System Modelling
For performance assessment and control tuning purposes, the system is modeled by following a linear lumped-parameter approach. The developed model is schematized in Figure 3. The model includes the motor and its controller along with the dynamic model of the autonomous steering system.
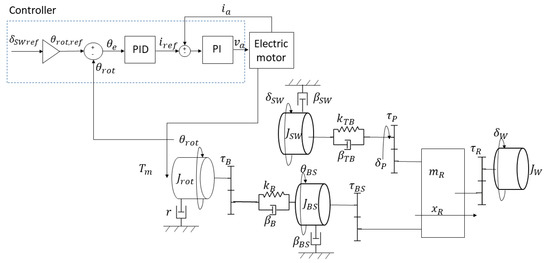
Figure 3.
Dynamic model of the studied system.
3.1. Electric Motor
For simplicity, the BLDC motor can be represented as a standard DC motor. Neglecting field-weakening operation, the electrical dynamic model of the BLDC motor can be described as
where is the motor terminal voltage, is the motor armature current, is the phase-to-phase terminal inductance, is the phase-to-phase terminal resistance and is the motor back-EMF, given by
and the electromagnetic motor torque provided by the motor is
being the machine characteristic constants and the angular position of the motor.
The damping coefficient of the electric motor representing the mechanical losses is computed as the ratio between the no load torque and the no load speed.
Relevant parameters from the motor manufacturer are reported in Table 1.

Table 1.
Electric motor model parameters.
3.2. Mechanical System
The mechanical dynamics of the steering actuator are described through a 3-DOF system, in which friction is modeled as viscous damping and constant gear ratios are used. For the ball screw, a viscous damper with coefficient is introduced. The ball screw transmission ratio is . The same approach is used to model the belt drive connecting the motor shaft with the ball screw nut. Damping coefficient and transmission ratio are used. Furthermore, the belt stiffness is accounted for through the coefficient . The steering column is modeled by considering it as a torsion bar with torsional stiffness and damping coefficient . The rack and pinion mechanism of the steering system of the vehicle is represented by the constant gear ratio that is equal to the C-factor of the rack. The ratio considers the ratio between the wheel steering angle and the linear displacement of the rack . It was experimentally determined based on the acquisitions from the on-vehicle sensor data. The term models the friction of the steering wheel.
The equations of motion are obtained through the Lagrangian approach with the motor angle , the ball-screw angle and the steering angle as generalized coordinates. The system differential equations are
The equivalent inertia at the ball screw is computed using an energetic approach as
The system is rearranged in the state-space form . The system state vector is . The input to the system is the driving torque provided to the electric motor: . The outputs of the system are the angle at the motor used to perform the PID position control and the angle at the steering column pinion end, compared with the measurement of the steering encoder sensor: . The angle at the pinion is computed considering the rigid transmission ratio of the ball screw and the rack C-factor as: .
A full description of the model transmission ratios and known masses and inertia are provided in Table 2. The missing parameters, i.e., the ball screw inertia , the steering wheel inertia , the wheel inertia , the belt damping , the belt stiffness , the damping of the ball screw , the damping of the steering wheel , the damping of the steering column and the stiffness of the steering column , are identified through the grey-box model parameters estimation optimization process described in Section 4.3.

Table 2.
Dynamic model parameters.
3.3. Electric Motor Control
The adopted control strategy for the BLDC motor has been designed and modeled based on the EPOS 4 controller architecture [24]. The most suitable operating mode for the autonomous steering actuator is the cyclic synchronous position mode provided by the EPOS 4 ECU. As presented in Figure 4, the reference steering angle () is computed by the trajectory planning algorithm implemented in dSPACETM. The reference is compared with the signal acquired by the steering wheel encoder sensor. Then, it is converted to a motor target position that is passed to the EPOS motor controller. Thus, the EPOS performs the position control loop and provides the current set to the inner (cascade) current control loop, which in turn will yield motion on the motor shaft.
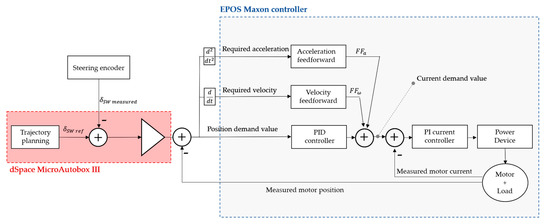
Figure 4.
Electric motor control block diagram.
The position control of the electric motor is implemented through a Proportional-Integral-Derivative (PID) algorithm and a feedforward control to improve the motion system setpoint. The velocity feedforward serves for compensation of speed-proportional friction and its coefficient is computed as
The acceleration feedforward accounts for the inertia of the system and its coefficient is determined by
The anti-windup method is used to prevent saturation of the command signals. The limit in current is set to 20 A according to the motor capabilities. The internal current control loop computes the voltage set to the motor. It consists of a Proportional-Integral (PI) control with an anti-windup algorithm to avoid saturation of the voltage command (24 V).
The block scheme of the controller architecture is depicted in Figure 4.
The tuning of the PI current controller is performed using the pole placement technique. Since the system can be analyzed as a linear canonical first-order system, an algebraic method can be adopted to define precise relationships between poles and the shape of the response. The tuning of the position PID controller has been performed by using the Tuning App (based on transfer functions) in the Simulink block PID controller of the Control Design MATLAB toolbox.
The parameters used for implementing the electric motor control are reported in Table 3.

Table 3.
Electric motor controller parameters.
4. Results and Discussion
4.1. Testbed Setup
The presented system has been installed on the chassis of the considered vehicle and the experimental campaign is carried out. The electric motor of the steering actuator and its embedded Hall sensor are connected to the EPOS ECU presented in the previous section via a dedicated wiring system. The ECU is fixed on the monocoque of the vehicle. An additional microcontroller (Texas InstrumentTM Launch XL-F28379d, Dallas, TX, USA) is installed on the vehicle to acquire the steering angle sensor data from the digital encoder sensor mounted on the steering rack and to provide the reference profile to the actuator ECU in real-time at a sampling frequency of 100 Hz. All the systems are connected via CAN to the PC to both provide the enabling and configurations messages to the system and to acquire the data of encoder sensor steering angle and steering profile from the TI microcontroller and the values of actual current and the actual position of the electric motor provided from the EPOS controller. Figure 5 schematizes the overall layout of the actuator testbed installed in the actual vehicle.
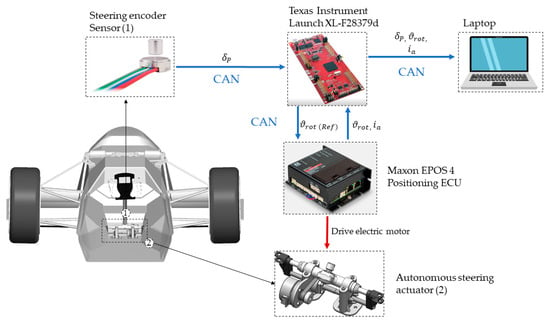
Figure 5.
Autonomous steering actuator testbed setup block scheme.
All the systems are powered by the Low Voltage (LV) battery of the car i.e., a 24 V lithium-ion battery.
The performed tests are sine-sweep steering maneuvers and steering maneuvers generated by the MPC strategy that controls the driverless vehicle dynamics. The sine-sweep maneuvers are performed with both suspended and on-ground vehicles aimed at the system identification and dynamic performance assessment. Furthermore, the system tracking performance is evaluated when a reference profile generated by the MPC for the autonomous mission is provided.
4.2. Sine-Sweep Test
Different sine-sweep steering maneuvers are conducted first. The test is performed for a frequency range from 0 Hz to 10 Hz, in a time interval of 10 s with an amplitude at the steering wheel of 10 degrees. Data are acquired for two different conditions of the vehicle, namely suspended and stationary vehicles on the ground. The response to the reference steering wheel position is measured by the encoder mounted on the steering column. Results obtained in the case of the suspended vehicle are reported in Figure 6a. Similarly, Figure 6b shows the motor current and position measured by the embedded sensors.
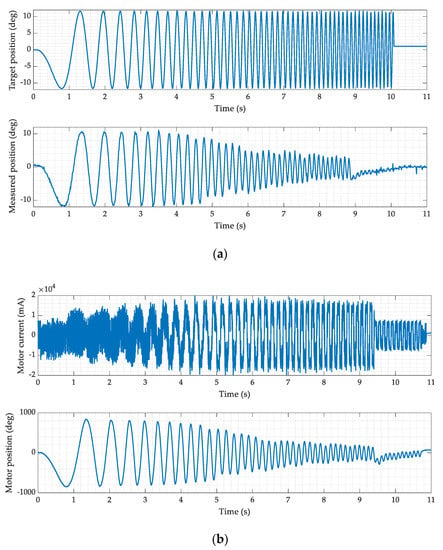
Figure 6.
Sine-sweep steering maneuver—suspended vehicle, 0–10 Hz, amplitude 10 degrees. (a) Reference steering wheel position and measured response by the steering encoder. (b) Measured motor current and position.
The current measured by the motor approaches the limit of 20 A provided by the motor manufacturer. By analyzing the trend of the current, we can see sections without steering angle variations for a short period despite the high motor current and torque output. This behavior is caused by the dead band in the actuator due to the backlash and the compliance of the elastic elements present in the system, for this reason, a dead band compensator should be implemented in the controller, as described in [15].
An equivalent sine-sweep test is repeated with the vehicle on the ground (dry asphalt). In Figure 7 the data collected by the steering encoder sensor and by the motor sensors are reported.
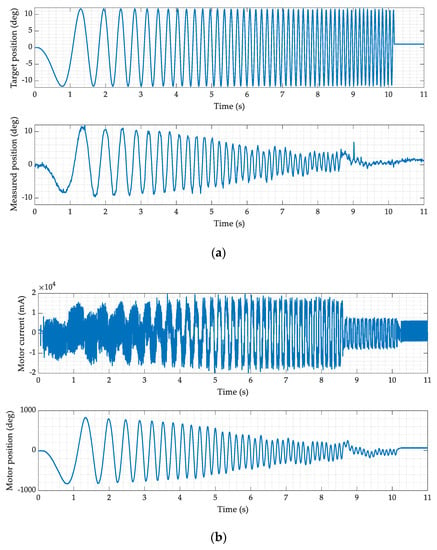
Figure 7.
Sine-sweep steering maneuver—stationary vehicle on the ground, dry asphalt, 0–10 Hz, amplitude 10 degrees. (a) Reference steering wheel position and measured response by the steering encoder. (b) Measured motor current and position.
The performed sine-sweep maneuvers in both the test conditions are processed to extract the frequency response function of the system. Figure 8 shows the Bode plot where the output and input to the system are the measured positions by the steering encoder sensor and the reference steering sine-sweep profile, respectively. The cut-off frequency for the suspended vehicle condition is at 5 Hz. The frequency response function of the test performed with the vehicle on the ground shows a cut-off frequency at 4.8 Hz.
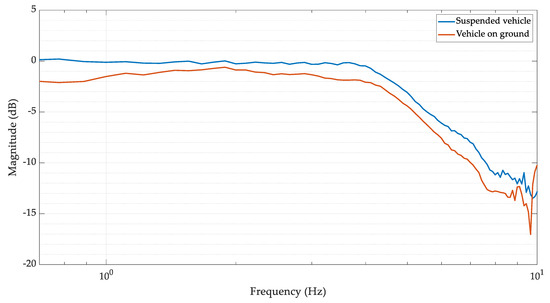
Figure 8.
Experimental frequency response function of the closed loop system: suspended vehicle (blue) and vehicle on the ground (orange).
From the analysis of the Bode plot for the vehicle on the ground case, reported in Figure 8, the stick slip effect is preponderant at low frequency in the case of the vehicle on the ground. Due to friction among tires and ground, the bandwidth of the system on the ground is slightly lower than in the suspended vehicle case. For both the test conditions, the dynamic performance of the system is consistent with the considered application. As the typical steering frequencies of the driver input are below 4 Hz [10], the designed actuator shows good tracking performance below 4 Hz for both the considered tests.
4.3. System Identification
The grey-box model estimation approach is used to identify damping and stiffness coefficients along with inertia terms related to the ball screw, steering wheel, steering column, and wheels. To this end, the experimental data reported in Section 4.2 are used. The friction losses of the system as the moments of inertia of the ball screw, of the steering wheel and column, and of the wheels were determined starting from the experimental acquisitions by using a grey-box model estimation approach. The first analytical esteem of the parameters is performed to determine the starting nominal values of the parameters.
The estimated system has nine design variables: the ball screw inertia , the steering wheel inertia , the wheel inertia , the belt damping , the belt stiffness , the damping of the ball screw , the damping of the steering wheel , the damping of the steering column and the stiffness of the steering column .
The software tunes the model parameters to obtain a simulated response () that tracks the measured response or reference signal (). The provided to the parameter estimation algorithm is the suspended vehicle sine sweep test response reported in Figure 6. The optimization method for the estimation of the parameters is the Nonlinear Least Squares aimed at minimizing the squares of the residuals in the system response. In Table 4, the identified parameters are reported.

Table 4.
Identified parameters.
The identified values are consistent with the considered application. The response of the identified numerical model is reported in Figure 9, compared with the signal acquired by the encoder sensor during an on-vehicle experimental testing campaign ().
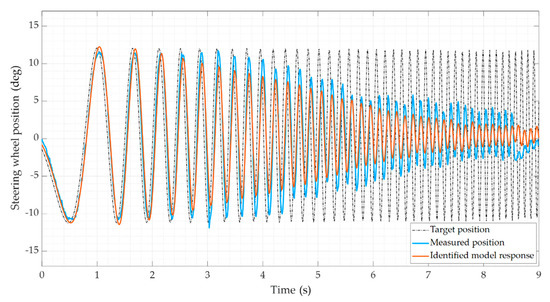
Figure 9.
Steering wheel position behavior during the performed sine-sweep maneuver for validating the system identification: target position (black, dash-dotted) vs. measured position (blue, solid) vs. identified model response (orange, solid).
The identified system features one pole at the origin and a real stable pole at 334 rad/s (53.2 Hz) that are the rigid body modes. Then, two complex conjugate sets of poles appear at 30.9 rad/s (4.9 Hz) and 131 rad/s (20.9 Hz). The former low-frequency pole represents the motor inertia mode vibrating due to the belt drive compliance. The latter is the ball screw inertia vibrating due to the torsional stiffness of the steering wheel and column. The target frequency range for the present application (1 Hz) is below the frequencies of the identified mechanical system.
The goodness-of-fit between the identified model and the actual actuator has been quantified as a function of the Normalized Root Mean Square Error (NRMSE) cost function, as follows:
where indicates the 2-norm of a vector, is the measured position and is the identified position. The proposed identification has a equal to 75%. The identified numerical response matches the experimental one.
4.4. Autonomous Driving Test
The performance of the proposed EPS system has been evaluated with a steering profile coming from the co-simulation of an autonomous driving mission. The vehicle is driven at a constant longitudinal speed equal to 5 km/h while the steering angle reference profile is properly given to the actuator for a time length of about 120 s. Figure 10a compares the steering wheel position from the encoder with the reference signal generated by the MPC strategy devoted to autonomous driving [18]. Accordingly, Figure 10b shows the followed track that yields the tracked position profile. From these results, an angular position RMSE of 3 degrees is computed for the whole track. This value is consistent with the required performance for the specific application.
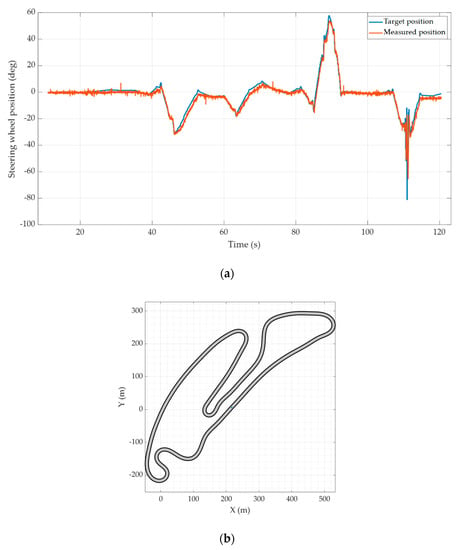
Figure 10.
Autonomous driving test. (a) Steering wheel position measured by the encoder sensor (orange, solid) vs. target position generated by the MPC strategy devoted to autonomous driving (blue, solid). (b) Spatial coordinates (X,Y) of the race track related to the performed autonomous driving test.
Furthermore, the applied realistic reference highlights important features of the control. The maximum overshoot is found at 89.4 s, reaching up to 4.5 degrees of error for a very narrow time interval. It is worth noting that the position activity around 111 s presents high dynamic content and thus puts in evidence the intrinsic limitations of the actuation system above 4 Hz (max. error up to 15.7 degrees). However, this behavior is beyond the bandwidth of interest.
5. Conclusions
This paper presented the design, integration, and performance assessment of an EPS system for a driverless vehicle. In detail, an FSD racing vehicle was considered and the proposed EPS was studied for system identification and performance assessment during different maneuvers. To this end, the actuator was designed to fulfill the competition rules and both design and packaging constraints. The system model was developed by considering both the electric motor and the existing mechanical steering subsystem. Furthermore, the applied control strategy was discussed, along with the performed system identification procedure that has been conducted exploiting a grey-box model. Experimental tests in a proper laboratory environment were carried out to assess the system performance while validating the described model and performing system identification. The performance of the proposed EPS system was tested on the racetrack, during both sine-sweep maneuvers and co-simulated driverless sessions.
Sine-sweep test results highlighted the actuator capabilities in terms of bandwidth. Also, favorable matching was found between the plant model and the prototype. Finally, the system performance was assessed in terms of position reference tracking. The investigated EPS system was able to satisfy the design requirement by showing favorable tracking metrics.
As future work, an extensive validation stage on-track could be required to test the proposed system under several demanding handling maneuvers in different road conditions.
Author Contributions
Conceptualization, R.M., S.C., I.K., S.F., S.L., N.A. and R.G.; Investigation, R.M., S.C. and I.K.; Methodology, R.M., S.C. and I.K.; Supervision, N.A., A.B. and R.G.; Validation, R.M., S.C., S.F. and I.K.; Writing—original draft, R.M.; Writing—review & editing, S.C., I.K., S.F., S.L. and R.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data available on request due to restrictions.
Acknowledgments
This work was developed in the framework of the activities of the Interdepartmental Center for Automotive Research and Sustainable Mobility (CARS) at Politecnico di Torino (www.cars.polito.it, accessed on 16 July 2021).
Conflicts of Interest
The authors declare no conflict of interest.
References
- PwC. Available online: https://www.pwc.com/en/industries/automotive/Publications/eascy.html (accessed on 15 January 2021).
- Mc Kinsey Center for Future Mobility. Available online: https://www.mckinsey.com/features/mckinsey-center-for-future-mobility/overview/autonomous-driving (accessed on 15 January 2021).
- SAE J3016—Levels of Driving Automation. Available online: https://www.sae.org/news/2019/01/sae-updatesj3016automateddrivinggraphic#:~:text=The%20J3016%20standard%20defines%20six,graphic%20first%20deployed%20in%202016 (accessed on 15 January 2021).
- Mehrabi, N.; Azad, N.L.; McPhee, J. Optimal disturbance rejection control design for electric power steering systems. In Proceedings of the 2011 50th IEEE Conference on Decision and Control and European Control Conference, Orlando, FL, USA, 12–15 December 2011; pp. 6584–6589. [Google Scholar]
- Baharom, M.B.; Hussain, K.; Day, A.J. Design of full electric power steering with enhanced performance over that of hydraulic power-assisted steering. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2013, 227, 390–399. [Google Scholar] [CrossRef]
- Würges, M. New electrical power steering systems. Encycl. Automot. Eng. 2014, 1–17. [Google Scholar] [CrossRef]
- Liao, Y.G.; Du, H.I. Modelling and analysis of electric power steering system and its effect on vehicle dynamic behaviour. Int. J. Veh. Auton. Syst. 2003, 1, 153–166. [Google Scholar] [CrossRef]
- Fankem, S.; Müller, S. A new model to compute the desired steering torque for steer-by-wire vehicles and driving simulators. Veh. Syst. Dyn. 2014, 52 (Suppl. 1), 251–271. [Google Scholar] [CrossRef]
- Chen, X.; Chen, X. Control-Oriented Model for Electric Power Steering System (No. 2006-01-0938); SAE Technical Paper; SAE International: Warrendale, PA, USA, 2006. [Google Scholar]
- Groll, M.V.; Mueller, S.; Meister, T.; Tracht, R. Disturbance compensation with a torque controllable steering system. Veh. Syst. Dyn. 2006, 44, 327–338. [Google Scholar] [CrossRef]
- Govender, V.; Khazardi, G.; Weiskircher, T.; Keppler, D.; Müller, S. A PID and state space approach for the position control of an electric power steering. In 16 Internationales Stuttgarter Symposium; Springer: Wiesbaden, Germany, 2016; pp. 755–769. [Google Scholar]
- Carriere, S.; Caux, S.; Fadel, M. Optimal lqi synthesis for speed control of synchronous actuator under load inertia variations. IFAC Proc. Vol. 2008, 41, 5831–5836. [Google Scholar] [CrossRef]
- Liao, Y.G.; Du, H.I. Cosimulation of multi-body-based vehicle dynamics and an electric power steering control system. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2001, 215, 141–151. [Google Scholar] [CrossRef]
- Falcone, P.; Borrelli, F.; Asgari, J.; Tseng, H.E.; Hrovat, D. Predictive active steering control for autonomous vehicle systems. IEEE Trans. Control. Syst. Technol. 2007, 15, 566–580. [Google Scholar] [CrossRef]
- Park, M.; Lee, S.; Han, W. Development of Steering Control System for Autonomous Vehicle Using Geometry-Based Path Tracking Algorithm. Etri J. 2015, 37, 617–625. [Google Scholar] [CrossRef]
- Govender, V.; Müller, S. Modelling and position control of an electric power steering system. IFAC PapersOnLine 2016, 49, 312–318. [Google Scholar] [CrossRef]
- Zakaria, M.I.; Husain, A.R.; Mohamed, Z.; Shah, M.B.N. Steering control of a steer-by-wire system vehicle with time delay and actuator saturation via anti-windup controller. Eng. Appl. Sci. Res. 2019, 46, 72–78. [Google Scholar]
- Khan, I.; Feraco, S.; Bonfitto, A.; Amati, N. A model predictive control strategy for lateral and longitudinal dynamics in autonomous driving. In Volume 4: 22nd International Conference on Advanced Vehicle Technologies (AVT), Proceedings of the ASME 2020 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Virtual, Online, 17–19 August 2020; ASME: New York, NY, USA, 2020; p. V004T04A004. [Google Scholar]
- Nguyen, V.G.; Guo, X.; Zhang, C.; Tran, X.K. Parameter Estimation, Robust Controller Design and Performance Analysis for an Electric Power Steering System. Algorithms 2019, 12, 57. [Google Scholar] [CrossRef] [Green Version]
- Naranjo, J.E.; González, C.; García, R.; de Pedro, T. Electric power steering automation for autonomous driving. In Proceedings of the International Conference on Computer Aided Systems Theory, Las Palmas de Gran Canaria, Spain, 7–11 February 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 519–524. [Google Scholar]
- Formula Student 2020 Rulebook. Available online: https://www.formulastudent.de/all/2020/rules/FSRules-2020-V1 (accessed on 7 December 2020).
- Kabzan, J.; de la Iglesia Valls, M.; Reijgwart, V.; Hendrikx, H.F.C.; Ehmke, C.; Prajapat, M.; Bühler, A.; Gosala, N.; Gupta, M.; Sivanesan, R.; et al. Amz driverless: The full autonomous racing system. J. Field Robot. 2020, 37, 1267–1294. [Google Scholar] [CrossRef]
- Feraco, S.; Luciani, S.; Bonfitto, A.; Amati, N.; Tonoli, A. A local trajectory planning and control method for autonomous vehicles based on the RRT algorithm. In Proceedings of the 2020 AEIT International Conference of Electrical and Electronic Technologies for Automotive (AEIT AUTOMOTIVE), Torino, Italy, 18–20 November 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Maxon Group. Epos 4 Positioning Controller Application Notes; Edition 2019-11; Maxon Group: Sachseln, Switzerland, 2019. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).