Abstract
The need for reducing the cost of and space in Electrically Assisted Bicycles (EABs) has led the research to the development of solutions able to sense the applied pedalling torque and to provide a suitable electrical assistance avoiding the installation of torque sensors. Among these approaches, this paper proposes a novel method for the estimation of the pedalling torque starting from an estimation of the motor load torque given by a Load Torque Observer (LTO) and evaluating the environmental disturbances that act on the vehicle longitudinal dynamics. Moreover, this work shows the robustness of this approach to rotor position estimation errors introduced when sensorless techniques are used to control the motor. Therefore, this method allows removing also position sensors leading to an additional cost and space reduction. After a mathematical description of the vehicle longitudinal dynamics, this work proposes a state observer capable of estimating the applied pedalling torque. The theory is validated by means of experimental results performed on a bicycle under different conditions and exploiting the Direct Flux Control (DFC) sensorless technique to obtain the rotor position information. Afterwards, the identification of the system parameters together with the tuning of the control system and of the LTO required for the validation of the proposed theory are thoroughly described. Finally, the capabilities of the state observer of estimating an applied pedalling torque and of recognizing the application of external disturbance torques to the motor is verified.
1. Introduction
Presently, the need for air pollution reduction together with the aging of the population have brought research in the mobility field to the development of EABs. In particular, the term EAB refers to bicycles whose motion is assisted by electrical motors. Thus, these vehicles present the advantages of increasing the mobility capabilities of standard bicycles thanks to the electrical assistance and to be environmentally friendly because they are zero-emission vehicles. Therefore, EABs results to be attractive for users who want to reduce the efforts while riding a bicycle such as elderly people. By means of EABs, the moving range of the bicycle can be extended without exhausting the rider and uphill riding efforts are considerably reduced. Moreover, EABs do not require a driving license and thus can be driven by the majority of people. In addition, through EABs one can save costs related to insurance and parking. A massive usage of these vehicles could, therefore, improve also the traffic flow in the cities. Also, riding an EAB reduces the energy cost per distance travelled compared to driving a car [1]. EABs can be divided into many categories depending on the motor type used to provide the electrical assistance, the motor placement, the type of assistance and the type of battery. A comprehensive characterization of different kinds of EABs can be found in [1]. Nevertheless, there are laws which vary from country to country regarding the electrical assistance. In particular, these laws limit the maximum power that can be provided to assist the motion and thus the applicable motor torque and the resulting vehicle speed. Therefore, sensors such as torque and speed sensors are necessary to measure these quantities in order to respect legislation.
Among the different kinds of EABs, there are bicycles which provide the electrical assistance level basing on the pedalling torque and bicycles in which the assistance is related to the speed of the vehicle. However, vehicles which rely on pedalling torque are more appreciated by the users in terms of cycling feeling than the velocity-based ones [2]. Thus, this work focuses the attention on bicycles whose electrical assistance is related to the pedalling torque applied by the rider. For this kind of EABs, a torque sensor is necessary in order to measure the pedalling torque and provide a proper electrical assistance with the objective of achieving certain vehicle dynamics performance. However, torque sensors are usually expensive and increase the overall cost of EABs which are categorized as expensive class bicycles. Moreover, torque sensors are weak against external shocks and risk to be damaged since they are installed directly where the pedalling force is applied. The need for cost and space reduction has led the current research to the development of solutions capable of avoiding the installation of such torque sensors.
Many approaches were proposed to address this issue. A common method is based on Disturbance Observers (DOBs) which were first proposed in [3,4]. The DOBs are widely used to achieve robustness to model uncertainties and disturbances in control systems. Also, a DOB can be used to estimate disturbances without using costly force sensors [5,6,7]. DOBs have been employed in many fields such as motion control [8,9,10], high friction systems [11] and vehicles [12,13]. Moreover, DOBs have been also applied in EABs for the pedalling torque estimation in many works. In [6], a pedalling torque estimation based on a DOB is proposed. Also, in [14,15,16,17] the average pedalling torque is evaluated starting from a Fourier series expansion of the disturbance torque estimated using a DOB. In these works, an estimation of the pedalling torque is obtained combining the information given by the DOB with a Recursive Least Square (RLS) algorithm. However, using this approach, a delay of one pedalling cycle is required to evaluate the Fourier series of the disturbance torque. Therefore, the pedalling torque cannot be estimated in real-time during the first pedalling revolution. Other works based on DOBs investigate the problem of providing a proper electrical assistance starting from the estimated pedalling torque. In particular, in [5], a method which exploits two DOBs is proposed. In this work, one DOB is used to realize a robust control by removing the estimated disturbance whereas an additional DOB estimates the applied pedalling torque in order to provide electrical assistance. Also, in [18], a DOB is designed with the objective of achieving the environmental disturbance rejection in order to obtain an uphill riding feeling equal to the level ground riding.
Many works focus the attention on the analysis of the repetitive nature of the pedalling torque due to the mechanical design of the bicycle crankset. In particular, these works are based on the Repetitive Control (RC) which is a common method used for periodic disturbance rejection or periodic reference signal tracking. The RC was first applied in many motion control problems such as Hard Disk drives [19], Compact Disk players [20] and also in non rotatory motion control applications [21,22]. Afterwards, the aforementioned technique has been employed also in power assist applications to generate the auxiliary torque [23]. Moreover, the RC has been also successfully applied in the field of EABs. In [24,25], a RC is used to reduce the speed fluctuations caused by the pedalling torque that are significant especially in uphill riding with the objective of enhancing the bicycle stability and safety.
In this work, a different approach, which estimates the pedalling torque starting from a motor Load Torque Observer (LTO) and from an estimation of the environmental load torque components that act in the bicycle longitudinal dynamics, is proposed. Thanks to a LTO, the external load torque applied to the motor shaft can be estimated relying on the motor mathematical model and on the rotor position information and, therefore, without using an expensive torque sensor. In recent decades, LTOs have been investigated using classical state observers and exploiting both sensored and sensorless methods. Among the works which rely on sensored techniques, several state observers based on different approaches have been employed. In [26], a nonlinear load torque estimation based on Lyapunov stability is proposed. Also, in [27], the state estimation is achieved considering an adaptive observer which exploits the Fourier analysis of the voltages and the currents of the motor. Another approach based on a Sliding Mode Observer (SMO) has been proposed in [28]. Many works exploit Kalman Filters (KFs) to achieve the motor load torque estimation. In particular, in [29], an Extended Kalman Filter (EKF) which linearizes the mathematical model of the motor has been implemented. However, EKFs do not account for model uncertainties due to parametric variations. Therefore, in order to improve the robustness to parametric variations, a H-Infinity Filter (HIF) has been proposed in [30]. To avoid the installation of encoders or resolvers and, therefore, to save cost and space, many LTOs exploit the rotor position and speed information given by sensorless techniques. In [31], the INFORM sensorless technique has been used to estimate the position information in a full order state observer. Other LTOs based on sensorless techniques are proposed in [32,33]. In these works, an Unscented Kalman Filter (UKF) is employed to reduce the error caused by the linearization performed when using an EKF. Also, in [34], a comparison between sensored and sensorless load torque estimation based on UKFs is reported. Moreover, in [35], several state observers which rely on the position information given by the DFC sensorless technique have been successfully implemented and compared. Also in this work, a LTO which exploits the DFC sensorless technique is proposed showing the robustness of the pedalling torque estimation to errors on the measured mechanical quantities. Therefore, using the proposed approach it is possible to estimate the pedalling torque also considering the information given by sensorless techniques which typically introduce an estimation error on the rotor position compared to high-resolution encoders. Thus, this method allows estimating the pedalling torque removing both the torque and the position sensors.
The objective of this work is to show the possibility of estimating the pedalling torque starting from a motor LTO which relies on sensorless position information. It has to be remarked that the proposed approach is valid for EABs whose motor is installed within the rear wheel of the vehicle. Moreover, the proposed theory has been validated neglecting the influence of the environmental load torque components. Therefore, under this assumption the estimated motor load torque results to be equal to the pedalling torque. Nevertheless, the capability of the LTO to estimate generic external disturbance torques different from the pedalling torque is verified. Eventually, it has to be remarked that the project of a control system able to provide a suitable electrical assistance starting from the estimated pedalling torque is not analyzed within this work.
After a mathematical description of the vehicle longitudinal dynamics, a technique capable of estimating the applied pedalling torque exploiting a LTO is explained. Then, in order to highlight the nature of the signal that has to be estimated by means of the LTO, an analysis of the pedalling torque is reported. Afterwards, the experimental setup used to validate the proposed theory is described. After a brief recall of the DFC sensorless technique, the identification of the machine parameters together with the control system design is reported. Then, a LTO for the pedalling torque estimation is tuned and different experiments that evaluate its load torque estimation capabilities are performed.
2. Theory
2.1. Bicycle Longitudinal Dynamics
The design of the control system for an EAB requires the modelling of its vehicle dynamics. Although the effects of the rolling rotation of the vehicle body together with the front fork effect are important in the bicycle stabilization, these effects can be neglected in this analysis since the vehicle stabilization is typically controlled by the human action [24]. Therefore, the analysis of the vehicle dynamics can be reduced to the longitudinal dynamics model of the bicycle described in Figure 1.
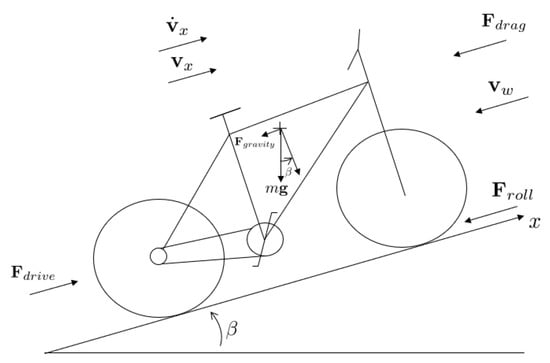
Figure 1.
Bicycle longitudinal dynamics.
Considering the dynamics along the x-axis one obtains the following equation:
where represents the driving force applied to the vehicle whereas , , , are respectively the effects of gravity, of the aerodynamic drag and of the rolling friction on the motion of the vehicle. In addition, m represents the global vehicle mass including the mass of the cyclist and is the acceleration of the vehicle along the longitudinal direction. In the following, a deeper analysis of the terms of (1) is presented. The driving force can be written as:
where is the driving force generated by the motor electrical assistance whereas represents the human force applied to the pedals and transmitted to the back wheel through the chain. A gravity component in vehicle longitudinal dynamics is due to the presence of a road slope and it results in a resistive force when going uphill and a driving force in downhill riding. This component has the following expression:
where g is the acceleration of gravity. The aerodynamic drag is proportional to the speed squared and depends on the dynamic pressure. As shown in [1], this component can be expressed as:
where is the aerodynamic drag coefficient, is the speed of the vehicle and is the speed of the wind. In particular, the coefficient depends on the cyclist and its posture while riding. Moreover, the stochastic nature of the speed of the wind and its variable direction can result in a driving or resistive force on the vehicle dynamics. The rolling friction component is an effect of the deformation of the wheels and can be written as:
where is the rolling friction coefficient which depends on the tire footprint variation due to its deformation in relation to the cyclist mass and the tire pressure. An analysis of the friction components has been presented in [1] leading to the following considerations. In absence of road slope, the influence of the rolling friction is more relevant at low speeds (). At higher speeds (), the aerodynamic drag component overcomes the rolling friction. In presence of road slope, the gravity component is dominant with respect to both the rolling and the aerodynamic friction components.
2.2. Pedalling Torque Estimation
Since the objective of this work is to estimate the pedalling torque starting from an analysis of the load torque applied to the electrical motor which provides the motion assistance, an analysis of the motor dynamics is necessary. Let us now consider a bicycle with the electrical motor installed on the back wheel and under the hypothesis of adherence conditions. The system can be considered constituted by three rigid bodies: the two wheels and the bicycle frame plus the cyclist. Since the applied pedalling torque is transmitted through the chain to the back wheel, the evaluation of the pedalling torque can be performed analyzing the back wheel dynamics. Let us consider the electromechanical equation of the motor which provides the electrical assistance to the vehicle:
where is the motor torque, is the motor load torque due to external forces applied to the motor, J is the inertia of the wheel expressed with respect to the revolute joint which constraints the motion between the back wheel and the bicycle frame, is its angular acceleration and represents the internal friction torque of the motor. In Figure 2, the dynamics of the back wheel of an EAB is reported. It has to be remarked that for the sake of brevity the reaction force due to the coupling between the wheel and the frame is not explicitly reported because it can be expressed as the sum of the friction and inertia forces acting on each rigid body. Therefore, the global forces acting on the bicycle dynamics, expressed in (1), are reported in the figure and will be considered in the mathematical analysis.
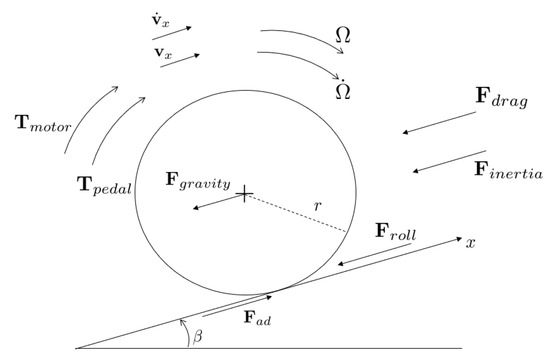
Figure 2.
Back wheel longitudinal dynamics.
Focusing on the motor load torque, the following expression can be obtained:
where is the static friction force, r is the radius of the wheel and is the torque applied to the motor due to the pedalling. It has to be remarked that the pedalling torque has an opposite sign with respect to the global load torque since it is a driving torque for the wheel. Under adherence conditions and considering the dynamics along the x-axis, the static friction force results to be equal to:
where is the inertia force. Therefore, the motor load torque results to be:
where , , , , .
Starting from (9) the pedalling torque can be expressed as:
Thus, given the environmental torque components , and , the inertia torque and the motor load torque a measurement of the applied pedalling torque can be obtained. The idea on which this work is based consists in estimating the pedalling torque starting from an estimation of the motor load torque given by a state observer and an estimation of the environmental torque components acting on the back wheel of the vehicle. Therefore, (10) can be written as:
where the is the estimated pedalling torque, is the estimated gravity component, is the estimated aerodynamic drag component, is the estimated rolling friction component, is the estimated inertia torque and is the estimated motor load torque component given by a state observer.
2.3. Motor Load Torque Observation
The estimation of the pedalling torque requires an estimation of the load torque applied to the motor . Focusing on (6), a more precise description of the internal friction of the motor is required in order to achieve a proper estimation of the external load torque applied to the motor. This phenomenon has been described considering a traditional Coulomb friction model which takes into account also the viscous friction effect. Thus, the internal friction torque presents the following expression:
where is the Coulomb friction torque that is equal to the maximum applicable motor torque in static conditions, b is the viscous friction coefficient and is the angular speed of the wheel. Let us now analyze the differential equations that describe the motor dynamics:
where (13) has been obtained from the motor electromechanical Equation (6), (14) is the definition of the mechanical speed where is the mechanical rotor position and (15) represents the chosen dynamics for the applied load torque. No assumptions on the behaviour of the applied load torque can be made, since this torque is an external unknown disturbance. Therefore, the only valid assumption is to consider the unknown disturbance applied to the motor to be invariable in a short time interval [32,35]. Considering the mechanical rotor position as the only measurable quantity, (13)–(15) can be written using a continuous-time state-variables representation:
The following quantities can be defined: the state vector , the input vector and the output equal to the measured mechanical rotor position given by a position sensor or a sensorless technique. Moreover, the following matrices can be defined:
where is the state matrix, is the input matrix and is the output matrix. The implementation of a state observer on a microcontroller requires the discretization of the state-variables representation and the selection of a proper sampling period . Considering the input to be constant over the sampling period, the system can be discretized as follows:
where , and are the discretized state, input and output matrices respectively. These matrices can be obtained as follows:
The expression of the discretized matrices can be simplified considering classical discretization methods such as the forward Euler, the backward Euler and the Tustin approximations. In particular, when a sampling time much smaller than the mechanical time constant of the system is chosen, the three discretization methods provide the same discretized matrices. Therefore, a forward Euler approximation has been used to simplify (21) and (22) due to the simplicity of its discretized matrices expression:
To observe the state using a state observer, the observability of the system must be proved. Therefore, the observability matrix has been evaluated:
Evaluating the rank of the observability matrix, one can conclude that the system is fully observable since the rank of the observability matrix is equal to the number of state variables n:
Therefore, given the measured input and output of the system, its state can be estimated using a discrete-time state observer.
2.4. Pedalling Torque Analysis
To evaluate the estimated pedalling torque and to choose the proper electrical assistance that the motor has to provide to achieve the desired vehicle dynamics specifications, it is important to analyze the nature of the applied pedalling torque. The pedalling torque is the sum of the torque contributions due to the forces applied to the left and right pedals:
where and are the left and right pedalling torques, respectively. To understand the behaviour of the pedalling torque, the forces applied to the pedals have to be analyzed. These forces can be decomposed in two components: a tangential component and a radial component . The only component which has an effect on the pedalling torque is the tangential one. In particular, its contribution to the pedalling torque is:
where is the crank arm lenght and i belongs to the set in dependence of the pedal on which the pedalling force is applied. Therefore, the pedalling torque presents a behaviour which depends on the direction of the applied force to each pedal and on the crank angle . In Figure 3, the pedalling torque generated by a pedalling force applied in a generic direction is shown.
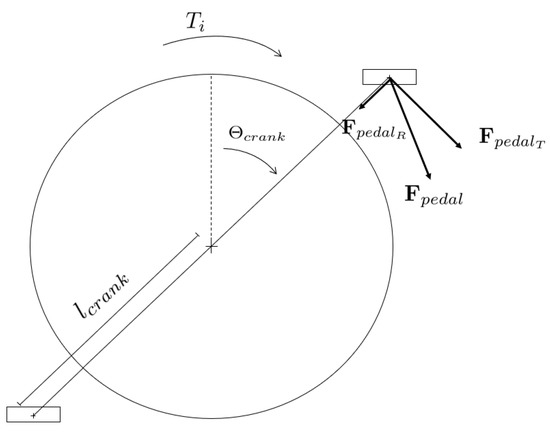
Figure 3.
Pedalling torque generated by an applied pedalling force in a generic direction.
Due to the design of the crankset, a typical pedalling torque presents a quasi-periodic profile which is close to a sinusoidal profile plus an offset [15,36,37,38]. The pedalling torque reaches its maximum and minimum twice during a pedalling cycle. In particular, the maximum is reached when the higher pedalling force tangential component is applied. This condition is typically satisfied when the pedals are close to the horizontal position depending on the direction of the applied pedalling force. In addition, depending on the crank angle, a typical pedalling torque increases in the first quarter period and decreases in the second quarter period. Within the second half period, similar considerations can be done when the pedalling force is applied on the other pedal. Figure 4 shows an example of the resulting pedalling torque obtained when a pedalling force with a constant module and a constant application direction is applied. One can notice that under these conditions the tangential pedalling force component results higher when the pedals are in horizontal position. Therefore, in this position one obtains the maximum value of the pedalling torque. Same considerations can be done when the pedalling torque is applied on the other pedal during the second half period.
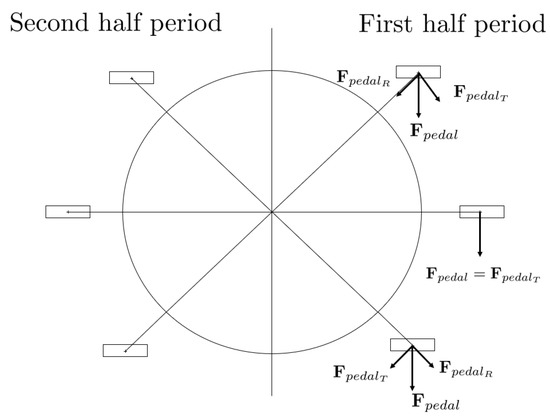
Figure 4.
Example of pedalling torque obtained when applying a pedalling force with a constant module and application direction.
3. Experimental Validation
In this section, a description of the experimental setup used to verify the validity of the proposed pedalling torque estimation method is reported. It has to be remarked that the experimental validation has been conducted neglecting the effects of the environmental torque components on the wheel longitudinal dynamics. Therefore, in this work, methods able to estimate and compensate the aforementioned components have not been analyzed. The objective of this analysis is to demonstrate the possibility of estimating the pedalling torque starting from the motor load torque estimation obtained using a LTO. Thus, a setup constituted by a bicycle with a motor installed on the back wheel has been considered. To evaluate the only effect of the pedalling torque on the motor load torque, all the experiments have been performed avoiding the contact between the wheels and the ground. Under these assumptions, expression (7) can be written as:
where represents the generic external load torque applied to the rear wheel. Therefore, the estimated motor load torque given by the LTO can be expressed as:
where is the estimated external disturbance torque.
3.1. Experimental Setup Description
This section describes the setup used for the experimental validation reported in Figure 5.
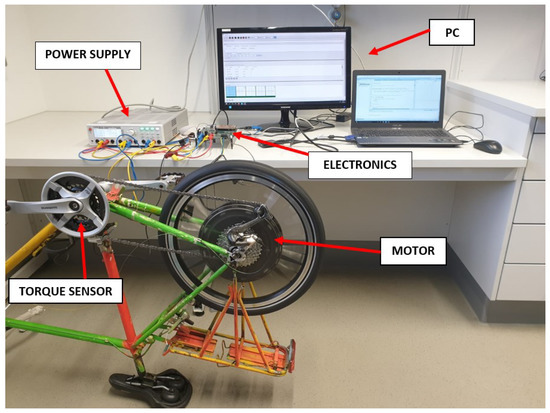
Figure 5.
Setup used for the experimental validation.
The setup is constituted of a bicycle with a motor installed on the rear wheel, a torque sensor necessary for the validation of the estimated pedalling torque and a custom electronic board. In the following, a more detailed description of the components that constitute the setup is provided. The motor under consideration is a star-connected Permanent Magnet Synchronous Machine (PMSM) with 23 pole pairs and surface mounted magnets. The nominal values of this motor are reported in Table 1. However, depending on the legislation of each country, the maximum output power and vehicle speed must be limited, i.e., 250 W and 25 according to the directive 2002/24/EC in the European Union. Therefore, in practical applications the motor will be driven with a reduced output power with respect to the nominal conditions.

Table 1.
Motor nominal values.
The torque sensor used for the pedalling torque measurement has been installed within the crankset of the bicycle. In particular, the sensor under consideration is commonly used in commercial EAB applications thanks to its robustness and compactness. This sensor measures the torque evaluating the twist of a torsional element placed in the middle of the sensor which is measured by an Hall effect sensor that evaluates the magnetic displacement. Moreover, the sensor returns a voltage proportional to the measured torque with a sensitivity of 10 . As stated in [39], this particular sensor is able to measure only the left pedalling torque. The torque generated by the right pedalling force is not measured due to the presence of the chainwheel on the right part of the pedalling shaft. Therefore, this sensor measures the torque generated by the left pedalling force and the weight of the left leg on the left pedal when the right leg applies a force. In particular, the weight of the left leg generates a negative torque measured by the sensor because non professional cyclists usually do not lift the leg while pushing the other pedal [40]. A reconstruction of the global pedalling torque starting from the measured torque is therefore necessary for the validation of the estimated pedalling torque. The pedalling torque reconstruction process will be described in detail in Section 4.2.
Moreover, an electronic board used for motor control, the torque sensor reading and the pedalling torque observation has been developed. In particular, the board is constituted by a 32-bit microcontroller, a three-phase inverter and sensing circuitry. The motor is driven with a PWM-frequency of 60 kHz whereas the motor control system and the state observer are discretized with a frequency of 10 kHz. Also, the measurements of phase currents and voltages are performed with a 16-bit AD converter and a sampling frequency of 10 kHz. In addition, the designed board allows sensorless operation based on the Direct Flux Control (DFC) sensorless technique. More details about this technique will be provided in Section 3.2. Thanks to an USB communication and a custom software, the useful information can be plotted and analyzed using a PC and exported to MATLAB environment.
3.2. Direct Flux Control DFC Sensorless Technique
The aim of this section is to provide a brief description of the DFC sensorless technique used for the estimation of the electrical rotor position. In electrical machines and drives, the position information is typically provided by encoders or resolvers causing an increase in cost and occupied space. In many applications, the cost and space reduction requirements have led to the employment of sensorless techniques. Nevertheless, sensorless operation typically introduces a rotor position estimation error and thus reduce the control performance with respect to high-resolution encoders. Therefore, in order to avoid the installation of a position sensor and to prove the robustness of the proposed pedalling torque estimation technique in presence of rotor position estimation errors, the motor under consideration has been controlled by means of a sensorless technique. However, it has to be remarked that using a sensorless technique to control the motor is not a strict requirement of the proposed pedalling torque estimation method.
DFC is an anisotropy-based sensorless technique able to estimate the electrical rotor position relying on measurements of the machine star-point voltage. This technique is applicable to Synchronous Machines (SMs) with an accessible star-point. The DFC estimated rotor position is obtained by exploiting the dependence of the machine inductances on the rotor position. Considering a SM driven by a power inverter, the DFC measures the difference between the star-point voltage of the machine and the voltage of a virtual star-point during the transition between the machine excitation states 0 and I. Figure 6 reports the schematic of a three-phase SM with an accessible star-point under DFC sensorless operation, where are the machine terminals, N is the star-point or neutral-point of the machine, V is the virtual star-point and O is the ground reference. In addition, is the phase currents vector, is the terminal voltages vector and is the Back Electro-Motive Forces (BEMFs) vector. Also, as the figure shows, the virtual star-point is obtained by connecting the machine terminals to three star-connected resistors. In Figure 7, it can be seen that during the machine excitation state 0 all machine terminals are grounded whereas in the excitation state I, a generic phase X, belonging to the set , switches to the inverter bus voltage . The measurement of the differential voltage necessary to obtain the anisotropy signals from which the electrical rotor position can be estimated requires for example in this specific implementation a modified edge-aligned PWM pattern which drives the machine between the excitation states 0 and I at the beginning of each PWM period. In particular, a new anisotropy signal related to one phase is calculated at each period. Therefore, after three periods a new updated measurement of the anisotropy signals can be used to extract the rotor position. Figure 8 shows the PWM excitation commonly used to obtain the aforementioned anisotropy signals. More details about the dynamics of the star-point voltage and about the estimation of the electrical rotor position using the DFC technique can be found in [41]. As stated in [42,43], the estimated electrical rotor position obtained with the DFC technique presents oscillations with respect to the real position which depend on the machine inductance matrix. In particular, the estimated position presents a ripple which is a nonlinear function of the 6th harmonic component of the rotor position.
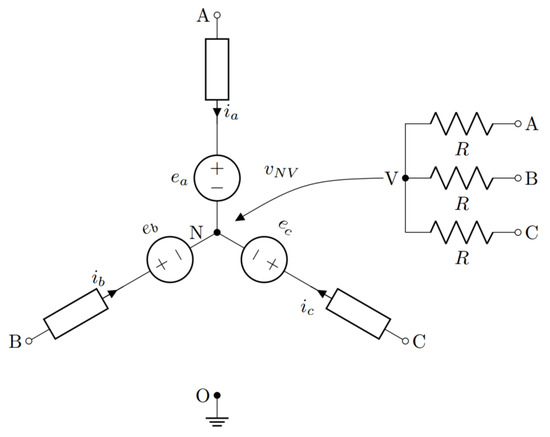
Figure 6.
Schematic of a SM with an accessible star-point under DFC sensorless operation.
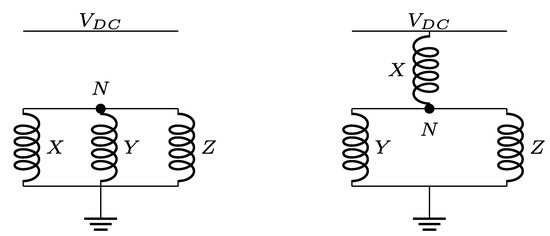
Figure 7.
Machine excitation states 0 (left) and I (right), where are the generic phases belonging to the set [41].
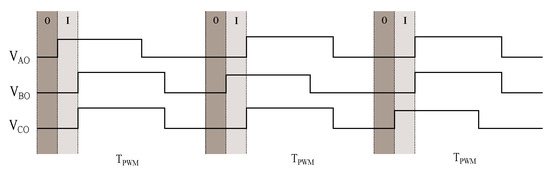
Figure 8.
PWM excitation used for the measurement of the voltage , where is the PWM period [41].
3.3. Electrical Parameters Identification
The tuning of a proper control system able to provide the electrical assistance and of a LTO requires the knowledge of the machine parameters which in many cases are not provided in the datasheets of the motors. In this section, the identification procedure used for evaluating the electrical parameters of the motor under consideration is analyzed. Since in the experimental setup no high-resolution encoder is available, a technique able to estimate the electrical machine parameters relying on the DFC estimated rotor position has been used. This technique, proposed in [44], combines a classical online parameter identification algorithm, the RLS, with the position information given by the DFC sensorless technique. Let us consider the electrical equations of a PMSM in the -reference frame:
where and are the voltages in the -reference frame, R is the phase resistance, and are the inductances in the -reference frame, is the permanent magnet flux linkage, and are the currents in the -reference frame, and are their derivatives and is the electrical rotor speed. After some manipulations, Equations (31) and (32) can be written in the form:
where is the system response, is the parameter vector and is the state vector. For systems in the form (33), the RLS algorithm can be used for the identification of the parameter vector . The estimation of the electrical parameters has been performed considering the following expressions for the terms which constitute Equation (33) and using the position information given by the DFC technique:
where is the estimated electrical rotor speed obtained as the derivative of the estimated electrical rotor position given by the DFC sensorless technique . The identification process has been performed using the same electronics described in [44]. A forgetting factor of has been chosen for the RLS algorithm in order to provide a significant number of samples for the parameters estimation. To estimate the parameters, the PMSM has to be driven with persistently exciting input signals. For the identification of the phase resistance and of the motor inductances a sinusoidal excitation has been provided to the motor in the form:
where A and f are respectively the amplitude and the frequency of the sinusoidal excitation and i belongs to the set . In particular, the chosen amplitude of the sinusoidal excitation used in the identification process is equal to V. Concerning the frequency, a value of Hz has been used for the measurement of R and whereas, in order to avoid measurements error due to position ripples generated by the electromagnetic torque, a higher frequency equal to Hz has been applied for the measurement of . The identification of the permanent magnet flux linkage has been achieved considering a constant voltage input V. Table 2 reports the steady-state values of the identified electrical parameters obtained with this approach together with the excitation inputs applied for the identification of each parameter. In [44], it has been shown that the combination of the RLS with the DFC estimated position grants a relative error on the identified values with respect to the given reference values smaller than the 10%. Such error on the knowledge of the parameters has been considered acceptable for the tuning of the control system and of the LTO.

Table 2.
Identified electrical parameters using the RLS and the DFC estimated electrical rotor position and excitation inputs used for the identification process.
3.4. Control System Design
The design of an EAB capable of providing an electrical assistance related to the pedalling torque applied by the cyclist requires the tuning of the motor control. In particular, providing an electrical assistance means applying a motor torque with the objective of achieving certain desired vehicle dynamics specifications. However, in this work the project of an electrical assistance able to obtain certain bicycle longitudinal dynamics performance will not be discussed. Nevertheless, the design of a proper control system is necessary for the experimental validation of the proposed theory. Providing a desired motor torque means controlling the motor currents. Thus, let us focus on the expression of the electromagnetic torque of a PMSM:
where is the number of pole pairs and is the motor anisotropy. Therefore, in order to control the motor torque a proper current control must be designed. For motors which present a small anisotropy, such as the motor under consideration, it is convenient to reduce the torque control to the control of the current considering a current reference on the d-axis equal to . Under these conditions the motor torque results proportional only to :
Both the and controllers have been tuned using a standard Field Oriented Control (FOC) based on the parameters identified in Section 3.3 and according to the delays introduced by the chosen PWM excitation, the AD conversion and the digital implementation of the control system.
3.5. Mechanical Parameters Identification
The estimation of the pedalling torque based on state observation techniques requires a good knowledge of the mathematical model of the motor. In particular, as Equations (13)–(15) show, the values of the motor inertia J, of the motor internal friction torque and of the applied motor torque must be identified. As (39) shows, the motor torque depends on the permanent magnet flux linkage which has been previously evaluated in Section 3.3. Therefore, in this section an analysis of the identification of the mechanical parameters is provided.
The motor inertia identification was performed considering a method based on the addition of sinusoidal perturbations on the drive system. The method under consideration has been proposed in [45] and it has the advantage of removing the influence of the viscous friction in the inertia identification. In particular, this method provides the following current references:
where is the reference amplitude of the sinusoidal excitation and is the chosen frequency. This results in a sinusoidal mechanical speed:
where is the amplitude of the sinusoidal mechanical speed and is the phase shift between and . As stated in [45], evaluating the current at the zero-crossing time instants of the mechanical rotor speed , the motor inertia can be calculated as follows:
The results obtained in the inertia identification experiments are reported in Table 3. The selection of the amplitude and of the frequency has been performed according to the indications reported in [45]. The average identified value of the motor inertia is .

Table 3.
Motor inertia identification.
Let us now analyze the internal friction torque identification. The Coulomb friction torque has been calculated by considering the maximum value of the motor torque which grants static conditions. In this particular motor, Nm when a current reference A is applied. The viscous friction coefficient b has been calculated considering (6) in steady-state conditions and in absence of an applied load torque Nm. Under these assumptions, the viscous friction coefficient can be obtained using the following expression:
where is the steady-state value of the mechanical rotor speed. The identification experiment was performed applying several motor torque steps and evaluating the corresponding steady-state mechanical speed. The obtained values of the viscous friction coefficient together with the applied motor torque and the resulting steady-state mechanical speed are reported in Table 4. Starting from the obtained results, the average value of the viscous friction coefficient has been calculated.

Table 4.
Viscous friction coefficient identification.
4. Pedalling Torque Estimation
In this section, the validation of the pedalling torque estimated using a LTO is performed. The tuning of a LTO observer is described considering the identified electrical parameters reported in Table 2 and the average values of the mechanical ones evaluated in Section 3.5. Also, in this section an analysis of the pedalling torque reconstruction starting from the measured pedalling torque given by the torque sensor is reported. Finally, the state estimation capabilities of the LTO are evaluated performing several experiments on the setup.
4.1. Pedalling Torque Observer
As described in Section 2.3, a LTO estimates the motor load torque which under the assumptions stated in Section 3 can be reduced to (29). In particular, in this work a KF has been chosen as LTO. Nevertheless, it has to be remarked that a generic state observer can be tuned for the estimation of the motor load torque. A KF whose nominal model is based on Equations (19) and (20) has been considered:
where the vector describes the noise on the process whereas v describes the noise on the measurement. In particular, in this case v represents the position error introduced by the DFC sensorless technique. In a KF both the elements of and v are modelled as white, uncorrelated Gaussian processes whose variance is described considering the covariance matrices and respectively. The selection of a KF as LTO has the advantage of granting a small state estimation error also in presence of model uncertainties and noise on the measurements. Nevertheless, in order to achieve a good state estimation, the KF must be properly tuned. Tuning a KF means initializing both the state estimation and the estimation error covariance matrix and properly selecting the covariance matrices and . Since no assumptions on the initial conditions of the system can be done, the following initial state and initial value of the error covariance matrix have been considered:
Concerning the selection of the covariance matrices, the following values have been chosen:
In this case, since the measurement is given by the DFC sensorless technique which is known to present an estimation error with respect to the real rotor position, a bigger value of the variance has been selected compared to the diagonal elements of the matrix . This means that the equations that describe the process are considered more reliable than the measurements because the deviations from the nominal model are considered smaller than the error on the measurement given by the sensorless technique. A standard KF algorithm as described in [46] has been implemented on the microcontroller with a digital implementation frequency of 10 kHz. Since the chosen sampling period s is much smaller than the mechanical time constant s, the expressions (24) can be used to represent the state and the input matrices of the KF. It has to be remarked that in order to reduce the errors related to the conversions of the phase currents and voltages from the phase to the rotor reference frame, the estimated rotor position given by the LTO has been used in the conversion instead of the measured DFC position leading to an improvement of the control system performance.
4.2. Pedalling Torque Reconstruction
The evaluation of the estimated pedalling torque requires the reconstruction of the pedalling torque starting from the measured one given by the torque sensor as stated in Section 3. There is a strong correlation between the torque of the left and right pedalling revolution in standard cycling operations [39]. In particular, the left and the right torque can be considered symmetric. Therefore, the right torque can be computed by applying the same torque profile applied on the left pedal in the previous half revolution without committing a considerable error in the torque reconstruction. Thus, the reconstructed right pedalling torque can be obtained as follows:
where is the estimated crankset angle. Since no sensor able to measure the crankset angle with a good resolution can be installed within the crankset, this angle has been computed from the estimated rotor position given by the state observer . In particular, the crankset angle has been calculated under the assumption of considering a constant transmission ratio between the crankset and the rear wheel using the following expression:
The global reconstructed pedalling torque can be obtained summing the measured left pedalling torque to the reconstructed right one:
An example of pedalling torque reconstruction is reported in Figure 9, where the upper subplot shows the comparison between the measured left pedalling torque and the reconstructed right one whereas the lower subplot shows the reconstructed pedalling torque according to (53).
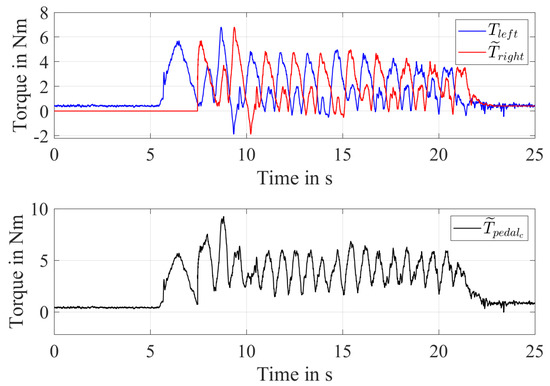
Figure 9.
Pedalling torque reconstruction.
4.3. Load Torque Observer LTO Validation
In this section the evaluation of the state estimation provided by the LTO tuned according to Section 4.1 is reported. The validation has been performed considering different experiments in the following conditions:
- E1:
- the motor is current controlled with A and A without an applied load torque Nm;
- E2:
- the motor is current controlled with progressively increasing steps and A and an external torque disturbance is applied ;
- E3:
- the motor is current controlled with A and A and a pedalling torque is applied .
- E4:
- the motor is current controlled with A and A and both a pedalling torque and an external torque disturbance are applied .
For each experiment, the following quantities have been analyzed: the current on the q-axis, the estimated electrical rotor position, the estimated mechanical rotor speed and the estimated load torque. In particular, the following quantities have been compared:
- the provided current reference given by the motor current control with the actual current ;
- the measured electrical rotor position obtained applying the DFC technique with the estimated electrical rotor position given by the LTO ;
- the measured rotor speed obtained as the derivative of the DFC rotor position with the estimated rotor speed given by the LTO ;
- the reconstructed pedalling torque reported to the motor side with the estimated motor load torque given by the LTO .
To evaluate the performance of the control system and of the state observation, the following indexes were calculated for each analyzed quantity:
where , , , are the q-axis current error, the position estimation error, the speed estimation error and the load torque estimation error, respectively. Moreover, it has to be remarked that the experiments have been performed considering a reduced motor power output when providing the electrical assistance with respect to the legislation limitations. Nevertheless, this does not limit the validity of the experimental results, whose main purpose is to validate the state observation capabilities of the LTO.
Figure 10 shows the results obtained in the experiment E1 which has been performed by applying a step current A in s while A when no load torque is applied to the wheel Nm. According to (38), in this condition the applied motor torque is Nm. One can notice that the actual current is capable of following the current reference with an error whose steady-state values are in the range A. Focusing on the electrical rotor position, one can see that as stated in Section 3.2, the measured electrical rotor position obtained applying the DFC technique presents an oscillation over the real position. Using a properly tuned state observer, it is possible to improve the measured electrical rotor position obtaining an estimated position closer to the real one. Considering the LTO designed in Section 4, the position estimation error results in the range rad. Concerning the rotor speed, one can notice that it presents a first order system step response profile. The figure reports also the corresponding speed estimation error whose range in steady-state condition is . Focusing on the estimated motor load torque , one can see that its average value is close to zero: Nm. Moreover, the load torque estimation error belongs to the range Nm in steady-state condition. Thus, the LTO is able to recognize that no external load torque is applied to the wheel.
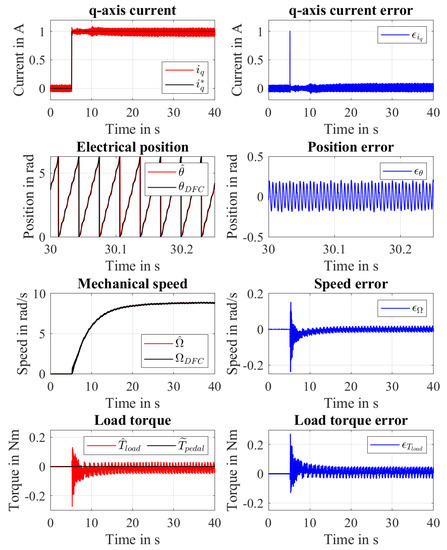
Figure 10.
Experiment E1: Torque control without an applied load torque.
Figure 11 shows the results obtained in the experiment E2 which has been performed by applying increasing step current references on the q-axis while A and an external breaking torque is applied . In particular, the following step current references have been applied: A, A, A, A and A. This means that the following motor torques have been provided: Nm, Nm, Nm, Nm and Nm. To evaluate the load torque estimation capability of the LTO in presence of an applied external disturbance torque, the wheel has been braked starting from s by means of a mechanical brake. Moreover, this breaking torque has been applied with the objective of keeping the speed of the wheel constant within the range . Focusing on the current , one can notice that the control system is also able to reject external disturbances such as an applied breaking torque. Moreover, similar considerations to E1 can be done concerning the range of the q-axis current error . Also, the figure shows the electrical rotor position behaviour in s when an increasing step current is applied and the mechanical brake is active. One can notice that the presence of the breaking torque and the application of the motor torque step do not affect significantly the position estimation error whose values are within the same range of the experiment E1. Focusing on the estimated speed, it can be noticed that the application of the mechanical brake in s causes a deceleration. Then, by means of the applied breaking torque, the speed is kept within the aforementioned range. In particular, the average value of the estimated speed when the brake is active results . In this experiment, due to the speed fluctuations caused by the application of the breaking torque, the speed estimation error increases with respect to the experiment E1 to the range . Analysing the estimated load torque , it can be noticed that the observer is capable of recognizing that after s an external disturbance torque is applied and that the breaking torque is progressively increased in order to keep the speed constant when increasing motor torques are provided. This means that by means of a LTO it is possible to recognize the presence of external torque disturbances acting on the wheel such as environmental torques. Since the external torque provided by the installed mechanical brake is not measurable, no plot that shows the load torque error is reported in the figure.
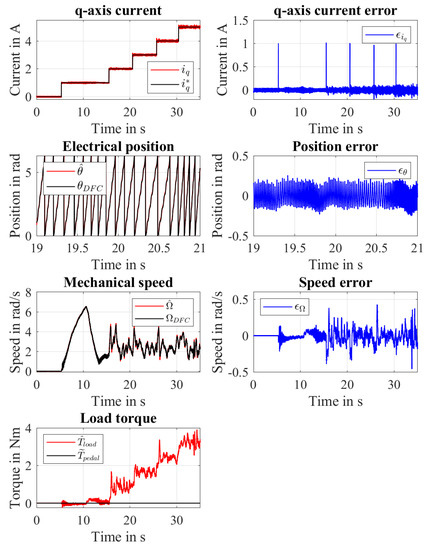
Figure 11.
Experiment E2: Torque control with an applied external torque disturbance.
Figure 12 shows the results obtained in the experiment E3 which was performed controlling the motor with a A when a pedalling torque is applied . Thus, no motor torque is provided by the motor Nm. In particular, the experiment has been performed applying the pedalling torque in s with the objective of reaching a speed in the range . Focusing on the speed, one can notice that the estimated speed is kept within the objective range in steady-state condition with an average estimated speed of . Nevertheless, the pedalling torque profile introduces speed fluctuations which cause an increase of the speed estimation and q-axis current errors whose ranges in steady-state condition are and A, respectively. Similar considerations to E1 and E2 can be done regarding the position estimation. Considering the estimated load torque, it can be seen that the average load torque estimation error is Nm while its fluctuation belongs to the range Nm over the mean value in steady-state condition. Thus, one can notice that the observer is able to estimate with good accuracy the average value of the applied pedalling torque. Focusing on the fluctuation of the load torque estimation error, one can conclude that it is related to the torque reconstruction process which is based on the assumption of a perfect symmetry between the left and the right pedalling torque and considers a constant transmission ratio between the crankset and the rear wheel sprocket. Since both these hypotheses are not completely true, an error on the torque reconstruction and consequently on the load torque estimation is expected. Therefore, it is important to verify that the state observer is able to achieve a small average value of the estimation error rather than a perfect following of the reconstructed signal. In Figure 13, the comparison between the estimated load torque given by the LTO and the reconstructed pedalling torque is reported. One can notice that the estimated pedalling torque presents a similar profile to the reconstructed pedalling torque and a similar mean value. This indicates that the state observer is capable of recognizing the fluctuations of the load torque caused by the pedalling.
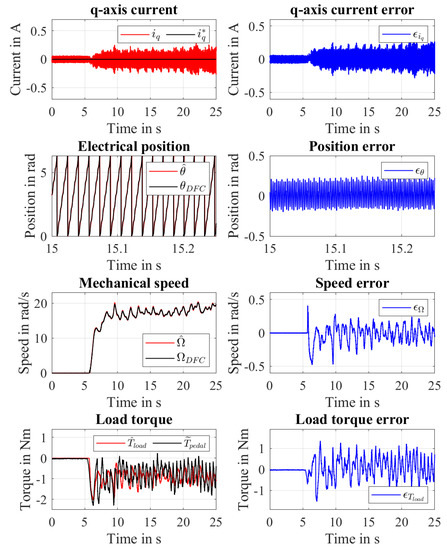
Figure 12.
Experiment E3: Applied pedalling torque with no additional torque disturbance.
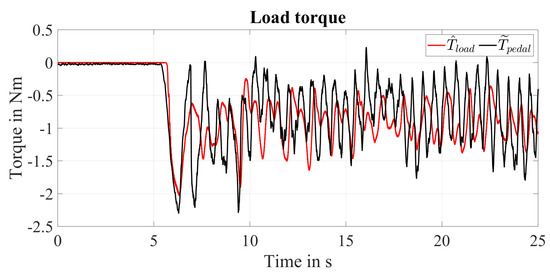
Figure 13.
Experiment E3: Comparison between the estimated load torque and the reconstructed pedalling torque.
Figure 14 shows the results obtained in the experiment E4 which has been performed controlling the motor with the following current references A and applying both a pedalling torque and a breaking torque . Therefore, the provided motor torque is Nm. In particular, a pedalling torque has been applied in s. Then, in s, the wheel is braked by means of the mechanical brake. Moreover, when the mechanical brake is active, the pedalling torque is applied with the objective of keeping the speed of the wheel within the range . Therefore, the applied pedalling torque is expected to increase as the breaking torque is applied in order to keep the speed within the objective range. Concerning the current and its error , similar considerations to E3 can be done. Also, regarding the estimated position and its error , there are no particular remarks with respect to the previous experiments. Focusing on the speed, one can notice that when both the pedalling and the breaking torque are applied the speed is kept within the objective range with an average estimated speed . Due to the speed oscillations introduced by the pedalling and the breaking torque, the speed estimation error range results increased to . Concerning the load torque estimation, one can notice that, when only the pedalling torque is applied, similar results to the ones of E3 are obtained. When also the breaking torque is provided, the applied pedalling torque increases to keep the speed in the objective range. Thus, the average value of decreases. It can be seen that the application of the breaking torque cannot easily be recognized by analysing only the estimated load torque. Focusing on the load torque estimation error , one can see that after s, its average value is Nm while its variability range is Nm over the mean value. Also in this case, the variability of the load torque estimation error can be explained by the imperfection of the pedalling torque reconstruction process plus the application of a not perfectly constant breaking torque. Therefore, also in this case, it is important to evaluate the mean value of the load torque estimation error. Neglecting the fluctuations introduced by the pedalling torque reconstruction process, the load torque estimation error is equal to the estimated external load torque with opposite sign . Therefore, the external torque disturbance can be considered as an offset between the applied pedalling torque and the estimated load torque given by the observer. Thus, the pedalling torque can be estimated from the estimated load torque considering (30). In Figure 15, a comparison between the estimated load torque, the reconstructed pedalling torque and the estimated pedalling torque with opposite sign in steady-state condition is reported. In this case, the pedalling torque has been estimated assuming . It can be noticed that the estimated pedalling torque presents a similar profile and mean value with respect to the reconstructed pedalling torque after compensating for the external torque disturbance. This indicates that by means of the LTO it is possible to estimate the applied pedalling torque also in presence of environmental torques which act on the bicycle longitudinal dynamics.
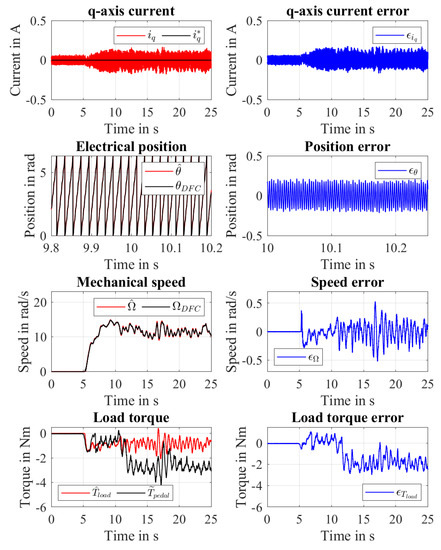
Figure 14.
Experiment E4: Applied pedalling torque with external torque disturbance.
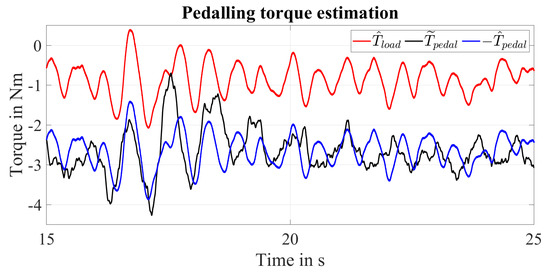
Figure 15.
Experiment E4: Comparison between the estimated load torque, the reconstructed pedalling torque and the estimated pedalling torque with opposite sign in steady-state condition.
5. Conclusions
In this work, a novel pedalling torque estimation approach based on the state observation of the dynamics of the driving wheel of an EAB is proposed. After analysing the vehicle longitudinal dynamics and in particular the back-wheel one, a technique capable of estimating the pedalling torque starting from an estimation of the motor load torque and of the environmental torques acting on the bicycle is presented. Then, a LTO for the estimation of the motor load torque is described. Moreover, a mathematical analysis of the pedalling torque is provided. An experimental validation of the proposed theory is performed showing the capability of the proposed LTO of estimating the pedalling torque and generic disturbance torques applied to the wheel. Also, the robustness of the load torque estimation to position estimation errors introduced when controlling the machine with a sensorless technique is verified. Therefore, with the proposed technique, it is possible to evaluate the pedalling torque avoiding the installation of both torque and position sensors leading to reduction of cost and space. The experimental validation has been performed relying on the DFC sensorless technique and controlling the machine with a standard FOC. To tune both the control system and the state observer, an identification of the electrical and mechanical parameters of the system has been performed. The load torque estimation has been achieved using a KF as LTO and exploiting the estimated rotor position given by the observer to control the machine. The evaluation of the pedalling torque estimation has been performed comparing the estimated load torque with the reconstructed pedalling torque obtained from the torque sensor measurements. Several experiments in different conditions have been performed highlighting the capability of the LTO of estimating the applied pedalling torque and recognizing external disturbances applied to the motor. Although the capability of the LTO of estimating external torque disturbances has been proved, the validation of the proposed theory has been performed neglecting the influence of the environmental torques. In future works, techniques capable of achieving an online estimation of the external disturbance torques with the objective of extracting the pedalling torque from the global estimated motor load torque when the vehicle operates on the road will be analyzed. In particular, techniques able to estimate the road slope, the vehicle mass, the aerodynamic drag and the rolling friction will be taken into account. The robustness of the proposed method in presence of position estimation errors has been also proved when the DFC sensorless technique is applied. Nevertheless, the proposed pedalling torque estimation approach can be implemented relying on the position information given by other sensorless techniques or position sensors which will be taken into account in future works in order to understand the impact of the different position measurement approaches on the pedalling torque estimation. Also, the analysis of control strategies able to achieve certain vehicle dynamics performance starting from the estimated pedalling torque within the entire output power range allowed from the legislation will be investigated in future works. Concerning the selection of the LTO, future works will analyze other approaches based on different state observers with the objective of enhancing the robustness of the state estimation in presence of model uncertainties.
Author Contributions
Conceptualization, R.M. and E.G.; methodology, R.M., S.F. and E.G.; software, R.M., S.F. and E.G.; validation, R.M. and S.F.; formal analysis, R.M.; investigation, R.M.; resources, R.M.; data curation, R.M.; writing—original draft preparation, R.M.; writing—review and editing, R.M., M.N. and E.G.; visualization, R.M.; supervision, E.G.; project administration, M.N.; funding acquisition, M.N. All authors have read and agreed to the published version of the manuscript.
Funding
This work has received financial support by H. Janocha.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to the particular format in which they are organized.
Acknowledgments
We acknowledge support by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) and Saarland University within the funding programme Open Access Publishing. Also, the authors would like to thank Niklas König and Rosario Gandolfo for the assistance provided in the experimental validation.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Muetze, A.; Tan, Y.C. Electric bicycles—A performance evaluation. IEEE Ind. Appl. Mag. 2007, 13, 12–21. [Google Scholar] [CrossRef]
- Cappelle, J.; Lataire, P.; Maggetto, G.; Van den Bossche, P.; Timmermans, J. Electrically Assisted Cycling around the World. In Proceedings of the 20th International Electric Vehicle Symposium (EVS 20), Long Beach, CA, USA, 15–19 November 2003. [Google Scholar]
- Ohnishi, K. A new servo method in mechatronics. Trans. Jpn. Soc. Electr. Eng. 1987, 107-D, 83–86. [Google Scholar]
- Murakami, T.; Ohnishi, K. Advanced motion control in mechatronics—A tutorial. In Proceedings of the IEEE International Workshop on Intelligent Control, Istanbul, Turkey, 20–22 August 1990; Volume 1, pp. SL9–SL17. [Google Scholar]
- Cheon, D.S.; Nam, K.H. Pedaling torque sensor-less power assist control of an electric bike via model-based impedance control. Int. J. Automot. Technol. 2017, 18, 327–333. [Google Scholar] [CrossRef]
- Sankaranarayanan, V.; Ravichandran, S. Torque sensorless control of a human-electric hybrid bicycle. In Proceedings of the International Conference on Industrial Instrumentation and Control (ICIC), Pune, India, 28–30 May 2015; pp. 806–810. [Google Scholar]
- Oh, S.; Ohri, Y. Sensor Free Power Assisting Control Based on Velocity Control and Disturbance Observer. In Proceedings of the IEEE International Symposium on Industrial Electronics (ISIE 2005), Dubrovnik, Croatia, 20–23 June 2005; pp. 1709–1714. [Google Scholar]
- Ohnishi, K.; Matsui, N.; Hori, Y. Estimation, identification, and sensorless control in motion control system. Proc. IEEE 1994, 82, 1253–1265. [Google Scholar] [CrossRef]
- Seki, H.; Iso, M.; Hori, Y. How to design force sensorless power assist robot considering environmental characteristics-position control based or force control based. In Proceedings of the IEEE 2002 28th Annual Conference of the Industrial Electronics Society (IECON 02), Seville, Spain, 5–8 November 2002; Volume 3, pp. 2255–2260. [Google Scholar]
- Kato, A.; Ohnishi, K. Robust force sensorless control in motion control system. In Proceedings of the 9th IEEE International Workshop on Advanced Motion Control, Istanbul, Turkey, 27–29 March 2006; pp. 165–170. [Google Scholar]
- Salvucci, V.; Oh, S.; Hori, Y. New approach to force sensor-less power assist control for high friction and high inertia systems. In Proceedings of the IEEE International Symposium on Industrial Electronics, Bari, Italy, 4–7 July 2010; pp. 3559–3564. [Google Scholar]
- Nam, K.; Kim, Y.; Oh, S.; Hori, Y. Steering Angle-Disturbance Observer (SA-DOB) based yaw stability control for electric vehicles with in-wheel motors. In Proceedings of the IICCAS 2010, Gyeonggi-do, Korea, 27–30 October 2010; pp. 1303–1307. [Google Scholar]
- Nam, K.; Fujimoto, H.; Hori, Y. Advanced Motion Control of Electric Vehicles Based on Robust Lateral Tire Force Control via Active Front Steering. IEEE/ASME Trans. Mechatron. 2014, 19, 289–299. [Google Scholar] [CrossRef]
- Kurosawa, T.; Fujimoto, Y.; Tokumaru, T. Estimation of pedaling torque for electric power assisted bicycles. In Proceedings of the IECON 2014—40th Annual Conference of the IEEE Industrial Electronics Society, Dallas, TX, USA, 29 October–1 November 2014; pp. 2756–2761. [Google Scholar]
- Kurosawa, T.; Fujimoto, Y. Torque Sensorless Control for an Electric Power Assisted Bicycle with Instantaneous Pedaling Torque Estimation. IEEJ J. Ind. Appl. 2017, 6, 124–129. [Google Scholar] [CrossRef][Green Version]
- Fukushima, N.; Fujimoto, Y. Estimation of pedaling torque for electric power-assisted bicycle on slope environment. In Proceedings of the IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Munich, Germany, 3–7 July 2017; pp. 1682–1687. [Google Scholar]
- Fukushima, N.; Fujimoto, Y. Experimental verification of torque sensorless control for electric power-assisted bicycles on sloped environment. In Proceedings of the IEEE 15th International Workshop on Advanced Motion Control (AMC), Tokyo, Japan, 9–11 March 2018; pp. 66–71. [Google Scholar]
- Fan, X.; Tomizuka, M. Robust disturbance observer design for a power-assist electric bicycle. In Proceedings of the 2010 American Control Conference, Baltimore, MD, USA, 30 June–2 July 2010; pp. 1166–1171. [Google Scholar]
- Chew, K.K.; Tomizuka, M. Digital control of repetitive errors in disk drive systems. IEEE Control. Syst. Mag. 1990, 10, 16–20. [Google Scholar] [CrossRef]
- Steinbuch, M. Repetitive control for systems with uncertain period-time. Automatica 2002, 38, 2103–2109. [Google Scholar] [CrossRef]
- Tsao, T.C.; Tomizuka, M. Robust Adaptive and Repetitive Digital Tracking Control and Application to a Hydraulic Servo for Noncircular Machining. J. Dyn. Syst. Meas. Control. 1994, 116, 24–32. [Google Scholar] [CrossRef]
- Hanson, R.D.; Tsao, T.C. Periodic Sampling Interval Repetitive Control and Its Application to Variable Spindle Speed Noncircular Turning Process. J. Dyn. Syst. Meas. Control. 1998, 122, 560–566. [Google Scholar] [CrossRef]
- Hatada, K.; Hirata, K. Energy-efficient power assist control for periodic motions. In Proceedings of the SICE Annual Conference 2010, Taipei, Taiwan, 18–21 August 2010; pp. 2004–2009. [Google Scholar]
- Hatano, R.; Namikawa, D.; Minagawa, R.; Iwase, M. Experimental verification of effectiveness on driving force assist control based on repetitive control for electrically-assisted bicycles. In Proceedings of the IEEE 13th International Workshop on Advanced Motion Control (AMC), Yokohama, Japan, 14–16 March 2014; pp. 237–241. [Google Scholar]
- Fan, X.; Iwase, M.; Tomizuka, M. Non-Uniform Velocity Profile Compensation for an Electric Bicycle Based on Repetitive Control With Sinusoidal and Non-Sinusoidal Internal Models. In Proceedings of the SME 2009 Dynamic Systems and Control Conference, Hollywood, CA, USA, 12–14 October 2009; Volume 1, pp. 765–772. [Google Scholar]
- Solsona, J.; Valla, M.I.; Muravchik, C. Nonlinear control of a permanent magnet synchronous motor with disturbance torque estimation. IEEE Trans. Energy Convers. 2000, 15, 163–168. [Google Scholar] [CrossRef]
- Aghili, F. Torque control of electric motors without using torque sensor. In Proceedings of the International Conference on Intelligent Robots and Systems, San Diego, CA, USA, 29 October–2 November 2007; pp. 3604–3609. [Google Scholar]
- Lian, C.; Xiao, F.; Gao, S.; Liu, J. Load Torque and Moment of Inertia Identification for Permanent Magnet Synchronous Motor Drives Based on Sliding Mode Observer. IEEE Trans. Power Electron. 2019, 34, 5675–5683. [Google Scholar] [CrossRef]
- Zedong, Z.; Yongdong, L.; Fadel, M.; Xi, X. A Rotor Speed and Load Torque Observer for PMSM Based on Extended Kalman Filter. In Proceedings of the IEEE International Conference on Industrial Technology, Mumbai, India, 15–17 December 2006; pp. 233–238. [Google Scholar]
- Peng, D. Exponential decay H-infinite load torque observer of permanent magnet synchronous motor. In Proceedings of the 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017; pp. 4747–4750. [Google Scholar]
- Thiemann, P.; Mantala, C.; Hordler, J.; Trautmann, A.; Groppe, D.; Strothmann, R.; Zhou, E. New sensorless rotor position detection technique of PMSM based on direct flux control. In Proceedings of the International Conference on Power Engineering, Energy and Electrical Drives, Malaga, Spain, 11–13 May 2011; pp. 1–6. [Google Scholar]
- Janiszewski, D. Load torque estimation in sensorless PMSM drive using Unscented Kalmana Filter. In Proceedings of the IEEE International Symposium on Industrial Electronics, Gdansk, Poland, 27–30 June 2011; pp. 643–648. [Google Scholar]
- Janiszewski, D. Load torque estimation for sensorless PMSM drive with output filter fed by PWM converter. In Proceedings of the IECON 2013—39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; pp. 2953–2959. [Google Scholar]
- Kyslan, K.; Šlapák, V.; Fedák, V.; Ďurovský, F.; Horváth, K. Design of load torque and mechanical speed estimator of PMSM with unscented Kalman filter —An engineering guide. In Proceedings of the 19th International Conference on Electrical Drives and Power Electronics (EDPE), Dubrovnik, Croatia, 4–6 October 2017; pp. 297–302. [Google Scholar]
- Fabbri, S.; D’Amato, D.; Palmieri, M.; Cupertino, F.; Nienhaus, M.; Grasso, E. Performance Comparison of Different Estimation Techniques of the External Load-torque applied on a PMSM using Direct Flux Control. In Proceedings of the International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Sorrento, Italy, 24–26 June 2020; pp. 688–693. [Google Scholar]
- Hatada, K.; Hirata, K.; Sato, T. Energy-Efficient Power Assist Control with Periodic Disturbance Observer and Its Experimental Verification Using an Electric Bicycle. SICE J. Control. Meas. Syst. Integr. 2017, 10, 410–417. [Google Scholar] [CrossRef]
- Hatada, K.; Hirata, K. Power assisting control for electric bicycles using an adaptive filter. In Proceedings of the IEEE International Conference on Industrial Technology (ICIT), Busan, Korea, 26 February–1 March 2014; pp. 51–54. [Google Scholar]
- Quintana-Duque, J.C.; Dahmen, T.; Saupe, D. Estimation of Torque Variation from Pedal Motion in Cycling. Int. J. Comput. Sci. Sport 2015, 14, 34–50. [Google Scholar]
- Spagnol, P.; Corno, M.; Savaresi, S.M. Pedaling torque reconstruction for half pedaling sensor. In Proceedings of the European Control Conference (ECC), Zurich, Switzerland, 17–19 July 2013; pp. 275–280. [Google Scholar]
- Capmal, S.; Vandewalle, H. Torque-velocity relationship during cycle ergometer sprints with and without toe clips. Eur. J. Appl. Physiol. Occup. Physiol. 1997, 79, 375–379. [Google Scholar] [CrossRef] [PubMed]
- Grasso, E.; Mandriota, R.; König, N.; Nienhaus, M. Analysis and Exploitation of the Star-Point Voltage of Synchronous Machines for Sensorless Operation. Energies 2019, 12, 4729. [Google Scholar] [CrossRef]
- Grasso, E.; Palmieri, M.; Mandriota, R.; Cupertino, F.; Nienhaus, M.; Kleen, S. Analysis and Application of the Direct Flux Control Sensorless Technique to Low-Power PMSMs. Energies 2020, 13, 1453. [Google Scholar] [CrossRef]
- Mandriota, R.; Palmieri, M.; Nienhaus, M.; Cupertino, F.; Grasso, E. Application of Star-Point Voltage Exploiting Sensorless Techniques to Low-Power PMSMs. In Proceedings of the IEEE 29th International Symposium on Industrial Electronics (ISIE), Delft, The Netherlands, 17–19 June 2020; pp. 1529–1534. [Google Scholar]
- König, N.; Grasso, E.; Schuhmacher, K.; Nienhaus, M. Parameter identification of star-connected PMSMs by means of a sensorless technique. In Proceedings of the Thirteenth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte Carlo, Monaco, 10–12 April 2018; pp. 1–7. [Google Scholar]
- Liu, K.; Zhu, Z.Q. Fast Determination of Moment of Inertia of Permanent Magnet Synchronous Machine Drives for Design of Speed Loop Regulator. IEEE Trans. Control. Syst. Technol. 2017, 25, 1816–1824. [Google Scholar] [CrossRef]
- Simon, D. Optimal State Estimation: Kalman, H Infinity, and Nonlinear Approaches; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).