Author Contributions
Conceptualization, A.P., H.W., S.K., K.W. and A.R.; software, H.W., S.K.; validation, A.P., H.W., S.K., K.W. and A.R.; writing—original draft preparation, A.P.; writing—review and editing, A.P., H.W. and S.K.; supervision, A.P. All authors have read and agreed to the published version of the manuscript.
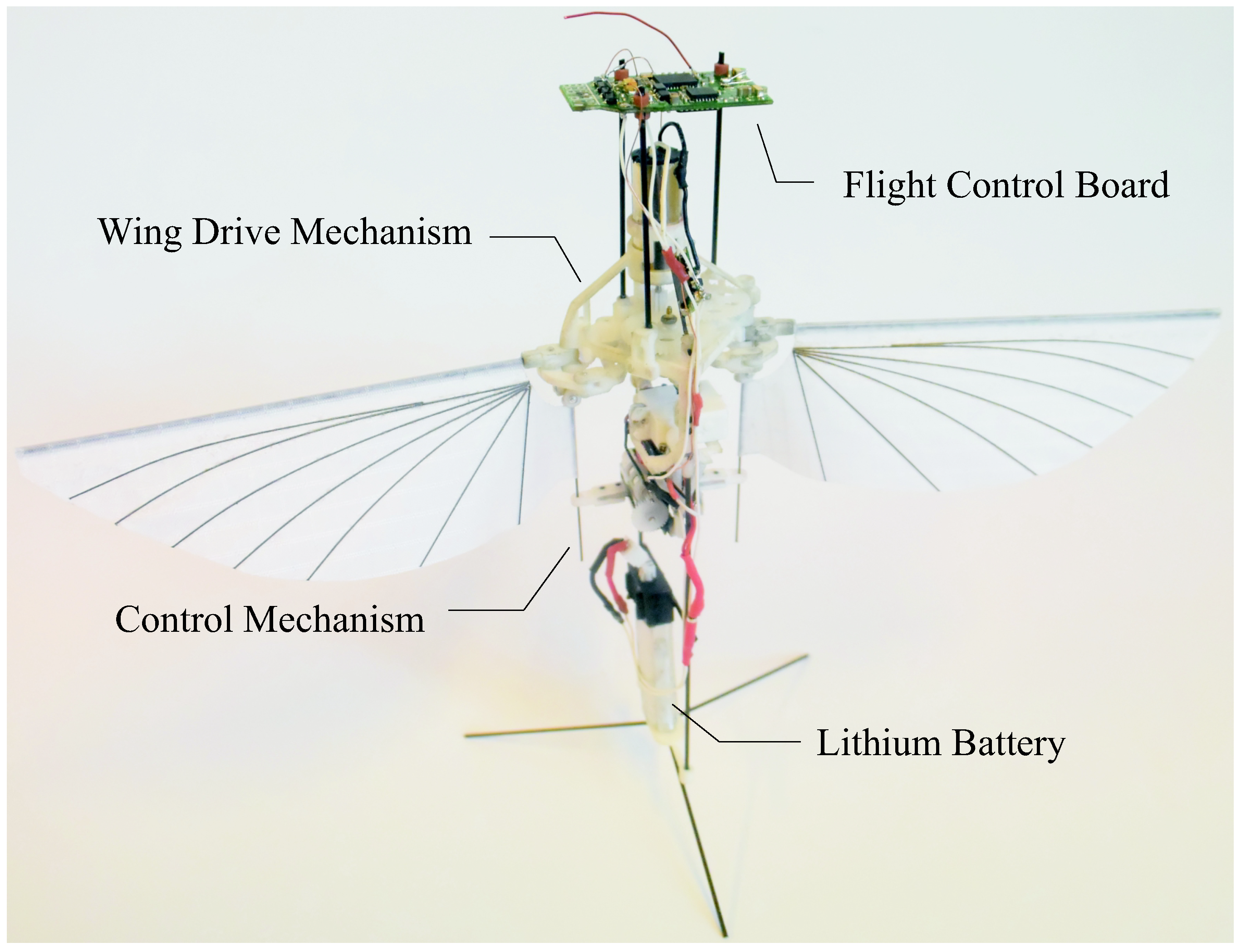
Figure 1.
The COLIBRI robot.
Figure 1.
The COLIBRI robot.
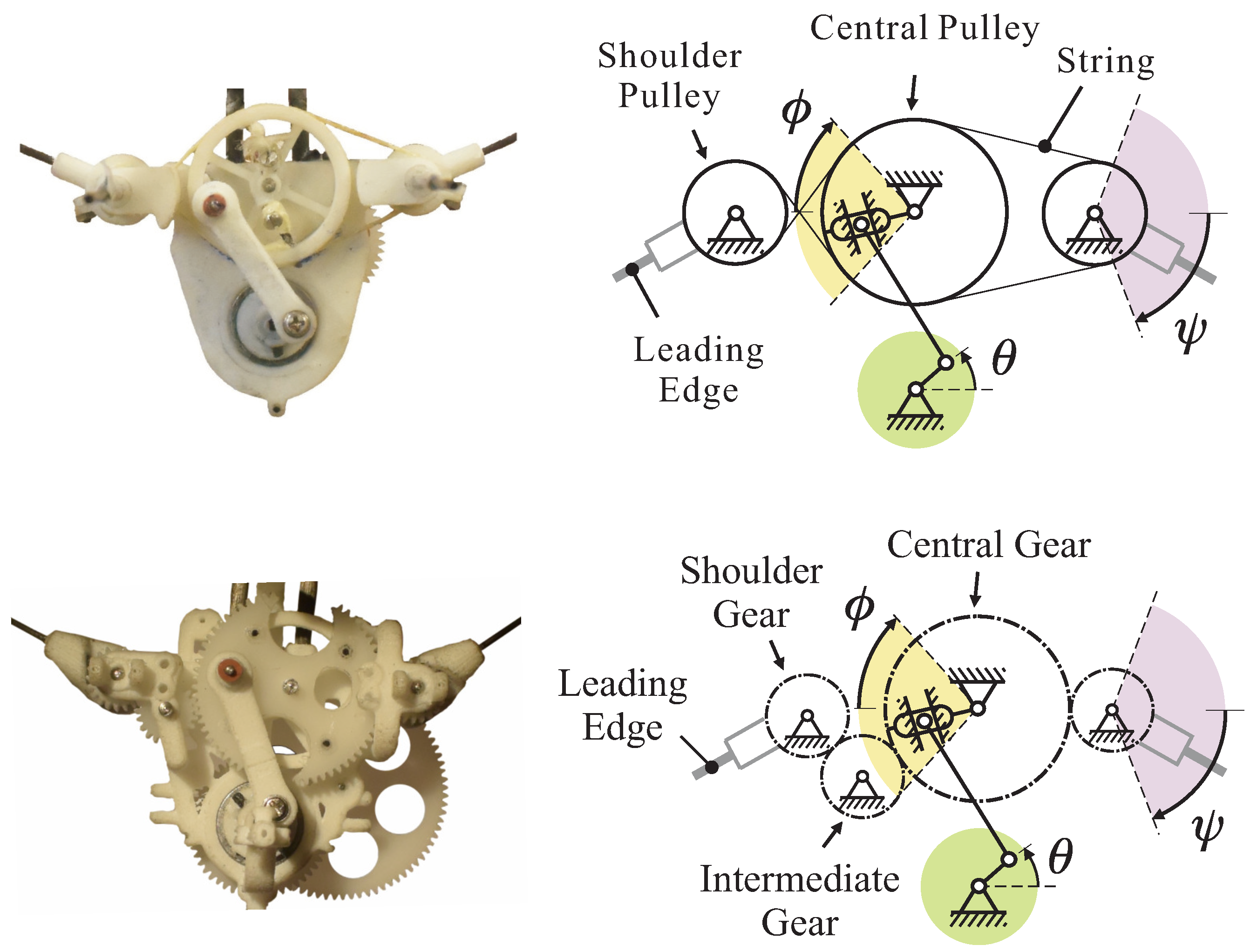
Figure 2.
Evolution of the transmission mechanism of the COLIBRI robot. Top: string transmission. Bottom: gear transmission.
Figure 2.
Evolution of the transmission mechanism of the COLIBRI robot. Top: string transmission. Bottom: gear transmission.
Figure 3.
Exploded view of the flapping mechanism with gear transmission of the COLIBRI robot.
Figure 3.
Exploded view of the flapping mechanism with gear transmission of the COLIBRI robot.
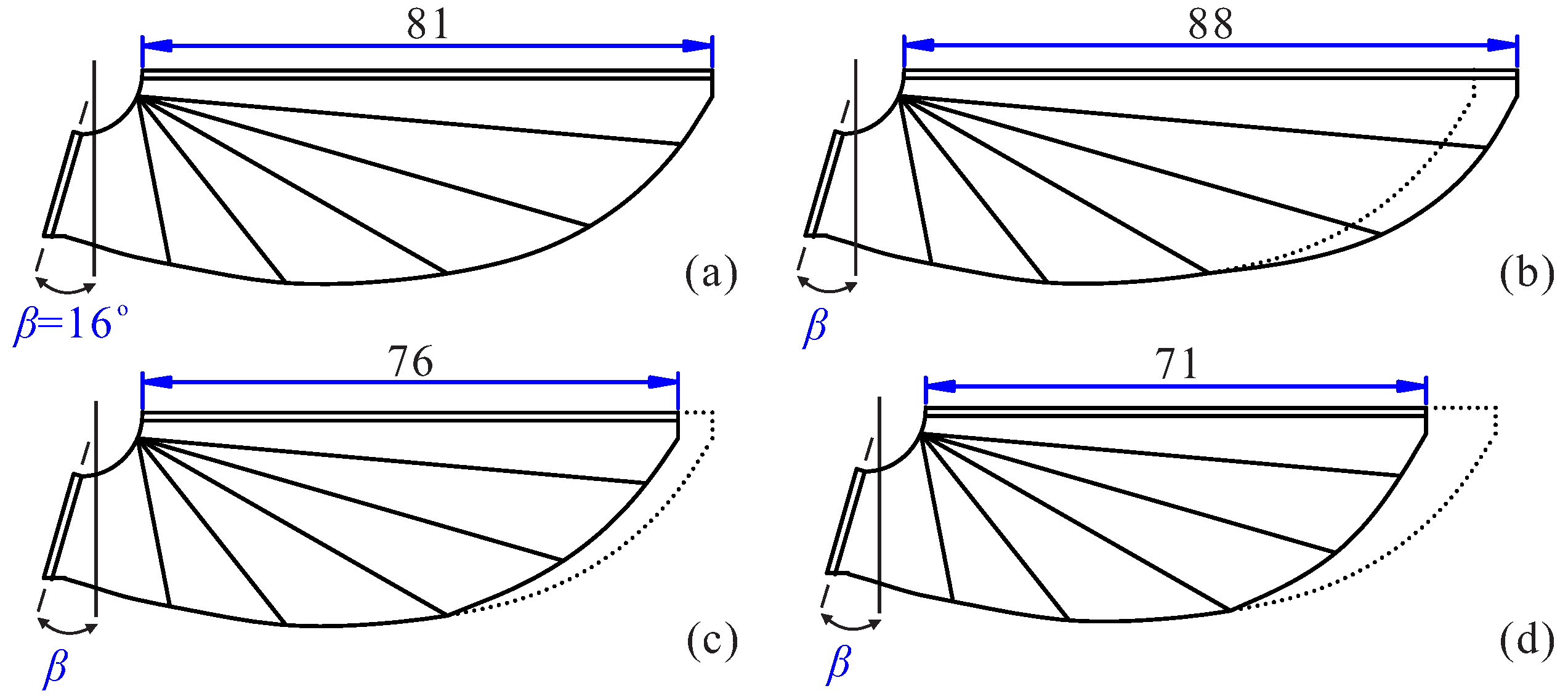
Figure 4.
Wings of various sizes, (a) 81 mm (nominal), (b) 88 mm, (c) 76 mm, (d) 71 mm. The nominal wing is represented in dotted lines.
Figure 4.
Wings of various sizes, (a) 81 mm (nominal), (b) 88 mm, (c) 76 mm, (d) 71 mm. The nominal wing is represented in dotted lines.
Figure 5.
Lift
L vs. flapping frequency
f for the various wings of
Figure 4.
Figure 5.
Lift
L vs. flapping frequency
f for the various wings of
Figure 4.
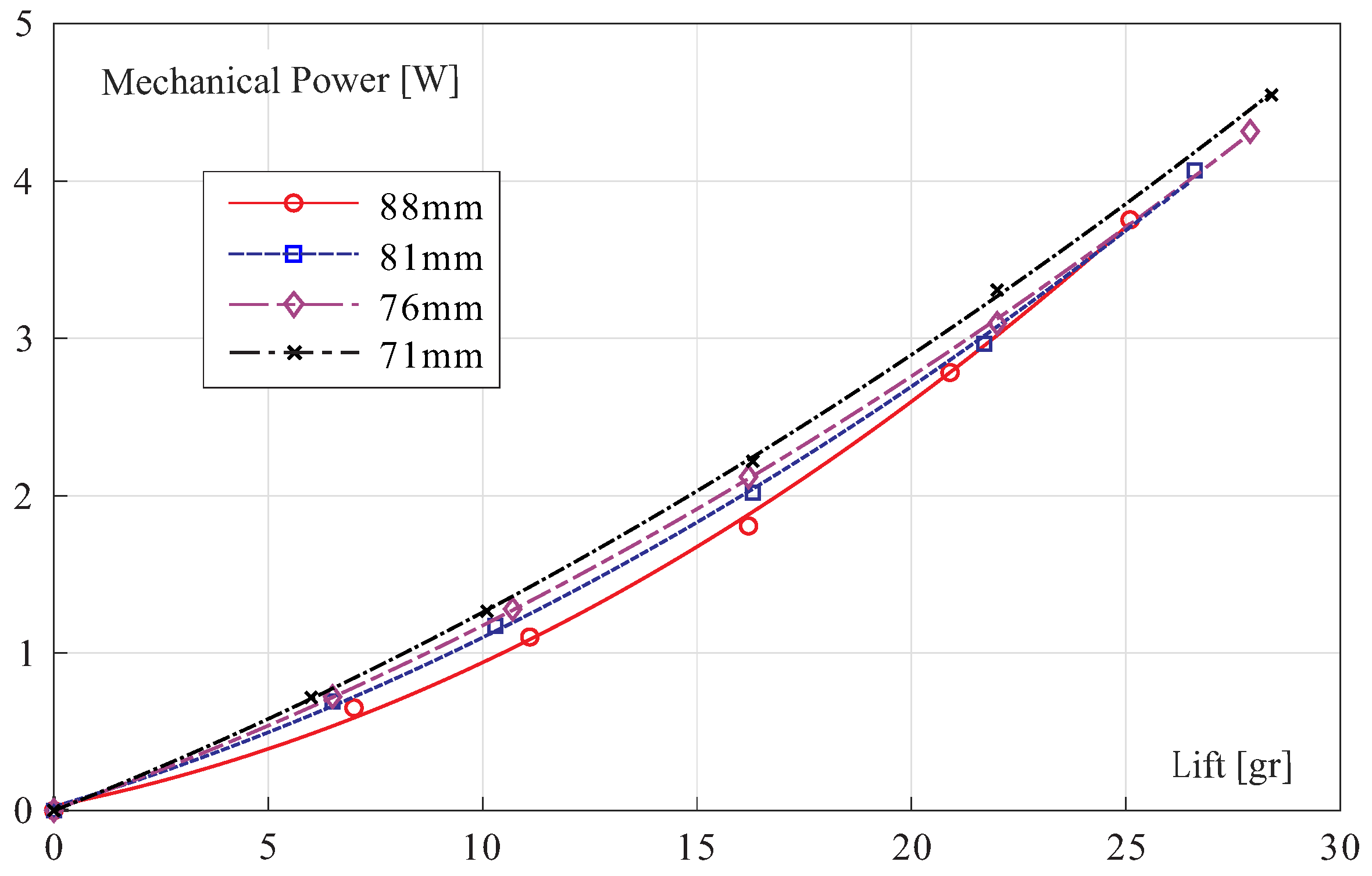
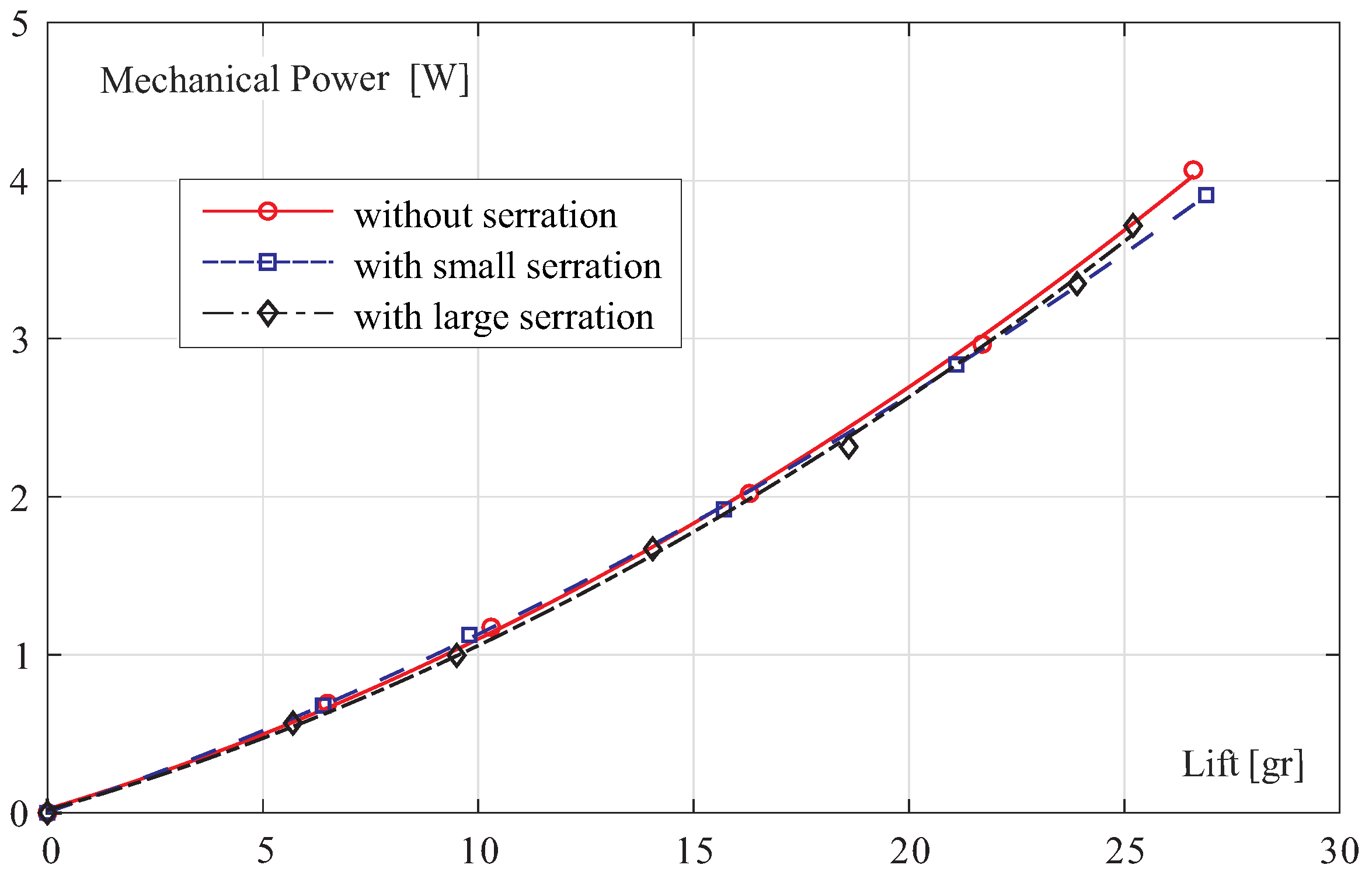
Figure 6.
Mechanical power
vs. lift
L for the wings of
Figure 4.
Figure 6.
Mechanical power
vs. lift
L for the wings of
Figure 4.
Figure 7.
Wings with trailing edge serration. (a) Hummingbird Chlorostilbon canivetii (source: Wikipedia). (b) Small serration. (c) Large serration. The nominal wing is in dotted line.
Figure 7.
Wings with trailing edge serration. (a) Hummingbird Chlorostilbon canivetii (source: Wikipedia). (b) Small serration. (c) Large serration. The nominal wing is in dotted line.
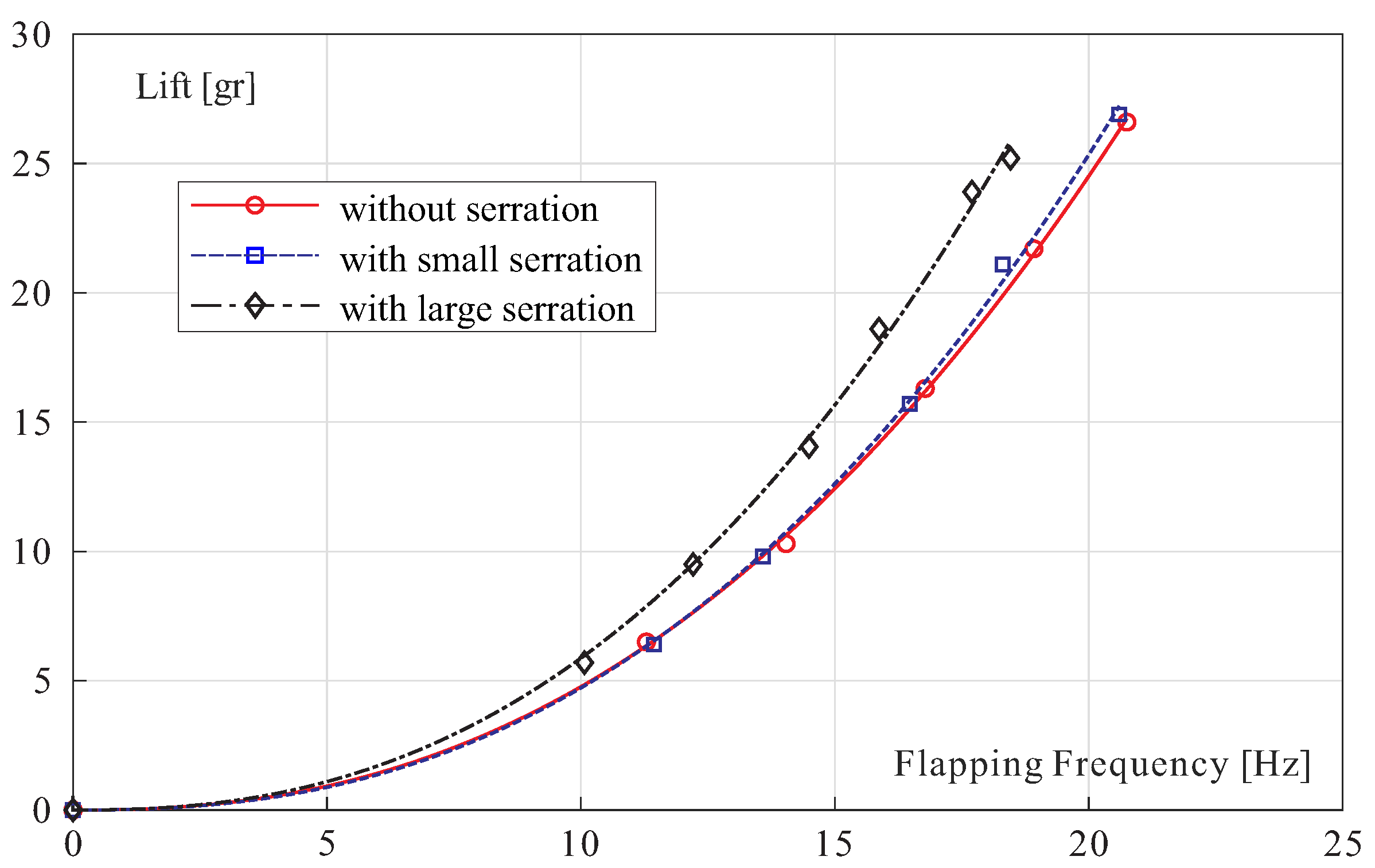
Figure 8.
Lift vs. flapping frequency for the wings with trailing edge serration.
Figure 8.
Lift vs. flapping frequency for the wings with trailing edge serration.
Figure 9.
Mechanical power vs. lift L for the wings with trailing edge serration.
Figure 9.
Mechanical power vs. lift L for the wings with trailing edge serration.
Figure 10.
Discharge curve of two batteries B2 in series for a discharge rate of 1.2 A (data from manufacturer). The dashed line is the best fit Shepherd model.
Figure 10.
Discharge curve of two batteries B2 in series for a discharge rate of 1.2 A (data from manufacturer). The dashed line is the best fit Shepherd model.
Figure 11.
22.8 gr. Discharge curve of two batteries B2 in series for a discharge rate of 1.07 A ( s) and 0.98 A ( s).
Figure 11.
22.8 gr. Discharge curve of two batteries B2 in series for a discharge rate of 1.07 A ( s) and 0.98 A ( s).
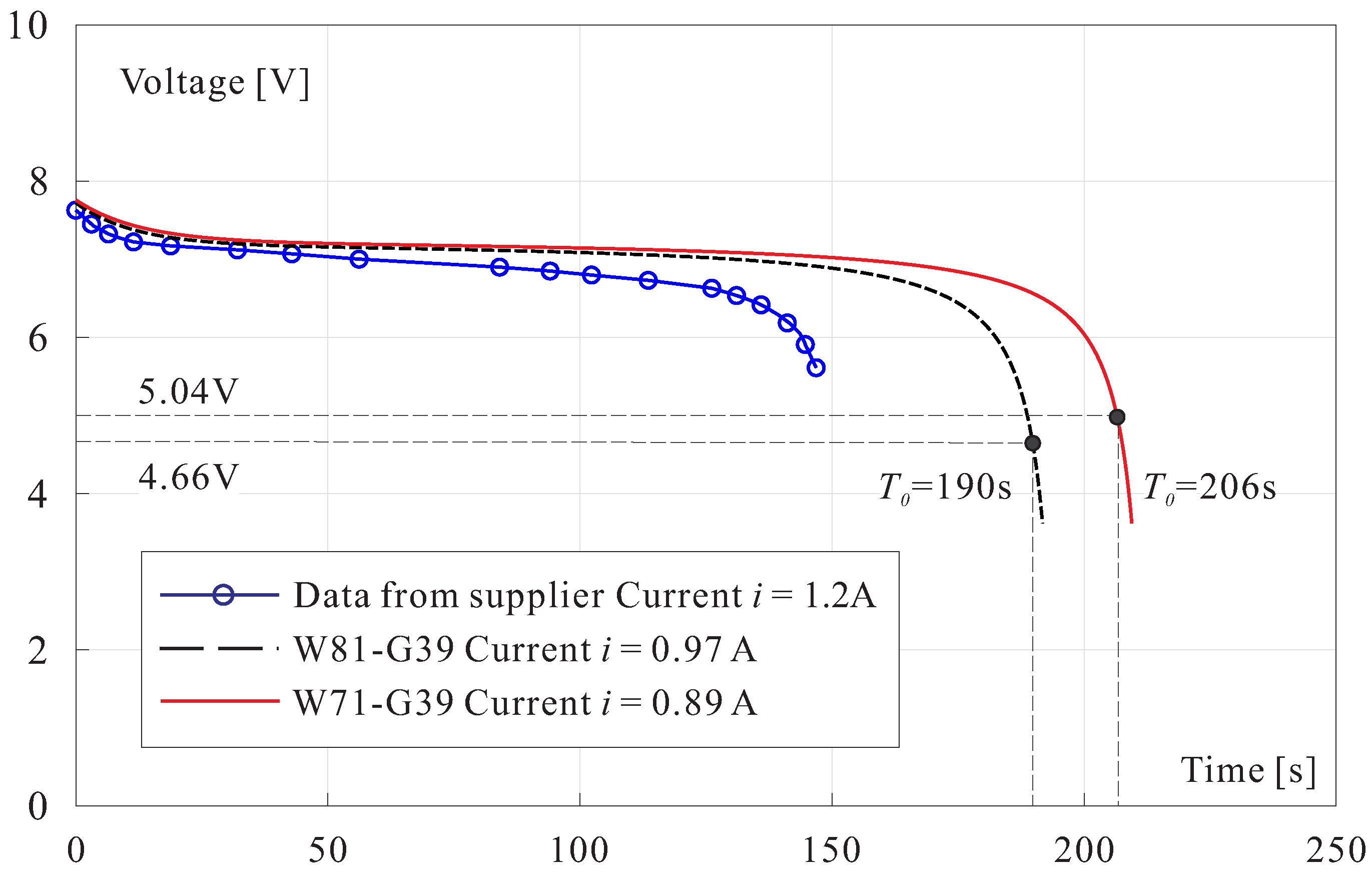
Figure 12.
20 gr. Discharge curve of two batteries B2 in series for a discharge rate of 0.97 A ( 190 s) and 0.89 A ( 206 s).
Figure 12.
20 gr. Discharge curve of two batteries B2 in series for a discharge rate of 0.97 A ( 190 s) and 0.89 A ( 206 s).
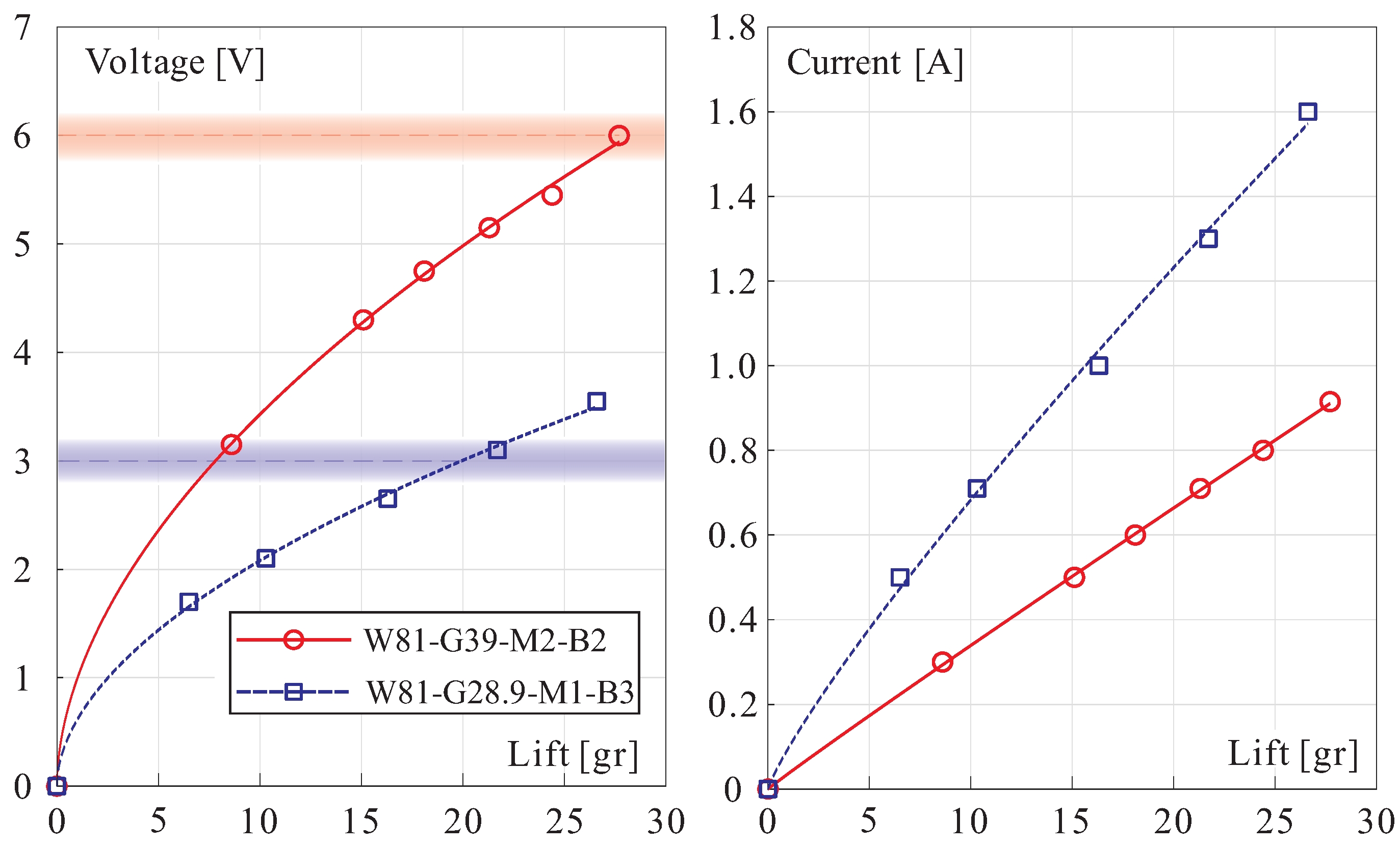
Figure 13.
Voltage vs. Lift (left) and Current vs. Lift (right) for two flight configurations (with a single battery B3 and two batteries B2 in series). The shaded areas correspond to the voltage limits.
Figure 13.
Voltage vs. Lift (left) and Current vs. Lift (right) for two flight configurations (with a single battery B3 and two batteries B2 in series). The shaded areas correspond to the voltage limits.
Figure 14.
Experimental set-up for the endurance test.
Figure 14.
Experimental set-up for the endurance test.
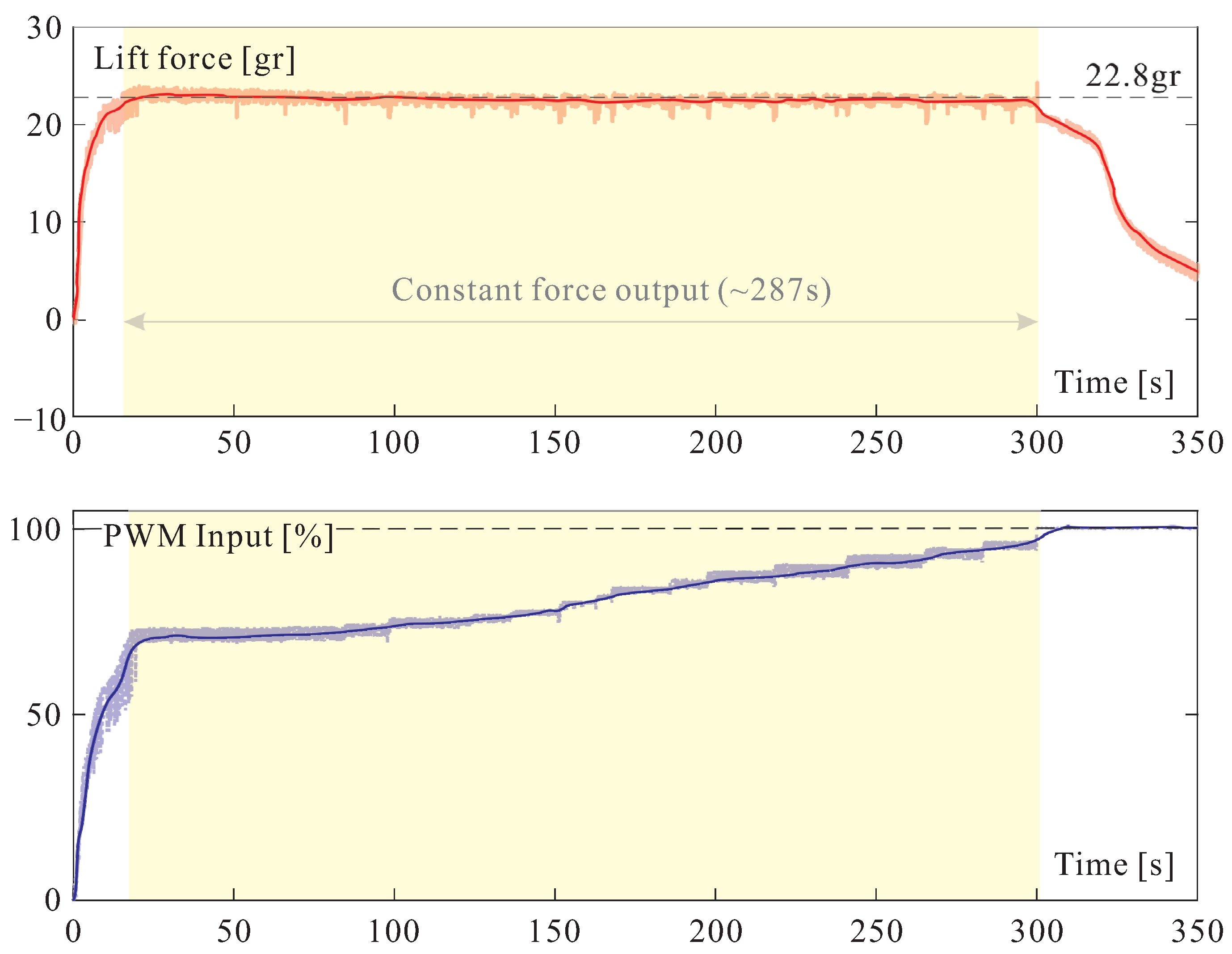
Figure 15.
Endurance experiment. Top: Time history of the lift force. Bottom: Time history of the duty factor of the PWM. The lift drops suddenly when reaches 100%.
Figure 15.
Endurance experiment. Top: Time history of the lift force. Bottom: Time history of the duty factor of the PWM. The lift drops suddenly when reaches 100%.
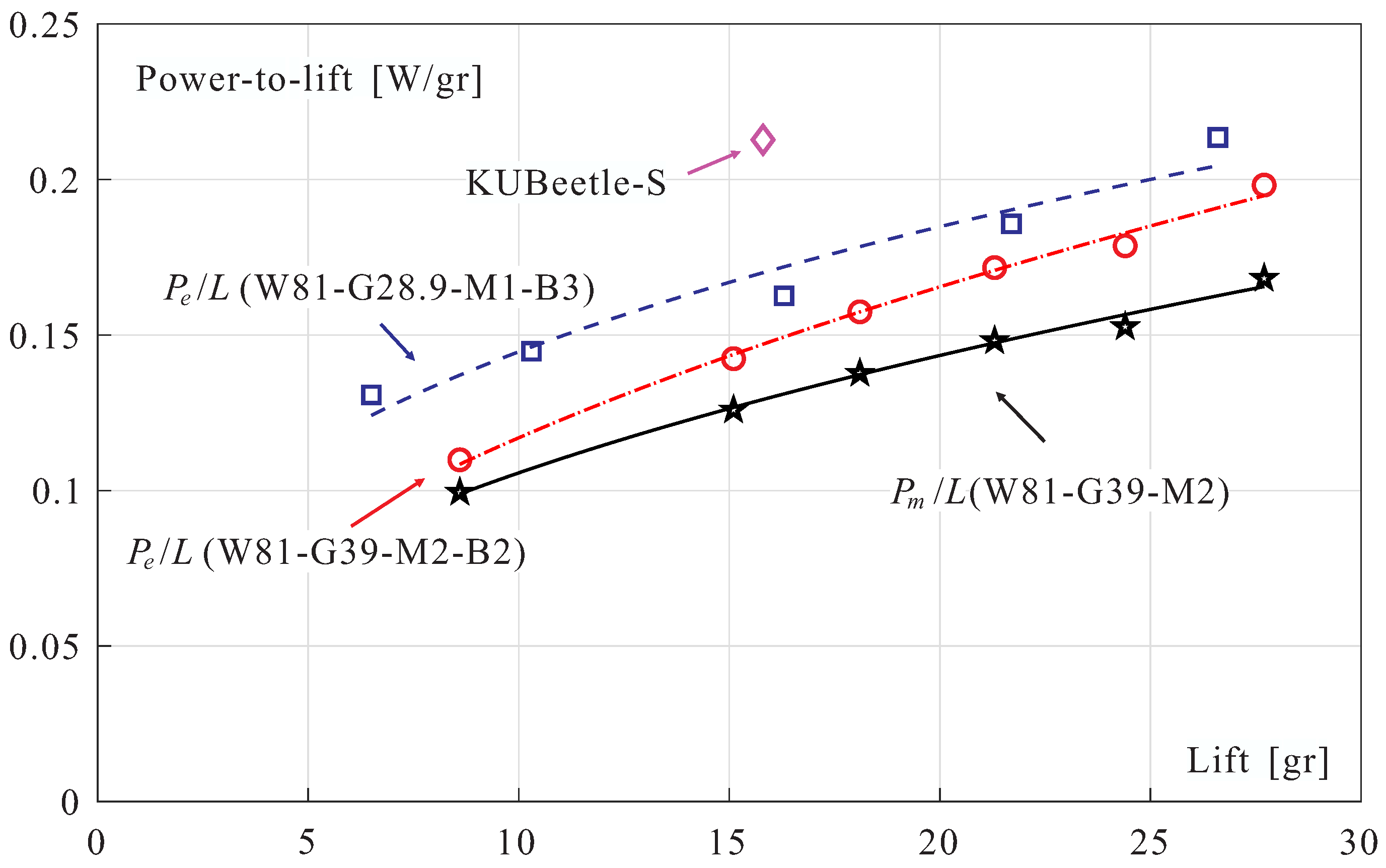
Figure 16.
Power-to-lift ratio vs. Lift. is the mechanical power and is the electrical power. The value of the KUBeetle-S project is given for comparison.
Figure 16.
Power-to-lift ratio vs. Lift. is the mechanical power and is the electrical power. The value of the KUBeetle-S project is given for comparison.
Table 1.
Weight breakdown excluding the battery. The motors M1 and M2 refer to Table 3.
Table 1.
Weight breakdown excluding the battery. The motors M1 and M2 refer to Table 3.
| Component | Weight [gr] |
|---|
| Flapping mechanism | 7.2 |
| Attitude control servos | 3.8 |
| Motor | 3.9 (M1) 3.6 (M2) |
| Avionics (including Bluetooth) | 2 |
| Carbon rods | 0.5 |
| Lines and connectors | 1.2 |
| Total | 18.6 (M1) 18.3 (M2) |
Table 2.
Characteristics of the batteries.
Table 2.
Characteristics of the batteries.
| N° | Reference | Capacity | Weight | Discharge Rate | Max. Current |
|---|
| [mAh] | [gr] | [A] |
|---|
| B1 | Zippy LiPo | 50 | 1.51 | 20C | 1 |
| B2 | Hyperion G5 | 70 | 2.26 * | 25C–30C | 1.75–2.1 |
| LiPo | (50C burst) |
| B3 | Hyperion G5 | 100 | 3.00 ** | 25C–30C | 2.5–3 |
| LiPo | (50C burst) |
| B4 | Eastfire LiPo | 100 | 3.01 | 30C | 3 |
Table 3.
Characteristics of the motors considered in this study.
Table 3.
Characteristics of the motors considered in this study.
| N° | Producer | Weight [gr] | | V·s] | [] |
|---|
| M1 | Chaoli | 3.87 | 0.63 | 6.75 | 0.0138 |
| M2 | Micron Wings | 3.59 | 1.2 | 8.44 | 0.0143 |
| M3 | Songyang | 3.56 | 0.76 | 7.09 | 0.0151 |
| M4 | Micron Wings | 2.88 | 0.87 | 5.90 | 0.025 |
Table 4.
Single battery B3 and Motor M1: Influence of the wing size and the gearbox. Flapping frequency f, mechanical power , current I, voltage e, heat power and total electric power . The lift is 21.6 gr in all cases.
Table 4.
Single battery B3 and Motor M1: Influence of the wing size and the gearbox. Flapping frequency f, mechanical power , current I, voltage e, heat power and total electric power . The lift is 21.6 gr in all cases.
| Wing-Gearbox | f [Hz] | [W] | I [A] | e [V] | [W] | [W] |
|---|
| W81-G28.9 | 18.96 | 2.84 | 1.22 | 3.10 | 0.94 | 3.78 |
| W81-G23.1 | 18.96 | 2.84 | 1.53 | 2.82 | 1.47 | 4.31 |
| W88-G28.9 | 17.75 | 2.84 | 1.31 | 3.00 | 1.08 | 3.93 |
| W88-G23.1 | 17.75 | 2.84 | 1.63 | 2.77 | 1.67 | 4.51 |
Table 5.
Two batteries B2 in series and Motor M2: Influence of the wing size and the gearbox. Flapping frequency f, mechanical power , current I, voltage e, heat power and total electric power . The lift is gr in all cases.
Table 5.
Two batteries B2 in series and Motor M2: Influence of the wing size and the gearbox. Flapping frequency f, mechanical power , current I, voltage e, heat power and total electric power . The lift is gr in all cases.
| Wing-Gearbox | f [Hz] | [W] | I [A] | e [V] | [W] | [W] |
|---|
| W81-G28.9 | 19.4 | 3.23 | 1.09 | 4.28 | 1.42 | 4.66 |
| W81-G39 | 19.4 | 3.23 | 0.82 | 4.99 | 0.80 | 4.03 |
| W71-G28.9 | 21.8 | 3.23 | 0.97 | 4.5 | 1.13 | 4.36 |
| W71-G39 | 21.8 | 3.23 | 0.73 | 5.39 | 0.62 | 3.86 |
Table 6.
Two batteries B2 in series and Motor M2. Lift: 22.8 gr. I is the motor current and i is the battery discharge current. T is the estimated flight time.
Table 6.
Two batteries B2 in series and Motor M2. Lift: 22.8 gr. I is the motor current and i is the battery discharge current. T is the estimated flight time.
| Wing-Gearbox | [W] | I [A] | e [V] | i [A] | [s] | T [s] |
|---|
| W81-G39 | 0.80 | 0.82 | 4.99 | 1.07 | 170 | 237 |
| W71-G39 | 0.62 | 0.73 | 5.39 | 0.98 | 185 | 241 |
Table 7.
Two batteries B2 in series and Motor M2. Lift: 20 gr. I is the motor current and i is the battery discharge current. T is the estimated flight time.
Table 7.
Two batteries B2 in series and Motor M2. Lift: 20 gr. I is the motor current and i is the battery discharge current. T is the estimated flight time.
| Wing-Gearbox | [W] | I [A] | e [V] | i [A] | [s] | T [s] |
|---|
| W81-G39 | 0.62 | 0.72 | 4.66 | 0.97 | 190 | 285 |
| W71-G39 | 0.49 | 0.64 | 5.04 | 0.89 | 206 | 288 |