Abstract
An online algebraic estimation technique for natural and forcing frequencies for a class of uncertain and lumped-parameter vibrating mechanical systems with n degrees of freedom is described. In general, realistic vibrating systems can be affected by unknown exogenous excitation forces with multiple and independent frequency harmonic components. Hence, natural frequencies as well as excitation force frequencies can be simultaneously computed from an algebraic approach into a small interval of time during online operation of the mechanical system. Measurements of an available output signal, associated with some specific degree of freedom, are only required for frequency estimation in time-domain. Information on mass, stiffness and damping matrices are not necessary for multifrequency estimation algorithms. Some analytical, numerical and experimental results on a cantilever Euler–Bernoulli beam are described to show and validate the acceptable estimation of multiple frequencies in forced multiple degrees of freedom vibrating systems.
1. Introduction
Several techniques for mainly offline modal parameter identification on vibrating mechanical systems have been proposed [1,2,3,4,5]. For instance, Fast Fourier Transform (FFT), spectral estimation, Kalman filtering, linear regression, least squares and zero-crossing techniques have been applied for estimation of frequency parameters in oscillating signals [6,7,8]. Some popular experimental modal analysis techniques based on Frequency Response Functions (FRF) are peak picking, mode-picking, circle-fit and curve fitting [1,2]. The wave finite element method can be also used to compute offline the natural frequencies of composite structures, which are widely used in automotive and aerospace industry [9]. The well-known FFT constitutes a standard offline method for multifrequency estimation as well. Nevertheless, the FFT is not suitable for implementation of adaptive or active vibration control schemes [10]. The FFT demands at least a sampling rate of the double of the frequencies in vibrating signals [11]. Moreover, FFT presents numerical errors depending on the information extracted from the measured signal during transient analysis, which makes necessary the application of additional filtering techniques. Thus, a measurement window of 12 cycles is commonly recommended to obtain an accurate parameter estimation using the discrete Fourier Transform for harmonic control in 60 Hz power systems, where harmonics are sinusoidal components with integer multiples of the known fundamental frequency [12]. A fundamental time versus frequency tradeoff is required for Fourier Transform-based algorithms, with a consequent observation time equals to at least one to ten waveform cycles, as described in [12].
In vibrating systems, parameter estimation can be used for detection of possible structural damage [13,14]. Damages in structural components may cause inherent changes on the stiffness distribution [14]. Changes in natural frequencies of damaged structures can be then exhibited. In fact, wear, fatigue and cracks are the most common defects in mechanical structures, and their opportune detection represents a major issue to anticipate failures [15]. In this regard, damage detection (cracks) in cantilever shaft beams has been carried out using information about natural frequencies of transverse vibrations [16]. Here, it has been concluded that changes on natural frequencies depend on the crack location and dimensions [16]. Similarly, changes on natural frequencies of beam-like structures due to presence of cracks has been discussed in the literature [17]. Thus, the fast estimation of natural frequencies represents a relevant issue to detect potential failures and quantify the remaining useful life on many mechanical structures. Moreover, real-time information on natural frequencies and/or excitation force frequencies can be used to implement efficient vibration control schemes in a wide variety of vibration engineering systems [18,19,20]. In this context, active vibration control on flexible smart structures, based on modal control techniques, requires information on the existing natural frequencies with a reasonable accuracy [20].
Online algebraic frequency estimation for active vibration control tasks has been introduced by the authors in [21]. Online estimation of natural frequencies has been also used for adaptive resonant vibration control in a flexible cantilever beam structure in [10]. Furthermore, online monitoring of natural frequencies of flexible structures can be used to readjust vibration control parameters, where an online estimator of a natural frequency in a flexible-link manipulator has been presented in [22].
Smart structures are mechanical and kinematic systems, which are partially actuated from a dynamical point of view [23]. In recent years, these smart structures have gained ground in a wide variety of engineering fields [18], ranging from civil structures, such as bridges and buildings, vehicles, such as automobiles, aircrafts and ships, heavy construction cranes [24] and oil rigs up to those of spatial applications such as flexible-link robots [25]. The aim of providing these systems with proper actuators is to improve their dynamic performance and robustness against external disturbances such as wind forces, road imperfections, seismic motions amidst the ever changing loading and operating conditions often imposed by the nature of their tasks [18,23]. In these cases, not only the knowledge of their natural frequencies but the frequency content of the external disturbances are required to design effective vibration control schemes that allow these systems to perform their tasks with accuracy, efficiency and safety. Indeed, the knowledge of the natural frequencies on a smart structure makes it possible for the control system to adapt its response, such that, when the natural frequencies of some of the plant modes fall within the bandwidth of its actuators, an active vibration control scheme may be turned-on in order to cancel or attenuate residual vibrations. However, when these natural frequencies change and exceed the bandwidth of the actuators, the strategy may be reconfigured to implement semiactive or passive vibration control to inject damping with the same actuators. For instance, in flexible-link robots, fast rotations of the flexible links and time-varying loading conditions often induce changes in the boundary conditions of these systems with distributed mass and stiffness, which in turns makes the natural frequencies of its links to abruptly change [26]. Thus, critical natural frequencies of flexible links are key parameters for the synthesis of an effective control system design [27,28]. In general, a precise knowledge of the so-called modal parameters allows the proper selection, location and tuning of actuators (e.g., electrical motors, piezoelectric patches, electromagnetic and hydraulic shakers, magnetorheological dampers) [25,29]. Therefore, a reasonable knowledge of a model and parameters of a mechanical structure and exogenous is a crucial part for analysis, design and control of modern smart structures.
This paper deals with the online parameter identification problem of both natural frequencies and exogenous excitation force frequencies into an operating bandwidth of interest for lumped-parameter vibrating mechanical systems of n degrees of freedom. The online algebraic parameter identification approach is based on operational calculus, differential algebra and module theory [30,31]. In contrast with other parameter identification techniques, in this multifrequency estimation approach natural and excitation frequencies are computed from an algebraic approach, online, in time-domain and using information of some simple and measurable signal. The main challenge is that, all system parameters are assumed to be completely unknown and the information is estimated from the dynamics in real-time oscillatory signals.
The main contributions of the present work are the following:
- A novel algebraic technique for online estimation in time-domain of multiple natural frequencies for an important class of forced and uncertain lumped-parameter vibrating mechanical systems of n degrees of freedom is proposed.
- Closed-form algebraic formulas to simultaneously estimate online multiple frequencies of possible exogenous excitation forces affecting a vibrating system are obtained.
- Compared with other parameter identification methods, the introduced multifrequency estimation approach is performed in time-domain, algebraically and online, into a small interval of time. System parameters of mass, stiffness and damping matrices are assumed to be completely unknown.
- Measurements of available output signals, associated with some degree of freedom, are only required. Then, multifrequency estimation can be carried out using measurements of either position, velocity or acceleration.
The work is organized as follows. The class of Multiple Degrees-Of-Freedom (MDOF) forced vibrating mechanical systems considered for multiple frequency estimation synthesis is described in Section 2. Closed-form algebraic formulas to obtain online estimates of natural and excitation frequencies are described in Section 3. Some analytical, numerical and experimental results to validate the effectiveness of the algebraic estimation of multiple frequencies in considerably disturbed MDOF vibrating systems are presented in Section 4. In general, the results reveal that the proposed estimation technique represents a very good and effective alternative to compute natural and excitation frequencies on uncertain and forced MDOF vibrating mechanical systems. Some conclusions and future research are finally described in Section 5.
2. Description of the MDOF Forced Vibrating Mechanical System
It is considered the online and simultaneous estimation of natural frequencies and excitation force frequencies occurring on lightly damped vibrating mechanical systems of n degrees of freedom. In general, this class of MDOF mechanical system can be described as follows
where is the generalized displacement vector and stands for an excitation force vector, whose values contains multiple harmonic components. As usual, are velocity and acceleration vectors, respectively. The matrices denote mass, damping and stiffness matrices described by
Moreover, the components in the excitation force can be described as a sum of m arbitrary, distinct and unknown frequency harmonic terms as follows
where , and are amplitudes, excitation frequencies and phase angles, respectively.
The vibrating system (1) can be also described in terms of modal (principal) coordinates (see, e.g., [1,2] and references therein) as follows
where ; , and are components of the modal matrix
The general model (1) has been widely used to describe forced oscillations for a large class of engineering systems. The mathematical model (1) is commonly adopted for vibration analysis and control [20,32]. In fact, vibrating behavior of rotating machinery, building and bridge structures, machine tools, dynamic vibration absorbers, cranes and flexible-link robots can be modeled, under certain operating conditions, as the MDOF mechanical system (1) [25,31,33,34,35,36].
Furthermore, some continuous vibrating mechanical systems (e.g., beams, plates, general structures) can be also approximated, into a specific interest bandwidth, by application of the well-known Rayleigh expansion theorem, modal analysis theory or finite element methods with a finite MDOF mechanical system (1) [1,2,32,37].
3. Algebraic Estimation of Natural and Forcing Frequencies
The proposed online algebraic estimation technique of natural and excitation forcing frequencies on MDOF vibrating systems, into an interest bandwidth, will be based on available information on some measurable output signal (e.g., position, velocity or acceleration). Moreover, the system parameters of mass, damping and stiffness matrices and excitation force vector are assumed to be unknown.
The presented online estimation approach considers that all vibration modes of interest in the vibrating system are excited by external forces or by changes in its initial conditions. Information about the natural frequencies of the vibrating system can be then extracted from the measured output signal. Estimation of natural frequencies can be then computed for operating scenarios in which measurements of free vibration responses are only available.
The frequency estimation is based on a perspective of oscillating signal modeling. In this fashion, harmonic excitation force components (3) can be modeled into a small interval of time and certain initial conditions as
with and . Then, solution of Equation (5) yields the harmonic components of the excitation force vector as follows
with
where and stand for unknown initial conditions of the dynamic model (5) at . Therefore, the excitation forces can be expressed as
The displacements , , for a lightly damped vibrating mechanical system (i.e., ) can be approximated as
where is the k-th natural frequency and is the j-th forcing excitation frequency to be simultaneously estimated. Similarly, from Equation (8) output displacement signals can be modeled by differential equations as
where the superscript notation is used to denote time derivatives of order . Then, the solution of the dynamic signal model (9) can be used to reconstruct harmonic terms of measured signals for certain initial conditions into an interval of time. It is important to remark that the system parameter information is contained into the coefficients , for .
Note that, by defining either or , the velocity and acceleration signals can be also modeled by Equation (9). Therefore, the proposed estimation technique can be also implemented for operational scenarios where measurements of velocity or acceleration may be preferred.
Now, from Equation (9) the natural and excitation frequencies are given by the imaginary roots of the polynomial
Nevertheless, parameters and initial condition of the vibrating signal model (9) are unknown. Thence, for synthesis of the multiple frequency estimation scheme, Equation (9) is first multiplied by to eliminate dependence on unknown initial conditions. Resulting expressions are then integrated times with respect to time to avoid information of time derivatives of measured signals up to -th order:
with
where and is the starting time to perform the estimation process. Here, the notation is used to stand for iterated integrals of the form . Henceforth, the superscript i is used to denote coefficient, matrix or vector associated with some measurable output variable used for natural and excitation frequency estimation.
Repeating more integrations, with respect to time, of the Equation (11), leads to the systems of linear equations
where is the vector of system parameters to be estimated, and are, respectively, and matrices given by
The components and are given by
with and .
The estimated parameters are computed as follows
Then, corresponding coefficients can be algebraically computed, into some short window of time, without singularities, by the estimators
where , is the gain for a first order invariant and smoothing filter. Here, the notation is used for estimated value and represents absolute value.
Therefore, algebraic formulas to simultaneously compute the natural frequencies and excitation frequencies are proposed as follows
where and are the roots of the characteristic polynomial given by
where the asterisk denotes complex conjugate.
4. Numerical and Experimental Validation
4.1. Numerical Results: 3 DOF Mass-Spring System
The proposed algebraic estimation technique of natural and excitation frequencies is validated on 3 DOF lightly damped vibrating mechanical system submitted to uncertain and multiple frequency disturbances.
The system parameters used as mass, viscous damping and stiffness of the forced mechanical system are detailed in Table 1.

Table 1.
Parameters of the 3 Multiple Degrees-Of-Freedom (DOF) forced vibrating mechanical system.
For reference and further evaluation, the natural frequencies of the oscillating system to be estimated are numerically computed as rad/s, rad/s and rad/s.
For application of the proposed algorithms, the algebraic estimation assumes that all the system parameters and excitation forces are unknown. Thus, multiple frequency estimation should be performed by using exclusive information on some specific measurable output signal.
The vibrating 3 DOF mechanical system dynamics with lumped parameters used for numerical estimation assessment purposes is governed by
with excitation forces
Therefore, three different, low and high frequencies contained into the excitation forces (19) to be estimated are rad/s, rad/s and rad/s.
In numerical tests, measurements of the position variable were only used. However, any measurable output signal can be employed to perform the proposed online algebraic estimation technique.
An effective and fast estimation of the three natural frequencies is verified in Figure 1. Similarly, in Figure 2 is depicted a satisfactory algebraic estimation of the three components with low and high excitation frequencies, that is, with multiple and arbitrary harmonics. It is important to note that, for numerical implementations, fifth-order Runge–Kutta methods with fixed small step time of 0.1 ms were used for computation of the natural and forcing frequencies before 0.5 s.
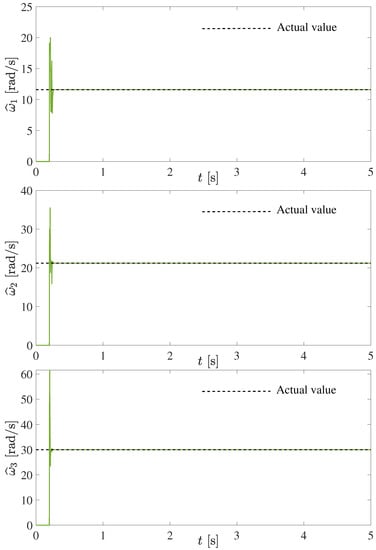
Figure 1.
Online algebraic estimation of the three natural frequencies for the 3 DOF vibrating mechanical system (18).
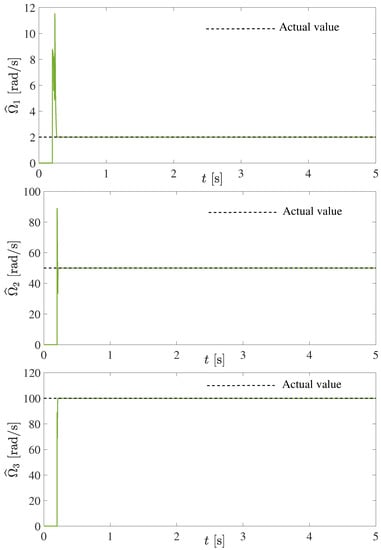
Figure 2.
Online algebraic estimation of the three excitation frequencies for the 3 DOF vibrating mechanical system (18).
Clearly, the numerical results for the case of this undamped 3 DOF mechanical system, submitted to forces containing up to three different harmonics, are certainly effective, fast and acceptable.
4.2. Experimental Results: A Cantilever Euler–Bernoulli Beam
The dynamic performance of the proposed estimation technique was evaluated on a distributed parameter system, that is, a cantilever Euler–Bernoulli beam with base excitation (shaker). The experimental setup is shown in Figure 3. This mechanical system consists of an instrumented aluminum beam (with strain gauge and accelerometer), whose physical dimensions are given in Table 2.

Figure 3.
Experimental setup of the cantilever beam submitted to forces with multiple excitation frequencies.

Table 2.
Specifications of the cantilever beam.
Note that a cantilever beam represents a flexible vibrating mechanical system, with distributed parameters of mass, stiffness and damping. In fact, distributed parameter systems have an infinite number of DOF and natural frequencies, which are modeled by partial differential equations [32,37].
In this case study, the algebraic estimation technique was performed to algebraically compute approximate values for the first three natural frequencies. The dynamics associated with higher order vibration modes were then considered as disturbances for evaluation of the robustness of the proposed estimation techniques. Moreover, unknown damping parameters were also neglected in the online and multifrequency estimation. Nevertheless, more frequencies can be considered in the estimation approach, according to a specific bandwidth, operating conditions and type of application.
The dynamic behavior of the cantilever beam can be numerically approximated by using the finite element methods with clamped-free boundary conditions into a certain frequency range. The finite element method was then used to compute the first three natural frequencies. Thus, the beam was discretized in 10 elements and 11 nodes, where each node has 2 DOF (i.e., lateral and angular displacements). The mass of the accelerometer was introduced to the finite element model by means of a concentrated mass of 0.050 kg at the node closest to the free-end of the beam. Applying the respective boundary conditions and by means of the solution of the eigenproblem, the natural frequencies of the first three modes of vibration were numerically obtained as: , and Hz. Moreover, the numerical model and its modal parameters associated with the cantilever beam were validated by means of experimental modal analysis techniques (see, e.g., [2]). Thus, the so-called Peak Picking technique was implemented to obtain offline approximate natural frequencies and modal dampings. The experimental Frequency Response Function (FRF) of the cantilever beam is shown in Figure 4 and its approximate modal parameters for the first three mode-shapes are reported in Table 3.
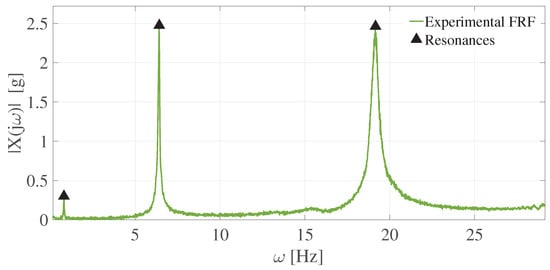
Figure 4.
Experimental Frequency Response Functions (FRF) of the cantilever beam for the first three mode-shapes.

Table 3.
Modal parameters of the cantilever beam obtained with Peak Picking techniques.
For online estimation purposes of multiple natural and excitation frequencies, the flexible structure was additionally perturbed close to the clamping and also at a middle point at the same time by two piezoelectric patch actuators mounted on the beam, as shown in Figure 3. In addition, a strain gauge was cemented at a point near to the physical clamping, in order to take precise strain measurements. The experimental setup features a MEMS accelerometer, attached to the free-end of the beam, which is used to get acceleration measurements. The data acquisition, signals processing and generation of the multiple frequency excitation forces are depicted in the schematic diagram Figure 5. The electrical signals were conditioned for the piezoelectric patch actuators (perturbations) and the electromagnetic shaker (base excitation) by a high voltage and a high current amplifier, respectively.
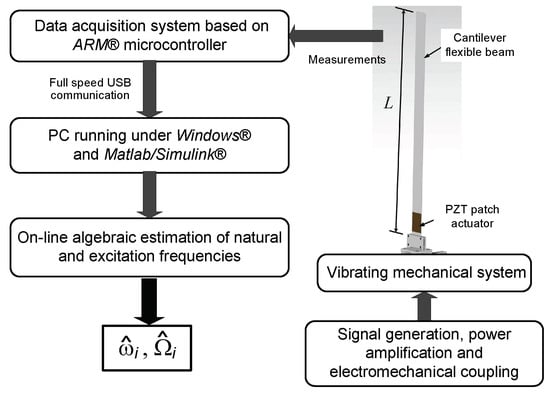
Figure 5.
Schematic diagram of the signal generation and data acquisition system for online algebraic identification.
The objective of this experiment was to estimate, in time domain and online, the first three natural frequencies as well as the three excitation frequencies corresponding to exogenous disturbance forces applied on the cantilever beam. In addition to the three first natural frequencies of the beam, the excitation force frequencies to be estimated online are rad/s (0.318 Hz), rad/s (7.96 Hz) and rad/s (15.91 Hz). The acceleration signal measurements at the free-end of the cantilever beam were used for application of the proposed algebraic frequency estimation.
The experimental results of the online algebraic estimation of the first three natural frequencies of the beam are shown in Figure 6. Moreover, the algebraic estimation of the three exogenous excitation frequencies is depicted in Figure 7. Thus, as shown in Table 4, reasonable expected estimation errors are obtained for the first three natural and excitation frequencies on the cantilever beam, which is approximately described by a lumped-parameter model. These are result of the filtering of low frequencies inherent to the data acquisition system as well as to the approximate discretization and implementations of numerical integrators. In general, all the results are also fast and effective.
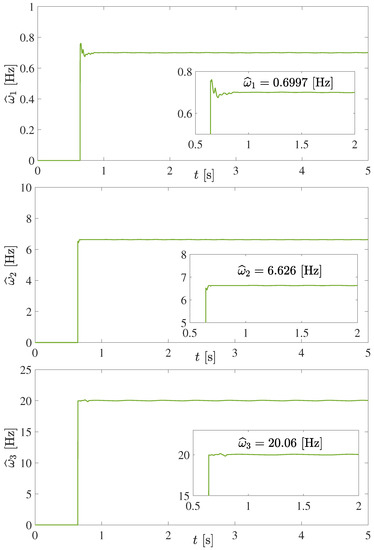
Figure 6.
Online algebraic estimation of the first three natural frequencies of the distributed-parameter system.
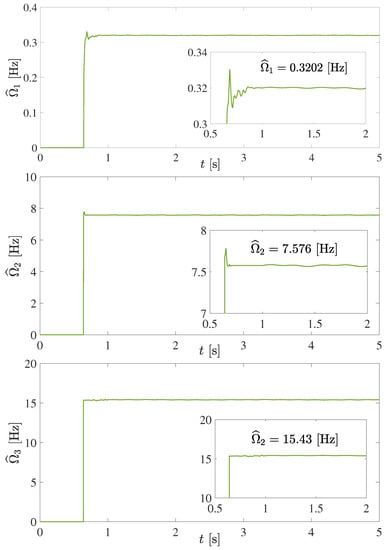
Figure 7.
Online algebraic estimation of exogenous excitation frequencies of the distributed-parameter system.

Table 4.
Online algebraic estimation of natural and excitation frequencies.
Finally, it is important to remark that, real-time algebraic estimation of multiple natural and excitation frequencies on more complex distributed parameter systems, modeled by partial differential equations, could be extended and improved to get more accurate estimates. Indeed, this is a relevant and future research topic.
5. Conclusions
In this paper, a novel time-domain and online algebraic estimation technique to compute the natural and excitation frequencies on forced lumped-parameter vibrating mechanical systems of n degrees of freedom was proposed and evaluated. Multiple and unknown, natural and forced, frequencies are estimated algebraically, simultaneously, and online into a small window of time. The proposed algebraic estimation technique does not require information on the system parameters as mass, damping and stiffness. Online estimation of natural and forced frequencies is independent of the initial conditions. Hence, algebraic estimators can be continuously reset and updated to supervise possible changes on natural frequencies and forcing excitation frequencies, during the real-time operation of a vibrating mechanical system. Measurements of a measurable output signal associated with some degree of freedom are only necessary to perform and apply the proposed algebraic estimation technique. Some analytical, numerical and experimental results have confirmed an effective performance of the algebraic estimation techniques for multiple natural and excitation frequencies for disturbed vibrating systems. Finally, the novel algebraic estimation techniques represent a good and fast alternative for estimation of natural and excitation frequencies on forced and uncertain MDOF vibrating mechanical systems.
Author Contributions
Research and writing, G.S.-N., F.B.-C., L.G.T.-F., J.F.P.-S., O.A.G.-P.; and Supervision G.S.-N., F.B.-C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest. The founders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Ewins, D. Modal Testing: Theory, Practice and Aplication, 2nd ed.; Research Studies Press Ltd.: Wiley, UK, 2001. [Google Scholar]
- Heylen, W.; Lammens, S.; Sas, P. Modal Analysis, Theory and Testing; Katholieke Universiteit: Leuven, Belgium, 2003. [Google Scholar]
- Vu, V.; Thomas, M.; Lafleur, F.; Marcouiller, L. Towards an automatic spectral and modal identification from operational modal analysis. J. Sound Vib. 2013, 332, 213–227. [Google Scholar] [CrossRef]
- Yang, Y.; Nagarajaiah, S. Output-only modal identification with limited sensors using sparse component analysis. J. Sound Vib. 2013, 332, 4741–4765. [Google Scholar] [CrossRef]
- Liao, Y.; Wells, V. Modal parameter identification using the log decrement method and band-pass filters. J. Sound Vib. 2011, 330, 5014–5023. [Google Scholar] [CrossRef]
- Oppenheim, A.V.; Willsky, A.S.; Young, I.T. Signals and Systems; Prentice-Hall: Englewood Cliffs, NJ, USA, 1983. [Google Scholar]
- Djurić, M.B.; Djurišić, Ž.R. Frequency measurement of distorted signals using Fourier and zero crossing techniques. Electr. Power Syst. Res. 2008, 78, 1407–1415. [Google Scholar] [CrossRef]
- Yilmaz, A.S.; Alkan, A.; Asyali, M.H. Applications of parametric spectral estimation methods on detection of power system harmonics. Electr. Power Syst. Res. 2008, 78, 683–693. [Google Scholar] [CrossRef]
- Chronopoulos, D.; Troclet, B.; Bareille, O.; Ichchou, M. Modeling the response of composite panels by a dynamic stiffness approach. Compos. Struct. 2013, 96, 111–120. [Google Scholar] [CrossRef]
- Tjahyadi, H.; He, F.; Sammut, K. Multi-mode vibration control of a flexible cantilever beam using adaptive resonant control. Smart Mater. Struct. 2006, 15, 270–278. [Google Scholar] [CrossRef]
- Walker, J.S. Fast Fourier Transforms, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Beltran-Carbajal, F.; Silva-Navarro, G.; Trujillo-Franco, L. On-line parametric estimation of damped multiple frequency oscillations. Electr. Power Syst. Res. 2018, 154, 423–432. [Google Scholar] [CrossRef]
- Maamar, A.; Abdelghani, M.; Le, T.P.; Gagnol, V.; Sabourin, L. Operational modal identification in the presence of harmonic excitation. Appl. Acoust. 2019, 147, 64–71. [Google Scholar] [CrossRef]
- Altunışık, A.C.; Okur, F.Y.; Kahya, V. Modal parameter identification and vibration based damage detection of a multiple cracked cantilever beam. Eng. Fail. Anal. 2017, 79, 154–170. [Google Scholar] [CrossRef]
- Elshamy, M.; Crosby, W.; Elhadary, M. Crack detection of cantilever beam by natural frequency tracking using experimental and finite element analysis. Alex. Eng. J. 2018, 57, 3755–3766. [Google Scholar] [CrossRef]
- Satpute, D.; Baviskar, P.; Gandhi, P.; Chavanke, M.; Aher, T. Crack detection in cantilever shaft beam using natural frequency. Mater. Today Proc. 2017, 4, 1366–1374. [Google Scholar] [CrossRef]
- Khatir, S.; Dekemele, K.; Loccufier, M.; Khatir, T.; Wahab, M.A. Crack identification method in beam-like structures using changes in experimentally measured frequencies and Particle Swarm Optimization. Comptes Rendus MÉCanique 2018, 346, 110–120. [Google Scholar] [CrossRef]
- Preumont, A. Vibration Control of Active Structures: An Introduction, 4th ed.; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Friswell, M.I.; Inman, D.J. The relationship between positive position feedback and output feedback controllers. Smart Mater. Struct. 1999, 8, 285–291. [Google Scholar] [CrossRef]
- Inman, D.J. Vibration with Control; John Wiley & Sons, Ltd.: Chichester, UK, 2006. [Google Scholar]
- Beltran-Carbajal, F.; Silva-Navarro, G.; Sira-Ramírez, H.J. Application of on-line algebraic identification in active vibration control. In Proceedings of the International Conference on Noise and Vibration Engineering (ISMA2004), Leuven, Belgium, 20–22 September 2004; pp. 157–162. [Google Scholar]
- Trapero, J.R.; Sira-Ramírez, H.; Batlle, V.F. A fast on-line frequency estimator of lightly damped vibrations in flexible structures. J. Sound Vib. 2007, 307, 365–378. [Google Scholar] [CrossRef]
- Gawronski, W.K. Advanced Structural Dynamics and Active Control of Structures; Springer: New York, NY, USA, 1998. [Google Scholar]
- Maghsoudi, M.J.; Mohamed, Z.; Husain, A.; Tokhi, M. An optimal performance control scheme for a 3D crane. Mech. Syst. Signal Process. 2016, 66–67, 756–768. [Google Scholar] [CrossRef]
- Garcia-Perez, O.; Silva-Navarro, G.; Peza-Solis, J. Flexible-link robots with combined trajectory tracking and vibration control. Appl. Math. Model. 2019, 70, 285–298. [Google Scholar] [CrossRef]
- Zhao, Z.; Liu, C.; Ma, W. Characteristics of steady vibration in a rotating hub–beam system. J. Sound Vib. 2016, 363, 571–583. [Google Scholar] [CrossRef]
- Dwivedy, S.K.; Eberhard, P. Dynamic analysis of flexible manipulators, a literature review. Mech. Mach. Theory 2006, 41, 749–777. [Google Scholar] [CrossRef]
- Lochan, K.; Roy, B.; Subudhi, B. A review on two-link flexible manipulators. Annu. Rev. Control 2016, 42, 346–367. [Google Scholar] [CrossRef]
- Kim, H.K.; Choi, S.B.; Thompson, B.S. Compliant control of a two-link flexible manipulator featuring piezoelectric actuators. Mech. Mach. Theory 2001, 36, 411–424. [Google Scholar] [CrossRef]
- Fliess, M.; Sira-Ramírez, H. An algebraic framework for linear identification. ESAIM Control Optim. Calc. Var. 2003, 9, 151–168. [Google Scholar] [CrossRef]
- Beltran-Carbajal, F.; Silva-Navarro, G. Adaptive-like vibration control in mechanical systems with unknown parameters and signals. Asian J. Control 2013, 15, 1613–1626. [Google Scholar] [CrossRef]
- Rao, S.S. Mechanical Vibrations; Prentice Hall Upper: Saddle River, NJ, USA, 2011. [Google Scholar]
- Ewins, D.J.; Braun, S.G.; Rao, S.S. Encyclopedia of Vibration, Three-Volume Set; Academic Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Piersol, A.G.; Paez, T.L. Harris’ Shock and Vibration Handbook; McGraw-Hill: New York, NY, USA, 2010. [Google Scholar]
- Beltran-Carbajal, F.; Silva-Navarro, G. Output feedback dynamic control for trajectory tracking and vibration suppression. Appl. Math. Model. 2020, 79, 793–808. [Google Scholar] [CrossRef]
- Arias-Montiel, M.; Beltran-Carbajal, F.; Silva-Navarro, G. On-line algebraic identification of eccentricity parameters in active rotor-bearing systems. Int. J. Mech. Sci. 2014, 85, 152–159. [Google Scholar] [CrossRef]
- Meirovitch, L. Fundamentals of Vibrations; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).