Optimal Design and Performance Analysis of Radial MR Valve with Single Excitation Coil
Abstract
1. Introduction
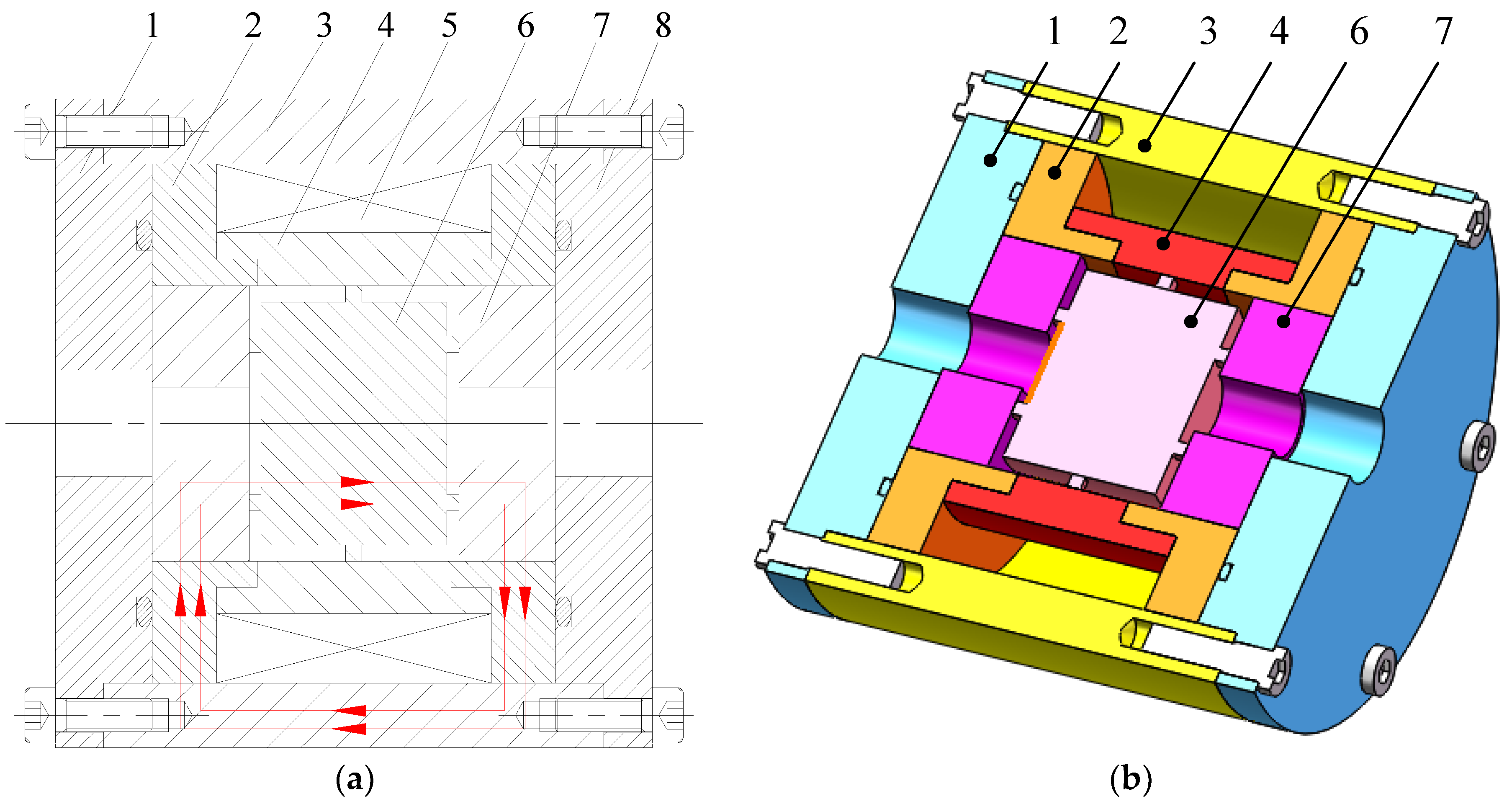
2. Working Principle and Structure
2.1. Working Principle
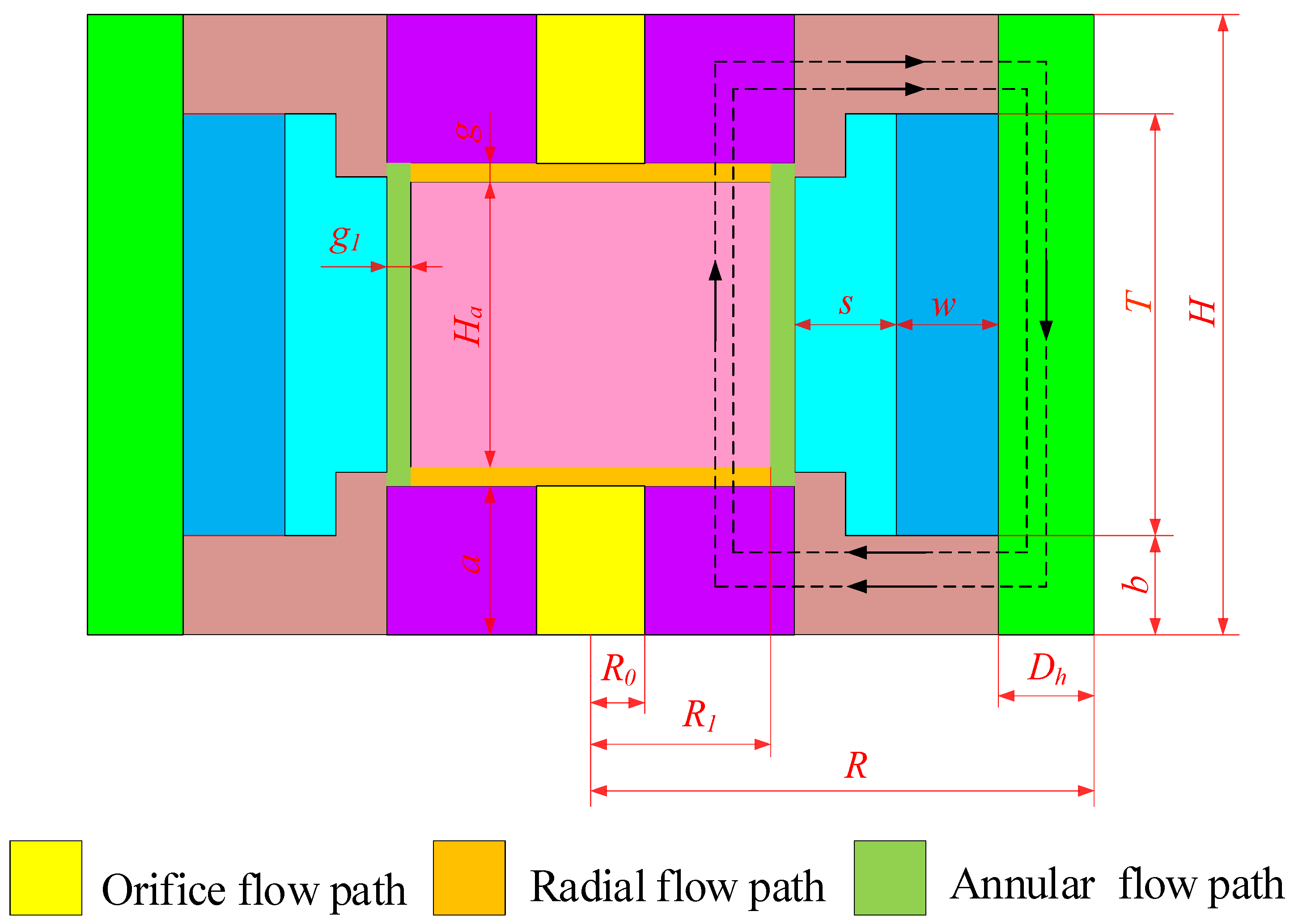
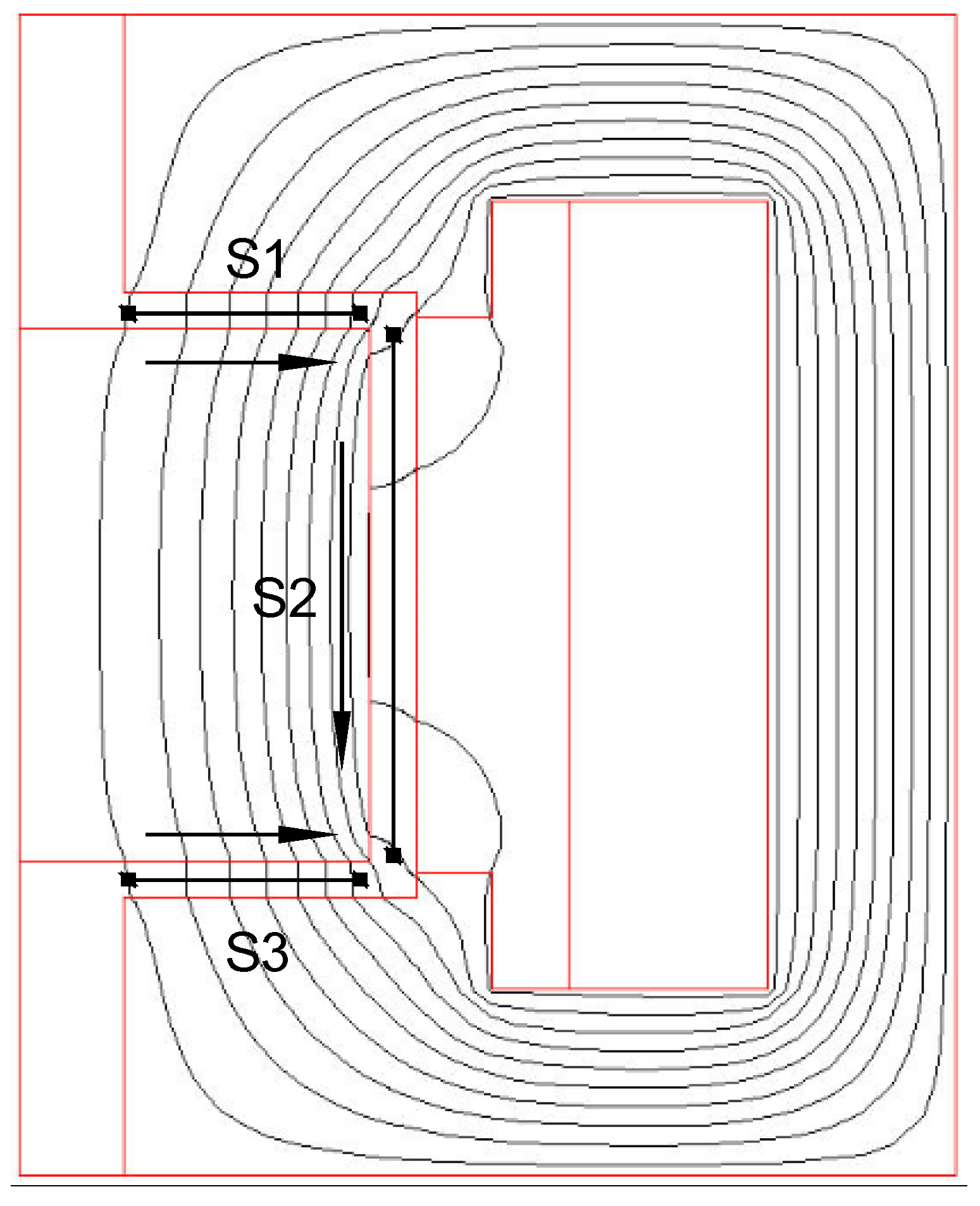
2.2. Magnetic Circuit Design
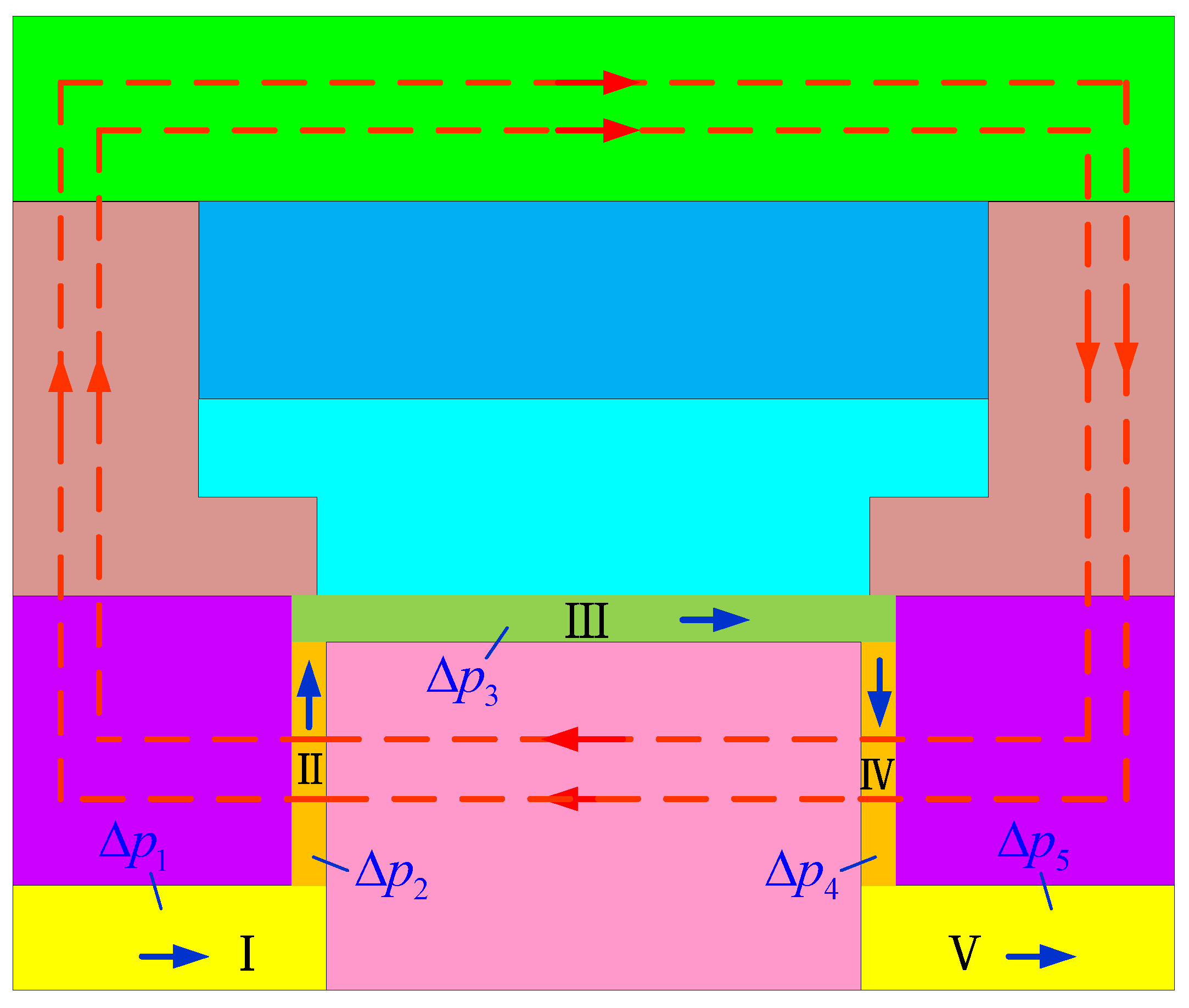
2.3. Mathematical Model of Pressure Drop
3. Simulation Analysis of Magnetic Field and Dimensional Parameters of the Radial Mr Valve with Single Excitation Coil
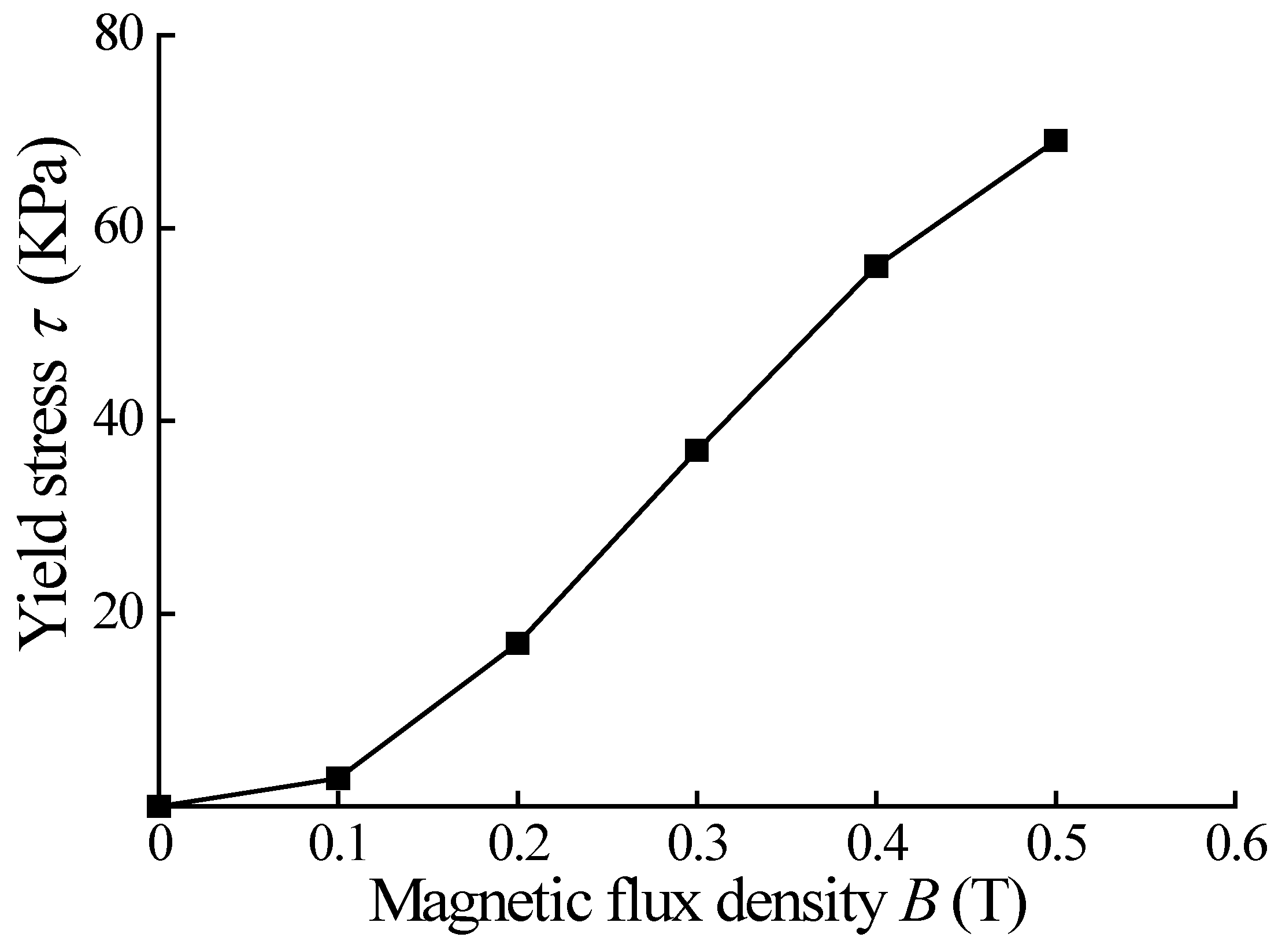
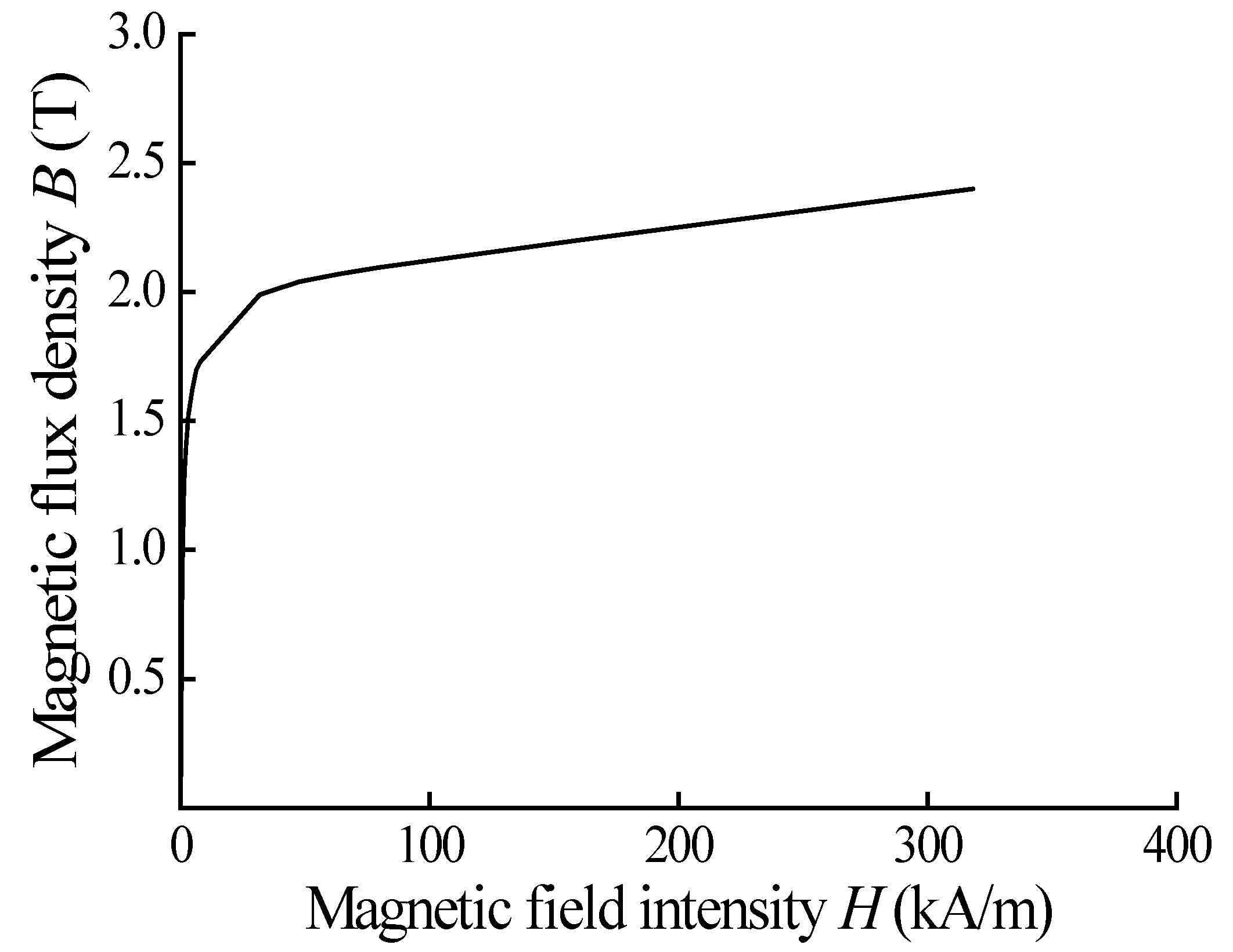
3.1. Working Characteristics of MR Fluids
3.2. Electromagnetic Field Simulation of MR Valve
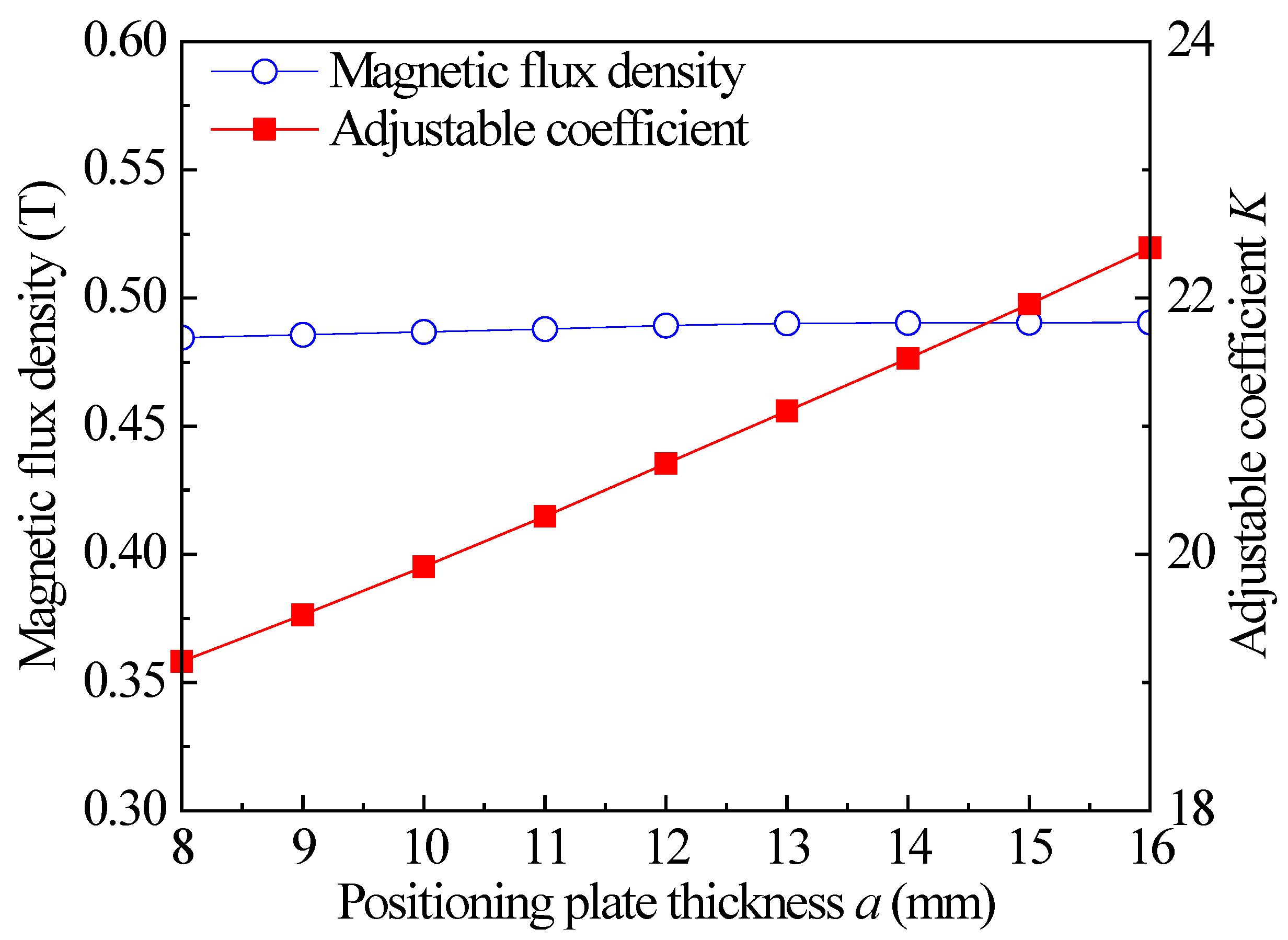
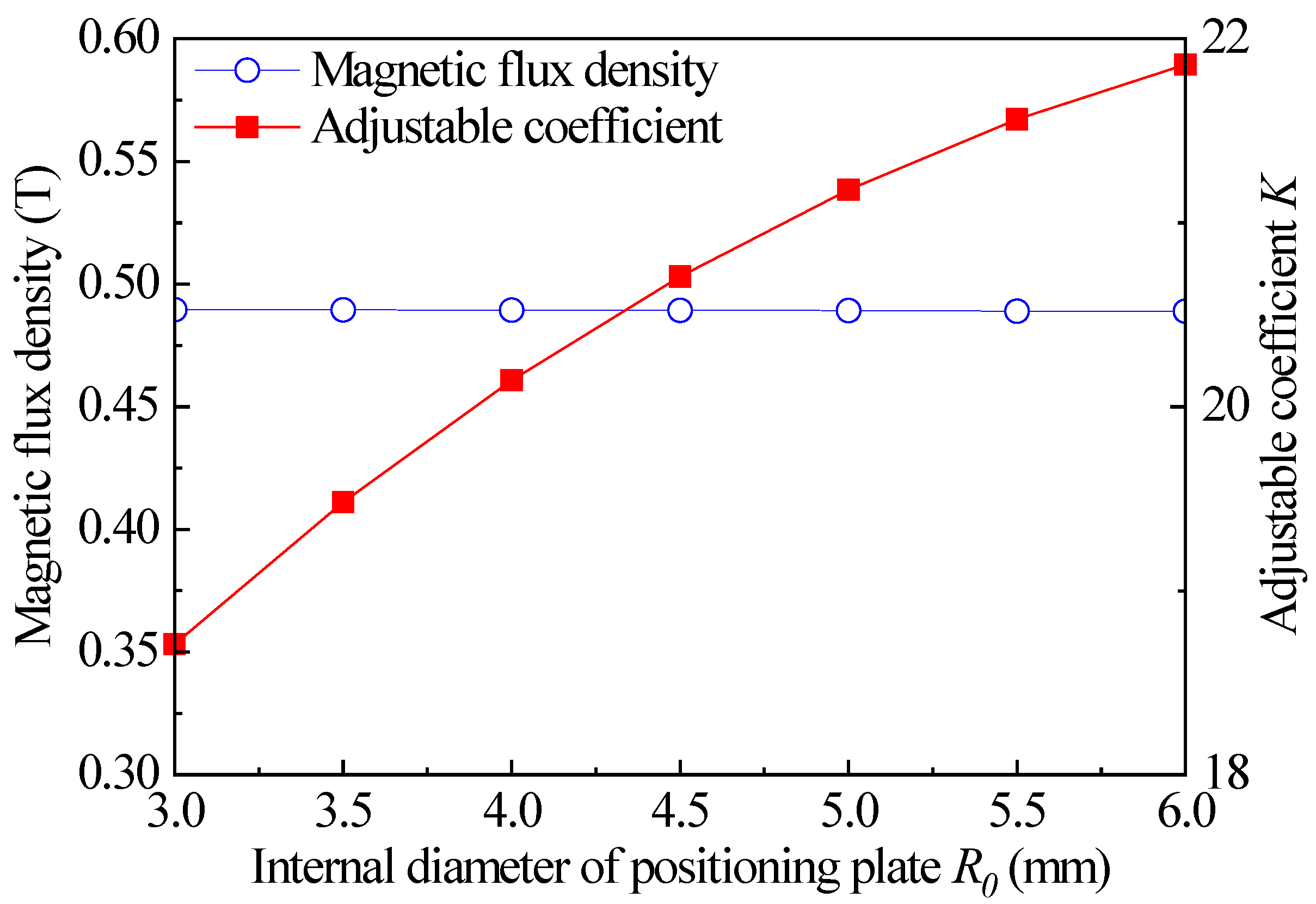
3.3. Effect of Dimensional Parameters on Performance of Magnetic Flux Density and Adjustable Coefficient
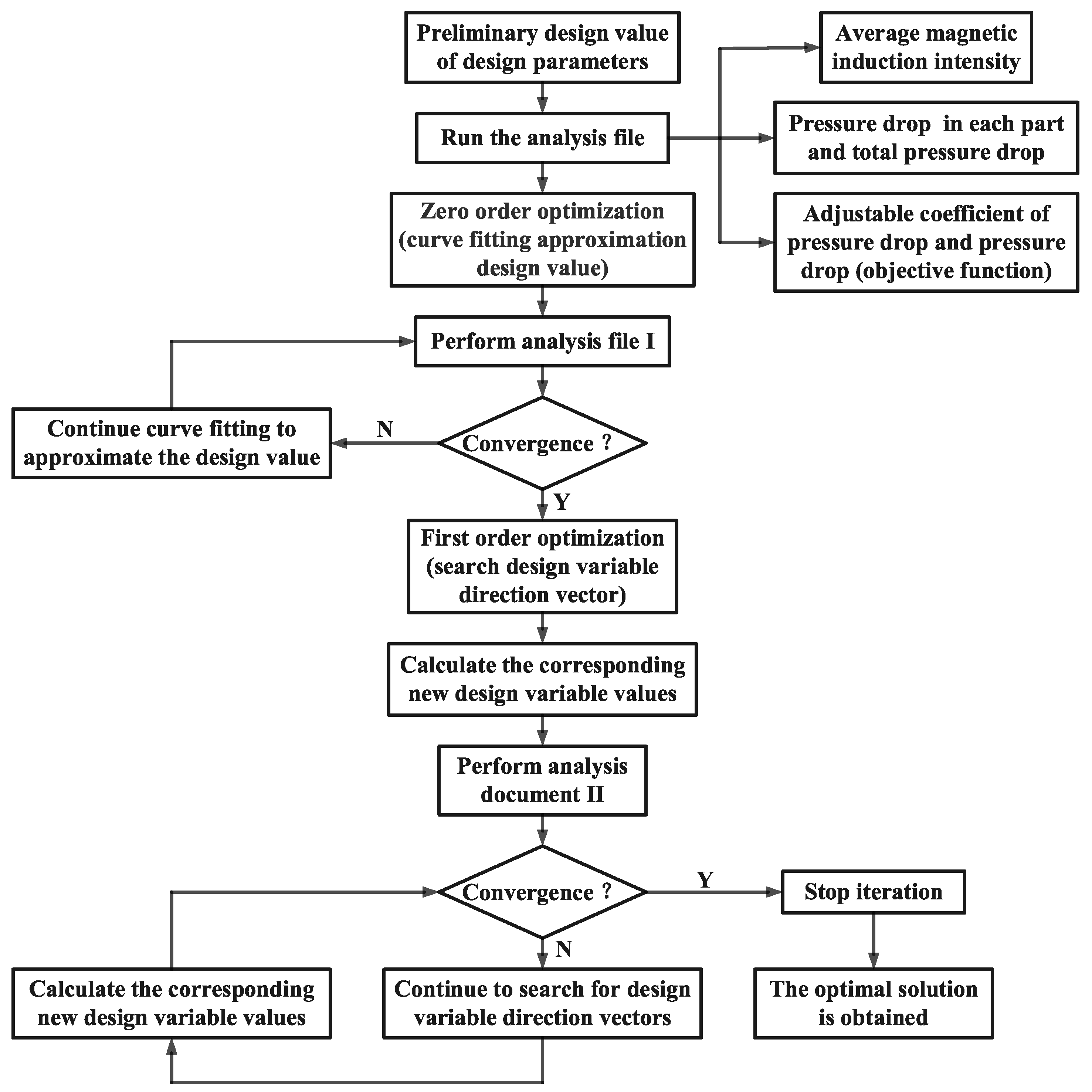
4. Optimization of Radial MR Valve with Single Excitation Coil
4.1. Optimization of Controlled Pressure Drops
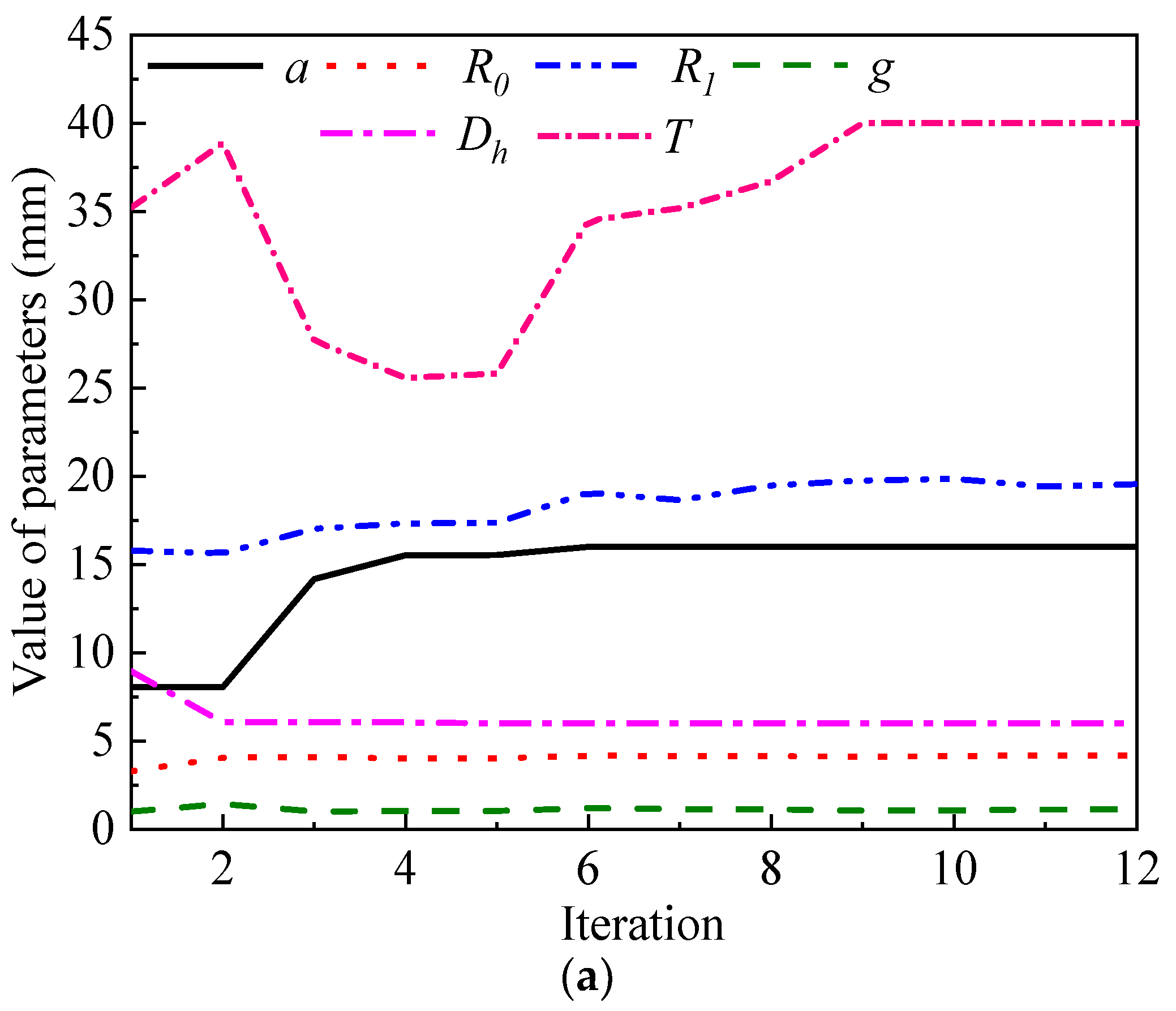
4.2. Optimal Results Analysis
5. Experimental Test and Analysis of Radial MR Valve
5.1. Prototype of Radial MR Valve with Single Excitation Coil
5.2. Performance Test System of Radial MR Valve
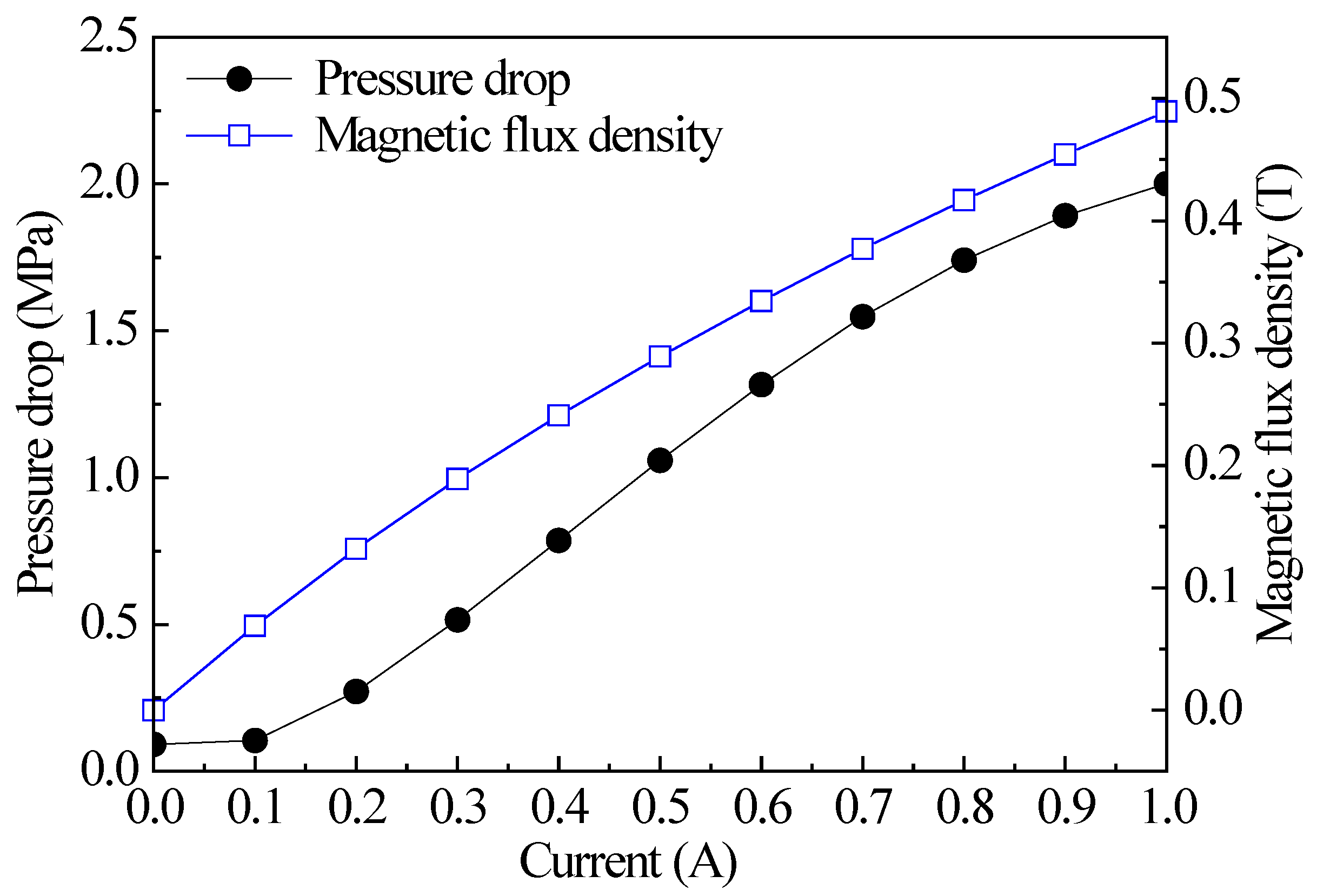
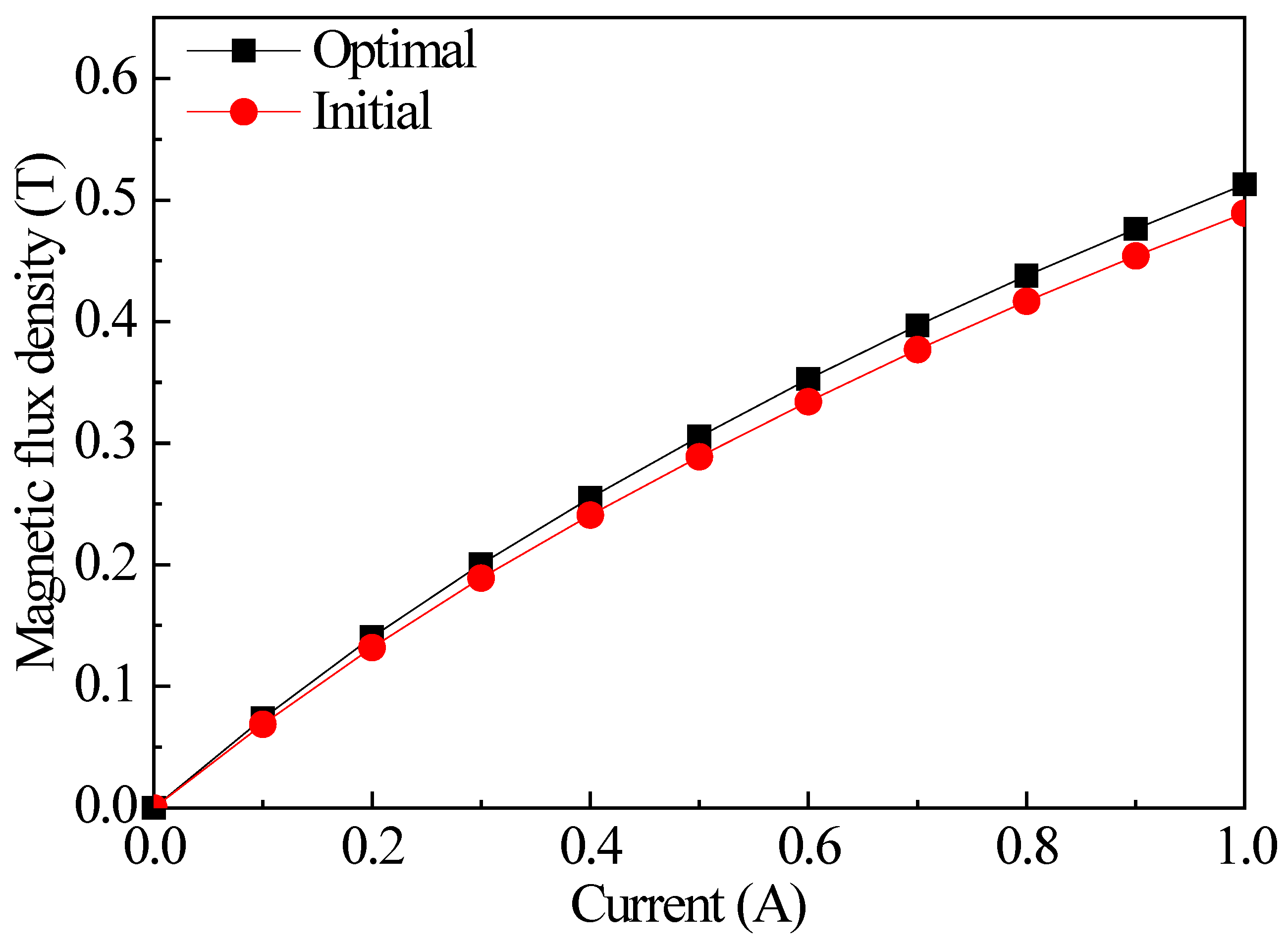
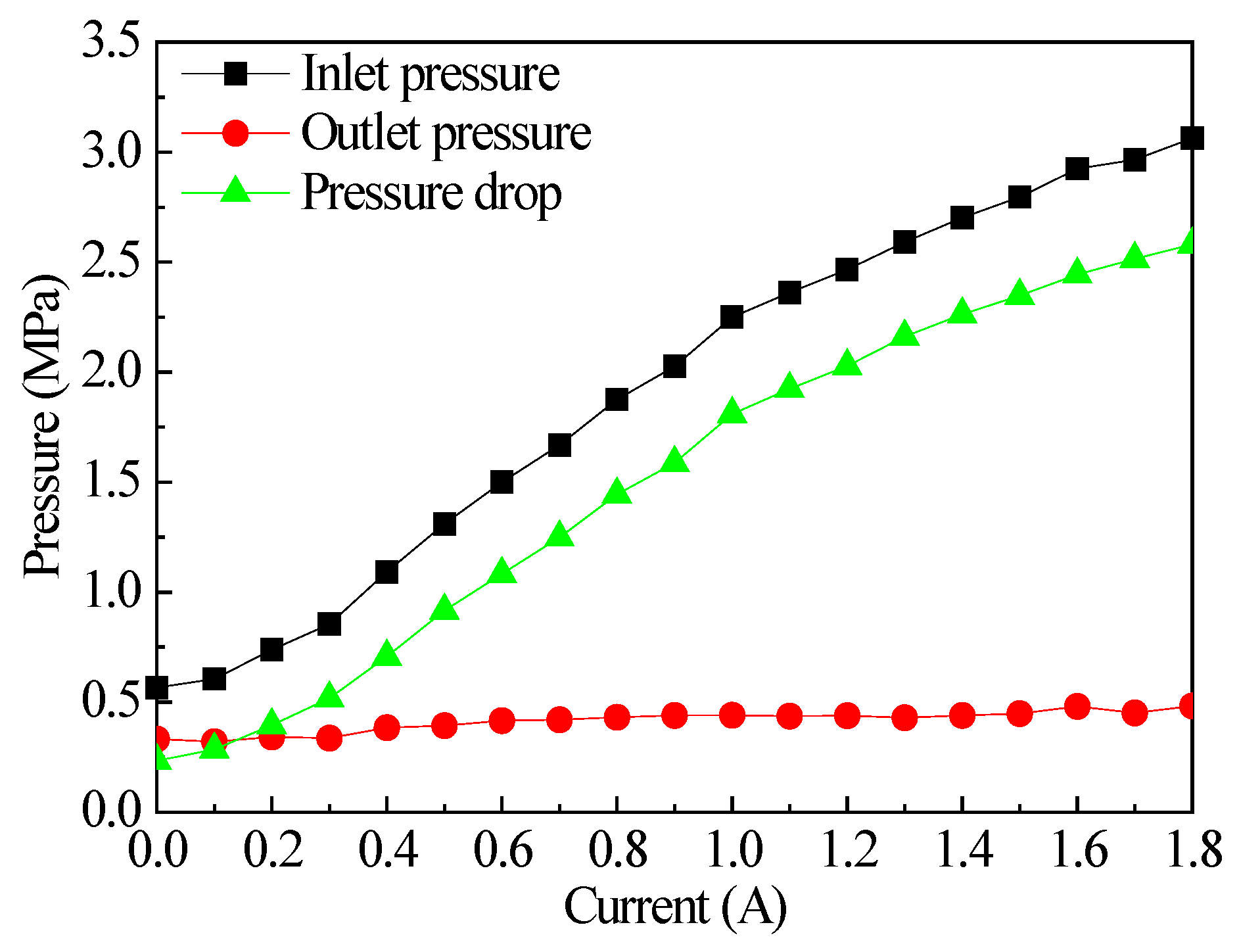
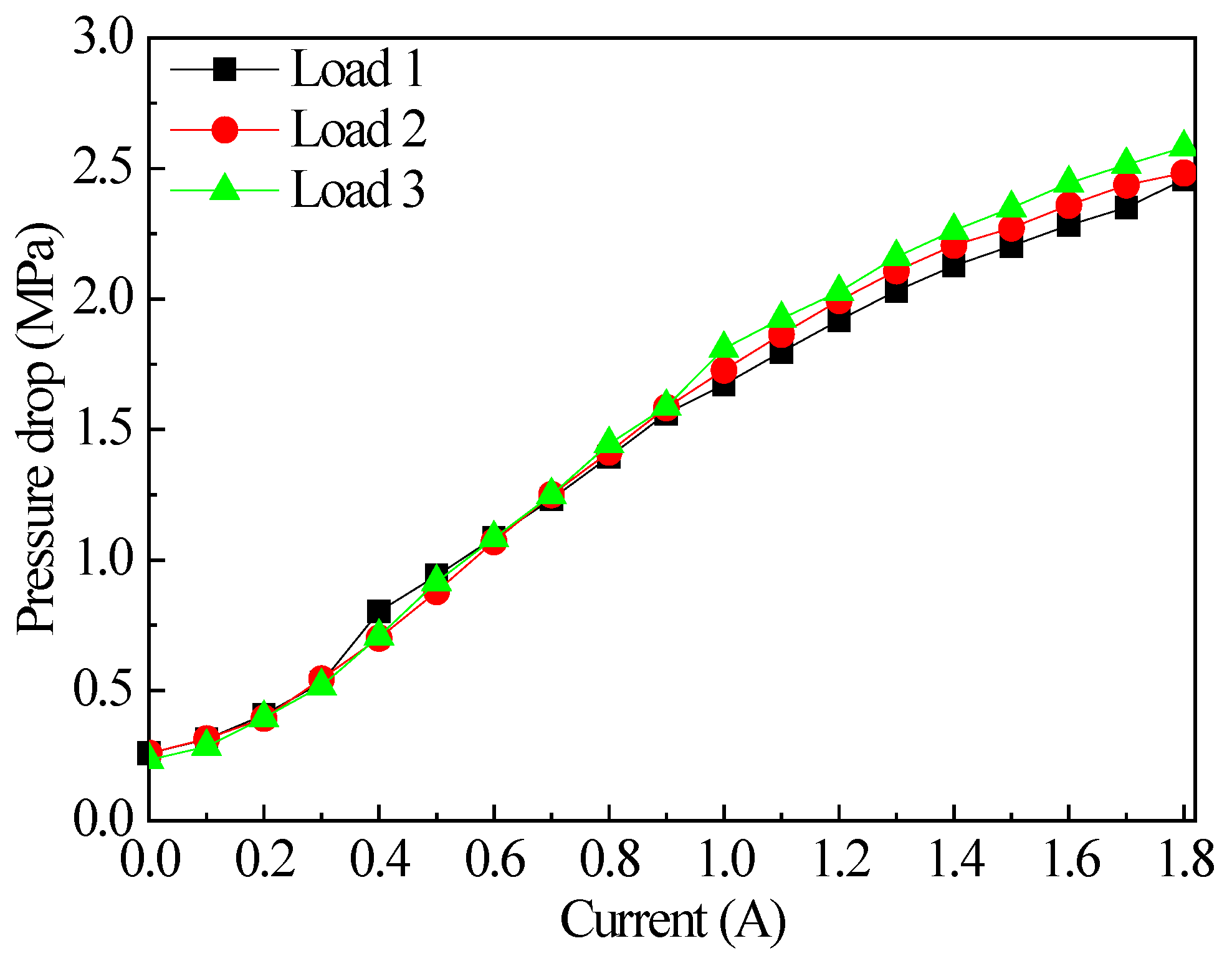
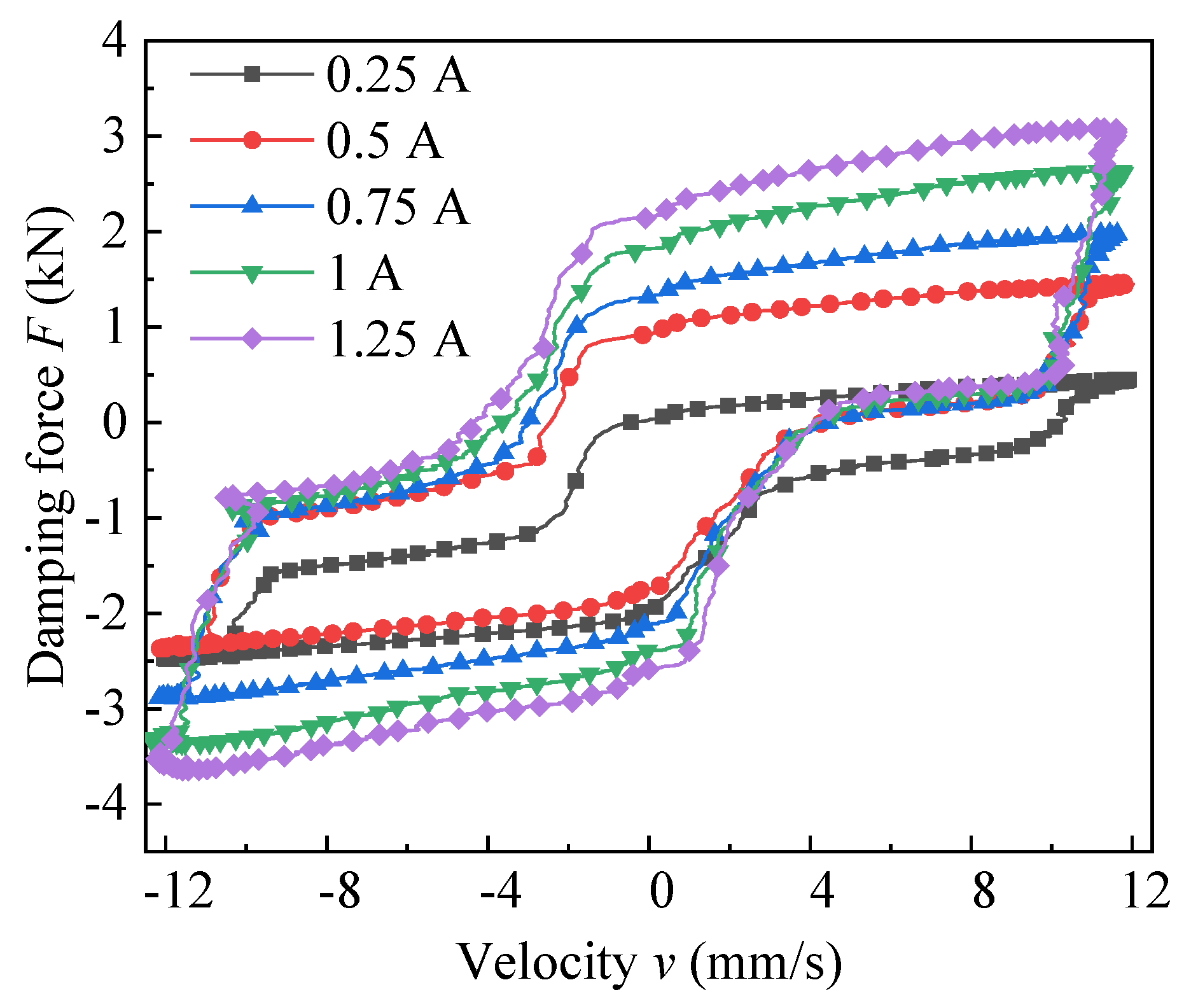
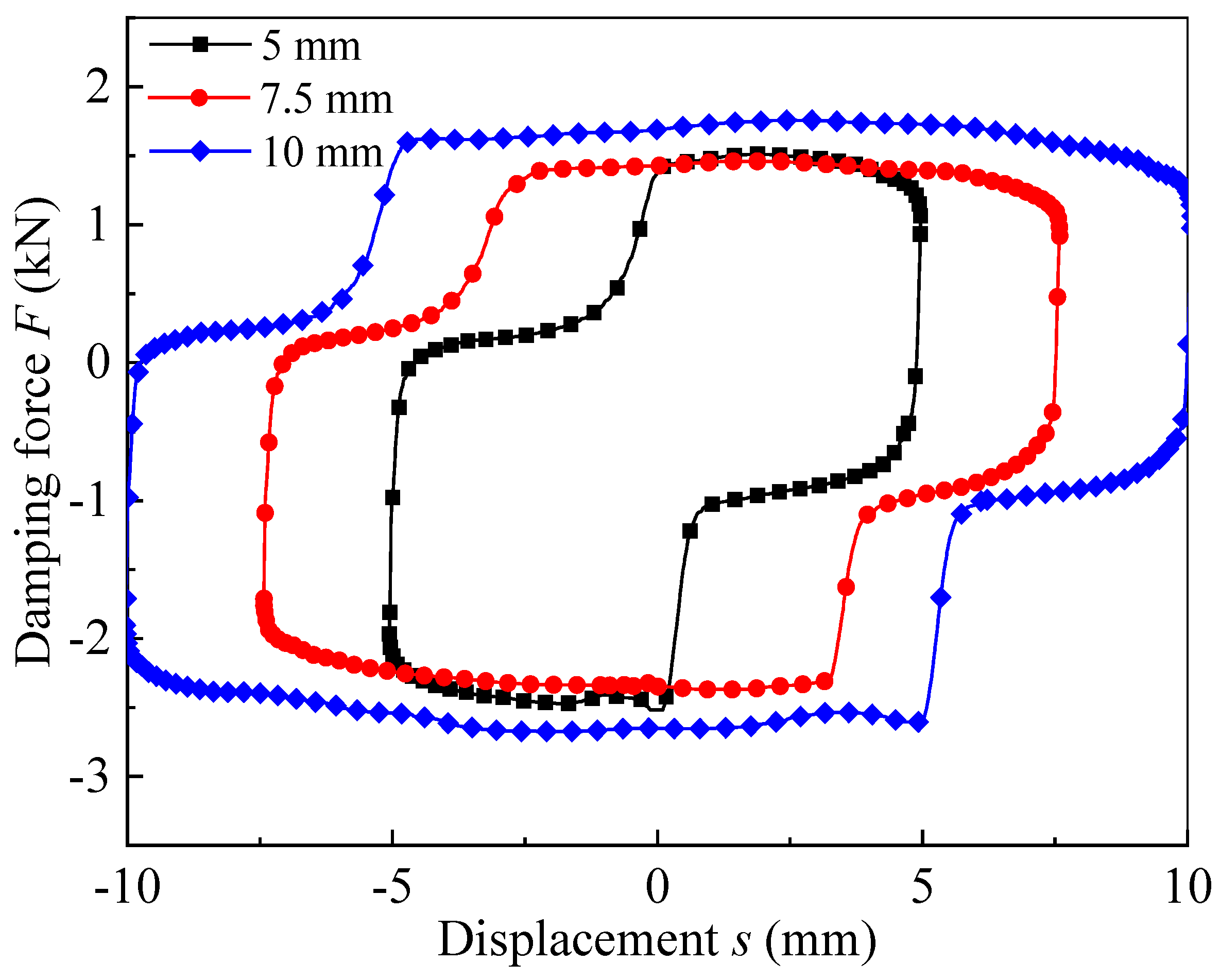
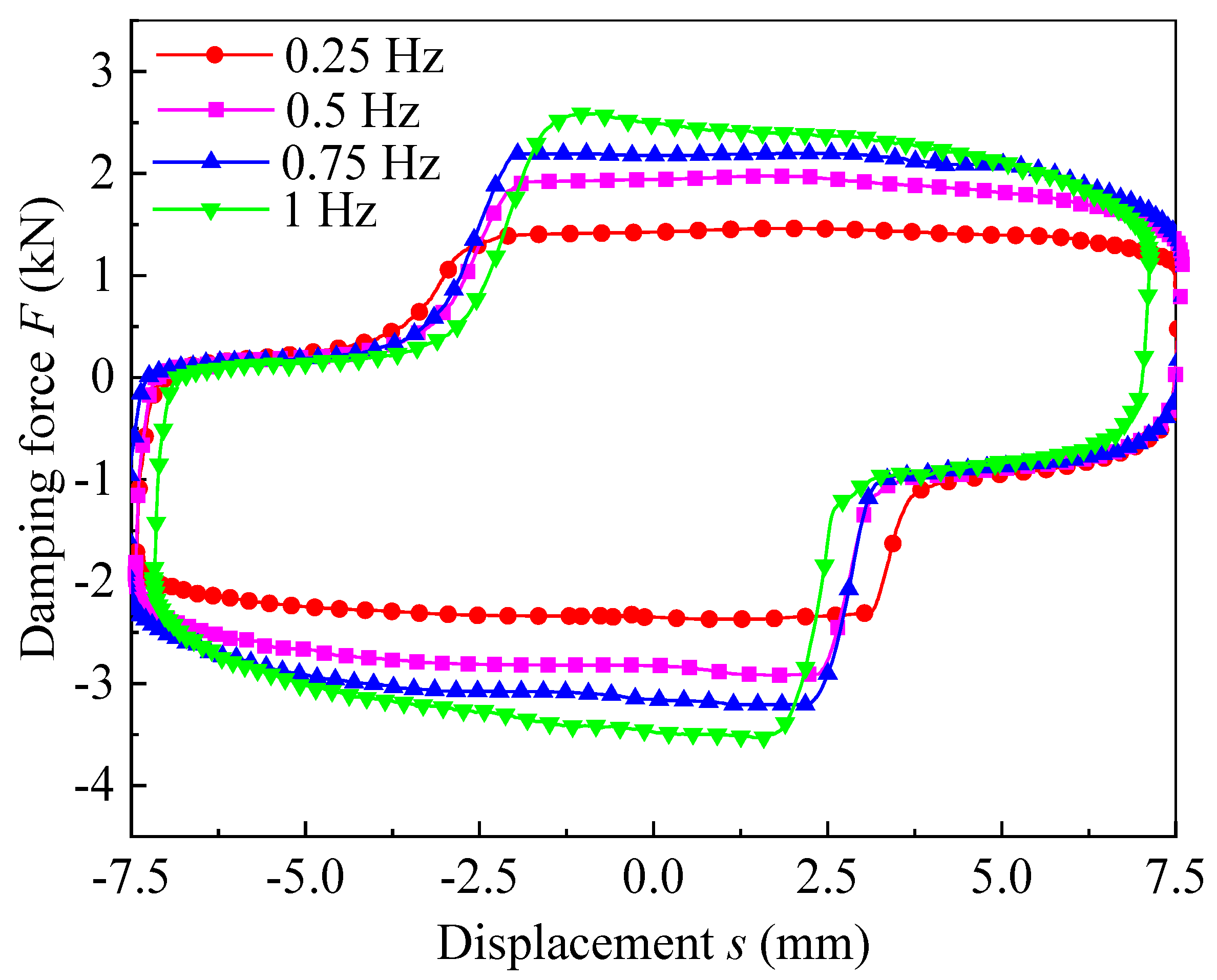
5.3. Pressure Performance Test of the Radial MR Valve
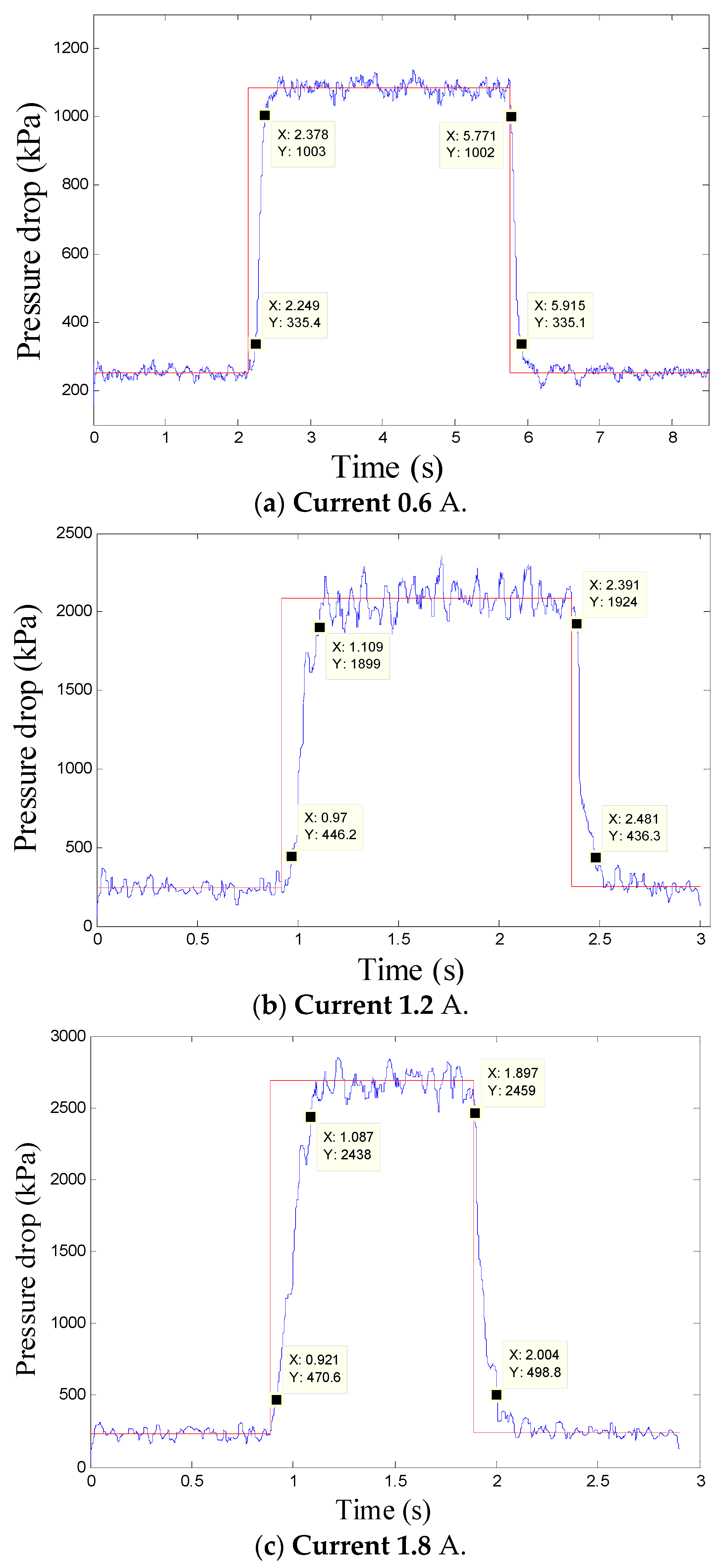
5.4. Response Performance Test of the Radial MR Valve
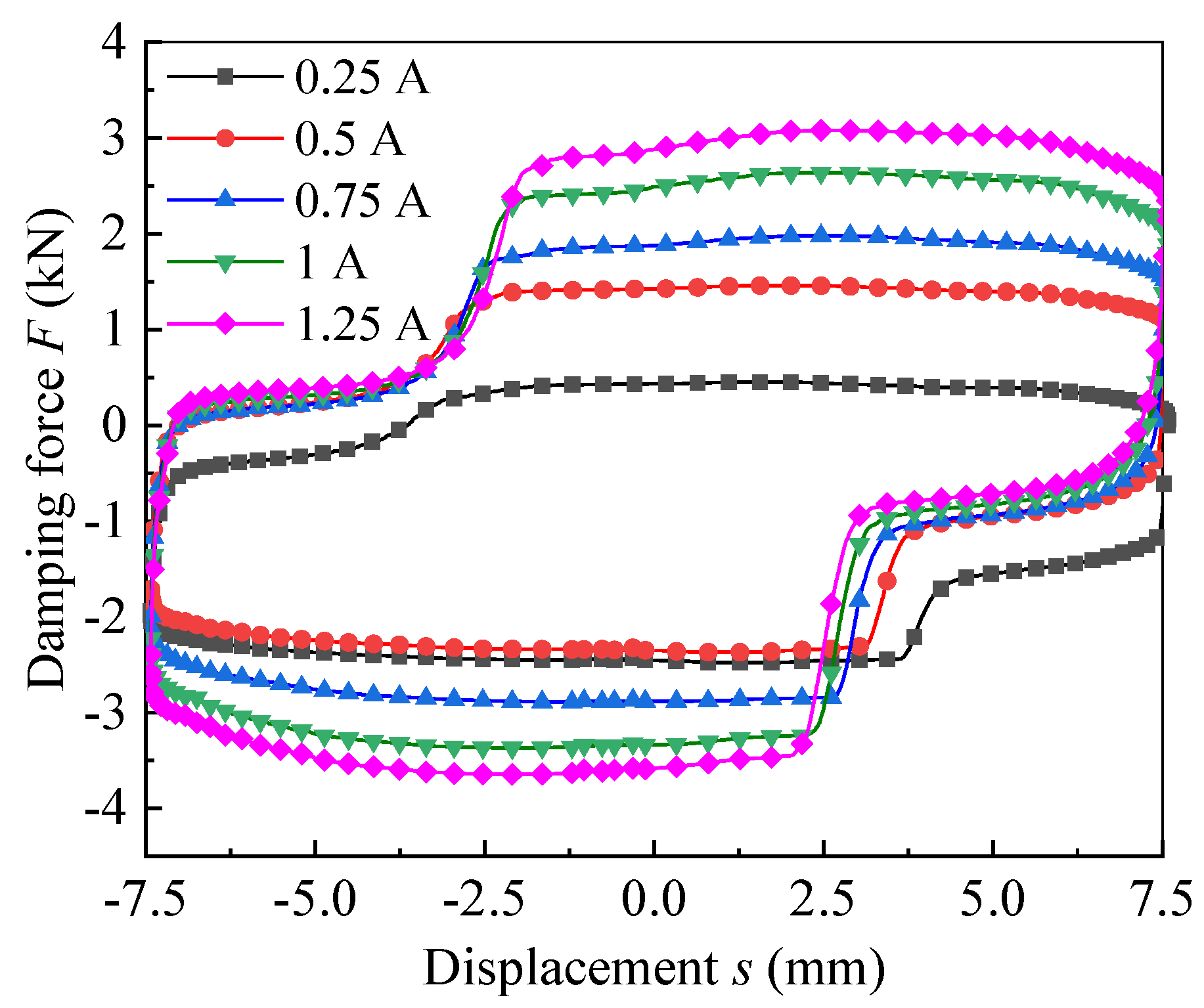
5.5. Experimental Analysis of Dynamic Performance of Radial Mr Valve Controlled Cylinder System
5.5.1. Dynamic Performance Test System of Radial Mr Valve Controlled Cylinder System
5.5.2. Dynamic Performance of the Optimal Radial Mr Valve Controlled Cylinder System
5.5.3. Comparison and Analysis of Dynamic Performance
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Heo, Y.H.; Choi, D.; Yun, I.; Kim, S. A tiny haptic knob based on magnetorheological fluids. Appl. Sci. 2020, 10, 5118. [Google Scholar] [CrossRef]
- Yang, J.; Sun, S.S.; Tian, T.F.; Li, W.H.; Du, H.P. Development of a novel multi-layer MRE isolator for suppression of building vibrations under seismic events. Mech. Syst. Signal Process. 2016, 70–71, 811–820. [Google Scholar] [CrossRef]
- Tian, T.F.; Nakano, M. Fabrication and characterisation of anisotropic magnetorheological elastomer with 45 degrees iron particle alignment at various silicone oil concentrations. J. Intell. Mater. Syst. Struct. 2017, 29, 151–159. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, D.; Cui, H.; Yang, J. A new modified model for the rheological properties of magnetorheological fluids based on different magnetic field. J. Magn. Magn. Mater. 2020, 500, 166377. [Google Scholar] [CrossRef]
- Hu, G.L.; Zhong, F.; Zhang, H.Y.; Ding, R.Q. Structure optimization and performance analysis of a multiple radial magnetorheological valve. J. Beijing Inst. Technol. 2017, 26, 458–467. [Google Scholar]
- Hu, G.L.; Zhang, J.W.; Liao, M.K.; Ding, R.Q. The effect of radial resistance gap on the pressure drop of a compact annular-radial-orifice flow magnetorheological valve. J. Beijing Inst. Technol. 2018, 27, 535–546. [Google Scholar]
- Ichwan, B.; Mazlan, S.A.; Imaduddin, F. Development of a modular MR valve using meandering flow path structure. Smart Mater. Struct. 2016, 25, 037001. [Google Scholar] [CrossRef]
- Hu, G.L.; Wu, L.F.; Li, L.S.; Yu, L.F. Performance Analysis of Rotary Magnetorheological Brake with Multiple Fluid Flow Channels. IEEE Access 2020, 8, 173323–173335. [Google Scholar] [CrossRef]
- Li, W.H.; Du, H. Design and experimental evaluation of a magnetorheological brake. Int. J. Adv. Manuf. Technol. 2003, 21, 508–515. [Google Scholar] [CrossRef]
- Bai, X.X.; Wereley, N.M.; Choi, Y.T. Magnetorheological energy absorber with dual concentric annular valves. J. Intell. Mater. Systerns Struct. 2016, 27, 944–958. [Google Scholar] [CrossRef]
- Tae-Hoon, L.; Chulhee, H.; Seung-Bok, C. Design and damping force characterization of a new magnetorheological damper activated by permanent magnet flux dispersion. Smart Mater. Struct. 2017, 27, 015013. [Google Scholar]
- Bai, X.X.; Cai, F.; Chen, P. Resistor-capacitor (RC) operator-based hysteresis model for magnetorheological (MR) dampers. Mech. Syst. Signal Pr. 2019, 117, 157–169. [Google Scholar] [CrossRef]
- Weber, F.; Distl, H.; Fischer, S.; Braun, C. MR Damper Controlled Vibration Absorber for Enhanced Mitigation of Harmonic Vibrations. Actuators 2016, 5, 27. [Google Scholar] [CrossRef]
- Sun, S.S.; Ning, D.H.; Yang, J. Development of an MR seat suspension with self-powered generation capability. J. Smart Mater. Struct. 2017, 26, 085025. [Google Scholar] [CrossRef]
- Yang, S.Y.; Han, C.; Shin, S.U.; Choi, S.B. Design and Evaluation of a Semi-Active Magneto-rheological Mount for a Wheel Loader Cabin. Actuators 2017, 6, 16. [Google Scholar] [CrossRef]
- Hu, G.L.; Long, M.; Huang, M.; Li, W.H. Design, Analysis, Prototyping, and Experimental Evaluation of an Efficient Double Coil Magnetorheological Valve. Adv. Mech. Eng. 2014, 6, 403410. [Google Scholar] [CrossRef]
- Ai, H.X.; Wang, D.H.; Liao, W.H. Design and Modeling of a Magnetorheological Valve with both Annular and Radial Flow Paths. J. Intell. Mater. Syst. Struct. 2006, 17, 328–334. [Google Scholar] [CrossRef]
- Hu, G.L.; Long, M.; Yu, L.F.; Li, W.H. Design and performance evaluation of a novel magnetorheological valve with a tunable resistance gap. Smart Mater. Struct. 2014, 23, 127001. [Google Scholar] [CrossRef]
- Hu, G.L.; Liao, M.K.; Li, W.H. Analysis of a compact annular-radial-orifice flow magnetorheological valve and evaluation of its performance. J. Intell. Mater. Syst. Struct. 2017, 28, 1322–1333. [Google Scholar] [CrossRef]
- Abd Fatah, A.Y.; Mazlan, S.A.; Koga, T.; Zamzuri, H.; Imaduddin, F. Design of magnetorheological valve using serpentine flux path method. Int. J. Appl. Electromagn. Mech. 2016, 50, 29–44. [Google Scholar] [CrossRef]
- Imaduddin, F.; Mazlan, S.A.; Zamzuri, H.; Yazid, I.I.M. Design and performance analysis of a compact magnetorheological valve with multiple annular and radial gaps. J. Intell. Mater. Syst. Struct. 2015, 26, 1038–1049. [Google Scholar] [CrossRef]
- Manjeet, K.; Sujatha, C. Magnetorheological valves based on Herschel–Bulkley fluid model: Modelling, magnetostatic analysis and geometric optimization. Smart Mater. Struct. 2019, 28, 115008. [Google Scholar] [CrossRef]
- Manjeet, K.; Sujatha, C. Chandramohan Geometric optimisation of magnetorheological valve using feedforward neural networks for distribution of magnetic flux density inside the valve. Smart Mater. Struct. 2019, 28, 105018. [Google Scholar]
- Xiong, S.P.; Wilfong, G.; Lumkes, J. Development of a novel high-speed actuation mechanism using a magneto-rheological fluid clutch and its application to a fluid control valve. J. Intell. Mater. Syst. Struct. 2019, 30, 2502–2516. [Google Scholar] [CrossRef]
- Seid, S.; Chandramohan, S.; Sujatha, S. Optimal design of an MR damper valve for prosthetic knee application. J. Mech. Sci. Technol. 2018, 32, 2959–2965. [Google Scholar] [CrossRef]
- Nguyen, Q.H.; Han, Y.M.; Choi, S.B.; Wereley, N.M. Geometry optimization of MR valves constrained in a specific volume using the finite element method. Smart Mater. Struct. 2007, 16, 2242–2252. [Google Scholar] [CrossRef]
- Shin, S.U.; Lee, T.H.; Cha, S.W. Optimal design and experimental analysis of a magnetorheological valve system for the vehicle lifter used in maintenance. J. Spie Smart Struct. Mater. Nondestruct. Eval. Health Monit. 2017, 10164, 101642C. [Google Scholar]
- Idris, M.H.; Imaduddin, F.; Mazlan, S.A.; Choi, S.B. A Concentric Design of a Bypass Magnetorheological Fluid Damper with a Serpentine Flux Valve. Actuators 2020, 9, 16. [Google Scholar] [CrossRef]
- Ntella, S.L.; Duong, M.T.; Civet, Y.; Pataky, Z.; Perriard, Y. Design Optimization of Miniature Magnetorheological Valves with Self-Sensing Capabilities Used for a Wearable Medical Application. In Proceedings of the 2020 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Boston, MA, USA, 6–9 July 2020; pp. 409–414. [Google Scholar]
- Hu, G.L.; Zhang, J.W.; Zhong, F.; Yu, L.F. Performance evaluation of an improved radial magnetorheological valve and its application in the valve controlled cylinder system. Smart Mater. Struct. 2019, 28, 047003. [Google Scholar] [CrossRef]
















| Project | Initial Valve | Optimal Valve | ||
|---|---|---|---|---|
| λ1 = 1 and λ2 = 0 | λ1 = 0 and λ2 = 1 | λ1 = 0.75 and λ2 = 0.25 | ||
| Objective function f | 1.00 | 0.39789 | 0.56721 | 0.68546 |
| Adjustable coefficient K | 20.71 | 12.10 | 36.51 | 16.77 |
| Field-dependent pressure drop pτ/MPa | 1.9091 | 4.7981 | 1.5145 | 3.8007 |
| Viscous pressure drop pη/MPa | 0.0922 | 0.0397 | 0.0414 | 0.2267 |
| Magnetic flux density /T | 0.4892 | 0.5262 | 0.4783 | 0.5182 |
| Project | Initial Valve | Optimal Valve | ||
|---|---|---|---|---|
| λ1 = 1 and λ2 = 0 | λ1 = 0 and λ2 = 1 | λ1 = 0.75 and λ2 = 0.25 | ||
| Radial damping gap g/mm | 1.5 | 1.0023 | 2 | 1.1323 |
| Positioning plate thickness a/mm | 12 | 13.950 | 16 | 16 |
| Damping gap radius of circular tube R0/mm | 4.5 | 3 | 4.8889 | 4.1819 |
| Valve spool radius R1/mm | 15 | 20 | 16.172 | 19.550 |
| Thickness of valve body Dh/mm | 8 | 6 | 6 | 6 |
| Width of winding grooves T/mm | 34 | 40 | 40 | 40 |
| Weight of valve G/kg | 2.41 | - | - | 2.22 |
| Current (A) | Rising Response Time (ms) | Falling Response Time (ms) | ||
|---|---|---|---|---|
| Initial Design | Optimal Design | Initial Design | Optimal Design | |
| 0.6 | 71 | 129 | 96 | 144 |
| 1.2 | 80 | 139 | 66 | 90 |
| 1.8 | 119 | 166 | 84 | 107 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, G.; Zhou, F.; Yu, L. Optimal Design and Performance Analysis of Radial MR Valve with Single Excitation Coil. Actuators 2021, 10, 34. https://doi.org/10.3390/act10020034
Hu G, Zhou F, Yu L. Optimal Design and Performance Analysis of Radial MR Valve with Single Excitation Coil. Actuators. 2021; 10(2):34. https://doi.org/10.3390/act10020034
Chicago/Turabian StyleHu, Guoliang, Feng Zhou, and Lifan Yu. 2021. "Optimal Design and Performance Analysis of Radial MR Valve with Single Excitation Coil" Actuators 10, no. 2: 34. https://doi.org/10.3390/act10020034
APA StyleHu, G., Zhou, F., & Yu, L. (2021). Optimal Design and Performance Analysis of Radial MR Valve with Single Excitation Coil. Actuators, 10(2), 34. https://doi.org/10.3390/act10020034





