Robust Control of a Class of Nonlinear Discrete-Time Systems: Design and Experimental Results on a Real-Time Emulator
Abstract
:1. Introduction
1.1. Background
- The problem of using previous measurements in the observer structure and estimated states in the control law, in presence of modeling uncertainties, has not been tackled before. For example, the Kalman filter uses the previous measurements with a single regression step () but what is proposed in this paper is to solve an estimation-control problem in dual form (a single resolution step from LMI) with sliding windows of estimated states and measurements ().
- The sliding window approach allows to introduce additional decision variables to the convex problem which add more degree of freedom.
- A more optimal use and introduction of Young’s inequality will be proposed other than the classical ones [5]. This will increase the degree of freedom when synthesizing a robust control law as well as the treatment of less conservative LMIs.
- A technique for handling and transforming BMI constraints into LMI is used. This technique is based on the inclusion of a “Slack-Variable”. This subsequently makes it possible to eliminate the difficulty of calculating or optimizing bilinear terms.
1.2. Notation
- In a matrix, the notation represents the blocks induced by symmetry.
- represents a vector of the canonical basis of , where, .
- is the Euclidean vector norm.
- is the transposed matrix of Z.
- represents the identity matrix of dimension p.
- Z is a square matrix. The notation () means that Z is positive definite (negative definite).
- The norm of the vector is given by and is defined as .
1.3. Preliminaries
- g is globally Lipschitz with respect to its argument, i.e.,
- there exist constants and so that for all ∈ there exist , , and functions satisfying the following equality:and where and .
2. Problem Formulation
3. New Sliding Window Observer-Based Controller Design Methodology
3.1. Stability Analysis
3.2. Converting BMI into LMI
4. Discussion on the Enhancement
4.1. Standard Approach
4.2. Comparison from LMI Feasibility Point of View
4.3. Comparison from Computational Complexity Point of View
4.3.1. Real-Time Application: Feasibility and Complexity
4.3.2. Computational Complexity in Solving the LMIs
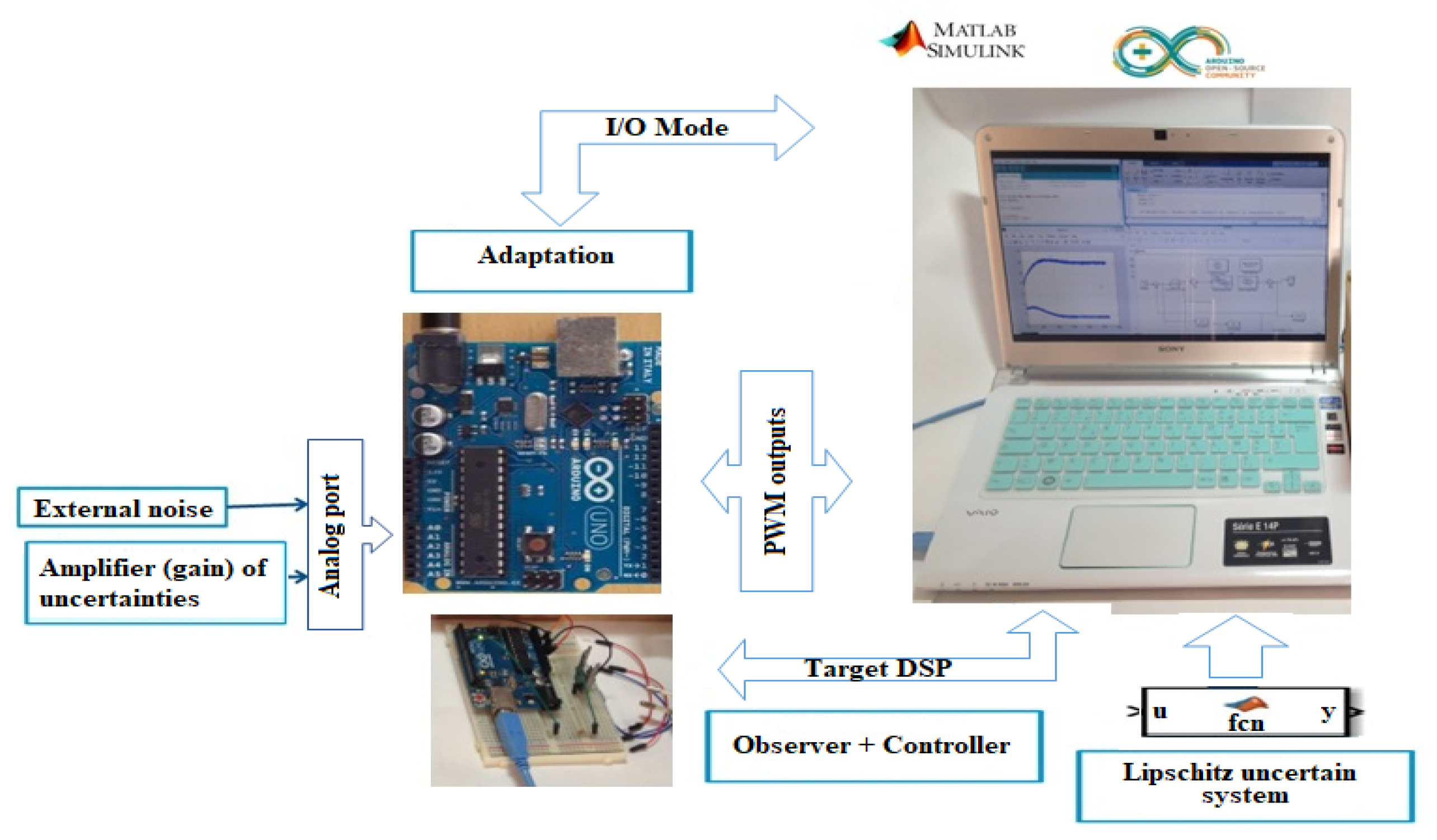
5. Simulation and Experimental Results
5.1. Example 1
5.1.1. Simulation Results
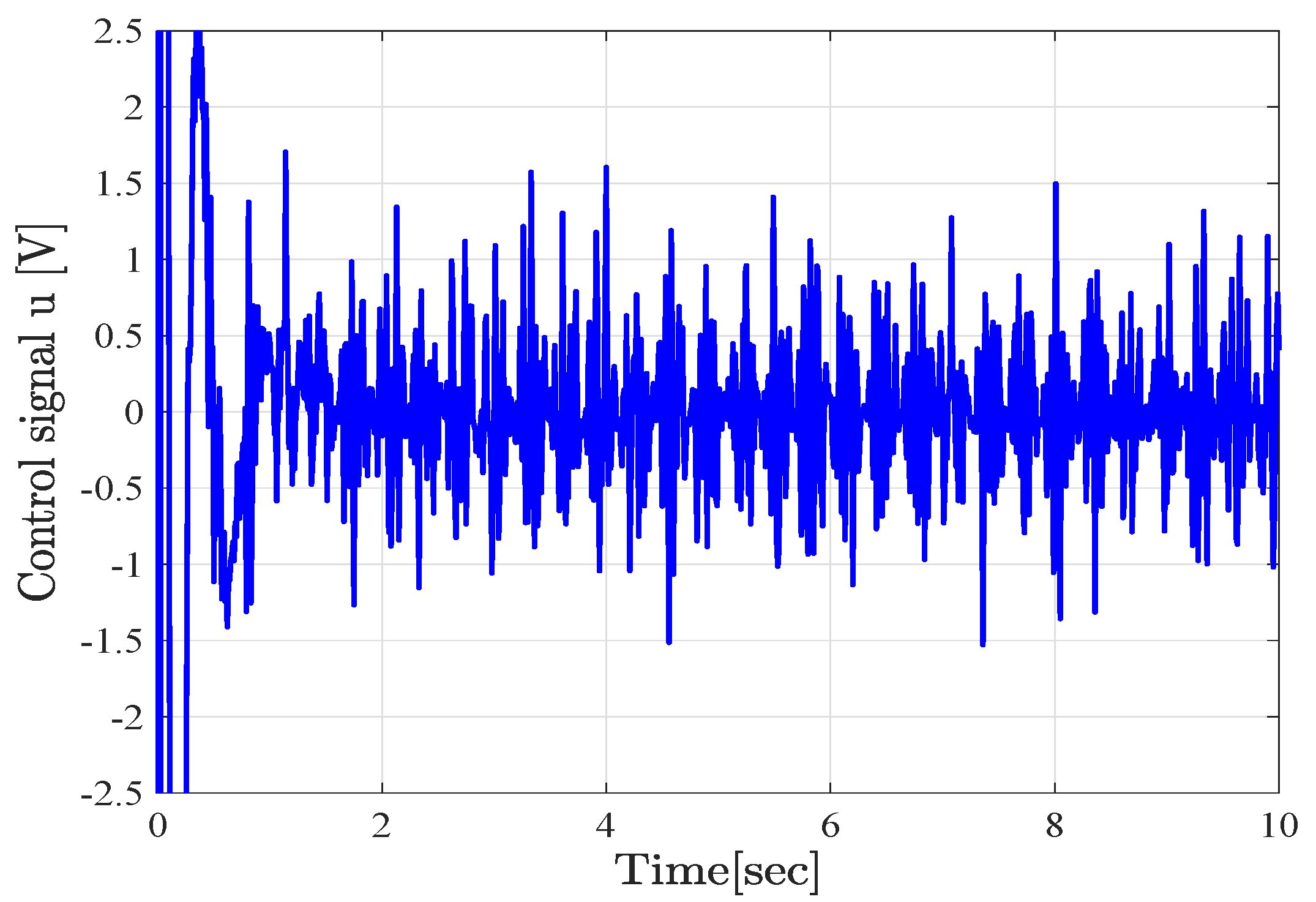
5.1.2. Experimental Results
5.2. Exemple 2
- Standard approach:
- Sliding window approach ():
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ho, D.; Lu, G. Robust stabilization for a class of discrete-time nonlinear systems via output feedback: The unified LMI approach. Int. J. Control 2003, 76, 105–115. [Google Scholar] [CrossRef]
- Auriol, J.; Di Meglio, F. Robust output feedback stabilization for two heterodirectional linear coupled hyperbolic PDEs. Automatica 2020, 115, 108896. [Google Scholar] [CrossRef]
- Kheloufi, H.; Bedouhene, F.; Zemouche, A.; Alessandri, A. Observer-based stabilisation of linear systems with parameter uncertainties by using enhanced LMI conditions. Int. J. Control 2015, 88, 1189–1200. [Google Scholar] [CrossRef] [Green Version]
- Monnet, D.; Ninin, J.; Clement, B. A global optimization approach to H∞ synthesis with parametric uncertainties applied to AUV control. In Proceedings of the IFAC World Congress, Toulouse, France, 9–14 July 2017; pp. 3953–3958. [Google Scholar]
- Kheloufi, H.; Zemouche, A.; Bedouhene, F.; Souley-Ali, H. A robust H∞ observer-based stabilization method for systems with uncertain parameters and Lipschitz nonlinearities. Int. J. Robust Nonlinear Control 2016, 26, 1962–1979. [Google Scholar] [CrossRef]
- Song, J.; He, S. Robust finite-time H∞ control for one-sided Lipschitz nonlinear systems via state feedback and output feedback. J. Frankl. Inst. 2015, 352, 3250–3266. [Google Scholar] [CrossRef]
- Ito, H.; Dinh, T.N. Interval observers for global feedback control of nonlinear systems with robustness with respect to disturbances. Eur. J. Control 2018, 39, 68–77. [Google Scholar] [CrossRef]
- Thabet, A.; Frej, G.B.H.; Boutayeb, M. Observer-based feedback stabilization for lipschitz nonlinear systems with extension to H∞ performance analysis: Design and experimental results. IEEE Trans. Control Syst. Technol. 2018, 26, 321–328. [Google Scholar] [CrossRef]
- Shao, K.; Zheng, J.; Huang, K.; Wang, H.; Man, Z.; Fu, M. Finite-Time Control of a Linear Motor Positioner Using Adaptive Recursive Terminal Sliding Mode. IEEE Trans. Ind. Electron. 2020, 67, 6659–6668. [Google Scholar] [CrossRef]
- Shao, K.; Zheng, J.; Wang, H.; Wang, X.; Lu, R.; Man, Z. Tracking Control of a Linear Motor Positioner Based on Barrier Function Adaptive Sliding Mode. IEEE Trans. Ind. Inform. 2021, 17, 7479–7488. [Google Scholar] [CrossRef]
- Mao, X.; Liu, W.; Hu, L.; Luo, Q.; Lu, J. Stabilization of hybrid stochastic differential equations by feedback control based on discrete-time state observations. Syst. Control Lett. 2014, 73, 88–95. [Google Scholar] [CrossRef] [Green Version]
- Gasmi, N.; Boutayeb, M.; Thabet, A.; Aoun, M. Enhanced LMI Conditions for Observer-Based H∞ Stabilization of Lipschitz Discrete-Time Systems. Eur. J. Control 2018, 44, 80–89. [Google Scholar] [CrossRef]
- Scholtz, E. Observer Based Monitors and Distributed Wave Controllers for Electromechanical Disturbances in Power Systems. Ph.D. Thesis, Massachusetts Institute Technology, Cambridge, MA, USA, 2004. [Google Scholar]
- Ibrir, S.; Xie, W.F.; Su, C.Y. Observer-based control of discrete-time Lipschitzian non-linear systems: Application to one-link flexible joint robot. Int. J. Control 2005, 78, 385–395. [Google Scholar] [CrossRef]
- Grandvallet, B.; Zemouche, A.; Boutayeb, M.; Changey, S. A sliding window filter for real-time attitude independent TAM calibration. In Proceedings of the 49th IEEE Conference on Decision and Control, Atlanta, GA, USA, 15–17 December 2010; pp. 467–472. [Google Scholar]
- Lin, W.; Byrnes, C. Remarks on linearization of discrete-time autonomous systems and nonlinear observer design. Syst. Control Lett. 1995, 25, 31–40. [Google Scholar] [CrossRef]
- Rajamani, R. Observer for Lipschitz nonlinear systems. IEEE Trans. Autom. Control 1998, 43, 397–401. [Google Scholar] [CrossRef]
- Ibrir, S. Static output feedback and guaranteed cost control of a class of discrete-time nonlinear systems with partial state measurements. Nonlinear Anal. Theory Methods Appl. 2008, 68, 1784–1792. [Google Scholar] [CrossRef]
- Grandvallet, B.; Zemouche, A.; Souley-Ali, H.; Boutayeb, M. New LMI Condition for Observer-Based H∞ Stabilization of a Class of Nonlinear Discrete-Time Systems. SIAM J. Control Optim. 2013, 51, 784–800. [Google Scholar] [CrossRef]
- Heemels, W.; Daafouz, J.; Millerioux, G. Observer-Based Control of Discrete-Time LPV Systems With Uncertain Parameters. IEEE Trans. Autom. Control 2010, 55, 2130–2135. [Google Scholar] [CrossRef] [Green Version]
- Grandvallet, B.; Zemouche, A.; Boutayeb, M.; Changey, S. Real-Time Attitude-Independent Three-Axis Magnetometer Calibration for Spinning Projectiles: A Sliding Window Approach. IEEE Trans. Control Syst. Technol. 2014, 22, 255–264. [Google Scholar] [CrossRef]
- Gasmi, N.; Boutayeb, M.; Thabet, A.; Aoun, M. Sliding Window Based Nonlinear H∞ Filtering: Design and Experimental Results. IEEE Trans. Circuits Syst. II Express Briefs 2019, 66, 302–306. [Google Scholar] [CrossRef]
- Zemouche, A.; Rajamani, R.; Phanomchoeng, G.; Boulkroune, B.; Rafaralahy, H.; Zasadzinski, M. Circle criterion-based H∞ observer design for Lipschitz and monotonic nonlinear systems–Enhanced LMI conditions and constructive discussions. Automatica 2017, 85, 412–425. [Google Scholar] [CrossRef] [Green Version]
- Ibrir, S.; Diopt, S. Novel LMI Conditions for observer-based stabilization of Lipschitzian nonlinear systems and uncertain linear systems in discrete-time. Appl. Math. Comput. 2008, 206, 579–588. [Google Scholar] [CrossRef]
- Petersen, I. A stabilization algorithm for a class of uncertain linear systems. Syst. Control Lett. 1987, 8, 351–357. [Google Scholar] [CrossRef]
- Spong, M. Modeling and control of elastic joint robots. Trans. ASME J. Dyn. Syst. Meas. Control 1987, 109, 310–319. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gasmi, N.; Boutayeb, M.; Thabet, A.; Bel Haj Frej, G.; Aoun, M. Robust Control of a Class of Nonlinear Discrete-Time Systems: Design and Experimental Results on a Real-Time Emulator. Actuators 2021, 10, 303. https://doi.org/10.3390/act10110303
Gasmi N, Boutayeb M, Thabet A, Bel Haj Frej G, Aoun M. Robust Control of a Class of Nonlinear Discrete-Time Systems: Design and Experimental Results on a Real-Time Emulator. Actuators. 2021; 10(11):303. https://doi.org/10.3390/act10110303
Chicago/Turabian StyleGasmi, Noussaiba, Mohamed Boutayeb, Assem Thabet, Ghazi Bel Haj Frej, and Mohamed Aoun. 2021. "Robust Control of a Class of Nonlinear Discrete-Time Systems: Design and Experimental Results on a Real-Time Emulator" Actuators 10, no. 11: 303. https://doi.org/10.3390/act10110303
APA StyleGasmi, N., Boutayeb, M., Thabet, A., Bel Haj Frej, G., & Aoun, M. (2021). Robust Control of a Class of Nonlinear Discrete-Time Systems: Design and Experimental Results on a Real-Time Emulator. Actuators, 10(11), 303. https://doi.org/10.3390/act10110303








