Robust Control Design Based on Perturbation Cancellation for Micro-Positioning Design with Hysteresis

Abstract

Based on the superiority of the piezoelectric elements, including lightweight, high electric mechanical transformation efficiency and a quick response time, a piezoelectric-based micro-positioning actuator is developed in this investigation. For eliminating the effects of hysteresis and modeling uncertainties that appeared in this micro-positioning actuator, a nonlinear adaptive fuzzy robust control design with a perturbation cancellation ability is proposed for this micro-positioning design to achieve a positioning resolution of 1 μm. Structurally, this proposed robust control methodology contains two particular parts: a universal fuzzy approximator and a robust compensator, which are employed to cancel the modeling uncertainties caused by the perturbed parts of the micro-positioning actuator and mitigate the approximation error between the modeling uncertainties and the universal fuzzy approximator, respectively. From both the numerical simulations and real validations, this proposed micro-positioning design performs a promising positioning performance in the micrometer level.

1. Introduction

Due to the ongoing development of the miniaturization of electronic elements and the dense integration of electronic chips on silicon wafers, there has been a tremendous and growing demand for more advanced and innovative micro/nano positioners in recent decades [1]. Implementations of micro/nano positioning systems have been exploited in numerous fields, including micro/nano manipulators [2]; aerial vehicles [3]; internal combustion engines [4]; image and optical systems [5]; and the applications involved in manufacturing communities and research disciplines, including mechanical systems [3,4], the semiconductor industry, and biotech, neuroscience, and materials science [6].

There exist several categories of micro/nano positioners, including the piezoelectric actuator [7], shape memory alloy (SMA) [8], electromagnetic actuator [9], electrostatic actuator [10], and electrothermal actuator [11], which are classified based on their mechanisms of actuation. Among all categories, much attention has been paid to the piezoelectric actuator owing to its superior characteristics, such as higher resolution in terms of displacement, overwhelming force [12], negligence of wear and tear [13], lightweight and high electric mechanical transformation efficiency [14], great stiffness, wide bandwidth, fast response, good stability, long lifespan, anti-electromagnetic interference [15], etc.

Except for these advantages, the piezoelectric actuator also attaches the harmful hysteresis effect, which results from its unique crystalline polarization effect [16]. The hysteresis effect induces a dynamic lag response between the input voltage and output displacement and demotes the linearity as well as the applicability of the piezoelectric actuator to perform high-accuracy positioning. Thereby, resolving the hysteresis effect of the piezoelectric actuator is one of the most considerable concerns in the micro-positioning design of piezoelectric-based actuators [17].

In the published literature, many approaches and methods regarding solving the hysteresis effect of piezoelectric actuators have been cultivated. These approaches and methods vary with the models and the controllers or compensators adopted on the piezoelectric-based micro-positioning actuators [17]. The mathematical representation of piezoelectric actuators mainly separates them into three approaches. One utilizes an operator modeling technique or polynomial technique, such as the Prandtl–Ishlinskii model, Preisach model, or Krasnoselskii–Pokrovskii model, to approximate the ascending and descending character of a hysteresis curve, while the Backslash model, Duhem model, and Bouc–Wen model aim to model a piezoelectric actuator through interpreting the system according to dynamic equations, with which it is easy to implement and determine the parameters of the dynamic equations to match the hysteresis curve. Among these three models, the Bouc–Wen model is presented with a set of first-order differential equations; it would be appropriate to apply them to the nonlinear control design of eliminating hysteresis. Several data-driven models based on neural networks have been proposed in the past decade [18,19,20]. Precise approximations for the hysteresis effect can be achieved, and an advantage of not knowing the inversion model of hysteresis can be obtained for developing the corresponding control laws via using neural network models of the above-mentioned published research. However, positioning error convergence and robustness properties with respect to modelling uncertainties and disturbances are not easy to guarantee from these designs, and higher computational power consumptions are always needed as well due to the structural complexities of adopted neural network models.

As to the control or compensated methods, Preisach- or Prandtl–Ishlinskii-based compensators [21,22,23] dominate the field. Through multiple operation points, the Preisach and Prandtl–Ishlinskii models transform the hysteresis curve of input–output coordinates into one-to-one mapping. As a result, an inversion-based compensator can reverse the one-to-one mapping, compensate for the dynamic lag, and then flatten the hysteresis curve. Nonetheless, the operator modeling approach requires a large amount of driven data, and its operation region is constrained by the operation points. On the other hand, control methods established on a set of first-order differential equations are more concrete from a structural perspective and are much easier to manipulate. It is also worth noting that there was an increasing trend of feedback control methods being applied in the design of piezoelectric actuators. By implementing an inversed-based compensator as an inner open loop and combining it with a feedback controller as an outer loop, several hybrid control methods have attempted to possess the advantages of inversed-based compensators in dealing with hysteresis and the closed-loop controller in converging tracking error according to time [24,25,26]. However, the overall control structures of these hybrid control methods are too complicated, and high calculation power is always required. Some feedback-linearization-based and sliding-model-based nonlinear controllers, which integrate the Bouc–Wen model for mitigating hysteresis, have been proposed recently [27,28], and these control designs have achieved acceptable micrometer positioning performances. Nevertheless, the dynamics of piezoelectric actuators in these investigations are assumed as exactly known functions without any parameter perturbations; hence, the effects of modelling uncertainties should not be considered in the control designs of these latest studies, and the robustness of these control designs cannot be guaranteed even though the Bouc–Wen model is used to compensate for the hysteresis of piezoelectric actuators. For the sake of achieving the control structure’s simplicity and a high positioning accuracy for the proposed micro-positioning system with modelling uncertainties, a nonlinear control methodology which integrates a Bouc–Wen model, a feedback linearization control law, an adaptive fuzzy approximator, and a robust compensator is exploited to actively cancel the uncertain perturbation and eliminate approximation errors and hysteresis without composing any inversed-based compensators. Based on the above arrangement, a nonlinear control method that possesses several good properties, including simplicity of the control structure, the global stability, the guaranteed convergence of positioning error, the guaranteed robustness with respect to modeling uncertainties, and the precise micro-positioning ability is delivered.

The organization of this investigation is arranged as follows: In Section 2, the hysteresis character of a used piezoelectric element and the dynamics of the micro-positioning actuator are briefly described. Derivation and proof of the proposed robust control design are revealed in Section 3. Next, simulation and discussion are investigated in Section 4, and the real verification is conducted in Section 5. Finally, the conclusion is made in Section 6.

2. Dynamics of the Controlled Piezoelectric Actuator

The micro-positioning actuator discussed in this investigation basically is constructed from the piezoelectric material. The Bouc–Wen model that is presented with a set of first-order differential equations is used to model the behavior of the piezoelectric material with the hysteresis effect. In the beginning, a brief introduction about hysteresis of piezoelectric material is given. Then, the dynamics of the overall micro-positioning actuator, which comprises of this piezoelectric material, will be formulated.

2.1. Hysteresis Effect

Hysteresis is a particular character of piezoelectric elements. As shown in Figure 1, the hysteresis loop of a controllable piezoelectric material is usually an unrepeated continuous loop that starts at the origin, saturates at a certain point, and lags to some degree when descending and ascending. Owing to this inherent property and the memory-like lagging dynamics, it is always a challenging issue to model hysteresis precisely and moderate the effect of hysteresis of the piezoelectric actuator.

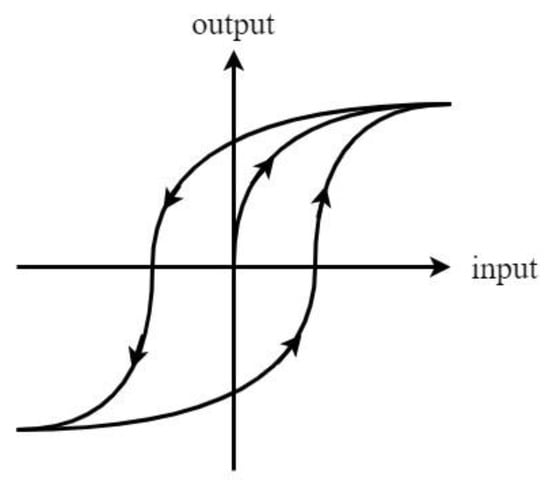
Figure 1. Illustration of the hysteresis loop.

2.2. Dynamic Model of Micro-Positioning Actuators

As depicted in Figure 2, except for the piezoelectric element, the micro-positioning actuator developed in this investigation consists of two symmetrical electrodes, A and B, and a fastener that can carry affordable loads. The micrometer displacement of the buckled fastener can be controlled by electrodes A and B.

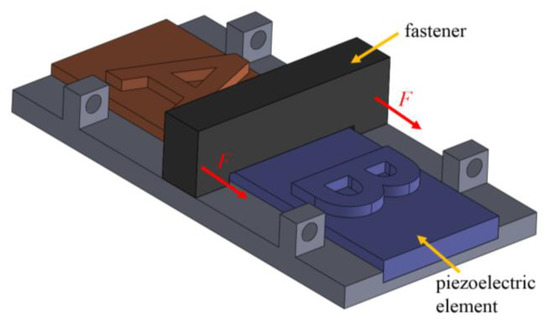
Figure 2. Schematics of a micro-positioning actuator with a piezoelectric element, a fastener, and two electrodes.

Theoretically, the dynamics of the piezoelectric-based micro-positioning actuator in Figure 3 are equivalent to a nonlinear spring–mass–damper system combining with a hysteresis model as plotted in Figure 3, and it could be presented by a set of differential equations such as:

$$m\ddot{z}+b\dot{z}+kz=k\left(du-l\right)$$

(1)

$$\dot{l}=\alpha d\dot{u}-\beta \left|\dot{u}\right|l{\left|l\right|}^{i-1}-\gamma \dot{u}{\left|l\right|}^i$$

(2)

$$y=z$$

(3)

where $m$, $b$, and $k$ denote the mass, the damping coefficient, and the stiffness of the equivalent spring–mass–damper system. Meanwhile, $l$ denotes the hysteretic displacement; parameters $d$, $\alpha$, $\beta$, and $\gamma$ are strictly positive coefficients; and $i$ denotes the transition state from elastic to plastic [29], where $i=1$ is chosen in general. The displacement of the micro-positioning actuator is defined as $z$. The derivative of $u$ physically denotes the input voltage of the controlled micro-positioning actuator, which is regarded as the real control input in this investigation. In the presence of modeling uncertainties, each system parameter ($m$, $b$, $k$, $d$, $\alpha$, $\beta$, and $\gamma$) is denoted as the combination of the nominal terms ($\overline{m}$, $\overline{b}$, $\overline{k}$, $\overline{d}$, $\overline{\alpha }$, $\overline{\beta }$, and $\overline{\gamma }$) and the perturbed terms: ($\tilde{m}$, $\tilde{b}$, $\tilde{k}$, $\tilde{d}$, $\tilde{\alpha }$, $\tilde{\beta }$, and $\tilde{\gamma }$), i.e., the system parameters can be expressed as $m=\overline{m}+\tilde{m}$, $b=\overline{b}+\tilde{b}$, $k=\overline{k}+\tilde{k}$, $d=\overline{d}+\tilde{d}$, $\alpha =\overline{\alpha }+\tilde{\alpha }$, $\beta =\overline{\beta }+\tilde{\beta }$, and $\gamma =\overline{\gamma }+\tilde{\gamma }$, respectively.

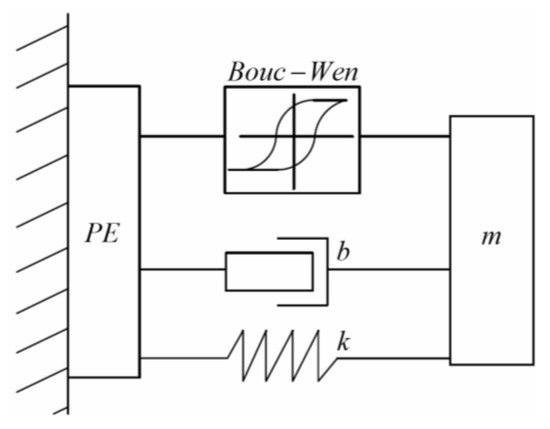
Figure 3. The equivalent illustration of a piezoelectric-based micro-positioning actuator.

3. Nonlinear Control Design of Micro-Positioning Actuators

For micro-positioning applications, development of an appropriate control scheme is the most crucial task, especially in facing of the modeling uncertainties (unmodeled dynamics or undetermined parameters). To begin with, a well-known feedback linearization (FL) control design is constructed with the nominal values: $\overline{m}$, $\overline{b}$, $\overline{k}$, $\overline{d}$, $\overline{\alpha }$, $\overline{\beta }$, and $\overline{\gamma }$; subsequently, it will be upgraded to a robust control form called adaptive fuzzy robust (AFR) control design for achieving the accurate micro-positioning. Concerning the existence of the modeling uncertainties, our control design objective is to cultivate a nonlinear controller for precisely converging the positioning error of the micro-positioning actuator at a micro-meter scale as small as possible.

We define the micro-positioning error as:

$$e=y-y_d$$

(4)

where $y_d\in C^{\infty }$ is the desired trajectory, which is continuously differentiable.

Taking the triple derivative for Equation (4), a third order error dynamic system with the control command $\dot{u}$ can be obtained:

$$\begin{array}{cc}\hfill \stackrel{⃛}{e}& =\stackrel{⃛}{y}-{\stackrel{⃛}{y}}_d\hfill \\ & =F\left(z\right)+G\left(z\right)\dot{u}-{\stackrel{⃛}{y}}_d\hfill \end{array}$$

(5)

where

$$\begin{gathered} F\left(z\right)=-\frac{b}{m}\ddot{z}-\frac{k}{m}\dot{z} \\ G\left(z\right)=\frac{k}{m}(d-\alpha d+\beta \mathrm{sgn}(\dot{u})l+\gamma \left|l\right|). \end{gathered}$$

3.1. Adaptive Fuzzy Robust Control Design with Respect to Unknown System Perturbations

Initially, if we assume all parameters of the dynamics of $F\left(z\right)$ and $G\left(z\right)$ in Equation (5) are exactly known, a feedback linearization control law can be easily derived as the following form:

$$\dot{u}=\frac{1}{G\left(z\right)}\left(-F\left(z\right)-{\lambda }_{0}e-{\lambda }_1\dot{e}-{\lambda }_2\ddot{e}+{\stackrel{⃛}{y}}_d\right)$$

(6)

Substituting Equation (6) into Equation (5), a third-order differential equation for the positioning error is obtained as below:

$$\stackrel{⃛}{e}+{\lambda }_2\ddot{e}+{\lambda }_1\dot{e}+{\lambda }_{0}e=0$$

(7)

Ideally, without considering the modeling uncertainties, the positioning error of the controlled micro-positioning actuator could be proven to asymptotically converge to zero if the control gains ${\lambda }_2$, ${\lambda }_1$, and ${\lambda }_0$ are appropriately chosen to let Equation (7) satisfy Hurwitz’s condition.

In practice, assuming all parameters of the dynamics of $F\left(z\right)$ and $G\left(z\right)$ are exactly known values is a strong assumption because parameters of piezoelectric elements are inevitably inconsistent after a batch manufacture and slight variations among piezoelectric elements can be found normally; hence, the perturbed terms ($\tilde{m}$, $\tilde{b}$, $\tilde{k}$, $\tilde{d}$, $\tilde{\alpha }$, $\tilde{\beta }$, and $\tilde{\gamma }$) do exist. For this reason, the feedback linearization control law in Equation (6) should be modified as:

$$\dot{u}=\frac{1}{\overline{G}\left(z\right)}\left(-\overline{F}\left(z\right)-{\lambda }_{0}e-{\lambda }_1\dot{e}-{\lambda }_2\ddot{e}+{\stackrel{⃛}{y}}_d\right)$$

(8)

where

$$\begin{gathered} \overline{F}\left(z\right)=-\frac{\overline{b}}{\overline{m}}\ddot{z}-\frac{\overline{k}}{\overline{m}}\dot{z} \\ \overline{G}\left(z\right)=\frac{\overline{k}}{\overline{m}}(\overline{d}-\overline{\alpha }\overline{d}+\overline{\beta }\mathrm{sgn}(\dot{u})l+\overline{\gamma }\left|l\right|). \end{gathered}$$

Based on the control law in Equation (8), dynamics of the positioning error for Equation (8) becomes a third-order differential equation with a perturbed input that is the integration of all modeling uncertainties:

$$\stackrel{⃛}{e}+{\lambda }_2\ddot{e}+{\lambda }_1\dot{e}+{\lambda }_{0}e=\omega$$

(9)

where $\omega$ is the overall modeling uncertainties caused by perturbed terms, and $\omega$ will be detailed in the following section.

Remark 1.

Obviously, the overall modeling uncertainties $\omega$strongly affect the convergence of the positioning error $e$and should be eliminated, and if the overall modeling uncertainties $\omega$can be perfectly canceled, the micro-positioning error in Equation (9) will asymptotically converge to zero.

3.2. Perturbation Elimination

From Remark 1, cancellation of modeling uncertainties would be the solution to the positioning problem of this micro-positioning actuator. For eliminating the effect of the overall modeling uncertainties $\omega$, a robust control law combined with an adaptive fuzzy approximator and a robust compensator with the perturbation elimination property is proposed. Merging the feedback linearization controller in Equation (8) with an adaptive fuzzy approximator $\widehat{\omega }\left(e,{\theta }_{\omega }\right)$ and a robust compensator $u_e$ yields a modified robust control law as the following:

$$\dot{u}=\frac{1}{\overline{G}\left(z\right)}\left(-\overline{F}\left(z\right)-\widehat{\omega }\left(e,{\theta }_{\omega }\right)+u_e+v+{\stackrel{⃛}{y}}_d\right)$$

(10)

where $v$ denotes a virtual controller that will expressed later, $u_e$ denotes a robust compensator, and the adaptive fuzzy approximator $\widehat{\omega }\left(e,{\theta }_{\omega }\right)$ that is utilized to approximate the overall modeling uncertainties $\omega$ can be expressed as a fuzzy regression form [30,31]:

$$\widehat{\omega }\left(e,{\theta }_{\omega }\right)={\theta }_{\omega }^T\xi \left(e\right)={\xi }^T\left(e\right){\theta }_{\omega }$$

(11)

where $\xi \left(e\right)$ is the fuzzy set vector, and ${\theta }_{\omega }$ is the tunable weight vector.

The optimal parameters ${\theta }_{\omega }^{*}$ of the parameters ${\theta }_{\omega }$ are denoted as:

$${\theta }_{\omega }^{*}=\arg \underset{{\theta }_{\omega }\in {\mathsf{\Omega }}_{\omega }}{\min }\left[\underset{e\in {\mathsf{\Omega }}_e}{\sup }\Vert \omega -\widehat{\omega }\left(e,{\theta }_{\omega }\right)\Vert \right]$$

(12)

where two suitable boundary sets for the parameter ${\theta }_{\omega }$ and the positioning error e are individually denoted as ${\mathsf{\Omega }}_{\omega }$ and ${\mathsf{\Omega }}_e$.

Remark 2.

It is worth mentioning that the number of fuzzy sets in$\xi \left(e\right)$is always a trade-off between the complexity of the approximator and the approximation capability. Normally, the more fuzzy sets that are applied, the more accurate approximation that can be obtained.

Details of the overall modeling uncertainties $\omega$ caused by the perturbed terms ($\tilde{m}$, $\tilde{b}$, $\tilde{k}$, $\tilde{d}$, $\tilde{\alpha }$, $\tilde{\beta }$, and $\tilde{\gamma }$) can be calculated as the following:

$$\omega =\left(F\left(z\right)-\overline{F}\left(z\right)\right)+\left(G\left(z\right)-\overline{G}\left(z\right)\right)\dot{u}$$

(13)

The overall modeling uncertainties $\omega$ can be approximated by using an adaptive fuzzy approximator $\widehat{\omega }\left(e,{\theta }_{\omega }^{*}\right)$ because of the universal approximation property of the fuzzy system in Equation (11) [30,31], and the remained approximation error can be presented as:

$${\omega }_a=\omega -\widehat{\omega }\left(e,{\theta }_{\omega }^{*}\right)$$

(14)

Substituting the modified robust control law in Equation (10) into dynamics of positioning error in Equation (5), we get:

$$\stackrel{⃛}{e}=v+\left(\widehat{\omega }\left(e,{\theta }_{{}_{\omega }}^{*}\right)-\widehat{\omega }\left(e,{\theta }_{\omega }\right)\right)+u_e+{\omega }_a$$

(15)

Or equivalently,

$$\dot{E}=v+B{\xi }^T\left(e\right){\tilde{\theta }}_{\omega }+B{u}_e+B{\omega }_a$$

(16)

where ${\tilde{\theta }}_{\omega }={\theta }_{\omega }^{*}-{\theta }_{\omega }$ is the parameter error vector, $E={\left[\begin{array}{ccc}e& \dot{e}& \ddot{e}\end{array}\right]}^T$, $B={\left[\begin{array}{ccc}0& 0& 1\end{array}\right]}^T$, $v=AE$ and

$$A=\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ -{\lambda }_0& -{\lambda }_1& -{\lambda }_2\end{array}\right]$$

in which, ${\lambda }_i>0$, for i = 0, 1, and 2.

The positioning problem of the proposed micro-positioning actuator with parameter perturbations is equivalent to optimize the H_∞ performance index denoted as the following form:

$$\underset{{\omega }_a\in L_2\left[0,t_f\right]}{\max }\underset{u_e\in L_2\left[0,t_f\right]}{\min }\frac{{\displaystyle {\int }_0^{t_f}\left[\begin{array}{l}{E}^T\left(t\right)QE\left(t\right)+u_e^T\left(t\right)R{u}_e\left(t\right)\\ +\frac{1}{r_{\omega }}{\tilde{\theta }}_{\omega }^T\left(t\right){\tilde{\theta }}_{\omega }\left(t\right)\end{array}\right]}dt }{{\displaystyle {\int }_0^{t_f}{\omega }_a^T\left(t\right){\omega }_a\left(t\right)}dt}\le {\rho }^2$$

(17)

Or equivalently,

$$\underset{{\omega }_a\in L_2\left[0,t_f\right]}{\max }\underset{u_e\in L_2\left[0,t_f\right]}{\min }{\displaystyle {\int }_0^{t_f}\left[\begin{array}{c}{E}^T\left(t\right)QE\left(t\right)+u_e^T\left(t\right)R{u}_e\left(t\right)\\ +\frac{1}{r_{\omega }}{\tilde{\theta }}_{\omega }^T\left(t\right){\tilde{\theta }}_{\omega }\left(t\right)\hfill \end{array}\right]}dt \le {\rho }^2{\displaystyle {\int }_0^{t_f}{\omega }_a^T\left(t\right){\omega }_a\left(t\right)}dt$$

(18)

where $t_f$ denotes the final time of the positioning process, $Q$ and R denote as strictly symmetric positive-definite weighting matrices, $r_{\omega }>0$ stands for a strictly positive scalar, and $\rho$ is the attenuation level for measuring the worst-case effect of the overall modeling uncertainties ${\omega }_a$ on the system output $z$. Normally, a value between 0 and 1 is the proper region of the attenuation value $\rho$ for a robust positioning design.

Furthermore, if the initial values are considered, then inequality in Equation (18) can be modified as:

$$\begin{array}{c}\underset{{\omega }_a\in L_2\left[0,t_f\right]}{\max }\underset{u_e\in L_2\left[0,t_f\right]}{\min }{\displaystyle {\int }_0^{t_f}\left[E^T\left(t\right)QE\left(t\right)+u_e^T\left(t\right)R{u}_e\left(t\right)\right]}dt\\ \le E^T\left(0\right)PE\left(0\right)+\frac{1}{r_{\omega }}{\tilde{\theta }}_{\omega }^T\left(0\right){\tilde{\theta }}_{\omega }\left(0\right)+{\rho }^2{\displaystyle {\int }_0^{t_f}{\omega }_a^T\left(t\right){\omega }_a\left(t\right)}dt\end{array}$$

(19)

where $P=P^T>0$ is a weighting matrix for the initial value of the error system $E\left(0\right)$.

Theorem 1.

The robust positioning problem of the proposed micro-positioning actuator with parameter perturbations can be solved, if the following adaptive fuzzy robust control law is applied for the nonlinear perturbed dynamics of the micro-positioning actuator in Equations (1)–(3):

$$\dot{u}=\frac{1}{\overline{G}\left(z\right)}\left(-\overline{F}\left(z\right)+{\xi }^T\left(e\right){\theta }_{\omega }+u_e+v+{\stackrel{⃛}{y}}_d\right)$$

(20)

where

$$u_e=-R^{-1}{B}^{T}PE$$

(21)

$${\dot{\theta }}_{\omega }=r_{\omega }\xi \left(e\right)B^{T}PE$$

(22)

As to the matrix $P=P^T>0$, it is the solution of the following Riccati-like equation:

$$PA+A^{T}P+Q+PB\left(\frac{1}{{\rho }^2}I-R^{-1}\right)B^{T}P=0$$

(23)

Proof of Theorem 1.

Choose a Lyapunov candidate as:

$$V=\frac{1}{2}{E}^{T}PE+\frac{1}{2r_{\omega }}{\tilde{\theta }}_{\omega }^T{\tilde{\theta }}_{\omega }$$

(24)

The time derivative of $V$ is:

$$\dot{V}=\frac{1}{2}\left({\dot{E}}^{T}PE+E^{T}P\dot{E}\right)+\frac{1}{r_{\omega }}{\dot{\tilde{\theta }}}_{\omega }^T{\tilde{\theta }}_{\omega }$$

(25)

Substituting Equations (16) and (21) into Equation (25), we obtain:

$$\begin{array}{cc}\hfill \dot{V}& =\frac{1}{2}{\left(v+B{\xi }^T\left(e\right){\tilde{\theta }}_{\omega }+B{u}_e+B{\omega }_a\right)}^{T}PE\hfill \\ & +\frac{1}{2}{E}^{T}P\left(v+B{\xi }^T\left(e\right){\tilde{\theta }}_{\omega }+B{u}_e+B{\omega }_a\right)+\frac{1}{r_{\omega }}{\dot{\tilde{\theta }}}_{\omega }^T{\tilde{\theta }}_{\omega }\hfill \\ & =\frac{1}{2}{E}^T\left(A^{T}P+PA\right)E-\frac{1}{2}{E}^T\left(PB{R}^{-1}{B}^{T}P+PB{R}^{-1}{B}^{T}P\right)E\hfill \\ & +\frac{1}{2}{\tilde{\theta }}_{\omega }{}^T\xi \left(e\right)B^{T}P{E}^T+\frac{1}{2}{E}^{T}PB{\xi }^T\left(e\right){\tilde{\theta }}_{\omega }\hfill \\ & +\frac{1}{r_{\omega }}{\dot{\tilde{\theta }}}_{\omega }^T{\tilde{\theta }}_{\omega }+\frac{1}{2}{\omega }_a^T{B}^{T}PE+\frac{1}{2}{E}^{T}PB{\omega }_a\hfill \end{array}$$

(26)

Noticing that Equation (21) can simplify the term $E^{T}PB{R}^{-1}{B}^{T}PE$, we thus obtain:

$$\begin{array}{cc}\hfill \dot{V}& =\frac{1}{2}{E}^T\left(A^{T}P+PA-PB{R}^{-1}{B}^{T}P\right)E-\frac{1}{2}{u}_e^{T}R{u}_e\hfill \\ & +\frac{1}{2}{\tilde{\theta }}_{\omega }{}^T\xi \left(e\right)B^{T}P{E}^T+\frac{1}{2}{E}^{T}PB{\xi }^T\left(e\right){\tilde{\theta }}_{\omega }+\frac{1}{r_{\omega }}{\dot{\tilde{\theta }}}_{\omega }^T{\tilde{\theta }}_{\omega }+\frac{1}{2}{\omega }_a^T{B}^{T}PE+\frac{1}{2}{E}^{T}PB{\omega }_a\hfill \end{array}$$

(27)

Since ${\dot{\tilde{\theta }}}_{\omega }=-{\dot{\theta }}_{\omega }$, Equation (27) can be rewritten as:

$$\begin{array}{cc}\hfill \dot{V}& =\frac{1}{2}{E}^T\left(A^{T}P+PA-PB{R}^{-1}{B}^{T}P\right)E-\frac{1}{2}{u}_e^{T}R{u}_e\hfill \\ & +\frac{1}{2}{\tilde{\theta }}_{\omega }{}^T\xi \left(e\right)B^{T}P{E}^T+\frac{1}{2}{E}^{T}PB{\xi }^T\left(e\right){\tilde{\theta }}_{\omega }-\frac{1}{r_{\omega }}{\dot{\theta }}_{\omega }^T{\tilde{\theta }}_{\omega }\hfill \\ & +\frac{1}{2}{\omega }_a^T{B}^{T}PE+\frac{1}{2}{E}^{T}PB{\omega }_a\hfill \end{array}$$

(28)

Moreover, it is easy to check out that ${\tilde{\theta }}_{\omega }{}^T\xi \left(e\right)B^{T}P{E}^T=E^{T}PB{\xi }^T\left(e\right){\tilde{\theta }}_{\omega }$; therefore, Equation (28) can be rearranged as:

$$\begin{array}{cc}\hfill \dot{V}& =\frac{1}{2}{E}^T\left(A^{T}P+PA-PB{R}^{-1}{B}^{T}P\right)E-\frac{1}{2}{u}_e^{T}R{u}_e\hfill \\ & +\left(E^{T}PB{\xi }^T\left(e\right)-\frac{1}{r_{\omega }}{\dot{\theta }}_{\omega }^T\right){\tilde{\theta }}_{\omega }\hfill \\ & +\frac{1}{2}{\omega }_a^T{B}^{T}PE+\frac{1}{2}{E}^{T}PB{\omega }_a\hfill \end{array}$$

(29)

Inserting the adaptive law in Equation (22) into Equation (29) yields:

$$\begin{array}{cc}\hfill \dot{V}& =\frac{1}{2}{E}^T\left(A^{T}P+PA-PB{R}^{-1}{B}^{T}P\right)E-\frac{1}{2}{u}_e^{T}R{u}_e+\frac{1}{2}{\omega }_a^T{B}^{T}PE+\frac{1}{2}{E}^{T}PB{\omega }_a\hfill \\ & =\frac{1}{2}{E}^T\left(A^{T}P+PA-PB{R}^{-1}{B}^{T}P\right)E-\frac{1}{2}{u}_e^{T}R{u}_e+\frac{1}{2}{\omega }_a^T{B}^{T}PE+\frac{1}{2}{E}^{T}PB{\omega }_a\hfill \\ & +\frac{1}{2{\rho }^2}{E}^{T}PB{B}^{T}PE-\frac{1}{2{\rho }^2}{E}^{T}PB{B}^{T}PE\hfill \\ & =\frac{1}{2}{E}^T\left(A^{T}P+PA+PB\left(\frac{1}{{\rho }^2}I-R^{-1}\right)B^{T}P\right)E-\frac{1}{2{\rho }^2}{E}^{T}PB{B}^{T}PE\hfill \\ & -\frac{1}{2}{u}_e^{T}R{u}_e+\frac{1}{2}{\omega }_a^T{B}^{T}PE+\frac{1}{2}{E}^{T}PB{\omega }_a\hfill \end{array}$$

(30)

Based on the result of Equation (23), the following result can be found:

$$\begin{array}{cc}\hfill \dot{V}& =-\frac{1}{2}{E}^{T}QE-\frac{1}{2}{u}_e^{T}R{u}_e\hfill \\ & -\frac{1}{2{\rho }^2}{E}^{T}PB{B}^{T}PE+\frac{1}{2}{\omega }_a^T{B}^{T}PE+\frac{1}{2}{E}^{T}PB{\omega }_a\hfill \\ & -\frac{1}{2}{\rho }^2{\omega }_a^T{\omega }_a+\frac{1}{2}{\rho }^2{\omega }_a^T{\omega }_a\hfill \\ & =-\frac{1}{2}{E}^{T}QE-\frac{1}{2}{u}_e{}^{T}R{u}_e\hfill \\ & -\frac{1}{2}{\left(\frac{1}{\rho }{B}^{T}PE-\rho {\omega }_a\right)}^T\left(\frac{1}{\rho }{B}^{T}PE-\rho {\omega }_a\right)+\frac{1}{2}{\rho }^2{\omega }_a^T{\omega }_a\hfill \end{array}$$

(31)

If the worst-case perturbation equals ${\omega }_a=\frac{1}{{\rho }^2}{B}^{T}PE$, then Equation (31) can be presented as a concise form as:

$$\dot{V}\le -\frac{1}{2}{E}^{T}QE-\frac{1}{2}{u}_e^{T}R{u}_e+\frac{1}{2}{\rho }^2{\omega }_a^T{\omega }_a$$

(32)

Integrating Equation (32) from $t=0$ to $t=t_f$, we obtain:

$$V\left(t_f\right)-V\left(0\right)\le -\frac{1}{2}{\displaystyle {\int }_0^{t_f}\left[E{\left(t\right)}^{T}QE\left(t\right)+u_e^T\left(t\right)R{u}_e\left(t\right)\right]dt} +\frac{{\rho }^2}{2}{\displaystyle {\int }_0^{t_f}{\omega }_a^T\left(t\right){\omega }_a\left(t\right) dt}$$

(33)

Since $V\left(t_f\right)\ge 0$, the above inequality indicates the following fact:

$$\begin{array}{cc}& \frac{1}{2}{\displaystyle {\int }_0^{t_f}\left[E^T\left(t\right)QE\left(t\right)+u_e{}^T\left(t\right)R{u}_e\left(t\right)\right]}dt \hfill \\ & \le \frac{1}{2}{E}^T\left(0\right)PE\left(0\right)+\frac{1}{2r_{\omega }}{\tilde{\theta }}_{\omega }^T\left(0\right){\tilde{\theta }}_{\omega }\left(0\right)+\frac{{\rho }^2}{2}{\displaystyle {\int }_0^{t_f}{\omega }_a^T\left(t\right){\omega }_a\left(t\right)}dt \hfill \end{array}$$

(34)

Obviously, Equation (34) can be described as the following equivalent form:

$$\begin{array}{cc}& {\displaystyle {\int }_0^{t_f}\left[E^T\left(t\right)QE\left(t\right)+u_e{}^T\left(t\right)R{u}_e\left(t\right)\right]dt}\hfill \\ & \le E^T\left(0\right)PE\left(0\right)+\frac{1}{r_{\omega }}{\tilde{\theta }}_{\omega }^T\left(0\right){\tilde{\theta }}_{\omega }\left(0\right)+{\rho }^2{\displaystyle {\int }_0^{t_f}{\omega }_a^T\left(t\right){\omega }_a\left(t\right) dt}\hfill \end{array}$$

(35)

Equation (35) is the same as Equation (19); hence, the proof of Theorem 1 is completed. □

4. Simulation and Discussion

4.1. Parameters of the Micro-Positioning Actuator and the Proposed Controller

By means of the particle swarm optimization (PSO) method, the nominal parameters of the micro-positioning actuator can be identified and listed in Table 1. To control parameters of this proposed method, they are resolved by a Ricatti solver that is provided in the control toolbox of the simulation platform MATLAB R2020b (Tainan, R.O.C.) and all related control parameters are listed in Table 2.

Table 1. Nominal parameters of the proposed micro-positioning actuator.

Parameter	Value	Unit
$\overline{m}$	$0.128$	$kg$
$\overline{b}$	$1.58\times {10}^1$	$Ns/m$
$\overline{k}$	$1.957\times {10}^3$	$N/m$
$\overline{d}$	$1.734\times {10}^{-6}$	$m/V$
$\overline{\alpha }$	$0.358$
$\overline{\beta }$	$0.036$
$\overline{\gamma }$	$0.027$

Table 2. Fuzzy membership functions and control parameters of this proposed method.

Fuzzy Membership Functions
$\begin{array}{cc}\begin{array}{l}{\xi }_{\omega }{}_{{}_1}=\left[\exp \left(\frac{-{\Vert e-c_j\cdot {10}^{-6}\Vert }^2}{r}\right),\dots ,\exp \left(\frac{-{\Vert e-c_j\cdot {10}^{-6}\Vert }^2}{r}\right)\right],\\ {\xi }_{\omega }{}_{{}_2}=\left[\exp \left(\frac{-{\Vert \dot{e}-d_j\cdot {10}^{-6}\Vert }^2}{r}\right),\dots ,\exp \left(\frac{-{\Vert \dot{e}-d_j\cdot {10}^{-6}\Vert }^2}{r}\right)\right]\end{array}& \begin{array}{cc}for& j=1,\dots ,21\end{array} \end{array}$
${\xi }_{\omega }=\left[\begin{array}{cc}{\xi }_{\omega }{}_{{}_1}& {\xi }_{\omega }{}_{{}_2}\end{array}\right]$
$c_1=-10,c_2=-9,\dots ,c_{20}=9,c_{21}=10$ $d_1=-10,d_2=-9,\dots ,d_{20}=9,d_{21}=10$
$r={10}^{-12}$ $r_{\omega }=100$
$\mathrm{Parameters} \mathrm{of} \mathrm{the} \mathrm{robust} \mathrm{compensator} u_e$
$\rho =0.5$ $R=0.01$
$Q=\left[\begin{array}{ccc}{10}^4& 0& 0\\ 0& {10}^3& 0\\ 0& 0& {10}^2\end{array}\right]$ $r_{\omega }=10$
Parameters of the virtual controller v ${\lambda }_0=10, {\lambda }_1=8, {\lambda }_2=6$

4.2. Simulation Results

In the following simulation verification, micrometer positioning performances of two developed control laws—1. feedback linearization (FL) control law and 2. adaptive fuzzy robust (AFR) control law—will be compared. The feedback linearization (FL) and adaptive fuzzy robust (AFR) methods are realized by using Equations (8) and (10), and related control parameters adopted for constructing the feedback linearization (FL) and the adaptive fuzzy robust (AFR) control laws are listed in Table 2. For validating the micrometer positioning performance, two desired trajectories, including a trapezoid-type trajectory (with the magnitude of ±90 μm) and a sinusoid-type trajectory (with the magnitude of ±100 μm and a frequency of π/3), are used. Concerning the arrangements of the model perturbed uncertainties ($\tilde{m}$, $\tilde{b}$, $\tilde{k}$, $\tilde{d}$, $\tilde{\alpha }$, $\tilde{\beta }$, and $\tilde{\gamma }$) in the following scenarios, ±1% random perturbations are set up for perturbed terms ($\tilde{m}$, $\tilde{b}$, $\tilde{k}$, $\tilde{d}$, $\tilde{\alpha }$, $\tilde{\beta }$, and $\tilde{\gamma }$) individually. The reason why only ±1% random perturbations are considered for these perturbed terms is that the feedback linearization (FL) design will diverge for a micro-positioning actuator with perturbed bounds beyond this value. Furthermore, a time-varying positive nominal perturbation will be added on the nominal value $\overline{m}$ of the actuator mass for performing the practical situation that fastener on the micro-positioning actuator in Figure 2 carries different loads.

In total, two simulative scenarios will be conducted and discussed in this section:

Scenario 1:

A trapezoid-type trajectory with the magnitude of ±90 μm is used as the desired trajectory. Moreover, ±1% random perturbations are arranged for perturbed terms ($\tilde{m}$, $\tilde{b}$, $\tilde{k}$, $\tilde{d}$, $\tilde{\alpha }$, $\tilde{\beta }$, and $\tilde{\gamma }$) and, a positive perturbation (20% of $\overline{m}$) is added for the mass $m$ during 0–5 s and 10–19 s.

Scenario 2:

A sinusoid-type trajectory with the magnitude of ±100 μm and a fixed frequency of π/3 is applied as the desired trajectory. Moreover, ±1% random perturbations are set up for perturbed terms ($\tilde{m}$, $\tilde{b}$, $\tilde{k}$, $\tilde{d}$, $\tilde{\alpha }$, $\tilde{\beta }$, and $\tilde{\gamma }$), and a fixed 20% positive nominal perturbation is arranged for the mass $m$.

In the following, discussions for both scenarios will be detailed individually.

Scenario 1:

Figure 4, Figure 5 and Figure 6 are the simulation results of the feedback linearization (FL) and the adaptive fuzzy robust (AFR) methods for Scenario 1. Initial positions of the controlled micro-positioning actuator for these two control methods are set up as 10 μm. From Figure 4, it is easy to find out that the controlled output displacement z of the proposed adaptive fuzzy robust (AFR) method precisely follows the desired trajectory. However, the tracking result of the feedback linearization (FL) method is worse due to modeling uncertainties $\omega$ caused by the dopped system parameters’ perturbations. Rapid convergence of the positioning error revealed in Figure 5 for the proposed method shows us the exponential convergent property of this proposed method in positioning errors. Additionally, a slight positioning error can be spotted in transient responses of each turning point when tracking the desired trapezoid-type trajectory, but all positioning errors vanish within a few seconds.

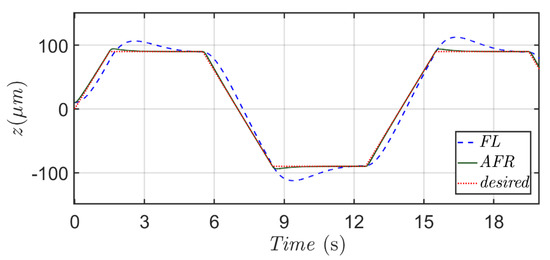
Figure 4. Micro-positioning results of output displacement z based on the proposed method (green line) and feedback linearization method (blue dash line) with respect to a desired trapezoid trajectory (red dotted line).

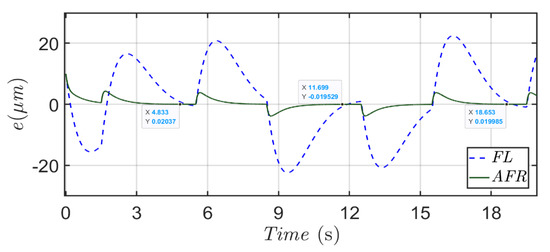
Figure 5. Histories of positioning errors for the proposed method (green line) and feedback linearization method (blue dash line) with respect to a desired trapezoid trajectory.

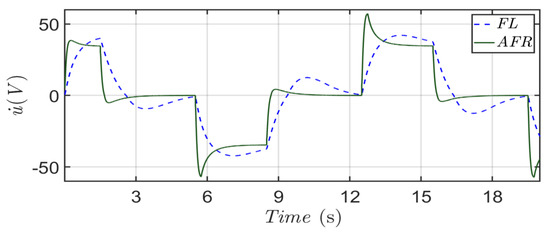
Figure 6. Histories of the overall control commands of the proposed method and feedback linearization method.

Figure 6 displays the overall control commands of feedback linearization (FL) and adaptive fuzzy robust (AFR) method, respectively. As shown in Figure 6, the range of the control inputs is within (−100 V, 50 V) for these two methods. Both of these two methods have the same tendency in control commands, but the feedback linearization (FL) method cannot generate proper control commands for achieving the micro-positioning mission in Scenario 1.

As displayed in Figure 7, a positive perturbation (20% of $\overline{m}$) is added for the mass $m$ during 0–5 s and 10–19 s for the micro-positioning verification of Scenario 1.

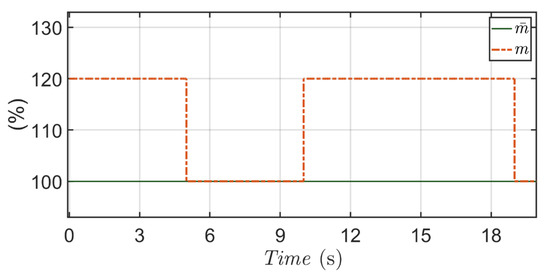
Figure 7. A time-varying positive perturbation (20% of $\overline{m}$) is added for $m$ during 0–5 s and 10–19 s (red dotted line) in Scenario 1.

The original model functions $F$ and $G$ described by using the nominal values and perturbed values for Scenario 1 are displayed with respect to $\overline{F}$ and $\overline{G}$ in Figure 8, respectively. From the comparisons in Figure 8, biases and model distortions caused by the time-varying variation of mass and 1% random perturbations for the other parameters can be easily observed. These perturbations in model functions downgrade the micro-positioning performance of the feedback linearization (FL) method that always requires the exact model functions. However, as shown in Figure 4 and Figure 5, modeling uncertainties $\omega$ due to these parameters’ variations do not influence the micro-positioning performance of the proposed method that integrates an adaptive fuzzy approximator $\widehat{\omega }\left(e,{\theta }_{\omega }\right)$ and a robust compensator u_e.

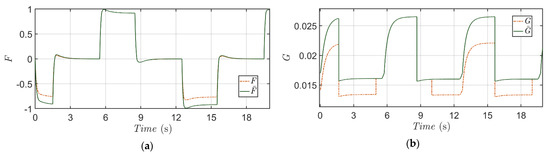
Figure 8. Comparisons of model functions $F$ and $G$ (green line) with $\overline{F}$ and $\overline{G}$ (red dotted line) in Scenario 1. (a) $F$ and $\overline{F}$, (b) $G$ and $\overline{G}$.

Scenario 2:

In Scenario 2, one more tough testing is examined in order to verify the robustness of this proposed method corresponding to a highly varying trajectory and modeling uncertainties. Figure 9 and Figure 10 are the simulation results of the feedback linearization (FL) method and the proposed method for Scenario 2. As the setting in Scenario 2, a sinusoid-type trajectory is adopted along with a fixed 20% variation of $\overline{m}$ being added on the mass m and 1% random variations being dopped to system parameters ($\tilde{m}$, $\tilde{b}$, $\tilde{k}$, $\tilde{d}$, $\tilde{\alpha }$, $\tilde{\beta }$, and $\tilde{\gamma }$). Initial positions of the micro-positioning actuator for these two control methods are set up as 10 μm in this case. From Figure 9, it is easy to find out that the micro-positioning of the proposed method precisely follows the desired trajectory. However, the positioning result of the feedback linearization (FL) method is worse, and a harmonic type positioning error appears (>1 μm) due to the dopped system parameters’ perturbations in Figure 10. Similar to the results in of Scenario 1, a rapid convergence of the positioning error to near zero can be found from Figure 10 for the proposed method under the effect of modeling uncertainties, and these results show us the exponential convergent property in positioning error and the robustness property of this proposed method.

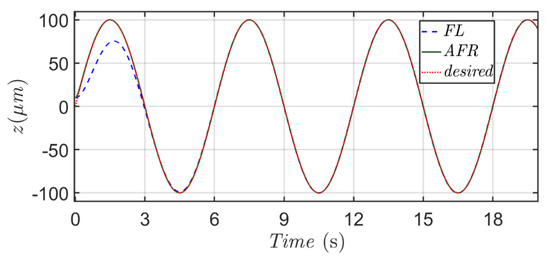
Figure 9. Micro-positioning results of output displacement z based on the proposed method (green line) and feedback linearization method (blue dash line) with respect to a desired sinusoidal trajectory.

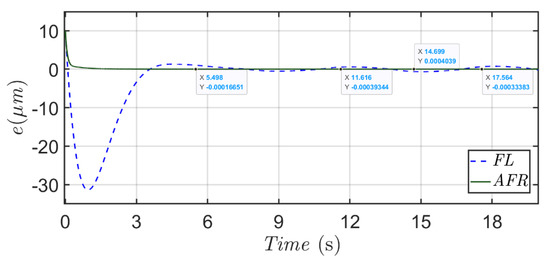
Figure 10. Histories of positioning errors for the proposed method (green line) and feedback linearization method (blue dash line) with respect to a desired sinusoidal trajectory.

Figure 11 displays the overall control commands of feedback linearization method and the proposed method, respectively. According to Figure 11, the control outputs are bounded around (−100 V, 100 V) for these two methods. Both methods have a similar sinusoidal profile in control commands, but the feedback linearization method cannot output appropriate control commands for achieving the micro-positioning requirement of Scenario 2.

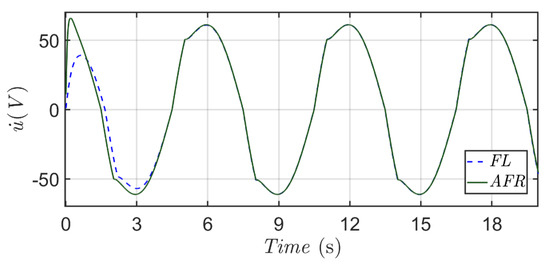
Figure 11. Histories of the overall control commands of the proposed method and feedback linearization method.

In this Scenario (Figure 12), a fixed 20% positive nominal perturbation is arranged for the mass $m$ for the purpose of verifying the micro-positioning performance of the proposed method.

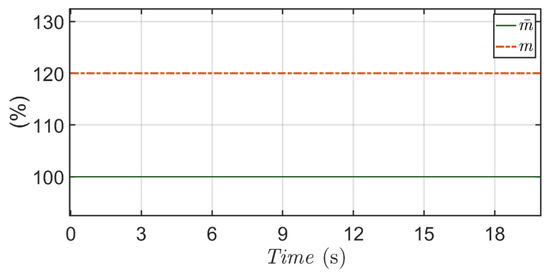
Figure 12. A fixed positive perturbation (20% of $\overline{m}$) is added for $m$ in Scenario 2.

Model functions $F$ and $G$ with the nominal values and perturbed values for Scenario 2 are displayed in Figure 13. From the comparisons in Figure 13, biases and model distortions caused by the 20% variation of mass and 1% random perturbation for the model parameters can be easily observed. These perturbations in model functions downgrade the micro-positioning performance of the feedback linearization (FL) method that always requires the exact model functions. However, as shown in Figure 9 and Figure 10, modeling uncertainties $\omega$ due to these parameters’ random variations do not affect the micro-positioning performance of the proposed method that integrates an adaptive fuzzy approximator and a robust compensator.

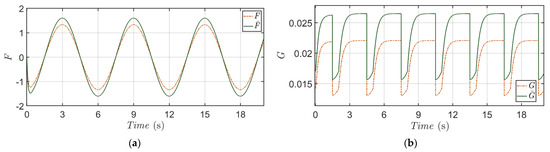
Figure 13. Comparisons of model functions $F$ and $G$ (green line) with $\overline{F}$ and $\overline{G}$ (red dotted line) in Scenario 2. (a) $F$ and $\overline{F}$, (b) $G$ and $\overline{G}$.

Obviously, from Scenarios 1 and 2, the proposed method outperforms the feedback linearization (FL) method for tracking a sinusoid-type and a trapezoid-type trajectory under effects of the above-mentioned modeling uncertainties and hysteresis. Significantly, this proposed method delivers a positioning accuracy of nanoscale (maximum 20 nm for scenario 1 and 0.4 nm for Scenario 2) which is far outstripping the required micro-positioning specification: “micrometer”.

5. Validation of Real Micro-Positioning System

For validation of the micrometer-level positioning ability of this proposed method, a micro-positioning platform integrates a mover (piezoelectric-based actuator), a position measuring system that has a resolution of 1 μm, a driving system, and a desktop for calculating the proposed control algorithm. These are exhibited in Figure 14b. The piezoelectric-based actuator used as a mover of loads and made of the piezoelectric element and a fastener is installed (as shown in Figure 14a) and the maximum range of this mover’s movable displacement is within (−5000 μm, 5000 μm). The black object mounted on the fastener of this mover is the added load, and its weight is 20% of the nominal mass. The above setting is established to verify the robustness of this proposed micro-positioning method with respect to a fixed modeling uncertainty. Electrodes A and B are set up on each side of the fastener symmetrically to precisely control the piezoelectric element to drive the loaded fastener to move along the x-direction forward or backward. The driving system contains a voltage amplifier, named THS4011, that can be adjusted via the digital signal processor DSP F28335. As for the desktop, it is used for realizing the real-time calculation of the proposed adaptive fuzzy robust control command. The communication between the digital signal processor DSP F28335 and the desktop will bear on the emulator through which the real-time feedback position of the load mounted on the fastener measured by Microtrack 7000, and the calculated control command of the desktop is transmitted. For practical verifications, three scenarios are arranged as:

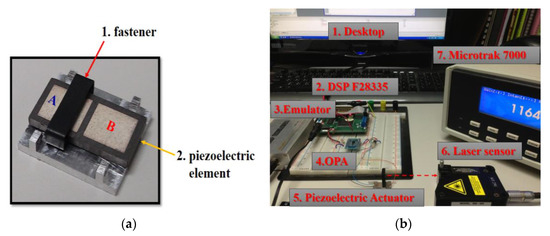
Figure 14. Experimental installation of the proposed micro-positioning design: (a) a piezoelectric-based actuator and (b) the overall micro-positioning system with a position measuring system, a piezoelectric-based actuator, and the proposed adaptive fuzzy robust control law carried out in the desktop.

Scenario 3:

A stair-type trajectory with magnitudes: −500 μm to 500 μm, is set up.

Scenario 4:

A trapezoidal-type trajectory with magnitudes: 0 μm to 1000 μm, is set up.

Scenario 5:

A sinusoidal-type trajectory with magnitudes: −300 μm to 300 μm, is preset up.

Initial value:

The initial position of the fastener with a load is set up at 0 μm for all these scenarios.

Figure 15 reveals the micro-positioning result with respect to the desired stair-type trajectory which is with magnitudes: 500 μm ∈ (0 s, 6 s), −500 μm ∈ (6 s, 12 s), and 0 μm ∈ (12 s, 18 s) in Scenario 3. Figure 16 is history of the micro-positioning error delivered via the proposed AFR method, and from this illustration, the positioning error converges to zero exponentially.

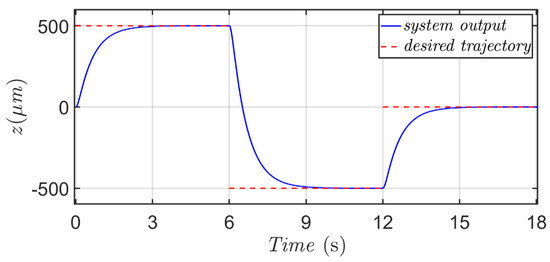
Figure 15. History of the proposed micro-positioning actuator for a desired stair-type trajectory.

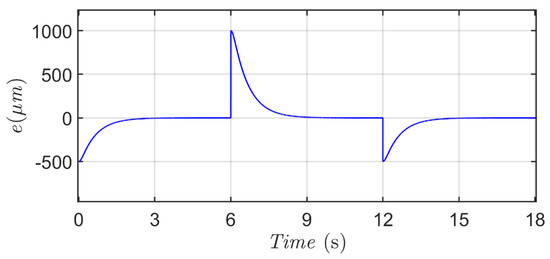
Figure 16. Micro-positioning error for a desired stair-type trajectory.

Figure 17 and Figure 18 display the micro-positioning results of this proposed micro-positioning actuator for Scenario 4. A similar exponential convergent character in the positioning error can be obtained, and a satisfactory micro-positioning performance is delivered corresponding to a desired trajectory with ascending and descending slopes.

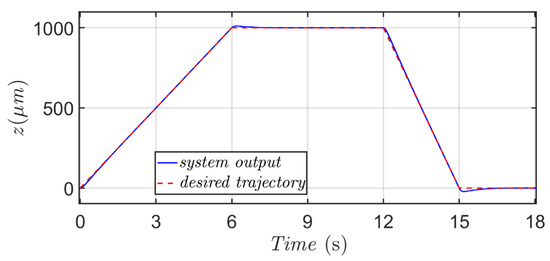
Figure 17. History of the proposed micro-positioning actuator for a desired trapezoidal-type trajectory.

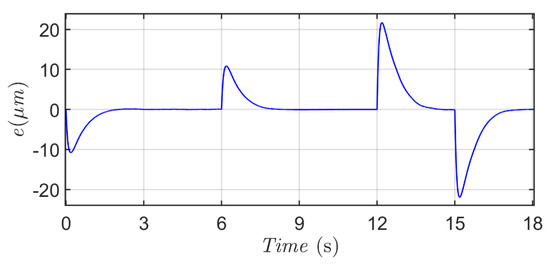
Figure 18. Micro-positioning error for a desired trapezoidal-type trajectory.

Figure 19 and Figure 20 indicate the micro-positioning results of this proposed micro-positioning design with respect to a desired sinusoidal-type trajectory. Since the desired sinusoidal-type trajectory is a signal that varies with a frequency, the micro-positioning task of this scenario is more sophisticated than the other two scenarios. An exponential convergent character in the positioning error can be easily observed for Scenario 5 as well, and this verification consists of the mathematical evaluation in Remark 1. From these positioning results, it is easy to observe from the outcome of this real test that the real-time instantaneous position of the moving fastener with a load quickly and precisely follows the desired sinusoidal-type trajectory after 2.5 s.

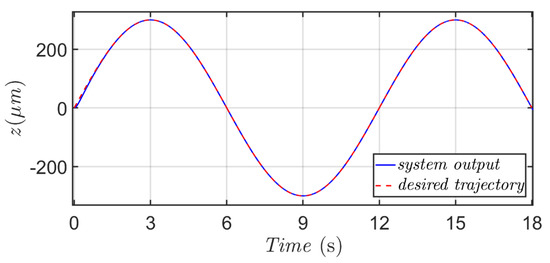
Figure 19. History of the proposed micro-positioning actuator for a desired sinusoidal-type trajectory.

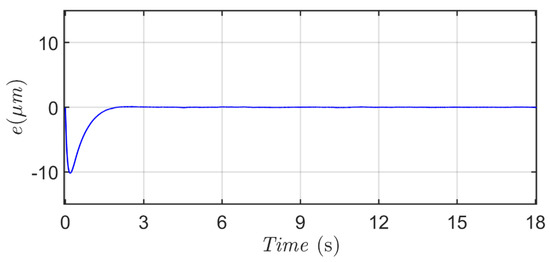
Figure 20. Micro-positioning error for a desired sinusoidal-type trajectory.

The RMS (root mean square) statistics of positioning errors in the steady state for the above-mentioned simulation and experiments with 100 runs are listed in Table 3.

Table 3. The RMS statistics of positioning errors in the steady state.

Desired Trajectory	RMS Positioning Errors of Simulation Results	RMS Positioning Errors of Practical Results
Trapezoidal Trajectory	0.010 (μm)	0.011 (μm)
Sinusoidal Trajectory	0.0003 (μm)	0.003 (μm)

Table 3 reveals the fact that statistics of positioning errors in simulation results and experiments are similar.

6. Conclusions

Integrating a piezoelectric actuator and a nonlinear adaptive fuzzy robust control law, a micro-positioning actuator is established in this investigation. For globally securing the stability and the micro-positioning ability under influences of hysteresis effect and the modeling uncertainties, a rigorous mathematical proof about the robustness and stability of this proposed method has been proven with respect to a specific robust performance index; the micro-positioning performance of this proposed method can be guaranteed as well. From the simulation results, it is easy to point out the fact that based on the perturbation cancellation of the on-line fuzzy approximator and the elimination ability to approximation error of the robust compensator, this proposed adaptive fuzzy robust control design performs far better than the feedback linearization control design in micro-positioning performance when encountering hysteresis and modeling uncertainties caused by the variations of system parameters. Practical tests of this proposed micro-positioning design are validated via adopting three desired trajectories with their own features, and all practical testing results achieve the required accuracy of 1 μm after a short transient response. Promising qualities of this proposed micro-positioning method, including stability, robustness, and micro-positioning performances in these practical tests are identical to the simulation results.