The Impact of Productivity, Investment and Real Wages on Employment Absorption Rate in South Africa

Abstract

Many developing countries are facing high levels of unemployment and most people who are employed are poorly remunerated due to low skills and productivity levels. Although jobs are important, a productive job is even more important, not only for employees, but also for employers. South Africa, being a developing country, is also facing the challenge of dramatically high levels of unemployment. This study’s aim was to examine both the short- and long-term impacts of real wages, labour productivity and investment spending on employment absorption rates in South Africa. To establish the existing relationship between variables, the study applied several econometric approaches, such as an autoregressive distributed lag (ARDL) model, error correction model (ECM) and a Toda–Yamamoto causality analysis on quarterly time series data from 1995Q1 to 2019Q1. The results revealed the existence of both short- and long-run relationships among the variables. While a positive relationship was found between employment absorption, investment spending and labour productivity, it was found that real wages negatively impact on long-run employment absorption rates. Additionally, the short-run analysis indicated that the lagged employment absorption rate influences the current rate of employment. Furthermore, the causality tests indicated that a bi-directional causal relationship exists between employment absorption and investment spending; and a uni-directional relationship between employment and both real wages and labour productivity. Based on the findings, the study recommends increments of investment spending and labour productivity that enables the South African economy to carry out more activities that would require more workers, thereby improving the employment absorption rate. The fact that labour productivity positively impacts the employment absorption rate infers the requirement for quality and skilled workers to be absorbed in the South African labour market. Therefore, labour skills improvements appear to be a prerequisite for productivity enhancement and job creation.

1. Introduction

Developing countries, with mostly limited resources, have focused development policy mostly on increasing levels of investment (Porter and Kramer 2019). Although investment is important for economic growth and employment, it has limitations, and a balance needs to be achieved between ongoing investment versus improvement in productivity for economic growth and development (Ahluwalia 1991). South Africa, over the last twenty years, has been affected by extremely high levels of unemployment and low levels of employment absorption. The latest data release by Statistics South Africa indicate still-rising levels of unemployment. Unemployment in South Africa increased from 27.2% in 2018 to 29.0% in 2019, while the employment absorption rate decreased from 43.1% to 42.4% over the same period (StatsSA 2019). These employment datasets are shocking compared to most other developing countries.

Table 1. Labour data for selected countries in 2018.

Country	Unemployment Rate in %	Min Wage in US $	Human Capital Index	Employment Rate in %	Labour Cost Index
Spain	13.6	890	65.6	64.5	100.4
Greece	17.6 *	793	64.7	72.0	93.3
Argentina	8.5	320	64.3	42.3 *	--
Brazil	12.3	288 *	59.7 *	54.3	116.6
Colombia	11.8	263 *	61.8	56.4	--
Turkey	13.7	485	60.3	45.8	188.5 *
South Africa	29.0 *	292	58.1 *	42.6 *	156.2 *

Source: (CountryEconomy 2019) and (TradingEconomics 2019). Note: * indicates worst performance or situation of the countries listed.

provides a summary of data for a range of countries that have, or are still experiencing, labour market problems where reliable data are available. Of all these countries, South Africa has by far the highest, and growing, unemployment rate, followed by Greece and Turkey. Colombia, Brazil and South Africa have the lowest minimum wages, at below $300. Looking at the Human Capital Index, again South Africa has the lowest index, followed by Brazil and Turkey. South Africa and Argentina have the lowest employment rates, of 42.6% and 42.3%, respectively, followed by Turkey. The countries with the highest labour cost indexes are Turkey and South Africa. The results from Table 1 paint a problematic labour market picture for most of these struggling countries, but especially for South Africa, where the market has been deteriorating.

The South African labour market is one of the worst performing markets in the world and, for this reason, it is important to analyse it from all angles in the quest to find answers to this problem. Other developing and unstable developing economies, such as Turkey, Brazil and Argentina, have similar problems in their labour markets, and the results from this study could be useful for these countries. This study has the aim of analysing the South African labour market from an employment absorption point of view, and its impact on and relationship with productivity, investment and real wages.

2. Review of the Literature

This section provides definitions of variables included in the study, followed by an empirical analysis of previous studies on this subject of research. The employment absorption rate is defined as “the proportion of the working-age population aged 15 to 65 years that is employed” (National Development Agency 2000). Higher levels of the employment absorption rate indicate more employment opportunities. Labour productivity is defined in simple terms as output per unit of labour input (OECD 2002); higher levels of productivity have a positive impact on output and economic growth. In economic terms, investment means the capital outlay of money usually for income or profit (Merriam-Webster 2019). Higher levels of domestic and foreign investment could lead to economic growth. Lastly, real wages are defined as the value of goods and services that could be purchased with the level of wages received as income, taking inflation into account (OECD 2002). The theoretical foundation of the study is based on the historical theories of Okun’s Law, who stated that unemployment is related to economic growth, and higher levels of economic growth are positively related to employment creation (Okun 1962). Okun’s Law, although it has some limitations, has been used over a number of decades as a theoretical guideline, estimating, in general, that a one percent decrease in the unemployment rate could lead to a three percent increase in economic output. This relationship is, however, also affected by other variables, such as labour supply, wages and productivity (Prachowny 1993). In addition, the Phillips curve states there is a trade-off between unemployment and inflation (Phillips 1958). Various studies have analysed this relationship and added variables such as productivity and wages (Ball and Moffittm 2001).

Regarding empirical studies, a comprehensive analysis is provided from across the world on the relationship between the variables included in the study. Mahadea and Simson (2010) analysed the employment situation in South Africa. Their study found that, although the economy has shown positive growth from 1994 to 2008, the formal sector could not provide adequate jobs during this period. The question of what impacts would result from the economy experiencing a recession, or period of low growth, could be asked. The study used a regression model to analyse the relationship between economic growth and employment and found that the employment elasticity was low over the period, and employment growth was limited in relation to economic growth. This situation could be described as jobless growth. Klein (2012) analysed the employment environment in South Africa during and since the financial crisis in 2008. The main finding from this research was that employment creation is limited and restricted when real wages grow faster than productivity in labour. The results from the research also indicate that, in the long run, cointegration exists between real wages and productivity, but not in the short run. In a comprehensive employment study in South Africa by Fourie (2011) he listed the key issues in the local employment environment, which included workers finding it difficult to transit from the informal to formal employment sectors; structural problems limiting the smooth functioning of the labour market, such as labour regulations and poverty; unemployment being affected by real wage elasticity of labour demand, which was approximately 0.7, and an output-elasticity of employment of only 0.5; and employment creation and the labour market being affected by poverty, social-welfare grants and supply of labour.

Barnichon (2010) analysed the correlation between unemployment and productivity. He found that technology shocks or impacts can lead to a positive relationship between unemployment and productivity, and non-technology shocks, such as aggregate demand, cause a negative relationship. Sawyer (2002) investigated the relationship between inflation, employment, wages and capital investment. Some of the findings include that rising aggregate demand drives the relationship between real wage and employment, and that investment plays a major role in the creation of employment opportunities. Meager and Speckesser (2011) state that a strong link exists between productivity and wages, and public policy has limited impact on this relationship. When wage increases are faster than growth in productivity, it has a negative impact on the economy, but the relationship will always attempt to move to equilibrium due to international competition. The study found that wage moderation could allow employment creation. Hellwig and Irmen (2001) analysed the interrelationships between wages, employment and endogenous productivity growth. This study found that “steady-state equilibria employment contracts at a constant rate equal to the difference between the growth rates of productivity and output”, which disagrees with the statement or view that equality of wage growth and productivity growth is a condition for constant employment. According to Rowthorn (1999), theory predicts that factors such as capital investment, innovation and technology do not have a long-run impact on the levels of unemployment or, on the other hand, employment creation. The study found, however, that if capital investment is endogenous, it may have a long-run impact on employment.

Results of studies in developed countries provide different results compared to developing countries. In a study by Guthrie (2001), in New Zealand, on employment and productivity, it was found that the productivity of firms is positively affected by employee retention strategies such as increased involvement in decision-making. Bresnahan et al. (2002) analysed factors that affect demand for labour in the United States and found that innovation and productivity are key factors. Businesses with increased levels of innovation usually make use of highly skilled labour. Van Ark et al. (2008) studied labour productivity in developed countries. Since the 1990s, European growth in labour productivity has been low, while in the US the growth has been much higher, leading to an increased productivity gap. The research found that the main reason for this growing gap is the difference in the growth rate of the knowledge economy. A number of factors were identified and one of them is productivity growth, which acts as a proxy for innovation and technology improvements. In Europe, the labour market is subjected to higher levels of regulations when compared to the US. Girma et al. (2001) analysed the possible existence of a gap in wages and productively between foreign and domestic firms. The interesting results from the study are that foreign managed firms actually have higher levels of productivity and wages when compared to local firms, and no proof of intra-industry spill-overs affecting productivity were established. Barry et al. (2005), however, found evidence of improved productivity spill-overs from FDI. Arnold and Javorcik (2009) also analysed the impact of FDI and foreign firms on productivity. The study established that foreign ownership had a significant positive impact on productivity at firm level, mostly due to increases in investment, employment and wages, as well as improved integration of firms for extended international trade into the global economy. Dearden et al. (2006) state that wages are used to predict the level of productivity and their study had tested this relationship in the UK. The study found that training of workers in an industry had a significant impact on improved productivity and also led to increased wages. Conti (2005) also analysed this relationship in Italy, and the study found similar results, with training leading to significant increases in productivity, but movements in wages were not detected. Blundell et al. (2014) analysed labour productivity in the UK, and found that both productivity and wages have been decreasing since the financial crisis. This phenomenon could possibly be explained via the over-supply of labour. Bedi and Cielik (2002) analysed the impact of FDI on employment and wages in Poland. Evidence from this study indicates that wages are higher in foreign owned companies. Lazear (2006) states that output and productivity are more than 30% higher in the US compared to other developed countries due to an environment of growth in capital and investment. Factors such as flexible labour regulations, entrepreneurship development, and ongoing skills development could lead to increased productivity.

Empirical results from developing countries indicate the following: Coniglio et al. (2015) indicate that employment creation is a major problem for most developing countries, and their study analysed the relationship between FDI and employment in sub-Saharan African countries. Results include that foreign firms use more skilled workers for employment and pay higher wages when compared to local firms. McMillan and Rodrik (2011) found that developing countries have a dilemma of productivity gaps between traditional and modern sectors, and that the ongoing flow from low-productivity sectors to high-productivity sectors drives growth and development in these countries. The study found an interesting result, in that the Asian countries followed this pattern for rapid development, while Africa and Latin America followed the opposite path, but with poor developmental results. Additional results from the study indicated that developing countries, where exports are dominated by raw natural resources, have a negative impact on structural change and economic growth, because these mostly highly productive sectors do not have the capacity to absorb excess labour from low-skilled and low-productivity traditional sectors. Debaere et al. (2010) analysed the impact of FDI on employment. The study found that investment by multi-national corporations in developing countries has a negative impact on the specific company’s possible short-term employment situation, while investment in developed countries does not affect employment growth significantly. In contrast to the previous findings, Habib and Sarwar (2013) state that FDI is critical for economic growth and development. The authors studied the relationship between FDI, economic growth and employment growth from 1970 to 2011 in Pakistan, using Johanson cointegration methodology. The study found significant long-term relationships with cointegration between variables. Aitken et al. (1996) investigated the relationship between FDI and foreign business ownership and wages in Mexico and Venezuela. Results indicate that FDI had a negative impact on wages at local firms. It should, however, be kept in mind that foreign involvement in the local economy could have different impacts on wages and productivity depending on the specific firm and sectors.

In summary, this specific study field allows for interesting empirical findings with contrasting views, and to find consensus on the impact and relationships between the variables is not possible in a dynamic environment. Herewith are some of the lessons from the literature view. In most countries, including South Africa, economic growth does not always translate to the creation of additional employment. If wages increase faster than productivity, the impact is negative on both employment creation and the economy. Wages and productivity should have a positive correlation. When local demand increases, wage pressure increases, as well as demand for labour, while it is also the case that, when wage moderation occurs, employment creation becomes a possibility. In addition, domestic investment drives economic growth and employment. In studies in developed countries, job security could lead to higher levels of productivity. Productivity increases are dependent on innovation and technology. From a negative perspective, labour and other regulations have a negative impact on employment creation. Foreign investment by foreign firms could have both positive and negative impacts. Foreign firms usually require and appoint mostly skilled labour and such firms usually have higher levels of productivity and wages and could lead to destroying the competitiveness of local firms and local employment. Higher levels of skill lead to improved productivity and higher wages, while an over-supply of labour leads to lower wages.

3. Methodology

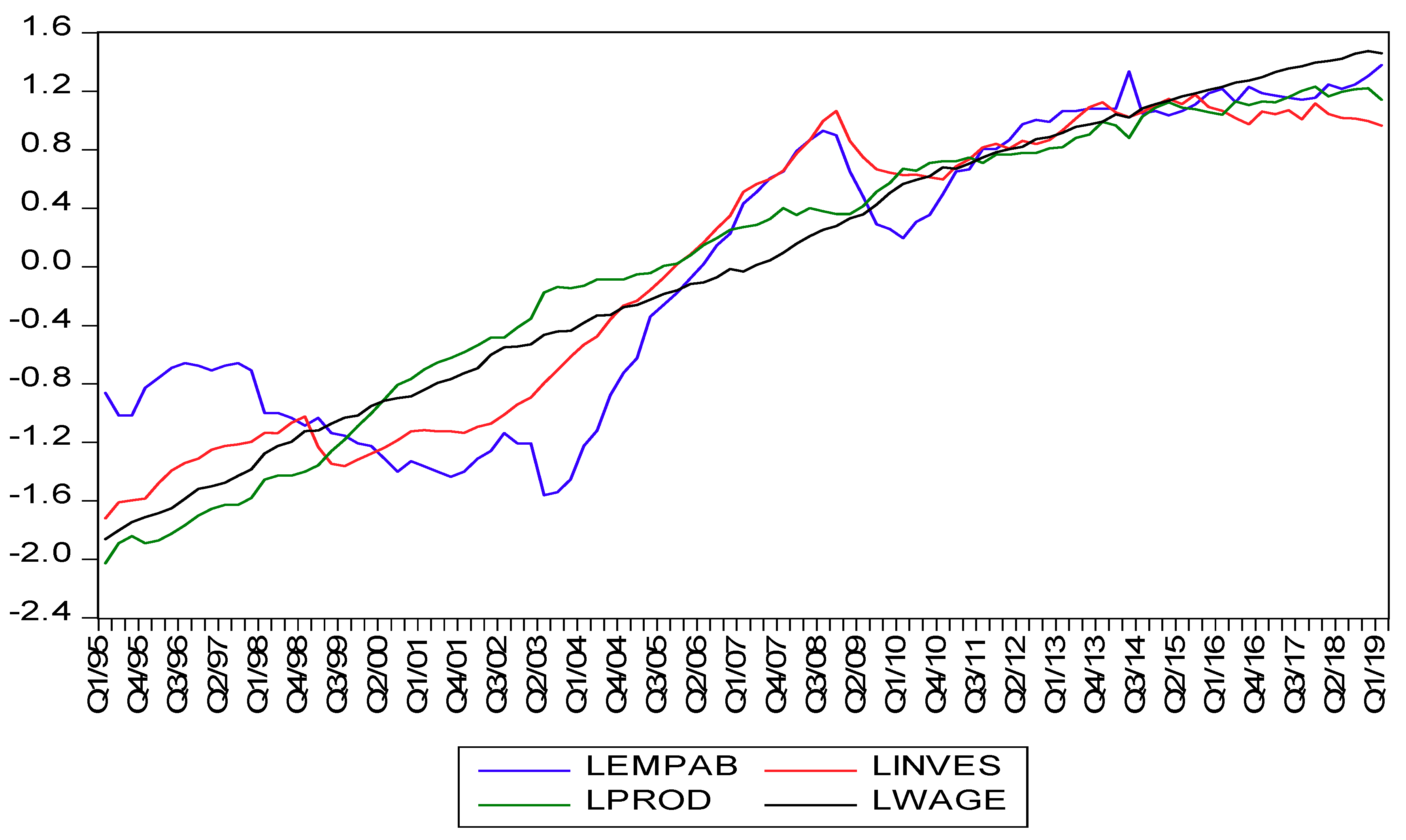
The dataset used in this study consists of employment absorption rate (LEMPAB), productivity (PROD), gross capital formation or investment spending (INVES) and real wages (WAGE). Quarterly data covered the period between the first quarter of 1995 and the first quarter of 2019. The time period was selected based on two reasons. The first is that the authors’ aim was to determine the extent to which employment absorption is affected by labour productivity, investment spending and real wages after the apartheid era (with the democratic government), and the second reason was the availability of data. The entire dataset was acquired from the South African Reserve Bank (SARB). Before the econometric estimation, the dataset was transformed into a natural logarithm. The augmented Dickey–Fuller (ADF) and the Phillips–Perron (PP) tests were employed to establish the presence or absence of unit roots within LEMPAB, LPROD, LINVES and LWAGE. Although it is noted that the ARDL model can be applied to a set of variables without performing unit root tests, it is advisable to carry out a unit root test to certify that data do not contain an I(2) variable, as the ARDL approach is only appropriate for variables that are integrated with order I(0) and I(1) or a combination of the two. The reason for this is that, according to Ouattara (2004), the ARDL model produces spurious results when applied to I (2) variables.

The augmented Dickey–Fuller (ADF) test for unit root was introduced in the econometrics field as an extension to the Dickey–Fuller (DF) test to eradicate the issue of error term that appeared unlikely to be white noise in the DF test. To achieve improved unit root test results, the ADF adds an extra lagged term of dependent variable (Dickey and Fuller 1979). The lag length on the extra terms, in this study, is achieved using the Schwarz information criterion (SIC). The SIC is considered a most effective criterion for model selection (Cavanaugh and Neath 1999). The ADF test can be performed in the following three ways:

$$\Delta y_t=\delta y_{t-1}+{\sum }_{i=1}^p{\beta }_i\Delta y_{t-i}+u_t$$

(1)

$$\Delta y_t={\alpha }_0+\delta y_{t-1}+{\sum }_{i=1}^p{\beta }_i\Delta y_{t-i}+u_t$$

(2)

$$\Delta y_t={\alpha }_0+\delta y_{t-1}+{\alpha }_{2}t+{\sum }_{i=1}^p{\beta }_i\Delta y_{t-i}+u_t$$

(3)

Mackinnon (1991) provides the critical values for each of the above presented three models. The null hypothesis of $y_t$ has unit root, and is rejected if the ADF statistic value is greater that the critical value (in absolute terms), and the conclusion will be that $y_t$ is stationary. Phillips and Perron (1988) established a general rule of the augmented Dickey–Fuller test process that allows for impartially mild assumptions regarding the error distribution. The Phillips and Perron test is the AR (1) procedure, which is stated as follows:

$$\Delta y_t={\alpha }_0+\delta y_{t-1}+e_t$$

(4)

The Phillips and Perron (PP) test rectifies the t-statistic of the coefficient δ from the AR (1) model to incapacitate the serial correlation within the $e_t$. Consequently, the PP test is an alteration of the ADF test, where it considers the restrictiveness nature of the error procedure. This test also uses the Mackinnon (1991) critical values. The Phillips and Perron is seen to be robust to general forms of heteroscedasticity within the error term, and it can be applied for regression without taking into account the lag length specification (Pinn et al. 2011).

Contrary, to ADF and PP unit root tests whose null hypotheses suggest the occurrence of a unit root in the series, the Kwiatkowski–Phillips–Schmidt–Shin (KPSS) employs the Lagrange multiplier (LM) test and suggests that series are initially stationary (Hadri 2000). Consequently, all three tests (ADF, PP and KPSS) are used in this study to ensure robust results.

Following the unit root tests, the cointegration test was performed using the bound testing approach. The aim of this test was to empirically establish a long-term relationship among variables of interest. The test was selected based on the results from unit root tests. The ARDL bound testing procedure is considered to be more robust and appropriate when applied to a dataset with a diminutive sample size. Moreover, it simultaneously provides the estimation for short- and long-term parameters (Haug 2002). The ARDL (p,q), developed by Pesaran et al. (2001), is applied to this study and presented as follows:

$$\Delta y_t={\propto }_0+{\propto }_1{y}_{t-1}+{\beta }_1{x}_{t-1}+{\sum }_{i=1}^p{\delta }_i\Delta y_{t-i}+{\sum }_{j=1}^q{\theta }_j\Delta x_{t-j}+{\epsilon }_t$$

(5)

Applying Equation (5) on variables of this study, the following Equation (6) was obtained:

$$\begin{gathered} \Delta LEMPA{B}_t={\propto }_0+{\propto }_{1}LEMPA{B}_{t-1}+{\propto }_{2}LPRO{D}_{t-1}+{\propto }_{3}LINVE{S}_{t-1}+ {\propto }_{4}LWAG{E}_{t-1}+ \\ {\sum }_{j=1}^k{\beta }_j\Delta LEMPA{B}_{t-I}+{\sum }_{j=1}^k{\gamma }_j\Delta LPRO{D}_{t-j}+{\sum }_{j=1}^k{\delta }_j\Delta LINVE{S}_{t-j}+{\sum }_{j=1}^k{\phi }_j\Delta LWAG{E}_{t-j}+ \\ {e}_t \end{gathered}$$

(6)

where ${\propto }_0$ is the drift, ${\propto }_1$, ${\propto }_2$, ${\propto }_3 ,$ and ${\propto }_4$ are the long-run coefficients and $e_t$ denotes white noise errors. The cointegration between variables is achieved by means of performing the F-test for the joint significance of the ${\propto }_1$, ${\propto }_2$, ${\propto }_3 ,$ and ${\propto }_4$ coefficients in Equation (6). The null hypothesis of no cointegration ($H_0$: ${\propto }_1$= ${\propto }_2$ = ${\propto }_3 =$ ${\propto }_4$ = 0) is tested against the alternative ($H_0$: ${\propto }_1$≠ ${\propto }_2$ ≠ ${\propto }_3$ ${\propto }_4$ ≠ 0). Pesaran et al. (2001) suggested two asymptotic critical values that are utilised to test for cointegration when the independent variables are considered as I(m) where 0 ≤ m ≤ 1. The lower bound values suggest that regressors are I(0), while the upper bound values suggest that these variables are I(1). Regardless of the order of integration, the null hypothesis ($H_0$) is rejected if the estimated F-statistic is larger than the critical value of the upper bound. Conversely, the study fails to reject $H_0$ if the estimated F-statistic falls below the lower bound critical value. Lastly, for the estimated F-statistic that falls between both critical values, the regression results are inconclusive. Once the cointegration among variables is established, the ARDL error correction model (ARDL-ECM) also has to be determined. Equation (7) determines the error correction model associated with the cointegration (long run) estimates:

$$\begin{gathered} \Delta LEMPA{B}_t={\alpha }_0+{\sum }_{j=1}^k{\beta }_j\Delta LEMPA{B}_{t-j}+{\sum }_{j=1}^k{\gamma }_j\Delta LPRO{D}_{t-j}+{\sum }_{j=1}^k{\delta }_j\Delta LINVE{S}_{t-j}+ \\ {\sum }_{j=1}^k{\tau }_j\Delta LWAG{E}_{t-j}+\lambda EC{T}_{t-1}+e_t \end{gathered}$$

(7)

where $ECT$ denotes error correction term and $\lambda$ is the coefficient of the ECT utilised to measure the model speed of adjustment towards long-run equilibrium. In the absence of cointegration among variables, the error correction model (ECM) without error correction term can be estimated following Equation (8):

$$\begin{gathered} \Delta LEMPA{B}_t={\alpha }_0+{\sum }_{j=1}^k{\beta }_j\Delta LEMPA{B}_{t-j}+{\sum }_{j=1}^k{\gamma }_j\Delta PRO{D}_{t-j}+{\sum }_{j=1}^k{\delta }_j\Delta INVE{S}_{t-j}+ \\ {\sum }_{j=1}^k{\tau }_j\Delta WAG{E}_{t-j}+e_t \end{gathered}$$

(8)

where ${\beta }_j$, ${\gamma }_j$, ${\delta }_j$ and ${\phi }_j$ are short run coefficients.

The presence of dynamic error correction model derived by Equation (7) does not automatically infer stability of the estimated coefficients. Therefore, Pesaran et al. (2001) recommended the stability test of estimated parameters on the studied model. This is done by the means of cumulative sum (CUSUM) and/or cumulative square sum (CUSUMSQ) tests.

Granger causality is one of the tests that can be utilised to establish a causal relationship among variables. However, this test can lead to spurious results on functions with time lags on integrated variables (Dritsaki 2017). Additionally, the standard granger causality tests suffer from inconvenience parameter dependency asymptotically (Toda and Phillips 1993); (Toda and Yamamoto 1995). The potency of Toda and Yamamoto’s procedures in establishing causal relationship among variables lies in its ability to overcome numerous deficiencies of the standard Granger causality procedures. The Toda and Yamamoto test for granger non-causality is conducted from the modified Wald test (Rambaldi and Doran 1996), and, therefore, the Wald statistic is valid irrespective of variables’ integration order, be it I(0), I(1) or I(2). For these reasons, the Toda and Yamamoto test for Granger non-causality test is applied to this study. In order to analyse Granger causality (1961), Toda and Yamamoto (1995) developed a model based on the estimation of augmented VAR model (k + $d_{max}$), where k denotes the optimal time lag and $d_{max}$ the maximum integrated order of variables in the VAR model. According to Toda and Yamamoto (1995), for d = 1, any lag selection process is always effective, since k ≥ 1 = d. However, if d = 2, the procedure is valid only if k ≠ 1. Using the VAR model, the Toda–Yamamoto causality is expressed as follows:

$$y_t={\mu }_0+\left[{\sum }_{i=i}^k{\alpha }_{1t}{y}_{t-i }+{\sum }_{i=k+1}^{d_{max}}{\alpha }_{2t}{y}_{t-i }\right]+\left[{\sum }_{i=1}^k{\beta }_{1t}{x}_{t-i }+{\sum }_{i=k+1}^{d_{max}}{\beta }_{2t}{x}_{t-1 }\right]+e_{1t}$$

(9)

$$x_t={\theta }_0+\left[{\sum }_{i=i}^k{\gamma }_{1t}{x}_{t-i }+{\sum }_{i=k+1}^{d_{max}}{\gamma }_{2t}{x}_{t-i }\right]+\left[{\sum }_{i=1}^k{\delta }_{1t}{y}_{t-i }+{\sum }_{i=k+1}^{d_{max}}{\delta }_{2t}{y}_{t-i }\right]+e_{2t}$$

(10)

where k is the optimum time lag and $d_{max}$ is the maximum integration order on variable (both in VAR model).

4. Empirical Estimation and Discussion of Results

4.1. Empirical Estimation

Figure 1 provides a summary of the trends over the study period (1995 to 2019) for the four variables included in the study. The South African employment absorption experiences its peak in 2007 and 2014, and the lowest labour absorption was experienced in 2003 and 2010. The graph employment trends, though it is not a constant rate, follow the trends of investment spending. Compared to both employment and investment spending, which appear to undergo fluctuation over the investigated period, labour productivity follows an upward trend while the real wages have been gradually increasing in an almost constant trend. From 2015 to date, employment, labour productivity and investment spending are experiencing decreasing trends and this might be resulting from poor economic conditions in the country.

Before empirical analysis, the paper determines the order of integration for each variable. To achieve this goal, a number of tests were performed. These tests include the ADF, PP and KPSS. These tests were selected based on the fact that ADF and PP produce almost similar results for unit root, and KPSS complements them by means of testing variables’ stationarity. Therefore, the null hypothesis for KPSS opposes the null hypothesis for ADF and PP (Brooks 2019). Following the KPSS results, as exhibited in

Table 2. Unit root and stability tests.

Variables	ADF		P-P		KPSS
	Const	Const and Trend	Const	Const and Trend	Const	Const and Trend
Levels I(0)
LEMPAB	0.8481	0.427	0.9143	0.5740	1.147	0.137 *
LINVES	0.545	0.753	0.488	0.657	0.533	0.111 *
LPROD	0.633	0.302	0.322	0.353	0.820	0.159
LWAGE	0.770	0.040 *	0.828	0.041 *	0.844	0.112 *
First difference I(1)
$\Delta$LEMPAB	0.001 *	0.001 *	0.0000 *	0.001 *	0.262 *	0.129 *
$\Delta$LINVES	0.001 *	0.001 *	0.0005 *	0.001 *	0.085 *	0.075 *
$\Delta$LPROD	0.001 *	0.001 *	0.0000 *	0.001 *	0.314 *	0.358
$\Delta$LWAGE	0.001 *	0.001 *	0.0000 *	0.001 *	0.097 *	0.036 *

Note: * denotes that a variable has no unit root and it is stationary. ∆ denotes variable at first difference.

, demonstrates that one of the four variables (PROD) become stationary after first difference and yet LEMPAB, LWAGE and LINVES are stationary at level. Accordingly, LEMPAB, LINVES and LWAGE are all I(1), while LPROD is I(0). The presence of a mixed order of integration calls for the usage of ARDL model, since there is no variable that integrated of order two [I(2)].

When the ADRL model is applied on the data series to determine cointegration and short-run relationships; unless otherwise, the E-views software automatically selects the optimum number of lags. However, given that causal relationship in this study is determined using the Toda–Yamamoto for Granger causality, it is necessary to determine the lag selection using the VAR approach. The results from the five information criteria are exhibited in

Table 3. Lag length selection.

Lag	LogL	LR	FPE	AIC	SC	HQ
0	−729.9703	NA	10,200,000	36.6985	36.8674	36.7595
1	−543.5467	326.2413	20,400,823	28.1773	29.0217 *	28.4826 *
2	−526.1788	26.9203 *	19,555,404 *	28.1089	29.6289	28.6585
3	−509.7557	22.1711	20,462,357	28.0877	30.2833	28.8816
4	−492.2648	20.1146	21,681,235	28.0132 *	30.8843	29.0513

Note: * Denotes the optimal lag selected. LR: sequential modified LR test statistic (each test at 5% level). FPE: Final prediction error. AIC: Akaike information criterion. SC: Schwarz information criterion. HQ: Hannan-Quinn information criterion.

, where four out of five criteria emphasise the use of one lag. Therefore, one lag is employed to determine causal relationships among variables.

The ARDL model was utilised for cointegration and its results are presented in

Table 4. Cointegration results and Bounds test.

F-Statistic	5.693	3
Pesaran Critical Values
Significance	I0 Bound	I1 Bound
10%	2.37	3.2
5%	2.79	3.67
1%	3.65	4.66

. The Wald test estimated that the F-value is 5.693 and is greater than the corresponding values of the lower and upper bound, which are 2.79 and 3.67, respectively. In other words, the estimated F-value is significant to infer the presence of cointegration among variables at the 5 percent significance level. Therefore, there is evidence of long-term relationships between labour productivity, investment spending, real wage and employment.

Following Equation (6), the results in

Table 5. Long-term coefficients.

Variable	Coefficient	Std. Error	t-Statistic	Prob.
LINVES	0.1880	0.1286	1.4615	0.1477
LPROD	0.7222	0.4203	1.7182	0.0895
LWAGE	−0.2335	0.0553	−4.2223	0.0001

suggest a negative long-term relationship between employment absorption and real wage. If the level of real wages increases by 1 percent, employment levels will decline by −0.235 percent. Similar findings of a positive relationship between investment spending were also found in the study of (Iocovoiu 2012), (Lach 2010), (Ncanywa and Makhenyane 2016). Contrary to real wages, both labour productivity and investment spending have a positive impact on the South African employment. A 1 percent increase in labour productivity leads to a 0.722 percent increase in employment levels, whilst a 1 percent increase in investment spending results in 0.118 increase in employment respectively. The following long-term equation is listed:

LEMPAB = 0.7222LPROD + 0.1880 LINVES − 0.2335 LWAGE

The presence of long-term relationships among variables implies the estimation error correction model, which indicates the speed of adjustment towards long-term equilibrium. The error correction model (ECM) results in

Table 6. Cointegrating form.

Variable	Coefficient	Std. Error	t−Statistic	Prob.
D(LEMPAB(−1))	0.3556	0.0983	3.6156	0.0005 *
D(LEMPAB(−2))	0.1608	0.0652	2.4638	0.0158 *
D(LINVES)	0.0456	0.0216	2.1079	0.0381 *
D(LINVES(−1))	−0.0267	0.0226	−1.1849	0.2394
D(LINVES(−2))	−0.0269	0.0217	−1.2415	0.2179
D(LPROD)	−0.6182	0.0658	−9.3852	0.0000 *
D(LPROD(−1))	0.2677	0.0962	2.7810	0.0067 *
D(LWAGE)	−0.0980	0.0314	−3.1213	0.0025 *
CointEq(−1) *	−0.0400	0.0082	−4.8586	0.0000 *

Note: * denote significant at 5 percent.

are interpreted based on their corresponding lower- and upper-bound critical t-values (Pesaran et al. 2001). The error correction term (ECT) meets the required features; that is, having a negative sign (−0.0400) and being statistically significant at the 5 percent level with its absolute t-Statistic of −4.858 and the p < 0.001. The coefficient of −0.0400 suggests that approximately 4 percent of any shocks in the model are corrected each quarter. That is to say, short-term changes in the model will take approximately 24.98 (1/−0.040029) quarters to come back to long-term equilibrium.

As confirmation of the long-term relationship, fluctuation in investment spending and labour productivity are statistically significant to influence short-term changes in employment absorption. However, the coefficients of labour, the real wages, have no significant influence on short-term changes within employment absorption. Additionally, a lagged employment absorption rate has a positive impact on the current rate of employment absorption. When a study follows econometric modelling and regression, it is important to conduct a number of diagnostics in order to determine the validity of the model’s results. This study utilised normality, heteroscedasticity, serial autocorrelation and stability tests. The results from these tests in

Table 7. Diagnostic test results.

Test Statistics	Probability (p-Value)	Decision
Normality	0.285	Residuals are normally distributed
Serial correlation	0.733	Residuals are serially uncorrelated
Heteroscedasticity	0.620	Residuals are homoscedastic
Stability	0.200	The model is stable

illustrate that probabilities for all these performed tests are more than 0.05 (5%), suggesting that the null hypotheses for normality, serial correlation and heteroscedasticity are rejected. In other words, the model residuals are normally distributed, uncorrelated and homoscedastic. Additionally, using the Ramsey RESET test, results in Table 6 confirm the stability of the used model.

Table 7 displays the Toda–Yamamoto causality testing obtained from the application of Equations (9) and (10). The results in

Table 8. Toda–Yamamoto causality test two-variate VAR model results.

Variables	Lag(k)	Lag (k+dmax)	Chi-sq	Prob.	Direction of Causality
LINVES vs. LEMPAB	1	1+1	4.36792	0.0155 *	LINVES → LEMPAB
LEMPAB vs. LINVES	1	1+1	3.50471	0.0342	LEMPAB ← LINVES
LPROD vs. LEMPAB	1	1+1	6.5769	0.0022 *	LPROD →LEMPAB
LEMPAB vs. LPROD	1	1+1	0.52023	0.5962	LEMPAB # LPROD
LWAGE vs. LEMPAB	1	1+1	4.66989	0.0118 *	LWAGE→LEMPAB
LEMPAB vs. LWAGE	1	1+1	1.24991	0.2915	LEMPAB # LWAGE

Note: * rejection of null hypothesis at 5 percent level. The (k+dmax) denotes VAR order. →Denotes a unidirectional (one–way) causality and, # represents no causality between variables.

suggest a two-way or bidirectional causal relationship between investment spending and employment absorption rate. These results suggest that an increase in domestic investment may result in employment absorption and vice versa. Additionally, both labour productivity and real wages, from the study findings, appear to be good predictors of employment fluctuation. In other words, unidirectional causality exists between employment and labour productivity, and between real wages and employment. This causal relationship between employment and explanatory variables confirms the short-term result represented in Table 6. Thus, Toda–Yamamoto test infers the presence of causality among the study variables.

4.2. Discussion of Results

One on the most critical objectives of any macroeconomic policy is to strive to reduce the level of unemployment by dealing with issues of wage flexibility, as argued within descriptions of the Philips Curve and the Keynesian theory of employment (Gokal and Hanif 2004), (Malik et al. 2000). The identified negative relationship between employment level and wages, as estimated in this study’s long-term estimations, implies that, if effective supply of labour is available, employers could decide to reduce wages. On the other hand, if labour supply declines, employees could demand increases in wages. These findings are supported by the study of Seputiene (2011), whose findings revealed a negative relationship between employment wages within some of the EU countries. This result is also in line with the Phillip’s curve theory, suggesting that a low rate of unemployment leads to high real wages. Following this theory, one can conclude that, among other factors, the high rate of unemployment in South Africa might be resulting from high wages demanded by the labour unions through labour regulations. Additionally, this study found that in the short-term, a negative relationship exists between employment and real wages. Thus, a negative relationship always exists between employment and real wages. Besides the result from both long and short-term relationships between real wages and employment level, the causality test infers that real wage can be used in forecasting employment. The findings of Adudu and Ojonye (2015) suggested that employment changes might be caused by wages fluctuations. Contrary to real wages that negatively influence the South African employment, the study found that both investment spending and labour productivity possess a positive impact on long-term employment. When domestic investment improves, more jobs could be created and the unemployed with specific skills could find work. This implies that firms that have a culture of growing their investment possess the capacity to employ growth and productive labour. This positive relationship was also found in the study of Baumol (1977), Birch (1979), Kerr et al. (2014), Saks (2008), whose findings support the existence of a long-term relationship between investment spending and employment. Additionaly, the positive relationship between employment growth and labour productivity was supported in studies conducted by Bjuggren (2018), stipulating that labour product stimulates firms’ employment. However, the study of Junankar (2013) found an inverse relationship between employment and productivity. That is, if employed workers are more productive, employers might decide to increase their wages to boost their productivity, rather than employing new workers.

5. Conclusions and Policy Implications

This study scrutinised relationships between employment absorption, labour productivity, investment spending and real wages in the South African economy. In the study, the Bounds test for cointegration, as developed by Pesaran et al. (2001), was used, as well as causality tests developed by Toda and Yamamoto (1995). The study results suggested the presence of long-term relationships among the four analysed variables (employment absorption, labour productivity, investment spending and real wages). The findings portrayed that a rise in investment spending by 1 percent causes employment absorption to increase by only 0.188 percent, and a 1 percent increase in labour productivity leads to 0.722 increase in the employment level, while a 1 percent increase in real wages could cause employment absorption to decline by 0.234 percent. Contrary to the long-term relationship estimation, the dynamic short-term analysis of the model indicated that different lags of the independent variables had different impacts on employment of the dependent variable. This result might infer that it takes time for any changes from explanatory variables to positively affect employment growth and, in terms of specific lags, the impact could be even negative. The Toda and Yamamoto causality results suggested a bi-directional relationship between investment spending and employment absorption, whilst a uni-directional causal relationship was found between labour productivity and employment, and between real wages and employment. Based on the findings, the study recommends increments of labour productivity and investment spending that could enable the South African economy to increase economic activities that would require more labour, thereby improving the employment absorption rate. The fact that labour productivity positively impacts the employment absorption rate infers a requirement for an increase in the quality and skills of workers in the South African labour market. Increased investment and a skilled labour force will lead to economic growth and, subsequently, the creation of employment. A number of additional variables could have been included in the study, but that would have made the study too wide in extent. Thus, future studies should consider including factors such as FDI, economic growth, inflation, and political risk.