2. Methods
System dynamics is a relatively new discipline that saw its formation in the mid-20th century and began to spread with the publication of
Industrial Dynamics by Jay Forrester [
12]. System dynamics is used when analyzing a domain as a system to understand the feedback within the system in order to develop solutions to inherent problems versus symptoms. The methodology was originally developed at MIT by a group dedicated to this academic pursuit [
13] and engaged by the Club of Rome to create the World3 model, which has been a cornerstone of sustainability and climate change analysis [
14]. System dynamics is an iterative, interdisciplinary process that views problems holistically. Essentially, using system dynamics involves identifying elements, subsystems, and the systems’ context, boundaries and properties of the system under investigation. System dynamics is both systematic and systemic in that there are systematic processes, and it is rooted in systemic thinking in order to recognize and solve complex problems by seeing the whole instead of only the parts [
15]. System dynamics is often preferred over other analysis methods because of its underlying computational rigor—see
Appendix A.
System dynamics is applied in this study to the Norwegian pension system in order to understand how elements in this system operate and interact. System dynamics modeling is aided by the use of software (this study uses iThink, see
Appendix A). The elements in a system dynamics model consist of stocks, flows, and variables (stock and flow diagram). Stocks are an accumulation of its flows over time, and flows represent addition and subtraction to the stock over time. Variables in stock and flow models are elements that affect the inflows and outflows. The variables are linked to each other and flows through instantaneous causal links. The accumulated causal behavior in the stock is affected by the flows, which are in turn affected by the variables.
The structure of a system yields the behavior over time (accumulated in stocks), and the goal is to discover all the elements and relationships in a system and reproduce the observable reference mode behavior (actual system behavior). In system dynamics models, there are endogenous and exogenous elements. Endogenous elements are incorporated in the model structure in relation to other structural elements. Exogenous elements are variables that contain data that are directly imported into the model structure.
Feedback Theory
A fundamental concept in system dynamics is feedback theory. In the evaluation of the relationships between elements in a system, there are often feedback loops operating in a system [
16]. A feedback loop is the interconnection of variables in a system that feeds back into itself. This is a closed loop system. Open loop systems do not have a feedback loop, and often the policy goal in these systems is to close the loop, especially in environmental management systems. Open loop systems have exogenous variables that influence the system structure from outside the system to generate the system behavior. Closed loop systems have endogenous variables, where the behavior is influenced by forces within the system. An example of this is climate change variables. When modeling societal collapse in history (e.g., the classic Mayans), climate change (drought) influenced societal collapse. Climate change is exogenous in this example because the population was not causing the drought. However, when modeling human-induced climate change in contemporary societies, climate change is endogenous because human activity influences climate change and climate change, in turn, affects human societies.
A causal loop diagram (CLD) of the stock and flow diagram shows the relationships between elements in a system (the feedback loop), which can be either positive or negative. A positive relationship means the elements develop in the same direction (when one increases, so does the other), and a negative relationship means the elements develop in opposite directions (when one increases, the other decreases). A balancing feedback loop means that the relationships between the elements keep the accumulated elements (stocks) at equilibrium. In addition to the balancing feedback loop, there is also a reinforcing feedback loop, where the behavior of the stock does not find an equilibrium and continues to increase or decrease over time.
One of the major goals of system dynamics is to understand the structure of the system that results in the observable behavior. This is the motivation for using system dynamics as the methodology for this study. The goal of this study is to understand how policy structure produces gender disparity in the pension system. Representing the pension system mathematically is an approach that serves to complement other methodological approaches. For more information about system dynamics modeling and its limitations, please see
Appendix A.
3. Results
The model presented in
Figure 1 is one part of a larger model. This section presents the stock and flow diagram of the Norwegian pension system (representing its structure). This is only a portion of the system however, and represents how income is accumulated over time (see
Appendix A for an expanded description of the model). Total lifetime income is the largest determining factor of pension payments. There are policies in place to equalize the pension payments between men and women. The main structural policy is the provision of childcare resources (i.e., pre-school daycare).
The stock and flow structure only represents childcare resources after parental leave ends. During parental leave, parents earn the same amount of pension points as they did before parental leave. The model only represents how women are enabled to enter the labor force after parental leave ends (the availability of childcare resources), and how this in turn affects income and pension. Only labor force participants who have worked 40 years (regardless of position percent/full time vs. part time) are represented in this model. This model assumes that the male position percent is not affected by child rearing, and this is recognized as a limitation of the model. Also, although this study only investigates pension transfers from the state, the pension system also includes a mandatory occupational pension. In addition to this, pensioners may have invested in private pension accounts to supplement their income at retirement. Therefore, the model does not represent total pension income, only total pension amount received from the state (in the Old Age Pension category).
The CLD of the system is presented in this section as well as the behavior (in the form of graphs) produced from the structure.
3.1. Stock and Flow Diagram of the Norwegian Pension System
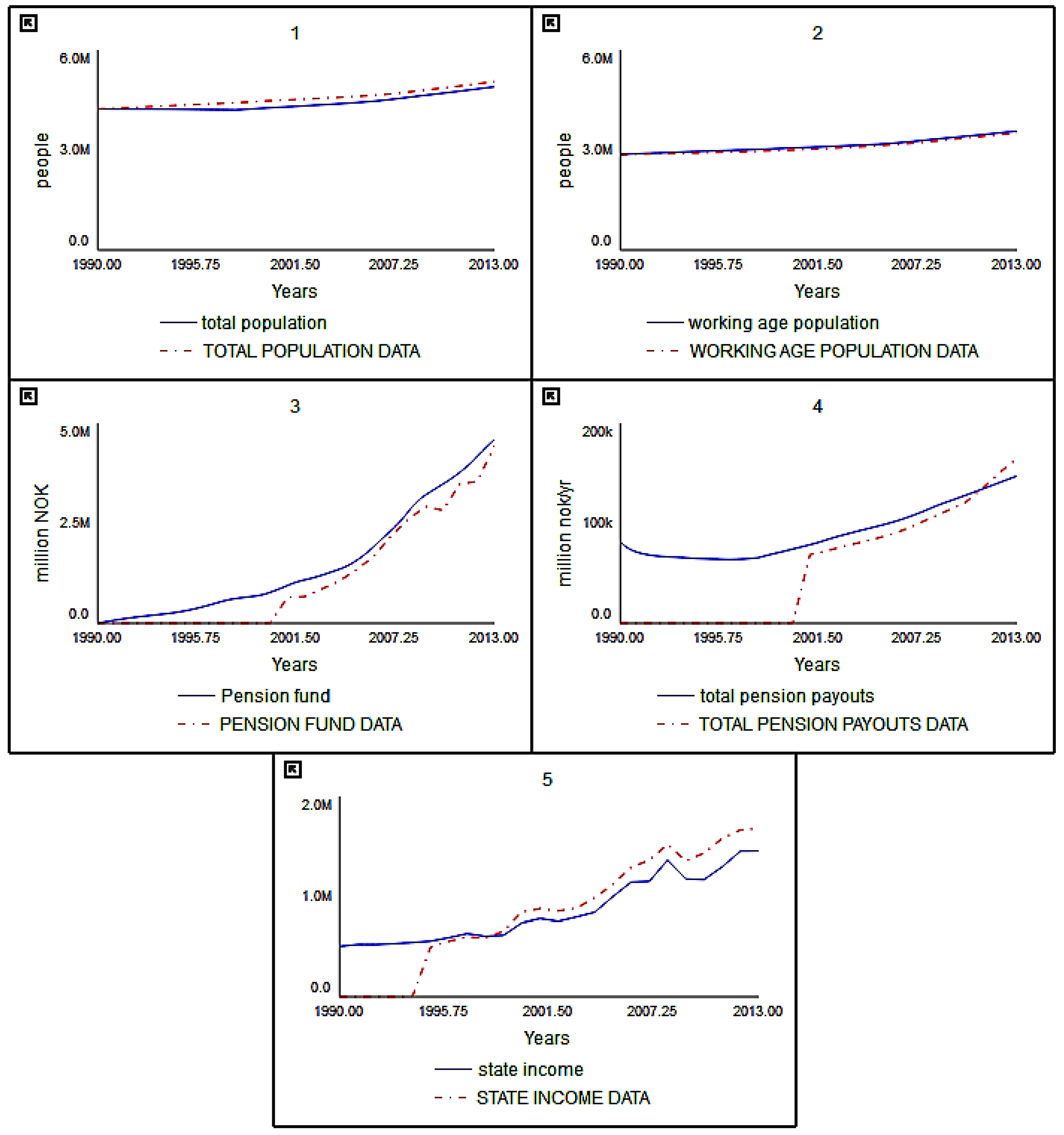
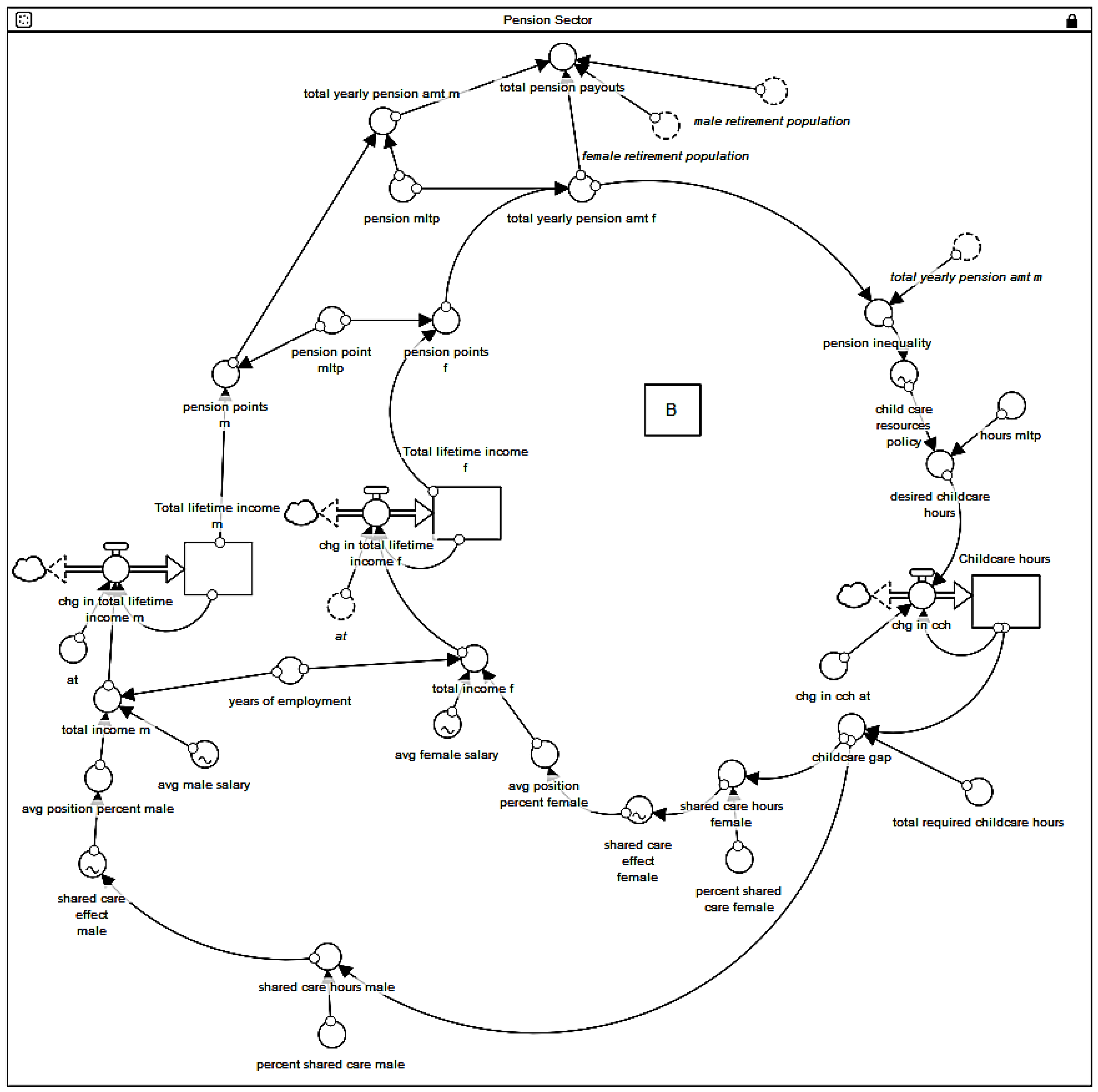
Figure 1 shows the stock and flow diagram of the section of the Norwegian pension system that represents how total lifetime income is accumulated for men and women. Total lifetime income for men is the stock on the left, and total lifetime income for women is the stock on the right. Total lifetime income is the largest determining factor for pension payments. Men and women earn different levels of pension as shown in
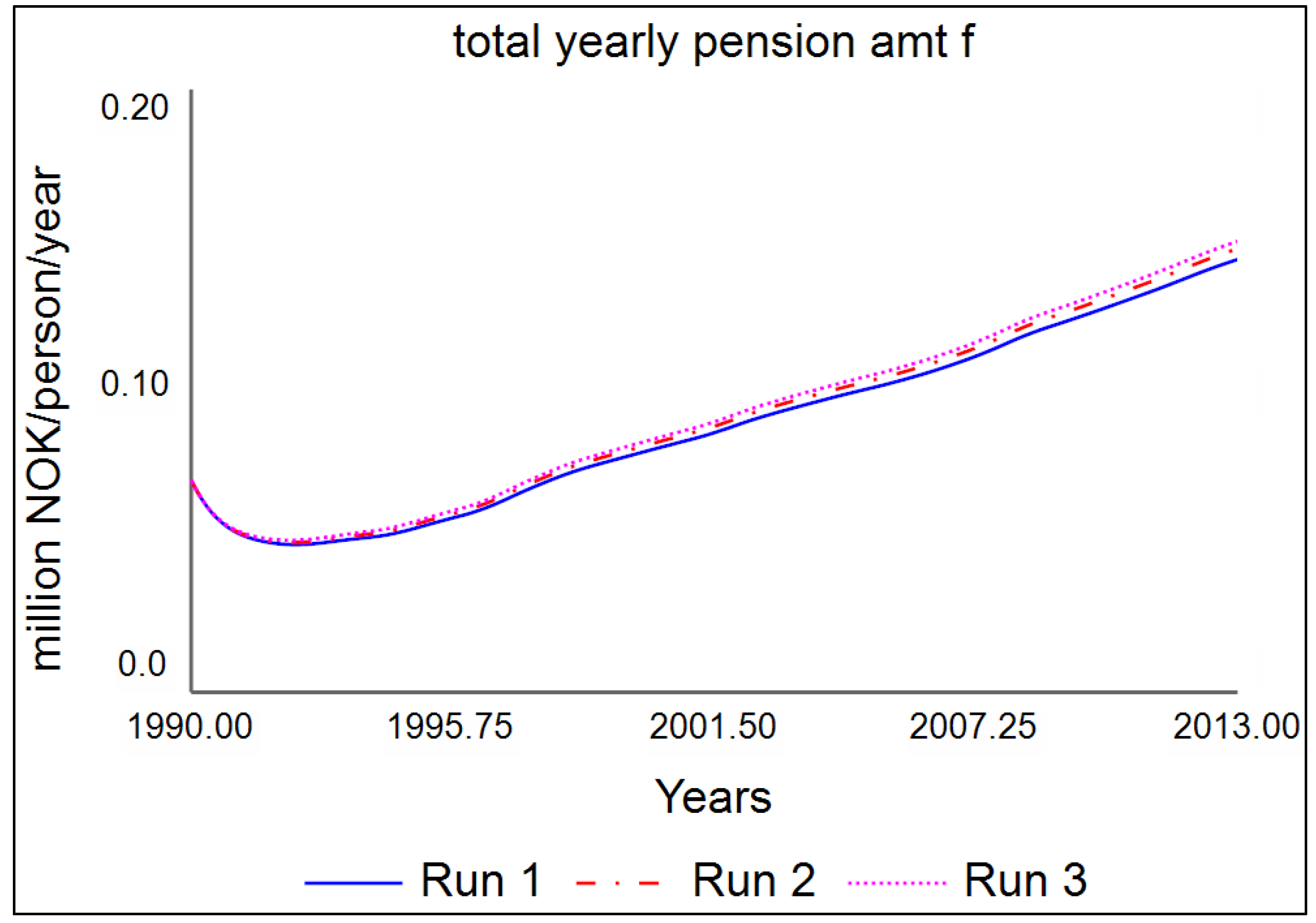
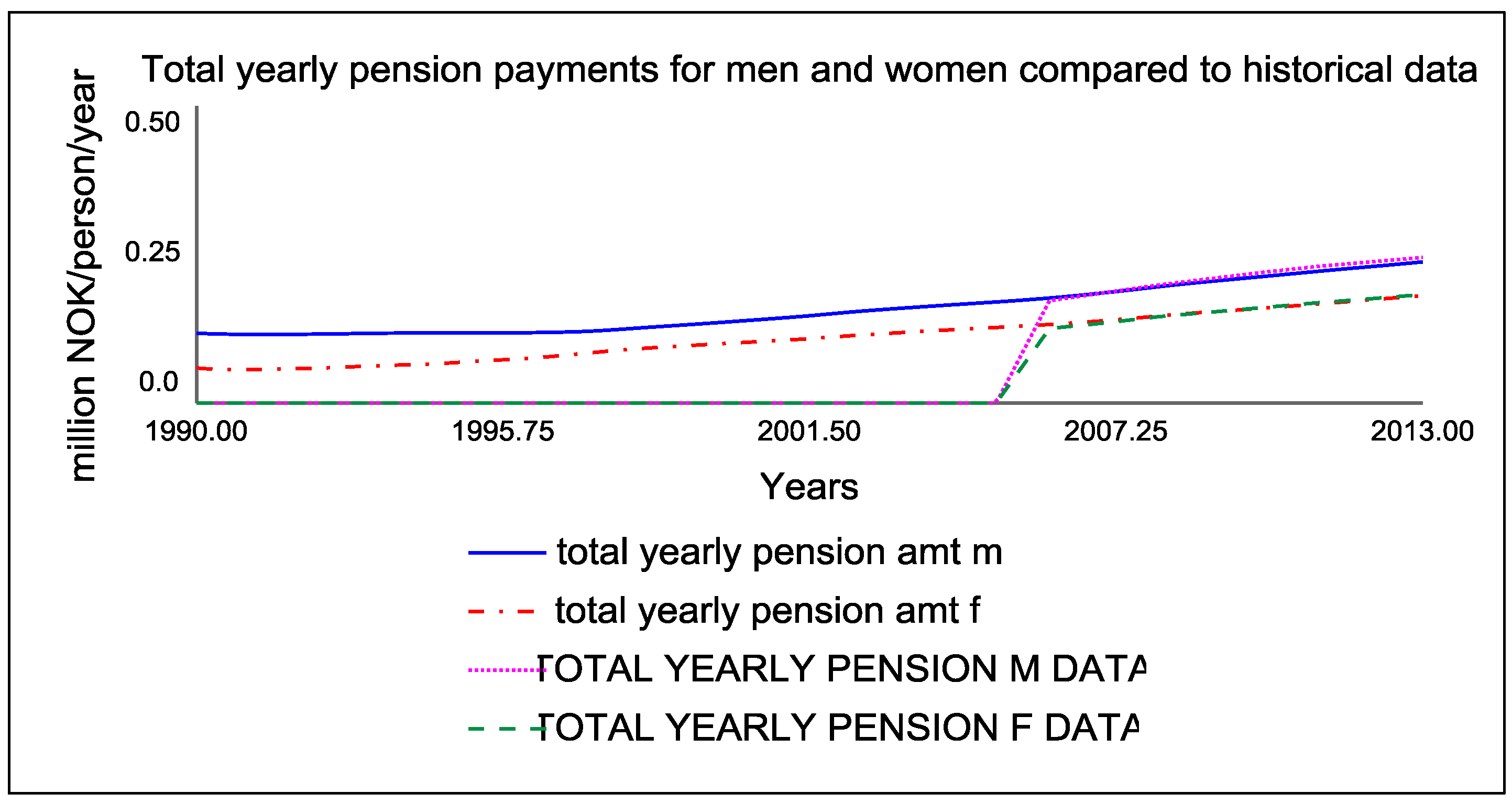
Figure 2. Total yearly pension payments are simulated in the model in
Figure 2 (blue-men and red-women) with the historical data (pink-men, green-women, no data before 2006).
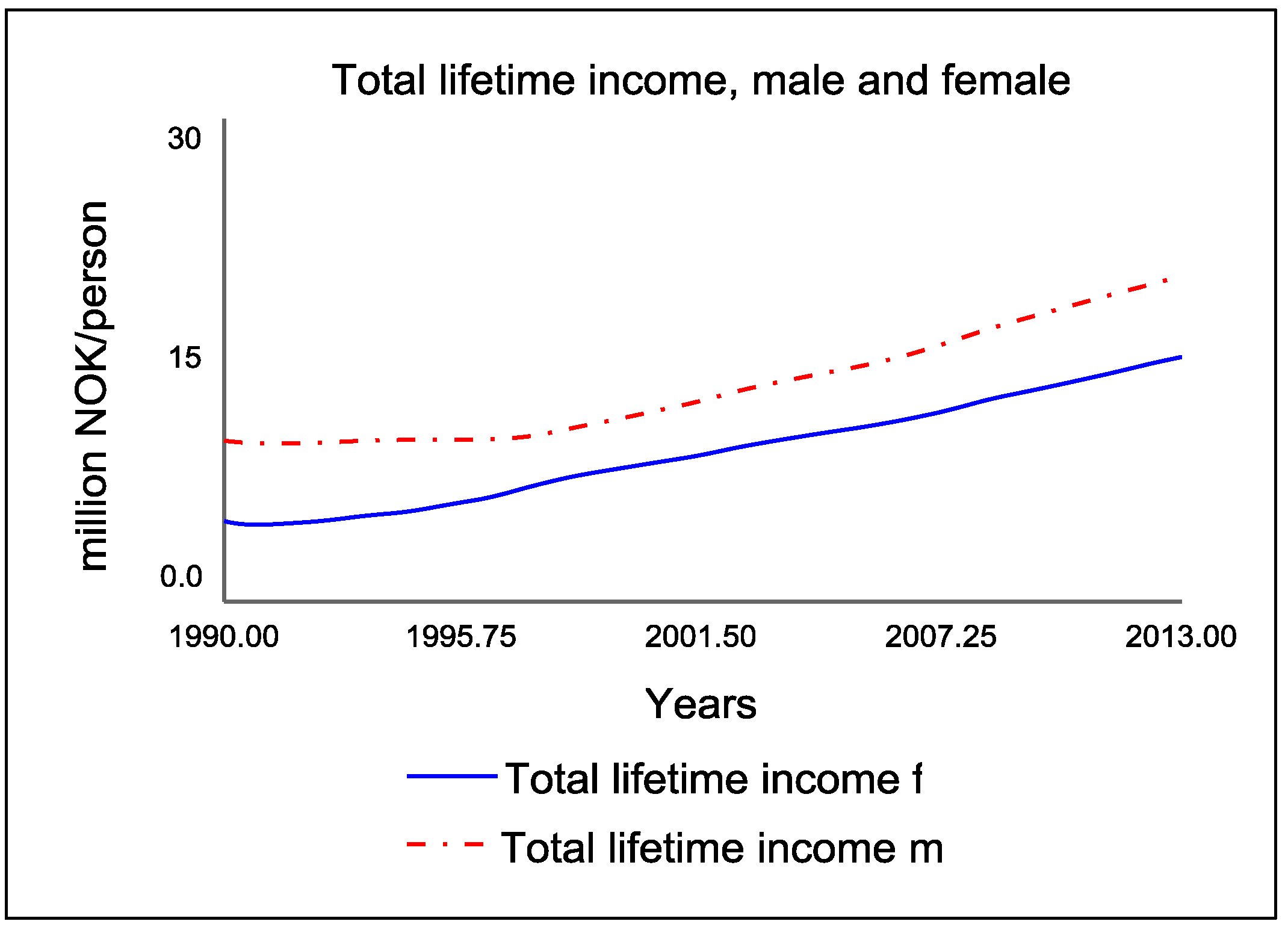
The total lifetime income for men and women (
Figure 3) differs because of several factors. There is wage inequality between men and women, which is around 83%–87% female/male income, although this has been decreasing with time [
10]. Another factor that affects the total lifetime income is the salary difference in male versus female dominated fields. Male dominated fields, such as engineering, have much higher salaries than typically female dominated fields, such as teaching [
10]. Wage inequality and male/female dominated fields are factors that are aggregated in the variables “avg male salary” and “avg female salary” in the model.
The purpose of this model is to investigate how state policies have worked to reduce pension inequality between men and women. As stated, there are policies to reduce wage inequality and goals to encourage women to enter male dominated fields. However, even if these inequalities disappear, the average position percent (full time position equals 100%) is still affected for women in childbearing/rearing years by a significant amount (ca. 20%). All else being equal, this large gap leads to major differences in pension, which is why the policies regarding this are investigated in this model.
Parental leave in Norway allows for men and women to stay home for 36 or 46 weeks after the birth of a child (number of weeks depends on whether they take 100% or 80% salary). Of these, the father must take 10 weeks of this, and the mother cannot take leave for the father [
17]. Parents receive pension points during this time. By the age of one, the child has a right to a place in daycare [
18]. This system allows for women (mothers are much more likely to be the parent taking the majority of parental leave) to be back at work as early as possible to start/resume earning income and pension points again.
Women are most likely to work part time versus full time (represented as “position percent” in the model), and this is usually due to childbearing and rearing even with childcare resources in place. Norwegian childcare resources include income for women who stay home with children and do not hold a job, but these women do not receive pension points for this (and this income is not included in the model.) This tendency to work part time is represented in the stock and flow diagram in
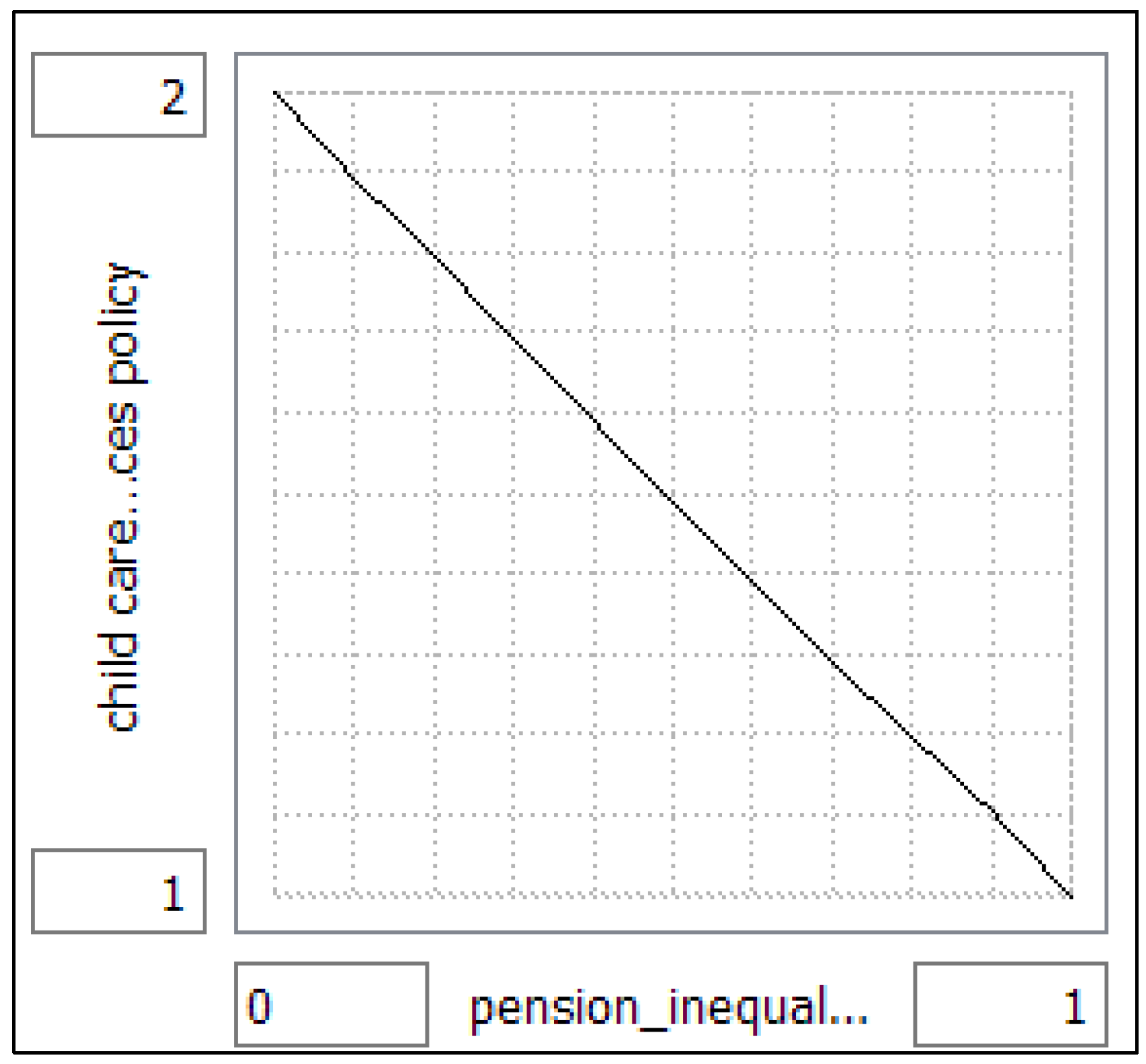
Figure 1. The “average position percent female” variable is affected by shared care hours. “Shared care hours” are the number of unpaid childcare hours parents must provide, which are not available to be outsourced to state childcare services. Either the mother or the father can provide unpaid childcare work, but this is (as a societal norm) usually provided by the mother. “Childcare resources policy” is a non-linear graphical function that states: as pension inequality increases, the childcare resources increase in availability in order to reduce pension inequality. This is a model assumption to represent policy decision-making. In short, policy makers will offer more childcare resources when pension inequality is higher. As pension inequality approaches 1, childcare resources increase by a decreasing percentage. In this sense, pension inequality between the genders is used as
one performance indicator of gender inequality in general. The representation of this in the model does not mean that the only influence on childcare resources is pension inequality. Many variables not investigated in this model influence the level of childcare resources, which is a supply and demand dynamic referred to as the childcare gap [
19]. Please see
Appendix A concerning assumptions in system dynamics modeling.
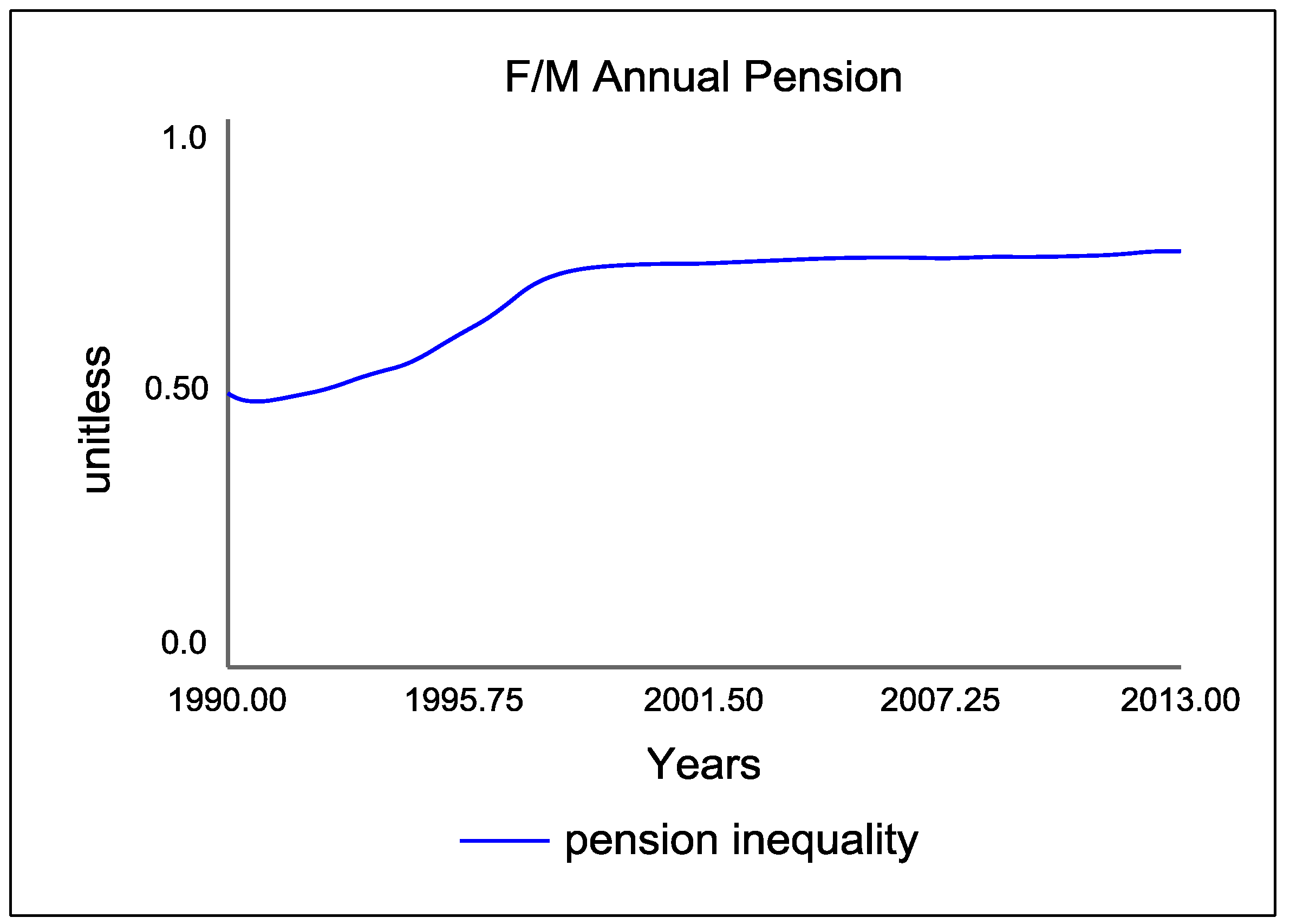
“Pension inequality” is the ratio between male and female pensions. The goal is to have this equal 1 (equal female/male pensions). The graph in
Figure 4 shows the behavior of this over time. The simulation runs until 2013, with the ratio at 0.75.
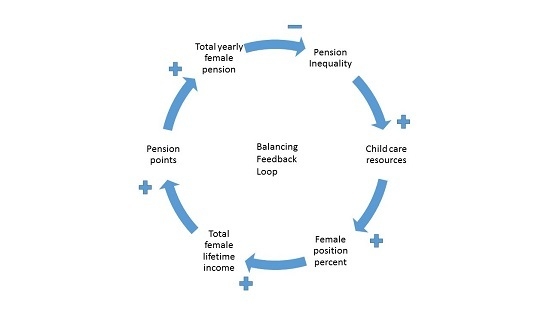
3.2. Causal Loop Diagram
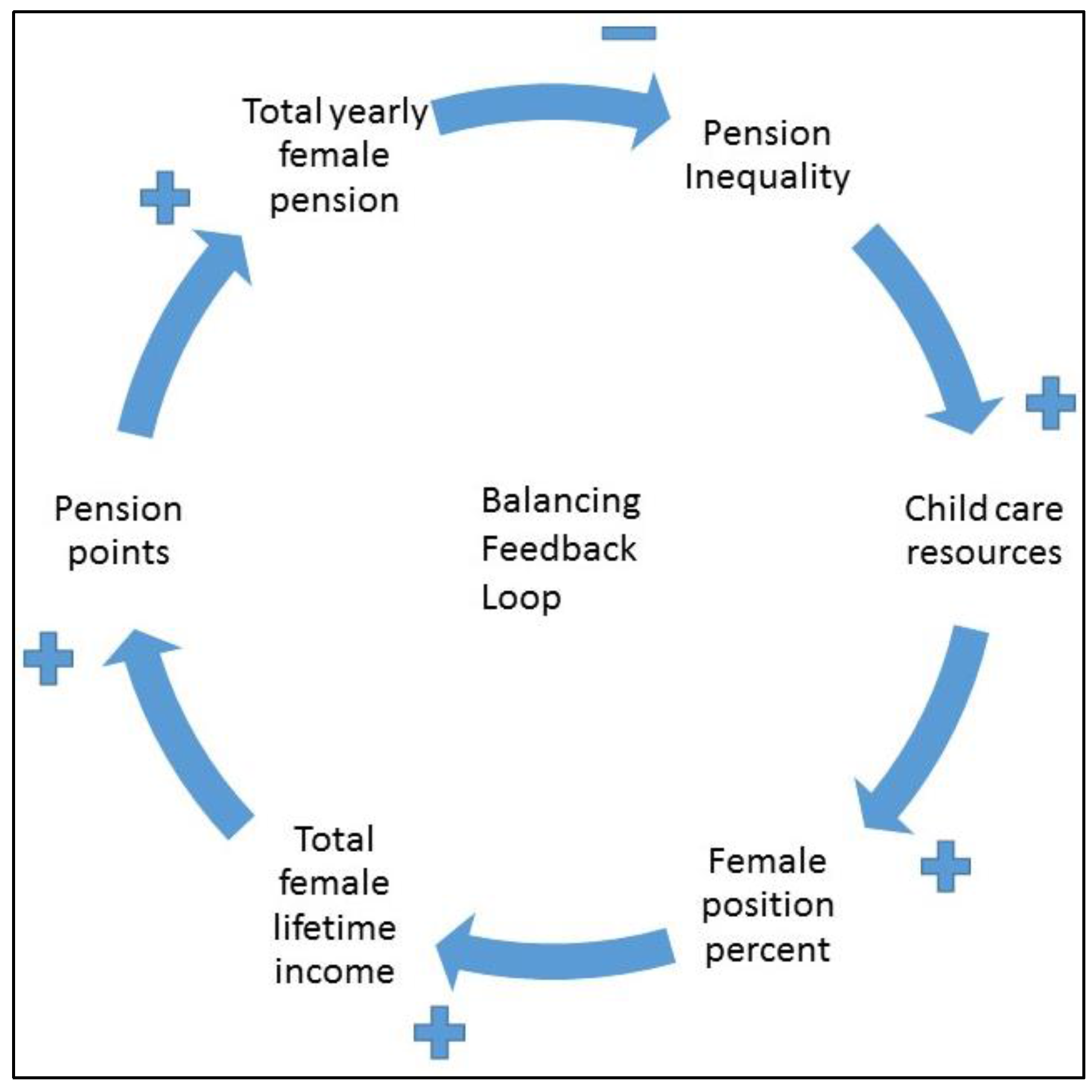
The relationship between the variables in the stock and flow diagram forms a balancing feedback loop, which is represented in the CLD in
Figure 5.
The CLD explains that as pension inequality increases, the amount of childcare resources increases. This increases the position percent (full versus part time work) that women are available to take. A higher position percent gives a higher total female lifetime income, which means more pension points for women. The more pension points women earn, the higher the pension they receive at retirement. As women receive higher pensions, pension inequality is reduced.
It seems from the CLD that the policy (childcare resources) in place helps to alleviate the pension inequality. As is often the case in policy implementation, as one problem is fixed, another arises. The next section discusses why this policy helps fix the problem, but with structural consequences for women.
4. Discussion
One important variable that is left out of the CLD is unpaid childcare work. The childcare policy relies on the importance of the dual earner household, but does not address the issue of shared caregiver, which is the other side of the dual earner relationship. This section explains how this structural oversight in policy leaves women disadvantaged.
There is a social dilemma with having children in Norway and most modern societies because of the large economic burden for the parents; yet children are valuable and necessary for the society [
20]. Having children is not a rational economic choice for women, but it is rational as a societal choice. Norway has an interest in keeping the fertility rate from dropping and socially investing in children because the welfare system depends on labor force participation. Therefore, investing in the welfare of the young supports the welfare of the elderly in this model [
18]. This is social investment strategy represented in the Norwegian pension system. However, the focus on children and childcare resources to increase female labor force participation (which increases the pension payment and hence female elderly welfare) keeps women locked into the balancing feedback loop shown in the CLD in
Figure 5. Is this fair? It is not a rational economic choice (in terms of pension) for women to provide their own childcare versus having it provided by the state. I am not indicating that most women that use state provided childcare resources would rather stay home with their children (though some most likely would), but many do choose to stay home either full time or part time and are not rewarded (in terms of their pension) for their contribution to the social investment (as shown in
Figure 2).
The “new gender contract,” advocated by Gøsta Esping-Andersen is the concept that welfare states should support a child-centered social investment strategy, where female labor force participation is necessary for the sustainability of the political economy [
21]. Norway’s social welfare policy has focused on making this a reality, and women are needed in the labor force to do so, making gender equality both an economic issue and a social issue [
22]. Increasing female labor force participation leads to what Esping-Andersen calls “female life course masculinization,” and men should hopefully adopt (and must in order for the new gender contract to work) a more “feminine life course” (higher rate of care duties at home). However, a more feminine life course for men is not easily achieved, and has as yet not been achieved to the level where childbearing/rearing does not affect female position percent (level of part time work). Although feminists are skeptical of the focus on children in social investment strategy having a positive outcome for women [
23], this problem with the new gender contract and social investment strategy should instead call for the revival of the concept of husbandry [
24]. Husbandry is a richer gender identity for men, where they identify beyond “the economic man.” Husbandry is not “a male mother;” and women need not become an “honorary man” or adhere to female life course masculinization. The argument in the revival of husbandry is that caring is a human trait, where men are leading less full lives without having it as part of their gender identity.
The CLD in
Figure 5 indicates that women are at a structural disadvantage in terms of future pension payments. Only those women who want to contribute to the welfare system with labor force participation (and hence contributing to social investment strategy) will achieve higher pensions. Women must adhere to social investment strategy with labor force participation, where there is the defamilialization of care [
23]; and if they choose not to adhere and provide childcare themselves, their lifetime earnings and hence pension will suffer. Even if women do adhere, care work at home is still largely the responsibility of mothers, which leads to higher rates of female part time work in childbearing/rearing years.
Regarding the recent report by the Nordic Council of Ministers [
11] mentioned at the beginning of this paper, their assertion that part time work during childbearing/rearing years has no significant effect on the pension payment for women (using economic forecasting) is a very simplistic view of the systemic forces at work in the Norwegian pension system. Because of the methodological differences and points of departure between that study and the one presented in this paper, different elements of this issue are highlighted. The Nordic Council of Ministers research highlights that female part time work does not economically influence the level of pension compared to her full time counterpart (not a male/female comparison). This study identifies the systemic forces that make this so (and compares her to her male counterpart) and argues that these forces are what leads to the structural disadvantage for women in the Norwegian pension system. The two main systemic forces that lead to this disadvantage are the policy requirement of outsourcing childcare to enable female labor force participation (female life course masculinization) and the policy requirement of the shared caregiver (male life course feminization-which is a hopeful, not a strategic policy requirement). It is this policy that determines whether or not a woman’s pension payment equals or comes close to her full time counterpart, but it is the policy requirements that are the disadvantage for women.
Though not coming from a systemic perspective, Jensen [
23], in an analysis of gender issues in social investment strategy, explains that structural factors (devaluation of women in the welfare system) must be attended to instead of worked around (male life course feminization). The structure of a system causes the behavior. Any realistic policy must address the structure to create real change [
25]. As an extension of “female life course masculinization,” the Norwegian pension system is considered a “masculine pension system” because there is a requirement of labor force participation to receive pension points [
26]. Women do not earn pension points for unpaid childcare work in the years after parental leave ends unless they are in paid employment. Women must “act like a man” and enter the labor force full time as soon as parental leave ends if they do not want to see a reduction in their pensions. However, there are only so many hours in the day, and women caught in this policy will never achieve maximum pension if men do not share childcare responsibilities. Because the policy relies on hope and not strategy to fulfill this shared caregiver requirement, in the evaluation of social investment strategy and its policies in regards to pension, the effect of solely focusing on children to enhance elderly welfare leaves women at a structural disadvantage.
This study does not model the Norwegian labor force and does not address the salary gap between male and female dominated professions, nor does it address the wage gap. This is important to address in relation to this study because labor force dynamics have a relationship with gender identity, as women are much more represented in care professions, and these are considered of lower value even when they are highly-skilled (such as nurses and teachers) [
27].
5. Concluding Remarks
This study uses system dynamics modeling to explore how the Norwegian pension system in its implementation of social investment strategy traps women in a structurally disadvantaged situation. There is no attempt in this paper to give policy recommendations, as is so often the purpose of system dynamics modeling studies, because further research must be done before policy can be addressed. This includes, for example, analyzing the results in relation to various household structures (e.g., single men and women, couples without children, couples with many children versus one child). This study assumes equal pension levels for men and women as the desired system behavior, which corresponds to Norwegian equality goals, and further analysis must address several policy scenarios to achieve this. For example, if the male population contributes unpaid childcare hours and this achieves the desired behavior, what are the possible side effects of this and are the implementation challenges insurmountable? To be relevant for Norway, policy analysis must include a thorough evaluation of implementation challenges and feasibility. The model presented in this paper is the first system dynamics model that focuses on gender and pension in Norway. Labor force dynamics and childcare gap dynamics beyond pension are important future model developments that will give new insight into Norwegian gender issues.