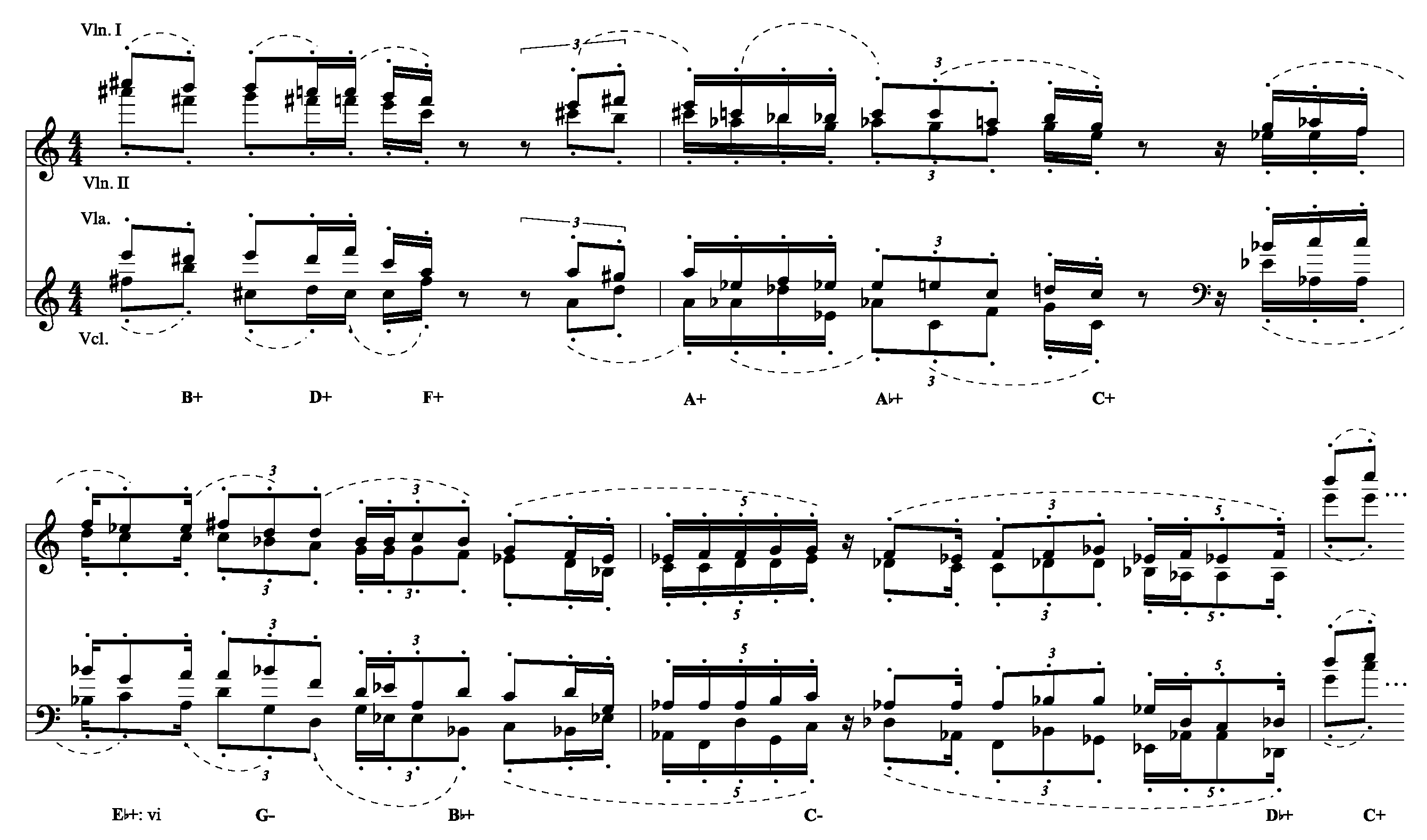1. Background and Introduction
Sky Macklay is an emerging, New York-based composer and oboist. Her music explores post-minimalist contrasts, audible processes, theatre, and the visceral nature of the cognition of sound. Her works have been performed by ensembles such as International Contemporary Ensemble (ICE), Yarn/Wire, Spektral Quartet, Mivos Quartet, Dal Niente, Da Capo Chamber Players, Firebird Ensemble, Hexnut, The University of Memphis Contemporary Chamber Players, The Luther College Concert Band, Luna Nova, and PRIZM. Her piece Dissolving Bands was commissioned and premiered by The Lexington Symphony in Lexington, Massachusetts. Dissolving Bands was the winner of The American Society of Composers, Authors, and Publishers (ASCAP) 2013 Leo Kaplan Award. In 2015, The International Alliance for Women in Music commissioned her sonic and kinetic installation of inflatable harmonica-playing robots aptly entitled Harmonibots. She has also received commissions from The New York Virtuoso Singers, The Walden School Faculty Commissioning Project, and from Saint John Lutheran Church (MN). Her multi-movement work for jazz ensemble, Mestiza, was performed at the 2010 Midwest Black History Conference. Lake Dublin for clarinet, piano, and water bowls, was a winner in the 2011 Iowa Composers Forum Spring Festival’s Composition Contest. The International Alliance for Women in Music has drawn much attention to her piece Before There Was Backspace There Was No Going Back for amplified electric typewriter and ensemble.
As an oboist, Sky plays with Ghost Ensemble Collective and performs her own and other composers’ works. Sky has toured internationally as a wind ensemble and orchestral oboist, and draws upon this background as a composer.
Hailing from Waseca (MN, USA), Sky graduated Magna Cum Laude from Luther College in Decorah (IA, USA) where she studied Composition with Brooke Joyce. In 2012, she earned her Master of Music degree in Composition from The University of Memphis (TN, USA) where she studied with Kamran Ince. Sky is currently pursuing her doctoral studies at Columbia University (NY, USA) where she has studied with Fred Lerdahl and George Lewis. Sky has taught at The Preparatory Center for the Performing Arts at Brooklyn College (NY, USA), and is currently an instructor at The Walden School Young Musicians Program in Dublin(NH, USA). Beyond composing, her current research interests include extended techniques for oboe and composition pedagogy.
1Sky Macklay has written a string quartet entitled
Many Many Cadences (
Macklay 2014), which inventively combines the basic operations of neo-Riemannian triadic transformations and voice leading (e.g., Parallel (P), Leading-tone (L), Relative (R), SLIDE, etc.). Concomitantly, predominant-dominant-tonic, dominant-tonic, deceptive, and plagal progressions, and expected resolutions of active scale degrees (e.g., the leading tone) in the standard cadential formulae of
Many Many Cadences (
Macklay 2014) are overwhelming. Macklay’s parsimonious voice leading is a systematic consequence of her transformational operations. In fact, Macklay’s harmonic use of ic1/2 voice-leading parsimony may often implicate a contextually fluid voice mapping involving a dual process of inversion. However, the single tonal/post-tonal identity this suggests is a model of local, event-to-event harmonic phenomena, as they exist as a part of the quartet’s superstructure, and systematized into ordinary language, quantitative measures, and/or diagrams. Appropriating Iannis Xenakis’ kinematic diagrams for this study’s own special, non-mathematical use, I will present Macklay’s return to pre-modern tonal expectations as both a literal return to common-practice tonality as well as a triadic post-tonality. As the first large-scale, in-depth analysis of any work by Sky Macklay, this detailed study explores the chord-note mapping premise of Macklay’s neo-Riemannianism and its relevance to twenty-first-century musical discourse.
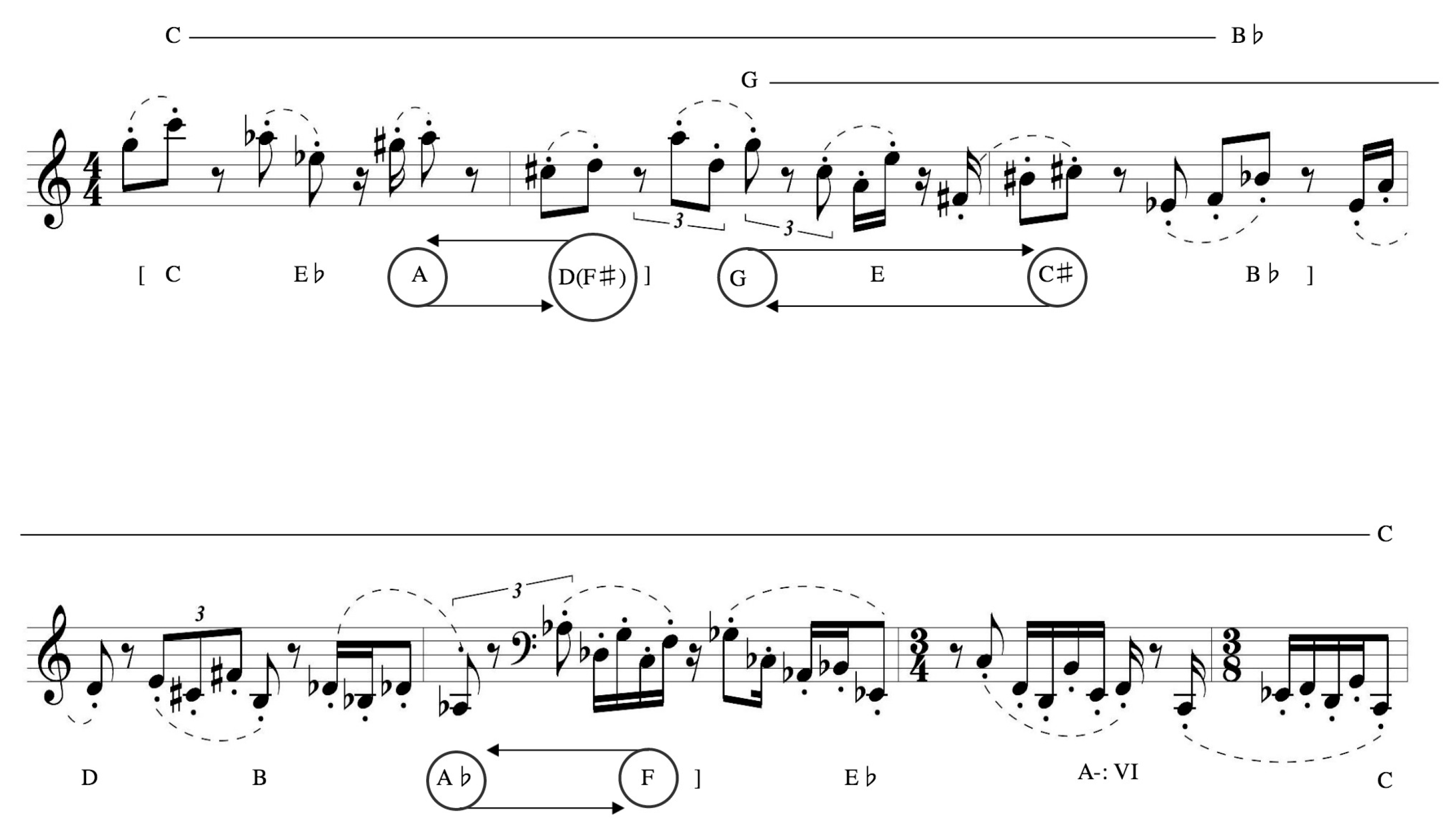
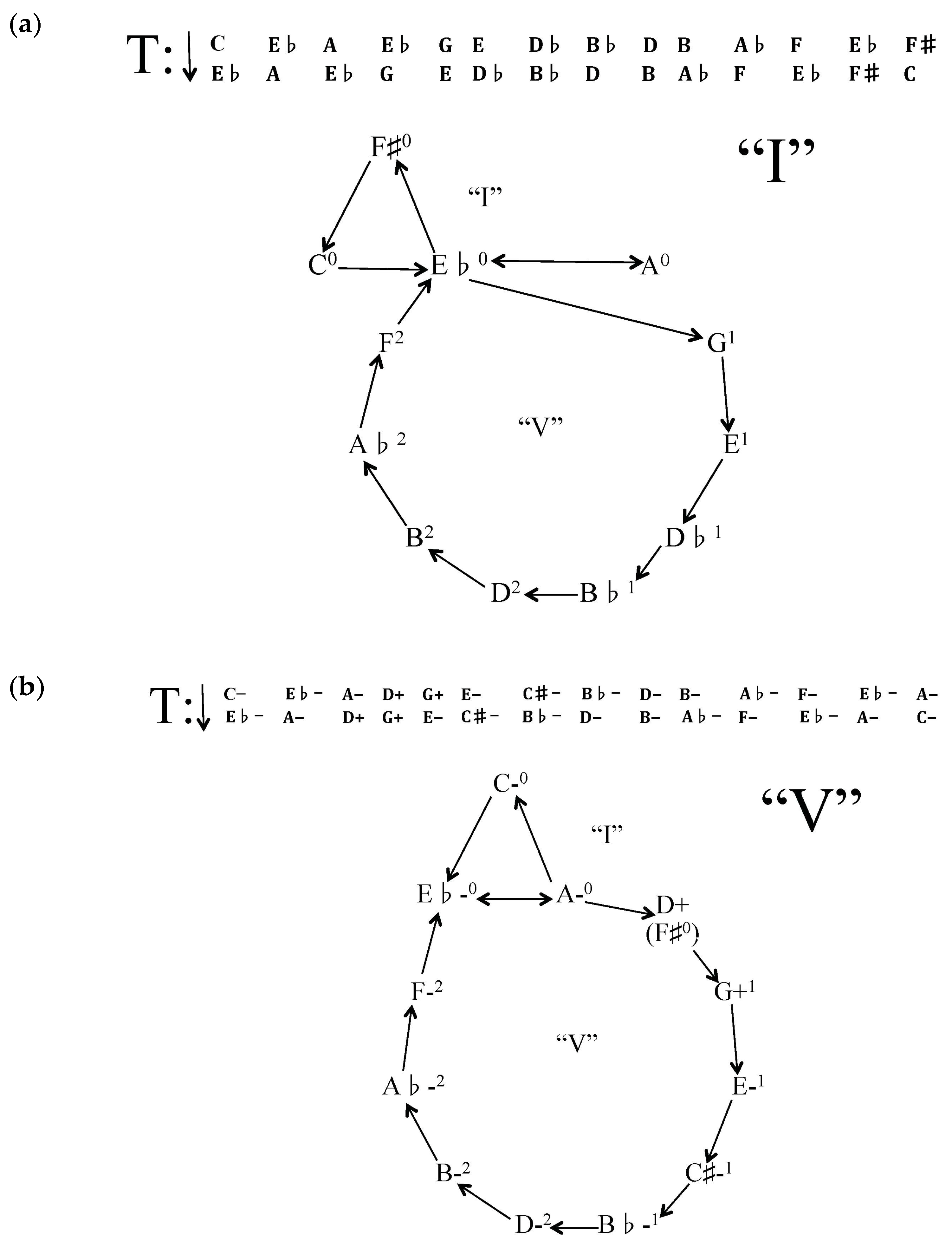
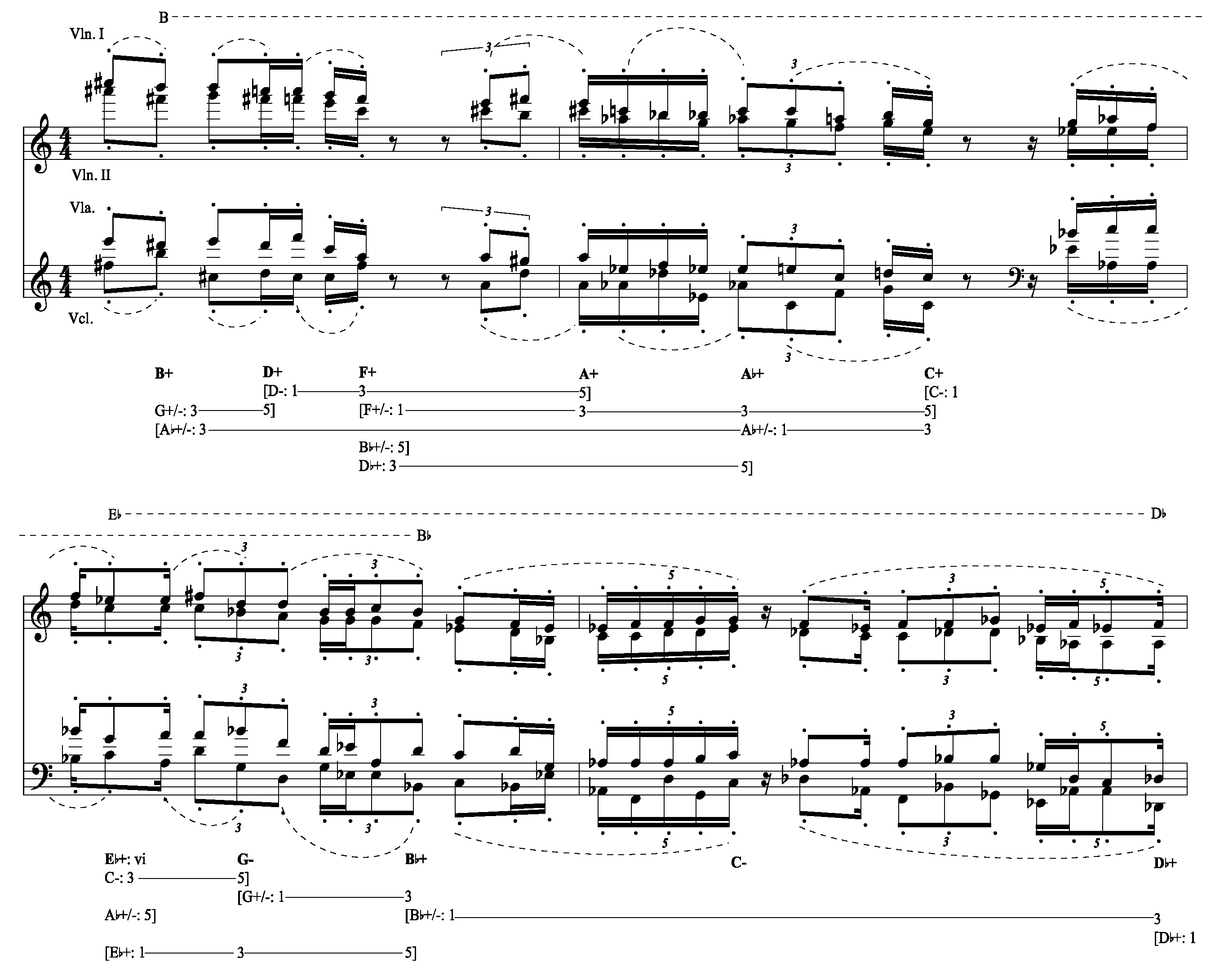
Figure 1 provides a piano-score reduction of the first six measures of Sky
Macklay’s (
2014)
Many Many Cadences. This music serves an expository function as the main idea and basic motivic pathway of the entire piece: the music that follows this excerpt introduces successive repetitions of this idea, each with its own time-span, rhythmic variances, and triadic transformations. Several features of this quartet conspicuously harken back to common-practice or
pre-modern tonality: tertian harmonies, triadic progressions, “teleological structural genesis”,
2 traditional instrumentation, continual developing variation, and familiar formal designs. Some of these can be heard in the six measures of
Figure 1: the relentless perfect authentic, leading tone imperfect authentic cadences, and plagal progressions involving the explicit tonicizations of 13 different triads are confined by framing C+ harmonies in measures 1 and 6 (the roots of triads will be given in capital letters with a + or − symbol to indicate major or minor chord quality, respectively), and wisps of melodic material with a generally downward trajectory rapidly discharge from this triadic post-tonal adumbration in measures 1–6.
One particular facet of neoconservative postmodernism
3 (i.e., the nonfunctional relation of triads) is found in Macklay’s music although in a manner that constitutes a paradox, namely, the adoption of tonal materials such as tertian harmonies with a regard for common-practice syntax that is congruent to its utter neglect. The predominant-dominant-tonic, dominant-tonic, deceptive, and plagal progressions, and the expected resolutions of active scale degrees (such as the leading tone) in all these individual standard cadential formulae are not only frequent, they are overwhelming. The excerpt from
Many Many Cadences (
Macklay 2014) offers an almost immodest example of this sudden regard for traditional tonality: each one of the 15 related melodic fragments in measures 1–6 ends completely resolved within its explicit tonality. The endings on A (violin I), in particular, although Macklay clearly abandons them in their fleeting tonal fields, are actually points of arrival, the letter names of the chordal roots of which spell out the components of the D+ triad; a tonal hearing of textbook cadential formulae in the key of A+ or F♯- will certainly find a G♯ resolving perhaps up to A or a B in the key of D+ descending to A. On the other hand, it is well known that the frustration of tonal expectations is not without ample precedent in the music of the common-practice period. Indeed, Macklay’s string quartet and other stylistically similar works greatly differ from common practice in that they seem to unremittingly eschew any kind of tonal suspension from beginning to end.
But this seemingly continual satisfaction of tonal expectations is indubitably a part of the music’s aesthetic: the pre-modern superficies ostensibly promises tonal successions that are always delivered. Yet tonal expectations are certainly not the only voice-leading expectations a listener should bring to this music, although I will use the term “voice leading” synonymously with the term “part writing”, or what Dmitri
Tymoczko (
2008a) formalized as “bijective” voice leadings, implying a fixed number of voices, in this case, three (pp. 1–49).
This study proposes the hypothesis that the highly constrained, traditionally normative characteristics of Macklay’s neoconservative postmodern music nonetheless avails itself of voice leading derived directly from certain post-tonal practices. In Part I, I will define this as an emergent property from a voice-leading perspective, focusing on the two principal post-tonal types of motivic projection and the triadic transformations of voice-leading parsimony and contextual inversion. Then, in Part II, I will establish an identity of essence between this new emergentistic model of triadic post-tonality and other models of triadic processes (i.e., neo-Riemannian, common-practice) from which it arises. In Part III, I will apply the model to an analysis of Macklay’s stylistically neoconservative postmodern music, and, in Part IV, I introduce a graphical and tabular means of surveying its supervenient metatonality.
2. Part I: Macklay’s Harmonic Style(s) As an Emergent Property of Voice Leading
A feature of Macklay’s neoconservative postmodern music is often referred to, in some form or other, as the “return to harmony” or the “return to tonality” (
Bernard 1995, p. 284).
4 However, in the context of this recent piece, this “return” may be better understood as an “assimilation”, which results in a very focused and concentrated presentation of tonal cadential progressions projected along a certain well-defined motivic pathway of which
Figure 1 is paradigmatic. First, atonal practices are paradoxically concurrent with the near exclusive use of well-known harmonic cadential progressions. Second, her neoconservative postmodern string quartet is largely both homophonic and homorhythmic. Third, and perhaps most simply, much of the harmonic rhythm in Macklay’s neoconservative postmodern string quartet is very fast, blurring any sense of discrete chord progressions.
Yet Macklay’s harmonic appropriations are hardly reversions to common practice: I suggest the term “assimilation” because, at the core, there remain two significant and generalizable features of post-tonal harmonic practice, one being motivic projection.
5 Generally defined, a triadic progression is motivic to the degree that triads are projected along a distinct motivic pathway; it involves triadic transformation to the degree that its triads either connect by having the voices move as economically as possible, or by inverting around one or two notes of the preceding triad. But before fleshing out these concepts with more precise definitions and examples, the issue of what does and does not constitute a harmonic progression in Macklay’s music requires some attention.
For the purposes of this study, I will define a harmonic progression as a totally ordered succession of single triadic sonorities involving idealized voice leadings between the I/i chords of each distinct key area (as established by a cadential formula), meaning that triadic progressions so defined are represented by their most efficient one-to-one voice leading (
Tymoczko 2008a, pp. 1–49). Furthermore, Macklay will often restate a harmonic progression while simultaneously varying one or more of the aspects of the original template several times by allowing each of these restatements to become the input, as it were, of the next iteration. These restatements are rarely separated by silence. Rather, they sometimes project a process involving interval cycles, although without strictly preserving clockwise motion around the cycle.
Figure 2, which provides the roots of the tonicized chords for the section in
Many Many Cadences (
Macklay 2014) that immediately follows the music of Example 1, displays one application of this procedure: the first four-root sequence C-E♭-A-D first accrues to C-E♭-A-D-G-E-C♯-B♭ in measures 7–9, and then, if one substitutes F♯ as the third active scale degree of the fourth key area of D+ of the first four-root sequence, immediately accrues to all three diminished-seventh chords of the three C3-cycles of [C-E♭-A-(F♯)]-[G-E-C♯-B♭]-[D-B-A♭-F]… (The brackets below
Figure 2 concern this accretion in that they show a progression of the roots of tonicized triads through a motivic pathway that ignores adjacency of pitch-class intervals of the C3-cycles). Therefore, in taking this practice into account, the root progression under scrutiny is devoid of both immediate repetitions of a pitch-class (pc), as well as immediate repetitions of the same ordered sequence of pcs.
Given this definition of a harmonic progression, one can see that, with the help of transposition, pc diversity is easy to come by when one starts on any pc (considered here as a temporary tonal center) and moves repeatedly and contiguously by any given generating pc interval. For example, an interval cycle without returning to its point of origin will always be non-duplicative, that is, all of the pcs will be different. This ceases to be the case if one continues to move around the clock-face, so to speak. But, with the exception of the C1 and C5 cycles, transposing an interval cycle allows for further avoidance of interior repetitions: starting on C, C30 gives C, E♭, F♯, A, C31 gives C♯, E, G, B♭, and C32 completes the aggregate with D, F, A♭, B. When examining Macklay’s harmonic practice as a whole, the maximal lengths of nonduplicative successions of transient pitch centers without interior repetitions are approximately seven to ten notes, demonstrating a “composing-out” of the composer’s motivic patterning.
Theorist Scott Murphy’s assessment of Penderecki’s overall melodic practice could be applicable to Macklay’s overall
harmonic practice: “This is not unlike an acknowledgment of certain liberties some serial composers take with their realizations of a row” (
Murphy 2007, p. 217). It is as though the fleeting centrically functioning pcs of her harmonies considered linearly are based on a freely atonal scale model. In other words, there are times when it seems Macklay is using approximately seven to ten scale degrees as the basis for constructing freely atonal music, if only in a purely linear sense. The movement of the harmony in measures 2–6 of
Many Many Cadences (
Macklay 2014) (
Figure 1) offers a good example of this diversity: no pc (as root) is repeated in its 11 tonicized triads. The roots of the tonicized triads in the chord progression of
Figure 2 have pc repetitions, but they are considerably spread out, as demonstrated by the analysis above the music. Each horizontal line represents a non-duplicative pc succession that begins and ends with the two pcs at the line’s two ends. These two series constitute a set of non-duplicative, tonicized root successions, in which neither member of the set is completely embedded within the other: their average length is 9.5 (
Tenney 1977, pp. 36–69).
Figure 3 provides a similar analysis for a line of tonicized triad roots from later in the quartet (from m. 25): the average length of the two successions is exactly seven. Ideally, a thorough statistical analysis of Macklay’s triadic-harmonic repertoire would confirm or correct this hypothesis; for now, a general familiarity with the music of this quartet will need to suffice. This kind of pc diversity that characterizes Macklay’s overall harmonic practice involves non-duplicative successions of tonal centers from approximately seven to ten notes which serve as essentially freely atonal melodic lines that are harmonized by her triadic vertical sonorities. Additionally, there is a subtler motivic link between the tonal-center “melody” in
Figure 3 and all the triads of this passage. There are 12 members of set-class (037) embedded in the linear succession of the tonicized triadic roots, and, vertically, all the triads themselves are members of the same set-class. So both the triads and the tonicized root progression follow a motivic path, one vertically; one horizontally.
Figure 4 shows a representative harmonic progression from a passage involving two complete musical textures occurring at the same time from
Many Many Cadences (
Macklay 2014). While the predominant-dominant-tonic, dominant-tonic, deceptive cadences, and plagal progressions continue above (see
Figure 4a), the harmonic progression shown in Example 4b is occurring underneath. Although there are seven nonduplicative successions of chordal roots among the sequences that make up this layer of the passage, all but one non-duplicative succession falls short of the approximate minimum of seven pcs. This type of writing takes Macklay farther away from European and closer to American modernism: Ruggles’s sacrifice of pc non-repetition for the sake of motivic repetition has been discussed (
Slottow 2009, p. 25),
6 and a very rapid, quasi-atonal change of key implication has been noted in Ives’ music.
7 The image of “total chromatic saturation”
8 that Mike Searby uses to describe Ligeti’s “textural” music of the late 1950s and early 1960s also serves as an appropriate metaphor for the pc diversity of Macklay’s “
basse fondamentale”
9: the composer’s priority to aspire toward the inclusion of the pitch-class aggregate by completely soaking the musical space, both vertically and horizontally.
10 There is also a different kind of motivic patterning evident in
Figure 4b. Notice that the four roots of the harmonies of each sequence are usually either members of set-class (016) or consist in whole or in part of (016) subsets, and that a certain normal form transposition of (016) is arranged symmetrically around the [0,1,6] subset of the third sequence [e,0,1,6]. Starting locally with [e,0,1,6] or rather [B, C, D♭, F♯], B and D♭ surround C symmetrically and wedge toward it. More globally, a member of set-class (016) with normal form [E, F, B♭] surround the third sequence, which contains three members of sc(016) ([C, D♭, F♯], [C, F, F♯], and [F♯, B, C]) whose first notes 0 (C) and 6 (F♯) are a tritone apart—the poles of the 0–6 inversional axis (sum 0)—creating a palindrome [C, E, F, F♯, B♭]. These poles together with [E, F, B♭] also constitute the normal form pitch set [4,5,6,t,0], subsets of which are [0,5,6] and [4,5,t] that are not only members of set-class (016), but begin with the notes C and E, respectively. In prime form, [4,5,6,t,0] is set-class (01268), the (016) subsets of which are pitch sets [0,1,6] and [8,1,2]. The first integer name of the latter, together with the C and E of the normal form pitch set, come very close to spelling the C+ triad. What is found instead is a motivic parallelism to the musical surface being enlarged or composed out as a concealed repetition of something nested at a deeper level of structure. This gives measures 46–88 a high degree of self-similarity across scale: the note G, the 5th active scale degree or dominant in the key of C, is repeated in the first sequence, and is given further centricity as the dominant of C by virtue of its upper leading-tone A♭ (integer name 8). Likewise, B is repeated in the second sequence, and, as a lower leading tone, gives further local centricity to C. The arrival at the C+ triad at measure 96 (the beginning of the B section of this quartet’s ternary form) resolves the harmonic major third on B (beginning in measure 46) and the two build-ups to a B+maj.7 chord in measures 54–57 and measure 60, respectively, as though these harmonies had served a prolongational leading-tone function. Knowing that the 12 inversional axes are analogous to the 12 major/minor keys of traditional tonality,
Figure 4c features yet another motivic structure that consists of all but one (A) of the 12 notes (as pc roots) of the chromatic scale that is not only symmetrical around both poles of the 0–6 inversional axis (which are adjacent to each other in measure 74), but is quite literally an incarnation of that axis. All roots in the measures leading up to the 0–6 adjacency are on the left side of the axis of symmetry on the pitch-class clockface, while all of the roots in the measures leading away from the 0–6 adjacency are on the right side. All this suggests is that C+ is the tonic, but its tonicity is created by both inversional symmetry as well as traditional harmonic functions simultaneously.
Along with the motivic projection of pc centers, the other feature that characterizes Macklay’s harmony from this neoconservative postmodern piece is triadic transformation via voice-leading parsimony (the most efficient) and contextual inversion. Parsimonious voice leading, in which the voices move from chord to chord by the shortest distances possible, is a trademark of many different Western musical styles. Musicians usually “find maximally efficient voice leadings with relative ease” (
Tymoczko 2008a, p. 49), and one does not need Roman numeral analysis to understand how harmonic successions of triads of different quality would likely show the more or less equidistribution of neo-Riemannian triadic transformations (i.e., Parallel (P), Leading-tone (L), Relative (R), as well as the secondary operations that combine these three) between adjacent chords. The only possible bias might be in the reduced number of SLIDE transformations in common-practice chord progressions, since this transformation involves parallel fifths, and so binds together tonally distant chords (
Lewin 2002, pp. 196–230). This theoretically flat distribution means the semitone unquestionably serves as the fundamental voice-leading building block of most of Macklay’s motion from triad to triad, although there are melodic interval classes that serve to relieve the semitonal motion change in a manner that preserves both her Pendereckian sonorism as well as her neoconservative postmodernism at the same time. Throughout her string quartet, most triadic transformations weight the minor second and (somewhat less so) the major second considerably more than the minor third and (much less so) any remaining interval class. The nonduplicative successions of chordal roots in
Figure 4 from
Many Many Cadences (
Macklay 2014) display intervallic voice-leading preferences very typical of Macklay’s triadic transformations: her triadic harmonies strongly gravitate toward parsimonious voice-leading transformations involving the semitone and the major second interval classes, or what Julian Hook refers to as
uniform triadic transformations or UTTs (
Hook 2007, p. 15).
Theorists John Roeder and Scott Alexander Cook also hear such triadic transformations as a hallmark of the music of prominent contemporary British composer Gavin Bryars (1943), beginning with his String Quartet No. 2: “This music appears promising for a neo-Riemannian analysis because, although it is consistently triadic, it lacks fifth progressions, and because the chords always connect parsimoniously”. Furthermore, they note “chord-sequences that are developed” within certain sections of Bryars’ music “demonstrate voice leading that is exclusively parsimonious”. Finally, they say of their analysis that it “demonstrates that Bryars’ harmonies are not to be dismissed simply as non-functional sonorities”. Instead, “The parsimonious voice leading apparent in the music is a systematic, not arbitrary, consequence of the transformational system Bryars employs” (
Roeder and Cook 2006, pp. 46, 55, 66). In a manner very similar to Bryars’, Macklay’s string quartet marks out this neo-Riemannian territory not only in its triadicism but also in its primary focus on two voice-leading intervals, the semitone and the major second. These intervals have been the unmistakable cornerstone of Macklay’s voice-leading vocabulary throughout her career, and connecting vertical sonorities in the smoothest way possible, with the moving voices commonly going no further afield than two semitones, is perhaps the most conspicuous aspect of her harmonic style. The excerpts from
Many Many Cadences (
Macklay 2014) discussed thus far exemplify this practice: if one were to connect the pc-center triads of the first three examples,
Figure 1 would be found to intersperse three minor thirds in voice leading that otherwise uses semitones and major seconds exclusively,
Figure 2 would be found to intersperse a single minor third, while the voice leading of
Figure 3 would be found to make truly exclusive use of semitones and major seconds. Of course, the most parsimonious and slightly less than most parsimonious voice leading of
Figure 1 and
Figure 2, and certainly that of
Figure 3, would, if realized, amount to “textbook” examples; Macklay does not exclusively use ic1/2 voice-leading parsimony in constructing
all of her neoconservative postmodern harmonic progressions—the minor third still makes a modest number of appearances—just as all of Macklay’s fundamental basses, so to speak, do not exclusively present an absolute minimum of seven nor an absolute maximum of 10 pcs before repeating one of them.
Although
Tymoczko (
2008a) defines triadic transformations (e.g., neo-Riemannian transformations) as a strictly harmonic phenomenon that “does not specify any particular mapping between its notes” (p. 10), Richard
Cohn (
1998) explains that these transformations invert a triad, “mapping major and minor triads to each other”, and that “because the inversional axis is defined in relation to the triad’s component pitch classes, rather than as a fixed point in pitch-class space, this class of transformations is now referred by the term “contextual inversion” (p. 170). The present study asserts that Macklay’s use of this class of triadic transformation is often equivalent to a contextually fluid voice mapping that can be described as a dual process of inversion. Works such as
Many Many Cadences (
Macklay 2014) include extended harmonic passages analyzable according to a form of contextual inversion in which relations by pitch-class inversion are camouflaged by numerous “assumed” transformations that do not actually appear in the passage(s). It explains why Macklay’s harmonic progressions generally do not appear to spotlight any single systematic standard to get from one triad to the next. Moreover, this seeming process of redaction is, according to Macklay herself, motivated by nothing more than the composer’s instinct. A dramatic application of a twofold brand of contextual inversion is provided in
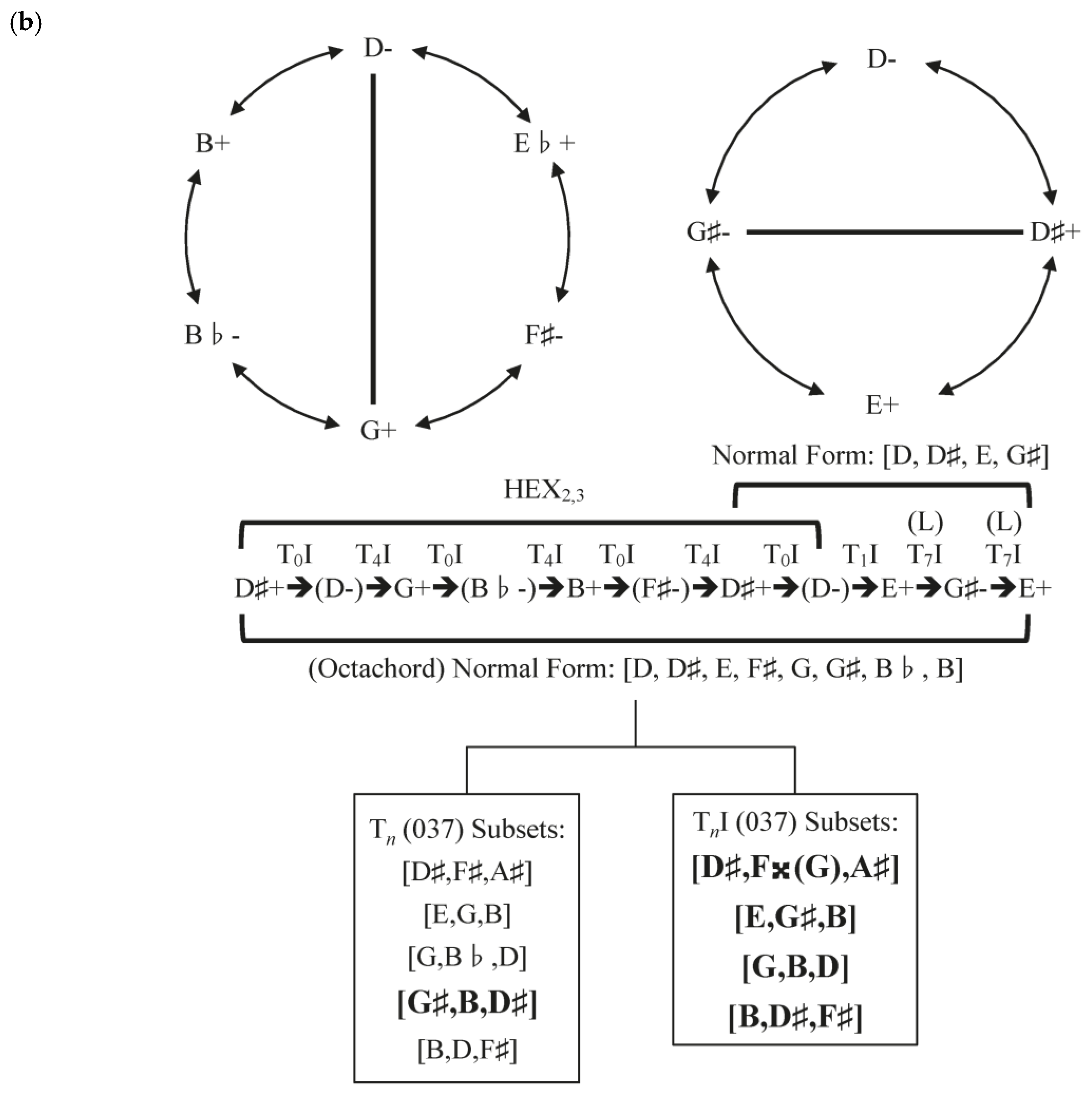
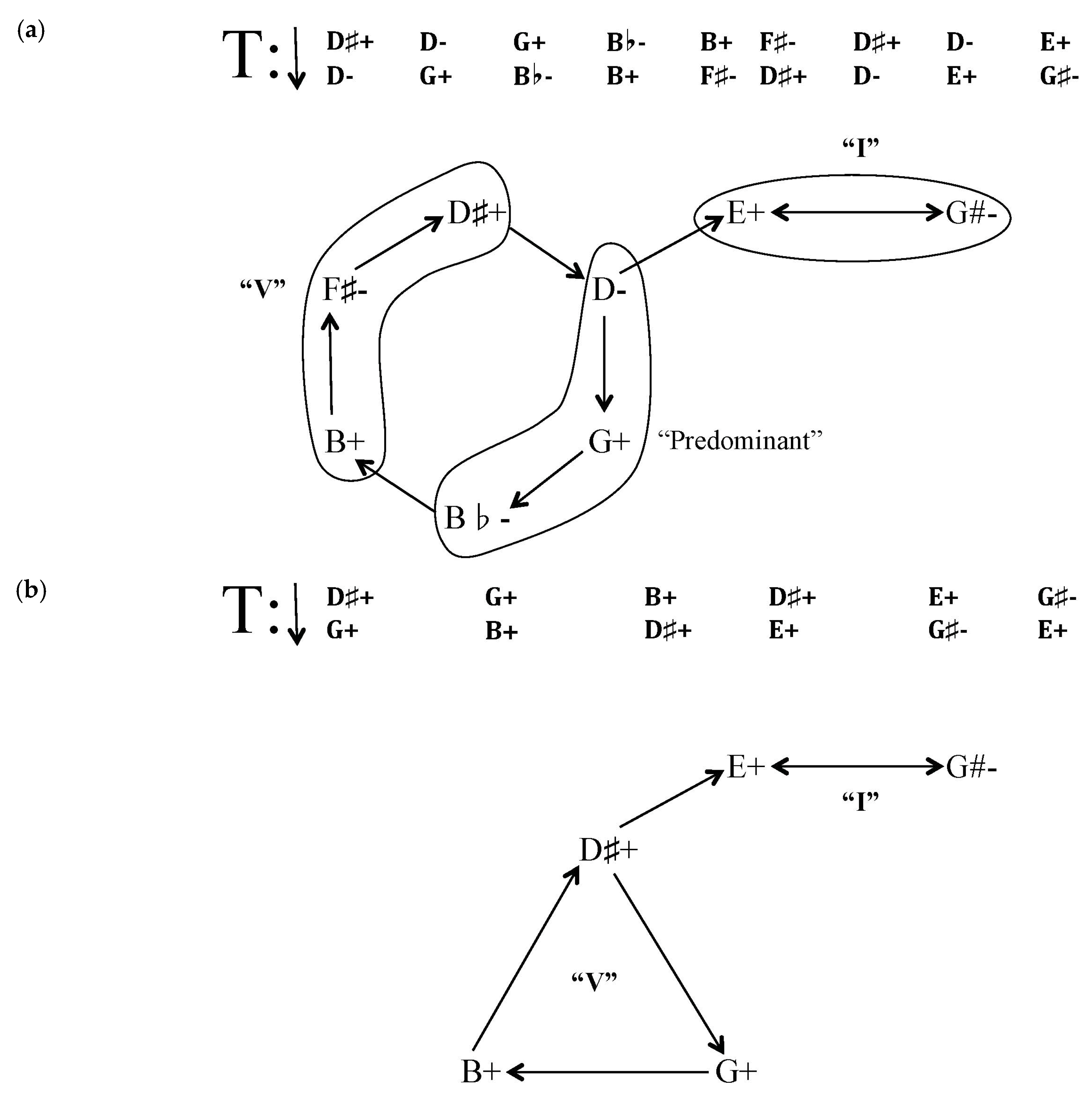
Figure 5: the last six measures before section A1, which brings an end to the B section of this quartet’s ternary form.
For the most part, this succession of triads can be interpreted simply as the result of transposition-
cum-parsimonious voice leading and vice versa, but I have expanded it through a process of double inversion into a much larger progression.
Figure 5 illustrates one very important abstract possibility. Beginning with D♯+ and moving by T
0I and T
4I in alternation, one arrives at a cycle of six triads: major and minor triads built on D♯, D, G, B♭, B, and F♯. Moving through the cycle involves leading the voices elsewhere by no more than two semitones, so the voice leading conforms to ic1/2 parsimony (i.e., each triad differs from its adjacent triads by semitonal and whole-tonal movement of voices). The cycle as a whole involves only six different pitch classes, and these correspond to the hexatonic collection HEX
2,3. When this cycle is written out as alternating 1s and 3s, the triads of the hexatonic poles (like D- and G+) seem to bear a minor dominant/tonic relationship to each other and together comprise set class (02469) (
Gollin 2011, p. 388).
11After arriving back at D♯+, a different double inversional cycle, moving by T
0I and T
1I, seems to begin, but this is instantly interrupted by an L transformation that is just as immediately reversed. This succession consists of four triads (two major and two minor) that, except for D-, share common tones with G♯-. In like manner, except for the progression from D- to E+, which (in parsimonious terms) involves one voice by moving by a minor 3rd, each triad in this final succession differs from its neighbors by voice leading consisting of movement by 1s and 2s. If one presents this chord progression in normal form as a cycle, two of the triads lying opposite of each other (D♯+ and G♯-) seem to bear a dominant/tonic relationship (
Gollin 2011, p. 388).
12Sky Macklay, if she is indeed using a double inversional process (often contextual in the sense of inverting around pitch class components shared between both “assumed” and/or “non-assumed” adjacent chords) to connect triads of the same quality in
Many Many Cadences (
Macklay 2014), then perhaps evidence may be found in the expanded fundamental bass of the entire passage considered as the octachord [2,3,4,6,7,8,t,e]. This octachord contains nine subsets belonging to the triad set class (037), five of which are the very triads which actually appear in the score in measures 130–136, and so along with the remaining parallel-minor versions of the four major-quality chords of this passage, produces what looks very much like significant evidence that a process of double inversional triadic transformation is taking place.
Thus, what sets the use of triadic transformation by inversion in a neoconservative postmodern work like
Many Many Cadences (
Macklay 2014) apart from its contextual formalization in, say, the music of Crumb, Adams, or Zwilich (
Straus 2005, pp. 158–66), is that, like the motivic projection of pc centers, it permeates the entire work not only as a harmonic
modus operandi but also as a supervenient metaprocess involving two rather than only one operation of inversion, both of which enjoy a rather occult, contextually fluid existence. The extreme degree to which
Many Many Cadences (
Macklay 2014) features ic1/2 voice-leading parsimony, apparently coupled with a peculiar system of dual-process, contextual-fluid inversion, coupled with pc-center motivic projection, is comparable to the noticeable concentration on the semitone and tritone that dominated Penderecki’s melodic writing from the mid-1970s onward (
Murphy 2007, p. 192). It should come as no surprise, therefore, that in a piece like her
Analytical Paper of a 21st-Century Piece for Dr. Philip Herbert-Dorbert’s Class for bassoon, cello, piano, and percussionist/actor (2011), where the seemingly disconnected paroxysms of pitch and timbre, the articulation of form by means other than shifts in tonality, and the total rejection of triadic harmony might make it difficult for even connoisseurs of her work unfamiliar with this piece to name its composer, the passages that unambiguously resonate with the sophomoric narrator’s attempts to analyze this post-tonal music in terms of tonal theoretical categories satirically discloses Macklay’s true musical identity.
3. Part II: Triadic Emergentism as a Single Processual Identity
Macklay’s consistent use of pc-center motivic projection, ic1/2 voice-leading parsimony, and dual-process, contextual-fluid inversion not only signifies a particular harmonic style, but also affords someone familiar with the style the ability to make reasonable guesses about how these harmonic progressions emerge. For example, given the eight-note triad incipit C+E♭+A+E♭-G+E+D♭+B♭-, the claim of both ic1/2 voice-leading parsimony and dual-process, contextual-fluid inversion is that any one of the 24-minus [B♭, D♭, F] vertical subsets of sc(037) of the aggregate could follow. Alternatively, the claim of pc-center motivic projection is that one or more of the five other pcs that have not yet been stated [F, F♯, A♭, B, D] will probably follow. Admittedly, there is also a fair but presumably smaller chance that a C will follow, since C occurred first in the melody, whereas the odds of E♭ coming next are much slimmer, since that pc has already been repeated in the incipit. It is by the means of such predictions that the composer herself decides what triad to go to next, and the stylistically informed performer or listener can try to anticipate subsequent harmonies. The homophonic and homorhythmic textures (sometimes compounded in textural simultaneity) that are ubiquitous in Macklay’s neoconservative postmodern quartet help to give clarity to the plausibility of these scenarios.
As discussed at the outset, although Macklay revisits many aspects of common-practice tonality in her neoconservative postmodern quartet, she slights common-practice style by concurrently failing to meet the expectations of the tonal ear. On the one hand, what is so strange about Macklay’ s music are the familiar experiences like the perceived instability of a dominant triad with its perceived tendency to move to the perceived stability of a tonic triad, as well as the sense of closure offered by one familiar cadential progression after another after another, virtually ad infinitum. One could interpret their ubiquity as the composer’s deliberate self-indulgence in stylistic regression. On the other hand, a consistent employment of pc-center motivic projection, ic1/2 voice-leading parsimony, and dual-process, contextual-fluid inversion between tonicized triads, manifests (as we have seen) continuous, often parallel, emergences of non-functional harmony that actually militate against the tonal expectations (amounting to a kind of anti-imitation of tonality). This points to a property specifically arising from within the domains of both tonality and post-tonality, revealing an identity of essence shared by these domains.
However, this single tonal/post-tonal identity is not a complex model of tonality, but rather a relatively simple model of tonality: local event-to-event harmonic phenomena, even as they exist as a part of the music’s superstructure, and as I have systematized them in ordinary language, “textbook” diagrams, and by quantitative measures. After all, one should eschew the attribution of structure to one’s models that is out of all proportion to one’s formalism, concealing mechanisms in a “black box” that obscures intuitive musicality (
Tymoczko 2008b, pp. 251–72). But if the emergent tonal/post-tonal identity is so rudimentary, how will it adequately capture the richness of Macklay’s neoconservative postmodern music? In one sense, it always/already has/does, in that this identity emerges from a single parameter that is the canvas of all music—a plane where, as Xenakis explains, “melodic and harmonic liaisons are effected and perceived” so that “unpredictability and entropy are both diminished” as a consequence. Thus, if we consider both harmony and melody as a single plane, the aftermath of the first cumulation of the aggregate will always display zero unpredictability, maximum constraint, nil choice, and zero entropy (
Xenakis 1992, pp. 75–6).
13 But, in another sense, such a higher-level identity simultaneously achieves an appreciably high degree of complexity within this ataxic stasis, as demonstrated by five conditions of correspondence (modified from
Xenakis (
1992, p. 73) and shared by most theories of harmony, both common-practice and post-tonal). To illustrate these conditions,
Figure 6 employs graphics that depict each condition’s
emergentistic identity profile for any given model of harmony. Equivalence relations hold between the five conditions of correspondence as members of a set that has been partitioned into five cells such that every element of the set is a member of one and only one cell of the partition. Yet the union of all the cells equals the original set, thus illustrating the degree to which every condition shares an identity of essence with every other condition. The following five conditions of correspondence are essentially identical to each other, thus constituting a single identity. Hence, I have related these cells by what is formally called an equivalence class that is at once a novel property that comes from a combination of all horizontal and vertical pitch constituents and which makes any model of harmonic progression the same as any other. To denote that the five elements of the set of the conditions of correspondence (C) are equivalent with respect to an equivalence relation R, I will use the notation 1 ~ 2 ~ 3 ~ 4 ~ 5. In these equivalence relations, as in all mathematics, an identity is an equality relation 1 ~ 2 ~ 3 ~ 4 ~ 5, such that conditions 1–5 contain some variables and every condition produces the same value as every other regardless of their respective variables. In other words, 1 ~ 2 ~ 3 ~ 4 ~ 5 is an identity if conditions 1, 2, 3, 4, and 5 define the same function. So for the purposes of illustrating the process of emergentism, a partition of C is a set of nonempty subsets of C (the conditions themselves) such that every element c in C is in every subsequent subset once it has been introduced (i.e., C itself is a union of the subsets). To rephrase, for any equivalence relation on C, the set of its equivalence class is five partitions of C.
14Every chord of a progression (I have broken down continuity into discrete chords as closely or as distantly related as desired) is an element of fluid determinacy that has a probability of continuation equal to every other chord in the progression for the very reason that each term of one chord is in a one-to-one correspondence with a term of the succeeding chord. Put simply, a fundamental aspect of triadic syntax is that one firmly expects one chord to be followed by another (
Moreno 2017, p. 239).
15 Triadic syntax therefore consists of elements whose likelihood of continuation is, for all practical purposes, limitless.
Figure 6a represents this condition with a grey circle for highly certain although highly indeterminate continuation.
Each step of the triadic transformative mechanism (i.e., whether common-practice rules of motion, tonal function, treatment of non-harmonic tones, modulation, chord alterations, post-tonal motivic projection, voice-leading parsimony, or contextual inversion, etc.) by virtue of its internal structure corresponds to an uninterrupted flow of high indeterminacy to the terms of the resulting chord, the continuation of which is possible to the same degree as that of the previous chord. Kostka and Payne purport that “any chord may follow” tonic harmony (
Kostka and Payne 2004, p. 109), but this results in an identity profile for the initial tonic triad, to borrow Schenkerian terminology, that is the same as that shown in
Figure 6b, which means that all continuations are equally possible, that is, all continuations exist, at least, as
potentia. Riemann applies the Hegelian dialectical terms to fundamental harmonic progressions, claiming that “thetic is the tonic” (
Riemann 2000/1872, p. 102; see also
Harrison 1994, p. 267). Riemann’s “principal” cadence is a progression in which the first I chord is thesis, from which proceed antithetical-, and, finally, synthetical-function chords. All other “secondary” chords are considered to be modifications or “transformations” of these primary chords, which themselves originate from the initial syntactical state (tonic) (
Harrison 1994, pp. 270–73). This interpretation befits the customary formal situation of all triads: since no chord by itself is partial regarding what comes next, a progression that opens with any given triad is full of possibilities; and, if nothing comes next, the last chord of a progression, while it may serve as a tonic-function conclusion, still has the same unlimited continuation potential as the penultimate chord. As Christopher Wm. White puts it, “in traditional tonal theory, one generally moves through” the tonic, predominant, and dominant categories “clockwise. Beginning with a tonic, one most often moves to the predominant cluster. There, one can either stay within the chords of that cluster, move back to tonic, or move to the dominant cluster. At this point, one has the option of choosing another dominant chord or returning back to the tonic cluster” (
White 2013, p. 198). According to White, the most frequent relational class—I—has a higher total frequency than all the remaining relational classes, and that due to its overwhelming frequency this chord plays “a defining role in our formulation of chord syntax”. The behavior of this class has a tendency to “influence the categorization of the remaining chord alphabet”. One particular behavior stands out: the tonic chord has “
more evenly distributed transition probabilities (italics added)” (
Gollin 2011, p. 259). Initial tonic harmony can therefore be defined as identical to any solitary harmony in that it has a maximum possibility for both continuation and termination.
If the set of elements (the chord progression) reaches a state and remains there (communal absorbing or communal stationary state), then the apparent variance enjoyed among the degrees to which elements are perceived to have, say, dominant or tonic functions or to be the result of some other transformative mechanism corresponds to an overall state that has no transform (i.e., no subsequent chord; it has come to an end). This definition, as applied to tonic and dominant functions or to any other kind of processual substitution of one set of pc triadic components with another, places these into imaginary categories, existing along an identity that is a continuum whose length, if measured by possible continuations from one chord to another, is effectively infinite. I could even make an argument for this condition from common-practice harmony’s tendency to cluster around one point of the continuum, that is, common-practice harmony is an overly deterministic system in which every harmony has a singular destiny that is artificially forced upon what is in truth a chaotic system depending on how much uncertainty we are willing to tolerate in the forecast, so to speak. Put differently, the identity profile of tonal harmony is like a segment or a detail of the continuum. In most textbook models, for example, pre-dominant harmony moves to dominant harmony (i.e., dominant and leading-tone harmonies). If a harmonic progression reaches this state and remains there, the focus of the pre-dominant harmony becomes quite sharp, while the dominant harmony becomes the term that corresponds to this absorbing or stationary state. In other words, it has no transform no matter how badly the listener wants it to go to the tonic, resulting in the partition seen in graph 6c. To explain this equivalence relation, take mediant and submediant triads. They can be said to have a quasi-tonic function: according to Walter Piston, “they have very little effect on the tonality but suggest the mode” (
Piston 1941, p. 50), which means that they are as multivalent as the tonic chord itself regarding what harmonies may follow. Ultimately, this continuum permits me to describe any of its elements relative to any other of its elements: each one with a high degree of indeterminacy; graphically, a partition consisting of conditions 1–3; its identity, no element is inherently “more dominant” or “more tonic” than another.
All triads can be generated, without regard for individual placement within a tonal hierarchy, if the states of a mechanism reproduce themselves in the same manner without end, equalizing the degrees of expectation for each of the elements that are made to follow each other in closed circuit. This condition, just as the preceding three, eliminates the distinction between dominant and tonic categories, as well as that between expected and unexpected. In other words, this condition, like the others, has no preference for an identity profile with a hierarchical structure over one without. For example, Robert Gauldin’s investigative categorization of a specific voice-leading practice of 19th-century harmony in which “divergent chromatic wedge progressions that exploit recurring patterns of either even or odd intervals between outer voices” succinctly captures this symmetrical concept that most would ascribe to the kind of centricity established through inversional axes in post-tonal music (
Gauldin 2004, pp. 1–22).
16 The graph of
Figure 6d offers yet another profile that meets its condition in a manner that makes it indistinguishable from its predecessors. The multidimensional nature of where a composer, listener, or analyst may envisage the placement of a triad within a cyclic set permits a “synonymical” view of my interpretation of harmonic continuations: compare, for instance, the object of Gauldin’s research with a symmetrical progression whose chords all belong to the same hexatonic system. Abstractly considered, they are identical to each other.
Halting a transformative mechanism and its start from a previous state is a displacement of the representative point in the chord progression, which is not due to the erstwhile transformation but to a compositional decision that can be evaluated using a different analytical technique. As has already been stated, a fundamental aspect of triadic tonal harmonic syntax is that one firmly expects one chord to be followed by another, different chord. It does not matter how this is achieved. Triadic harmony therefore consists of elements whose likelihood of continuation is not only theoretically inexhaustible, but the changeability of the means of realizing this prospect is equally inexhaustible. Therefore,
Figure 6e represents this condition as a clone of the other four: the high certainty and exceeding indeterminacy of the selfsame concept of harmonic continuation put forward by every condition of this list.
How well do the two principal types of triadic post-tonality associated with Macklay’s neoconservative postmodern harmonic style identify with a single emergent tonal property according to these five conditions (or what I will now refer to as the quinary condition)? Triadic transformative harmonic practice, applied to any set of harmonies, plainly satisfies all of them. All harmonic progressions have the same identity profile: a non-binary paradigm, in which all chords and transformative mechanisms are each equally likely as not to follow or give rise to all other chords. The number of possible successors is always fixed, encompassing all 23 subsets of sc(037) remaining after the preceding chord, and therefore completely capable of satisfying the quinary condition. Consequently, triadic transformative harmonic practice not only embraces both complete determinism and complete chaos, it completely desegregates these two states, producing a rather exciting experience as gauged by the quinary condition.
Pc-center motivic projection, applied to non-duplicative successions of harmonized roots that do not exceed nine or ten notes, fares nearly as well. A single triad amply meets the quinary condition, since any one of 22 other chords (i.e., those with roots other than that of the first chord) have an equal chance of following. This makes formal sense in its identity with common-practice tonality: pc-center motivic projection regards every beginning of a Macklay fundamental bass as a “tonic” with its potential to head in the highest number of directions. Yet this “tonicity” is measured by the number of possible continuations, and so is determined by the possible return of a chord within a harmonic progression, for as it adds triad after triad, the number of continuations that are likely to occur, which is equatable to the “tonic” valence of each successive chord of the progression, remains immutable at a ratio 1:21.
Obviously, this evinces the possibility of both a communal absorbing (or communal stationary) state as well as the possible return of triads that have already appeared. In other words, all harmonic progressions of both equal and unequal length and content will have the same identity profile—the potential, variably realized from case to case, of an exceedingly heterogeneous yet somehow unvaried model of harmonic emergentism. Furthermore, while the quinary condition appears to imply that a harmonic progression’s possible continuations are equally probable, this is just an impression conveyed by the pseudo-stochastic independence that may be inferred from it. Nevertheless, such a conclusion undermines while at the same time permitting hierarchical systematization: if there is no hierarchy, then any hierarchy may be imposed. It is in this manner that pc-center motivic projection fully meets the quinary condition: there is no triadic progression, whether it involves root movements as predicted by pc-center motivic projection or even pre-modern functional harmony, that is categorically more probable than any other except by means of artifice.
In light of its absolute fulfillment of the quinary condition, perhaps a model for emergentism in Macklay’s neoconservative postmodern music should be based on observations simpler than these two summations of the composer’s harmonic style. After all, a model that proposes to share a single identity with all other tonal models as embodied in the quinary condition can be achieved by considering pc-center motivic practice and triadic transformative harmonic practice to be themselves identical. That is, a chord is expected to follow another only if it meets both pc-center motivic projection and triadic transformative harmonic practice criteria. The first and most obvious product of their unification is the great promotion (or slight demotion, depending on one’s point of view) of the probable continuations of a chord progression as predicted by ic1/2 voice-leading parsimony and dual-process, contextual-fluid inversion: namely, a progression’s next chord. In the case of C+ E♭+, although ic1/2 voice-leading parsimony and dual-process, contextual-fluid inversion expects C+ or C- to the same degree as any of the other remaining 23 triads after E♭+, pc-center motivic projection does not really expect E♭- at all, since a triad with that letter-name root was just presented. Thus, the combination of these two features leaves 22 equally probable continuations for the first chord and every chord thereafter. This is not to say that this equation has any affect on the possibility of a communal absorbing or communal stationary state: it is always the case that all harmonic progressions, even those theoretical singularities that go on forever, would have 22 equally probable continuations from chord to chord. As shown in the following analysis, this creates a virtually universal equalization of an expectancy that holds among all harmonic progressions, which, at any given point, have exactly 22 continuations that meet both criteria, and so fulfills the quinary condition.
4. Part III: Analytical Application
Wilfred Meller’s examination of the avant-garde in America begins as follows: “In a sense, avant-garde music is a rear-, not an advance-guard action, for it is both a consequence of, and a reaction against, five hundred years of European ‘consciousness’. The Renaissance started with man’s dualistic awareness of the distinction between the Self and the Non-Self: which in musical terms became the dualistic, and peculiarly European, phenomenon of harmony” (
Mellers 1963–1964, p. 1).
17With this in mind,
Figure 7a lays out the roots of the major- and minor-key areas of Macklay’s American harmonic “consciousness” in the opening of
Many Many Cadences (
Macklay 2014) (
Figure 1): C+E♭+A+E♭-G+E+D♭+B♭-D+B+A♭+F+E♭+F-C+. The alphanumeric designation with superscript above each triad letter name is the C3-interval cycle to which the pc root belongs and which, without conflicting with either pc-center motivic projection or ic1/2 voice-leading parsimony and dual-process, contextual-fluid inversion, largely determines the content of the harmonic progression. The kinematic or transition diagram in which each term is connected to its transform by an arrow is a general, graphical expression of triadic connectivity, regardless of transformation type.
18 After the first state of the graph beginning with C, the harmonic progression entertains three potential continuations (according to the kinematic diagram) for its second tonicized root: E♭ could continue to F♯, A, or G, F♯ could continue back to C, A could continue to toggle between itself and E♭, and G could continue around both C3
1 and C3
2, until arriving back at E♭. However, when the tonicized root movement goes to A before executing the switchback to E♭, the ground covered so far greatly decreases the possibility that the same tritone leap will follow the E♭, as this would duplicate yet another pc already used. The progression therefore is left with two pc continuations from the E♭ to the F♯, or from the E♭ to the G, “locking” it either way into a journey through all three C3-interval cycles and exhausting the aggregate. However, when the progression arrives at and finishes with C, the circuit is set to start all over again, which might mean a return to the ambivalence presented earlier in the progression. The sequence from three continuations near the beginning, down to two at the first tonicized E♭ root, then back up to three as implied by the circuitry is in a one-to-one correspondence with the transition from C3
0 to [C3
1-C3
2] back to C3
0. One might just as well draw an identity of essence between this and the minimal Schenkerian
Ursatz I-V-I to apply the true significance not directly expressed by the unification of the two principal types of triadic post-tonality introduced earlier.
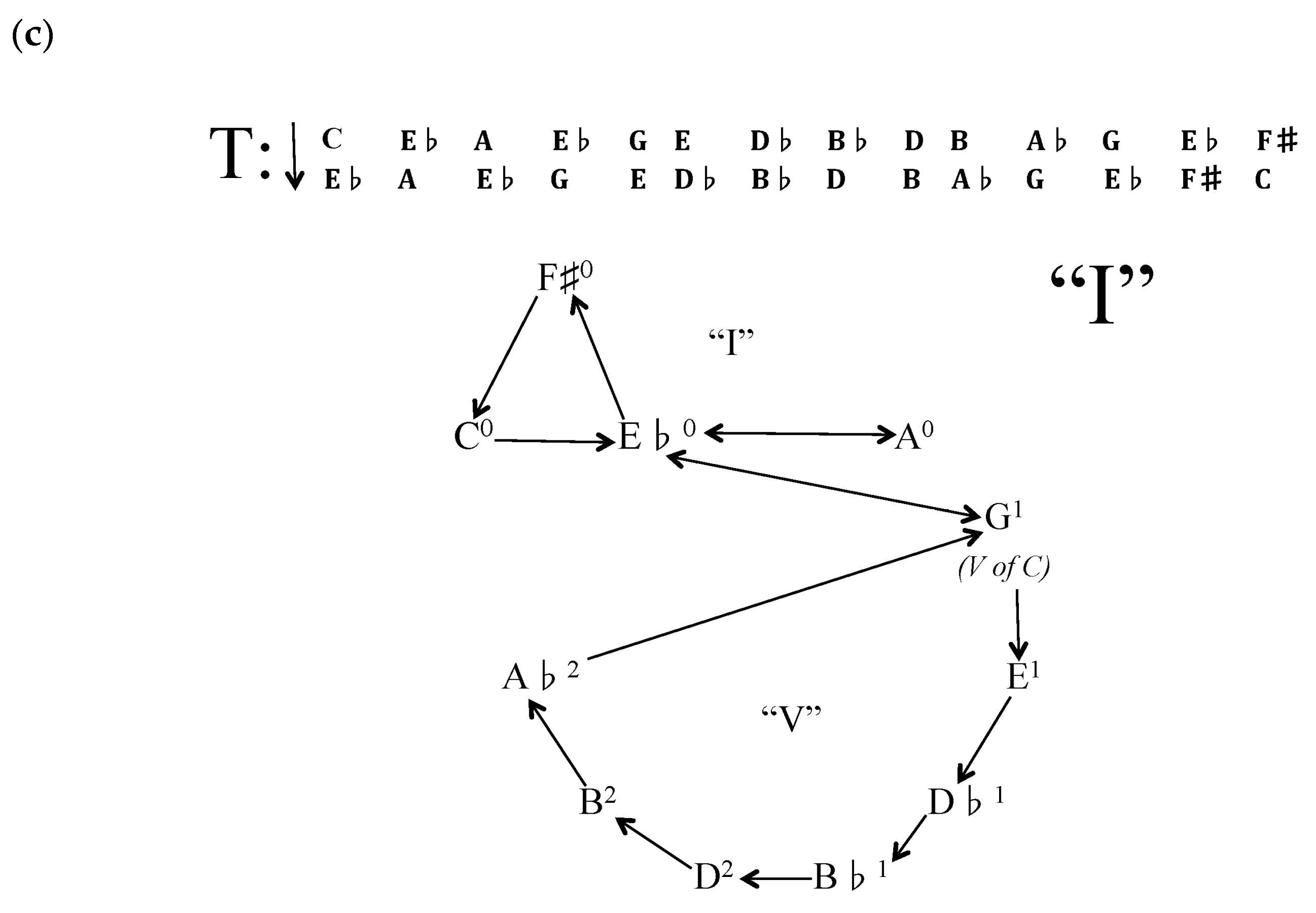
Recalling the quote above, and taking care to notice the harmonized “fundamental bass” with mostly minor-quality triads in measures 7–13—C-E♭-A-D+G+E-C#-B♭-D-B-A♭-F-E♭-A-C-,
Mellers (
1963–1964) might have looked upon this as further evidence that “the American retreat from the West has been more empirically spontaneous” (p. 2). This harmonic sequence is analyzed in Example 7b. The remarkable claim made by Mellers that the American avant-garde is derived from experience, particularly from sensory observation, and not derived from the application of logic may explain the omission of an F♯ triad from this progression, eliminating it from the upper circuit of the kinematic graph, although without affecting the “resolution” to the final “I” of the “I-V-I” progression, belying F#
’s true “function” as an analogue to mediant/submediant harmony: there is a continuation, from Example 7a, that might reasonably be expected in Example 7b, yet, insofar as the progression concludes with a three-note segment of C3
0, it ends just as the last one did. Furthermore, not only is F♯ surreptitiously given as an individual pc component of the D+ triad, the respective triad-quality preponderance of three consecutive harmonic statements—the template in measures 1–6, its minor-quality version in measures 7–13, and its full restatement (with the exception of the substitution of G- for F+ in measure 17, G being the dominant of C which belongs to the C3
0 interval cycle) in measures 14–19, may be thought of as an abstraction of the “I-V-I” progression of the initial template on a larger scale.
Therefore, the C triads are forced into a tonally determinate role regarding the Western expectations generated from a “book-end” perspective, as discussed earlier, but they offer the same effect regarding expectations generated by the combination of Macklay’s two idiosyncratic harmonic features. An identity of essence regarding the play between tonal expectations and the expectations as generated by Macklay’s two harmonic features occurs in a foreshortened iteration of the template. The three C-centered statements give way to an abridged statement that begins by tonicizing B+ and continuing with a composed rhythmic acceleration culminating with the appearance of a 16th-note quintuplet in measure 28, followed by a return to the C centricity of the first 24 measures, replete with nontuplet 16th notes as the smallest rhythmic value.
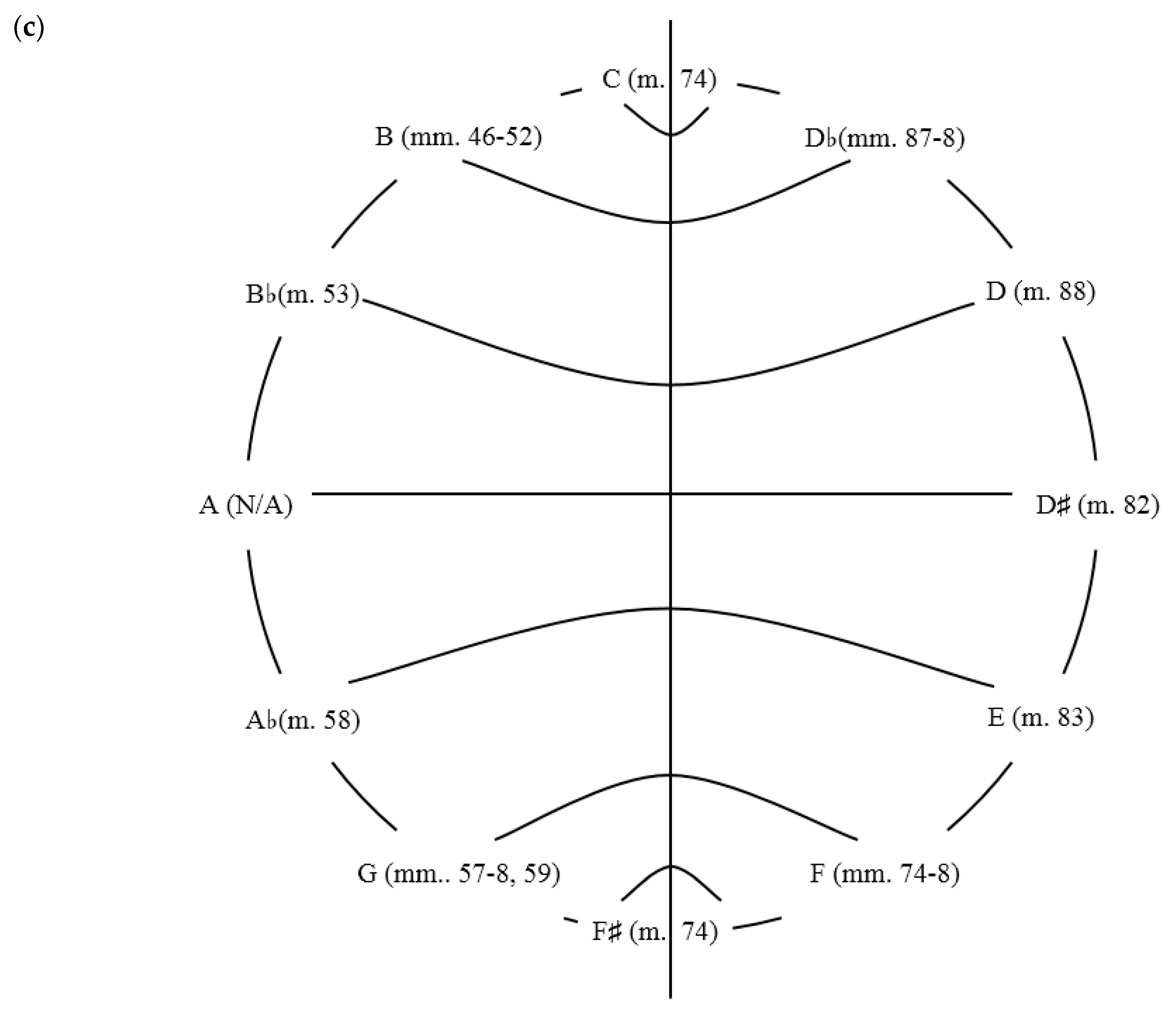
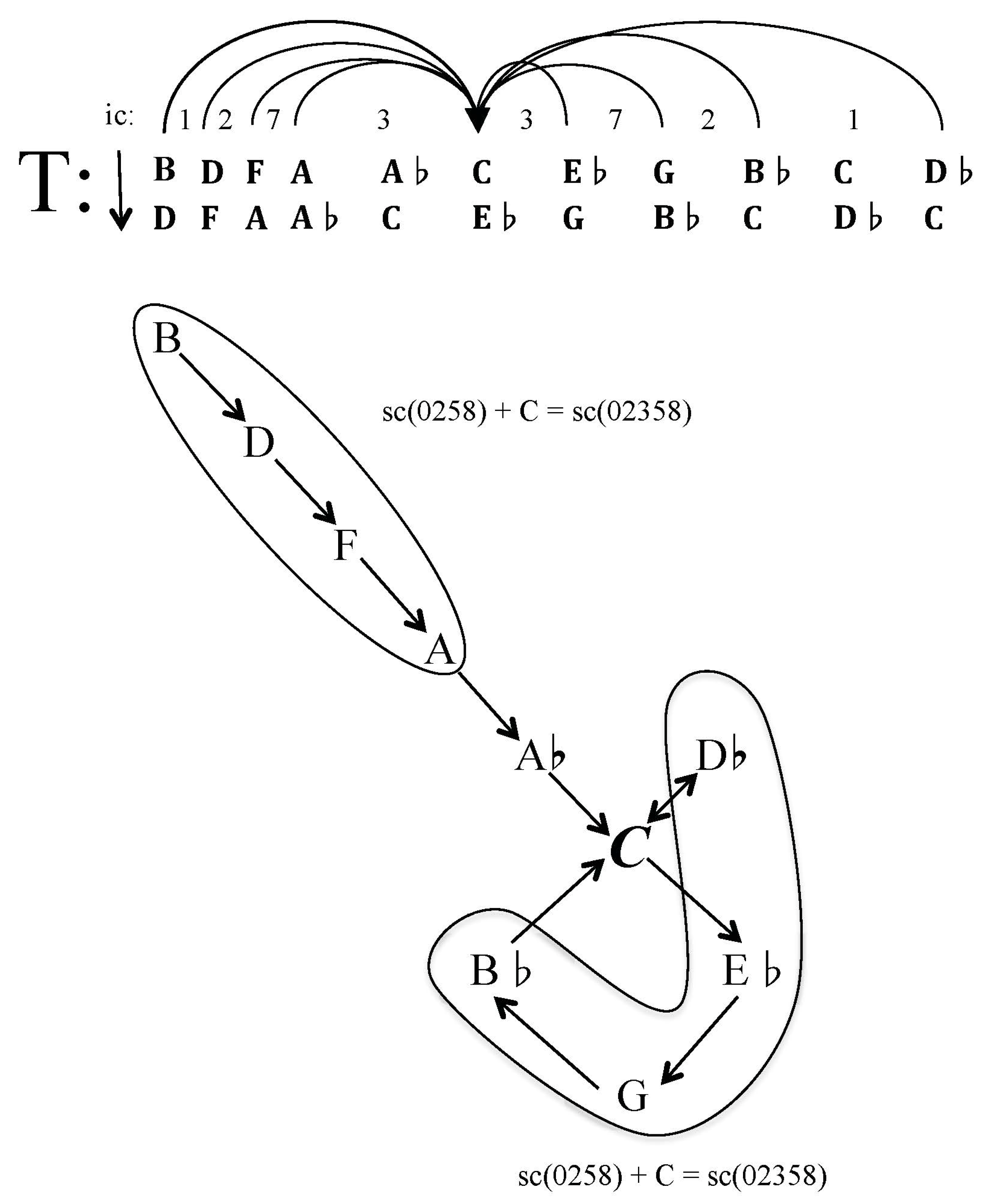
Figure 8 displays this music that brings the briefest respite from the erstwhile C centricity. The two non-duplicative successions that are not completely imbedded in each other are a line of ten notes and a line of five notes that ultimately descends by semitone with an upper leading tone back to C, forming with the initial B of the first non-duplicative succession a large scale statement of sc(012) that serves as a contracting wedge converging on the axis note C. Actually, the two lines together form a larger contracting wedge whose inversional symmetry begins with the minor third above and below C: the tritone between E♭ (to the right of the C+ chord at the midpoint of the progression) and A (to the left of the C+ midpoint). Moving outward from the center, there are the pcs a perfect fifth above and below C as well as pcs a major second above and below C: the minor seventh between G on the right and F on the left, and the major third between B♭ on the right and D on the left. At the endpoints themselves, there are the minor seconds above and below C: the major second between D♭ (enharmonic C♯) and B, which finally resolve to C in the next measure. This subliminal but very real inversionally symmetrical contracting wedge converges on the axis note C, and so has a very strong centripetal force. C has been predetermined and is, in fact, the axis of symmetry. As shown in
Figure 9, all the pitches (except for A♭) leading to C from both sides of the diagram are both members of sc(0258); likewise, the inclusion of C in either of these members of sc(0258) results in a member of sc(02358) and so further evinces the use of an inversional axis. As proposed earlier, every chord of a progression is an element of fluid determinacy that has a probability of continuation equal to every other chord in the progression. Thus, the fusion of pc-center motivic and triadic transformative practice provides an environment that fosters the strong anticipation of C at the end of this harmonic progression, the balancing of notes against other notes around C, because both triadic transformative harmonic practice as well as pc-center motivic projection embrace both complete determinism and complete chaos, undermining while at the same time
permitting hierarchical systematization: as stated earlier, if there is no hierarchy, than any hierarchy may be imposed, in this case, the use of an inversional axis. This warrants a comparison to the first four iterations of the template that concluded with no less an establishment of C by other kinds of direct emphasis and reinforcement. What is more, the next five measures are, in the sense of a succession of tonicized, harmonized roots, an exact restatement of the template.
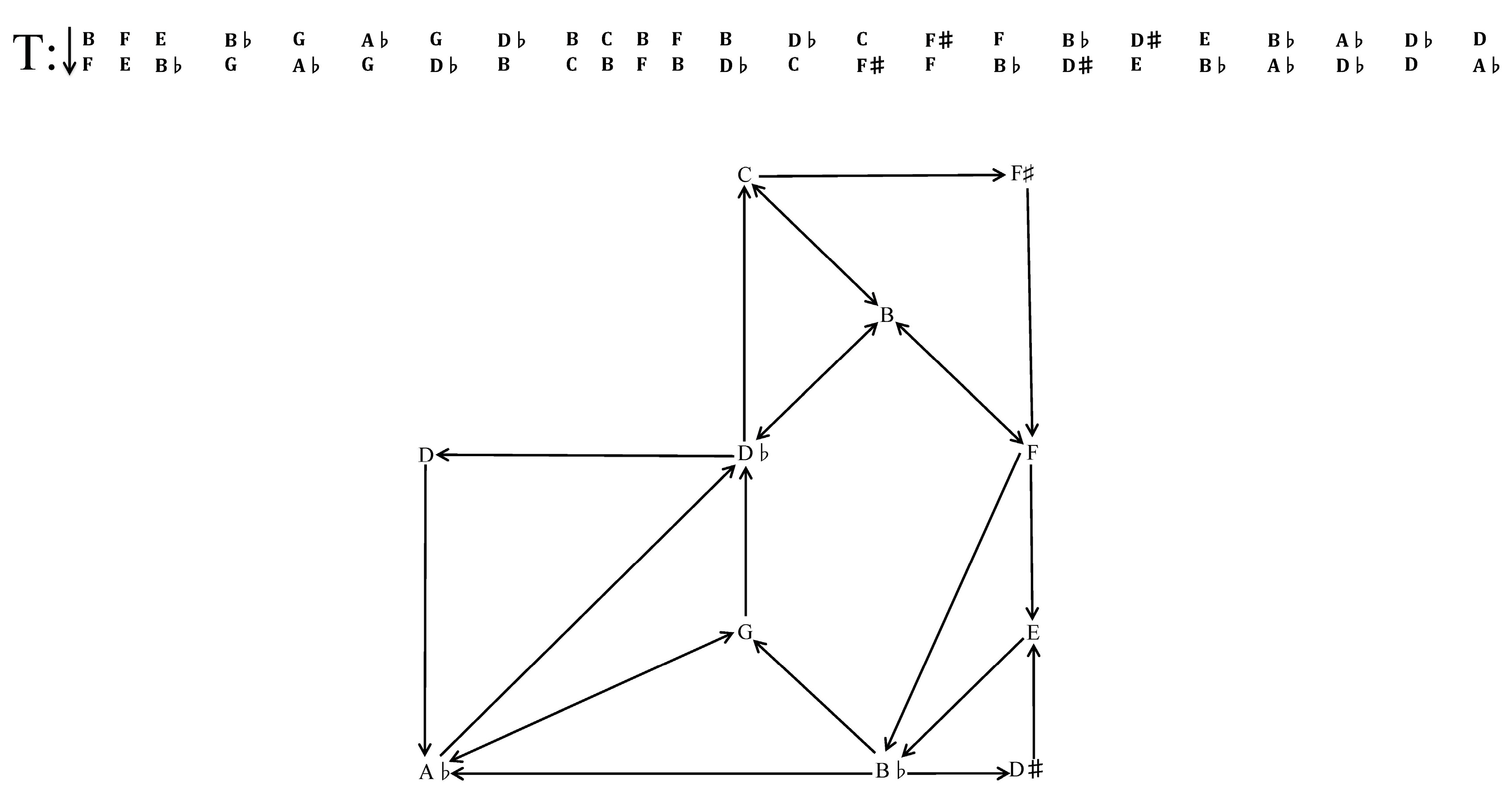
A return to
Figure 4 provides an attractive example of a succession of triadic simultaneities in the quartet that has no readily discernable compositional scheme. In this saturational root progression, all but one of the twelve tones (as roots of tertian harmonies), presented in order of appearance B F E B♭ G A♭ D♭ C F♯ D♯ D, make up a harmonic texture below the faster texture made up of the ongoing cadential formulae. As shown in
Figure 10, this 11-note line nearly exhausts the aggregate. A continuation that honored ic1/2 voice-leading parsimony or dual-process, contextual-fluid inversion might reuse a former pc, while a continuation that honored pc-center motivic projection would obviously go to A. Therefore, in considering both features, there is no hierarchical system that is especially illuminating, making the A that one might expect to end this 11note succession very mysterious by its omission. Or, to put it another way, the first six pc roots—[B, F, E, B♭, G, A♭]—belongs to the set class whose Forte name is 6-z13, while the last six pc roots (if they included A)—[D♭, C, F♯, D♯, D, A]—belongs to the set class whose Forte name is 6-z42, the zygotic mate of 6-z13. To complete this Z-relation, Macklay would not have had to violate either of the two features. In the excerpt of Example 4, she could have placed A anywhere in the progression without violating either ic1/2 voice-leading parsimony or dual-process, contextual-fluid inversion, while continuing a strict observance of pc-center motivic projection by completing a saturational presentation of the aggregate.
However, unlike the tonicization of C throughout this quartet, Macklay does nothing to articulate the “tonicity” of A in this passage of textural simultaneity beyond omitting it in a manner reminiscent of an axis which passes between two notes a semitone apart. Yet later in the quartet, Macklay brings back a tetrachordal member of a subset of this material (the 11-note root progression is made up of no less than 16 subsets of sc(0136)) at different dynamic levels, at a slower tempo, and for what is arguably the express purpose of comprising A. The quartet boasts five statements of the progression C+, A−, F♯
0, B+ (the roots of which constitute a member of sc(0136) at a transposition which includes A) in the middle section of its ternary form, of which the first (measure 108) is shown in
Figure 11. She begins with sc(0136), but instead of using any of the (0136) subsets that could have been culled from the 11-note collection from measures 46–88, she uses a transposition of sc(0136) that includes A (as well as C with which each of the five statements of the untransposed set class begins). The slower tempo and portamento texture may afford an opportunity for an expert listener familiar with Macklay’s harmonic style to expect somewhat less than what (s)he has heard so far (namely, the repetition of longer triadic progressions), especially when remembering that A was completely omitted from the passage from Example 10 and from the chord progressions in measures 89–95, and recognizing that this may very well be the reason the A− triad is included in every triadically-harmonized, tetrachordal root progression (sc(0136) or otherwise) throughout the B section until measure 129. It makes good compositional sense to match the appearance of A− in every set of four chords with the attempt to compensate for its absence in the 50 measures leading up to the B section: repeating the same harmonization of the sc(0136) root movement at the same transpositional level as just one of a myriad number of ways to achieve this.
Another example of a root progression that coincides with a conclusion articulated by the conspicuous repetition of one or more pcs (E and its leading tone D♯, in this case) is the excerpt from
Many Many Cadences (
Macklay 2014) introduced earlier (
Figure 5), a line of five harmonized roots that conforms to both pc-center motivic projection and ic1/2 voice-leading parsimony and dual-process, contextual-fluid inversion.
Figure 12 provides an analysis, showing how this progression does not violate either of these two features. Both the motivic design and triadic transformative process can be seen in measures 130–36 (i.e., after the last repetition of the sc(0136) root-movement harmonization) as a rather concentrated composing-out and tonicization of the E+ triad involving a progression of mostly major quality chords, and signaling the end of the B section. One might contest that, as stated earlier, this last succession of triads can be interpreted simply as the result of transposition-
cum-parsimonious voice leading and vice versa, or it can be explained by a process of double inversion and so expanded into a much larger progression. However, the analytical subject need not be the entire eight-note line of both “real” and “assumed” chords, but merely the five that actually appear in the score, since the roots of the lower part of the diagram spell out B aug. or, rather, the dominant of E+ that then toggles between itself and G♯−—E, G♯, and B—all three components (as roots of triads) of E+ (being itself the dominant of A- which has been present in every set of four chords since the beginning of this section) occur within this final span.
5. Part IV: The Macklay Kinematic and a Tabular Survey of the Entire Quartet
The above examples provide a few instances of communal absorbing or communal stationary states among the harmonic progressions, but not in the sense that it is impossible to leave these states, rather, in the sense that the state space in which they occur is finite even when the features of pc-center motivic projection and ic1/2 voice-leading parsimony and dual-process, contextual-fluid inversion are considered in tandem. But is this state space “permeable” (
Ligeti (
1965), pp. 5–19)
19 by the emergence of all possible harmonic progressions (i.e., the particular behavior Macklay’s harmonic practice tends to demonstrate)? The process of answering this question can begin by enumerating the set of specific triads along with every triad, with which it forms a two-chord harmonic simultaneity succession that employs voice leading of mostly unordered pc intervals 1 and 2: what I call
Macklay progressions that form the
Macklay set. Since transposition and/or inversion do not change a harmonic progression’s identity profile, the Macklay set is partitioned into
harmonic classes equivalent under these canonic operations. However, rather than present the Macklay set first in tabular form, the set may instead assume a more compact form that has already been adopted. A compression of any one of the kinematic graphs in the analyses of
Figure 7,
Figure 9,
Figure 10, or
Figure 12 to show all the possible Macklay progressions that begin with any given chord root would result in a transition diagram isomorphic to
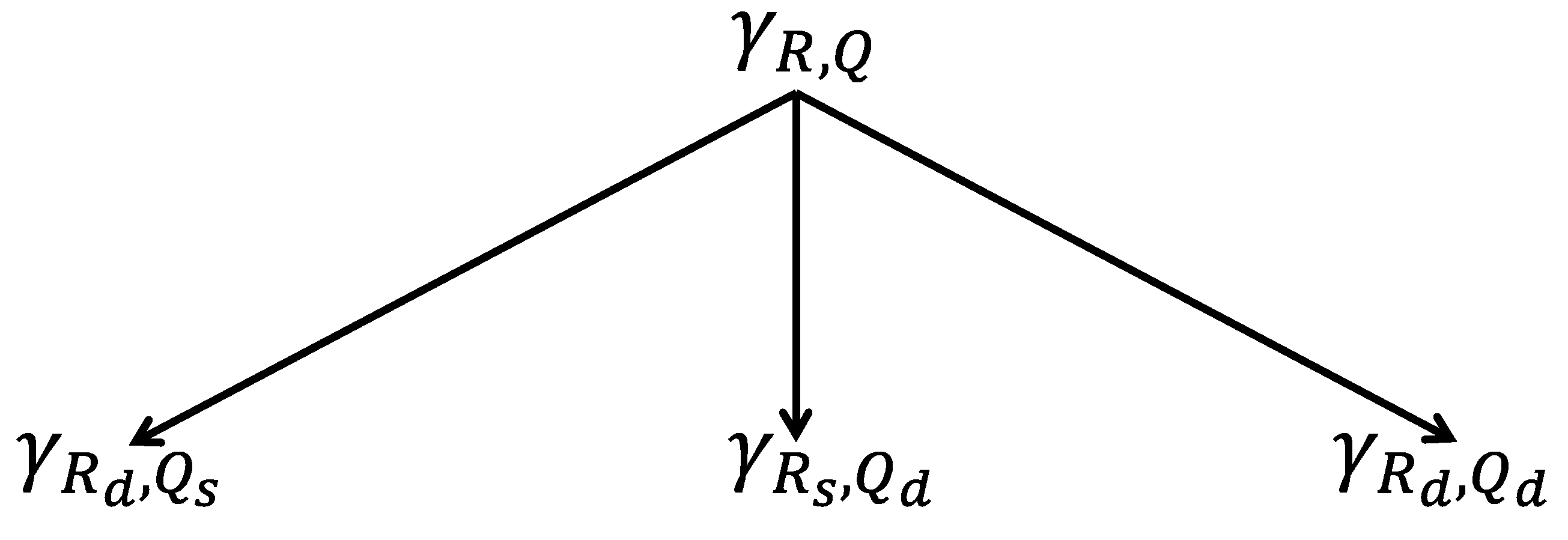
Figure 13, the
Macklay kinematic. As in the kinematic graphs of earlier analyses, the arrows connect terms to their transforms (i.e., triads signified by ϒ or gamma, the third letter of the Greek alphabet), therefore representing triadic transformations (usually involving voice leading by unordered pc intervals 1 and 2), and epitomizing the imaginary representative point that “jumps” from term to term, representing every possible progression. Like
Tymoczko’s (
2008a) systems, the terms of the Macklay kinematic represent particular chords (e.g., “C +”), and not just chord types (e.g., “major triad”) (pp. 1–49). However, the three arrows that radiate from the kinematic’s “tonal center”—the topmost term—correspond bijectively with a Macklay harmonic class. Therefore, the Macklay kinematic is also representative of the harmonic classes, because the three arrows in the diagram represent the transformational means by which the content of each class is generated.
As a theorist who has adequately described the general principles or procedures for formalizing the notion of voice leading, Tymoczko “shows how to classify voice leadings according to transpositional and inversional equivalence, and supplies algorithms for identifying maximally efficient voice leadings between arbitrarily chosen chords”. However, the details of his algorithms for solving this problem are exceedingly technical (
Gollin 2011). Ironically enough, transpositional and inversional equivalence allows for the comparative simplicity of the Macklay kinematic. First, the root (
R) and quality (
Q) of the initial term could be chosen arbitrarily and the graph would look the same. Second, the arrows of the graph assume such parsimony that <1> voice leading is equated with its exact inversion, namely, <e> voice leading or, as Tymoczko puts it, “they do not…distinguish one-semitone ascending motion from eleven-semitone descending motion” (
Tymoczko 2010, p. 42).
To save space, the kinematic diagram of the entire string quartet has been distilled into the formula of
Figure 13, in which
s stands for “same” and
d stands for “different”.
This kinematic proposes a method for semantically describing triadic harmonic content directly from triadic transformations, abstractly considered. The goal is not necessarily to do a formal harmonic analysis or to achieve chord transcription, but to produce a consistent harmonic description (a blueprint, if you will) useful for similarity-based operations. This is accomplished without attempting to estimate the pitch content in the transforms. By avoiding this, one also avoids its constraints, allowing one to operate on a wide variety of triadic music. The approach combines a rudimentary kinematic representation of a system that is assumed to have unobserved (hidden) states initialized with musical knowledge and trained on the given data (i.e., triad root, quality, the chord lexicon of the 24 major and minor triads, and “idealized” chord connectivity). The output, which is a function of voice leading (“bijective” part writing) instead of Julian Hook’s algebraic structures, for example, symbolically represents all possible sequences of major and minor triads that outwardly extend the basic triadic character of the initial term. While it is clear that I am reducing the harmony of triadic music to a mere succession of major and minor triads, as this choice of lexicon assumes, I believe that this is a sound basis for a highly abstract approach to labeling. In other words, the lexicon, and therefore the Mackay kinematic itself, is a robust representation of the salient harmonic characteristics of many types of triadic music.
Although Macklay employs pc-center motivic projection (the aim of which usually seems to be the possibility of attaining 12-pc diversity), the collective roots of her harmonic progressions without interior repetitions never comprehend the entire aggregate. Therefore, among all harmonic classes (consisting of a specific chord followed by all the chords to which it goes over the course of
Many Many Cadences (
Macklay 2014)), there seems to be a strong correlation between this fact and the record of observing that the largest class has only 10 pc roots. These harmonic classes are tabulated in the
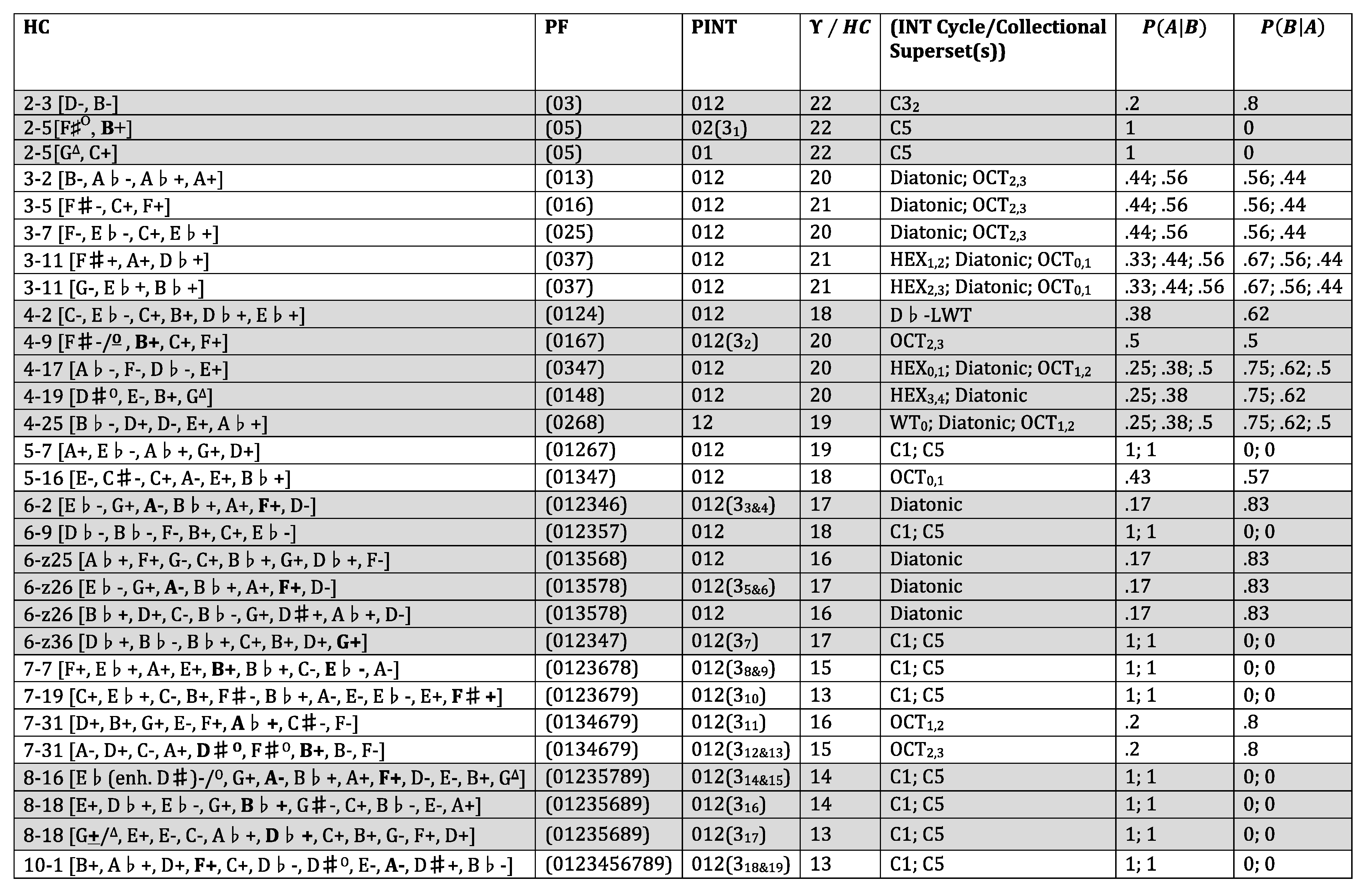
Appendix. Following Allen Forte’s nomenclature for unordered set classes, each harmonic class is assigned a twonumber label (abbreviated HC in the
Appendix) and a prime form (PF) in the two leftmost columns (
Morris 1983/1984, pp. 187–217). Transposing and/or inverting the tonicized roots of a chord progression so that it begins with 0 and is most packed to the left is to put it in “prime form”. For example, C-E♭-C+B+D♭+E♭+ is a member of class 4–2 with a prime form of (0124). This harmonic class can be graphed kinematically according to the formula above: as one traces the pitches of the prime form through the graph, the number of arrows (i.e., transitions, transformations, and representative points) from term to term in the progressions represent the number of times the first chord goes to another chord of root
d and quality
s or
d (e.g., the arrow of the harmonic progression from C- to E♭+ is the same as
). In the next column of the table, each prime form is also characterized by the unordered pc intervals required for parsimonious transformational voice leading, borrowed from what Robert Morris calls INT
1, modified to PINT (
Morris 1987, p. 107) (incidentally, the triads in bold in the first column are those which required one voice from the initial chord to move by three semitones. I have underlined the quality of the initial chord responsible for voice leading by a three in cases involving classes whose first triads have two major- or two minor-triad qualities. The third column provides the number of triads not included in the harmonic class). I will discuss the remaining columns shortly.
Although the Macklay kinematic is structurally redundant, this is overshadowed by the diagram’s symmetric yet reiterative complexity, an overall testament to the synergistic union of the two relatively simple harmonic features of pc-center motivic projection and ic1/2 voice-leading parsimony and dual-process, contextual-fluid inversion. The appended table also facilitates an analysis of these tandem expectations according to the quinary condition outlined earlier. The
Appendix column entitled “
” displays the number of triads not included in a harmonic class. Setting the continuations of the initial triad aside, this column reveals a communal absorbing or communal stationary state that cuts across class cardinality: some harmonic classes tend toward the saturational, as if to levy less entropy on other harmonic classes excluding more than 13 triads, notwithstanding the communal stationary or communal absorbing state imposed on all harmonic classes. It is of primary analytical interest that, among these harmonic classes, the most saturational harmonic class—10-1—is by far the most rare, occurring on the table only once. This would seem to indicate, to continue the waterlogging analogy, that there seem to be very few exclusively linear ways availed by the composer to soak her musical space so thoroughly that the horizontal surface becomes completely drenched. Most of these near saturational harmonic classes end with harmonic class 3–2; this can be seen by finding 3–2’s interval series of <12> at the end of each of their interval series. Upon closer inspection, 3–2 actually enjoys considerable numerical superiority as a subset of the larger harmonic-class supersets. This promotes 3–2 to an extremely special and nearly singular status among the harmonic classes, not unlike the singular status tonic harmony has among the seven diatonic
Stufen. The progressions of tonicized roots in sections A and A1, which terminate at the end of a contour descent and a return to a C triad of major or minor quality, contain conspicuously high concentrations of 3–2.
To reiterate, the general heterogeneity and symmetry of the Macklay kinematic correlates with the general heterogeneity and symmetry of all tonal models, and the model of emergentism that combines pc-center motivic projection and ic1/2 voice-leading parsimony and dual-process, contextual-fluid inversion has been said to meet the quinary condition of correspondence deemed necessary to be analogous to any tonal model. But what of the fourth condition that implies the use of inversional axes, referential collections, and interval cycles? Regardless of how many triads of different roots the model generates, there still seems to be a binary distinction between those triads that are expected by ordered means of some generating pc interval, and those that are less obviously the result of inversional symmetry, a referential collection (due perhaps to multi-collectional resemblances), or a cyclic set. One could dedifferentiate these two groups by, for example, claiming that triads generated by either pc-center motivic or triadic transformative practice are to be as expected as those generated by the forms of centricity just listed. In the case of the previously discussed incipit of C+E♭+A+E♭-G+E+D♭+B♭-, this would assign F, F♯, A♭, B, D as the most probable continuations, the C and A, as less probable continuations, and the E♭, G, E, and D♭ as even less probable. One could further simplify this view of pc-center motivic projection by remembering the actual distribution that exists around the purported mean of 7 to 10 note that reflects a more realistic analysis of the frequency of certain lengths of non-duplicative root successions. At least this would reflect Macklay’s harmonic practice by effectively eliminating most concrete expectations about what will follow and what will not.
A suitable means of creating a sense of focus on a particular note or harmony is inversional symmetry. Take, once again, the F, F♯, A♭, B, and D in relation to C+E♭+A+E♭-G+E+D♭+B♭-. What could make one of these triadically harmonized, tonicized pc roots more centric than the others? Since the 8-note incipit actually goes on to include the remaining five pcs of the aggregate, the continuations to D+, B+, A♭+, F+, E♭+, F♯-, and C+ evince something significant. If C is to be established as a root of the central harmony, all of the other chords in this progression should be found to balance around C at the same time they are pressing on toward a seven- to ten-note, well-formed fundamental bass that is devoid of internal repetitions. Yet, because the progression of the entire phrase contains all 12 tones, the tonicized root succession is thereby linearly saturational: a sense of atonality can only be tempered by the establishment of centricity. This can be seen easily enough: the second chord E♭+, at 3 or 15 semitones above C is balanced by the third chord A+, 3 or 15 semitones below C; the fifth chord G+ is balanced by the fourth to last chord F+; the sixth chord E+ is balanced by the fifth to last chord A♭+; the seventh chord D♭+ is balanced by the sixth to last chord B+; and the eighth chord B♭- is balanced by the seventh to last chord D+. In a kinematic diagram, the 2 that is the third term in the prime-form path [01234565789te] would be followed by an arrow that goes to e, which is itself followed by an arrow that goes to 8, which is followed by an arrow that goes to 5, spelling out with these tonicized triad roots the components of what is vii
07 in the key of C and prosecuting a considerably “heavy” sweep to C+, the axis of symmetry and literally the central tone of the passage. One may remember from
Figure 9, that for B+D+F+A+A♭+C+E♭+G-B♭+C-D♭+ there are four pairs of pcs that balance around C in the progression.
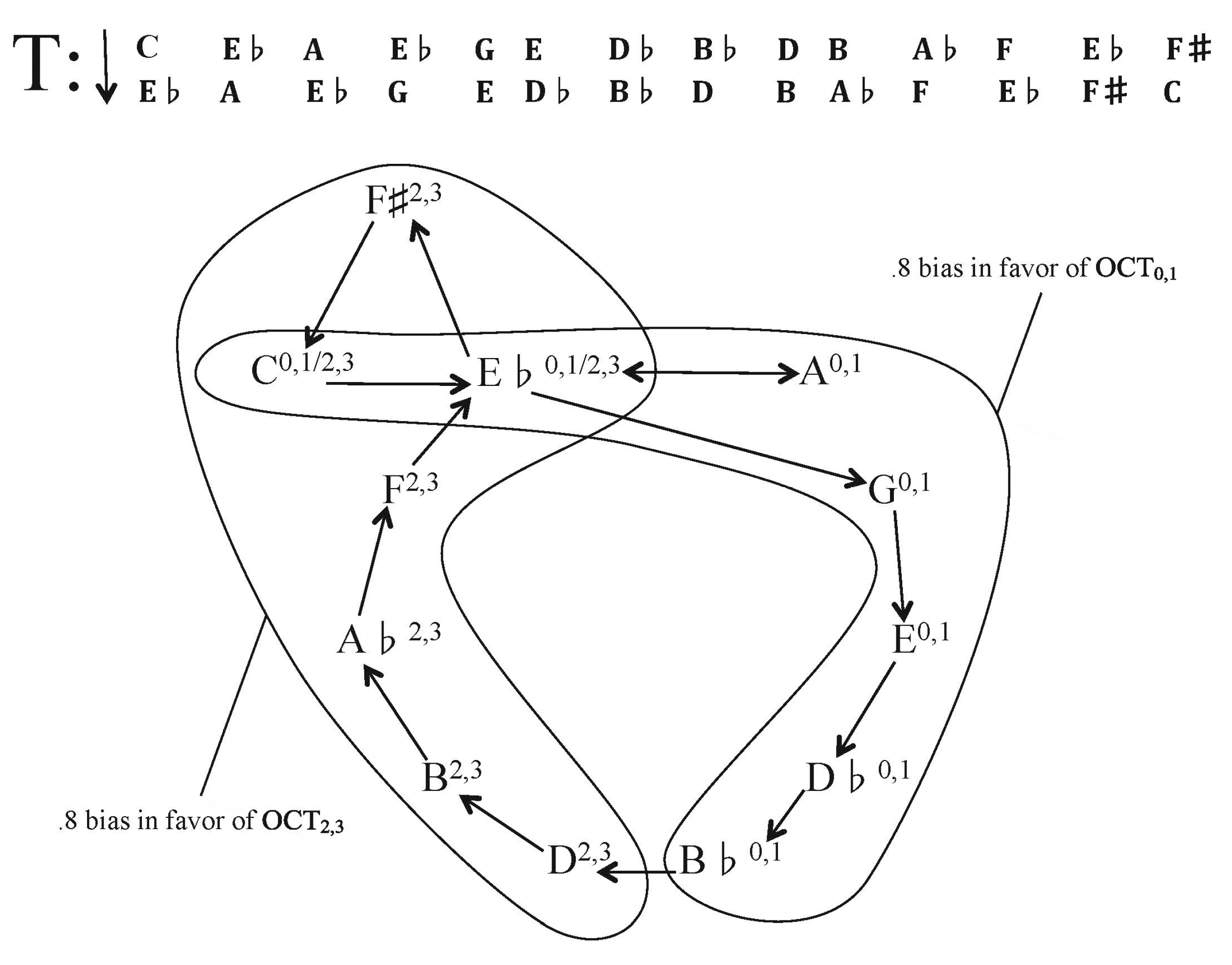
The fifth column in the table located in the
Appendix deals with the possibility that the sources of harmonic-class pitch material are certain large sets. It is labeled “(INT Cycle/Collectional Superset(s))”, and shows for a given harmonic class the referential set(s) or interval cycle(s) to which the class bears a degree of kinship. For example, for a harmonic class with no apparent relatedness to a diatonic, octatonic, hexatonic, or whole-tone collection, the likeliest generating pc intervals that most conveniently account for the content of a harmonic class usually belong to the C1-, and C5-cycles, respectively. The column under the “
” heading gives the conditional probability that a harmonic class (expressed as a pc set) will actually become the referential collection(s)/interval cycle(s) of which it is a subset. The last column under the “
” heading expresses the conditional probability that a harmonic class (expressed as a pc set) is actually derived from the referential collection(s)/interval cycle(s) of which it is a subset. Thus, all values are between 0 and 1, where 0 in the former column would represent a total bias in favor of one collection or another in the latter. 1 in the former column would represent in the latter a harmonic class (expressed as a pc set) that is not merely derived from, but actually is one, of the four large collections that have attracted the most compositional and theoretical attention (i.e., diatonic, octatonic, hexatonic, and whole-tone). The numbers in between flesh out the continuum of the communicating class (to borrow a Markovian term) of referential sets and harmonic classes or, rather, between no bias and complete bias in favor of one of the four major collections or one of the six interval cycles and their transpositions. In the case of a harmonic progression belonging to class 7–31, the cardinality is seven, meaning that there are five remaining pcs in the aggregate, but only one of those is needed if 7–31 is to become OCT
0,1; therefore, the value is
or 0.8 in favor of a bias toward OCT
0,1. This relatively high number represents a strong negative correlation with the probability (0.2) that 7–31 will, in fact, become OCT
0,1. The continuum from 0 to 1 is mutually inclusive of a continuum along which music may be understood in terms of the shift of observable referential-collectional or interval-cyclical partiality. Thus, because they seem to have their origins in either the C1- or C5-cycle, saturational harmonic progressions are often assigned a value of 1 in the former column (i.e., 100% probability that the set will go on to comprehend the aggregate), and 0 in the latter (i.e., 0% probability that the set is not the result of generating pc intervals 1, 11 and/or 5, 7).
These points of shared identity with common-practice tonality provide a higher-resolution picture of the simultaneous and indeed equivalent phenomena in the previously analyzed harmonic progressions.
Figure 14 revisits the opening of
Many Many Cadences (
Macklay 2014), where the enclosures contain the harmonic class (7–31), to which both tonicized root successions belong, and the value between 0 and 1 in the callouts indicate the collectional bias of this harmonic class. The graph below charts the change of bias from OCT
0,1 to OCT
2,3. The harmonic progression starts on its “tonic” with negligible bias, then the bias increases significantly with the arrival of D♭, forming with the following B♭, harmonic class 7–31. Consulting the table in the
Appendix, harmonic class 7–31’s fairly strong association (0.8) with OCT
0,1 begs to be extended with an F♯ to harmonic class 8–28, since this is the distinctive sound world implied by its linear structural properties. However, the
basse fondamentale of tonicized roots descends 9 semitones to D, taking an unexpected path. This demonstrates how an emergentistic model accounts for the earlier observation of the compositional decision at this point in Macklay’s harmonic progression to go to a chord other than F♯+ or F♯-, that nonetheless contains the pc F♯ as a chord member.
The probability that 7–31 will become an octatonic scale, amazingly enough, predicts this decision: this harmonic class, with 1:4 odds against it, only has a 0.2 probability of becoming a “diminished scale”. After its channeled continuations from D+ to F♯− that begins to invoke OCT
2,3, the progression rests on C+, which by no means completes that collection (0.8), but comes as close to completing it as the first half of the chord progression came to completing OCT
0,1.
Figure 15 revisits the B section and its recurrent sc(0136) root progression, an important subset of harmonic classes 10–1, 8–18, and 7–31. This four-chord succession stays centered on C because it begins with that pc root and the succession is repeated, untransposed, four times after its first presentation; the bias in favor of OCT
2,3 (0.5) is almost self-evident, and is promoted by the root of the third chord of each of the two preceding four-chord successions, which help to expand the collection to [9,11,0,2,3,6] with a 0.67 bias in favor of OCT
2,3. The repetitions of the sc(0136) harmonic progression continue until the D♯+ in measure 130, where the probability that the subsequent progression will develop into HEX
3,4 begins to become much higher (one possible outcome (1) divided by the only favorable outcome (1) with the continuation to the terminal C+ in measure 136). This provides an element common to the ensuing OCT
1,2-subset on C and to HEX
3,4, namely, pitch set [0,3,4,7], whose members (as triadically harmonized roots) constitute harmonic class 4–17, but, in this case, a C triad with both major and minor third. Thus, it links the contrasting B section with sections A and A1. The harmonic organization of the transition between B and A1 involves contrasting hexatonic and octatonic collections, with an important interaction and link between the two that happens to be emblematic of the “tonic” of the entire quartet. This dramatic change in collectional bias from OCT
2,3 to HEX
3,4 at the end of B through to OCT
1,2 of the first three measures of A1 is analogous to the effect of the minimal Schenkerian
Ursatz I-V-I, and so is another place in this piece where the tonal cadential analogy works.
Although two successive moments in a harmonic progression can be analogous to if not actually dominant and tonic because of the kind and degree of determinism imposed on them, the elements that contribute to the centric moment have no intrinsic reason to do so on their own. In this model, dominant and tonic have no psychological sense, purpose, or significance, no meaning, except by dint of a composer’s stratagems; rather, they exist in a three-dimensional space consisting of two spatial coordinates and one for time in which it is possible to locate harmonic events.
One final observation: In addition to Macklay’s ubiquitous voice-leading interval classes 1 and 2, the three-dimensional continuum in which tonic and dominant functionality are real (although arbitrary) categories is only possible by combining into one the attributes of traditional common-practice music with the triadic post-tonality of neoconservative postmodernism via the restoration of the importance of superposed 3s and 4s in the Western art tradition. Since the triad inverts into another triad of opposite quality, ic1/2 voice-leading parsimony and dual-process, contextual-fluid inversion avails only three unordered pc intervals for voice leading (i.e., 1, 2, and 3, in order of declension), and it seems that pc-center motivic projection would tend to limit the number of possible continuations to 22, since a triad followed by its inverse could, after transposition, result in premature pc-root duplication. I could even compare the Macklay kinematic to a world line in physics (i.e., the path of an object in space-time) tracing the history of its location in 3-dimensional musical space at each instant in time. A world line is a general way of representing the course of events, and its use is not bound to any specific field. Thus, as an extension of general usage, a world line could be used to track the sequential path of harmonic progressions (with time and space as dimensions), marking the history of a piece of music—starting at the beginning of the first measure and going until the end of the last. Ultimately, it is a metric that would, like the kinematic diagrams of the present study, effect the reduction of dimensions to one, and raise the rhetorical question which asks, to paraphrase British mathematician and science fiction author C. H. Hinton: “Why, then, should not music be its successive harmonic states and the passing of them through the three-dimensional space to which the percipient’s musical consciousness is confined?” (
Hinton 1884, p. 18).
Arguing that this music engages the emergence of a harmonic practice that is analogous to common-practice tonal expectations might be understood as a reinforcement of the view that Macklay’s move toward neoconservative postmodernism is actually a step backwards, a view that is not shared by the composer herself. In her program notes from a recent performance of
Many Many Cadences (
Macklay 2014) by the Mivos Quartet in a concert of new works by Columbia University graduate composers held on Friday, 27 February 2015 at 8:00 p.m., Macklay talks about placing functional harmony within a suitable contemporary context as she describes and defends her return to more traditional idioms (
Macklay 2015). She notes that even in year 2015, “Western ears are vey sensitive to certain formulaic chord progressions commonly used at the ends of phrases in tonal music (cadences)” (
Macklay 2015). It is for this reason that, in speaking for herself, and, in a broader sense, for many other composers of the early 21st century, she states that her intention was to “stretch the listener’s perception of cadences by recontexualizing these predictable chord progressions in very fast cells that are constantly changing key and register” (
Macklay 2015). In her final sentence, Macklay’s tone is that of a composer who has found a new path of development for old material: “These lonely, disjunct ends of phrases eventually congeal and transform into new kinds of phrases and sound objects” (
Macklay 2015).
On the other hand, as opposed to a literal return to the common-practice, it has been proposed here that Macklay’s “pre-modernism” is produced from and identical to post-tonally centric, referential collectional, and triadic tissue. Therefore, the “neo” in Macklay’s “neoconservative postmodernism” may signify more than an expression of the Ovidian adage “omnia mutantur, nihil interit”
20 and recontextualization. It may also signify the discovery of something that, while theoretically identical to pre-modern functional tonal expectations, stems in its balance of chance and determinism from the undivided wholeness of two harmonic characteristics that,
prima facie, do not appear to lend themselves to common-practice tonality. Ic1/2 voice-leading parsimony and dual-process, contextual-fluid inversion employ the two most common interval classes in all referential collections, and pc-center motivic projection offers one means, akin to Schoenberg’s conception of the twelve-tone system, to avoid a bias toward a central pitch.
21 As Pieter van den Toorn puts it, “With Schoenberg, connections were pursued primarily from the standpoint of motives…, while, with Schenker, they were pursued from that of harmony and voice leading”, but Schoenberg and Schenker were both right because “in a larger sense”, motive, harmony, and voice leading are all part of “an organic whole, of parts reciprocally both defining and being defined by a whole” (
Van den Toorn 1996, p. 373, 389).
22 The abstract descriptions of non-binary integration of the two principal types of triadic post-tonality involved in Macklay’s recontextualization and van den Toorn’s “organic whole” bear a striking resemblance to each other. Macklay may have retreated from category distinctions in many obvious ways, but this retreat was, as a logical consequence, accompanied by an unconscious insight into a holism the application of which has lifted neoconservative postmodernism in music to a new level, imparting monistic transcendence to merely pouring old wine into new wineskins.