Abstract
All the studies on the thermoelastic behaviour of materials, including the revised higher order theory on the thermoelastic effect, are based on several assumptions that limit the application of such theory to the cases of isotropic materials in the presence of uniaxial residual stresses and undergoing uniaxial applied loads. These assumptions lead to some discrepancies in the description of the real thermoelastic behaviour of materials in the presence of residual stresses. In this work, by rewriting the thermoelastic equation in a different way, it was possible to study the behaviour of homogeneous and non-isotropic materials undergoing any loading conditions and residual stresses. Firstly, the error made by the calibration procedures of thermoelastic stress analysis (TSA) data in the presence of residual stresses has been investigated. Then, a statistical analysis was carried out to determine the minimum value of residual stress which would lead to significant and measurable variations in the thermoelastic signal. The simulations involved two non-ferrous metals: AA6082 and Ti6Al4V, which exhibit a specific thermoelastic behaviour.
1. Introduction
Thermoelastic stress analysis (TSA) is a well-established, non-contact technique used to assess the superficial stress field exploiting the thermoelastic effect. This technique is based on the generation of small and reversible temperature variations linked to the volume variation in components subjected to a dynamic load in the linear elastic range [1].
In recent years, TSA found large employment in many applications on sample specimens [2,3] and real components [4,5], due to the advantages of being contactless, full field, totally safe for the component and not requiring substantial surface preparation. In this regard, such a technique is very useful to validate structural finite element modelling (FEM) and to predict stress concentration in real components. In particular, its applicability has been already demonstrated in complex air frame modelling [4] and in the qualification of additively manufactured components [5].
Under adiabatic conditions and for a homogeneous isotropic material, if the dependence on temperature of thermal and mechanical characteristics of the material are neglected, the thermoelastic signal is proportional to the sum of the principal stress amplitude [1,6]. If this dependence is not neglected, the thermoelastic signal shows a dependence also on the mean stress. Some materials, including steels, do not show sensitivity to this effect, while it is not negligible for non-ferrous titanium and aluminium alloys that are widely used in the design of lightweight structures. This result has been widely demonstrated both analytically and experimentally by Wong et al. through the revised higher order theory [7,8] showing the possibility to use the TSA for residual stresses estimation [9,10,11,12,13,14,15,16].
So far, there have been two different approaches to evaluate residual stresses by means of the TSA. The first, proposed by Wong and et al. [10], considers residual stresses as a mean stress which remains constant during the dynamic load application. Several researchers followed this approach. Gyekenyesi et al. [11] demonstrated how to simultaneously obtain the stress amplitude and the mean stress from the first and second harmonics; the latter is approximately 2% of the first harmonic [12] and its measurements represent the main limitation of this technique. Patterson et al. [14,15] proposed an alternative technique based on a calibration procedure to directly relate the stress amplitude to the detector response, in such a way that the second harmonic evaluation is not necessary. In their work, Galietti et al. [17] proposed a calibration procedure and showed the applicability of this approach in the simple case of uniaxial load and assuming uniaxial residual stresses directed as the applied load.
The second approach has been proposed by Quinn et al. [18], and it assumes that residual stresses associated to plastic deformation can be evaluated through TSA by determining the variation of the linear thermal expansion coefficient. This relation has been empirically proved but has the limit to neglect the second order effect.
All the studies present in literature, including the revised higher order theory, are based on several assumptions that limit the application of such theory to the cases of isotropic materials subjected to uniaxial residual stresses and uniaxial applied loads. It follows that the description of the real phenomenon contains some discrepancies.
The aim of this work is to propose a general model for thermoelastic stress analysis that is able to provide the value of a thermoelastic signal as a function of either the general biaxial applied load or the general biaxial residual stress (or mean load) with different principal axes. Moreover, the model provides the possibility to assess the thermoelastic signal for material with generic constitutive equations (i.e., isotropic/orthotropic/anisotropic behaviour).
The proposed equation was firstly used for evaluating the error made in neglecting the principal residual stresses in terms of modulus, sign and direction with respect to the applied amplitude and mean stresses. In particular, two approaches for calibrating the TSA data were considered, based on the classical TSA equation [1,6] and the revised high order theory (mean stress effect) [19]. In both cases, the error was investigated as a function of the residual stresses.
Similar simulations with the proposed equation were used to carry out a statistical analysis with the aim to evaluate the minimum value of residual stresses which lead to significant and measurable variations in the thermoelastic signal for aluminium and titanium alloys.
The proposed approach could represent a useful tool to obtain information about the residual stresses on real components subjected to actual loading conditions. The assessment of the effective stress map of real components in the presence of residual stresses is of great importance together with their estimation in many industrial applications. This is the case, for instance, for mechanical components produced by means of the Additive Manufacturing process in which the residual stresses play a key role on the material stresses distribution, and then its mechanical behaviour.
2. Theory
In this work, the thermoelastic signal has been evaluated through an equation based on Wong’s second order equation [7,8] and the more general equation presented by Potter and Graves [20].
Under isentropic and adiabatic conditions and considering the material macroscopically homogeneous, the thermoelastic general equation obtained by Potter and Graves [20] can be written in tensorial form:
In Equation (1), dT is the infinitesimal temperature difference due to the thermoelastic effect associated with the strain field , while ρ and Cε respectively represent the density and the specific heat at constant strain and T is the reference temperature.
, , and represent the state of deformation in a point, the vector of the linear thermal expansion coefficients and the material stiffness matrix, respectively. All these quantities are expressed in the reference system x, y, z:
The dependence of from temperature has been neglected. In fact, in most cases this term is negligible, being it of the order of 10−9 K for ΔT ≈ 10−2 K and α ≈ 10−7 K−1.
The strain and the stress vectors are linked through the constitutive relation:
Substituting in Equation (1):
Equation (4) describes the temperature variation due to the thermoelastic effect associated with the variation of the stress state , for a homogeneous material in adiabatic conditions. It can be also applied to describe the thermoelastic behaviour in any load conditions and for anisotropic materials.
If the stress vector components change in phase with sinusoidal law, it results in
where and are respectively the mean and the amplitude stress vectors that can be expressed as vectors in the reference system as
Substituting Equations (5) and (6) in Equation (4):
Integrating between t0 = 0 and t, with T(t0) = T0, Equation (8) became
Typical TSA analysis are carried out by a lock-in amplifier, allowing to discriminate the amplitude of the signal at the same frequency of the mechanical imposed load.
By focusing on the amplitude of the temperature running at the same frequency as the applied load, the temperature variations are
where the mean stress vector () represents all the stress contributions remaining constant during the sinusoidal loading. It can be described as composed by the sum of:
- The applied mean stress , here considered proportional to for each pixel in a fixed test;
- the residual stress; and
- own weight of the structure.
In general, the latter is negligible, as well as, as a first approximation, the bending moments. Therefore, can be considered as the sum of the applied mean load and the residual stresses vector.
In this case, Equation (10) became
In Equation (11), the residual stress vector is expressed in the principal stress reference system, while the tensor R is the rotation matrix that allows to write in the reference system used to write the equation.
Using Equation (11), it is possible to evaluate the thermoelastic signal in the case of uniaxial stresses and isotropic material but with biaxial residual stresses, which is the case of main interest for practical applications.
Assuming and are uniaxial (σmxx, Δσxx), and considering the material isotropic and θ the angle between the residual stress principal system and the loading system, see Figure 1, Equation (11) became
where E is the isotropic Young Modulus, α is the isotropic coefficient of thermal expansion, and ν is the isotropic Poisson Modulus.
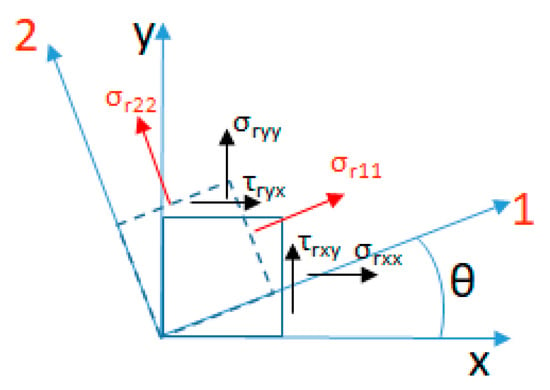
Figure 1.
Residual stresses in the principal system (1, 2) and in the loading system (x, y).
It is possible to assume [21,22], therefore Equation (12) became
Following the approach already used by Patterson et al. [13,14], Galietti et al. [17] and Palumbo [19], the two thermoelastic parameters a and b can be defined as:
where a and b can be determined through literature or experimentally.
In this work, to consider the term linked to the residual stress, the parameter c has been defined as follows:
with γr = σr22/σr11.
Substituting in Equation (13), and defining γ as the ratio between σmxx and Δσxx, it can be obtained that
Therefore, the stress can be evaluated by measuring the thermoelastic signal ΔT and solving
3. Materials and Methods
Two different materials were used for simulating TSA data: Titanium alloy Ti-6Al-4V and Aluminium alloy AA6082; both alloys show a non-negligible second order effect on the thermoelastic signal [7,8,9,10,11,16,17,19]. In Table 1 are the values of the mechanical and thermo-physical properties of materials [1,7,23,24,25,26].

Table 1.
Mechanical and thermo-physical characteristic of the considered materials.
In each simulation, a reference temperature of 293 K was assumed. In order to simulate the real thermoelastic signal in different stress and residual stress conditions, Equation (13) was employed and the statistical analysis was carried out by considering a white gaussian noise. Experimental measurements were performed on a uniform temperature target (about 297 K), by using a cooled IR camera FLIR X6540sc (Flir System, Inc. Winstonville, OR, USA) with a frame rate of 200 Hz and an integration time of 0.596 ms, which are the settings used in TSA tests. The results demonstrated a standard deviation for the noise of 0.01 K (Figure 2) and, therefore, this was the value adopted in this study.
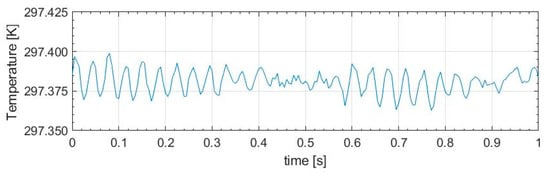
Figure 2.
Sampling of a real signal using a cooled IR camera FLIR X6540sc.
3.1. Error Analysis in Stresses Evaluation if Residual Stresses Are Neglected
In this paragraph, by using the proposed approach, the error made in stresses evaluation using TSA when the residual stresses are neglected, has been determined. In particular, the error was evaluated by considering two approaches for calibrating the TSA data: The one based on the classical TSA equation [1] and the one based on the revised high order theory (mean stress effect) [19]. In both cases, the error was investigated as a function of the residual stresses.
By imposing a stress amplitude ∆σxx for fixed values of γ (σmxx/Δσxx), σr1 and γr (σr22/σr11), the thermoelastic amplitude signal is
The classical thermoelastic equation provides the following relations between temperature and stress amplitude:
where is the stress amplitude evaluated by using such an approach. It is affected by the error related to neglected residual stresses.
By including Equation (19) in Equation (18) one can obtain
By writing the stress amplitude of the classic technique affected by error as the sum of the effective value and a real number , Equation (20) becomes
Hence, the error can be directly assessed by the following equation, when the ε turns into for readability:
This error can be also evaluated by taking into account the calibration procedure proposed by Galietti and Palumbo [17,19]. In this case, the thermoelastic signal was expressed as the polynomial sum of amplitude stress terms:
where the stress amplitude clearly contains the error. By expressing the latter as , and by substituting Equation (23) in Equation (18), it is possible to obtain
Finally, the error made by using the procedure is
When σr1 = 0, the error is
Since εGal has been defined as the error made by neglecting residual stresses, it has to be null in the case σr1 = 0. Therefore, the only solution which has to be considered for evaluating the error using the technique in Reference [19], is the one with the negative sign of the radical term in Equation (25), being −(2bγΔσxx + a), a positive term. By considering the materials characteristics in Table 1, the parameter a has a negative value of order 10−10 for the AA60082 and 10−11 for the Ti6Al4V, while the product 2bγΔσxx can be both positive or negative (depending on the loading system) and it has the order of 10−23 for the AA60082 and 10−24 for the Ti6Al4V. Therefore the term −(2bγΔσxx + a) always has a positive value.
Furthermore, in the manuscript the errors evaluated by using Equations (22) and (25) will be graphically shown and discussed.
3.2. TSA Capability in Evaluating Residual Stresses: Statistical Analysis
A statistical study was carried out by simulating temperature measurements during TSA tests under different residual stress conditions in order to determine the minimum value of residual stress which leads to a measurable variation in the thermoelastic signal for the considered materials.
In this regard, two representative cases have been investigated as will be shown in the following section. In particular, the variation of the principal residual stress σr11 has been studied, by keeping the residual stress ratio γr constant.
The simulation involved the following steps:
- Signal amplitude calculation (Equation (13));
- Signal temporal reconstruction, assuming a sampling frequency of 200 Hz;
- Adding the gaussian noise according to the experimental value found with a cooled IR camera FLIR X6540sc, as described in the previous section; and
- Performing a Fast Fourier Transform to obtain the amplitude of the signal.
The classical and the Palumbo et al. [19] approaches were then used to calculate the stress. A total of 1000 repetitions were performed for each approach in order to evaluate the mean and standard deviation values.
A statistical inference analysis allowed to carry out a hypothesis test and to calculate the probability of a second type error β that is to accept the null hypothesis when it is false [27]. In this study the null hypothesis is represented by the absence of residual stress, and the β-error is made when residual stresses are not null [27].
The second type error probability was calculated for each approach assuming a confidence interval of 95% and using 1 as samples dimension.
4. Results and Discussion
4.1. Effects of Biaxial Residual Stresses on TSA Signal
In this section the effect of the residual stresses on the thermoelastic signal (ΔT) has been investigated. To study this effect, Equation (13) has been considered, in which the thermoelastic signal is expressed as a function of the principal residual stresses and their direction with respect to the applied loads. In particular, to represent and compact all the data, the ratio between the residual stresses has been considered. In this way, the analyses have been performed at specific ratios between the principal residual stresses (γr = σr22/σr11): 1, 0, −1 and −2.
The material characteristics of the alloys used for the analysis were resumed in Table 1, while the load conditions are shown in Table 2. The amplitude and the mean load were selected considering the mechanical characteristics of the material and the yield strength in order to ensure the linear elastic conditions.

Table 2.
Ranges of residual stress system modelled for AA6082 and Ti6Al4V alloys.
In Figure 3 and Figure 4, the thermoelastic signal is represented as a function of the two independent variables σr11 and θ.
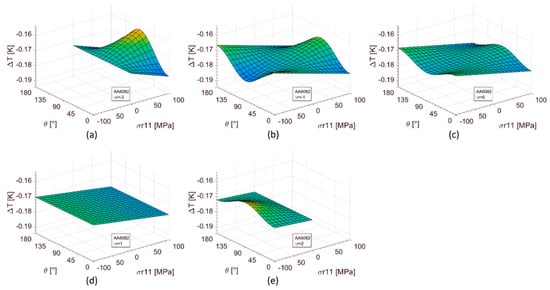
Figure 3.
Thermoelastic signal as a function of the two independent variables σr11 and θ for the AA6082 alloy: (a) γr = −2 (b) γr = −1 (c) γr = 0 (d) γr = −1 (e) γr = −2.
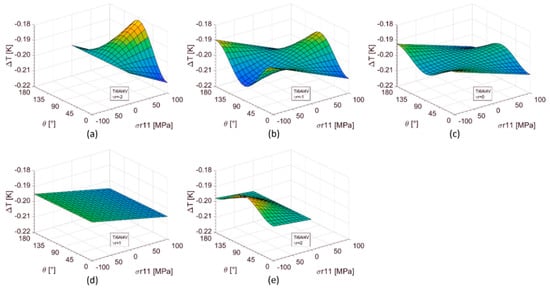
Figure 4.
Thermoelastic signal as a function of the two independent variables σr11 and θ for the Ti6Al4V alloy: (a) γr = −2 (b) γr = −1 (c) γr = 0 (d) γr = −1 (e) γr = −2.
The signal varies periodically with θ, with a period of 180°. The dependence of the signal on θ decreases, with ranging γr from −2 to 1. In particular, for γr = 1, there is no more an effect of θ on the thermoelastic signal.
Figure 5a,b shows the effect of the load amplitude on thermoelastic variations for three specific values of ∆σxx. Clearly, the higher the stress the stronger is the effect of residual stresses affecting the signal. In fact, a higher value of the stresses ensures also a higher signal and therefore better detection capacity with equal noise.
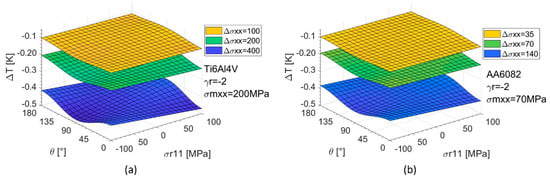
Figure 5.
Effect of the load amplitude on temperature variations for AA6082 (a) and Ti6Al4V (b) alloys.
As it is possible to observe in Figure 5, by fixing the value of θ and γr, the two alloys present the same trends in terms of temperature variations. Their different physical and mechanical properties determine a difference in the signal magnitude: At the same amplitude and mean stress, the AA6082 alloy responds with a signal which is higher than the Ti6Al4V alloy response. However, the possibility to apply higher stresses to the titanium alloy allows obtaining a signal of the same order and with a higher variability induced by the residual stresses.
Based on the trends resulted from the analysis presented in Figure 3 and Figure 4, two representative cases were selected for the following investigations. In both cases, ∆σxx, γ and σr11 are fixed. The first case represents a condition with the higher signal variation due to residual stresses with respect to the reference conditions (absence of residual stress, σr11 = 0), with γr = −2 and θ = 90°, while the second case represents a condition with a lower signal variation obtained by imposing γr = 1 and θ = 0°. These cases will be deeply investigated in the next sections.
4.2. Error Analysis: Results
The error ε defined in Section 3.1 has been calculated for the two alloys in order to compare the error made in the evaluation of the stress amplitude (uniaxial and uniform applied stress) by using two different calibration approaches.
The imposed load conditions (Table 3) were the two case studies representative of high (γr = −2, θ = 90°) and low (γr = 1, θ = 0°) residual stresses effect, as just discussed in the previous section. Furthermore, the effects of the mean load and of the load amplitude were also investigated.

Table 3.
Ranges of stress values used for modelling AA6082 and Ti6Al4V alloys.
The simulations were performed by using the mechanical and physical characteristics in Table 1 and the stress values in Table 3.
As expected, the approach which leads to the minimum error is the calibration procedure proposed by Galietti et al. [17] which considers the mean stress effect (Figure 6 and Figure 7c,d). Indeed, by increasing the mean stress, the error due to neglecting the residual stresses decrease, while the classical approach (Figure 6 and Figure 7a,b) presents an increasing error with the mean load. This effect is related to the analytical definition of the two terms that were modelled as additives.
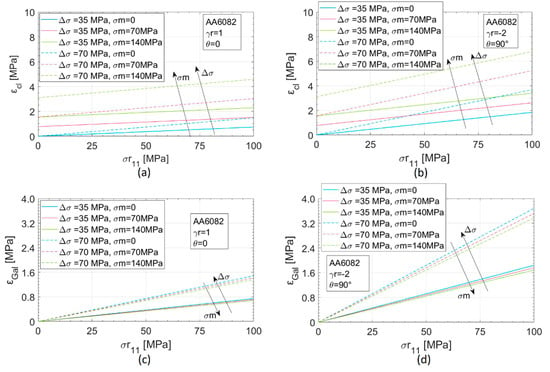
Figure 6.
Parameter ε as function of σr11 for the AA6082 alloy: (εcl) for the classical technique and (εGal) for the method proposed in Reference [17] are compared for the case of (a,c) for low and (b,d) for high residual stresses effect.
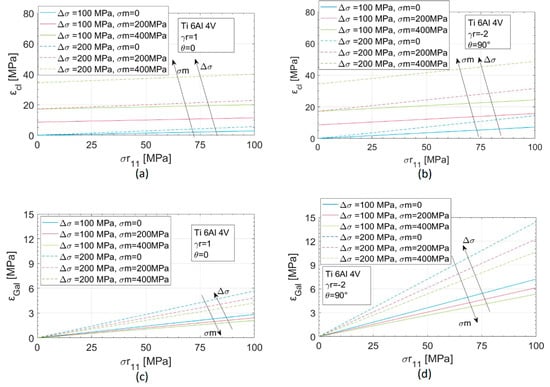
Figure 7.
Parameter ε as function of σr11 for the Ti6Al4V alloy: (εcl) for the classical technique and (εGal) for the method proposed in Reference [17] are compared for the case of (a,c) for low and (b,d) for high residual stresses effect.
The two alloys present a similar behaviour, so for both materials the following considerations can be made:
- The classical procedure presents the higher error;
- In the case of higher residual stress influence (γr = −2, θ = 90°), both the procedures give significant errors in stress amplitude evaluation, above 10%;
- The error increases as the stress amplitude increases for both the approaches. It is more significant for the Galietti et al. [17] approach in which the effect of the mean stress is considered; and
- The error always increases as the mean stress increases for the classic procedure while it decreases for the Galietti et al. [17] approach.
By resuming, the effect of neglecting residual stresses can involve significant errors in stresses evaluation by means of the TSA technique. However, when the modulus and directions of the residual stresses are known, the error in stress evaluation can be estimated by adopting the proposed approach.
4.3. Capability in Evaluating Residual Stresses: Results
In this section, the capability in residual stresses estimation will be investigated. In this regard, the second type error was evaluated as described in Section 3.2 for the two considered approaches.
In order to separate the effect of the mean stress from the residual stress influence, the second type error for the classical approach was calculated only for σmxx = 0 and for the same stress amplitude used in the error analysis. As expected, the results were equivalent to those obtained from the approach proposed by Galietti et al. [17] in the same stress conditions.
The stress conditions modelled to study the second type error made by using the method proposed by Galietti et al. [17] are reported in Table 3.
Figure 8 and Figure 9 show how the mean stress does not affect the minimum value of σr11 for which β is null, while it varies significantly depending on the residual stress conditions and on the stress amplitude. Considering the case of a single TSA test and then of a single thermoelastic measurement, for the AA6082 alloy, this value is equal to 27 MPa if ∆σxx is 35 MPa and the residual stress condition is biaxial, with γr = −2 and θ = 0 (Figure 8b). If the residual stress system is uniaxial with θ = 0, at least a σr11 of 75 MPa is needed to have a discernible thermoelastic signal variation with the same ∆σxx (Figure 8a).
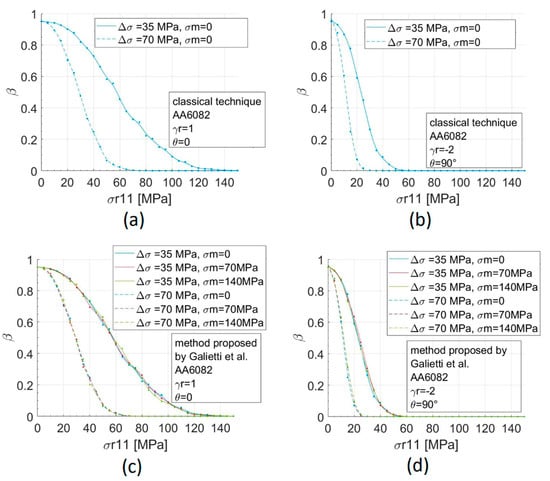
Figure 8.
Second type error as function of σr11 for the AA6082 alloy: The classical technique and the method proposed in Reference [17] are compered for the case of (a,c) for low and (b,d) for high residual stresses effect.
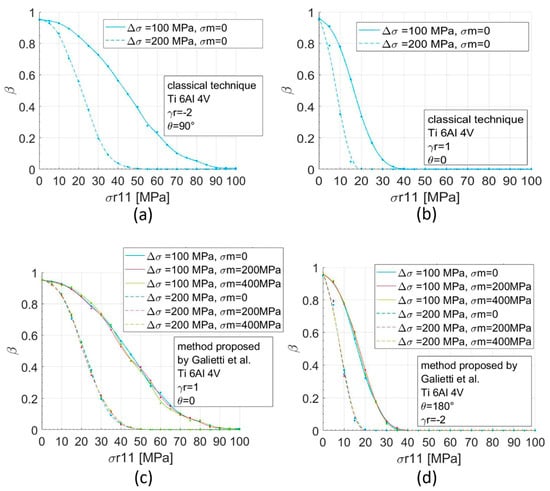
Figure 9.
Second type error as function of σr11 for the Ti6Al4V alloy: The classical technique and the method proposed in Reference [17] are compered for the case of (a,c) for low and (b,d) for high residual stresses effect.
If ∆σxx is 70 MPa, the two discernible values of the amplitude stress become 65 and 150 MPa, respectively (Figure 8a,b).
In the case of the alloy Ti6Al4V, the minimum σr11 values are lower, in both the considered residual stress conditions (Figure 9). For the two considered cases, values of 20 MPa and 55 MPa were obtained, respectively, for ∆σxx = 100 MPa and values of 45 MPa and 100 MPa for ∆σxx = 200 MPa. It is important to underline that the better capability for titanium in evaluating the residual stresses is due to the possibility to apply higher loads.
5. Conclusions
In this work, a new equation for describing the thermoelastic behaviour of materials was proposed. In particular, the proposed equation allows to study the behaviour of homogeneous and non-isotropic materials undergoing any loading conditions and residual stresses. By using this equation, the error made by the two calibration approaches of thermoelastic stress analysis (TSA) data in presence of residual stresses has been investigated. Moreover, the minimum value of residual stresses leading to significant and measurable variations in the thermoelastic signal has been evaluated.
The main results obtained for uniaxial and uniform applied stresses, can be summarized as follows:
- The error in stress amplitude evaluation with TSA if the residual stresses are neglected depends on the modulus, direction and angle of the principal residual stresses with respect to the applied stresses. Significant errors (above 10%) can be made in stresses evaluation;
- This error depends also on the applied stresses (amplitude and mean) and on the considered material (thermo-physical and mechanical property); and
- In the same way, the capability of TSA in residual stresses evaluation depend on the considered material and on the modulus, direction and angle of the principal residual stresses with respect to the applied stresses.
Further works will be focused on experimental tests on samples or components to obtain a quantitative measurement of residual stresses with the proposed approach.
Author Contributions
F.D.C. wrote the paper; methodology was setup by F.D.C., D.P. and R.D.F.; and supervision was done by U.G.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| dT | [K] | Infinitesimal temperature difference due to the thermoelastic effect |
| T | [K] | Reference temperature |
| [μm/m] | Vector of Infinitesimal strain variations | |
| [μm/m] | Vector of strains in a point | |
| [Pa] | Stiffness matrix | |
| [K−1] | Vector of the linear thermal expansion coefficients | |
| ρ | [kg/m3] | Density |
| Cε | [J/kg·K] | Specific Heat at constant strain |
| x, y, z | - | Reference system |
| [Pa] | Vector of stress in a point | |
| [Pa] | Vector of Infinitesimal stress variations | |
| [Pa] | Amplitude stress vector | |
| [Pa] | Total mean stress vector | |
| [Pa] | Applied mean stress vector | |
| [Pa] | Residual stress vector | |
| 1,2,3 | - | Principal system |
| R | - | Rotation matrix |
| θ | - | Angle between the residual stress principal system and the loading system |
| a, b | [Pa−1], [Pa−2] | Thermoelastic parameters [16,17] |
| c | [Pa−1] | Parameter depending on thermoelastic behaviour and residual stress |
| γr | - | Ratio between the principal residual stress components |
| γ | - | Ratio between the mean and amplitude of the load |
| K | [Pa−1] | Thermoelastic constant [1] |
| ε | - | Error affecting the stress amplitude measurement |
| - | Error affecting the stress amplitude measurement using the classical technique | |
| - | Error affecting the stress amplitude measurement using the method proposed by Galietti et al. [17] | |
| β | - | Second type error |
References
- Harwood, N.; Cummings, W.M. Thermoelastic Stress Analysis; Adam Hilger: Philadelphia, PA, USA, 1991. [Google Scholar]
- De Finis, R.; Palumbo, D.; Galietti, U. A multianalysis thermography-based approach for fatigue and damage investigation of ASTM A182 F6NM steel at two stress ratios. Fatigue Fract. Eng. Mater. Struct. 2019, 42, 267–283. [Google Scholar] [CrossRef]
- De Finis, R.; Palumbo, D.; Da Silva, M.M.; Galietti, U. Is the temperature plateau of a self-heating test a robust parameter to investigate the fatigue limit of steels with thermography? Fatigue Fract. Eng. Mater. Struct. 2019, 41, 917–934. [Google Scholar] [CrossRef]
- Rajic, N.; McSwiggen, D.; McDonald, M.; Whiteley, D. In situ thermoelastic stress analysis—An improved approach to airframe structural model validation. QIRT J. 2018, 16, 8–34. [Google Scholar] [CrossRef]
- Allevi, G.; Cibeca, M.; Fioretti, R.; Marsili, R.; Montanini, R.; Rossi, G. Qualification of additively manufactured aerospace brackets: A comparison between thermoelastic stress analysis and theoretical results. Measurement 2018, 126, 252–258. [Google Scholar] [CrossRef]
- Pitarresi, G.; Patterson, E.A. A review of the general theory of thermoelastic stress analysis. J. Strain Anal. Eng. Des. 2003, 38, 405–417. [Google Scholar] [CrossRef]
- Wong, A.K.; Jones, R.; Sparrow, J.G. Thermoelastic constant or thermoelastic parameter? J. Phys. Chem. Solids 1987, 48, 749–753. [Google Scholar] [CrossRef]
- Wong, A.K.; Sparrow, J.G.; Dunn, S.A. On the revised theory of the thermoelastic effect. J. Phys. Chem. Solids 1988, 48, 395–400. [Google Scholar] [CrossRef]
- Gyekenyesi, A.L.; Baaklini, G.Y. Thermoelastic Stress Analysis: The Mean Stress Effect in Metallic Alloys. In Proceedings of the SPIE 3585, Nondestructive Evaluation of Aging Materials and Composites III, Newport Beach, CA, USA, 8 February 1999. [Google Scholar]
- Wong, A.K.; Dunn, S.A.; Sparrow, J.G. Residual stress measurement by means of the thermoelastic effect. Nature 1988, 332, 613–615. [Google Scholar] [CrossRef]
- Gyekenyesi, A.L.; Baaklini, G.Y. Quantifying Residual Stresses by Means of Thermoelastic Stress Analysis. In Proceedings of the SPIE 3993, Nondestructive Evaluation of Aging Materials and Composites IV, Newport Beach, CA, USA, 13 May 2000. [Google Scholar]
- Robinson, A.F.; Dulieu-Barton, J.M.; Quinn, S.; Burguete, L. A Review of Residual Stress Analysis using Thermoelastic Techniques. In Proceedings of the 7th International Conference on Modern Practice in Stress and Vibration Analysis, Murray Edwards College, Cambridge, UK, 8–10 September 2009; p. 012029. [Google Scholar]
- Robinson, A.F.; Dulieu-Barton, J.M.; Quinn, S.; Burguete, L. The potential for assessing residual stress using thermoelastic stress analysis: A study of cold expanded holes. Exp. Mech. 2013, 53, 299–317. [Google Scholar] [CrossRef]
- Patterson, E.A. The Potential for Quantifying Residual Stress Using Thermoelastic Stress Analysis. In Proceedings of the SEM Annual Conference and Exposition on Experimental and Applied Mechanics 2007, Springfield, MA, USA, 3–6 June 2007; pp. 664–669. [Google Scholar]
- Du, Y.; Backman, D.; Patterson, E.A. A New Approach to Measuring Surface Residual Stress Using Thermoelasticity. In Proceedings of the SEM Annual Conference and Exposition on Experimental and Applied Mechanics 2008, Orlando, FL, USA, 2–5 June 2008; Volume 2, pp. 673–680. [Google Scholar]
- Palumbo, D. Analisi Termoelastica di Componenti in Titanio e Contemporanea Valutazione Delle Tensioni Residue. In Proceedings of the Atti del XXXVIII Convegno Nazionale AIAS, Torino, Italy, 9–11 September 2009. [Google Scholar]
- Galietti, U.; Palumbo, D. Thermoelastic Stress Analysis of Titanium Components and Simultaneous Assessment of Residual Stress. In Proceedings of the EPJ Web of Conferences, ICEM 14—14th International Conference on Experimental Mechanics, Poitiers, France, 4–9 July 2010; p. 38012. [Google Scholar]
- Quinn, S.; Dulieu-Barton, J.M.; Langlands, J.M. Progress in thermoelastic residual stress measurements. Strain 2004, 40, 127–133. [Google Scholar] [CrossRef]
- Palumbo, D.; Galietti, U. Data correction for thermoelastic stress analysis on titanium components. Exp. Mech. 2016, 56, 451–462. [Google Scholar] [CrossRef]
- Potter, R.T.; Greaves, L.J. The Application of Thermoelastic Stress Analysis Techniques to Fibre Composites. In Proceedings of the SPIE 0817, Optomechanical Systems Engineering, San Diego, CA, USA, 1 January 1987. [Google Scholar]
- Fukuhara, M.; Sanpei, A. Elastic moduli and internal frictions of Inconel 718 and Ti-6Al-4V as a function of temperature. J. Mater. Sci. Lett. 1993, 12, 1112–1124. [Google Scholar] [CrossRef]
- Naimon, E.R.; Ledbetter, M.H.; Weston, W.F. Low-temperature elastic properties of four wrought and annealed aluminium alloys. J. Mater. Sci. 1975, 10, 1309–1316. [Google Scholar] [CrossRef]
- Boyer, R.; Collings, E.W.; Welsch, G. Materials Properties Handbook: Titanium Alloys; ASM International: Materials Park, OH, USA, 1994. [Google Scholar]
- ASM International. ASM Handbook Volume 2: Properties and Selection: Nonferrous Alloys and Special-Purpose Materials; ASM International: Materials Park, OH, USA, 1990. [Google Scholar]
- Benjamin, D.; Kirkpatrick, C.W. Properties and Selection: Stainless Steels, Tool Materials and Special-Purpose Metals, 9th ed.; American Society for Metals: Metals Park, OH, USA, 1980. [Google Scholar]
- Holt, H.J. Structural Alloys Handbook; West Lafayette, Ind., CINDAS/Purdue University: West Lafayette, IN, USA, 1996. [Google Scholar]
- Montgomery, D.C.; Runger, G.C. Applied Statistics and Probability for Engineers, 5th ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2010; p. 768. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).