Micromechanical Modeling of Fatigue Crack Nucleation around Non-Metallic Inclusions in Martensitic High-Strength Steels
Abstract
1. Introduction
2. Material and Experimental Investigations
2.1. Martensitic Microstructure
2.2. Failure-Relevant Non-Metallic Inclusions
3. Modeling Methodology and Constitutive Model
3.1. Modeling Statistical Volume Elements
3.1.1. Modeling Martensitic Statistical Volume Elements without Defects
3.1.2. Modeling Martensitic Statistical Volume Elements with Defects
3.2. Local Crystal Plasticity Model
3.2.1. Constitutive Equations
3.2.2. Calibration of the Crystal Plasticity Model
3.3. Simulation Methodology for Residual Stress Development
3.4. Fatigue Indicator Parameters and Fatigue Crack Nucleation Model
3.5. Strategy of the Numerical Design of Experiment
4. Results and Discussion
4.1. Influence of Microstructural Variability
4.2. Effect of Residual Stresses
4.3. Influence of Interface Properties on Fatigue Response
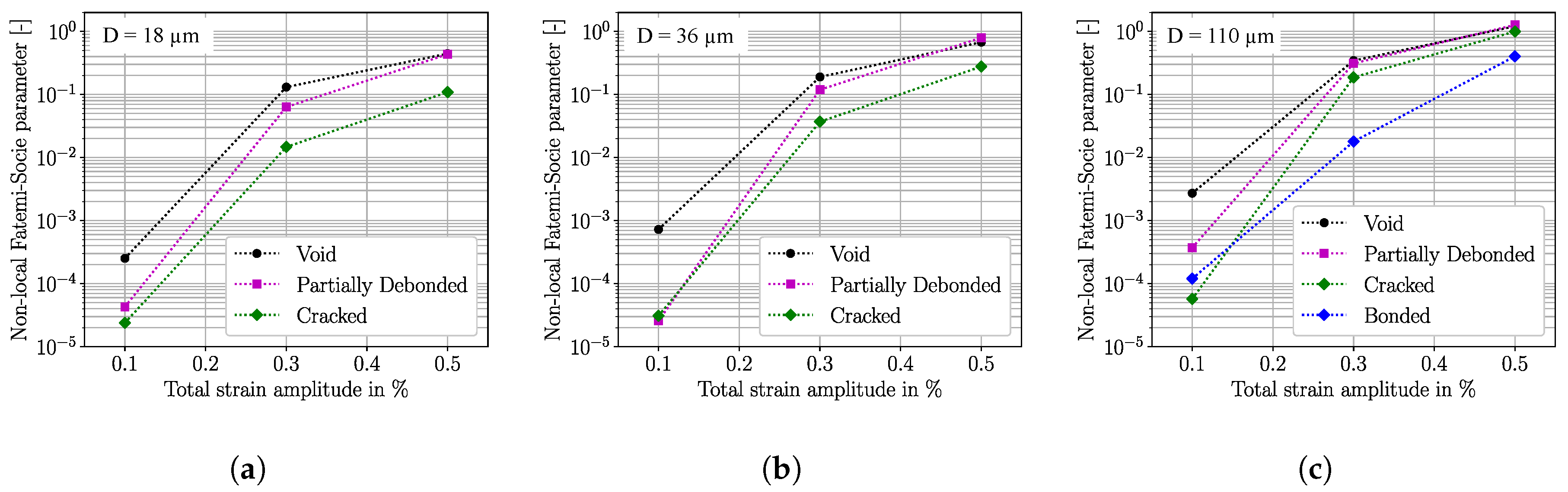
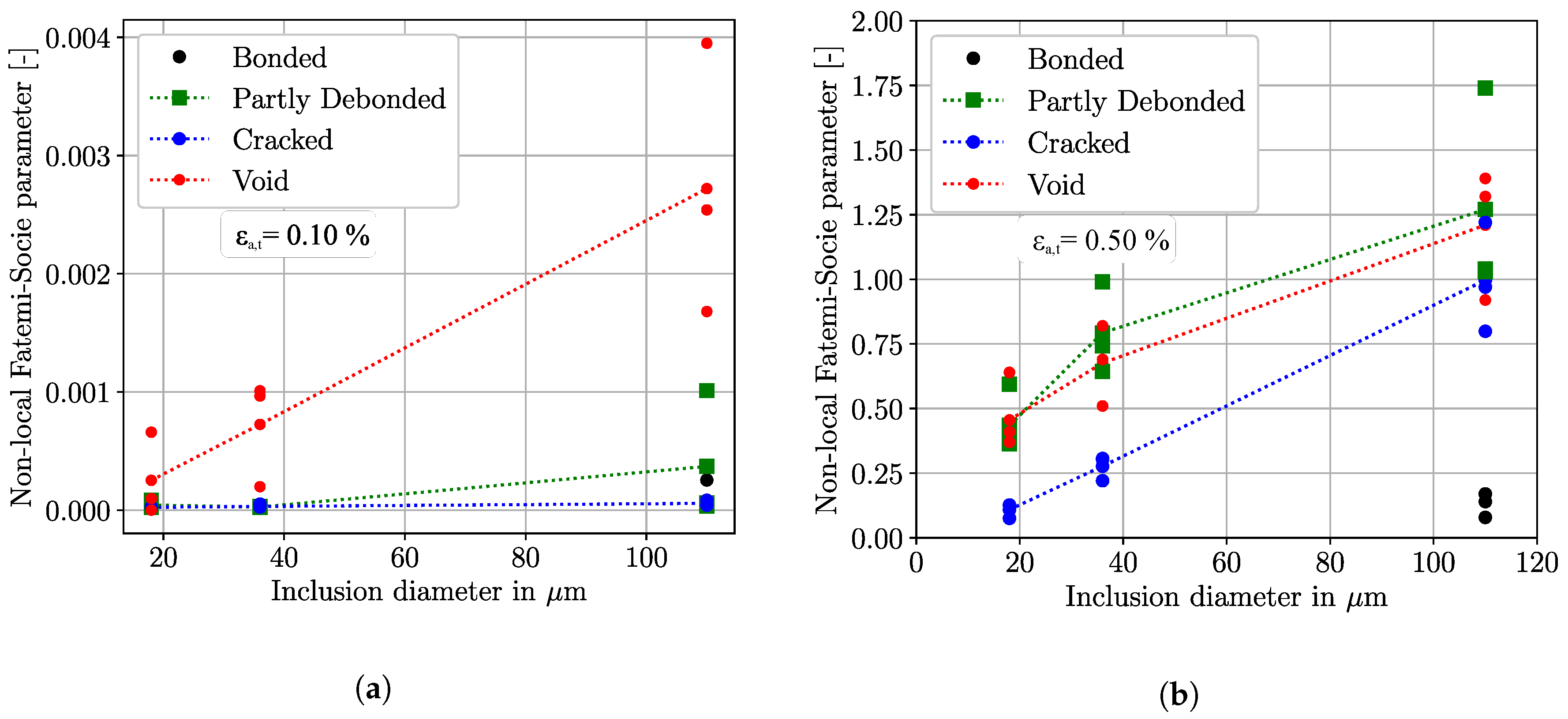
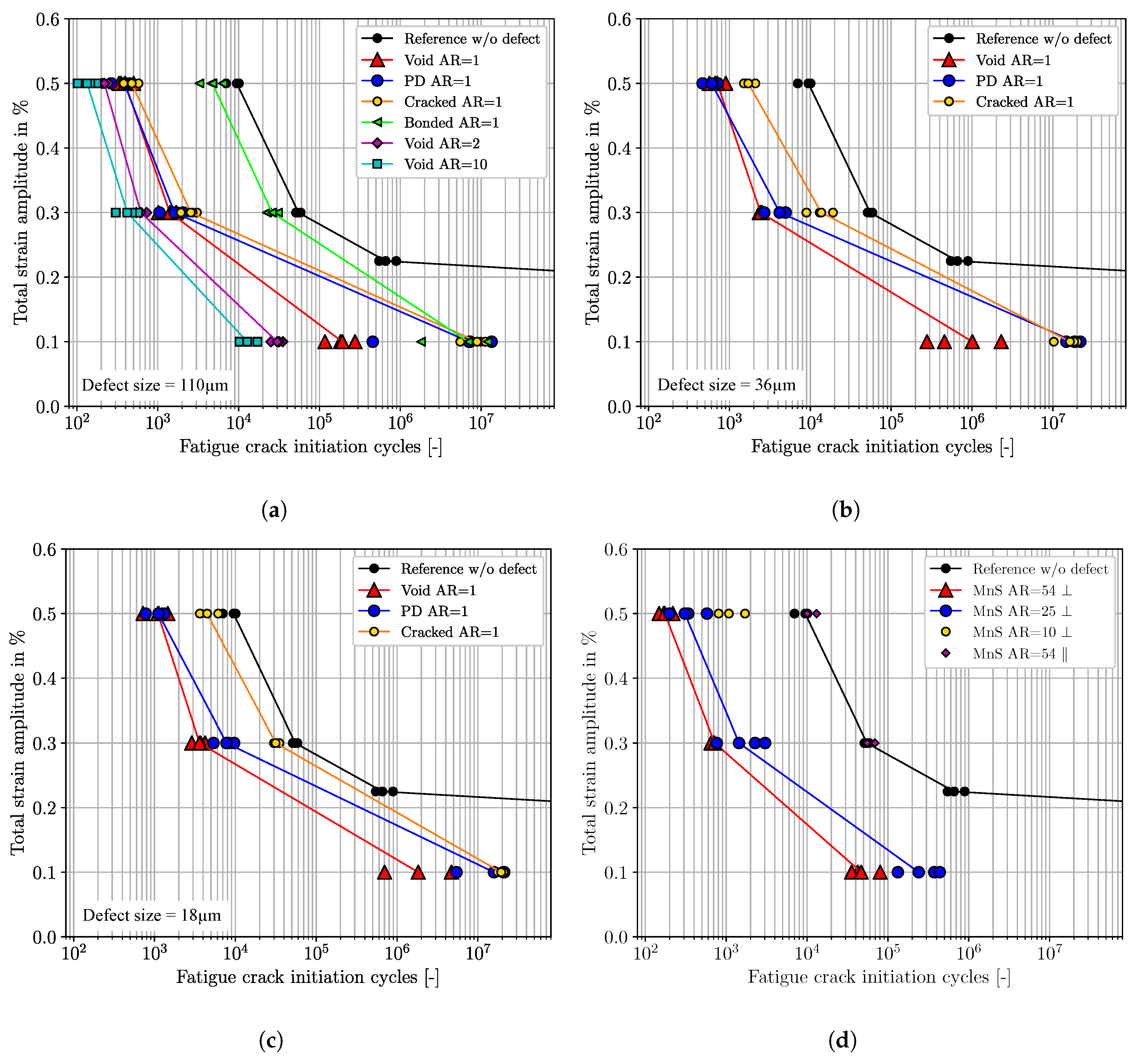
4.4. Influence of Defect Size
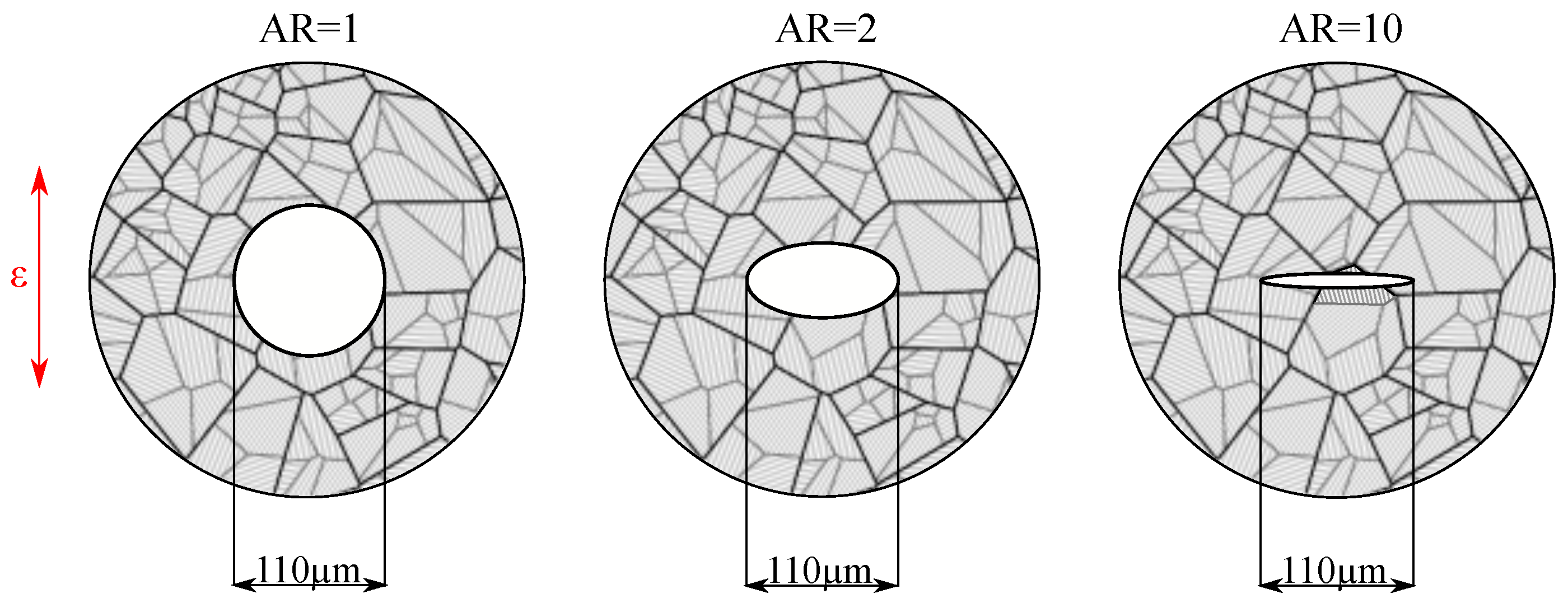
4.5. Influence of Aspect Ratio of Voids
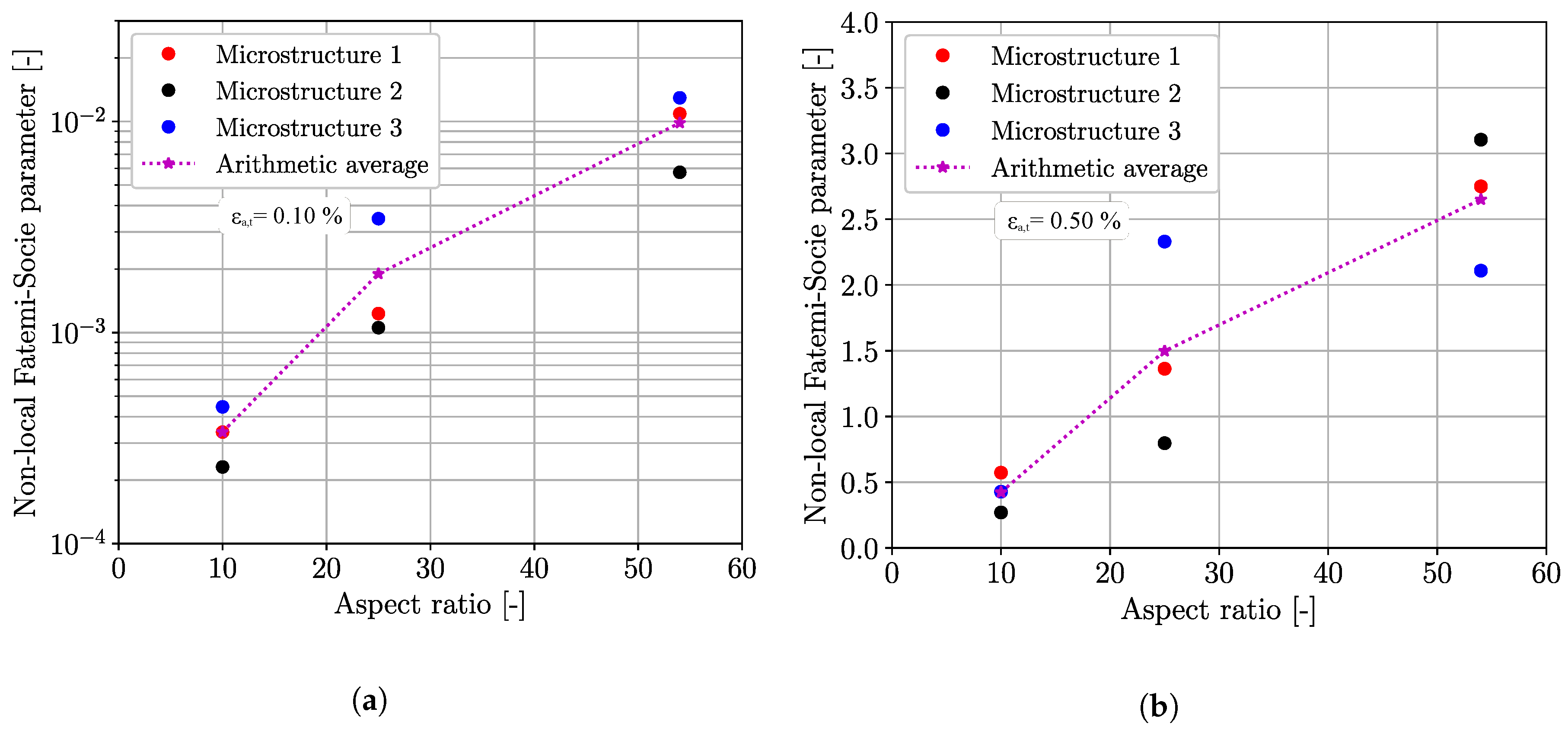
4.6. Influence of Manganese Sulfide Aspect Ratio and Orientation
4.7. Fatigue Crack Initiation Lifetime Results
5. Conclusions
- Residual stresses around oxidic inclusions
- Microstructural variability around defects
- Varying interface properties between non-metallic inclusions and the surrounding matrix
- Defect size
- Defect shape
- Alignment of manganese sulfides to loading axis
- The consideration of the residual stresses around oxidic inclusions due to previous heat treatments result in an increased fatigue crack nucleation potential, in particular for fatigue loading levels close to the elastic regime.
- The local fatigue crack nucleation responses around defects and inclusions depend strongly on the defect size, defect shape, martensitic block size and the crystallographic properties at the hot spot. Therefore, multiple martensitic microstructural realizations were considered in the numerical study to create a certain kind of statistical basis.
- In the present study, voids with increasing aspect ratios represent the most severe defects under fully reversed strain-controlled loading conditions. In particular, for loading levels within the elastic regime, the different inclusion–matrix interface conditions influence the fatigue crack nucleation lives substantially.
- The micromechanical investigations of the manganese sulfide fatigue crack nucleation behavior exhibit an influence of the aspect ratio (size of manganese sulfide) as well as a significant influence of the alignment of the manganese sulfide to the loading axis. These results correlate qualitatively well with the corresponding experimentally observed fracture behavior.
Author Contributions
Funding
Conflicts of Interest
References
- Lewis, A.M.; Kelly, J.C.; Keoleian, G.A. Vehicle lightweighting vs. electrification: Life cycle energy and GHG emissions results for diverse powertrain vehicles. Appl. Energy 2014, 126, 13–20. [Google Scholar] [CrossRef]
- Tervo, H.; Kaijalainen, A.; Pikkarainen, T.; Mehtonen, S.; Porter, D. Effect of impurity level and inclusions on the ductility and toughness of an ultra-high-strength steel. Mater. Sci. Eng. A 2017, 697, 184–193. [Google Scholar] [CrossRef]
- Murakami, Y. Metal Fatigue: Effects of Small Defects and Nonmetallic Inclusions, 1st ed.; Elsevier: Oxford, UK, 2002. [Google Scholar]
- Yang, Z.; Zhang, J.; Li, S.; Li, G.; Wang, Q.; Hui, W.; Weng, Y. On the critical inclusion size of high strength steels under ultra-high cycle fatigue. Mater. Sci. Eng. A 2006, 427, 167–174. [Google Scholar] [CrossRef]
- Klösch, G.; Huemer, K.; Frank, G. Nichtmetallische Einschlüsse in Langprodukten: Entstehung, Bestimmung, Auswirkungen—Ein Überblick. BHM Berg-Und Hüttenmännische Monatshefte 2009, 154, 27–32. [Google Scholar] [CrossRef]
- Krewerth, D.; Lippmann, T.; Weidner, A.; Biermann, H. Influence of non-metallic inclusions on fatigue life in the very high cycle fatigue regime. Int. J. Fatigue 2016, 84, 40–52. [Google Scholar] [CrossRef]
- Juvonen, P. Effects of Non-Metallic Inclusions on Fatigue Properties of Calcium Treated Steels. Ph.D. Thesis, Helsinki University of Technology, Espoo, Finland, 2004. [Google Scholar]
- Tanaka, K.; Mura, T. A theory of fatigue crack initiation at inclusions. Metall. Trans. A 1982, 13, 117–123. [Google Scholar] [CrossRef]
- Sinz, U. Schwingfestigkeit von Common-Rail Komponenten unter Berücksichtigung von seltenen nichtmetallischen Einschlüssen. Ph.D. Thesis, Technische Universität Kaiserslautern, Kaiserslautern, Germany, 2017. [Google Scholar]
- Cyril, N.; Fatemi, A.; Cryderman, B. Effects of Sulfur Level and Anisotropy of Sulfide Inclusions on Tensile, Impact, and Fatigue Properties of SAE 4140 Steel. SAE Int. J. Mater. Manuf. 2009, 1, 218–227. [Google Scholar] [CrossRef]
- Temmel, C.; Ingesten, N.G.; Karlsson, B. Fatigue anisotropy in cross-rolled, hardened medium carbon steel resulting from MnS inclusions. Metall. Mater. Trans. A 2006, 37, 2995–3007. [Google Scholar] [CrossRef]
- Hosseini, S.B.; Temmel, C.; Karlsson, B.; Ingesten, N.G. An In-Situ Scanning Electron Microscopy Study of the Bonding between MnS Inclusions and the Matrix during Tensile Deformation of Hot-Rolled Steels. Metall. Mater. Trans. A 2007, 38, 982–989. [Google Scholar] [CrossRef]
- Maciejewski, J. The Effects of Sulfide Inclusions on Mechanical Properties and Failures of Steel Components. J. Fail. Anal. Prev. 2015, 15, 169–178. [Google Scholar] [CrossRef]
- Åman, M.; Okazaki, S.; Matsunaga, H.; Marquis, G.B.; Remes, H. Interaction effect of adjacent small defects on the fatigue limit of a medium carbon steel. Fatigue Fract. Eng. Mater. Struct. 2017, 40, 130–144. [Google Scholar] [CrossRef]
- Murakami, Y. Effects of Small Defects and Nonmetallic Inclusions on the Fatigue Strength of Metals. JSME Int. J. Ser. 1 Solid Mech. Strength Mater. 1989, 32, 167–180. [Google Scholar] [CrossRef]
- Murakami, Y.; Kodama, S.; Konuma, S. Quantitative evaluation of effects of non-metallic inclusions on fatigue strength of high strength steels. I: Basic fatigue mechanism and evaluation of correlation between the fatigue fracture stress and the size and location of non-metallic inclusions. Int. J. Fatigue 1989, 11, 291–298. [Google Scholar] [CrossRef]
- Zhou, S.; Murakami, Y.; Beretta, S.; Fukushima, Y. Experimental investigation on statistics of extremes for three-dimensional distribution of non-metallic inclusions. Mater. Sci. Technol. 2002, 18, 1535–1543. [Google Scholar] [CrossRef]
- Manonukul, A.; Dunne, F.P.E. High- and low-cycle fatigue crack initiation using polycrystal plasticity. Proc. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 2004, 460, 1881–1903. [Google Scholar] [CrossRef]
- McDowell, D.; Dunne, F. Microstructure-sensitive computational modeling of fatigue crack formation. Int. J. Fatigue 2010, 32, 1521–1542. [Google Scholar] [CrossRef]
- Roters, F.; Eisenlohr, P.; Hantcherli, L.; Tjahjanto, D.; Bieler, T.; Raabe, D. Overview of constitutive laws, kinematics, homogenization and multiscale methods in crystal plasticity finite-element modeling: Theory, experiments, applications. Acta Mater. 2010, 58, 1152–1211. [Google Scholar] [CrossRef]
- Przybyla, C.; Prasannavenkatesan, R.; Salajegheh, N.; McDowell, D.L. Microstructure-sensitive modeling of high cycle fatigue. Int. J. Fatigue 2010, 32, 512–525. [Google Scholar] [CrossRef]
- Shenoy, M.; Zhang, J.; McDowell, D. Estimating fatigue sensitivity to polycrystalline Ni-base superalloy microstructures using a computational approach. Fatigue Fract. Eng. Mater. Struct. 2007, 30, 889–904. [Google Scholar] [CrossRef]
- Cruzado, A.; LLorca, J.; Segurado, J. Modeling cyclic deformation of inconel 718 superalloy by means of crystal plasticity and computational homogenization. Int. J. Solids Struct. 2017, 122–123, 148–161. [Google Scholar] [CrossRef]
- Briffod, F.; Shiraiwa, T.; Enoki, M. Microstructure modeling and crystal plasticity simulations for the evaluation of fatigue crack initiation in alpha-iron specimen including an elliptic defect. Mater. Sci. Eng. A 2017, 695, 165–177. [Google Scholar] [CrossRef]
- Boeff, M.; ul Hassan, H.; Hartmaier, A. Micromechanical modeling of fatigue crack initiation in polycrystals. J. Mater. Res. 2017, 32, 4375–4386. [Google Scholar] [CrossRef]
- Gillner, K.; Münstermann, S. Numerically predicted high cycle fatigue properties through representative volume elements of the microstructure. Int. J. Fatigue 2017, 105, 219–234. [Google Scholar] [CrossRef]
- Briffod, F.; Shiraiwa, T.; Enoki, M. Modeling and Crystal Plasticity Simulations of Lath Martensitic Steel under Fatigue Loading. Mater. Trans. 2018, 60. [Google Scholar] [CrossRef]
- Schäfer, B.J.; Sonnweber-Ribic, P.; ul Hassan, H.; Hartmaier, A. Micromechanical Modelling of the Influence of Strain Ratio on Fatigue Crack Initiation in a Martensitic Steel-A Comparison of Different Fatigue Indicator Parameters. Materials 2019, 12, 2852. [Google Scholar] [CrossRef] [PubMed]
- Brückner-Foit, A.; Huang, X. Numerical simulation of micro-crack initiation of martensitic steel under fatigue loading. Int. J. Fatigue 2006, 28, 963–971. [Google Scholar] [CrossRef]
- Hallberg, H.; Ås, S.K.; Skallerud, B. Crystal plasticity modeling of microstructure influence on fatigue crack initiation in extruded Al6082-T6 with surface irregularities. Int. J. Fatigue 2018, 111, 16–32. [Google Scholar] [CrossRef]
- Castelluccio, G.M.; McDowell, D.L. A mesoscale approach for growth of 3D microstructurally small fatigue cracks in polycrystals. Int. J. Damage Mech. 2014, 23, 791–818. [Google Scholar] [CrossRef]
- Musinski, W.D.; McDowell, D.L. On the eigenstrain application of shot-peened residual stresses within a crystal plasticity framework: Application to Ni-base superalloy specimens. Int. J. Mech. Sci. 2015, 100, 195–208. [Google Scholar] [CrossRef]
- Gallo, P. On the Crack-Tip Region Stress Field in Molecular Systems: The Case of Ideal Brittle Fracture. Adv. Theory Simul. 2019, 2. [Google Scholar] [CrossRef]
- Gallo, P.; Hagiwara, Y.; Shimada, T.; Kitamura, T. Strain energy density approach for brittle fracture from nano to macroscale and breakdown of continuum theory. Theor. Appl. Fract. Mech. 2019, 103. [Google Scholar] [CrossRef]
- Ye, W.; Efthymiadis, P.; Pinna, C.; Ma, A.; Shollock, B.; Dashwood, R. Experimental and modelling study of fatigue crack initiation in an aluminium beam with a hole under 4-point bending. Int. J. Solids Struct. 2018, 138, 87–96. [Google Scholar] [CrossRef]
- Fan, J.; McDowell, D.L.; Horstemeyer, M.F.; Gall, K. Cyclic plasticity at pores and inclusions in cast Al–Si alloys. Eng. Fract. Mech. 2003, 70, 1281–1302. [Google Scholar] [CrossRef]
- Gall, K.; Horstemeyer, M.F.; Degner, B.W.; McDowell, D.L.; Fan, J. On the driving force for fatigue crack formation from inclusions and voids in a cast A356 aluminum alloy. Int. J. Fract. 2001, 108, 207–233. [Google Scholar] [CrossRef]
- Carroll, J.; Brewer, L.; Battaile, C.; Boyce, B.; Emery, J. The effect of grain size on local deformation near a void-like stress concentration. Int. J. Plast. 2012, 39, 46–60. [Google Scholar] [CrossRef]
- Battaile, C.C.; Emery, J.M.; Brewer, L.N.; Boyce, B.L. Crystal plasticity simulations of microstructure-induced uncertainty in strain concentration near voids in brass. Philos. Mag. 2015, 95, 1069–1079. [Google Scholar] [CrossRef]
- Gillner, K.; Henrich, M.; Münstermann, S. Numerical study of inclusion parameters and their influence on fatigue lifetime. Int. J. Fatigue 2018, 111, 70–80. [Google Scholar] [CrossRef]
- Prasannavenkatesan, R.; Przybyla, C.P.; Salajegheh, N.; McDowell, D. Simulated extreme value fatigue sensitivity to inclusions and pores in martensitic gear steels. Eng. Fract. Mech. 2011, 78, 1140–1155. [Google Scholar] [CrossRef]
- Salajegheh, N. Microstructure-Sensitive Weighted Probability Approach for Modeling Surface to Bulk Transition of High Cycle Fatigue Failures Dominated by Primary Inclusions. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, Georgia, 2011. [Google Scholar]
- Prithivirajan, V.; Sangid, M.D. The role of defects and critical pore size analysis in the fatigue response of additively manufactured IN718 via crystal plasticity. Mater. Des. 2018, 150, 139–153. [Google Scholar] [CrossRef]
- Bandyopadhyay, R.; Sangid, M.D. Crystal plasticity assessment of inclusion- and matrix-driven competing failure modes in a nickel-base superalloy. Acta Mater. 2019, 177, 20–34. [Google Scholar] [CrossRef]
- Gu, C.; Lian, J.; Bao, Y.; Münstermann, S. Microstructure-based fatigue modelling with residual stresses: Prediction of the microcrack initiation around inclusions. Mater. Sci. Eng. A 2019, 751, 133–141. [Google Scholar] [CrossRef]
- Clark, B.; Castelluccio, G.; Reiterer, M.; McDowell, D.; Neu, R. Microstructure-sensitive fatigue modelling of medical-grade fine wire. Fatigue Fract. Eng. Mater. Struct. 2019, 42, 152–165. [Google Scholar] [CrossRef]
- Zhang, T.; Jiang, J.; Britton, B.; Shollock, B.; Dunne, F. Crack nucleation using combined crystal plasticity modelling, high-resolution digital image correlation and high-resolution electron backscatter diffraction in a superalloy containing non-metallic inclusions under fatigue. Proc. R. Soc. A Math. Phys. Eng. Sci. 2016, 472, 20150792. [Google Scholar] [CrossRef] [PubMed]
- Naragani, D.; Sangid, M.D.; Shade, P.A.; Schuren, J.C.; Sharma, H.; Park, J.S.; Kenesei, P.; Bernier, J.V.; Turner, T.J.; Parr, I. Investigation of fatigue crack initiation from a non-metallic inclusion via high energy x-ray diffraction microscopy. Acta Mater. 2017, 137, 71–84. [Google Scholar] [CrossRef]
- Schäfer, B.J.; Song, X.; Sonnweber-Ribic, P.; ul Hassan, H.; Hartmaier, A. Micromechanical Modelling of the Cyclic Deformation Behavior of Martensitic SAE 4150—A Comparison of Different Kinematic Hardening Models. Metals 2019, 9, 368. [Google Scholar] [CrossRef]
- Kitahara, H.; Ueji, R.; Tsuji, N.; Minamino, Y. Crystallographic features of lath martensite in low-carbon steel. Acta Mater. 2006, 54, 1279–1288. [Google Scholar] [CrossRef]
- Morito, S.; Tanaka, H.; Konishi, R.; Furuhara, T.; Maki, T. The morphology and crystallography of lath martensite in Fe-C alloys. Acta Mater. 2003, 51, 1789–1799. [Google Scholar] [CrossRef]
- Cayron, C. ARPGE: A computer program to automatically reconstruct the parent grains from electron backscatter diffraction data. J. Appl. Crystallogr. 2007, 40, 1183–1188. [Google Scholar] [CrossRef]
- Kitahara, H.; Ueji, R.; Ueda, M.; Tsuji, N.; Minamino, Y. Crystallographic analysis of plate martensite in Fe—28.5 at. % Ni by FE-SEM/EBSD. Mater. Charact. 2005, 54, 378–386. [Google Scholar] [CrossRef]
- Murakami, Y. Inclusion Rating by Statistics of Extreme Values and Its Application to Fatigue Strength Prediction and Quality Control of Materials. J. Res. Natl. Inst. Stand. Technol. 1994, 99, 345–351. [Google Scholar] [CrossRef]
- Sandström, R.; Karlsson, L. Transfer of two dimensional inclusion size distribution to three dimensions. In Proceedings of the Swedish Symposium on Non-Metallic Inclusions in Steel, Uddeholm, Sweden, 27–29 April 1981; pp. 242–268. [Google Scholar]
- Anderson, C.; Shi, G.; Atkinson, H.; Sellars, C. The precision of methods using the statistics of extremes for the estimation of the maximum size of inclusions in clean steels. Acta Mater. 2000, 48, 4235–4246. [Google Scholar] [CrossRef]
- Spriestersbach, D.; Grad, P.; Kerscher, E. Influence of different non-metallic inclusion types on the crack initiation in high-strength steels in the VHCF regime. Int. J. Fatigue 2014, 64, 114–120. [Google Scholar] [CrossRef]
- Dassault Systèmes. Abaqus Documentation; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Lu, S.; Pister, K. Decomposition of deformation and representation of the free energy function for isotropic thermoelastic solids. Int. J. Solids Struct. 1975, 11, 927–934. [Google Scholar] [CrossRef]
- Lee, E.H. Elastic-plastic deformation at finite strains. J. Appl. Mech. 1969, 36, 1–6. [Google Scholar] [CrossRef]
- Sherby, O.D.; Wadsworth, J.; Lesuer, D.R.; Syn, C.K. Revisiting the Structure of Martensite in Iron-Carbon Steels. Mater. Trans. 2008, 49, 2016–2027. [Google Scholar] [CrossRef]
- Michiuchi, M.; Nambu, S.; Ishimoto, Y.; Inoue, J.; Koseki, T. Relationship between local deformation behavior and crystallographic features of as-quenched lath martensite during uniaxial tensile deformation. Acta Mater. 2009, 57, 5283–5291. [Google Scholar] [CrossRef]
- Rice, J. Inelastic constitutive relations for solids: An internal-variable theory and its application to metal plasticity. J. Mech. Phys. Solids 1971, 19, 433–455. [Google Scholar] [CrossRef]
- Hutchinson, J.W. Bounds and self-consistent estimates for creep of polycrystalline materials. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1976, 348, 101–127. [Google Scholar] [CrossRef]
- Peirce, D.; Asaro, R.; Needleman, A. Material rate dependence and localized deformation in crystalline solids. Acta Metall. 1983, 31, 1951–1976. [Google Scholar] [CrossRef]
- Ohno, N.; Wang, J.D. Kinematic hardening rules with critical state of dynamic recovery, part I: Formulation and basic features for ratchetting behavior. Int. J. Plast. 1993, 9, 375–390. [Google Scholar] [CrossRef]
- Lubarda, V.A. Constitutive theories based on the multiplicative decomposition of deformation gradient: Thermoelasticity, elastoplasticity, and biomechanics. Const. Theor. Based Mult. Decompos. Deform. Gradient Thermoelast. Elastoplast. Biomech. 2004, 57, 95–108. [Google Scholar] [CrossRef]
- Vujosevic, L.; Lubarda, V.A. Finite-strain thermo elasticity based on multiplicative decomposition of deformation gradient. Theor. Appl. Mech. 2002, 28–29, 379–399. [Google Scholar] [CrossRef]
- Sweeney, C.; Dunne, F.; McHugh, P.; Leen, S. Micro-scale testing and micromechanical modelling for high cycle fatigue of CoCr stent material. J. Mech. Behav. Biomed. Mater. 2015, 46, 244–260. [Google Scholar] [CrossRef] [PubMed]
- Fatemi, A.; Socie, D.F. A critical plane approach to multiaxial fatigue damage including ou-of-phase loading. Fatigue Fract. Eng. Mater. Struct. 1988, 11, 149165. [Google Scholar] [CrossRef]
- Pineau, A.; Forest, S. Effects of inclusions on the very high cycle fatigue behaviour of steels. Fatigue Fract. Eng. Mater. Struct. 2017, 40, 1694–1707. [Google Scholar] [CrossRef]
- Kitagawa, H.; Takahashi, S. Applicability of fracture mechanics to very small cracks or cracks in the early stage. In Proceedings of the second international conference on mechanical behavior of materials, Boston, MA, USA, 16–20 August 1976; pp. 627–631. [Google Scholar]

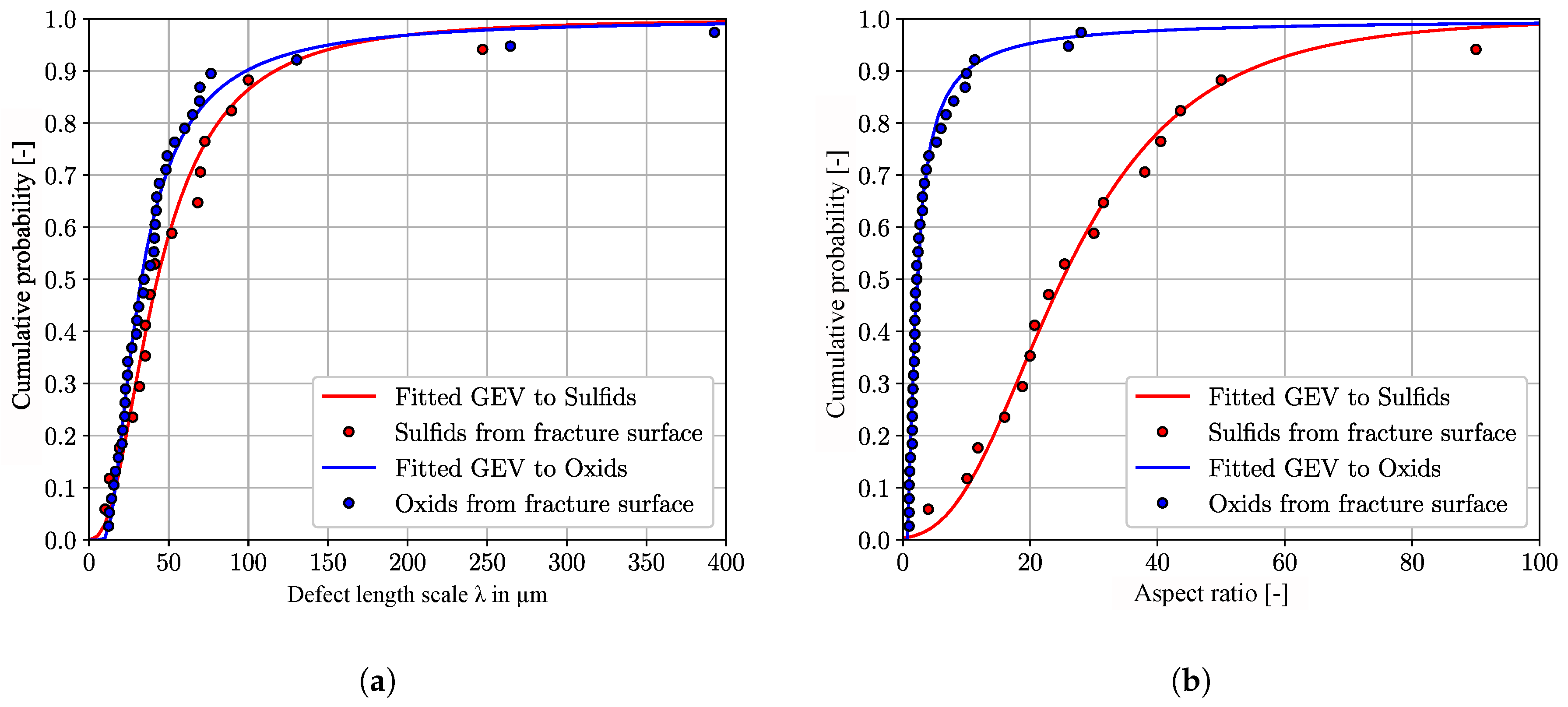

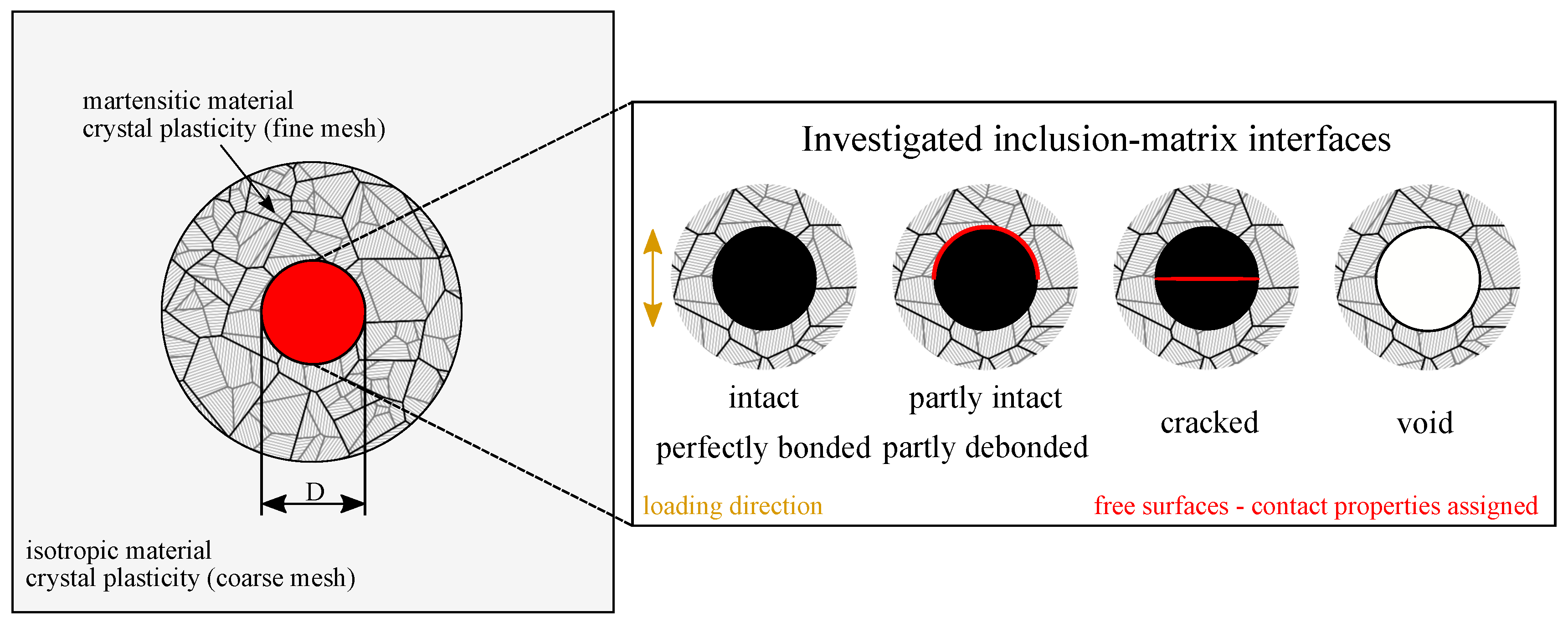

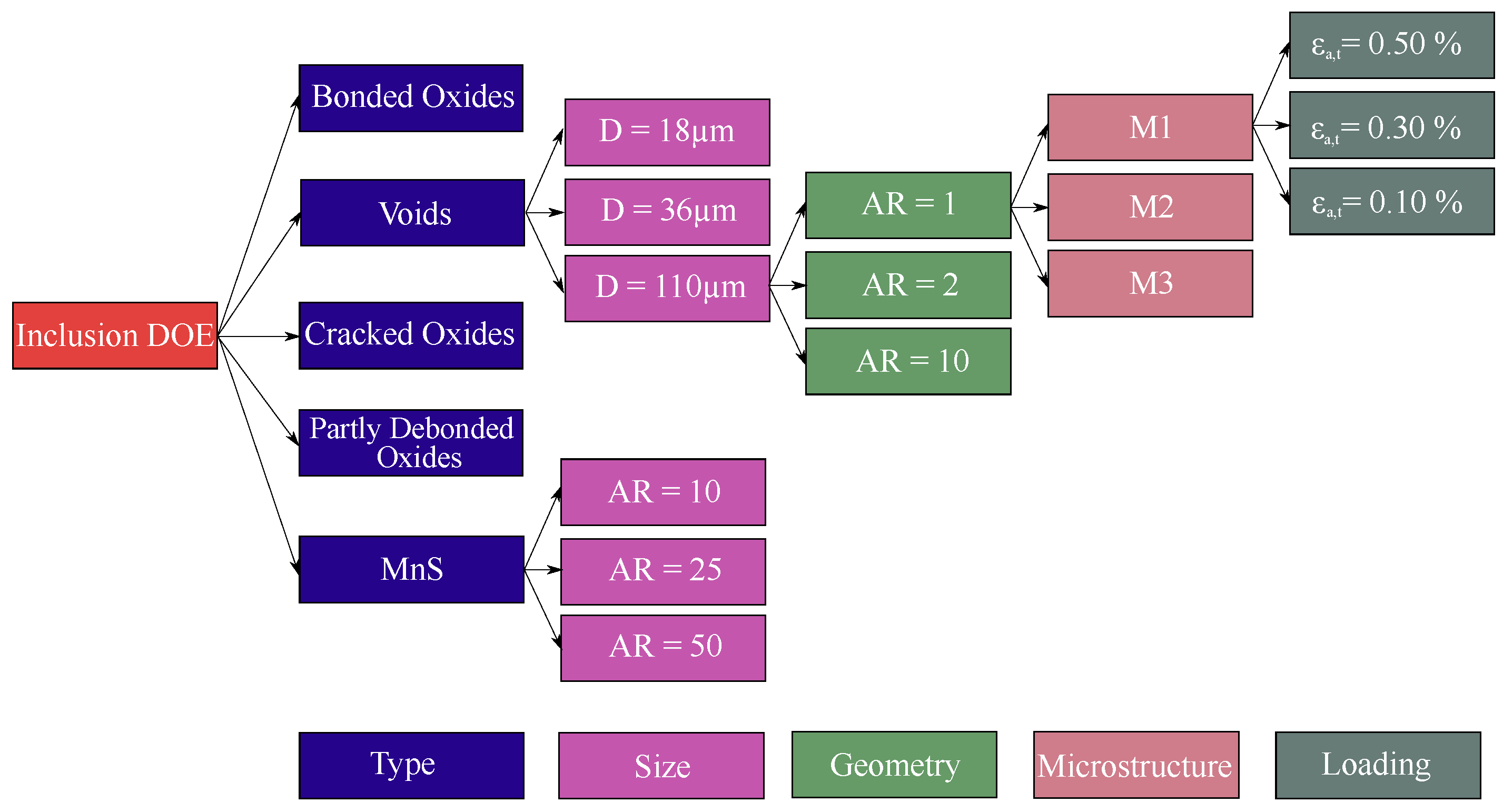

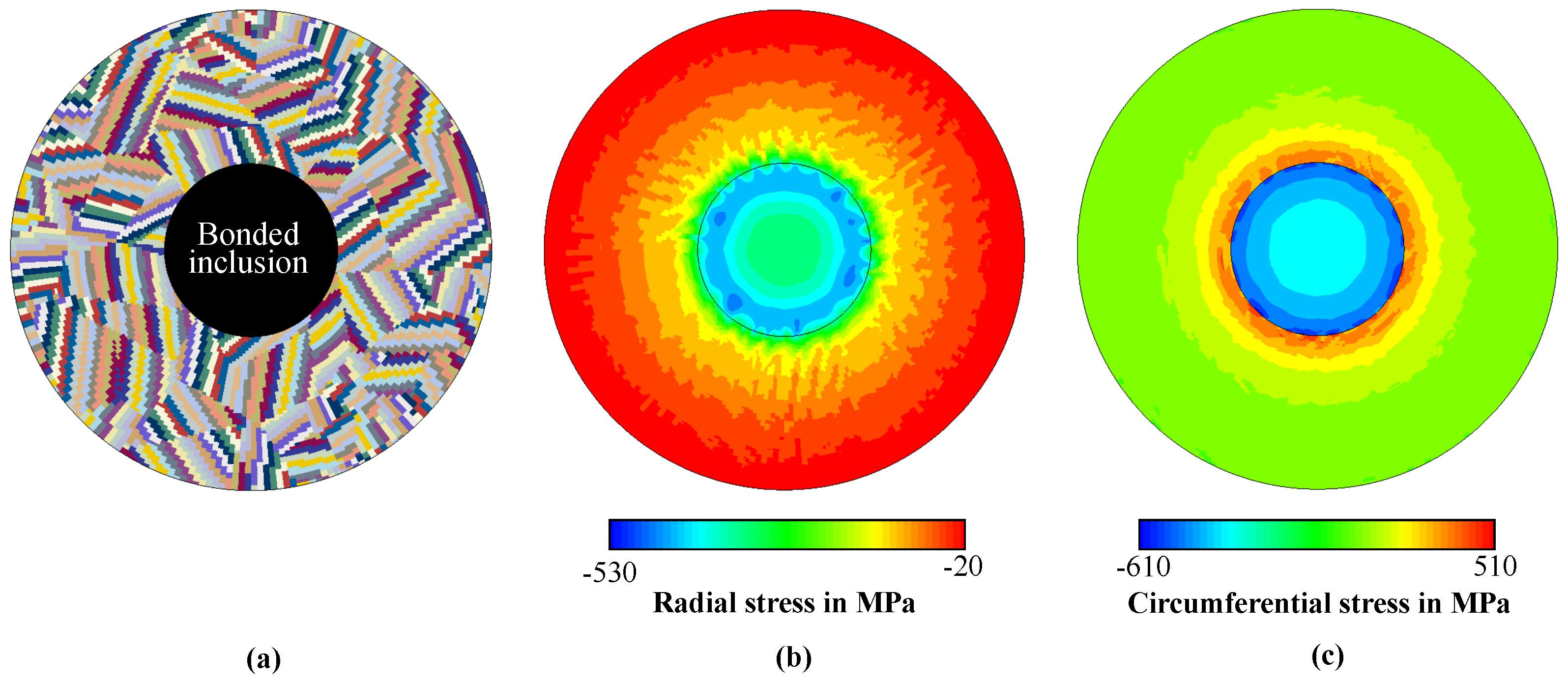



| Material | C | Si | Mn | P | S | Cr | Mo |
|---|---|---|---|---|---|---|---|
| SAE 4150 | 0.52 | 0.26 | 0.74 | 0.014 | 0.008 | 1.31 | 0.18 |
| Cumulative Probability | Oxidic Non-Metallic Inclusions | Sulfidic Non-Metallic Inclusions | ||||
|---|---|---|---|---|---|---|
| P = 10% | P = 50% | P = 90% | P = 10% | P = 50% | P = 90% | |
| Defect length scale λ in μm | 16 | 32 | 97 | 16 | 43 | 116 |
| Diameter in μm | 18 | 36.2 | 110 | - | - | - |
| Aspect ratio [-] | 1.2 | 2.2 | 10 | 10 | 25 | 54 |
| Chemical Composition | Young’s Modulus E | Poisson’s Ratio ν | Coefficient of Thermal Expansion |
|---|---|---|---|
| Al2O3 | 389 GPa | 0.25 | 8.0 × 1/K |
| MnS | 69 GPa | 0.30 | 18.1 × 1/K |
| Steel Matrix | - | - | 12.5 × 1/K |
| Elastic Constants | Flow Rule Parameters | Kinematic Hardening Parameters | |||
|---|---|---|---|---|---|
| 253.1 GPa | 0.001 s | A | 65.506 GPa | ||
| 132.4 GPa | 209 MPa | B | 499 | ||
| 75.8 GPa | m | 100 | M | 8 | |
| Strain Amplitude | D = 110 m | D = 36 m | D = 18 m |
|---|---|---|---|
| 0.10% | 2.35 | 5.10 | 1.98 × |
| 0.30% | 1.66 | 1.08 | 1.46 |
| 0.50% | 1.52 | 1.60 | 2.02 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schäfer, B.J.; Sonnweber-Ribic, P.; ul Hassan, H.; Hartmaier, A. Micromechanical Modeling of Fatigue Crack Nucleation around Non-Metallic Inclusions in Martensitic High-Strength Steels. Metals 2019, 9, 1258. https://doi.org/10.3390/met9121258
Schäfer BJ, Sonnweber-Ribic P, ul Hassan H, Hartmaier A. Micromechanical Modeling of Fatigue Crack Nucleation around Non-Metallic Inclusions in Martensitic High-Strength Steels. Metals. 2019; 9(12):1258. https://doi.org/10.3390/met9121258
Chicago/Turabian StyleSchäfer, Benjamin Josef, Petra Sonnweber-Ribic, Hamad ul Hassan, and Alexander Hartmaier. 2019. "Micromechanical Modeling of Fatigue Crack Nucleation around Non-Metallic Inclusions in Martensitic High-Strength Steels" Metals 9, no. 12: 1258. https://doi.org/10.3390/met9121258
APA StyleSchäfer, B. J., Sonnweber-Ribic, P., ul Hassan, H., & Hartmaier, A. (2019). Micromechanical Modeling of Fatigue Crack Nucleation around Non-Metallic Inclusions in Martensitic High-Strength Steels. Metals, 9(12), 1258. https://doi.org/10.3390/met9121258






