A Study on the Zener-Holloman Parameter and Fracture Toughness of an Nb-Particles-Toughened TiAl-Nb Alloy
Abstract
:1. Introduction
2. Experimental
3. Results
3.1. Starting Microstructure
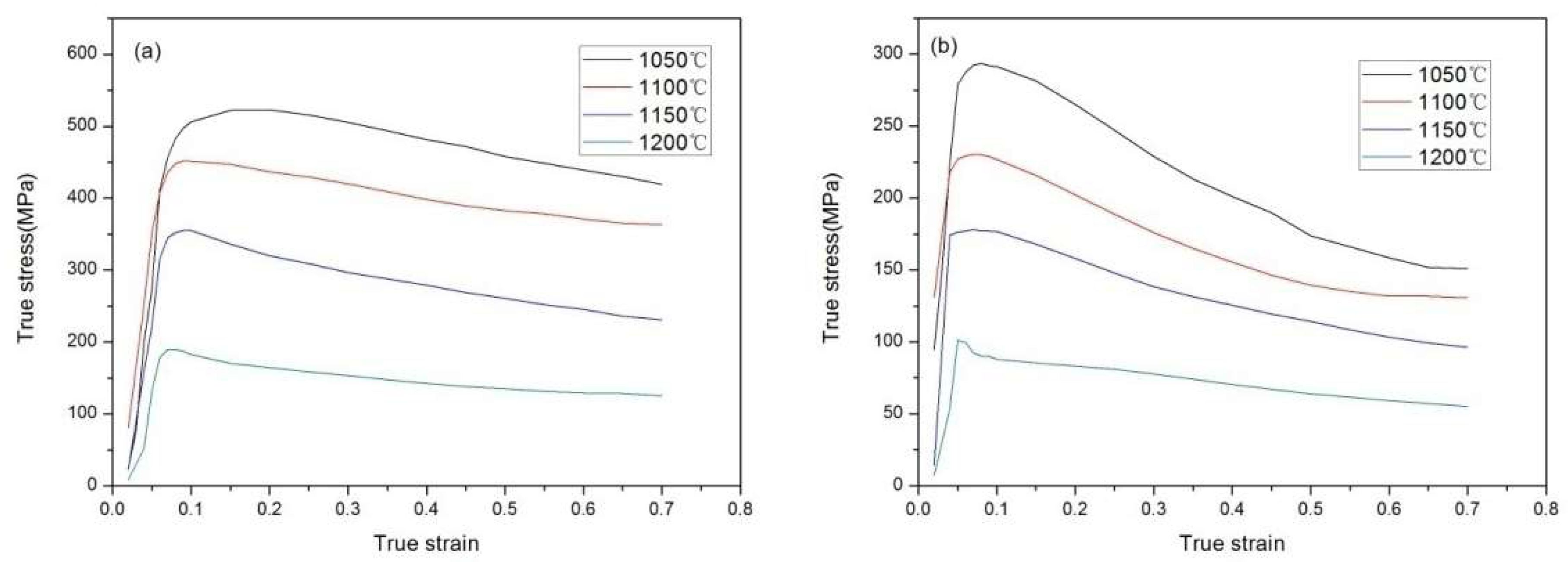
3.2. Deformation Behavior
3.3. Tensile Tests
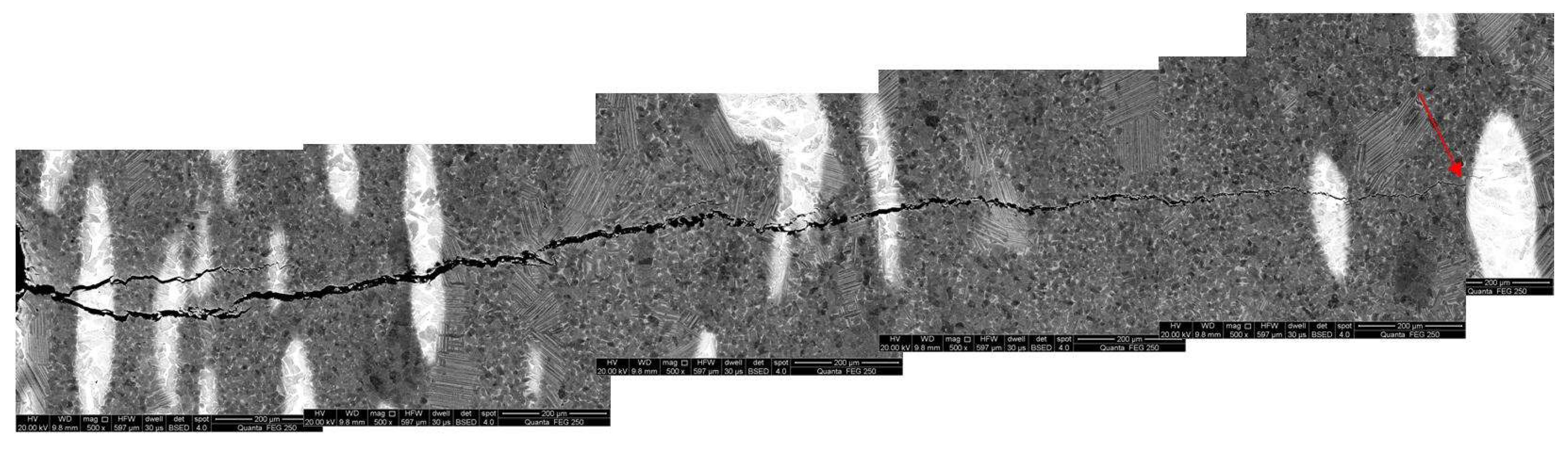
3.4. Bending Tests
4. Discussions
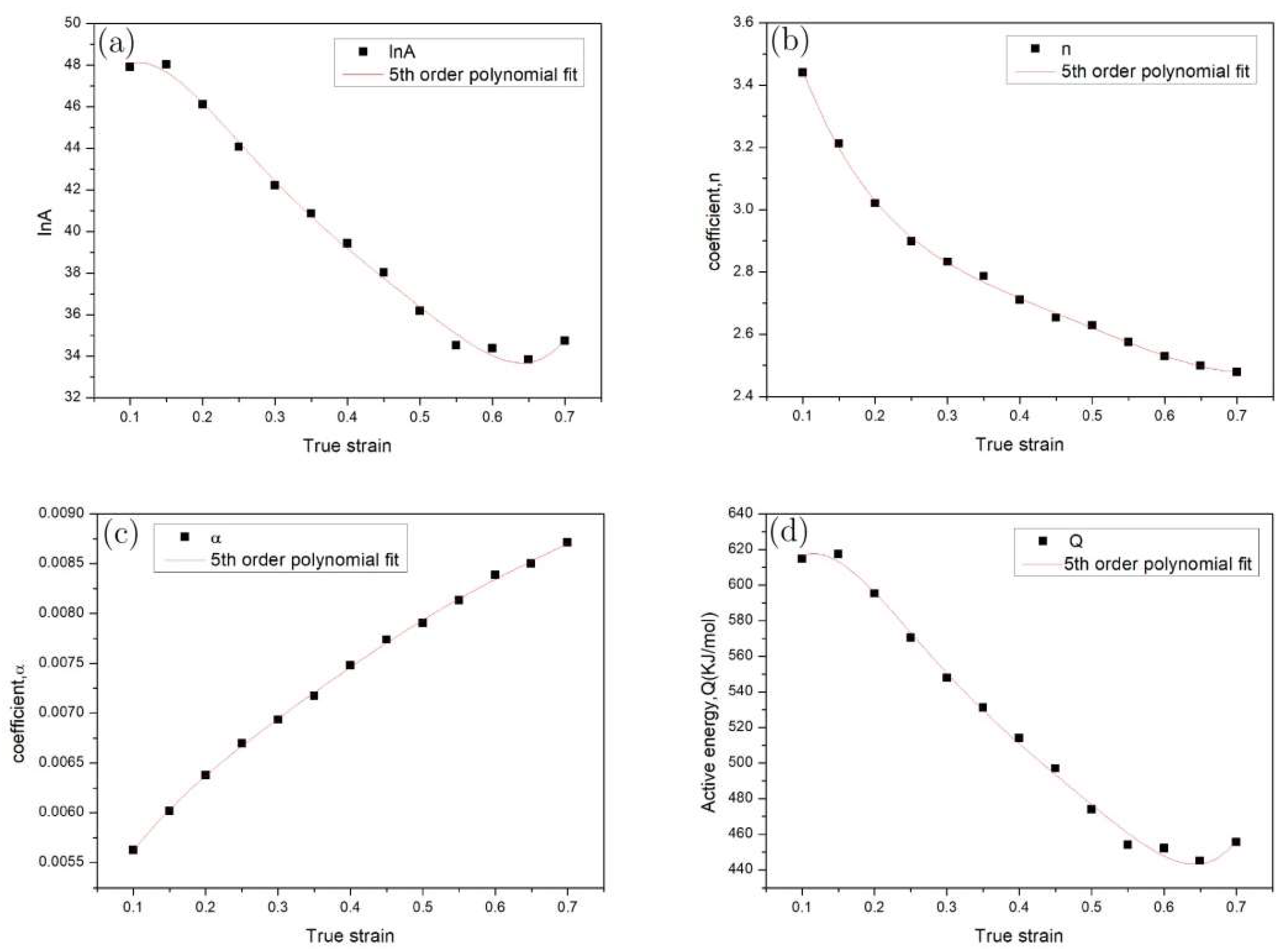
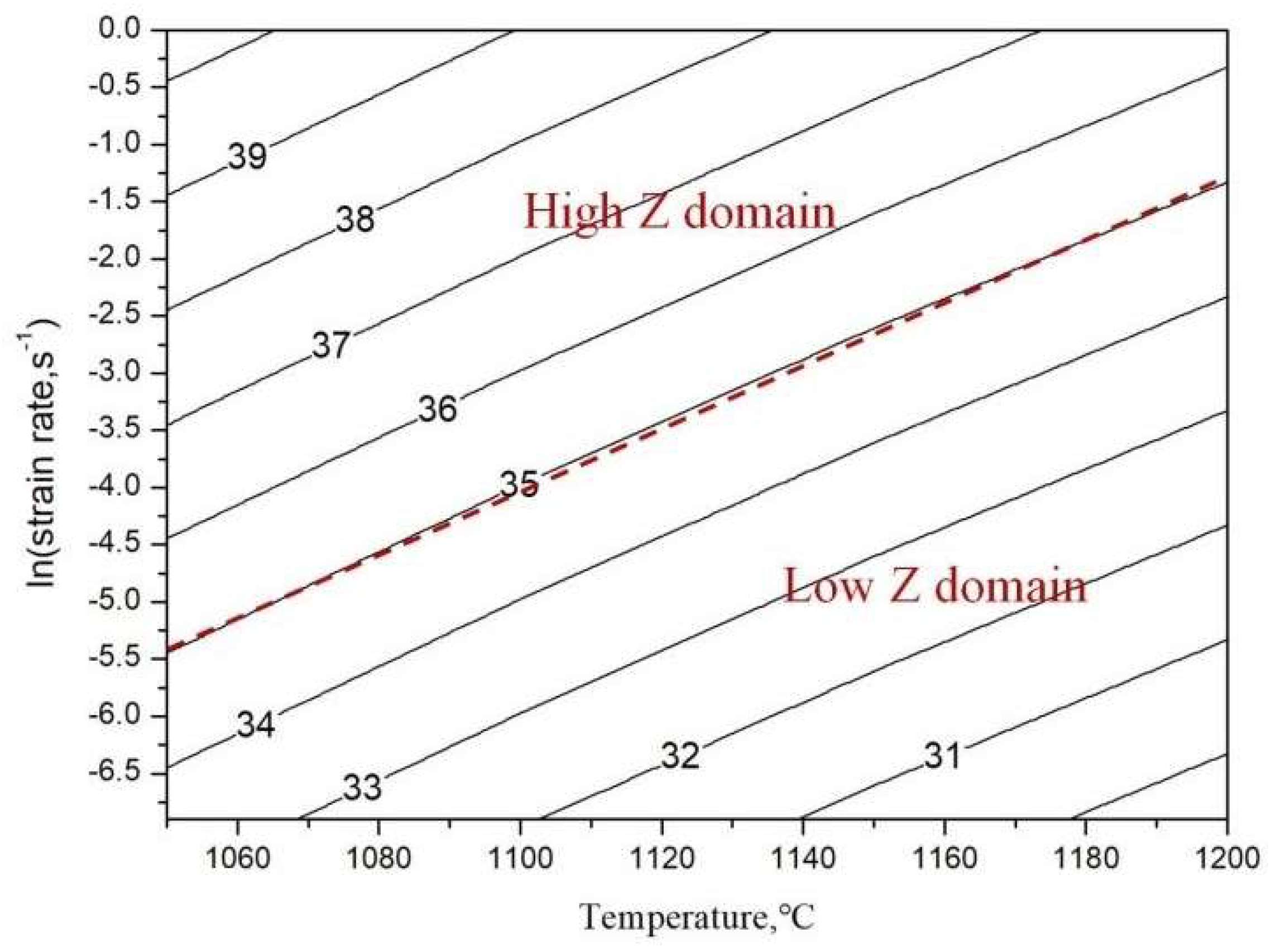
4.1. Effect of Zener-Holloman Parameter on Hot Deformation Mechanism
4.2. Effect of Nb Particles on Fracture Toughness Mechanism
4.3. Prediction of KIC
5. Conclusions
- (1)
- The Zener-Hollomon parameter can affect the hot deformation mechanism significantly. At a high Z condition, Nb particles played an important role in coordinating the deformation. At a low Z condition, deformation of Nb particles accompanied by dynamic recrystallization (DRX) became the dominant softening mechanism.
- (2)
- For the notched 3PB-tested Nb-particles-toughened high-Nb-containing γ-TiAl alloy with DP specimen, the fracture toughness was almost not affected by the loading rate, with a peak fracture toughness of about 12.9 MPa·m1/2.
- (3)
- The toughness of the TiAl alloy with a duplex microstructure can be improved by reinforcing it with ductile Nb particles. Nb particles can retard crack propagation and crack branching and crack deflection can further contribute to toughening.
- (4)
- The fracture toughness prediction model based on the Griffith-Orowan-Irwin relation is quite suitable for predicting the facture toughness of the Nb-particles-toughened DP specimen using tensile properties.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Clemens, H.; Mayer, S. Design, processing, microstructure, and applications of advanced intermetallic TiAl alloys. Adv. Eng. Mater. 2013, 15, 191–215. [Google Scholar] [CrossRef]
- Kunal, K.; Ramachandran, R.; Norman, M.W. Advances in gamma titanium aluminides and their manufacturing techniques. Prog. Mater. Sci. 2012, 55, 1–16. [Google Scholar]
- Liss, K.D.; Funakoshi, K.I.; Dippenaar, R.J.; Higo, Y.; Shiro, A.; Reid, M.; Suzuki, H.; Shobu, T.; Akita, K. Hydrostatic compression behavior and high-pressure stabilized β-phase in γ-based titanium aluminide intermetallics. Metals 2016, 6, 165. [Google Scholar] [CrossRef]
- Xiang, L.; Tang, B.; Xue, X.Y.; Kou, H.C.; Li, J.S. Characteristics of the dynamic recrystallization behavior of Ti-45Al-8.5Nb-0.2W-0.2B-0.3Y alloy during high temperature deformation. Metals 2017, 7, 261. [Google Scholar] [CrossRef]
- Ding, J.; Lin, J.P.; Zhang, M.H.; Dong, C.L.; Liang, Y.F. High-temperature torsion induced gradient microstructures in high Nb-TiAl alloy. Mater. Lett. 2017, 209, 193–196. [Google Scholar] [CrossRef]
- He, W.W.; Liu, Y.; Tang, H.P.; Li, Y.P.; Liu, B.; Liang, X.P.; Xi, Z.P. Microstructural characteristics and densification behavior of high-Nb TiAl powder produced by plasma rotating electrode process. Mater. Des. 2017, 132, 275–282. [Google Scholar] [CrossRef]
- Wu, Z.E.; Hu, R.; Zhang, T.B.; Zhou, H.; Li, J.S. Moisture induced environmental embrittlement of a high Nb containing TiAl alloy. Mater. Sci. Eng. A 2017, 701, 214–220. [Google Scholar] [CrossRef]
- Djanarthany, S.; Viala, J.C.; Bouix, J. Development of SiC/TiAl composites: Processing and interfacial phenomena. J. Mater. Sci. Eng. A 2001, 300, 211–218. [Google Scholar] [CrossRef]
- Liu, Y.X.; Wang, F.; Zhu, J.F.; Wang, X.F. Mechanical properties and microstructure of Al2O3/TiAl in situ composites doped with Cr2O3. Mater. Sci. Eng. A 2011, 528, 3337–3341. [Google Scholar]
- Lapin, M.; Štamborská, T.; Pelachová, O. Fracture behaviour of cast in-situ TiAl matrix composite reinforced with carbide particles. J. Mater. Sci. Eng. A 2018, 721, 1–7. [Google Scholar] [CrossRef]
- Rao, K.P.; Zhou, J.B. Characterization and mechanical properties of in situ synthesized Ti5Si3/TiAl composites. Mater. Sci. Eng. A 2003, 356, 208–218. [Google Scholar] [CrossRef]
- Hu, D. Effect of boron addition on tensile ductility in lamellar TiAl alloys. Intermetallics 2002, 10, 851–858. [Google Scholar] [CrossRef]
- Heredia, F.E.; He, M.Y.; Lucas, G.E.; Evans, A.G.; Deve, H.E.; Konitzer, D. The fracture resistance of directionally solidified dual–phase NiAl reinforced with refractory metals. Acta Metall. Mater. 1993, 41, 505–511. [Google Scholar] [CrossRef]
- Krstic, V.D. On the fracture of brittle–matrix/ductile–particle composites. Philos. Mag. A 1983, 48, 695–708. [Google Scholar] [CrossRef]
- Sun, X.; Yeomans, J.A. Ductile phase toughened brittle materials. J. Mater. Sci. Technol. 1996, 12, 124–134. [Google Scholar]
- Yang, X.; Xi, Z.P.; Liu, Y.; Tang, H.P.; Hu, K.; Jia, W.P. Microstructure and fracture toughness of a TiAl−Nb composite consolidated by spark plasma sintering. Trans. Nonferr. Met. Soc. China 2012, 22, 2628–2632. [Google Scholar] [CrossRef]
- Chen, Y.Y.; Niu, H.Z.; Kong, F.T.; Xiao, S.L. Microstructure and fracture toughness of a β phase containing TiAl alloy. Intermetallics 2011, 19, 1405–1410. [Google Scholar] [CrossRef]
- Rao, K.T.V.; Odette, G.R.; Ritchie, R.O. Ductile-reinforcement toughening in γ-TiAl intermetallic-matrix composites: Effects on fracture toughness and fatigue-crack propagation resistance. Acta Metall. Mater. 1994, 42, 893–911. [Google Scholar]
- Yoo, M.H.; Fu, C.L. Cleavage fracture of ordered intermetallic alloys. Mater. Sci. Eng. A 1992, 153, 470–478. [Google Scholar] [CrossRef]
- Li, J.B.; Liu, Y.; Liu, B.; Wang, Y.; Zhao, K.; He, Y.H. Effect of Nb particles on the flow behavior of TiAl alloy. Intermetallics 2014, 46, 22–28. [Google Scholar] [CrossRef]
- Sellars, C.M. Proceedings of the International Conference on Mathematical Modelling of Hot Rolling of Steel; Yue, S., Ed.; CIMM: Hamilton, ON, USA, 1990. [Google Scholar]
- Wang, L.; Liu, Y.; Zhang, W.; Wang, H.; Li, Q. Optimization of pack parameters for hot deformation of TiAl alloys. Intermetallics 2011, 19, 68–74. [Google Scholar] [CrossRef]
- Cao, R.; Lei, M.X.; Chen, J.H.; Zhang, J. Effects of loading rate on damage and fracture behavior of TiAl alloys. Mater. Sci. Eng. A 2007, 465, 183–193. [Google Scholar] [CrossRef]
- Nicolas, B.; Frédéric, D.; Russell, G.; Andreas, M. Fracture of convoluted and lamellar α2 + γ TiAl alloys. Intermetallics 2012, 22, 176–188. [Google Scholar]
- Gupta, R.K.; Narayana Murtya, S.V.S.; Panta, B.; Agarwalab, V.J.Y.; Sinha, P.P. Constitutive modeling and processing map for elevated temperature flow behaviors of a powder metallurgy titanium aluminide alloy. Mater. Sci. Eng. A 2012, 551, 169–186. [Google Scholar] [CrossRef]
- Kong, F.T.; Chen, Y.Y.; Zhang, D.L.; Zhang, S.Z. High temperature deformation behavior of Ti-46Al-2Cr-4Nb-0.2Y alloy. Mater. Sci. Eng. A 2012, 539, 107–114. [Google Scholar] [CrossRef]
- Marketza, W.T.; Fischera, F.D.; Clemens, H. Deformation mechanisms in TiAl intermetallics–experiments and modeling. Int. J. Plast. 2003, 19, 281–321. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Y.; Yang, G.Y.; Li, J.B.; Liu, B.; Wang, J.W.; Li, H.Z. Hot deformation behaviors of β phase containing Ti-43Al-4Nb-1.4W-based alloy. Mater. Sci. Eng. A 2013, 577, 210–217. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, C.; Liu, Y.; Zhao, S.X.; Li, J.B. Microstructure characterization and mechanical properties of TiAl-based alloys prepared by mechanical milling and spark plasma sintering. Mater. Charact. 2017, 128, 75–84. [Google Scholar] [CrossRef]
- Song, L.; Xu, X.J.; You, L.; Liang, Y.F.; Lin, J.P. Phase transformation and decomposition mechanisms of the βo(ω) phase in cast high Nb containing TiAl alloy. J. Alloys Compd. 2014, 616, 483–491. [Google Scholar] [CrossRef]
- Liu, B.; Liu, Y.; Li, Y.P.; Zhang, W.; Chiba, A. Thermomechanical characterization of β-stabilized Ti-45Al-7Nb-0.4W-0.15B alloy. Intermetallics 2011, 19, 1184–1190. [Google Scholar] [CrossRef]
- Li, J.B.; Liu, Y.; Wang, Y.; Liu, B.; He, Y.H. Dynamic recrystallization behavior of an as-cast TiAl alloy during hot compression. Mater. Charact. 2014, 97, 169–177. [Google Scholar] [CrossRef]
- Appel, F.; Paul, J.D.H.; Oehring, M. Gamma Titanium Aluminide Alloys—Science and Technology; Wiley VCH: Weinheim, Germany, 2011. [Google Scholar]
- Makhutov, N.A.; Matvienko, Y.G. Griffith theory and development of fracture mechanics criteria. Mater. Sci. 1993, 29, 316–319. [Google Scholar] [CrossRef]
- Zheng, Y.P.; Zeng, W.D.; Li, D.; Zhao, Q.Y.; Liang, X.B.; Zhang, J.W.; Ma, X. Fracture toughness of the bimodal size lamellar O phase microstructures in Ti-22Al-25Nb (at. %) orthorhombic alloy. J. Alloys Compd. 2017, 709, 511–518. [Google Scholar] [CrossRef]
- Boehlert, C.J. The tensile behavior of Ti-Al-NbO + Bcc Orthorhombic alloys. Metall. Mater. Trans. A 2001, 34, 1977–1988. [Google Scholar] [CrossRef]
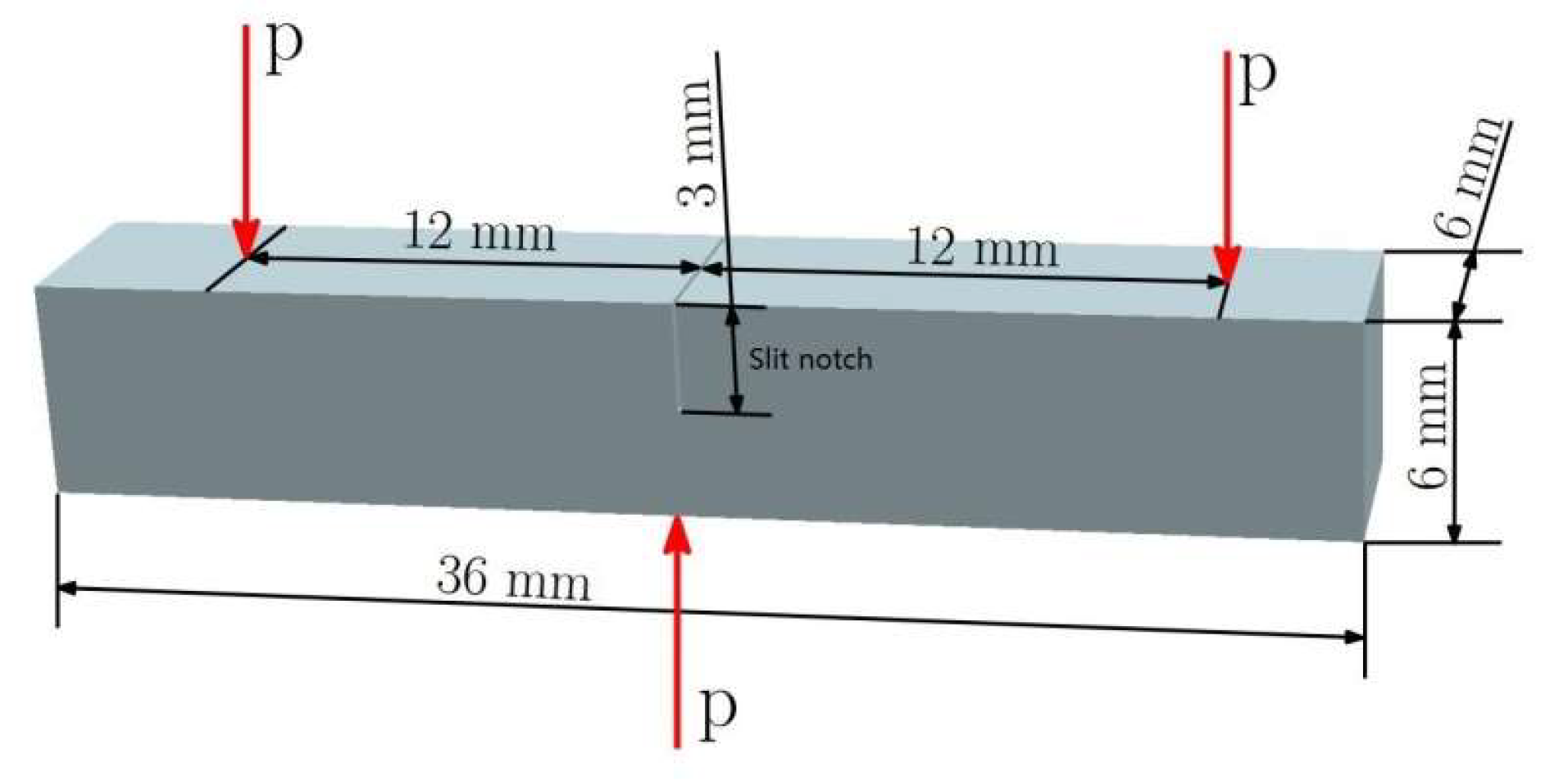






| V (mm/min) | Pmax (N) | KIC (MPa·m1/2) |
|---|---|---|
| 0.05 | 550 | 12.65 |
| 0.5 | 561 | 12.90 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Liu, B.; Wang, Y.; Tang, S.; Liu, Y.; Lu, X. A Study on the Zener-Holloman Parameter and Fracture Toughness of an Nb-Particles-Toughened TiAl-Nb Alloy. Metals 2018, 8, 287. https://doi.org/10.3390/met8040287
Li J, Liu B, Wang Y, Tang S, Liu Y, Lu X. A Study on the Zener-Holloman Parameter and Fracture Toughness of an Nb-Particles-Toughened TiAl-Nb Alloy. Metals. 2018; 8(4):287. https://doi.org/10.3390/met8040287
Chicago/Turabian StyleLi, Jianbo, Bin Liu, Yan Wang, Shan Tang, Yong Liu, and Xiaofang Lu. 2018. "A Study on the Zener-Holloman Parameter and Fracture Toughness of an Nb-Particles-Toughened TiAl-Nb Alloy" Metals 8, no. 4: 287. https://doi.org/10.3390/met8040287
APA StyleLi, J., Liu, B., Wang, Y., Tang, S., Liu, Y., & Lu, X. (2018). A Study on the Zener-Holloman Parameter and Fracture Toughness of an Nb-Particles-Toughened TiAl-Nb Alloy. Metals, 8(4), 287. https://doi.org/10.3390/met8040287




