Neural Network Modeling for the Extraction of Rare Earth Elements from Eudialyte Concentrate by Dry Digestion and Leaching
Abstract
:1. Introduction
2. Theoretical Background
2.1. Multiple Linear Regression
2.2. Stepwise Regression
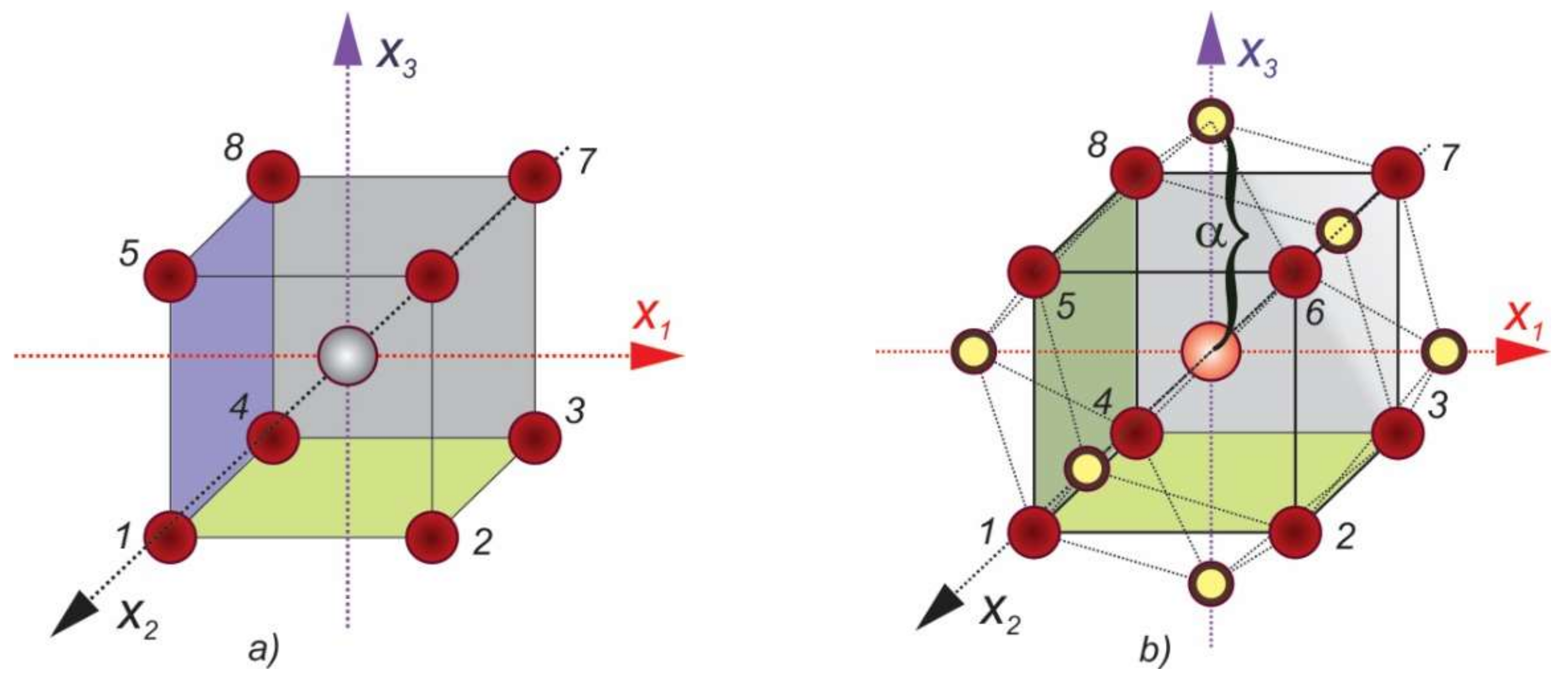
2.3. Design of Experiments
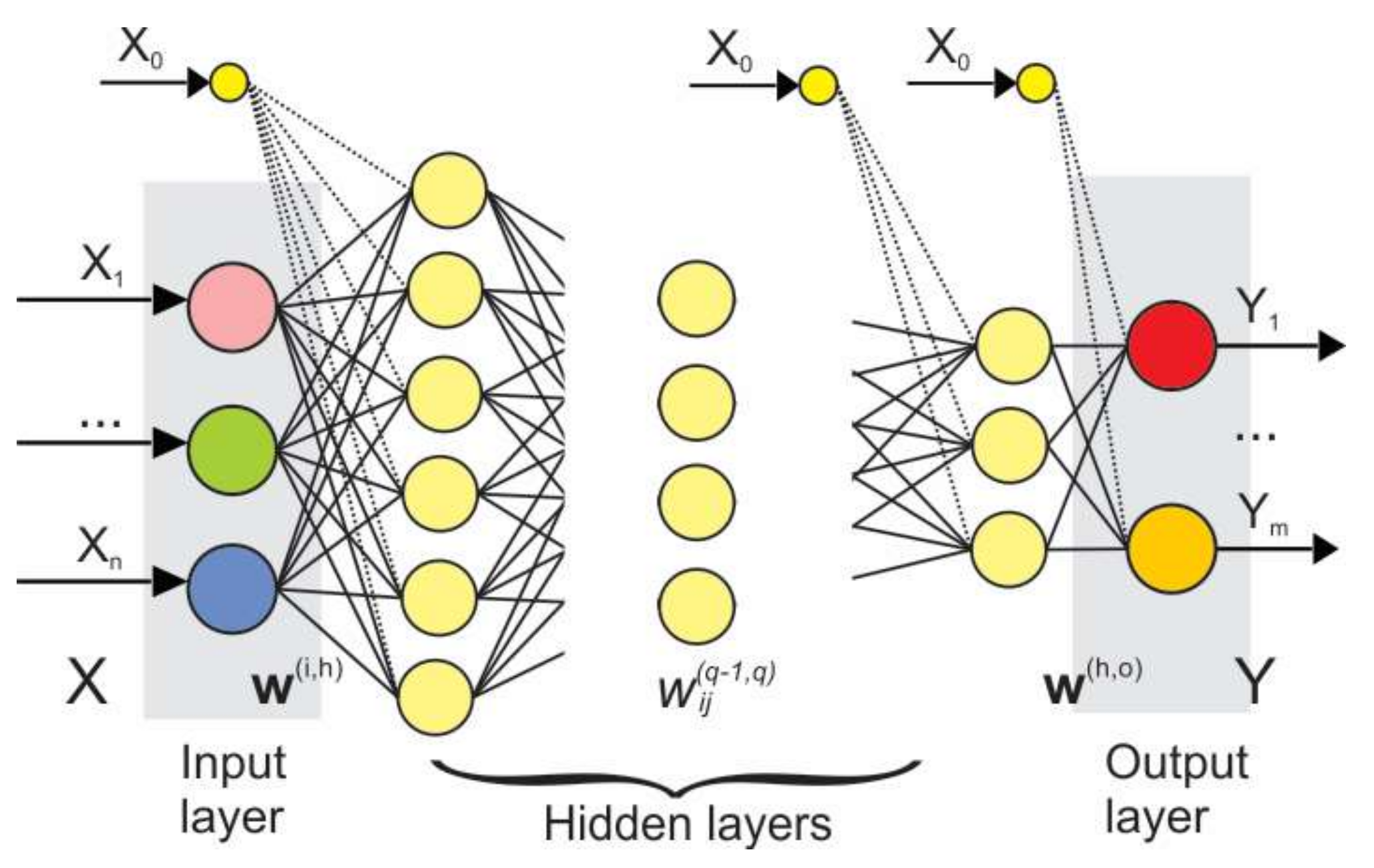
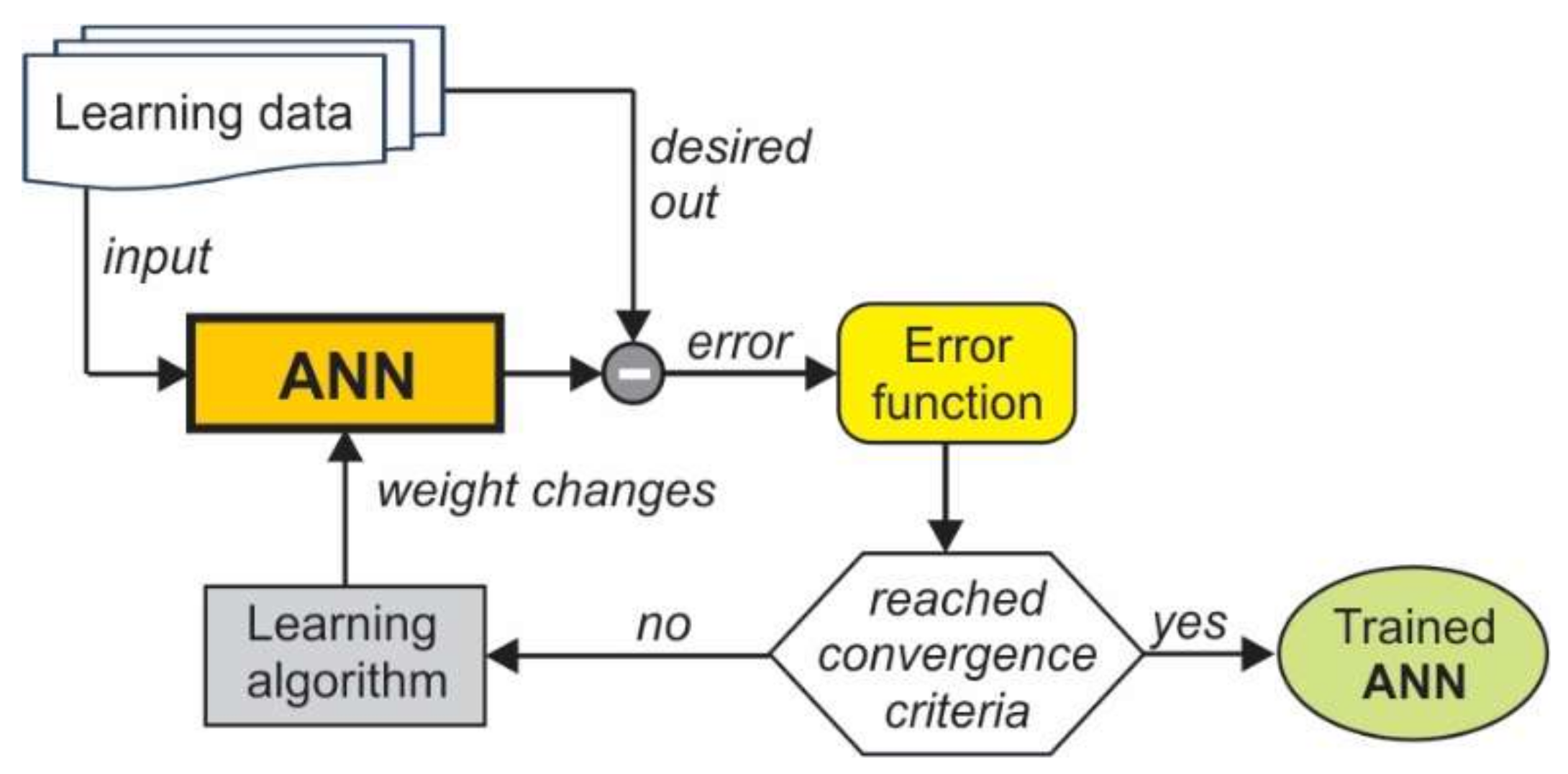
2.4. Artificial Neural Network
3. Materials and Methods
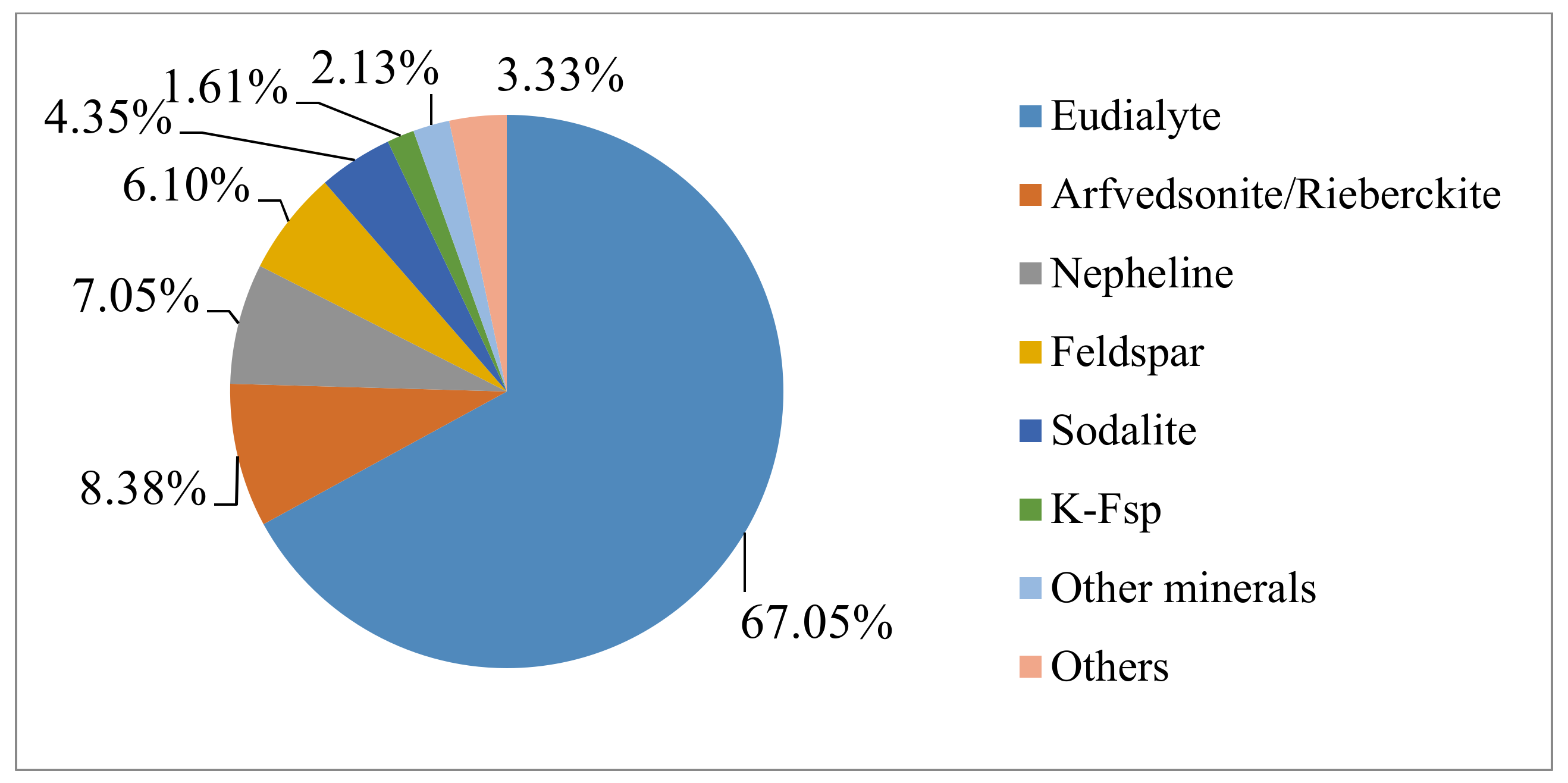
3.1. Material and Analysis
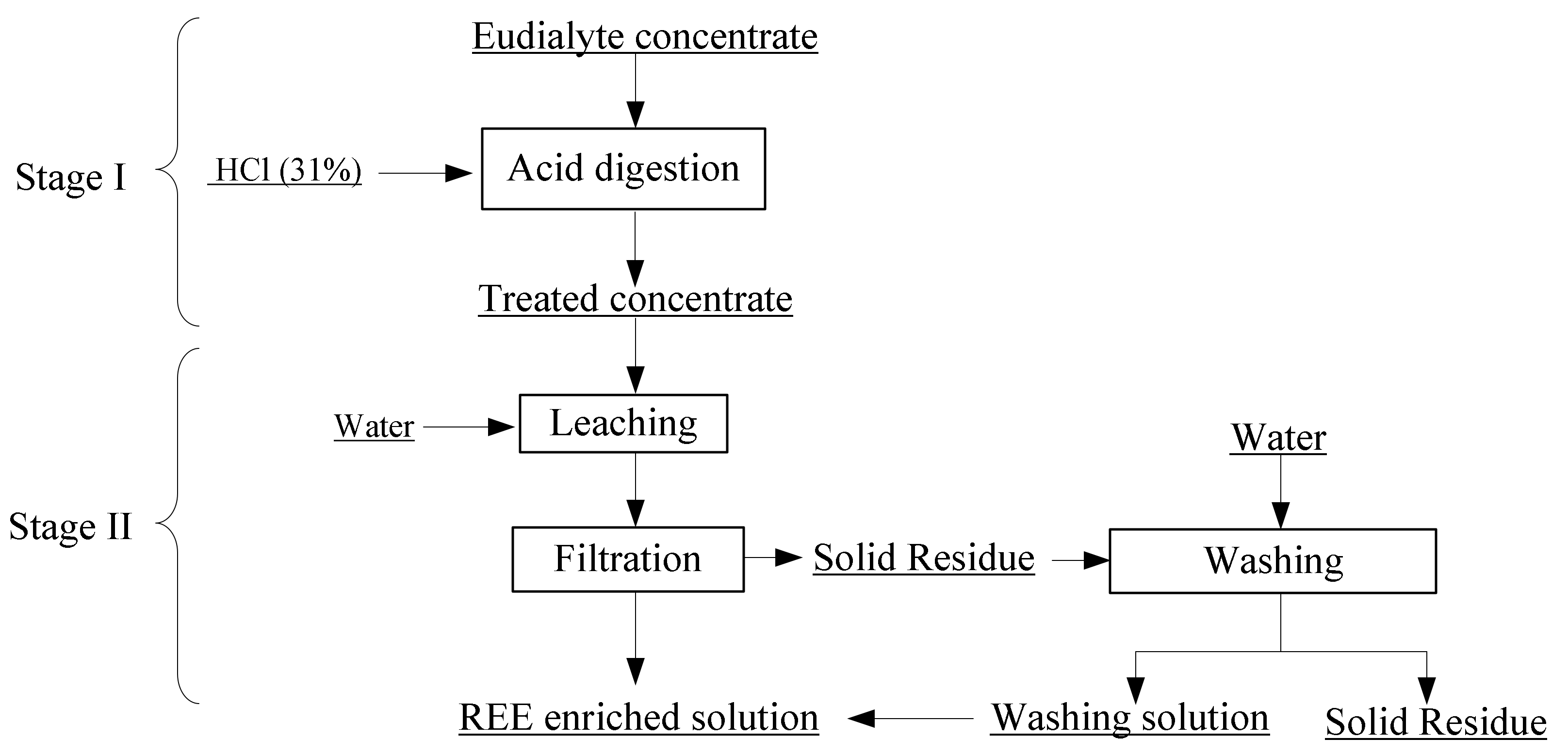
3.2. Extraction Procedure
4. Experiments and Obtained Measurements of Process Outputs
5. Model Setup and Results
5.1. Process Modeling in MLR Form
- (a)
- first order multiple linear regression
- (b)
- first order multiple linear regression with interaction effectswhere denotes the number of input factors ().
5.2. Modeling with Stepwise Regression
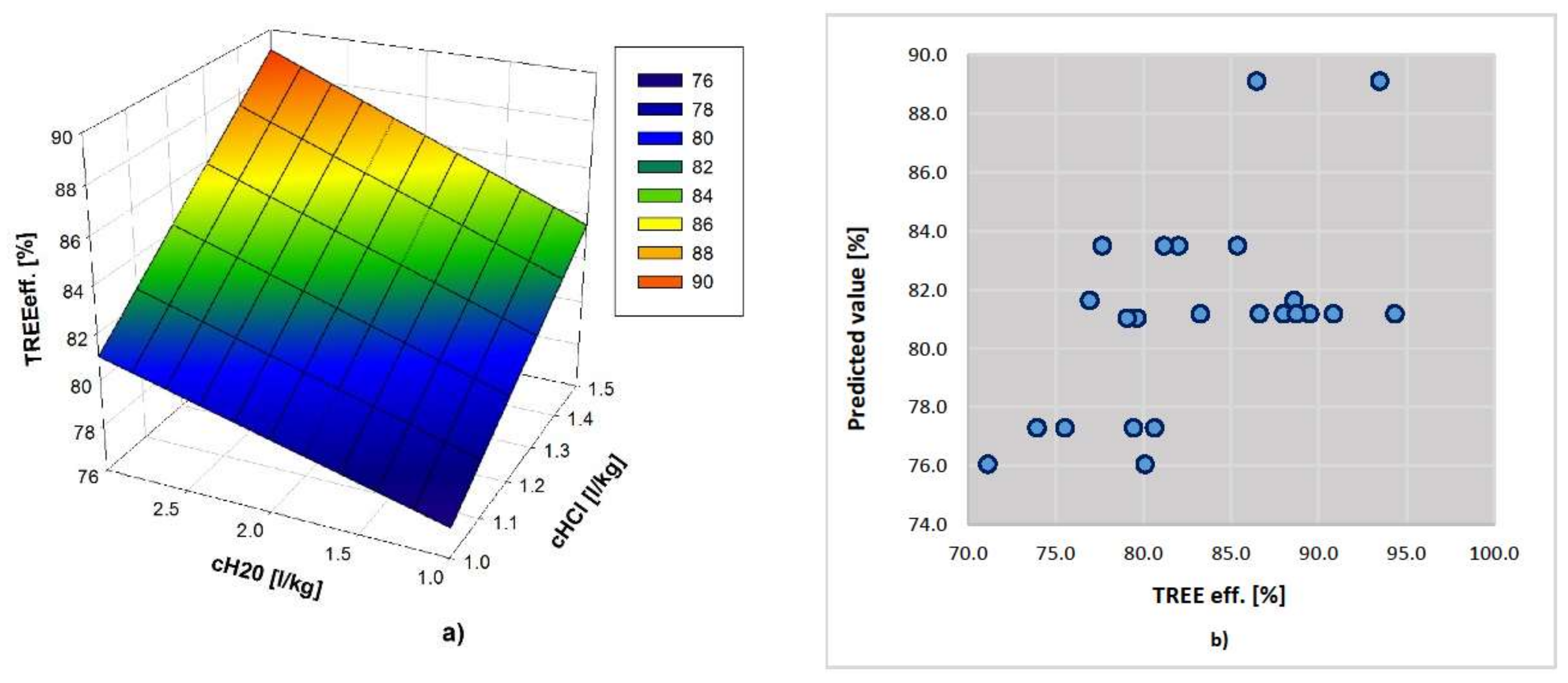
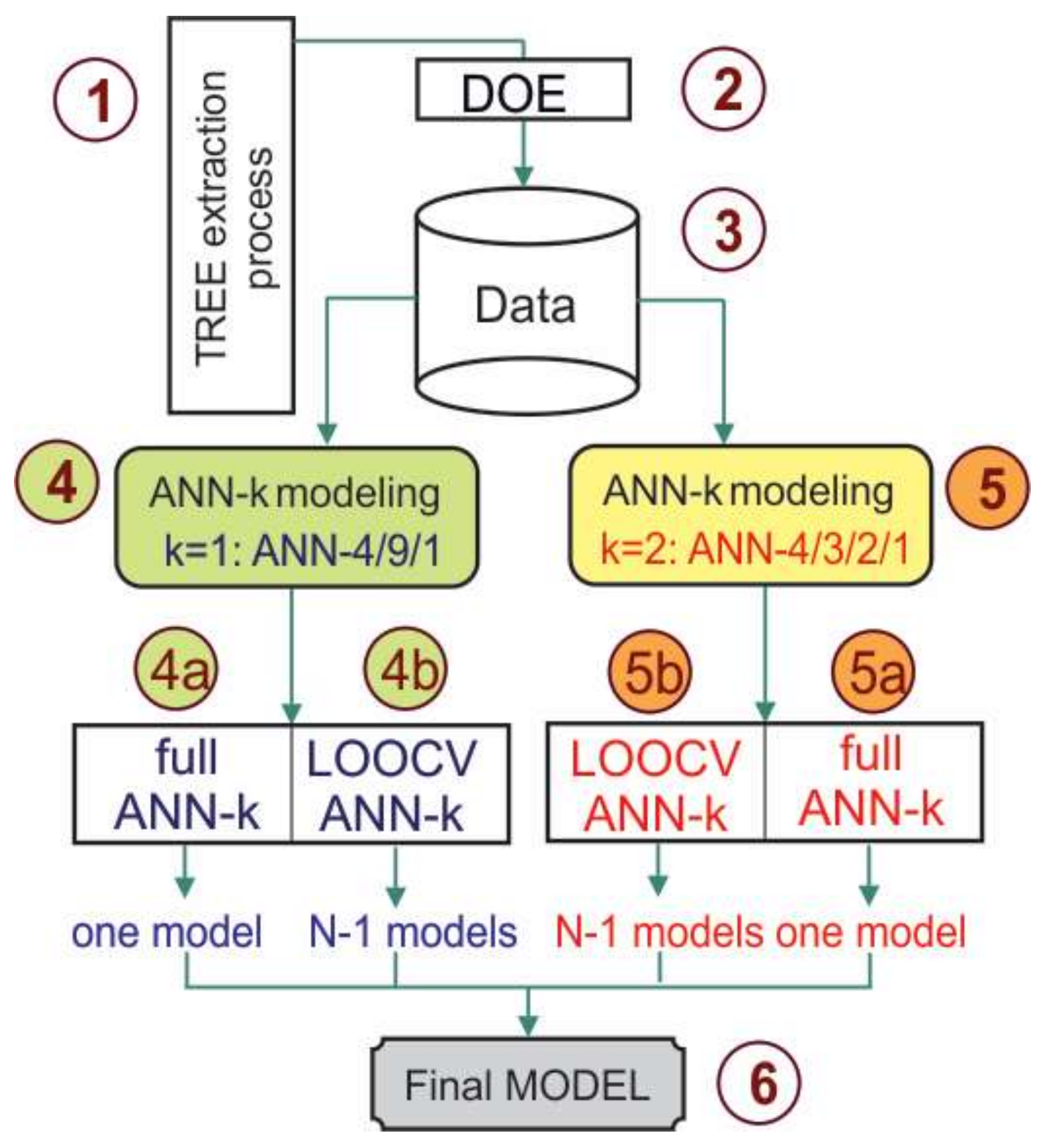
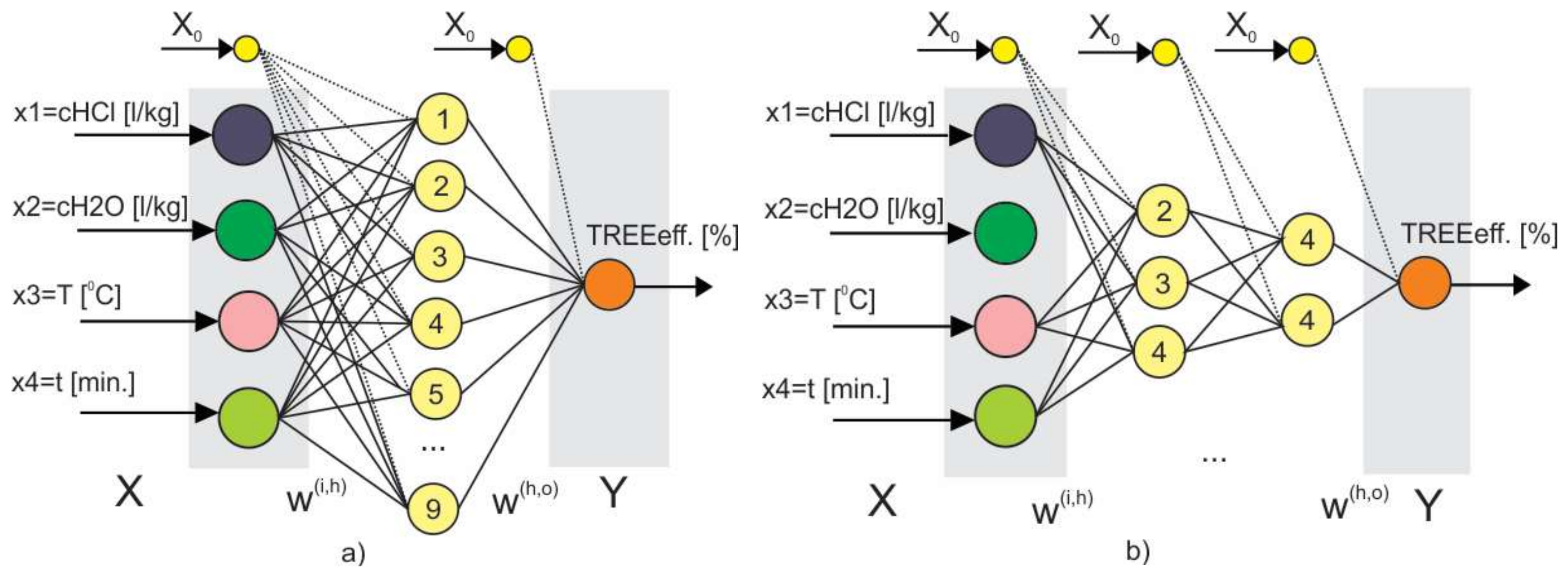
5.3. Modeling with ANN
5.3.1. ANN Modeling of TREE Extraction Based on LOO CV
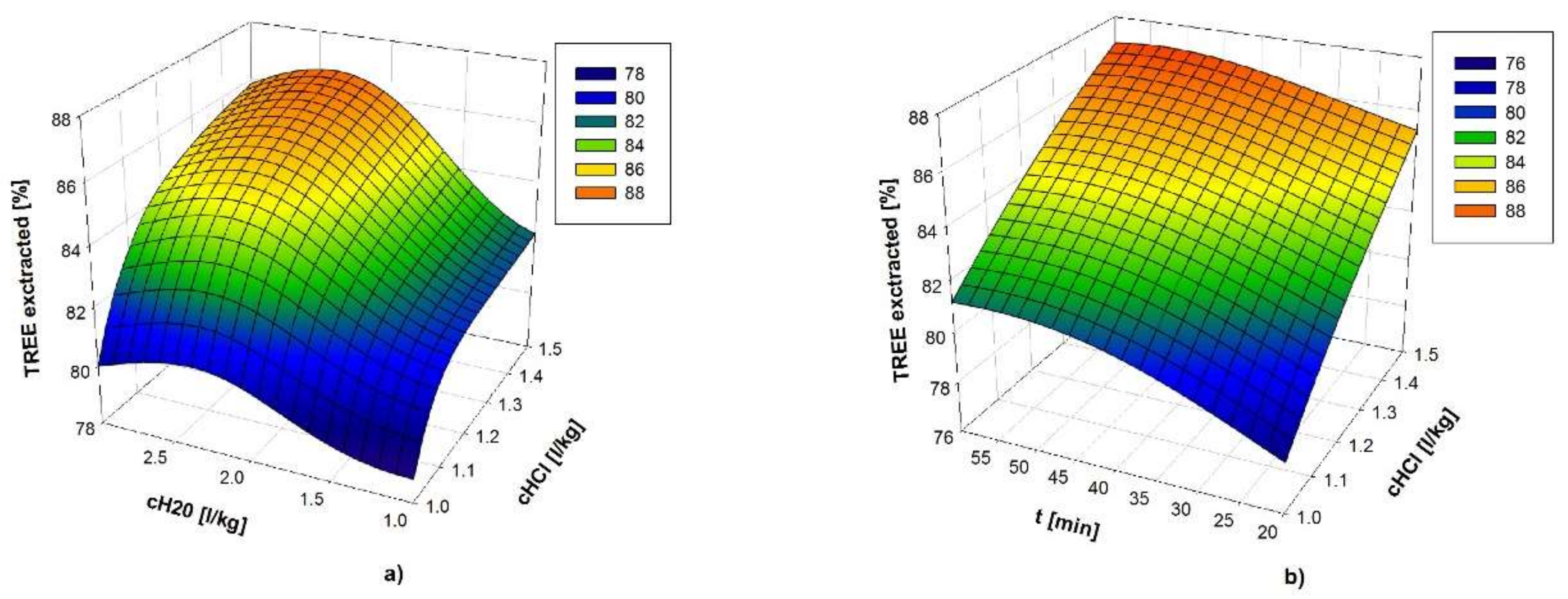
5.3.2. Simulation and Prediction Based on ANN Models
6. Validation of the Model and Scale-up
6.1. Validation of REE Extraction Model and Obtained Optimal Process Regimes
6.2. Dry Digestion and Leaching Process Scale-Up
7. Discussion
7.1. REE Extraction Modeling and Optimal Regimes
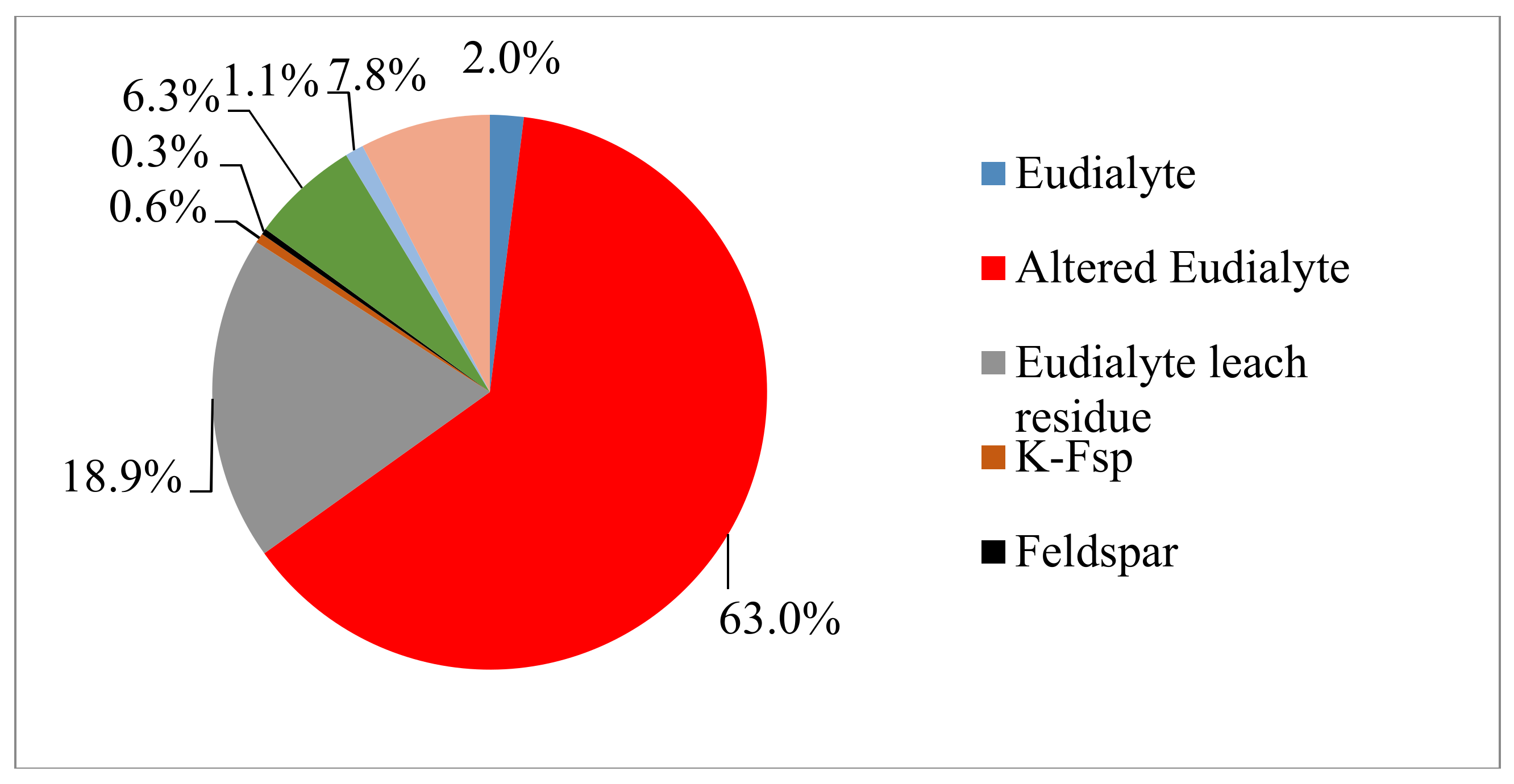
7.2. Phase Changes during REE Extraction
8. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Thomas, P.J.; Carpenter, D.; Boutin, C.; Allison, J.E. Rare earth elements (REEs): Effects on germination and growth of selected crop and native plant species. Chemosphere 2014, 96, 57–66. [Google Scholar] [CrossRef] [PubMed]
- Morais, C.A.; Ciminelli, V.S.T. Process development for the recovery of high-grade lanthanum by solvent extraction. Hydrometallurgy 2004, 73, 237–244. [Google Scholar] [CrossRef]
- Maestro, P.; Huguenin, D. Industrial applications of rare earths: Which way for the end of the century? J. Alloys Compd. 1995, 225, 520–528. [Google Scholar] [CrossRef]
- Krishnamurthy, N.; Gupta, C.K. The Rare Earths, Extractive Metallurgy of Rare Earths; CRC Press: Boca Raton, FL, USA, 2015; pp. 1–84. [Google Scholar]
- Hoshino, M.; Sanematsu, K.; Watanabe, Y. REE mineralogy and resources. In Handbook on the Physics and Chemistry of Rare Earths; Elsevier: New York, NY, USA, 2016; Volume 49, pp. 129–291. [Google Scholar]
- McLemore, V.T. Rare earth elements (REE) deposits associated with great plain margin deposits (alkaline-related), southwestern united states and eastern mexico. Resources 2018, 7, 8. [Google Scholar] [CrossRef]
- Möller, V.; Williams-Jones, A.E. A hyperspectral study (V-NIR-SWIR) of the Nechalacho REE-Nb-Zr deposit, Canada. J. Geochem. Explor. 2018, 188, 194–215. [Google Scholar] [CrossRef]
- Alonso, E.; Sherman, A.M.; Wallington, T.J.; Everson, M.P.; Field, F.R.; Roth, R.; Kirchain, R.E. Evaluating rare earth element availability: A case with revolutionary demand from clean technologies. Environ. Sci. Technol. 2012, 46, 3406–3414. [Google Scholar] [CrossRef] [PubMed]
- Golev, A.; Scott, M.; Erskine, P.D.; Ali, S.H.; Ballantyne, G.R. Rare earths supply chains: Current status, constraints and opportunities. Resour. Policy 2014, 41, 52–59. [Google Scholar] [CrossRef]
- Goodenough, K.; Schilling, J.; Jonsson, E.; Kalvig, P.; Charles, N.; Tuduri, J.; Deady, E.; Sadeghi, M.; Schiellerup, H.; Müller, A. Europe’s rare earth element resource potential: An overview of REE metallogenetic provinces and their geodynamic setting. Ore Geol. Rev. 2016, 72, 838–856. [Google Scholar] [CrossRef]
- Balomenos, E.; Davris, P.; Deady, E.; Yang, J.; Panias, D.; Friedrich, B.; Binnemans, K.; Seisenbaeva, G.; Dittrich, C.; Kalvig, P. The EURARE project: Development of a sustainable exploitation scheme for Europe’s Rare Earth Ore deposits. Johns. Matthey Technol. Rev. 2017, 61, 142–153. [Google Scholar] [CrossRef]
- García, M.V.R.; Krzemień, A.; Del Campo, M.Á.M.; Álvarez, M.M.; Gent, M.R. Rare earth elements mining investment: It is not all about China. Resour. Policy 2017, 53, 66–76. [Google Scholar] [CrossRef]
- Torró, L.; Proenza, J.; Aiglsperger, T.; Bover-Arnal, T.; Villanova-de-Benavent, C.; Rodríguez-García, D.; Ramírez, A.; Rodríguez, J.; Mosquea, L.; Salas, R. Geological, geochemical and mineralogical characteristics of REE-bearing Las Mercedes bauxite deposit, Dominican Republic. Ore Geol. Rev. 2017, 89, 114–131. [Google Scholar] [CrossRef]
- Edahbi, M.; Benzaazoua, M.; Plante, B.; Doire, S.; Kormos, L. Mineralogical characterization using QEMSCAN® and leaching potential study of REE within silicate ores: A case study of the Matamec project, Québec, Canada. J. Geochem. Explor. 2018, 185, 64–73. [Google Scholar] [CrossRef]
- Mikhailova, J.; Pakhomovsky, Y.A.; Ivanyuk, G.Y.; Bazai, A.; Yakovenchuk, V.; Elizarova, I.; Kalashnikov, A. REE mineralogy and geochemistry of the Western Keivy peralkaline granite massif, Kola Peninsula, Russia. Ore Geol. Rev. 2017, 82, 181–197. [Google Scholar] [CrossRef]
- Deymar, S.; Yazdi, M.; Rezvanianzadeh, M.R.; Behzadi, M. Alkali metasomatism as a process for Ti–REE–Y–U–Th mineralization in the Saghand Anomaly 5, Central Iran: Insights from geochemical, mineralogical, and stable isotope data. Ore Geol. Rev. 2018, 93, 308–336. [Google Scholar] [CrossRef]
- Davris, P.; Stopic, S.; Balomenos, E.; Panias, D.; Paspaliaris, I.; Friedrich, B. Leaching of rare earth elements from eudialyte concentrate by suppressing silica gel formation. Miner. Eng. 2017, 108, 115–122. [Google Scholar] [CrossRef]
- Borst, A.M.; Friis, H.; Andersen, T.; Nielsen, T.; Waight, T.E.; Smit, M.A. Zirconosilicates in the kakortokites of the Ilímaussaq complex, South Greenland: Implications for fluid evolution and high-field-strength and rare-earth element mineralization in agpaitic systems. Miner. Mag. 2016, 80, 5–30. [Google Scholar] [CrossRef]
- Anthony, J.W.; Bideaux, R.A.; Bladh, K.W.; Nichols, M.C. Handbook of Mineralogy, Volume IV, Arsenates, Phosphates, Vanadates; Mineralogical Society of America: Chantilly, VA, USA, 2000. [Google Scholar]
- Johnsen, O.; Ferraris, G.; Gault, R.A.; Grice, J.D.; Kampf, A.R.; Pekov, I.V. The nomenclature of eudialyte-group minerals. Can. Miner. 2003, 41, 785–794. [Google Scholar] [CrossRef]
- Zakharov, V.; Maiorov, D.; Alishkin, A.; Matveev, V. Causes of insufficient recovery of zirconium during acidic processing of lovozero eudialyte concentrate. Rus. J. Non-Ferr. Met. 2011, 52, 423–428. [Google Scholar] [CrossRef]
- Lebedev, V. Sulfuric acid technology for processing of eudialyte concentrate. Rus. J. Appl. Chem. 2003, 76, 1559–1563. [Google Scholar] [CrossRef]
- Lebedev, V.; Shchur, T.; Maiorov, D.; Popova, L.; Serkova, R. Specific features of acid decomposition of eudialyte and certain rare-metal concentrates from Kola peninsula. Rus. J. Appl. Chem. 2003, 76, 1191–1196. [Google Scholar] [CrossRef]
- Voßenkaul, D.; Birich, A.; Müller, N.; Stoltz, N.; Friedrich, B. Hydrometallurgical processing of eudialyte bearing concentrates to recover rare earth elements via low-temperature dry digestion to prevent the silica gel formation. J. Sustain. Metall. 2017, 3, 79–89. [Google Scholar] [CrossRef]
- Alkan, G.; Yagmurlu, B.; Cakmakoglu, S.; Hertel, T.; Kaya, Ş.; Gronen, L.; Stopic, S.; Friedrich, B. Novel Approach for Enhanced Scandium and Titanium Leaching Efficiency from Bauxite Residue with Suppressed Silica Gel Formation. Nat. Sci. Rep. 2018, 8, 5676. [Google Scholar] [CrossRef] [PubMed]
- Vaccarezza, V.; Anderson, C. Beneficiation and Leaching Study of Norra Kärr Eudialyte Mineral; TMS Annual Meeting & Exhibition; Springer: Berlin, Germany, 2018; pp. 39–51. [Google Scholar]
- Rivera, R.M.; Ulenaers, B.; Ounoughene, G.; Binnemans, K.; Van Gerven, T. Extraction of rare earths from bauxite residue (red mud) by dry digestion followed by water leaching. Miner. Eng. 2018, 119, 82–92. [Google Scholar] [CrossRef]
- Milivojevic, M.; Stopic, S.; Friedrich, B.; Stojanovic, B.; Drndarevic, D. Computer modeling of high-pressure leaching process of nickel laterite by design of experiments and neural networks. Int. J. Miner. Metall. Mater. 2012, 19, 584–594. [Google Scholar] [CrossRef]
- Milivojevic, M.; Stopic, S.; Stojanovic, B.; Drndarevic, D.; Bernd, F. Forward stepwise regression in determining dimensions of forming and sizing tools for self-lubricated bearings. METALL 2013, 67, 92–98. [Google Scholar]
- Mata, J. Interpretation of concrete dam behaviour with artificial neural network and multiple linear regression models. Eng. Struct. 2011, 33, 903–910. [Google Scholar] [CrossRef]
- Cohen, J.; Cohen, P.; West, S.G.; Aiken, L.S. Applied Multiple Regression/Correlation Analysis for the Behavioral Sciences; Routledge: Abingdon, UK, 2013. [Google Scholar]
- Fisher, R.A. The Design of Experiments; Oliver and Boyd: Edinburgh, UK; London, UK, 1937. [Google Scholar]
- Box, G.E.; Wilson, K.B. On the experimental attainment of optimum conditions. In Breakthroughs in Statistics; Springer: Berlin, Germany, 1992; pp. 270–310. [Google Scholar]
- Dong, L.; Park, K.-H.; Zhan, W.; Guo, X.-Y. Response surface design for nickel recovery from laterite by sulfation-roasting-leaching process. Trans. Nonferr. Met. Soc. China 2010, 20, s92–s96. [Google Scholar]
- Rumelhalt, D. Learning Internal Representation by Error Propogation, Parallel Distributed Processing: Explorations in the Microstructure of Cognition (Vol. 1); MIT Press: Cambridge, MA, USA, 1986. [Google Scholar]
- Drndarevic, D. Modeling and Optimization of Powder Metallurgy Process by Neural Networks. Ph.D. Thesis, University of Belgrade, Beograd, Serbia, 1996. [Google Scholar]
- Law, R. Back-propagation learning in improving the accuracy of neural network-based tourism demand forecasting. Tour. Manag. 2000, 21, 331–340. [Google Scholar] [CrossRef]
- Majdi, A.; Beiki, M. Evolving neural network using a genetic algorithm for predicting the deformation modulus of rock masses. Int. J. Rock Mech. Min. Sci. 2010, 47, 246–253. [Google Scholar] [CrossRef]
- Yu, Z. Feed-Forward Neural Networks and Their Applications in Forecasting; University of Houston: Houston, TX, USA, 2000. [Google Scholar]
- Heaton, J. Programming Neural Networks with Encog 3 in c#; Heaton Research, Inc.: St. Louis, MI, USA, 2015. [Google Scholar]
- Riedmiller, M.; Braun, H. A Direct Adaptive Method for Faster Backpropagation Learning: The RPROP algorithm. In Proceedings of the IEEE International Conference on Neural Networks, San Francisco, CA, USA, 28 March–1 April 1993; pp. 586–591. [Google Scholar]
- Riedmiller, M. Advanced supervised learning in multi-layer perceptrons—From backpropagation to adaptive learning algorithms. Comput. Stand. Interfaces 1994, 16, 265–278. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv. 2014. arXiv.org e-Print archive. Available online: https://arxiv.org/abs/1412.6980 (accessed on 22 December 2014).
- Milivojević, M. Methods of Development and Adaptation of Regression Models Based on Genetic Algorithms. Ph.D. Thesis, University of Kragujevac, Kragujevac, Serbia, 2016. [Google Scholar]
- Pallant, J. SPSS Survival Manual, 3rd ed.; Mc Graw Hill: New York, NY, USA, 2007. [Google Scholar]
- Team, R. RR Development Core Team: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2012; ISBN 3-900051-07-0. [Google Scholar]
- Hecht-Nielsen, R. Kolmogorov’s mapping neural network existence theorem. In Proceedings of the International Conference on Neural Networks, San Diego, CA, USA, 21–24 June 1987; pp. 11–14. [Google Scholar]
- McCaffrey, J. Understanding and using K-fold cross validation for neural networks. Visual Studio Magazine, 24 October 2013. [Google Scholar]
- Sadri, F.; Nazari, A.M.; Ghahreman, A. A review on the cracking, baking and leaching processes of rare earth element concentrates. J. Rare Earths 2017, 35, 739–752. [Google Scholar] [CrossRef]
- Krebs, D.; Furfaro, D. Processing of Rare Earth and Uranium Containing Ores and Concentrates. Patent WO 2014/082113 A1, 5 June 2014. [Google Scholar]






| Element | Content (wt %) | Element | Content (wt %) |
|---|---|---|---|
| Al | 3.2 | Ce | 0.52 |
| Ca | 5.7 | Pr | 532 mg/kg |
| Fe | 6.04 | Nd | 0.21 |
| Mn | 0.39 | Sm | 440 mg/kg |
| Nb | 0.36 | Gd | 239 mg/kg |
| Zr | 5.08 | Dy | 580 mg/kg |
| Hf | 0.11 | Y | 0.33 |
| Si | 23.1 | Yb | 368 mg/kg |
| La | 0.25 | TREE | 1.52 |
| No. | X1:HCl:Con. (L:kg) | X2:Water:Con. (L:kg) | X3:Leaching Temp. (°C) | X4:Leaching Time (min.) | Y:TREE Extr. (%) | ||||
|---|---|---|---|---|---|---|---|---|---|
| 1:1, 1.25:1, 1.5:1 | 1:1, 2:1, 3:1 | 20, 50, 80 | 20, 40, 60 | [0–100] | |||||
| c.v. | a.v. | c.v. | a.v. | c.v. | a.v. | c.v. | a.v. | ||
| A1 | 1 | 1.5:1 | 1 | 3:1 | 1 | 20 | 1 | 60 | 93.475 |
| A2 | −1 | 1:1 | 1 | 3:1 | 1 | 20 | 1 | 60 | 79.640 |
| A3 | 1 | 1.5:1 | −1 | 1:1 | 1 | 20 | 1 | 60 | 82.010 |
| A4 | −1 | 1:1 | −1 | 1:1 | 1 | 20 | 1 | 60 | 73.940 |
| A5 | 1 | 1.5:1 | 1 | 3:1 | −1 | 20 | 1 | 60 | 86.465 |
| A6 | −1 | 1:1 | 1 | 3:1 | −1 | 20 | 1 | 60 | 79.070 |
| A7 | 1 | 1.5:1 | −1 | 1:1 | −1 | 20 | 1 | 60 | 81.170 |
| A8 | −1 | 1:1 | −1 | 1:1 | −1 | 20 | 1 | 60 | 79.450 |
| A9 | 1 | 1.5:1 | 1 | 3:1 | 1 | 20 | −1 | 20 | 85.350 |
| A10 | −1 | 1:1 | 1 | 3:1 | 1 | 20 | −1 | 20 | 80.630 |
| A11 | 1 | 1.5:1 | −1 | 1:1 | 1 | 20 | −1 | 20 | 76.940 |
| A12 | −1 | 1:1 | −1 | 1:1 | 1 | 20 | −1 | 20 | 71.140 |
| A13 | 1 | 1.5:1 | 1 | 3:1 | −1 | 20 | −1 | 20 | 77.650 |
| A14 | −1 | 1:1 | 1 | 3:1 | −1 | 20 | −1 | 20 | 75.525 |
| A15 | 1 | 1.5:1 | −1 | 1:1 | −1 | 20 | −1 | 20 | 88.600 |
| A16 | −1 | 1:1 | −1 | 1:1 | −1 | 20 | −1 | 20 | 80.090 |
| A17 * | 0 | 1.25:1 | 0 | 2:1 | 0 | 50 | 1 | 40 | 89.49, 87.99, 88.74, 90.85, 86.63, 94.35, 83.24 |
| First-Order MLR Model: | |||
|---|---|---|---|
, | |||
| Coefficients a | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model | Unstandard. Coeff. | Standard. Coeff. | t | Sig. | 95.0% Confidence Interval for B | Correlations | Collinearity Statistics | ||||||
| B | Std. Error | Beta | Lower Bound | Upper Bound | Zero-Order | Partial | Part | Tolerance | VIF | ||||
| 1 | (Constant) | 64.866 | 6.293 | 10.307 | 0.000 | 51.452 | 78.280 | ||||||
| 13.044 | 4.943 | 0.563 | 2.639 | 0.019 | 2.509 | 23.579 | 0.563 | 0.563 | 0.563 | 1.000 | 1.000 | ||
| 2 | (Constant) | 64.866 | 5.651 | 11.478 | 0.000 | 52.746 | 76.986 | ||||||
| 10.554 | 4.587 | 0.456 | 2.301 | 0.037 | 0.715 | 20.393 | 0.563 | 0.524 | 0.441 | 0.936 | 1.068 | ||
| 0.031 | 0.015 | 0.425 | 2.146 | 0.050 | 0.000 | 0.062 | 0.540 | 0.497 | 0.411 | 0.936 | 1.068 | ||
| Parameter | Units | B1 | B2 | B3 | B4 |
|---|---|---|---|---|---|
| HCl:Concentrate | L:kg | 1.3:1 | 1.4:1 | 1.4:1 | 1.5:1 |
| Water:Concentrate | L:kg | 2.25:1 | 2.25:1 | 2.5:1 | 3:1 |
| Leaching time | min | 40 | 50 | 50 | 60 |
| Predicted value | 85.35% | 87.90% | 89.40% | 89.40% | |
| Actual value | 87.65% | 89.40% | 89.70% | 91.20% |
| Element | Concentration (g/L) | Element | Concentration (g/L) |
|---|---|---|---|
| Al | 0.56 | Ce | 0.951 |
| Ca | 10.49 | Pr | 0.105 |
| Fe | 2.02 | Nd | 0.370 |
| Mn | 0.269 | Sm | 0.094 |
| Nb | <0.0001 | Gd | 0.075 |
| Zr | 0.02 | Dy | 0.105 |
| Hf | 0.010 | Y | 0.601 |
| Si | 0.099 | Yb | 0.069 |
| La | 0.425 | TREE | 2.80 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Y.; Stopic, S.; Gronen, L.; Milivojevic, M.; Obradovic, S.; Friedrich, B. Neural Network Modeling for the Extraction of Rare Earth Elements from Eudialyte Concentrate by Dry Digestion and Leaching. Metals 2018, 8, 267. https://doi.org/10.3390/met8040267
Ma Y, Stopic S, Gronen L, Milivojevic M, Obradovic S, Friedrich B. Neural Network Modeling for the Extraction of Rare Earth Elements from Eudialyte Concentrate by Dry Digestion and Leaching. Metals. 2018; 8(4):267. https://doi.org/10.3390/met8040267
Chicago/Turabian StyleMa, Yiqian, Srecko Stopic, Lars Gronen, Milovan Milivojevic, Srdjan Obradovic, and Bernd Friedrich. 2018. "Neural Network Modeling for the Extraction of Rare Earth Elements from Eudialyte Concentrate by Dry Digestion and Leaching" Metals 8, no. 4: 267. https://doi.org/10.3390/met8040267
APA StyleMa, Y., Stopic, S., Gronen, L., Milivojevic, M., Obradovic, S., & Friedrich, B. (2018). Neural Network Modeling for the Extraction of Rare Earth Elements from Eudialyte Concentrate by Dry Digestion and Leaching. Metals, 8(4), 267. https://doi.org/10.3390/met8040267







