AC Iron Loss Prediction and Magnetic Properties of Fe-6.5 wt. % Si Ribbons Prepared by Melt-Spinning
Abstract
:1. Introduction
2. Materials and Methods
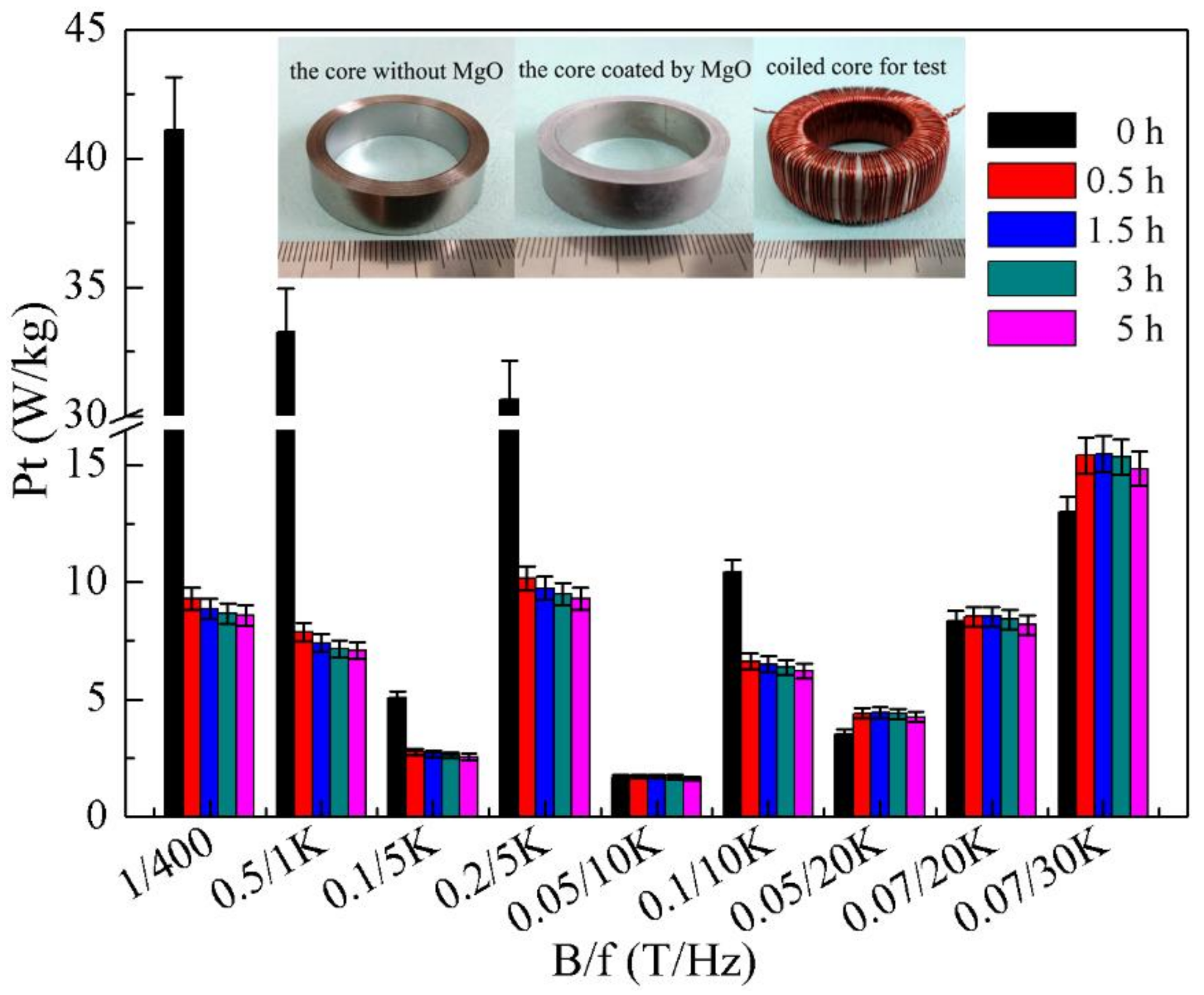
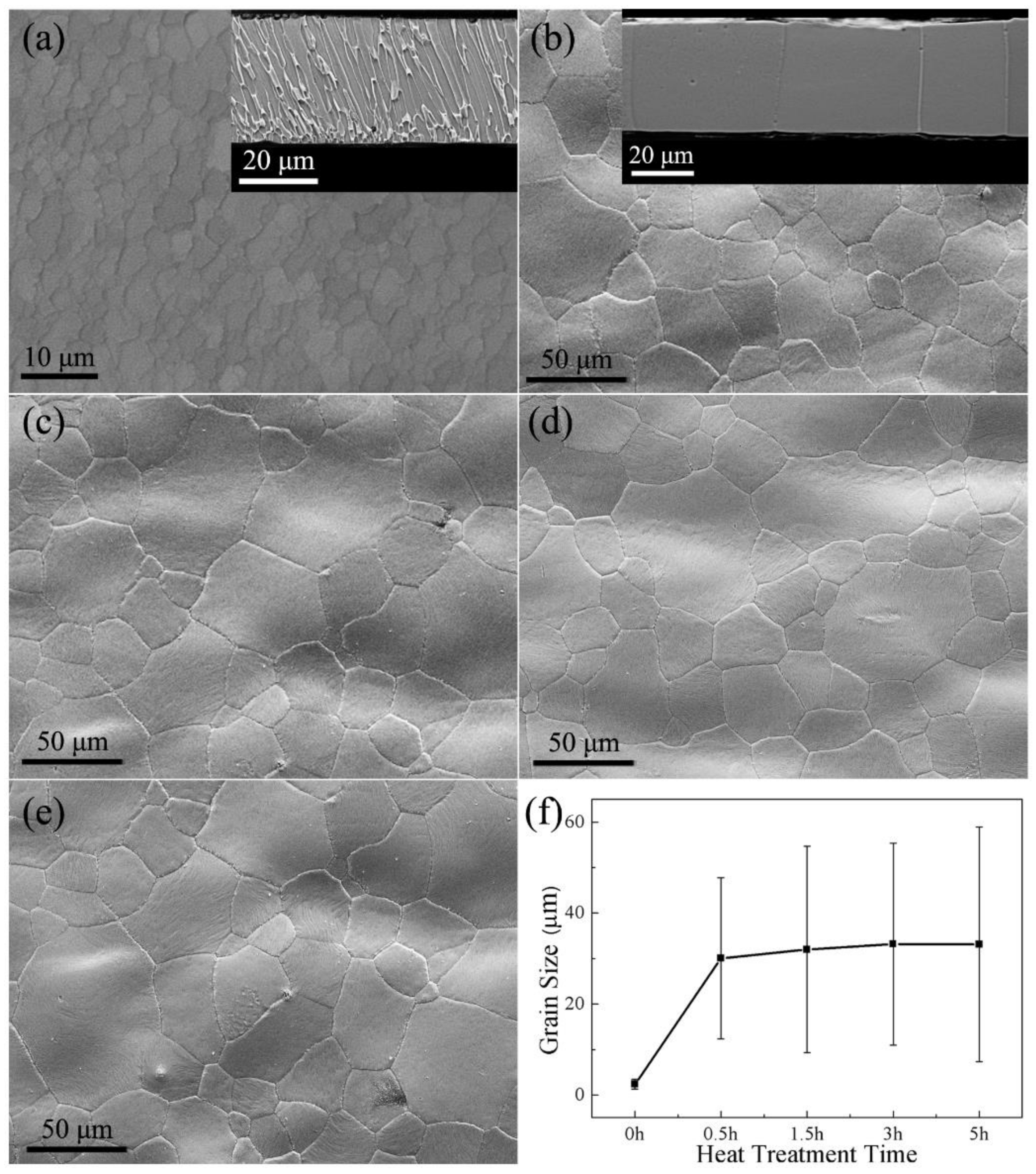
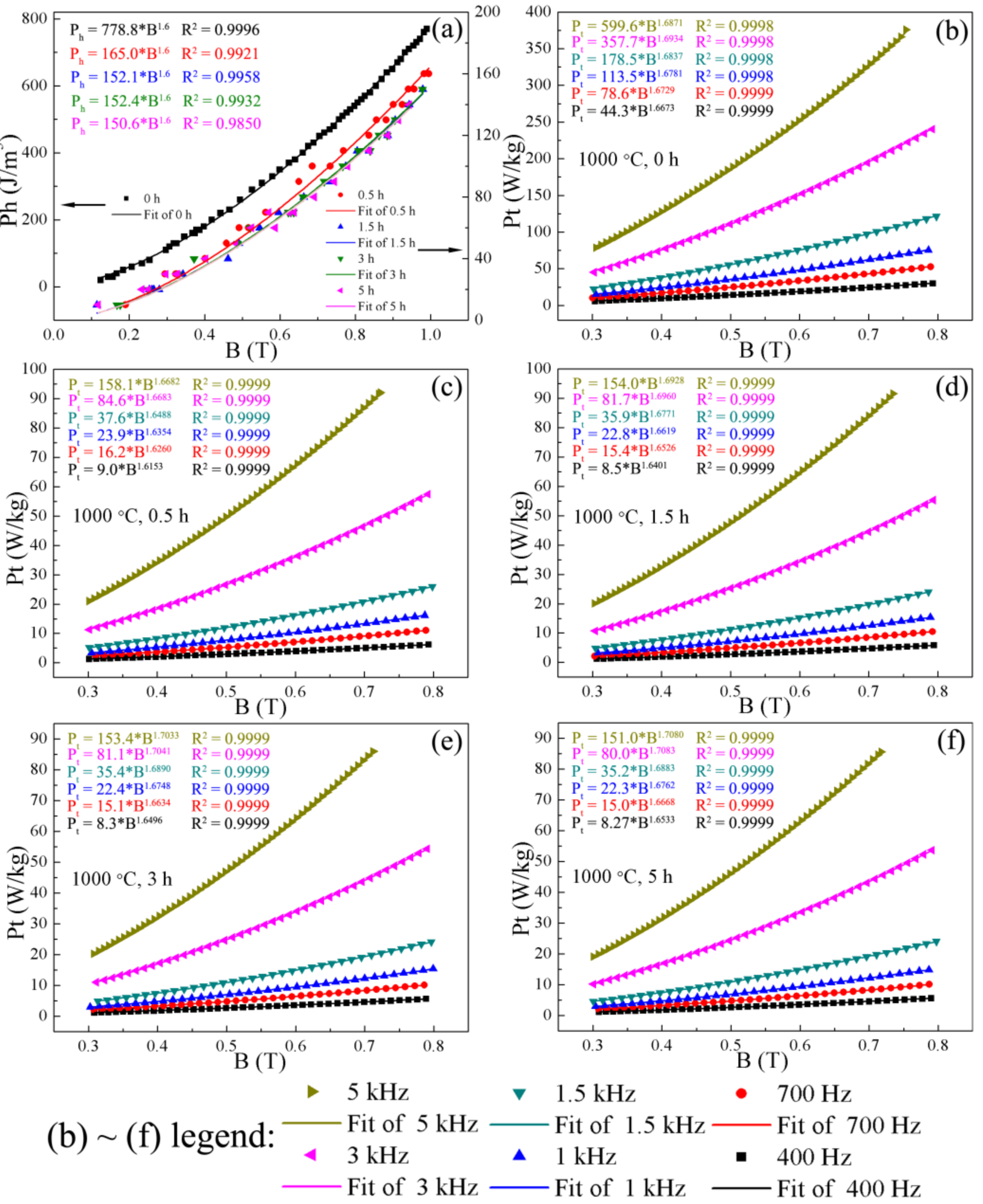
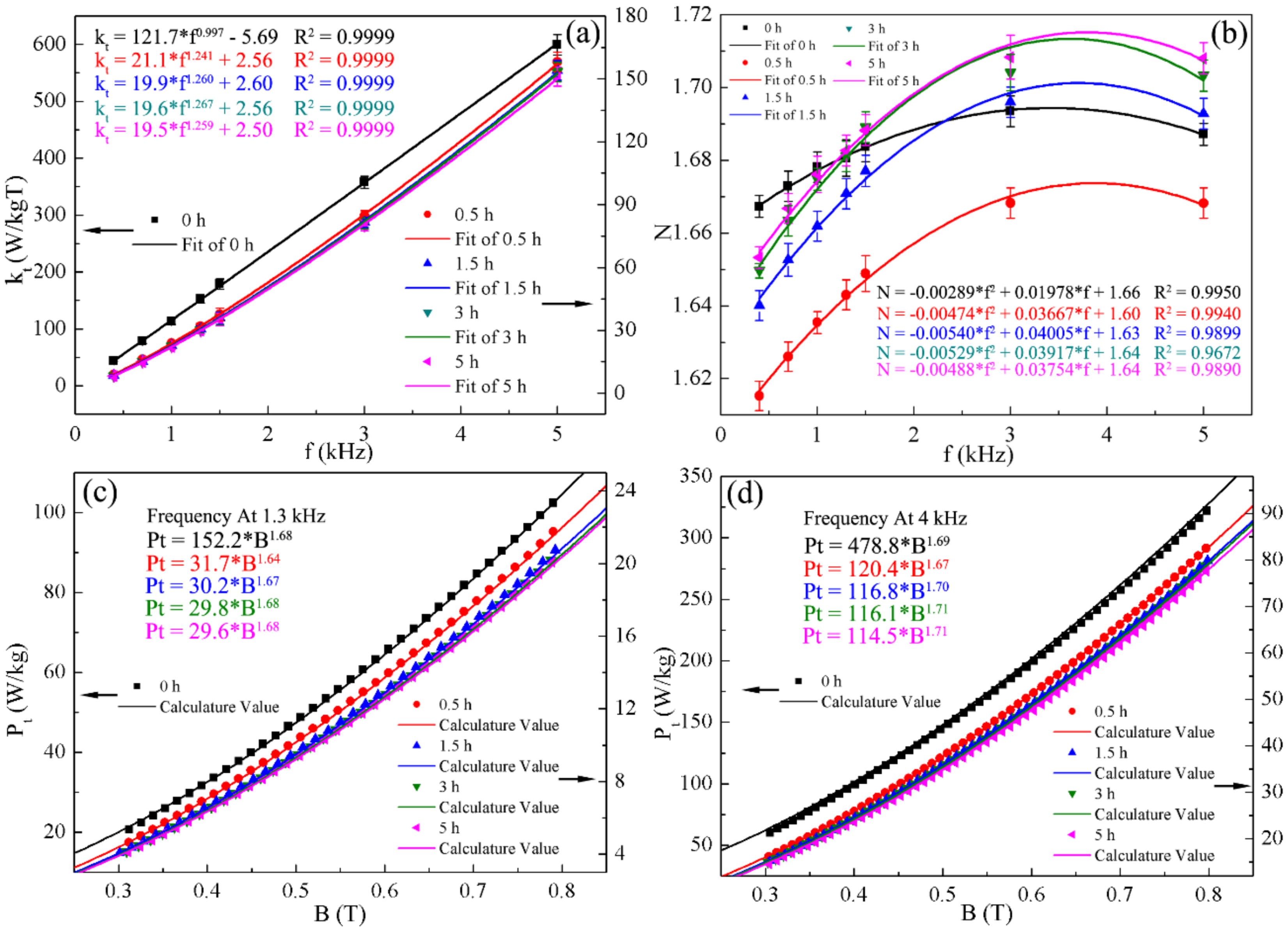
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bozorth, R.M. Ferromagnetism; Van Nostrand-Reinhold: New York, NY, USA, 1951; Volume 595, pp. 50–52. ISBN 0-7803-1032-2. [Google Scholar]
- Viala, B.; Degauque, J.; Baricco, M.; Ferrara, E.; Pasquale, M.; Fiorillo, F. Magnetic and mechanical properties of rapidly solidified Fe-Si 6.5 wt. % alloys and their interpretation. J. Magn. Magn. Mater. 1996, 160, 315–317. [Google Scholar] [CrossRef]
- Haiji, H.; Okada, K.; Hiratani, T.; Abe, M.; Ninomiya, M. Magnetic properties and workability of 6.5% Si steel sheet. J. Magn. Magn. Mater. 1996, 160, 109–114. [Google Scholar] [CrossRef]
- Li, H.; Liang, Y.F.; Ye, F. Effect of heat treatment on ordered structures and mechanical properties of Fe-6.5 mass % Si Alloy. Mater. Trans. 2015, 56, 759–765. [Google Scholar] [CrossRef]
- Liu, S.Q.; Cui, C.X.; Wang, X.; Li, N.; Shi, J.J.; Cui, S.; Chen, P. Effect of Cooling Rate on Microstructure and Grain Refining Behavior of In Situ CeB6/Al Composite Inoculant in Aluminum. Metals 2017, 7, 204. [Google Scholar] [CrossRef]
- Tan, X.; Li, H.Y.; Xu, H.; Han, K.; Li, W.D.; Zhang, F. A Cost-Effective Approach to Optimizing Microstructure and Magnetic Properties in Ce17Fe78B6 Alloys. Materials 2017, 10, 869. [Google Scholar] [CrossRef] [PubMed]
- Liang, Y.F.; Wang, S.; Li, H.; Jiang, Y.M.; Ye, F.; Lin, J.P. Fabrication of Fe-6.5 wt. % Si ribbons by melt spinning method on large scale. Adv. Mater. Sci. Eng. 2015, 2015, 296197. [Google Scholar] [CrossRef]
- Palmer, J.; Thompson, C.V.; Smith, H.I. Grain growth and grain size distributions in thin germanium films. J. Appl. Phys. 1987, 62, 2492–2497. [Google Scholar] [CrossRef]
- Steinmetz, C.P. On the law of hysteresis. Proc. IEEE 1984, 72, 197–221. [Google Scholar] [CrossRef]
- Kollár, P.; Olekšáková, D.; Vojtek, V.; Füzer, J.; Fáberová, M.; Bureš, R. Steinmetz law for ac magnetized iron-phenolformaldehyde resin soft magnetic composites. J. Magn. Magn. Mater. 2017, 424, 245–250. [Google Scholar] [CrossRef]
- Svensson, L.; Frogner, K.; Jeppsson, P.; Cedell, T.; Andersson, M. Soft magnetic moldable composites: Properties and applications. J. Magn. Magn. Mater. 2012, 324, 2717–2722. [Google Scholar] [CrossRef]
| Sample | μm | B (T) | Hc (A/m) | |
|---|---|---|---|---|
| B8 | B50 | |||
| 0 h | 1843 ± 60 | 1.16 ± 0.02 | 1.55 ± 0.03 | 237.6 ± 6.8 |
| 0.5 h | 10,589 ± 311 | 1.31 ± 0.03 | 1.55 ± 0.04 | 48.9 ± 1.6 |
| 1.5 h | 10,931 ± 327 | 1.31 ± 0.04 | 1.55 ± 0.03 | 46.6 ± 1.3 |
| 3 h | 11,082 ± 295 | 1.31 ± 0.03 | 1.55 ± 0.05 | 45.7 ± 1.0 |
| 5 h | 11,051 ± 301 | 1.32 ± 0.04 | 1.56 ± 0.04 | 45.3 ± 1.1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Liang, Y.; Chen, B.; Ye, F.; Lin, J. AC Iron Loss Prediction and Magnetic Properties of Fe-6.5 wt. % Si Ribbons Prepared by Melt-Spinning. Metals 2018, 8, 259. https://doi.org/10.3390/met8040259
Wang S, Liang Y, Chen B, Ye F, Lin J. AC Iron Loss Prediction and Magnetic Properties of Fe-6.5 wt. % Si Ribbons Prepared by Melt-Spinning. Metals. 2018; 8(4):259. https://doi.org/10.3390/met8040259
Chicago/Turabian StyleWang, Shuai, Yongfeng Liang, Biao Chen, Feng Ye, and Junpin Lin. 2018. "AC Iron Loss Prediction and Magnetic Properties of Fe-6.5 wt. % Si Ribbons Prepared by Melt-Spinning" Metals 8, no. 4: 259. https://doi.org/10.3390/met8040259
APA StyleWang, S., Liang, Y., Chen, B., Ye, F., & Lin, J. (2018). AC Iron Loss Prediction and Magnetic Properties of Fe-6.5 wt. % Si Ribbons Prepared by Melt-Spinning. Metals, 8(4), 259. https://doi.org/10.3390/met8040259






