Direct Numerical Study of a Molten Metal Drop Solidifying on a Cold Plate with Different Wettability
Abstract
:1. Introduction
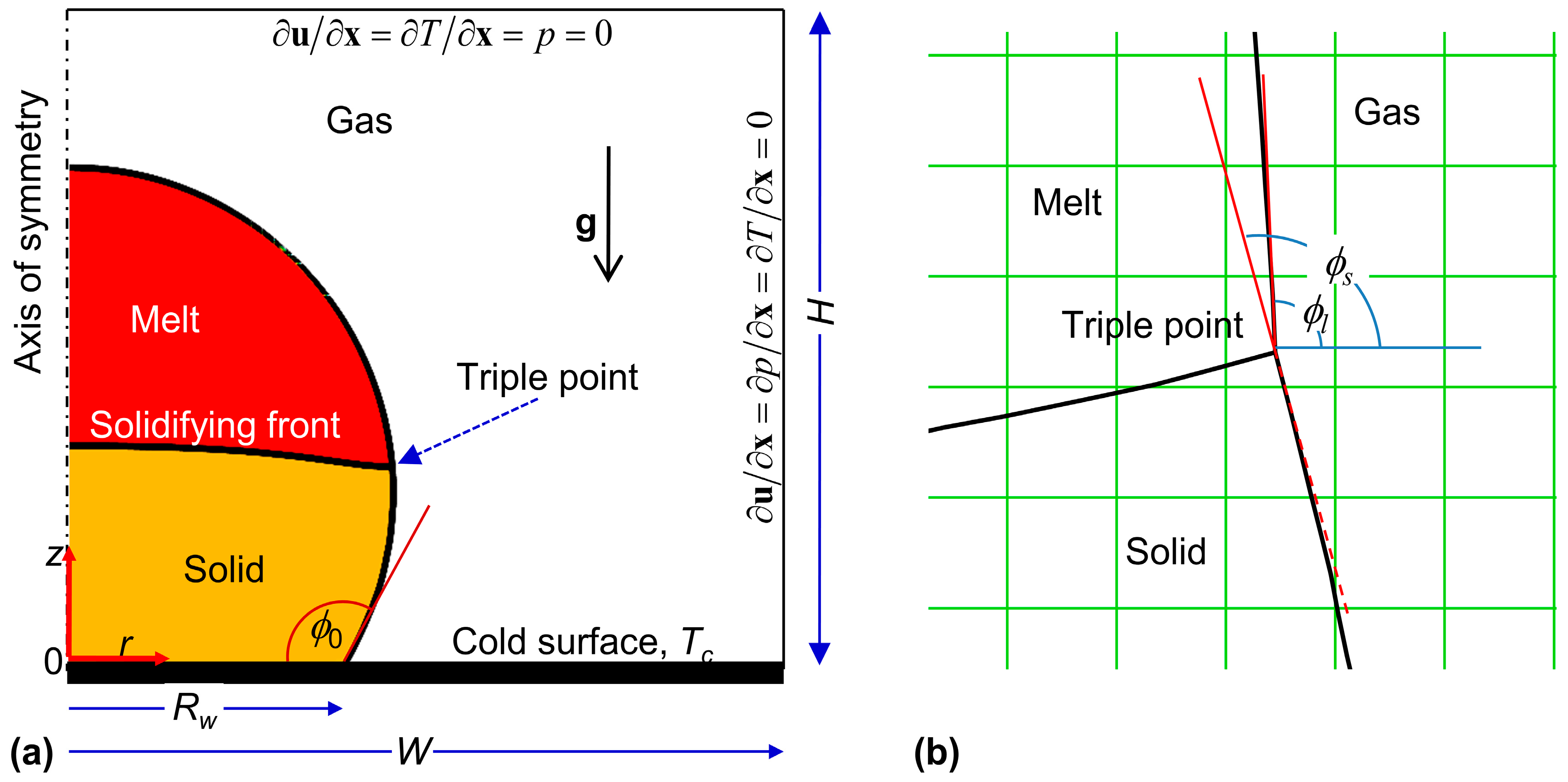
2. Numerical Problem and Method
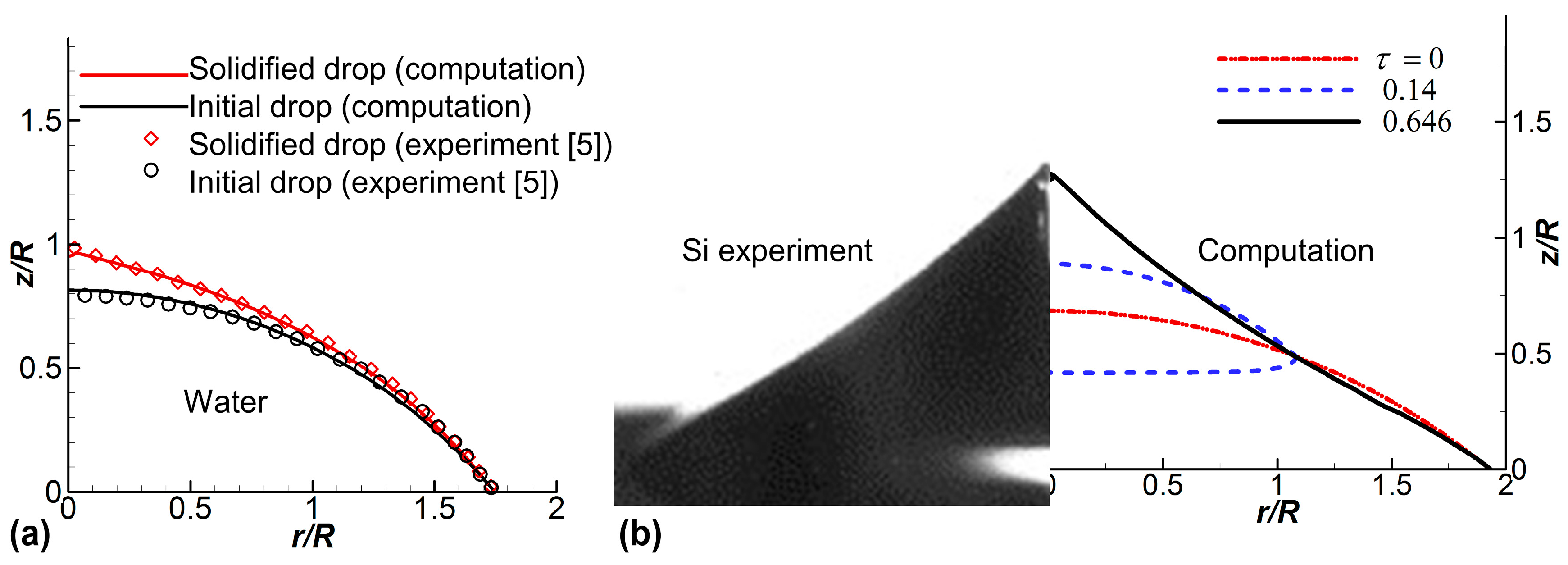
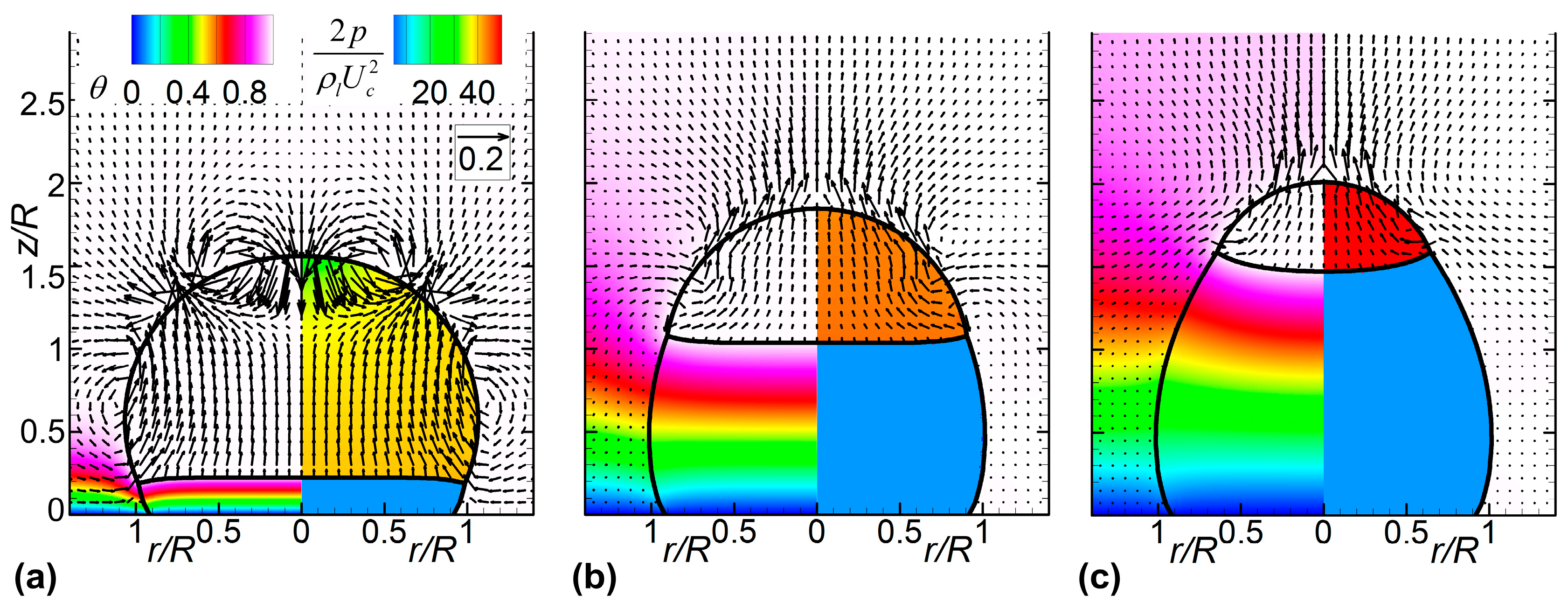
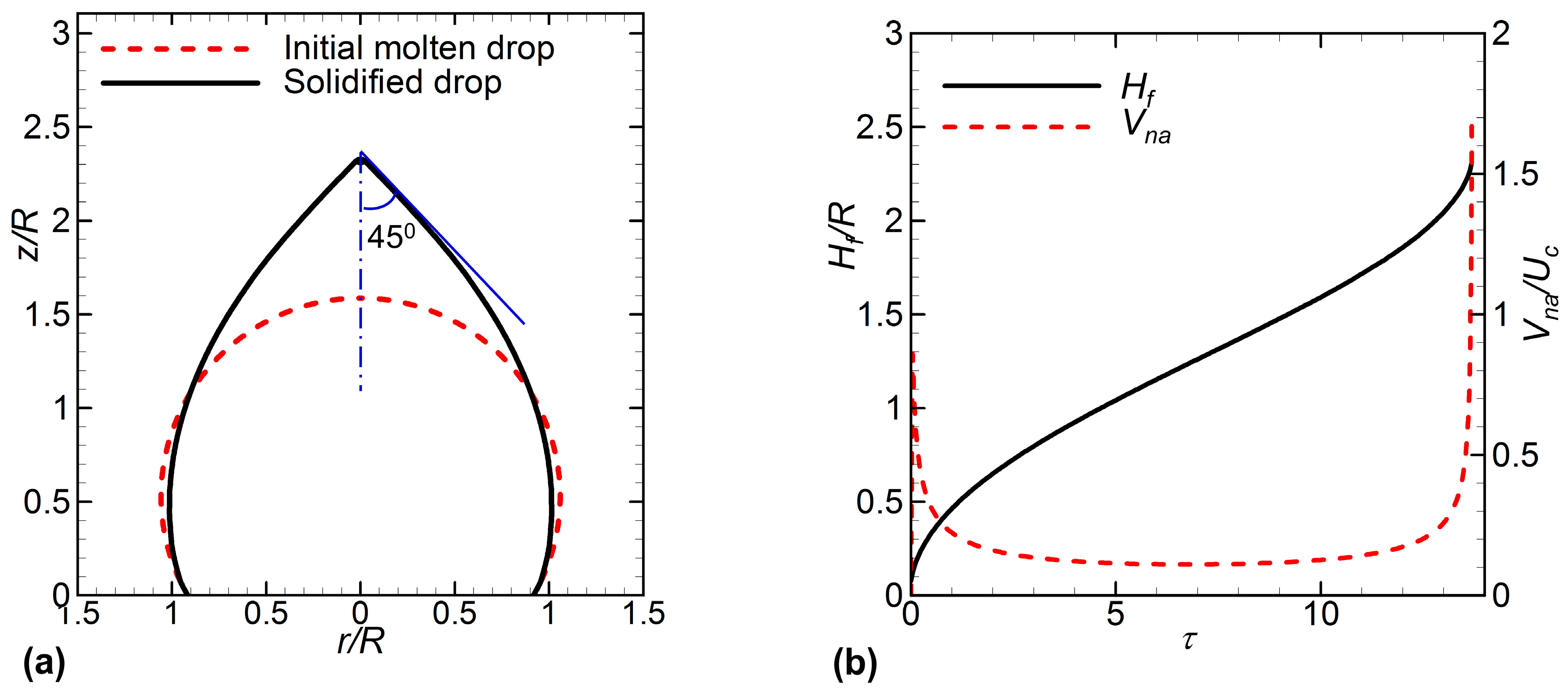
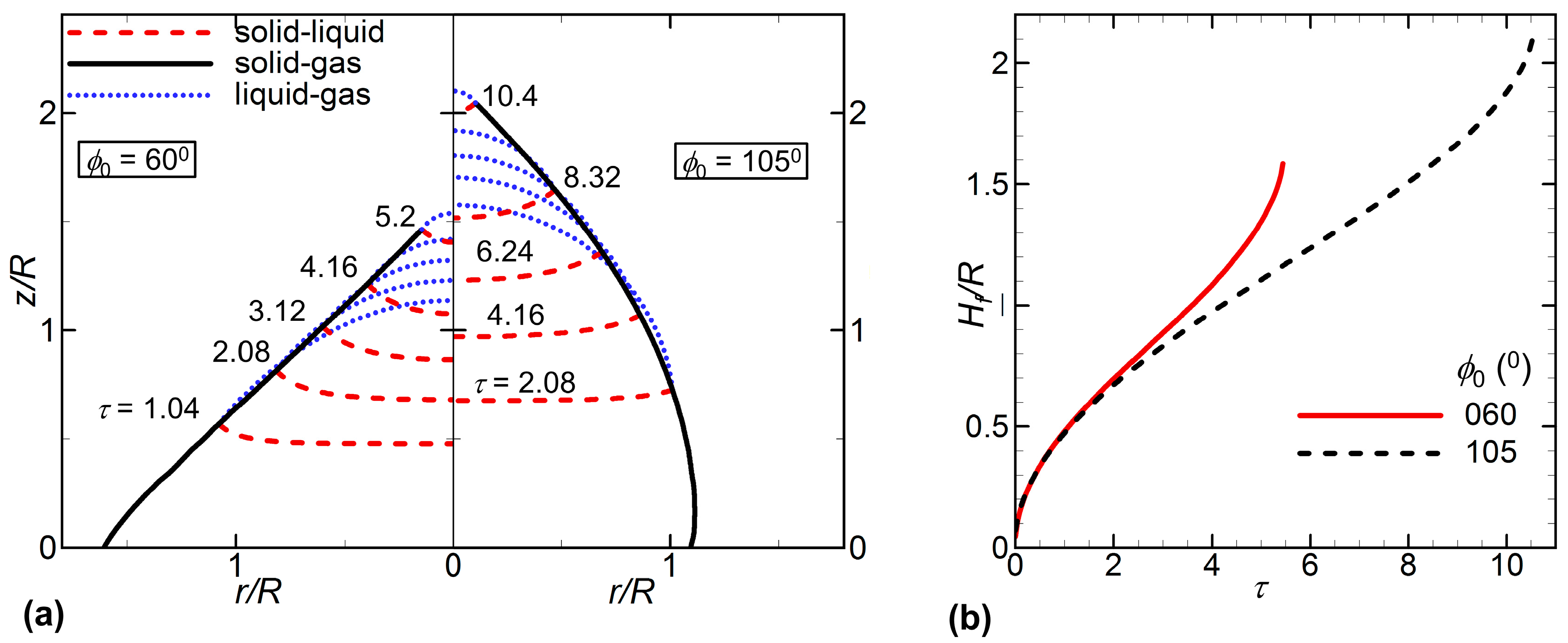
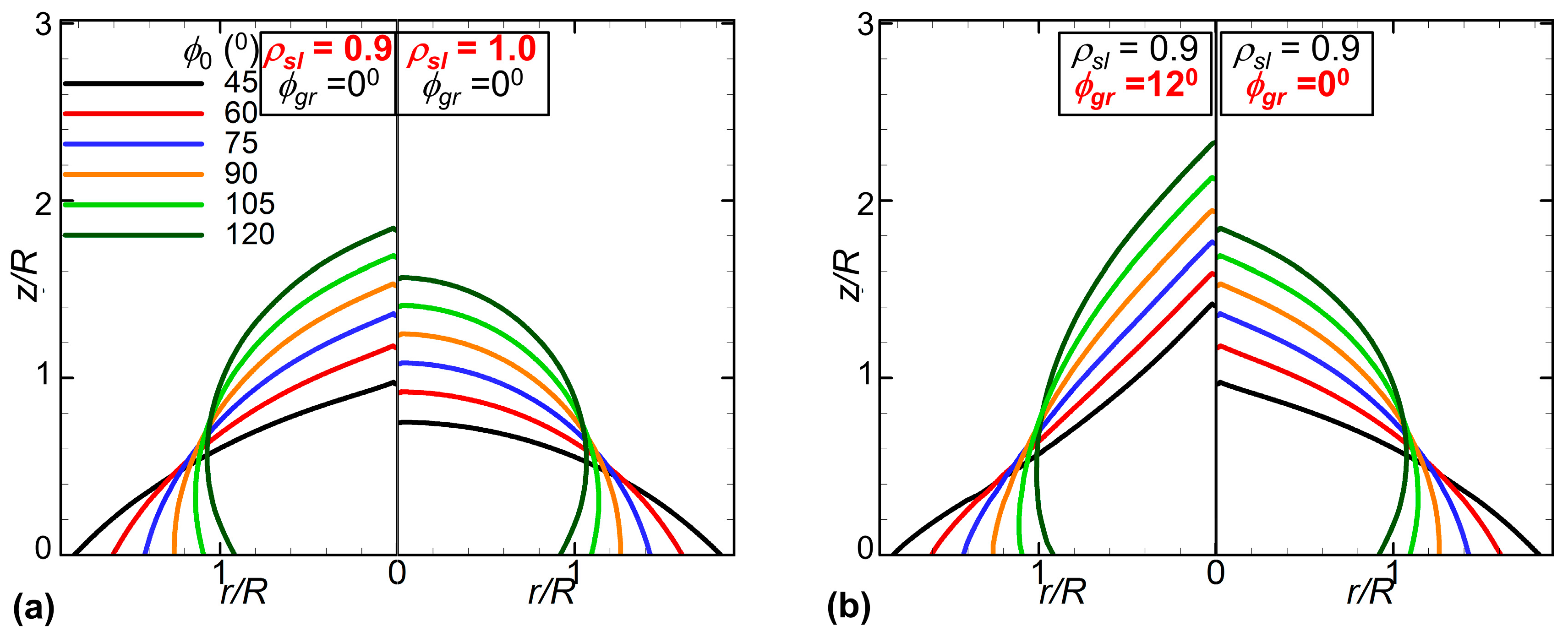
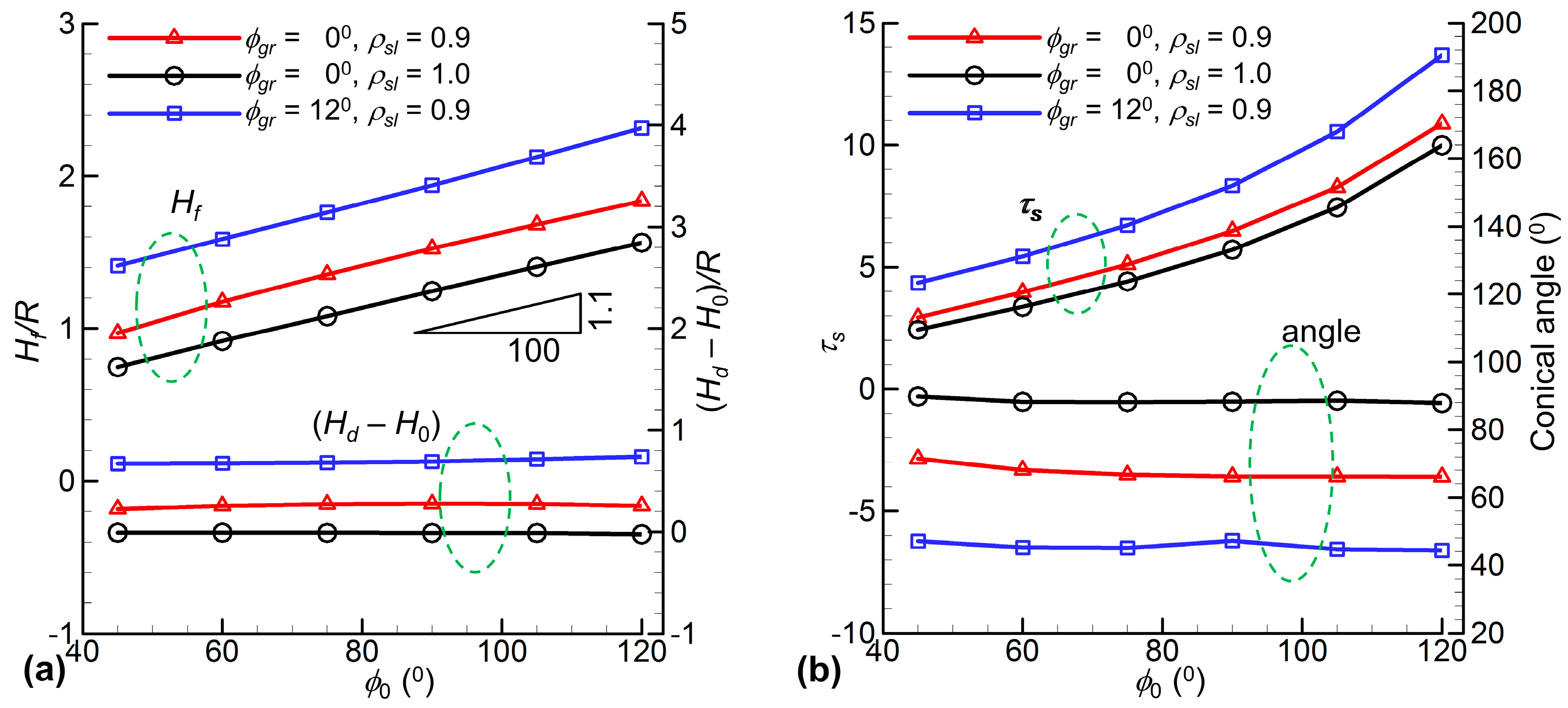
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Huang, L.; Liu, Z.; Liu, Y.; Gou, Y.; Wang, L. Effect of contact angle on water droplet freezing process on a cold flat surface. Exp. Therm. Fluid Sci. 2012, 40, 74–80. [Google Scholar] [CrossRef]
- Boinovich, L.; Emelyanenko, A.M.; Korolev, V.V.; Pashinin, A.S. Effect of Wettability on Sessile Drop Freezing: When Superhydrophobicity Stimulates an Extreme Freezing Delay. Langmuir 2014, 30, 1659–1668. [Google Scholar] [CrossRef] [PubMed]
- Hao, P.; Lv, C.; Zhang, X. Freezing of sessile water droplets on surfaces with various roughness and wettability. Appl. Phys. Lett. 2014, 104, 161609. [Google Scholar] [CrossRef]
- Jin, Z.; Cheng, X.; Yang, Z. Experimental investigation of the successive freezing processes of water droplets on an ice surface. Int. J. Heat Mass Transf. 2017, 107, 906–915. [Google Scholar] [CrossRef]
- Anderson, D.M.; Worster, M.G.; Davis, S.H. The case for a dynamic contact angle in containerless solidification. J. Cryst. Growth 1996, 163, 329–338. [Google Scholar] [CrossRef]
- Enríquez, O.R.; Marín, Á.G.; Winkels, K.G.; Snoeijer, J.H. Freezing singularities in water drops. Phys. Fluids 2012, 24, 091102. [Google Scholar] [CrossRef]
- Snoeijer, J.H.; Brunet, P. Pointy ice-drops: How water freezes into a singular shape. Am. J. Phys. 2012, 80, 764. [Google Scholar] [CrossRef]
- Hu, H.; Jin, Z. An icing physics study by using lifetime-based molecular tagging thermometry technique. Int. J. Multiph. Flow 2010, 36, 672–681. [Google Scholar] [CrossRef]
- Jin, Z.; Sui, D.; Yang, Z. The impact, freezing, and melting processes of a water droplet on an inclined cold surface. Int. J. Heat Mass Transf. 2015, 90, 439–453. [Google Scholar] [CrossRef]
- Satunkin, G.A. Determination of growth angles, wetting angles, interfacial tensions and capillary constant values of melts. J. Cryst. Growth 2003, 255, 170–189. [Google Scholar] [CrossRef]
- Itoh, H.; Okamura, H.; Nakamura, C.; Abe, T.; Nakayama, M.; Komatsu, R. Growth of spherical Si crystals on porous Si3N4 substrate that repels Si melt. J. Cryst. Growth 2014, 401, 748–752. [Google Scholar] [CrossRef]
- Hariharan, A.V.; Ravi, J. Laser Conversion of High Purity Silicon Powder to Densified Garnular Forms. U.S. Patent 9067792B1, 30 June 2015. [Google Scholar]
- Zhang, H.; Zhao, Y.; Lv, R.; Yang, C. Freezing of sessile water droplet for various contact angles. Int. J. Therm. Sci. 2016, 101, 59–67. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, X.; Min, J.; Liu, X. Modelling of sessile water droplet shape evolution during freezing with consideration of supercooling effect. Appl. Therm. Eng. 2017, 125, 644–651. [Google Scholar] [CrossRef]
- Schultz, W.W.; Worster, M.G.; Anderson, D.M. Solidifying sessile water droplets. In Interactive Dynamics of Convection and Solidification; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2001; pp. 209–226. ISBN 978-90-481-5719-8. [Google Scholar]
- Virozub, A.; Rasin, I.G.; Brandon, S. Revisiting the constant growth angle: Estimation and verification via rigorous thermal modeling. J. Cryst. Growth 2008, 310, 5416–5422. [Google Scholar] [CrossRef]
- Chaudhary, G.; Li, R. Freezing of water droplets on solid surfaces: An experimental and numerical study. Exp. Therm. Fluid Sci. 2014, 57, 86–93. [Google Scholar] [CrossRef]
- Vu, T.V.; Tryggvason, G.; Homma, S.; Wells, J.C.; Takakura, H. A front-tracking method for three-phase computations of solidification with volume change. J. Chem. Eng. Jpn. 2013, 46, 726–731. [Google Scholar] [CrossRef]
- Vu, T.V.; Tryggvason, G.; Homma, S.; Wells, J.C. Numerical investigations of drop solidification on a cold plate in the presence of volume change. Int. J. Multiph. Flow 2015, 76, 73–85. [Google Scholar] [CrossRef]
- Cao, Y.; Wu, Z.; Su, Y.; Xu, Z. Aircraft flight characteristics in icing conditions. Prog. Aerosp. Sci. 2015, 74, 62–80. [Google Scholar] [CrossRef]
- Dalili, N.; Edrisy, A.; Carriveau, R. A review of surface engineering issues critical to wind turbine performance. Renew. Sustain. Energy Rev. 2009, 13, 428–438. [Google Scholar] [CrossRef]
- Vu, T.V.; Homma, S.; Tryggvason, G.; Wells, J.C.; Takakura, H. Computations of breakup modes in laminar compound liquid jets in a coflowing fluid. Int. J. Multiph. Flow 2013, 49, 58–69. [Google Scholar] [CrossRef]
- Unverdi, S.O.; Tryggvason, G. A front-tracking method for viscous, incompressible, multi-fluid flows. J. Comput. Phys. 1992, 100, 25–37. [Google Scholar] [CrossRef]
- Vu, T.V.; Truong, A.V.; Hoang, N.T.; Tran, D.K. Numerical investigations of solidification around a circular cylinder under forced convection. J. Mech. Sci. Technol. 2016, 30, 5019–5028. [Google Scholar] [CrossRef]
- Vu, T.V.; Wells, J.C. Numerical simulations of solidification around two tandemly-arranged circular cylinders under forced convection. Int. J. Multiph. Flow 2017, 89, 331–344. [Google Scholar] [CrossRef]
- Liao, C.-C.; Chang, Y.-W.; Lin, C.-A.; McDonough, J.M. Simulating flows with moving rigid boundary using immersed-boundary method. Comput. Fluids 2010, 39, 152–167. [Google Scholar] [CrossRef]
- Vu, T.V. Three-phase computation of solidification in an open horizontal circular cylinder. Int. J. Heat Mass Transf. 2017, 111, 398–409. [Google Scholar] [CrossRef]
- Sun, Y.; Beckermann, C. Effect of solid–liquid density change on dendrite tip velocity and shape selection. J. Cryst. Growth 2009, 311, 4447–4453. [Google Scholar] [CrossRef]
- Nauenberg, M. Theory and experiments on the ice–water front propagation in droplets freezing on a subzero surface. Eur. J. Phys. 2016, 37, 045102. [Google Scholar] [CrossRef]
- Ajaev, V.S.; Davis, S.H. The effect of tri-junction conditions in droplet solidification. J. Cryst. Growth 2004, 264, 452–462. [Google Scholar] [CrossRef]
- Taira, K.; Nakata, J. Catching rays. Nat. Photonics 2010, 4, 602–603. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vu, T.V.; Nguyen, C.T.; Khanh, D.T. Direct Numerical Study of a Molten Metal Drop Solidifying on a Cold Plate with Different Wettability. Metals 2018, 8, 47. https://doi.org/10.3390/met8010047
Vu TV, Nguyen CT, Khanh DT. Direct Numerical Study of a Molten Metal Drop Solidifying on a Cold Plate with Different Wettability. Metals. 2018; 8(1):47. https://doi.org/10.3390/met8010047
Chicago/Turabian StyleVu, Truong V., Cuong T. Nguyen, and Duong T. Khanh. 2018. "Direct Numerical Study of a Molten Metal Drop Solidifying on a Cold Plate with Different Wettability" Metals 8, no. 1: 47. https://doi.org/10.3390/met8010047
APA StyleVu, T. V., Nguyen, C. T., & Khanh, D. T. (2018). Direct Numerical Study of a Molten Metal Drop Solidifying on a Cold Plate with Different Wettability. Metals, 8(1), 47. https://doi.org/10.3390/met8010047





