Choosing the Production Function Model for an Optimal Measurement of the Restructuring Efficiency of the Polish Metallurgical Sector in Years 2000–2015
Abstract
:1. Introduction
- A radical reduction of employment (127,000 people leaving the sector in years 1990–2015) [3];
- Lowering steel production to the market demand level (actually yearly average is around 9 mln. tons, in comparison to more than 13 mln. tons in the 90ties) [4];
- Increase in labour efficiency (switch from 84 tons/employee in the 90ties to 465 tons/employee in 2015);
- Withdrawal of outdated open-hearth furnace technology—completed in 2002 [5];
- Development of BOF and EAF technologies and implementation of production automation—actually 55% of Polish steel is being produced in converters (BOF) and the rest with EAF technology, with a tendency to lower the share of converter production during market downturn periods (down to 45% in 2009);
- Introducing new methods of organization and management, which allowed Polish ironworks to reach World Class Manufacturing global production standards [11].
2. Materials and Methods
2.1. Production Function Models
2.2. Decision-Making Model
3. Results
4. Discussion
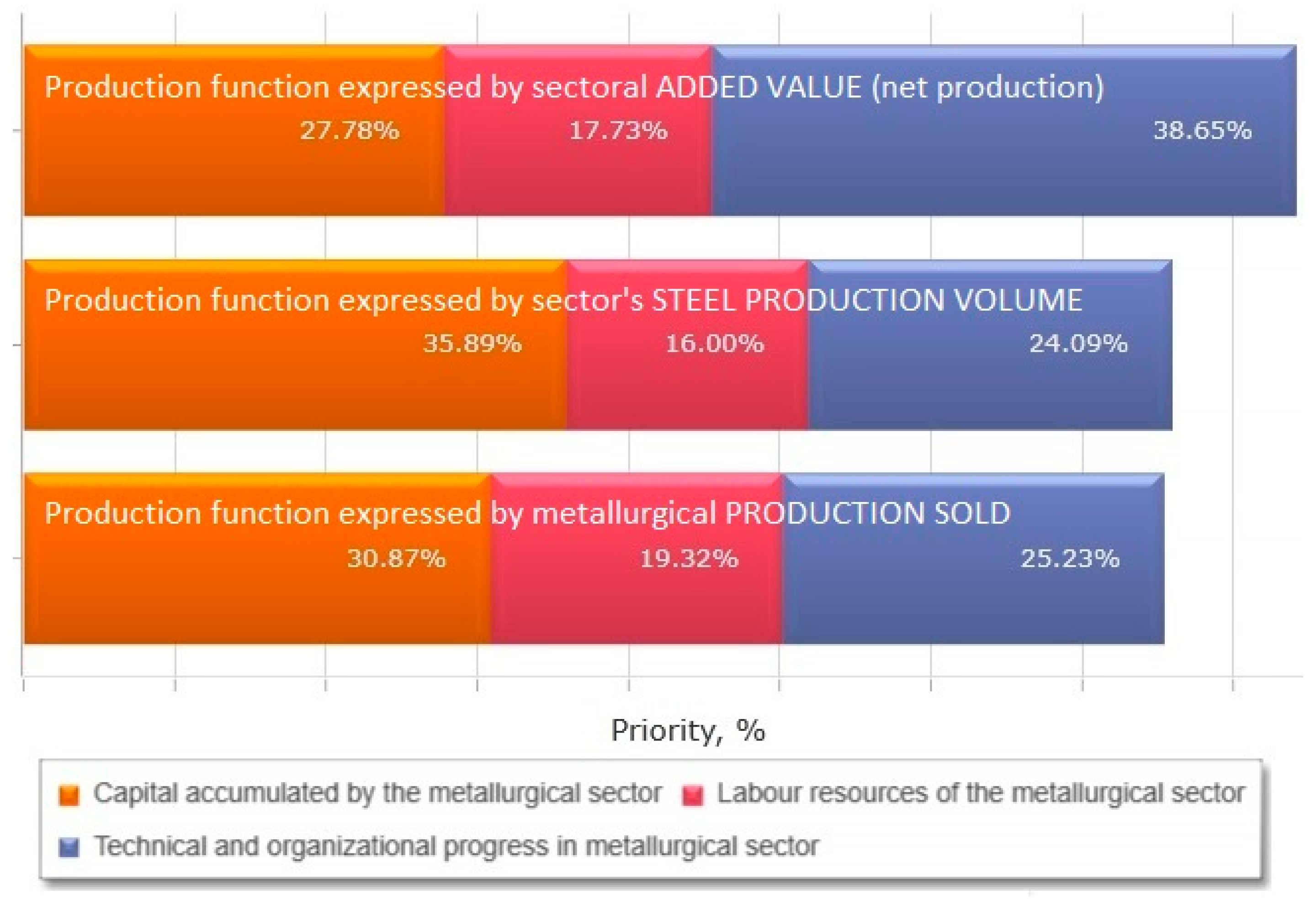
- From decision-maker’s perspective: as the 1st decision alternative obtained a significantly higher ranking that both 2nd and 3rd, neither 2nd nor 3rd can be perceived as a credible second-best solution—they both need to be rejected.
- From the perspective of former quantitative research: for the needs of econometric analysis of restructuring efficiency of Polish metallurgical sector, the dependent variable P expressed by the steel production volume (in mln. tons), together with explanatory variables C and L did not pass the statistical verification. Therefore, no production function models could be constructed on basis of this variable. Nevertheless, the rejection of this dependent variable in econometric analysis did not exclude its utilization in qualitative research. It can happen that the steel production volume, in reality, does reflect some aspects of the efficiency of restructuring processes, but the issue needs further research.
- In frames of AHP methodology: the IR ≤ 0.1 inconsistency ratio assumption still leaves space for a 10% inconsistency in expert evaluations; a very low distance between 2nd and 3rd decision alternatives (∆ = 0.23%) suggests a possibility of misinterpreting the evaluations with regard to ranking of two last decision alternatives.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Borowiecki, R. Effectiveness of Enterprises’s Restructuring and Economic Analysis as an Instrument of Restructuring Management. Acta Oeconomica Cassoviensia 1998, 2, 17–23. [Google Scholar]
- Gajdzik, B. The road of Polish steelworks towards market success—Changes after restructuring process. Metalurgija 2013, 52, 421–424. [Google Scholar]
- Gajdzik, B.; Ocieczek, W. Soft restructuring process in metallurgical enterprises in Poland. Metalurgija 2015, 54, 729–732. [Google Scholar]
- Gajdzik, B. Analysis of the size of steel production in Polish steel industry. In Proceedings of the METAL 2016 25th Anniversary International Conference on Metallurgy and Materials, Brno, Czech Republic, 25–27 May 2016; Tanger: Ostrava, Czech Republic, 2016; pp. 1787–1792. [Google Scholar]
- Gajdzik, B.; Janiszewski, K. Technological effects of metallurgical industry restructuring in Poland. Solid State Phenomena 2013, 212, 187–190. [Google Scholar] [CrossRef]
- Kłosok-Bazan, I.; Gajdzik, B.; Machnik-Słomka, J.; Ocieczek, W. Environmental aspects of innovation and new technology implementation in metallurgical industry. Metalurgija 2015, 54, 433–436. [Google Scholar]
- Gajdzik, B. The ecological value of metallurgical enterprise after privatization and restructuring. Metalurgija 2012, 51, 129–132. [Google Scholar]
- Gajdzik, B.; Burchart-Korol, D. Eco-innovation in manufacturing plants illustrated with an example of steel products development. Metalurgija 2011, 50, 63–66. [Google Scholar]
- Gajdzik, B. Comprehensive classification of environmental aspects in metallurgical enterprise. Metalurgija 2012, 51, 541–544. [Google Scholar]
- Szczucka-Lasota, B.; Gajdzik, B.; Węgrzyn, T.; Wszołek, Ł. Steel Weld Metal Deposit Measured Properties after Immediate Micro-Jet Cooling. Metals 2017, 7, 339. [Google Scholar] [CrossRef]
- Gajdzik, B. World Class Manufacturing in metallurgical enterprise. Metalurgija 2013, 52, 131–134. [Google Scholar]
- Szymszal, J.; Gajdzik, B.; Kaczmarczyk, G. The use of modern statistical methods to optimize production systems in foundries. Arch. Foundry Eng. 2016, 16, 115–120. [Google Scholar] [CrossRef]
- Cobb, C.W.; Douglas, P.H. A Theory of Production. Am. Econ. Rev. 1928, 18, 139–165. [Google Scholar]
- Chenery, H.B.; Clark, P. Interindustry Economics; John Willey & Son, Inc.: New York, NY, USA, 1959. [Google Scholar]
- Walters, A.A. Production and cost functions: An econometric survey. Econometrica 1963, 31, 1–66. [Google Scholar] [CrossRef]
- Brown, M. (Ed.) The Theory and Empirical Analysis of Production; Columbia University Press: New York, NY, USA, 1967. [Google Scholar]
- Intriligator, M.D. Mathematical Optimization and Economic Theory; Prentice Hall: Englewood Cliffs, NJ, USA, 1971. [Google Scholar]
- Pawłowski, Z. An Econometric Analysis of the Production Process; PWN: Warsaw, Poland, 1976. [Google Scholar]
- Welfe, W. The Econometric Models of the Polish Economy; PWE: Warsaw, Poland, 1992. [Google Scholar]
- Arrow, K.J.; Chenery, H.; Minhas, B.; Solow, R.W. Capital-labor substitution and economic efficiency. Rev. Econ. Stat. 1963, 42, 225–250. [Google Scholar] [CrossRef]
- Tinbergen, J. Production, Income and Welfare: The Search for an Optimal Social Order; University of Nebraska Press: Lincoln, NE, USA, 1985. [Google Scholar]
- Borkowski, B.; Dudek, H.; Szczęsny, W. Ekonometria: Wybrane Zagadnienia; PWN: Warsaw, Poland, 2004. [Google Scholar]
- Intriligator, M.D. Econometric Models, Techniques and Applications; North-Holland: Amsterdam, The Netherlands, 1978. [Google Scholar]
- Młody, M. Backshoring in Light of the Concepts of Divestment and De-internationalization: Similarities and Differences. Entrep. Bus. Econ. Rev. 2016, 4, 167–180. [Google Scholar] [CrossRef]
- Database of the Central Statistical Office of Poland (GUS). Available online: www.stat.gov.pl (accessed on 7 December 2017).
- Peleckis, K. The Use of Game Theory for Making Rational Decisions in Business Negotiations: A Conceptual Model. Entrep. Bus. Econ. Rev. 2015, 3, 105–121. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Hierarchy Process; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Kou, C.; Xiao, P.; Kang, A.; Mikhailenko, P.; Baaj, H.; Wu, Z. Methods to Evaluate the Aging Grades of Reclaimed Asphalt Binder. Appl. Sci. 2017, 7, 1209. [Google Scholar] [CrossRef]
- Gawlik, R. The use of Analytic Hierarchy Process to analyse international corporations’ operating environment. Crac. Rev. Econ. Manag. 2012, 891, 19–30. [Google Scholar]
- Gawlik, R. Encompassing the work-life balance into early career decision-making of future employees through the Analytic Hierarchy Process. In Advances in Intelligent Systems and Computing Series: Advances in Human Factors, Business Management and Leadership; Kantola, J.I., Barath, T., Nazir, S., Eds.; AHFE 2017. Advances in Intelligent Systems and Computing, vol. 594; Springer International Publishing AG: Cham, Switzerland, 2018; pp. 137–147. ISBN 978-3-319-60371-1. [Google Scholar] [CrossRef]
- Belton, V.; Gear, A.E. On a shortcoming of Saaty’s method of analytic hierarchies. Omega 1983, 11, 228–230. [Google Scholar] [CrossRef]
- Dyer, J.S. Remarks on the Analytic Hierarchy Process. Manag. Sci. 1990, 36, 249–258. [Google Scholar] [CrossRef]
- Barzilai, J. Notes on the Analytic Hierarchy Process. In Proceedings of the 2001 NSF Design, Service & Manufacturing Grantees & Research Conference, Tampa, FL, USA, 7–10 January 2001; National Science Foundation: Tampa, FL, USA; pp. 1–6. [Google Scholar]
- Saaty, T.L.; Vargas, L.; Whitaker, R. Addressing with brevity criticism of the Analytic Hierarchy Process. Int. J. Anal. Hierarchy Process 2009, 1, 121–134. [Google Scholar] [CrossRef]
- Wang, G.; Tian, X.; Hu, Y.; Evans, R.D.; Tian, M.; Wang, R. Manufacturing Process Innovation-Oriented Knowledge Evaluation Using MCDM and Fuzzy Linguistic Computing in an Open Innovation Environment. Sustainability 2017, 9, 1630. [Google Scholar] [CrossRef]
- Poh, K.L.; Liang, Y. Multiple-Criteria Decision Support for a Sustainable Supply Chain: Applications to the Fashion Industry. Informatics 2017, 4, 36. [Google Scholar] [CrossRef]
- Dinmohammadi, A.; Shafiee, M. Determination of the Most Suitable Technology Transfer Strategy for Wind Turbines Using an Integrated AHP-TOPSIS Decision Model. Energies 2017, 10, 642. [Google Scholar] [CrossRef]
- Gajdzik, B. Application of the Cobb-Douglas production function for analysis of production in Polish steel industry. In Proceedings of the METAL 2017 26th Anniversary International Conference on Metallurgy and Materials, Brno, Czech Republic, 24–26 May 2017; Tanger: Ostrava, Czech Republic, 2017. [Google Scholar]
- Marona, B.; Wilk, A. Tenant Mix Structure in Shopping Centres: Some Empirical Analyses from Poland. Entrep. Bus. Econ. Rev. 2016, 4, 51–65. [Google Scholar] [CrossRef]
- Gajdzik, B. Prognostic modeling of total steel production and according to production technology in Poland. Metalurgija 2017, 56, 241–244. [Google Scholar]
- Gajdzik, B. The Predictive Scenario Analysis in a Business Model: Variants of Possible Steel Production Trajectories and Efficiency in Poland. In Strategic Performance Management, New Concepts and Contermproray Trends; Jabłoński, M., Ed.; Nova Science Publishers, Inc.: Hauppauge, NY, USA, 2017; pp. 235–252. ISBN 978-1-53612-682-2. [Google Scholar]
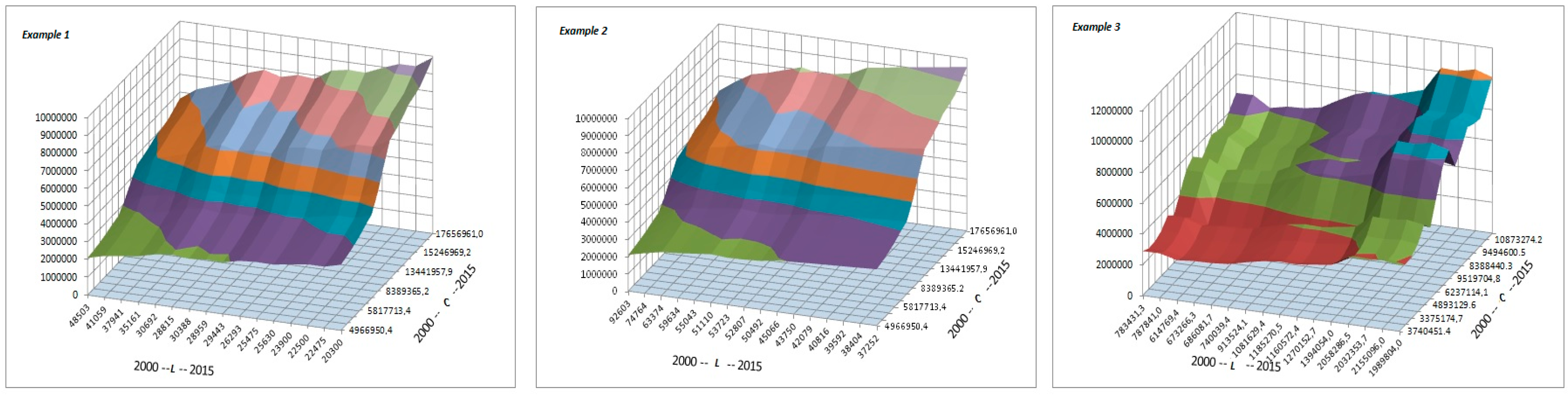
| Year | Steel Prod. | Net Product.* | Production Sold * | Employment | Working Time ** | Personnel Costs | Noncurrent Assets * | Depreciation Costs * | Inventories |
|---|---|---|---|---|---|---|---|---|---|
| Units | mln. Tons | kPLN | kPLN | Persons | hrs | kPLN | kPLN | kPLN | kPLN |
| 2000 | 10.498 | 2,368,816 | 5,594,079 | 48,503 | 92,603 | 960,635 | 3,740,451 | 475,558 | 1,200,118 |
| 2001 | 8.809 | 2,354,104 | 6,510,389 | 41,059 | 74,764 | 1,001,291 | 3,303,025 | 455,410 | 880,650 |
| 2002 | 8.367 | 2,478,104 | 7,634,910 | 37,941 | 63,374 | 805,283 | 3,375,175 | 363,009 | 771,513 |
| 2003 | 9.107 | 2,855,602 | 8,732,778 | 35,161 | 59,634 | 861,849 | 3,826,378 | 521,455 | 945,948 |
| 2004 | 10.578 | 3,510,601 | 11,034,345 | 30,692 | 55,043 | 877,946 | 4,893,130 | 475,292 | 1,761,401 |
| 2005 | 8.336 | 3,726,759 | 11,749,752 | 28,815 | 51,110 | 951,725 | 4,112,924 | 504,061 | 1,704,774 |
| 2005 | 9.992 | 4,333,148 | 14,068,288 | 30,388 | 53,723 | 1,181,508 | 6,237,114 | 520,332 | 2,217,204 |
| 2007 | 10.631 | 5,059,092 | 16,948,513 | 28,959 | 52,807 | 1,282,866 | 8,479,986 | 616,023 | 2,783,153 |
| 2008 | 9.727 | 5,639,094 | 18,559,869 | 29,443 | 50,492 | 1,500,126 | 9,519,705 | 620,372 | 3,465,137 |
| 2009 | 7.128 | 6,246,660 | 18,630,690 | 26,293 | 45,066 | 1,413,797 | 7,243,792 | 632,130 | 2,731,506 |
| 2010 | 7.993 | 6,808,157 | 21,225,904 | 25,475 | 43,750 | 1,616,132 | 8,388,440 | 733,173 | 3,242,684 |
| 2011 | 8.776 | 7,893,795 | 25,711,174 | 25,630 | 42,079 | 1,782,271 | 9,849,655 | 804,536 | 4,515,567 |
| 2012 | 8.348 | 8,531,358 | 27,069,137 | 23,900 | 40,816 | 2,458,427 | 9,494,601 | 861,211 | 4,509,595 |
| 2013 | 7.950 | 8,527,592 | 27,558,472 | 22,500 | 39,592 | 2,034,230 | 9,343,192 | 845,370 | 5,141,268 |
| 2014 | 8.558 | 9,324,705 | 29,113,443 | 22,475 | 38,404 | 2,157,034 | 10,873,274 | 842,098 | 5,155,518 |
| 2015 | 9.202 | 1,0353,553 | 30,943,324 | 20,300 | 37,252 | 2,309,704 | 12,408,001 | 659,700 | 5,522,684 |
| CRITERIA and Sub-Criteria | Prioritization (%) | |
|---|---|---|
| Local | Global | |
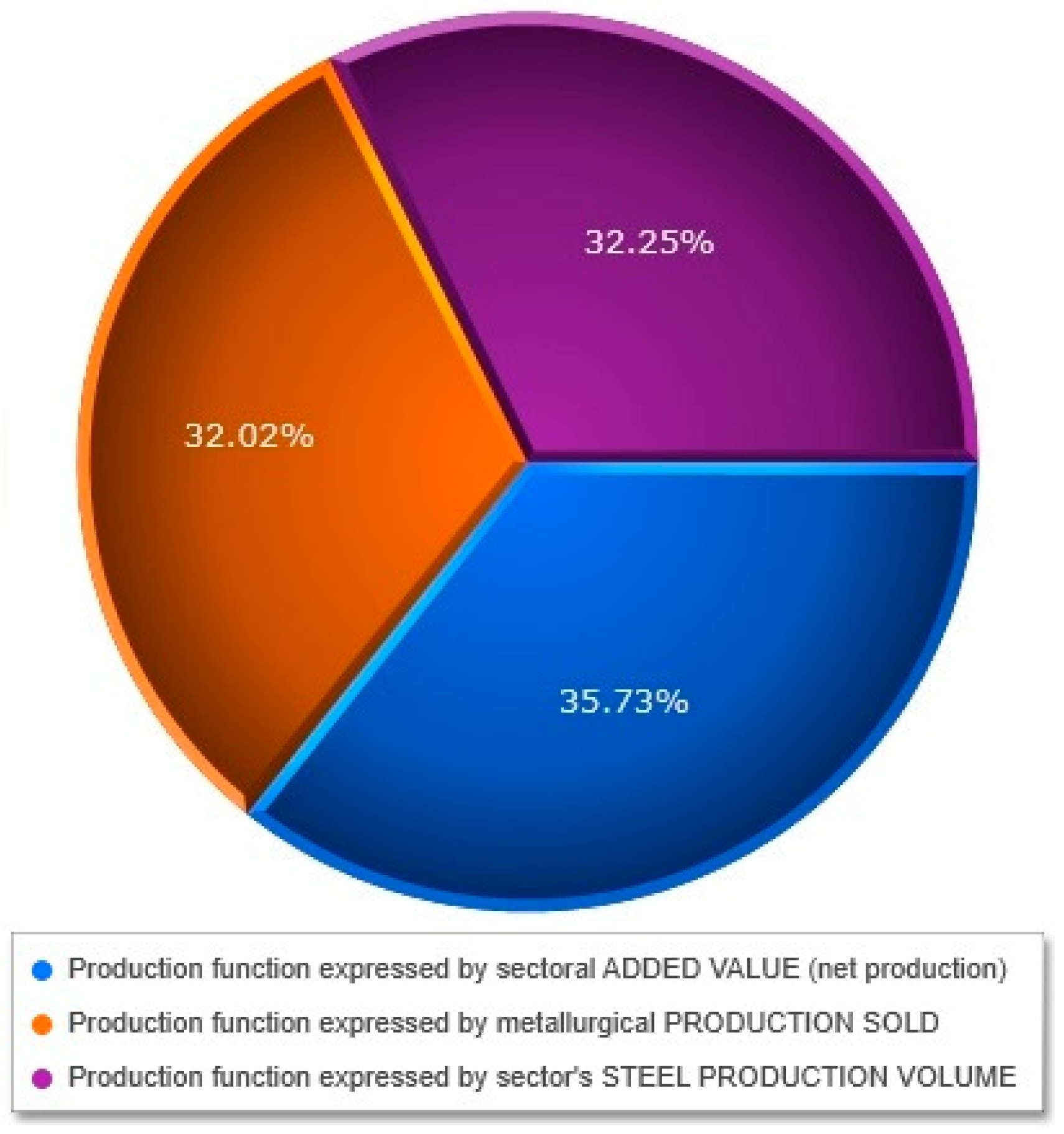
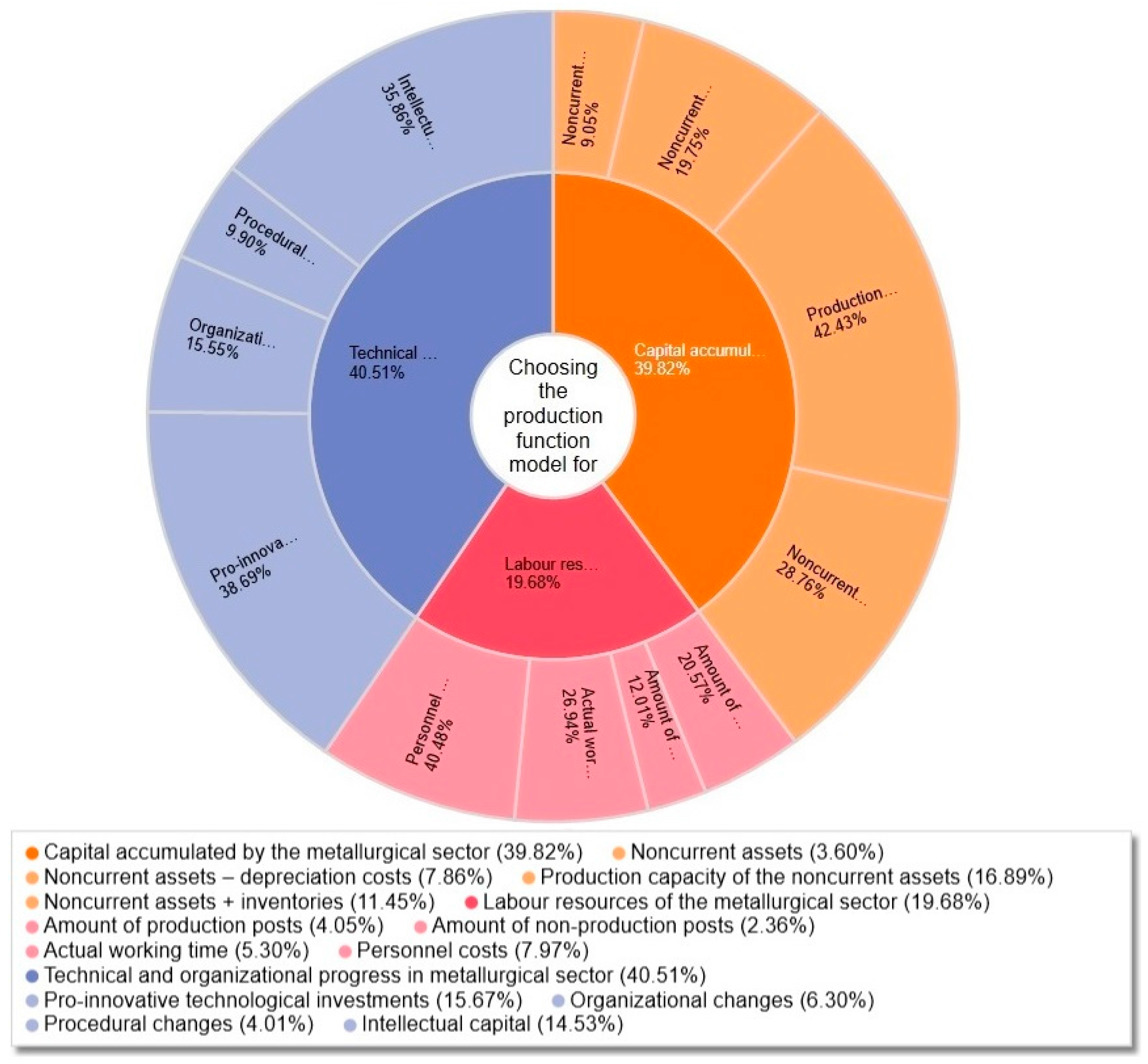
| CAPITAL ACCUMULATED BY THE METALLURGICAL SECTOR | 39.82% | 39.82% |
| Noncurrent assets | 9.05% | 3.60% |
| Noncurrent assets—depreciation costs | 19.75% | 7.86% |
| Production capacity of the noncurrent assets | 42.43% | 16.89% |
| Noncurrent assets + inventories | 28.76% | 11.45% |
| LABOUR RESOURCES OF THE METALLURGICAL SECTOR | 19.68% | 19.68% |
| Amount of production posts | 20.57% | 4.05% |
| Amount of non-production posts | 12.01% | 2.36% |
| Actual working time | 26.94% | 5.30% |
| Personnel costs | 40.48% | 7.97% |
| TECHNICAL AND ORGANIZATIONAL PROGRESS IN METALLURGICAL SECTOR | 40.51% | 40.51% |
| Pro-innovative technological investments | 38.69% | 15.67% |
| Organizational changes | 15.55% | 6.30% |
| Procedural changes | 9.90% | 4.01% |
| Intellectual capital | 35.86% | 14.53% |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gajdzik, B.; Gawlik, R. Choosing the Production Function Model for an Optimal Measurement of the Restructuring Efficiency of the Polish Metallurgical Sector in Years 2000–2015. Metals 2018, 8, 23. https://doi.org/10.3390/met8010023
Gajdzik B, Gawlik R. Choosing the Production Function Model for an Optimal Measurement of the Restructuring Efficiency of the Polish Metallurgical Sector in Years 2000–2015. Metals. 2018; 8(1):23. https://doi.org/10.3390/met8010023
Chicago/Turabian StyleGajdzik, Bożena, and Remigiusz Gawlik. 2018. "Choosing the Production Function Model for an Optimal Measurement of the Restructuring Efficiency of the Polish Metallurgical Sector in Years 2000–2015" Metals 8, no. 1: 23. https://doi.org/10.3390/met8010023
APA StyleGajdzik, B., & Gawlik, R. (2018). Choosing the Production Function Model for an Optimal Measurement of the Restructuring Efficiency of the Polish Metallurgical Sector in Years 2000–2015. Metals, 8(1), 23. https://doi.org/10.3390/met8010023






