Local Buckling Behavior and Plastic Deformation Capacity of High-Strength Pipe at Strike-Slip Fault Crossing
Abstract
:1. Introduction
2. State of the Art in Buckling Failure Criteria for Line Pipes
2.1. CSA Z662 Model (2015)
2.2. UOA Model (2006)
2.3. CRES-GB 50470 Model (2017)
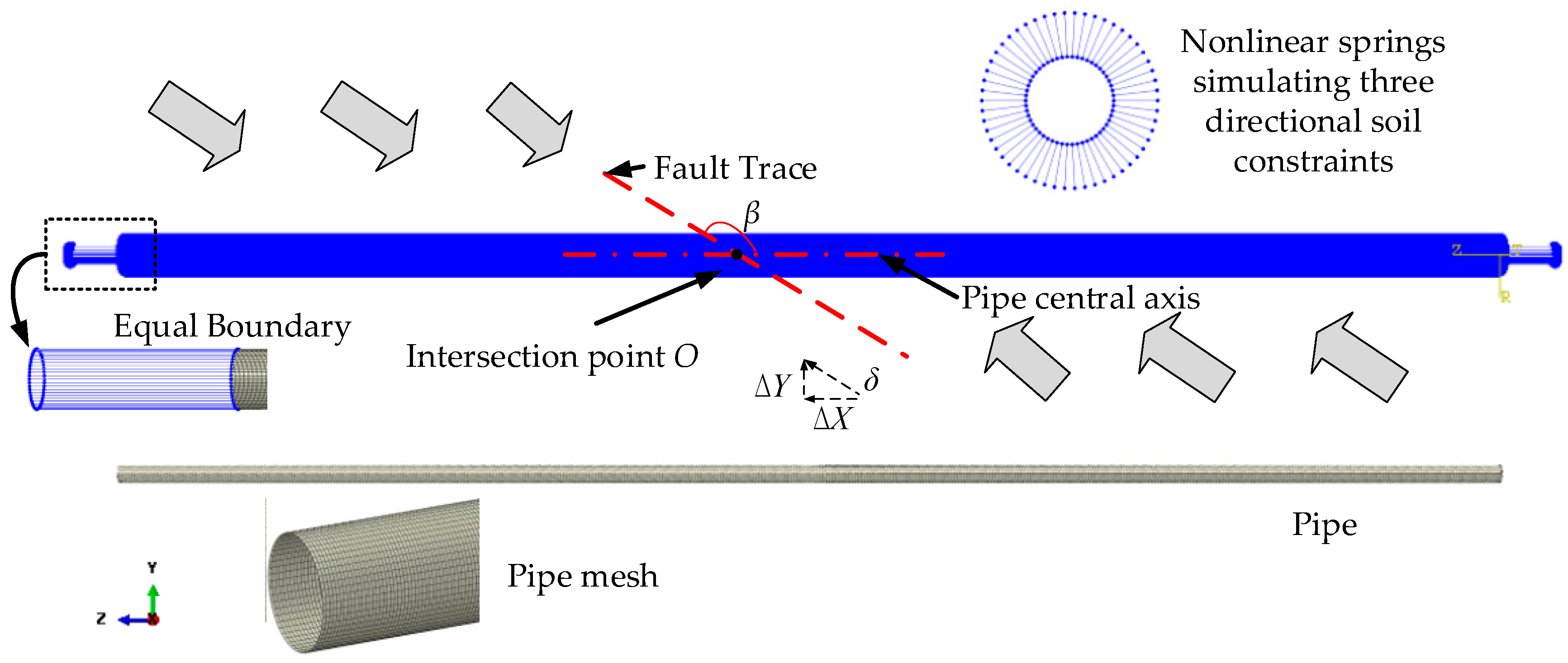
3. Finite Element Model
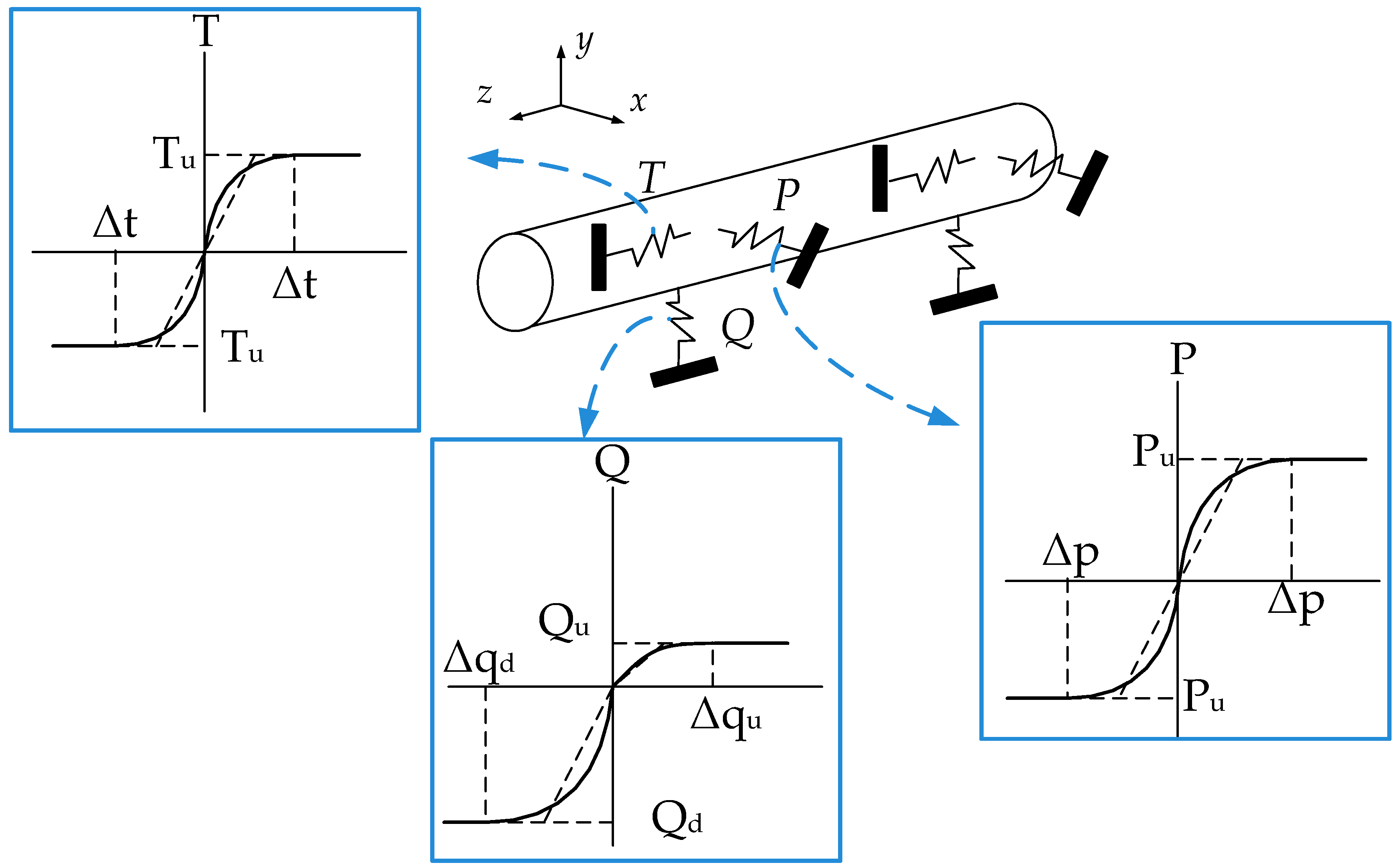
3.1. Modelling Pipe-Soil Interaction with Discrete Nonlinear Soil Springs
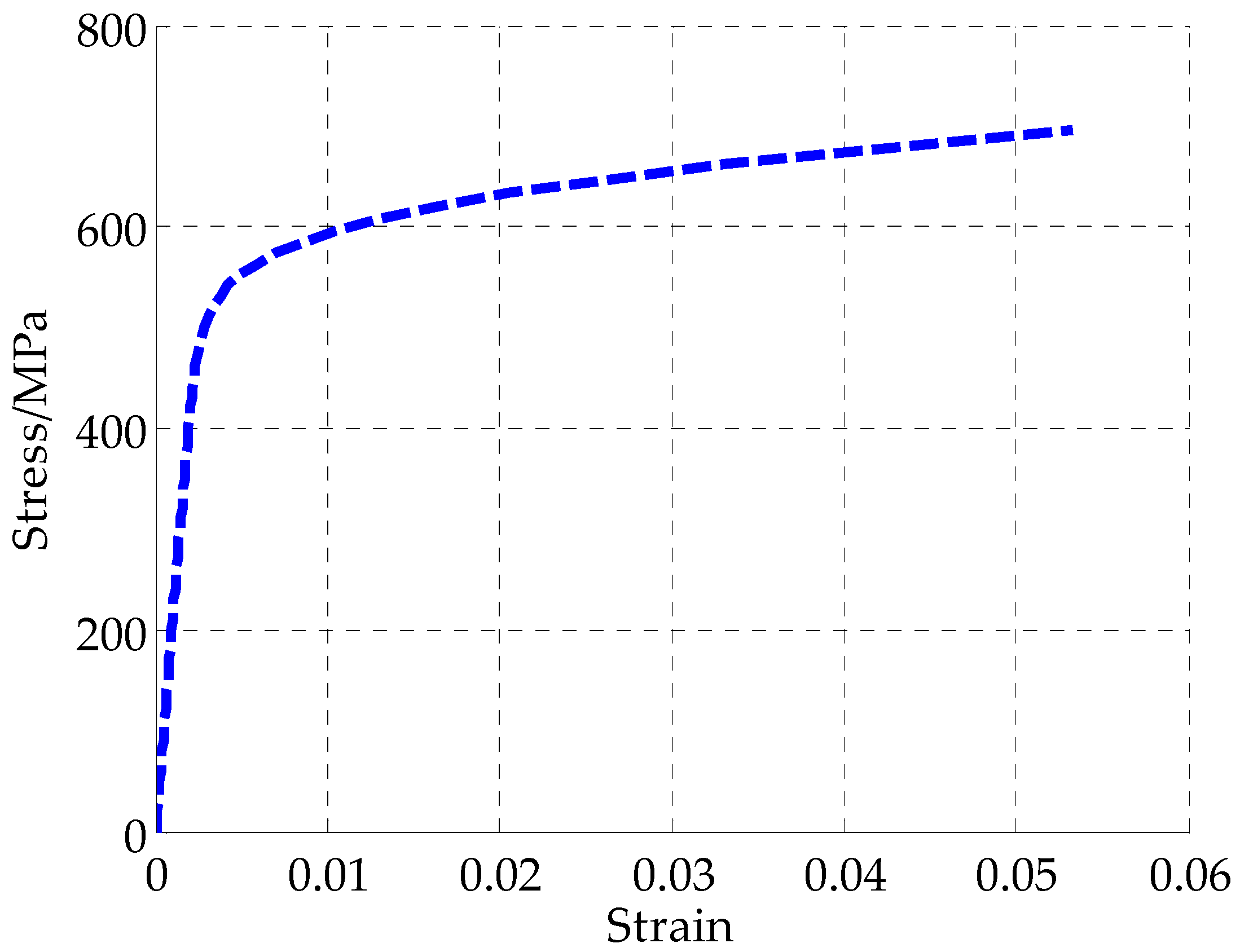
3.2. Modelling of Pipe
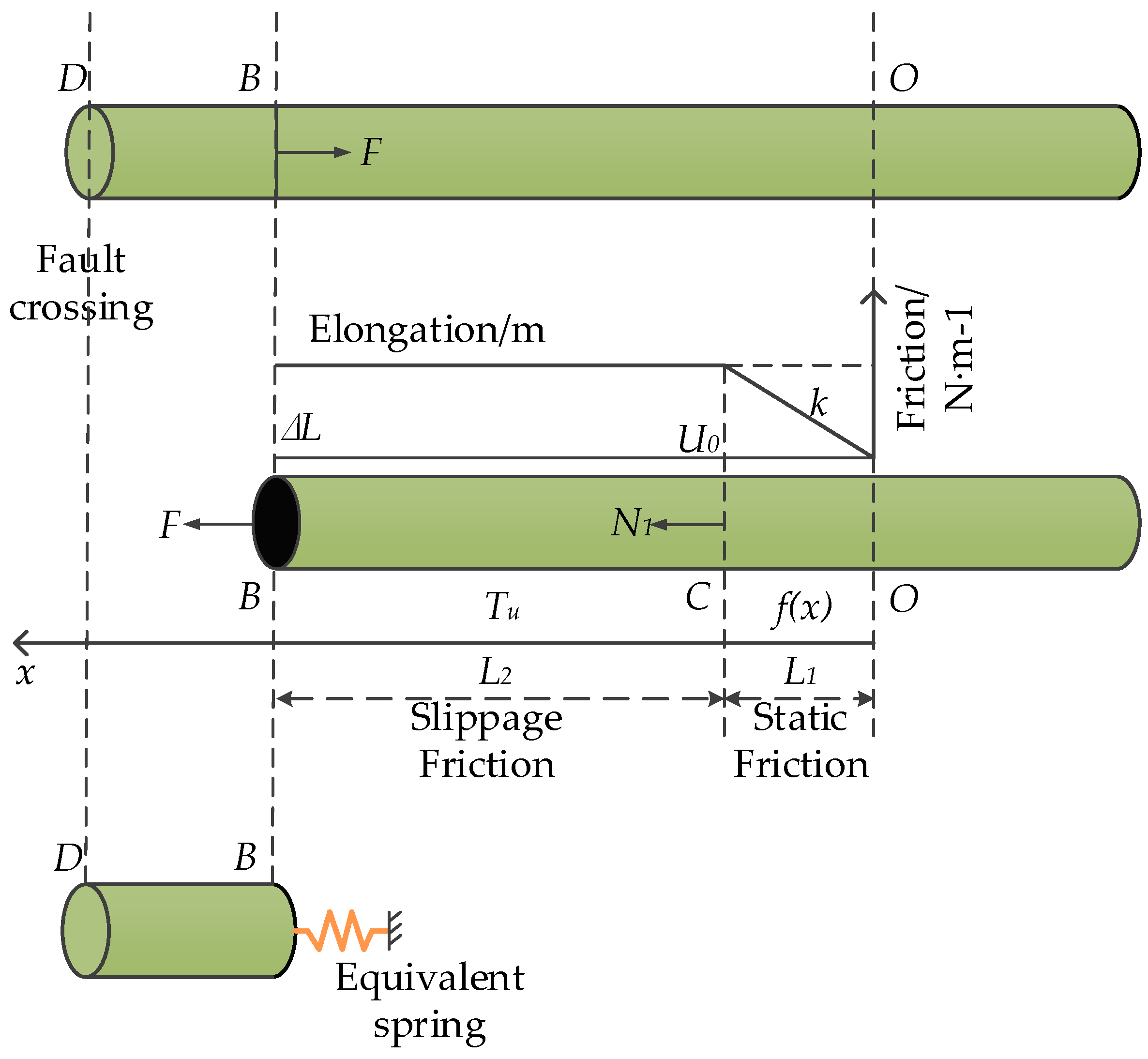
3.3. Constitutive Model of Equivalent Boundary
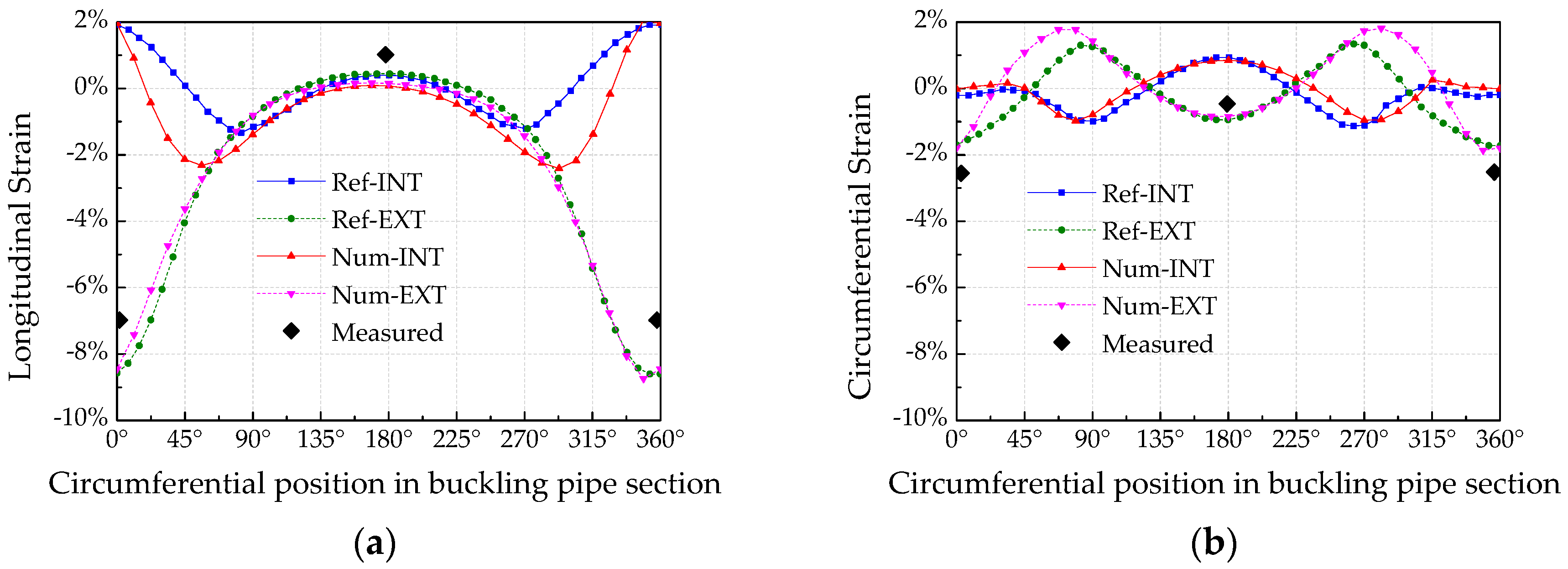
3.4. Validation of Proposed Model
4. Results and Discussion
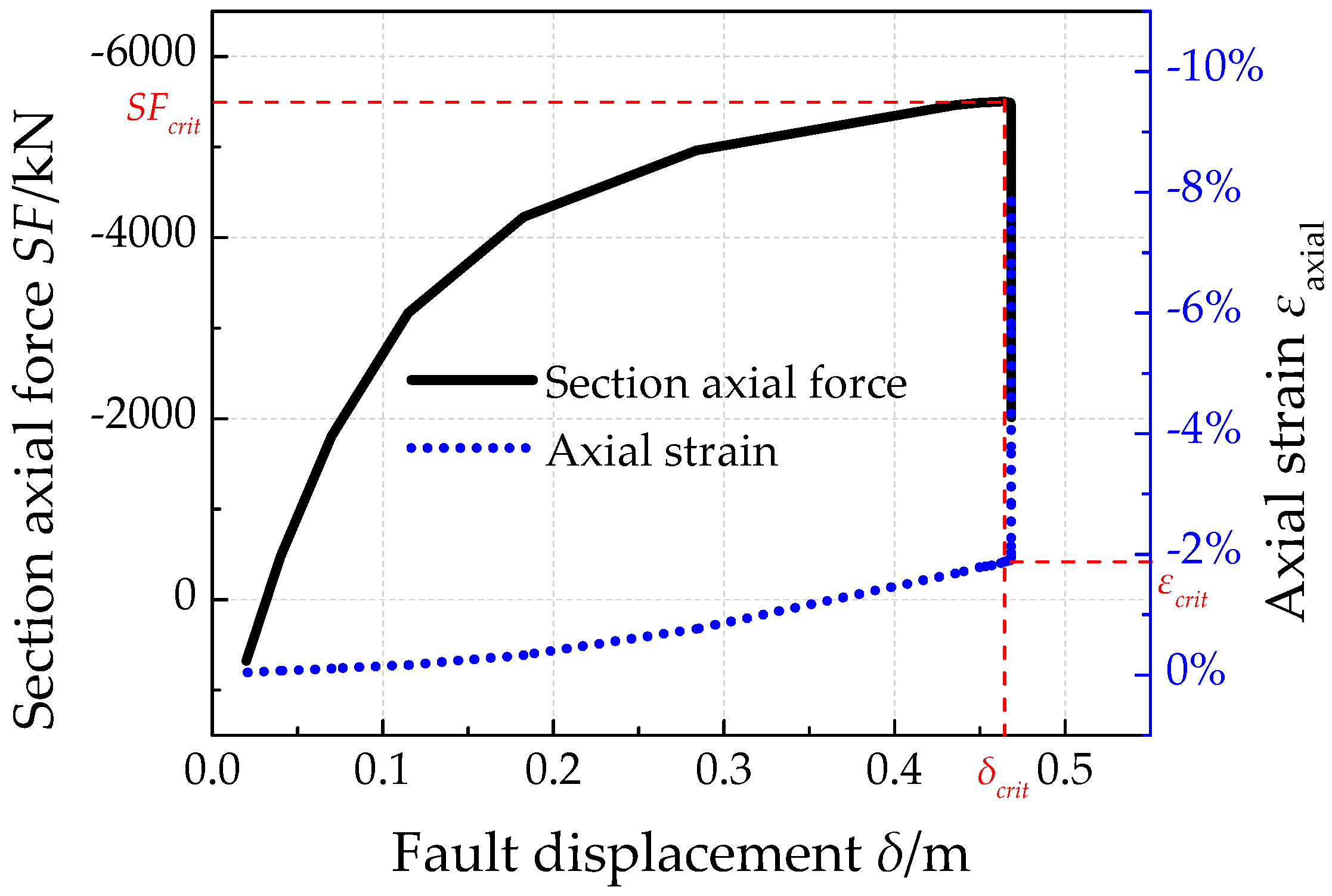
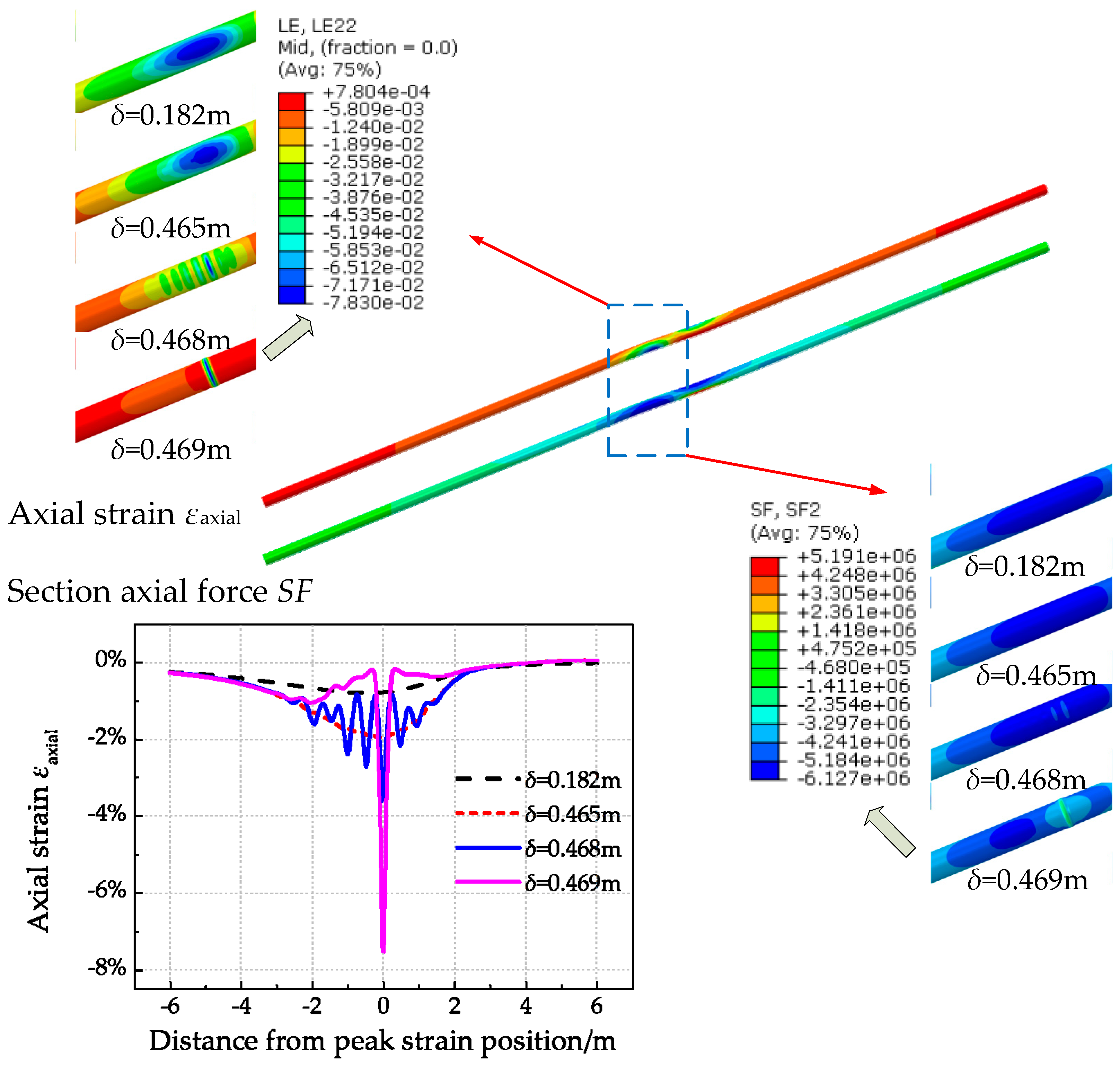
4.1. Baseline Analysis for the Local Buckling Failure of X80 Pipe Steel
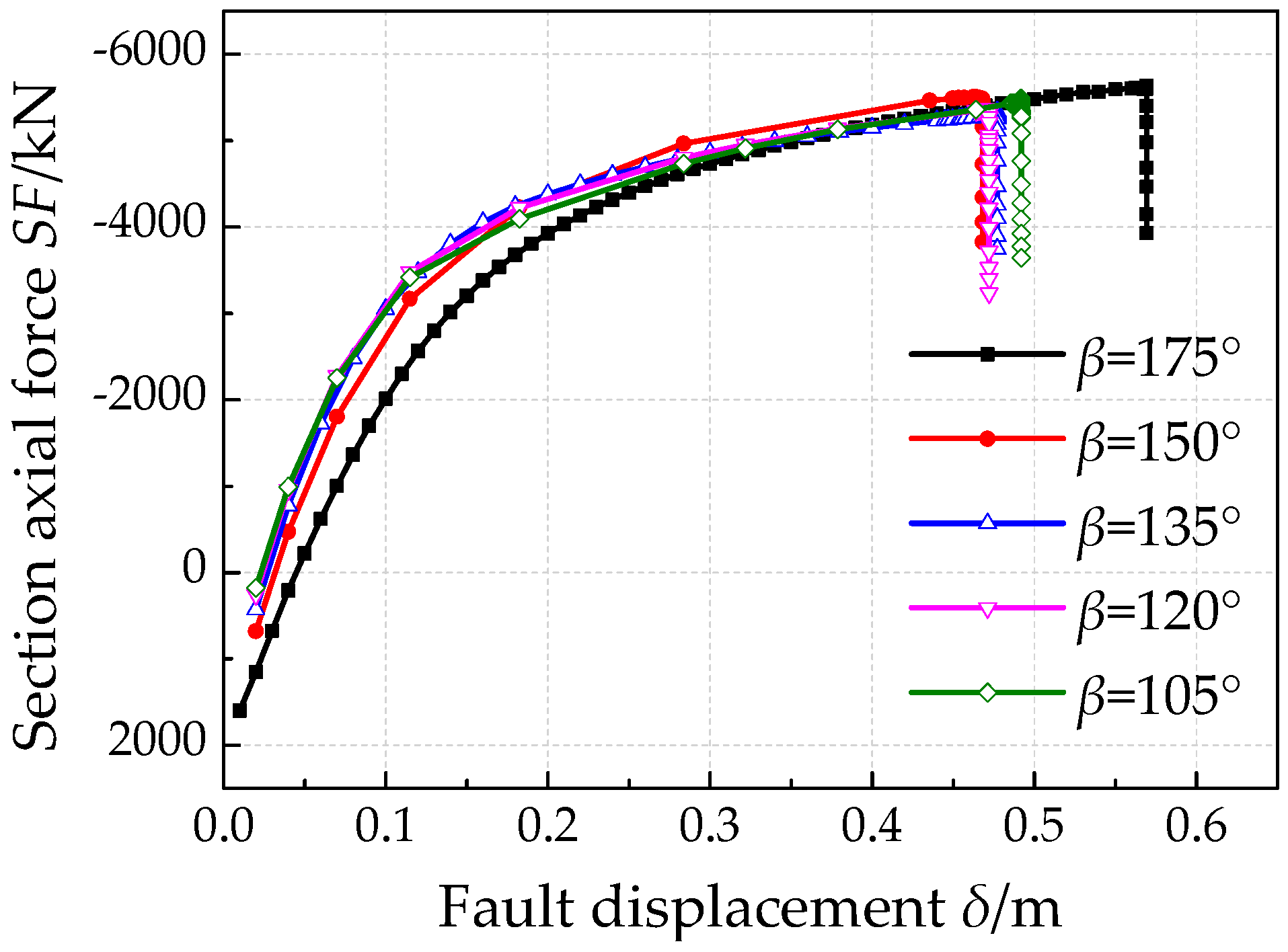
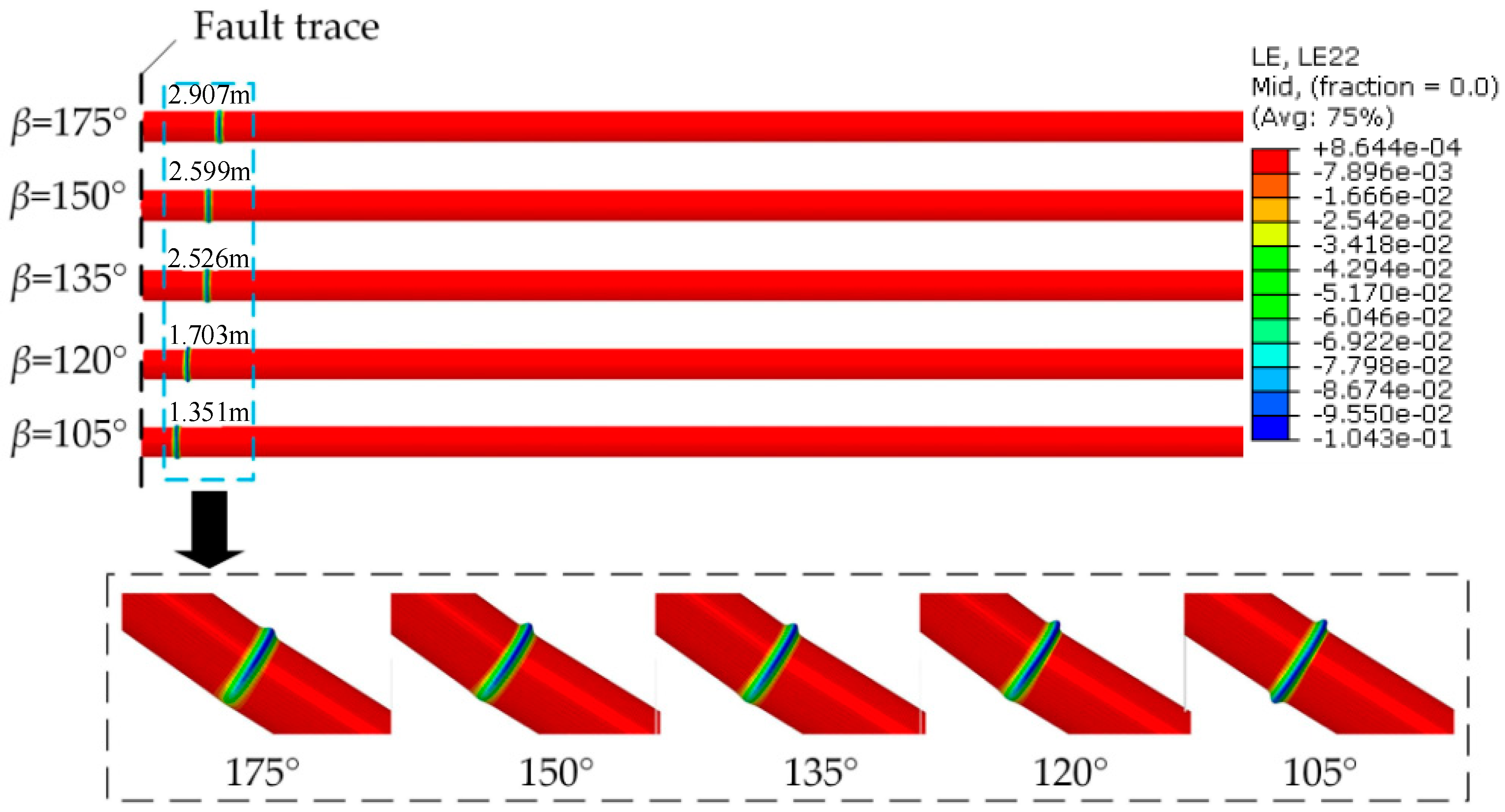
4.2. Effects of Pipe-Fault Intersection Angle
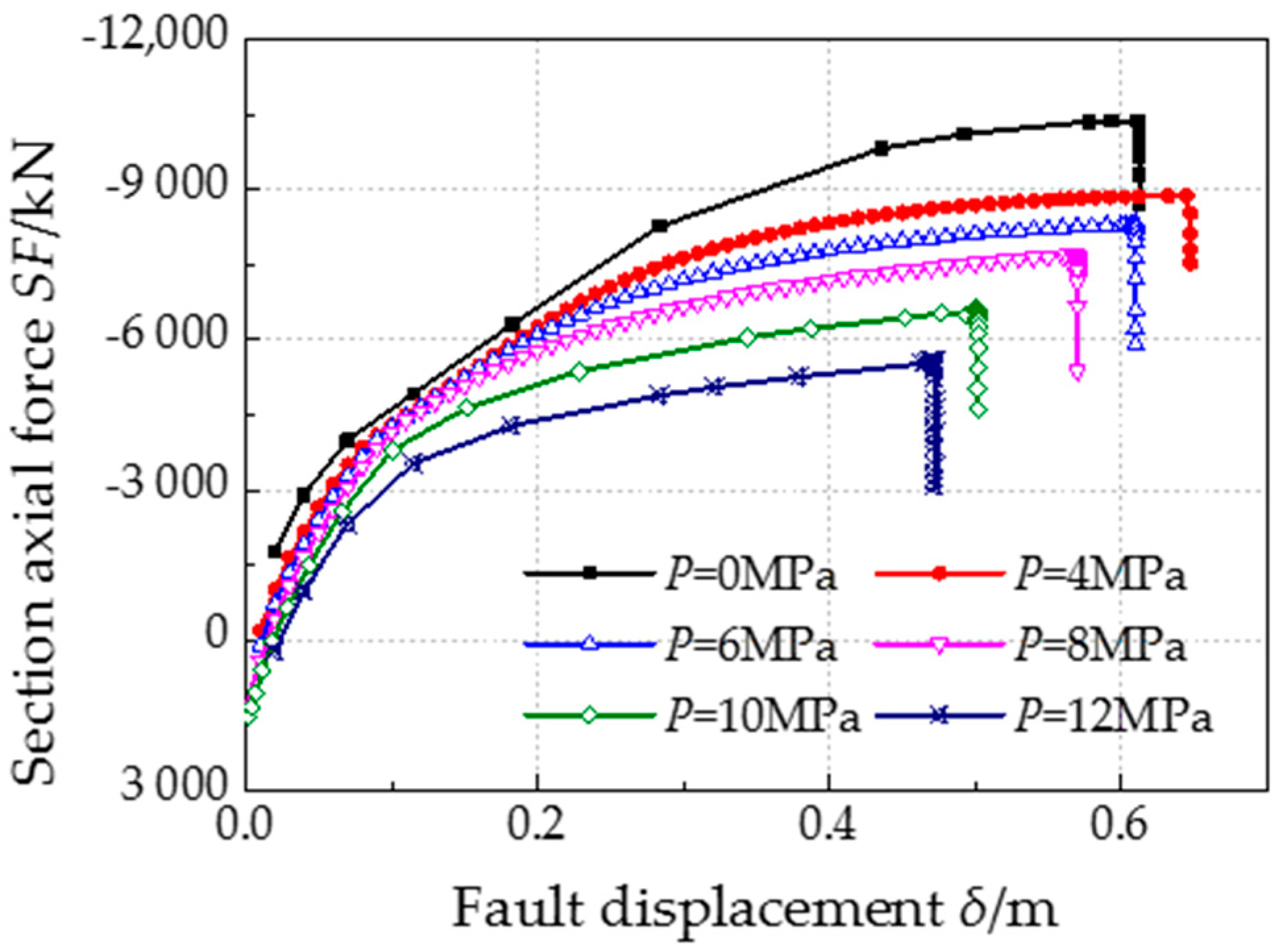
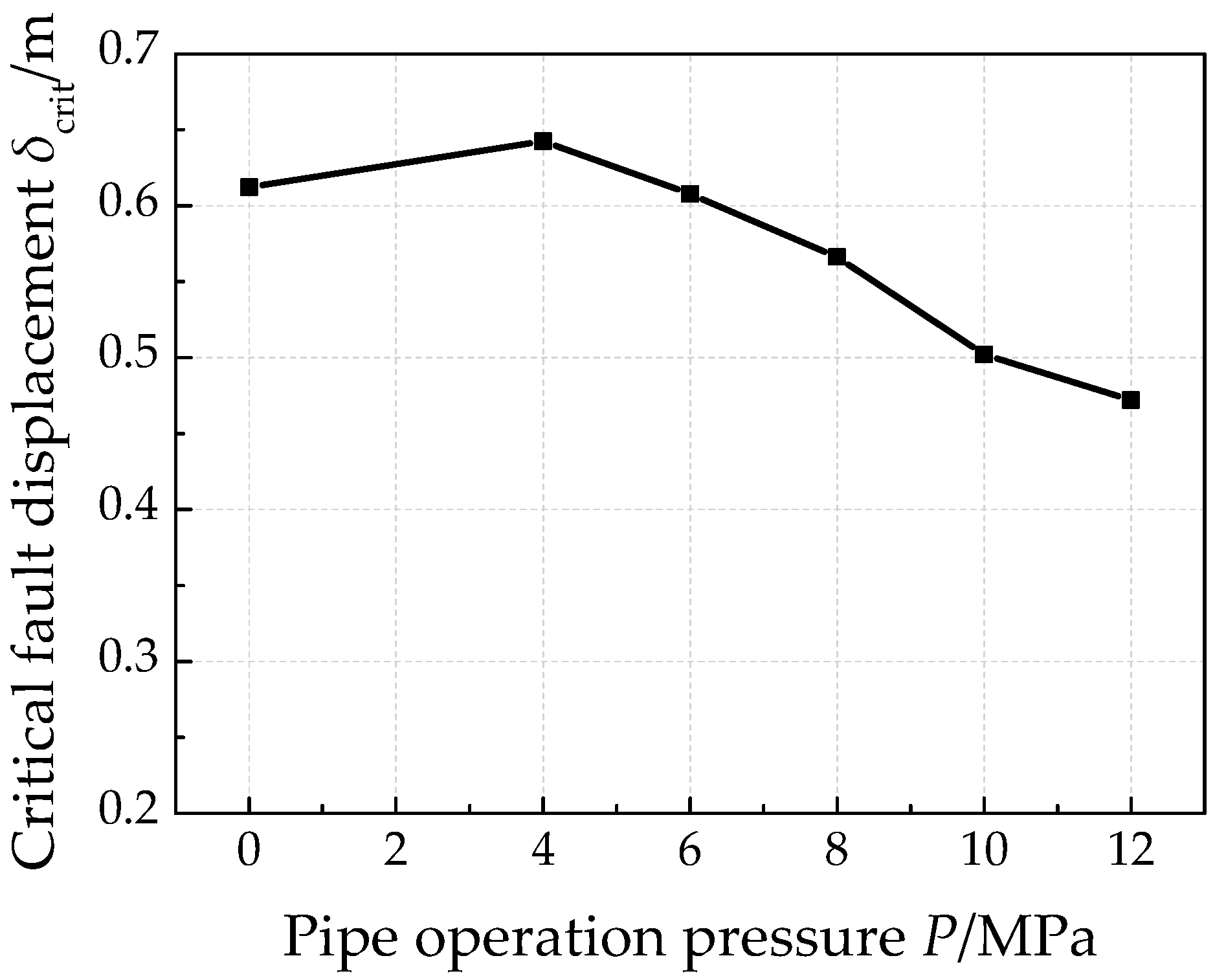
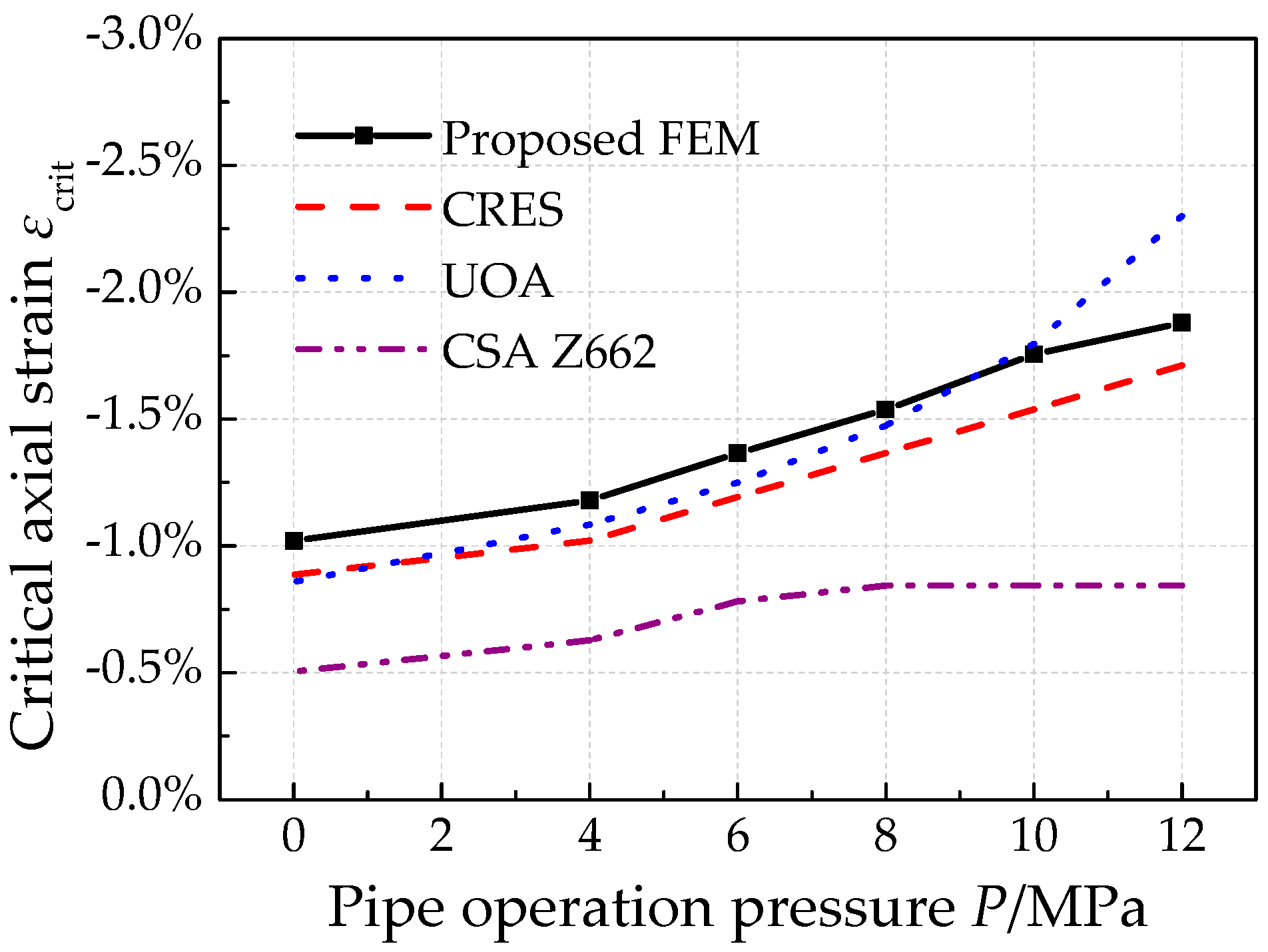
4.3. Effects of Pipe Operation Pressure
4.4. Effects of Pipe Wall Thickness
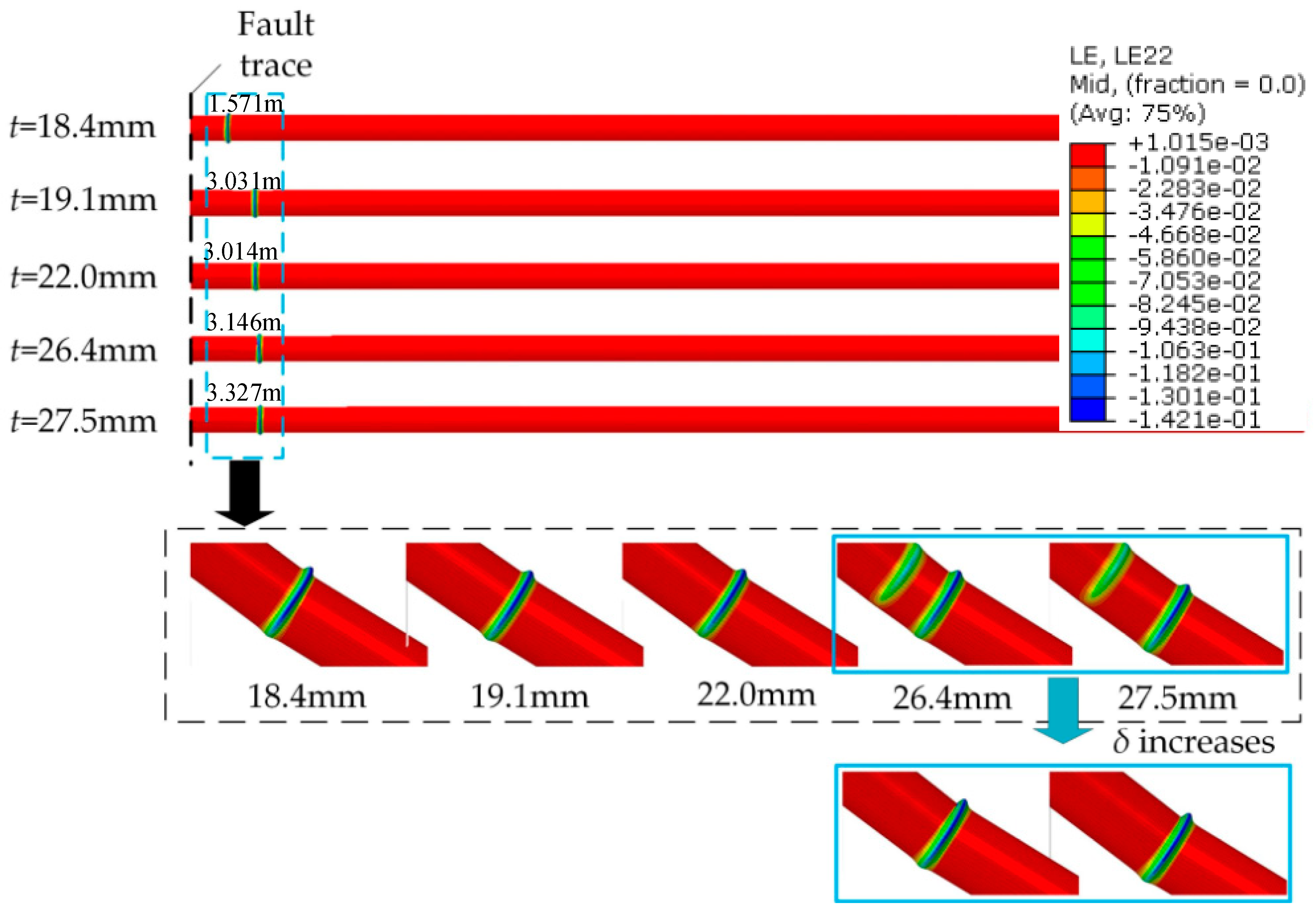
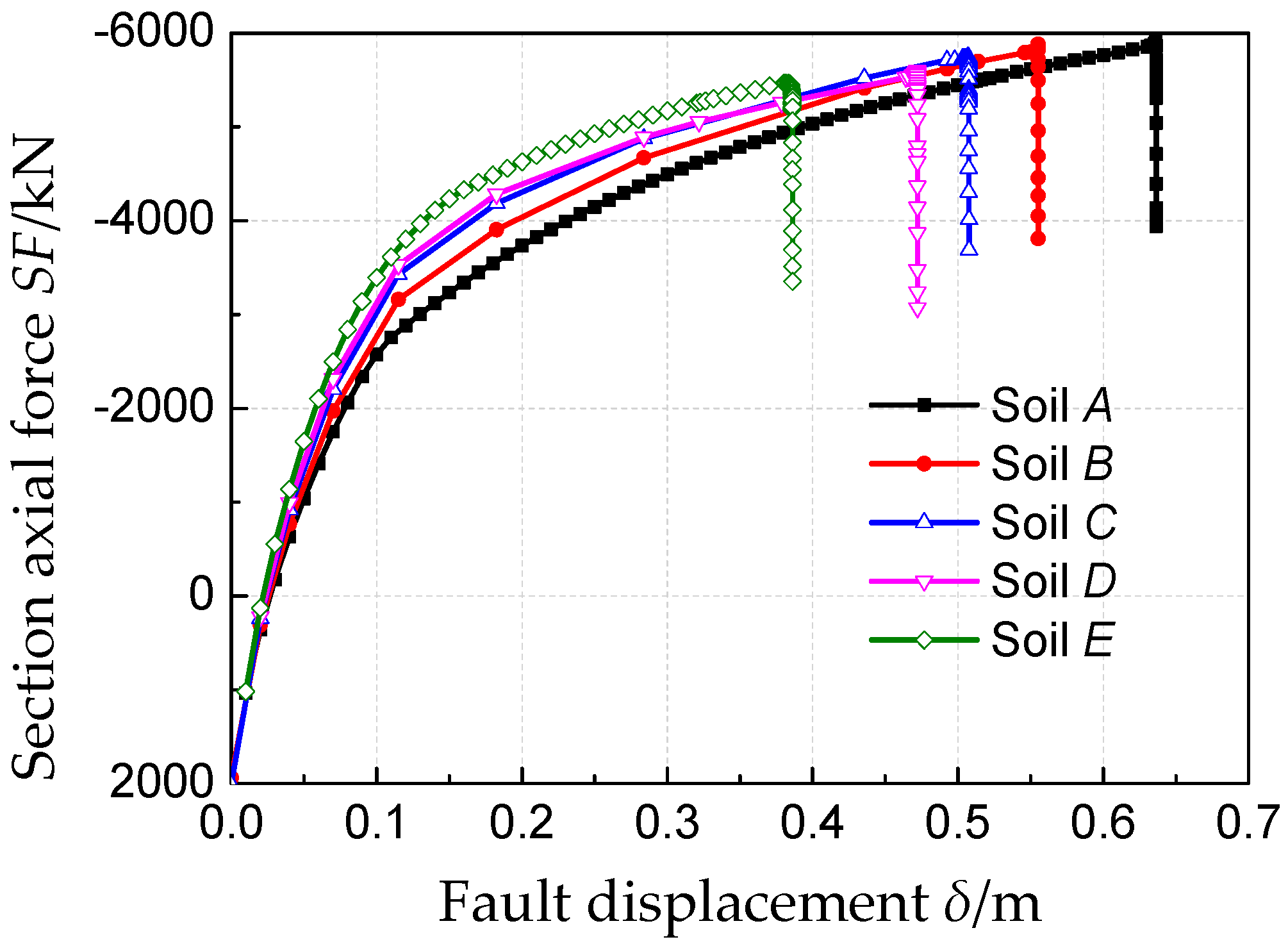
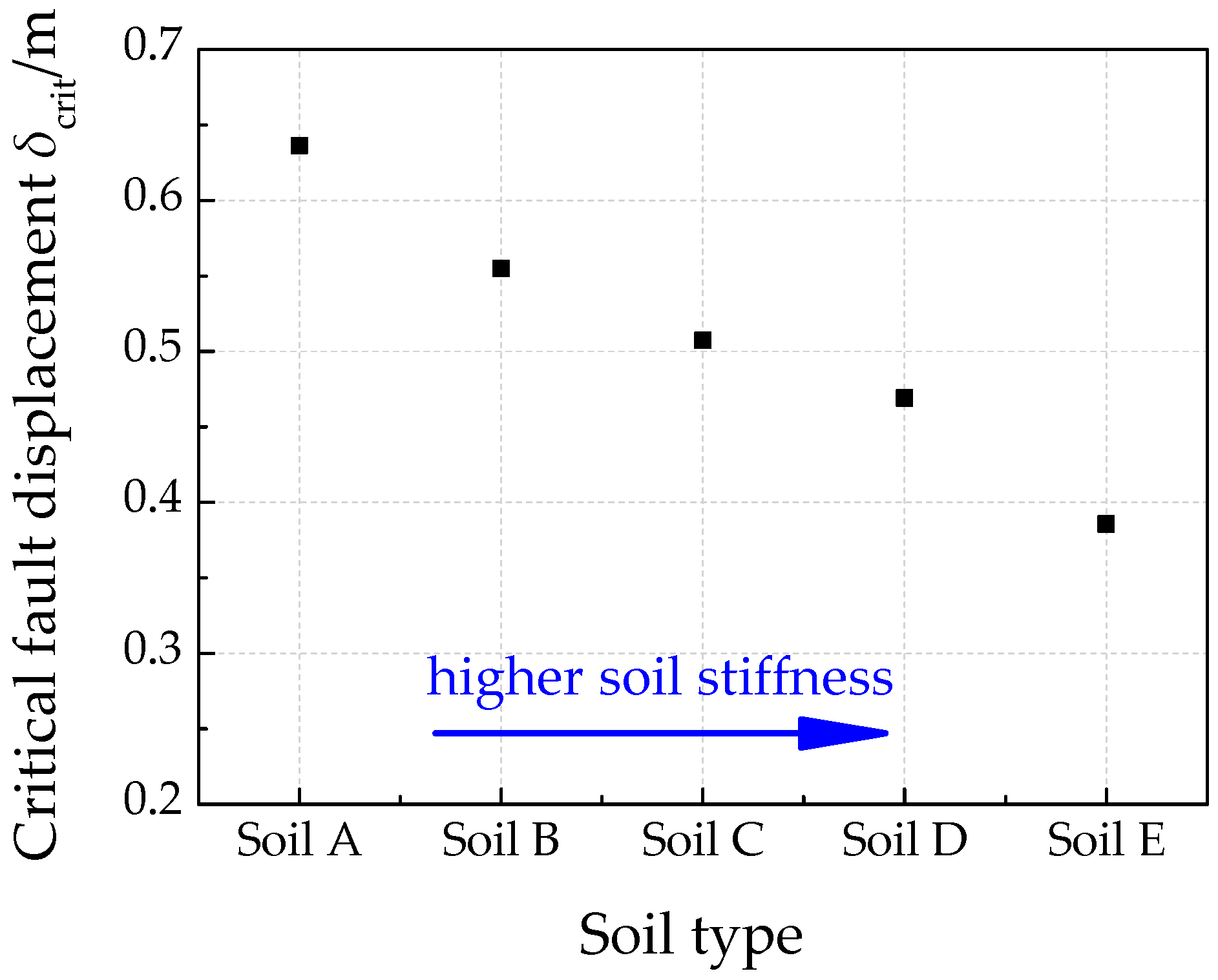
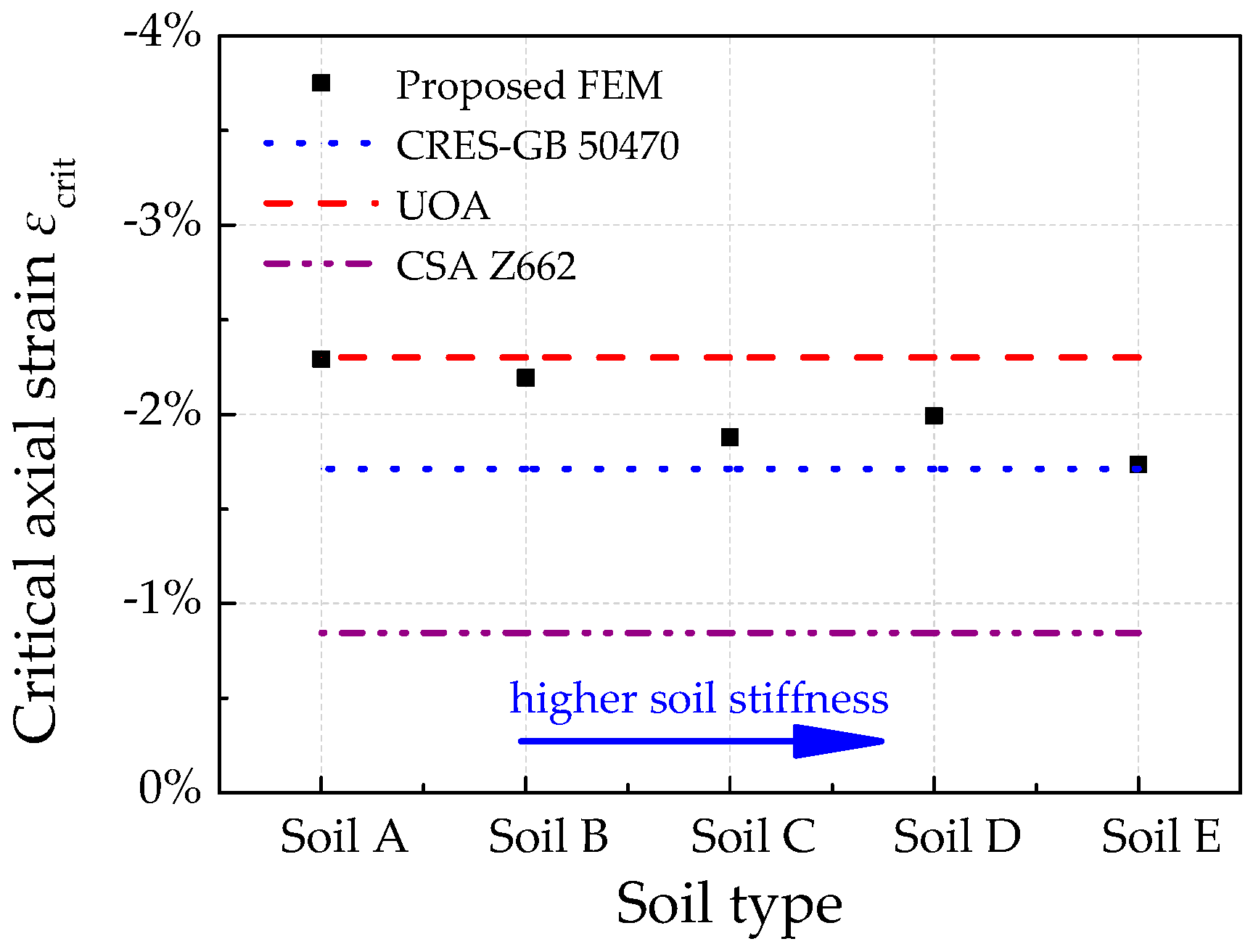
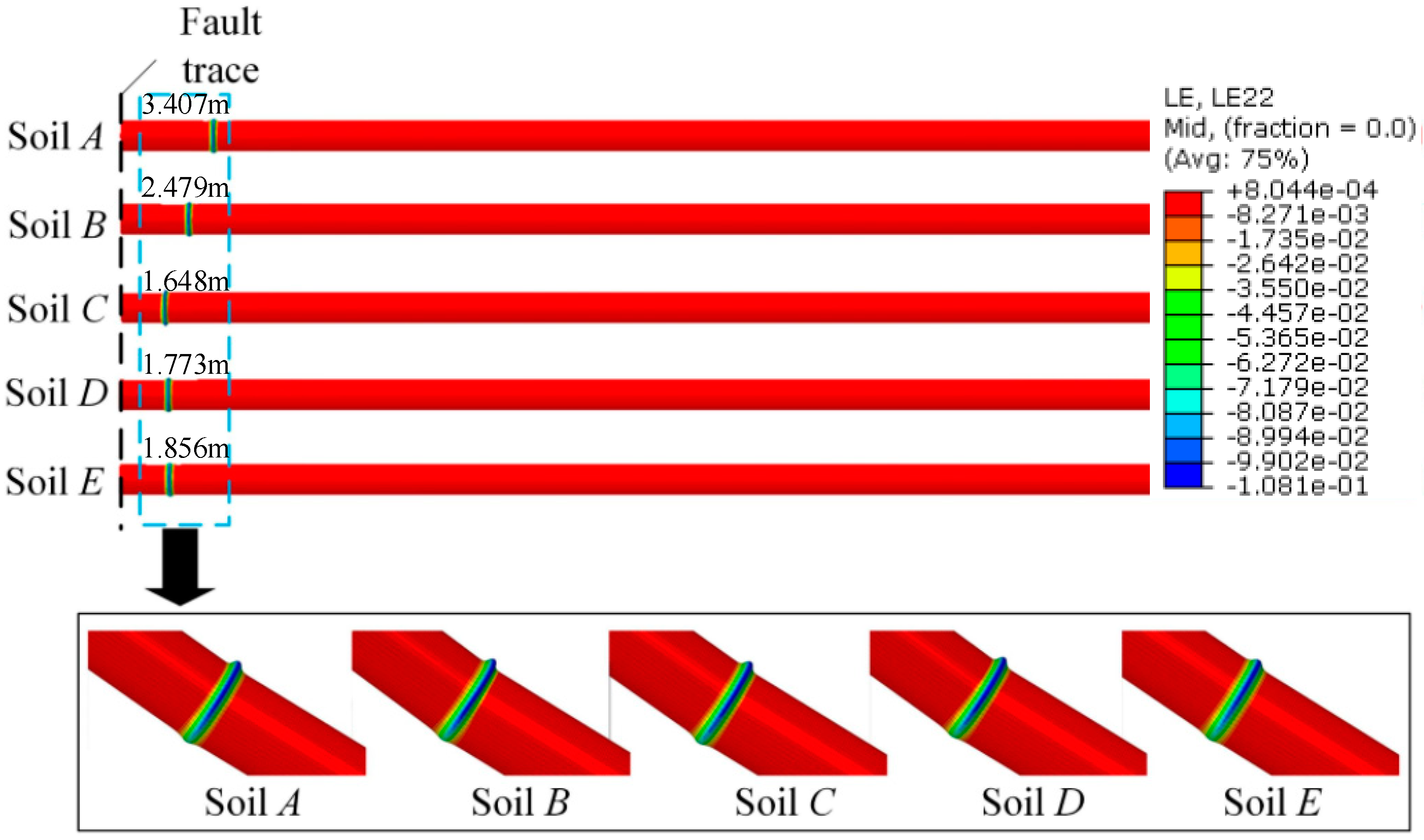
4.5. Effects of Soil Parameters
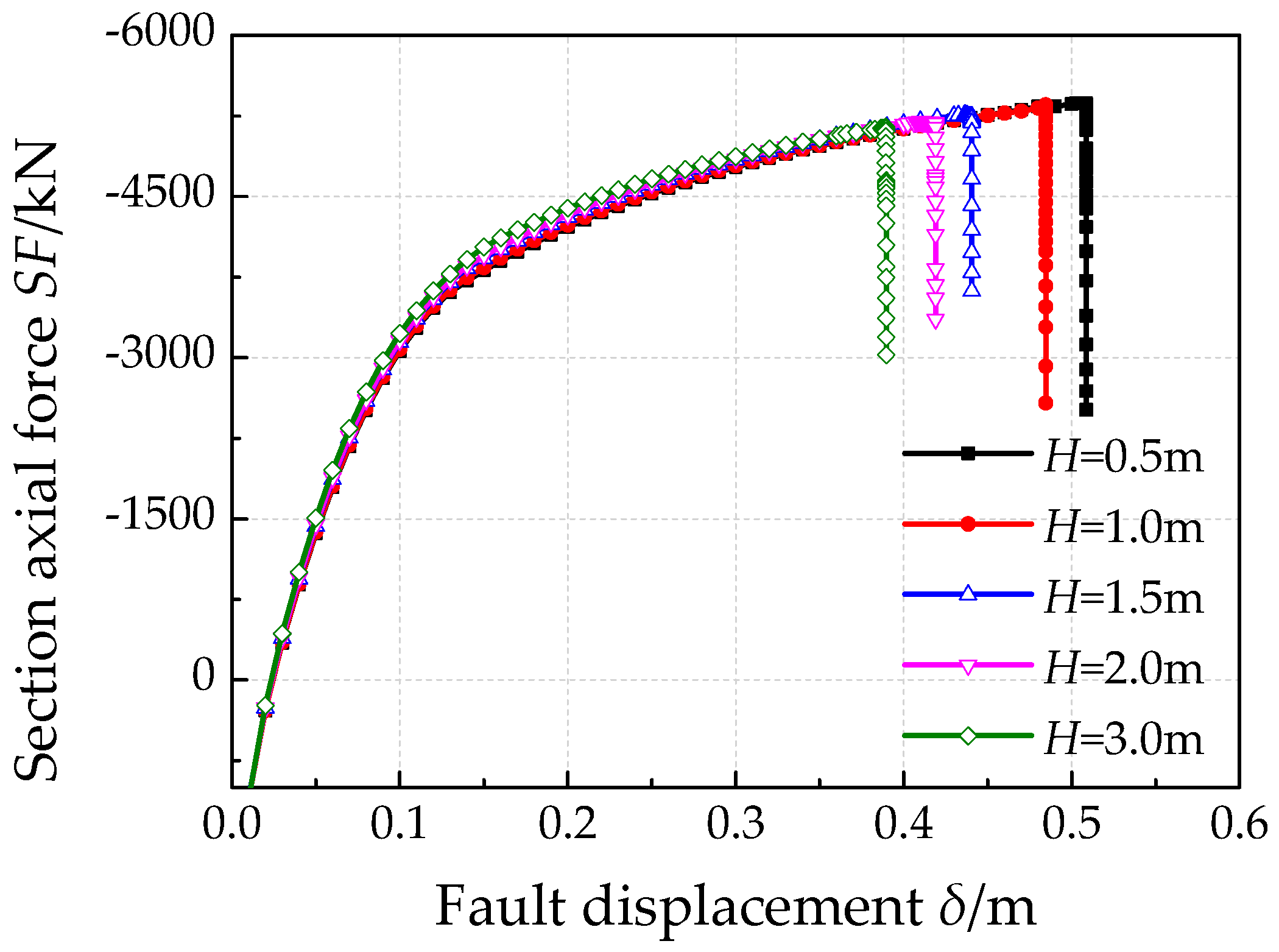
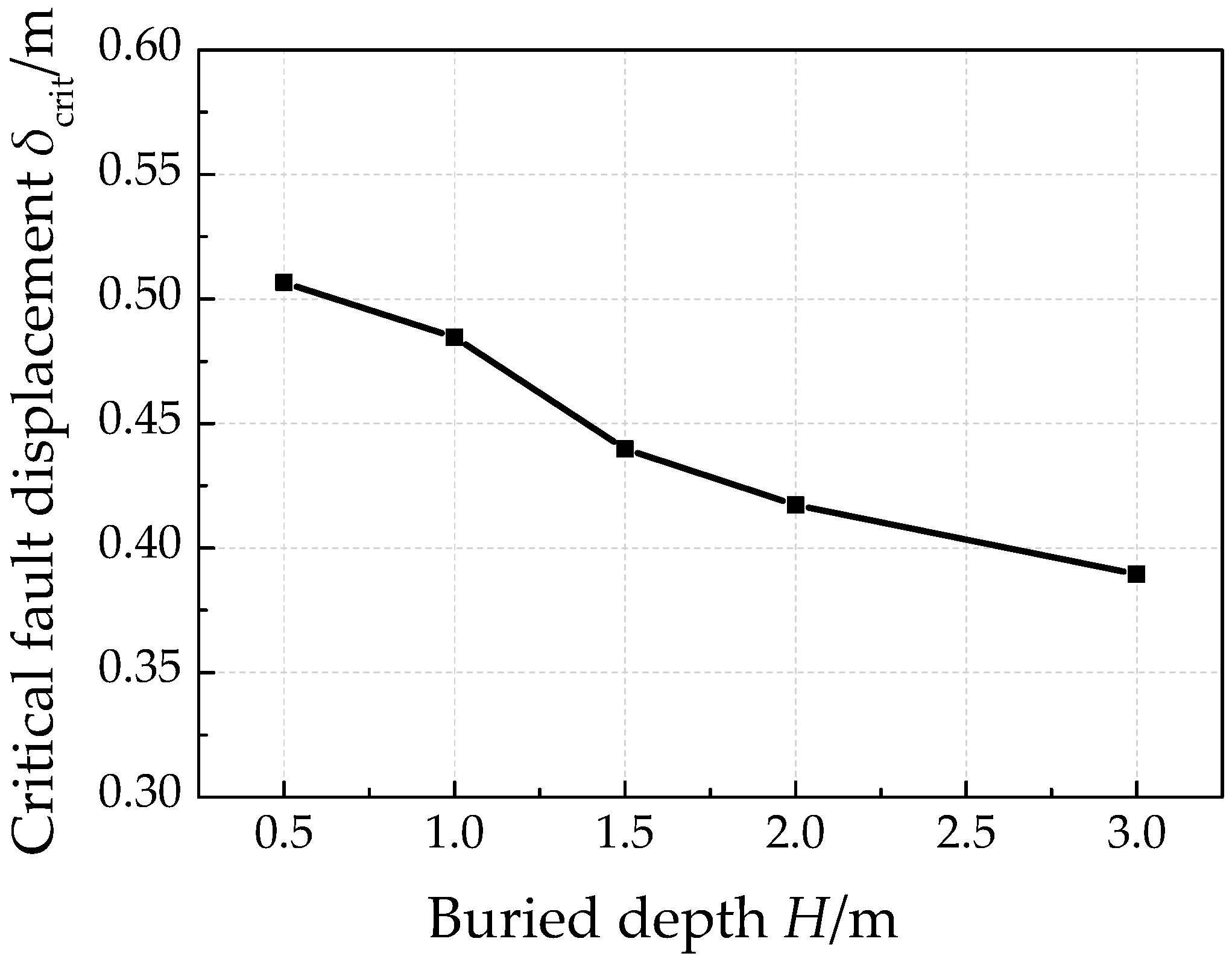
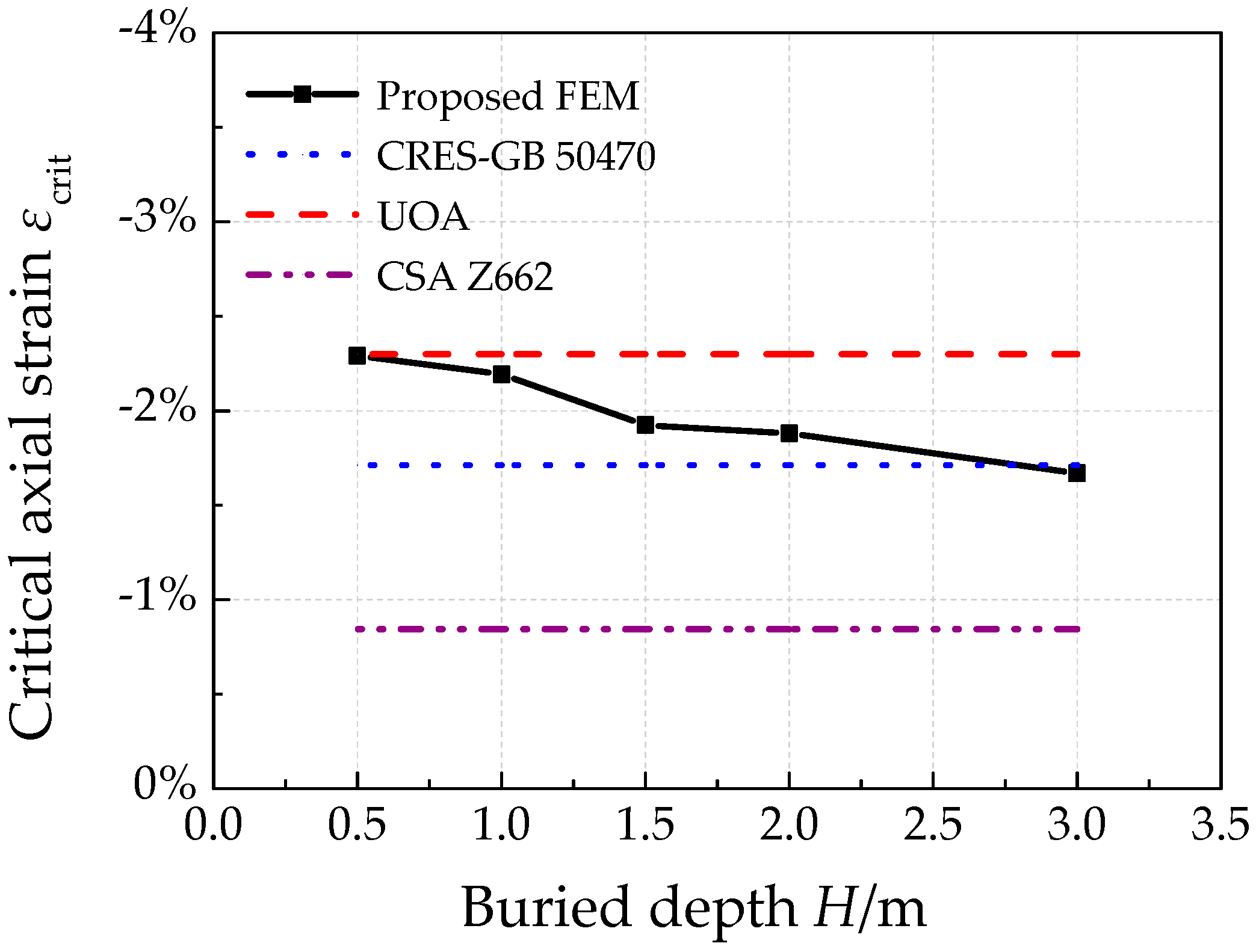
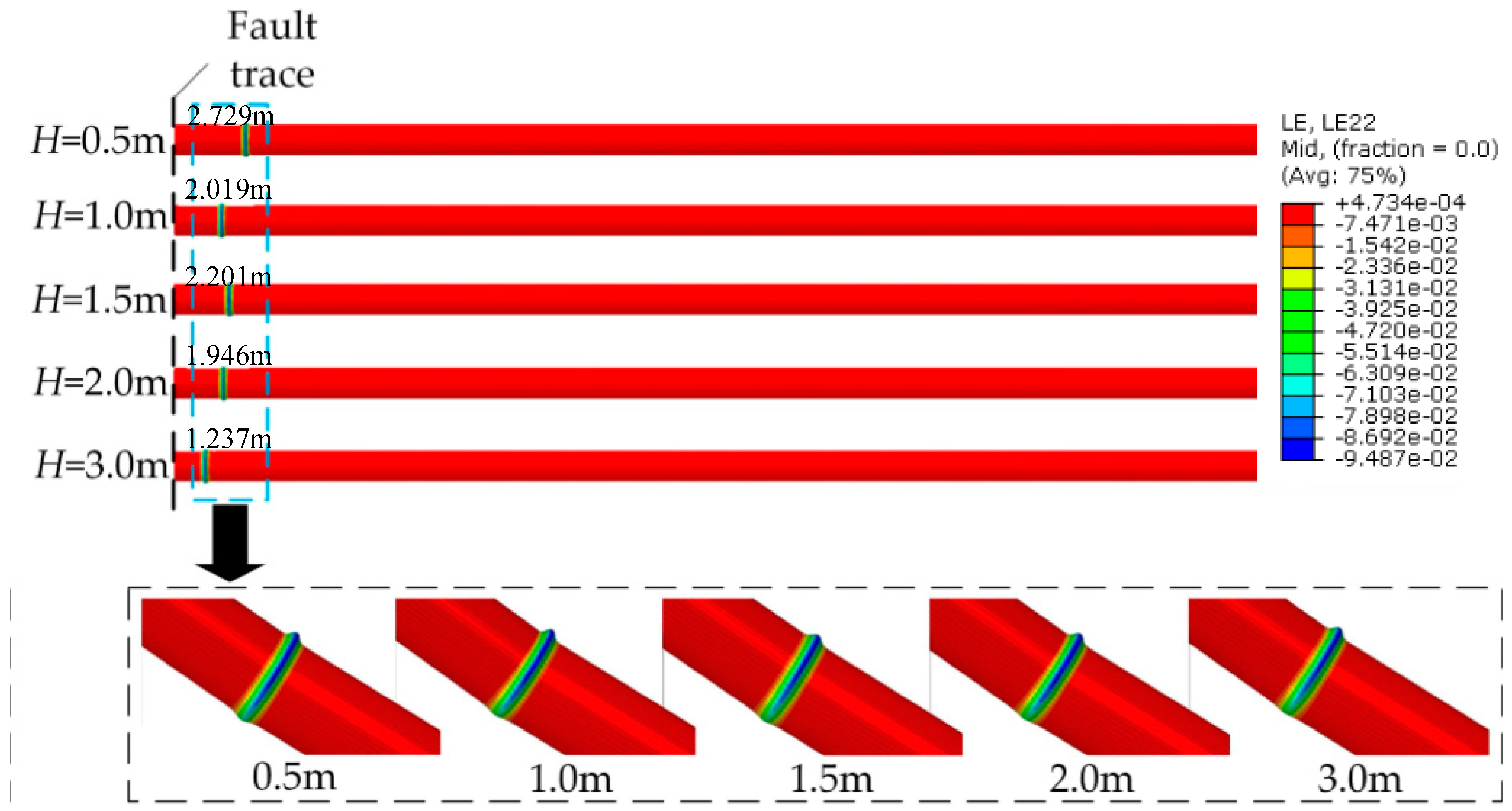
4.6. Effects of Pipe Buried Depth
5. Conclusions
- For compressive strike-slip fault, the critical fault displacement increases initially and decrease afterwards with pipe fault intersection angle. When pipe fault intersection angle equals 135°, the pipe is most likely to be buckled and fail. The failure section of pipe locates further with increase of pipe fault intersection angle.
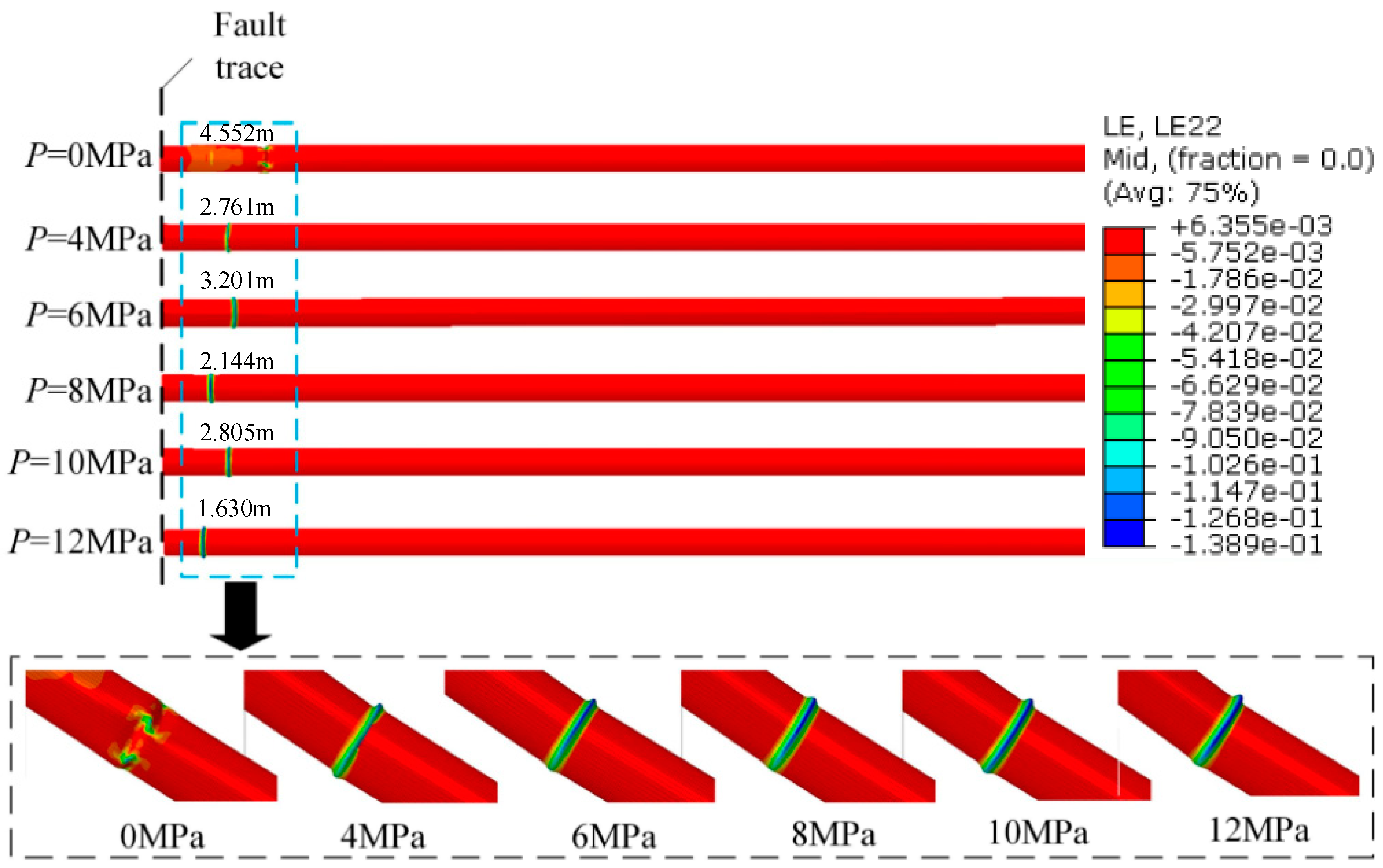
- Pipe operation pressure decreases pipe’s anti-buckling capacity generally, although a positive correlation between the critical compressive strain and pipe operation pressure was also found. In addition, operation pressure affects pipe’s plastic deformation shape in post buckling stage. For the pipe investigated, when P is larger than 4 MPa, the pipe performs an elephant’s foot buckling, and when P is 0 MPa, the pipe exhibits diamond buckling.
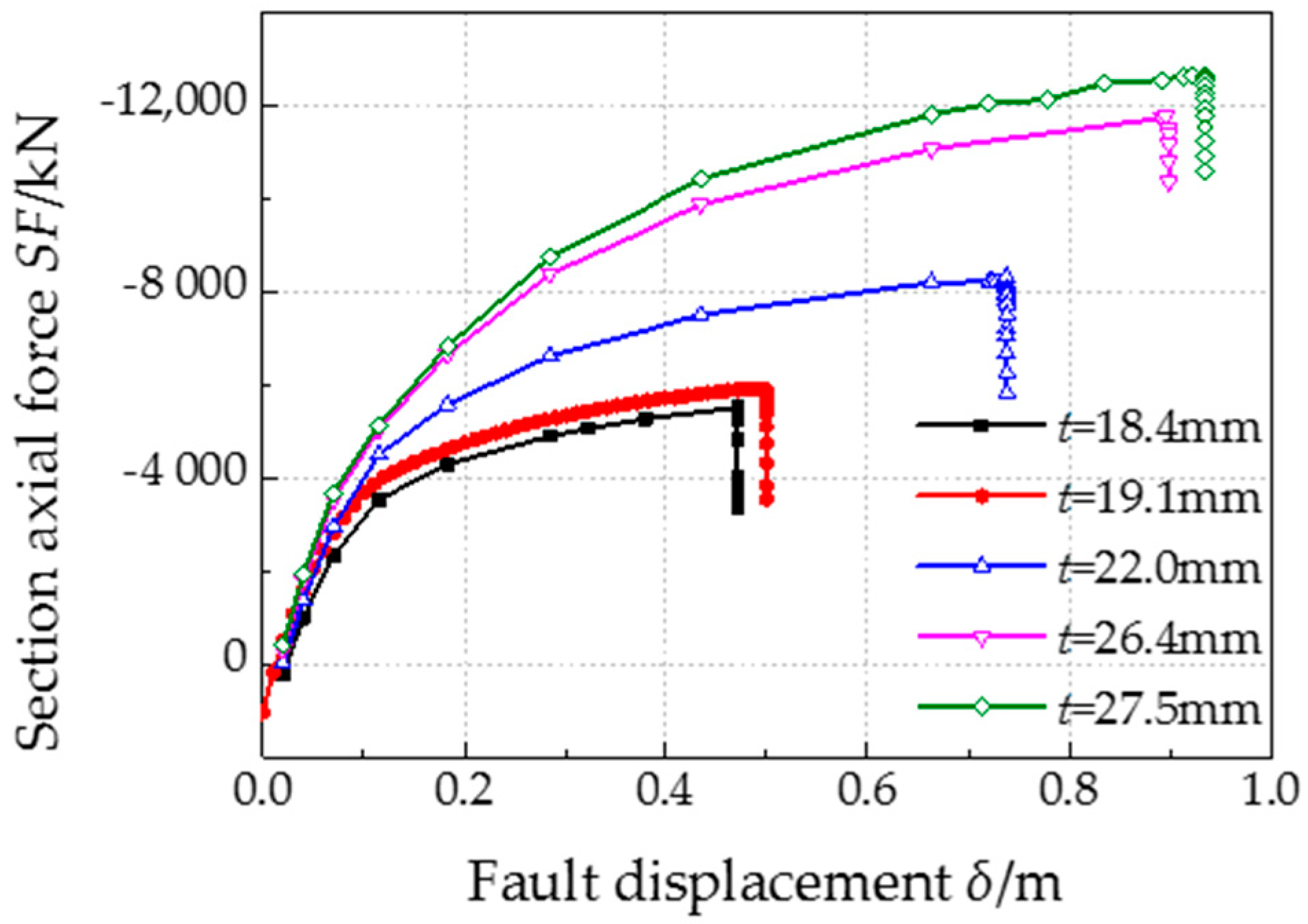
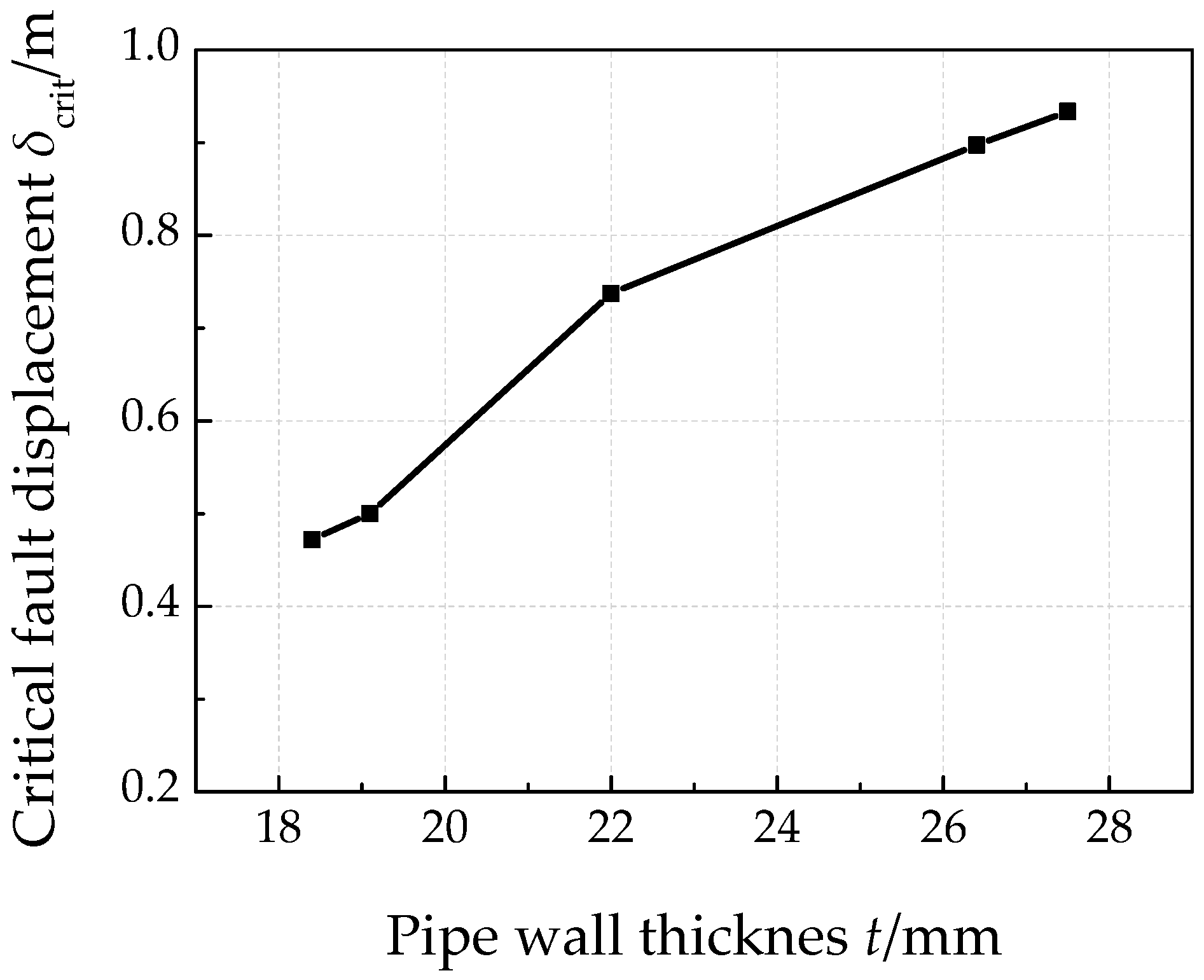
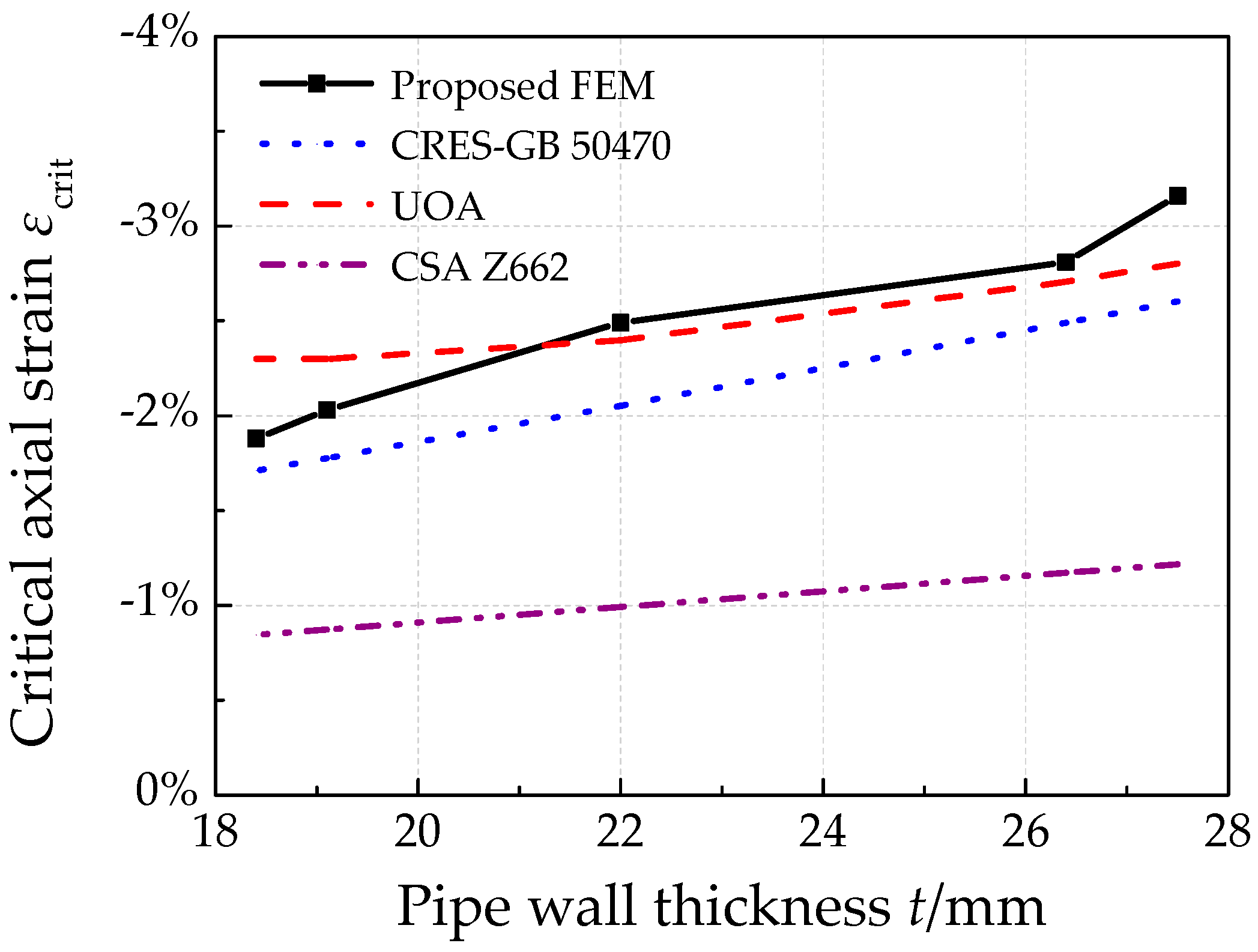
- Pipe wall thickness has a positive relationship with both the critical fault displacement and critical axial strain for pipe. The failure pipe section of thicker pipes locates further away from fault trace.
- Both increasing soil stiffness and pipe buried depth increase soil constraints on pipe, which will lead to a smaller critical fault displacement. In addition, pipe failure locations are nearer to fault trace with stronger constraints by surrounding soil.
- For pure pipes without considering the geometry imperfections, the CSA Z662 model predicts too conservative results for compressive strain capacity. Generally, both the CRES-GB 50470 model and the UOA model have rather good critical compressive strain results compared with the numerical derived results for various conditions. Among them, the CRES-GB 50470 model is recommended for pipe failure assessment, because it is relatively conservative.
- Numerical results show that not only the pipe parameters (i.e., geometrical parameters and internal pressure) but also external loads (pipe fault intersection angle, soil constraints on pipe) also have some minor effects on pipe’s critical compressive strain, which is not considered by the commonly available buckling failure criteria.
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| D | the pipe diameter (m) |
| t | the pipe wall thickness (m) |
| P | the pipe operation pressure (MPa) |
| the compressive strain capacity of steel pipes | |
| σy | the yield strength of pipe steel (MPa) |
| E | the initial elastic modulus (MPa) |
| hg | the height of the geometry imperfection (mm) |
| σu | the tensile strength of pipe material (MPa) |
| σa | the applied net-section stress in the longitudinal direction of pipe (MPa) |
| Tu | the axial peak resistant force per unit length of soil springs (kN/m) |
| Pu | the lateral peak resistant force per unit length of soil springs (kN/m) |
| Qu | the vertical uplift peak resistant force per unit length of soil springs (kN/m) |
| Qd | the vertical bearing peak resistant force per unit length of soil springs (kN/m) |
| Δt | the yield displacement in the axial direction (m) |
| Δp | the yield displacement in the lateral direction (m) |
| Δqu | the yield displacement in the vertical uplift direction (m) |
| Δqd | the yield displacement in the vertical bearing direction (m) |
| σtrue | the true stress (MPa) |
| εtrue | the true strain |
| r | the strain hardening exponent |
| α | the yield offset parameter |
| A | the pipe cross section area (m2) |
| ΔL | the pipe extension at Point B (m) |
| δ | the fault displacement (m) |
| ΔX | the fault displacement in the pipe axial direction (m) |
| ΔY | the fault displacement in the pipe perpendicular direction (m) |
| β | the pipe fault intersection angle (°) |
| εcrit | the critical compressive strain |
| SF | the section axial force in buckled area (kN) |
| SFcrit | the critical section axial force in buckled area (kN) |
| K | the coefficient of theory critical axial force |
| εaxial | the axial compressive strain |
| δcrit | the critical fault displacements (m) |
| the internal friction angle of the soil (°) | |
| c | the soil cohesion representative (kPa) |
| γ | the effective unit weight of soil (kN/m3) |
| f | the pipe–soil friction coefficient |
| H | the pipe buried depth (m) |
References
- Lower, M.D. Strain-Based Design Methodology of Large Diameter Grade X80 Linepipe. Ph.D. Thesis, University of Tennessee, Knoxville, TN, USA, 2014. [Google Scholar]
- Liu, X.B.; Zhang, H.; Wu, K.; Xia, M.Y.; Chen, Y.F.; Li, M. Buckling failure mode analysis of buried X80 steel gas pipeline under reverse fault displacement. Eng. Fail. Anal. 2017, 77, 50–64. [Google Scholar] [CrossRef]
- Newmark, N.M.; Hall, W.J. Pipeline design to resist large fault displacement. In Proceedings of the U.S. National Conference on Earthquake Engineering, Ann Arbor, MI, USA, 18–20 June 1975; pp. 416–425. [Google Scholar]
- Kennedy, R.P.; Chow, A.W.; Williamson, R.A. Fault movement effects on buried oil pipeline. Transp. Eng. J. 1977, 103, 617–633. [Google Scholar]
- Wang, R.L.; Yeh, Y.H. A refined seismic analysis and design of buried pipeline for fault movement. Earthq. Eng. Struct. Dyn. 1985, 13, 75–96. [Google Scholar] [CrossRef]
- Karamitros, D.K.; Bouckovalas, G.D.; Kouretzis, G.P. Stress analysis of buried steel pipelines at strike-slip fault crossings. Soil Dyn. Earthq. Eng. 2007, 27, 200–211. [Google Scholar] [CrossRef]
- Trifonov, O.V.; Cherniy, V.P. A semi-analytical approach to a nonlinear stress-strain analysis of buried steel pipelines crossing active faults. Soil Dyn. Earthq. Eng. 2010, 30, 1298–1308. [Google Scholar] [CrossRef]
- Zhang, L.; Zhao, X.; Yan, X.; Yang, X. Elastoplastic analysis of mechanical response of buried pipelines under strike-slip faults. Int. J. Geomech. 2016, 17. [Google Scholar] [CrossRef]
- Ha, D.; Abdoun, T.H.; O’Rourke, M.J.; Symans, M.D.; O’Rourke, T.D.; Palmer, M.C.; Steward, H.E. Buried high-density polyethylene pipelines subjected to normal and strike-slip faulting-a centrifuge investigation. Can. Geotech. J. 2008, 45, 1733–1742. [Google Scholar] [CrossRef]
- Ha, D.; Abdoun, T.H.; O’Rourke, M.J.; Symans, M.D. Centrifuge modeling of earthquake effects on buried high-density polyethylene (HDPE) pipelines crossing fault zones. J. Geotech. Geoenviron. Eng. 2008, 134, 1501–1515. [Google Scholar] [CrossRef]
- O’Rourke, T.D.; Jung, J.K.; Argyrou, C. Underground pipeline response to earthquake-induced ground deformation. Soil Dyn. Earthq. Eng. 2016, 91, 272–283. [Google Scholar] [CrossRef]
- Jung, J.K.; O’Rourke, T.D.; Argyrou, C. Multi-directional force–displacement response of underground pipe in sand. Can. Geotech. J. 2016, 53, 1763–1781. [Google Scholar] [CrossRef]
- Jalali, H.H.; Rofooei, F.R.; Attari, N.K.A. Performance of Buried Gas Distribution Pipelines Subjected to Reverse Fault Movement. J. Earthq. Eng. 2017, 10, 1–24. [Google Scholar] [CrossRef]
- Jalali, H.H.; Rofooei, F.R.; Attari, N.K.A.; Samadian, M. Experimental and finite element study of the reverse faulting effects on buried continuous steel gas pipelines. Soil Dyn. Earthq. Eng. 2016, 86, 1–14. [Google Scholar] [CrossRef]
- Rofooei, F.R.; Jalali, H.H.; Attari, N.K.A.; Kenarangi, H.; Samadian, M. Parametric study of buried steel and high density polyethylene gas pipelines due to oblique-reverse faulting. Can. J. Civ. Eng. 2015, 42, 178–189. [Google Scholar] [CrossRef]
- Trifonov, O.V. Numerical stress-strain analysis of buried steel pipelines crossing active strike-slip faults with an emphasis on fault modeling aspects. J. Pipeline Syst. Eng. Pract. 2015, 6. [Google Scholar] [CrossRef]
- Xie, X.J.; Symans, M.D.; O’Rourke, M.J.; Abdoun, T.H.; O’Rourke, T.D.; Palmer, M.C.; Stewart, H.E. Numerical modeling of buried HDPE pipelines subjected to normal faulting: A case study. Earthq. Spectra 2013, 29, 609–632. [Google Scholar] [CrossRef]
- Xie, X.J.; Symans, M.D.; O’Rourke, M.J.; Abdoun, T.H.; O’Rourke, T.D.; Palmer, M.C.; Stewart, H.E. Numerical modeling of buried HDPE pipelines subjected to strike-slip faulting. J. Earthq. Eng. 2011, 15, 1273–1296. [Google Scholar] [CrossRef]
- Joshi, S.; Prashant, A.; Deb, A.; Jain, S.K. Analysis of buried pipelines subjected to reverse fault motion. Soil Dyn. Earthq. Eng. 2011, 31, 930–940. [Google Scholar] [CrossRef]
- Uckan, E.; Akbas, B.; Shen, J.; Rou, W.; Paolacci, W.; O’Rourke, M. A simplified analysis model for determining the seismic response of buried steel pipes at strike-slip fault crossings. Soil Dyn. Earthq. Eng. 2015, 75, 55–65. [Google Scholar] [CrossRef]
- Liu, X.B.; Zhang, H.; Han, Y.S.; Xia, M.Y.; Zheng, W. A semi-empirical model for peak strain prediction of buried X80 steel pipelines under compression and bending at strike-slip fault crossings. J. Nat. Gas Sci. Eng. 2016, 32, 465–475. [Google Scholar] [CrossRef]
- Melissianos, V.E.; Vamvatsikos, D.; Gantes, C.J. Performance assessment of buried pipelines at fault crossings. Earthq. Spectra 2017, 33, 201–218. [Google Scholar] [CrossRef]
- Melissianos, V.E.; Vamvatsikos, D.; Gantes, C.J. Performance-based assessment of protection measures for buried pipes at strike-slip fault crossings. Soil Dyn. Earthq. Eng. 2017, 101, 1–11. [Google Scholar] [CrossRef]
- Liu, X.B.; Zhang, H.; Gu, X.T.; Chen, Y.F.; Xia, M.Y.; Wu, K. Strain demand prediction method for buried X80 steel pipelines crossing oblique-reverse faults. Earthq. Struct. 2017, 12, 321–332. [Google Scholar] [CrossRef]
- Xu, L.; Lin, M. Analysis of buried pipelines subjected to reverse fault motion using the vector form intrinsic finite element method. Soil Dyn. Earthq. Eng. 2017, 93, 61–83. [Google Scholar] [CrossRef]
- Kaya, E.S.; Uckan, E.; O’Rourke, M.J.; Karamanos, S.A.; Akbas, B.; Cakir, F.; Cheng, Y. Failure analysis of a welded steel pipe at Kullar fault crossing. Eng. Fail. Anal. 2016, 71, 43–62. [Google Scholar] [CrossRef]
- Zhang, J.; Liang, Z.; Han, C.J. Buckling behavior analysis of buried gas pipeline under strike-slip fault displacement. J. Nat. Gas Sci. Eng. 2014, 21, 921–928. [Google Scholar] [CrossRef]
- Zhang, J.; Liang, Z.; Han, C.J.; Zhang, H. Numerical simulation of buckling behavior of the buried steel pipeline under reverse fault displacement. Mech. Sci. 2015, 6, 203–210. [Google Scholar] [CrossRef]
- Vazouras, P.; Karamanos, S.A.; Dakoulas, P. Finite element analysis of buried steel pipelines under strike-slip fault displacements. Soil Dyn. Earthq. Eng. 2010, 30, 1361–1376. [Google Scholar] [CrossRef]
- Vazouras, P.; Karamanos, S.A.; Dakoulas, P. Mechanical behavior of buried steel pipes crossing active strike-slip faults. Soil Dyn. Earthq. Eng. 2012, 41, 164–180. [Google Scholar] [CrossRef]
- Vazouras, P.; Dakoulas, P.; Karamanos, S.A. Pipe-soil interaction and pipeline performance under strike-slip fault movements. Soil Dyn. Earthq. Eng. 2015, 72, 48–65. [Google Scholar] [CrossRef]
- Vazouras, P.; Karamanos, S.A. Structural behavior of buried pipe bends and their effect on pipeline response in fault crossing areas. Bull. Earthq. Eng. 2017, 4, 1–26. [Google Scholar] [CrossRef]
- Liu, X.B.; Zhang, H.; Li, M.; Xia, M.Y.; Zheng, W.; Wu, K.; Han, Y.S. Effects of steel properties on the local buckling response of high strength pipelines subjected to reverse faulting. J. Nat. Gas Sci. Eng. 2016, 33, 378–387. [Google Scholar] [CrossRef]
- Kainat, M.; Lin, M.; Cheng, J.R.; Martens, M.; Adeeb, S. Effects of the initial geometric imperfections on the buckling behavior of high-strength UOE manufactured steel pipes. J. Press. Vessel Technol. 2016, 138. [Google Scholar] [CrossRef]
- Neupane, S.; Adeeb, S.; Cheng, R.; Ferguson, J.; Martens, M. Modeling the deformation response of high strength steel pipelines—Part I: Material characterization to model the plastic anisotropy. J. Appl. Mech. 2012, 136, 272–275. [Google Scholar] [CrossRef]
- Neupane, S.; Adeeb, S.; Cheng, R.; Ferguson, J.; Martens, M. Modeling the deformation response of high strength steel pipelines—Part II: Effects of material characterization on the deformation response of pipes. J. Appl. Mech. 2012, 79, 051003. [Google Scholar] [CrossRef]
- Canadian Standard Association (CSA). Oil and Gas Pipeline Systems; CSA Standard; CSA Z662-11; Canadian Standard Association: Mississauga, ON, Canada, 2015. [Google Scholar]
- Gresnigt, A.M. Plastic Design of Buried Steel Pipelines in Settlement Areas; STEVIN-laboratory of the Department of Civil Engineering, Delft University of Technology: Delft, The Netherlands, 1987. [Google Scholar]
- American Lifelines Alliance. American Society of Civil Engineers, Guidelines for the Design of Buried Steel Pipe (with Addenda through February 2005); American Lifelines Alliance: Reston, VA, USA, 2005. [Google Scholar]
- Indian Institute of Technology Kanpur. IITK-GSDMA Guidelines for Seismic Design of Buried Pipelines, Gandhinagar: Gujarat State Disaster Management Authority; Indian Institute of Technology Kanpur: Kalyanpur, India, 2007. [Google Scholar]
- Dorey, A.B.; Murray, D.W.; Cheng, J.J.R. Critical buckling strain equations for energy pipelines—A parametric study. J. Offshore Mech. Arct. Eng. 2006, 128, 248–255. [Google Scholar] [CrossRef]
- Liu, M.; Wang, Y.Y.; Zhang, F.; Kotian, K. Realistic Strain Capacity Models for Pipeline Construction and Maintenance; US DOT PHMSA Other Transaction Agreement #DTPH56-10-T-000016, Draft Final Report; Center For Reliable Energy Systems: Dublin, OH, USA, 2013. [Google Scholar]
- Codeofchina Inc. GB 50470-2008 Seismic Technical Code for Oil and Gas Transmission Pipeline Engineering; Codeofchina Inc.: Beijing, China, 2017. [Google Scholar]
- American Petroleum Institute (API). Design, Construction, Operation, and Maintenance of Offshore Hydrocarbon Pipelines (Limit State Design); API Recommended Practice, API RP 1111; American Petroleum Institute: Washington, DC, USA, 1991. [Google Scholar]
- Det Norske Veritas (DNV). Submarine Pipeline Systems; DNV Offshore Standard, DNV-OS-F101; Det Norske Veritas: Oslo, Norway, 2010. [Google Scholar]
- Committee on Gas and Liquid Fuel Lifelines of the American Society of Civil Engineers Technical Council on Lifeline Earthquake Engineering. Guidelines for the Seismic Design of Oil and Gas Pipeline Systems; ASCE: Reston, VA, USA, 1984; pp. 10–12. [Google Scholar]
- Hibbitt, D.; Karlsson, B.; Sorensen, P. ABAQUS Standard User’s and Reference Manuals; Version 6.14; Hibbitt, Karlsson & Sorensen, Inc.: Johnston, RI, USA, 2007. [Google Scholar]
- Ramberg, W.; Osgood, W.R. Description of Stress-Strain Curves by Three Parameters; NACA Technical Note; No. 902; National Advisory Committee for Aeronautics (NACA): Washington, DC, USA, 1943.
- Liu, X.B.; Zhang, H.; Xia, M.Y. Buckling behavior of buried steel pipeline under compression strike-slip fault. In Proceedings of the 2017 ASME Pressure Vessels & Piping Conference, Waikoloa, HI, USA, 16–20 July 2017. [Google Scholar]
- Martini, A.; Troncossi, M.; Rivola, A. Leak Detection in Water-Filled Small-Diameter Polyethylene Pipes by Means of Acoustic Emission Measurements. Appl. Sci. 2017, 7, 2. [Google Scholar] [CrossRef]
- Juliano, T.M.; Meegoda, J.N.; Watts, D.J. Acoustic Emission Leak Detection on a Metal Pipeline Buried in Sandy Soil. J. Pipeline Syst. Eng. Pract. 2013, 4, 149–155. [Google Scholar] [CrossRef]
- Martini, A.; Troncossi, M.; Rivola, A. Vibroacoustic Measurements for Detecting Water Leaks in Buried Small-Diameter Plastic Pipes. J. Pipeline Syst. Eng. Pract. 2017, 8, 1–10. [Google Scholar] [CrossRef]
- Yazdekhasti, S.; Piratla, K.R.; Atamturktur, S.; Khan, A. Experimental evaluation of a vibration-based leak detection technique for water pipelines. Struct. Infrastruct. Eng. 2017, 14, 46–55. [Google Scholar] [CrossRef]
- Liu, A.; Hu, Y.; Zhao, F.; Li, X.; Takada, S.; Zhao, L. An equivalent-boundary method for the shell analysis of buried pipelines under fault movement. Acta Seismol. Sin. 2004, 17, 150–156. [Google Scholar] [CrossRef]
- American Society of Mechanical Engineers. Pipeline Transportation Systems for Liquid Hydro Carbons and Other Liquids; ANSI/ASME2016, B31:4; American Society of Mechanical Engineers: New York, NY, USA, 2016. [Google Scholar]
- American Society of Mechanical Engineers. Gas Transmission and Distribution Piping Systems; ANSI/ASME2016, B31:8; American Society of Mechanical Engineers: New York, NY, USA; 2016. [Google Scholar]


| Soil Sites Type | Internal Friction Angle ψ (°) | Cohesion c (kPa) | Effective Unit Weight of Soil γ (kN/m3) | Pipe-Soil Friction Coefficient f |
|---|---|---|---|---|
| Soil A | 30 | 30 | 22 | 0.6 |
| Soil B | 30 | 40 | 22 | 0.6 |
| Soil C | 33 | 50 | 22 | 0.6 |
| Soil D | 33 | 60 | 22 | 0.6 |
| Soil E | 33 | 70 | 22 | 0.6 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Zhang, H.; Wang, B.; Xia, M.; Wu, K.; Zheng, Q.; Han, Y. Local Buckling Behavior and Plastic Deformation Capacity of High-Strength Pipe at Strike-Slip Fault Crossing. Metals 2018, 8, 22. https://doi.org/10.3390/met8010022
Liu X, Zhang H, Wang B, Xia M, Wu K, Zheng Q, Han Y. Local Buckling Behavior and Plastic Deformation Capacity of High-Strength Pipe at Strike-Slip Fault Crossing. Metals. 2018; 8(1):22. https://doi.org/10.3390/met8010022
Chicago/Turabian StyleLiu, Xiaoben, Hong Zhang, Baodong Wang, Mengying Xia, Kai Wu, Qian Zheng, and Yinshan Han. 2018. "Local Buckling Behavior and Plastic Deformation Capacity of High-Strength Pipe at Strike-Slip Fault Crossing" Metals 8, no. 1: 22. https://doi.org/10.3390/met8010022
APA StyleLiu, X., Zhang, H., Wang, B., Xia, M., Wu, K., Zheng, Q., & Han, Y. (2018). Local Buckling Behavior and Plastic Deformation Capacity of High-Strength Pipe at Strike-Slip Fault Crossing. Metals, 8(1), 22. https://doi.org/10.3390/met8010022






