Effect of Computational Parameters on Springback Prediction by Numerical Simulation
Abstract
:1. Introduction
2. Materials and Methods
3. Numerical Model
4. Results
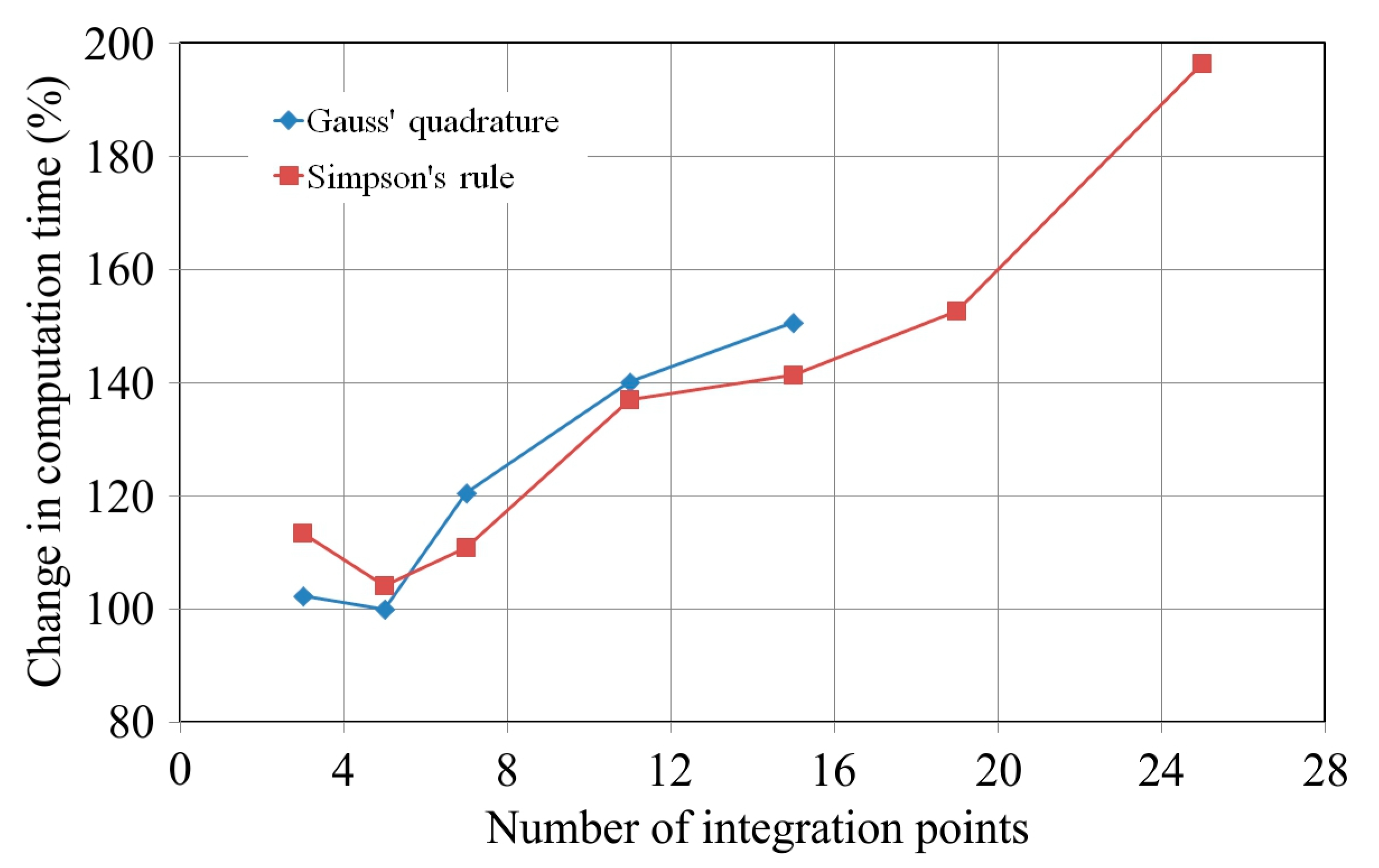
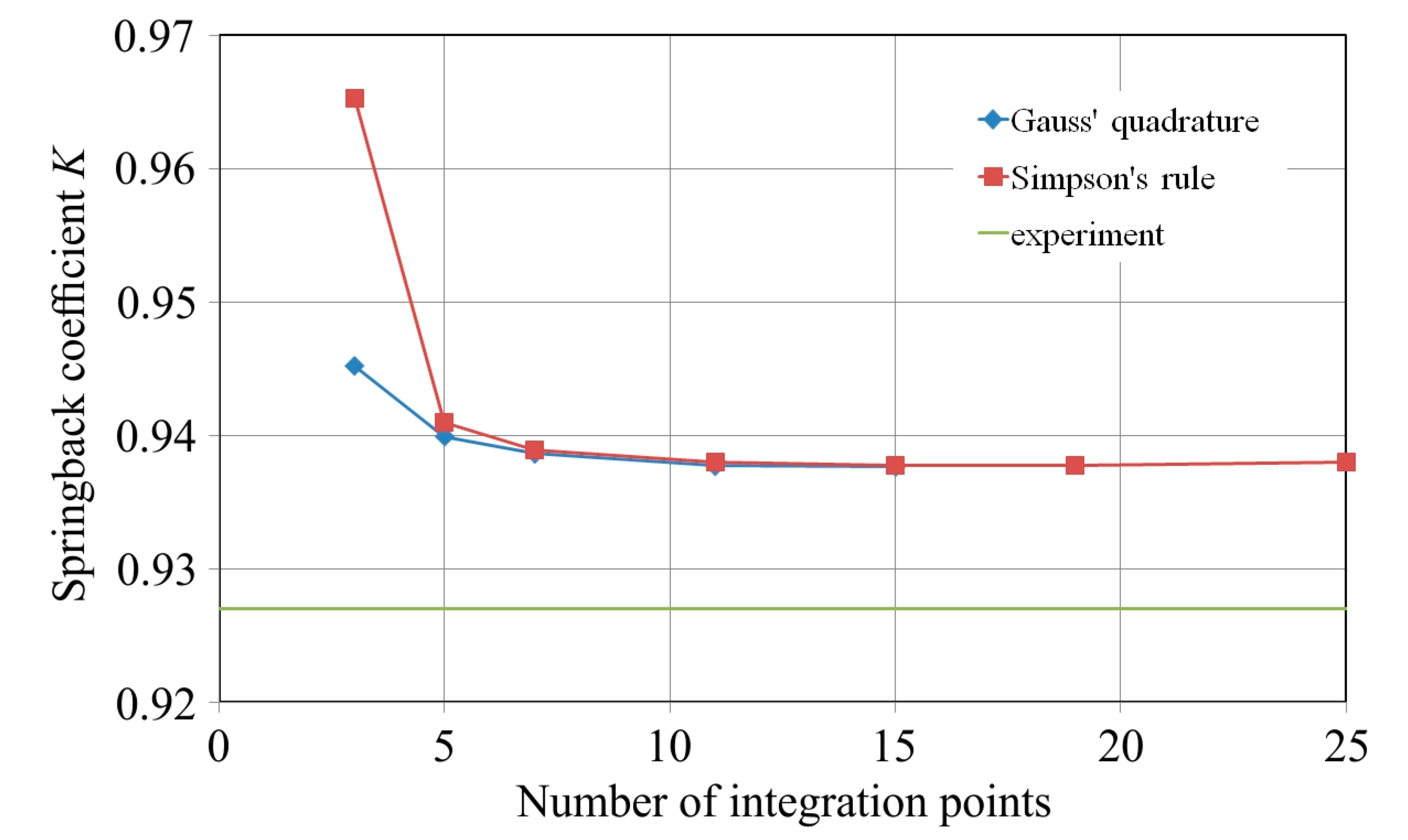
4.1. Effect of the Number of Integration Points
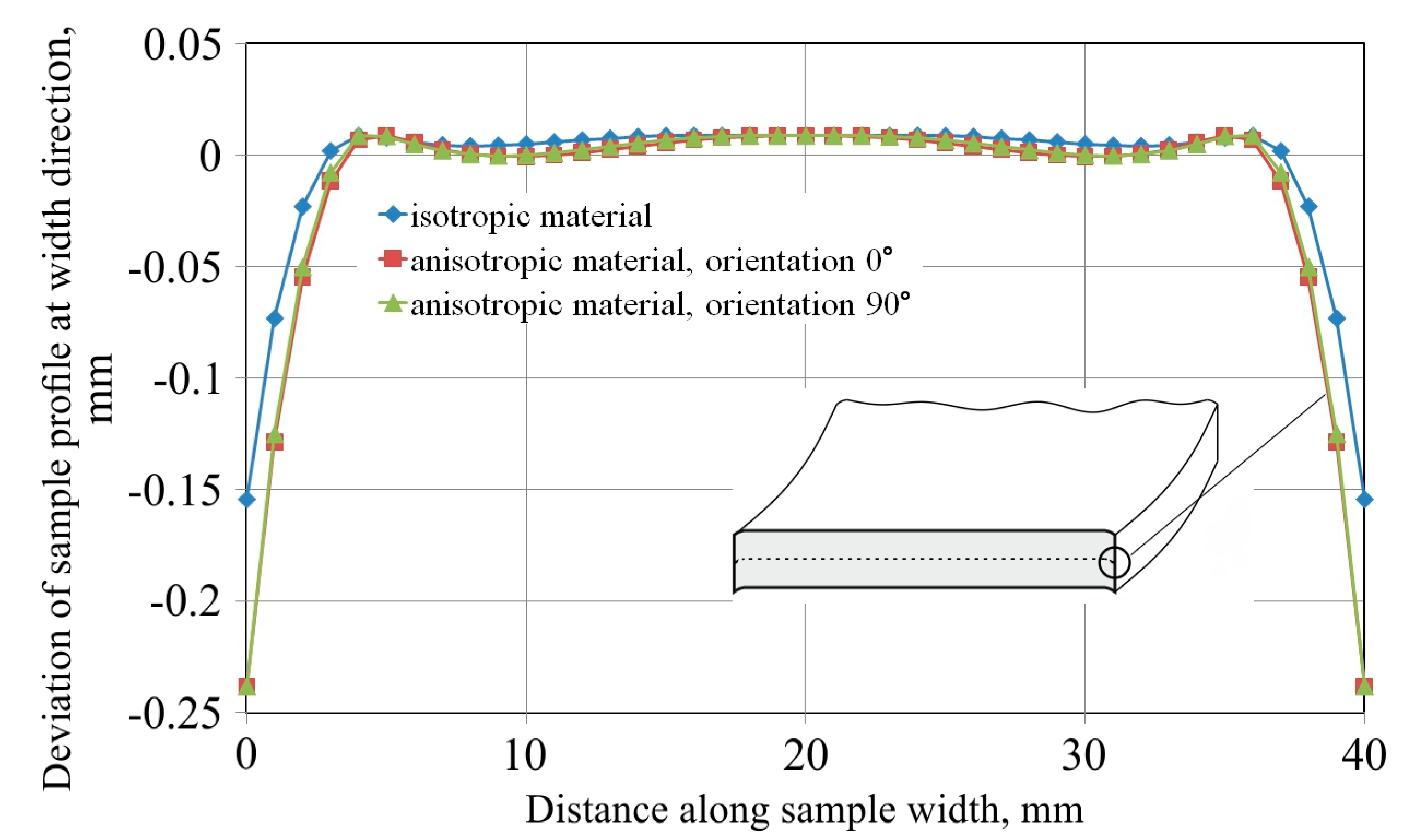
4.2. Sample Orientation
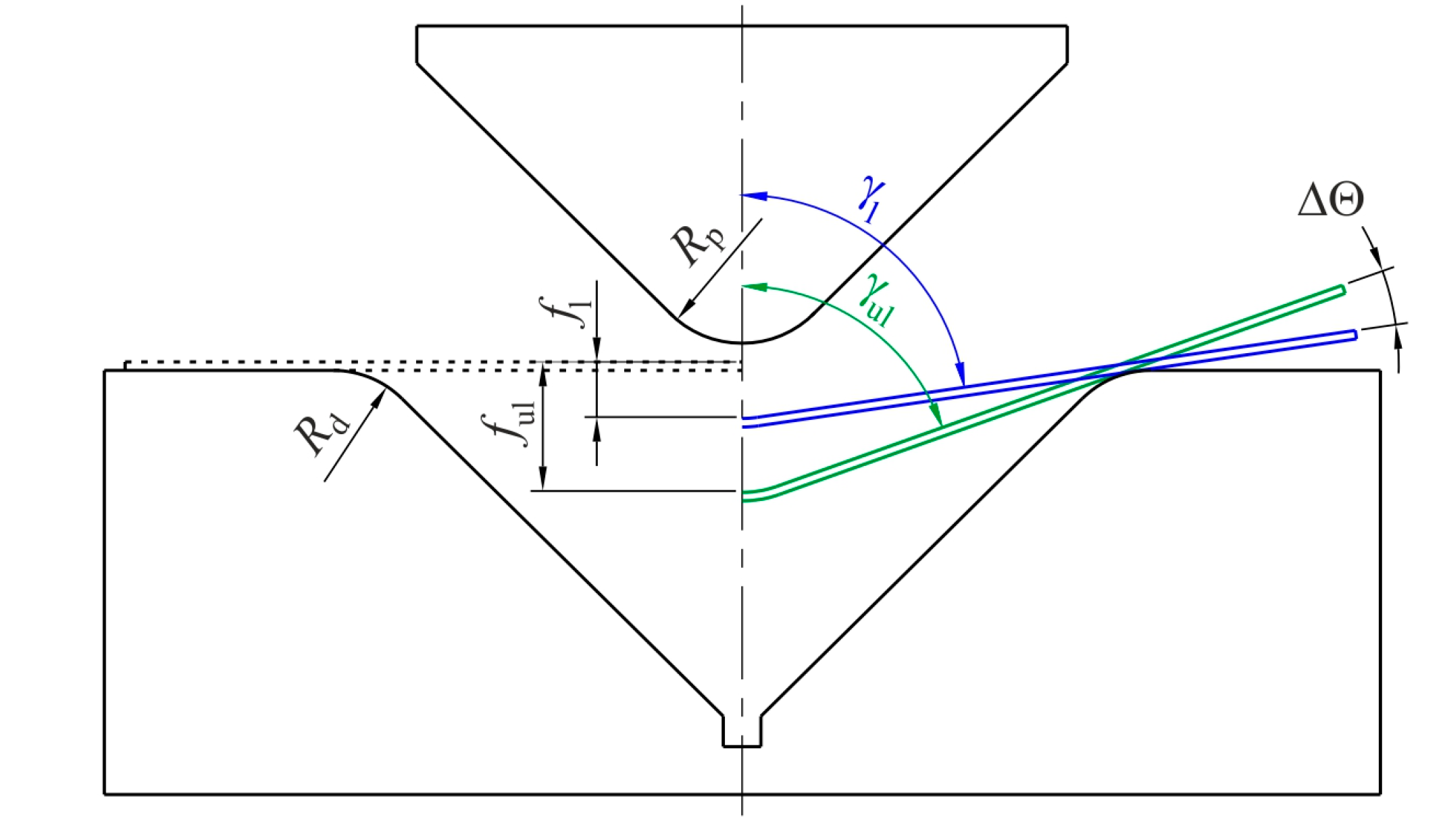
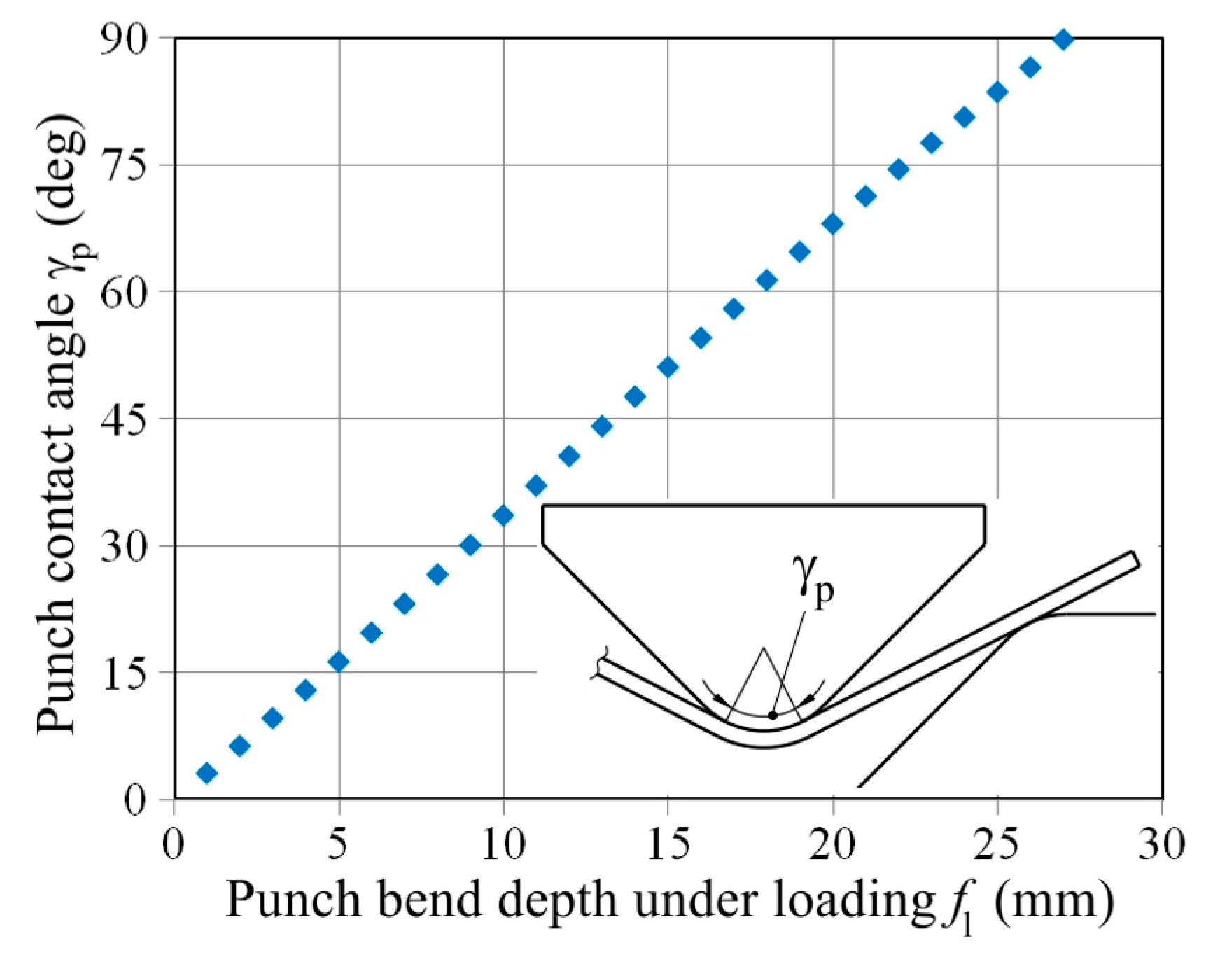
4.3. Sheet Deformation during Bending
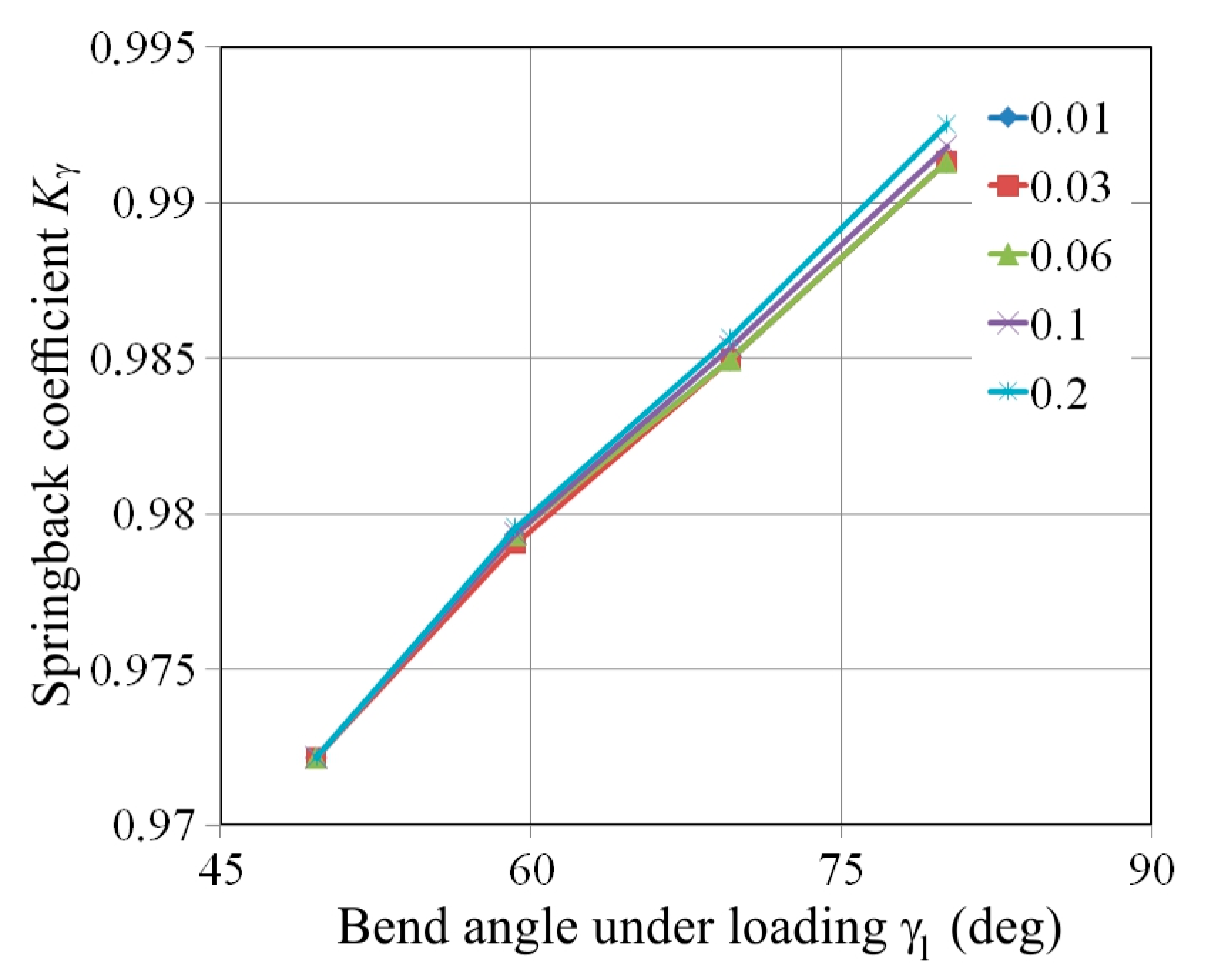
4.4. Effect of Friction Coefficient
5. Conclusions
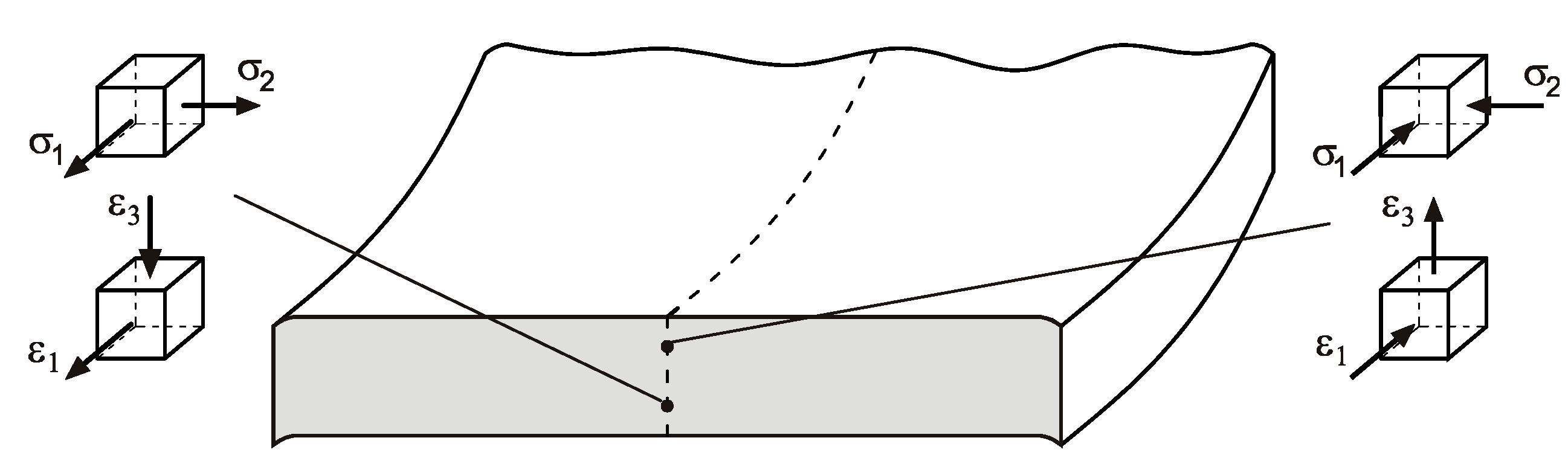
- The samples cut along the transverse direction exhibit greater springback than the blank cut in the rolling direction.
- The variation of the springback coefficient value almost shows linear dependence between the springback coefficient value and bend angle under loading.
- The results of the numerical model indicate that five integration points are the minimum acceptable considering the computation time and accuracy of springback prediction.
- Analyses of the sheet material with seven or more integration points through the thickness indicated that both Simpson’s and Gauss’ rules provide similar accuracy of prediction.
- The Gauss’ rule with five integration points is optimal to obtain the accurate results of springback prediction.
- The friction coefficient value slightly influences the springback amounts.
Author Contributions
Conflicts of Interest
References
- Dai, H.L.; Jiang, H.J.; Dai, T.; Xu, W.L.; Luo, A.H. Investigation on the influence of damage to springback of U-shape HSLA steel plates. J. Alloys Compd. 2017, 708, 575–586. [Google Scholar] [CrossRef]
- Carden, W.D.; Geng, L.M.; Matlock, D.K.; Wagoner, R.H. Measurement of springback. Int. J. Mech. Sci. 2002, 44, 79–101. [Google Scholar] [CrossRef]
- Yang, X.A.; Ruan, F. A die design method for springback compensation based on displacement adjustment. Int. J. Mech. Sci. 2011, 53, 399–406. [Google Scholar] [CrossRef]
- Eggertsen, P.A.; Mattiasson, K. On constitutive modeling for springback analysis. Int. J. Mech. Sci. 2010, 52, 804–818. [Google Scholar] [CrossRef]
- Nilsson, A.; Melin, L.; Magnusson, C. Finite-element simulation of V-die bending: A comparison with experimental results. J. Mater. Process. Technol. 1997, 65, 52–58. [Google Scholar] [CrossRef]
- Trzepiecinski, T.; Lemu, H.G. Prediction of springback in V-die air bending process by using finite element method. MATEC Web Conf. 2017, 121, 03023. [Google Scholar] [CrossRef]
- Karağaç, I. The experimental investigation of springback in V-bending using the flexforming process. Arab. J. Sci. Eng. 2017, 42, 1853–1864. [Google Scholar] [CrossRef]
- Leu, D.K.; Hsieh, C.M. The influence of coining force on spring-back reduction in V-die bending process. J. Mater. Process. Technol. 2008, 196, 230–235. [Google Scholar] [CrossRef]
- Bakhshi-Jooybari, M.; Rahmani, B.; Daeezadeh, V.; Gorji, A. The study of spring-back of CK67 steel sheet in V-die and U-die bending processes. Mater. Des. 2009, 30, 2410–2419. [Google Scholar] [CrossRef]
- Firat, M.; Osman, M.; Kocabicak, U.; Ozsoy, M. Stamping process design using FEA in conjunction with orthogonal regression. Finite Elem. Anal. Des. 2010, 46, 992–1000. [Google Scholar] [CrossRef]
- Huang, Y.M.; Leu, D.K. Effects of process variables on V-die bending process of steel sheet. Int. J. Mech. Sci. 1998, 40, 631–650. [Google Scholar] [CrossRef]
- Garcia-Romeu, M.L.; Ciurana, J.; Ferrer, I. Springback determination of sheet metals in air bending process based on an experimental work. J. Mater. Process. Technol. 2007, 191, 174–177. [Google Scholar] [CrossRef]
- Ragai, I.; Lazim, D.; Nemes, J.A. Anisotropy and springback in draw bending of stainless steel 410: Experimental and numerical study. J. Mater. Process. Technol. 2005, 166, 116–127. [Google Scholar] [CrossRef]
- Vin, L.J.; Streppel, A.H.; Singh, U.P.; Kals, H.J.J. A process model for air bending. J. Mater. Process. Technol. 1996, 57, 48–54. [Google Scholar] [CrossRef]
- Thipprakmas, S.; Rojananan, S. Investigation of spring-go phenomenon using finite element method. Mater. Des. 2008, 29, 1526–1532. [Google Scholar] [CrossRef]
- Tekıner, Z. An experimental study of the examination of spring-back of sheet metals with several thicknesses and properties in bending dies. J. Mater. Process. Technol. 2004, 145, 109–117. [Google Scholar] [CrossRef]
- Lingbeek, R.; Huétink, J.; Ohnimus, S.; Petzoldt, M.; Weiher, J. The development of a finite elements based springback compensation tool for sheet metal products. J. Mater. Process. Technol. 2005, 169, 115–125. [Google Scholar] [CrossRef]
- Del Pozo, D.; López de Lacalle, L.N.; López, J.M.; Hernández, A. Prediction of press/die deformation for an accurate manufacturing of drawing dies. Int. J. Adv. Manuf. Technol. 2008, 37, 649–656. [Google Scholar] [CrossRef]
- López de Lacalle, L.N.; Lamikiz, A.; Muñoa, J.; Salgado, M.A.; Sánchez, J.A. Improving the high-speed fnishing of forming tools for advanced high-strength steels (AHSS). Int. J. Adv. Manuf. Technol. 2006, 29, 49–63. [Google Scholar] [CrossRef]
- Sumikawa, S.; Ishiwatari, A.; Hiramoto, J.; Urabe, T. Improvement of springback prediction accuracy using material model considering elastoplastic anisotropy and Bauschinger effect. J. Mater. Process. Technol. 2016, 230, 1–7. [Google Scholar] [CrossRef]
- Yoshida, T.; Katayama, K.; Hashimoto, Y.; Kuriyama, Y. Shape control techniques for high strength steel in sheet metal forming. Nippon Steel Tech. Rep. 2003, 88, 27–32. [Google Scholar]
- Hattori, Y.; Furakawa, K.; Hamasaki, H.; Yoshida, F. Experimental and simulated springback after stamping of copper-based spring materials. In Proceedings of the 59th Holm Conference on Electrical Contacts, Newport, RI, USA, 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Yoshida, F.; Uemori, T. A model of large-strain cyclic plasticity and its application to springback simulation. Int. J. Mech. Sci. 2003, 45, 1687–1702. [Google Scholar] [CrossRef]
- Rashid, M.; Liebert, C. Finite Element Analysis of a Lifting Portable Offshore Unit. Master’s Thesis, Chalmers University of Technology, Goteborg, Sweden, 2015. [Google Scholar]
- Xu, W.L.; Ma, C.H.; Li, C.H.; Feng, W.J. Sensitive factors in springback simulation for sheet metal forming. J. Mater. Proc. Technol. 2004, 151, 217–222. [Google Scholar] [CrossRef]
- Wagoner, R.H.; Li, M. Simulation of springback: Through-thickness integration. Int. J. Plast. 2007, 23, 345–360. [Google Scholar] [CrossRef]
- Martínez Krahmer, D.; Polvorosa, R.; López de Lacalle, L.N.; Alonso-Pinillos, U.; Abate, G.; Riu, F. Alternatives for specimen manufacturing in tensile testing of steel plates. Exp. Tech. 2016, 40, 1555–1565. [Google Scholar] [CrossRef]
- Hollomon, J.H. Tensile deformation. Trans. Metall. Soc. AIME 1945, 162, 268–290. [Google Scholar]
- ABAQUS 2016. Theory Guide; Dassault Systèmes: Vélizy-Villacoublay Codex, France, 2015.
- ABAQUS 2016. Analysis User’s Guide. Volume IV: Elements; Dassault Systèmes: Vélizy-Villacoublay Codex, France, 2015.
- Hill, R. A theory of the yielding and plastic flow of anisotropic metals. Proc. R. Soc. A 1948, 193, 281–297. [Google Scholar] [CrossRef]
- Trzepieciński, T.; Gelgele, H.L. Investigation of anisotropy problems in sheet metal forming using finite element method. Int. J. Mater. Form. 2011, 4, 357–369. [Google Scholar] [CrossRef]
- Von Mises, R. Mechanik der festen Körper im plastisch-deformablen Zustand. Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse 1913, 1913, 582–592. [Google Scholar]
- Frącz, W.; Stachowicz, F. Springback phenomenon in sheet metal V-die air bending—Experimental and numerical study. Manuf. Ind. Eng. 2008, 2, 34–37. [Google Scholar]
- Burgoyne, C.J.; Crisfield, M.A. Numerical integration strategy for plates and shells. Int. J. Numer. Methods Eng. 1990, 29, 105–121. [Google Scholar] [CrossRef]
- Albrut, A.; Brabie, G. The influence of the rolling direction of the joined steel sheets on the springback intensity in the case of Ω-shape parts made from tailor welded strips. Arch. Civ. Mech. Eng. 2006, 6, 5–12. [Google Scholar] [CrossRef]
- Papeleux, L.; Ponthot, J.P. Finite element simulation of springback in sheet metal forming. J. Mater. Proc. Technol. 2002, 125–126, 785–791. [Google Scholar] [CrossRef]
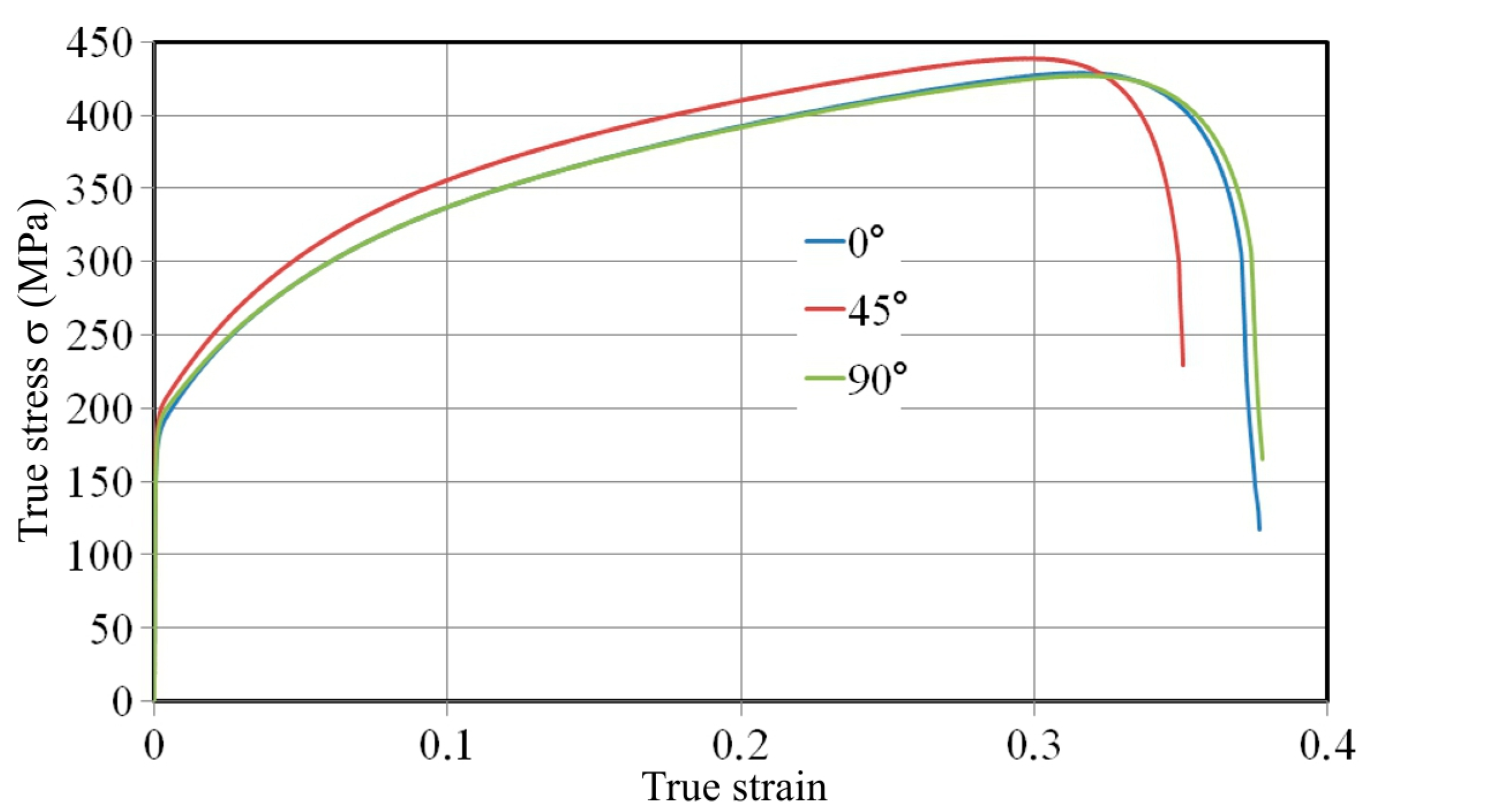





| Orientation | Yield Stress σy (MPa) | Ultimate Tensile Strength σm (MPa) | Strain Hardening Coefficient C (MPa) | Strain Hardening Exponent n | Lankford’s Coefficient r |
|---|---|---|---|---|---|
| 0° | 182.1 | 322.5 | 549.3 | 0.214 | 1.751 |
| 45° | 196 | 336.2 | 564.9 | 0.205 | 1.124 |
| 90° | 190 | 320.9 | 555.2 | 0.209 | 1.846 |
| Average value | 191.02 | 328.9 | 558.57 | 0.208 | 1.461 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trzepiecinski, T.; Lemu, H.G. Effect of Computational Parameters on Springback Prediction by Numerical Simulation. Metals 2017, 7, 380. https://doi.org/10.3390/met7090380
Trzepiecinski T, Lemu HG. Effect of Computational Parameters on Springback Prediction by Numerical Simulation. Metals. 2017; 7(9):380. https://doi.org/10.3390/met7090380
Chicago/Turabian StyleTrzepiecinski, Tomasz, and Hirpa G. Lemu. 2017. "Effect of Computational Parameters on Springback Prediction by Numerical Simulation" Metals 7, no. 9: 380. https://doi.org/10.3390/met7090380
APA StyleTrzepiecinski, T., & Lemu, H. G. (2017). Effect of Computational Parameters on Springback Prediction by Numerical Simulation. Metals, 7(9), 380. https://doi.org/10.3390/met7090380






