Low Field Magnetic and Thermal Hysteresis in Antiferromagnetic Dysprosium
Abstract
:1. Introduction
2. Materials and Methods
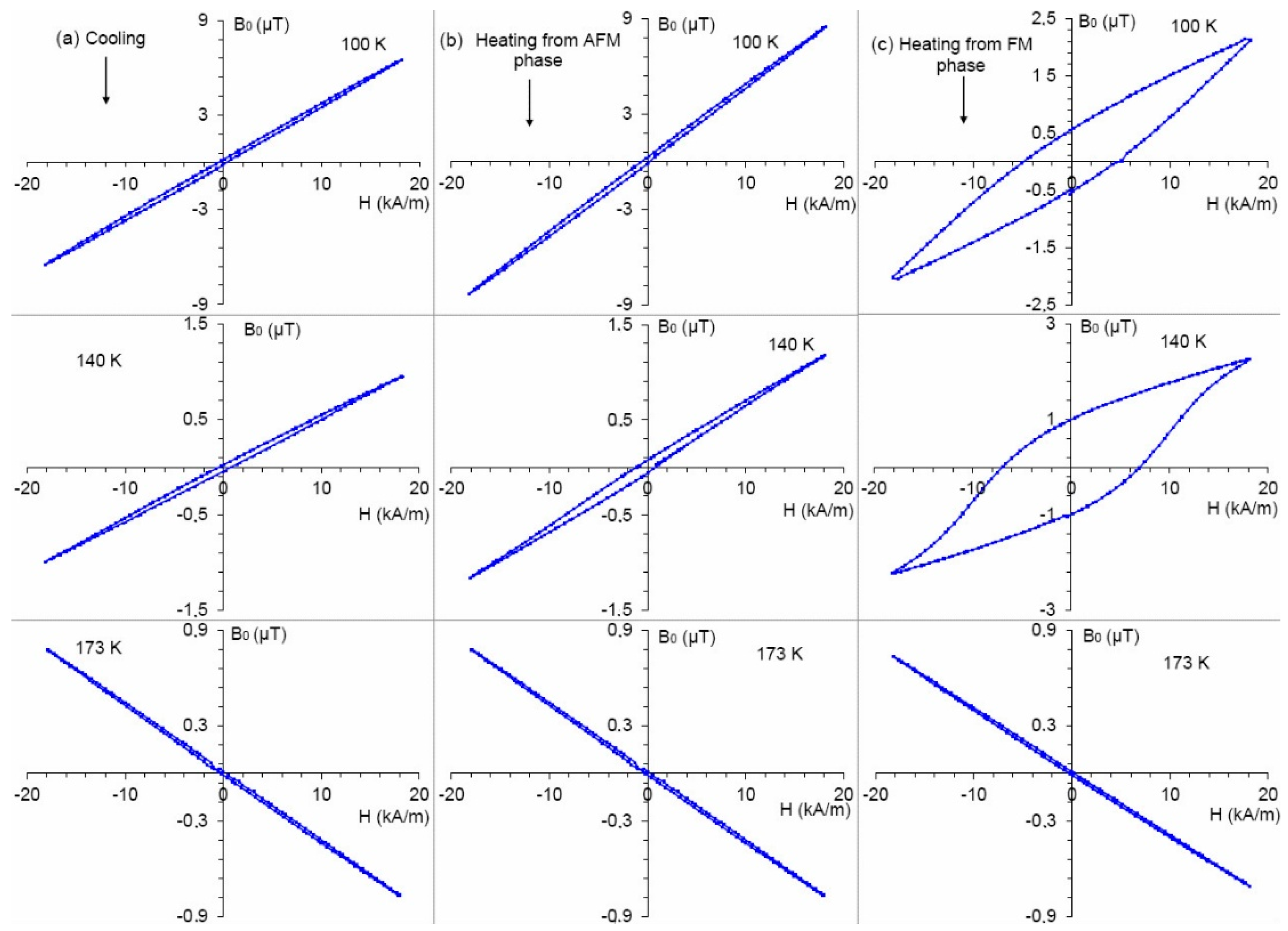
3. Results
4. Discussion
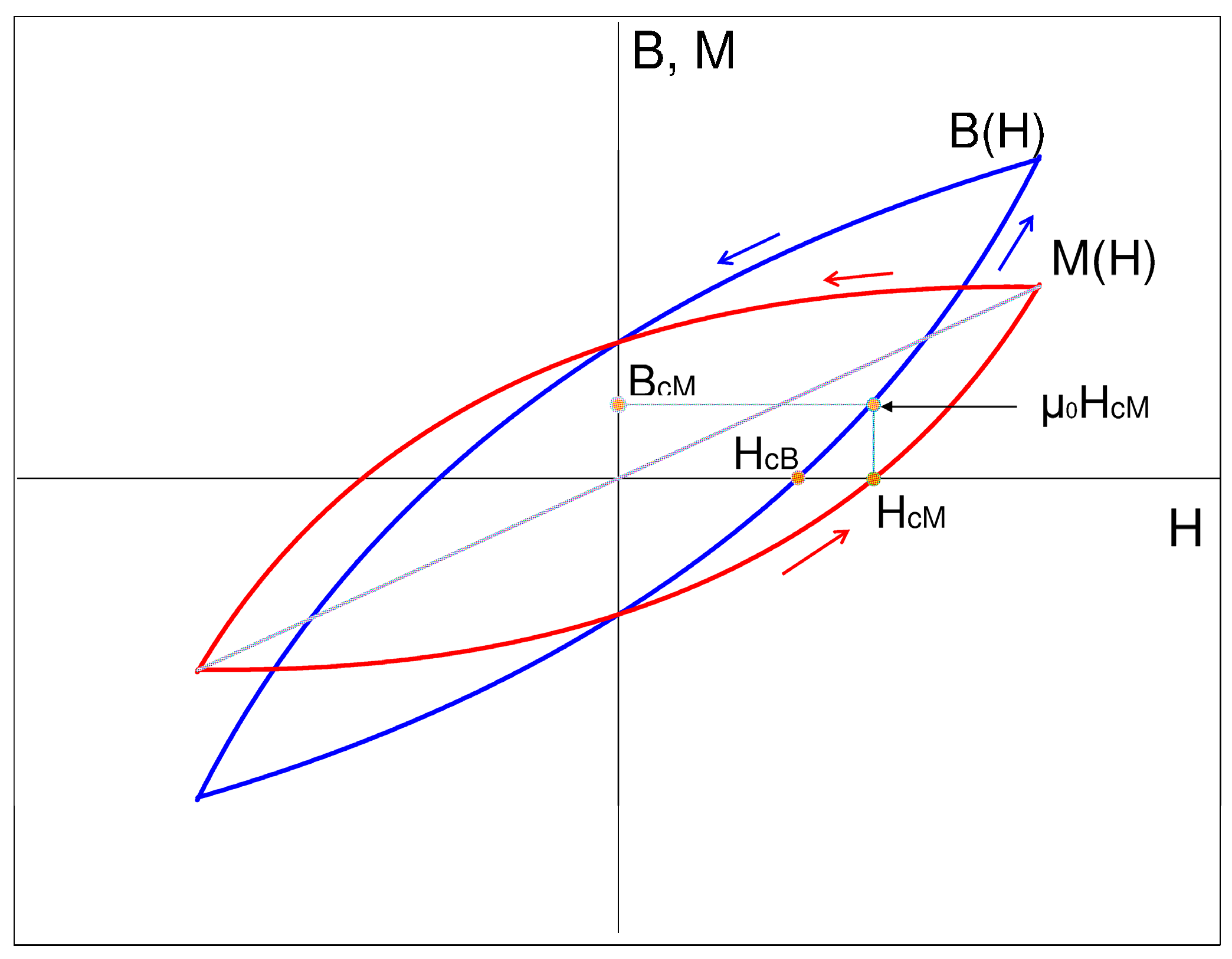
4.1. Relationship Between the Width of and Hysteresis
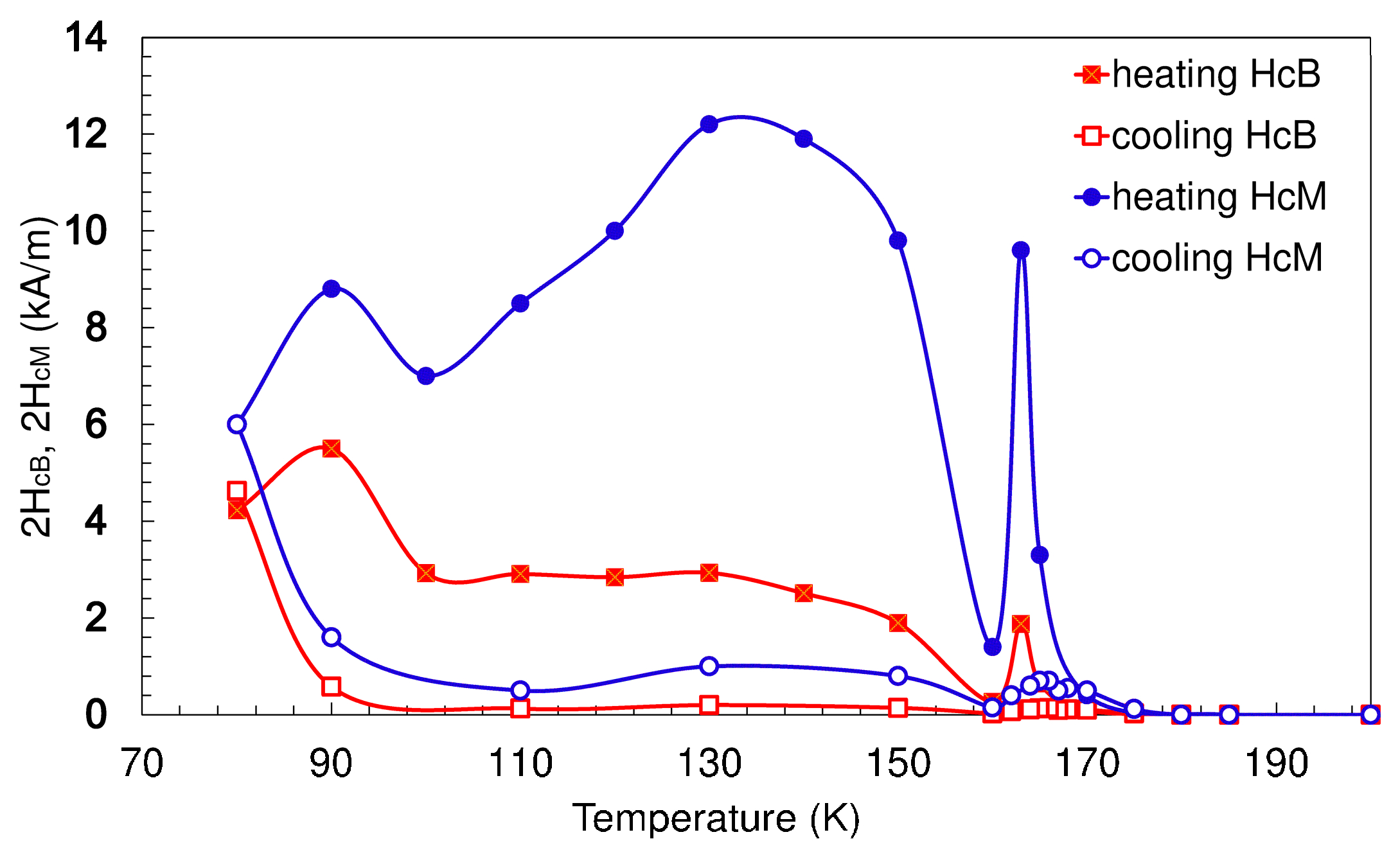
4.2. Temperature Dependence of the Magnetic Hysteresis Width
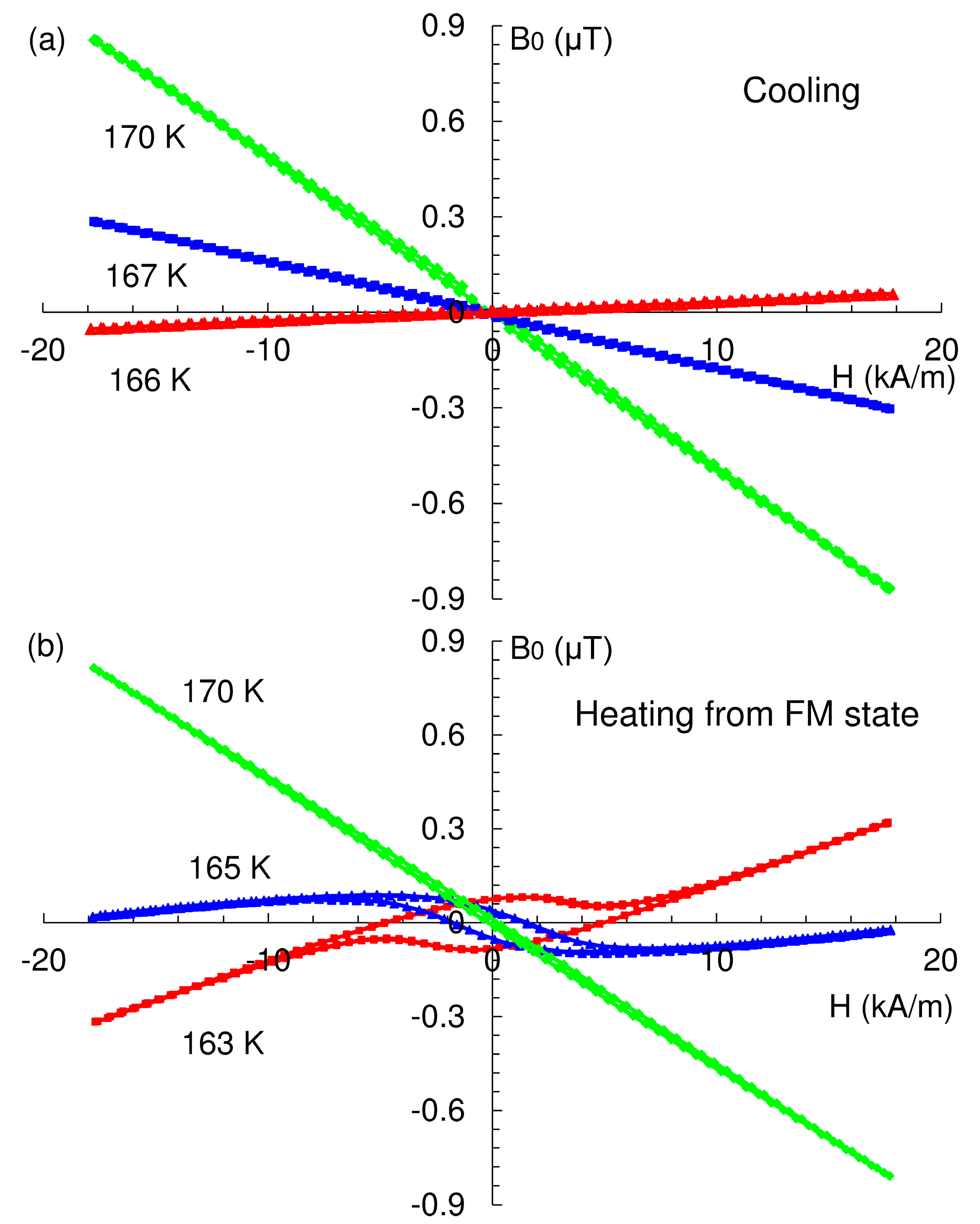
4.3. Thermal Hysteresis and Relaxation in the Helical Phase
- direct contribution of the FM phase to the dissipation;
- pinning of the AFM domain walls by residual FM phase in addition to the direct contribution of the latter to the dissipation.
5. Conclusions
- (1)
- We showed that mechanomagnetic spectroscopy is much more sensitive to magnetic hysteresis in the AFM phase than the conventional experimental method based on registration of hysteresis.
- (2)
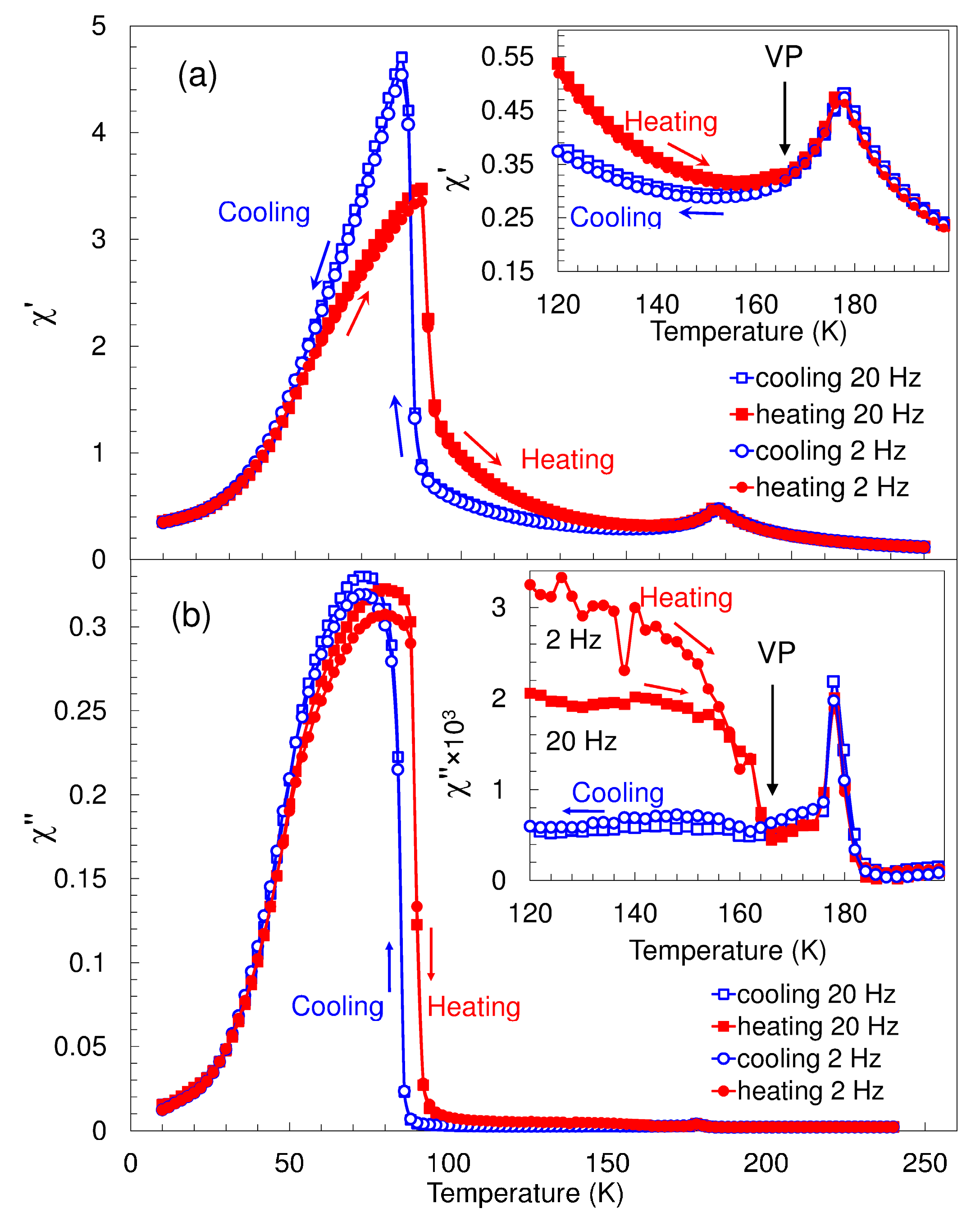
- A number of regularities in magnetic properties of polycrystalline Dy in the spiral AFM phase, including the crucial role of the Villari point at 166 K, revealed by means of RVE measurements, were confirmed by using studies of AC susceptibility:
- Thermal hysteresis persists in AC susceptibility, and is most intense in its imaginary part. The thermal hysteresis in AC susceptibility vanishes at the temperature of the Villari point at 166 K, as is the case for the thermal hysteresis in the reversible Villari effect.
- The imaginary part of the AC susceptibility is strongly frequency dependent in the helical antiferromagnetic phase during heating from the ferromagnetic state. The frequency dependence disappears at the Villari point. This behavior is consistent with the previously reported relaxation in the reversible Villari effect.
- (3)
- We suggest that thermal hysteresis in polycrystalline Dy, other rare earth elements, and their alloys, is related to the ferromagnetic phase, stabilized in the antiferromagnetic structure by lattice defects, possessing intense strain fields, like lattice dislocations.
- (4)
- Since the Villari point at 166 K controls several magnetic properties of Dy, this temperature can be ranked to be nearly as important as the TN and TC. Keeping in mind similar behavior of thermal hysteresis in Dy and other rare earth elements and their alloys, the effects reported in the present work should be generic for a wide range of helical antiferromagnets.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Elliott, J.; Legvold, S.; Spedding, F.H. Some magnetic properties of Dy metal. Phys. Rev. 1954, 94, 1143–1145. [Google Scholar] [CrossRef]
- Griffel, M.; Skochdopole, R.E.; Spedding, F.H. Heat capacity of dysprosium from 15 to 300°k. J. Chem. Phys. 1956, 25, 75–79. [Google Scholar] [CrossRef]
- Wilkinson, M.K.; Koehler, W.C.; Wollan, E.O.; Cable, J.W. Neutron diffraction investigation of magnetic ordering in dysprosium. J. Appl. Phys. 1961, 32, 48S–49S. [Google Scholar] [CrossRef]
- Darnell, F.J. Temperature dependence of lattice parameters for Gd, Dy, and Ho. Phys. Rev. 1963, 130, 1825–1828. [Google Scholar] [CrossRef]
- Darnell, F.J.; Moore, E.P. Crystal structure of dysprosium at low temperatures . J. Appl. Phys. 1963, 34, 1337–1338. [Google Scholar] [CrossRef]
- Rosen, M. Elastic moduli and ultrasonic attenuation of gadolinium, terbium, dysprosium, holmium, and erbium from 4.2 to 300°k. Phys. Rev. 1968, 174, 504–514. [Google Scholar] [CrossRef]
- Belov, K.P.; Levitin, R.Z.; Nikitin, S.A.; Ped'ko, A.V. Magnetic and magnetoelastic properties of dysprosium and gadolinium. Soviet Phys. JETP 1961, 13, 1096–1101. [Google Scholar]
- Doerr, M.; Rotter, M.; Lindbaum, A. Magnetostriction in rare-earth based antiferromagnets. Adv. Phys. 2005, 54, 1–66. [Google Scholar] [CrossRef]
- McKenna, T.J.; Campbell, S.J.; Chaplin, D.H.; Wilson, G.V.H. Temperature modulation and temperature hysteresis studies of dysprosium. Phys. Status Solidi (A) 1983, 75, 421–432. [Google Scholar] [CrossRef]
- Amitin, E.B.; Bessergenev, W.G.; Kovalevskaya, Y.A.; Paukov, I.E.J. Thermodynamic properties of dysprosium from 7 to 300 K. Chem. Thermodyn. 1983, 15, 181–188. [Google Scholar] [CrossRef]
- McKenna, T.J.; Campbell, S.J.; Chaplin, D.H.; Wilson, G.V.H. Domain effects near the order-disorder and order-order ferromagnetic transitions in Gd and Dy. J. Magn. Magn. Mater. 1980, 20, 207–211. [Google Scholar] [CrossRef]
- Arzhavitin, V.M.; Derevyanko, V.V.; Sukhareva, T.V.; Finkel, V.A. Anomalies of kinetic, magnetic and relaxation properties of dysprosium in the region of helicoidal antiferromagnetic structure. Funct. Mater. 2006, 13, 30–34. [Google Scholar]
- Herz, E.; Kronmuller, H. Field-induced phase transitions in the helical state of dysprosium. Phys. Status Solidi (A) 1978, 47, 451–458. [Google Scholar] [CrossRef]
- Isci, C.; Palmer, S.B. An ultrasonic study of the magnetic phases of dysprosium. J. Phys. F 1978, 8, 247–260. [Google Scholar] [CrossRef]
- Chernyshov, A.S.; Mudryk, Y.; Pecharsky, V.K.; Gschneidner, K.A., Jr. Temperature and magnetic field-dependent x-ray powder diffraction study of dysprosium. Phys. Rev. B 2008, 77, 094132. [Google Scholar] [CrossRef]
- Amitin, E.B.; Bessergenev, V.G.; Kovalevskaya, Y.A. Features of the thermodynamic properties of dysprosium as a quasi-two-dimensional magnetic system. Zh. Eksp. Teor. Fiz 1983, 84, 205–214. [Google Scholar]
- Andrianov, A.V.; Gaidukov, Y.P.; Vasil’ev, A.N.; Fawcett, E. The magnetic phase diagrams of dysprosium. J. Magn. Magn. Mater. 1991, 97, 246–250. [Google Scholar] [CrossRef]
- Chernyshov, A.S.; Tsokol, A.O.; Tishin, A.M.; Gschneidner, Jr.K.A.; Pecharsky, V.K. Magnetic and magnetocaloric properties and the magnetic phase diagram of single-crystal dysprosium. Phys. Rev. B 2005, 71, 184410. [Google Scholar] [CrossRef]
- Alkhafaji, M.T.; Ali, N. Magnetic phase diagram of dysprosium. J. Alloys Compd. 1997, 250, 659–661. [Google Scholar] [CrossRef]
- Del Moral, A.; Lee, E.W. The reversible susceptibilities of dysprosium and terbium. J. Phys. F 1974, 4, 280–290. [Google Scholar] [CrossRef]
- Palmer, S.B.; Lee, E.W. The elastic constants of dysprosium and holmium. In Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, London, UK, 25 April 1972. [Google Scholar]
- Palmer, S.B. Antiferromagnetic domains in rare earth metals and alloys. J. Phys. F 1975, 5, 2370–2378. [Google Scholar] [CrossRef]
- Kobayashi, S. Universal hysteresis scaling for incommensurate magnetic order in dysprosium. Phys. Rev. Lett. 2011, 106, 057207. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.-W.; Guo, H.; Seu, K.A.; Dumesnil, K.; Roy, S.; Sinha, S.K. Jamming behavior of domains in a spiral antiferromagnetic systems. Phys. Rev. Lett. 2013, 110, 217201. [Google Scholar] [CrossRef] [PubMed]
- Corró, M.L.; El Hichou, A.; Cesari, E.; Kustov, S. Study of magnetic transitions in Dy by means of reversible Villari effect. J. Phys. D 2016, 49, 015001. [Google Scholar] [CrossRef]
- Kustov, S.; Masdeu, F.; Cesari, E. Mechanomagnetic spectroscopy of phase transitions in ferromagnetic shape memory alloys. Appl. Phys. Lett. 2006, 89, 061917. [Google Scholar] [CrossRef]
- Kustov, S.; Corró, M.L.; Cesari, E. Mechanomagnetic spectroscopy of ferromagnetic shape memory alloys. Mater. Sci. Eng. A 2009, 521, 194–200. [Google Scholar] [CrossRef]
- Kustov, S.; Corró, M.L.; Cesari, E.; Pérez-Landazábal, J.I.; Recarte, V. Peculiarities of magnetoelastic coupling in Ni–Fe–Ga–Co ferromagnetic martensite. J. Phys. D 2010, 43, 175002. [Google Scholar] [CrossRef]
- Kustov, S.; Golyandin, S.; Ichino, A.; Gremaud, G. A new design of automated piezoelectric composite oscillator technique. Mater. Sci. Eng. A 2006, 442, 532–537. [Google Scholar] [CrossRef]
- Robinson, W.H.; Edgar, A. The piezoelectric method of determining mechanical damping at frequencies of 30 to 200 kHz. IEEE Trans. Sonics Ultrason. 1974, 21, 98–105. [Google Scholar] [CrossRef]
- Bozorth, R.M. Ferromagnetism; Wiley-IEEE Press: Hoboken, NJ, USA, 2003; Chapter 13; pp. 595–712. [Google Scholar]
- Gignoux, D.; Schlenker, M.; de Lacheisserie, É.D. T. Magnetism: Fundamentals; Springer: New York, NY, USA, 2005; Chapter 12; pp. 351–397. [Google Scholar]
- Corró, M.L.; El Hichou, A.; Kustov, S. A review of mechanomagnetic spectroscopy. Case study: Dy polycrystals. J. Magn. Magn. Mater. 2016, 400, 141–144. [Google Scholar]
- Sugiyama, I.; Shibata, N.; Wang, Z.; Kobayashi, S.; Yamamoto, T.; Ikuhara, Y. Ferromagnetic dislocations in antiferromagnetic NiO. Nat. Nanotechnol. 2013, 8, 266–270. [Google Scholar] [CrossRef] [PubMed]


© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liubimova, I.; Corró Moyà, M.L.; Torrens-Serra, J.; Recarte, V.; Pérez-Landazábal, J.I.; Kustov, S. Low Field Magnetic and Thermal Hysteresis in Antiferromagnetic Dysprosium. Metals 2017, 7, 215. https://doi.org/10.3390/met7060215
Liubimova I, Corró Moyà ML, Torrens-Serra J, Recarte V, Pérez-Landazábal JI, Kustov S. Low Field Magnetic and Thermal Hysteresis in Antiferromagnetic Dysprosium. Metals. 2017; 7(6):215. https://doi.org/10.3390/met7060215
Chicago/Turabian StyleLiubimova, Iuliia, Miguel Lluís Corró Moyà, Joan Torrens-Serra, Vicente Recarte, José Ignacio Pérez-Landazábal, and Sergey Kustov. 2017. "Low Field Magnetic and Thermal Hysteresis in Antiferromagnetic Dysprosium" Metals 7, no. 6: 215. https://doi.org/10.3390/met7060215
APA StyleLiubimova, I., Corró Moyà, M. L., Torrens-Serra, J., Recarte, V., Pérez-Landazábal, J. I., & Kustov, S. (2017). Low Field Magnetic and Thermal Hysteresis in Antiferromagnetic Dysprosium. Metals, 7(6), 215. https://doi.org/10.3390/met7060215






