Abstract
A mathematical model was developed to describe the hydrodynamics of a batch reactor for aluminum degassing utilizing the rotor-injector technique. The mathematical model uses the Eulerian algorithm to represent the two-phase system including the simulation of vortex formation at the free surface, and the use of the RNG k-ε model to account for the turbulence in the system. The model was employed to test the performances of three different impeller designs, two of which are available commercially, while the third one is a new design proposed in previous work. The model simulates the hydrodynamics and consequently helps to explain and connect the performances in terms of degassing kinetics and gas consumption found in physical modeling previously reported. Therefore, the model simulates a water physical model. The model reveals that the new impeller design distributes the bubbles more uniformly throughout the ladle, and exhibits a better-agitated bath, since the transfer of momentum to the fluids is better. Gas is evenly distributed with this design because both phases, gas and liquid, are dragged to the bottom of the ladle as a result of the higher pumping effect in comparison to the commercial designs.
1. Introduction
The metallurgical industry today is facing a twofold problem: new technologies are restricted by tighter environmental and safety regulations, while economic margins and the quality of metal required have increased for most applications.
During recent decades, Computational Fluid Dynamics (CFD) has become a very powerful tool in the metallurgical industry not only for the research and development of new processes but also for the understanding and optimization of existing ones. Agitated vessels where gas is injected through an impeller that mixes the liquid with the injected gas is a commonplace process in chemical and metallurgical operations. In the aluminum industry, dissolved hydrogen is removed from molten aluminum by using the impeller injector technique, in which purge gas is injected by the impeller, providing global stirring in the vessel, breaking and dispersing bubbles through the molten metal. Since there is a lack of experimental data regarding this process, mainly due to the cost and hazard of the systems with nontransparent fluids such as molten metal, CFD has been used to predict fluid flow structures, gas hold-up in the vessel, formation and shape of the vortex.
In the two-fluid flow models, separate continuity and momentum equations are derived for the liquid and gas phases, with appropriate interfacial mass and momentum transfer relations. Two-phase flow formulation can be categorized into two types: namely, the Euler–Euler, or continuum, approach where a set of transport equations is solved for the gas phase; and the Eulerian–Lagrangian approach, where the gas phase is treated as particles which interact with the continuous phase. Model development should also consider how the results and obtained data can be verified. Common verification sources include experimental water model results, plant operating data, results from similar CFD models, etc. Experimental techniques such as particle image velocimetry have provided detailed flow field data for validation and improvement of CFD models [1,2]. Deen et al. [3] compared sliding mesh, Eulerian simulations to PIV data and replicated the presence of gas cavities behind impeller blades observed in experiments.
While it is clear CFD is already becoming an important tool for the design of impellers and stirred tanks, there is room for improvement in this burgeoning field, specifically in the area of turbulence. Numerical simulation of the degassing of aluminum by using rotor injector techniques faces the difficulty of modeling a complex two-phase system: the molten aluminum; and a gas phase, which is composed of two gases: the purge gas and dissolved hydrogen. This difficulty in modeling such a system arises from the inability of software and hardware to handle mathematical models able to provide a detailed description of the flow patterns in the metal bath, including the turbulence created by the rotation of the impeller and the flow of injected purge gas, the interaction between the liquid and gas phases, and the interaction between the purge gas and the dissolved hydrogen. The two standard k-ε turbulence models, employing the concept of isotropic turbulent viscosity, performs well for a wide variety of flows, but for strong swirl flows, the RNG k-ε improves the prediction of turbulence. To simplify the analysis and get a viable solution, early work has focused on the flow patterns induced by injecting gas bubbles [4,5]. Johansen [6] and Hop [7] modeled flow patterns induced by the rotor by means of transport equations for one phase, assuming that purge gas bubbles are introduced into the computational domain as a disperse phase, and monitoring their trajectory using a Lagrange reference frame. All previous studies restrict the movement of metal at the free surface to simplify the model and therefore excluded that effect on flow patterns and analysis. Maniruzzaman and Makhlouf [8,9] used a Eulerian–Eulerian multiphase model, in which they modeled the system of interacting phases as two separate but interdependent systems. The first subsystem involves turbulent flow patterns resulting from the rotation of the impeller and the gas flow; and the second subsystem involves particle dynamics, it thereby being possible to contain the system complexity without computational cost. Furthermore, the study included the movement of the melt surface, showing the formation of the vortex, even though it used a two-dimensional geometry model. The last relevant contribution to the modeling of rotary degassing was the model of Warke et al. [10,11] who simulated the turbulent multiphase flow field that develops in the melt during rotary degassing calculating the mean turbulence dissipation energy and the distribution of gas bubbles in the melt and used both quantities as input into other mathematical models to simulate the removal of dissolved hydrogen and impure solid particles from the melt.
Numerous CFD simulations for single-phase turbulent flow in agitated vessels for aluminum degassing using the rotor injector technique can be found in the literature, establishing CFD as a viable tool for the investigation of fluid dynamics in complex systems. These have been done using commercial codes such as FIDAP [12], Fluent [10,13], Phoenics [1], and others [14]. Although these models are complex and help to understand the agitation phenomena inside the reactor, they do not provide a proper connection between the fluid flow and mass transport phenomena to predict the removal of solid inclusions and dissolved hydrogen. Warke [10,11] modeled degassing by the rotor injector technique dividing the system into three separate but interconnected subsystems which included the turbulent flow fields caused by the impeller rotation, the gas flow injected, and the removal dynamics of particles and dissolved hydrogen. The approach was done using a standard turbulence model and the Eulerian approach for the multiphase fluid, and the connection of the subsystems was performed with parameters like turbulent energy dissipation and bubble distribution.
Recent work in this area includes 3D modeling of the entire system as well as the modeling of the free surface for the formation of the vortex, as shown by the work done by Ramos et al. [1], based on a Eulerian–Eulerian approach where the effects of critical operating parameters, such as rotational impeller speed, flow gas injected, and gas point injection, were analyzed. Clearly the CFD approach is well suited for studying the aluminum degasification using the rotor injector technique, since high temperatures and production schedules limit experimental research. More recently, a couple of experimental studies [15,16] present results on the degassing kinetics and on the hydrodynamics features of the three impellers tested in this work. Two of them are commercially available designs while the third design is a new design proposed in previous work [15].
In this paper, a CFD analysis is presented to study the performance of three different impeller designs based on the flow dynamics and turbulence in a water physical model of an aluminum batch degassing unit implementing the rotor injector technique. The analysis was used to explain, based on first principles, the superior performance of a new impeller design proposed in this work against two commercially-available designs in terms of gas consumption and degassing kinetics.
2. Materials and Methods
2.1. Mathematical Model
The system is schematically presented in Figure 1a, while its dimensions and characteristics are shown in Table 1. The fluid dynamics of the aluminum batch degassing reactor may be represented by simultaneously solving the principles of conservation of mass and the turbulent Navier-Stokes equations under a Multiple Reference Frame (MRF). Figure 1b shows the regions where two different frames of reference apply: (a) A rotating frame of reference for the shaft and the impeller, which is separated from the fluids and (b) A fixed frame of reference. To treat the two-fluid system gas-liquid in order to resolve the vortex shape and size, and gas holdup, the Eulerian two-phase model was considered in the fluid system.
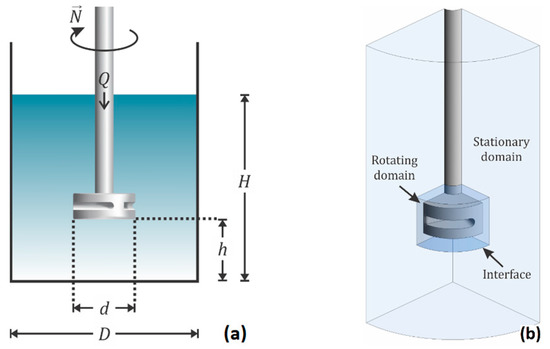
Figure 1.
(a) Schematic representation of the batch degassing ladle, indicating the rotating speed, , and the gas flow rate, Q and the geometric features of the ladle; (b) Interphase between the rotating frame of reference and the fixed frame of reference showing the two regions of the ladle (the mobile frame of reference and the fixed frame of reference).

Table 1.
Characteristics of the system.
The three different designs, including the shaft, are depicted in Figure 2.
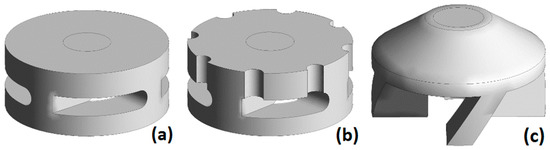
Figure 2.
Three impeller designs tested in this research. (a) Commercial impeller design A; (b) Commercial impeller design B; (c) New design proposed in previous work [16] design C.
2.2. Assumptions
The assumptions of the model are listed below:
- Physical properties for all the fluids in the system are taken as constants.
- Liquid phase is considered as a continuous phase, while gas is considered an interpenetrated phase in the liquid phase.
- All fluids are considered to be incompressible and Newtonian.
- Gas phase interpenetrated in the liquid is considered to comprise rigid spheres of constant size (1 mm).
- The system is considered to be isothermal without the presence of thermal gradients.
- All walls are considered to be impermeable and the fluid meets the non-slip condition for every mobile or static wall, while the well-known standard wall functions are used to connect the laminar region near the static walls to the turbulent core of the fluid.
- Turbulence in the ladle can be represented by the dispersed RNG k-ε turbulence model and is only present in the liquid phase.
- The volume rate of gas removed from the liquid is negligible in comparison with the input gas flow rate.
2.3. Governing Equations
2.3.1. Mass Conservation for the Liquid and Gas Phase
Equations (1) and (2) are mass balances for liquid and gas phases respectively, where , and are the velocity vector, the volume fraction and the density of the fluids, while subscripts and represents liquid and gas phases.
2.3.2. Momentum Conservation for Liquid and Gas Phases
Equations (3) and (4) are the momentum conservation equations for liquid and gas phases respectively, where the transient, convective, pressure, diffusive, gravitational, the momentum exchange between phases and a source term associated to the Multiple Reference Frames (MFR) are the terms from left to right in these equations. P is the pressure shared by both phases, and , , and are the gravitational constant, the momentum exchange between phases, and the effective viscosity, respectively. The effective viscosity is the sum of the liquid molecular viscosity, and the turbulent viscosity, , (). and have the same value but different sign and can be expressed by the following expression:
where the subscripts and may be either or and is the exchange coefficient between liquid and gas defined as:
where is the bubble diameter, is the interfacial concentration area, is the drag function (Equation (9)) in terms of the drag coefficient, , is a drag modification based on Brucato’s correlation [17], and is the particle relax time (Equation (7)).
where is the relative Reynolds number including the relative velocity (). For this work, the drag coefficient was taken from the Schiller-Naumann correlation [18].
The source term represents Coriolis and centrifugal forces in the rotating frame of reference:
where is the angular velocity and is the radial position vector. This term is needed to transform the momentum and mass fluxes from the rotating frame to the static frame of reference.
2.3.3. RNG k-ε Model
The dispersed RNG k-ε model for a two-phase system with bubbles dispersed through a continuous liquid phase accounts for the turbulence exclusively in the liquid phase, and the model consists of two additional conservation equations: one equation represents a balance of the turbulent kinetic energy, , and the other conservation equation is for its dissipation rate, :
where is the transformation of turbulent kinetic energy due to the velocity gradients, and the constants are 0.0845, 1.42, 1.68, and the inverse Prandtl numbers for and are 2.5. The link between the turbulence model and the turbulent Navier-Stokes equation is made by means of turbulent viscosity, which is computed for high Reynolds number systems in the RNG k-ε model as:
This turbulent viscosity is affected by the rotation or swirl in the main flow, and then the prediction can be improved by using a RNG swirl modification, where the turbulent viscosity computed with Equation (14) is affected by a function :
where is a characteristic swirl number and is a constant of typical value of 0.07 but that can be increased in the case of a higher Reynolds system.
The term in Equation (13) works like the standard k-ɛ model for moderate strained flows, but for rapidly-strained flows, this term causes the RNG model to give lower turbulent viscosity and therefore is more responsive to the effects of rapid-strained and streamlined curvatures than the standard k-ε model. The term is computed as:
where , , , , and is the strain-rate tensor.
Finally, according to the Sato’s model, the contribution of the dispersed phase on the turbulence equations of the liquid may be expressed as:
where 0.45 and 0.75.
2.4. Boundary and Initial Conditions
At the static walls all components of velocity are zero due to the non-slip condition and the impermeability of the walls. Standard wall functions are used to interpolate the velocity fields from the turbulent core to the laminar region at the wall.
At the rotating walls there is a thin layer of fluid that exchanges momentum between the rotating bodies (shaft and impeller) and the fluid.
At the open boundary, atmospheric fixed pressure is set and finally, at the impeller’s nozzles, gas inlet is set with a constant velocity inlet corresponding to the gas flow rate used in the ladle.
Finally, a periodic or cyclic condition in angular direction was set due to impeller symmetry, which allows only ¼ of the volume of the ladle to be solved.
Initial conditions correspond to a static liquid without initial gas holdup and static gas above the liquid level.
2.5. Solution
Figure 3 shows meshes of each ladle including the three different designs. The differences in the mesh can be seen between the rotating frame (tetrahedric elements) and the fixed frame (hexahedric elements), and the interphase between them, while in Table 2 the number of elements and characteristics of the elements are presented for each mesh. These meshes were the results of a grid sensitivity study, which represent the optimum meshes for each case in terms of precision of results and computational time.
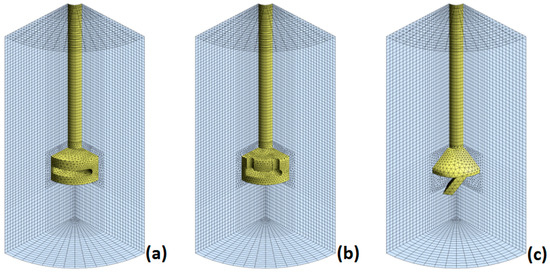
Figure 3.
Meshes used in this work. (a) Impeller design A; (b) design B; (c) design C.

Table 2.
Characteristics of the different meshes for the three impellers tested in this work.
Three simulations were performed by using the CFD commercial code Fluent Ansys® version 14.5 for each impeller in transient mode with a time step of 0.001 s until a quasi-steady fluid flow condition was reached at 20 s. A PC with a Core i7, 3.4 GHz processor was used to compute the numerical solutions and every computation took around 5 days, to get the final converged results.
2.6. Experimental Procedure
Velocity fields were obtained experimentally in a full-scale water physical model operating at 10 L per minute and 400 rpm with all the impellers made of Nylamid® (Wayne, NJ, USA), by using the Particle Image Velocimetry equipment (PIV) (Dantec Dynamics© (Skovlunde, Denmark) model LDY 302), which includes a high-speed camera (Vision Research model Dk 2740), and a high-intensity laser using only 45% of the power at 800 Hz in single-frame mode. Image statistics processing was handled by the software Dynamics Studio v4.00© (Dantec Dynamics©, v4.00, c Skovlunde, Denmark). 800 photographs were taken for the purposes of statistical analysis and the fluid was seeded with polyamid particles of 50 micrometers in diameter covered with rodamine B, since the camera was equipped with a 550 nm optical filter in order to discriminate between the tracers light and the light scattered from the bubbles within the flow. The high-speed camera was positioned perpendicularly with respect to the laser sheet. PIV technique details can be seen in [15].
Degassing trials were carried out in the physical model by saturating water with oxygen, achieved by blowing air for 30 min until a dissolved oxygen content of around 6 ppm was set. Then, nitrogen was blown at 10 L per minute and the rotating speed was set to 400 rpm and the oxygen concentration was measured with a portable oxymeter Hanna® (Woonsocket, RI, USA) model HI 9146 to get the degassing kinetics for each impeller tested in this work. A complete and detailed description of the technique can be found in [16].
3. Results and Discussion
3.1. Validation
Figure 4 shows measured and computed flow patterns in a r-z plane (axial and radial velocity components) for each impeller running at 400 rpm and with a gas flow rate of 10 L/min for impellers A, B and C. In general, good agreement is found between computations and experiments both in magnitude and in trend. For all the impellers it can be seen that fluid is radially pushed away by the rotor to the inner wall surface of the vessel aided by the additional momentum provided by the incoming gas flow at the impeller level, in that manner the flow in this zone becomes completely radial. This is apparently a combined effect of the fluid pushed away from the impeller, reinforced by the passing bubbles, generating a strong flow; at first in the radial direction and later, upward by means of the ascending bubbles, showing two circulation loops for each impeller: one counterclockwise below the impeller line, and a second one clockwise above the impeller line. Commercial impeller designs A and C show radial velocities projected horizontally from the impeller to the ladle walls. On the other hand, the design B presents an inclined projection of liquid from the impeller.
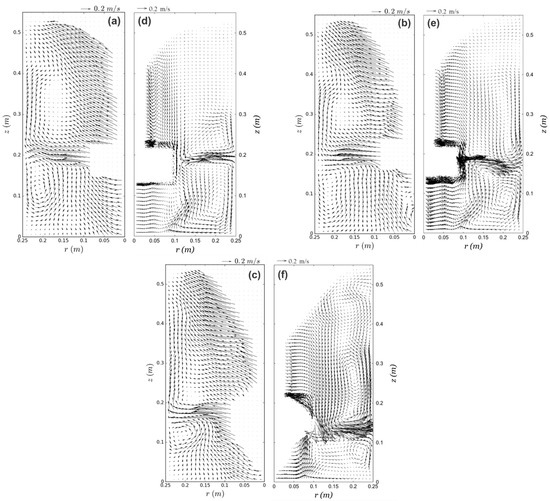
Figure 4.
Measured (left) and computed (right) velocity fields at 400 rpm and 10 L/min for impeller A (a,d), for impeller B (b,e) and for impeller C (c,f).
Impeller A shows the smallest vortex size, while impeller B presents a wider circulation loop at the bottom of the ladle than the other impellers. Impeller C, on the other hand presents a higher radial projection of fluid than the other impellers, produced by the stronger pumping effect of impeller C, setting a critical difference when compared to the other two impellers.
Figure 5 shows the gas holdup fields, computed by the model and measured with a high-speed camera, again showing excellent agreement in terms of gas dispersion, gas distribution and vortex shapes and sizes, where impeller A presents lower vortex than impellers B and C. Also, the gas coming down from impellers B and C is remarkably described by the simulations. The observed bubble distribution and the computed gas holdup fields shown in Figure 5 clearly show that gas bubbles are more evenly distributed by impellers B and C than in the case of impeller A. It is also seen from these graphical results that bubbles dispersed by impeller C are the most evenly distributed and more consistently reach regions closer to the lateral walls and bottom wall, and that all the mentioned effects can be clearly observed both in the measured and predicted results. These comparisons indicate the model is describing both flow patterns and gas behavior in the system accurately, and that, consequently, validation is more than satisfactory.

Figure 5.
Comparison between measured and computed gas holdup fields. Gas holdup in the r-z plane of the ladle for the three impellers tested at 400 rpm and 10 L/min. Experimental: (a) Impeller A; (b) impeller B; (c) impeller C. Computed: (d) Impeller A; (e) impeller B; (f) impeller C.
3.2. Process Analysis
The results observed in Figure 4 and Figure 5 suggest that impeller C transfers momentum more efficiently than impeller designs A and B, which in turn enhances bubble dispersion in the whole ladle giving rise to conditions promoting a faster degasification of the system.
Accordingly, Figure 6 shows results of degassing kinetics (deoxidation of water by purging nitrogen) in a physical model [16] of the three impellers under the same operating conditions (400 rpm and 10 L/min), where the new design promotes the fastest degassing kinetics. A duration of almost 3 min for complete degassing is saved by using impeller design C in comparison to impeller A, which shows the worst performance. In the following results, this behavior is explained in terms of hydrodynamic characteristics.
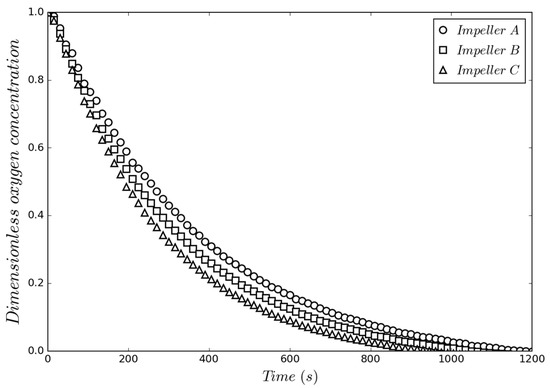
Figure 6.
Deoxidation kinetics in a water model using the three impellers at 400 rpm and 10 L/min.
Figure 5d–f show the gas holdup computed for the three impellers under the same operating conditions. Numerical diffusion does not appear in the computations indicating that these numerical calculations have been performed using the proper numerical techniques and grids. The impeller A presents the smaller vortex while impellers B and C present bigger vortexes. Impellers A and B show gas fraction coming down from the impeller, promoted by the well-known pumping effect, while impeller C shows a much higher pumping effect and a bigger gas fraction coming out from the impeller, which is confirmed by the photos of the experiments in Figure 5c. Also, this impeller presents the most homogeneous gas distribution throughout the entire ladle, while impeller A shows the worst gas distribution. Impeller C presents gas bubbles even below the impeller height due to the higher pumping effect creating the strongest radial fluid projection and circulation loops, as seen in Figure 4 and Figure 5.
Figure 7 shows the angular velocities at the impeller height of the three impellers under the same operating conditions, as predicted by the numerical model. Impeller A shows the worst liquid agitation, while impellers B and C are better agitated, with impeller C presenting the highest angular velocities and the highest momentum transfer of all impellers. This fact indicates that impeller C not only promotes more pumping from its bottom, but also transfers more momentum to the liquid than the commercial impellers.
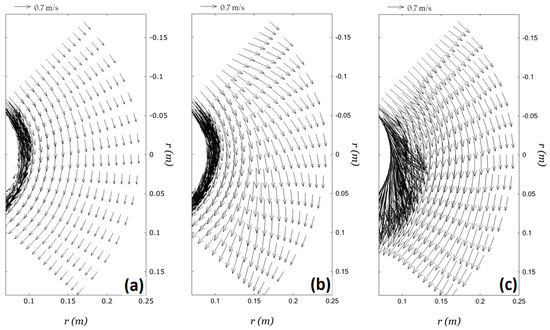
Figure 7.
Predicted angular velocity component fields in a θ-r plane at the height of the impeller for the three impellers tested at 400 rpm and 10 L/min. (a) impeller A; (b) impeller B; (c) impeller C.
Figure 8 shows the pressure contours for the three impellers predicted by the model. The higher pumping effect of impeller design C is clearly seen in this figure in comparison to the other two impellers, which do not promote pressure drops below the impeller as large as the one presented by impeller C. The zone of low pressure formed below impeller C allows this rotor to suck fluid and gas more efficiently from the bottom of the ladle, and eject these through the lateral nozzles in a radial direction towards the side wall. This pressure drop drags fluid and gas towards the bottom of the ladle as can be confirmed by the velocity and gas holdup fields of Figure 4 and Figure 5.
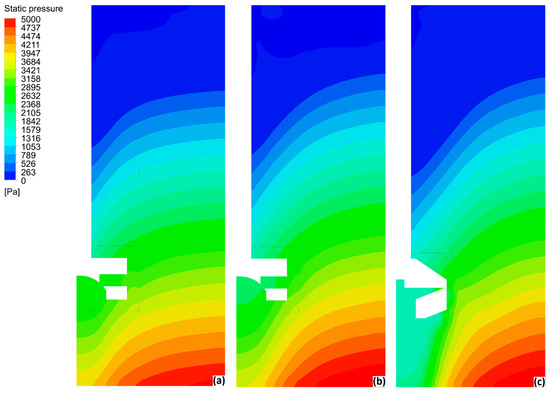
Figure 8.
Pressure fields in the r-z plane of the ladle for the three impellers tested at 400 rpm and 10 L/min. (a) Impeller A; (b) impeller B; (c) impeller C.
Finally, Figure 9 shows the water eddy viscosity contours for the three impellers, where it can be noted that impeller design C presents the most turbulence, followed by impeller B; with the least turbulent flow field being promoted by design A. It is to be noted that the fluid at the bottom of the ladle presents highly-turbulent behavior, which contrasts with the low turbulence presented in this region for impellers A and B. Turbulence accelerates momentum and mass transfer and the increment in turbulence is associated with better degassing kinetics.
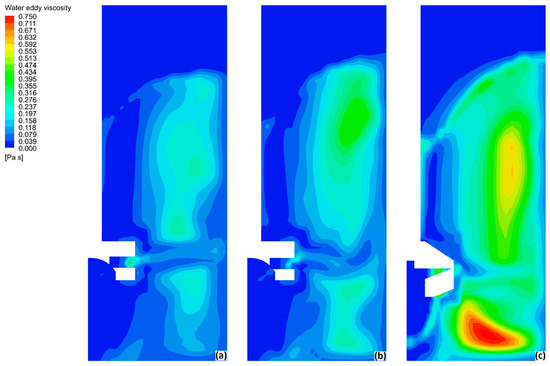
Figure 9.
Water eddy viscosity fields in the r-z plane of the ladle for the three impellers tested at 400 rpm and 10 L/min. (a) Impeller A; (b) impeller B; (c) impeller C.
These hydrodynamic characteristics, (i.e., velocity, pressure, gas holdup and turbulent kinetic energy fields) may be used to explain the superior performance of impeller design C, since it promotes a much higher pumping effect, creating a huge pressure drop below the impeller, whichdrags more fluid and gas ejected radially from the impeller towards the bottom of the ladle. Also, the gas holdup is distributed more evenly throughout the ladle, and the turbulent kinetic energy increased by using this impeller. Therefore, impeller C increases the pumping effect, distributes better the purging gas and adequately agitates the liquid, promoting high velocities and turbulence. Consequently, the mass transfer is accelerated and this results in the fastest degassing kinetics when compared with the other impellers. Another feature to explain the accelerated degassing kinetics is the bubble-size distribution achieved by each impeller. However, the photos do not show a conclusive effect of the impeller on the bubble-size distribution, and the mathematical model developed cannot, in its current state, predict the size distribution.
4. Conclusions
Agreement between flow patterns measured by PIV and computed by the model is sufficient, both in magnitude and in trend, for each impeller under study.
The observed bubble distribution and the computed gas holdup fields show that bubbles dispersed by impeller C are the most evenly distributed in the ladle, and more consistently reach regions closer to the walls.
The hydrodynamic characteristics (i.e., velocity, gas holdup, pressure and eddy viscosity fields) predicted by the model for the cases under study suggest that the superior performance of impeller design C, promoting the fastest degassing kinetics, may be a result of the following factors:
The pressure contours and gas holdup computed by the model for the three impellers shows that the design of impeller C promotes the biggest pressure drops below the impeller, which in turn apparently drags more fluid and gas towards the bottom of the ladle, showing the highest pumping effect and the biggest gas fraction coming out, down from the impeller, which promotes the largest projection of liquid from the impeller to the ladle walls while also promoting more turbulence, as shown by computed turbulent eddy viscosity fields, and improving the distribution of gas bubbles throughout the entire ladle. This design, then, displays a better performance in terms of degassing kinetics than the commercial impellers tested and, since this design is new, it can be recommended for industrial degassing units.
Acknowledgments
Authors would like to thank DGAPA-UNAM for financial support through the project PAPIIT IN114115. Technical assistance from Cándido Atlatenco and Arturo Sánchez is acknowledged.
Author Contributions
Diego Abreu-López and Marco A. Ramírez-Argáez developed the mathematical model and performed the numerical simulations; Adrián Amaro-Villeda performed the experiments to validate the model; Francisco A. Acosta-González and Carlos González-Rivera analyzed the data. All the authors helped to write the paper.
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
Abbreviations
| List of symbols | ||
| Interfacial area concentration | ||
| inverse Prandtl number for turbulent kinetic energy | ||
| Swirl modification constant | ||
| inverse Prandtl number for dissipation rate of turbulent kinetic energy | ||
| Drag coefficient | ||
| Drag function | ||
| RNG k-ε model constant | ||
| RNG k-ε model constant | ||
| RNG k-ε model constant | ||
| Turbulent dispersed model constant | ||
| Turbulent dispersed model constant | ||
| Impeller diameter | ||
| Ladle diameter | ||
| Bubble diameter | ||
| Swirl modification function | ||
| Momentum exchange between phases | ||
| Gravity acceleration | ||
| Generation of turbulent kinetic energy | ||
| Distance from bottom to impeller line | ||
| Height of liquid | ||
| Turbulent kinetic energy | ||
| Exchange coefficient between phase and phase | ||
| Angular velocity | ||
| Pressure | ||
| Gas flow rate | ||
| Radial position vector | ||
| Coriolis and centrifugal forces in the rotating frame of reference | ||
| Term from RNG k-ε model | ||
| Reynolds number | ||
| Strain rate magnitude | ||
| Strain rate tensor | ||
| Time | ||
| Velocity | ||
| Greek symbols | ||
| Volume fraction | ||
| RNG k-ε model constant | ||
| Dissipation rate of turbulent kinetic energy | ||
| RNG k-ε model relation | ||
| RNG k-ε model constant | ||
| Drag modification of Brucato’s model | ||
| Viscosity | ||
| Source term of turbulent kinetic energy | ||
| Source term of dissipation rate of turbulent kinetic energy | ||
| Density | ||
| Particle relaxation time | ||
| Characteristic swirl number | ||
| Subscripts | ||
| Liquid phase | ||
| Gas phase | ||
| Turbulent | ||
| Effective | ||
References
- Ramos Gomez, E.; Zenit, R.; González Rivera, C.; Trápaga, G.; Ramírez Argáez, M.A. Mathematical Modeling of Fluid Flow in a Water Physical Model of an Aluminum Degassing Ladle Equipped with Impeller-Injector. Metall. Mater. Trans. B 2013, 44, 423–435. [Google Scholar] [CrossRef]
- Lane, G.L.; Schwarz, M.P.; Evans, G.M. Numerical modeling of gas-liquid flow in stirred tanks. Chem. Eng. Sci. 2005, 60, 2203–2213. [Google Scholar] [CrossRef]
- Deen, N.G.; Solberg, T.; Hjertager, B.H. Flow generated by an aerated Rushton impeller: Two-phase PIV experiments and numerical simulations. Can. J. Chem. Eng. 2002, 80, 638–652. [Google Scholar] [CrossRef]
- Johansen, S.T.; Boysan, F. Fluid Dynamics in Bubbled Stirred Ladles. Part II: Mathematical Modeling. Metall. Trans. B 1988, 19, 755–764. [Google Scholar] [CrossRef]
- Ilegbusi, O.J.; Szekely, J. The Modeling of Gas-Bubble Driven Circulations Systems. ISIJ Int. 1990, 30, 731–739. [Google Scholar] [CrossRef]
- Johansen, S.T.; Fredriksen, A.; Rasch, B. Particle Flotation to Bubbles in Rotor-Stirred reactors for Melt Treatment. In Light Metals, the Minerals, Metals and Materials Society; TMS: Las Vegas, NV, USA, 1995; pp. 1203–1206. [Google Scholar]
- Hop, B.; Johansen, S.T.; Rasch, B. A 3D Numerical Model for Removal of Inclusions to Gas Bubbles. In Light Metals, the Minerals, Metals and Materials Society; TMS: Anaheim, CA, USA, 1996; pp. 647–656. [Google Scholar]
- Maniruzamman, M.; Makhlouf, M. Mathematical Modeling and Computer Simulation of the Rotating Impeller Particle Flotation Process: Part II. Particle Agglomeration and Flotation. Metall. Mater. Trans. B 2002, 33, 305–314. [Google Scholar] [CrossRef]
- Maniruzamman, M.; Makhlouf, M. Mathematical Modeling and Computer Simulation of the Rotating Impeller Particle Flotation Process: Part I. Fluid Flow. Metall. Mater. Trans. B 2002, 33, 297–303. [Google Scholar] [CrossRef]
- Warke, V.S.; Tryggvason, G.; Makhlouf, M.M. Mathematical Modeling and Computer Simulation of Molten Metal Cleansing by the Rotating Impeller Degasser: Part I. Fluid Flow. J. Mater. Process. Technol. 2005, 168, 112–118. [Google Scholar] [CrossRef]
- Warke, V.S.; Shankar, S.; Makhlouf, M.M. Mathematical Modeling and Computer Simulation of Molten Metal Cleansing by the Rotating Impeller Degasser: Part II. Removal of hydrogen gas and solid particles. J. Mater. Process. Technol. 2005, 168, 119–126. [Google Scholar] [CrossRef]
- Mirgaux, A.; Ablitzer, D.; Waz, E.; Bellot, J.E. Mathematical modeling and computer simulation of molten aluminum purification by flotation in stirred reactor. Metall. Mater. Trans. B 2009, 40, 363–375. [Google Scholar] [CrossRef]
- Hop, B.; Frisvold, F.; Rasch, B.; Johansen, S.T. The fluid mechanics in the H110 Hycast reactor. In Light Metals, the Minerals, Metals and Materials Society; TMS: Orlando, FL, USA, 1997; pp. 837–841. [Google Scholar]
- Dong, L.; Johansen, S.T.; Engh, T.A. Flow induced by an impeller in an unbaffled tank—II. Numerical Modeling. Chem. Eng. Sci. 1994, 49, 3511–3518. [Google Scholar] [CrossRef]
- Mancilla, E.; Cruz-Mendez, W.; Garduño, I.; González-Rivera, C.; Ramírez-Argáez, M.; Ascanio, G. Comparison of the hydrodynamic performance of rotor-injector devices in a water physical model of an aluminum degassing ladle. Chem. Eng. Res. Des. 2016, 118, 158–169. [Google Scholar] [CrossRef]
- Hernández-Hernández, M.; Camacho-Martínez, J.L.; González-Rivera, C.; Ramirez-Argáez, M.A. Impeller Design Assisted by Physical Modeling and Pilot Plant Trials. J. Mater. Process. Technol. 2016, 236, 1–8. [Google Scholar] [CrossRef]
- Brucato, A.; Grisafi, F.; Montante, G. Particle drag coefficients in turbulent fluids. Chem. Eng. Sci. 1998, 53, 3295–3314. [Google Scholar] [CrossRef]
- Schiller, L.; Naumann, Z. A drag coefficient correlation. Z. Ver. Deutsch. Ing. 1935, 77, 51. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).