Amplitude Dependent Internal Friction in a Mg-Al-Zn Alloy Studied after Thermal and Mechanical Treatment
Abstract
:1. Introduction
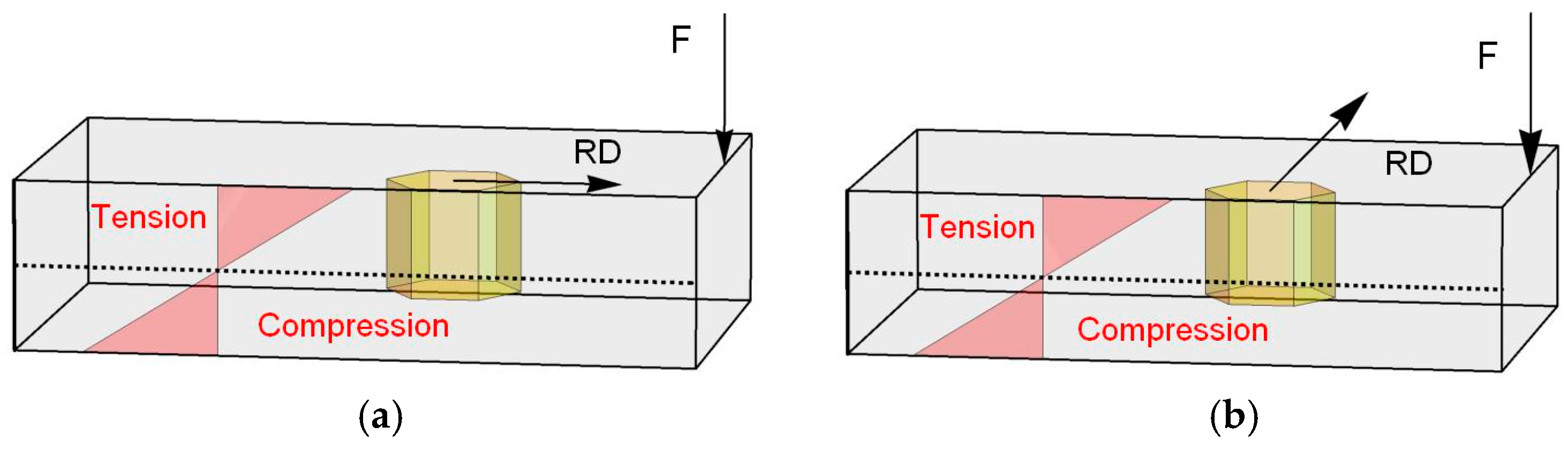
2. Materials and Methods
- Electromagnetic excitation and recording of vibrations—the principle is described in [21]. The resonant frequency was ~40 Hz.
- Manual excitation and record of vibrations by a laser. The resonant frequency was 14 Hz. Manual excitation was used for AZ31 sheets.
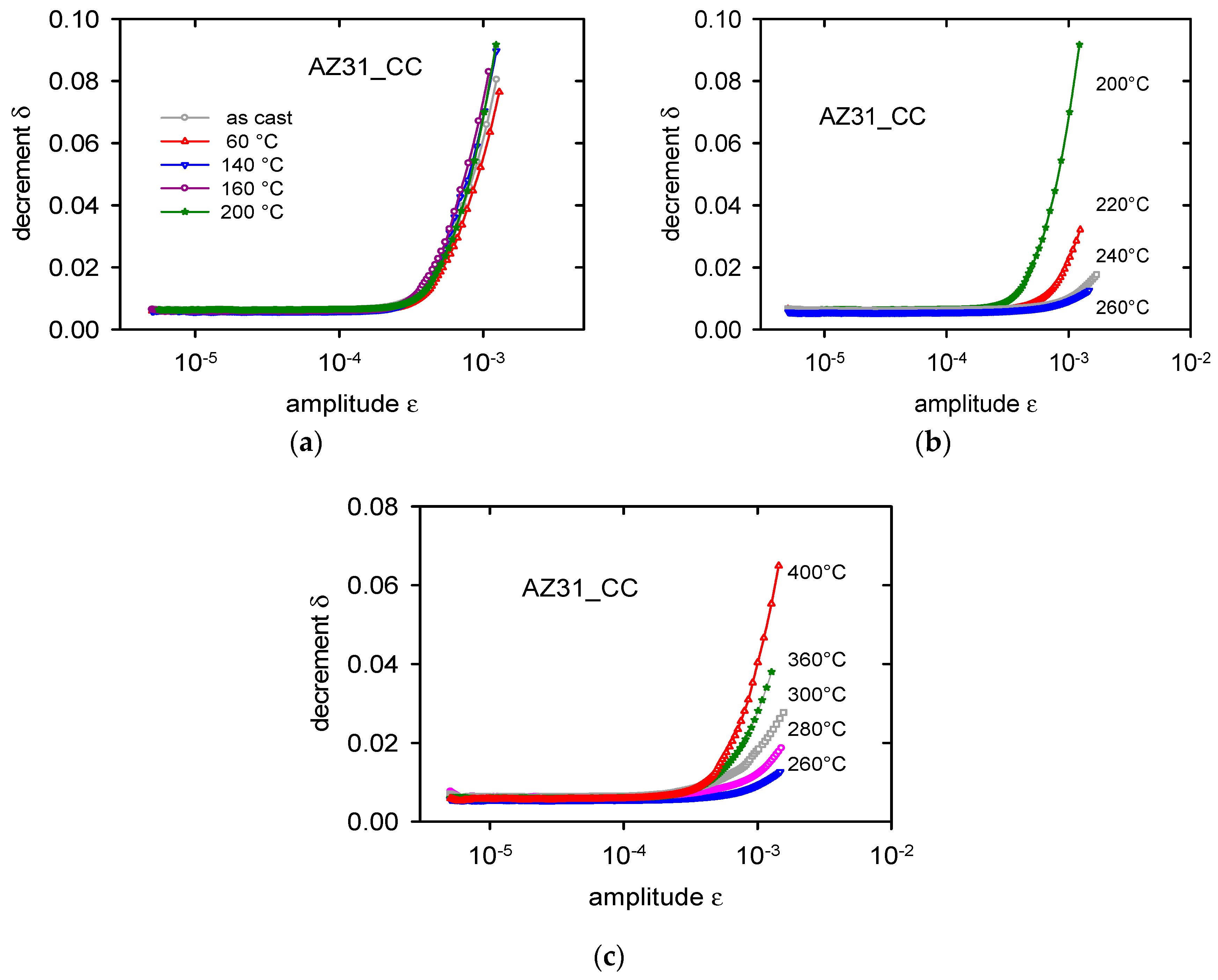
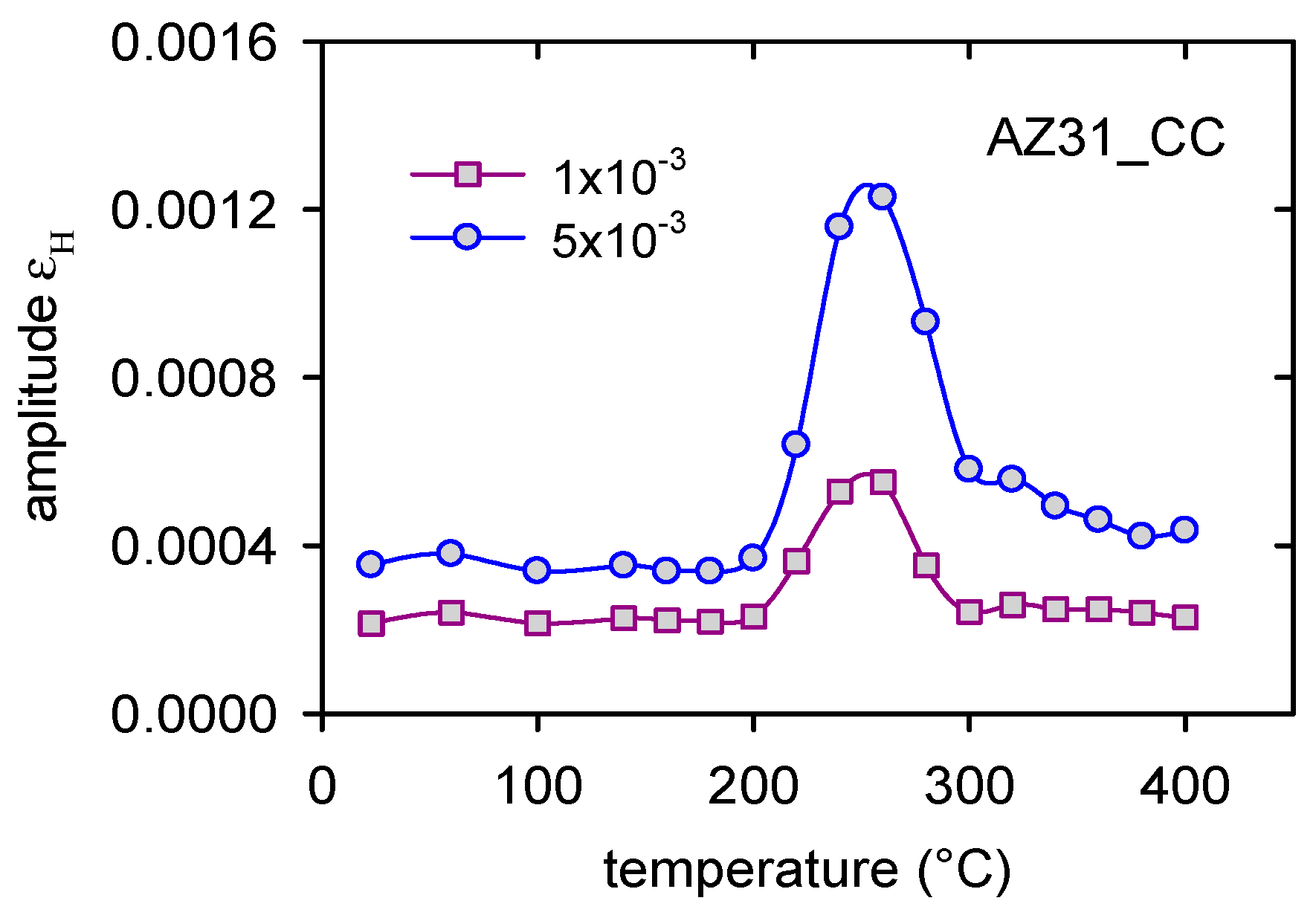
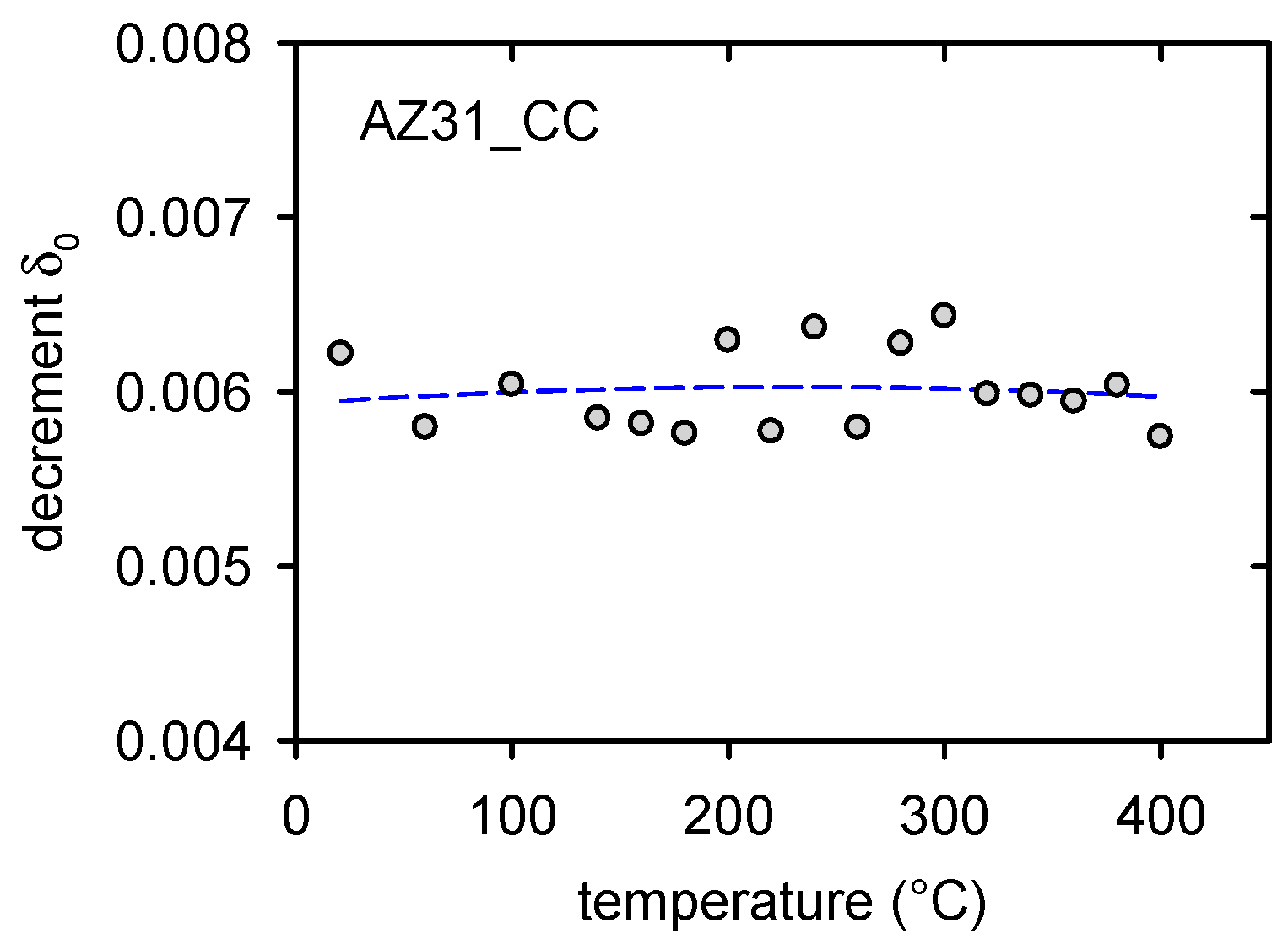
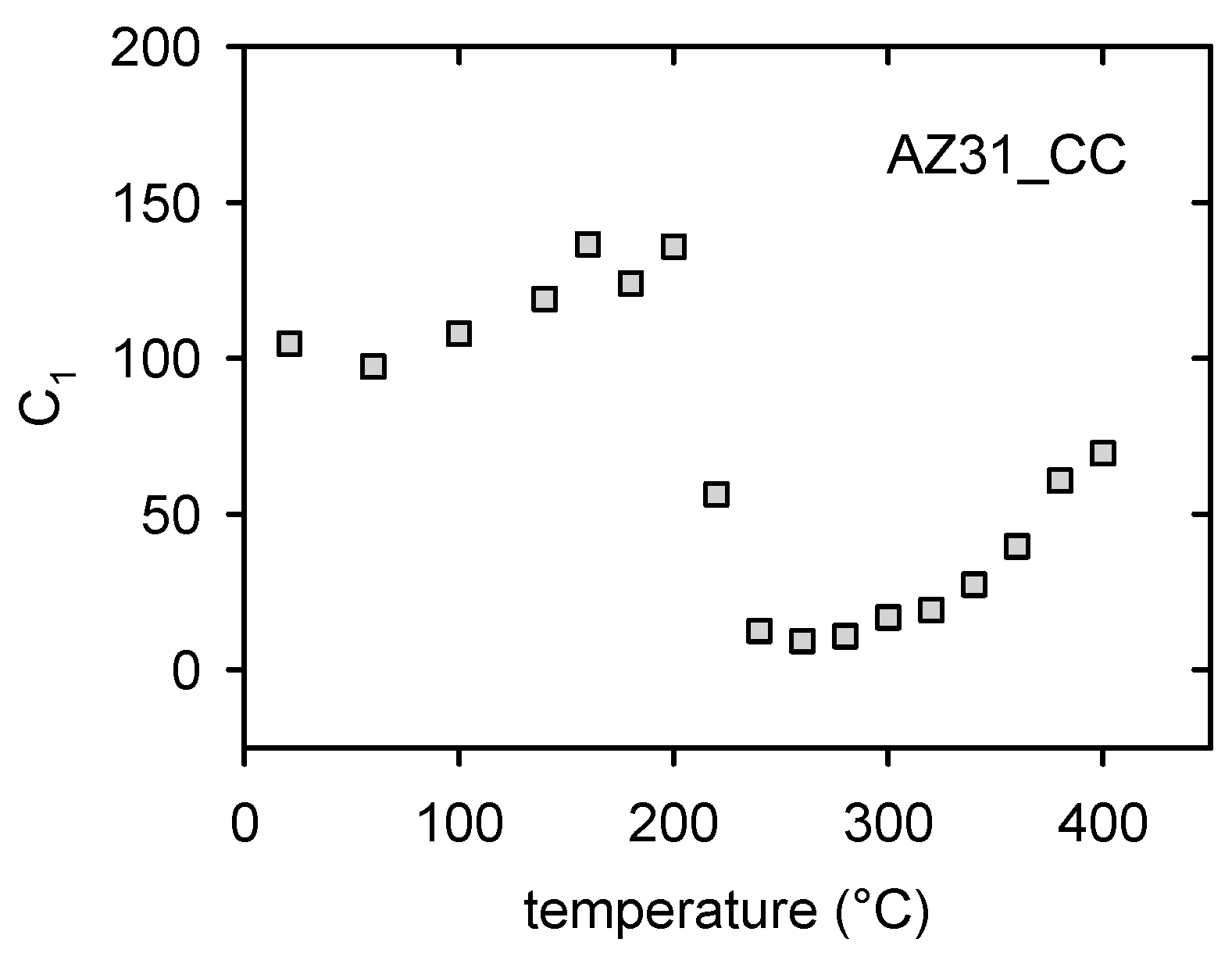
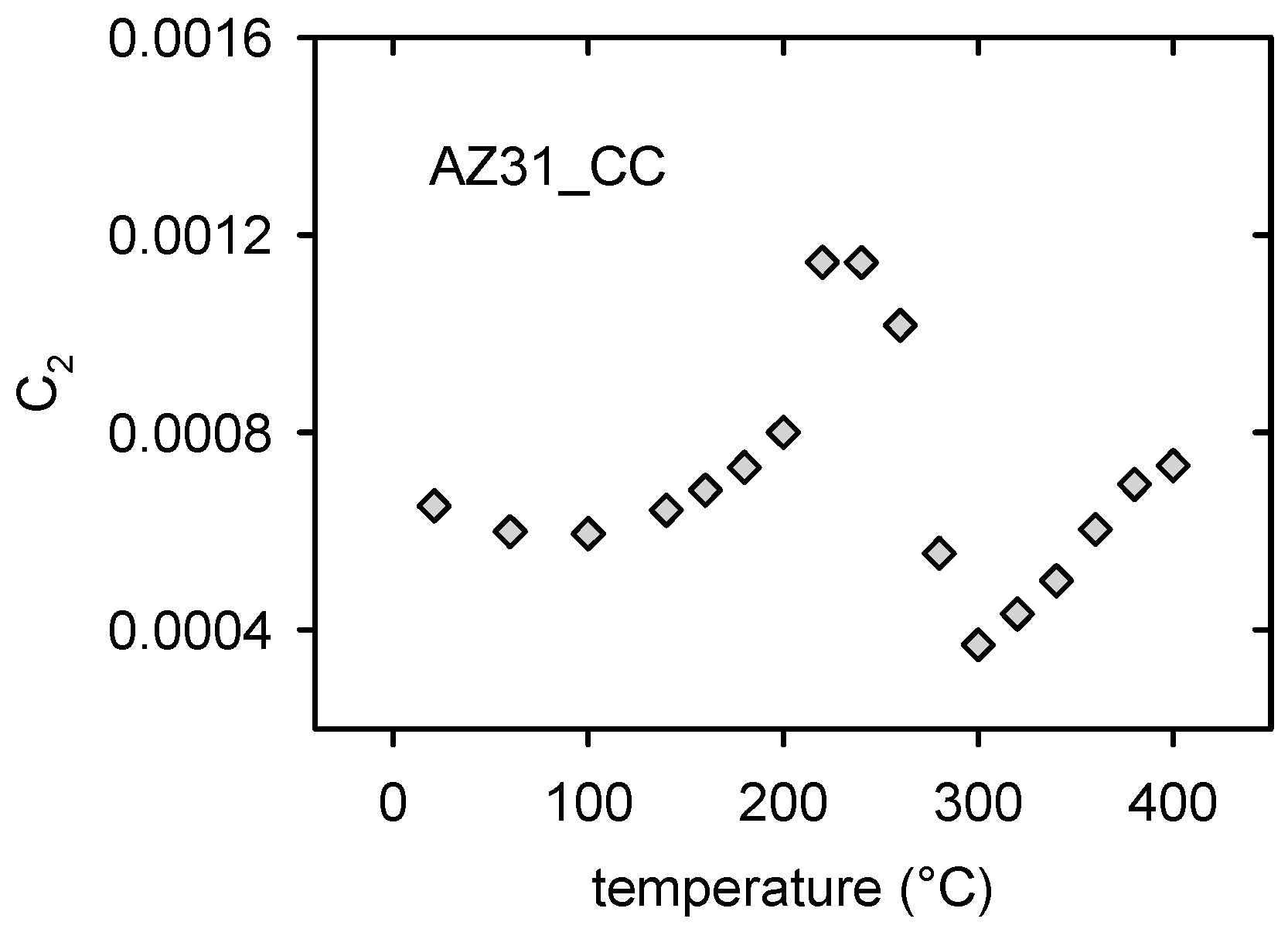
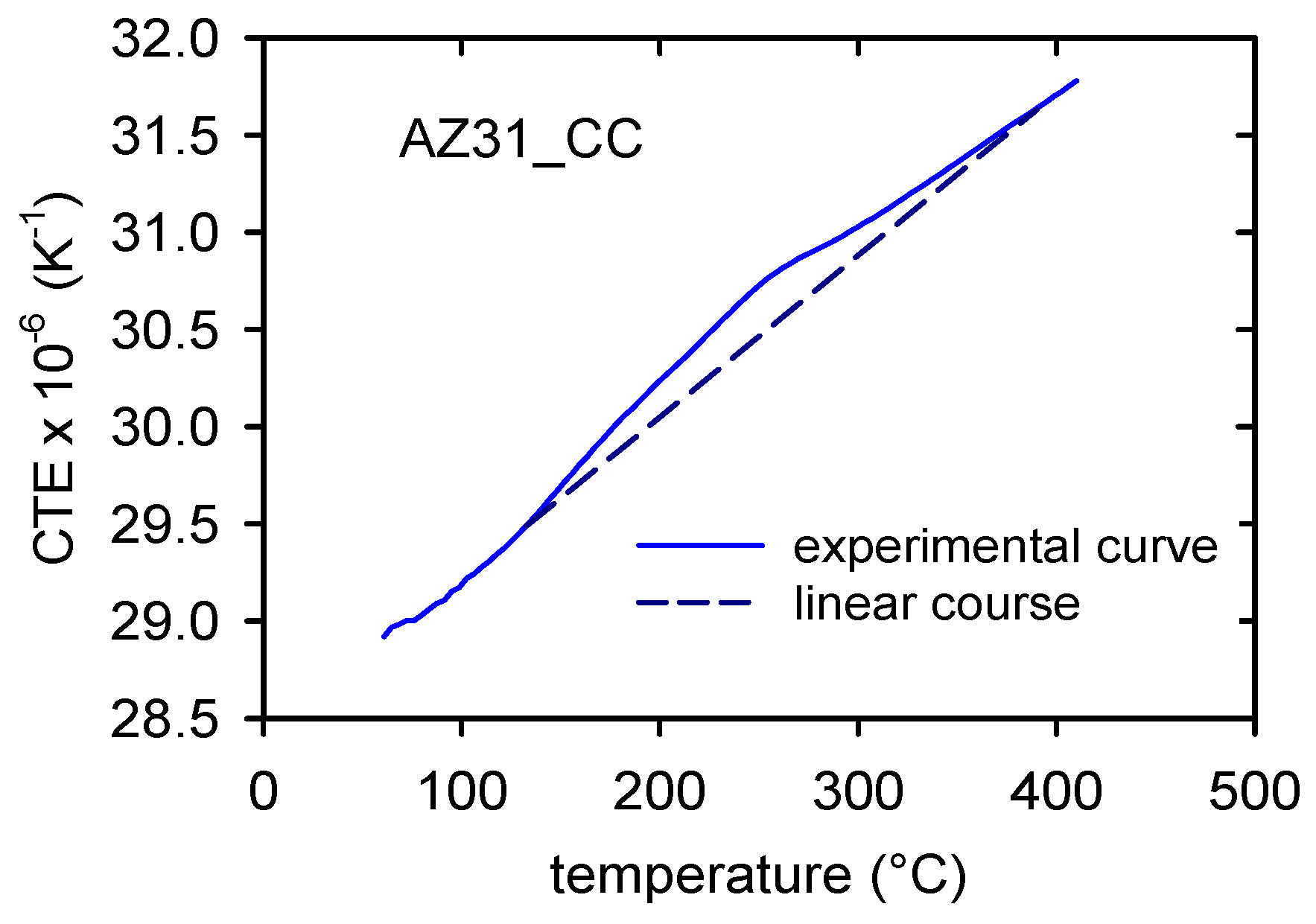
3. Experimental Results
4. Discussion
4.1. Annealing and Quenching of the Cast Alloy
4.2. Rolled Alloy
5. Conclusions
- Microstructure changes in the cast alloy after step by step annealing and quenching are manifested with the effects in the amplitude dependent internal friction.
- The main contribution to the internal friction in the cast alloy is the dislocation internal friction, i.e., vibration of dislocation segments and their thermally-activated movement in the slip plane.
- Main changes in the microstructure of the cast alloy occurred in the temperature region from 200 to 300 °C.
- Redistribution of solute atoms due to the thermal treatment caused a decrease of the dislocation internal friction in the temperature range of 200–260 °C.
- Thermal residual stresses formed due to quenching at temperatures higher than 260 °C caused microplastic deformation of the continuously cast alloy.
- Basal texture in the rolled sheets strongly influences the internal friction. While dislocation internal friction is the dominant mechanism in the sample with the longest axis in the rolling direction, twins’ formation and twin boundary movement is very probably the deciding mechanism in the sample cut in the transversal direction.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Granato, A.V.; Lücke, K. Theory of mechanical damping due to dislocations. J. Appl. Phys. 1956, 27, 586–596. [Google Scholar] [CrossRef]
- Granato, A.V.; Lücke, K. Application of dislocation theory to internal friction phenomena at high frequencies. J. Appl. Phys. 1956, 27, 789–805. [Google Scholar] [CrossRef]
- Granato, A.V. Internal studies in dislocation motion. In Dislocation Dynamics; Rosenfield, A.R., Hahn, G.T., Bement, A.L., Jr., Jaffee, R.I., Eds.; McGraw-Hill: New York, NY, USA, 1968; p. 117. [Google Scholar]
- Granato, A.V.; Lücke, K. Temperature dependence of amplitude-dependent dislocation damping. J. Appl. Phys. 1981, 52, 7136–7142. [Google Scholar] [CrossRef]
- Teutonico, L.J.; Granato, A.V.; Lücke, K. Theory of the thermal breakaway of a pinned dislocation line with application to damping phenomena. J. Appl. Phys. 1964, 35, 220–234. [Google Scholar] [CrossRef]
- Marchesoni, F.; Segoloni, D. The string model of dislocation damping revisited. Acta Phys. Pol. B 1993, 24, 865–889. [Google Scholar]
- Gremaud, G.; Kustov, S. Non-linear elasticity due to dislocation-solute atom interaction in solid solutions. J. Alloys Compd. 2000, 310, 85–90. [Google Scholar] [CrossRef]
- Gremaud, G. Dislocation—Point defect interaction. In Mechanical Spectroscopy Q−1; Schaller, R., Fantozzi, G., Gremaud, G., Eds.; Trans Tech Publications: Zurich, Switzerland, 2001; pp. 178–246. [Google Scholar]
- D’Anna, G.; Benoit, W.; Vinokur, V.M. Internal friction and dislocation collective pinning in disordered quenched solid solutions. J. Appl. Phys. 1997, 82, 5983–5990. [Google Scholar] [CrossRef]
- Gremaud, G. Overview on dislocation-point defect interaction: The brownian picture of dislocation motion. Mater. Sci. Eng. A 2004, 370, 191–198. [Google Scholar] [CrossRef]
- Puga, H.; Carneiro, V.H.; Barbosa, J.; Soares, D. Effect of grain and secondary phase morphologies in the mechanical and damping behavior of Al7075 alloys. Met. Mater. Int. 2016, 22, 863–871. [Google Scholar] [CrossRef]
- Murai, T.; Matsuoka, S.; Miyamoto, S.; Oki, Y. Effects of extrusion conditions on microstructure and mechanical properties of AZ31B magnesium alloy extrusions. J. Mater. Proc. Technol. 2003, 141, 207–212. [Google Scholar] [CrossRef]
- Granato, A.V.; Higata, A.; Lücke, K. Recovery of damping and modulus changes following plastic deformation. Acta Metall. 1958, 6, 470–480. [Google Scholar] [CrossRef]
- González-Martínez, R.; Göken, J.; Letzig, D.; Timmerberg, J.; Steinhoff, K. Influence of heat treatment on damping behaviour of the magnesium wrought alloy AZ61. Acta Metall. Sin. 2007, 20, 235–240. [Google Scholar] [CrossRef]
- González-Martínez, R.; Göken, J.; Letzig, D.; Steinhoff, K.; Kainer, K.U. Influence of aging on damping of the magnesium-aluminium-zinc series. J. Alloys Compd. 2007, 437, 127–132. [Google Scholar] [CrossRef]
- Göken, J.; Riehemann, W. Damping behaviour of AZ91 magnesium alloy with cracks. Mater. Sci. Eng. A 2004, 370, 417–421. [Google Scholar] [CrossRef]
- Trojanová, Z.; Mielczarek, A.; Riehemann, W.; Lukáč, P. Cyclic bending and the damping behaviour of short fibre-reinforced magnesium alloy AZ91. Compos. Sci. Technol. 2000, 66, 585–590. [Google Scholar] [CrossRef]
- Jun, J.-H. Damping behaviour of Mg-Zn-Al castings. Mater. Sci. Eng. A 2016, 665, 86–89. [Google Scholar] [CrossRef]
- Lu, L.; Dahle, A.K.; Taylor, J.A.; StJohn, D.H. Theoretical and practical considerations of grain refinement of Mg-Al alloys. Mater. Sci. Forum 2005, 488–489, 299–302. [Google Scholar] [CrossRef]
- Vidrich, G. Grain Refinement and Dispersion-Strengthening With Finest Ceramic Particles. Ph.D. Thesis, Clausthal University of Technology, Clausthal-Zellerfeld, Germany, 2008. [Google Scholar]
- Trojanová, Z.; Lukáč, P.; Chmelík, F.; Riehemann, W. Microstructural changes in ZE41 composite estimated by acoustic measurements. J. Alloys Compd. 2003, 355, 113–119. [Google Scholar] [CrossRef]
- Trojanová, Z.; Palček, P.; Chalupová, M.; Lukáč, P.; Hlaváčová, I. High frequency cycling behaviour of three AZ magnesium alloys—Microstructural characterization. Int. J. Mater. Res. 2016, 107, 903–915. [Google Scholar] [CrossRef]
- Wang, J.; Duo, J.; Ding, Y.; Tang, B. Thermal Cycling Behavior of Mg-4%Sn-2.5%Pb Alloy. J. Residuals Sci. Technol. (JRST) 2017, 14, 420–425. [Google Scholar] [CrossRef]
- Debye, P. Zur Theorie der spezifischen Wärmen. Annalen der Physik 1912, 39, 789–839. [Google Scholar] [CrossRef]
- Bohlen, J.; Chmelík, F.; Dobroň, P.; Kaiser, F.; Letzig, D.; Lukáč, P.; Kainer, K.U. Orientation effects on acoustic emission during tensile deformation of hot rolled magnesium alloy AZ31. J. Alloys Compd. 2004, 378, 207–213. [Google Scholar] [CrossRef]
- Victoria-Hernandez, J.; Yi, J.; Bohlen, J.; Kurz, G.; Letzig, D. The influence of the recrystallization mechanisms and grain growth on the texture of a hot rolled AZ31 sheet during subsequent isochronal annealing. J. Alloys Compd. 2014, 616, 189–197. [Google Scholar] [CrossRef]
- Wang, Y.N.; Huang, J.C. The role of twinning and untwinning in yielding behavior in hot-extruded Mg-Al-Zn alloy. Acta Mater. 2007, 55, 897–905. [Google Scholar] [CrossRef]
- Klimanek, P.; Pötzsch, A. Microstructure evolution under compressive plastic deformation of magnesium at different temperatures and strain rates. Mater. Sci. Eng. A 2002, 324, 145–150. [Google Scholar] [CrossRef]
- Huang, H.T.; Godfrey, A.; Zheng, J.P.; Liu, W. Influence of locat strain on twinning behavior during compression of AZ31 magnesium alloy. Mater. Sci. Eng. A 2015, 640, 330–337. [Google Scholar] [CrossRef]
- Yang, P.; Yu, Y.; Chen, L.; Mao, W. Experimental determination and theoretical prediction of twin orientations in magnesium alloy AZ31. Scr. Mater. 2014, 50, 1163–1168. [Google Scholar] [CrossRef]
- Hou, D.; Liu, T.; Luo, L.; Lu, L.; Chen, H.; Shi, D. Twinning behaviors of a rolled AZ31 magnesium alloy under multidirectional loading. Mater. Charact. 2017, 124, 122–128. [Google Scholar] [CrossRef]
- Wu, L.; Agnew, S.R.; Ren, Y.; Brown, D.W.; Clausen, B.; Stoica, G.M.; Wenk, H.R.; Liaw, P.K. The effects of texture and extension twinning on the low-cycle fatigue behavior of a rolled magnesium alloy, AZ31B. Mater. Sci. Eng. A 2010, 527, 7057–7706. [Google Scholar] [CrossRef]
- Watanabe, H.; Sasakura, Y.; Ikeo, N.; Mukai, T. Effect of deformation twins on damping capacity in extruded pure magnesium. J. Alloys Compd. 2015, 626, 60–64. [Google Scholar] [CrossRef]
- Stráská, J.; Janeček, M.; Čížek, J.; Stráský, J.; Hadzima, B. Microstructure stability of ultra-fine grained magnesium alloy AZ31 processed by extrusion and equal channel angular pressing (EX-ECAP). Mater. Charact. 2014, 94, 69–79. [Google Scholar] [CrossRef]
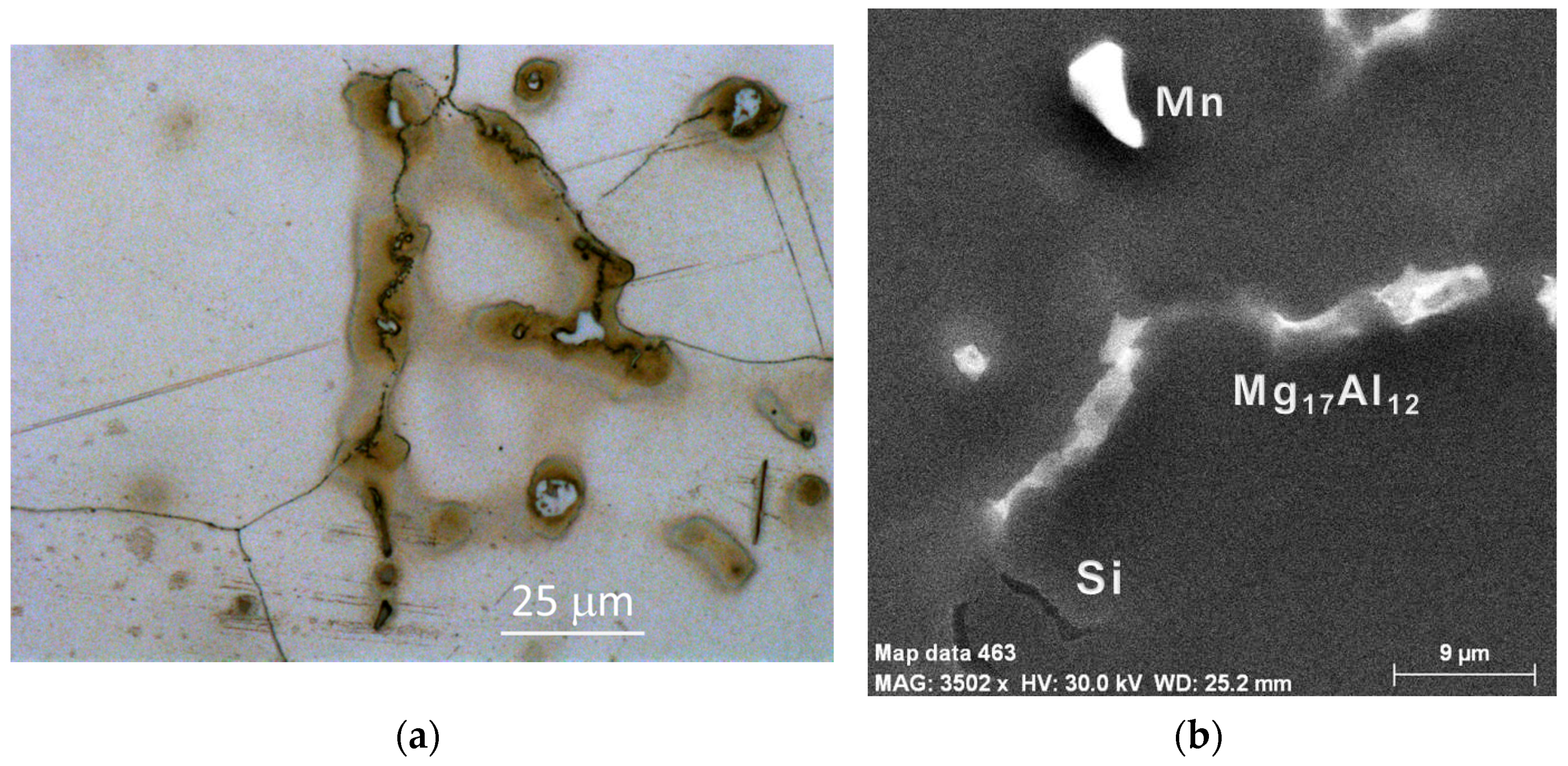
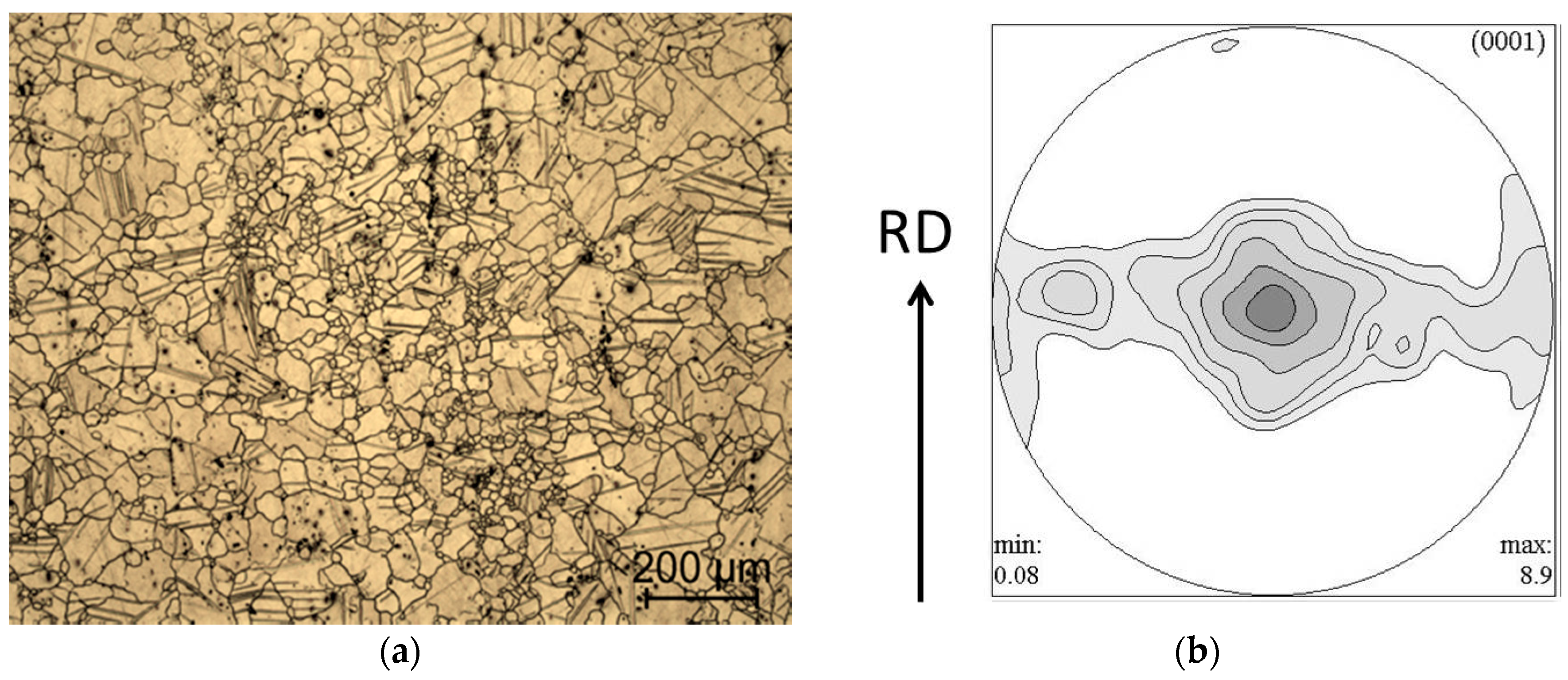
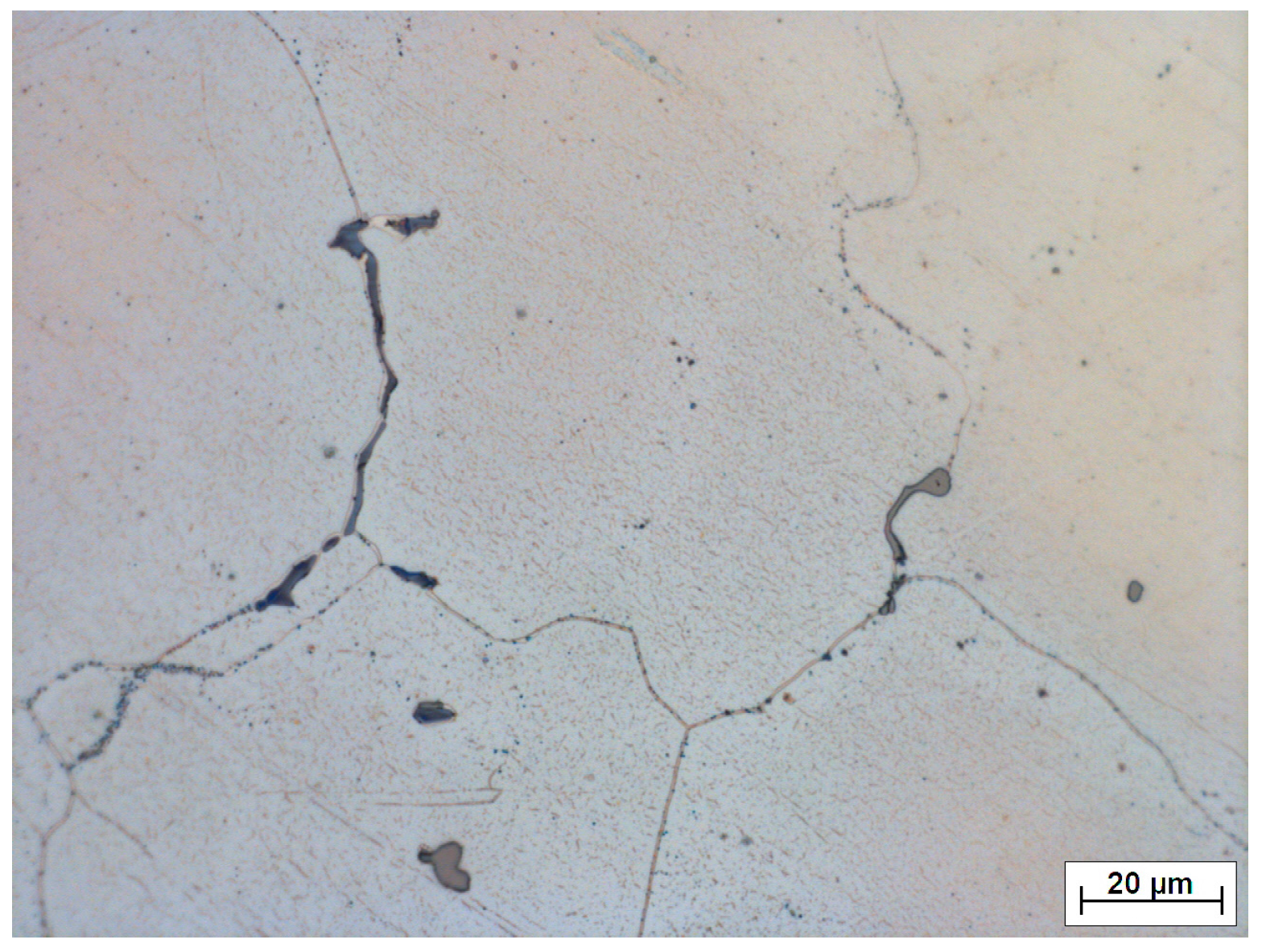
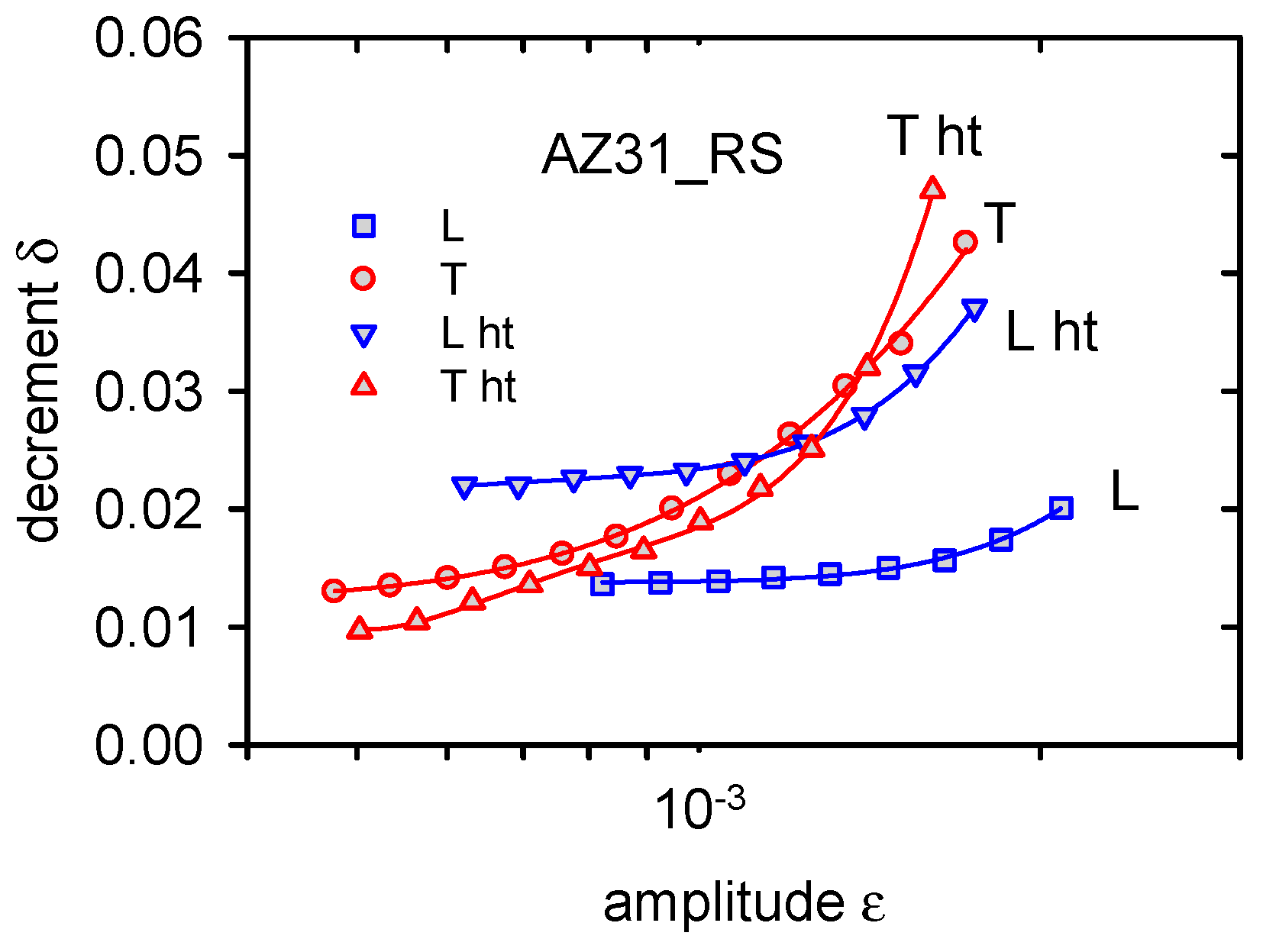

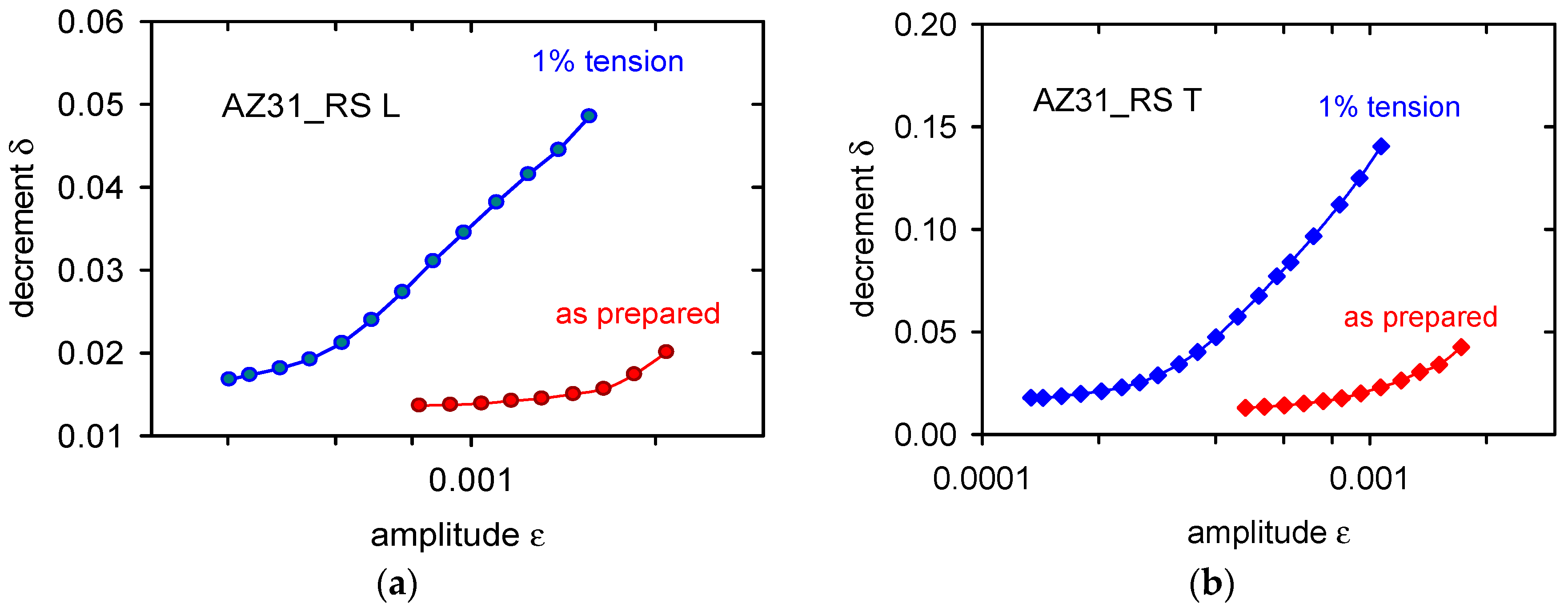
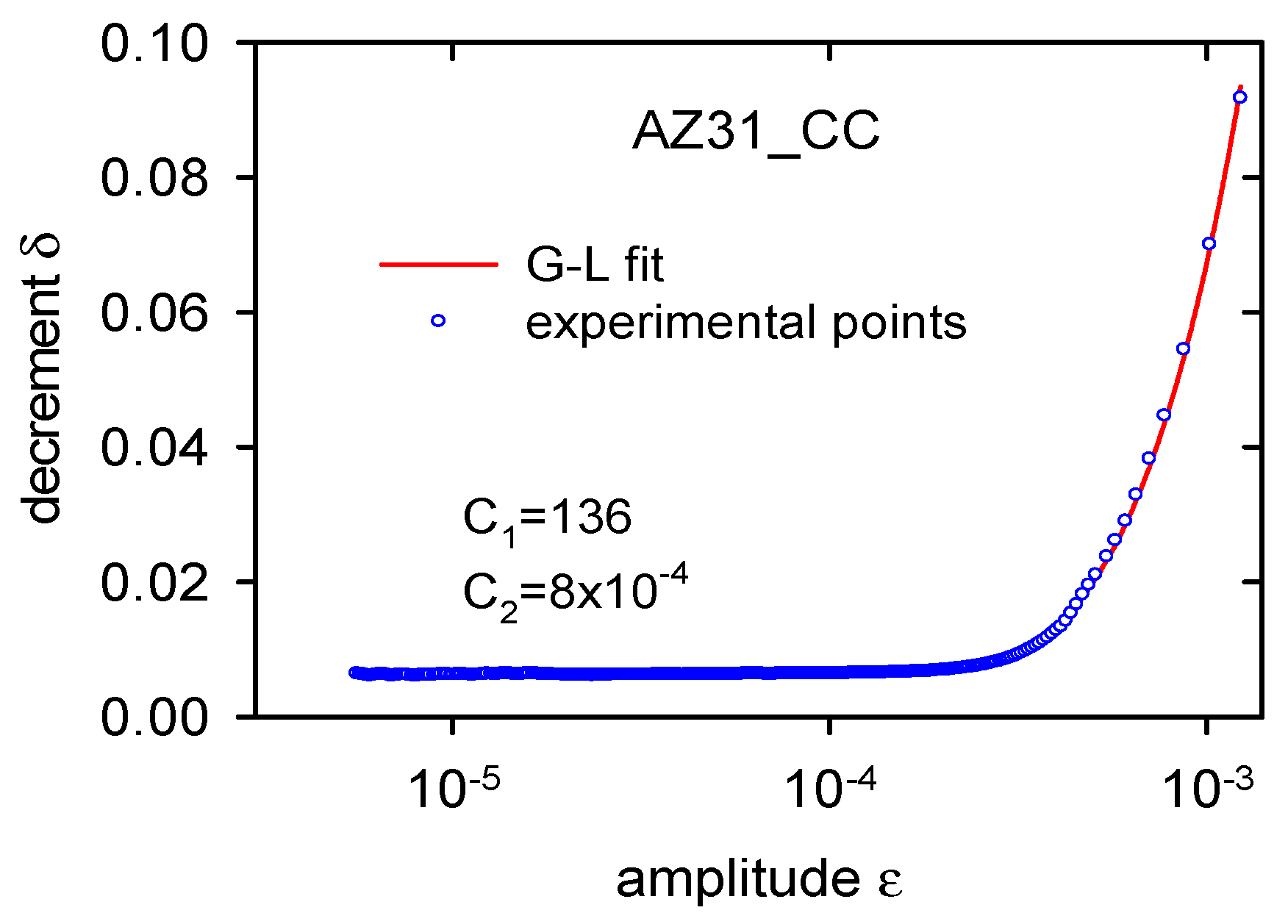
| Material | Al | Zn | Mn | Si | Fe | Ce | Mg |
|---|---|---|---|---|---|---|---|
| AZ31_CC | 3.5 | 0.9 | 0.4 | 0.06 | <0.01 | - | Bal. |
| AZ31_RS | 3.2 | 1.3 | 0.4 | 0.015 | 0.03 | 0.06 | Bal. |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trojanová, Z.; Lukáč, P.; Džugan, J.; Halmešová, K. Amplitude Dependent Internal Friction in a Mg-Al-Zn Alloy Studied after Thermal and Mechanical Treatment. Metals 2017, 7, 433. https://doi.org/10.3390/met7100433
Trojanová Z, Lukáč P, Džugan J, Halmešová K. Amplitude Dependent Internal Friction in a Mg-Al-Zn Alloy Studied after Thermal and Mechanical Treatment. Metals. 2017; 7(10):433. https://doi.org/10.3390/met7100433
Chicago/Turabian StyleTrojanová, Zuzanka, Pavel Lukáč, Ján Džugan, and Kristýna Halmešová. 2017. "Amplitude Dependent Internal Friction in a Mg-Al-Zn Alloy Studied after Thermal and Mechanical Treatment" Metals 7, no. 10: 433. https://doi.org/10.3390/met7100433
APA StyleTrojanová, Z., Lukáč, P., Džugan, J., & Halmešová, K. (2017). Amplitude Dependent Internal Friction in a Mg-Al-Zn Alloy Studied after Thermal and Mechanical Treatment. Metals, 7(10), 433. https://doi.org/10.3390/met7100433







